第28章: 模型选择、斯坦因收缩和模型平均

28 模型选择、斯坦因收缩和模型平均

28.1 介绍

本章回顾了模型选择、James-Stein 收缩和模型平均。

模型选择是从一组模型中选择一个模型（或估计器）的工具。不同的模型选择方法通过用于对模型进行排序和比较的标准来区分。

模型平均是模型选择的概括。模型和估计量使用数据相关权重进行平均。

James-Stein 收缩通过收缩到合理的目标来修改经典估计量。收缩可减少均方误差。

Burnham 和 Anderson (1998) 以及 Claeskens 和 Hjort (2008) 是关于模型选择和平均的两本优秀专着。 Lehmann 和 Casella (1998) 全面阐述了 James-Stein 收缩理论。另请参见 Wasserman (2006) 和 Efron (2010)。

28.2 选型

在应用项目的过程中，经济学家通常会估计多个模型。事实上，大多数应用论文都包含显示不同规格结果的表格。问题出现了：哪种模型最好？实际中应该使用哪个？我们怎样才能做出最好的选择呢？这就是模型选择的问题。

以工资回归为例。假设我们想要一个包含教育、经验、地区和婚姻状况的模型。我们应该如何着手？我们应该估计一个简单的线性模型加上经验的二次模型吗？教育应该线性输入，如图 2.6(a) 所示的简单样条曲线，还是为每个教育级别使用单独的虚拟变量？婚姻状况应该作为一个简单的虚拟变量（已婚或未婚）输入还是允许所有记录的类别？是否应该包括互动？哪个？多少？综上所述，我们需要选择要包含在回归模型中的特定回归量。

模型“选择”可能被错误命名。将这个问题称为“估计器选择”会更合适。当我们检查包含多重回归结果的表格时，我们正在比较同一回归的多个估计值。一个估计量可能比另一个估计量包含更少的变量；这是一个受限估计量。一个可以通过最小二乘法估计，另一个可以通过 2SLS 估计。另一个可能是非参数的。底层模型是相同的；差异在于估计量。无论如何，文献已经采用了“模型选择”这个术语，我们将遵守这个惯例。为了获得一些基本的理解，从一个程式化的例子开始可能会有所帮助。假设我们有一个 $K \times 1$ 估计器 $\widehat{\theta}$，它具有期望 $\theta$ 和已知的协方差矩阵 $\boldsymbol{V}$。另一种可行的估计器是 $\widetilde{\theta}=0$。后者可能看起来像一个愚蠢的估计器，但它捕获了模型选择通常涉及排除限制的特征。在这种情况下，我们可以通过加权均方误差（WMSE）来比较两个估计器的准确性。对于给定的权重矩阵 $\boldsymbol{W}$ 定义

\[ \text { wmse }[\widehat{\theta}]=\operatorname{tr}\left(\mathbb{E}\left[(\widehat{\theta}-\theta)(\widehat{\theta}-\theta)^{\prime}\right] \boldsymbol{W}\right)=\mathbb{E}\left[(\widehat{\theta}-\theta)^{\prime} \boldsymbol{W}(\widehat{\theta}-\theta)\right] \text {. } \]

通过设置 $\boldsymbol{W}=\boldsymbol{V}^{-1}$ 来简化计算，我们对剩余的计算进行了设置。

对于我们的两个估计器，我们计算出

\[ \begin{aligned} \text { wmse }[\hat{\theta}] &=K \\ \text { wmse }[\widetilde{\theta}] &=\theta^{\prime} \boldsymbol{V}^{-1} \theta \stackrel{\text { def }}{=} \lambda . \end{aligned} \]

（参见练习 28.1）如果 $K<\lambda$，则 $\widehat{\theta}$ 的 WMSE 较小；如果 $K>\lambda$，则 $\widetilde{\theta}$ 的 WMSE 较小。从这个简单的分析中得出的一个见解是，当潜在省略的变量相对于估计方差具有较小的系数时，我们应该更喜欢较小（更简单）的模型，而当这些变量相对于估计方差具有较大的系数时，我们应该更喜欢更大（更复杂）的模型。另一个见解是这种选择是不可行的，因为 $\lambda$ 是未知的。

（28.1）和（28.2）之间的比较是基本的偏差-方差权衡。估计器 $\widehat{\theta}$ 是无偏的，但方差贡献为 $K$。估计器 $\widetilde{\theta}$ 的方差为零，但具有平方偏差贡献 $\lambda$。 WMSE 结合了这两个组件。

基于 WMSE 的选择表明，理想情况下，如果 $K<\lambda$，我们应该选择估计器 $\widehat{\theta}$，如果 $K>\lambda$，则选择 $\tilde{\theta}$。一个可行的实现是用估计器替换 $\lambda$。插件估计器是 $\hat{\lambda}=\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}=W$，用于检验 $\theta=0$ 的 Wald 统计量。然而，估计器 $\widehat{\lambda}$ 有期望

\[ \mathbb{E}[\widehat{\lambda}]=\mathbb{E}\left[\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \hat{\theta}\right]=\theta^{\prime} \boldsymbol{V}^{-1 \prime} \theta+\mathbb{E}\left[(\widehat{\theta}-\theta)^{\prime} \boldsymbol{V}^{-1}(\widehat{\theta}-\theta)\right]=\lambda+K \]

所以是有偏见的。无偏估计量是 $\tilde{\lambda}=\widehat{\lambda}-K$。请注意，$\tilde{\lambda}>K$ 与 $W>2 K$ 相同。这导致了模型选择规则：如果 $W>2 K$，则使用 $\widehat{\theta}$，否则使用 $\widetilde{\theta}$。

这是一个过于简单化的设置，但强调了基于标准的模型选择的基本要素。比较不同估计量的 MSE 通常涉及偏差和方差之间的权衡，更复杂的模型表现出较小的偏差但增加了估计方差。实际的权衡是未知的，因为偏差取决于未知的真实参数。然而，偏差是可以估计的，从而产生 MSE 的经验估计和经验模型选择规则。

大量的模型选择标准被提出。我们在这里列出了应用计量经济学中最常用的那些。

我们首先列出线性回归模型 $Y=X^{\prime} \beta+e$ 与 $\sigma^{2}=\mathbb{E}\left[e^{2}\right]$ 和 $k \times 1$ 系数向量 $\beta$ 的选择标准。令 $\widehat{\beta}$ 为最小二乘估计器，$\widehat{e}_{i}$ 为最小二乘残差估计器，$\widehat{\sigma}^{2}=n^{-1} \sum_{i=1}^{n} \widehat{e}_{i}^{2}$ 为方差估计器。估计参数 $\left(\beta\right.$ 和 $\left.\sigma^{2}\right)$ 的数量为 $Y=X^{\prime} \beta+e$。

28.3 贝叶斯信息准则

\[ \mathrm{BIC}=n+n \log \left(2 \pi \widehat{\sigma}^{2}\right)+K \log (n) . \]

28.4 赤池信息准则

\[ \mathrm{AIC}=n+n \log \left(2 \pi \widehat{\sigma}^{2}\right)+2 K . \]

28.5 交叉验证

\[ \mathrm{CV}=\sum_{i=1}^{n} \widetilde{e}_{i}^{2} \]

其中 $\widetilde{e}_{i}$ 是最小二乘留一预测误差。

接下来我们列出了基于似然估计的两个常用选择标准。令 $f(y, \theta)$ 为带有 $K \times 1$ 参数 $\theta$ 的参数密度。似然度 $L_{n}(\theta)=\prod_{i=1}^{n} f\left(Y_{i}, \theta\right)$ 是根据观测值评估的密度。最大似然估计器 $\widehat{\theta} \operatorname{maximizes} \ell_{n}(\theta)=\log L_{n}(\theta)$。

28.6 贝叶斯信息准则

\[ \mathrm{BIC}=-2 \ell_{n}(\widehat{\theta})+K \log (n) . \]

28.7 赤池信息准则

\[ \mathrm{AIC}=-2 \ell_{n}(\widehat{\theta})+2 K . \]

在以下部分中，我们推导并讨论这些和其他模型选择标准。

28.8 贝叶斯信息准则

贝叶斯信息准则 (BIC)，也称为 Schwarz 准则，由 Schwarz (1978) 提出。它适用于通过最大似然估计的参数模型，用于选择作为真实模型的近似概率最高的模型。

令 $\pi(\theta)$ 为 $\theta$ 的先验密度。 $Y$ 和 $\theta$ 的联合密度为 $f(y, \theta) \pi(\theta)$。 $Y$ 的边际密度为

\[ p(y)=\int f(y, \theta) \pi(\theta) d \theta \]

根据观测值评估的边际密度 $p(Y)$ 称为边际似然。

Schwarz (1978) 建立了以下近似值。

定理 28.1 施瓦茨。如果模型 $f(y, \theta)$ 满足标准正则性条件并且先验 $\pi(\theta)$ 是扩散的，则

\[ -2 \log p(Y)=-2 \ell_{n}(\widehat{\theta})+K \log (n)+O(1) \]

其中 $O(1)$ 项的边界为 $n \rightarrow \infty$。

第 28.32 节给出了正态线性回归的启发式证明。 “扩散”先验是将权重均匀分布在参数空间上的先验。

施瓦茨定理表明，边际似然大约等于最大似然乘以根据估计参数数量和样本大小进行的调整。近似值 (28.6) 通常称为贝叶斯信息准则或 BIC。 BIC 是惩罚的 $\log$ 可能性。术语 $K \log (n)$ 可以解释为过度参数化惩罚。对数似然乘以 $-2$ 是传统做法，因为它将标准放入与对数似然统计量相同的单位中。在正态线性回归的背景下，我们在（5.6）中计算出

\[ \ell_{n}(\widehat{\theta})=-\frac{n}{2}(\log (2 \pi)+1)-\frac{n}{2} \log \left(\widehat{\sigma}^{2}\right) \]

其中 $\widehat{\sigma}^{2}$ 是残差方差估计。因此，BIC 等于 (28.3) $K=k+1$。

由于 $n \log (2 \pi)+n$ 不会因模型而异，因此该术语通常被省略。然而，最好按上述方式定义 BIC，以便不同参数族具有可比性。了解一些作者通过将上述表达式除以 $n$ 来定义 BIC（例如 $\mathrm{BIC}=\log \left(2 \pi \widehat{\sigma}^{2}\right)+$ $K \log (n) / n)$ 不会改变模型之间的排名）也是有用的。然而，这是一个不明智的选择，因为它改变了缩放比例，使得比较模型之间的差异程度变得困难。

现在假设我们有两个模型 $\mathscr{M}_{1}$ 和 $\mathscr{M}_{2}$，它们具有边际似然 $p_{1}(Y)$ 和 $p_{2}(Y)$。假设两个模型具有相同的先验概率。贝叶斯定理指出，给定数据时模型正确的概率与其边际似然成正比。具体来说

\[ \begin{aligned} &\mathbb{P}\left[\mathscr{M}_{1} \mid Y\right]=\frac{p_{1}(Y)}{p_{1}(Y)+p_{2}(Y)} \\ &\mathbb{P}\left[\mathscr{M}_{2} \mid Y\right]=\frac{p_{2}(Y)}{p_{1}(Y)+p_{2}(Y)} . \end{aligned} \]

贝叶斯选择选择概率最高的模型。因此，如果 $p_{1}(Y)>p_{2}(Y)$ 我们选择 $\mathscr{M}_{1}$。如果 $p_{1}(Y)<p_{2}(Y)$ 我们选择 $\mathscr{M}_{2}$。

查找边际似然最高的模型与查找 $-2 \log p(Y)$ 值最低的模型相同。定理 $28.1$ 表明后者大约等于 BIC。 BIC 选择选择 BIC 的 ${ }^{1}$ 值最低的模型。因此，BIC 选择是近似贝叶斯选择。

上述讨论涉及两个模型，但适用于任意数量的模型。 BIC 选择选择 BIC 最小的型号。为了实现，您只需估计每个模型、计算其 BIC 并进行比较。模型。

BIC 可以在 Stata 中通过使用估计统计命令获得

28.9 回归的 Akaike 信息准则

Akaike 信息准则 (AIC) 由 Akaike (1973) 提出。用于选择估计密度最接近真实密度的模型。它专为通过最大似然估计的参数模型而设计。

令 $\widehat{f}(y)$ 为观测向量 $Y=\left(Y_{1}, \ldots, Y_{n}\right)$ 的未知真实密度 $g(y)$ 的估计量。例如，$g(y)$ 的正态线性回归估计为 $\widehat{f}(y)=\prod_{i=1}^{n} \phi_{\widehat{\sigma}}\left(Y_{i}-X_{i}^{\prime} \widehat{\beta}\right)$。

为了测量两个密度 $g$ 和 $\widehat{f}$ 之间的距离，Akaike 使用了 Kullback-Leibler 信息准则 (KLIC)

\[ \operatorname{KLIC}(g, f)=\int g(y) \log \left(\frac{g(y)}{f(y)}\right) d y . \]

请注意 $\operatorname{KLIC}(g, f)=0$ 和 $f(y)=g(y)$。根据詹森不等式，

\[ \operatorname{KLIC}(g, f)=-\int g(y) \log \left(\frac{f(y)}{g(y)}\right) d y \geq-\log \int f(y) d y=0 . \]

因此，$\operatorname{KLIC}(g, f)$ 是 $f$ 与 $g$ 偏差的非负度量，值越小表示偏差越小。

${ }^{1}$ 当 BIC 为负数时，这意味着取最大的负值。真实密度和估计密度之间的 KLIC 距离为

\[ \begin{aligned} \operatorname{KLIC}(g, \widehat{f}) &=\int g(y) \log \left(\frac{g(y)}{\widehat{f}(y)}\right) d y \\ &=\int g(y) \log (g(y)) d y-\int g(y) \log (\widehat{f}(y)) d y . \end{aligned} \]

这是随机的，因为它取决于估计器 $\widehat{f}$。 Akaike 提出了预期的 KLIC 距离

\[ \mathbb{E}[\operatorname{KLIC}(g, \widehat{f})]=\int g(y) \log (g(y)) d y-\mathbb{E}\left[\int g(y) \log (\widehat{f}(y)) d y\right] . \]

(28.8) 中的第一项不依赖于模型。因此，预期 KLIC 距离的最小化就是第二项的最小化。乘以 2（类似于 BIC），这是

\[ T=-2 \mathbb{E}\left[\int g(y) \log (\widehat{f}(y)) d y\right] . \]

期望超过随机估计器 $\widehat{f}$。

另一种解释是注意到 (28.9) 中的积分是相对于真实数据密度 $g(y)$ 对 $Y$ 的期望。因此我们可以将(28.9)写成

\[ T=-2 \mathbb{E}[\log (\widehat{f}(\widetilde{Y}))] \]

其中 $\tilde{Y}$ 是 $Y$ 的独立副本。理解这个表达式的关键是估计器 $\widehat{f}$ 和评估点 $\widetilde{Y}$ 都是随机且独立的。 $T$ 是使用样本外实现 $\widetilde{Y}$ 的估计模型 $\widehat{f}$ 的预期对数似然拟合。因此 $T$ 可以解释为预期的预测对数似然。基于样本外对数似然，具有较低 $T$ 值的模型具有良好的拟合度。

为了获得进一步的理解，我们考虑具有 $K$ 回归量的正态线性回归模型的简单情况。观测模型的对数密度为

\[ \log f(Y, \boldsymbol{X}, \theta)=-\frac{n}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(Y_{i}-X_{i}^{\prime} \beta\right)^{2} . \]

真实参数值的预期值为 $-\frac{n}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{n}{2}$。这意味着 $T$ 的理想值是 $T_{0}=n \log \left(2 \pi \sigma^{2}\right)+n$。如果没有估计误差，这将是获得的值。

为了简化计算，我们添加方差 $\sigma^{2}$ 已知的假设。

定理 28.2 假设 $\widehat{f}(y)$ 是一个估计的正态线性回归模型，具有 $K$ 回归量和已知方差 $\sigma^{2}$。假设真实密度 $g(y)$ 是方差为 $\sigma^{2}$ 的条件同方差回归。然后

\[ \begin{aligned} T &=n \log \left(2 \pi \sigma^{2}\right)+n+K=T_{0}+K \\ \mathbb{E}\left[-2 \ell_{n}(\widehat{\theta})\right] &=n \log \left(2 \pi \sigma^{2}\right)+n-K=T_{0}-K . \end{aligned} \]

证明在 $28.32$ 节中给出。这些表达很有趣。表达式 (28.12) 显示预期 KLIC 距离 $T$ 等于理想值 $T_{0}$ 加上 $K$。后者是参数估计的成本，以预期 KLIC 距离来衡量。通过估计参数（而不是使用真实值），预期 KLIC 距离会增加 $K$。

表达式（28.13）显示了相反的情况。它表明样本对数似然函数比理想值 $T_{0}$ 小 $K$。这是样本内过度拟合的成本。样本对数似然是样本内的拟合度量，因此低估了总体对数似然。这两个表达式一起表明预期样本对数似然比目标值 $T$ 小 $2 K$。这是过度拟合和参数估计的综合成本。

结合这些表达式，我们可以为 $T$ 提出一个无偏估计。在正态回归模型中，我们使用（28.4）。由于 $n \log (2 \pi)+n$ 不会因模型而异，因此通常会被省略。因此，对于线性回归，通常使用定义 $\mathrm{AIC}=n \log \left(\widehat{\sigma}^{2}\right)+2 K$。

有趣的是，AIC 的形式与 BIC 类似。 AIC 和 BIC 都是惩罚对数似然，并且两种惩罚都与估计参数 $K$ 的数量成正比。不同之处在于，AIC 惩罚是 $2 K$，而 BIC 惩罚是 $K \log (n)$。由于 $2<\log (n)$ if $n \geq 8$，BIC 使用更强的参数化惩罚。

通过 AIC 选择模型相当于计算每个模型的 AIC 并选择 ${ }^{2}$ 值最低的模型。

定理 28.3 在定理 28.2 的假设下，$\mathbb{E}[\mathrm{AIC}]=T$。因此，AIC 是 $T$ 的无偏估计器。

这些结果的有趣特征之一是它们是精确的 - 没有近似值，并且不要求真实误差呈正态分布。关键假设是条件同方差。如果同方差性失败，则 AIC 就会失去有效性。

AIC 可以在 Stata 中通过使用估计模型后的估计统计命令来获得。

28.10 似然性的 Akaike 信息准则

对于一般似然上下文，Akaike 提出了标准（28.7）。这里，$\widehat{\theta}$是最大似然估计，$\ell_{n}(\widehat{\theta})$是最大化对数似然函数，$K$是估计参数的数量。这专门针对正态线性回归模型的情况（28.4）。

对于回归，AIC 选择是通过估计一组模型、计算每个模型的 AIC，并选择 AIC 最小的模型来执行的。

AIC的优点是计算简单、易于实现、解释简单。它很直观，因为它是一个简单的惩罚可能性。

缺点是它的简单性可能具有欺骗性。证明表明该标准基于对数似然的二次近似和经典 Wald 统计量的渐近卡方近似。当这些条件失败时，AIC 可能不准确。例如，如果模型是近似（拟）似然而不是真实似然，则信息矩阵等式的失败意味着经典 Wald 统计量不是渐近卡方。在这种情况下，AIC 的准确性就会失效。另一个问题是许多非线性模型都存在参数识别失败的参数区域。在这些模型中，对数的二次近似

${ }^{2}$ 当 AIC 为负时，这意味着取最大的负值。似然函数无法在参数空间中保持一致，因此 AIC 的准确性失败。这些条件对解释非线性模型中的 AIC 提出了挑战。

以下是定理 28.3 的模拟。

定理 28.4 在最大似然估计的标准正则条件下，加上某些统计量（在证明中确定）一致可积的假设，$\mathbb{E}[\mathrm{AIC}]=T+O\left(n^{1 / 2}\right)$。因此，AIC 是 $T$ 的近似无偏估计量

$28.32$ 节给出了证明的草图。

该结果表明，一般来说，AIC 是估计参数模型的 KLIC 拟合的合理估计器。该定理广泛适用于最大似然估计，因此 AIC 可以用于多种情况。

28.11 锦葵准则

Mallows 准则由 Mallows (1973) 提出，通常称为 $C_{p}$ 准则。它适用于同方差回归模型的线性估计。

采取同方差回归框架

\[ \begin{aligned} Y &=m+e \\ m &=m(X) \\ \mathbb{E}[e \mid X] &=0 \\ \mathbb{E}\left[e^{2} \mid X\right] &=\sigma^{2} . \end{aligned} \]

将 $n$ 观测值的第一个方程以向量表示法写为 $\boldsymbol{Y}=\boldsymbol{m}+\boldsymbol{e}$。令 $\widehat{\boldsymbol{m}}=\boldsymbol{A} \boldsymbol{Y}$ 为 $\boldsymbol{m}$ 的线性估计器，这意味着 $\boldsymbol{A}$ 只是回归矩阵 $\boldsymbol{X}$ 的某个 $n \times n$ 函数。残差为 $\widehat{\boldsymbol{e}}=\boldsymbol{Y}-\widehat{\boldsymbol{m}}$。线性估计器的类别包括最小二乘、加权最小二乘、核回归、局部线性回归和级数回归。例如，使用回归矩阵 $\boldsymbol{Z}$ 的最小二乘估计就是 $n$ 的情况。

Mallows (1973) 提出了该准则

\[ C_{p}=\widehat{\boldsymbol{e}}^{\prime} \widehat{\boldsymbol{e}}+2 \widetilde{\sigma}^{2} \operatorname{tr}(\boldsymbol{A}) \]

其中 $\widetilde{\sigma}^{2}$ 是 $\sigma^{2}$ 的初步估计器（通常基于拟合大型模型）。在使用 $K$ 系数进行最小二乘回归的情况下，这可以简化为

\[ C_{p}=n \widehat{\sigma}^{2}+2 K \widetilde{\sigma}^{2} . \]

Mallows 标准的使用方式与 AIC 类似。估计一组回归模型，并为每个模型计算标准 $C_{p}$。 $C_{p}$ 值最小的模型是 Mallows 选择的模型。

Mallows 设计了标准 $C_{p}$ 作为以下拟合度量的无偏估计量

\[ R=\mathbb{E}\left[\sum_{i=1}^{n}\left(\widehat{m}_{i}-m_{i}\right)^{2}\right] . \]

这是根据观测值评估的估计回归与真实回归之间的预期平方差。

$R$ 的另一个动机是预测准确性。考虑一组独立的观测值 $\widetilde{Y}_{i}, i=1, \ldots, n$，它们具有与样本中相同的回归量 $X_{i}$。考虑给定 $X_{i}$ 和拟合回归对 $\widetilde{Y}_{i}$ 的预测。最小二乘预测器是 $\widehat{m}_{i}$。预期预测误差平方和为

\[ \text { MSFE }=\sum_{i=1}^{n} \mathbb{E}\left[\left(\widetilde{Y}_{i}-\widehat{m}_{i}\right)^{2}\right] . \]

该数量的最佳可能（不可行）值为

\[ \operatorname{MSFE}_{0}=\sum_{i=1}^{n} \mathbb{E}\left[\left(\widetilde{Y}_{i}-m_{i}\right)^{2}\right] . \]

差异在于估计器的预测精度：

\[ \begin{aligned} \operatorname{MSFE}^{-\operatorname{MSFE}_{0}} &=\sum_{i=1}^{n} \mathbb{E}\left[\left(\widetilde{Y}_{i}-\widehat{m}_{i}\right)^{2}\right]-\sum_{i=1}^{n} \mathbb{E}\left[\left(\widetilde{Y}_{i}-m_{i}\right)^{2}\right] \\ &=\mathbb{E}\left[\sum_{i=1}^{n}\left(\widehat{m}_{i}-m_{i}\right)^{2}\right] \\ &=R \end{aligned} \]

这等于马洛斯的拟合度。因此 $R$ 是预测准确性的衡量标准。

我们指出，Mallows 准则是 $R$ 的无偏估计量。更准确地说，调整后的标准 $C_{p}^{*}=C_{p}-\boldsymbol{e}^{\prime} \boldsymbol{e}$ 对于 $R$ 是无偏的。比较模型时，$C_{p}$ 和 $C_{p}^{*}$ 是等效的，因此这种替换对模型选择没有影响。

定理 28.5 如果 $\widehat{\boldsymbol{m}}=\boldsymbol{A} \boldsymbol{Y}$ 是线性估计量，回归误差有条件均值为零且同方差，并且 $\widetilde{\sigma}^{2}$ 对于 $\sigma^{2}$ 是无偏的，则

\[ \mathbb{E}\left[C_{p}^{*}\right]=R \]

因此调整后的 Mallows 准则 $C_{p}^{*}$ 是 $R$ 的无偏估计量。

第 28.32 节给出了证明。

28.12 坚持标准

将样本分为两部分，一部分用于估计，第二部分用于评估，创建了一个用于模型评估和选择的简单装置。此过程通常被标记为保留评估。在最近的机器学习文献中，数据划分通常被描述为训练样本和测试样本。

样本通常是随机划分的，以便估计（训练）样本具有 $N$ 观测值，评估（测试）样本具有 $P$ 观测值，其中 $N+P=n$。 $N \& P$ 的选择没有通用规则，但 $N=P=n / 2$ 是标准选择。对于更复杂的过程，例如模型选择方法的评估，最好将样本分为（1）训练、（2）模型选择和（3）最终估计和评估。当需要获得其分布不被模型选择过程扭曲的参数估计器时，这可能特别有用。这种划分最适合样本量极大的情况。

采用二分除法的标准情况，其中 $1 \leq i \leq N$ 是估计样本，$N+1 \leq$ $i \leq N+P$ 是评估样本。在估计样本上，我们构建参数估计，例如最小二乘系数

\[ \widetilde{\beta}_{N}=\left(\sum_{i=1}^{N} X_{i} X_{i}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} X_{i} Y_{i}\right) \]

将此系数与评估样本相结合，我们计算 $i \geq N+1$ 的预测误差 $\widetilde{e}_{N, i}=Y_{i}-X_{i}^{\prime} \widetilde{\beta}_{N}$。

在 $4.12$ 节中，我们将基于大小 $N$ 的估计样本的均方预测误差 (MSFE) 定义为样本外预测误差平方 $\operatorname{MSFE}_{N}=\mathbb{E}\left[\widetilde{e}_{N, i}^{2}\right]$ 的期望。 MSFE 的保留估计量是预测误差平方的平均值

\[ \widetilde{\sigma}_{N, P}^{2}=\frac{1}{P} \sum_{i=N+1}^{N+P} \widetilde{e}_{N, i}^{2} . \]

我们可以看到 $\widetilde{\sigma}_{N, P}^{2}$ 对于 $\mathrm{MSFE}_{N}$ 是无偏的。

当 $N=P$ 时，我们可以通过翻转过程来改进 MSFE 的估计。交换估计和评估样本的角色，我们获得第二个 MSFE 估计器，例如 $\widetilde{\omega}_{N, P}^{2}$。全局估计量是他们的平均值 $\widetilde{\sigma}_{N, P}^{* 2}=\left(\widetilde{\sigma}_{N, P}^{2}+\widetilde{\omega}_{N, P}^{2}\right) / 2$。该估计量也具有期望 MSFE ${ }_{N}$，但方差有所减少。

估计的 MSFE $\widetilde{\sigma}_{N, P}^{* 2}$ 可用于模型选择。数量 $\widetilde{\sigma}_{N, P}^{* 2}$ 是针对一组建议模型计算的。所选模型是 $\widetilde{\sigma}_{N, P}^{* 2}$ 值最小的模型。该方法直观、通用、灵活，不依赖于技术假设。

保留方法有两个缺点。首先，如果我们的目标是使用完整样本进行估计，那么我们期望的估计是 $\mathrm{MSFE}_{n}$，而不是 $\operatorname{MSFE}_{N}$。留出估计提供了基于使用显着减少的样本量的估计的MSFE的估计器，并且因此对于基于使用完整样本的估计的MSFE是有偏差的。其次，估计器 $\widetilde{\sigma}_{N, P}^{* 2}$ 对将观测值随机分类到估计和评估样本中很敏感。这会影响模型的选择。结果可能取决于初始样本排序，因此部分是任意的。

28.13 交叉验证标准

在应用统计学和机器学习中，模型选择和调整参数选择的默认方法是交叉验证。我们已经介绍了整本书中的一些概念，现在对这些概念进行回顾和统一。交叉验证与上一节中介绍的保留标准密切相关。

在 $3.20$ 节中，我们将留一估计量定义为通过将估计公式应用于省略 $i^{t h}$ 观察的样本而获得的估计量。这与前面描述的保留问题相同，其中估计样本是 $N=n-1$，评估样本是 $P=1$。省略观察 $i$ 获得的估计量写为 $\widehat{\beta}_{(-i)}$。预测误差为 $\widetilde{e}_{i}=Y_{i}-X_{i}^{\prime} \widehat{\beta}_{(-i)}$。样本外均方误差“估计”为 $\widetilde{e}_{i}^{2}$。此操作重复 $n$ 次，每次观测 $3.20$ 一次，MSFE 估计值是 $3.20$ 预测误差平方的平均值

\[ \mathrm{CV}=\frac{1}{n} \sum_{i=1}^{n} \widetilde{e}_{i}^{2} . \]

估计器 CV 称为交叉验证 (CV) 准则。它是保留标准的自然推广，消除了上一节中描述的两个缺点。首先，CV 准则是 MSFE ${ }_{n-1}$ 的无偏估计量，本质上与 MSFE 相同。因此CV $_{n}$。对于模型选择来说本质上是无偏的。其次，CV 标准不依赖于观察值的随机排序。由于没有随机分量，该标准在任何实现中都取相同的值。

在最小二乘估计中，CV 准则具有简单的计算实现。定理 3.7 表明留一最小二乘估计量 (3.42) 等于

\[ \widehat{\beta}_{(-i)}=\widehat{\beta}-\frac{1}{\left(1-h_{i i}\right)}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} X_{i} \widehat{e}_{i} \]

其中 $\widehat{e}_{i}$ 是最小二乘残差，$h_{i i}$ 是杠杆值。因此预测误差等于

\[ \widetilde{e}_{i}=Y_{i}-X_{i}^{\prime} \widehat{\beta}_{(-i)}=\left(1-h_{i i}\right)^{-1} \widehat{e}_{i} \]

其中第二个等式来自定理 3.7。因此 CV 标准是

\[ \mathrm{CV}=\frac{1}{n} \sum_{i=1}^{n} \widetilde{e}_{i}^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(1-h_{i i}\right)^{-2} \widehat{e}_{i}^{2} . \]

还记得在我们的非参数回归研究（第 19.12 节）中，我们将核回归的交叉验证标准定义为预测误差平方的加权平均值

\[ \mathrm{CV}=\frac{1}{n} \sum_{i=1}^{n} \tilde{e}_{i}^{2} w\left(X_{i}\right) . \]

定理 $19.7$ 表明 $\mathrm{CV}$ 对于积分均方误差 (IMSE) 近似无偏，IMSE 是非参数回归精度的标准度量。这些结果表明 CV 是 MSFE 和 IMSE 的无偏估计量，显示出这些准确性度量之间的密切联系。

在 $20.17$ 节和方程 (20.30) 中，我们定义了级数回归的 CV 标准，如 (28.5) 中所示。选择序列回归的变量与模型选择相同。上述结果表明，CV 标准是回归模型 MSFE 和 IMSE 的估计量，因此是评估模型精度的良好候选标准。 CV 标准的有效性比 AIC 广泛得多，因为 CV 定理不需要条件同方差。这不是证明方法的产物；而是证明方法的产物。交叉验证本质上比 AIC 或 BIC 更稳健。

CV 模型选择的实施与其他标准相同。估计一组回归模型。对于每个 CV 标准进行计算。 CV 值最小的模型是 CVselected 模型。

CV 方法在概念和潜在应用方面也更广泛。它适用于任何估计方法，只要可以计算出“留一”误差即可。它还可以应用于平方误差损失之外的其他损失函数。例如，绝对损失的交叉验证估计是

\[ \mathrm{CV}=\frac{1}{n} \sum_{i=1}^{n}\left|\widetilde{e}_{i}\right| . \]

从计算和概念上讲，通过最小化此类标准来选择模型是很简单的。然而，将 CV 应用于一般标准的属性尚不清楚。

Stata 没有标准命令来计算回归模型的 CV 标准。

28.14 K 折交叉验证

CV 标准有两个缺陷，可以通过密切相关的 K 折交叉验证标准来缓解。第一个缺陷是，当样本量非常大或估计方法不是最小二乘法时，CV 计算的计算成本可能很高。对于最小二乘以外的估计量，可能需要计算 $n$ 单独的估计值。在某些情况下，这在计算上可能会令人望而却步。第二个缺陷是 CV 标准（被视为 $\operatorname{MSFE}_{n}$ 的估计量）具有很高的方差。来源是留一估计量 $\widehat{\beta}_{(-i)}$ 在 $i$ 上的变化最小，因此高度相关。

另一种方法是将样本分成 $K$ 组（或“折叠”），并将每个组视为保留样本。这有效地将估计数量从 $n$ 减少到 $K$。（这个 $K$ 不是估计系数的数量。我为可能的符号混淆表示歉意，但这是标准标签。）一个常见的选择是 $K=10$，导致所谓的 $\mathbf{1 0}$-fold cross-验证。

该方法按以下步骤进行。此描述用于使用估计器 $\widehat{\theta}$ 估计回归模型 $Y=g(X, \theta)+e$

对观察值进行随机排序。
将观测值分割为（大致）相等大小 $n_{k} \simeq n / K$ 的折叠 $k=1, \ldots, K$。让 $I_{k}$ 表示折叠 $k$ 中的观察值
对于 $k=1, . ., K$

从数据集中排除折叠 $I_{k}$。这会生成一个具有 $n-n_{k}$ 观测值的样本。
计算该样本的估计量 $\widehat{\theta}_{(-k)}$。
计算 $i \in I_{k}$ 的预测误差 $\widetilde{e}_{i}=Y_{i}-g\left(X_{i}, \widehat{\theta}_{(-k)}\right)$。
计算$\mathrm{CV}_{k}=n_{k}^{-1} \sum_{i \in I_{k}} \widetilde{e}_{i}^{2}$

计算$\mathrm{CV}=K^{-1} \sum_{k=1}^{K} \mathrm{CV}_{k}$。

如果 $K=n$ 该方法与留一交叉验证相同。

$K$-fold CV 的一个有用功能是我们可以计算近似标准误差。它基于 $\operatorname{var}[\mathrm{CV}] \simeq K^{-1} \operatorname{var}\left[\mathrm{CV}_{k}\right]$ 的近似值，该近似值基于 $\mathrm{CV}_{k}$ 是近似不相关的 acros 折叠的想法。这会导致标准错误

\[ s(\mathrm{CV})=\sqrt{\frac{1}{K(K-1)} \sum_{k=1}^{K}\left(\mathrm{CV}_{k}-\mathrm{CV}\right)^{2}} . \]

这类似于聚类方差公式，其中折叠被视为聚类。可以报告标准误差 $s$ (CV)，以评估 CV 作为 MSFE 估计值的精度。

K 折交叉验证的一个缺点是 CV 可能对观测值的初始随机排序敏感，导致部分任意的结果。这个问题可以通过一种称为重复 CV 的技术来减少，该技术重复 K 折 CV 算法 $M$ 次（每次使用不同的随机排序），从而得到 $C$ 的 $M$ 值。对它们进行平均以产生重复的 CV 值。随着 $M$ 的增加，排序带来的随机性被消除。可以通过平均平方标准误差的平方根来获得相关的标准误差。

CV模型选择通常是通过选择CV值最小的模型来实现的。另一种实现称为单标准误差 (1se) 规则，它选择 CV 值在最小 CV 的一个标准误差范围内的最简约模型。（非正式）的想法是，$\mathrm{CV}$ 的值彼此在一个标准误差范围内的模型在统计上是不可区分的，并且在其他条件相同的情况下，我们应该倾向于简约。 1se 规则是流行的 cv.glmnet R 函数中的默认规则。 LSE 规则是一种过度平滑的选择，这意味着它倾向于更高的偏差和更低的方差。相比之下，为了进行推理，许多计量经济学家建议使用欠平滑带宽，这意味着选择比 CV 最小化选择更简洁的模型。

28.15 许多选择标准都是相似的

对于线性回归模型，引入了许多选择标准。然而，许多这些替代标准彼此非常相似。在本节中，我们将回顾其中的一些联系。以下讨论针对带有 $n$ 观测值、$K$ 估计系数和最小二乘方差估计器 $\widehat{\sigma}_{K}^{2}$ 的标准回归模型 $Y=X^{\prime} \beta+e$。

Shibata (1980) 提出了该标准

\[ \text { Shibata }=\widehat{\sigma}_{K}^{2}\left(1+\frac{2 K}{n}\right) \]

作为 MSFE 的估计器。回顾回归的 Mallows 准则 (28.15)，如果我们用 $\widehat{\sigma}_{K}^{2}$ 替换初步估计器 $\widetilde{\sigma}^{2}$，我们会看到 Shibata = $C_{p} / n$。因此，两者在实践中非常相似。

对小$x$取对数并使用$\log (1+x) \simeq x$的近似值

\[ n \log (\text { Shibata })=n \log \left(\widehat{\sigma}_{K}^{2}\right)+n \log \left(1+\frac{2 K}{n}\right) \simeq n \log \left(\widehat{\sigma}_{K}^{2}\right)+2 K=\text { AIC. } \]

因此 Shibata 准则的最小化和 AIC 是相似的。

Akaike (1969) 提出了最终预测误差准则

\[ \mathrm{FPE}=\widehat{\sigma}_{K}^{2}\left(\frac{1+K / n}{1-K / n}\right) . \]

使用扩展 $(1-x)^{-1} \simeq 1+x$ 和 $(1+x)^{2} \simeq 1+2 x$，我们看到 $\mathrm{FPE} \simeq$ Shibata。

Craven 和 Wahba (1979) 提出了广义交叉验证

\[ \mathrm{GCV}=\frac{n \widehat{\sigma}_{K}^{2}}{(n-K)^{2}} . \]

通过展开 $(1-x)^{-2} \simeq 1+2 x$ 我们发现

\[ n \mathrm{GCV}=\frac{\widehat{\sigma}_{K}^{2}}{(1-K / n)^{2}} \simeq \widehat{\sigma}_{K}^{2}\left(1+\frac{2 K}{n}\right)=\text { Shibata. } \]

上述计算表明，当 $K / n$ 很小时，WMSE、AIC、Shibata、FPE、GCV 和 Mallows 准则都非常接近。对于大型 $K$，有限样本会出现差异。但从上述分析可以看出，这些标准之间并无根本区别。他们都在估计同一个目标。这与 BIC 形成鲜明对比，BIC 使用不同的参数化惩罚并且渐近不同。有趣的是，$\mathrm{CV}$ 和上述标准之间也存在联系。再次使用展开式 $(1-x)^{-2} \simeq 1+2 x$ 我们发现

\[ \begin{aligned} \mathrm{CV} &=\sum_{i=1}^{n}\left(1-h_{i i}\right)^{-2} \widehat{e}_{i}^{2} \\ & \simeq \sum_{i=1}^{n} \widehat{e}_{i}^{2}+\sum_{i=1}^{n} 2 h_{i i} \widehat{e}_{i}^{2} \\ &=n \widehat{\sigma}_{K}^{2}+2 \sum_{i=1}^{n} X_{i}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} X_{i} \widehat{e}_{i}^{2} \\ &=n \widehat{\sigma}_{K}^{2}+2 \operatorname{tr}\left(\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\sum_{i=1}^{n} X_{i} X_{i}^{\prime} \widehat{e}_{i}^{2}\right)\right) \\ & \simeq n \widehat{\sigma}_{K}^{2}+2 \operatorname{tr}\left(\left(\mathbb{E}\left[X X^{\prime}\right]\right)^{-1}\left(\mathbb{E}\left[X X^{\prime} e^{2}\right]\right)\right) \\ &=n \widehat{\sigma}_{K}^{2}+2 K \sigma^{2} \\ & \simeq S h i b a t a . \end{aligned} \]

倒数第三条线由 WLLN 渐近成立。以下等式在条件同方差性下成立。最终近似值用估计器 $\widehat{\sigma}_{K}^{2}$ 替换 $\sigma^{2}$。该计算表明，在条件同方差的假设下，CV 标准与其他标准类似。然而，它在异方差性下有所不同，这是其主要优点之一。

28.16 与似然比检验的关系

由于 AIC 和 BIC 是惩罚对数似然，因此 AIC 和 BIC 选择与似然比检验相关。假设我们有两个嵌套模型 $\mathscr{M}_{1}$ 和 $\mathscr{M}_{2}$，其估计参数为对数似然 $\ell_{1 n}\left(\widehat{\theta}_{1}\right)$ 和 $\ell_{2 n}\left(\widehat{\theta}_{2}\right)$ 和 $K_{1}<K_{2}$。如果 $\operatorname{AIC}\left(K_{1}\right)<\operatorname{AIC}\left(K_{2}\right)$ 发生，AIC 选择 $\mathscr{M}_{1}$

\[ \left.-2 \ell_{1 n}\left(\widehat{\theta}_{1}\right)+2 K_{1}<-2 \ell_{2 n}\left(\widehat{\theta}_{2}\right)\right)+2 K_{2} \]

或者

\[ \mathrm{LR}=2\left(\ell_{2 n}\left(\widehat{\theta}_{2}\right)-\ell_{1 n}\left(\widehat{\theta}_{1}\right)\right)<2 r \]

其中 $r=K_{2}-K_{1}$.因此，AIC 选择类似于通过具有不同临界值的似然比检验进行的选择。 “临界值”不是使用卡方分布中的临界值，而是 $2 r$。这并不是说 AIC 选择是测试（事实并非如此）。而是该决定中有类似的结构。

有两个有用的实际意义。其一是，当测试统计数据以 $F$ 形式报告时（除以系数 $r$ 的差值），则 AIC“临界值”为 2 。如果 $F<2$，AIC 选择受限（较小）模型。如果 $F>2$，它会选择无限制（更大）的模型。

另一个有用的含义是在考虑单个系数的情况下（当 $r=1$ 时）。 AIC 选择 $\mathrm{LR}>2$ 的系数（较大的模型）。相反，如果 LR $>3.84$，则 $5 %$ 显着性检验“选择”较大的模型（拒绝较小的模型）。因此AIC在选择更大型号方面更加慷慨。看待这一问题的一种等效方法是，如果 t 比率超过 $1.41$，则 AIC 选择系数，而 $5 %$ 显着性检验则选择 t 比率超过 $1.96$。

尽管有效临界值不同，但类似的评论也适用于 BIC 选择。为了比较模型与系数 $K_{1}<K_{2}$，如果 $\mathrm{LR}<\log (n) r$，BIC 选择 $\mathscr{M}_{1}$。 $F$ 统计量的“临界值”是 $\log (n)$。因此，随着样本量的增加，BIC 选择变得更加严格。

28.17 一致的选择

模型选择过程的一个重要属性是它是否在大样本中选择真实模型。我们称这样的过程为一致的。

为了进一步讨论这个问题，我们需要仔细地定义什么是“真实”模型。答案取决于模型的类型。

当模型是参数密度或分布 $f(y, \theta)$ 和 $\theta \in \Theta$ 时（如似然估计），如果存在一些 $\theta_{0} \in \Theta$ 使得 $f\left(y, \theta_{0}\right)$ 等于真实密度或分布，则该模型为真。请注意，在这种情况下，正确定义函数类 $f(y, \theta)$ 和参数空间 $\Theta$ 非常重要。

在半参数条件矩条件模型中，如果存在 $\theta_{0} \in \Theta$ 使得 $\mathbb{E}\left[g\left(Y, X, \theta_{0}\right) \mid X\right]=0$ 满足 $\mathbb{E}[g(Y, X, \theta) \mid X]=0$ 和 $\theta \in \Theta$，则该模型为真。这包括回归模型 $Y=m(X, \theta)+e$ 和 $\mathbb{E}[e \mid X]=0$，其中如果存在一些 $\theta_{0} \in \Theta$ 使得 $m\left(X, \theta_{0}\right)=\mathbb{E}[Y \mid X]$ 则该模型为真。它还包括同方差回归模型，该模型增加了 $\mathbb{E}\left[e^{2} \mid X\right]=\sigma^{2}$ 是常量的要求。

在半参数无条件矩条件模型 $\mathbb{E}[g(Y, X, \theta)]=0$ 中，如果存在某个 $\theta_{0} \in \Theta$ 使得 $\mathbb{E}\left[g\left(Y, X, \theta_{0}\right)\right]=0$ 满足，则该模型为真。这里的一个微妙问题是，当模型刚刚被识别并且 $\Theta$ 不受限制时，这个条件通常成立，因此模型通常为真。这包括解释为投影的最小二乘回归和刚刚确定的工具变量回归。

在非参数模型中，例如 $Y \sim f \in \mathscr{F}$，其中 $\mathscr{F}$ 是某个函数类（例如二阶可微密度），则如果真实密度是函数类 $\mathscr{F}$ 的成员，则该模型为真。

可能存在多个真实模型，因此出现了一个复杂情况。当模型严格非嵌套（意味着两个模型类中没有公共元素）时，这种情况不会发生，但严格非嵌套模型很少见。大多数模型都有重要的交叉点。例如，不包含公共元素的线性回归模型 $Y=\alpha+X_{1}^{\prime} \beta_{1}+e$ 和 $Y=\alpha+X_{2}^{\prime} \beta_{2}+e$ 以及 $X_{1}$ 和 $X_{2}$ 可能会显示为非嵌套，但它们在 $\beta_{1}=0$ 和 $\beta_{2}=0$ 时相交。另一个例子是线性模型 $Y=\alpha+X^{\prime} \beta+e$ 和 $\log$-线性模型 $\log (Y)=\alpha+X^{\prime} \beta+e$。如果我们添加 $Y=\alpha+X_{1}^{\prime} \beta_{1}+e$ 的假设，那么模型是不相交的。但是，如果我们放宽正态性并使用条件均值假设 $Y=\alpha+X_{1}^{\prime} \beta_{1}+e$，则模型在 $Y=\alpha+X_{1}^{\prime} \beta_{1}+e$ 和 $Y=\alpha+X_{1}^{\prime} \beta_{1}+e$ 时相交。

最常见的相交模型类型是嵌套的。在回归中，当两个模型为 $Y=X_{1}^{\prime} \beta_{1}+e$ 和 $Y=X_{1}^{\prime} \beta_{1}+X_{2}^{\prime} \beta_{2}+e$ 时，就会发生这种情况。如果 $\beta_{2} \neq 0$ 则只有第二个模型为真。但如果 $\beta_{2}=0$ 则两者都是真实模型。

一般来说，给定一组模型 $\overline{\mathscr{M}}=\left\{\mathscr{M}_{1}, \ldots, \mathscr{M}_{M}\right\}$，子集 $\overline{\mathscr{M}}^{*}$ 是真实模型（如上所述），而其余部分不是真实模型。

模型选择规则 $\widehat{M}$ 从集合 $\bar{M}$ 中选择一个模型。如果一个方法渐进地选择了一个真实的模型，我们就说它是一致的。

定义 28.1 如果 $\mathbb{P}\left[\widehat{M} \in \bar{M}^{*}\right] \rightarrow 1$ 与 $n \rightarrow \infty$ 相同，则模型选择规则是模型选择一致

这表明模型选择规则选择一个真实模型，随着样本量的变化，概率趋于 1。

一类广泛的模型选择方法满足一致性的定义。要了解这一点，请考虑信息标准的类别

\[ \mathrm{IC}=-2 \ell_{n}(\widehat{\theta})+c(n, K) . \]

这包括 AIC $(c=2 K), \mathrm{BIC}(c=K \log (n))$ 和基于测试的选择（$c$ 等于 $\chi_{K}^{2}$ 分布的固定分位数）。

定理 28.6 在最大似然估计的标准正则条件下，如果 $c(n, K)=o(n)$ 与 $n \rightarrow \infty$ 相同，则基于 IC 的选择是模型选择一致的。

证明在 $28.32$ 节中给出。

此结果涵盖 AIC、BIC 和基于测试的选择。因此，所有模型选择都是一致的。

该结果的一个主要限制是模型选择一致性的定义很弱。模型可能是真实的，但过度参数化。要理解其中的区别，请考虑模型 $Y=$、$X_{1}^{\prime} \beta_{1}+e$ 和 $Y=X_{1}^{\prime} \beta_{1}+X_{2}^{\prime} \beta_{2}+e$。如果 $\beta_{2}=0$ 则 $\mathscr{M}_{1}$ 和 $\mathscr{M}_{2}$ 都为 true，但 $\mathscr{M}_{1}$ 是首选模型，因为它更简洁。当两个嵌套模型都是真实模型时，通常将更简约的模型视为正确的模型。在这种情况下，我们不会将较大的模型描述为不正确的模型，而是将其描述为过度参数化。如果选择规则渐进地选择过度参数化模型，我们就说它“过度选择”。

定义 28.2 如果存在模型 $\mathscr{M}_{1} \subset \mathscr{M}_{2}$ 使得 $\liminf _{n \rightarrow \infty} \mathbb{P}\left[\widehat{\mathscr{M}}=\mathscr{M}_{2} \mid \mathscr{M}_{1}\right]>0$ 存在，则模型选择规则渐近过度选择。

该定义指出，当两个模型嵌套并且较小的模型为真（因此两个模型都是真实模型，但较小的模型更简约）时，如果以正概率渐近选择较大的模型，就会发生过度选择。

定理 28.7 在最大似然估计的标准正则条件下，如果 $c(n, K)=O(1)$ 为 $n \rightarrow \infty$，则基于 IC 的选择会渐近过度选择。

证明在 $28.32$ 节中给出。

此结果包括 AIC 和基于测试的选择。因此，这些过程是过度选择的。例如，如果模型为 $Y=X_{1}^{\prime} \beta_{1}+e$ 和 $Y=X_{1}^{\prime} \beta_{1}+X_{2}^{\prime} \beta_{2}+e$ 且 $\beta_{2}=0$ 成立，则这些过程会选择具有正概率的过参数化回归。

遵循这一推理思路，区分真实模型和简约模型是很有用的。我们将简约模型集 $\bar{M}^{0} \subset \overline{\mathscr{M}}^{*}$ 定义为参数数量最少的真实模型集。当 $\bar{M}^{*}$ 中的模型嵌套时，$\overline{\mathscr{M}}^{0}$ 将是单例。在 $\beta_{2}=0$ 的回归示例中，$\mathscr{M}_{1}$ 是 $\left\{\mathscr{M}_{1}, \mathscr{M}_{2}\right\}$ 中唯一的简约模型。我们为渐近选择简约模型的过程引入了更强的一致性定义。定义 28.3 如果 $\mathbb{P}\left[\widehat{\mathscr{M}} \in \overline{\mathscr{M}}^{0}\right] \rightarrow 1$ 为 $n \rightarrow \infty$，则模型选择规则对于简约模型是一致的

正如我们现在所展示的，在我们回顾的方法中，只有 BIC 选择对于简约模型是一致的。

定理 28.8 在最大似然估计的标准正则条件下，如果对于所有 $K_{2}>K_{1}$，基于 IC 的选择对于简约模型是一致的

\[ c\left(n, K_{2}\right)-c\left(n, K_{1}\right) \rightarrow \infty \]

为 $n \rightarrow \infty$，而 $c(n, K)=o(n)$ 为 $n \rightarrow \infty$。

第 28.32 节给出了证明。

该条件包括 BIC，因为 $c\left(n, K_{2}\right)-c\left(n, K_{1}\right)=\left(K_{2}-K_{1}\right) \log (n) \rightarrow \infty$ if $K_{2}>K_{1}$。

一些经济学家将定理 $28.8$ 解释为表明 BIC 选择优于其他方法。这是一个不正确的推论。在下一节中，我们将展示其他选择程序在模型拟合和样本外预测方面是渐近最优的。因此，一致的模型选择只是几个理想的统计特性之一。

28.18 渐近选择最优性

AIC/Shibata/Mallows/CV 类的回归器选择在相当广泛的条件下对于样本外预测来说是渐近最优的。这可能看起来与上一节的结果相冲突，但事实并非如此，因为一致的模型选择和准确预测的目标之间存在重大差异。

我们的分析将在以回归矩阵 $\boldsymbol{X}$ 为条件的同方差回归模型中进行。我们将回归模型写为

\[ \begin{aligned} Y &=m+e \\ m &=\sum_{j=1}^{\infty} X_{j} \beta_{j} \\ \mathbb{E}[e \mid X] &=0 \\ \mathbb{E}\left[e^{2} \mid X\right] &=\sigma^{2} \end{aligned} \]

其中 $X=\left(X_{1}, X_{2}, \ldots\right)$.我们还可以用矩阵表示法将回归方程写为$\boldsymbol{Y}=\boldsymbol{m}+\boldsymbol{e}$。

$K^{t h}$ 回归模型使用第一个 $K$ 回归变量 $X_{K}=\left(X_{1}, X_{2}, \ldots, X_{K}\right)$。矩阵表示法中的最小二乘估计是

\[ \boldsymbol{Y}=\boldsymbol{X}_{K} \widehat{\beta}_{K}+\widehat{\boldsymbol{e}}_{K} . \]

如 $28.6$ 节中所示，将拟合值 $\widehat{\boldsymbol{m}}=\boldsymbol{X}_{K} \widehat{\beta}_{K}$ 和回归拟合（预期预测误差平方和）定义为

\[ R_{n}(K)=\mathbb{E}\left[(\widehat{\boldsymbol{m}}-\boldsymbol{m})^{\prime}(\widehat{\boldsymbol{m}}-\boldsymbol{m}) \mid \boldsymbol{X}\right] \]

尽管现在我们通过样本大小 $n$ 和模型 $K$ 对 $R$ 进行索引。

在任何样本中，都有一个最优模型 $K$ 可以最小化 $R_{n}(K)$ ：

\[ K_{n}^{\mathrm{opt}}=\underset{K}{\operatorname{argmin}} R_{n}(K) . \]

模型$K_{n}^{\text {opt }}$获得$R_{n}(K)$的最小值

\[ R_{n}^{\mathrm{opt}}=R_{n}\left(K_{n}^{\mathrm{opt}}\right)=\min _{K} R_{n}(K) . \]

现在考虑使用回归模型的马洛准则进行模型选择

\[ C_{p}(K)=\widehat{\boldsymbol{e}}_{K}^{\prime} \widehat{\boldsymbol{e}}_{K}+2 \sigma^{2} K \]

其中我们明确地通过 $K$ 进行索引，并且为了简单起见，我们假设误差方差 $\sigma^{2}$ 是已知的。（如果用一致估计器替换，结果不会改变。）令所选模型为

\[ \widehat{K}_{n}=\underset{K}{\operatorname{argmin}} C_{p}(K) . \]

使用 Mallows 选择的模型的预测精度为 $R_{n}\left(\widehat{K}_{n}\right)$。如果预测精度渐近等于不可行的最优值，我们就说选择过程是渐近最优的。这可以写成

\[ \frac{R_{n}\left(\widehat{K}_{n}\right)}{R_{n}^{\mathrm{opt}}} \underset{p}{\longrightarrow} 1 . \]

我们根据风险比考虑 (28.18) 中的收敛，因为 $R_{n}^{\text {opt }}$ 随着样本量的增加而发散。

Li（1987）建立了渐近最优性（28.18）。他的结果取决于以下条件。

观测值 $\left(Y_{i}, X_{\boldsymbol{i}}\right), i=1, \ldots, n$ 是独立且同分布的。

2.$\mathbb{E}[e \mid X]=0$。

3.$\mathbb{E}\left[e^{2} \mid X\right]=\sigma^{2}$。

$\mathbb{E}\left[|e|^{4 r} \mid X\right] \leq B<\infty$ 对应一些 $r>1$。
$R_{n}^{\mathrm{opt}} \rightarrow \infty$ 为 $n \rightarrow \infty$
估计模型是嵌套的。

假设 28.1.2 和 28.1.3 表明真实模型是条件同方差回归。假设 28.1.4 是一个技术条件，即误差的条件矩是一致有界的。假设 28.1.5 很微妙。它有效地表明不存在正确指定的有限维模型。要看到这一点，假设有一个 $K_{0}$ 以便正确指定模型，这意味着 $m_{i}=\sum_{j=1}^{K_{0}} X_{j i} \beta_{j}$。在这种情况下，我们可以证明 $K \geq K_{0}, R_{n}(K)=R_{n}\left(K_{0}\right)$ 不会随 $n$ 变化，违反假设 28.1.5。假设28.1.6是限制估计模型数量的技术条件。这种假设可以推广到允许非嵌套模型，但在这种情况下，需要对估计模型的数量进行替代限制。

定理 28.9 假设 $28.1$ 意味着 (28.18)。因此，Mallows 选择渐近等价于使用不可行的最优模型。

第 28.32 节给出了证明。

定理 $28.9$ 指出条件同方差回归中的 Mallows 选择是渐近最优的。关键假设是同方差性，并且所有有限维模型都被错误指定（不完整），这意味着总是有遗漏的变量。后者意味着无论样本大小如何，遗漏变量偏差和估计方差之间总是存在权衡。所述定理特定于 Mallows 选择，但可扩展到 AIC、Shibata、GCV、FPE 和 CV，并需要一些额外的技术考虑。主要信息是上一节中讨论的选择方法渐进地选择一系列模型，这些模型在最小化预测误差的意义上是最佳拟合的。

Andrews (1991c) 使用类似的论点表明，通过交叉验证进行的选择满足相同的渐近最优性条件，而不需要条件同方差。该治疗方法更具技术性，因此我们在此不进行评论。这表明交叉验证选择相对于其他方法具有重要优势。

28.19 重点信息标准

Claeskens 和 Hjort (2003) 引入了聚焦信息准则 (FIC) 作为标量参数 MSE 的估计量。当估计模型之一嵌套其他模型时，该标准适用于正确指定的似然模型。令 $f(y, \theta)$ 为带有 $K \times 1$ 参数 $\theta$ 的参数模型密度。

允许的模型类别（子模型）是由一组可微分限制 $r(\theta)=0$ 定义的模型类别。令 $\widetilde{\theta}$ 为受限 MLE，它最大化受 $r(\theta)=0$ 影响的似然度。

FIC 的一个关键特征是它专注于实值参数 $\mu=g(\theta)$，其中 $g$ 是一些可微函数。 Claeskens 和 Hjort 将 $\mu$ 称为目标参数。 $\mu$ 的选择是由研究人员做出的，是一个关键的选择。在大多数应用中，$\mu$ 是应用中的关键系数（例如，工资回归中的教育回报）。 $\mu$ 的无限制 MLE 是 $\widehat{\mu}=g(\widehat{\theta})$，受限制的 MLE 是 $\widetilde{\mu}=g(\widetilde{\theta})$。

估计精度通过目标参数估计器的 MSE 来衡量，即偏差平方加上方差：

\[ \operatorname{mse}[\widetilde{\mu}]=\mathbb{E}\left[(\widetilde{\mu}-\mu)^{2}\right]=(\mathbb{E}[\widetilde{\mu}]-\mu)^{2}+\operatorname{var}[\widetilde{\mu}] . \]

事实证明，通过无限制估计量来标准化 MSE 是很方便的。我们将其定义为焦点

\[ \mathrm{F}=\operatorname{mse}[\widetilde{\mu}]-\operatorname{mse}[\widehat{\mu}] . \]

Claeskens-Hjort FIC 是 F 的估计量。具体来说，

\[ \mathrm{FIC}=(\widetilde{\mu}-\widehat{\mu})^{2}-2 \widehat{\boldsymbol{G}}^{\prime} \widehat{\boldsymbol{V}}_{\widehat{\theta}} \widehat{\boldsymbol{R}}\left(\widehat{\boldsymbol{R}}^{\prime} \widehat{\boldsymbol{V}}_{\widehat{\theta}} \widehat{\boldsymbol{R}}^{-1} \widehat{\boldsymbol{R}}^{\prime} \widehat{\boldsymbol{V}}_{\widehat{\theta}} \widehat{\boldsymbol{G}}\right. \]

其中 $\widehat{\boldsymbol{V}}_{\widehat{\theta}}, \widehat{\boldsymbol{G}}$ 和 $\widehat{\boldsymbol{R}}$ 是 $\operatorname{var}[\widehat{\theta}], \boldsymbol{G}=\frac{\partial}{\partial \theta^{\prime}} g(\theta)$ 和 $\boldsymbol{R}=\frac{\partial}{\partial \theta^{\prime}} r(\theta)$ 的估计器。

在具有线性限制 $\boldsymbol{R}^{\prime} \beta=0$ 和感兴趣的线性参数 $\mu=\boldsymbol{G}^{\prime} \beta$ 的最小二乘回归 $\boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{e}$ 中，FIC 等于

\[ \begin{aligned} \mathrm{FIC} &=\left(\boldsymbol{G}^{\prime} \boldsymbol{R}\left(\boldsymbol{R}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{R}\right)^{-1} \boldsymbol{R}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \widehat{\beta}\right)^{2} \\ &-2 \widehat{\sigma}^{2} \boldsymbol{G}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{R}\left(\boldsymbol{R}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{R}\right)^{-1} \boldsymbol{R}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{G} . \end{aligned} \]

FIC 的使用方式与 AIC 类似。计算每个感兴趣的子模型的 FIC，并选择 FIC 值最低的模型。

FIC的优点是它专门针对最小化目标参数的MSE。因此，当目标是估计特定目标参数时，FIC 是合适的。缺点是它不一定会产生对其他参数具有良好估计的模型。例如，在线性回归$Y=X_{1} \beta_{1}+X_{2} \beta_{2}+e$中，如果$X_{1}$和$X_{2}$不相关，并且焦点参数为$\beta_{1}$，那么FIC将倾向于选择没有$X_{2}$的子模型，从而选择模型将产生 $\beta_{2}$ 的高度偏差估计。因此，当使用 FIC 时，是否应该注意 $\mu$ 之外的估计值是值得怀疑的。

在计算上，使用替代公式来实现 FIC 可能会很方便。定义调整焦点

\[ \mathrm{F}^{*}=n(\mathrm{~F}+2 \operatorname{mse}[\widehat{\mu}])=n(\operatorname{mse}[\widetilde{\mu}]+\operatorname{mse}[\widehat{\mu}]) . \]

这会向所有模型添加相同的数量，因此不会改变最小化模型。乘以 $n$ 将 FIC 置于更易于报告的单位中。调整后焦点的估计是调整后的 FIC，可以写为

\[ \begin{aligned} \text { FIC }^{*} &=n(\widetilde{\mu}-\widehat{\mu})^{2}+2 n \widehat{\boldsymbol{V}}_{\widetilde{\mu}} \\ &=n(\widetilde{\mu}-\widehat{\mu})^{2}+2 n s(\widetilde{\mu})^{2} \end{aligned} \]

在哪里

\[ \widehat{\boldsymbol{V}}_{\widetilde{\mu}}=\widehat{\boldsymbol{G}}^{\prime}\left(\boldsymbol{I}_{k}-\widehat{\boldsymbol{V}}_{\widehat{\theta}} \widehat{\boldsymbol{R}}\left(\widehat{\boldsymbol{R}}^{\prime} \widehat{\boldsymbol{V}}_{\widehat{\theta}} \widehat{\boldsymbol{R}}\right)^{-1} \widehat{\boldsymbol{R}}^{\prime} \widehat{\boldsymbol{V}}_{\widehat{\theta}}\right) \widehat{\boldsymbol{G}} \]

是 $\operatorname{var}[\widetilde{\mu}]$ 的估计量，$s(\widetilde{\mu})=\widehat{V}_{\widetilde{\mu}}^{1 / 2}$ 是 $\widetilde{\mu}$ 的标准误差。

这意味着 $\mathrm{FIC}^{*}$ 可以使用传统软件轻松计算，无需额外编程。估计器 $\widehat{\mu}$ 可以根据完整模型（长回归）计算，估计器 $\widetilde{\mu}$ 及其标准误差 $s(\widetilde{\mu})$ 可以根据受限模型（短回归）计算。然后可以应用公式(28.20)来获得FIC $^{*}$。

公式（28.19）也提供了对FIC的直观理解。当我们最小化 FIC* 时，我们正在最小化目标参数 $\left(\widehat{\boldsymbol{V}}_{\widetilde{\mu}}\right)$ 估计量的方差，同时不会将估计 $\widetilde{\mu}$ 与无限制估计 $\widehat{\mu}$ 相比改变太多。

当从两个模型中进行选择时，如果 $(\widetilde{\mu}-\widehat{\mu})^{2}+2 \widehat{\boldsymbol{V}}_{\widetilde{\mu}}<$ 0 与 $(\widetilde{\mu}-\widehat{\mu})^{2} / \widehat{V}_{\widetilde{\mu}}<2$ 相同，FIC 将选择受限模型。不等式左边的统计量是受限模型中的平方 t 统计量，用于检验 $\mu$ 等于无限制估计量 $\widehat{\mu}$ 的假设，但忽略后者的估计误差。因此，一个简单的实现（当仅比较两个模型时）是估计长回归和短回归，获取感兴趣系数的两个估计值的差异，并使用短（受限）回归的标准误差计算 t 比。如果此 t 比率超过 $1.4$，FIC 将选择长回归估计。如果 t 比小于 $1.4$，FIC 将选择短期回归估计。 Claeskens 和 Hjort 使用局部错误指定渐近框架来激励 FIC。我们使用更简单的启发式动机。首先采用无限制 MLE。在标准条件下，$\widehat{\mu}$ 具有渐近方差 $\boldsymbol{G}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{G}$，其中 $\boldsymbol{V}_{\theta}=\mathscr{I}^{-1}$。由于估计量是渐近无偏的，因此得出：

\[ \operatorname{mse}[\widehat{\mu}] \simeq \operatorname{var}[\widehat{\mu}] \simeq n^{-1} \boldsymbol{G}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{G} . \]

其次采用受限 MLE。标准条件下 $\widetilde{\mu}$ 具有渐近方差

\[ \boldsymbol{G}^{\prime}\left(\boldsymbol{V}_{\theta}-\boldsymbol{V}_{\theta} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\right)^{-1} \boldsymbol{R} \boldsymbol{V}_{\theta}\right) \boldsymbol{G} . \]

$\widetilde{\mu}$ 也有一个概率限制，例如 $\mu_{R}$，它（通常）与 $\mu$ 不同。我们一起发现

\[ \operatorname{mse}[\widetilde{\mu}] \simeq B+n^{-1} \boldsymbol{G}^{\prime}\left(\boldsymbol{V}_{\theta}-\boldsymbol{V}_{\theta} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\right)^{-1} \boldsymbol{R} \boldsymbol{V}_{\theta}\right) \boldsymbol{G} \]

其中 $B=\left(\mu-\mu_{R}\right)^{2}$.相减，我们发现焦点是

\[ \mathrm{F} \simeq B-n^{-1} \boldsymbol{G}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\right)^{-1} \boldsymbol{R} \boldsymbol{V}_{\theta} \boldsymbol{G} . \]

$B$ 的插件估计器 $\widehat{B}=(\widehat{\mu}-\widetilde{\mu})^{2}$ 有偏差，因为

\[ \begin{aligned} \mathbb{E}[\widehat{B}] &=(\mathbb{E}[\widehat{\mu}-\widetilde{\mu}])^{2}+\operatorname{var}[\widehat{\mu}-\widetilde{\mu}] \\ & \simeq B+\operatorname{var}[\widehat{\mu}]-\operatorname{var}[\widetilde{\mu}] \\ & \simeq B+n^{-1} \boldsymbol{G}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\right)^{-1} \boldsymbol{R}_{\theta} \boldsymbol{G} . \end{aligned} \]

由此可见，$F$ 的近似无偏估计量为

\[ \widehat{B}-2 n^{-1} \boldsymbol{G}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V}_{\theta} \boldsymbol{R}\right)^{-1} \boldsymbol{R} \boldsymbol{V}_{\theta} \boldsymbol{G} . \]

FIC 是通过用估计值替换未知的 $\boldsymbol{G}, \boldsymbol{R}$ 和 $n^{-1} \boldsymbol{V}_{\theta}$ 来获得的。

28.20 最佳子集和逐步回归

假设我们有一组潜在的回归量 $\left\{X_{1}, \ldots, X_{K}\right\}$ 并且我们想要选择回归量的子集用于回归。令 $S_{m}$ 表示回归量的子集，并让 $m=1, \ldots, M$ 表示潜在子集的集合。给定模型选择标准（例如 AIC、Mallows 或 CV），最佳子集模型是最小化 $M$ 模型中的标准的模型。这是通过估计 $M$ 模型并比较模型选择标准来实现的。

如果 $K$ 很小，则比较所有子集模型在计算上是可行的。然而，当 $K$ 很大时，这可能不可行。这是因为潜在子集的数量是 $M=2^{K}$，它随着 $K$ 的增加而快速增加。例如，$K=10$ 意味着 $M=1024, K=20$ 意味着 $M \geq 1,000,000$，$K=40$ 意味着 $M$ 超过一万亿。在这种情况下估计所有子集回归根本没有意义。

如果目标是找到产生最小选择标准的回归器集合，那么我们似乎应该能够以大大降低的计算成本找到回归器的近似集合。实现此目标的一些特定算法称为逐步回归、阶段回归和最小角度回归。这些程序实际上都没有达到最小化任何特定选择标准的目标；相反，它们被视为有用的计算近似值。由于不同的作者似乎对有些不同的实现使用相同的术语，因此还存在一些潜在的混乱。我们在这里使用 Hastie、Tibshirani 和 Friedman (2008) 中描述的术语。

在下面的描述中，我们使用 $\operatorname{SSE}(m)$ 来指代拟合模型的残差平方和，使用 $C(m)$ 来指代用于模型比较的选择标准（最常使用 AIC）。

28.21 向后逐步回归

从“活动集”中包含的所有回归量 $\left\{X_{1}, \ldots, X_{K}\right\}$ 开始。
对于 $m=0, \ldots, K-1$

估计 $Y$ 在活动集上的回归。
确定其遗漏将对 $C(m)$ 影响最小的回归量。
将此回归量放入槽 $K-m$ 中并从活动集中删除。
计算$C(m)$并存储在槽$K-m$中。

$C(m)$ 值最小的模型为所选模型。

向后逐步回归需要 $K<n$，以便所有变量的回归都是可行的。它产生从“最相关”到“最不相关”的回归量排序。一个简化的版本是当 $C(m)$ 增加时退出循环。（这可能不会产生与完成循环相同的结果。）对于 AIC 选择的情况，步骤 (b) 可以通过计算每个主动回归量的经典（同方差）t 比来实现，并找到具有最小绝对值的回归量t 比率。（参见练习 28.3。）

28.22 前向逐步回归

首先将空集 $\{\varnothing\}$ 作为“活动集”，将所有回归量 $\left\{X_{1}, \ldots, X_{K}\right\}$ 作为“非活动集”。
对于 $m=1, \ldots, \min (n-1, K)$

估计 $Y$ 在活动集上的回归。
确定非活动集中的回归量，其包含将对 $C(m)$ 产生最大影响。
将此回归量放入槽 $m$ 中，并将其从非活动集移动到活动集。
计算$C(m)$并存储在槽$m$中。

$C(m)$ 值最小的模型为所选模型。

一个简化的版本是当 $C(m)$ 增加时退出循环。（这可能不会产生与完成循环相同的答案。）对于 AIC 选择的情况，可以通过在非活动集中查找与步骤 (a) 的残差具有最大绝对相关性的回归器来实现步骤 (b)。（参见练习 28.4。）

有组合算法可以检查每一步的向前和向后运动。该算法还可以通过按组组织的回归器来实现（以便在每个步骤中包含或排除所有元素）。还有一些老式版本使用显着性检验而不是选择标准（通常不建议这样做）。

基于老式显着性检验的逐步回归可以在 Stata 中使用 stepwise 命令实现。如果注意力仅限于一次包含一个回归量的模型，则可以通过将显着性水平设置为等于 $p=0.32$ 来实现 AIC 选择。因此，命令stepwise, $\operatorname{pr}$ (.32) 使用AIC 准则实现向后逐步回归，stepwise, pe (.32) 使用AIC 准则实现向前逐步回归。

可以使用 lars 命令在 R 中实现逐步回归。

28.23 模型选择估计量的 MSE

模型选择可能会导致估计器的采样性能较差。在本节中，我们将表明，通过模型选择，估计的均方误差不一定会得到改善，而且可能会大大恶化。

为了简单起见，请考虑具有精确正态分布和已知协方差矩阵的估计器。将后者标准化为我们考虑的设置的身份

\[ \widehat{\theta} \sim \mathrm{N}\left(\theta, I_{K}\right) \]

以及模型选择估计器的类别

\[ \widehat{\theta}_{\mathrm{pms}}=\left\{\begin{array}{lll} \widehat{\theta} & \text { if } & \widehat{\theta}^{\prime} \widehat{\theta}>c \\ 0 & \text { if } & \widehat{\theta}^{\prime} \hat{\theta} \leq c \end{array}\right. \]

对于一些 $c$。 AIC 设置 $c=2 K$、BIC 设置 $c=K \log (n)$ 和 $5 %$ 显着性测试集 $c$ 等于 $\chi_{K}^{2}$ 分布的 $95 %$ 分位数。通常将 $\widehat{\theta}_{\mathrm{pms}}$ 称为模型选择后 (PMS) 估计器

我们可以显式计算 $\widehat{\theta}_{\mathrm{pms}}$ 的 MSE。

定理 28.10 如果 $\widehat{\theta} \sim \mathrm{N}\left(\theta, \boldsymbol{I}_{K}\right)$ 那么

\[ \operatorname{mse}\left[\widehat{\theta}_{\mathrm{pms}}\right]=K+(2 \lambda-K) F_{K+2}(c, \lambda)-\lambda F_{K+4}(c, \lambda) \]

其中 $F_{r}(x, \lambda)$ 是具有 $r$ 自由度和非中心参数 $\lambda=\theta^{\prime} \theta$ 的非中心卡方分布函数。

证明在 $28.32$ 节中给出。

MSE 仅由 $K, \lambda$ 决定，而 $c . \lambda=\theta^{\prime} \theta$ 是 MSE 的重要参数。作为欧几里德长度的平方，它索引了系数 $\theta$ 的大小。

我们可以看到以下限制情况。如果 $\lambda=0$ 则 mse $\left[\widehat{\theta}_{\mathrm{pms}}\right]=K\left(1-F_{K+2}(c, 0)\right)$。作为 $\lambda \rightarrow \infty$ 然后 mse $\left[\widehat{\theta}_{\mathrm{pms}}\right] \rightarrow K$。无限制估计器获得 if $c=0$，在这种情况下获得 mse $\left[\widehat{\theta}_{\mathrm{pms}}\right]=K$。作为 $c \rightarrow \infty$，mse $\left[\widehat{\theta}_{\mathrm{pms}}\right] \rightarrow \lambda$。后一个事实意味着基于 BIC 的 PMS 估计器的 MSE $\rightarrow \infty$ 为 $\lambda=0$。

使用定理 $28.10$ 我们可以数值计算 MSE。在图 28.1(a) 和 (b) 中，我们针对 $\sqrt{\lambda}$ 的一系列值绘制了一组估计量的 MSE。面板 (a) 适用于 $K=1$，面板 (b) 适用于 $K=5$。请注意，未选择的估计器 $\widehat{\theta}$ 的 MSE 对于 $\lambda$ 是不变的，因此它的 MSE 图在 $K$ 处是一条平坦的线。绘制的其他估计量是 AIC 选择 ( $c=2 K$ )、5% 显着性检验选择（卡方临界值）以及 $28.10$ 和 $28.10$ 的 BIC 选择 $(c=K \log (n))$。

在图中，您可以看到，对于 $\lambda<K$，PMS 估计器的 MSE 大致低于未选择的估计器，但对于 $\lambda>K$ 的 MSE 较高。 AIC 估计器的 MSE 与未选择的估计器相比失真最小，对于 $K=1$ 达到约 $1.5$ 的峰值。然而，对于较大的 $\lambda$ 值，BIC 估计量具有非常大的 MSE，并且失真随着 $n$ 的增加而增加。选择估计量的 MSE 随着 $\lambda$ 增加，直到达到峰值，然后缓慢下降并渐近回到 $K$。此外，由于 $n$ 发散，BIC 的 MSE 是无界的。因此，对于非常大的样本量，BIC 选择的估计器的 MSE 可以是未选择的估计器的 MSE 的很大倍数。该图显示，如果 $\lambda<K$ 很小，则模型选择有优势，因为 MSE 可以大大降低。然而，如果 $\lambda<K$ 很大，那么如果使用 BIC，MSE 会大大增加，如果使用 AIC，MSE 会适度增加。对图的合理解读会导致实际建议不要使用 BIC 进行模型选择，并谨慎使用 AIC。

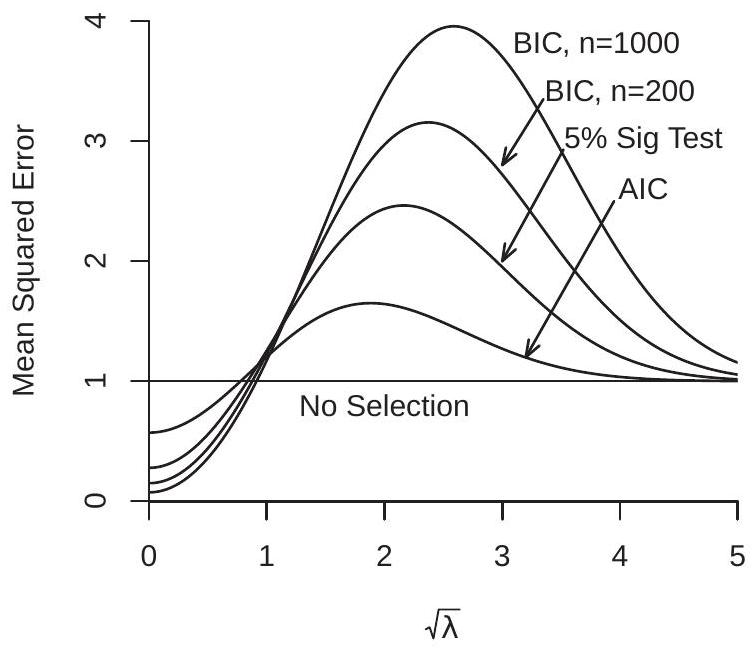
MSE，$K=1$

MSE，$K=5$

图 28.1：模型选择后估计量的 MSE

数值计算表明，当 $\lambda$ 较小时，MSE 会因选择而降低，而当 $\lambda$ 适度较大时，MSE 会增加。这在实践中意味着什么？当 $\theta$ 较小时，$\lambda$ 也较小，这意味着比较模型在估计精度方面相似。在这些情况下，模型选择可能很有价值，因为它有助于选择较小的模型来提高精度。然而，当 $\lambda$ 适度大时（这意味着 $\theta$ 适度大），较小的模型具有有意义的遗漏变量偏差，但选择标准很难检测要使用哪个模型。保守的 BIC 选择程序倾向于选择较小的模型，因此会产生较大的偏差，导致较高的 MSE。这些考虑表明，在选择具有相似估计精度的模型时，最好使用 AIC。不幸的是，不可能先验地知道适当的模型。

本节的结果可能看起来与定理 $28.8$ 相矛盾，该定理表明 BIC 对于简约模型是一致的，因为对于图中的所有 $\lambda>0$ 来说，正确的简约模型是较大的模型。然而，BIC 并未以足够的频率选择该模型来产生低 MSE。这并不矛盾。 BIC 的一致性出现在图的下部，其中 BIC 估计器的 MSE 非常小，并且接近于零（$\lambda \rightarrow 0$）。事实上，AIC 估计器的 MSE 在此区域略高于 BIC 的 MSE，这是由于 AIC 的超选特性造成的。

28.24 模型选择后的推理

经济学家通常对推理问题感兴趣，例如假设检验和置信区间。如果通过 AIC 或 CV 等程序选择了计量经济模型，则应用于所选模型的统计检验的属性是什么？

具体来说，考虑回归模型 $Y=X_{1} \beta_{1}+X_{2} \beta_{2}+e$ 和变量 $X_{2}$ 的选择。也就是说，我们将 $Y=X_{1} \beta_{1}+e$ 与 $Y=X_{1} \beta_{1}+X_{2} \beta_{2}+e$ 进行比较。在这种情况下，在所选模型中对 $\beta_{2}$ 进行常规推理是不合适的，这并不是太深刻的认识。如果我们选择较小的模型，则不会估计 $\beta_{2}$。如果我们选择较大的值，那是因为 $\beta_{2}$ 的 $\mathrm{t}$ 比率超过了临界值。以超过临界值为条件的 t 比分布不是传统分布的，似乎没有必要进一步推动这个问题。

更有趣和微妙的问题是对 $\beta_{1}$ 推理的影响。这确实是一个典型的兴趣背景。一位经济学家对给定一组 $X_{2}$ 控制条件下 $X_{1}$ 对 $Y$ 的影响感兴趣。通常在这些控制中进行选择以找到合适的经验模型。一旦获得这一点，我们就想对 $\beta_{1}$ 做出推理陈述。对控件的选择是否会影响推理？

我们用数字来说明这个问题。假设 $\left(X_{1}, X_{2}\right)$ 是具有单位方差和相关性的联合正态分布，$\rho, e$ 是独立且标准正态分布，并且 $n=30$ 是独立的且标准正态分布。我们单独估计 $Y$ 对 $\left(X_{1}, X_{2}\right)$ 的长回归和 $Y$ 对 $X_{1}$ 的短回归。我们在长回归中为 $\beta_{2}=0$ 构建 t 统计量 ${ }^{3}$，如果 t 统计量在 $\left(X_{1}, X_{2}\right)$ 水平上显着，则选择长回归；如果 $\left(X_{1}, X_{2}\right)$ 统计量不显着，则选择短回归。我们在所选回归中为 $\left(X_{1}, X_{2}\right)$ 构建标准 $\left(X_{1}, X_{2}\right)$ 置信区间 $\left(X_{1}, X_{2}\right)$。当没有选择并且估计模型正确时，这些置信区间将具有精确的 $\left(X_{1}, X_{2}\right)$ 覆盖范围，因此与 $\left(X_{1}, X_{2}\right)$ 的偏差是由于模型选择和错误指定造成的。我们通过使用一百万次重复、不同的 $\left(X_{1}, X_{2}\right)$ 和 $\left(X_{1}, X_{2}\right)$ 进行模拟来计算实际覆盖概率。

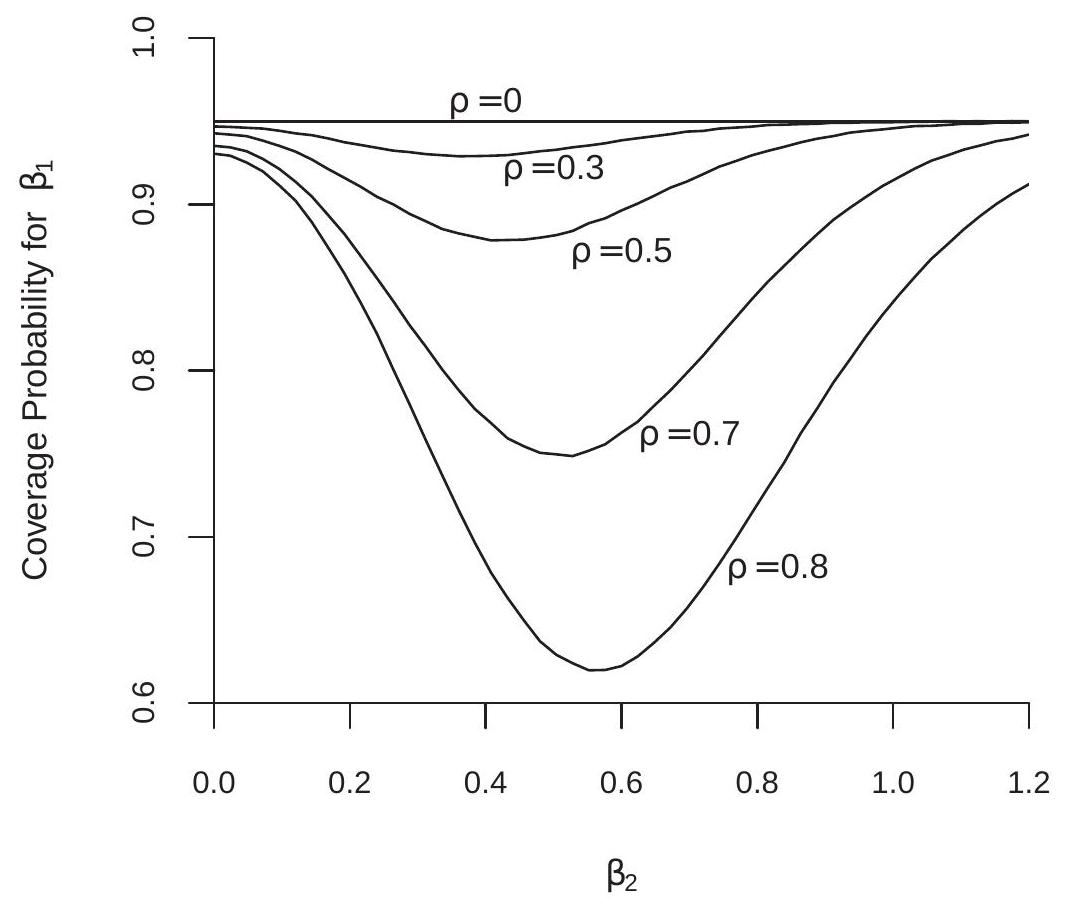
图 28.2：模型选择后的覆盖概率

我们在图 $28.2$ 中显示了 $\rho$ 的多个值的覆盖概率作为 $\beta_{2}$ 的函数。如果

${ }^{3}$ 使用同方差公式并假设误差方差已知。这样做是为了关注选择问题而不是协方差矩阵估计。

${ }^{4}$ 使用同方差公式并假设正确的误差方差已知。

${ }^{5}$ 覆盖概率对于 $\beta_{1}$ 是不变的。回归量与 $(\rho=0)$ 不相关，则实际覆盖概率等于 $0.95$ 的名义水平。这是因为在此正态回归模型中，$\beta_{2}$ 的 t 统计量独立于 $\beta_{1}$ 的 t 统计量，并且短回归和长回归中 $X_{1}$ 的系数相同。

对于 $\rho \neq 0$，这种不变性被打破。随着 $\rho$ 的增加，置信区间的覆盖概率会降至名义水平以下。失真度受 $\beta_{2}$ 值的强烈影响。对于 $\beta_{2}=0$ 来说，失真程度是轻微的。原因是，当 $\beta_{2}=0$ 时，选择 t 统计量以高概率 (95%) 选择短回归，这会导致近似有效的推理。此外，作为 $\beta_{2} \rightarrow \infty$，覆盖概率收敛到名义水平。原因是，对于较大的 $\beta_{2}$，选择 t 统计量以高概率选择长回归，再次导致近似有效的推理。然而，对于 $\beta_{2}$ 的中间值，失真很大。对于 $\rho=0.5$，覆盖概率降至 $\rho \neq 0$，对于 $\rho \neq 0$，覆盖概率低至 $\rho \neq 0$。原因是，对于 $\rho \neq 0$ 的中间值，选择 $\rho \neq 0$ 统计量会选择具有有意义概率的两个模型，并且此选择决策与 $\rho \neq 0$ 的 t 统计量相关。覆盖率不足的程度是巨大的并且非常令人不安。

此显示的消息是模型选择后的推理存在问题。传统的推理过程不具有传统的分布，并且扭曲可能是无限的。

28.25 实证说明

我们通过一个应用来说明模型选择方法。采用 CPS 数据集和具有 $n=1149$ 观察值的亚洲女性子样本。考虑对数工资回归，主要关注以 0 到 30 年经验之间的预期工资之间的百分比差异来衡量的经验回报。我们考虑并比较九种最小二乘回归。所有指标均包括一项已婚指标和三项地区指标。估计模型的复杂性涉及教育和经验的影响。

表 28.1：亚洲女性的经验回归估计

	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9
Return	$13 %$	$22 %$	$20 %$	$29 %$	$40 %$	$37 %$	$33 %$	$47 %$	$45 %$
s.e.	7	8	7	11	11	11	17	18	17
BIC	956	$\mathbf{9 0 7}$	924	964	913	931	977	925	943
AIC	915	861	858	914	858	$\mathbf{8 5 5}$	916	860	857
CV	405	387	386	405	385	$\mathbf{3 8 5}$	406	387	386
FIC	86	48	53	58	$\mathbf{3 2}$	34	86	71	68
Education	College	Spline	Dummy	College	Spline	Dummy	College	Spline	Dummy
Experience	2	2	2	4	4	4	6	6	6

经验条款：

模型1-3包含经验及其平方。
模型 4-6 包括高达 4 次方的经验值。
模型 7-9 包括高达 6 次方的经验值。

教育术语： - 模型 1、4 和 7 包括一个虚拟变量 College，表明受教育年限为 16 或更高。

模型 2、5 和 8 包括 education 中的线性样条，在 education=9 处有一个单结。
模型 3、6 和 9 包括六个虚拟变量，教育程度分别为 12、13、14、16、18 和 20。

表 $28.1$ 报告了九个模型的关键估计。报告的内容包括以工资差异百分比表示的经验回报的估计、其标准误差 (HC1)、BIC、AIC、CV 和 FIC*，后者将经验回报作为重点。我们可以看到，估计值有很大差异，范围从 $13 %$ 到 $47 %$。一些估计值还存在较大的标准误差。（在大多数模型中，经验回报具有“统计显着性”，但通过较大的标准误差，我们意味着很难确定经验回报的精确值。）我们还可以看到，影响幅度的最重要因素点估计的超越了经验的二次规范，也超越了教育的最简单规范。另一个需要注意的事项是标准误差受经验项数量的影响最大。

BIC 选择了一个简约模型，其中教育为线性样条，经验为二次。 AIC 和 CV 选择一个不太节俭的模型，具有完整的虚拟教育规范和 $4^{\text {th }}$ 阶多项式的经验。 FIC 选择一个中间模型，在教育中使用线性样条，在经验中使用 $4^{t h}$ 阶多项式。

当使用信息标准选择模型时，检查几个标准很有用。在应用中，决策应结合判断和正式标准来做出。在这种情况下，交叉验证标准选择具有估计值 $37 %$ 的模型 6，但具有估计值 $20 %$ 和 $45 %$ 的模型 3 和 9 获得了接近相似的 CV 标准值。 FIC 专注于这个特定系数，选择模型 5，其点估计 $40 %$ 与 CV 选择的模型类似。总体而言，基于这一证据，CV 选择的模型及其 $37 %$ 的点估计似乎是一个合适的选择。然而，CV 标准的平坦度所反映的不确定性表明，规格的选择仍然存在不确定性。

28.26 收缩方法

收缩方法是一类广泛的估计器，它通过将估计器 $\hat{\theta}$ 移向预先选定的点（例如零向量）来减少方差。在高维度中，方差的减少足以补偿偏差的增加，从而在均方误差测量时提高效率。本节和接下来的几节回顾了《经济学家的概率与统计》第 15 章中介绍的材料。

对于某些收缩权重 $w \in[0,1]$，最简单的收缩估计器采用 $\widetilde{\theta}=(1-w) \widehat{\theta}$ 的形式。设置 $w=0$ 我们获得 $\widetilde{\theta}=\widehat{\theta}$ （无收缩），设置 $w=1$ 我们获得 $\widetilde{\theta}=0$ （完全收缩）。计算该估计器的 MSE 很简单。假设$\widehat{\theta} \sim(\theta, V)$。那么 $\widetilde{\theta}$ 有偏差

\[ \operatorname{bias}[\widetilde{\theta}]=\mathbb{E}[\widetilde{\theta}]-\theta=-w \theta, \]

方差

\[ \operatorname{var}[\widetilde{\theta}]=(1-w)^{2} \boldsymbol{V}, \]

和加权均方误差（使用权重矩阵 $\boldsymbol{W}=\boldsymbol{V}^{-1}$ ）

\[ \text { wmse }[\widetilde{\theta}]=K(1-w)^{2}+w^{2} \lambda \]

其中 $\lambda=\theta^{\prime} \boldsymbol{V}^{-1} \theta$.定理 28.11 如果 $\widehat{\theta} \sim(\theta, V)$ 和 $\widetilde{\theta}=(1-w) \widehat{\theta}$ 那么

wmse $[\widetilde{\theta}]<$ wmse $[\hat{\theta}]$ 如果 $0<w<2 K /(K+\lambda)$。
wmse $[\widetilde{\theta}]$ 通过收缩权重 $w_{0}=K /(K+\lambda)$ 最小化。
最小化的 WMSE 为 wmse $[\widetilde{\theta}]=K \lambda /(K+\lambda)$。

证明参见练习$28.6$。

定理的第 1 部分表明，对于收缩权重 $w$ 的一系列值，收缩估计器降低了 WMSE。定理的第 2 部分表明，WMSE 最小化收缩权重是 $K$ 和 $\lambda$ 的简单函数。后者是 $\theta$ 相对于估计方差的大小的度量。当 $\lambda$ 很大（系数很大）时，最优收缩权重 $w_{0}$ 很小；当 $\lambda$ 较小（系数较小）时，最佳收缩权重 $w_{0}$ 较大。第 3 部分计算相关的最佳 WMSE。这可能大大小于原始估计器 $\widehat{\theta}$ 的 WMSE。例如，如果 $w$ 则 wmse $w$，即原始估计器的 WMSE 的二分之一。

为了构造最佳收缩权重，我们需要未知的 $\lambda$。无偏估计量是 $\hat{\lambda}=$ $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}-K$ （参见练习 28.7），表示收缩权重

\[ \widehat{w}=\frac{K}{\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}} . \]

将 $K$ 替换为自由参数 $c$ （我们称之为收缩系数），我们得到

\[ \widetilde{\theta}=\left(1-\frac{c}{\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}}\right) \widehat{\theta} . \]

这通常称为斯坦因规则估计器。

该估计器具有许多吸引人的特性。它可以被视为平滑选择估计器。数量 $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}$ 是假设 $\mathbb{H}_{0}: \theta=0$ 的 Wald 统计量。因此，当 Wald 统计量很大时（当证据表明零系数的假设是错误时），收缩估计量接近原始估计量 $\widehat{\theta}$。然而，当 Wald 统计量很小时（当证据与零系数的假设一致时），收缩估计器会将原始估计器移向零。

28.27 James-Stein 收缩估计器

James 和 Stein (1961) 做出了以下发现。

定理28.12 假设$\widehat{\theta} \sim \mathrm{N}(\theta, V), \widetilde{\theta}$ 在(28.25) 中定义，并且$K>2$ 被定义。

如果 $0<c<2(K-2)$ 则 wmse $[\widetilde{\theta}]<$ wmse $[\widehat{\theta}]$。
通过设置 $c=K-2$ 来最小化 WMSE 并等于

\[ \text { wmse }[\widetilde{\theta}]=K-(K-2)^{2} \mathbb{E}\left[Q_{K}^{-1}\right] \]

其中 $Q_{K} \sim \chi_{K}^{2}(\lambda)$.请参阅《经济学家概率与统计》定理 $15.3$。

这一结果震惊了统计界。第 1 部分表明，收缩估计器对于所有参数值都具有严格较小的 WMSE，因此主导了原始估计器。后者是 MLE，因此该结果表明 MLE 占主导地位，因此不可接受。这是一个令人震惊的结果，因为之前人们认为不可能找到一个主导 MLE 的估计器。

定理 $28.12$ 关键取决于条件 $K>2$。这意味着收缩率仅在三维或更大维度上实现均匀改善。

收缩系数 $c=K-2$ 的最小化选择导致了通常所说的 James-Stein 估计量

\[ \widetilde{\theta}=\left(1-\frac{K-2}{\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}}\right) \widehat{\theta} . \]

实际上 $\boldsymbol{V}$ 是未知的，因此我们用估计器 $\widehat{\boldsymbol{V}}$ 代替。这导致

\[ \widetilde{\theta}_{\mathrm{JS}}=\left(1-\frac{K-2}{\widehat{\theta}^{\prime} \widehat{\boldsymbol{V}}^{-1} \widehat{\theta}}\right) \widehat{\theta} \]

这是完全可行的，因为它不依赖于未知数或调整参数。 $\widehat{\boldsymbol{V}}$ 替换 $\boldsymbol{V}$ 可以通过有限样本或渐近参数来证明。

28.28 斯坦因效应的解释

詹姆斯-斯坦定理似乎与经典统计理论相冲突。原始估计器 $\widehat{\theta}$ 是最大似然估计器。它是公正的。它是无偏最小方差。 CramerRao 的效率很高。 James-Stein 收缩估计器如何实现一致更小的均方误差？

部分答案是经典理论有一些警告。例如，克拉默-饶定理将注意力限制在无偏估计量上，从而排除了对收缩估计量的考虑。 James-Stein 估计量降低了 MSE，但不是 Cramer-Rao 有效的，因为它有偏差。因此詹姆斯-斯坦定理与克拉默-拉奥定理并不冲突。相反，它们是互补的结果。一方面，当无偏性是估计的重要属性时，克拉默-饶定理描述了最佳可能的方差。另一方面，詹姆斯-斯坦定理表明，如果无偏性不是关键属性，而是 MSE 很重要，那么就有比 MLE 更好的估计量。

James-Stein 定理似乎也与我们在 $28.16$ 节中的结果相冲突，该结果表明选择估计器并未实现相对于 MLE 的统一 MSE 改进。这可能看起来是冲突，因为 James-Stein 估计器具有与选择估计器类似的形式。不同之处在于选择估计器是硬阈值规则 - 它们是数据的不连续函数 - 而 James-Stein 估计器是软阈值规则 - 它是数据的连续函数。硬阈值往往会导致高方差；软阈值往往会导致低方差。 James-Stein 估计器能够减少方差，因为它是一个软阈值函数。

当 $\lambda$ 很小时，James-Stein 估计器实现的 MSE 改进最大。当参数 $\theta$ 相对于估计方差 $\boldsymbol{V}$ 而言较小时，就会发生这种情况。这意味着用户需要明智地选择中心点。

28.29 正部分估计器

简单的 James-Stein 估计器有一个奇怪的特性，它可以“过度收缩”。当 $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}<K-2$ 时，$\widetilde{\theta}$ 的符号与 $\widehat{\theta}$ 相反。这是没有意义的，表明可以进行进一步的改进。标准解决方案是通过将收缩权重 (28.24) 限制在 0 和 1 之间来使用“正部分”修剪。该估计器可以写为

\[ \begin{aligned} \widetilde{\theta}^{+} &=\left\{\begin{array}{cc} \widetilde{\theta}, & \widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta} \geq K-2 \\ 0, & \widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}<K-2 \end{array}\right.\\ &=\left(1-\frac{K-2}{\hat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}}\right)_{+} \widehat{\theta} \end{aligned} \]

其中 $(a)_{+}=\max [a, 0]$ 是“正部分”函数。或者，它可以写成

\[ \widetilde{\theta}^{+}=\widehat{\theta}-\left(\frac{K-2}{\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}}\right)_{1} \widehat{\theta} \]

其中 $(a)_{1}=\min [a, 1]$

正部分估计器同时执行“选择”和“收缩”。如果 $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}$ 足够小，则 $\widetilde{\theta}^{+}$“选择” 0 。当 $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}$ 大小适中时，$\widetilde{\theta}^{+}$ 将 $\widehat{\theta}$ 缩小到零。当 $\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}$ 非常大时，$\widetilde{\theta}^{+}$ 接近原始估计器 $\widehat{\theta}$。

与我们的直觉一致，正部分估计量的 WMSE 均低于未调整的 James-Stein 估计量。

定理28.13 在定理$28.12$的假设下

\[ \operatorname{wmse}\left[\widetilde{\theta}^{+}\right]<\operatorname{wmse}[\tilde{\theta}] . \]

证明参见《经济学家概率与统计》定理 $15.6$。《经济学家概率与统计》定理 $15.7$ 为正部分估计量提供了 MSE 的明确数值评估。

在图 $28.3$ 中，我们将 wmse $\left[\widetilde{\theta}^{+}\right] / K$ 绘制为 $K=4,6,12$ 和 48 的 $\lambda / K$ 的函数。这些图均低于 1（MLE 的归一化 WMSE），并且对于较小和中等的 $\lambda$ 值来说基本上如此。 WMSE 函数随着 $K$ 的增加而下降，这表明当 $K$ 较大时，MSE 的减少幅度更大。

总之，正部分变换是对未经调整的 James-Stein 估计量的重要改进。更加合理，减少了均方误差。更广泛的信息是，对收缩权重施加边界条件可以提高估计效率。

28.30 向限制收缩

经典的 James-Stein 估计器在应用中没有直接使用，因为我们很少希望将整个参数向量收缩到特定点。相反，更常见的做法是将参数向量缩小到一组限制。这里有一些例子：

将长回归缩小为短回归。

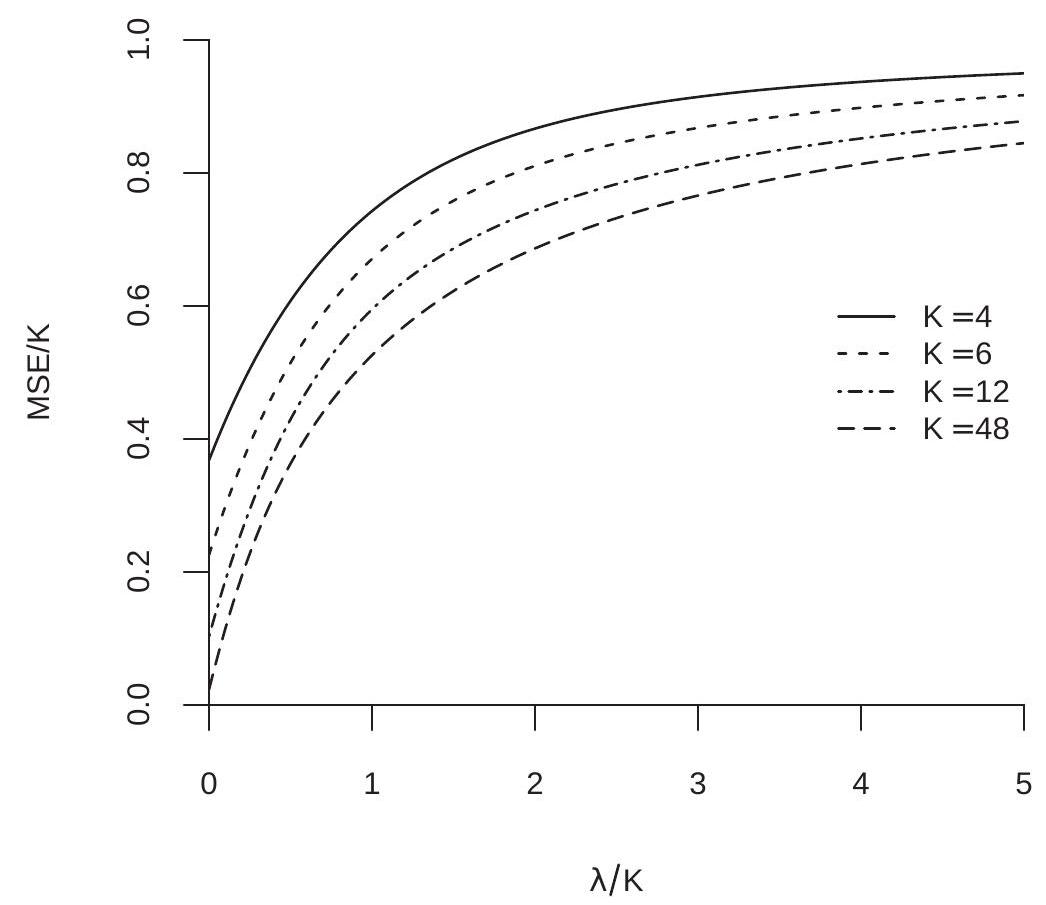
图 28.3：James-Stein 估计器的 WMSE

将回归缩小为仅截距模型。
将回归系数缩小到一组限制条件。
将一组估计值（或系数）缩小到它们的共同平均值。
将一组估计（或系数）缩小为参数模型。
将非参数序列模型缩小为参数模型。

一般思考这些应用的方式是，研究人员希望允许大型模型的通用性，但相信较小的模型可能是一个有用的近似值。收缩估计器允许数据根据两个规格的信息强度在这两个选项之间平滑地进行选择。

令 $\widehat{\theta} \sim \mathrm{N}(\theta, \boldsymbol{V})$ 为原始估计量，例如一组回归系数估计值。正态性假设用于精确理论，但也可以基于渐近近似来证明其合理性。研究人员考虑了一组 $q>2$ 线性限制，可以将其写为 $\boldsymbol{R}^{\prime} \theta=\boldsymbol{r}$，其中 $\boldsymbol{R}$ 是 $K \times q$，$\boldsymbol{r}$ 是 $q \times 1$。 $\theta$ 的最小距离估计器是

\[ \widehat{\theta}_{\boldsymbol{R}}=\widehat{\theta}-\boldsymbol{V} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{V} \boldsymbol{R}\right)^{-1}\left(\boldsymbol{R}^{\prime} \widehat{\theta}-\boldsymbol{r}\right) . \]

具有正部分修剪的 James-Stein 估计量为

\[ \widetilde{\theta}^{+}=\widehat{\theta}-\left(\frac{q-2}{\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right)^{\prime} \boldsymbol{V}^{-1}\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right)}\right)_{1}\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right) . \]

函数 $(a)_{1}=\min [a, 1]$ 将收缩权重限制在 1 以下。

定理28.14 在定理28.12的假设下，如果$q>2$那么

\[ \operatorname{wmse}\left[\widetilde{\theta}^{+}\right]<\operatorname{wmse}[\widetilde{\theta}] . \]

如果限制数量为 3 或更多，则收缩估计器将获得一致较小的 MSE。限制数量 $q$ 与经典 James-Stein 估计器中参数数量 $K$ 的作用相同。当限制 $q$ 更多时，收缩会获得更大的收益，并且当限制接近在总体中得到满足时，收缩会获得更大的收益。如果所施加的限制远未得到满足，则收缩估计器将具有与原始估计器相似的性能。因此，仔细选择限制非常重要。

实际上，协方差矩阵 $\boldsymbol{V}$ 是未知的，因此它被替换为估计器 $\widehat{\boldsymbol{V}}$。因此估计器的可行版本等于

\[ \widehat{\theta}_{\boldsymbol{R}}=\widehat{\theta}-\widehat{\boldsymbol{V}} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \widehat{\boldsymbol{V}} \boldsymbol{R}\right)^{-1}\left(\boldsymbol{R}^{\prime} \widehat{\theta}-\boldsymbol{r}\right) \]

和

\[ \widetilde{\theta}^{+}=\widehat{\theta}-\left(\frac{q-2}{J}\right)_{1}\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right) \]

在哪里

\[ J=\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right)^{\prime} \widehat{\boldsymbol{V}}^{-1}\left(\widehat{\theta}-\widehat{\theta}_{\boldsymbol{R}}\right) . \]

值得注意的是，$J$ 是检验假设 $\mathbb{H}_{0}$ : $\boldsymbol{R}^{\prime} \theta=\boldsymbol{r}$ 与 $\mathbb{H}_{1}: \boldsymbol{R}^{\prime} \theta \neq \boldsymbol{r}$ 的最小距离统计量。因此，收缩程度是标准测试限制的平滑版本。当 $J$ 很大时（因此证据表明限制是错误的），收缩估计器接近无限制估计器 $\widehat{\theta}$。当 $J$ 很小时（因此证据表明限制可能是正确的），收缩估计器等于限制估计器 $\widehat{\theta}_{\boldsymbol{R}}$。对于 $J$ 的中间值，收缩估计器将 $J$ 收缩到 $J$。

我们可以用任何类似的渐近卡方统计量代替 $J$，包括 Wald、似然比和分数统计量。如果乘以 $q$，我们还可以使用 F 统计量（通常由统计软件生成）。这些替换不会产生完全相同的有限样本分布，但渐近等效。

在线性回归中，我们有一些非常方便的简化方法。一般来说，$\widehat{\boldsymbol{V}}$ 可以是异方差稳健或集群稳健协方差矩阵估计器。然而，如果无限制估计器的维度 $K$ 非常大或具有稀疏的虚拟变量，那么这些协方差矩阵估计器的行为就会很差，最好使用经典的协方差矩阵估计器来执行收缩。如果这样做，则 $\widehat{\boldsymbol{V}}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} s^{2}, \widehat{\theta}_{\boldsymbol{R}}$ 是约束最小二乘估计量（在大多数应用中是短回归的最小二乘估计量），而 $J$ 是用于测试限制的传统（同方差）Wald 统计量。我们可以将后者写成F统计量的形式

\[ J=\frac{n\left(\widehat{\sigma}_{R}^{2}-\widehat{\sigma}^{2}\right)}{s^{2}} \]

其中 $\widehat{\sigma}_{R}^{2}$ 和 $\widehat{\sigma}^{2}$ 是受限制和无限制模型的最小二乘误差方差估计量。收缩权重 $\left((q-2) / J_{1}\right.$ 可以从标准回归输出轻松计算出来。

28.31 詹姆斯·斯坦集团

James-Stein 估计器可以应用于参数组（块）。假设我们将参数向量 $\theta=\left(\theta_{1}, \theta_{2}, \ldots, \theta_{G}\right)$ 划分为 $G$ 组，每个组的维度为 $K_{g} \geq 3$。我们有一个带有协方差矩阵 $\boldsymbol{V}$ 的标准估计器 $\widehat{\theta}=\left(\widehat{\theta}_{1}, \widehat{\theta}_{2}, \ldots, \widehat{\theta}_{G}\right)$（例如，最小二乘回归或 MLE）。群 James-Stein 估计量为

\[ \begin{aligned} \widetilde{\theta} &=\left(\widetilde{\theta}_{1}, \widetilde{\theta}_{2}, \ldots, \widetilde{\theta}_{G}\right) \\ \widetilde{\theta}_{g} &=\widehat{\theta}_{g}\left(1-\frac{K_{g}-2}{\hat{\theta}_{g}^{\prime} \boldsymbol{V}_{g}^{-1} \widehat{\theta}_{g}}\right)_{+} \end{aligned} \]

其中 $\boldsymbol{V}_{g}$ 是 $\boldsymbol{V}$ 的 $g^{t h}$ 对角线块。估算器的可行版本将 $\boldsymbol{V}$ 替换为 $\widehat{\boldsymbol{V}}$，将 $\boldsymbol{V}_{g}$ 替换为 $\widehat{V}_{g}$。

James-Stein 群估计器分别缩小每个系数块。相对于经典的 James-Stein 估计器的优点是，这允许收缩权重在不同的块上变化。某些参数块可以使用大量收缩，而其他参数块可以使用最小量。由于使用了正部分修剪，估计器同时执行收缩和选择。影响较小的区块将被缩小至零并被消除。该估计器的缺点是，由于收缩维数减小，收缩带来的好处可能会减少。这些因素之间的权衡将取决于最佳收缩权重在参数之间变化的异质性。

应根据两个标准选择组。首先，应该选择它们，以便各组根据预期的收缩量来分隔变量。因此，预期相对于其估计方差“大”的系数应该被分组在一起，并且预期相对于其估计方差“小”的系数应该被分组在一起。这将使估计的收缩权重根据组的不同而变化。例如，研究人员可能期望多项式回归中的高阶系数相对于其估计方差较小。因此，将多项式变量分为“低阶”和“高阶”是适当的。其次，应选择组，以便研究人员的损失（效用）可以在系数组之间分离。这是因为最优理论（如下所示）依赖于损失是可分离的假设。要理解这些建议的含义，请考虑工资回归。如果我们将教育系数和经验系数用于不同的目的，例如估计教育回报和经验回报，那么我们对教育系数和经验系数的解释是可分离的。在这种情况下，将教育和经验系数分成不同的组是适当的。

对于最优理论，我们定义相对于块对角权重矩阵 $\boldsymbol{W}=\operatorname{diag}\left(\boldsymbol{V}_{1}^{-1}, \ldots, \boldsymbol{V}_{G}^{-1}\right)$ 的加权 MSE

定理 28.15 在定理 28.12 的假设下，如果针对所有 $g=1, \ldots, G$ 的 $\boldsymbol{W}=\operatorname{diag}\left(\boldsymbol{V}_{1}^{-1}, \ldots, \boldsymbol{V}_{G}^{-1}\right)$ 和 $K_{g}>2$ 定义 WMSE，则

\[ \operatorname{wmse}[\widetilde{\theta}]<\operatorname{wmse}[\widehat{\theta}] \text {. } \]

该证明是经典詹姆斯-斯坦理论的简单扩展。 $W$ 的块对角线结构意味着 WMSE 是各组 WMSE 之和。经典的 James-Stein 理论可以应用于每个组，发现 WMSE 通过逐组收缩而降低。因此，总 WMSE 因收缩而降低。

28.32 实证例证

我们通过三个实证应用来说明詹姆斯-斯坦收缩。

第一个应用是第 28.18 节中使用的样本，即 CPS 数据集，其子样本为亚洲女性 ( $n=1149$ )，重点关注回归经验概况。我们考虑模型 9（经验中的 $6^{t h}$ 阶多项式）向模型 3（经验中的 $2^{\text {nd }}$ 阶多项式）的收缩。估计系数的数量差异为 4 。我们将 $\widehat{\boldsymbol{V}}$ 设置为等于 $\mathrm{HCl}$ 协方差矩阵估计器。经验确定的收缩权重为 $0.46$，这意味着斯坦因规则估计量大约是两个模型估计值的相等加权平均值。估计的经验概况如图 28.4(a) 所示。

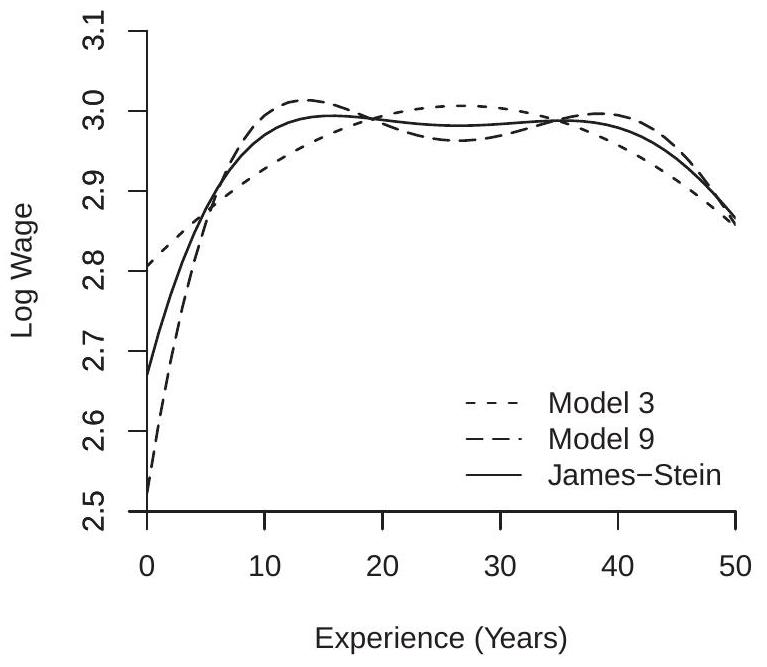
经验简介

企业效应

图 28.4：收缩图解

两个最小二乘估计在视觉上是不同的。 $6^{t h}$ 阶多项式（模型 9）显示前 10 年的经验急剧回归，然后长达 40 年的经验曲线不稳定，并在此之后下降。它还显示出大约 25 年的下降。二次规范忽略了其中一些特征。 James-Stein 估计量本质上是两个轮廓的平均值。它保留了四次规范的大部分功能，只是它消除了 25 年以来毫无吸引力的下降。

第二个应用是第 17 章中使用的 Invest1993 数据集。这是企业投资决策年度观察的面板数据集。我们关注公司特定的影响。这些在研究公司异质性时很有趣，并且对于特定公司的预测也很重要。当每个公司的时间序列观察数量很少时，准确估计公司效应是具有挑战性的。

为了保持分析的重点，我们将注意力限制在纽约证券交易所或美国证券交易所交易的公司以及样本的最后十年（1982-1991）。由于回归量是滞后的，这意味着每个公司最多有九个时间序列观察值。该样本总共有 $N=786$ 个公司和 $n=5692$ 个观测值用于估计。我们的基线模型是双向固定效应线性回归，如表 17.2 第四列所示。我们的受限模型用 19 个行业特定的虚拟变量取代了公司固定效应。这与表 $17.2$ 的第一列类似，只是省略了交易虚拟变量并添加了时间虚拟变量。因此，斯坦因规则估计器将固定效应模型缩小为行业效应模型。如果大多数固定效应是由行业而不是公司特定的变化来解释的，那么后者会表现得很好。

由于无限制模型中存在大量估计系数，我们使用同方差权重矩阵作为简化。这允许使用统计量 $J$ 的简单公式 (28.28) 来计算收缩权重。异方差协方差矩阵不合适，并且由于稀疏虚拟规范，集群鲁棒协方差矩阵将不可靠。

经验确定的收缩权重为 $0.35$，这意味着斯坦因规则估计器对行业效应规范赋予约 $1 / 3$ 权重，对公司特定规范赋予 $2 / 3$ 权重。

为了报告我们的结果，我们重点关注公司特定效应的分布。对于固定效应模型，这些是估计的固定效应。对于行业效应模型，这些是估计的行业虚拟系数（针对每个公司）。对于斯坦因规则估计，它们是两者的加权平均值。我们通过固定效应和斯坦因规则估计量来估计 ${ }^{6}$ 估计的公司特定效应的密度，并将它们绘制在图 28.4(b) 中。

您可以看到，公司特定密度的固定效应估计更加分散，而 Stein 估计量则更加尖锐且更加尖峰，这表明固定效应估计量比 Stein 估计量归因于公司特定因素的更多变化。 Stein 估计器将固定效应拉向其共同平均值，并根据其估计来调整随机性。我们的预期是，斯坦因估计如果用于特定公司预测等应用，将会更加准确，因为相对于固定效应估计，它们的方差会减少。

第三个应用程序使用带有黑人子样本的 CPS 数据集（ $n=2413)$ 重点关注美国各地区（东北部、中西部、南部、西部）的教育回报率。假设要求您灵活估计黑人男性的教育回报率允许教育回报因地区而异。鉴于 $28.18$ 节中的模型选择信息，模型 6 的自然基线被增强，以允许不同地区之间存在更大的差异。灵活的规范将六个教育虚拟变量与四个区域相互作用dummies（省略截距），增加了 18 个系数，并允许教育回报在每个地区不受限制地变化。

按地区划分的教育回报的最小二乘估计如图 28.5(a) 所示。为简单起见，我们将省略的教育群体（教育程度低于 12 年）合并为“11 年”。由于样本较小，估计值显得嘈杂。我们可以看到的一个特征是，这四条线在 12 到 18 岁之间的教育年限中相互追踪。也就是说，它们在教育年限中大致呈线性，具有相同的斜率但截距不同。

为了提高估计的精度，我们将四个配置文件缩小为模型 6。这意味着我们不是在缩小彼此的轮廓，而是在缩小具有相同教育效果但针对特定区域的截距的模型。我们再次使用 HCl 协方差矩阵估计。限制数量为 18 。经验确定的收缩权重为 $0.49$，这意味着斯坦因规则估计器对两个模型赋予相同的权重。

斯坦因规则估计如图 28.5(b) 所示。估计值比面板 (a) 的噪声要小，并且更容易看到模式。这四条线相互跟踪，并且在 1218 年内近似呈线性。在 20 年的教育中，这四条线分散，这似乎可能是由于样本较小。在面板 (b) 中，更容易看到跨区域的模式。看来东北地区的工资最高（以教育程度为条件），而西部地区的工资最低。这个排名对于几乎所有级别的教育都是不变的。

虽然斯坦因规则估计将非参数估计缩小到共同教育因素规范，但它并不强加后者的规范。斯坦因规则估计器能够

${ }^{6}$ 使用共同的带宽来估计两种密度以帮助比较。选择带宽是为了在为两个样本选择的带宽之间进行折衷。

最小二乘估计

斯坦因规则估计

图 28.5：各地区教育概况的斯坦因规则估计

对公因子模型赋予接近于零的权重。事实上，估计对两个模型都赋予 $1 / 2$ 权重，这是斯坦因规则选择的选择，并且是数据驱动的。

这三个应用程序传达的信息是，詹姆斯-斯坦收缩方法可以建设性地用于减少经济应用中的估计方差。这些应用说明了潜在应用的常见形式：将灵活的规范缩减为更简单的规范；将异质估计缩减为同质估计；固定效应对群体虚拟估计的缩小。这三个应用程序还采用了中等大的样本量（ $n=1149,2413$ 和 5692 ），但发现收缩权重接近 $50 %$ 。这表明斯坦因收缩的好处并不局限于“小”样品，而是可以建设性地用于结构复杂的中等大样品。

28.33 模型平均

回想一下，模型选择的问题是如何从一组通用模型中选择单个模型。 James-Stein 收缩估计器通过取两个估计器的加权平均值在两个嵌套模型之间进行平滑。更一般地，我们可以取任意数量估计量的平均值。这些估计量称为模型平均估计量。估计的关键问题是如何选择平均权重。

假设我们有一组 $M$ 模型 $\overline{\mathscr{M}}=\left\{\mathcal{M}_{1}, \ldots, \mathcal{M}_{M}\right\}$。对于每个模型，都有一个参数 $\theta$ 的估计器 $\widehat{\theta}_{m}$。考虑多个模型、参数和估计器的自然方法与模型选择相同。所有模型都是通用超集（重叠）模型的子集，该模型包含所有子模型作为特殊情况。

对应于模型集我们引入一组权重$w=\left\{w_{1}, \ldots, w_{M}\right\}$。通常将权重限制为非负并将总和限制为 1。这些权重的集合称为 $\mathbb{R}^{M}$ 概率单纯形。定义 28.4 概率单纯形。向量集 $\mathscr{S} \subset \mathbb{R}^{M}$ 使得 $\sum_{m=1}^{M} w_{m}=1$ 和 $w_{i} \geq 1$ 对应于 $i=1, \ldots, M$。

$\mathbb{R}^{2}$ 和 $\mathbb{R}^{3}$ 中的概率单纯形如图 $28.6$ 的两个面板所示。 $\mathbb{R}^{2}$ 中的单纯形（图 (a)）是顶点 $(1,0)$ 和 $(0,1)$ 之间的线。示例元素是由点 $w$ 指示的点 $(.7, .3)$。这是权重向量，它将权重 $0.7$ 放在模型 1 上，将权重 $\mathbb{R}^{2}$ 放在模型 2 上。顶点 $\mathbb{R}^{2}$ 是将所有权重放在模型 1 上的权重向量，对应于模型选择，类似地，顶点 $\mathbb{R}^{2}$ 是将所有权重放在模型 2 上的权重向量。

$\mathbb{R}^{3}$ 中的单纯形（图 (b)）是 $(1,0,0),(0,1,0)$ 和 $(0,0,1)$ 之间形成的等边三角形。一个示例元素是由桥 $w$ 指示的点 $(.1, .5, .4)$。边缘是权重向量，是三个模型中两个模型之间的平均值。例如，底部边缘是权重向量，它将权重分配在模型 1 和 2 之间，不对模型 3 施加权重。顶点是将所有权重放在三个模型之一上的权重向量，并对应于模型选择。\

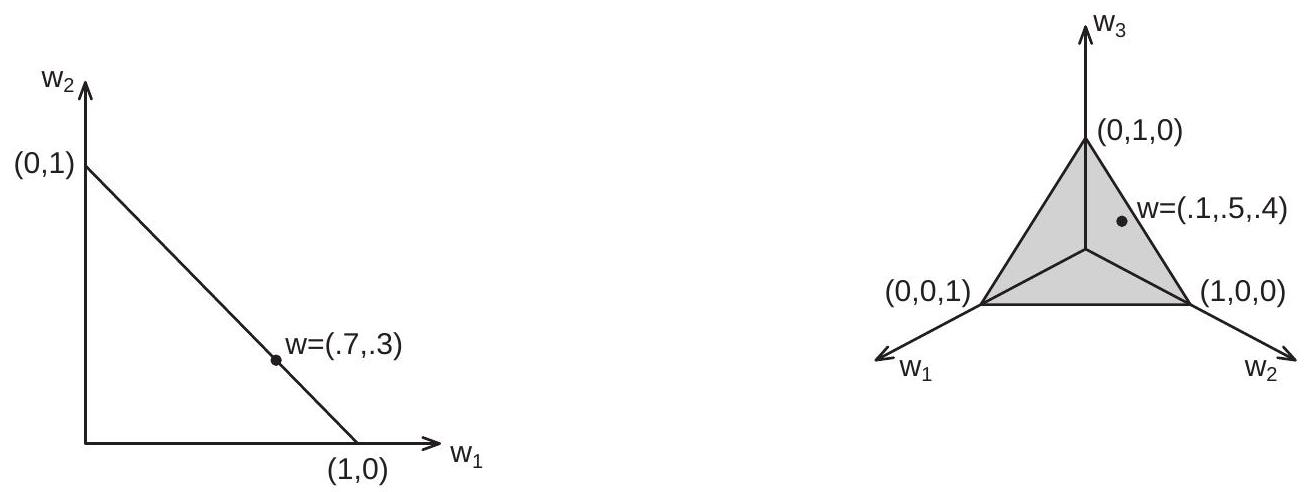
图 28.6：$\mathbb{R}^{2}$ 和 $\mathbb{R}^{3}$ 中的概率单纯形

由于概率单纯形上的权重之和为 1，因此另一种表示方法是通过替换来消除一个权重。因此，我们可以设置 $w_{M}=1-\sum_{m=1}^{M-1} w_{m}$ 并定义位于 $\mathbb{R}^{M-1}$ 单位单纯形中的向量集 $w=\left\{w_{1}, \ldots, w_{M-1}\right\}$，该单位单纯形是由概率单纯形和原点包围的区域。

给定一个权重向量，我们定义平均估计器

\[ \widehat{\theta}(w)=\sum_{m=1}^{M} w_{m} \widehat{\theta}_{m} . \]

选择估计器作为权重向量 $w$ 是单位向量的特殊情况出现，例如图 28.6 中的顶点。

不一定有必要将平均估计器的权重向量限制在概率单纯形 $\mathscr{S}$ 中，但在大多数情况下，这是一个可以提高性能的合理限制。例如，未调整的 James-Stein 估计器是一种平均估计器，它不强制权重的非负性。然而，正部分版本强加了非负性并因此实现了 MSE 的降低。

在 $28.19$ 节和定理 $28.11$ 中，我们探索了简单收缩估计器的 MSE，它将无限制估计器收缩到零向量。这与模型平均估计器相同，其中两个估计器之一是零向量。在定理 $28.11$ 中，我们表明最优收缩（模型平均）估计器的 MSE 小于无限制估计器。该结果扩展到任意数量的估计器之间求平均的情况。最佳平均估计器的 MSE 小于任何给定样本中完整模型的估计器的 MSE。

然而，最佳平均权重是未知的。已经提出了多种方法来选择平均权重。

一种简单的方法是等权重。这是通过设置 $w_{m}=1 / M$ 和估计器中的结果来实现的

\[ \widehat{\theta}^{*}=\frac{1}{M} \sum_{m=1}^{M} \widehat{\theta}_{m} . \]

等权的优点是简单、易于激励、权重估计不会引入随机性。因为权重是固定的，所以可以计算等权估计量的方差。另一个重要的优点是，可以在不知道如何构建基于经验的权重的情况下构建估计器，例如对来自完全不同的概率族的模型进行平均时。等权重的缺点是该方法可能对所考虑的模型集敏感，不能保证估计器的性能优于无限制的估计器，并且样本信息的使用效率低下。在实践中，等权重最好用在模型集已经过预先筛选的情况下，以便所有模型都被认为是“合理的”模型。从计量经济学方法论的角度来看，等权重不是一种正确的统计方法，因为它是一种不完整的方法论。

尽管存在这些担忧，但在为非技术受众总结信息时，可以建设性地采用同等权重。相关上下文是指您通常使用不同的假设做出少量合理但不同的估计。提出不同的估计是为了说明可能结果的范围以及代表“共识”或“推荐”估计的平均值。

如上所述，已经提出了多种方法来选择平均权重。在以下部分中，我们概述了四种流行的方法：平滑 BIC、平滑 AIC、Mallows 平均和 Jackknife 平均。

28.34 平滑的 BIC 和 AIC

回想一下，施瓦茨定理 $28.1$ 指出，对于概率模型 $f(y, \theta)$ 和扩散先验，边际似然 $p(Y)$ 满足

\[ -2 \log p(Y) \simeq-2 \ell_{n}(\widehat{\theta})+K \log (n)=\mathrm{BIC} . \]

这被解释为意味着右侧值最高的模型大约具有最高的边际似然，因此是成为真实模型的概率最高的模型。

对施瓦茨的结果还有另一种解释。边际似然与模型正确的概率大致成正比，以数据为条件。施瓦茨定理意味着这大约是

\[ p(Y) \simeq \exp (-\mathrm{BIC} / 2) \]

这是 BIC 的简单指数变换。通过设置与此变换成比例的模型权重可以实现后验概率加权。这些称为 BIC 权重，并生成平滑的 BIC 估计器。

为了完整地描述该方法，我们有一组模型 $\overline{\mathscr{M}}=\left\{\mathscr{M}_{1}, \ldots, \mathscr{M}_{M}\right\}$。每个模型 $f_{m}\left(y, \theta_{m}\right)$ 都依赖于通过最大似然估计的 $K_{m} \times 1$ 参数向量 $\theta_{m}$。最大似然值为 $L_{m}\left(\widehat{\theta}_{m}\right)=f_{m}\left(Y, \widehat{\theta}_{m}\right)$。模型 $m$ 的 BIC 是 $\operatorname{BIC}_{m}=-2 \log L_{m}\left(\widehat{\theta}_{m}\right)+K_{m} \log (n)$。

$\mathrm{BIC}$ 权重是

\[ w_{m}=\frac{\exp \left(-\mathrm{BIC}_{m} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\mathrm{BIC}_{j} / 2\right)} . \]

BIC 权重的一些属性如下。它们是非负的，因此所有模型都会获得正权重。一些模型可以接收任意接近于零的权重，并且实际上许多估计模型可能接收到基本上为零的 BIC 权重。 BIC选择的模型接收最大权重，BIC值接近最小的模型接收最接近最大权重的模型。 $\mathrm{BIC}$ 不接近最小权重的模型接近于零。

平滑 BIC (SBIC) 估计量为

\[ \widehat{\theta}_{\text {sbic }}=\sum_{m=1}^{M} w_{m} \widehat{\theta}_{m} . \]

SBIC 估计器是比 BIC 选择更平滑的数据函数，因为模型之间不存在不连续跳跃。

平滑 BIC 权重和估计器的优点是它可用于组合来自不同概率族的模型。对于 BIC，重要的是所有模型都在同一样本上进行估计。在组合来自不同概率族的模型时，将完整公式用于 BIC（不遗漏常数）也很重要。

在计算上，最好使用所谓的“BIC 差异”而不是 BIC 的实际值来实现平滑的 BIC，因为所编写的公式可能会产生数值溢出问题。困难在于公式中的求幂。这个问题可以通过如下方式消除。让

\[ \mathrm{BIC}^{*}=\min _{1 \leq m \leq M} \mathrm{BIC}_{m} \]

表示模型中最低的 BIC 并定义 BIC 差异

\[ \Delta \mathrm{BIC}_{m}=\mathrm{BIC}_{m}-\mathrm{BIC}^{*} . \]

然后

\[ \begin{aligned} w_{m} &=\frac{\exp \left(-\mathrm{BIC}_{m} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\mathrm{BIC}_{j} / 2\right)} \\ &=\frac{\exp \left(-\mathrm{BIC}_{m} / 2\right) \exp \left(\mathrm{BIC}^{*} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\mathrm{BIC}_{j} / 2\right) \exp \left(\mathrm{BIC}^{*} / 2\right)} \\ &=\frac{\exp \left(-\Delta \mathrm{BIC}_{m} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\Delta \mathrm{BIC}_{j} / 2\right)} . \end{aligned} \]

因此，无论是在 $\mathrm{BIC}_{m}$ 还是 $\Delta \mathrm{BIC}_{m}$ 上计算，权重在代数上都是相同的。由于 $\Delta \mathrm{BIC}_{m}$ 的量级小于 $\mathrm{BIC}_{m}$，因此不太可能发生溢出问题。

由于指数的属性，如果 $\Delta \mathrm{BIC}_{m} \geq 10$ 则 $w_{m} \leq 0.01$。因此，平滑的 BIC 通常将权重集中在 BIC 值接近最小值的模型上。这意味着在实践中，平滑的 BIC 会对少数模型施加有效的非零权重。 Burnham 和 Anderson（1998）遵循 Akaike 提出的建议，即如果我们对 AIC 进行与 BIC 相同的变换以获得平滑的 BIC 权重，我们就可以获得模型的频率近似概率。具体来说，他们提出了 AIC 权重

\[ w_{m}=\frac{\exp \left(-\mathrm{AIC}_{m} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\mathrm{AIC}_{j} / 2\right)} . \]

他们没有为这种特定的变换选择提供强有力的理论依据，但考虑到平滑的 BIC 公式，这似乎很自然，并且在模拟中效果很好。

AIC 权重的代数性质与 BIC 权重的代数性质相似。所有模型都收到正权重，尽管有些模型收到的权重任意接近于零。 AIC 最小的模型获得最大的 AIC 权重，AIC 值相似的模型获得相似的 AIC 权重。

在计算上，AIC 权重应使用 AIC 差值来计算。定义

\[ \begin{aligned} \mathrm{AIC}^{*} &=\min _{1 \leq m \leq M} \mathrm{AIC}_{m} \\ \Delta \mathrm{AIC}_{m} &=\mathrm{AIC}_{m}-\mathrm{AIC}^{*} . \end{aligned} \]

AIC 权重在代数上相等

\[ w_{m}=\frac{\exp \left(-\Delta \mathrm{AIC}_{m} \mathrm{AIC}_{m} / 2\right)}{\sum_{j=1}^{M} \exp \left(-\Delta \mathrm{AIC}_{j} / 2\right)} . \]

至于 BIC 权重 $w_{m} \leq 0.01$ if $\Delta \mathrm{AIC}_{m} \geq 10$，因此 AIC 权重将集中在 AIC 值接近最小值的模型上。然而，在实践中，AIC 标准的集中程度普遍低于 BIC 标准，因为 AIC 对大处罚的处罚较小。 AIC 权重往往比相应的 BIC 权重更分散在模型中。

平滑 AIC (SAIC) 估计量为

\[ \widehat{\theta}_{\text {saic }}=\sum_{m=1}^{M} w_{m} \widehat{\theta}_{m} . \]

SAIC 估计器是比 AIC 选择更平滑的数据函数。

回想一下，AIC 选择和 BIC 选择都是模型选择一致的，因为随着样本量变大，所选模型是真实模型的概率任意接近 1。此外，BIC 对于简约模型是一致的，而 AIC 渐近过度选择。

这些属性延伸至SBIC 和SAIC。在大样本中，SAIC 和 SBIC 权重将仅集中于真实模型；不正确模型的权重将逐渐接近于零。然而，SAIC 将渐近地将权重分散到简约真实模型和过度参数化真实模型上，而 SBIC 渐近地将权重仅集中在简约真实模型上。

平滑估计量的一个有趣的特性是可以在等拟合简约模型中渐近分布权重。假设我们有两个非嵌套模型，它们具有相同数量的参数和相同的 KLIC 值，因此它们是相等的近似值。在大样本中，SBIC 和 SAIC 都将是两个估计量的加权平均值，而不是简单地选择两者之一。

28.35 Mallows 模型平均

在线性回归中，Mallows 准则 (28.14) 直接应用于模型平均估计器 (28.29)。同方差回归模型为

\[ \begin{aligned} Y &=m+e \\ m &=m(X) \\ \mathbb{E}[e \mid X] &=0 \\ \mathbb{E}\left[e^{2} \mid X\right] &=\sigma^{2} . \end{aligned} \]

假设 $m(X)$ 有 $M$ 模型，每个模型对于某个 $K_{m} \times 1$ 回归向量 $X_{m}$ 都采用 $\beta_{m}^{\prime} X_{m}$ 的形式。系数的 $m^{t h}$ 模型估计量为 $\widehat{\beta}_{m}=\left(\boldsymbol{X}_{m}^{\prime} \boldsymbol{X}_{m}\right)^{-1} \boldsymbol{X}_{m}^{\prime} \boldsymbol{Y}$，向量 $\boldsymbol{m}$ 的估计量为 $\widehat{\boldsymbol{m}}_{m}=\boldsymbol{P}_{m} \boldsymbol{Y}$，其中 $M$。对应的残差向量是$M$$M$。

固定权重的模型平均估计量为

\[ \widehat{\boldsymbol{m}}_{m}(w)=\sum_{m=1}^{M} w_{m} \boldsymbol{P}_{m} \boldsymbol{Y}=\boldsymbol{P}(w) \boldsymbol{Y} \]

在哪里

\[ \boldsymbol{P}(w)=\sum_{m=1}^{M} w_{m} \boldsymbol{P}_{m} . \]

模型平均残差为

\[ \widehat{\boldsymbol{e}}(w)=\left(\boldsymbol{I}_{n}-\boldsymbol{P}(w)\right) \boldsymbol{Y}=\sum_{m=1}^{M} w_{m}\left(\boldsymbol{I}_{n}-\boldsymbol{P}_{m}\right) \boldsymbol{Y} . \]

估计器 $\widehat{\boldsymbol{m}}_{m}(w)$ 在 $\boldsymbol{Y}$ 中是线性的，因此可以应用 Mallows 准则。它等于

\[ \begin{aligned} C(w) &=\widehat{\boldsymbol{e}}(w)^{\prime} \widehat{\boldsymbol{e}}(w)+2 \widetilde{\sigma}^{2} \operatorname{tr}(\boldsymbol{P}(w)) \\ &=\widehat{\boldsymbol{e}}(w)^{\prime} \widehat{\boldsymbol{e}}(w)+2 \widetilde{\sigma}^{2} \sum_{m=1}^{M} w_{m} K_{m} \end{aligned} \]

其中 $\widetilde{\sigma}^{2}$ 是 $\sigma^{2}$ 的初步 ${ }^{7}$ 估计器。

在模型选择的情况下，马洛斯惩罚与估计系数的数量成正比。在模型平均情况下，Mallows 罚分是估计系数的平均数。

Mallows 选择的权重向量是最小化 Mallows 准则的权重向量。它等于

\[ \widehat{w}_{\mathrm{mma}}=\underset{w \in \mathscr{S}}{\operatorname{argmin}} C(w) . \]

从计算角度来看，观察 $C(w)$ 是 $w$ 中的二次函数是有用的。事实上，通过定义残差向量的 $n \times M$ 矩阵 $\widehat{\boldsymbol{E}}=\left[\widehat{\boldsymbol{e}}_{1}, \ldots, \widehat{\boldsymbol{e}}_{M}\right]$ 和 $M \times 1$ 向量 $\boldsymbol{K}=\left[K_{1}, \ldots, K_{M}\right]$，标准是

\[ C(w)=w^{\prime} \widehat{\boldsymbol{E}}^{\prime} \widehat{\boldsymbol{E}} w+2 \widetilde{\sigma}^{2} \boldsymbol{K}^{\prime} w . \]

概率单纯形 $\mathscr{S}$ 由一个等式和 $2 M$ 不等式约束定义。最小化问题 (28.30) 属于二次规划的范畴，这意味着优化

${ }^{7}$ 通常使用来自最大模型的偏差校正最小二乘方差估计器。二次受线性等式和不等式约束。这是数值优化的一个经过深入研究的领域，数值解被广泛使用。在 R 中，使用quadprog 包中的命令solve.QP。在 MATLAB 中使用命令quadprog。

图 $28.7$ 说明了 Mallows 权重计算问题。显示的是 $\mathbb{R}^{3}$ 中的概率单纯形 $\mathscr{S}$。轴是权重向量。椭圆是无约束误差平方和的轮廓，作为投影到约束集 $\sum_{m=1}^{M} w_{m}=1$ 上的权重向量的函数。这是 $\mathbb{R}^{3}$ 中概率单纯形作为二维平面的扩展。轮廓的中点是最小化权重向量，允许权重超出 $[0,1]$。最低轮廓椭圆与概率单纯形相交的点是解 (28.30)，即 Mallows 选择的权重向量。左侧面板中显示的示例中，解为顶点 $(0,1,0)$，因此所选权重向量将所有权重放在模型 2 上。右侧面板中显示的示例中，解位于 $(1,0,0)$ 和 $ 之间的边缘上matheq9$，这意味着所选权重向量对模型 1 和 3 进行平均，但不对模型 2 赋予权重。由于轮廓集是椭圆形且约束集是单纯形，因此解点往往位于边和顶点上，这意味着某些模型接收零重量。事实上，在存在大量模型的情况下，解决方案的一般特征是大多数模型的权重为零；选定的权重向量对合格模型的一小部分赋予正权重。\

图 28.7：锦葵权重选择

获得权重 $\widehat{w}$ 后，通过使用权重对模型估计 $\widehat{\beta}_{m}$ 进行平均来找到系数的模型平均估计器。

在两个嵌套模型的特殊情况下，Mallows 准则可以写为

\[ \begin{aligned} C(w) &=(w, 1-w)\left(\begin{array}{cc} \widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{1} & \widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{2} \\ \widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{1} & \widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2} \end{array}\right)\left(\begin{array}{c} w \\ 1-w \end{array}\right)+2 \widetilde{\sigma}^{2}\left(w K_{1}+(1-w) K_{2}\right) \\ &=(w, 1-w)\left(\begin{array}{ll} \widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{1} & \widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2} \\ \widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2} & \widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2} \end{array}\right)\left(\begin{array}{c} 1-w \\ w \end{array}\right)+2 \widetilde{\sigma}^{2}\left(w K_{1}+(1-w) K_{2}\right) \\ &=w^{2}\left(\widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{1}-\widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2}\right)+\widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2}-2 \widetilde{\sigma}^{2}\left(K_{2}-K_{1}\right) w+2 \widetilde{\sigma}^{2} \end{aligned} \]

我们假设 $K_{1}<K_{2}$ 以便 $\widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{2}=\boldsymbol{Y}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{P}_{1}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{P}_{2}\right) \boldsymbol{Y}=\boldsymbol{Y}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{P}_{2}\right) \boldsymbol{Y}=\widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2}$。该标准的最小值是

\[ \widehat{w}=\left(\frac{\widetilde{\sigma}^{2}\left(K_{2}-K_{1}\right)}{\widehat{\boldsymbol{e}}_{1}^{\prime} \widehat{\boldsymbol{e}}_{1}-\widehat{\boldsymbol{e}}_{2}^{\prime} \widehat{\boldsymbol{e}}_{2}}\right)_{1} . \]

这与斯坦因规则权重 (28.27) 相同，但收缩常数略有不同。因此 $M=2$ 的 Mallows 平均估计器是斯坦因规则估计器。因此，对于 $M>2$，Mallows 平均估计器是 James-Stein 估计器对多个模型的推广。

基于后一种观察，B. E. Hansen (2014) 表明，当模型是嵌套线性回归、误差同方差且模型相距 4 个或更大系数时，MMA 估计器的 WMSE 低于无限制最小二乘估计器。后一个条件类似于斯坦因规则理论中的改进条件。

B. E. Hansen (2007) 表明，MMA 估计量在类似条件下使用 Li (1987) 的理论渐近地实现了与不可行的最优最佳加权平均相同的 MSE。这表明使用模型选择工具来选择平均权重对于回归拟合和点预测是渐近最优的。

28.36 Jackknife (CV) 模型平均

Mallows 选择的缺点是该标准仅在误差条件同方差时才有效。相反，通过交叉验证进行选择不需要同方差。因此，使用交叉验证而不是 Mallows 来选择权重向量似乎是明智的。事实证明，这是一个简单的扩展，具有出色的有限样本性能。在机器学习文献中，这种方法称为堆叠。

拟合平均回归（具有固定权重）可以写为

\[ Y_{i}=\sum_{m=1}^{M} w_{m} X_{m i}^{\prime} \widehat{\beta}_{m}+\widehat{e}_{i}(w) \]

其中 $\widehat{\beta}_{m}$ 是模型 $m$ 的最小二乘系数估计值。相应的留一方程为

\[ Y_{i}=\sum_{m=1}^{M} w_{m} X_{m i}^{\prime} \widehat{\beta}_{m,(-i)}+\widetilde{e}_{i}(w) \]

其中 $\widehat{\beta}_{m,(-i)}$ 是删除观测值 $i$ 时模型 $m$ 的最小二乘系数估计值。留一预测误差满足简单关系

\[ \widetilde{e}_{i}(w)=\sum_{m=1}^{M} w_{m} \widetilde{e}_{m i} \]

其中 $\widetilde{e}_{m i}$ 是模型 $m$ 的留一预测误差。采用矩阵表示法 $\widetilde{\boldsymbol{e}}(w)=\widetilde{\boldsymbol{E}} w$，其中 $\widetilde{\boldsymbol{E}}$ 是留一预测误差的 $n \times M$ 矩阵。

这意味着方差的折刀估计（或等效的交叉验证标准）等于

\[ \mathrm{CV}(w)=w^{\prime} \widetilde{\boldsymbol{E}}^{\prime} \widetilde{\boldsymbol{E}} w \]

这是权重向量的二次函数。权重向量的交叉验证选择是最小化

\[ \widehat{w}_{\mathrm{jma}}=\underset{w \in \mathscr{S}}{\operatorname{argmin}} \mathrm{CV}(w) . \]

给定权重，可以通过使用权重向量 $\widehat{w}_{\text {jma. }}$ 对模型估计值进行加权平均来找到系数估计值（以及任何其他感兴趣的参数）。 B. E. Hansen 和 Racine (2012) 将其称为 Jackknife 模型平均 (JMA) 估计器。

该解的代数性质与 Mallows 类似。由于 (28.31) 最小化受单纯形约束的二次函数，因此解往往位于边和顶点上，这意味着许多（或大多数）模型的权重为零。因此，JMA权重选择同时执行选择和收缩。通过二次规划以数值方式找到解决方案，即使模型 $M$ 的数量很大，计算也简单且快速。

B. E. Hansen 和 Racine (2012) 表明，JMA 估计量渐近等效于基于回归拟合标准的最小二乘估计的不可行最优加权平均值。他们的结果在相当温和的条件下成立，包括条件异方差。这个结果类似于 Andrews (1991c) 对 Li (1987) 的模型选择结果的推广。

该理论的含义是JMA权重选择计算简单并且具有优异的采样性能。

28.37 格兰杰-拉马纳森平均

Granger 和 Ramanathan (1984) 提出了一种类似于 JMA 的基于保留样本的预测组合方法，该方法已成为现代机器学习文献中的流行方法。

将样本随机分为两部分：估计样本和评估样本。使用估计样本，估计 $M$ 回归模型，获得系数 $\widehat{\beta}_{m}$。使用这些系数和评估样本构建 $M$ 模型的拟合值 $\widetilde{Y}_{m i}=X_{m i}^{\prime} \widehat{\beta}_{m}$。然后通过 $Y_{i}$ 对 $\widetilde{Y}_{m i}$ 的最小二乘回归来估计模型权重，并且使用评估样本进行无截距。这个回归是

\[ Y_{i}=\sum_{m=1}^{M} \widehat{w}_{m} \widetilde{Y}_{m i}+\widehat{e}_{i} . \]

最小二乘系数 $\widehat{w}_{m}$ 是 Granger-Ramanathan 权重。

基于非正式的争论，Granger 和 Ramanathan (1984) 建议使用无约束最小二乘回归来获得权重，但不建议这样做，因为这会产生极其不稳定的经验权重，特别是当 $M$ 很大时。相反，建议使用约束回归，施加约束 $\widehat{w}_{m} \geq 0$ 和 $\sum_{m=1}^{M} \widehat{w}_{m}=1$。为了施加非负约束，最好使用二次规划。

这种 Granger-Ramanathan 方法最适合样本量非常大的应用，在这种情况下，保留样本分割带来的效率损失不构成问题。

28.38 实证说明

我们通过第 28.18 节的实证应用来说明模型平均方法，该节报告了亚洲女性 CPS 子样本的工资回归估计，重点关注 0 到 30 年间的经验回报。

表 $28.2$ 报告了使用 SBIC、SAIC、Mallows 模型平均 (MMA) 和 Jackknife 模型平均 (JMA) 方法获得的模型平均权重。最后一栏中还报告了经验回报的加权平均估计百分比。

结果表明，这些方法偏重于有些不同的模型。 SBIC 几乎把所有的重心都放在了模型 2 上。 SAIC 将近 $1 / 2$ 的权重放在模型 6 上，其余大部分分配在模型 5 和 9 之间。MMA 将近 $1 / 2$ 的权重放在模型 5 上的模型 $9,30 %$ 上，将 $9 %$ 上的权重放在模型 1 上。 JMA 与 MMA 类似，但更强调简约性，模型 5 上的权重为 $1 / 2$，模型 1 上的模型 $9,17 %$ 为 $17 %$，模型 3 上的 $8 %$ 为权重。 MMA/JMA 方法的一个有趣的事情是它们可以在完全不同的模型之间分配权重，例如型号 1 和 9。

非 BIC 方法的平均估计量彼此相似，但 SBIC 产生的估计值比其他方法小得多。

表 28.2：亚洲女性的模型平均权重和经验回报估计

	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9	Return
SBIC	$.02$	$.96$	$.00$	$.00$	$.04$	$.00$	$.00$	$.00$	$.00$	$22 %$
SAIC	$.00$	$.02$	$.10$	$.00$	$.15$	$.44$	$.00$	$.06$	$.22$	$38 %$
MMA	$.09$	$.02$	$.02$	$.00$	$.30$	$.00$	$.00$	$.00$	$.57$	$39 %$
JMA	$.17$	$.00$	$.08$	$.00$	$.57$	$.01$	$.00$	$.00$	$.17$	$34 %$

28.39 技术证明*

定理28.1 的证明我们在具有$K \times 1$ 系数向量$\beta$ 和已知方差$\sigma^{2}$ 的正态线性回归模型的简化假设下建立了定理。似然函数是

\[ L_{n}(\beta)=\left(2 \pi \sigma^{2}\right)^{-n / 2} \exp \left(-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(Y_{i}-X_{i}^{\prime} \beta\right)^{2}\right) . \]

在 MLE $\widehat{\beta}$ 上进行评估，这等于

\[ L_{n}(\widehat{\beta})=\left(2 \pi \sigma^{2}\right)^{-n / 2} \exp \left(-\frac{\sum_{i=1}^{n} \widehat{e}_{i}^{2}}{2 \sigma^{2}}\right) . \]

利用(8.21)我们可以写出

\[ \begin{aligned} L_{n}(\beta) &=\left(2 \pi \sigma^{2}\right)^{-n / 2} \exp \left(-\frac{1}{2 \sigma^{2}}\left(\sum_{i=1}^{n} \widehat{e}_{i}^{2}+(\widehat{\beta}-\beta)^{\prime} \boldsymbol{X}^{\prime} \boldsymbol{X}(\widehat{\beta}-\beta)\right)\right) \\ &=L_{n}(\widehat{\beta}) \exp \left(-\frac{1}{2 \sigma^{2}}(\widehat{\beta}-\beta)^{\prime} \boldsymbol{X}^{\prime} \boldsymbol{X}(\widehat{\beta}-\beta)\right) . \end{aligned} \]

对于扩散先验 $\pi(\beta)=C$，边际似然为

\[ \begin{aligned} p(Y) &=L_{n}(\widehat{\beta}) \int \exp \left(-\frac{1}{2 \sigma^{2}}(\widehat{\beta}-\beta)^{\prime} \boldsymbol{X}^{\prime} \boldsymbol{X}(\widehat{\beta}-\beta)\right) C d \beta \\ &=L_{n}(\widehat{\beta}) n^{-K / 2}\left(2 \pi \sigma^{2}\right)^{K / 2} \operatorname{det}\left(\frac{1}{n} \boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1 / 2} C \end{aligned} \]

其中最终的等式是多元正态积分。重写并记录日志

\[ \begin{aligned} -2 \log p(Y) &=-2 \log L_{n}(\widehat{\beta})+K \log n-K \log \left(2 \pi \sigma^{2}\right)+\log \operatorname{det}\left(\frac{1}{n} \boldsymbol{X}^{\prime} \boldsymbol{X}\right)+\log C \\ &=-2 \ell_{n}(\widehat{\beta})+K \log n+O(1) . \end{aligned} \]

这就是定理。

定理 28.2 的证明来自 (28.11)

\[ \begin{aligned} \int g(y) \log f(y, \widehat{\theta}) d y &=-\frac{n}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n} \int\left(y-X_{i}^{\prime} \widehat{\beta}\right)^{2} g\left(y \mid X_{i}\right) d y \\ &=-\frac{n}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{1}{2 \sigma^{2}} \sum_{i=1}^{n}\left(\sigma^{2}+(\widehat{\beta}-\beta)^{\prime} X_{i} X_{i}^{\prime}(\widehat{\beta}-\beta)\right) \\ &=-\frac{n}{2} \log \left(2 \pi \sigma^{2}\right)-\frac{n}{2}-\frac{1}{2 \sigma^{2}} \boldsymbol{e}^{\prime} \boldsymbol{P} \boldsymbol{e} . \end{aligned} \]

因此

\[ T=-2 \mathbb{E}\left[\int g(y) \log \widehat{f}(y) d y\right]=n \log \left(2 \pi \sigma^{2}\right)+n+\frac{1}{\sigma^{2}} \mathbb{E}[\boldsymbol{e} \boldsymbol{P} \boldsymbol{e}]=n \log \left(2 \pi \sigma^{2}\right)+n+K . \]

这是(28.12)。最终的等式在条件同方差的假设下成立。

在 $\widehat{\beta}$ 处评估 (28.11)，我们获得对数似然

\[ -2 \ell_{n}(\widehat{\beta})=n \log \left(2 \pi \sigma^{2}\right)+\frac{1}{\sigma^{2}} \sum_{i=1}^{n} \widehat{e}_{i}^{2}=n \log \left(2 \pi \sigma^{2}\right)+\frac{1}{\sigma^{2}} \boldsymbol{e}^{\prime} \boldsymbol{M} \boldsymbol{e} . \]

这个有期待

\[ -\mathbb{E}\left[2 \ell_{n}(\widehat{\beta})\right]=n \log \left(2 \pi \sigma^{2}\right)+\frac{1}{\sigma^{2}} \mathbb{E}\left[\boldsymbol{e}^{\prime} \boldsymbol{M e}\right]=n \log \left(2 \pi \sigma^{2}\right)+n-K . \]

这是(28.13)。最终的等式在条件同方差下成立。

定理 28.4 的证明该证明使用泰勒展开式，类似于非线性模型中 MLE 渐近分布理论所使用的泰勒展开式。我们避免了技术细节，因此这不是完整的证明。

将模型密度写为 $f(y, \theta)$，将估计模型写为 $\widehat{f}(y)=f(y, \widehat{\theta})$。回想一下（28.10），我们可以将目标 $T$ 写为

\[ T=-2 \mathbb{E}[\log f(\widetilde{Y}, \widehat{\theta})] \]

其中 $\widetilde{Y}$ 是 $Y$ 的独立副本。令 $\widetilde{\theta}$ 为在样本上计算的 MLE $\widetilde{Y} . \widetilde{\theta}$ 是 $\widehat{\theta}$ 的独立副本。根据对称性，我们可以将 $T$ 写为

\[ T=-2 \mathbb{E}[\log f(Y, \widetilde{\theta})] . \]

定义 Hessian $H=-\frac{\partial}{\partial \theta \partial \theta^{\prime}} \mathbb{E}[\log f(Y, \theta)]>0$。现在对 $\log$ 似然 $\log f(Y, \widetilde{\theta})$ 对 $\widehat{\theta}$ 进行二阶泰勒级数展开。这是

\[ \begin{aligned} \log f(Y, \widetilde{\theta}) &=\log f(Y, \widehat{\theta})+\frac{\partial}{\partial \theta^{\prime}} \log f(Y, \widehat{\theta})(\widetilde{\theta}-\widehat{\theta})-\frac{1}{2}(\widetilde{\theta}-\widehat{\theta})^{\prime} H(\widetilde{\theta}-\widehat{\theta})+O_{p}\left(n^{-1 / 2}\right) \\ &=\log f(Y, \widehat{\theta})-\frac{n}{2}(\widetilde{\theta}-\widehat{\theta})^{\prime} H(\widetilde{\theta}-\widehat{\theta})+O_{p}\left(n^{-1 / 2}\right) . \end{aligned} \]

由于 MLE $\widehat{\theta}$ 的一阶条件，第二个等式成立。如果 (28.34) 中的 $O_{p}\left(n^{-1 / 2}\right)$ 项是一致可积的 (28.33) 和 (28.34) 意味着

\[ \begin{aligned} T &=-\mathbb{E}[2 \log f(Y, \widehat{\theta})]+\mathbb{E}\left[n(\widetilde{\theta}-\widehat{\theta})^{\prime} H(\widetilde{\theta}-\widehat{\theta})\right]+O\left(n^{-1 / 2}\right) \\ &=-\mathbb{E}[2 \log L(\widehat{\theta})]+\mathbb{E}\left[n(\widetilde{\theta}-\theta)^{\prime} H(\widetilde{\theta}-\theta)\right]+\mathbb{E}\left[n(\widehat{\theta}-\theta)^{\prime} H(\widehat{\theta}-\theta)\right] \\ &+2 \mathbb{E}\left[n(\widetilde{\theta}-\theta)^{\prime} H(\widehat{\theta}-\theta)\right]+O\left(n^{-1 / 2}\right) \\ &=-\mathbb{E}\left[2 \ell_{n}(\widehat{\theta})\right]+\mathbb{E}\left[\chi_{K}^{2}\right]+\mathbb{E}\left[\widetilde{\chi}_{K}^{2}\right]+O\left(n^{-1 / 2}\right) \\ &=-\mathbb{E}\left[2 \ell_{n}(\widehat{\theta})\right]+2 K+O\left(n^{-1 / 2}\right) \end{aligned} \]

其中 $\chi_{K}^{2}$ 和 $\widetilde{\chi}_{K}^{2}$ 是具有 $K$ 自由度的卡方随机变量。倒数第二个等式成立，如果

\[ n(\widehat{\theta}-\theta)^{\prime} H(\widehat{\theta}-\theta) \underset{d}{\longrightarrow} \chi_{K}^{2} \]

(28.35) 左侧的 Wald 统计量是一致可积的。在标准正则条件（包括正确的规范）下，MLE 的渐近收敛性 (28.35) 成立。

定理 28.5 的证明使用矩阵符号我们可以写成$\widehat{\boldsymbol{m}}-\boldsymbol{m}=-\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{m}+\boldsymbol{A} \boldsymbol{e}$。然后我们可以将拟合写为

\[ \begin{aligned} R &=\mathbb{E}\left[(\widehat{\boldsymbol{m}}-\boldsymbol{m})^{\prime}(\widehat{\boldsymbol{m}}-\boldsymbol{m}) \mid \boldsymbol{X}\right] \\ &=\mathbb{E}\left[\boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{m}-2 \boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right) \boldsymbol{A} \boldsymbol{e}+\boldsymbol{e}^{\prime} \boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{e} \mid \boldsymbol{X}\right] \\ &=\boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{m}+\sigma^{2} \operatorname{tr}\left(\boldsymbol{A}^{\prime} \boldsymbol{A}\right) . \end{aligned} \]

请注意，此计算依赖于条件同方差的假设。

现在考虑 Mallows 准则。我们发现

\[ \begin{aligned} C_{p}^{*} &=\widehat{\boldsymbol{e}}^{\prime} \widehat{\boldsymbol{e}}+2 \widetilde{\sigma}^{2} \operatorname{tr}(\boldsymbol{A})-\boldsymbol{e}^{\prime} \boldsymbol{e} \\ &=(\boldsymbol{m}+\boldsymbol{e})^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right)(\boldsymbol{m}+\boldsymbol{e})+2 \widetilde{\sigma}^{2} \operatorname{tr}(\boldsymbol{A})-\boldsymbol{e}^{\prime} \boldsymbol{e} \\ &=\boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{m}+2 \boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{e}+\boldsymbol{e}^{\prime} \boldsymbol{A}^{\prime} \boldsymbol{A} \boldsymbol{e}-2 \boldsymbol{e}^{\prime} \boldsymbol{A} \boldsymbol{e}+2 \widetilde{\sigma}^{2} \operatorname{tr}(\boldsymbol{A}) . \end{aligned} \]

采取期望并使用条件同方差和 $\mathbb{E}\left[\widetilde{\sigma}^{2} \mid \boldsymbol{X}\right]=\sigma^{2}$ 的假设

\[ \mathbb{E}\left[C_{p}^{*} \mid \boldsymbol{X}\right]=\boldsymbol{m}^{\prime}\left(\boldsymbol{I}_{n}-\boldsymbol{A}^{\prime}\right)\left(\boldsymbol{I}_{n}-\boldsymbol{A}\right) \boldsymbol{m}+\sigma^{2} \operatorname{tr}\left(\boldsymbol{A}^{\prime} \boldsymbol{A}\right)=R \]

这就是所说的结果。

定理 28.6 的证明取任意两个模型 $\mathscr{M}_{1}$ 和 $\mathscr{M}_{2}$，其中 $\mathcal{M}_{1} \notin \overline{\mathscr{M}}^{*}$ 和 $\mathscr{M}_{2} \in \overline{\mathscr{M}}^{*}$。令他们的信息标准写为

\[ \begin{aligned} &\mathrm{IC}_{1}=-2 \ell_{1}\left(\widehat{\theta}_{1}\right)+c\left(n, K_{1}\right) \\ &\mathrm{IC}_{2}=-2 \ell_{2}\left(\widehat{\theta}_{2}\right)+c\left(n, K_{2}\right) . \end{aligned} \]

如果满足以下条件，则选择模型 $\mathscr{M}_{1}$ 而不是 $\mathscr{M}_{2}$

\[ \mathrm{LR}<c\left(n, K_{2}\right)-c\left(n, K_{1}\right) \]

其中 $\mathrm{LR}=2\left(\ell_{2}\left(\widehat{\theta}_{2}\right)-\ell\left(\widehat{\theta}_{1}\right)\right)$ 是测试 $\mathcal{M}_{1}$ 与 $\mathcal{M}_{2}$ 的似然比统计量。由于我们假设 $\mathscr{M}_{1}$ 不是真实模型，而 $\mathscr{M}_{2}$ 为真，那么 LR 以 $n$ 的速率发散到 $+\infty$。这意味着对于任何 $\alpha>0, n^{-1+\alpha} \mathrm{LR} \underset{p}{\rightarrow}+\infty$.此外，假设意味着 $n^{-1+\alpha}\left(c\left(n, K_{1}\right)-c\left(n, K_{2}\right)\right) \longrightarrow 0$。修复 $\mathrm{LR}=2\left(\ell_{2}\left(\widehat{\theta}_{2}\right)-\ell\left(\widehat{\theta}_{1}\right)\right)$。有一个足够大的 $\mathrm{LR}=2\left(\ell_{2}\left(\widehat{\theta}_{2}\right)-\ell\left(\widehat{\theta}_{1}\right)\right)$ 使得 $\mathrm{LR}=2\left(\ell_{2}\left(\widehat{\theta}_{2}\right)-\ell\left(\widehat{\theta}_{1}\right)\right)$ 成立。因此

\[ \begin{aligned} \mathbb{P}\left[\widehat{M}=\mathscr{M}_{1}\right] & \leq \mathbb{P}\left[n^{-1+\alpha} \operatorname{LR}<n^{-1+\alpha}\left(c\left(n, K_{2}\right)-c\left(n, K_{1}\right)\right)\right] \\ & \leq \mathbb{P}[\mathrm{LR}<\epsilon] \rightarrow 0 . \end{aligned} \]

由于这适用于任何 $\mathscr{M}_{1} \notin \overline{\mathscr{M}}^{*}$，我们推断所选模型在 $\overline{\mathscr{M}}^{*}$ 中的概率接近 1。这意味着选择标准与所声称的模型选择一致。

定理证明 28.7 采用定理 $28.6$ 证明中描述的设置，但现在假设 $\mathscr{M}_{1} \subset$、$\mathcal{M}_{2}$ 和 $\mathscr{M}_{1}, \mathscr{M}_{2} \in \overline{\mathcal{M}}^{*}$。似然比统计量满足 LR $\underset{d}{\longrightarrow} \chi_{r}^{2}$ 其中 $r=K_{2}-K_{1}$。让

\[ B=\limsup _{n \rightarrow \infty}\left(c\left(n, K_{1}\right)-c\left(n, K_{2}\right)\right)<\infty . \]

令 $F_{r}(u)$ 表示 $\chi_{r}^{2}$ 分布函数

\[ \begin{aligned} \mathbb{P}\left[\widehat{\mathscr{M}}=\mathscr{M}_{2}\right] &=\mathbb{P}\left[\operatorname{LR}>\left(c\left(n, K_{2}\right)-c\left(n, K_{1}\right)\right)\right] \\ & \geq \mathbb{P}[\operatorname{LR}>B] \\ & \rightarrow \mathbb{P}\left[\chi_{r}^{2}>B\right]=1-F_{r}(B)>0 \end{aligned} \]

因为 $\chi_{r}^{2}$ 在正实数线和 $B<\infty$ 上有支撑。这表明选择标准以正概率渐近过度选择。

定理证明$28.8$ 由于$c(n, K)=o(n)$，该过程与模型选择一致。采用两个模型 $\mathscr{M}_{1}, \mathscr{M}_{2} \in \overline{\mathscr{M}}^{*}$ 和 $K_{1}<K_{2}$。由于两个模型都是正确的，因此 LR $=O_{p}(1)$。修复 $\epsilon>0$。存在 $B<\infty$ 使得 $\mathrm{LR} \leq B$ 的概率超过 $1-\epsilon$。到 (28.16) 时，$28.8$ 足够大，使得 $28.8$ 成立。因此

\[ \mathbb{P}\left[\widehat{\mathscr{M}}=\mathscr{M}_{2}\right] \leq \mathbb{P}\left[\mathrm{LR}>\left(c\left(n, K_{2}\right)-c\left(n, K_{1}\right)\right)\right] \leq \mathbb{P}[\mathrm{LR}>B] \leq \epsilon . \]

由于 $\epsilon$ 是任意的 $\mathbb{P}\left[\widehat{\mathscr{M}}=\mathscr{M}_{2}\right] \longrightarrow 0$ 。

定理 28.9 的证明首先，我们检查 $R_{n}(K)$。将预测值以矩阵表示法写为 $\widehat{\boldsymbol{m}}_{K}=$ $\boldsymbol{X}_{K} \widehat{\beta}_{K}=\boldsymbol{P}_{K} \boldsymbol{Y}$ 其中 $\boldsymbol{P}_{K}=\boldsymbol{X}_{K}\left(\boldsymbol{X}_{K}^{\prime} \boldsymbol{X}_{K}\right)^{-1} \boldsymbol{X}_{K}^{\prime}$。观察 $\boldsymbol{m}-\widehat{\boldsymbol{m}}_{K}=\boldsymbol{M}_{K} \boldsymbol{m}-\boldsymbol{P}_{K} \boldsymbol{e}$ 与 $\boldsymbol{M}_{K}=\boldsymbol{I}_{K}-\boldsymbol{P}_{K}$ 的关系很有用。我们发现预测风险等于

\[ \begin{aligned} R_{n}(K) &=\mathbb{E}\left[\left(\boldsymbol{m}-\widehat{\boldsymbol{m}}_{K}\right)^{\prime}\left(\boldsymbol{m}-\widehat{\boldsymbol{m}}_{K}\right) \mid \boldsymbol{X}\right] \\ &=\mathbb{E}\left[\left(\boldsymbol{M}_{K} \boldsymbol{m}-\boldsymbol{P}_{K} \boldsymbol{e}\right)^{\prime}\left(\boldsymbol{M}_{K} \boldsymbol{m}-\boldsymbol{P}_{K} \boldsymbol{e}\right) \mid \boldsymbol{X}\right] \\ &=\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m}+\mathbb{E}\left[\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e} \mid \boldsymbol{X}\right] \\ &=\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m}+\sigma^{2} K . \end{aligned} \]

回归量的选择通过最后一行中的两项影响 $R_{n}(K)$。第一项 $\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m}$ 是由于省略变量而导致的平方偏差。随着 $K$ 的增加，该术语减少，反映出遗漏变量偏差的减少。第二项 $\sigma^{2} K$ 是估计方差。回归量的数量正在增加。增加回归量的数量会减少偏差但增加方差，从而影响样本外预测的质量。接下来我们检查调整后的马洛斯标准。我们发现

\[ \begin{aligned} C_{n}^{*}(K) &=\widehat{\boldsymbol{e}}_{K}^{\prime} \widehat{\boldsymbol{e}}_{K}+2 \sigma^{2} K-\boldsymbol{e}^{\prime} \boldsymbol{e} \\ &=(\boldsymbol{m}+\boldsymbol{e})^{\prime} \boldsymbol{M}_{K}(\boldsymbol{m}+\boldsymbol{e})+2 \sigma^{2} K-\boldsymbol{e}^{\prime} \boldsymbol{e} \\ &=\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m}+2 \boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{e}-\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e}+2 \sigma^{2} K . \end{aligned} \]

下一步是证明

\[ \sup _{K}\left|\frac{C_{n}^{*}(K)-R_{n}(K)}{R_{n}(K)}\right| \underset{p}{\longrightarrow} 0 \]

作为 $n \rightarrow \infty$。为了建立 (28.36)，观察到

\[ C_{n}^{*}(K)-R_{n}(K)=2 \boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{e}-\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e}+\sigma^{2} K . \]

选择 $\epsilon>0$ 和一些序列 $B_{n} \rightarrow \infty$ 使得 $B_{n} /\left(R_{n}^{\text {opt }}\right)^{r} \rightarrow 0$ 。（根据假设 28.1.5，这是可行的。）根据布尔不等式 (B.24)、惠特尔不等式 (B.48)，事实是 $\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m} \leq R_{n}(K)$ 和 $R_{n}(K) \geq \sigma^{2} K$、$B_{n} /\left(R_{n}^{\text {opt }}\right)^{r} \rightarrow 0$ 和 $\sum_{K=1}^{\infty} K^{-r}<\infty$

\[ \begin{aligned} & \mathbb{P}\left[\sup _{K}\left|\frac{\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{e}}{R_{n}(K)}\right|>\epsilon \mid \boldsymbol{X}\right] \leq \sum_{K=1}^{\infty} \mathbb{P}\left[\left|\frac{\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{e}}{R_{n}(K)}\right|>\epsilon \mid \boldsymbol{X}\right] \\ & \leq \frac{C_{1} r}{\epsilon^{2 r}} \sum_{K=1}^{\infty} \frac{\left|\boldsymbol{m}^{\prime} \boldsymbol{M}_{K} \boldsymbol{m}\right|^{r}}{R_{n}(K)^{2 r}} \\ & \leq \frac{C_{1 r}}{\epsilon^{2 r}} \sum_{K=1}^{\infty} \frac{1}{R_{n}(K)^{r}} \\ & =\frac{C_{1} r}{\epsilon^{2 r}} \sum_{K=1}^{B_{n}} \frac{1}{R_{n}(K)^{r}}+\frac{C_{1 r}}{\epsilon^{2 r}} \sum_{K=B_{n}+1}^{\infty} \frac{1}{R_{n}(K)^{r}} \\ & \leq \frac{C_{1 r}}{\epsilon^{2 r}} \frac{B_{n}}{\left(R_{n}^{\mathrm{opt}}\right)^{r}}+\frac{C_{1 r}}{\epsilon^{2 r} \sigma^{2 r}} \sum_{K=B_{n}+1}^{\infty} \frac{1}{K^{r}} \\ & \rightarrow 0 \text {. } \end{aligned} \]

通过类似的论证，但使用 Whittle 不等式 (B.49)、$\operatorname{tr}\left(\boldsymbol{P}_{K} \boldsymbol{P}_{K}\right)=\operatorname{tr}\left(\boldsymbol{P}_{K}\right)=K$ 和 $K \leq \sigma^{-2} R_{n}(K)$

\[ \begin{aligned} \mathbb{P}\left[\sup _{K}\left|\frac{\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e}-\sigma^{2} K}{R_{n}(K)}\right|>\epsilon \mid \boldsymbol{X}\right] & \leq \sum_{K=1}^{\infty} \mathbb{P}\left[\left|\frac{\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e}-\mathbb{E}\left(\boldsymbol{e}^{\prime} \boldsymbol{P}_{K} \boldsymbol{e}\right)}{R_{n}(K)}\right|>\epsilon \mid \boldsymbol{X}\right] \\ & \leq \frac{C_{2 r}}{\epsilon^{2 r}} \sum_{K=1}^{\infty} \frac{\operatorname{tr}\left(\boldsymbol{P}_{K} \boldsymbol{P}_{K}\right)^{r}}{R_{n}(K)^{2 r}} \\ &=\frac{C_{2 r}}{\epsilon^{2 r}} \sum_{K=1}^{\infty} \frac{K^{r}}{R_{n}(K)^{2 r}} \\ & \leq \frac{C_{1 r}}{\epsilon^{2 r} \sigma^{2 r}} \sum_{K=1}^{\infty} \frac{1}{R_{n}(K)^{r}} \\ & \rightarrow 0 . \end{aligned} \]

这些一起意味着（28.36）。

最后我们证明 (28.36) 蕴涵 (28.18)。该论证类似于非线性估计量的标准一致性证明。 (28.36) 指出 $C_{n}^{*}(K)$ 在概率上均匀收敛于 $R_{n}(K)$。这意味着 $C_{n}^{*}(K)$ 的极小值在概率上收敛于 $R_{n}(K)$ 的极小值。形式上，因为 $K_{n}^{\mathrm{opt}}$ 最小化了 $R_{n}(K)$

\[ \begin{aligned} 0 & \leq \frac{R_{n}\left(\widehat{K}_{n}\right)-R_{n}\left(K_{n}^{\mathrm{opt}}\right)}{R_{n}\left(\widehat{K}_{n}\right)} \\ &=\frac{C_{n}^{*}\left(\widehat{K}_{n}\right)-R_{n}\left(K_{n}^{\mathrm{opt}}\right)}{R_{n}\left(\widehat{K}_{n}\right)}-\frac{C_{n}^{*}\left(\widehat{K}_{n}\right)-R_{n}\left(\widehat{K}_{n}\right)}{-R_{n}\left(\widehat{K}_{n}\right)} \\ & \leq \frac{C_{n}^{*}\left(\widehat{K}_{n}\right)-R_{n}\left(K_{n}^{\mathrm{opt}}\right)}{R_{n}\left(\widehat{K}_{n}\right)}+o_{p}(1) \\ & \leq \frac{C_{n}^{*}\left(K_{n}^{\mathrm{opt}}\right)-R_{n}\left(K_{n}^{\mathrm{opt}}\right)}{R_{n}\left(K_{n}^{\mathrm{opt}}\right)}+o_{p}(1) \\ & \leq o_{p}(1) . \end{aligned} \]

第二个不等式是(28.36)。下面使用 $\widehat{K}_{n}$ 最小化 $C_{n}^{*}(K)$ 和 $K_{n}^{\text {opt }}$ 最小化 $R_{n}(K)$ 的事实。决赛时间为（28.36）。这是（28.18）。

在提供定理 $28.10$ 的证明之前，我们提出两个与自由度 $K$ 和非中心参数 $\lambda$ 的非中心卡方密度函数相关的技术结果，该函数等于

\[ f_{K}(x, \lambda)=\sum_{i=0}^{\infty} \frac{e^{-\lambda / 2}}{i !}\left(\frac{\lambda}{2}\right)^{i} f_{K+2 i}(x) \]

其中 $f_{r}(x)=\frac{x^{r / 2-1} e^{-x / 2}}{\left.2^{r / 2} \Gamma(r / 2)\right)}$ 是 $\chi_{K}^{2}$ 密度函数。

定理 28.16 非中心卡方密度函数 (28.37) 遵循递归关系 $f_{K}(x, \lambda)=\frac{K}{x} f_{K+2}(x, \lambda)+\frac{\lambda}{x} f_{K+4}(x, \lambda)$。

定理 $28.16$ 的证明是对非中心卡方密度函数 (28.37) 的直接操作。

第二个技术结果来自 Bock（1975，定理 A&B）。

定理 28.17 如果 $X \sim \mathrm{N}\left(\theta, \boldsymbol{I}_{K}\right)$ 那么对于任何函数 $h(u)$

\[ \begin{aligned} \mathbb{E}\left[X h\left(X^{\prime} X\right)\right] &=\theta \mathbb{E}\left[h\left(Q_{K+2}\right)\right] \\ \mathbb{E}\left[X^{\prime} X h\left(X^{\prime} X\right)\right] &=K \mathbb{E}\left[h\left(Q_{K+2}\right)\right]+\lambda \mathbb{E}\left[h\left(Q_{K+4}\right)\right] \end{aligned} \]

其中$\lambda=\theta^{\prime} \theta$和$Q_{r} \sim \chi_{r}^{2}(\lambda)$是非中心卡方随机变量，具有$r$自由度和非中心参数$\lambda$。

定理 28.17 的证明为了证明 (28.38)，我们首先证明对于 $Z \sim \mathrm{N}(\mu, 1)$，然后对于任何函数 $g(u)$

\[ \mathbb{E}\left[Z g\left(Z^{2}\right)\right]=\mu \mathbb{E}\left[g\left(Q_{3}\right)\right] . \]

假设$\mu>0$。使用变量变化 $y=x^{2}$

\[ \begin{aligned} \mathbb{E}\left[Z g\left(Z^{2}\right)\right] &=\int_{-\infty}^{\infty} \frac{x}{\sqrt{2 \pi}} g\left(x^{2}\right) \exp \left(-\frac{1}{2}(x-\mu)^{2}\right) d x \\ &=\int_{0}^{\infty} \frac{y}{2 \sqrt{2 \pi}} e^{-\left(y+\mu^{2}\right) / 2}\left(e^{\sqrt{y} \mu}-e^{-\sqrt{y} \mu}\right) g(y) d y . \end{aligned} \]

通过展开式和勒让德复制公式

\[ e^{x}-e^{-x}=2 \sum_{i=0}^{\infty} \frac{x^{1+2 i}}{(1+2 i) !}=\sqrt{\pi} x \sum_{i=0}^{\infty} \frac{\left(x^{2} / 2\right)^{i}}{2^{i} i ! \Gamma(i+3 / 2)} . \]

那么 (28.41) 等于

\[ \mu \int_{0}^{\infty} y e^{-\left(y+\mu^{2}\right) / 2} \sum_{i=0}^{\infty} \frac{\left(\mu^{2} / 2\right)^{i} y^{i+1 / 2}}{2^{3 / 2+i} i ! \Gamma(i+3 / 2)} g(y) d y=\mu \int_{0}^{\infty} y f_{3}\left(y, \mu^{2}\right) g(y) d y=\mu \mathbb{E}\left[g\left(Q_{3}\right)\right] \]

其中 $f_{3}(y, \lambda)$ 是具有 3 个自由度的非中心卡方密度 (28.37)。这是（28.40）。

取 (28.38) 的 $j^{t h}$ 行。写$X^{\prime} X=X_{j}^{2}+J$，其中$X_{j} \sim \mathrm{N}\left(\theta_{j}, 1\right)$ 和$J \sim \chi_{K-1}^{2}\left(\lambda-\theta_{j}^{2}\right)$ 是独立的。设置 $g(u)=h(u+J)$ 并使用 (28.41)

\[ \begin{aligned} \mathbb{E}\left[X_{j} h\left(X^{\prime} X\right)\right] &=\mathbb{E}\left[X_{j} h\left(X_{j}^{2}+J\right)\right] \\ &=\mathbb{E}\left[\mathbb{E}\left[X_{j} g\left(X_{j}^{2}\right) \mid J\right]\right] \\ &=\mathbb{E}\left[\theta_{j} \mathbb{E}\left[g\left(Q_{3}\right) \mid J\right]\right] \\ &=\theta_{j} \mathbb{E}\left[h\left(Q_{3}+J\right)\right] \\ &=\theta_{j} \mathbb{E}\left[h\left(Q_{K+2}\right)\right] \end{aligned} \]

即 (28.38)。最终的等式使用了 $Q_{3}+J \sim Q_{K+2}$ 这一事实。

观察 $X^{\prime} X$ 的密度为 $f_{K}(x, \lambda)$。使用定理 $28.16$

\[ \begin{aligned} \mathbb{E}\left[X^{\prime} X\left(X^{\prime} X\right)\right] &=\int_{0}^{\infty} x h(x) f_{K}(x, \lambda) d x \\ &=K \int_{0}^{\infty} h(x) f_{K+2}(x, \lambda) d x+\lambda \int_{0}^{\infty} h(x) f_{K+4}(x, \lambda) d x \\ &=K \mathbb{E}\left[h\left(Q_{K+2}\right)\right]+\lambda \mathbb{E}\left[h\left(Q_{K+4}\right)\right] \end{aligned} \]

即 (28.39)。

定理28.10的证明通过二次结构我们可以计算出

\[ \begin{aligned} \operatorname{MSE}\left[\widehat{\theta}^{*}\right] &=\mathbb{E}\left[\left(\widehat{\theta}-\theta-\widehat{\theta} \mathbb{1}\left\{\widehat{\theta}^{\prime} \hat{\theta} \leq c\right\}\right)^{\prime}\left(\widehat{\theta}-\theta-\widehat{\theta} \mathbb{1}\left\{\widehat{\theta}^{\prime} \widehat{\theta} \leq c\right\}\right)\right] \\ &=\mathbb{E}\left[(\widehat{\theta}-\theta)^{\prime}(\widehat{\theta}-\theta)\right]-\mathbb{E}\left[\widehat{\theta}^{\prime} \widehat{\theta} \mathbb{1}\left\{\widehat{\theta}^{\prime} \widehat{\theta} \leq c\right\}\right]+2 \mathbb{E}\left[\theta^{\prime} \widehat{\theta} \mathbb{1}\left\{\widehat{\theta}^{\prime} \widehat{\theta} \leq c\right\}\right] \\ &=K-K \mathbb{E}\left[\mathbb{1}\left\{Q_{K+2} \leq c\right\}\right]-\lambda \mathbb{E}\left[\mathbb{1}\left\{Q_{K+4} \leq c\right\}\right]+2 \lambda \mathbb{E}\left[\mathbb{1}\left\{Q_{K+2} \leq c\right\}\right] \\ &=K+(2 \lambda-K) F_{K+2}(c, \lambda)-\lambda F_{K+4}(c, \lambda) . \end{aligned} \]

第三个等式使用定理 28.17 的两个结果，设置 $h(u)=\mathbb{1}\{u \leq c\}$。

28.40 练习

练习 28.1 验证方程 (28.1)-(28.2)。

练习 28.2 求权重为 $\omega_{i}$ 的线性回归 $Y_{i}=X_{i}^{\prime} \beta+e_{i}$ 的加权最小二乘估计量的 Mallows 准则（假设条件同方差）。

练习28.3 向后逐步回归。验证以下主张：对于 AIC 选择的情况，算法的步骤 (b) 可以通过计算每个主动回归量的经典（同方差）t 比来实现，并找到具有最小绝对 t 比的回归量。

提示：使用似然比和 F 统计量之间的关系以及 $\mathrm{F}$ 和 Wald 统计量之间的等式来表明，对于一个系数的检验，AIC 中的最小变化与识别最小平方 t 统计量相同。

练习28.4 前向逐步回归。验证以下主张：对于 AIC 选择的情况，可以通过识别非活动集中与步骤 (a) 残差具有最大绝对相关性的回归量来实现算法的步骤 (b)。

提示：这很有挑战性。首先表明目标是找到最能降低 SSE $=\widehat{\boldsymbol{e}}^{\prime} \widehat{\boldsymbol{e}}=\|\widehat{\boldsymbol{e}}\|^{2}$ 的回归量。使用几何参数表明与 $\widehat{\boldsymbol{e}}$ 最平行的回归量将使 $\|\widehat{\boldsymbol{e}}\|$ 减少最多。证明该回归量与 $\widehat{\boldsymbol{e}}$ 具有最大的绝对相关性。

练习28.5 一位经济学家估计了几个模型并报告了一个选定的规范，指出“其他规范的系数不显着”。我们应该如何解释报告的参数估计值和 t 比率？

练习28.6 验证定理28.11，包括(28.21)、(28.22)和(28.23)。

练习28.7 在定理28.11的假设下，证明$\hat{\lambda}=\widehat{\theta}^{\prime} \boldsymbol{V}^{-1} \widehat{\theta}-K$是$\lambda=\theta^{\prime} \boldsymbol{V}^{-1} \theta$的无偏估计量。

练习 28.8 针对未调整（非正部分）Stein 估计器 $\widetilde{\theta}, \boldsymbol{V}=\boldsymbol{I}_{K}$ 和 $r=0$ 的更简单情况证明定理 $28.14$。

额外的挑战：在这些假设下证明

\[ \begin{aligned} \operatorname{wmse}[\tilde{\theta}] &=K-(q-2)^{2} J_{q}\left(\lambda_{R}\right) \\ \lambda_{\boldsymbol{R}} &=\theta^{\prime} \boldsymbol{R}\left(\boldsymbol{R}^{\prime} \boldsymbol{R}\right)^{-1} \boldsymbol{R}^{\prime} \theta . \end{aligned} \]

练习28.9 假设你有参数向量$\widehat{\theta}$的两个无偏估计量$\widehat{\theta}_{1}$和$\widehat{\theta}_{2}$，以及协方差矩阵$\boldsymbol{V}_{1}$和$\boldsymbol{V}_{2}$。以最小化未加权均方误差为目标，例如$\operatorname{tr} \boldsymbol{V}_{1}$ 对应 $\widehat{\theta}_{1}$。假设 $\widehat{\theta}_{1}$ 和 $\widehat{\theta}_{2}$ 不相关。

证明最优加权平均估计量等于

\[ \frac{\frac{1}{\operatorname{tr} \boldsymbol{V}_{1}} \widehat{\theta}_{1}+\frac{1}{\operatorname{tr} \boldsymbol{V}_{2}} \widehat{\theta}_{2}}{\frac{1}{\operatorname{tr} \boldsymbol{V}_{1}}+\frac{1}{\operatorname{tr} \boldsymbol{V}_{2}}} . \]

推广到 $M$ 无偏不相关估计量的情况。
解释公式。练习 28.10 您通过最小二乘估计 $M$ 线性回归 $Y=X_{m}^{\prime} \beta_{m}+e_{m}$。令 $\widehat{Y}_{m i}=X_{m i}^{\prime} \widehat{\beta}_{m}$ 为拟合值。
表明 Mallows 平均标准与

\[ \sum_{i=1}^{n}\left(Y_{i}-w_{1} \widehat{Y}_{1 i}-w_{2} \widehat{Y}_{2 i}-\cdots-w_{M} \widehat{Y}_{M i}\right)^{2}+2 \sigma^{2} \sum_{m=1}^{M} w_{m} k_{m} \]

假设模型嵌套，$M$ 是最大模型。如果先前的标准在概率单纯形中最小化到 $w$ 但忽略了惩罚，那么解决方案是什么？（最小化权重向量是什么？）

练习28.11 你用最小二乘法估计$M$线性回归$Y=X_{m}^{\prime} \beta_{m}+e_{m}$。令 $\widetilde{Y}_{m i}=X_{m i}^{\prime} \widehat{\beta}_{m(-i)}$ 为留一回归的预测值。证明 JMA 准则等于

\[ \sum_{i=1}^{n}\left(Y_{i}-w_{1} \widetilde{Y}_{1 i}-w_{2} \widetilde{Y}_{2 i}-\cdots-w_{M} \widetilde{Y}_{M i}\right)^{2} \]

练习 28.12 使用 cps09mar 数据集执行类似于 $28.18$ 节中介绍的分析，但使用西班牙裔女性的子样本。该样本有 3003 个观测值。 BIC、AIC、CV、FIC 选用哪些型号？（您检查的精确信息标准可能会受到限制，具体取决于您的软件。）您如何解释结果？您会选择哪种型号/估价作为您的首选？

	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9	Return
SBIC	\(.02\)	\(.96\)	\(.00\)	\(.00\)	\(.04\)	\(.00\)	\(.00\)	\(.00\)	\(.00\)	\(22 %\)
SAIC	\(.00\)	\(.02\)	\(.10\)	\(.00\)	\(.15\)	\(.44\)	\(.00\)	\(.06\)	\(.22\)	\(38 %\)
MMA	\(.09\)	\(.02\)	\(.02\)	\(.00\)	\(.30\)	\(.00\)	\(.00\)	\(.00\)	\(.57\)	\(39 %\)
JMA	\(.17\)	\(.00\)	\(.08\)	\(.00\)	\(.57\)	\(.01\)	\(.00\)	\(.00\)	\(.17\)	\(34 %\)