第21章: 断点回归

21 断点回归

21.1 介绍

应用计量经济学的核心目标之一是估计治疗效果。一个主要障碍是观察数据处理很少是外生的。到目前为止，本书讨论的处理潜在内生性的技术包括工具变量、固定效应和差异中的差异。另一种重要的方法出现在回归不连续性设计的背景下。这是一种相当特殊的情况（不受计量经济学家的控制），其中处理是由阈值交叉规则确定的。例如：（1）现任政治人物在选举中是否有优势？现任者是上次选举的获胜者，这意味着他们的投票份额超过了阈值。 (2) 上大学有什么影响？大学生是根据入学考试录取的，这意味着他们的考试成绩超过了特定的门槛。在这些情况下，待遇（在职、大学入学）可以被视为随机分配给接近截止点的个人。（在示例中，针对投票份额接近获胜阈值的候选人以及入学考试分数接近截止阈值的学生。）此设置称为回归不连续性设计 (RDD)。当它应用时，有一些简单的技术可以估计治疗的因果效应。

Thistlethwaite 和 Campbell (1960) 首次使用了断点回归。它由 Black (1999)、Ludwig 和 Miller (2007) 以及 Lee (2008) 在经济学中推广。重要评论包括 Imbens 和 Leimieux (2008)、Lee 和 Leimieux (2010) 以及 Cattaneo、Idrobo 和 Titiunik (2020，$2021)$

核心模型是尖锐回归不连续性，其中处理是可观察量的不连续确定性规则。然而，大多数应用都涉及模糊回归不连续性，其中处理概率在可观察值中是不连续的。我们首先回顾尖锐回归不连续性，然后介绍模糊回归不连续性。

21.2 急剧回归不连续性

以潜在结果框架为例。如果个人为 $D=0$，则未接受治疗；如果为 $D=1$，则接受治疗。如果不治疗，个体的结果为 $Y_{0}$，如果治疗，则结果为 $Y_{1}$。个体的治疗效果是 $\theta=Y_{1}-Y_{0}$，它是随机的。可观察的协变量是 $X$。 $X=x$ 子群体的条件平均治疗效果 (ATE) 为 $\theta(x)=\mathbb{E}[\theta \mid X=x]$。

当治疗由 $X$ 阈值函数确定时，就会出现急剧回归不连续性设计，例如$D=\mathbb{1}\{X \geq c\}$。在大多数应用程序中，阈值 $c$ 由策略或规则确定。决定治疗的协变量 $X$ 通常称为运行变量。阈值 $c$ 通常称为“截止”。

讨论一个具体的例子可能会有所帮助。 Ludwig 和 Miller (2007) 使用锐回归断点设计来评估名为 Head Start 的美国联邦反贫困计划。 Head Start 成立于 1965 年，旨在为 3 至 5 岁的贫困儿童及其家庭提供学前教育、保健和其他社会服务。启蒙资金通过竞争性赠款申请授予当地市政当局。由于担心贫困地区的申请率可能不如资金充足的地区，1965年春，联邦政府向美国300个最贫困的县提供了拨款援助。这 300 个县是根据 1960 年美国人口普查的贫困率选出的。

正如路德维希和米勒所记录的那样，结果是受援助县的申请激增，从而导致项目资金激增。 300 个接受治疗的县中的 $80 %$ 获得了启蒙支持，而其余县中只有 $43 %$ 获得了支持。因此，可以合理地得出结论，这些县获得了外源性资金的大幅增加。

路德维希和米勒有兴趣了解启蒙资金的增加是否会导致结果发生可衡量的变化。他们的论文研究了死亡率和教育。我们将只关注死亡率。具体来说，他们感兴趣的是对 5-9 岁儿童死亡率的影响，他们将死亡编码为“Head Start 相关”（例如结核病），这意味着 Head Start 计划的目标是减少这些事件。他们还对这种干预措施的长期影响感兴趣，因此重点关注 1973 年至 1983 年期间的死亡率，即拨款撰写干预措施后的八到十八年。他们的数据子集（由 Cattaneo、Titiunik 和 VazquezBare (2017) 汇总）以 LM2007 的形式发布在教科书网站上。

总而言之，路德维希和米勒提出的问题是，1965 年向根据贫困指数选出的 300 个美国县提供赠款援助是否对八到十八年后同一县的儿童死亡率产生了可衡量的影响（相对于那些提供资助的县）没有获得拨款写作援助。

在此应用程序中，测量单位是美国县。结果变量 $Y$ 是 1973-1983 年县死亡率。运行变量 $X$ 是 1960 年县贫困率（贫困线以下人口的百分比）。$c$ 的截止值是 59.1984。（后者只是因为有 300 个县的贫困率等于或高于这个界限。）

21.3 鉴别

在本节中，我们提出回归不连续模型的核心识别定理。回想一下，$\theta$ 是随机个体治疗效果，$\theta(x)=\mathbb{E}[\theta \mid X=x]$ 是条件 ATE。设置 $\bar{\theta}=\theta(c)$，即截止时子群体的条件 ATE。这是由于将截止值设置为 $c$ 的决定而受到边际影响的子群体。核心识别定理指出，$\bar{\theta}$ 是通过温和假设下的回归不连续性设计来识别的。

让$m(x)=\mathbb{E}[Y \mid X=x], m_{0}(x)=\mathbb{E}\left[Y_{0} \mid X=x\right]$和$m_{1}(x)=\mathbb{E}\left[Y_{1} \mid X=x\right]$。请注意 $\theta(x)=m_{1}(x)-$ $m_{0}(x)$。设置 $m(x+)=\lim _{z \downarrow x} m(z)$ 和 $m(x-)=\lim _{z \uparrow x} m(z)$。

以下是断点回归设计的核心辨识定理。这是 Hahn、Todd 和 Van der Klaauw (2001) 的贡献。

定理 21.1 假设处理被指定为 $D=\mathbb{1}\{X \geq c\}$。假设 $m_{0}(x)$ 和 $m_{1}(x)$ 在 $x=c$ 处连续。然后是$\bar{\theta}=m(c+)-m(c-)$。定理 $21.1$ 的条件是最小的。 $m_{0}(x)$ 和 $m_{1}(x)$ 的连续性意味着未处理和处理结果的条件期望持续受到运行变量的影响。以先发制人为例。 $m_{0}(x)$ 是未获得赠款援助的县在考虑贫困率的情况下的平均死亡率。 $D=\mathbb{1}\{X \geq c\}$ 是接受赠款写作援助的县的平均死亡率。没有理由预期这两个函数会出现不连续性。

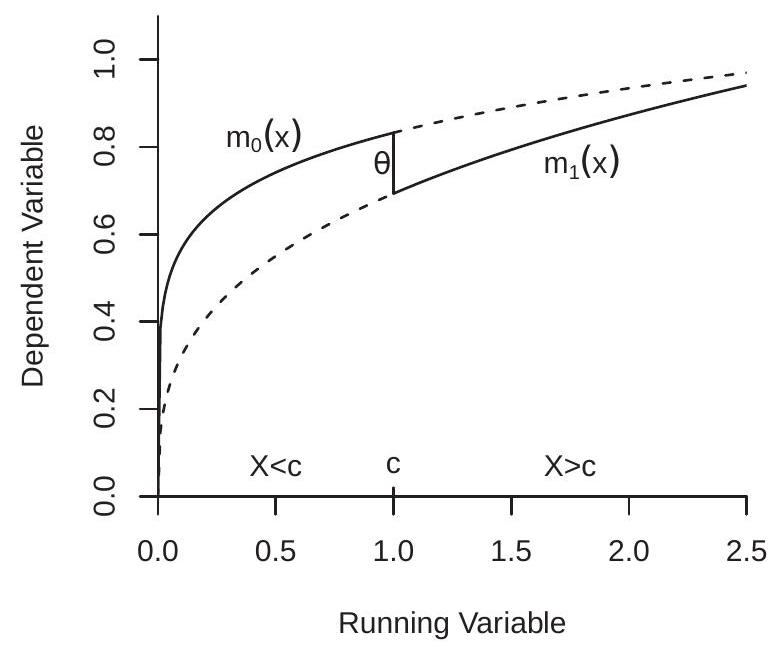
该定理的直觉如图 21.1(a) 所示。绘制的两个连续函数是 CEF $m_{0}(x)$ 和 $m_{1}(x)$。这些函数之间的垂直距离是条件 ATE 函数 $\theta(x)$。由于治疗规则将所有具有 $X \geq c$ 的县分配为治疗组，将所有具有 $X<c$ 的县分配为非治疗组，因此观察到的结果 $m(x)$ 的 CEF 是实线，对于 $x<c$ 和 $m_{1}(x)$ 来说，它等于 $m_{0}(x)$ $ 为 $m_{0}(x)$。 $m_{0}(x)$ 处 $m_{0}(x)$ 的不连续性等于 RDD 处理效果 $m_{0}(x)$。

图 21.1 (a) 中的图旨在模拟我们在 Head Start 应用程序中的预期。我们将 $m_{0}(x)$ 和 $m_{1}(x)$ 绘制为 $x$ 的增函数，这意味着死亡率随着贫困率的增加而增加。我们还绘制了函数图，使 $m_{1}(x)$ 低于 $m_{0}(x)$，因为我们预计拨款援助应该会降低死亡率。

我们从回归理论得知，CEF $m(x)$ 是通用确定的。因此 RDD 治疗效果 $\bar{\theta}=m(c+)-m(c-)$ 也是如此。这是辨识定理的关键要点。回归不连续性设计确定了治疗截止时的条件 ATE。在 Head Start 示例中，这是贫困率为 $59.1984 %$ 的县的 ATE。使用 $\bar{\theta}$ 推断其他县的 ATE 是外推法。如图21.1(a)所示，全部识别为实线，虚线未识别。因此，RDD 方法的局限性在于它估计的治疗效果范围狭窄。

RDD 处理效果的识别与函数 $m_{0}(x)$ 和 $m_{1}(x)$ 的非参数处理交织在一起。如果采用参数（例如线性）形式，则 $x<c$ 和 $x \geq c$ 的最佳拟合近似值通常会具有不连续性，即使真正的 CEF 是连续的。因此，非参数处理对于防止将非线性错误地标记为不连续性至关重要。

定理 $21.1$ 的形式证明很简单。我们可以将观察到的结果写为 $Y=Y_{0} \mathbb{1}\{X<c\}+$ $Y_{1} \mathbb{1}\{X \geq c\}$。我们发现以 $X=x$ 为条件的期望

\[ m(x)=m_{0}(x) \mathbb{1}\{x<c\}+m_{1}(x) \mathbb{1}\{x \geq c\} . \]

由于 $m_{0}(x)$ 和 $m_{1}(x)$ 在 $x=c$ 处连续，因此我们推导出 $m(c+)=m_{1}(c)$ 和 $m(c-)=m_{0}(c)$。因此，正如所声称的，$m(c+)-m(c-)=m_{1}(c)-m_{0}(c)=\theta(c)$。

21.4 预估

我们的目标是在给定观测值 $\left\{Y_{i}, X_{i}\right\}$ 和已知截止值 $c$ 的情况下估计条件 ATE $\bar{\theta}$。条件 ATE 可以根据 CEF $m(x)$ 计算。考虑到不连续性的非参数 CEF 估计与分别估计未处理观测值 $X_{i}<c$ 和已处理观测值 $X_{i} \geq c$ 的 CEF 相同。 $\bar{\theta}$ 的估计量是相邻估计端点之间的差异。

前两章研究了非参数核和级数回归。研究结果之一是，对于边界估计，首选方法是局部线性 (LL) 回归（第 19.4 节）。相比之下，Nadaraya-Watson 估计量在边界点有偏差（参见第 19.10 节），并且级数估计量在边界处具有较高方差（参见 $20.14$ 节以及 Gelman 和 Imbens (2019)）。因此，局部线性估计是首选，并且是回归不连续性设计中使用最广泛的技术 ${ }^{1}$。

${ }^{1}$ 一些作者除了局部线性估计之外还使用多项式来呼吁“鲁棒性”。正如 Gelman 和 Imbens (2019) 中所主张的那样，应该阻止这种情况。

急剧回归不连续性

领先地位对儿童死亡率的影响

图 21.1：急剧回归不连续性设计

描述估计器集

\[ Z_{i}(x)=\left(\begin{array}{c} 1 \\ X_{i}-x \end{array}\right) . \]

令 $K(u)$ 为核函数，$h$ 为带宽。 $x<c$ 的 LL 系数估计器为

\[ \widehat{\beta}_{0}(x)=\left(\sum_{i=1}^{n} K\left(\frac{X_{i}-x}{h}\right) Z_{i}(x) Z_{i}(x)^{\prime} \mathbb{1}\left\{X_{i}<c\right\}\right)^{-1}\left(\sum_{i=1}^{n} K\left(\frac{X_{i}-x}{h}\right) Z_{i}(x) Y_{i} \mathbb{1}\left\{X_{i}<c\right\}\right) \]

对于 $x \geq c$ 来说是

\[ \widehat{\beta}_{1}(x)=\left(\sum_{i=1}^{n} K\left(\frac{X_{i}-x}{h}\right) Z_{i}(x) Z_{i}(x)^{\prime} \mathbb{1}\left\{X_{i} \geq c\right\}\right)^{-1}\left(\sum_{i=1}^{n} K\left(\frac{X_{i}-x}{h}\right) Z_{i}(x) Y_{i} \mathbb{1}\left\{X_{i} \geq c\right\}\right) . \]

CEF 的估计量是系数向量的第一个元素

\[ \widehat{m}(x)=\left[\widehat{\beta}_{0}(x)\right]_{1} \mathbb{1}\{x<c\}+\left[\widehat{\beta}_{1}(x)\right]_{1} \mathbb{1}\{x \geq c\} . \]

$\bar{\theta}$ 的估计量是 $x=c$ 处的差值

\[ \widehat{\theta}=\left[\widehat{\beta}_{1}(c)\right]_{1}-\left[\widehat{\beta}_{0}(c)\right]_{1}=\widehat{m}(c+)-\widehat{m}(c-) . \]

为了有效估计边界点，建议使用三角核。然而，Epanechnikov 和 Gaussian 具有相似的效率（参见第 19.10 节）。一些作者为矩形内核提供了案例，因为这允许使用标准回归软件。这种便利性的回报是效率损失（根 AMSE 为 3%）。

应绘制 CEF 估计 $\widehat{m}(x)$ 以目视检查回归函数和不连续性。许多作者仅在 $x=c$ 附近的支撑上绘制 CEF，以强调估计的局部性质。应按照第 19.17 节所述计算和绘制置信带。这些是针对未处理和处理子样本分别计算的，但在其他方面与第 19.17 节中描述的相同。

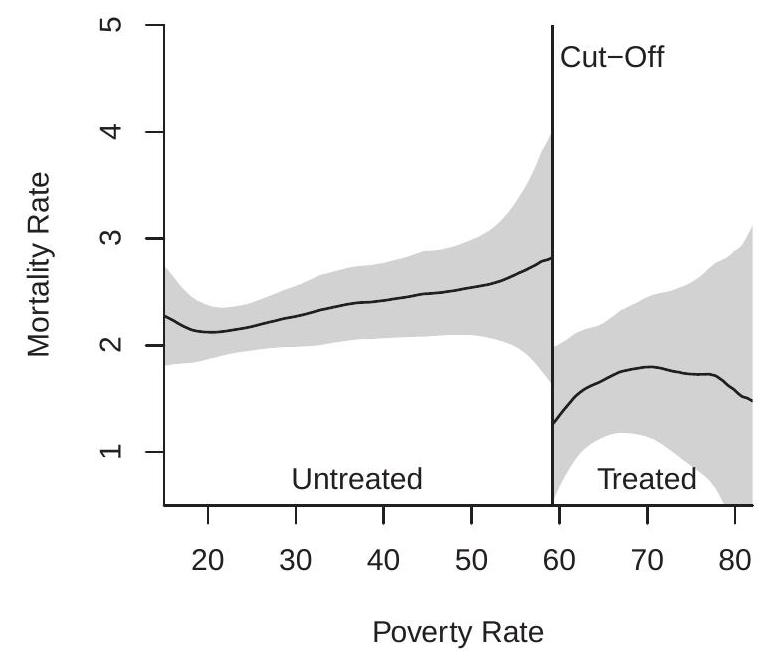
为了说明这一点，图 21.1(b) 显示了我们对 Ludwig-Miller (2007) Head Start RDD 模型对由于热射病相关原因导致的儿童死亡率的估计。我们使用归一化的 ${ }^{2}$ 三角核和 $h=8$ 的带宽。该带宽选择在第 21.6 节中描述。 X 轴是 1960 年的贫困率。截止值是 $59.1984 %$。低于截止线的县没有获得拨款援助，高于截止线的县获得了援助。 y 轴为死亡率（每 100,000 人的死亡人数）。估计结果显示，死亡率随着贫困率的增加而增加（几乎呈线性），并且在 $59.1984 %$ 截止点处出现显着的向下不连续性。不连续性约为每 100,000 人死亡 $1.5$ 。置信带表明估计的 CEF 在边界处具有相当大的不确定性。处理过的样品中的 CEF 呈现非线性且置信带非常宽。

应用经济学文献中习惯于以不同的方式显示图 21.1(b)。许多应用经济学家并不显示置信区间和局部线性估计，而是显示分箱均值。分箱均值以正方形或三角形显示，旨在指示 CEF 非参数形状的原始估计。这种习惯是一个糟糕的选择，一个坏习惯，应该避免。这种做法有两个问题。首先，符号的使用产生了原始数据散点图的视觉印象，而实际上显示的是分箱均值。后者是非参数直方图形状的估计器，应显示为直方图而不是散点图。其次，分箱均值并不是真正的原始数据，而是不同的（且不准确的）非参数估计量。分箱均值与使用矩形核的 Nadaraya-Watson 估计器相同，并且仅在点网格上而不是连续地进行评估。局部线性估计优于 Nadaraya-Watson，任何内核都优于矩形，并且没有理由仅在任意网格上进行评估。这些图并不是“最佳实践”；而是“最佳实践”。相反，它们是由于不规范的实践而产生的坏习惯。最佳实践是绘制最佳的非参数估计量并绘制置信区间以表达不确定性。

21.5 推理

如定理 $19.6$ 和 19.9 中所述，LL 估计量 $\widehat{m}(x)$ 在标准正则条件下是渐近正态的。这扩展到 RDD 估计器 $\widehat{\theta}$。它具有渐近偏差

\[ \operatorname{bias}[\widehat{\theta}]=\frac{h^{2} \sigma_{K^{*}}^{2}}{2}\left(m^{\prime \prime}(c+)-m^{\prime \prime}(c-)\right) \]

和方差

\[ \operatorname{var}[\widehat{\theta}]=\frac{R_{K}^{*}}{n h}\left(\frac{\sigma^{2}(c+)}{f(c+)}+\frac{\sigma^{2}(c-)}{f(c-)}\right) . \]

渐近方差可以通过两个边界回归估计量的渐近方差估计量之和来估计，如第 19.16 节所述。令 $\widetilde{e}_{i}$ 为留一预测误差并设置

\[ \begin{gathered} Z_{i}=\left(\begin{array}{c} 1 \\ X_{i}-c \end{array}\right) \\ K_{i}=K\left(\frac{X_{i}-c}{h}\right) . \end{gathered} \]

${ }^{2}$ 标准化为具有单位方差。某些软件实现了缩放后的三角内核以支持 [-1,1]。如果带宽乘以 $\sqrt{6}$，结果是相同的。例如，我使用 $h=8$ 和归一化三角核的估计与使用带宽为 $h=19.6$ 的 $[-1,1]$ 三角核的估计相同。协方差矩阵估计量是

\[ \begin{aligned} \widehat{\boldsymbol{V}}_{0} &=\left(\sum_{i=1}^{n} K_{i} Z_{i} Z_{i}^{\prime} \mathbb{1}\left\{X_{i}<c\right\}\right)^{-1}\left(\sum_{i=1}^{n} K_{i}^{2} Z_{i} Z_{i}^{\prime} \widetilde{e}_{i}^{2} \mathbb{1}\left\{X_{i}<c\right\}\right)\left(\sum_{i=1}^{n} K_{i} Z_{i} Z_{i}^{\prime} \mathbb{1}\left\{X_{i}<c\right\}\right)^{-1} \\ \widehat{\boldsymbol{V}}_{1} &=\left(\sum_{i=1}^{n} K_{i} Z_{i} Z_{i}^{\prime} \mathbb{1}\left\{X_{i} \geq c\right\}\right)^{-1}\left(\sum_{i=1}^{n} K_{i}^{2} Z_{i} Z_{i}^{\prime} \widetilde{e}_{i}^{2} \mathbb{1}\left\{X_{i} \geq c\right\}\right)\left(\sum_{i=1}^{n} K_{i} Z_{i} Z_{i}^{\prime} \mathbb{1}\left\{X_{i} \geq c\right\}\right)^{-1} . \end{aligned} \]

$\widehat{\theta}$ 的渐近方差估计量是这两个协方差矩阵估计量 $\left[\widehat{\boldsymbol{V}}_{0}\right]_{11}+\left[\widehat{\boldsymbol{V}}_{0}\right]_{11}$ 的第一个对角元素之和。 $\hat{\theta}$ 的标准误差是方差估计量的平方根。

关于治疗效果 $\bar{\theta}$ 的推论陈述会受到偏差的影响，就像在任何非参数估计环境中一样。一般来说，偏差的程度是不确定的。有两个建议可能有助于减少有限样本偏差。首先，使用公共带宽来估计每个子样本的 LL 回归。当 $m(x)$ 在 $x=c$ 处具有连续二阶导数时，这将导致零一阶渐近偏差。其次，使用小于 AMSE 最佳带宽的带宽。这减少了偏差，但代价是增加了方差和标准误差。总的来说，这会导致更诚实的推理陈述。

表 21.1：启蒙援助对儿童死亡率影响的 RDD 估计

为了说明这一点，表 $21.1$ 展示了 Head Start 治疗效果的 RDD 估计（拨款援助对贫困率处于政策截止点的县的影响）。这等于图 21.1(b) 中估计的 CEF 之间的垂直距离。点估计值为 $-1.51$，标准误差为 $0.71$。无效果检验的 t 统计量的 p 值为 $3 %$，与传统水平的统计显着性一致。估计政策影响很大。报告指出，联邦拨款援助以及由此导致的 Head Start 计划支出激增，导致目标死亡率长期下降，每 10 万名儿童下降约 5 美元。鉴于截止时未经治疗的儿童死亡率估计为每 100,000 名儿童 $3.3$，死亡率下降了近 $50 %$。

21.6 带宽选择

在非参数估计中，最关键的选择是带宽。这在 RDD 估计中尤其重要，因为对于最佳带宽选择方法尚未达成广泛共识。因此，在估计之前计算几个基于数据的带宽规则是谨慎的。我将描述两种基于 RDD 估计器全局拟合的简单方法。

我们的第一个建议是修改 Fan 和 Gijbels (1996) 的经验法则 (ROT) 带宽 (19.9)，以允许 $x=c$ 处出现不连续性。该方法需要参考模型。 FanGijbels 方法的适度扩展是 $q^{t h}$ 阶多项式加上电平移位不连续性。这个型号是

\[ m(x)=\beta_{0}+\beta_{1} x+\beta_{2} x^{2}+\cdots+\beta_{q} x^{q}+\beta_{q+1} D \]

其中 $D=\mathbb{1}\{x \geq c\}$.通过最小二乘法估计该模型，获得系数估计值和方差估计值 $\widehat{\sigma}^{2}$。根据系数估计值计算估计的二阶导数

\[ \widehat{m}^{\prime \prime}(x)=2 \widehat{\beta}_{2}+6 \widehat{\beta}_{3} x+12 \widehat{\beta}_{4} x^{2}+\cdots+q(q-1) \widehat{\beta}_{q} x^{q-2} . \]

(19.9) 中的常数 $\bar{B}$ 估计为

\[ \widehat{B}=\frac{1}{n} \sum_{i=1}^{n}\left(\frac{1}{2} \widehat{m}^{\prime \prime}\left(X_{i}\right)\right)^{2} \mathbb{1}\left\{\xi_{1} \leq X_{i} \leq \xi_{2}\right\} \]

其中 $\left[\xi_{1}, \xi_{2}\right]$ 是评估区域（当 $X$ 有界时，可以设置为等于 $X$ 的支持度）。参考带宽 (19.9) 则为

\[ h_{\mathrm{rot}}=0.58\left(\frac{\widehat{\sigma}^{2}\left(\xi_{2}-\xi_{1}\right)}{\widehat{B}}\right)^{1 / 5} n^{-1 / 5} . \]

Fan-Gijbels 推荐 $q=4$，但其他选择也可用于多项式阶数。 ROT 带宽 (21.3) 适用于任何标准化（方差一）内核。对于 $|u| \leq 1$ 的非标准化矩形核 $K(u)=1 / 2$，将常量 $0.58$ 替换为 $1.00$。对于 $|u| \leq 1$ 的非标准化三角核 $K(u)=1-|u|$，将常量 $0.58$ 替换为 $1.42$。

另一种有用的方法是交叉验证。 RDD 估计器的 CV 本质上与任何其他非参数估计器相同。对于每个带宽，计算留一残差并记录它们的平方和。最小化此标准的带宽是 CV 选择的选择。作为 $h$ 函数的 CV 准则图可以帮助确定拟合相对于带宽的敏感度。

这两个提案旨在产生具有全局精度的带宽 $h$。另一种选择是带宽选择规则，其目标是达到或接近截止值的精度。全局方法的优点是它是一个更简单的估计问题，因此更准确且变量更少。带宽估计是一个难题。带宽估计中的噪声将转化为 RDD 估计的估计噪声。另一方面，以截止精度为目标的方法则针对感兴趣的对象。这是一个具有挑战性的估计问题，因此我不会进一步审查它。具体提案请参见 Imbens 和 Kalyanaraman (2012)、Arai 和 Ichimura (2018) 以及 Cattaneo、Idrobo、Titiunik (2020)。

折衷方案是计算 CV 标准，评估区域 $\left[\xi_{1}, \xi_{2}\right]$ 是 $X$ 完全支持的子集，中心接近截止值。一些早期的评论论文推荐了这种方法。这种方法的挑战在于 CV 标准是一个噪声估计器，通过限制评估区域，我们增加了其估计方差。这会增加噪音。

在应用程序中，我建议您首先计算多项式阶 $q$ 的多个值的 Fan-Gijbels ROT 带宽。比较结果时要注意多项式回归中系数的精度。如果高阶功率估计不精确，则带宽估计也可能有噪声。其次，找到最小化交叉验证标准的带宽。绘制 CV 标准。如果它相对平坦，则表明您很难对带宽进行排名。结合以上信息来选择 AMSE 最小化带宽。然后稍微减少此带宽（也许 25%）以减少估计偏差。

一些稳健性检查（使用替代带宽进行估计）是谨慎的，但也仅限于此。鲁棒性热潮的一个相当奇怪的含义是希望结果不随带宽而变化。相反，如果真正的回归函数是非线性的，那么结果将随带宽而变化。您应该期望的是，当您减少带宽时，估计函数将显示形状和噪声的组合，并伴随更宽的置信带。当您增加带宽时，估计值将会变直，置信带也会变窄。狭窄意味着估计值减少了方差，但这是以增加（且不确定）偏差为代价的。我们使用 Ludwig-Miller (2007) Head Start 应用程序进行说明。我们使用 $q=2,3$ 和 4 计算修改后的 FanGijbels ROT，获得 $h_{\mathrm{rot}}(q=2)=24.6, h_{\mathrm{rot}}(q=3)=11.0$ 和 $h_{\text {rot }}(q=4)=5.2$ 的带宽。这些结果对多项式的选择敏感。检查这些多项式回归，我们发现第三和第四个系数估计值具有较大的标准误差，因此存在噪声。接下来我们评估了区域 [1,30] 上的交叉验证标准（未显示）。我们发现 CV 标准随着 $h$ 单调递减，尽管对于 $h \geq 20$ 来说相当平坦。本质上，CV 标准建议使用无限带宽，这意味着使用同等权重的所有观测值。由于我们想要小于 AMSE 最优的带宽，因此我们倾向于较小的带宽，并使用 $q=3$ 和 $q=4$ 对 ROT 带宽进行粗略平均，以获得 $h=8$。这是本章所示的经验结果中使用的带宽。

较大的带宽会导致更平坦（更线性）的估计条件平均函数和更小的估计先行效应。较小的带宽会导致估计的条件平均函数的曲率更大，特别是对于截止以上的部分。

21.7 带有协变量的 RDD

定理 $21.1$ 的一个强大含义是协变量对于识别条件 ATE 不是必需的。这意味着增强回归模型以包含协变量对于估计和推断来说并不是必需的。但估计的精度会受到影响。包含相关协变量可以减少方程误差。因此，应谨慎考虑在可用时添加相关协变量。

将变量表示为 $(Y, X, Z)$，其中 $Z$ 是协变量向量。再次考虑潜在结果框架，其中 $Y_{0}$ 和 $Y_{1}$ 是经过治疗和未经治疗的结果。假设 CEF 采用部分线性形式

\[ \begin{aligned} &\mathbb{E}\left[Y_{0} \mid X=x, Z=z\right]=m_{0}(x)+\beta^{\prime} z \\ &\mathbb{E}\left[Y_{1} \mid X=x, Z=z\right]=m_{1}(x)+\beta^{\prime} z . \end{aligned} \]

为简单起见，我们假设两个方程中的线性系数相同。这不是必需的，但可以简化估计策略。由此可见，$Y$ 的 CEF 等于

\[ m(x, z)=m_{0}(x) \mathbb{1}\{x, c\}+m_{1}(x) \mathbb{1}\{x \geq c\}+\beta^{\prime} z . \]

定理 $21.1$ 的小扩展表明条件 ATE 是 $\bar{\theta}=m(c+, z)-m(c-, z)$。

不同的作者提出了使用协变量模型估计 RDD 的不同方法。首选方法是 Robinson (1988) 的估计。参见第 19.24 节。（这是首选，因为罗宾逊证明了它是半参数有效的，而其他建议没有效率依据。）估计方法如下。

使用 RDD 局部线性估计器在 $X_{i}$ 上回归 $Y_{i}$，得到第一步拟合值 $\widehat{m}_{i}=$ $\widehat{m}\left(X_{i}\right)$
使用 LL 回归，将 $Z_{i 1}$ 回归到 $X_{i}, \ldots$ 上的 $X_{i}, Z_{i 2}$ 上，将 $Z_{i k}$ 回归到 $X_{i}$ 上，获得协变量的拟合值，例如 $\widehat{g}_{1 i}, \ldots, \widehat{g}_{k i}$。
对 $Z_{1 i}-\widehat{g}_{1 i}, \ldots, Z_{k i}-\widehat{g}_{k i}$ 回归 $Y_{i}-\widehat{m}_{i}$ 以获得系数估计值 $\widehat{\beta}$ 和标准误差。
构造残差$\widehat{e}_{i}=Y_{i}-Z_{i}^{\prime} \widehat{\beta}$。 5. 使用 RDD 局部线性估计器在 $X_{i}$ 上回归 $\widehat{e}_{i}$，以获得非参数估计器 $\widehat{m}(x)$、条件 ATE $\widehat{\theta}$ 和相关标准误差。

正如 Robinson (1988) 所示以及第 19.24 节中所讨论的，上述估计量是半参数有效的，传统的渐近理论有效，并且传统的推理也是有效的。因此，估计器可用于评估条件 ATE。

如上所述，在正确的规范下，包含协变量不会改变条件 ATE 参数 $\bar{\theta}$。然而，包含协变量可能会影响远离不连续点 $x$ 的条件均值函数 $m(x)$。协变量还会影响估计器的精度和标准误差。

为了说明这一点，我们用两个协变量来增强 Ludwig-Miller Head Start 估计：县级黑人人口百分比和县级城市人口百分比。这些变量可以被视为收入的代理。我们使用罗宾逊估计器来估计模型。估计的非线性函数$m(x)$如图21.2(a)所示，系数估计见表21.1。

比较图 21.2(a) 和图 21.1(b)，估计的条件 ATE（政策的治疗效果）大致相同，但 $m(x)$ 的形状不同。包含协变量后，$m(x)$ 变得相当平坦。检查表 $21.1$ 我们可以看到估计的治疗效果与没有协变量的基线模型几乎相同。我们还看到黑人百分比的系数为正，城市百分比的系数为负，这与这些作为收入代理的观点一致。

带有协变量的 RDD

贫困率直方图

图 21.2：RDD 诊断

21.8 一个简单的 RDD 估计器

简单的 RDD 估计器可以通过使用传统软件的标准回归来实现。它相当于具有非归一化矩形带宽的 LL 估计器。估计回归

\[ Y=\beta_{0}+\beta_{1} X+\beta_{3}(X-c) D+\theta D+e \]

对于观测值的子样本，使得$|X-c| \leq h$。系数估计 $\widehat{\theta}$ 是估计的条件 ATE，并且可以使用回归标准误差按常规方式进行推理。最重要的选择是带宽。 ROT 选择是 (21.3)，用 $1.00$ 替换常量 $0.58$。

为了说明这一点，请看 Head Start 示例。对于归一化三角核，我们使用了 $h=8$ 的带宽。这与非标准化矩形核的 $h=8 \sqrt{3} \simeq 13.8$ 带宽一致。我们选取贫困率在 $59.1984 \pm 13.8=[45.4,72.0]$ 区间内的 482 个子样本，并通过最小二乘法估计方程 (21.4)。估计是

\[ \widehat{Y}=\begin{array}{cc} -3.11+ \\ (9.13) & 0.11 \\ (0.17) \end{array} \quad X+\underset{(0.23)}{0.18}(X-59.2) D-\underset{(1.06)}{2.20} D . \]

条件 ATE 的点估计 $-2.2$ 大于表 $21.1$ 中报告的值，但在抽样变化范围内。效果的标准误差也较大，这与我们的预期一致，即矩形核估计器不太准确。

21.9 密度不连续性测试

核心辨识定理假设 CEF $m_{0}(x)$ 和 $m_{1}(x)$ 在截止点连续。如果运行变量被寻求或避免治疗的个人操纵，这些假设可能会被违反。为获得治疗而进行的操纵可能会导致运行变量集中在临界值之上或之下。如果没有操纵，我们预计 $X$ 的密度在 $x=c$ 处是连续的，但如果有操纵，我们预计 $X$ 的密度在 $x=c$ 处可能会不连续。

合理的规格检查是评估 $X$ 的密度 $f(x)$ 在 $x=c$ 处是否连续。然而，在实现过程中需要注意一些，因为传统的密度估计器会平滑不连续性，并且传统的密度估计器在边界点处有偏差（类似于 Nadaraya-Watson 估计器在边界点处的偏差）。

一个简单的目视检查是带有窄箱的运行变量的直方图，经过精心构建，以便没有箱跨越截止值。如果直方图箱在截止点的一侧没有显示聚束的证据，则这与密度在截止点处连续的假设是一致的；另一方面，如果任一侧都有明显的尖峰，则这与正确规格的假设不一致。

在 Head Start 示例中，运行变量是由各个县操纵的，这是不可信的，因为它是由联邦机构在 1965 年根据 1960 年人口普查构建的。尽管如此，我们还是可以检查证据。在图 21.2(b) 中，我们显示了运行变量（县贫困率）的频率计数直方图，箱宽度为 2，构建后箱端点之一恰好落在截止点（实线）。直方图似乎在其支撑范围内不断下降。特别是没有视觉证据表明在截止点周围聚集。

McCrary (2008) 对截止处的密度连续性进行了正式测试。我在这里只做一个简单的总结；详细信息请参阅他的论文。第一步是精细直方图估计器，类似于图 21.2(b)，但箱宽度更窄。第二步是应用 RDD 局部线性估计器，将直方图高度视为结果变量，并将箱中点视为运行变量。这是一个局部线性密度估计器，不受传统核密度估计器的边界偏差问题的影响。 RDD 条件 ATE 是截止处的密度差。 McCrary 推导了密度差估计量的渐近分布，并提出了适当的 t 统计量来检验连续密度的假设。如果统计数据很大，这就是反对无操纵假设的证据，表明 RDD 设计不合适。

21.10 模糊回归不连续性

急剧的回归不连续性要求截止点将治疗与未治疗完全分开。另一种情况是这种分离不完美，但治疗的条件概率在截止点是不连续的。这称为模糊回归不连续性 (FRD)。

再次考虑潜在结果框架，其中 $Y_{0}$ 和 $Y_{1}$ 是未经治疗和经过治疗的结果，$\theta=Y_{1}-Y_{0}$ 是治疗效果，$X$ 是运行变量，截止时的条件平均治疗效果为 $ matheq5$ 和 $D=1$ 表示治疗。定义治疗的条件概率

\[ p(x)=\mathbb{P}[D=1 \mid X=x] . \]

以及 $p(c+)$ 和 $p(c-)$ 截止处的左右极限。 FRD 在 $p(c+) \neq p(c-)$ 时适用。

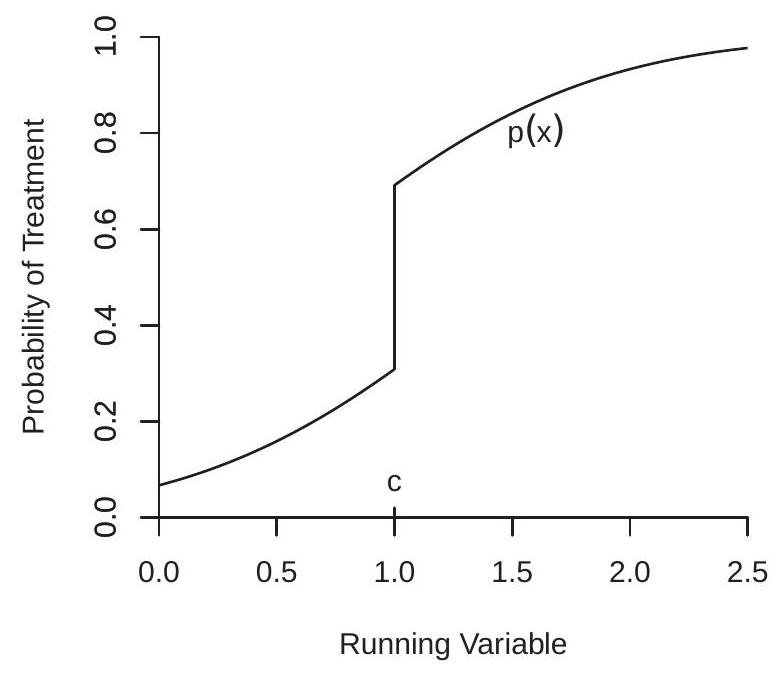
这种情况如图 21.3(a) 所示。这将治疗的条件概率显示为运行变量 $X$ 的函数，在 $X=c$ 处存在不连续性。

条件治疗概率

模糊回归不连续性

图 21.3：模糊回归不连续性设计

以下是断点回归设计的核心辨识定理。这是 Hahn、Todd 和 Van der Klaauw (2001) 的成果。

定理 21.2 假设 $m_{0}(x)$ 和 $m_{1}(x)$ 在 $x=c, p(x)$ 处连续，在 $x=c$ 处不连续，并且对于 $c$ 附近的 $X$，$D$ 独立于 $\theta$。然后

\[ \bar{\theta}=\frac{m(c+)-m(c-)}{p(c+)-p(c-)} . \]

定理 $21.2$ 是比定理 $21.1$ 更实质性的识别结果，因为它本质上令人惊讶。它指出，条件 ATE 由 CEF 和条件概率函数在所述假设下的不连续性之比来确定。这拓宽了断点回归框架的潜在应用范围，超越了 Sharp RDD。

除了 $p(x)$ 的不连续性之外，与定理 $21.1$ 相关的关键附加假设是治疗 $D$ 独立于 $X=x$ 的治疗效果 $\theta$。这是一个强有力的假设。这意味着治疗分配是随机分配给 $X$ 接近 $c$ 的个体。例如，这不允许个体选择治疗，因为治疗效果高的个体 $\theta$ 比治疗效果低的个体 $\theta$ 更有可能寻求治疗。 Hahn、Todd 和 Van der Klaauw（2001）使用了更强的假设，即治疗效果 $p(x)$ 在个体之间是恒定的。

图 21.3(b) 显示了结果。两条虚线是平均潜在结果 $m_{0}(x)$ 和 $m_{1}(x)$。实现的 CEF $m(x)$ 是使用面板 (a) 中显示的概率函数的这两个函数的概率加权平均值。由于概率函数在 $x=c$ 处不连续，因此 CEF $m(x)$ 在 $x=c$ 处也是不连续的。然而，不连续性并不是完整的条件 ATE $\bar{\theta}$。定理 $21.2$ 的重要贡献是条件 ATE 等于面板 (b) 和 (a) 中不连续性的比率。

为了证明该定理，首先观察观察到的结果是

\[ \begin{aligned} Y &=Y_{0} \mathbb{1}\{D=0\}+Y_{1} \mathbb{1}\{D=1\} \\ &=Y_{0}+\theta \mathbb{1}\{D=1\} . \end{aligned} \]

以 $X=x$ 为条件对 $x$ 接近 $c$ 进行期望，我们得到

\[ \begin{aligned} m(x) &=m_{0}(x)+\mathbb{E}[\theta \mathbb{1}\{D=1\} \mid X=x] \\ &=m_{0}(x)+\theta(x) p(x) \end{aligned} \]

其中第二个等式使用以下假设：$\theta$ 和 $D$ 对于 $c$ 附近的 $X$ 是独立的。 $c$ 的左极限和右极限是

\[ \begin{aligned} &m(c+)=m_{0}(c)+\bar{\theta} p(c+) \\ &m(c-)=m_{0}(c)+\bar{\theta} p(c-) . \end{aligned} \]

采取差异并重新排列我们建立定理。

21.11 FRD的估计

如 (21.2) 所示，间断点 $m(c+)-m(c-)$ 的 LL 估计量是通过在截止点两侧 $X$ 上 $Y$ 的局部线性回归获得的，从而导致

\[ \widehat{m}(c+)-\widehat{m}(c-)=\left[\widehat{\beta}_{1}(c)\right]_{1}-\left[\widehat{\beta}_{0}(c)\right]_{1} . \]

类似地，不连续性 $p(c+)-p(c-)$ 的 LL 估计器 $\hat{p}(c+)-\widehat{p}(c-)$ 可以通过 $Y$ 在截止点两侧 $D$ 上的局部线性回归来获得。除以我们得到条件 ATE 的估计量

\[ \widehat{\theta}=\frac{\widehat{m}(c+)-\widehat{m}(c-)}{\widehat{p}(c+)-\widehat{p}(c-)} . \]

这概括了尖锐的 RDD 估计器，在这种情况下为 $p(c+)-p(c-)=1$。

该估计量与二元工具 IV 回归中的结构系数和估计量 (12.28) 的 Wald 表达式 (12.27) 非常相似。事实上，$\widehat{\theta}$ 可以被认为是 $Y$ 使用工具 $D$ 在 $X$ 上进行回归的局部加权 IV 估计器。然而，实现估计的最简单方法是使用上面的 $\widehat{\theta}$ 表达式。

估计器 (21.7) 需要四个 LL 回归。目前尚不清楚分子和分母是否应使用公共带宽，或者不同的带宽是否是更好的选择。带宽选择至关重要。除了评估 $Y$ 回归对 $X$ 的拟合度之外，检查 $D$ 对 $X$ 回归对估计器 $\hat{p}(x)$ 的拟合度也很重要。后者是 IV 模型的简化形式。识别取决于其精度。

FRD 条件 ATE 的识别取决于 $x=c$ 处条件概率 $p(x)$ 的不连续性大小。一个小的不连续性将导致仪器故障问题。

标准误差的计算方法与 IV 回归类似。令 $s(\widehat{\theta})$ 为标准错误 $\widehat{m}(c+)-$ $\widehat{m}(c-)$。那么 $\widehat{\theta}$ 的标准错误是 $s(\widehat{\theta}) /|\widehat{p}(c+)-\widehat{p}(c-)|$。

在 FRD 应用中，建议绘制估计函数 $\widehat{m}(x)$ 和 $\widehat{p}(x)$ 以及置信带以评估精度。您正在寻找证据证明 $p(x)$ 中的不连续性是真实且有意义的，以便识别条件 ATE $\theta$。 $m(x)$ 中的不连续性指示条件 ATE 是否非零。如果 $m(x)$ 中没有不连续性，则 $\theta=0$ 中没有不连续性。条件 ATE 的估计是这两个估计的不连续性的比率。

21.12 练习

练习21.1 我们已经描述了$D=\mathbb{1}\{X \geq c\}$ 进行处理时的RDD。假设对 $D=\mathbb{1}\{X \leq c\}$ 进行处理。描述估计条件 ATE $\bar{\theta}$ 时涉及的差异（如果有）。

练习 21.2 假设对 $D=\mathbb{1}\left\{c_{1} \leq X \leq c_{2}\right\}$ 进行处理，其中 $c_{1}$ 和 $c_{2}$ 都位于 $X$ 支撑的内部。确定了哪些治疗效果？

练习21.3 证明(21.1)是通过采用所描述的条件期望得到的。

练习 21.4 解释为什么方程（21.4）对子样本进行估计，其中 $|X-c| \leq h$ 与具有矩形带宽的局部线性回归相同。

练习21.5 使用课本网页上的数据文件LM2007。使用贫困率在 $59.1984 \pm 13.8$ 区间内的子样本（如文本中所述）复制回归 (21.5)。以 $59.1984 \pm 7$ 和 $59.1984 \pm 20$ 为间隔重复。报告您对条件 ATE 和标准误差的估计。因变量是 mort_age59_related_postHS。（运行变量是 povrate60。）

练习21.6 使用课本网页上的数据文件LM2007。复制表 21.1 中报告的基线 RDD 估计。这使用带宽为 $h=8$ 的归一化三角内核。（如果您使用非标准化三角核（例如在 Stata 中使用的），这对应于 $h=19.6$ 的带宽）。使用 $h=4$ 和 $h=12$ 的带宽重复此操作（如果使用非标准化三角核，则使用 $h=9.8$ 和 $h=29.4$）。报告您对条件 ATE 和标准误差的估计。

练习21.7 使用课本网页上的数据文件LM2007。 Ludwig 和 Miller (2007) 表明，对其他形式的死亡率的类似 RDD 估计并未表现出类似的不连续性。执行类似的检查。使用因变量 mort_age59_injury_postHS（5-9 岁年龄组因伤害而导致的死亡率）估计条件 ATE。练习 21.8 进行与上一个练习类似的估计，但使用因变量 mort_age25plus_related_postHS（$25+$ 年龄组中因 HS 相关原因导致的死亡率）。

练习 21.9 进行与上一个练习类似的估计，但使用因变量 mort_age59_related_preHS（在 Head Start 计划实施之前，1959 年至 1964 年 5-9 岁年龄组中因 HS 相关原因导致的死亡率）开始）。