第18章: 双重差分法

18 双重差分法

18.1 介绍

估计政策变化影响的最流行的方法之一是差异中的差异法，通常称为“差异中的差异”。估计通常是双向面板数据回归，以政策指标作为回归量。通常建议使用聚类方差估计进行推理。

为了将差异估计的差异解释为政策效应，需要满足三个关键条件。首先，估计的回归是正确的条件期望。特别是，这要求正确包含所有趋势和相互作用。其次，政策是外生的，它满足条件独立性。第三，不存在与政策变化同时发生的其他相关未纳入因素。如果满足这些假设，则差异估计值的差异是有效的因果效应。

18.2 新泽西州最低工资

差异法中的差异最著名的应用是 Card 和 Krueger (1994)，他们研究了新泽西州 1992 年将最低小时工资从 \(\$ 4.25\) 提高到 \(\$ 5.05\) 的影响。古典经济学告诉我们，最低工资的提高将导致就业减少和物价上涨。为了调查这种影响的严重程度，作者在 1992 年 2 月 15 日至 1992 年 3 月 4 日（最低工资增长颁布之前）期间对新泽西州的 331 家快餐店进行了调查，并在此期间再次进行了调查1992年5月11日至1992年12月31日（颁布后）。快餐店被选为调查对象，因为它们是最低工资雇员的主要雇主。变化前，大约 \(30 %\) 的抽样工人的最低工资为 \(\$ 4.25\)。

表 18.1：快餐店的平均就业人数

	New Jersey	Pennsylvania	Difference
Before Increase	\(20.43\)	\(23.38\)	\(2.95\)
After Increase	\(20.90\)	\(21.10\)	\(0.20\)
Difference	\(0.47\)	\(-2.28\)	\(\mathbf{2 . 7 5}\)

数据文件CK1994是从原始Card-Krueger数据集中提取的，并发布在教科书网页上。表 \(18.1\)（第一列）显示最低工资上涨前后新泽西州快餐店全职等效员工 \({ }^{2}\) 的平均人数 \({ }^{1}\)。增加之前，平均员工人数为 20.4 人。增加后平均员工人数为20.9人。与传统理论的预测相反，就业人数略有增加（每家餐厅增加 \(0.5\) 员工）而不是减少。

这种估计——就业变化——可以称为差异估计。这是就业的变化与政策的变化同时发生。解释上的一个困难是，所有的就业变化都归因于政策。它没有提供反事实的直接证据——如果最低工资没有增加会发生什么。

差异估计器中的差异通过将处理样本中的变化与对照样本中的可比变化进行比较来改进差异估计器。

卡德和克鲁格选择宾夕法尼亚州东部作为他们的对照样本。 1992 年，宾夕法尼亚州的最低工资保持在每小时 1 美元。年初，两个州的快餐店起薪相似。这两个地区（新泽西州和宾夕法尼亚州东部）还有更多相似之处。影响一个州的任何趋势或经济冲击都可能影响两个州。因此卡德和克鲁格认为将宾夕法尼亚州东部作为对照是合适的。这意味着，在没有提高最低工资的情况下，他们预计新泽西州和宾夕法尼亚州东部的就业情况也会发生同样的变化。

卡德和克鲁格在调查新泽西州餐馆的同时，还对宾夕法尼亚州东部的 79 家快餐店进行了调查。表 18.1 的第二列显示了相当于全职员工的平均人数。政策变更前，平均员工人数为 23.4 人。政策改变后，平均数量为 21.1。因此，在宾夕法尼亚州，每家餐厅的平均就业人数减少了 \(2.3\) 员工。

将宾夕法尼亚州视为对照意味着将新泽西州 (0.5) 的变化与宾夕法尼亚州 \((-2.3)\) 的变化进行比较。差异（每家餐厅 \(2.75\) 员工）是最低工资增长影响的双重差分估计。与传统经济理论完全相反，这一估计表明就业人数增加而不是减少。这一令人惊讶的估计已在经济学家 \({ }^{3}\) 和大众媒体中广泛讨论。

以回归格式重写表 \(18.1\) 中的估计值是有建设性的。令 \(Y_{i t}\) 表示在 \(t\) 时间调查的餐厅 \(i\) 的就业情况。令 State \(_{i}\) 为指示州的虚拟变量，其中 State \(_{i}=1\) 代表新泽西州，State \(_{i}=0\) 代表宾夕法尼亚州。令 Time \({ }_{t}\) 为指示时间段的虚拟变量，其中 Time \(e_{t}=0\) 表示政策更改之前的时间段，Time \(18.1\) 表示政策更改之后的时间段。让 \(18.1\) 表示治疗虚拟变量，如果最低工资等于 \(18.1\)，则使用 \(18.1\)；如果最低工资等于 \(18.1\)，则使用 \(18.1\)。在此应用程序中，它等于交互虚拟 \(18.1\) 状态 \(18.1\) 时间 \(18.1\)。

表 \(18.1\) 是两个虚拟变量的饱和回归，因此可以写为回归方程

\[ Y_{i t}=\beta_{0}+\beta_{1} \text { State }_{i}+\beta_{2} \text { Time }_{t}+\theta D_{i t}+\varepsilon_{i t} . \]

事实上，系数可以通过以下对应关系用表 \(18.1\) 来写：

\({ }^{1}\) 如果餐馆在两项调查中缺少全类型等效员工的数量，我们的计算就会下降。

\({ }^{2}\) 跟随卡和克鲁格全职当量员工定义为全职员工、经理和助理经理人数的总和，加上兼职员工人数的二分之一。

\({ }^{3}\) 大多数经济学家并不从字面上理解这一估计 - 他们不相信提高最低工资会导致就业增加。相反，它被解释为证据，表明最低工资的微小变化可能只会对就业水平产生轻微影响。

	New Jersey	Pennsylvania	Difference
Before Increase	\(\beta_{0}+\beta_{1}\)	\(\beta_{0}\)	\(\beta_{1}\)
After Increase	\(\beta_{0}+\beta_{1}+\beta_{2}+\theta\)	\(\beta_{0}+\beta_{2}\)	\(\beta_{1}+\theta\)
Difference	\(\beta_{2}+\theta\)	\(\beta_{2}\)	\(\theta\)

我们看到回归（18.1）中的系数对应于可解释的差异和差异估计值的差异。 \(\beta_{1}\) 是政策变更前一段时间内“新泽西州与宾夕法尼亚州”效果的差异估计值。 \(\beta_{2}\) 是控制状态下时间效应的差异估计量。 \(\theta\) 是差异估计值的差异 - 新泽西州相对于宾夕法尼亚州的变化。

我们对回归（18.1）的估计是

\[ \begin{aligned} & Y_{i t}=23.4-2.9 \text { State }_{i}-2.3 \text { Time }_{t}+2.75 D_{i t}+\varepsilon_{i t} . \\ & \text { (1.4) (1.5) (1.2) (1.34) } \end{aligned} \]

标准误按餐厅进行聚类。正如预期的那样，治疗假人的系数 \(\widehat{\theta}\) 精确等于表 18.1 中差异估计的差异。系数估计可以如所描述的那样进行解释。新泽西州和宾夕法尼亚州之间的变更前差异为 \(-2.9\)，时间效应为 \(-2.3\)。差异效应的差异是\(2.75\)。检验零效应假设的 t 统计量略高于 2，渐近 \(p\) 值为 \(0.04\)。

由于观测值分为状态 \(_{i}=0\) 和状态 \(_{i}=1\) 组，并且时间 \(_{t}\) 相当于时间指数，因此该回归与状态为 \(D_{i t}\) 的 \(Y_{i t}\) 的双向固定效应回归相同和时间固定效应。此外，由于回归量 \(D_{i t}\) 不会因州内个体的不同而变化，如果包含餐厅级别的固定效应而不是州固定效应，则固定效应回归不会改变。 （餐厅固定效应与州一级贬低的任何变量正交。请参见练习 18.1。）因此，上述回归与双向固定效应回归相同

\[ Y_{i t}=\theta D_{i t}+u_{i}+v_{t}+\varepsilon_{i t} \]

其中 \(u_{i}\) 是餐厅固定效应，\(v_{t}\) 是时间固定效应。实现这一目标的最简单方法是使用时间虚拟变量进行单向固定效应回归。估计是

\[ Y_{i t}=\underset{(1.34)}{2.75} D_{i t}-\begin{gathered} 2.3 \\ (1.2) \end{gathered} \text { Time }_{t}+u_{i}+\varepsilon_{i t} \]

与之前的回归相同。

方程（18.3）是基本的双重差分模型。它是响应 \(Y_{i t}\) 对二元策略 \(D_{i t}\) 的双向固定效应回归。系数 \(\theta\) 对应于样本均值的双重差异，可以解释为 \(D\) 对 \(Y\) 的政策影响（也称为处理效果）。 （我们将在下一节中讨论识别。）我们的演示（以及卡德-克鲁格示例）重点关注两个聚合单位（状态）和两个时间段的基本情况。回归公式（18.3）很方便，因为它可以很容易地推广到允许多个状态和时间段。这样做可以为已确定的政策效果提供更有说服力的证据。方程（18.3）也可以通过改变趋势规范和使用连续处理变量来推广。

另一个常见的概括是使用控件 \(X_{i t}\) 来增强回归。这个型号是

\[ Y_{i t}=\theta D_{i t}+X_{i t}^{\prime} \beta+u_{i}+v_{t}+\varepsilon_{i t} \]

许多实证研究报告估计了基本模型和控制回归。例如，我们可以增强 Card-Krueger 回归，以包含变量 hoursopen，即餐厅每天营业的小时数。营业时间较长的餐厅往往会拥有更多的员工。

\[ Y_{i t}=\underset{(1.31)}{2.84} D_{i t}-\underset{(1.2)}{2.2} \text { Time }_{t}+\underset{(0.4)}{1.2} \text { hoursopen }_{i t}+u_{i}+\varepsilon_{i t} . \]

估计的影响是，餐厅每营业一小时就会雇佣额外的 \(1.2\) 员工，并且这种影响在统计上是显着的。估计的治疗效果没有发生有意义的改变。

18.3 鉴别

考虑 \(i=1, \ldots, N\) 和 \(t=1, \ldots, T\) 的双重差分方程 (18.5)。我们感兴趣的是系数 \(\theta\) 是治疗 \(D_{i t}\) 对结果 \(Y_{i t}\) 的因果影响的条件。通过应用 \(2.30\) 节中的定理 \(2.12\) 可以找到答案。

在 \(2.30\) 节中，我们介绍了潜在结果框架，该框架将结果写为治疗、控制和不可观察量的函数。结果（例如在餐馆就业）被写为 \(Y=h(D, X, e)\)，其中 \(D\) 是治疗（最低工资政策），\(X\) 是控制，\(e\) 是未观察因素的向量。模型 (18.5) 指定 \(h(D, X, e)\) 在其参数中是可分离和线性的，并且不可观察量由个体特定、时间特定和特殊效应组成。

我们现在提出了足够的条件，在该条件下系数 \(\theta\) 可以被解释为因果效应。回想一下变换中的双向 (17.65) 并设置 \(\ddot{Z}_{i t}=\left(\ddot{D}_{i t}, \ddot{X}_{i t}^{\prime}\right)^{\prime}\)。

定理 18.1 假设以下条件成立：

1.\(Y_{i t}=\theta D_{i t}+X_{i t}^{\prime} \beta+u_{i}+v_{t}+\varepsilon_{i t}\)。

2.\(\mathbb{E}\left[\ddot{Z}_{i t} \ddot{Z}_{i t}^{\prime}\right]>0\)。

3. \(\mathbb{E}\left[X_{i t} \varepsilon_{i s}\right]=0\) 适用于所有 \(t\) 和 \(s\)。

4. 以 \(X_{i 1}, X_{i 2}, \ldots, X_{i T}\) 为条件，随机变量 \(D_{i t}\) 和 \(\varepsilon_{i s}\) 对于所有 \(t\) 和 \(s\) 在统计上是独立的。

那么 (18.5) 中的系数 \(\theta\) 等于 \(D\) 对 \(Y\) 的平均因果效应（以 \(X\) 为条件）。

条件 1 表明结果等于指定的线性回归模型，该模型在可观察量、个体效应和时间效应中可加性分离。

条件 2 表明变换回归量内的双向具有非奇异设计矩阵。这要求 \(D_{i t}\) 和 \(X_{i t}\) 的所有元素随时间和个体而变化。

条件 3 是固定效应模型中回归量的标准外生性假设。

条件 4 表明治疗变量有条件地独立于特殊误差。这是固定效应回归的条件独立假设。

为了证明定理 18.1，应用 (17.65) 到 (18.5) 内的双向变换。我们获得

\[ \ddot{Y}_{i t}=\theta \ddot{D}_{i t}+\ddot{X}_{i t}^{\prime} \beta+\ddot{\varepsilon}_{i t} . \]

在条件 2 下，投影系数 \((\theta, \beta)\) 是唯一定义的，在条件 3 和 4 下，它们等于线性回归系数。因此 \(\theta\) 是相对于 \(D\) 的回归导数。条件 4 意味着以 \(\ddot{X}_{i t}\) 为条件，随机变量 \(\ddot{D}_{i t}\) 和 \(\ddot{\varepsilon}_{i s}\) 在统计上是独立的。定理 \(2.12\) 表明回归导数 \(\theta\) 等于所述的平均因果效应。

\(D\) 和 \(\varepsilon\) 独立的假设是基本的外生性假设。要将 \(\theta\) 解释为治疗效果，重要的是 \(D\) 被定义为治疗而不是简单地作为交互（时间和状态）虚拟变量。这很微妙。检查方程 (18.5)，回顾 \(D\) 被定义为治疗（最低工资的增加）。在此方程中，误差 \(\varepsilon_{i t}\) 包含回归中未包含的所有变量和效应。因此，如果新泽西州存在与最低工资增长同时发生的其他变化，则假设 \(D\) 和 \(\varepsilon\) 是独立的，这意味着这些同时发生的变化独立于 \(\varepsilon\)，因此不会影响就业。这是一个强有力的假设。条件 4 再次规定，与最低工资增长同时发生的所有其他影响对就业没有影响。如果没有这个假设，就不可能声称差异回归确定了治疗的因果效应。

此外，\(D_{i t}\) 和 \(\varepsilon_{i s}\) 的独立性意味着两者都不会受到对方的影响。这意味着政策（处理）不是根据对任一时期的响应变量的了解而制定的，也意味着在第一个时期的结果（就业）没有因预期即将到来的政策变化而改变。

很难知道 \(D\) 的外生性是否是一个合理的假设。它类似于工具变量回归中的工具外生性。它的有效性取决于清晰的结构论证。基于双重差分规范的实证研究需要明确说明 \(D\) 的外生性，类似于 IV 回归。

就卡德-克鲁格申请而言，作者认为该政策是外生的，因为它是在生效前两年通过的。在该立法通过时，经济处于扩张状态，但在通过时，经济已陷入衰退。这表明，假设 1990 年的政策决定不受 1992 年就业水平的影响是可信的。此外，对经济衰退期间提高最低工资的影响的担忧引发了关于扭转政策的认真讨论，这意味着在第一次调查时，不确定该政策是否会真正实施。因此，当时的就业决定并不是根据即将到来的最低工资上涨而做出的，这似乎是可信的。

然而，作者没有讨论 1992 年新泽西州或宾夕法尼亚州经济中是否发生了其他同时发生的事件，这些事件可能对两个州的就业产生不同的影响。类似的巧合事件可能发生过很多次，这似乎是合理的。这似乎是他们的认同论证中最大的弱点。

辨识（定理 18.1 的条件）还要求正确指定回归模型。这意味着真实模型在指定变量中是线性的，并且包括所有相互作用。由于基本 \(2 \times 2\) 规范是饱和虚拟变量模型，因此它必然是条件期望，因此可以正确指定。在具有两个以上状态或时间段的应用中，情况并非如此，因此在这种情况下需要仔细考虑模型规范。

18.4 多个单位

基本的双重差分模型具有两个聚合单位（例如状态）和两个时间段。如果存在多个单位或多个时间段，则可以获得附加信息。在本节中，我们重点关注多个单元的情况。可以有多个处理单元、多个控制单元或两者都有。在本节中，我们假设周期数为 \(T=2\)。令 \(N_{1} \geq 1\) 为未处理（对照）单元的数量，\(N_{2} \geq 1\) 为已处理单元的数量，\(N=N_{1}+N_{2}\) 为已处理单元的数量。

基本回归模型

\[ Y_{i t}=\theta D_{i t}+u_{i}+v_{t}+\varepsilon_{i t} \]

施加了两个严格的限制。首先，所有单位都同样受到时间的影响，因为 \(v_{t}\) 在 \(i\) 中很常见。其次，治疗效果 \(\theta\) 在所有治疗单位中都是常见的。

卡德-克鲁格数据集仅包含来自两个州的观察结果，但作者确实记录了包括该州区域在内的其他变量。他们将新泽西州分为三个区域（北部、中部和南部），将宾夕法尼亚州东部分为两个区域（1 个区域用于费城东北部郊区，2 个区域用于其余区域）。

表 \(18.2\) 显示了最低工资上涨前后按地区划分的全职等效雇员的平均人数。我们观察到，新泽西州三个地区中的两个地区的就业增长几乎相同，并且所有三个地区的变化都很小。我们还可以观察到，宾夕法尼亚州的两个地区的就业人数均出现下降，但幅度不同。

我们可以通过回归排除检验来检验同等治疗效果 \(\theta\) 的假设。这可以通过向回归添加交互虚拟对象并测试排除交互来完成。由于新泽西州有三个处理区域，因此我们包括与时间指数交互的三个新泽西州区域虚拟中的两个。一般来说，我们会包含 \(N_{2}-1\) 这样的交互。这些系数衡量了不同地区治疗效果的差异。测试这两个系数是否为零，我们得到 \(0.60\) 的 p 值，该值远不显着。因此，我们接受这样的假设：治疗效果 \(\theta\) 在新泽西州地区很常见。

相反，当治疗效果 \(\theta\) 发生变化时，我们将其称为异质治疗效果。这并不违反治疗效果框架，但分析起来可能要复杂得多。 （错误地施加同质治疗效果的模型被错误指定并产生不一致的估计。）

如果控制效果是异质的，则会出现更严重的问题。控制效果是对照组的变化。表 \(18.2\) 详细列出了宾夕法尼亚州两个地区的估计控制效果。虽然这两种估计都是负面的，但彼此之间有些不同。如果效果明显，则不存在同质控制效果。我们可以通过回归排除检验来检验相等控制效应的假设。由于有两个宾夕法尼亚州地区，我们将宾夕法尼亚州地区之一与时间索引的交互纳入其中。 （一般来说，我们会包括 \(N_{1}-1\) 交互作用。）该系数衡量各区域控制效果的差异。我们测试该系数是否为零，获得 \(1.2\) 的 t 统计量和 \(0.23\) 的 p 值。它在统计上不显着，这意味着我们不能拒绝控制效应是同质的假设。

相反，如果控制效果是异质的，那么双重差分估计策略就会被错误指定。该方法依赖于识别可信对照样本的能力。因此，如果相等控制效应的检验拒绝同质控制效应的假设，则应将其视为反对将双重差分参数解释为治疗效应的证据。

表 18.2：快餐店的平均就业人数

	South NJ	Central NJ	North NJ	PA 1	PA 2
Before Increase	\(16.6\)	\(22.0\)	\(22.0\)	\(24.8\)	\(22.2\)
After Increase	\(17.3\)	\(21.4\)	\(22.7\)	\(21.0\)	\(21.2\)
Difference	\(0.7\)	\(-0.6\)	\(0.7\)	\(-3.8\)	\(-1.0\)

18.5 警察能减少犯罪吗？

DiTella 和 Schargrodsky (2004) 使用双重差分法来研究警察在街上的存在是否会减少汽车盗窃的问题。理性犯罪模型预测，可观察到的警察部队的存在将由于威慑作用而降低犯罪率（至少在当地）。然而，因果效应很难衡量，因为警察部队的分配不是外生的，而是根据需求进行分配的。双重差分估计器需要改变警察分配的外生事件。 DiTella-Schargrodsky 的创新在于利用警方对恐怖袭击的反应作为外生变量。

1994 年 7 月，阿根廷布宜诺斯艾利斯的主要犹太中心发生了可怕的恐怖袭击。两周内，联邦政府向该国所有犹太和穆斯林建筑提供了警察保护。 DiTella 和 Schargrodsky (2004) 假设，他们的存在虽然是为了阻止恐怖或报复性袭击，但也能阻止其他街头犯罪，例如部署在当地的警察盗窃汽车。作者收集了 1994 年 4 月至 12 月布宜诺斯艾利斯选定街区的汽车盗窃详细信息，形成了涵盖 876 个城市街区的小组。他们假设恐怖袭击和政府的反应对于汽车盗窃来说是外生的，因此是一种有效的治疗方法。他们假设，对于任何包含犹太机构（以及警察保护）的城市街区来说，威慑效果将是最强的。由于被抓的威胁，潜在的偷车贼将不敢入室行窃。随着与受保护地点距离的增加，威慑效果预计会减弱。因此，作者根据恐怖袭击前后每个街区的平均汽车盗窃数量以及有和没有犹太机构的城市街区之间的平均汽车盗窃数量提出了双重差分估计器。他们的样本有 37 个有犹太机构的街区（处理样本）和 839 个没有机构的街区（对照样本）。

数据文件DS2004是作者的AER复制文件的稍微修改版本，并发布在教科书网页上。

表 18.3：按城市街区划分的汽车盗窃案数量

	Same Block	Not on Same Block	Difference
April-June	\(0.112\)	\(0.095\)	\(-0.017\)
August-December	\(0.035\)	\(0.105\)	\(0.070\)
Difference	\(-0.077\)	\(0.010\)	\(-\mathbf{0 . 0 8 7}\)

表 \(18.3\) 显示每个街区的平均汽车盗窃数量，分别为 7 月袭击前的几个月和 7 月袭击后的几个月，以及有犹太机构（因此从 7 月下旬开始受到警察保护）的城市街区）以及其他城市街区。我们可以看到，受保护的城市街区的平均汽车盗窃数量急剧下降，从每月 \(0.112\) 下降到 0.035 起，而不受保护的街区的平均汽车盗窃数量几乎保持不变，从 \(0.095\) 上升到 \(0.105\) 。取差中之差，我们发现警察存在的效果使汽车盗窃减少了 \(0.087\)，大约为 \(78 %\)。

估计 diff-in-diff 模型的一般方法是形式 (18.3) 的回归，其中 \(Y_{i t}\) 是 \(t\)、\(u_{i}\) 和 \(v_{t}\) 月期间 \(i\) 块上的汽车盗窃数量是区块和月份固定效应。此回归 \(^{4}\) 产生与 \(0.087\) 相同的估计值，因为面板是平衡的并且没有控制变量。

模型 (18.3) 做出了强有力的假设，即治疗效果在五个治疗个月内保持不变。我们在表 \(18.4\) 中研究了这一假设，该表按月份细分了汽车盗窃案。对于对照样本，汽车盗窃数量在几个月内几乎保持不变。对于八个中的七个

\({ }^{4}\) 我们省略了 7 月份的观察结果，因为汽车盗窃数据仅是该月的上半个月。表 18.4：按城市街区划分的汽车盗窃案数量

Pre-Attack	April	Same Block	Not on Same Block	Difference
	May	\(0.112\)	\(0.110\)	\(-0.012\)
	June	\(0.088\)	\(0.100\)	\(0.012\)
Post-Attack	August	\(0.128\)	\(0.076\)	\(-0.052\)
	September	\(0.014\)	\(0.111\)	\(0.064\)
	October	\(0.061\)	\(0.099\)	\(0.085\)
	November	\(0.027\)	\(0.108\)	\(0.047\)
	December	\(0.027\)	\(0.100\)	\(0.073\)
			\(0.106\)	\(0.079\)

每个区块的平均数量从 \(0.10\) 到 \(0.11\) 不等，只有一个月（六月）略低，为 \(0.08\)。在处理样本中，恐怖袭击发生前三个月内每个区块的平均盗窃次数与对照样本中的平均值相似。但在袭击发生后的五个月里，汽车盗窃案的数量普遍减少。平均值范围从 \(0.014\) 到 \(0.061\)。在攻击发生后的每个月，控制样本的盗窃率都较低，平均范围从 \(0.047\) 到 \(0.085\)。鉴于治疗样本的样本量较小（37），这是惊人的一致证据。

我们可以通过包含四个虚拟变量来正式测试治疗效果的同质性，这些虚拟变量用于攻击后四个月与治疗样本的相互作用，然后测试这些变量的排除。此测试的 \(\mathrm{p}\) 值是 \(0.81\)，远非显着。因此，数据中没有理由怀疑同质性假设。

目标是评估警察存在对犯罪威慑的因果效应。让我们对案件进行评估以进行鉴定。将恐怖袭击视为外因似乎是合理的。政府的反应也显得是外生的。两者都与汽车盗窃率没有合理的相关性。我们还观察到，表 \(18.3\) 和 \(18.4\) 中的证据表明，攻击前处理样本和对照样本的盗窃率相似。因此，额外的警察保护似乎是为了预防袭击而提供的，而不是作为预防犯罪的借口。一旦考虑到处理效应，几个月内盗窃率的总体同质性就使警方的反应是因果效应的说法可信。恐怖袭击本身并没有降低汽车盗窃率，因为在治疗样本之外似乎没有可测量的影响。最后，虽然该论文没有明确说明 1994 年 7 月是否有任何其他同时发生的事件可能影响了这些特定的城市街区，但很难为如此大的影响想出其他解释。我们的结论是，这是一个强有力的认同论证。警察的存在大大减少了汽车盗窃的发生率。

作者断言警察的存在可以更广泛地阻止犯罪。这是一个脆弱的扩展，因为该论文没有提供这一主张的直接证据。虽然这似乎是合理的，但我们应该谨慎对待没有证据支持的概括。

总体而言，DiTella 和 Schargrodsky（2004）是对重要政策效果进行清晰阐述和可信识别的双重差异估计的一个极好的例子。

18.6 趋势规范

一些应用程序（包括本章前面介绍的两种）适用于较短的时间段，例如一年，在这种情况下，我们可能不会期望变量具有趋势。其他应用涵盖许多年或几十年，在这种情况下，变量可能会呈趋势。这些趋势可以反映长期增长、商业周期影响、品味变化或许多其他特征。如果趋势指定不正确，则模型将被错误指定，并且由于遗漏变量偏差，估计的政策效果将不一致。考虑双重差分方程 (18.5)。该模型强加了一个强有力的假设，即 \(Y_{i t}\) 的趋势完全由所包含的控件 \(X_{i t}\) 和常见的未观察到的时间分量 \(v_{t}\) 来解释。这可能是相当有限制的。可以合理地预期，不同单位的趋势可能有所不同，并且观察到的控制不能完全捕获趋势。

思考这个问题的一种方法是过度识别。为简单起见，假设没有控件并且面板是平衡的。然后是 \(N T\) 观察值。具有政策效应的双向模型具有 \(N+T\) 系数。除非 \(N=T=2\) 这个模型被过度识别。除了考虑异质治疗效果之外，考虑异质趋势也是合理的。

一种概括是包括线性趋势与控制变量的相互作用。这个型号是

\[ Y_{i t}=\theta D_{i t}+X_{i t}^{\prime} \beta+Z_{i}^{\prime} \delta t+u_{i}+v_{t}+\varepsilon_{i t} . \]

它指定 \(Y_{i t}\) 中的趋势因单位而异，具体取决于控件 \(Z_{i}\)。

更广泛的概括是包括特定于单位的线性时间趋势。这个型号是

\[ Y_{i t}=\theta D_{i t}+X_{i t}^{\prime} \beta+u_{i}+v_{t}+t w_{i}+\varepsilon_{i t} . \]

在此模型中，\(w_{i}\) 是时间趋势固定效应，随单位的不同而变化。如果没有控制，则该模型具有 \(2 N+T\) 系数，并且只要 \(T \geq 4\) 即可识别。

模型（18.6）的估计可以通过三种方式之一来完成。如果 \(N\) 很小（例如，具有状态级数据的应用程序），则可以使用显式虚拟变量方法来估计回归。令 \(d_{i}\) 和 \(S_{t}\) 为虚拟变量，指示 \(i^{t h}\) 单位和 \(t^{t h}\) 时间段。设置\(d_{i t}=d_{i} t\)，个体虚拟人与时间趋势的交互。该方程是通过 \(Y_{i t}\) 在 \(D_{i t}, X_{i t}\)、\(d_{i}, S_{t}\) 和 \(N\) 上的回归来估计的。同样，可以使用回归量 \(N\) 和 \(N\) 应用单向固定效应。

当 \(N\) 很大时，计算上更有效的方法是使用残差回归。对于每个单元 \(i\)，估计每个变量 \(Y_{i t}, D_{i t}, X_{i t}\) 和 \(S_{t}\) 的时间趋势模型。也就是说，对于每个 \(i\) 估计

\[ Y_{i t}=\widehat{\alpha}_{0}+\widehat{\alpha}_{1} t+\dot{Y}_{i t} . \]

这是一个概括性的内部转变。使用残差 \(\dot{Y}_{i t}\) 代替原始观测值。对 \(\dot{D}_{i t}, \dot{X}_{i t}\) 和 \(\dot{S}_{t}\) 进行回归 \(\dot{Y}_{i t}\) 以获得 (18.6) 的估计值。

趋势固定效应 \(\nu_{t}\) 的相关性可以通过显着性检验进行评估。具体来说，可以使用标准排除测试来测试周期虚拟变量的系数为零的假设。类似地，可以使用标准排除检验来测试趋势交互项的显着性。如果测试具有统计显着性，则表明它们的包含与正确的规范相关。不幸的是，当协方差矩阵在单元级别聚集时，无法测试特定于单元的线性时间趋势的显着性。这类似于通过单个观察来测试虚拟变量的显着性的问题。仅当协方差矩阵聚集在更精细的级别时，才能测试特定于单位的时间趋势的显着性。否则协方差矩阵估计是奇异的并且向下偏置。简单的测试会夸大其重要性。

为了简单起见，我们的讨论集中在平衡面板的情况上。这些方法同样适用于使用标准面板数据估计的不平衡面板。

18.7 蓝色法律会影响酒类销售吗？

历史上，美国许多州都禁止或限制周日销售酒精饮料。这些法律被称为“蓝色法律”。近年来，这些法律有所放松。这些变化是否导致酒精饮料的消费增加？ Bernheim、Meer 和 Novarro（2016）利用关于酒精消费和销售时间的详细小组调查了这个问题。观察到的与法律变化同时发生的变化可能反映了潜在的趋势。不同州在不同年份改变法律的事实允许采用双重差分方法来确定治疗效果。

该论文重点关注蒸馏酒销售，尽管葡萄酒和啤酒销售也包含在其数据中。他们的数据集 BMN2016 的删节版本发布在教科书网页上。酒量以人均加仑纯乙醇当量来衡量。这些数据是 1970-2007 年美国 47 个州的州级数据，不平衡。

作者仔细收集了有关周日允许出售酒类的时间的信息。他们区分了在场外消费的场外销售（酒类商店、超市）和在场内消费的场内销售（餐馆、酒吧）。令 \(Y_{i t}\) 表示 \(t\) 年 \(i\) 州人均酒类销量的自然对数。他们的基本模型的简化版本是

OnHours 和 OffHours 是允许的周日场内和场外销售时间数。 UR 是州失业率。 OnOutFlows (OffOutFlows) 是少于邻近州的店内（店外）销售时间的加权数量。添加这些是为了调整可能的跨境交易。该模型包括州和年份固定效应。标准误按州进行聚类。

估计表明，店内销售时间的增加导致酒类销量小幅增长。这与酒精在社交（餐厅和酒吧）环境中作为补充品是一致的。 OffHours 的小且微不足道的系数表明，场外销售时间的增加不会导致酒类销量的增加。这与根据已知时间调整购买的理性消费者是一致的。失业率的负面影响意味着白酒销售是顺周期的。

作者担心他们的动态和趋势规范是否正确指定，因此尝试了一些替代规范和交互。为了理解趋势问题，我们在图 \(18.1\) 中绘制了三个州人均酒类销量对数的时间序列路径：加利福尼亚州、爱荷华州和纽约州。您可以看到，从 1970 年到 1995 年左右，这三个指标均呈现下降趋势，然后又呈上升趋势。然而，这三个系列的趋势组成部分并不相同。这表明将这些趋势视为各州的共同趋势可能是不正确的。

如果我们扩展基本模型以包括特定于州的线性趋势，则估计如下。

\[ \begin{aligned} & +0.005 \text { OnOutFlows }{ }_{i t}-0.005 \text { OffOutFlows }{ }_{i t}+t w_{i}+u_{i}+v_{t}+\varepsilon_{i t} \text {. } \\ & (0.005) \quad(0.005) \end{aligned} \]

OnHours 的估计系数降至零并且变得微不足道。其他估计值没有发生有意义的变化。作者仅在脚注中讨论了这种回归，指出添加特定于州的趋势“需要大量数据，而留下的变化太少，无法识别感兴趣的影响”。这是一个不幸的说法，因为实际上标准误差已经减少，而不是增加，

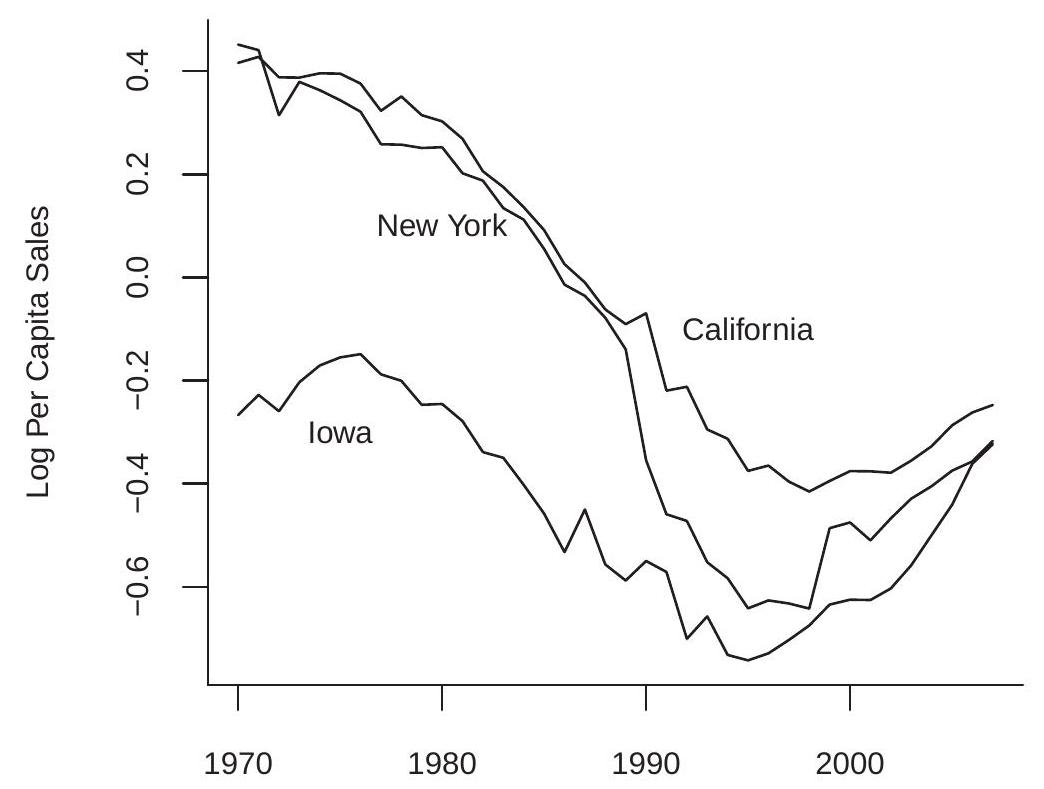
图 18.1：按州划分的酒类销售情况

表明效果得到了更好的识别。问题在于 OnHours 和 OffHours 是有趋势的，而且趋势因州而异。这意味着这些变量与状态趋势相互作用相关。忽略趋势交互作用会导致遗漏变量偏差。这就解释了为什么当趋势规范改变时系数估计值也会改变。

Bernheim、Meer 和 Novarro（2016）是细致的实证工作的一个很好的例子，仔细关注细节并隔离治疗策略。这也是一个很好的例子，说明了对趋势规范的关注如何影响结果。

18.8 检查您的代码：堕胎会影响犯罪吗？

在一篇备受讨论的论文中，Donohue 和 Levitt (2001) 使用双重差分方法发展了一种不同寻常的理论。 20 世纪 90 年代，美国各地的犯罪率急剧下降。多诺休和莱维特推测，一个重要的解释是 1973 年具有里程碑意义的堕胎合法化。后者可能通过两个潜在渠道影响犯罪率。首先，它减少了年轻男性的群体规模。其次，它减少了面临犯罪行为风险的年轻男性的群体规模。这表明 20 年后，20 世纪 70 年代初堕胎数量的大幅增加将转化为犯罪率的大幅减少。

正如您可能想象的那样，这篇论文在多个方面都存在争议。该论文的实证分析也很细致，使用各种工具和不同的粒度级别来调查潜在的联系。最详细的回归在论文的最后提出，作者利用了不同年龄组的差异。这些回归的形式为

\[ \log \left(\text { Arrests }_{i t b}\right)=\beta \text { Abortion }_{i b}+u_{i}+\lambda_{t b}+\theta_{i t}+\varepsilon_{i t b} \]

其中 \(i, t\) 和 \(b\) 索引状态、年份和出生队列。逮捕是指因特定犯罪而被捕的原始人数，堕胎是指每活产堕胎的比率。回归包括州固定效应、同类年交互作用和州年交互作用。通过包括所有这些相互作用效应，回归估计了三重差异，并确定了堕胎对州内跨队列变异的影响，这是比简单的跨州差异回归更强的识别论据。 Donohue 和 Levitt 报告了 \(\beta\) 的估计值等于 \(-0.028\)，但标准误差较小。根据这些估计，Donohue 和 Levitt 认为堕胎合法化可以减少大约 15-25% 的犯罪率。

不幸的是，他们的估计存在错误。在尝试复制 Donohue-Levitt 的工作时，Foote 和 Goetz (2008) 发现 Donohue-Levitt 的计算机代码无意中省略了状态年交互 \(\theta_{i t}\)。这是一个重要的遗漏，因为如果没有 \(\theta_{i t}\)，估计值是基于跨州和跨队列变异的混合，而不仅仅是声称的跨队列变异。 Foote 和 Goetz 重新估计了回归，发现 \(\beta\) 的估计值等于 \(-0.010\)。虽然在统计上仍然不同于零，但幅度的减小大大降低了估计的影响。富特和古茨还进行了更广泛的实证分析。

不管错误和政治后果如何，多诺休-莱维特的论文都是对双重差分法的非常聪明和创造性的运用。不幸的是，这项创造性的工作在某种程度上被关于计算机代码的争论所掩盖。

我相信这一集有两个重要信息。首先，包括适当的控件！在多诺休-莱维特回归中，他们正确地主张回归包括州年相互作用，因为这可以最精确地测量所需的因果影响。其次，检查你的代码！计算错误在应用经济工作中普遍存在。很容易出错；将它们从冗长的代码中清除是非常困难的。大多数论文中的错误都会被忽略，因为细节很少受到关注。然而，重要且有影响力的论文会受到审查。如果你有幸写了一篇受到广泛关注的论文，那么如果在发表后发现编码错误，你会发现这是最尴尬的。解决办法是积极主动、保持警惕。

18.9 推理

许多双重差分应用程序使用高度聚合（例如州级）数据，因为它们正在调查聚合级别发生的政策变化的影响。在最近的文献中，使用聚类方法来计算标准误差并在高聚合水平上应用聚类已成为惯例。

为了理解这种选择的动机，回顾一下聚类方差估计的传统论点是有用的。假设组 \(g\) 中个体 \(i\) 的误差 \(e_{i g}\) 独立于回归量，具有方差 \(\sigma^{2}\)，并且组内个体之间具有相关性 \(\rho\)。如果每组中的人数为 \(N\)，则最小二乘估计量的精确方差（回想方程 \((4.53))\) 为

\[ \boldsymbol{V}_{\widehat{\beta}}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \sigma^{2}(1+\rho(N-1)) \]

最初由 Moulton (1990) 得出。这会使“通常”方差增大 \((1+\rho(N-1))\) 因子。即使 \(\rho\) 非常小，如果 \(N\) 很大，那么这个通货膨胀因子也可能很大。

聚类方差估计器不对每组内的条件方差和相关性强加任何结构。它允许任意关系。优点是所得到的方差估计器对于广泛的相关结构具有鲁棒性。缺点是估计器可能不太精确。实际上，聚类方差估计量应该被视为是根据组的数量构建的。如果您使用美国各州作为组（如应用程序中常见的那样），则组数（最多）为 51。这意味着您将使用 51 个观测值来估计协方差矩阵，而不管“观测值”的数量有多少例子。一个含义是，如果您估计的系数超过 51 个，则样本协方差矩阵估计器将不是满秩的，这可能会使潜在相关的推理方法无效。

Bertrand、Duflo 和 Mullainathan (2004) 在一篇有影响力的论文中令人信服地阐述了聚类标准误差的案例。这些作者通过采用著名的 CPS 数据集，然后添加随机生成的回归量来证明他们的观点。他们发现，如果使用非聚类方差估计量，那么标准误差将太小，并且研究人员会不恰当地得出随机生成的“变量”对回归有显着影响的结论。可以通过使用在州级别聚集的聚集标准误差来消除错误拒绝。根据本文的建议，经济学研究人员现在通常聚集在州一级。

然而，也有一些限制。以前面介绍的 Card-Krueger (1994) 为例。他们的样本只有两个州（新泽西州和宾夕法尼亚州）。如果标准误差集中在州一级，那么只有两个有效观测值可用于标准误差计算，这太少了。对于此应用程序，在州级别进行集群是不可能的。一个暗示可能是，这会对仅涉及少数几个州的申请产生怀疑。如果我们不能排除聚类依赖结构，并且由于状态数量少而不能使用聚类方法，那么信任报告的标准错误可能是不合适的。

当处理 \(\left(D_{i t}=1\right)\) 仅适用于少数单位时，就会出现另一个挑战。最极端的情况是只有一个处理单元。例如，当您有兴趣衡量仅一个州采用的政策的效果时，可能会出现这种情况。这种情况特别危险，并且在代数上与稀疏虚拟变量的鲁棒协方差矩阵估计问题相同。 （参见第 4.16 节。）正如我们从该分析中了解到的，在单个处理单元的极端情况下，稳健的协方差矩阵估计量是奇异的并且高度偏向于零。问题是因为子组的方差是根据单个观测值估计的。

相同的分析适用于聚类方差估计器。如果存在单个处理单元，则标准聚类协方差矩阵估计器将是奇异的。如果您计算子组平均值的标准误差，尽管它是最不精确的估计系数，但在代数上它将为零。治疗效果将具有非零报告的标准误差，但它是不正确的并且高度偏向于零。有关更详细的分析和推理建议，请参阅 Conley 和 Taber (2011)。

18.10 练习

练习18.1 文中声称，在平衡样本中，个人层面的固定效应与州层面贬低的任何变量都是正交的。

1. 展示这一主张。

2. 这个断言在不平衡样本中是否成立？

3. 解释为什么这个主张意味着回归

\[ Y_{i t}=\beta_{0}+\beta_{1} \text { State }_{i}+\beta_{2} \text { Time }_{t}+\theta D_{i t}+\varepsilon_{i t} \]

和

\[ Y_{i t}=\theta D_{i t}+u_{i}+\delta_{t}+\varepsilon_{i t} \]

产生与 \(\theta\) 相同的估计值。

练习 18.2 在 \(T=2\) 和 \(N=2\) 的回归 (18.1) 中，假设时间变量被省略。因此估计方程是

\[ Y_{i t}=\beta_{0}+\beta_{1} \text { State }_{i}+\theta D_{i t}+\varepsilon_{i t} . \]

其中 \(D_{i t}=\) 状态 \(_{i}\) 时间 \(_{t}\) 是治疗指标。

1. 找到最小二乘估计器 \(\widehat{\theta}\) 的代数表达式。

2. 表明 \(\hat{\theta}\) 仅是已处理子样本的函数，而不是未处理子样本的函数。

3. \(\hat{\theta}\) 是双重差分估计器吗？

4. 在什么假设下 \(\widehat{\theta}\) 可能是治疗效果的适当估计量？

练习18.3 采用基本的双重差分模型

\[ Y_{i t}=\theta D_{i t}+u_{i}+\delta_{t}+\varepsilon_{i t} . \]

假设我们有一个工具变量 \(Z_{i t}\)，它独立于 \(\varepsilon_{i t}\)，但与 \(D_{i t}\) 相关，而不是假设 \(D_{i t}\) 和 \(\varepsilon_{i t}\) 是独立的。描述如何估计 \(\theta\)。

提示：复习第 17.28 节。

练习 18.4 对于第 18.4 节的规范测试，请解释为什么同质治疗效果的回归测试仅包括 \(N_{2}-1\) 交互虚拟变量而不是所有 \(N_{2}\) 交互虚拟变量。还要解释为什么相等控制效应的回归测试仅包括 \(N_{1}-1\) 交互虚拟变量而不是所有 \(N_{1}\) 交互虚拟变量。

练习 18.5 一位经济学家对威斯康星州 2011 年“第 10 号法案”立法对工资的影响感兴趣。 （作为背景，第 10 号法案削弱了工会的权力。）她计算了第 10 号法案颁布前后几十年威斯康星州和邻近的明尼苏达州平均工资率的统计数据 \({ }^{5}\)。

	Years	Average Wage
Wisconsin	\(2001-2010\)	\(15.23\)
Wisconsin	\(2010-2020\)	\(16.72\)
Minnesota	\(2001-2010\)	\(16.42\)
Minnesota	\(2010-2020\)	\(18.10\)

1. 根据这些信息，她对第 10 号法案对平均工资影响的估计是多少？

2. 上表中的数字按县平均数计算。 （经济学家得到了每个县的平均工资。她通过取各县的平均值来计算该州的平均工资。）现在假设她估计以下线性回归，将各个县视为观察值。

\[ \text { wage }=\alpha+\beta \text { Act } 10+\gamma \text { Wisconsin }+\delta \text { Post } 2010+e \]

\({ }^{5}\) 这个数字完全是虚构的。这三个回归变量是“第 10 号法案在该州生效”、“县位于威斯康星州”和“时间段为 2011-2020 年”的虚拟变量。

她发现 \(\widehat{\beta}\) 有什么价值？

3. 她发现 \(\widehat{\gamma}\) 的值是多少？

练习18.6 使用课本网页上的数据文件CK1994。古典经济学告诉我们，提高最低工资会提高产品价格。因此，您可以使用 Card-Krueger diffin-diff 方法来估计 1992 年新泽西州最低工资上涨对产品价格的影响。数据文件包含变量priceentree、pricefry 和pricesoda。将可变价格创建为这三者的总和，指示典型膳食的成本。

1. 缺少一些价格值。删除这些观察。这将产生不平衡的面板，因为两项调查中仅一项可能缺少价格。通过删除配对观察来平衡面板。这可以在 Stata 中通过以下命令完成：

• 如果价格为 \(==\)，则下降。

• bys store: gen nperiods \(=\) [_N \(]\)

• 如果 n 个周期 \(==2\) 则保留

2. 创建表 \(18.1\) 的模拟，但使用一顿饭的价格而不是员工数量。解释结果。

3. 估计以价格作为因变量的回归模拟 (18.2)。

4. 以状态固定效应和价格作为因变量来估计回归 (18.4) 的类似情况。

5. 以餐厅固定效应和价格作为因变量来估计回归 (18.4) 的类比。

6. 这些回归的结果相同吗？

7. 创建一个表 \(18.2\) 的模拟表来表示一顿饭的价格。解释结果。

8. 测试各地区的同质治疗效果。

9. 检验各地区的同等控制效果。

练习18.7 使用课本网页上的数据文件DS2004。作者认为，外在的警察存在将阻止汽车盗窃。本章中提供的证据表明，受到警察保护的城市街区的汽车盗窃案有所减少。这种威慑效果是否延伸到同一区块之外？该数据集具有虚拟变量 oneblock，它指示该城市街区是否距离受保护机构只有一个街区。

1. 计算表 \(18.3\) 的模拟，该表显示距离受保护机构一个街区的城市街区和距离受保护机构一个街区以上的城市街区之间的差异。

2. 估计具有街区和月份固定效应的回归，其中包括两个处理变量：对于与受保护机构位于同一街区的城市街区，以及对于相隔一个街区的城市街区，两者都与 7 月后的虚拟变量相互作用。排除 7 月份的观察结果。 (c) 对您的发现发表评论。威慑效果是否超出了同一个街区？

练习18.8 使用课本网页上的数据文件BMN2016。作者报告了酒类销售结果。该数据文件包含啤酒和葡萄酒销售的相同信息。对于啤酒或葡萄酒销售，估计类似于 (18.7) 和 (18.8) 的 diff-in-diff 模型并解释你的结果。一些相关变量包括 \(i d\)（州识别）、年份、unempw（失业率）。对于啤酒，相关变量包括 logbeer（啤酒销售的日志）、beeronsun（允许的内部销售小时数）、beeroffsun（允许的外部销售小时数）、beerOnOutflows、beerOffOutflows。对于葡萄酒来说，变量具有相似的名称。