第23章: 非线性最小二乘法
23 非线性最小二乘法
23.1 介绍
非线性回归模型是参数回归函数\(m(x, \theta)=\mathbb{E}[Y \mid X=x]\),其参数\(\theta \in \Theta\) 是非线性的。我们将模型写为
\[ \begin{aligned} Y &=m(X, \theta)+e \\ \mathbb{E}[e \mid X] &=0 . \end{aligned} \]
在非线性回归中,普通最小二乘估计器不适用。相反,参数通常通过非线性最小二乘法 (NLLS) 进行估计。 NLLS 是一个需要数值优化的 m 估计器。
我们用三个例子来说明非线性回归。
我们的第一个例子是 Box-Cox 回归模型。严格正变量 \(x>0\) 的 Box-Cox 变换(Box 和 Cox,1964)为
\[ x^{(\lambda)}= \begin{cases}\frac{x^{\lambda}-1}{\lambda}, & \text { if } \lambda \neq 0 \\ \log (x), & \text { if } \lambda=0 .\end{cases} \]
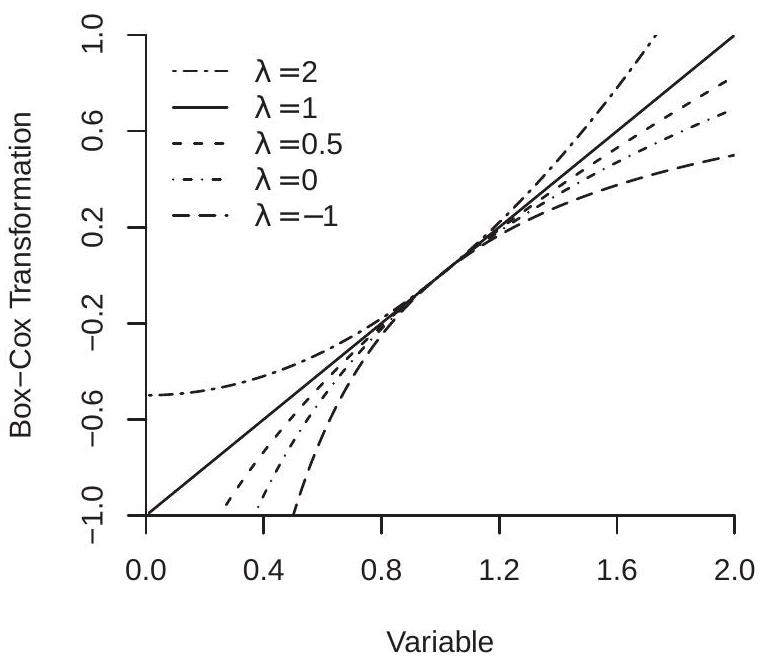
Box-Cox 变换连续嵌套线性 \((\lambda=1)\) 和对数 \((\lambda=0)\) 函数。图 23.1(a) 显示了 \(\lambda=2,1,0,0.5,0\) 和 \(-1\) 在 \(x \in(0,2]\) 上的 Box-Cox 变换 (23.1)。参数 \(\lambda\) 控制函数的曲率。
Box-Cox 回归模型为
\[ Y=\beta_{0}+\beta_{1} X^{(\lambda)}+e \]
它有参数 \(\theta=\left(\beta_{0}, \beta_{1}, \lambda\right)\)。回归函数在 \(\left(\beta_{0}, \beta_{1}\right)\) 中是线性的,但在 \(\lambda\) 中是非线性的。
为了说明这一点,我们重新审视 Acemoglu、Johnson 和 Robinson (2001) 提出的 \(\log\)(死亡率)风险的简化形式回归 (12.87)。一个合理的问题是,为什么作者将方程指定为 \(\log\)(死亡率)而不是死亡率的回归。 Box-Cox 回归模型允许两者作为特殊情况,并且等于
\[ \text { risk }=\beta_{0}+\beta_{1} \text { mortality }{ }^{(\lambda)}+e . \]
我们的第二个例子是恒定替代弹性 (CES) 生产函数,它是由 Arrow、Chenery、Minhas 和 Solow (1961) 提出的,作为流行的柯布-道格拉斯生产函数的推广。两个输入的 CES 函数为
\[ Y=\left\{\begin{array}{cc} A\left(\alpha X_{1}^{\rho}+(1-\alpha) X_{2}^{\rho}\right)^{v / \rho}, & \text { if } \rho \neq 0 \\ A\left(X_{1}^{\alpha} X_{2}^{(1-\alpha)}\right)^{v}, & \text { if } \rho=0 . \end{array}\right. \]
其中 \(A\) 是异构(随机)生产率,\(v>0, \alpha \in(0,1)\) 和 \(\rho \in(-\infty, 1]\)。系数\(v\)是规模弹性。系数 \(\alpha\) 是份额参数。系数 \(\rho\) 是输入之间替代弹性 \(\sigma\) 的重写 \({ }^{1}\),并且满足 \(\sigma=1 /(1-\rho)\)。如果 \(A\),则弹性满足 \(A\);如果 \(A\),则弹性满足 \(A\)。在 \(A\) 处,我们获得单位弹性柯布-道格拉斯函数。设置 \(A\) 和 \(A\) 我们得到一个线性生产函数。取极限 \(A\),我们得到 Leontief 生产函数。
设置 \(\log A=\beta+e\)。该框架隐含着回归模型
\[ \log Y=\beta+\frac{v}{\rho} \log \left(\alpha X_{1}^{\rho}+(1-\alpha) X_{2}^{\rho}\right)+e \]
参数为 \(\theta=(\rho, v, \alpha, \beta)\)。
我们通过对 Papageorgiou、Saam 和 Schulte (2017) 的修改来说明 CES 生产函数估计。这些作者估计了电力生产的 CES 生产函数,其中 \(X_{1}\) 是使用“清洁”技术的发电能力,\(X_{2}\) 是使用“肮脏”技术的发电能力。他们利用 26 个国家的小组对 1995 年至 2009 年的模型进行了估算。他们的目标是衡量清洁发电和污染发电之间的替代弹性。数据文件 PPS2017 是作者数据集的摘录。
我们的第三个例子是回归扭结模型。这本质上是分段连续线性样条,其中结被视为自由参数。我们的应用中使用的模型是非线性 AR(1) 模型
\[ Y_{t}=\beta_{1}\left(X_{t-1}-c\right)_{-}+\beta_{2}\left(X_{t-1}-c\right)_{+}+\beta_{3} Y_{t-1}+\beta_{4}+e_{t} \]
其中\((a)_{-}\)和\((a)_{+}\)是负部分和正部分函数,\(c\)是拐点,斜率是拐点两侧的\(\beta_{1}\)和\(\beta_{2}\)。参数是 \(\theta=\left(\beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}, c\right)\)。回归函数在 \(\left(\beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}\right)\) 中是线性的,在 \(c\) 中是非线性的。
我们使用 B. E. Hansen (2017) 的应用来说明回归扭结模型,该模型是 Reinhart 和 Rogoff (2010) 的形式化。这些数据是 1791-2009 年美国实际 GDP 增长 \(Y_{t}\) 和联邦债务与 GDP 比率 \(X_{t}\) 的年度观察时间序列。莱因哈特-罗格夫对债务水平超过阈值时 GDP 增长率放缓的假设感兴趣。为了说明这一点,图 23.1 (b) 显示了回归扭结函数。扭结 \(c=44\) 由正方形标记。您可以看到函数对于 \(X<c\) 向上倾斜,对于 \(X>c\) 向下倾斜。
23.2 鉴别
如果存在参数值 \(\theta_{0}\) 使得 \(m\left(x, \theta_{0}\right)=\mathbb{E}[Y \mid X=x]\) 正确,则回归模型 \(m(x, \theta)\) 被正确指定。如果 \(\theta_{0}\) 是唯一的,则参数是点标识的。在正确指定的非线性回归模型中,如果存在唯一的真实参数,则参数被点识别。
假设\(\mathbb{E}\left[Y^{2}\right]<\infty\)。由于条件期望是最佳均方预测器,因此真实参数 \(\theta_{0}\) 满足优化表达式
\[ \theta_{0}=\underset{\theta \in \Theta}{\operatorname{argmin}} S(\theta) \]
\({ }^{1}\) 将模型编写为替代弹性 \(\sigma\) 的函数而不是其变换 \(\rho\) 是很诱人的。然而,这是不建议的,因为它会使回归函数更加非线性并且难以优化。
- Box-Cox 变换
.jpg)
- 回归扭结模型
图 23.1:非线性回归模型
在哪里
\[ S(\theta)=\mathbb{E}\left[(Y-m(X, \theta))^{2}\right] \]
是期望的平方误差。这将参数表示为 \((Y, X)\) 分布的函数。
如果没有 \(\theta\) 使得 \(m(x, \theta)=\mathbb{E}[Y \mid X=x]\) 存在,则回归模型指定错误。在这种情况下,我们将伪真值 \(\theta_{0}\) 定义为最佳拟合参数 (23.5)。很难给出解唯一的一般条件。因此,错误指定下的伪真值的识别通常是假设的,而不是推断的。
23.3 预估
预期平方误差 \(S(\theta)\) 的模拟估计量是平方误差的样本平均值
\[ S_{n}(\theta)=\frac{1}{n} \sum_{i=1}^{n}\left(Y_{i}-m\left(X_{i}, \theta\right)\right)^{2} . \]
由于 \(\theta_{0}\) 最小化 \(S(\theta)\),因此它的模拟估计器最小化 \(S_{n}(\theta)\)
\[ \widehat{\theta}_{\mathrm{nlls}}=\underset{\theta \in \Theta}{\operatorname{argmin}} S_{n}(\theta) . \]
这称为非线性最小二乘 (NLLS) 估计器。它包括 OLS 作为特殊情况,即 \(m\left(X_{i}, \theta\right)\) 在 \(\theta\) 中呈线性。它是一个带有 \(\rho_{i}(\theta)=\left(Y_{i}-m\left(X_{i}, \theta\right)\right)^{2}\) 的 m 估计器。
由于 \(S_{n}(\theta)\) 是 \(\theta\) 的非线性函数,因此 \(\widehat{\theta}_{\text {nlls. }}\) 的解没有明确的代数表达式,而是通过数值最小化找到。 《经济学家的概率与统计》第 12 章提供了概述。 NLLS 残差为 \(\widehat{e}_{i}=Y_{i}-m\left(X_{i}, \widehat{\theta}_{\text {nlls }}\right)\)。
在某些情况下,包括第 23.1 节中的第一个和第三个示例,模型 \(m(x, \theta)\) 在大多数参数中都是线性的。在这些情况下,计算捷径是使用嵌套最小化(也称为集中或分析)。以示例 1(Box-Cox 回归)为例。给定 Box-Cox 参数 \(\lambda\),回归是线性的。系数\(\left(\beta_{0}, \beta_{1}\right)\)可以通过最小二乘法估计,获得残差和样本集中均方误差\(S_{n}^{*}(\lambda)\)。后者可以使用一维方法最小化。最小化器 \(\hat{\lambda}\) 是 \(\lambda\) 的 NLLS 估计器。给定 \(\hat{\lambda}_{\text {nlls }}\),NLLS 系数估计量 \(\left(\widehat{\beta}_{0}, \widehat{\beta}_{1}\right)\) 是通过 \(Y_{i}\) 在常数和 \(m(x, \theta)\) 上的 OLS 回归找到的。
- Box-Cox 回归
.jpg)
- CES 生产函数
图 23.2:平方误差函数的平均值
我们用两个例子来说明。
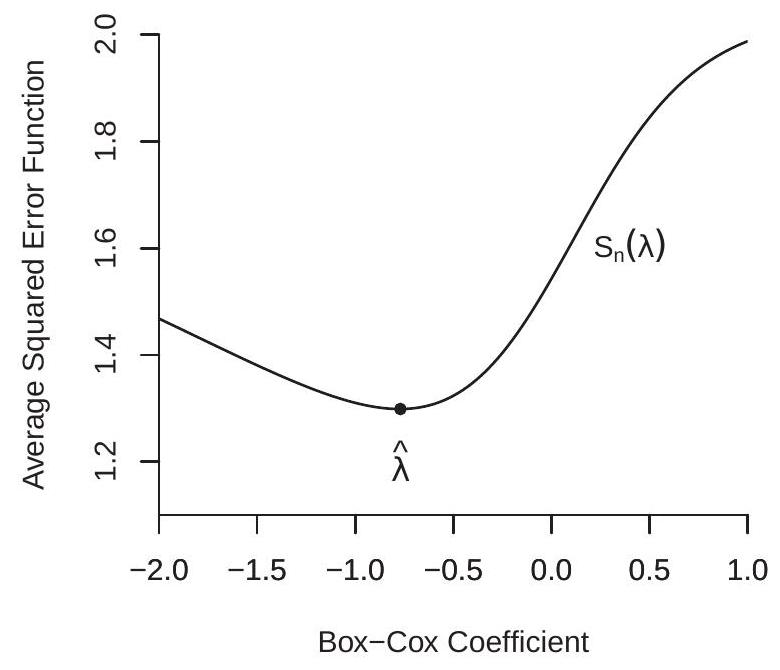
图 23.2(a) 显示了应用于 (23.2) 的 Box-Cox 回归模型的平方误差 \(S_{n}^{*}(\lambda)\) 的集中平均值,显示为 Box-Cox 参数 \(\lambda\) 的函数。您可以看到 \(S_{n}^{*}(\lambda)\) 既不是二次函数也不是全局凸函数,但在 \(\widehat{\lambda}=-0.77\) 处有明确定义的最小值。这是一个参数值,它产生的回归模型比 Acemoglou 等人使用的对数规范更加弯曲。等人。
图 23.2(b) 显示了 CES 生产函数应用程序的平方误差平均值,显示为 \((\rho, \alpha)\) 的函数,其他参数设置为最小值。您可以看到最小值是在 \((\widehat{\rho}, \widehat{\alpha})=(.36, .39)\) 处获得的。我们通过函数 \(S_{n}(\rho, \alpha)\) 的等高线曲面来显示它。二次函数具有椭圆形轮廓表面。您可以看到,该函数在最小值附近似乎接近二次函数,但在远离最小值时变得越来越非二次函数。
三个模型的参数估计值和标准误差如表 23.1 所示。标准误差计算将在第 23.5 节中讨论。 Box-Cox 和 Regression Kink 模型的标准误差是使用异方差稳健公式计算的,CES 生产函数的标准误差是通过集群稳健公式计算的,按国家进行聚类。
采用 Box-Cox 回归。估计值 \(\hat{\lambda}=-0.77\) 显示风险与死亡率之间的估计关系比对数函数具有更强的曲率,而估计值 \(\widehat{\beta}_{1}=-17\) 正如预测的那样为负值。然而,\(\widehat{\beta}_{1}\) 的较大标准误差表明斜率系数并未精确估计。
采用 CES 生产函数。 \(\widehat{\rho}=0.36\) 的估计值为正,表明清洁技术和肮脏技术是替代品。 \(\sigma=1 /(1-\rho)\) 的隐含替代弹性是 \(\widehat{\sigma}=1.57\)。估计表 23.1:示例模型的 NLLS 估计
| \(\lambda\) | \(-0.77\) | \(0.28\) | |
|---|---|---|---|
| CES Production Function | \(\rho\) | \(0.36\) | \(0.29\) |
| \(v\) | \(1.05\) | \(0.03\) | |
| \(\alpha\) | \(0.39\) | \(0.06\) | |
| \(\beta\) | \(1.66\) | \(0.31\) | |
| \(\sigma\) | \(1.57\) | \(0.46\) | |
| Regression Kink Regression | \(\beta_{1}\) | \(0.033\) | \(0.026\) |
| \(\beta_{2}\) | \(-0.067\) | \(0.046\) | |
| \(\beta_{3}\) | \(0.28\) | \(0.09\) | |
| \(\beta_{4}\) | \(3.78\) | \(0.68\) | |
| \(c\) | \(43.9\) | \(11.8\) |
规模弹性 \(\widehat{v}=1.05\) 略高于 1,与规模报酬递增一致。清洁技术 \(\widehat{\alpha}=0.39\) 的份额参数略小于二分之一,表明肮脏技术是主要输入。
采用回归扭结函数。低债务水平 \(\widehat{\beta}_{1}=0.03\) 的 GDP 增长估计斜率为正,高债务水平 \(\widehat{\beta}_{2}=-0.07\) 的估计 GDP 增长斜率为负。这与莱因哈特-罗格夫假说一致,即高债务水平导致经济增长放缓。估计的扭结点为 \(\widehat{c}=44 %\),远低于 Reinhart-Rogoff 根据其非正式分析建议的假定 \(90 %\) 扭结点。
应深思熟虑地解释非线性模型中的常规 t 比和 p 值。在这种情况下,在所有“显着”系数估计值上附加星号的烦人的经验习惯是特别不合适的。以表 23.1 中的 CES 估计为例。 \(v\) 的“t 比”用于检验 \(v=0\) 的假设,这是一个毫无意义的假设。类似地,\(\alpha\) 的 t 比率是针对一个无趣的假设。在这些估计值后面附加星号并将其描述为“显着”是没有意义的,因为没有理由将 0 作为参数的有趣值。同样,在 Box-Cox 回归中,没有理由将 \(\lambda=0\) 作为重要假设。在回归扭结模型中,假设 \(c=0\) 通常毫无意义,并且很容易位于参数空间之外。
23.4 渐近分布
我们首先考虑 NLLS 估计量的一致性。我们诉诸定理 \(22.3\) 和 \(22.4\) 作为 m 估计量。
假设 $23.1
\(\left(Y_{i}, X_{i}\right)\) 是独立同分布的。
\(m(X, \theta)\) 在 \(\theta \in \Theta\) 中连续,概率为 1。
3.\(\mathbb{E}\left[Y^{2}\right]<\infty\)。
\(|m(X, \theta)| \leq m(X)\) 和 \(\mathbb{E}\left[m(X)^{2}\right]<\infty\)。
\(\Theta\) 是紧凑的。
对于所有\(\theta \neq \theta_{0}, S(\theta)>S\left(\theta_{0}\right)\)。
假设 1-4 是相当标准的。假设5不是必需的,但简化了证明。假设 6 很关键。它指出最小化器 \(\theta_{0}\) 是唯一的。
定理23.1 NLLS估计器的一致性 如果假设 \(23.1\) 成立,则 \(\widehat{\theta} \underset{p}{\longrightarrow} \theta_{0}\) 为 \(n \rightarrow \infty\)。
接下来我们讨论可微模型的渐近分布。我们首先提出主要结果,然后讨论假设。设置 \(m_{\theta}(x, \theta)=\frac{\partial}{\partial \theta} m(x, \theta), m_{\theta \theta}(x, \theta)=\frac{\partial^{2}}{\partial \theta \partial \theta^{\prime}} m(x, \theta)\) 和 \(m_{\theta i}=\) \(m_{\theta}\left(X_{i}, \theta_{0}\right)\)。定义 \(\boldsymbol{Q}=\mathbb{E}\left[m_{\theta i} m_{\theta i}^{\prime}\right]\) 和 \(\Omega=\mathbb{E}\left[m_{\theta i} m_{\theta i}^{\prime} e_{i}^{2}\right]\)
假设 \(23.2\) 对于 \(\theta_{0}\) 的某个邻域 \(\mathscr{N}\),
1.\(\mathbb{E}[e \mid X]=0\)。
2.\(\mathbb{E}\left[Y^{4}\right]<\infty\)。
\(m(x, \theta)\) 和 \(m_{\theta}(X, \theta)\) 在 \(\theta \in \mathcal{N}\) 中可微。
\(\mathbb{E}|m(X, \theta)|^{4}<\infty, \mathbb{E}\left\|m_{\theta}(X, \theta)\right\|^{4}<\infty\) 和 \(\mathbb{E}\left\|m_{\theta \theta}(X, \theta)\right\|^{4}<\infty\) 对应 \(\theta \in \mathcal{N}\)。
5.\(\boldsymbol{Q}=\mathbb{E}\left[m_{\theta i} m_{\theta i}^{\prime}\right]>0\)。
- \(\theta_{0}\) 位于 \(\Theta\) 的内部。
假设 1 强制指定模型是正确的。如果我们放宽这个假设,渐近分布仍然是正态的,但协方差矩阵会发生变化。假设 2 是渐近正态性所需的矩界。假设 3 表明回归函数是二阶可微的。这可以放宽,但条件和推导会变得复杂。假设 4 说明了回归函数及其导数的矩界限。假设 5 表明“线性回归器”\(m_{\theta i}\) 具有满秩总体设计矩阵。如果这个假设失败,那么 \(m_{\theta i}\) 将是多重共线性的。假设6要求参数不在参数空间的边界上。这很重要,否则抽样分布将不对称。
定理$23.2 Asymptotic Normality of NLLS Estimator 如果假设 \(23.1\) 和 \(23.2\) 成立,则 \(\sqrt{n}\left(\widehat{\theta}-\theta_{0}\right) \underset{d}{\longrightarrow} \mathrm{N}(0, \boldsymbol{V})\) 为 \(n \rightarrow \infty\),其中 \(V=Q^{-1} \Omega Q^{-1}\)
定理 \(23.2\) 表明,在一般条件下,NLLS 估计量具有渐近分布,其结构与 OLS 估计量相似。估计器以传统速率收敛到具有三明治形式协方差矩阵的正态分布。此外,渐近方差与使用线性回归量 \(m_{\theta i}\) 的假设 OLS 回归中的渐近方差相同。因此,NLLS 的分布渐近与线性回归相同。
渐近分布在条件同方差下得到简化。如果 \(\mathbb{E}\left[e^{2} \mid X\right]=\sigma^{2}\) 则渐近方差为 \(\boldsymbol{V}=\sigma^{2} \boldsymbol{Q}^{-1}\)。
23.5 协方差矩阵估计
渐近协方差矩阵 \(\boldsymbol{V}\) 的估计与线性回归类似,但我们使用线性回归量 \(m_{\theta i}\) 的估计进行调整。这个估计是
\[ \widehat{m}_{\theta i}=m_{\theta}\left(X_{i}, \widehat{\theta}\right)=\frac{\partial}{\partial \theta} m\left(X_{i}, \widehat{\theta}\right) . \]
最好以代数方式计算导数,但也可以用数值导数(离散导数)代替。
以 \(m\left(x, \beta_{0}, \beta_{1}, \lambda\right)=\beta_{0}+\beta_{1} x^{(\lambda)}\) 的 Box-Cox 回归模型为例。我们计算 \(\lambda \neq 0\)
\[ m_{\theta}\left(x, \beta_{0}, \beta_{1}, \lambda\right)=\left(\begin{array}{c} \frac{\partial}{\partial \beta_{0}}\left(\beta_{0}+\beta_{1} x^{(\lambda)}\right) \\ \frac{\partial}{\partial \beta_{1}}\left(\beta_{0}+\beta_{1} x^{(\lambda)}\right) \\ \frac{\partial}{\partial \beta_{\lambda}}\left(\beta_{0}+\beta_{1} x_{i}^{(\lambda)}\right) \end{array}\right)=\left(\begin{array}{c} 1 \\ x^{(\lambda)} \\ \frac{x^{\lambda} \log (x)-x^{(\lambda)}}{\lambda} \end{array}\right) . \]
对于 \(\lambda=0\),第三个条目是 \(\log ^{2}(x) / 2\)。通过将 \(\lambda\) 替换为估计器 \(\hat{\lambda}\) 来获得估计值。因此对于 \(\widehat{\lambda} \neq 0\)
\[ \widehat{m}_{\theta i}=\left(\begin{array}{c} 1 \\ x^{(\widehat{\lambda})} \\ \frac{1-x^{\hat{\lambda}}+\lambda x^{\hat{\lambda}} \log (x)}{\hat{\lambda}^{2}} \end{array}\right) . \]
协方差矩阵分量估计为
\[ \begin{aligned} \widehat{\boldsymbol{Q}} &=\frac{1}{n} \sum_{i=1}^{n} \widehat{m}_{\theta i} \widehat{m}_{\theta i}^{\prime} \\ \widehat{\Omega}=\frac{1}{n} \sum_{i=1}^{n} \widehat{m}_{\theta i} \widehat{m}_{\theta i}^{\prime} \widehat{e}_{i}^{2} \\ \widehat{\boldsymbol{V}} &=\widehat{\boldsymbol{Q}}^{-1} \widehat{\Omega} \widehat{\boldsymbol{Q}}^{-1} \end{aligned} \]
其中 \(\widehat{e}_{i}=Y_{i}-m\left(X_{i}, \widehat{\theta}\right)\) 是 NLLS 残差。标准误差按照惯例计算为 \(n^{-1} \widehat{\boldsymbol{V}}\) 对角线元素的平方根。
如果误差是同方差的,则可以使用以下公式估计协方差矩阵
\[ \begin{aligned} \widehat{\boldsymbol{V}}^{0} &=\widehat{\boldsymbol{Q}}^{-1} \widehat{\sigma}^{2} \\ \widehat{\sigma}^{2} &=\frac{1}{n} \sum_{i=1}^{n} \widehat{e}_{i}^{2} . \end{aligned} \]
如果观测值满足聚类依赖性,则可以使用标准聚类方差估计器,再次将线性回归器估计 \(\widehat{m}_{\theta i}\) 视为有效回归器。
为了说明这一点,表 23.1 显示了我们三个估计模型的标准误差。第一个和第三个模型的标准误差使用公式(23.6)计算。 CES 模型的标准误差按国家/地区进行聚类。
在小样本中,NLLS 的标准误差可能不可靠。另一种方法是使用引导方法进行推理。非参数引导程序从观测对 \(\left(Y_{i}, X_{i}\right)\) 中进行替换提取以创建引导程序样本,并对其应用 NLLS 以获得引导程序参数估计值 \(\widehat{\theta}^{*}\)。从 \(\widehat{\theta}^{*}\) 我们可以计算引导标准误差和/或引导置信区间,例如通过偏差校正百分位数方法。
23.6 面板数据
考虑具有加性个体效应的非线性回归模型
\[ \begin{aligned} Y_{i t} &=m\left(X_{i t}, \theta\right)+u_{i}+\varepsilon_{i t} \\ \mathbb{E}\left[\varepsilon_{i t} \mid X_{i t}\right] &=0 . \end{aligned} \]
为了消除个体效应,我们可以应用内变换或一阶差分变换。应用我们获得的内变换
\[ \dot{Y}_{i t}=\dot{m}\left(X_{i t}, \theta\right)+\dot{\varepsilon}_{i t} \]
在哪里
\[ \dot{m}\left(X_{i t}, \theta\right)=m\left(X_{i t}, \theta\right)-\frac{1}{T_{i}} \sum_{t \in S_{i}} m\left(X_{i t}, \theta\right) \]
使用面板数据符号。因此 \(\dot{m}\left(X_{i t}, \theta\right)\) 是应用于 \(m\left(X_{i t}, \theta\right)\) 的内变换。它不是 \(m\left(\dot{X}_{i t}, \theta\right)\)。方程(23.7)是一个非线性面板模型。该系数可以通过 NLLS 来估计。当 \(X_{i t}\) 严格为外生时,该估计量是合适的,因为 \(\dot{m}\left(X_{i t}, \theta\right)\) 是所有时间段内 \(X_{i s}\) 的函数。
另一种方法是应用一阶差分变换。因此产量
\[ \Delta Y_{i t}=\Delta m\left(X_{i t}, \theta\right)+\Delta \varepsilon_{i t} \]
其中 \(\Delta m\left(X_{i t}, \theta\right)=m\left(X_{i t}, \theta\right)-m\left(X_{i, t-1}, \theta\right)\).方程(23.8)可以通过NLLS来估计。这再次要求 \(X_{i t}\) 是严格外生的,以实现一致的估计。
如果回归量 \(X_{i t}\) 包含滞后因变量 \(Y_{i, t-1}\),则 NLLS 不是合适的估计量。 GMM 可以应用于类似于线性动态面板回归模型的(23.8)。
23.7 阈值模型
非线性回归的一个极端例子是阈值回归模型类。这些是不连续的回归模型,其中扭结点被视为自由参数。它们已在经济学中成功用于模拟阈值效应和临界点。它们也是回归树和随机森林的现代机器学习方法的核心工具。在本节中,我们将进行评论。
阈值回归模型采用以下形式
\[ \begin{aligned} Y &=\beta_{1}^{\prime} X_{1}+\beta_{2}^{\prime} X_{2} \mathbb{1}\{Q \geq \gamma\}+e \\ \mathbb{E}[e \mid X] &=0 \end{aligned} \]
其中 \(X_{1}\) 和 \(X_{2}\) 分别是 \(k_{1} \times 1\) 和 \(k_{2} \times 1\),\(Q\) 是标量。变量 \(Q\) 称为阈值变量,\(\gamma\) 称为阈值。
通常,\(X_{1}\) 和 \(X_{2}\) 都包含截距,\(X_{2}\) 和 \(Q\) 是 \(X_{1}\) 的子集。在后一种情况下,\(\beta_{2}\) 是阈值处斜率的变化。阈值变量 \(Q\) 应该是连续分布的或有序的。
在完整的阈值规范 \(X_{1}=X_{2}=X\) 中。在这种情况下,所有系数都在阈值处切换。这个回归也可以写成
\[ Y=\left\{\begin{array}{cc} \theta_{1}^{\prime} X+e, & Q<\gamma \\ \theta_{2}^{\prime} X+e, & Q \geq \gamma \end{array}\right. \]
其中 \(\theta_{1}=\beta_{1}\) 和 \(\theta_{2}=\beta_{1}+\beta_{2}\)。
当只有一个回归器 \(X\) 时,就会出现一个简单但完整的阈值模型。回归可以写成
\[ Y=\alpha_{1}+\beta_{1} X+\alpha_{2} \mathbb{1}\{X \geq \gamma\}+\beta_{2} X \mathbb{1}\{X \geq \gamma\}+e . \]
这类似于回归扭结模型,但更通用,因为它允许 \(X=\gamma\) 处的不连续性。回归扭结模型施加了限制 \(\alpha+\beta \gamma=0\)。
阈值模型最适合经济模型预测 CEF 不连续性的情况。它也可以用作一种灵活的近似,用于认为 CEF 相对于一个变量具有尖锐的非线性或具有尖锐的相互作用效应的情况。例如,回归扭结模型不允许扭结交互效应。
阈值模型主要取决于阈值变量 \(Q\) 的选择。该变量控制回归模型显示非线性的能力。原则上,这可以通过将多个阈值合并到可能不同的变量中来概括,但这种概括受到样本大小和信息的限制。
阈值模型在系数 \(\beta=\left(\beta_{1}, \beta_{2}\right)\) 中是线性的,在 \(\gamma\) 中是非线性的。参数 \(\gamma\) 至关重要,因为它决定了模型的非线性 - 样本分割。
许多经验应用使用非正式的临时方法来估计阈值模型。您可能会看到根据回归量特征将样本分为“子组”。当后一个分割基于连续回归量时,分割点恰好是阈值参数。当您看到这样的表格时,谨慎的做法是持怀疑态度。这个阈值参数是如何选择的?基于直觉?还是基于数据探索?如果是前者,您认为结果会提供信息吗?如果是后者,您应该相信报告的测试吗?
为了说明阈值回归,我们回顾了 Card、Mas 和 Rothstein (2008) 的一篇有影响力的论文。他们对美国城市的种族隔离过程感兴趣。关于美国白人行为的一个常见假设是,他们只有在少数族裔居民比例很小的社区中才能舒适地生活。这种行为的一个简单模型(在他们的论文中进行了探讨)预测,这种偏好会导致少数族裔中不稳定的混血平衡。他们称这种平衡为临界点。如果少数派超过这个临界点,结果将发生不连续的变化。其经济机制是,如果少数族裔以大致连续的速度迁入一个社区,当达到临界点时,白人居民将大量退出,因为他们感到不舒服而选择搬迁。这预测了在临界点处不连续的阈值回归。数据文件 CMR2008 是作者数据集的删节版本。
- 估计标准
.jpg)
- 阈值回归估计
图 23.3:阈值回归 - Card-Mas-Rothstein (2008) 模型
作者使用类似于以下的规范
\[ \begin{aligned} \Delta W_{c i t} &=\delta_{0} \mathbb{1}\left\{M_{c i t-1} \geq \gamma\right\}+\delta_{1}\left(M_{c i t-1}-\gamma\right) \mathbb{1}\left\{M_{c i t-1} \geq \gamma\right\} \\ &+\beta_{1} M_{c i t-1}+\beta_{2} M_{c i t-1}^{2}+\theta^{\prime} X_{c i t-1}+\alpha+u_{c}+e_{c i t} \end{aligned} \]
其中 \(c\) 是城市 (MSA),\(i\) 是城市内的人口普查区域,\(t\) 是时间段(十年),\(\Delta W_{c i t}\) 是十年来该区域的白人人口百分比变化,$ matheq5$ 是该地区中少数民族的比例,\(u_{c}\) 是对城市的固定效应,\(X_{c i t}\) 是地区层面的回归控制。该样本基于每十年收集一次的人口普查数据。他们估算了三十年的模型;我们关注1970-1980年。因此 \(\Delta W_{c i t}\) 是 1970-1980 年间白人人口的变化,其余变量是 1970 年的。回归中使用的控制因素包括失业率、对数平均家庭收入、住房空置率、租户份额、单体建筑中的住房比例以及乘坐公共交通通勤的工人比例。该模型有 \(n=35,656\) 观测值和 \(c\) 城市。此规范允许 \(c\) 和 \(c\) 之间的关系是非线性(二次)关系,并且阈值处的截距和斜率不连续移动。作者的主要预测是 \(c\) 应该很大且为负。阈值参数 \(c\) 是触发不连续的白色向外迁移的少数分数。
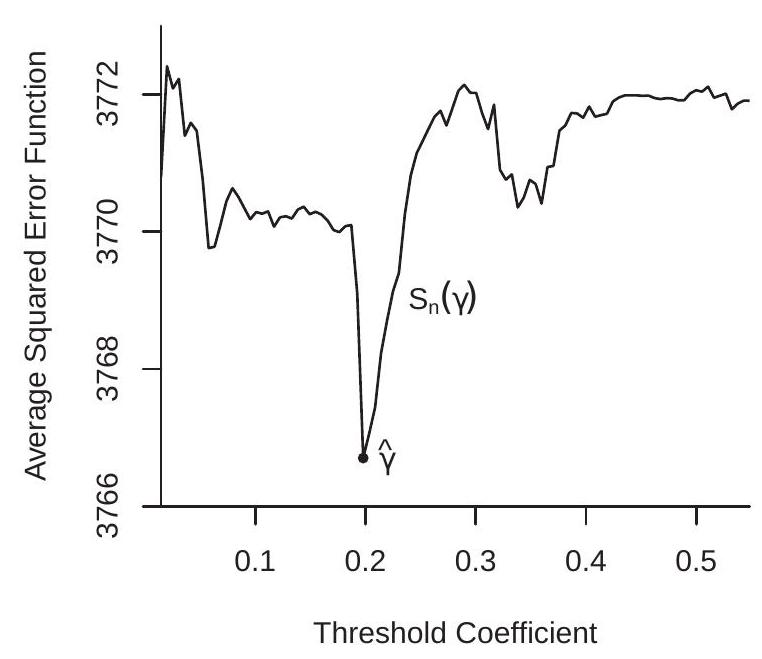
\({ }^{2}\) 大都市统计区 (MSA)。作者使用了包含至少 100 个人口普查区的 104 个 MSA。由于阈值回归模型是显式非线性回归,因此合适的估计方法是NLLS。由于模型除 \(\gamma\) 之外的所有系数都是线性的,因此最好的计算技术是集中最小二乘法。对于每个 \(\gamma\),模型都是线性的,并且可以通过最小二乘法估计系数。这会产生平方误差 \(S_{n}^{*}(\gamma)\) 的集中平均值,可以将其最小化以找到 NLLS 估计器 \(\widehat{\gamma}\)。为了说明这一点,Card-Mas-Rothstein 数据集 \({ }^{3}\) 的集中最小二乘准则如图 23.3(a) 所示。正如您所看到的,标准 \(S_{n}^{*}(\gamma)\) 是高度非平滑的。这在阈值应用中是典型的。因此,需要通过网格搜索来最小化该标准。该标准是一个阶跃函数,每次观察都有一个阶跃。完整搜索将计算 \(\gamma\) 的 \(S_{n}^{*}(\gamma)\) 等于样本中 \({ }^{2}\) 的每个值。一种简化(我们采用的)是在较少数量的网格点上计算标准。在我们的插图中,我们在 \({ }^{2}\) 的 \({ }^{2}\) 和 \({ }^{2}\) 分位数 \({ }^{2}\) 之间使用 100 个等距的网格点。 (这些分位数是所显示图形的边界。)您可以看到,对于 \({ }^{2}\) 和 \({ }^{2}\) 之间的 \({ }^{2}\) 值,该标准通常较低,对于 \({ }^{2}\){ }^{2}$ 值尤其较低$。最小值是在 \(\gamma\) 处获得的。这就是 NLLS 估计器。在应用程序的上下文中,这意味着临界点的点估计为 \(\gamma\),这意味着当社区少数族裔比例超过 \(\gamma\) 时,白人家庭会不连续地改变其行为。剩余的 NLLS 估计值通过最小二乘回归 (23.9) 设置 \(\gamma\) 获得。
我们的估计见表 23.2。按照 Card、Mas 和 Rothstein (2008) 的说法,标准误差按城市 (MSA) 对 \({ }^{5}\) 进行聚类。检查表 \(23.2\) 我们可以看到,估计表明少数族裔中白人人口的社区下降正在增加,在 \(20 %\) 的临界点之上急剧且加速下降。估计的不连续性为 \(-11.6 %\)。这与 Card、Mas 和 Rothstein (2008) 使用临时估计方法获得的估计几乎相同。
白人人口也因失业率、租房者份额和公共交通的使用而减少,但因空置率而增加。另一个有趣的观察是,尽管样本具有非常大的 \((35,656)\) 观测值,但参数估计的标准误差相当大,表明相当大的不精确性。这主要是由于聚类协方差矩阵计算造成的,因为只有 \(N=104\) 聚类。
阈值回归的渐近理论是非标准的。 Chan (1993) 表明,在正确的规范下,阈值估计器 \(\widehat{\gamma}\) 以快速 \(O_{p}\left(n^{-1}\right)\) 的概率收敛到 \(\gamma\),并且其他参数估计器具有传统的渐近分布,证明了表 23.2 中报告的标准误差。他还表明,阈值估计器 \(\widehat{\gamma}\) 具有非标准渐近分布,不能用于置信区间构建。
B. E. Hansen (2000) 在连续阈值变量 \(Q\) 的“小阈值效应”渐近框架下推导出 \(\widehat{\gamma}\) 的渐近分布和相关检验统计量。该分布理论允许简单地构造 \(\gamma\) 的渐近置信区间。简而言之,他表明在正确的规范、独立观察和同方差性下,用于检验的 F 统计量
\({ }^{3}\) 使用 1970-1980 年样本和模型 (23.9)。
\({ }^{4}\) 重要的是,搜索应限制在 \(\gamma\) 的值内,该值很好地位于阈值变量的支持范围内。否则回归可能不可行。所需的修剪程度(远离支撑边界)取决于具体应用。
\({ }^{5}\) 我不清楚集群是否适合此应用程序。聚类的动机之一是包含固定效应,因为这会引起聚类内观察值之间的相关性。然而,在这种情况下,每个簇的典型观测值数量为数百,因此这种相关性接近于零。聚类的另一个动机是回归误差 \(e_{c i t}\)(白人人口变化的未观察到的因素)在城市内的各个区域之间相关。虽然可以预期白人对少数族裔的态度可能在城市内相关,但我们是否应该预期人口变化之间存在无条件相关性似乎不太清楚。表 23.2:阈值估计:Card-Mas-Rothstein (2008) 模型
| Variable | Estimate | Standard Error |
|---|---|---|
| Intercept Change | \(-11.6\) | \(3.7\) |
| Slope Change | \(-74.1\) | \(42.6\) |
| Minority Fraction | \(-54.4\) | \(28.8\) |
| Minority Fraction \({ }^{2}\) | \(142.3\) | \(23.9\) |
| Unemployment Rate | \(-81.1\) | \(38.8\) |
| \(\log (\) Mean Family Income) | \(3.4\) | \(3.6\) |
| Housing Vacancy Rate | \(324.9\) | \(40.2\) |
| Renter Share | \(-62.7\) | \(13.6\) |
| Fraction Single-Unit | \(-4.8\) | \(9.5\) |
| Fraction Public Transport | \(-91.6\) | \(24.5\) |
| Intercept | \(14.8\) | na |
| MSA Fixed Effects | yes | |
| Threshold | \(0.198\) | |
| \(99 %\) Confidence Interval | \([0.198,0.209]\) | |
| \(N=\) Number of MSAs | 104 | |
| \(n=\) Number of observations | 35,656 |
假设 \(\mathbb{H}_{0}: \gamma=\gamma_{0}\) 具有渐近分布
\[ \frac{n\left(S_{n}^{*}\left(\gamma_{0}\right)-S_{n}^{*}(\widehat{\gamma})\right)}{S_{n}^{*}(\widehat{\gamma})} \underset{d}{\longrightarrow} \xi \]
其中 \(\mathbb{P}[\xi \leq x]=(1-\exp (-x / 2))^{2}\). \(\xi\) 的 \(1-\alpha\) 分位数可以通过求解 \(\left(1-\exp \left(-c_{1-\alpha} / 2\right)\right)^{2}=\) \(1-\alpha\) 找到,并且等于 \(c_{1-\alpha}=-2 \log (1-\sqrt{1-\alpha})\)。例如,\(c_{.95}=7.35\) 和 \(c_{.99}=10.6\)。
基于测试反演,\(\gamma\) 的有效 \(1-\alpha\) 渐近置信区间是一组 \(F\) 统计数据,小于 \(c_{1-\alpha}\) 并且等于
\[ C_{1-\alpha}=\left\{\gamma: \frac{n\left(S_{n}^{*}(\gamma)-S_{n}^{*}(\widehat{\gamma})\right)}{S_{n}^{*}(\widehat{\gamma})} \leq c_{1-\alpha}\right\}=\left\{\gamma: S_{n}^{*}(\gamma) \leq S_{n}^{*}(\widehat{\gamma})\left(1+\frac{c_{1-\alpha}}{n}\right)\right\} \]
这是通过网格搜索以数字方式构建的。在我们的示例中 \(C_{0.99}=[0.198,0.209]\)。这是一个狭窄的置信区间。然而,这个区间没有考虑集群依赖性。根据汉森的理论,我们可以预期,在簇依赖下,渐近分布 \(\xi\) 需要重新缩放。这将导致将上述公式中的 \(1+c_{1-\alpha} / n\) 替换为 \(1+\rho c_{1-\alpha} / n\),以获得某些调整因子 \(\rho\)。这将扩大置信区间。根据图 \(23.3(\mathrm{a})\) 的形状,调整后的置信区间可能不会太宽。然而,这是一个猜想,因为理论还没有制定出来,所以我们无法估计调整因子 \(\rho\)。
经验实践和模拟结果表明,除非使用适度大的样本(例如 \(n \geq 500\) ),否则阈值估计往往相当不精确。阈值参数是通过接近阈值的观察来识别的,而不是通过远离阈值的观察来识别的。这需要大量样本来确保在阈值附近有足够数量的观测值,以便能够确定其位置
给定系数估计值,可以将回归函数与传统计算的置信区间一起绘制出来。在图 23.3(b) 中,我们使用基于估计值 \(\left(\widehat{\beta}_{1}, \widehat{\beta}_{2}, \widehat{\delta}_{1}, \widehat{\delta}_{2}\right)\) 的协方差矩阵计算的 \(95 %\) 渐近置信区间绘制估计回归函数。如果以平均值评估回归函数,则估计 \(\widehat{\theta}\) 没有贡献。我们忽略截距 \(\widehat{\alpha}\) 的估计,因为在聚类依赖性下未识别其方差,并且我们主要对相对比较的幅度感兴趣。我们在图 23.3(b) 中看到的是,回归函数总体呈向下倾斜,这表明白人人口的变化总体上随着少数族裔比例的增加而减少,正如预期的那样。视觉上的倾斜效果很强。当少数派越过临界点时,回归函数的水平和斜率都会急剧下降。估计回归函数的水平还表明,白人人口的预期变化在临界点从正转为负,这与种族隔离假设一致。尽管样本很大,但观察到置信带相当宽是有启发性的。这很大程度上是由于决定使用聚类协方差矩阵估计器。因此,回归函数的位置存在相当大的不确定性。置信区间在估计的临界点处最宽。
本节中提出的实证结果与 Card、Mas 和 Rothstein (2008) 中报告的结果不同但相似。这是一篇有影响力的论文,因为它使用了严格的经济模型来深入了解隔离行为,并使用丰富的详细数据集来研究强临界点预测。
23.8 非线性元件测试
在非线性回归模型中识别可能很棘手。假设
\[ m(X, \theta)=X^{\prime} \beta+X(\gamma)^{\prime} \delta \]
其中 \(X(\gamma)\) 是 \(X\) 的函数和未知参数 \(\gamma\)。 \(X(\gamma)\) 的示例包括 Box-Cox 变换和 \(X \mathbb{1}\{X>\gamma\}\)。后者出现在回归扭结和阈值回归模型中。
当 \(\delta=0\) 时,模型是线性的。这通常是一个需要考虑的有用假设(子模型)。例如,在 Card-Mas-Rothstein(2008)的应用中,这是没有临界点的假设,这是他们论文中探讨的关键问题。
在本节中,我们考虑假设 \(\mathbb{H}_{0}: \delta=0\) 的检验。在 \(\mathbb{H}_{0}\) 下,模型是 \(Y=X^{\prime} \beta+e\),\(\delta\) 和 \(\gamma\) 都已退出。这意味着在 \(\mathbb{H}_{0}\) 下,参数 \(\gamma\) 未被识别。这使得标准分布理论无效。当事实为 \(\delta=0\) 时,\((\beta, \delta, \gamma)\) 的 NLLS 估计量不是渐近正态分布的。如果应用传统的临界值,经典测试会过度拒绝 \(\mathbb{H}_{0}: \delta=0\)。
作为一个例子,考虑阈值回归(23.9)。无临界点的假设对应于联合假设\(\delta_{0}=0\)和\(\delta_{1}=0\)。在此假设下,参数 \(\gamma\) 未被识别。
为了检验假设,标准检验是拒绝较大的 F 统计值
\[ \mathrm{F}=\frac{n\left(\widetilde{S}_{n}-S_{n}^{*}(\widehat{\gamma})\right)}{S_{n}^{*}(\widehat{\gamma})} \]
其中 \(\widetilde{S}_{n}=n^{-1} \sum_{i=1}^{n}\left(Y_{i}-X_{i}^{\prime} \widehat{\beta}\right)^{2}\) 和 \(\widehat{\beta}\) 是 \(Y\) 对 \(X\) 回归的最小二乘系数。这是基于在空 \(\left(\widetilde{S}_{n}\right)\) 和替代 \(\left(S_{n}^{*}(\widehat{\gamma})\right)\) 下计算的估计值的误差方差估计器之间的差异。
F 统计量可以写为
\[ \mathrm{F}=\max _{\gamma} \mathrm{F}_{n}(\gamma)=\mathrm{F}_{n}(\widehat{\gamma}) \]
在哪里
\[ \mathrm{F}_{n}(\gamma)=\frac{n\left(\widetilde{S}_{n}-S_{n}^{*}(\gamma)\right)}{S_{n}^{*}(\gamma)} \]
统计量 \(\mathrm{F}_{n}(\gamma)\) 是经典的 \(\mathrm{F}\) 统计量,用于在 \(\gamma\) 已知时测试 \(\mathbb{H}_{0}: \delta=0\)。从这个表示中我们可以看到 \(\mathrm{F}\) 是非标准的,因为它是潜在大量统计数据 \(\mathrm{F}_{n}(\gamma)\) 的最大值
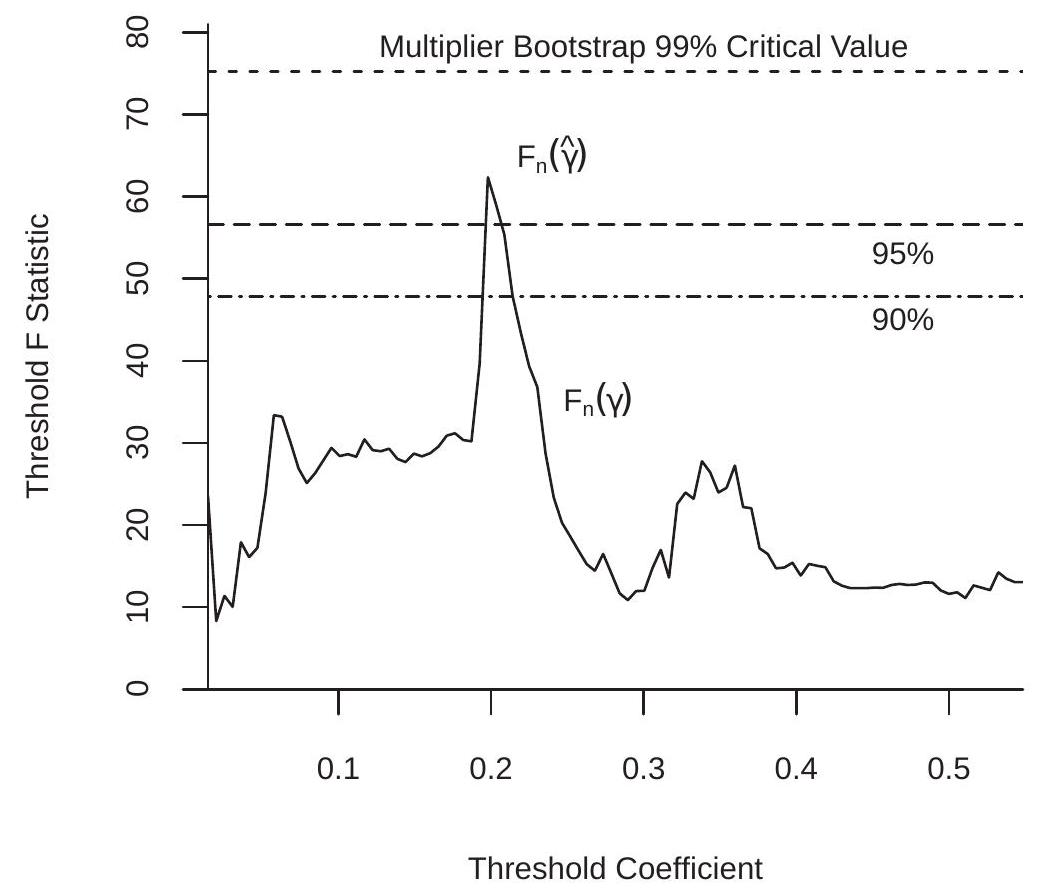
图 23.4:CMR 模型中的阈值回归测试
为了说明这一点,图 \(23.4\) 将检验统计量 \(\mathrm{F}_{n}(\gamma)\) 绘制为 \(\gamma\) 的函数。您可以看到该函数不稳定,类似于集中标准 \(S_{n}^{*}(\gamma)\)。这是明智的,因为 \(\mathrm{F}_{n}(\gamma)\) 是 \(S_{n}^{*}(\gamma)\) 的反函数的仿射函数。由于这种对偶性,统计量在 \(\widehat{\gamma}\) 处最大化。最大值为 \(\mathrm{F}=\mathrm{F}_{n}(\hat{\gamma})\)。在此应用程序中,我们找到 \(\mathrm{F}=62.4\)。以传统标准来看,这是非常高的。
检验的渐近理论由 Andrews 和 Ploberger (1994) 以及 B. E. Hansen (1996) 制定。特别是,Hansen 展示了乘数引导程序用于计算独立观测值的 p 值的有效性。方法如下。
根据观测值 \(\left(Y_{i}, X_{i}\right)\) 计算 \(\mathbb{H}_{0}\) 相对于 \(\mathbb{H}_{1}\) 的 \(\mathrm{F}\) 检验统计量(或任何其他标准统计量,例如 Wald 或似然比)。
对于 \(b=1, \ldots, B\) :
生成均值为零、方差为 1 的 \(n\) 随机变量 \(\xi_{i}^{*}\)(标准选择为正态和 Rademacher)。
设置 \(Y_{i}^{*}=\widehat{e}_{i} \xi_{i}^{*}\),其中 \(\widehat{e}_{i}\) 是 NLLS 残差。
\(\operatorname{On}\left(Y_{i}^{*}, X_{i}\right)\) 相对于 \(\mathbb{H}_{1}\) 计算 \(\mathbb{H}_{0}\) 的 \(\mathrm{F}\) 统计量 \(\mathrm{F}_{b}^{*}\)。 3. 乘数引导 p 值为 \(p_{n}^{*}=\frac{1}{B} \sum_{b=1}^{B} \mathbb{1}\left\{\mathrm{F}_{b}^{*}>\mathrm{F}\right\}\)。
如果 \(p_{n}^{*}<\alpha\) 检验在 \(\alpha\) 水平上显着。
可以将临界值计算为引导统计数据 \(\mathrm{F}_{b}^{*}\) 的经验分位数。
在步骤 \(2 \mathrm{~b}\) 中,您也可以设置 \(Y_{i}^{*}=\widehat{\beta}^{\prime} Z_{i}+\widehat{e}_{i} \xi_{i}^{*}\)。 \(\delta\) 上的测试对于 \(\delta\) 的引导值是不变的。重要的是引导数据满足原假设。
对于聚类样本,我们需要进行较小的修改。将聚类回归写为
\[ \boldsymbol{Y}_{g}=\boldsymbol{X}_{g} \beta+\boldsymbol{X}_{g}(\gamma) \delta+\boldsymbol{e}_{g} . \]
通过更改上面的步骤 \(2 \mathrm{a}\) 和 \(2 \mathrm{~b}\) 来修改引导方法。让 \(N\) 表示簇的数量。修改后的算法使用以下步骤。
- 生成均值为 0、方差为 1 的 \(N\) 随机变量 \(\xi_{g}^{*}\)。
- \(\operatorname{Set} \boldsymbol{Y}_{g}^{*}=\widehat{\boldsymbol{e}}_{g} \xi_{g}^{*}\)
为了说明这一点,我们将此测试应用于使用 Card-Mas-Rothstein (2008) 数据估计的阈值回归 (23.9)。我们使用 \(B=10,000\) 引导复制。应用第一个算法(适合独立观察),引导 p 值为 \(0 %\)。 \(99 %\) 的临界值为 \(16.7\),因此 \(\mathrm{F}=62.4\) 的观测值远远超过此阈值。应用第二种算法(适用于集群依赖性),引导 p 值为 \(3.1 %\)。 \(95 %\) 临界值为 \(56.6\),\(99 %\) 为 \(B=10,000\)。因此,\(B=10,000\) 的观测值在 \(B=10,000\) 水平上“显着”,但在 \(B=10,000\) 水平上则不显着。对于大小为 \(B=10,000\) 的样本来说,这是令人惊讶的轻微意义。这些临界值在图 \(B=10,000\) 上用虚线表示。 F 统计过程打破了 \(B=10,000\) 和 \(B=10,000\) 临界值,但没有打破 \(B=10,000\)。因此,尽管上一节中的倾斜效应在视觉上有强有力的证据,但这种效应的统计证据是强有力的,但不是压倒性的。
23.9 计算
Stata 有一个内置命令 nl 用于 NLLS 估计。您需要指定非线性方程并给出数值搜索的起始值。尝试多个起始值是谨慎的做法,因为该算法不能保证收敛到全局最小值。
在 R 或 MATLAB 中估计 NLLS 需要更多编程,但很简单。您编写一个函数,计算平均平方误差 \(S_{n}(\theta)\) (或集中平均平方误差)作为参数的函数。然后,您调用数值优化器来最小化此函数。例如,在 R 中,对于向量值参数,标准优化器是 optim。对于标量参数,请使用优化。
23.10 技术证明*
定理23.1的证明。我们诉诸定理 \(22.3\),它在五个条件下成立。假设 23.1 第 1、2、5 和 6 部分直接满足条件 1,2、4 和 5。要验证条件 3,请通过 \(c_{r}\) 不等式 (B.5) 和 \(|m(X, \theta)| \leq m(X)\) 观察
\[ (Y-m(X, \theta))^{2} \leq 2 Y^{2}+2 m(X)^{2} . \]
根据假设 23.1 第 3 部分和第 4 部分,右侧的期望是有限的。我们的结论是 \(\widehat{\theta} \underset{p}{\longrightarrow} \theta_{0}\) 如所述。
定理23.2的证明。我们诉诸定理 \(22.4\),它在五个条件下成立(除了在定理 23.1 中建立的一致性之外)。重新调整标准以便 \(\rho_{i}(\theta)=\frac{1}{2}\left(Y_{i}-m\left(X_{i}, \theta\right)\right)^{2}\) 很方便。然后是\(\psi_{i}=-m_{\theta i} e_{i}\)。
为了显示条件 1,由 Cauchy-Schwarz 不等式 (B.32) 和假设 23.2.2 和 23.2.4
\[ \mathbb{E}\left\|\psi_{i}\right\|^{2}=\mathbb{E}\left\|m_{\theta i} e_{i}\right\|^{2} \leq\left(\mathbb{E}\left\|m_{\theta i}\right\|^{4} \mathbb{E}\left[e_{i}^{4}\right]\right)^{1 / 2}<\infty . \]
接下来我们展示条件 3。使用假设 23.2.1,我们计算出
\[ S(\theta)=\mathbb{E}\left[\rho_{i}(\theta)\right]=\frac{1}{2} \mathbb{E}\left[e^{2}\right]+\frac{1}{2} \mathbb{E}\left[\left(m\left(X, \theta_{0}\right)-m(X, \theta)\right)^{2}\right] . \]
因此
\[ \psi(\theta)=\frac{\partial}{\partial \theta} S(\theta)=-\mathbb{E}\left[m_{\theta}(X, \theta)\left(m\left(X, \theta_{0}\right)-m(X, \theta)\right)\right] \]
与衍生品
\[ \begin{aligned} \boldsymbol{Q}(\theta) &=-\frac{\partial}{\partial \theta^{\prime}} \mathbb{E}\left[m_{\theta}(X, \theta)\left(m\left(X, \theta_{0}\right)-m(X, \theta)\right)\right] \\ &=\mathbb{E}\left[m_{\theta}(X, \theta) m_{\theta}(X, \theta)^{\prime}\right]-\mathbb{E}\left[m_{\theta \theta}\left(X, \theta_{0}\right)\left(m\left(X, \theta_{0}\right)-m(X, \theta)\right)\right] . \end{aligned} \]
在假设 23.2.4 下,这对于 \(\theta \in \mathcal{N}\) 来说是存在且连续的。
在 \(\theta_{0}\) 处评估 (23.10) 我们得到
\[ \boldsymbol{Q}=\boldsymbol{Q}\left(\theta_{0}\right)=\mathbb{E}\left[m_{\theta i} m_{\theta i}^{\prime}\right]>0 \]
根据假设 23.2.5。这验证了条件 2。
如果 \(\psi(Y, X, \theta)=m_{\theta}(X, \theta)(Y-m(X, \theta))\) 在 \(\theta \in \mathscr{N}\) 中是 Lipschitz 连续的,则条件 4 成立。这是成立的,因为 \(m_{\theta}(X, \theta)\) 和 \(m(X, \theta)\) 在紧集 \(\theta \in \mathscr{N}\) 中都是可微的,并且有界四阶矩(假设 \(23.2 .2\) 和 23.2.4)意味着 \(\psi(Y, X, \theta)\) 的 Lipschitz 边界具有有限二阶矩。
条件 5 由假设 23.2.6 隐含。
定理 \(22.4\) 的五个条件一起满足,结果如下。
23.11 练习
练习 23.1 采用模型 \(Y=\exp (\theta)+e\) 和 \(\mathbb{E}[e]=0\)。
\(\theta\) 中的 CEF 是线性的还是非线性的?这是非线性回归模型吗?
有没有办法使用线性方法来估计模型?如果是这样,请解释如何获得 \(\theta\) 的估计器 \(\widehat{\theta}\)。
- 部分的答案与 NLLS 估计器相同还是不同?
练习23.2 采用模型\(Y^{(\lambda)}=\beta_{0}+\beta_{1} X+e\)和\(\mathbb{E}[e \mid X]=0\),其中\(Y^{(\lambda)}\)是\(Y\)的Box-Cox变换。 (a) 这是参数 \(\left(\lambda, \beta_{0}, \beta_{1}\right)\) 的非线性回归模型吗? (小心,这很棘手。)
练习 23.3 采用模型 \(Y=\frac{\beta_{1}}{\beta_{2}+\beta_{3} X}+e\) 和 \(\mathbb{E}[e \mid X]=0\)。
参数 \(\left(\beta_{1}, \beta_{2}, \beta_{3}\right)\) 是否已识别?
如果不是,则确定哪些参数?您将如何估计模型?
练习 23.4 采用模型 \(Y=\beta_{1} \exp \left(\beta_{2} X\right)+e\) 和 \(\mathbb{E}[e \mid X]=0\)。
参数 \(\left(\beta_{1}, \beta_{2}\right)\) 是否已识别?
找到一个表达式来计算 NLLS 估计值 \(\left(\widehat{\beta}_{1}, \widehat{\beta}_{2}\right)\) 的协方差矩阵。
练习 23.5 采用模型 \(Y=m(X, \theta)+e\) 和 \(e \mid X \sim \mathrm{N}\left(0, \sigma^{2}\right)\)。求 \(\theta\) 和 \(\sigma^{2}\) 的 MLE。
练习23.6 采用模型\(Y=\exp \left(X^{\prime} \theta\right)+e\)和\(\mathbb{E}[Z e]=0\),其中\(X\)是\(k \times 1\),\(Z\)是\(\ell \times 1\)。
\(\ell\) 和 \(k\) 之间的什么关系对于识别 \(\theta\) 是必要的?
描述如何通过 GMM 估计 \(\theta\)。
描述渐近协方差矩阵的估计量。
练习23.7 假设\(Y=m(X, \theta)+e\)和\(\mathbb{E}[e \mid X]=0, \widehat{\theta}\)是NLLS估计器,\(\widehat{\boldsymbol{V}}\)是\(\operatorname{var}[\widehat{\theta}]\)的估计器。您对 CEF \(\mathbb{E}[Y \mid X=x]=m(x)\) 和 \(x\) 感兴趣。求 \(m(x)\) 的渐近 \(95 %\) 置信区间。
练习 23.8 文件 PSS2017 包含 Papageorgiou、Saam 和 Schulte (2017) 的数据子集。为了进行稳健性检查,他们使用近似资本存量而不是产能作为投入指标,重新估计了 CES 生产函数。使用此替代措施估计模型 (23.3)。 \(Y, X_{1}\) 和 \(X_{2}\) 的变量分别是 EG_total、EC_c_alt 和 EC_d_alt。将估计值与表 23.1 中报告的值进行比较。
练习 23.9 文件 RR2010 包含来自 Reinhart 和 Rogoff (2010) 的美国观察结果。该数据集包含对实际 GDP 增长、债务/GDP 和通货膨胀率的观察。估计模型 (23.4),将 \(Y\) 设置为通货膨胀率,将 \(X\) 设置为债务比率。
练习 23.10 在练习 9.26 中,您估计了电力公司横截面的成本函数。考虑非线性规范
\[ \log T C=\beta_{1}+\beta_{2} \log Q+\beta_{3}(\log P L+\log P K+\log P F)+\beta_{4} \frac{\log Q}{1+\exp (-(\log Q-\gamma))}+e . \]
该模型称为平滑阈值模型。对于远低于 \(\gamma\) 的 \(\log Q\) 值,变量 \(\log Q\) 的回归斜率为 \(\beta_{2}\)。对于远高于 \(\beta_{7}\) 的值,回归斜率为 \(\beta_{2}+\beta_{4}\)。该模型在这些制度之间实现了平稳过渡。
当选择 \(\gamma\) 且 \(\log Q_{i}\) 的多个值(在本例中至少为 10 到 15)均低于和高于 \(\gamma\) 时,模型效果最佳。检查数据并为 \(\gamma\) 选择适当的范围。
通过 NLLS 使用 \(\left(\beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}, \gamma\right)\) 上的全局数值搜索来估计模型。
通过 NLLS 使用 \(\gamma\) 上的集中数值搜索来估计模型。你得到相同的结果吗?
计算所有参数估计值 \(\left(\beta_{1}, \beta_{2}, \beta_{3}, \beta_{4}, \gamma\right)\) 的标准误差。