第17章: 面板数据

17 面板数据

17.1 介绍

经济学家传统上使用术语面板数据来指代由多个时间段的个人观察组成的数据结构。其他领域（例如统计学）通常将这种结构称为纵向数据。观察到的“个人”可以是例如人、家庭、工人、公司、学校、生产工厂、行业、地区、州或国家。与横截面数据集相关的显着特征是每个个体存在多个观察结果。更广泛地说，面板数据方法可以应用于具有聚类类型依赖性的任何上下文。

相对于横截面数据，面板数据有几个明显的优点。一是无需使用工具变量即可控制未观察到的时不变内生性的可能性。第二个是允许更广泛形式的异质性的可能性。第三是对动态关系和效果进行建模。

经济应用中的面板数据集有两大类：微观面板和宏观面板。微型小组通常是对个人的调查或管理记录，其特点是个体数量大（通常为 1000 人或更多）和相对较少的时间段（通常为 2 至 20 年）。宏观面板通常是国家或地区宏观经济变量，其特征是适度数量的个体（例如 7-20 人）和适度数量的时间段（20-60 年）。

面板数据曾经在应用经济实践中相对深奥。现在，它已成为应用研究的一个显着特征。

微型面板的一个典型的假设（我们在本章中遵循）是个体相互独立，而对给定个体的观察在不同时间段内是相关的。这意味着观察结果遵循聚集的依赖结构。因此，当前的计量经济学实践是在可能的情况下使用集群鲁棒协方差矩阵估计器。类似的假设经常用于宏观面板，尽管个人（例如国家）之间的独立性假设不那么令人信服。

面板数据方法在计量经济学中的应用始于 Mundlak (1961) 以及 Balestra 和 Nerlove (1966) 的开创性工作。

关于面板计量经济学，已经撰写了几本优秀的专着和教科书，包括 Arellano (2003)、Hsiao (2003)、Wooldridge (2010) 和 Baltagi (2013)。本章将总结一些主要主题，但要进行更深入的处理，请参阅这些参考资料。

面板数据应用中出现的一项挑战是计算方法可能需要对细节一丝不苟。因此，建议对常规应用程序使用已建立的软件包。对于经济学中的大多数面板数据应用，Stata 是标准软件包。

17.2 时间索引和不平衡面板

通常按个体 $i$ 和时间段 $t$ 对观测值进行索引，因此 $Y_{i t}$ 表示个体 $i$ 在周期 $t$ 中的变量。我们将个人索引为 $i=1, \ldots, N$，将时间段索引为 $t=1, \ldots T$。因此 $N$ 是面板中的个体数量，$T$ 是时间序列周期的数量。

尽管典型应用涉及年度数据，但面板数据集可以涉及任何时间序列频率的数据。数据集中的观测值将按日历时间索引，对于年度观测值来说，日历时间是年份。为了符号方便，通常将时间段表示为 $t=$ $1, \ldots, T$，因此 $t=1$ 是观察到的第一个时间段，$T$ 是最后一个时间段。

当在同一时间段内对所有个体进行观察时，我们说该小组是平衡的。在这种情况下，每个个体都有相同数量的 $T$ 观察值，观察值总数为 $n=N T$。

当样本中的个体有不同的时间段时，我们说该小组不平衡。这是最常见的面板数据集类型。它不会给应用程序带来问题，但确实使符号变得麻烦并且使计算机编程变得复杂。

为了说明这一点，请考虑教科书网页上的数据集 Invest 1993。这是从 Compustat 中提取的 1962 年美国公司样本，由 Bronwyn Hall 汇总，并用于 Hall 和 Hall (1993) 的实证研究中。在表 17.1 中，我们显示了前 13 个观测值的数据集中的一组变量。第一个变量是公司代码。第二个变量是观察年份。这两个变量对于任何面板数据分析都是必不可少的。在表 $17.1$ 中，您可以看到第一家公司 (#32) 是在 1970 年到 1977 年期间观察到的。第二家公司 (#209) 是在 1987 年到 1991 年期间观察到的。您可以看到，各个年份之间的差异很大所以这是一个不平衡的小组。

对于不平衡面板，时间索引 $t=1, \ldots, T$ 表示完整的时间段集。例如，在数据集 Invest 1993 中，有 1960 年至 1991 年的观测值，因此时间段总数为 $T=32$。每个人都会在 $T_{i}$ 周期的子集内进行观察。个人 $i$ 的时间段集合表示为 $S_{i}$，因此个人特定的总和（在时间段内）被写为 $\sum_{t \in S_{i}}$。

给定个体的观察时间段通常是连续的（例如，在表 17.1 中，从 1970 年到 1977 年，每年观察到公司 #32），但在某些情况下是不连续的（例如，如果缺少 1973 年）对于公司#32）。样本中的观测总数为 $n=\sum_{i=1}^{N} T_{i}$。

表 17.1：投资数据集的观察结果

Firm Code Number	Year	$I_{i t}$	$\bar{I}_{i}$	$\dot{I}_{i t}$	$Q_{i t}$	$\bar{Q}_{i}$	$\dot{Q}_{i t}$	$\widehat{e}_{i t}$
32	1970	$0.122$	$0.155$	$-0.033$	$1.17$	$0.62$	$0.55$	.
32	1971	$0.092$	$0.155$	$-0.063$	$0.79$	$0.62$	$0.17$	$-0.005$
32	1972	$0.094$	$0.155$	$-0.061$	$0.91$	$0.62$	$0.29$	$-0.005$
32	1973	$0.116$	$0.155$	$-0.039$	$0.29$	$0.62$	$-0.33$	$0.014$
32	1974	$0.099$	$0.155$	$-0.057$	$0.30$	$0.62$	$-0.32$	$-0.002$
32	1975	$0.187$	$0.155$	$0.032$	$0.56$	$0.62$	$-0.06$	$0.086$
32	1976	$0.349$	$0.155$	$0.194$	$0.38$	$0.62$	$-0.24$	$0.248$
32	1977	$0.182$	$0.155$	$0.027$	$0.57$	$0.62$	$-0.05$	$0.081$
209	1987	$0.095$	$0.071$	$0.024$	$9.06$	$21.57$	$-12.51$	.
209	1988	$0.044$	$0.071$	$-0.027$	$16.90$	$21.57$	$-4.67$	$-0.244$
209	1989	$0.069$	$0.071$	$-0.002$	$25.14$	$21.57$	$3.57$	$-0.257$
209	1990	$0.113$	$0.071$	$0.042$	$25.60$	$21.57$	$4.03$	$-0.226$
209	1991	$0.034$	$0.071$	$-0.037$	$31.14$	$21.57$	$9.57$	$-0.283$

17.3 符号

本章重点介绍面板数据回归模型，其观测值为 $\left(Y_{i t}, X_{i t}\right)$ 对，其中 $Y_{i t}$ 是因变量，$X_{i t}$ 是回归量的 $k$ 向量。这些是 $t$ 时间段内个人 $i$ 的观察结果。

在个体层面上对观察结果进行聚类是很有用的。我们借用 $4.21$ 节中的符号，将 $\boldsymbol{Y}_{i}$ 写为 $T_{i} \times 1$ 在 $t \in S_{i}$ 的 $Y_{i t}$ 上堆叠的观察结果，按时间顺序堆叠。类似地，我们将 $\boldsymbol{X}_{i}$ 写为 $t \in S_{i}$ 的堆叠 $X_{i t}^{\prime}$ 的 $T_{i} \times k$ 矩阵，按时间顺序堆叠。

有时我们还会对完整样本使用矩阵表示法。为此，让 $\boldsymbol{Y}=\left(\boldsymbol{Y}_{1}^{\prime}, \ldots, \boldsymbol{Y}_{N}^{\prime}\right)^{\prime}$ 表示堆叠的 $\boldsymbol{Y}_{i}$ 的 $n \times 1$ 向量，并类似地设置 $\boldsymbol{X}=\left(\boldsymbol{X}_{1}^{\prime}, \ldots, \boldsymbol{X}_{N}^{\prime}\right)^{\prime}$。

17.4 汇总回归

面板回归中最简单的模型是合并回归

\[ \begin{aligned} Y_{i t} &=X_{i t}^{\prime} \beta+e_{i t} \\ \mathbb{E}\left[X_{i t} e_{i t}\right] &=0 . \end{aligned} \]

其中 $\beta$ 是 $k \times 1$ 系数向量，$e_{i t}$ 是错误。该模型可以在个人层面上写为

\[ \begin{aligned} \boldsymbol{Y}_{i} &=\boldsymbol{X}_{i} \beta+\boldsymbol{e}_{i} \\ \mathbb{E}\left[\boldsymbol{X}_{i}^{\prime} \boldsymbol{e}_{i}\right] &=0 \end{aligned} \]

其中 $\boldsymbol{e}_{i}$ 是 $T_{i} \times 1$。完整样本的方程为 $\boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{e}$，其中 $\boldsymbol{e}$ 为 $n \times 1$。

合并回归模型中 $\beta$ 的标准估计量是最小二乘法，可以写为

\[ \begin{aligned} \widehat{\beta}_{\text {pool }} &=\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} X_{i t} X_{i t}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} X_{i t} Y_{i t}\right) \\ &=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{Y}_{i}\right) \\ &=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{Y}\right) . \end{aligned} \]

在面板数据中，$\widehat{\beta}_{\text {pool }}$ 被称为合并回归估计器。 $i^{t h}$ 个体的残差向量是 $\widehat{\boldsymbol{e}}_{i}=\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \widehat{\beta}_{\text {pool }}$。

合并回归模型非常适合误差 $e_{i t}$ 满足严格均值独立性的情况：

\[ \mathbb{E}\left[e_{i t} \mid \boldsymbol{X}_{i}\right]=0 . \]

当所有时间段 $j=1, \ldots, T$ 的误差 $e_{i t}$ 均值独立于所有回归量 $X_{i j}$ 时，就会发生这种情况。严格均值独立性强于成对均值独立性 $\mathbb{E}\left[e_{i t} \mid X_{i t}\right]=0$ 以及投影 (17.1)。严格均值独立性要求 $X_{i t}$ 的滞后值和未来值都不能帮助预测 $e_{i t}$。它从 $X_{i t}$ 中排除滞后因变量（例如 $Y_{i t-1}$ ）（否则 $e_{i t}$ 在给定 $e_{i t}$ 的情况下是可预测的）。它还要求 $e_{i t}$ 在第 12 章讨论的意义上是外生的。

我们现在在（17.2）下描述 $\widehat{\beta}_{\text {pool }}$ 的一些统计特性。首先，请注意，通过线性和簇级符号，我们可以将估计器写为

\[ \widehat{\beta}_{\mathrm{pool}}=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime}\left(\boldsymbol{X}_{i} \beta+\boldsymbol{e}_{i}\right)\right)=\beta+\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{e}_{i}\right) . \]

使用（17.2）

\[ \mathbb{E}\left[\widehat{\beta}_{\text {pool }} \mid \boldsymbol{X}\right]=\beta+\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \mathbb{E}\left[\boldsymbol{e}_{i} \mid \boldsymbol{X}_{i}\right]\right)=\beta \]

所以 $\widehat{\beta}_{\text {pool }}$ 对于 $\beta$ 是无偏的。

在误差 $e_{i t}$ 序列不相关且同方差的附加假设下，协方差估计量采用经典形式，并且可以使用经典同方差估计量。如果误差 $e_{i t}$ 是异方差但序列不相关，则可以使用异方差鲁棒协方差矩阵估计器。

然而，一般来说，我们预计对于给定个体，误差 $e_{i t}$ 在时间 $t$ 上是相关的。这不一定违反（17.2），但会使经典协方差矩阵估计无效。传统的解决方案是使用集群鲁棒协方差矩阵估计器，它允许任意的集群内依赖。合并回归等于的集群鲁棒协方差矩阵估计器

\[ \widehat{\boldsymbol{V}}_{\text {pool }}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \widehat{\boldsymbol{e}}_{i} \widehat{\boldsymbol{e}}_{i}^{\prime} \boldsymbol{X}_{i}\right)\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} . \]

如 (4.55) 中所示，这可以乘以自由度调整。 Stata回归命令使用的调整是

\[ \widehat{\boldsymbol{V}}_{\text {pool }}=\left(\frac{n-1}{n-k}\right)\left(\frac{N}{N-1}\right)\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \widehat{\boldsymbol{e}}_{i} \widehat{\boldsymbol{e}}_{i}^{\prime} \boldsymbol{X}_{i}\right)\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \]

可以使用 Stata 命令 regress cluster(id) 获得具有集群稳健标准误差的汇总回归估计量，其中 id 表示个体。

当严格均值独立性 (17.2) 失败时，合并最小二乘估计器 $\widehat{\beta}_{\text {pool }}$ 不一定与 $\beta$ 一致。由于严格均值独立性是一种强烈且不受欢迎的限制，因此通常优选采用以下各节中描述的替代估计器之一。

为了说明合并回归估计器，请考虑前面描述的 Invest1993 数据集。我们考虑一个简单的投资模型

\[ I_{i t}=\beta_{1} Q_{i t-1}+\beta_{2} D_{i t-1}+\beta_{3} C F_{i t-1}+\beta_{4} T_{i}+e_{i t} \]

其中 $I$ 是投资/资产，$Q$ 是市场价值/资产，$D$ 是长期债务/资产，$C F$ 是现金流/资产，$T$ 是虚拟变量，指示公司的股票是否在纽约证券交易所或美国证券交易所交易。回归还包括 19 个指示行业代码的虚拟变量。 $Q$ 投资理论表明 $\beta_{1}>0$ 而 $\beta_{2}=\beta_{3}=0$。流动性约束理论表明 $\beta_{2}<0$ 和 $I$。我们将在本章中使用这个例子。前 13 个观测值的 $I$ 和 $I$ 值也显示在表 17.1 中。

在表 $17.2$ 中，我们在第一列中展示了 (17.3) 的汇总回归估计，并具有集群鲁棒性标准误差。

17.5 单向错误组件模型

面板数据回归的一种方法是对回归误差 $e_{i t}$ 的相关结构进行建模。最常见的选择是错误组件结构。最简单的形式

\[ e_{i t}=u_{i}+\varepsilon_{i t} \]

表 17.2：投资方程估算

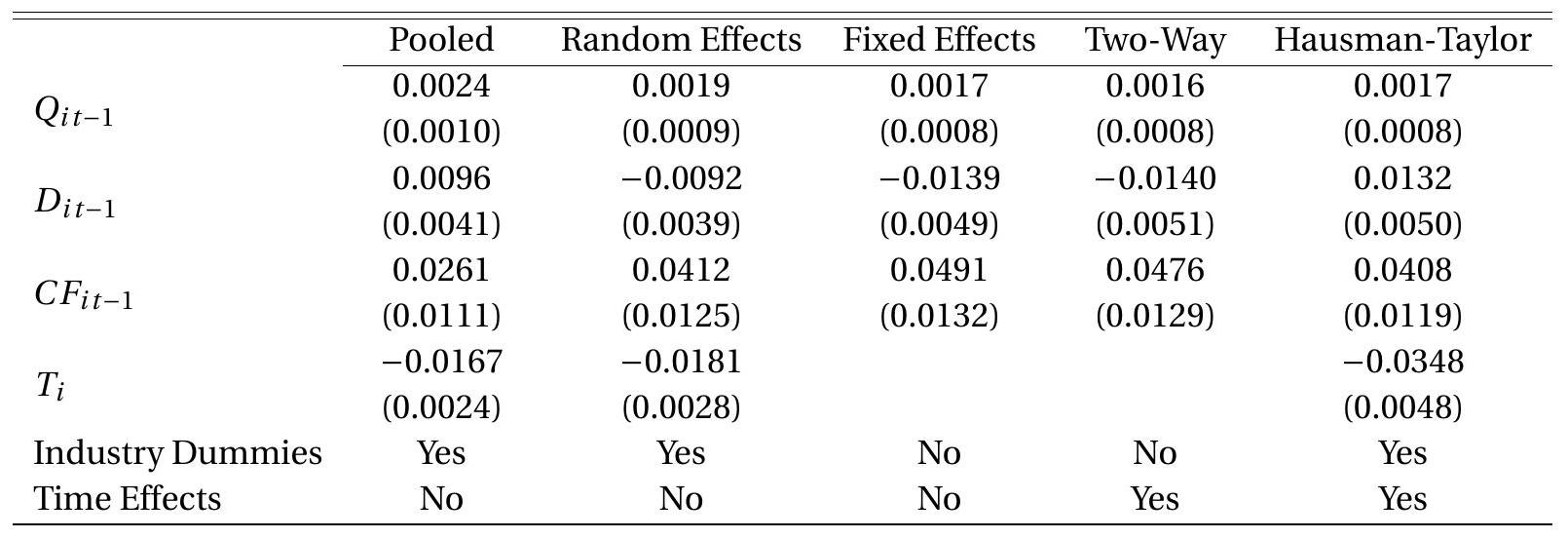
括号中的集群稳健标准错误。

其中 $u_{i}$ 是个体特定效应，$\varepsilon_{i t}$ 是特殊 (i.i.d.) 错误。这称为单向错误组件模型。

在向量表示法中，我们可以写成 $\boldsymbol{e}_{i}=\mathbf{1}_{i} u_{i}+\boldsymbol{\varepsilon}_{i}$，其中 $\mathbf{1}_{i}$ 是由 1 组成的 $T_{i} \times 1$ 向量。

单向误差分量回归模型为

\[ Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} \]

写在观察的层面上，或者 $\boldsymbol{Y}_{i}=\boldsymbol{X}_{i} \beta+\mathbf{1}_{i} u_{i}+\boldsymbol{\varepsilon}_{i}$ 写在个人的层面上。

为了说明为什么像 (17.4) 这样的误差分量结构可能是合适的，请检查表 17.1。在最后一列中，我们包含了这些观测值的汇总回归残差 $\widehat{e}_{i t}$。（由于缺乏该观察的滞后回归量，每家公司第一年都没有残差。）非常引人注目的是第二家公司（#209）的残差都是负数，集中在 $-0.25$ 周围。虽然非正式，但这表明使用（17.4）对这些错误进行建模可能是合适的，期望公司#209对其个体效应$u$具有较大的负值。

17.6 随机效应

随机效应模型假设 (17.4) 中的误差 $u_{i}$ 和 $\varepsilon_{i t}$ 有条件均值为零、不相关且同方差。

假设 17.1 随机效应。模型 (17.4) 成立

\[ \begin{aligned} \mathbb{E}\left[\varepsilon_{i t} \mid \boldsymbol{X}_{i}\right] &=0 \\ \mathbb{E}\left[\varepsilon_{i t}^{2} \mid \boldsymbol{X}_{i}\right] &=\sigma_{\varepsilon}^{2} \\ \mathbb{E}\left[\varepsilon_{i t} \varepsilon_{j s} \mid \boldsymbol{X}_{i}\right] &=0 \\ \mathbb{E}\left[u_{i} \mid \boldsymbol{X}_{i}\right] &=0 \\ \mathbb{E}\left[u_{i}^{2} \mid \boldsymbol{X}_{i}\right] &=\sigma_{u}^{2} \\ \mathbb{E}\left[u_{i} \varepsilon_{i t} \mid \boldsymbol{X}_{i}\right] &=0 \end{aligned} \]

其中 (17.7) 对于所有 $s \neq t$ 都成立。假设 $17.1$ 被称为随机效应规范。这意味着个体 $i$ 的误差向量 $\boldsymbol{e}_{i}$ 具有协方差结构

\[ \begin{aligned} \mathbb{E}\left[\boldsymbol{e}_{i} \mid \boldsymbol{X}_{i}\right] &=0 \\ \mathbb{E}\left[\boldsymbol{e}_{i} \boldsymbol{e}_{i}^{\prime} \mid \boldsymbol{X}_{i}\right] &=\mathbf{1}_{i} \mathbf{1}_{i}^{\prime} \sigma_{u}^{2}+\boldsymbol{I}_{i} \sigma_{\varepsilon}^{2} \\ &=\left(\begin{array}{cccc} \sigma_{u}^{2}+\sigma_{\varepsilon}^{2} & \sigma_{u}^{2} & \cdots & \sigma_{u}^{2} \\ \sigma_{u}^{2} & \sigma_{u}^{2}+\sigma_{\varepsilon}^{2} & \cdots & \sigma_{u}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{u}^{2} & \sigma_{u}^{2} & \cdots & \sigma_{u}^{2}+\sigma_{\varepsilon}^{2} \end{array}\right) \\ &=\sigma_{\varepsilon}^{2} \Omega_{i}, \end{aligned} \]

比如说，其中 $\boldsymbol{I}_{i}$ 是维度为 $T_{i}$ 的单位矩阵。矩阵 $\Omega_{i}$ 取决于 $i$，因为它的维度取决于观察到的时间段 $T_{i}$ 的数量。

假设 17.1.1 和 17.1.4 表明，特殊误差 $\varepsilon_{i t}$ 和个体特定误差 $u_{i}$ 是严格均值独立的，因此组合误差 $e_{i t}$ 也是严格均值独立的。

随机效应模型相当于等相关模型。也就是说，假设误差 $e_{i t}$ 满足

\[ \begin{aligned} \mathbb{E}\left[e_{i t} \mid \boldsymbol{X}_{i}\right] &=0 \\ \mathbb{E}\left[e_{i t}^{2} \mid \boldsymbol{X}_{i}\right] &=\sigma^{2} \end{aligned} \]

和

\[ \mathbb{E}\left[e_{i s} e_{i t} \mid \boldsymbol{X}_{i}\right]=\rho \sigma^{2} \]

为 $s \neq t$。这些条件意味着 $e_{i t}$ 可以写成 (17.4)，其组件满足假设 $17.1$、$\sigma_{u}^{2}=\rho \sigma^{2}$ 和 $\sigma_{\varepsilon}^{2}=(1-\rho) \sigma^{2}$。因此，随机效应和等相关是相同的。

随机效应回归模型为

\[ Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} \]

或 $\boldsymbol{Y}_{i}=\boldsymbol{X}_{i} \beta+\mathbf{1}_{i} u_{i}+\boldsymbol{\varepsilon}_{i}$，其中误差满足假设 17.1。

给定误差结构，$\beta$ 的自然估计量是 GLS。假设 $\sigma_{u}^{2}$ 和 $\sigma_{\varepsilon}^{2}$ 已知。 $\beta$ 的 GLS 估计量为

\[ \widehat{\beta}_{\mathrm{gls}}=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{Y}_{i}\right) . \]

可行的 GLS 估计器用估计器替换未知的 $\sigma_{u}^{2}$ 和 $\sigma_{\varepsilon}^{2}$。请参阅 $17.15$ 节。

我们现在描述假设 17.1 下估计器的一些统计特性。按线性度

\[ \widehat{\beta}_{\mathrm{gls}}-\beta=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{e}_{i}\right) . \]

因此

\[ \mathbb{E}\left[\widehat{\beta}_{\mathrm{gls}}-\beta \mid \boldsymbol{X}\right]=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \mathbb{E}\left[\boldsymbol{e}_{i} \mid \boldsymbol{X}_{i}\right]\right)=0 . \]

因此 $\widehat{\beta}_{\text {gls }}$ 对于 $\beta$ 有条件无偏。 $\widehat{\beta}_{\text {gls }}$ 的条件方差为

\[ \boldsymbol{V}_{\mathrm{gls}}=\left(\sum_{i=1}^{n} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1} \sigma_{\varepsilon}^{2} \]

现在让我们将 $\widehat{\beta}_{\text {gls }}$ 与池估计器 $\widehat{\beta}_{\text {pool. }}$ 进行比较。在假设 $17.1$ 下，后者对于 $\beta$ 也是有条件无偏的，并且具有条件方差

\[ \boldsymbol{V}_{\text {pool }}=\left(\sum_{i=1}^{n} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{n} \boldsymbol{X}_{i}^{\prime} \Omega_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{n} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1} . \]

使用高斯-马尔可夫定理的代数我们推导出

\[ \boldsymbol{V}_{\text {gls }} \leq \boldsymbol{V}_{\text {pool }} \]

因此，在假设 17.1 下，随机效应估计器 $\widehat{\beta}_{\text {gls }}$ 比合并估计器 $\widehat{\beta}_{\text {pool }}$ 更有效。（参见练习 17.1。）当 $\boldsymbol{V}_{\text {gls }}=\boldsymbol{V}_{\text {pool }}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \sigma_{\varepsilon}^{2}$ 没有个体特定效应时（当 $\sigma_{u}^{2}=0$ 时），两个方差矩阵是相同的。

假设随机效应模型是一个有用的近似值，但实际上并不正确，那么我们可以考虑使用集群稳健的协方差矩阵估计器，例如

\[ \widehat{\boldsymbol{V}}_{\mathrm{gls}}=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \widehat{\boldsymbol{e}}_{i} \widehat{\boldsymbol{e}}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)\left(\sum_{i=1}^{n} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1} \]

其中 $\widehat{\boldsymbol{e}}_{i}=\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \widehat{\beta}_{\mathrm{gls}}$.如果需要，可以通过自由度调整来重新缩放。

随机效应估计器 $\widehat{\beta}_{\text {gls }}$ 可以使用 Stata 命令 xtreg 获得。默认协方差矩阵估计量为 (17.11)。对于集群鲁棒协方差矩阵估计器 (17.14)，请使用命令 xtreg vce(robust)。（必须先使用xtset命令声明组标识符。例如，cusip是表17.1中的组标识符。）

为了说明这一点，在表 $17.2$ 的第二列中，我们提出了具有集群稳健标准误 (17.14) 的投资模型 (17.3) 的随机效应回归估计。点估计与合并回归估计有相当大的不同。债务系数由正转为负（后者与流动性约束理论一致），现金流系数大幅增加。如果假设 $17.1$ 正确，这些变化的幅度似乎比预期的要大。在下一节中，我们将考虑限制较少的规范。

17.7 固定效应模型

考虑单向误差分量回归模型

\[ Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} \]

或者

\[ \boldsymbol{Y}_{i}=\boldsymbol{X}_{i} \beta+\mathbf{l}_{i} u_{i}+\boldsymbol{\varepsilon}_{i} . \]

在许多应用中，将个体特定效应 $u_{i}$ 解释为时不变的未观察到的缺失变量是有用的。例如，在工资回归中，$u_{i}$ 可能是个人 $i$ 的不可观察能力。在投资模型 (17.3) 中，$u_{i}$ 可能是公司特定的生产率因素。

当 $u_{i}$ 被解释为省略变量时，很自然地期望它与回归量 $X_{i t}$ 相关。当 $X_{i t}$ 包含选择变量时尤其如此。

为了说明这一点，请考虑表 17.1 中的条目。最后一列显示前 13 个观测值的汇总回归残差 $\widehat{e}_{i t}$，我们将其解释为误差 $e_{i t}=u_{i}+\varepsilon_{i t}$ 的估计值。如前所述，残差特别引人注目的是，它们对公司 #209 都是强烈的负面影响，集中在 $-0.25$ 周围。我们可以将此解释为对该公司的 $u_{i}$ 的估计。检查两家公司的回归量 $Q$ 的值，我们可以看到公司 #209 对于 $Q$ 具有非常大的值（在所有时间段内）。（两家公司的平均值 $\bar{Q}_{i}$ 出现在第七列中。）因此，（尽管我们只查看两个观察结果）$u_{i}$ 和 $Q_{i t}$ 是相关的。从这些有限的观察中推断太多是不合理的，但相关性在于这种相关性违反了严格的均值独立性。

在计量经济学文献中，如果 $u_{i}$ 的随机结构被视为未知且可能与 $X_{i t}$ 相关，则 $u_{i}$ 称为固定效应。

$u_{i}$ 和 $X_{i t}$ 之间的相关性将导致汇总效应估计量和随机效应估计量出现偏差。这是由于遗漏变量偏差和内生性的经典问题造成的。要在生成的示例视图中查看这一点，请参见图 17.1。这显示了来自三个公司的三个观察值 $\left(Y_{i t}, X_{i t}\right)$ 的散点图。真实模型是 $Y_{i t}=9-X_{i t}+u_{i}$。（真实的斜率系数为 $-1$。）变量 $u_{i}$ 和 $X_{i t}$ 高度相关，因此通过九个观测值拟合的合并回归线的斜率接近 +1。（随机效应估计量是相同的。）$Y$ 和 $X$ 之间明显的正相关关系完全是由 $u_{i}$ 和 $u_{i}$ 之间的正相关关系驱动的。然而，以 $u_{i}$ 为条件，斜率为 $u_{i}$。因此，不控制 $u_{i}$ 的回归技术将产生有偏差且不一致的估计量。

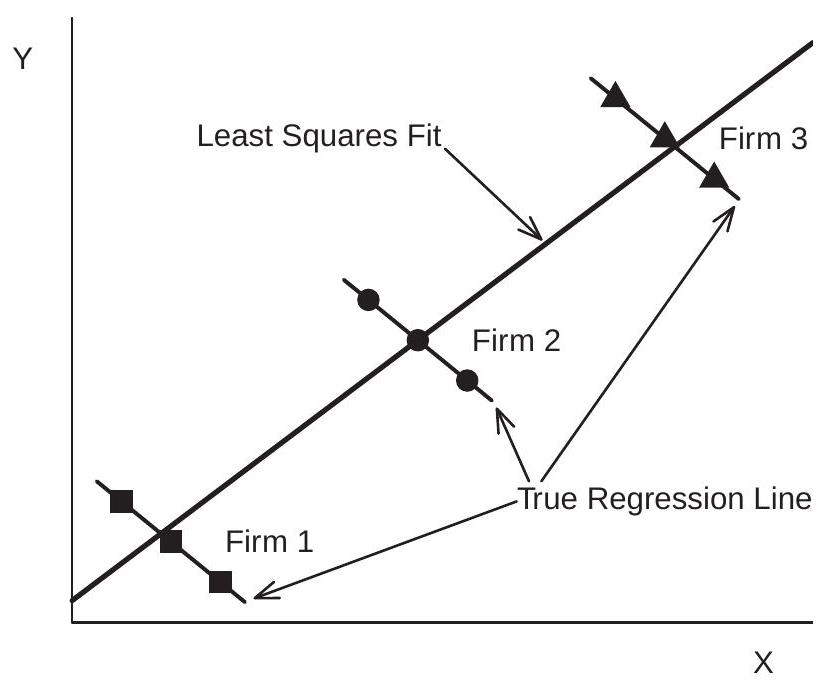
图 17.1：散点图和合并回归线

非结构化个体效应 $u_{i}$ 的存在意味着在简单的投影假设（例如 $\mathbb{E}\left[X_{i t} \varepsilon_{t}\right]=0$）下不可能识别 $\beta$。事实证明，识别的充分条件如下。定义 17.1 回归量 $X_{i t}$ 对于错误 $\varepsilon_{i t}$ 是严格外生的，如果

\[ \mathbb{E}\left[X_{i s} \varepsilon_{i t}\right]=0 \]

对于所有 $s=1, \ldots, T$。

严格外生性是一个强投影条件，这意味着如果任何 $s \neq t$ 的 $X_{i s}$ 添加到 (17.15)，它将具有零系数。严格外生性是严格均值独立性的投影模拟

\[ \mathbb{E}\left[\varepsilon_{i t} \mid \boldsymbol{X}_{i}\right]=0 . \]

(17.18) 蕴含(17.17)，但反之则不然。虽然 (17.17) 足以用于识别和渐近理论，但我们还将使用更强的条件 (17.18) 进行有限样本分析。

虽然 (17.17) 和 (17.18) 是强假设，但它们比 (17.2) 或假设 17.1 弱得多，后者要求个体效应 $u_{i}$ 也严格均值独立。相反，(17.17) 和 (17.18) 没有对 $u_{i}$ 做出任何假设。

严格的外生性（17.17）通常不适用于动态模型。在 $17.41$ 节中，我们讨论了预定回归量较弱假设下的估计。

17.8 转型之内

在上一节中，我们表明，如果 $u_{i}$ 和 $X_{i t}$ 相关，那么汇总和随机效应估计量将会有偏差且不一致。如果我们让 $u_{i}$ 和 $X_{i t}$ 之间的关系完全非结构化，那么一致估计系数 $\beta$ 的唯一方法是使用对 $u_{i}$ 不变的估计器。这可以通过消除 $u_{i}$ 的转换来实现。

其中一种转变就是内在转变。在本节中，我们将详细描述这种转变。

将给定个体的变量平均值定义为

\[ \bar{Y}_{i}=\frac{1}{T_{i}} \sum_{t \in S_{i}} Y_{i t} . \]

我们将其称为个体特定均值，因为它是给定个体的均值。相反，一些作者将其称为时间平均或时间平均值，因为它是一段时间内的平均值。

从变量中减去个体特定平均值，我们得到偏差

\[ \dot{Y}_{i t}=Y_{i t}-\bar{Y}_{i} . \]

这称为内部转换。我们还将 $\dot{Y}_{i t}$ 称为贬值值或与个体平均值的偏差。一些作者将 $\dot{Y}_{i t}$ 称为与时间平均值的偏差。重要的是这种侮辱发生在个人层面。

一些代数也可能有用。我们可以将个体特定平均值写为 $\bar{Y}_{i}=\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1} \mathbf{1}_{i}^{\prime} \boldsymbol{Y}_{i}$。堆叠单个 $i$ 的观察结果，我们可以使用符号编写内部变换

\[ \begin{aligned} \dot{\boldsymbol{Y}}_{i} &=\boldsymbol{Y}_{i}-\mathbf{1}_{i} \bar{Y}_{i} \\ &=\boldsymbol{Y}_{i}-\mathbf{1}_{i}\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1} \mathbf{1}_{i}^{\prime} \boldsymbol{Y}_{i} \\ &=\boldsymbol{M}_{i} \boldsymbol{Y}_{i} \end{aligned} \]

其中 $\boldsymbol{M}_{i}=\boldsymbol{I}_{i}-\mathbf{1}_{i}\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1} \mathbf{1}_{i}^{\prime}$ 是特定于个人的贬低运算符。请注意，$\boldsymbol{M}_{i}$ 是一个幂等矩阵。

同样，对于回归量，我们定义了个体特定的平均值和贬低值：

\[ \begin{aligned} \bar{X}_{i} &=\frac{1}{T_{i}} \sum_{t \in S_{i}} X_{i t} \\ \dot{X}_{i t} &=X_{i t}-\bar{X}_{i} \\ \dot{\boldsymbol{X}}_{i} &=\boldsymbol{M}_{i} \boldsymbol{X}_{i} . \end{aligned} \]

我们在表 17.1 中说明了贬低行为。在第四和第七列中，我们显示公司特定的平均值 $\bar{I}_{i}$ 和 $\bar{Q}_{i}$，在第五和第八列中显示贬值值 $\dot{I}_{i t}$ 和 $\dot{Q}_{i t}$。

我们还可以定义运算符内的完整样本。定义 $\boldsymbol{D}=\operatorname{diag}\left\{\mathbf{1}_{T_{1}}, \ldots, \mathbf{1}_{T_{N}}\right\}$ 和 $\boldsymbol{M}_{\boldsymbol{D}}=\boldsymbol{I}_{n}-$ $\boldsymbol{D}\left(\boldsymbol{D}^{\prime} \boldsymbol{D}\right)^{-1} \boldsymbol{D}^{\prime}$。请注意 $\boldsymbol{M}_{\boldsymbol{D}}=\operatorname{diag}\left\{\boldsymbol{M}_{1}, \ldots, \boldsymbol{M}_{N}\right\}$。因此

\[ \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Y}=\dot{\boldsymbol{Y}}=\left(\begin{array}{c} \dot{\boldsymbol{Y}}_{1} \\ \vdots \\ \dot{\boldsymbol{Y}}_{N} \end{array}\right), \quad \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}=\dot{\boldsymbol{X}}=\left(\begin{array}{c} \dot{\boldsymbol{X}}_{1} \\ \vdots \\ \dot{\boldsymbol{X}}_{N} \end{array}\right) \]

现在将这些运算应用到方程（17.15）中。取具体个体的平均值，我们得到

\[ \bar{Y}_{i}=\bar{X}_{i}^{\prime} \beta+u_{i}+\bar{\varepsilon}_{i} \]

其中 $\bar{\varepsilon}_{i}=\frac{1}{T_{i}} \sum_{t \in S_{i}} \varepsilon_{i t}$.从 (17.15) 中减去我们得到

\[ \dot{Y}_{i t}=\dot{X}_{i t}^{\prime} \beta+\dot{\varepsilon}_{i t} \]

其中 $\dot{\varepsilon}_{i t}=\varepsilon_{i t}-\bar{\varepsilon}_{i t}$.个体效应 $u_{i}$ 已被消除！获得

我们也可以用向量表示法来写它。将贬义运算符 $\boldsymbol{M}_{i}$ 应用于 (17.16) 我们

\[ \dot{\boldsymbol{Y}}_{i}=\dot{\boldsymbol{X}}_{i} \beta+\dot{\boldsymbol{\varepsilon}}_{i} . \]

由于 $\boldsymbol{M}_{i} \mathbf{1}_{i}=0$，个体效应 $u_{i}$ 被消除。方程（17.22）是（17.21）的向量版本。

方程（17.21）是变换（贬值）变量的线性方程。根据需要，个体效应 $u_{i}$ 已被消除。因此，从 (17.21) （或等效的 (17.22)）构造的估计量对于 $u_{i}$ 的值将是不变的。这意味着上一节中描述的内生性偏差将被消除。

然而，另一个结果是所有时不变回归量也被消除。也就是说，如果原始模型 (17.15) 包含任何回归量 $X_{i t}=X_{i}$ ，这些回归量对于每个个体来说随着时间的推移都是恒定的，那么对于这些回归量来说，贬低值完全相同 0 。这意味着，如果使用方程 (17.21) 来估计 $\beta$，则无法估计（或识别）任何时不变回归量的系数。这不是估计方法的结果，而是模型假设的结果。换句话说，如果个体效应 $u_{i}$ 没有已知的结构，那么就不可能解开任何时不变回归量 $X_{i}$ 的效应。两者在观察上具有相同的效果，无法单独识别。

内变换可以大大减少回归量的方差。这可以在表 17.1 中看到，您可以看到转换变量 $\dot{I}_{i t}$ 和 $\dot{Q}_{i t}$ 的元素之间的变异小于未转换变量的变异，因为大部分变异是由公司特定的方法捕获的。

通常不需要直接对内部转换进行编程，但如果需要，可以使用以下 Stata 命令轻松实现。

Stata Commands for Within Transformation
$* \quad \quad \mathrm{x}$ is the original variable
$* \quad$ id is the group identifier
$* \quad$ xdot is the within-transformed variable
egen xmean $=$ mean $(\mathrm{x})$, by(id) gen xdot $=\mathrm{x}-\mathrm{xmean}$

17.9 固定效应估计器

考虑将最小二乘应用于贬低方程（17.21）或等效方程（17.22）。这是

\[ \begin{aligned} \widehat{\beta}_{\mathrm{fe}} &=\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{Y}_{i t}\right) \\ &=\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{Y}}_{i}\right) \\ &=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{Y}_{i}\right) \end{aligned} \]

这称为固定效应或 $\beta$ 的估计量内。它被称为固定效应估计量，因为它适用于固定效应模型（17.15）。它被称为内部估计器，因为它基于每个个体内数据的变化。

上述定义隐含地假设矩阵 $\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}$ 是满秩的。这要求 $X_{i t}$ 的所有组成部分对于样本中的至少某些个体都具有时间变化。

固定效应残差为

\[ \begin{aligned} \widehat{\varepsilon}_{i t} &=\dot{Y}_{i t}-\dot{X}_{i t}^{\prime} \widehat{\beta}_{\mathrm{fe}} \\ \widehat{\boldsymbol{\varepsilon}}_{i} &=\dot{\boldsymbol{Y}}_{i}-\dot{\boldsymbol{X}}_{i} \widehat{\beta}_{\mathrm{fe}} \end{aligned} \]

让我们描述严格均值独立性下估计量的一些统计特性（17.18）。通过线性度和事实 $\boldsymbol{M}_{i} \mathbf{1}_{i}=0$，我们可以写

\[ \widehat{\beta}_{\mathrm{fe}}-\beta=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{\varepsilon}_{i}\right) \]

那么 (17.18) 意味着

\[ \mathbb{E}\left[\widehat{\beta}_{\mathrm{fe}}-\beta \mid \boldsymbol{X}\right]=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \mathbb{E}\left[\boldsymbol{\varepsilon}_{i} \mid \boldsymbol{X}_{i}\right]\right)=0 \]

因此，在 (17.18) 下，$\widehat{\beta}_{\mathrm{fe}}$ 对于 $\beta$ 是无偏的。

让 $\Sigma_{i}=\mathbb{E}\left[\boldsymbol{\varepsilon}_{i} \boldsymbol{\varepsilon}_{i}^{\prime} \mid \boldsymbol{X}_{i}\right]$ 表示特殊误差的 $T_{i} \times T_{i}$ 条件协方差矩阵。 $\widehat{\beta}_{\mathrm{fe}}$ 的方差是

\[ \boldsymbol{V}_{\mathrm{fe}}=\operatorname{var}\left[\widehat{\beta}_{\mathrm{fe}} \mid \boldsymbol{X}\right]=\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \Sigma_{i} \dot{\boldsymbol{X}}_{i}\right)\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1} \]

当特异误差同方差且序列不相关时，该表达式得到简化：

\[ \begin{aligned} \mathbb{E}\left[\varepsilon_{i t}^{2} \mid \boldsymbol{X}_{i}\right] &=\sigma_{\varepsilon}^{2} \\ \mathbb{E}\left[\varepsilon_{i j} \varepsilon_{i t} \mid \boldsymbol{X}_{i}\right] &=0 \end{aligned} \]

对于所有 $j \neq t$。在这种情况下，$\Sigma_{i}=\boldsymbol{I}_{i} \sigma_{\varepsilon}^{2}$ 和 (17.24) 简化为

\[ \boldsymbol{V}_{\mathrm{fe}}^{0}=\sigma_{\varepsilon}^{2}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1} . \]

比较 (17.25)(17.26) 下的固定效应和汇总估计量的方差以及不存在个体特定效应 $u_{i}=0$ 的假设是有启发性的。在这种情况下我们看到

\[ \boldsymbol{V}_{\mathrm{fe}}^{0}=\sigma_{\varepsilon}^{2}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1} \geq \sigma_{\varepsilon}^{2}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{X}_{i}\right)^{-1}=\boldsymbol{V}_{\text {pool }} \]

由于贬低变量 $\dot{\boldsymbol{X}}_{i}$ 相对于原始观测值 $\boldsymbol{X}_{i}$ 的变化减少，因此不等式成立。（参见练习 17.28。）这显示了使用相对于汇总估计的固定效应的成本。由于回归变量的变化减少，估计方差增加。这种效率的降低是估计器对个体效应 $u_{i}$ 的稳健性的必然副产品。

17.10 差分估计器

内部转变并不是唯一消除个体特异性效应的转变。另一个具有相同作用的重要变换是一阶差分。

一阶差分变换是 $\Delta Y_{i t}=Y_{i t}-Y_{i t-1}$。这可以应用于除第一个观察（基本上丢失）之外的所有观察。在个人层面，这可以写为 $\Delta \boldsymbol{Y}_{i}=\boldsymbol{D}_{i} \boldsymbol{Y}_{i}$，其中 $\boldsymbol{D}_{i}$ 是 $\left(T_{i}-1\right) \times T_{i}$ 矩阵差分运算符

\[ \boldsymbol{D}_{i}=\left[\begin{array}{cccccc} -1 & 1 & 0 & \cdots & 0 & 0 \\ 0 & -1 & 1 & & 0 & 0 \\ \vdots & & & \ddots & & \vdots \\ 0 & 0 & 0 & \cdots & -1 & 1 \end{array}\right] . \]

将变换 $\Delta$ 应用于 (17.15) 或 (17.16) 我们得到 $\Delta Y_{i t}=\Delta X_{i t}^{\prime} \beta+\Delta \varepsilon_{i t}$ 或

\[ \Delta \boldsymbol{Y}_{i}=\Delta \boldsymbol{X}_{i} \beta+\Delta \boldsymbol{\varepsilon}_{i} . \]

我们可以看到个体效应$u_{i}$已经被消除了。

应用于差分方程 (17.29) 的最小二乘为

\[ \begin{aligned} \widehat{\beta}_{\Delta} &=\left(\sum_{i=1}^{N} \sum_{t \geq 2} \Delta X_{i t} \Delta X_{i t}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \geq 2} \Delta X_{i t} \Delta Y_{i t}\right) \\ &=\left(\sum_{i=1}^{N} \Delta \boldsymbol{X}_{i}^{\prime} \Delta \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \Delta \boldsymbol{X}_{i}^{\prime} \Delta \boldsymbol{Y}_{i}\right) \\ &=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{D}_{i}^{\prime} \boldsymbol{D}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{D}_{i}^{\prime} \boldsymbol{D}_{i} \boldsymbol{Y}_{i}\right) \end{aligned} \]

(17.30) 称为差分估计器。对于 $T=2, \widehat{\beta}_{\Delta}=\widehat{\beta}_{\mathrm{fe}}$ 等于固定效应估计量。参见练习 17.6。然而，它们对于 $T>2$ 是不同的。

当误差 $\varepsilon_{i t}$ 连续不相关且同方差时，(17.29) 中的误差 $\Delta \boldsymbol{\varepsilon}_{i}=\boldsymbol{D}_{i} \boldsymbol{\varepsilon}_{i}$ 具有协方差矩阵 $\boldsymbol{H} \sigma_{\varepsilon}^{2}$，其中

\[ \boldsymbol{H}=\boldsymbol{D}_{i} \boldsymbol{D}_{i}^{\prime}=\left(\begin{array}{cccc} 2 & -1 & 0 & 0 \\ -1 & 2 & \ddots & 0 \\ 0 & \ddots & \ddots & -1 \\ 0 & 0 & -1 & 2 \end{array}\right) . \]

我们可以通过使用 GLS 来减少估计方差。当错误 $\varepsilon_{i t}$ 为独立同分布时（序列不相关且同方差），这是

\[ \begin{aligned} \widetilde{\beta}_{\Delta} &=\left(\sum_{i=1}^{N} \Delta \boldsymbol{X}_{i}^{\prime} \boldsymbol{H}^{-1} \Delta \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \Delta \boldsymbol{X}_{i}^{\prime} \boldsymbol{H}^{-1} \Delta \boldsymbol{Y}_{i}\right) \\ &=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{D}_{i}^{\prime}\left(\boldsymbol{D}_{i} \boldsymbol{D}_{i}^{\prime}\right)^{-1} \boldsymbol{D}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{D}_{i}^{\prime}\left(\boldsymbol{D}_{i} \boldsymbol{D}_{i}^{\prime}\right)^{-1} \boldsymbol{D}_{i} \boldsymbol{Y}_{i}\right) \\ &=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \boldsymbol{M}_{i} \boldsymbol{Y}_{i}\right) \end{aligned} \]

其中 $\boldsymbol{M}_{i}=\boldsymbol{D}_{i}^{\prime}\left(\boldsymbol{D}_{i} \boldsymbol{D}_{i}^{\prime}\right)^{-1} \boldsymbol{D}_{i}$.回想一下，矩阵 $\boldsymbol{D}_{i}$ 是 $\left(T_{i}-1\right) \times T_{i}$，秩为 $T_{i}-1$，并且与 $\mathbf{1}_{i}$ 的向量正交。这意味着 $\boldsymbol{M}_{i}$ 与 $\mathbf{1}_{i}$ 正交投影，因此等于内部变换矩阵。因此$\widetilde{\beta}_{\Delta}=\widehat{\beta}_{\mathrm{fe}}$，固定效应估计器！

我们所展示的是在 i.i.d. 下。误差，应用于一阶微分方程的 GLS 精确等于固定效应估计量。由于高斯-马尔可夫定理表明 GLS 的方差低于最小二乘法，这意味着在 $\varepsilon_{i t}$ 为 i.i.d 的假设下，固定效应估计器比一阶差分更有效。

这个论点扩展到消除固定效应的任何其他变换。在此类变换之后应用的 GLS 等于固定效应估计器，并且比独立同分布下在相同变换之后应用的最小二乘更有效。错误。这表明，在这些假设下，固定效应估计量在消除固定效应的估计量类别中是高斯-马尔可夫有效的。

17.11 虚拟变量回归

估计固定效应模型的另一种方法是通过 $Y_{i t}$ 对 $X_{i t}$ 的最小二乘和一整套虚拟变量，样本中的每个人都有一个。事实证明，这在代数上等价于组内估计器。

要了解这一点，请从没有回归器的误差分量模型开始：

\[ Y_{i t}=u_{i}+\varepsilon_{i t} . \]

考虑固定效应向量 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 的最小二乘估计。由于每个固定效应 $u_{i}$ 是个体特定均值，并且截距的最小二乘估计是样本均值，因此 $u_{i}$ 的最小二乘估计是 $\widehat{u}_{i}=\bar{Y}_{i}$。最小二乘残差就是 $\widehat{\varepsilon}_{i t}=Y_{i t}-\bar{Y}_{i}=$ $\dot{Y}_{i t}$，即内变换。如果您更喜欢代数参数，请让 $d_{i}$ 为 $N$ 虚拟变量的向量，其中 $i^{t h}$ 元素表示 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 个体。因此，$u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 的 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 元素为 1，其余元素为零。请注意，$u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 和 (17.32) 等于 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$。这是回归量 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 和系数 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 的回归。我们还可以在个体层面将其写为 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$ 或使用完整矩阵表示法 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$（其中 $u=\left(u_{1}, \ldots, u_{N}\right)^{\prime}$）。

$u$ 的最小二乘估计为

\[ \begin{aligned} \widehat{\boldsymbol{u}} &=\left(\boldsymbol{D}^{\prime} \boldsymbol{D}\right)^{-1}\left(\boldsymbol{D}^{\prime} \boldsymbol{Y}\right) \\ &=\operatorname{diag}\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1}\left\{\mathbf{1}_{i}^{\prime} \boldsymbol{Y}_{i}\right\}_{i=1, \ldots, n} \\ &=\left\{\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1} \mathbf{1}_{i}^{\prime} \boldsymbol{Y}_{i}\right\}_{i=1, \ldots, n} \\ &=\left\{\bar{Y}_{i}\right\}_{i=1, \ldots, n} . \end{aligned} \]

最小二乘残差为

\[ \widehat{\boldsymbol{\varepsilon}}=\left(\boldsymbol{I}_{n}-\boldsymbol{D}\left(\boldsymbol{D}^{\prime} \boldsymbol{D}\right)^{-1} \boldsymbol{D}^{\prime}\right) \boldsymbol{Y}=\dot{\boldsymbol{Y}} \]

如(17.19)所示。因此，简单误差分量模型的最小二乘残差是内变换变量。

现在考虑带有回归器的误差分量模型，可以写为

\[ Y_{i t}=X_{i t}^{\prime} \beta+d_{i}^{\prime} u+\varepsilon_{i t} \]

由于 $u_{i}=d_{i}^{\prime} u$ 如上所述。用矩阵表示法

\[ \boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{D} u+\boldsymbol{\varepsilon} . \]

我们考虑通过最小二乘法估计 $(\beta, u)$ 并将估计值写为 $\boldsymbol{Y}=\boldsymbol{X} \widehat{\beta}+\boldsymbol{D} \widehat{u}+\widehat{\boldsymbol{\varepsilon}}$。我们将其称为固定效应模型的虚拟变量估计量。

根据 Frisch-Waugh-Lovell 定理（定理 3.5），虚拟变量估计量 $\widehat{\beta}$ 和残差 $\widehat{\boldsymbol{\varepsilon}}$ 可以通过残差的最小二乘回归从 $\boldsymbol{Y}$ 对 $\boldsymbol{D}$ 对残差的回归获得$\boldsymbol{X}$ 对 $\boldsymbol{D}$ 的回归。我们在上面了解到，$\boldsymbol{D}$ 回归的残差是内部变换。因此，虚拟变量估计器 $\widehat{\beta}$ 和残差 $\widehat{\boldsymbol{\varepsilon}}$ 可以通过内部变换 $\widehat{\beta}$ 对内部变换 $\widehat{\beta}$ 的最小二乘回归来获得。这正是固定效应估计器 $\widehat{\beta}$。因此 $\widehat{\beta}$ 的虚拟变量和固定效应估计量是相同的。

这非常重要，我们将这个结果表述为定理。

定理 17.1 $\beta$ 的固定效应估计量在代数上等于 $\beta$ 的虚拟变量估计量。两个估计量具有相同的残差。

这可能是弗里施-沃-洛弗尔定理最重要的实际应用。它表明我们可以通过应用内变换或包含虚拟变量（样本中的每个个体一个）来估计系数。这很重要，因为在某些情况下，一种方法比另一种方法更方便，并且了解这两种方法在代数上是等效的很重要。

当 $N$ 很大时，建议使用内变换而不是虚拟变量方法。这是因为后者需要更多的计算机内存。要了解这一点，请考虑平衡情况下 (17.34) 中的矩阵 $\boldsymbol{D}$。它具有必须创建并存储在内存中的 $T N^{2}$ 元素。当 $N$ 很大时，这可能会过多。例如，如果 $T=10$ 和 $N=10,000$，则矩阵 $\boldsymbol{D}$ 有 10 亿个元素！一个包在技术上是否可以处理这个维度的矩阵取决于几个细节（系统 RAM、操作系统、包版本），但即使它可以执行计算，计算时间也很慢。因此，对于较大 $N$ 的固定效应估计，建议使用内变换而不是虚拟变量回归。

虚拟变量公式可以增加关于固定效应估计器如何实现固定效应不变性的见解。给定回归方程 (17.34)，我们可以使用残差回归公式编写 $\beta$ 的最小二乘估计量：

\[ \begin{aligned} \widehat{\beta}_{\mathrm{fe}} &=\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Y}\right) \\ &=\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}}(\boldsymbol{X} \beta+\boldsymbol{D} u+\boldsymbol{\varepsilon})\right) \\ &=\beta+\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{\varepsilon}\right) \end{aligned} \]

从 $\boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{D}=0$ 开始。表达式 (17.35) 不受向量 $u$ 的影响，因此 $\widehat{\beta}_{\mathrm{fe}}$ 对于 $u$ 是不变的。这是固定效应估计量对于固定效应的实际值不变的另一个证明，因此其统计属性不依赖于关于 $u_{i}$ 的假设。

17.12 固定效应协方差矩阵估计

首先考虑（17.27）中定义的经典协方差矩阵 $\boldsymbol{V}_{\mathrm{fe}}^{0}$ 的估计。这是

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}^{0}=\widehat{\sigma}_{\varepsilon}^{2}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \]

和

\[ \widehat{\sigma}_{\varepsilon}^{2}=\frac{1}{n-N-k} \sum_{i=1}^{n} \sum_{t \in S_{i}} \widehat{\varepsilon}_{i t}^{2}=\frac{1}{n-N-k} \sum_{i=1}^{n} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i} . \]

$N+k$ 自由度调整是由虚拟变量表示驱动的。您可以在假设 (17.18)、(17.25) 和 (17.26) 下验证 $\widehat{\sigma}_{\varepsilon}^{2}$ 对于 $\sigma_{\varepsilon}^{2}$ 是无偏的。参见练习 17.8。

请注意，假设 (17.18)、(17.25) 和 (17.26) 与假设 17.1 的 (17.5)-(17.7) 相同。不需要假设(17.8)-(17.10)。因此，固定效应模型通过消除 $u_{i}$ 的假设但保留 $\varepsilon_{i t}$ 的假设来削弱随机效应模型。

当误差 $\varepsilon_{i t}$ 同方差且序列不相关时，固定效应估计量的经典协方差矩阵估计量 (17.36) 有效，但在其他情况下无效。协方差矩阵估计器允许 $\varepsilon_{i t}$ 在 $t$ 上异方差且序列相关，是集群稳健的协方差矩阵估计器，按个体进行聚类

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \]

其中 $\widehat{\boldsymbol{\varepsilon}}_{i}$ 是（17.23）中定义的固定效应残差。（17.38）首先由Arellano（1987）提出。如 (4.55) 中所示，$\widehat{V}_{\text {fe }}^{\text {cluster }}$ 可以乘以自由度调整。 C. Hansen (2007) 的理论建议的调整是

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}=\left(\frac{N}{N-1}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \]

对应于 $(4.55)$ 的是

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}=\left(\frac{n-1}{n-N-k}\right)\left(\frac{N}{N-1}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \text {. } \]

这些估算器很方便，因为它们易于应用并且允许不平衡面板。

在典型的微型面板应用中，$N$ 非常大，而 $k$ 则较小。因此，(17.39) 中的调整很小，而 (17.40) 中的调整约为 $\bar{T} /(\bar{T}-1)$，其中 $\bar{T}=n / N$ 是每个人的平均时间段数。当 $\bar{T}$ 很小时，这可能是一个非常大的调整。因此，(17.38)、(17.39) 和 (17.40) 之间的选择可能很大。

要了解 (17.40) 中的自由度调整是否合适，请考虑简化设置，其中残差是用真实的 $\beta$ 但估计的固定效应 $u_{i}$ 构建的。这是一个有用的近似值，因为估计的斜率系数 $\beta$ 的数量相对于样本大小 $n$ 来说很小。然后 $\widehat{\boldsymbol{\varepsilon}}_{i}=\dot{\boldsymbol{\varepsilon}}_{i}=\boldsymbol{M}_{i} \boldsymbol{\varepsilon}_{i}$ 所以 $\dot{\boldsymbol{X}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i}=\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}$ 和 (17.38) 等于

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \varepsilon_{i} \varepsilon_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \]

这是具有真实误差而不是残差的理想化估计量。由于 $\mathbb{E}\left[\varepsilon_{i} \varepsilon_{i}^{\prime} \mid \boldsymbol{X}_{i}\right]=\Sigma_{i}$ ，因此 $\mathbb{E}\left[\widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }} \mid \boldsymbol{X}\right]=\boldsymbol{V}_{\mathrm{fe}}$ 和 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}$ 对于 $\boldsymbol{V}_{\mathrm{fe}}$ 是无偏的！因此不需要自由度调整。尽管事实上已经估计了 $N$ 固定效应。虽然此分析涉及理想化情况，其中残差是用真实系数 $\beta$ 构建的，因此不会转化为对可行估计量的直接建议，但它仍然表明 (17.40) 中的强烈临时调整是没有根据的。

此（粗略）分析表明，对于固定效应回归的聚类稳健协方差估计量，C. Hansen (17.39) 建议的调整是最合适的。它通常可以通过未调整的估计量 (17.38) 很好地近似。根据目前的理论，没有理由进行临时调整（17.40）。后者的主要论点是它产生最大的标准误差，因此是最保守的选择。

在当前实践中，估计器 (17.38) 和 (17.40) 是固定效应估计中最常用的协方差矩阵估计器。

在 $17.22$ 和 $17.23$ 部分中，我们讨论异方差但无序列相关下的协方差矩阵估计。

为了说明这一点，在表 $17.2$ 中，我们在第三列中展示了投资模型 (17.3) 的固定效应回归估计，并具有集群稳健的标准误差。交易指标 $T_{i}$ 和行业虚拟指标不能包含在内，因为它们是时不变的。点估计与随机效应估计相似，尽管债务和现金流量的系数增加了。

17.13 Stata 中的固定效应估计

Stata 中有多种方法可以获取固定效应估计量 $\widehat{\beta}_{\mathrm{fe}}$。

第一种方法是虚拟变量回归。这可以通过 Stata regress 命令获得，例如 reg y $\mathrm{x}$ , cluster(id)，其中 id 是组（个人）标识符。在大多数情况下，如第 17.11 节所述，由于计算机内存需求过多且计算速度较慢，因此不建议这样做。如果执行此命令，则可能有助于抑制系数估计的完整列表的显示。为此，请安静地输入 reg y $x$ , cluster(id) 后跟估计表，keep( $x_{-}$cons) be se。第二个命令将仅报告 $x$ 上的系数，而不是索引变量 id 上的系数。（也可以报告其他统计数据。）第二种方法是手动创建内部转换变量，如第 17.8 节所述，然后使用回归。

第三种方法是$x t r e g ~ f e$，它是专门为面板数据编写的。这使用部分化方法来估计斜率系数。默认的协方差矩阵估计器是经典的，如（17.36）中定义的那样。集群鲁棒协方差矩阵 (17.38) 可以使用选项 vce(robust) 或 $r$ 获得。

第四种方法是aregsorb(id)。此命令是partiallingout 回归的替代实现。默认协方差矩阵估计器是经典的 (17.36)。可以使用 cluster(id) 选项获得集群鲁棒协方差矩阵估计器 (17.40)。当指定 $\mathrm{r}$ 或 $\mathrm{v} c e$（稳健）时，将获得异方差鲁棒协方差矩阵，但不建议这样做，除非 $T_{i}$ 很大（如 $17.22$ 节中将讨论的那样）。

Stata xtreg 和 areg 命令之间的一个重要区别是，它们实现了不同的集群鲁棒协方差矩阵估计器：对于 xtreg 为 (17.38)，对于 areg 为 (17.40)。正如上一节中所讨论的，areg 使用的调整是临时的且没有充分理由，但会产生最大且因此最保守的标准误差。

命令之间的另一个区别是它们如何报告方程 $R^{2}$。这种差异可能是巨大的，并且源于他们正在估计不同的人口对应物这一事实。完整虚拟变量回归和 areg 命令以相同的方式计算 $R^{2}$：$Y_{i t}$ 与所有预测变量（包括各个虚拟变量）的拟合回归之间的平方相关性。 $x t r e g ~ f e$ 命令报告 $R^{2}$ 的三个值：内部、之间和总体。 “内部”$R^{2}$ 与使用内部变换变量从第二阶段回归获得的结果相同。（上述第二种方法。）“总体”$R^{2}$ 是 $Y_{i t}$ 与不包括个体效应的拟合回归之间的平方相关性。

应该报告哪个$R^{2}$？答案取决于添加回归量之前的基线模型。如果我们将基线视为个体特定的平均值，那么内部计算是合适的。如果基线是所有观测值的单一平均值，则完整回归 (areg) 计算是合适的。后者 (areg) 计算通常比内部计算高得多，因为固定效应通常“解释”大部分方差。无论如何，由于 $R^{2}$ 没有单一的定义，因此如果报告了该方法，则明确该方法非常重要。

在当前的计量经济学实践中，xtreg 和 areg 都被使用，尽管 areg 似乎是更流行的选择。由于后者通常会产生更高的 $R^{2}$ 值，因此应以怀疑的态度看待报告的 $R^{2}$ 值，除非作者记录了其计算方法。

17.14 估计器之间

间估计量是根据个体均值方程 (17.20) 计算的

\[ \bar{Y}_{i}=\bar{X}_{i}^{\prime} \beta+u_{i}+\bar{\varepsilon}_{i} . \]

估计可以在个体层面或观察层面进行。在 $N$ 个体级别应用于 (17.41) 的最小二乘为

\[ \widehat{\beta}_{\mathrm{be}}=\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{Y}_{i}\right) . \]

在观测级别应用于 (17.41) 的最小二乘为

\[ \widetilde{\beta}_{\mathrm{be}}=\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \bar{X}_{i} \bar{Y}_{i}\right)=\left(\sum_{i=1}^{N} T_{i} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} T_{i} \bar{X}_{i} \bar{Y}_{i}\right) . \]

在平衡面板 $\widetilde{\beta}_{\mathrm{be}}=\widehat{\beta}_{\text {be }}$ 中，但它们在不平衡面板上有所不同。 $\widetilde{\beta}_{\mathrm{be}}$ 等于在权重为 $T_{i}$ 的个体级别应用的加权最小二乘法。

在随机效应假设下（假设 17.1）$\widehat{\beta}_{\text {be }}$ 对于 $\beta$ 是无偏的并且有方差

\[ \boldsymbol{V}_{\mathrm{be}}=\operatorname{var}\left[\widehat{\beta}_{\mathrm{be}} \mid \boldsymbol{X}\right]=\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1}\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{X}_{i}^{\prime} \sigma_{i}^{2}\right)\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1} \]

在哪里

\[ \sigma_{i}^{2}=\operatorname{var}\left[u_{i}+\bar{\varepsilon}_{i}\right]=\sigma_{u}^{2}+\frac{\sigma_{\varepsilon}^{2}}{T_{i}} \]

是 (17.41) 中误差的方差。当面板平衡时，方差公式简化为

\[ \boldsymbol{V}_{\mathrm{be}}=\operatorname{var}\left[\widehat{\beta}_{\mathrm{be}} \mid \boldsymbol{X}\right]=\left(\sum_{i=1}^{N} \bar{X}_{i} \bar{X}_{i}^{\prime}\right)^{-1}\left(\sigma_{u}^{2}+\frac{\sigma_{\varepsilon}^{2}}{T}\right) . \]

在随机效应假设下，间估计器 $\widehat{\beta}_{\text {be }}$ 对于 $\beta$ 是无偏的，但效率低于随机效应估计器 $\widehat{\beta}_{\text {gls }}$。因此，线性面板数据应用中似乎很少直接使用间估计器。

相反，它的主要应用是构建 $\sigma_{u}^{2}$ 的估计。首先，考虑估计

\[ \sigma_{b}^{2}=\frac{1}{N} \sum_{i=1}^{N} \sigma_{i}^{2}=\sigma_{u}^{2}+\frac{1}{N} \sum_{i=1}^{N} \frac{\sigma_{\varepsilon}^{2}}{T_{i}}=\sigma_{u}^{2}+\frac{\sigma_{\varepsilon}^{2}}{\bar{T}} \]

其中 $\bar{T}=N / \sum_{i=1}^{N} T_{i}^{-1}$ 是 $T_{i}$ 的调和平均值。（在平衡面板 $\bar{T}=T$ 的情况下。）$\sigma_{b}^{2}$ 的自然估计量是

\[ \widehat{\sigma}_{b}^{2}=\frac{1}{N-k} \sum_{i=1}^{N} \widehat{e}_{b i}^{2} . \]

其中 $\widehat{e}_{b i}=\bar{Y}_{i}-\bar{X}_{i}^{\prime} \widehat{\beta}_{\text {be }}$ 是残差之间的值。（可以使用 $\widehat{\beta}_{\text {be }}$ 或 $\widetilde{\beta}_{\text {be }}$。）

从关系 $\sigma_{b}^{2}=\sigma_{u}^{2}+\sigma_{\varepsilon}^{2} / \bar{T}$ 和 (17.42) 我们可以推导出 $\sigma_{u}^{2}$ 的估计量。我们已经在（17.37）中为固定效应模型描述了 $\sigma_{\varepsilon}^{2}$ 的估计器 $\widehat{\sigma}_{\varepsilon}^{2}$。由于固定效应模型在比随机效应模型更弱的条件下成立，因此 $\widehat{\sigma}_{\varepsilon}^{2}$ 对于后者也有效。这建议使用以下 $\sigma_{u}^{2}$ 估计器

\[ \widehat{\sigma}_{u}^{2}=\widehat{\sigma}_{b}^{2}-\frac{\widehat{\sigma}_{\varepsilon}^{2}}{\bar{T}} . \]

总而言之，$\widehat{\sigma}_{\varepsilon}^{2}$ 使用固定效应估计器，$\widehat{\sigma}_{b}^{2}$ 使用间估计器，$\widehat{\sigma}_{u}^{2}$ 由两者构建。

(17.43) 可能为负数。通常使用约束估计器

\[ \widehat{\sigma}_{u}^{2}=\max \left[0, \widehat{\sigma}_{b}^{2}-\frac{\widehat{\sigma}_{\varepsilon}^{2}}{\bar{T}}\right] . \]

(17.44) 是随机效应模型中 $\sigma_{u}^{2}$ 最常见的估计量。

间估计器 $\widehat{\beta}_{\text {be }}$ 可以使用 Stata 命令 xtreg be 获得。估计器 $\widetilde{\beta}_{\text {be }}$ 可以通过 xtreg be wls 获得。

17.15 可行的GLS

随机效应估计量可以写为

\[ \widehat{\beta}_{\mathrm{re}}=\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{X}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \boldsymbol{X}_{i}^{\prime} \Omega_{i}^{-1} \boldsymbol{Y}_{i}\right)=\left(\sum_{i=1}^{N} \widetilde{\boldsymbol{X}}_{i}^{\prime} \widetilde{\boldsymbol{X}}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \widetilde{\boldsymbol{X}}_{i}^{\prime} \widetilde{\boldsymbol{Y}}_{i}\right) \]

其中 $\widetilde{\boldsymbol{X}}_{i}=\Omega_{i}^{-1 / 2} \boldsymbol{X}_{i}$ 和 $\widetilde{\boldsymbol{Y}}_{i}=\Omega_{i}^{-1 / 2} \boldsymbol{Y}_{i}$。研究这些转变是有启发性的。

定义 $\boldsymbol{P}_{i}=\mathbf{1}_{i}\left(\mathbf{1}_{i}^{\prime} \mathbf{1}_{i}\right)^{-1} \mathbf{1}_{i}^{\prime}$ 以便 $\boldsymbol{M}_{i}=\boldsymbol{I}_{i}-\boldsymbol{P}_{i}$。因此，虽然 $\boldsymbol{M}_{i}$ 是内部运算符，但自 $\boldsymbol{P}_{i} \boldsymbol{Y}_{i}=\mathbf{1}_{i} \bar{Y}_{i}$ 以来，$\boldsymbol{P}_{i}$ 可以称为个体均值运算符。我们可以写

\[ \Omega_{i}=\boldsymbol{I}_{i}+\mathbf{1}_{i} \mathbf{1}_{i}^{\prime} \sigma_{u}^{2} / \sigma_{\varepsilon}^{2}=\boldsymbol{I}_{i}+\frac{T_{i} \sigma_{u}^{2}}{\sigma_{\varepsilon}^{2}} \boldsymbol{P}_{i}=\boldsymbol{M}_{i}+\rho_{i}^{-2} \boldsymbol{P}_{i} \]

在哪里

\[ \rho_{i}=\frac{\sigma_{\varepsilon}}{\sqrt{\sigma_{\varepsilon}^{2}+T_{i} \sigma_{u}^{2}}} . \]

由于矩阵 $\boldsymbol{M}_{i}$ 和 $\boldsymbol{P}_{i}$ 是幂等且正交的，我们发现 $\Omega_{i}^{-1}=\boldsymbol{M}_{i}+\rho_{i}^{2} \boldsymbol{P}_{i}$ 和

\[ \Omega_{i}^{-1 / 2}=\boldsymbol{M}_{i}+\rho_{i} \boldsymbol{P}_{i}=\boldsymbol{I}_{i}-\left(1-\rho_{i}\right) \boldsymbol{P}_{i} . \]

因此 GLS 估计器使用的变换是

\[ \tilde{\boldsymbol{Y}}_{i}=\left(\boldsymbol{I}_{i}-\left(1-\rho_{i}\right) \boldsymbol{P}_{i}\right) \boldsymbol{Y}_{i}=\boldsymbol{Y}_{i}-\left(1-\rho_{i}\right) \mathbf{1}_{i} \bar{Y}_{i} \]

这是转换中的一部分。

所写的转换取决于未知的 $\rho_{i}$。可以用估计器代替

\[ \widehat{\rho}_{i}=\frac{\widehat{\sigma}_{\varepsilon}}{\sqrt{\widehat{\sigma}_{\varepsilon}^{2}+T_{i} \widehat{\sigma}_{u}^{2}}} \]

其中估计量 $\widehat{\sigma}_{\varepsilon}^{2}$ 和 $\widehat{\sigma}_{u}^{2}$ 在 (17.37) 和 (17.44) 中给出。我们得到了可行的变换

\[ \widetilde{\boldsymbol{Y}}_{i}=\boldsymbol{Y}_{i}-\left(1-\widehat{\rho}_{i}\right) \mathbf{1}_{i} \bar{Y}_{i} \]

和

\[ \widetilde{\boldsymbol{X}}_{i}=\boldsymbol{X}_{i}-\left(1-\widehat{\rho}_{i}\right) \mathbf{1}_{i} \bar{X}_{i}^{\prime} . \]

可行的随机效应估计量是使用（17.49）和（17.50）的（17.45）。

在上一节中我们注意到 $\widehat{\sigma}_{u}^{2}=0$ 是可能的。在本例中为 $\widehat{\rho}_{i}=1$ 和 $\widehat{\beta}_{\text {re }}=\widehat{\beta}_{\text {pool }}$。

这表明了以下内容。随机效应估计器 (17.45) 是应用于 (17.50) 和 (17.49) 中定义的变换变量 $\widetilde{\boldsymbol{X}}_{i}$ 和 $\widetilde{\boldsymbol{Y}}_{i}$ 的最小二乘法。当 $\widehat{\rho}_{i}=0$ 时，这些是内部变换，因此 $\widetilde{\boldsymbol{X}}_{i}=\dot{\boldsymbol{X}}_{i}, \widetilde{\boldsymbol{Y}}_{i}=\dot{\boldsymbol{Y}}_{i}$ 和 $\widehat{\beta}_{\mathrm{re}}=\widehat{\beta}_{\mathrm{fe}}$ 是固定效应估计器。当 $\widehat{\rho}_{i}=1$ 时，数据未转换为 $\widetilde{\boldsymbol{X}}_{i}=\boldsymbol{X}_{i}, \widetilde{\boldsymbol{Y}}_{i}=\boldsymbol{Y}_{i}$，而 $\widehat{\beta}_{\mathrm{re}}=\widehat{\beta}_{\text {pool }}$ 是池化估计器。一般来说，$\widetilde{\boldsymbol{X}}_{i}$ 和 $\widetilde{\boldsymbol{X}}_{i}$ 可以被视为转换中的部分。

回顾 $\widehat{\rho}_{i}=\widehat{\sigma}_{\varepsilon} / \sqrt{\widehat{\sigma}_{\varepsilon}^{2}+T_{i} \widehat{\sigma}_{u}^{2}}$ 的定义，我们发现当特殊误差方差 $\widehat{\sigma}_{\varepsilon}^{2}$ 相对于 $T_{i} \widehat{\sigma}_{u}^{2}$ 较大时，则 $\widehat{\rho}_{i} \approx 1$ 和 $\widehat{\beta}_{\text {re }} \approx \widehat{\beta}_{\text {pool. }}$ 相对较大。因此，当方差估计表明个体效应相对较小时，随机效应估计量会简化为合并估计量。另一方面，当个体效应误差方差 $\widehat{\sigma}_{u}^{2}$ 相对于 $\widehat{\sigma}_{\varepsilon}^{2}$ 较大时，则 $\widehat{\rho}_{i} \approx 0$ 和 $\widehat{\beta}_{\mathrm{re}} \approx \widehat{\beta}_{\mathrm{fe}}$ 相对较大。因此，当方差估计表明个体效应相对较大时，随机效应估计量接近固定效应估计量。

17.16 固定效应回归中的截距

固定效应估计量不适用于对所有个体都是时不变的任何回归量。这包括拦截。然而，一些作者和软件包（例如 Amemiya (1971) 和 Stata 中的 xtreg）报告了拦截。要了解如何构造截距估计量，请使用添加显式截距的分量回归方程

\[ Y_{i t}=\alpha+X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} . \]

我们已经讨论过通过 $\widehat{\beta}_{\mathrm{fe}}$ 来估计 $\beta$。将方程中的 $\beta$ 替换为 $\widehat{\beta}_{\mathrm{fe}}$，然后通过最小二乘估计 $\alpha$，我们得到

\[ \widehat{\alpha}_{\mathrm{fe}}=\bar{Y}-\bar{X}^{\prime} \widehat{\beta}_{\mathrm{fe}} \]

其中 $\bar{Y}$ 和 $\bar{X}$ 是完整样本的平均值。这是 xtreg 报告的估计器。

17.17 固定效应的估计

对于大多数应用，研究人员感兴趣的是系数 $\beta$，而不是固定效应 $u_{i}$。但在某些情况下，固定效应本身很有趣。当我们想要测量 $u_{i}$ 的分布以了解其异质性时，就会出现这种情况。它也出现在预测的背景下。正如 $17.11$ 节中所讨论的，固定效应估计 $\widehat{u}$ 是通过应用于回归的最小二乘法获得的 (17.33)。要找到他们的解决方案，请将 (17.33) 中的 $\beta$ 替换为最小二乘最小化器 $\widehat{\beta}_{\mathrm{fe}}$ 并应用最小二乘。由于这是个体特定的截距，因此解决方案是

\[ \widehat{u}_{i}=\frac{1}{T_{i}} \sum_{t \in S_{i}}\left(Y_{i t}-X_{i t}^{\prime} \widehat{\beta}_{\mathrm{fe}}\right)=\bar{Y}_{i}-\bar{X}_{i}^{\prime} \widehat{\beta}_{\mathrm{fe}} . \]

或者，使用 (17.34) 这是

\[ \begin{aligned} \widehat{u} &=\left(\boldsymbol{D}^{\prime} \boldsymbol{D}\right)^{-1} \boldsymbol{D}^{\prime}\left(\boldsymbol{Y}-\boldsymbol{X} \widehat{\beta}_{\mathrm{fe}}\right) \\ &=\operatorname{diag}\left\{T_{i}^{-1}\right\} \sum_{i=1}^{N} d_{i} \mathbf{1}_{i}^{\prime}\left(\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \widehat{\beta}_{\mathrm{fe}}\right) \\ &=\sum_{i=1}^{N} d_{i}\left(\bar{Y}_{i}-\bar{X}_{i}^{\prime} \widehat{\beta}_{\mathrm{fe}}\right) \\ &=\left(\widehat{u}_{1}, \ldots, \widehat{u}_{N}\right)^{\prime} \end{aligned} \]

因此，固定效应的最小二乘估计可以从个体特定的平均值中获得，并且不需要使用 $N+k$ 回归器进行回归。

如果已估计截距（如上一节所述），则应从 (17.51) 中减去该截距。在这种情况下，估计的固定效应是

\[ \widehat{u}_{i}=\bar{Y}_{i}-\bar{X}_{i}^{\prime} \widehat{\beta}_{\mathrm{fe}}-\widehat{\alpha}_{\mathrm{fe}} \]

使用任一估计器，当时间序列观测值 $T_{i}$ 的数量较小时，$\widehat{u}_{i}$ 都将是 $u_{i}$ 的不精确估计器。因此基于 $\widehat{u}_{i}$ 的计算应谨慎解释。

固定效应 (17.52) 可以在 Stata 中在 ivreg、fe 之后使用 Predict u 命令获得，或者在 areg 之后使用 Predict d 命令获得。

17.18 固定效应的 GMM 解释

我们还可以通过广义矩方法来解释固定效应估计量。

采用应用内变换（17.21）后的固定效应模型。我们可以将其视为一个 $T$ 方程组，每个方程对应一个时间段 $t$。这是一个多元回归模型。使用第 11 章的符号定义 $T \times k T$ 回归矩阵

\[ \overline{\boldsymbol{X}}_{i}=\left(\begin{array}{cccc} \dot{X}_{i 1}^{\prime} & 0 & \cdots & 0 \\ \vdots & \dot{X}_{i 2}^{\prime} & & \vdots \\ 0 & 0 & \cdots & \dot{X}_{i T}^{\prime} \end{array}\right) . \]

如果我们将每个时间段视为一个单独的方程，我们就有 $k T$ 矩条件

\[ \mathbb{E}\left[\overline{\boldsymbol{X}}_{i}^{\prime}\left(\dot{\boldsymbol{Y}}_{i}-\dot{\boldsymbol{X}}_{i} \beta\right)\right]=0 . \]

当 $T \geq 3$ 存在 $k$ 系数和 $k T$ 矩时，这是一个过度识别的方程组。（但是，由于内变换，矩是共线的。存在 $k(T-1)$ 有效矩。）在多元回归的背景下解释此模型，过度识别是通过系数向量 $\beta$ 在不同时间段内保持恒定的限制来实现的。

该模型可以解释为使用工具 $\overline{\boldsymbol{X}}_{i}$ 对 $\dot{\boldsymbol{X}}_{i}$ 进行 $\dot{\boldsymbol{Y}}_{i}$ 的回归。使用矩阵表示法的 2SLS 估计器是

\[ \widehat{\beta}=\left(\left(\dot{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{X}}\right)\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)\right)^{-1}\left(\left(\dot{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{X}}\right)\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Y}}\right)\right) \]

请注意

\[ \begin{aligned} & \overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{X}}=\sum_{i=1}^{n}\left(\begin{array}{cccc}\dot{X}_{i 1} & 0 & \cdots & 0 \\\vdots & \dot{X}_{i 2} & & \vdots \\0 & 0 & \cdots & \dot{X}_{i T}\end{array}\right)\left(\begin{array}{cccc}\dot{X}_{i 1}^{\prime} & 0 & \cdots & 0 \\\vdots & \dot{X}_{i 2}^{\prime} & & \vdots \\0 & 0 & \cdots & \dot{X}_{i T}^{\prime}\end{array}\right) \\ & =\left(\begin{array}{cccc}\sum_{i=1}^{n} \dot{X}_{i 1} \dot{X}_{i 1}^{\prime} & 0 & \cdots & 0 \\\vdots & \sum_{i=1}^{n} \dot{X}_{i 2} \dot{X}_{i 2}^{\prime} & & \vdots \\0 & 0 & \cdots & \sum_{i=1}^{n} \dot{X}_{i T} \dot{X}_{i T}^{\prime}\end{array}\right) \text {, } \\ & \overline{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}=\left(\begin{array}{c}\sum_{i=1}^{n} \dot{X}_{i 1} \dot{X}_{i 1}^{\prime} \\\vdots \\\sum_{i=1}^{n} \dot{X}_{i T} \dot{X}_{i T}^{\prime}\end{array}\right) \text {, } \end{aligned} \]

和

\[ \overline{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Y}}=\left(\begin{array}{c} \sum_{i=1}^{n} \dot{X}_{i 1} \dot{Y}_{i 1} \\ \vdots \\ \sum_{i=1}^{n} \dot{X}_{i T} \dot{Y}_{i T} \end{array}\right) \text {. } \]

因此 2SLS 估计器简化为

\[ \begin{aligned} \widehat{\beta}_{2 \mathrm{sls}} &=\left(\sum_{t=1}^{T}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)^{-1}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\right)^{-1} \\ & \times\left(\sum_{t=1}^{T}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)^{-1}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{Y}_{i t}\right)\right) \\ &=\left(\sum_{t=1}^{T} \sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)^{-1}\left(\sum_{t=1}^{T} \sum_{i=1}^{n} \dot{X}_{i t} \dot{Y}_{i t}\right) \\ &=\widehat{\beta}_{\mathrm{fe}} \end{aligned} \]

固定效应估计器！

这表明，如果我们将每个时间段视为具有单独矩方程的单独方程，从而使系统过度识别，然后使用 2SLS 权重矩阵通过 GMM 进行估计，则得到的 GMM 估计器等于简单固定效应估计器。添加附加力矩条件不会带来任何变化。

当方程误差序列不相关且同方差时，2SLS 估计器是合适的 GMM 估计器。如果我们使用允许异方差性和序列相关性的两步有效权重矩阵，则 GMM 估计量为

\[ \begin{aligned} \widehat{\beta}_{\mathrm{gmm}} &=\left(\sum_{t=1}^{T}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime} \widehat{e}_{i t}^{2}\right)^{-1}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\right)^{-1} \\ & \times\left(\sum_{t=1}^{T}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\right)\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{X}_{i t}^{\prime} \widehat{e}_{i t}^{2}\right)^{-1}\left(\sum_{i=1}^{n} \dot{X}_{i t} \dot{Y}_{i t}\right)\right) \end{aligned} \]

其中 $\widehat{e}_{i t}$ 是固定效应残差。

值得注意的是，这个 GMM 估计器是为平衡面板编写的。对于不平衡面板，$i$ 上的总和需要替换为 $t$ 期间观察到的个人的总和。否则无需进行任何更改。

17.19 固定效应模型中的识别

固定效应回归中斜率系数 $\beta$ 的识别与传统回归中的相似，但更细致一些。

考虑变换内方程是最有用的，它可以写为 $\dot{Y}_{i t}=\dot{X}_{i t}^{\prime} \beta+\dot{\varepsilon}_{i t}$ 或 $\dot{\boldsymbol{Y}}_{i}=\dot{\boldsymbol{X}}_{i} \beta+\dot{\boldsymbol{\varepsilon}}_{i}$

从回归理论我们知道系数$\beta$是$\dot{X}_{i t}$对$\dot{Y}_{i t}$的线性效应。变量 $\dot{X}_{i t}$ 是回归量与其特定个体平均值的偏差，$\dot{Y}_{i t}$ 也类似。因此，固定效应模型并不能识别 $X_{i t}$ 的平均水平对 $Y_{i t}$ 的平均水平的影响，而是识别 $X_{i t}$ 的偏差对 $Y_{i t}$ 的影响。

在任何给定样本中，仅当 $\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}$ 满秩时才定义固定效应估计量。总体类比（当个体独立同分布时）是

\[ \mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]>0 . \]

方程（17.54）是固定效应估计量的识别条件。它要求回归矩阵在应用内变换后期望是满秩的。回归量不能包含任何在个体水平上不具有时间变化的变量，也不能包含在个体水平上的时间变化是共线的一组回归量。

17.20 固定效应估计量的渐近分布

在本节中，我们提出平衡面板中固定效应估计量的渐近分布理论。下一节将考虑不平衡面板。

我们使用以下假设。

假设 $17.2

$Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t}$ 对应 $i=1, \ldots, N$，$t=1, \ldots, T$ 对应 $T \geq 2$。
变量$\left(\boldsymbol{\varepsilon}_{i}, \boldsymbol{X}_{i}\right), i=1, \ldots, N$ 是独立且同分布的。
$\mathbb{E}\left[X_{i s} \varepsilon_{i t}\right]=0$ 对于所有 $s=1, \ldots, T$。

4.$\boldsymbol{Q}_{T}=\mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]>0$。

5.$\mathbb{E}\left[\varepsilon_{i t}^{4}\right]<\infty$。

6.$\mathbb{E}\left\|X_{i t}\right\|^{4}<\infty$

给定假设 $17.2$，我们可以为 $\widehat{\beta}_{\mathrm{fe}}$ 建立渐近正态性。

定理 17.2 在假设 17.2 下，作为 $N \rightarrow \infty, \sqrt{N}\left(\widehat{\beta}_{\mathrm{fe}}-\beta\right) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{V}_{\boldsymbol{\beta}}\right)$ 其中 $\boldsymbol{V}_{\beta}=\boldsymbol{Q}_{T}^{-1} \Omega_{T} \boldsymbol{Q}_{T}^{-1}$ 和 $\Omega_{T}=\mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i} \boldsymbol{\varepsilon}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]$。

这种渐近分布是随着个体数量 $N$ 发散至无穷大而时间段 $T$ 的时间数量保持固定而得出的。因此，归一化是 $\sqrt{N}$ 而不是 $\sqrt{n}$ （尽管可以使用其中任何一个，因为 $T$ 是固定的）。这种近似适用于大量个体的情况。我们也可以得出 $N$ 和 $T$ 都发散到无穷大的情况的近似值，但这不会是一个更强的结果。思考这个问题的一种方法是定理 $17.2$ 不要求 $T$ 很大。

考虑到我们的渐近理论库，定理 $17.2$ 可能看起来很标准，但从根本上讲，它与我们引入的任何其他结果有很大不同。固定效应回归有效地估计 $N+k$ 系数 - $k$ 斜率系数 $\beta$ 加上 $N$ 固定效应 $u$ - 并且理论指定 $N \rightarrow \infty$。因此，估计参数的数量以与样本大小相同的速率发散至无穷大，但估计器获得了传统的均值零三明治形式渐近分布。从这个意义上说，定理 $17.2$ 是新的且特殊的。

我们现在讨论假设。

假设 17.2.2 表明观察结果在个体 $i$ 之间是独立的。这通常用于面板数据渐近理论。一个重要的隐含限制是，这意味着我们从回归量中排除任何序列相关的聚合时间序列变化。假设 17.2.3 强制 $X_{i t}$ 对于 $\varepsilon_{i t}$ 来说是严格外生的。这比简单投影更强，但比严格平均独立性（17.18）弱。它不会对特定于个人的效果 $u_{i}$ 施加任何条件。

假设17.2.4是上一节讨论的辨识条件。

中心极限定理需要假设 17.2.5 和 17.2.6。

现在我们证明定理17.2。这些假设意味着变量 $\left(\dot{\boldsymbol{X}}_{i}, \boldsymbol{\varepsilon}_{i}\right)$ 是独立同分布的。跨越 $i$ 并且具有有限的四阶矩。因此由 WLLN

\[ \frac{1}{N} \sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i} \underset{p}{\longrightarrow} \mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]=\boldsymbol{Q}_{T} . \]

假设 17.2.3 意味着

\[ \mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}\right]=\sum_{t=1}^{T} \mathbb{E}\left[\dot{X}_{i t} \varepsilon_{i t}\right]=\sum_{t=1}^{T} \mathbb{E}\left[X_{i t} \varepsilon_{i t}\right]-\sum_{t=1}^{T} \sum_{j=1}^{T} \mathbb{E}\left[X_{i j} \varepsilon_{i t}\right]=0 \]

所以它们的均值为零。假设 17.2.5 和 17.2.6 意味着 $\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}$ 具有有限协方差矩阵 $\Omega_{T}$。 CLT 的假设（定理 6.3）成立，因此

\[ \frac{1}{\sqrt{N}} \sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \varepsilon_{i} \underset{d}{\longrightarrow} \mathrm{N}\left(0, \Omega_{T}\right) \]

我们一起发现

\[ \sqrt{N}\left(\widehat{\beta}_{\mathrm{fe}}-\beta\right)=\left(\frac{1}{N} \sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1}\left(\frac{1}{\sqrt{N}} \sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}\right) \underset{d}{\longrightarrow} \boldsymbol{Q}_{T}^{-1} \mathrm{~N}\left(0, \Omega_{T}\right)=\mathrm{N}\left(0, \boldsymbol{V}_{\beta}\right) \]

就像声明的那样。

17.21 不平衡面板的渐近分布

在本节中，我们将上一节的理论扩展到随机选择下的不平衡面板。我们的演示基于 Wooldridge (2010) 的 $17.1$ 部分。

将不平衡面板视为理想化平衡面板的缩短版本，其中缩短是由于随机选择导致的“缺失”观察结果造成的。因此，假设基础（潜在）变量是 $\boldsymbol{Y}_{i}=\left(Y_{i 1}, \ldots, Y_{i T}\right)^{\prime}$ 和 $\boldsymbol{X}_{i}=\left(X_{i 1}, \ldots, X_{i T}\right)^{\prime}$。令 $\boldsymbol{s}_{i}=\left(s_{i 1}, \ldots, s_{i T}\right)^{\prime}$ 为选择指标的向量，这意味着如果对单个 $i$ 观察到时间段 $t$，则为 $s_{i t}=1$，否则为 $s_{i t}=0$。然后我们可以用代数方式描述估计量如下。

设 $\boldsymbol{S}_{i}=\operatorname{diag}\left(\boldsymbol{s}_{i}\right)$ 和 $\boldsymbol{M}_{i}=\boldsymbol{S}_{i}-\boldsymbol{s}_{i}\left(\boldsymbol{s}_{i}^{\prime} \boldsymbol{s}_{i}\right)^{-1} \boldsymbol{s}_{i}^{\prime}$ 是幂等的。内变换可以写为 $\dot{\boldsymbol{Y}}_{i}=\boldsymbol{M}_{i} \boldsymbol{Y}_{i}$ 和 $\dot{\boldsymbol{X}}_{i}=\boldsymbol{M}_{i} \boldsymbol{X}_{i}$。它们具有以下属性：如果 $s_{i t}=0$（因此缺少时间段 $t$），则 $\dot{\boldsymbol{Y}}_{i}$ 的 $t^{t h}$ 元素和 $\boldsymbol{S}_{i}=\operatorname{diag}\left(\boldsymbol{s}_{i}\right)$ 的 $t^{t h}$ 行均为零。缺失的观测值已被零替换。因此，它们不会出现在矩阵乘积和和中。

基于观察样本的 $\beta$ 的固定效应估计量为

\[ \widehat{\beta}_{\mathrm{fe}}=\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{Y}}_{i}\right) . \]

中心化和规范化，

从概念上讲，这似乎与平衡面板的情况相同，但不同之处在于，内部运算符 $\boldsymbol{M}_{i}$ 合并了由不平衡面板结构引起的样本选择。

要导出 $\widehat{\beta}_{\text {fe we }}$ 的分布理论，需要明确 $\boldsymbol{s}_{i}$ 的随机性质。也就是说，为什么有些时间段被观察到，而有些则没有？我们可以采取几种方法：

我们可以将 $s_{i}$ 视为固定（非随机）。这是最简单的方法，但也是最不令人满意的。
我们可以将 $s_{i}$ 视为随机但独立于 $\left(\boldsymbol{Y}_{i}, \boldsymbol{X}_{i}\right)$。这被称为“随机缺失”，是用于证明缺失观测值的方法合理性的常见假设。当未观察到观察的原因与观察无关时，这是合理的。例如，这适用于个人以“波浪”形式进入和退出的面板数据集。统计处理与固定$s_{i}$的情况没有本质上的不同。
我们可以将 $\left(\boldsymbol{Y}_{i}, \boldsymbol{X}_{i}, \boldsymbol{s}_{i}\right)$ 视为联合随机，但施加一个足以一致估计 $\beta$ 的条件。这就是我们下面采取的方法。事实证明，这种情况是一种卑鄙的独立性。这种方法的优点是它比完全独立的限制更少。缺点是我们必须使用条件均值限制而不是不相关性来识别系数。

我们施加的具体假设如下。

假设17.3

$Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t}$ 对于 $i=1, \ldots, N$ 和 $T_{i} \geq 2$。
变量$\left(\boldsymbol{\varepsilon}_{i}, \boldsymbol{X}_{i}, \boldsymbol{s}_{i}\right), i=1, \ldots, N$ 是独立且同分布的。

3.$\mathbb{E}\left[\varepsilon_{i t} \mid \boldsymbol{X}_{i}, s_{i}\right]=0$。

4.$\boldsymbol{Q}_{T}=\mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]>0$。

5.$\mathbb{E}\left[\varepsilon_{i t}^{4}\right]<\infty$。

6.$\mathbb{E}\left\|X_{i t}\right\|^{4}<\infty$。

与假设 $17.2$ 的主要区别在于，我们将严格的外生性加强为严格的均值独立性。这意味着回归模型已正确指定，并且选择不会影响 $\varepsilon_{i t}$ 的平均值。它比完全独立的限制性要小，因为 $\boldsymbol{s}_{i}$ 可以影响 $\varepsilon_{i t}$ 的其他时刻，更重要的是不限制 $\boldsymbol{s}_{i}$ 和 $\boldsymbol{X}_{i}$ 之间的联合依赖。

鉴于上述发展，建立渐近正态性是很简单的。

定理 17.3 在假设 17.3 下，作为 $N \rightarrow \infty, \sqrt{N}\left(\widehat{\beta}_{\mathrm{fe}}-\beta\right) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{V}_{\beta}\right)$ 其中 $\boldsymbol{V}_{\beta}=\boldsymbol{Q}_{T}^{-1} \Omega_{T} \boldsymbol{Q}_{T}^{-1}$ 和 $\Omega_{T}=\mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i} \boldsymbol{\varepsilon}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]$。现在我们证明定理17.3。这些假设意味着变量 $\left(\dot{\boldsymbol{X}}_{i}, \boldsymbol{\varepsilon}_{i}\right)$ 是独立同分布的。跨越 $i$ 并且具有有限的四阶矩。由 WLLN 提供

随机向量 $\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}$ 是独立同分布的。矩阵 $\dot{\boldsymbol{X}}_{i}$ 仅是 $\left(\boldsymbol{X}_{i}, \boldsymbol{s}_{i}\right)$ 的函数。假设 17.3.3 和迭代期望定律意味着

\[ \mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i}\right]=\mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime} \mathbb{E}\left[\boldsymbol{\varepsilon}_{i} \mid \boldsymbol{X}_{i}, \boldsymbol{s}_{i}\right]\right]=0 . \]

因此 $\dot{\boldsymbol{X}}_{i}^{\prime} \varepsilon_{i}$ 的平均值为零。假设 17.3.5 和 17.3.6 以及 $\boldsymbol{s}_{i}$ 有界这一事实意味着 $\dot{\boldsymbol{X}}_{i}^{\prime} \varepsilon_{i}$ 具有有限协方差矩阵，即 $\Omega_{T}$。 CLT 的假设成立，因此

\[ \frac{1}{\sqrt{N}} \sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \varepsilon_{i} \underset{d}{\longrightarrow} \mathrm{N}\left(0, \Omega_{T}\right) \]

我们共同获得了所陈述的结果。

17.22 异方差-鲁棒协方差矩阵估计

我们为固定效应估计器引入了两个协方差矩阵估计器。经典估计量 (17.36) 适用于特殊误差 $\varepsilon_{i t}$ 同方差且序列不相关的情况。集群鲁棒估计器 (17.38) 允许异方差性和任意序列相关性。在本节和下一节中，我们考虑中间情况，其中 $\varepsilon_{i t}$ 是异方差但序列不相关的。

假设(17.18)和(17.26)成立，但不一定(17.25)成立。定义条件方差

\[ \mathbb{E}\left[\varepsilon_{i t}^{2} \mid \boldsymbol{X}_{i}\right]=\sigma_{i t}^{2} . \]

然后是$\Sigma_{i}=\mathbb{E}\left[\boldsymbol{\varepsilon}_{i} \boldsymbol{\varepsilon}_{i}^{\prime} \mid \boldsymbol{X}_{i}\right]=\operatorname{diag}\left(\sigma_{i t}^{2}\right)$。协方差矩阵 (17.24) 可以写为

\[ \boldsymbol{V}_{\mathrm{fe}}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{X}_{i t}^{\prime} \sigma_{i t}^{2}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \]

$\sigma_{i t}^{2}$ 的自然估计量是 $\widehat{\varepsilon}_{i t}^{2}$。将(17.56)中的$\sigma_{i t}^{2}$替换为$\widehat{\varepsilon}_{i t}^{2}$并进行自由度调整，我们得到White型协方差矩阵估计器

\[ \widehat{\boldsymbol{V}}_{\mathrm{fe}}=\frac{n}{n-N-k}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{X}_{i t}^{\prime} \widehat{\varepsilon}_{i t}^{2}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} . \]

根据 White (1980) 的见解，期望 $\widehat{\boldsymbol{V}}_{\text {fe }}$ 是 $\boldsymbol{V}_{\text {fe. }}$ 的合理估计量似乎是合适的。不幸的是，斯托克和沃森（2008）发现的情况并非如此。问题是 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}$ 是个体特定均值 $\bar{\varepsilon}_{i}$ 的函数，只有当时间序列观测值 $T_{i}$ 的数量很大时，该均值才可以忽略不计。

我们可以通过简单的偏差计算看到这一点。假设样本是平衡的，并且残差是用真实的 $\beta$ 构建的。然后

\[ \widehat{\varepsilon}_{i t}=\dot{\varepsilon}_{i t}=\varepsilon_{i t}-\frac{1}{T} \sum_{t=1}^{T} \varepsilon_{i j} . \]

使用 (17.26) 和 (17.55)

\[ \mathbb{E}\left[\widehat{\varepsilon}_{i t}^{2} \mid \boldsymbol{X}_{i}\right]=\left(\frac{T-2}{T}\right) \sigma_{i t}^{2}+\frac{\bar{\sigma}_{i}^{2}}{T} \]

其中 $\bar{\sigma}_{i}^{2}=T^{-1} \sum_{t=1}^{T} \sigma_{i t}^{2}$. （参见练习17.10。）使用（17.57）并设置$k=0$，我们得到

\[ \begin{aligned} \mathbb{E}\left[\widehat{\boldsymbol{V}}_{\mathrm{fe}} \mid \boldsymbol{X}\right] &=\frac{T}{T-1}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{X}_{i t}^{\prime} \mathbb{E}\left[\widehat{\varepsilon}_{i t}^{2} \mid \boldsymbol{X}_{i}\right]\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \\ &=\left(\frac{T-2}{T-1}\right) \boldsymbol{V}_{\mathrm{fe}}+\frac{1}{T-1}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i} \bar{\sigma}_{i}^{2}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} . \end{aligned} \]

因此 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}$ 偏向于 $O\left(T^{-1}\right)$ 阶。除非 $T \rightarrow \infty$ 这种偏见将持续存在，因为 $N \rightarrow \infty . \widehat{\boldsymbol{V}}_{\mathrm{fe}}$ 在两种情况下都是无偏见的。第一个是当错误 $\varepsilon_{i t}$ 同方差时。第二个是当 $T=2$ 时。（要证明后者需要一些代数，所以被省略。）

为了纠正案例 $T>2$ 的偏差，Stock 和 Watson (2008) 提出了估计器

\[ \begin{aligned} \widetilde{\boldsymbol{V}}_{\mathrm{fe}} &=\left(\frac{T-1}{T-2}\right) \widehat{\boldsymbol{V}}_{\mathrm{fe}}-\frac{1}{T-1} \widehat{\boldsymbol{B}}_{\mathrm{fe}} \\ \widehat{\boldsymbol{B}}_{\mathrm{fe}} &=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i} \widehat{\sigma}_{i}^{2}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \\ \widehat{\sigma}_{i}^{2} &=\frac{1}{T-1} \sum_{t=1}^{T} \widehat{\varepsilon}_{i t}^{2} . \end{aligned} \]

您可以检查 $\mathbb{E}\left[\widehat{\sigma}_{i}^{2} \mid \boldsymbol{X}_{i}\right]=\bar{\sigma}_{i}^{2}$ 和 $\mathbb{E}\left[\widetilde{\boldsymbol{V}}_{\text {fe }} \mid \boldsymbol{X}_{i}\right]=\boldsymbol{V}_{\text {fe }}$ ，因此 $\widetilde{\boldsymbol{V}}_{\text {fe }}$ 对于 $\boldsymbol{V}_{\text {fe }}$ 是无偏的。（参见练习 17.11。）

Stock 和 Watson (2008) 表明 $\widetilde{\boldsymbol{V}}_{\text {fe }}$ 与 $T$fixed 和 $N \rightarrow \infty$ 一致。在模拟中，他们表明 $\widetilde{\boldsymbol{V}}_{\mathrm{fe}}$ 具有出色的性能。

由于 Stock-Watson 分析，当使用 xtreg 命令计算固定效应估计量时，Stata 不再计算异方差稳健协方差矩阵估计量 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}$。相反，当请求稳健标准错误时，会报告集群稳健估计器 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}^{\text {cluster }}$。然而，固定效应通常使用 areg 命令来实现，如果需要稳健的标准误差，该命令会报告有偏差的估计器 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}$。这些导致实际建议 areg 应与 cluster(id) 选项一起使用。

目前，校正估计器 (17.58) 尚未被编程为 Stata 选项。

17.23 异方差-稳健估计-不平衡情况

Stock 和 Watson (2008) 的偏差校正稳健协方差矩阵估计器的一个局限性是它仅针对平衡面板得出。在本节中，我们将其估计器概括为涵盖不平衡面板。

估计量是

\[ \begin{aligned} &\widetilde{\boldsymbol{V}}_{\mathrm{fe}}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \widetilde{\Omega}_{\mathrm{fe}}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \\ &\widetilde{\Omega}_{\mathrm{fe}}=\sum_{i=1}^{N} \sum_{t \in S_{i}} \dot{X}_{i t} \dot{X}_{i t}^{\prime}\left[\left(\frac{T_{i} \widehat{\varepsilon}_{i t}^{2}-\widehat{\sigma}_{i}^{2}}{T_{i}-2}\right) \mathbb{1}\left\{T_{i}>2\right\}+\left(\frac{T_{i} \widehat{\varepsilon}_{i t}^{2}}{T_{i}-1}\right) \mathbb{1}\left\{T_{i}=2\right\}\right] \end{aligned} \]

在哪里

\[ \widehat{\sigma}_{i}^{2}=\frac{1}{T_{i}-1} \sum_{t \in S_{i}} \widehat{\varepsilon}_{i t}^{2} . \]

为了证明这个估计量的合理性，如上一节所述，做出简化假设，即残差是用真实的 $\beta$ 构建的。我们计算出

\[ \begin{aligned} &\mathbb{E}\left[\widehat{\varepsilon}_{i t}^{2} \mid \boldsymbol{X}_{i}\right]=\left(\frac{T_{i}-2}{T_{i}}\right) \sigma_{i t}^{2}+\frac{\bar{\sigma}_{i}^{2}}{T_{i}} \\ &\mathbb{E}\left[\widehat{\sigma}_{i}^{2} \mid \boldsymbol{X}_{i}\right]=\bar{\sigma}_{i}^{2} . \end{aligned} \]

您可以证明，在这些假设下，$\mathbb{E}\left[\widetilde{\boldsymbol{V}}_{\mathrm{fe}} \mid \boldsymbol{X}\right]=\boldsymbol{V}_{\mathrm{fe}}$ 以及 $\widetilde{\boldsymbol{V}}_{\mathrm{fe}}$ 对于 $\boldsymbol{V}_{\mathrm{fe}}$ 是无偏的。（参见练习 17.12。）

在平衡面板中，估计器 $\widetilde{\boldsymbol{V}}_{\mathrm{fe}}$ 简化为 Stock-Watson 估计器（使用 $k=0$ ）。

17.24 随机效应与固定效应的豪斯曼检验

随机效应模型是固定效应模型的特例。因此，我们可以针对固定效应的替代方案来检验随机效应的零假设。豪斯曼检验通常用于此目的。该统计量是固定效应和随机效应估计量之间差异的二次方。统计数据是

\[ \begin{aligned} H &=\left(\widehat{\beta}_{\mathrm{fe}}-\widehat{\beta}_{\mathrm{re}}\right)^{\prime} \widehat{\operatorname{var}}\left[\widehat{\beta}_{\mathrm{fe}}-\widehat{\beta}_{\mathrm{re}}\right]^{-1}\left(\widehat{\beta}_{\mathrm{fe}}-\widehat{\beta}_{\mathrm{re}}\right) \\ &=\left(\widehat{\beta}_{\mathrm{fe}}-\widehat{\beta}_{\mathrm{re}}\right)^{\prime}\left(\widehat{\boldsymbol{V}}_{\mathrm{fe}}-\widehat{\boldsymbol{V}}_{\mathrm{re}}\right)^{-1}\left(\widehat{\beta}_{\mathrm{fe}}-\widehat{\beta}_{\mathrm{re}}\right) \end{aligned} \]

其中 $\widehat{\boldsymbol{V}}_{\mathrm{fe}}$ 和 $\widehat{\boldsymbol{V}}_{\mathrm{re}}$ 均采用经典（非鲁棒）形式。

该测试可以在系数 $\beta$ 的子集上实现。特别是，如果回归量 $X_{i t}$ 包含时不变元素，则需要执行此操作，以便随机效应估计器包含比固定效应估计器更多的系数。在这种情况下，应仅对时变回归量的系数进行检验。

如果 $H$ 超过 $\chi_{k}^{2}$ 分布的 $1-\alpha^{t h}$ 分位数（其中 $k=$ $\operatorname{dim}(\beta)$），则渐近 $100 \alpha %$ 检验将被拒绝。如果测试拒绝，则表明个体效应 $u_{i}$ 与回归变量相关，因此随机效应模型不合适。另一方面，如果检验未能拒绝该证据，则表明随机效应假设不能被拒绝。

使用豪斯曼检验来选择是使用固定效应估计器还是随机效应估计器是很诱人的。人们可以想象，如果豪斯曼检验未能拒绝随机效应假设，则使用随机效应估计器，否则使用固定效应估计器。然而，这并不是一个明智的做法。这个过程——根据测试选择一个估计器——被称为预测试估计器并且是有偏差的。出现偏差是因为测试结果是随机的并且与估计量相关。

相反，豪斯曼测试可以用作规范测试。如果您计划使用随机效应估计器（并且相信随机效应假设适合您的情况），则可以使用豪斯曼检验来检查此假设并提供证据来支持您的方法。

17.25 随机效应还是固定效应？

我们提出了回归系数的随机效应和固定效应估计量。实际中应该使用哪个？我们应该如何看待这种差异？

基本区别在于随机效应估计器要求个体误差 $u_{i}$ 满足条件均值假设 (17.8)。固定效应估计器不需要 (17.8) 并且对其违规具有鲁棒性。特别是，个体效应 $u_{i}$ 可以与回归量任意相关。另一方面，随机效应估计器在随机效应下是有效的（假设 17.1）。当前的计量经济学实践更看重稳健性而非效率。因此，当前的做法（几乎一致）是对线性面板数据模型使用固定效应估计器。随机效应估计器仅用于固定效应估计未知或具有挑战性的情况（这发生在许多非线性模型中）。

“随机效应”和“固定效应”标签具有误导性。这些标签出现在早期文献中，而我们今天仍被这些标签所困扰。在以前的时代，回归量被视为“固定的”。将个体效应视为未观察到的回归变量会导致个体效应被贴上“固定”的标签。如今，在处理观测数据时，我们很少将回归量称为“固定”。我们将所有变量视为随机的。因此，将 $u_{i}$ 描述为“固定”没有多大意义，并且它很难与“随机效应”标签形成对比，因为在任一假设下 $u_{i}$ 都被视为随机的。标签再次令人遗憾，但关键区别在于 $u_{i}$ 是否与回归量相关。

17.26 时间趋势

一般来说，我们预计经济主体将在同一时期经历共同的冲击。例如，商业周期波动、通货膨胀和利率会影响经济中的所有主体。因此，通常需要在面板回归模型中包含时间效应。

最简单的规范是线性时间趋势

\[ Y_{i t}=X_{i t}^{\prime} \beta+\gamma t+u_{i}+\varepsilon_{i t} . \]

有关时间趋势的介绍，请参阅第 14.42 节。还可以使用更灵活的规格（例如二次）。为了进行估计，最好将时间趋势 $t$ 作为回归向量 $X_{i t}$ 的元素，然后应用固定效应。

在某些情况下，时间趋势可能因人而异。系列可能以不同的速度增长或下降。线性时间趋势规范仅提取共同的时间趋势。为了考虑到个人特定的时间趋势，我们需要包括交互效应。这可以写成

\[ Y_{i t}=X_{i t}^{\prime} \beta+\gamma_{i} t+u_{i}+\varepsilon_{i t} . \]

在固定效应规范中，系数 $\left(\gamma_{i}, u_{i}\right)$ 被视为可能与回归量相关。为了从模型中消除它们，我们将它们视为未知参数并通过最小二乘法估计所有参数。根据 FWL 定理，$\beta$ 的估计量等于 $\dot{\boldsymbol{Y}}$ 在 $\dot{\boldsymbol{X}}$ 上的最小二乘，其中它们的元素是分别适合每个个体和变量的线性时间趋势的最小二乘回归的残差。

17.27 双向误差分量

在上一节中，我们讨论了时间趋势和个人特定时间趋势的包含。线性时间趋势所施加的函数形式是有限制的。没有经济理由认为系列的“趋势”是线性的。商业周期“趋势”是周期性的。这表明希望比线性（或多项式）规范更灵活。在本节中，我们考虑最灵活的规范，其中允许趋势采取任意形状，但要求它是常见的而不是特定于个人的。

我们考虑的模型是双向误差分量模型

\[ Y_{i t}=X_{i t}^{\prime} \beta+v_{t}+u_{i}+\varepsilon_{i t} . \]

在此模型中，$u_{i}$ 是未观察到的个体特定效应，$v_{t}$ 是未观察到的时间特定效应，$\varepsilon_{i t}$ 是特殊误差。

双向模型 (17.63) 可以使用随机效应或固定效应来处理。在随机效应框架中，误差 $v_{t}$ 和 $u_{i}$ 按照假设 17.1 进行建模。当面板平衡时，误差向量 $\boldsymbol{e}=v \otimes \mathbf{1}_{N}+\mathbf{1}_{T} \otimes u+\boldsymbol{\varepsilon}$ 的协方差矩阵为

\[ \operatorname{var}[\boldsymbol{e}]=\Omega=\left(\boldsymbol{I}_{T} \otimes \mathbf{1}_{N} \mathbf{1}_{N}^{\prime}\right) \sigma_{v}^{2}+\left(\mathbf{1}_{T} \mathbf{1}_{T}^{\prime} \otimes \boldsymbol{I}_{N}\right) \sigma_{u}^{2}+\boldsymbol{I}_{n} \sigma_{\varepsilon}^{2} . \]

当面板不平衡时，可以导出类似但繁琐的 (17.64) 表达式。该方差 (17.64) 可用于 $\beta$ 的 GLS 估计。

更典型的是（17.63）是使用固定效应来处理的。双向变换减去特定于个体的均值和特定于时间的均值，以从双向模型 (17.63) 中消除 $v_{t}$ 和 $u_{i}$。对于变量 $Y_{i t}$，我们定义特定时间的平均值如下。令 $S_{t}$ 为样本中包含观测值 $t$ 的个体 $i$ 的集合，并令 $N_{t}$ 为这些个体的数量。那么时间 $t$ 的特定时间平均值为

\[ \widetilde{Y}_{t}=\frac{1}{N_{t}} \sum_{i \in S_{t}} Y_{i t} . \]

这是在 $t$ 时刻观察到的所有 $Y_{i t}$ 值的平均值。

对于平衡面板的情况，变换中的双向是

\[ \ddot{Y}_{i t}=Y_{i t}-\bar{Y}_{i}-\widetilde{Y}_{t}+\bar{Y} \]

其中 $\bar{Y}=n^{-1} \sum_{i=1}^{N} \sum_{t=1}^{T} Y_{i t}$ 是全样本平均值。如果$Y_{i t}$满足双向分量模型

\[ Y_{i t}=v_{t}+u_{i}+\varepsilon_{i t} \]

然后是 $\bar{Y}_{i}=\bar{v}+u_{i}+\bar{\varepsilon}_{i}, \widetilde{Y}_{t}=v_{t}+\bar{u}+\widetilde{\varepsilon}_{t}$ 和 $\bar{Y}=\bar{v}+\bar{u}+\bar{\varepsilon}$。因此

\[ \begin{aligned} \ddot{Y}_{i t} &=v_{t}+u_{i}+\varepsilon_{i t}-\left(\bar{v}+u_{i}+\bar{\varepsilon}_{i}\right)-\left(v_{t}+\bar{u}+\widetilde{\varepsilon}_{t}\right)+\bar{v}+\bar{u}+\bar{\varepsilon} \\ &=\varepsilon_{i t}-\bar{\varepsilon}_{i}-\widetilde{\varepsilon}_{t}+\bar{\varepsilon}=\ddot{\varepsilon}_{i t} \end{aligned} \]

这样就消除了个人和时间的影响。

应用于 (17.63) 的双向内变换得到

\[ \ddot{Y}_{i t}=\ddot{X}_{i t}^{\prime} \beta+\ddot{\varepsilon}_{i t} \]

这对于 $v_{t}$ 和 $u_{i}$ 都是不变的。双向内估计器是应用于 (17.66) 的最小二乘法。

对于不平衡的情况，有两种计算方法来实现估计器。两者都是基于这样的认识：估计量相当于包含所有时间段的虚拟变量。令 $\tau_{t}$ 为一组 $T$ 虚拟变量，其中 $t^{t h}$ 表示 $t^{t h}$ 时间段。因此，$\tau_{t}$ 的 $t^{t h}$ 元素为 1，其余元素为零。将 $v=\left(\nu_{1}, \ldots, \nu_{T}\right)^{\prime}$ 设置为时间固定效应的向量。请注意 $v_{t}=\tau_{t}^{\prime} \nu$。我们可以将双向模型写为

\[ Y_{i t}=X_{i t}^{\prime} \beta+\tau_{t}^{\prime} \nu+u_{i}+\varepsilon_{i t} . \]

这是双向误差分量模型的虚拟变量表示。

模型 (17.67) 可以通过回归量 $X_{i t}$ 和 $\tau_{t}$ 以及系数向量 $\beta$ 和 $\nu$ 的单向固定效应进行估计。这可以通过标准单向固定效应方法（包括 Stata 中的 xtreg 或 areg）来实现。这会产生斜率 $\beta$ 以及时间效应 $\nu$ 的估计。为了实现识别，从 $\tau_{t}$ 中省略了一次虚拟变量，因此估计的时间效应均与该基线时间段相关。这是实践中估计双向固定效应模型最常用的方法。由于时间段的数量通常是适度的，因此这是一种在计算上有吸引力的方法。

第二种计算方法是通过残差回归消除时间影响。这是通过以下步骤完成的。首先，减去 (17.67) 的个体特定均值。这产生

\[ \dot{Y}_{i t}=\dot{X}_{i t}^{\prime} \beta+\dot{\tau}_{t}^{\prime} v+\dot{\varepsilon}_{i t} . \]

其次，在 $\dot{\tau}_{t}$ 上回归 $\dot{Y}_{i t}$ 以获得残差 $\ddot{Y}_{i t}$，并在 $\dot{\tau}_{t}$ 上回归 $\dot{X}_{i t}$ 的每个元素以获得残差 $\ddot{X}_{i t}$。第三，在 $\ddot{X}_{i t}$ 上回归 $\ddot{Y}_{i t}$ 以获得 $\beta$ 的内估计量。这些步骤消除了固定效应 $\dot{Y}_{i t}$，因此估计量对其值而言是不变的。这个两步过程的重要之处在于，第二步不是跨时间索引的内部转换，而是标准回归。

如果使用双向内估计器，则回归器 $X_{i t}$ 不能包含任何时不变变量 $X_{i}$ 或常见时间序列变量 $X_{t}$。两者都被双向变换所消除。仅针对在个体和时间上都有变化的回归量来确定系数。

如果需要，可以通过对系数 $\nu$ 进行排除测试来测试时间效应的相关性。如果检验拒绝零系数的假设，则表明时间效应在回归模型中相关。

(17.63) 的固定效应估计量对于 $v_{t}$ 和 $u_{i}$ 的值是不变的，因此不需要对它们的随机属性做出假设。

为了说明这一点，表 $17.2$ 的第四列呈现了投资方程的固定效应估计，并增加了年份虚拟指标，因此是一个双向固定效应模型。在此示例中，包含年份虚拟变量不会对系数估计值和标准误差产生太大影响。

17.28 工具变量

采用固定效应模型

\[ Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} . \]

如果 $\mathbb{E}\left[X_{i t} \varepsilon_{i t}\right]=0$，我们说 $X_{i t}$ 对于 $\varepsilon_{i t}$ 是外生的，如果 $\mathbb{E}\left[X_{i t} \varepsilon_{i t}\right] \neq 0$，我们说 $X_{i t}$ 对于 $\varepsilon_{i t}$ 是内生的。在第 12 章中，我们讨论了内生性的几个经济例子，同样的问题也适用于面板数据背景。主要区别在于，在固定效应模型中，我们只需要关心回归量是否与特殊误差 $\varepsilon_{i t}$ 相关，因为允许 $X_{i t}$ 和 $u_{i}$ 之间存在相关性。

如第 12 章中所示，如果回归量是内生的，则固定效应估计量对于结构系数 $\beta$ 将会有偏差且不一致。处理内生性的标准方法是指定工具变量 $Z_{i t}$ ，这些变量既相关（与 $X_{i t}$ 相关）又是外生的（与 $\varepsilon_{i t}$ 不相关）。

令 $Z_{i t}$ 为 $\ell \times 1$ 工具变量，其中 $\ell \geq k$。与横截面情况一样， $Z_{i t}$ 可能包含包含的外生变量（ $X_{i t}$ 中的外生变量）和排除的外生变量（不在 $X_{i t}$ 中的变量）。令 $\boldsymbol{Z}_{i}$ 为个人的堆叠工具，$\boldsymbol{Z}$ 为完整样本的堆叠工具。

固定效应模型的虚拟变量公式为 $Y_{i t}=X_{i t}^{\prime} \beta+d_{i}^{\prime} u+\varepsilon_{i t}$，其中 $d_{i}$ 是虚拟变量的 $N \times 1$ 向量，样本中的每个个体都有一个虚拟变量。完整样本的矩阵表示法模型为

\[ \boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{D} u+\boldsymbol{\varepsilon} . \]

定理 $17.1$ 表明 $\beta$ 的固定效应估计量可以通过 (17.69) 的最小二乘估计来计算。因此，虚拟变量 $\boldsymbol{D}$ 应被视为包含的外生变量。考虑使用工具 $\boldsymbol{Z}$ 对 $\boldsymbol{X}$ 进行 $\beta$ 的 2SLS 估计。由于 $\boldsymbol{D}$ 是一个包含的外生变量，因此它也应该用作工具。因此，固定效应模型 (17.68) 的 2SLS 估计是使用 $17.1$ 作为工具的 $\boldsymbol{Y}$ 对 $(\boldsymbol{X}, \boldsymbol{D})$ 的回归 (17.69) 的代数 2SLS。

由于 $\boldsymbol{D}$ 的维度可能太大，如第 17.11 节中所述，建议使用残差回归来计算 2SLS 估计量，正如我们现在所描述的。

在 12.12 节中，我们描述了 2SLS 估计器的几种替代表示。第五个（方程（12.32））表明 $\beta$ 的 2SLS 估计量等于

\[ \widehat{\beta}_{2 \text { sls }}=\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Z}\left(\boldsymbol{Z}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Z}\right)^{-1} \boldsymbol{Z}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Z}\left(\boldsymbol{Z}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Z}\right)^{-1} \boldsymbol{Z}^{\prime} \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Y}\right) \]

其中 $\boldsymbol{M}_{\boldsymbol{D}}=\boldsymbol{I}_{n}-\boldsymbol{D}\left(\boldsymbol{D}^{\prime} \boldsymbol{D}\right)^{-1} \boldsymbol{D}^{\prime}$.后者是运算符内的矩阵，即 $\boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Y}=\dot{\boldsymbol{Y}}, \boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{X}=\dot{\boldsymbol{X}}$ 和 $\boldsymbol{M}_{\boldsymbol{D}} \boldsymbol{Z}=\dot{Z}$。由此可见 2SLS 估计量为

\[ \widehat{\beta}_{2 \text { sls }}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{Z}\left(\dot{Z}^{\prime} \dot{Z}\right)^{-1} \dot{Z}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\dot{\boldsymbol{X}}^{\prime} \dot{Z}\left(\dot{\boldsymbol{Z}}^{\prime} \dot{Z}\right)^{-1} \dot{Z}^{\prime} \dot{\boldsymbol{Y}}\right) . \]

这很方便。它表明固定效应模型的 2SLS 估计量可以通过将 2SLS 应用于变换内的 $Y_{i t}, X_{i t}$ 和 $Z_{i t}$ 来计算。 2SLS 残差为 $\widehat{\boldsymbol{e}}=\dot{\boldsymbol{Y}}-\dot{\boldsymbol{X}} \widehat{\beta}_{2 s l s}$。

该估计量可以使用 Stata 命令 xtivreg fe 获得。也可以在进行内变换后使用 Stata 命令 ivregress 获得。

为了清楚起见，上述演示重点关注单向固定效应模型。双向固定效应模型没有实质性变化

\[ Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+v_{t}+\varepsilon_{i t} . \]

估计双向模型的最简单方法是将 $T-1$ 时间段虚拟变量添加到回归模型中，并将这些虚拟变量作为回归量和工具。

17.29 工具变量的识别

为了理解固定效应模型中结构斜率系数 $\beta$ 的识别，有必要检查内生回归变量 $X_{i t}$ 的简化形式方程。这是

\[ X_{i t}=\Gamma Z_{i t}+W_{i}+\zeta_{i t} \]

其中 $W_{i}$ 是 $k$ 回归量的固定效应的 $k \times 1$ 向量，$\zeta_{i t}$ 是一个特殊误差。

系数矩阵 $\Gamma$ 是 $Z_{i t}$ 对 $X_{i t}$ 的线性效应，固定效应 $W_{i}$ 保持不变。因此，$\Gamma$ 与固定效应回归模型中的系数 $\beta$ 具有类似的解释。它是 $Z_{i t}$ 的个体特定均值变化对 $X_{i t}$ 的影响。

2SLS 估计器是内部变换变量的函数。将内变换应用到简化形式，我们发现$\dot{X}_{i t}=\Gamma \dot{Z}_{i t}+\dot{\zeta}_{i t}$。这表明 $\Gamma$ 是内部转换工具对回归量的影响。如果转换内的工具不存在时间变化，或者在删除个体特定均值后工具与回归变量之间不存在相关性，则系数 $\Gamma$ 将无法识别或为奇异。无论哪种情况，系数 $\beta$ 都不会被识别。

因此，为了识别固定效应工具变量模型，我们需要

\[ \mathbb{E}\left[\dot{Z}_{i}^{\prime} \dot{Z}_{i}\right]>0 \]

和

\[ \operatorname{rank}\left(\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]\right)=k . \]

条件 (17.70) 与固定效应回归中的识别条件相同 - 工具在内部变换后必须具有完全变异。条件 (17.71) 类似于在横截面上下文中识别工具变量回归的相关条件，但适用于内部转换的工具和回归量。

条件 (17.71) 表明，要检查固定效应 2SLS 背景下的工具有效性，重要的是使用固定效应（内）回归来估计简化形式方程。可以应用仪器有效性的标准测试（对排除的仪器进行 $F$ 测试）。然而，由于简化形式方程的相关结构通常是未知的，因此适合使用在个体水平上聚类的聚类鲁棒协方差矩阵。

17.30 固定效应 2SLS 估计器的渐近分布

在本节中，我们提出固定效应估计量的渐近分布理论。我们为平衡面板的情况提供了正式的理论，并讨论了对不平衡情况的扩展。

我们对平衡面板使用以下假设。

假设 $17.4

$Y_{i t}=X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t}$ 对应 $i=1, \ldots, N$，$t=1, \ldots, T$ 对应 $T \geq 2$。
变量$\left(\boldsymbol{\varepsilon}_{i}, \boldsymbol{X}_{i}, \boldsymbol{Z}_{i}\right), i=1, \ldots, N$ 是独立且同分布的。
$\mathbb{E}\left[Z_{i s} \varepsilon_{i t}\right]=0$ 对于所有 $s=1, \ldots, T$。

4.$\boldsymbol{Q}_{Z Z}=\mathbb{E}\left[\dot{Z}_{i}^{\prime} \dot{Z}_{i}\right]>0$。

$\operatorname{rank}\left(\boldsymbol{Q}_{Z X}\right)=k$ 其中 $\boldsymbol{Q}_{Z X}=\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right]$。

6.$\mathbb{E}\left[\varepsilon_{i t}^{4}\right]<\infty$。

7.$\mathbb{E}\left\|X_{i t}\right\|^{2}<\infty$。

8.$\mathbb{E}\left\|Z_{i t}\right\|^{4}<\infty$。

给定假设 $17.4$，我们可以为 $\widehat{\beta}_{2 s l s}$ 建立渐近正态性。

定理 17.4 在假设 17.4 下，如 $N \rightarrow \infty, \sqrt{N}\left(\widehat{\beta}_{2 s l s}-\beta\right) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{V}_{\beta}\right)$ 其中

\[ \begin{aligned} \boldsymbol{V}_{\beta} &=\left(\boldsymbol{Q}_{Z X}^{\prime} \Omega_{Z Z}^{-1} \boldsymbol{Q}_{Z X}\right)^{-1}\left(\boldsymbol{Q}_{Z X}^{\prime} \Omega_{Z Z}^{-1} \Omega_{Z \varepsilon} \Omega_{Z Z}^{-1} \boldsymbol{Q}_{Z X}\right)\left(\boldsymbol{Q}_{Z X}^{\prime} \Omega_{Z Z}^{-1} \boldsymbol{Q}_{Z X}\right)^{-1} \\ \Omega_{Z \varepsilon} &=\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime} \boldsymbol{\varepsilon}_{i} \boldsymbol{\varepsilon}_{i}^{\prime} \dot{\boldsymbol{Z}}_{i}\right] . \end{aligned} \]

结果证明与定理$17.2$类似，故略。关键条件是假设 17.4.3，它指出工具对于特殊误差来说是严格外生的。识别条件是假设 17.4.4 和 17.4.5，这在上一节中已经讨论过。

该定理是针对平衡面板提出的。对于不平衡面板，我们可以通过添加选择指标 $\boldsymbol{s}_{i}$ 并将假设 $17.4 .3$ 替换为 $\mathbb{E}\left[\varepsilon_{i t} \mid \boldsymbol{Z}_{i}, \boldsymbol{s}_{i}\right]=$ 0 来修改定理 $17.3$ 中的定理，这表明特殊误差的平均值与仪器和选择无关。

如果特殊误差 $\varepsilon_{i t}$ 是同方差且序列不相关，则协方差矩阵简化为

\[ \boldsymbol{V}_{\beta}=\left(\boldsymbol{Q}_{Z X}^{\prime} \Omega_{Z Z}^{-1} \boldsymbol{Q}_{Z X}\right)^{-1} \sigma_{\varepsilon}^{2} . \]

在这种情况下，可以使用经典的同方差协方差矩阵估计器。否则，可以使用集群鲁棒协方差矩阵估计器，并采用以下形式

\[ \begin{aligned} \widehat{\boldsymbol{V}}_{\widehat{\beta}} &=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Z}}\left(\dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{Z}}\right)^{-1} \dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Z}}\right)\left(\dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{Z}}\right)^{-1}\left(\sum_{i=1}^{N} \dot{\boldsymbol{Z}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \dot{\boldsymbol{Z}}_{i}\right) \\ & \times\left(\dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{Z}}\right)^{-1}\left(\dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{X}}\right)\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Z}}\left(\dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{Z}}\right)^{-1} \dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1} \end{aligned} \]

对于固定效应回归的情况，不推荐使用异方差鲁棒协方差矩阵估计器，因为 $T$ 较小时存在偏差，并且尚未开发出偏差校正版本。

Stata 命令 xtivreg, fe 默认报告经典同方差协方差矩阵估计量。要获得集群稳健协方差矩阵，请使用选项 vce（稳健）或vce（集群 ID）。

17.31 线性高斯模

考虑刚刚确定的 2SLS 估计器。它求解方程 $\dot{\boldsymbol{Z}}^{\prime}(\dot{\boldsymbol{Y}}-\dot{\boldsymbol{X}} \beta)=0$。这些是总体矩条件 $\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime}\left(\dot{\boldsymbol{Y}}_{i}-\dot{\boldsymbol{X}}_{i} \beta\right)\right]=0$ 的样本模拟。这些总体条件保持在真实的 $\beta$ 上，因为 $\dot{\boldsymbol{Z}}^{\prime} u=\boldsymbol{Z}^{\prime} \boldsymbol{M D} u=0$ 作为 $u$ 位于 $\boldsymbol{D}$ 的零空间中，并且 $\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime} \boldsymbol{\varepsilon}\right]=0$ 由假设 17.4.3 隐含。

总体正交条件在过度识别的情况下也成立。在这种情况下，2SLS 的替代方案是 GMM。例如，让 $\widehat{\boldsymbol{W}}$ 为 $\boldsymbol{W}=\mathbb{E}\left[\dot{\boldsymbol{Z}}_{i}^{\prime} \varepsilon_{i} \varepsilon_{i}^{\prime} \dot{Z}_{i}\right]$ 的估计器

\[ \widehat{\boldsymbol{W}}=\frac{1}{N} \sum_{i=1}^{N} \dot{\boldsymbol{Z}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \dot{\boldsymbol{Z}}_{i} \]

其中 $\widehat{\boldsymbol{\varepsilon}}_{i}$ 是 2SLS 固定效应残差。 GMM 固定效应估计量为

\[ \widehat{\beta}_{\mathrm{gmm}}=\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Z}} \widehat{\boldsymbol{W}}^{-1} \dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{X}}\right)^{-1}\left(\dot{\boldsymbol{X}}^{\prime} \dot{\boldsymbol{Z}} \widehat{\boldsymbol{W}}^{-1} \dot{\boldsymbol{Z}}^{\prime} \dot{\boldsymbol{Y}}\right) . \]

估计器 (17.73)-(17.72) 没有 Stata 命令，但可以通过生成内部变换变量 $\dot{\boldsymbol{X}}, \dot{Z}$ 和 $\dot{\boldsymbol{Y}}$ 来获得，然后使用 $ 通过 GMM 估计 $\dot{\boldsymbol{Y}}$ 对 $\dot{\boldsymbol{X}}$ 的回归matheq5$ 作为使用按个体聚类的权重矩阵的工具。

17.32 使用时不变回归器进行估计

固定效应估计量的令人失望的地方之一是它无法估计时不变回归量的影响。它们不与固定效应分开识别，并通过内部变换消除。相比之下，随机效应估计量允许时不变回归量，但只有通过假设严格的外生性才能做到这一点，该外生性比经济应用中通常期望的更强。

事实证明，我们可以考虑一种中间情况，它保持时变回归量的固定效应假设，但对时不变回归量使用更强的假设。在我们的阐述中，我们将用 $k \times 1$ 向量 $X_{i t}$ 表示时变回归量，用 $\ell \times 1$ 向量 $Z_{i}$ 表示时不变回归量。

考虑线性回归模型

\[ Y_{i t}=X_{i t}^{\prime} \beta+Z_{i}^{\prime} \gamma+u_{i}+\varepsilon_{i t} . \]

在个人层面，这可以写成

\[ \boldsymbol{Y}_{i}=\boldsymbol{X}_{i} \beta+\boldsymbol{Z}_{i} \gamma+\boldsymbol{\imath}_{i} u_{i}+\boldsymbol{\varepsilon}_{i} \]

其中 $Z_{i}=\boldsymbol{\imath}_{i} Z_{i}^{\prime}$.对于矩阵表示法的完整样本，我们可以将其写为

\[ \boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{Z} \gamma+\boldsymbol{u}+\boldsymbol{\varepsilon} . \]

我们维持这样的假设：特殊误差 $\varepsilon_{i t}$ 在所有时间范围内与 $X_{i t}$ 和 $Z_{i}$ 不相关：

\[ \begin{aligned} \mathbb{E}\left[X_{i s} \varepsilon_{i t}\right] &=0 \\ \mathbb{E}\left[Z_{i} \varepsilon_{i t}\right] &=0 . \end{aligned} \]

在本节中，我们考虑 $Z_{i}$ 与个体级别误差 $u_{i}$ 不相关的情况，因此

\[ \mathbb{E}\left[Z_{i} u_{i}\right]=0, \]

但 $X_{i t}$ 和 $u_{i}$ 的相关性不受限制。在这种情况下，我们说 $Z_{i}$ 相对于固定效应 $u_{i}$ 是外生的，而 $X_{i t}$ 相对于 $u_{i}$ 是内生的。请注意，这是一种与工具变量部分中考虑的不同类型的内生性：内生性意味着与特殊误差 $\varepsilon_{i t}$ 的相关性。这里的内生性意味着与固定效应$u_{i}$的相关性。

我们考虑通过工具变量估计 (17.74)，因此需要与误差 $u_{i}+\varepsilon_{i t}$ 不相关的工具。由于 (17.76) 和 (17.77)，时不变回归量 $Z_{i}$ 满足此条件，因此

\[ \mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime}\left(\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \beta-\boldsymbol{Z}_{i} \gamma\right)\right]=0 . \]

虽然时变回归量 $X_{i t}$ 与 $u_{i}$ 相关，但变换后的变量 $\dot{X}_{i t}$ 与 (17.75) 下的 $u_{i}+\varepsilon_{i t}$ 不相关，因此

\[ \mathbb{E}\left[\dot{\boldsymbol{X}}_{i}^{\prime}\left(\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \beta-\boldsymbol{Z}_{i} \gamma\right)\right]=0 . \]

因此，我们可以使用工具集 $(\dot{\boldsymbol{X}}, \boldsymbol{Z})$ 通过工具变量回归来估计 $(\beta, \gamma)$。具体来说，$\boldsymbol{Y}$ 对 $\boldsymbol{X}$ 和 $\boldsymbol{Z}$ 的回归将 $\boldsymbol{X}$ 视为内生的，将 $\boldsymbol{Z}$ 视为外生的，并使用工具 $\dot{\boldsymbol{X}}$。将此估计器写为 $(\widehat{\beta}, \widehat{\gamma})$。这可以在构造内部转换的 $(\beta, \gamma)$ 后使用 Stata ivregress 命令来实现。

该工具变量估计器在代数上等于简单的两步估计器。第一步 $\widehat{\beta}=\widehat{\beta}_{\text {fe }}$ 是固定效应估计器。第二步设置 $\widehat{\gamma}=\left(\boldsymbol{Z}^{\prime} \boldsymbol{Z}\right)^{-1}\left(\boldsymbol{Z}^{\prime} \widehat{\boldsymbol{u}}\right)$，即估计固定效应 $\widehat{u}_{i}$ 对 $Z_{i}$ 的回归的最小二乘系数。要查看这种等价性，请观察工具变量估计器估计器求解样本矩方程

\[ \begin{aligned} &\dot{\boldsymbol{X}}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta-\boldsymbol{Z} \gamma)=0 \\ &\boldsymbol{Z}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta-\boldsymbol{Z} \gamma)=0 . \end{aligned} \]

请注意 $\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{Z}_{i}=\dot{\boldsymbol{X}}_{i}^{\prime} \boldsymbol{l}_{i} Z_{i}^{\prime}=0$ 和 $\dot{\boldsymbol{X}}^{\prime} \boldsymbol{Z}=0$。因此 (17.78) 与 $\dot{\boldsymbol{X}}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta)=0$ 相同，其解为 $\widehat{\beta}_{\mathrm{fe}}$。将其代入 (17.79) 的左侧，我们得到

\[ \boldsymbol{Z}^{\prime}\left(\boldsymbol{Y}-\boldsymbol{X} \widehat{\beta}_{\mathrm{fe}}-\boldsymbol{Z} \gamma\right)=\boldsymbol{Z}^{\prime}\left(\overline{\boldsymbol{Y}}-\overline{\boldsymbol{X}} \widehat{\beta}_{\mathrm{fe}}-\boldsymbol{Z} \gamma\right)=\boldsymbol{Z}^{\prime}(\widehat{\boldsymbol{u}}-\boldsymbol{Z} \gamma) \]

其中 $\overline{\boldsymbol{Y}}$ 和 $\overline{\boldsymbol{X}}$ 是堆叠的个体，意味着 $\boldsymbol{\imath}_{i} \bar{Y}_{i}$ 和 $\boldsymbol{\imath}_{i} \bar{X}_{i}^{\prime}$。设置等于 0 并求解，我们得到了所声称的最小二乘估计量 $\widehat{\gamma}=\left(\boldsymbol{Z}^{\prime} \boldsymbol{Z}\right)^{-1}\left(\boldsymbol{Z}^{\prime} \widehat{\boldsymbol{u}}\right)$。这种等价性首先由 Hausman 和 Taylor (1981) 观察到。

对于标准误差计算，建议通过工具变量回归联合估计 $(\beta, \gamma)$，并使用在个体级别聚类的集群鲁棒协方差矩阵。由于个体特定效应 $u_{i}$，经典估计量和异方差稳健估计量被错误指定。

估计器 $(\widehat{\beta}, \widehat{\gamma})$ 是下一节中描述的 Hausman-Taylor 估计器的特例。（出于未知原因，无法使用 Stata 的 xthtaylor 命令来估计上述估计器。）

17.33 豪斯曼泰勒模型

Hausman 和 Taylor (1981) 考虑了先前模型的推广。他们的模型是

\[ Y_{i t}=X_{1 i t}^{\prime} \beta_{1}+X_{2 i t}^{\prime} \beta_{2}+Z_{1 i}^{\prime} \gamma_{1}+Z_{2 i}^{\prime} \gamma_{2}+u_{i}+\varepsilon_{i t} \]

其中 $X_{1 i t}$ 和 $X_{2 i t}$ 是时变的，$Z_{1 i}$ 和 $Z_{2 i}$ 是时不变的。令 $X_{1 i t}$、$X_{2 i t}, Z_{1 i}$ 和 $Z_{2 i}$ 的维度分别为 $k_{1}, k_{2}, \ell_{1}$ 和 $\ell_{2}$。

将模型用矩阵表示法写为

\[ \boldsymbol{Y}=\boldsymbol{X}_{1} \beta_{1}+\boldsymbol{X}_{2} \beta_{2}+\boldsymbol{Z}_{1} \gamma_{1}+\boldsymbol{Z}_{2} \gamma_{2}+\boldsymbol{u}+\boldsymbol{\varepsilon} . \]

令 $\overline{\boldsymbol{X}}_{1}$ 和 $\overline{\boldsymbol{X}}_{2}$ 表示个体特定均值的一致矩阵，并让 $\dot{\boldsymbol{X}}_{1}=\boldsymbol{X}_{1}-\overline{\boldsymbol{X}}_{1}$ 和 $\dot{\boldsymbol{X}}_{2}=\boldsymbol{X}_{2}-\overline{\boldsymbol{X}}_{2}$ 表示内变换变量。

Hausman-Taylor 模型假设所有回归量在所有时间范围内都与特殊误差 $\varepsilon_{i t}$ 不相关，并且 $X_{1 i t}$ 和 $Z_{1 i}$ 相对于固定效应 $u_{i}$ 是外生的，因此

\[ \begin{aligned} \mathbb{E}\left[X_{1 i t} u_{i}\right] &=0 \\ \mathbb{E}\left[Z_{1 i} u_{i}\right] &=0 . \end{aligned} \]

然而，回归量 $X_{2 i t}$ 和 $Z_{2 i}$ 允许与 $u_{i}$ 相关。

设置 $\boldsymbol{X}=\left(\boldsymbol{X}_{1}, \boldsymbol{X}_{2}, \boldsymbol{Z}_{1}, \boldsymbol{Z}_{2}\right)$ 和 $\beta=\left(\beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}\right)$。这些假设意味着以下人口矩条件

\[ \begin{aligned} &\mathbb{E}\left[\dot{\boldsymbol{X}}_{1}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta)\right]=0 \\ &\mathbb{E}\left[\dot{\boldsymbol{X}}_{2}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta)\right]=0 \\ &\mathbb{E}\left[\overline{\boldsymbol{X}}_{1}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta)\right]=0 \\ &\mathbb{E}\left[\boldsymbol{Z}_{1}^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta)\right]=0 . \end{aligned} \]

有 $2 k_{1}+k_{2}+\ell_{1}$ 矩条件和 $k_{1}+k_{2}+\ell_{1}+\ell_{2}$ 系数。识别需要 $k_{1} \geq \ell_{2}$ ：外生时变回归量至少与内生时不变回归量一样多。（这包括上一节中 $k_{1}=\ell_{2}=0$ 的模型。）给定矩条件，系数 $\beta=\left(\beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}\right)$ 可以使用工具 $\boldsymbol{Z}=\left(\dot{\boldsymbol{X}}_{1}, \dot{\boldsymbol{X}}_{2}, \overline{\boldsymbol{X}}_{1}, \boldsymbol{Z}_{1}\right)$ 或等效的 $\boldsymbol{Z}=\left(\boldsymbol{X}_{1}, \dot{\boldsymbol{X}}_{2}, \overline{\boldsymbol{X}}_{1}, \boldsymbol{Z}_{1}\right)$ 通过 (17.80) 的 2SLS 回归来估计。这是 2SLS 回归，使用排除的工具 $2 k_{1}+k_{2}+\ell_{1}$ 和 $2 k_{1}+k_{2}+\ell_{1}$ 将 $\boldsymbol{X}_{1}$ 和 $Z_{1}$ 视为外生，将 $2 k_{1}+k_{2}+\ell_{1}$ 和 $2 k_{1}+k_{2}+\ell_{1}$ 视为内生

建议使用在个体级别聚类的聚类鲁棒协方差矩阵估计。不应使用传统协方差矩阵估计器或异方差稳健协方差矩阵估计器，因为它们由于个体特定效应 $u_{i}$ 而被错误指定。

当模型刚刚被识别时，估计器简化如下。 $\widehat{\beta}_{1}$ 和 $\widehat{\beta}_{2}$ 是固定效应估计器。 $\widehat{\gamma}_{1}$ 和 $\widehat{\gamma}_{2}$ 等于使用 $\bar{X}_{1 i}$ 作为 $Z_{2 i}$ 工具对 $\widehat{u}_{i}$ 对 $Z_{1 i}$ 和 $Z_{2 i}$ 进行回归的 2 SLS 估计器。（参见练习 17.14。）

当模型被过度识别时，也可以使用相同的方程和仪器，通过具有集群鲁棒权重矩阵的 GMM 来估计方程。

在构造转换变量 $\dot{\boldsymbol{X}}_{2}$ 和 $\overline{\boldsymbol{X}}_{1}$ 后，可以使用 Stata ivregress cluster(id) 命令计算具有集群稳健标准误差的估计量。

上述 2SLS 估计量与刚刚确定的平衡面板情况下的 Hausman 和 Taylor (1981) 估计量相对应。

Hausman 和 Taylor 在误差 $\varepsilon_{i t}$ 和 $u_{i}$ 严格均值独立且同方差的更强假设下导出了他们的估计量，并因此提出了一种 GLS 型估计量，当这些假设正确时，该估计量会更有效。定义 $\Omega=\operatorname{diag}\left(\Omega_{i}\right)$，其中 $\Omega_{i}=\boldsymbol{I}_{i}+$、$\mathbf{1}_{i} \mathbf{1}_{i}^{\prime} \sigma_{u}^{2} / \sigma_{\varepsilon}^{2}$、$\sigma_{\varepsilon}^{2}$ 和 $\sigma_{u}^{2}$ 是误差分量 $\varepsilon_{i t}$ 和 $u_{i}$ 的方差。还定义转换后的变量 $\varepsilon_{i t}$ 和 $\varepsilon_{i t}$。豪斯曼泰勒估计量是

\[ \begin{aligned} \widehat{\beta}_{\mathrm{ht}} &=\left(\boldsymbol{X}^{\prime} \Omega^{-1} \boldsymbol{Z}\left(\boldsymbol{Z}^{\prime} \Omega^{-1} \boldsymbol{Z}\right)^{-1} \boldsymbol{Z}^{\prime} \Omega^{-1} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \Omega^{-1} \boldsymbol{Z}\left(\boldsymbol{Z}^{\prime} \Omega^{-1} \boldsymbol{Z}\right)^{-1} \boldsymbol{Z}^{\prime} \Omega^{-1} \boldsymbol{Y}\right) \\ &=\left(\widetilde{\boldsymbol{X}}^{\prime} \widetilde{\boldsymbol{Z}}\left(\widetilde{\boldsymbol{Z}}^{\prime} \widetilde{\boldsymbol{Z}}\right)^{-1} \widetilde{\boldsymbol{Z}}^{\prime} \widetilde{\boldsymbol{X}}\right)^{-1}\left(\widetilde{\boldsymbol{X}}^{\prime} \widetilde{\boldsymbol{Z}}\left(\widetilde{\boldsymbol{Z}}^{\prime} \widetilde{\boldsymbol{Z}}\right)^{-1} \widetilde{\boldsymbol{Z}}^{\prime} \widetilde{\boldsymbol{Y}}\right) . \end{aligned} \]

回想一下（17.47）中的 $\Omega_{i}^{-1 / 2}=\boldsymbol{M}_{i}+\rho_{i} \boldsymbol{P}_{i}$，其中 $\rho_{i}$ 在（17.46）中定义。因此

\[ \begin{aligned} \widetilde{Y}_{i} &=Y_{i}-\left(1-\rho_{i}\right) \bar{Y}_{i} \\ \widetilde{X}_{1 i} &=X_{1 i}-\left(1-\rho_{i}\right) \bar{X}_{1 i} \\ \widetilde{X}_{2 i} &=X_{2 i}-\left(1-\rho_{i}\right) \bar{X}_{2 i} \\ \widetilde{Z}_{1 i} &=\rho_{i} Z_{1 i} \\ \widetilde{Z}_{2 i} &=\rho_{i} Z_{2 i} \\ \widetilde{\dot{X}}_{1 i} &=\dot{X}_{1 i} \\ \widetilde{\dot{X}}_{2 i} &=\dot{X}_{2 i} . \end{aligned} \]

由此可见，Hausman-Taylor 估计量可以使用工具 $\left(\dot{\boldsymbol{X}}_{1 i}, \dot{\boldsymbol{X}}_{2 i}, \rho_{i} \overline{\boldsymbol{X}}_{1 i}, \rho_{i} \boldsymbol{Z}_{2 i}\right)$ 通过 $\widetilde{\boldsymbol{Y}}_{i}$ 在 $\left(\widetilde{\boldsymbol{X}}_{1 i}, \widetilde{\boldsymbol{X}}_{2 i}, \rho_{i} \boldsymbol{Z}_{1 i}, \rho_{i} \boldsymbol{Z}_{2 i}\right)$ 上的 2SLS 回归来计算

当面板平衡时，系数 $\rho_{i}$ 全部相等并从工具中横向扩展。因此，可以使用工具 $\left(\dot{\boldsymbol{X}}_{1 i}, \dot{\boldsymbol{X}}_{2 i}, \overline{\boldsymbol{X}}_{1 i}, \boldsymbol{Z}_{2 i}\right)$ 通过 $\widetilde{\boldsymbol{Y}}_{i}$ 在 $\left(\widetilde{\boldsymbol{X}}_{1 i}, \widetilde{\boldsymbol{X}}_{2 i}, Z_{1 i}, \boldsymbol{Z}_{2 i}\right)$ 上的 2SLS 回归来计算估计量

实际上 $\rho_{i}$ 是未知的。可以按照 (17.48) 中的方式进行估计，并修改为根据未变换的 2SLS 回归来估计误差方差。在 Hausman 和 Taylor 使用的同方差假设下，估计器 $\widehat{\beta}_{\text {ht }}$ 具有经典的渐近协方差矩阵。当放宽这些假设时，可以使用集群鲁棒方法来估计协方差矩阵。具有集群鲁棒标准误的 Hausman-Taylor 估计器可以通过命令 xthtaylor vce(robust) 在 Stata 中实现。由于未知原因，该 Stata 命令要求至少存在一个外生时不变变量 $\left(\ell_{1} \geq 1\right)$ 和至少一个外生时变变量 $\left(k_{1} \geq 1\right)$，即使模型已识别也是如此。否则，可以使用上述工具变量方法来实现估计器。

Hausman-Taylor 估计器由 Amemiya 和 MaCurdy (1986) 以及 Breusch、Mizon 和 Schmidt (1989) 进行了改进，他们提出了使用附加工具的更有效版本，这些工具在更强的正交性条件下有效。 Gardner (1998) 观察到，在不平衡的情况下，工具应按 $\rho_{i}$ 进行加权。

在过度识别的情况下，尚不清楚是否优选使用更简单的 2SLS 估计器 $\widehat{\beta}_{2 s l s}$ 还是 GLS 型 Hausman-Taylor 估计器 $\widehat{\beta}_{\mathrm{ht}}$。 $\widehat{\beta}_{\mathrm{ht}}$ 的优点是它在规定的同方差和序列相关条件下是渐近有效的，并且 Stata 中有一个可用的程序。 $\widehat{\beta}_{2 \text { sls }}$ 的优点是编程更简单（如果您自己这样做），可能具有更好的有限样本属性（因为它避免了方差分量估计），并且从现代 GMM 的角度来看是自然估计器。

为了说明这一点，表 $17.2$ 的最后一列包含投资模型的 Hausman-Taylor 估计，将 $Q_{i t-1}, D_{i t-1}$ 和 $T_{i}$ 视为内生的 $u_{i}$ 和 $C F_{i t-1}$，并将行业虚拟变量视为外生。相对于固定效应模型，这允许估计交易指标 $T_{i}$ 的系数。与之前的估计相比，最有趣的变化是交易指标 $T_{i}$ 的系数相对于随机效应估计的幅度增加了一倍。这与 $T_{i}$ 与固定效应相关的假设是一致的，因此随机效应估计是有偏差的。

17.34 折刀协方差矩阵估计

作为渐近推理的替代方法，删除簇折刀可用于协方差矩阵计算。在固定效应估计的背景下，删除簇估计量采用以下形式

\[ \widehat{\beta}_{(-i)}=\left(\sum_{j \neq i} \dot{\boldsymbol{X}}_{j}^{\prime} \dot{\boldsymbol{X}}_{j}\right)^{-1}\left(\sum_{j \neq i} \dot{\boldsymbol{X}}_{j}^{\prime} \dot{\boldsymbol{Y}}_{j}\right)=\widehat{\beta}_{\mathrm{fe}}-\left(\sum_{i=1}^{N} \dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1} \dot{\boldsymbol{X}}_{i}^{\prime} \widetilde{\boldsymbol{e}}_{i} \]

在哪里

\[ \begin{aligned} &\widetilde{\boldsymbol{e}}_{i}=\left(\boldsymbol{I}_{i}-\dot{\boldsymbol{X}}_{i}\left(\dot{\boldsymbol{X}}_{i}^{\prime} \dot{\boldsymbol{X}}_{i}\right)^{-1} \dot{\boldsymbol{X}}_{i}^{\prime}\right)^{-1} \widehat{\boldsymbol{e}}_{i} \\ &\widehat{\boldsymbol{e}}_{i}=\dot{\boldsymbol{Y}}_{i}-\dot{\boldsymbol{X}}_{i} \widehat{\beta}_{\mathrm{fe}} \end{aligned} \]

$\widehat{\beta}_{\mathrm{fe}}$ 方差的删除簇折刀估计量为

\[ \begin{aligned} \widehat{\boldsymbol{V}}_{\widehat{\beta}}^{\text {jack }} &=\frac{N-1}{N} \sum_{i=1}^{N}\left(\widehat{\beta}_{(-i)}-\bar{\beta}\right)\left(\widehat{\beta}_{(-i)}-\bar{\beta}\right)^{\prime} \\ \bar{\beta} &=\frac{1}{N} \sum_{i=1}^{N} \widehat{\beta}_{(-i)} . \end{aligned} \]

删除簇折刀估计器 $\widehat{\boldsymbol{V}}_{\widehat{\beta}}^{\text {jack }}$ 类似于簇鲁棒协方差矩阵估计器。

对于作为固定效应估计器的函数 $\widehat{\theta}_{\mathrm{fe}}=r\left(\widehat{\beta}_{\mathrm{fe}}\right)$ 的参数，$\widehat{\theta}_{\mathrm{fe}}$ 方差的删除簇 Jack-Knife 估计器为

\[ \begin{aligned} \widehat{\boldsymbol{V}}_{\widehat{\theta}}^{\mathrm{jack}} &=\frac{N-1}{N} \sum_{i=1}^{N}\left(\widehat{\theta}_{(-i)}-\bar{\theta}\right)\left(\widehat{\theta}_{(-i)}-\bar{\theta}\right)^{\prime} \\ \widehat{\theta}_{(-i)} &=r\left(\widehat{\beta}_{(-i)}\right) \\ \bar{\theta} &=\frac{1}{N} \sum_{i=1}^{N} \widehat{\theta}_{(-i)} . \end{aligned} \]

估计器 $\widehat{\boldsymbol{V}}_{\widehat{\theta}}^{\text {jack }}$ 类似于 $\widehat{\theta}$ 的 Delta 方法集群鲁棒协方差矩阵估计器。

正如在 i.i.d. 的上下文中一样。样本折刀协方差矩阵估计器的一个优点是它不需要用户对渐近分布进行技术计算。缺点是计算成本增加，因为 $N$ 单独的回归是有效估计的。对于拥有大量 $N$ 个体的微型小组来说，这可能特别昂贵。

在 Stata jackknife 中，固定效应估计量的标准误差是通过使用 $x$ treg $f e$ vce(jackknife) 或 aregsorb(id) cluster(id) vce(jackknife) 获得的，其中 id 是簇变量。对于固定效应 2SLS 估计器，请使用xtivreg fe vce(jackknife)。

17.35 面板引导程序

引导方法还可以通过直接应用成对聚类引导方法应用于面板数据，该引导方法对整个个体而不是单个观察结果进行采样。在面板数据中，我们将其称为面板非参数引导程序。

面板非参数引导程序对 $N$ 各个历史记录 $\left(\boldsymbol{Y}_{i}, \boldsymbol{X}_{i}\right)$ 进行采样以创建引导程序样本。将固定效应（或任何其他估计方法）应用于引导样本以获得系数估计。通过重复 $B$ 次，可以计算系数估计的引导标准误差或系数估计的函数。可以计算百分位数类型和百分位数 t 置信区间。 $\mathrm{BC}_{a}$ 区间需要一个加速度系数 $a$ 的估计器，它是估计器三阶矩的缩放折刀估计。在面板数据中，应使用删除簇折刀来估计 $a$。

在 Stata 中，要获取 bootstrap 标准误差和置信区间，请使用 xtreg、vce(bootstrap,reps (#)) 或 areg,absorb(id) cluster(id) vce(bootstrap,reps(#))，其中 id 是cluster 变量，# 是引导复制的数量。对于固定效应 2SLS 估计器，请使用 xtivreg, fe vce(bootstrap,reps(#))。

17.36 动态面板模型

到目前为止，本章考虑的模型都是静态的，没有动态关系。在许多经济背景下，人们很自然地期望行为和决策是动态的，明确取决于过去的行为。例如，在我们的投资方程中，经济模型预测公司在任何给定年份的投资将取决于前几年的投资决策。这些考虑使我们考虑明确的动态模型。

面板框架中的主力动态模型是带有回归器和单向误差组件结构的 $p^{t h}$ 阶自回归。这是

\[ Y_{i t}=\alpha_{1} Y_{i, t-1}+\cdots+\alpha_{p} Y_{i, t-p}+X_{i t}^{\prime} \beta+u_{i}+\varepsilon_{i t} . \]

其中 $\alpha_{j}$ 是自回归系数，$X_{i t}$ 是 $k$ 回归向量向量，$u_{i}$ 是个体效应，$\varepsilon_{i t}$ 是特殊误差。通常假设误差 $u_{i}$ 和 $\varepsilon_{i t}$ 相互独立，并且 $\varepsilon_{i t}$ 连续不相关且均值为零。目前，我们假设回归量 $X_{i t}$ 是严格外生的 (17.17)。在 $\alpha_{j}$ 节中，我们讨论预定的回归量。

对于许多插图，我们将重点关注 AR(1) 模型

\[ Y_{i t}=\alpha Y_{i, t-1}+u_{i}+\varepsilon_{i t} \]

动态应该逐个解释。 (17.82) 中的系数 $\alpha$ 等于一阶自相关。当 $\alpha=0$ 时，该系列是序列不相关的（以 $u_{i}$ 为条件）。 $\alpha>0$ 表示 $Y_{i t}$ 呈正序列相关。 $\alpha<0$ 表示 $Y_{i t}$ 呈负序列相关。当 $\alpha=1$ 时，自回归单位根成立，这意味着 $Y_{i t}$ 遵循可能存在漂移的随机游走。由于 $\alpha$ 对于给定个体来说是恒定的，因此应将其视为特定于个体的截距。特殊错误 $\alpha$ 在标准时间序列自回归中扮演错误的角色。

如果 $|\alpha|<1$ 模型 (17.82) 是平稳的。通过标准自回归向后递归，我们计算出

\[ Y_{i t}=\sum_{j=0}^{\infty} \alpha^{j}\left(u_{i}+\varepsilon_{i t}\right)=(1-\alpha)^{-1} u_{i}+\sum_{j=0}^{\infty} \alpha^{j} \varepsilon_{i, t-j} \]

因此，以 $u_{i}$ 为条件，$Y_{i t}$ 的均值和方差分别为 $(1-\alpha)^{-1} u_{i}$ 和 $\left(1-\alpha^{2}\right)^{-1} \sigma_{\varepsilon}^{2}$。 $k^{t h}$ 自相关（以 $u_{i}$ 为条件）为 $\alpha^{k}$。请注意，$u_{i}$ 中横截面变化的影响是改变平均值，而不是方差或序列相关性。这意味着，如果我们查看一组个体 $u_{i}$ 的 $Y_{i t}$ 对时间的时间序列图，则序列 $u_{i}$ 将具有不同的均值，但具有相似的方差和序列相关性。

与时间序列数据的情况一样，序列相关性（大 $\alpha$ ）可以代表其他因素，例如时间趋势。因此，在应用中，包含时间效应以消除虚假串行相关性通常很有用。

17.37 固定效应估计的偏差

为了估计面板自回归 (17.81)，使用固定效应（内部）估计器似乎很自然。事实上，内变换消除了个体效应 $u_{i}$。问题在于，within 运算符会引起 AR(1) 滞后和误差之间的相关性。结果是，当 $T$ 固定时，组内估计器的系数不一致。 Nickell (1981) 中有详尽的解释。我们在本节中重点描述 AR(1) 模型 (17.82) 的基本问题。

将 inside 运算符应用到 (17.82) 我们得到

\[ \dot{Y}_{i t}=\alpha \dot{Y}_{i t-1}+\dot{\varepsilon}_{i t} \]

为 $t \geq 2$。正如预期的那样，个体效应被消除。困难在于$\mathbb{E}\left[\dot{Y}_{i t-1} \dot{\varepsilon}_{i t}\right] \neq 0$，因为$\dot{Y}_{i t-1}$和$\dot{\varepsilon}_{i t}$都是整个时间序列的函数。

为了在一个简单的例子中清楚地看到这一点，假设我们有一个带有 $T=3$ 的平衡面板。每个个体有两个观察对 $\left(Y_{i t}, Y_{i t-1}\right)$，因此内部估计量等于差分估计量。将差分运算符应用于 $t=3$ 的 (17.82) 我们发现

\[ \Delta Y_{i 3}=\alpha \Delta Y_{i 2}+\Delta \varepsilon_{i 3} . \]

由于滞后因变量和差异，每个人实际上只有一个观察结果。请注意，个体效应已被消除。

$\alpha$ 的固定效应估计量等于应用于 (17.84) 的最小二乘估计量，即

\[ \widehat{\alpha}_{\mathrm{fe}}=\left(\sum_{i=1}^{N} \Delta Y_{i 2}^{2}\right)^{-1}\left(\sum_{i=1}^{N} \Delta Y_{i 2} \Delta Y_{i 3}\right)=\alpha+\left(\sum_{i=1}^{N} \Delta Y_{i 2}^{2}\right)^{-1}\left(\sum_{i=1}^{N} \Delta Y_{i 2} \Delta \varepsilon_{i 3}\right) . \]

差分回归量和误差呈负相关。的确

\[ \begin{aligned} \mathbb{E}\left[\Delta Y_{i 2} \Delta \varepsilon_{i 3}\right] &=\mathbb{E}\left[\left(Y_{i 2}-Y_{i 1}\right)\left(\varepsilon_{i 3}-\varepsilon_{i 2}\right)\right] \\ &=\mathbb{E}\left[Y_{i 2} \varepsilon_{i 3}\right]-\mathbb{E}\left[Y_{i 1} \varepsilon_{i 3}\right]-\mathbb{E}\left[Y_{i 2} \varepsilon_{i 2}\right]+\mathbb{E}\left[Y_{i 1} \varepsilon_{i 2}\right] \\ &=0-0-\sigma_{\varepsilon}^{2}+0 \\ &=-\sigma_{\varepsilon}^{2} \end{aligned} \]

使用 $\operatorname{AR}(1)$ 模型的方差公式（假设 $|\alpha|<1)$ 我们计算 $\mathbb{E}\left[\left(\Delta Y_{i 2}\right)^{2}\right]=2 \sigma_{\varepsilon}^{2} /(1+$ $\alpha$ ）。由此可见 (17.84) 中 $\alpha$ 的固定效应估计量 $\widehat{\alpha}_{\mathrm{fe}}$ 的概率极限为

\[ \operatorname{plim}_{N \rightarrow \infty}\left(\widehat{\alpha}_{\mathrm{fe}}-\alpha\right)=\frac{\mathbb{E}\left[\Delta Y_{i 2} \Delta \varepsilon_{i 3}\right]}{\mathbb{E}\left[\left(\Delta Y_{i 2}\right)^{2}\right]}=-\frac{1+\alpha}{2} . \]

通常将 (17.85) 称为 $\widehat{\alpha}_{\text {fe }}$ 的“偏差”，尽管它在技术上是一个概率极限。

(17.85) 中发现的偏差很大。对于 $\alpha=0$，偏差为 $-1 / 2$，并随着 $\alpha \rightarrow 1$ 向 1 增加。因此，对于任何 $\alpha<1$，$\widehat{\alpha}_{\mathrm{fe}}$ 的概率极限都是负数！这是极端的偏见。

现在以 $T>3$ 为例。根据 Nickell (1981) 的表达式和一些代数，我们可以计算出 $|\alpha|<1$ 的固定效应估计量的概率极限为

\[ \operatorname{plim}_{N \rightarrow \infty}\left(\widehat{\alpha}_{\mathrm{fe}}-\alpha\right)=\frac{1+\alpha}{\frac{2 \alpha}{1-\alpha}-\frac{T-1}{1-\alpha^{T-1}}} . \]

由此可见，偏差的阶数为 $O(1 / T)$。

人们经常断言，如果 $T$ 足够大，则可以使用固定效应，例如$T \geq 30$。然而，从（17.86）我们可以计算出，对于$T=30$，当$\alpha=0.5$时，固定效应估计器的偏差为$-0.056$，当$\alpha=0.9$时，偏差为$-0.15$。对于 $T=60$ 和 $\alpha=0.9$，偏差为 $T$。这些幅度大得令人无法接受。这包括宏观面板中遇到的较长时间序列。因此，镍偏差问题适用于微型和宏观面板应用。

此分析的结论是，即使时间序列维度 $T$ 很大，固定效应估计量也不应用于具有滞后因变量的模型。

17.38 Anderson-Hsiao 估计器

Anderson 和 Hsiao (1982) 取得了重要突破，证明简单的工具变量估计量对于 (17.81) 的参数是一致的。

该方法首先通过 $t \geq p+1$ 的一阶差分 (17.81) 消除个体效应 $u_{i}$

\[ \Delta Y_{i t}=\alpha_{1} \Delta Y_{i, t-1}+\alpha_{2} \Delta Y_{i, t-2}+\cdots+\alpha_{p} \Delta Y_{i, t-p}+\Delta X_{i t}^{\prime} \beta+\Delta \varepsilon_{i t} . \]

这消除了个体效应$u_{i}$。挑战在于一阶差分会导致 $\Delta Y_{i t-1}$ 和 $\Delta \varepsilon_{i t}$ 之间的相关性：

\[ \mathbb{E}\left[\Delta Y_{i, t-1} \Delta \varepsilon_{i t}\right]=\mathbb{E}\left[\left(Y_{i, t-1}-Y_{i, t-2}\right)\left(\varepsilon_{i t}-\varepsilon_{i t-1}\right)\right]=-\sigma_{\varepsilon}^{2} . \]

其他回归量与 $\Delta \varepsilon_{i t}$ 不相关。对于 $s>1, \mathbb{E}\left[\Delta Y_{i t-s} \Delta \varepsilon_{i t}\right]=0$，并且当 $X_{i t}$ 是严格外生的 $\mathbb{E}\left[\Delta X_{i t} \Delta \varepsilon_{i t}\right]=0$ 时。

$\Delta Y_{i t-1}$ 和 $\Delta \varepsilon_{i t}$ 之间的相关性是内生性。解决内生性的一种方法是使用工具。 Anderson-Hsiao 指出 $Y_{i t-2}$ 是一个有效的工具，因为它与 $\Delta Y_{i, t-1}$ 相关但与 $\Delta \varepsilon_{i t}$ 不相关。

\[ \mathbb{E}\left[Y_{i, t-2} \Delta \varepsilon_{i t}\right]=\mathbb{E}\left[Y_{i, t-2} \varepsilon_{i t}\right]-\mathbb{E}\left[Y_{i, t-2} \varepsilon_{i t-1}\right]=0 . \]

Anderson-Hsiao 估计器是 IV，使用 $Y_{i, t-2}$ 作为 $\Delta Y_{i, t-1}$ 的工具。等效地，这是使用 $\left(Y_{i, t-2}, \ldots, Y_{i, t-p-1}\right)$ 工具对 $\left(\Delta Y_{i, t-1}, \ldots, \Delta Y_{i, t-p}\right)$ 进行的 IV。估算器需要 $T \geq p+2$。

为了证明这个估计量是一致的，为了简单起见，假设我们有一个包含 $T=3$、$p=1$ 的平衡面板，并且没有回归器。在这种情况下，Anderson-Hsiao IV 估计量为

\[ \widehat{\alpha}_{\mathrm{iv}}=\left(\sum_{i=1}^{N} Y_{i 1} \Delta Y_{i 2}\right)^{-1}\left(\sum_{i=1}^{N} Y_{i 1} \Delta Y_{i 3}\right)=\alpha+\left(\sum_{i=1}^{N} Y_{i 1} \Delta Y_{i 2}\right)^{-1}\left(\sum_{i=1}^{N} Y_{i 1} \Delta \varepsilon_{i 3}\right) . \]

假设 $\varepsilon_{i t}$ 是序列不相关的，(17.88) 显示 $\mathbb{E}\left[Y_{i 1} \Delta \varepsilon_{i 3}\right]=0$。一般来说，$\mathbb{E}\left[Y_{i 1} \Delta Y_{i 2}\right] \neq 0$。作为 $N \rightarrow \infty$

\[ \widehat{\alpha}_{\mathrm{iv}} \underset{p}{\longrightarrow} \alpha-\frac{\mathbb{E}\left[Y_{i 1} \Delta \varepsilon_{i 3}\right]}{\mathbb{E}\left[Y_{i 1} \Delta Y_{i 2}\right]}=\alpha . \]

因此 IV 估计量对于 $\alpha$ 是一致的。

Anderson-Hsiao IV 估计器依赖于两个关键假设。首先，工具的有效性（与方程误差的不相关性）依赖于正确指定动力学的假设，因此 $\varepsilon_{i t}$ 是序列不相关的。例如，许多应用程序使用 AR(1)。相反，如果真实模型是 $\operatorname{AR}(2)$，则 $Y_{i t-2}$ 不是有效的工具，并且 IV 估计将会有偏差。其次，工具的相关性（与内生回归量的相关性）需要 $\mathbb{E}\left[Y_{i 1} \Delta Y_{i 2}\right] \neq 0$。事实证明这是有问题的，并在第 17.40 节中进一步探讨。这些考虑因素表明估计器的有效性和准确性可能对这些未知特征敏感。

17.39 阿雷拉诺债券估计器

正交条件 (17.88) 是动态面板模型隐含的众多条件之一。事实上，所有滞后 $Y_{i t-2}, Y_{i t-3}, \ldots$ 都是有效的工具。如果 $T>p+2$ 这些可以用来潜在地提高估计效率。这首先由 Holtz-Eakin、Newey 和 Rosen (1988) 指出，并由 Arellano 和 Bond (1991) 进一步发展。

使用这些额外的工具有一个复杂之处，即每个时间段都有不同数量的工具。解决方案是将模型视为 $T$ 方程组，如第 17.18 节所示。

首先用矢量表示法编写模型会很有用。将差分回归量 $\left(\Delta Y_{i, t-1}, \ldots\right.$、$\Delta Y_{i, t-p}, \Delta X_{i t}^{\prime}$ 堆叠到矩阵 $\Delta \boldsymbol{X}_{i}$ 中，并将系数堆叠到向量 $\theta$ 中。我们可以将 (17.87) 写为 $\Delta \boldsymbol{Y}_{i}=$ $\Delta \boldsymbol{X}_{i} \theta+\Delta \boldsymbol{\varepsilon}_{i}$。将所有 $N$ 个体堆叠起来，可以写为 $\Delta \boldsymbol{Y}=\Delta \boldsymbol{X} \theta+\Delta \boldsymbol{\varepsilon}$。

对于 $t=p+2$ 期间，我们有 $p+k$ 有效工具 $\left[Y_{i 1} \ldots, Y_{i p}, \Delta X_{i, p+2}\right]$。对于 $t=p+3$ 期间，有 $p+1+k$ 有效工具 $\left[Y_{i 1} \ldots, Y_{i p+1}, \Delta X_{i, p+3}\right]$。对于 $t=p+4$ 期间，有 $p+2+k$ 工具。一般来说，对于任何 $t \geq p+2$ 都有 $t=p+2$ 工具 $t=p+2$。与 (17.53) 类似，我们可以将单个 $t=p+2$ 的工具矩阵定义为

\[ \boldsymbol{Z}_{i}=\left[\begin{array}{ccc} {\left[Y_{i 1}, \ldots, Y_{i p}, \Delta X_{i, p+2}^{\prime}\right]} & 0 & 0 \\ 0 & {\left[Y_{i 1}, \ldots, Y_{i, p+1}, \Delta X_{i, p+3}^{\prime}\right]} & \\ 0 & \ddots & 0 \\ & 0 & {\left[Y_{i 1}, Y_{i 2}, \ldots, Y_{i, T-2}, \Delta X_{i, T}^{\prime}\right]} \end{array}\right] . \]

这是 $(T-p-1) \times \ell$，其中 $\ell=k(T-p-1)+((T-2)(T-1)-(p-2)(p-1)) / 2$。该工具矩阵由数据集中可用的所有滞后值 $Y_{i, t-2}, Y_{i, t-3}, \ldots$ 以及差分严格外生回归量组成。

$\ell$ 矩条件是

\[ \mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime}\left(\Delta \boldsymbol{Y}_{i}-\Delta \boldsymbol{X}_{i} \alpha\right)\right]=0 \]

如果 $T>p+2$ 则 $\ell>p$ 并且模型被过度识别。定义矩条件的 $\ell \times \ell$ 协方差矩阵

\[ \Omega=\mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime} \Delta \boldsymbol{\varepsilon}_{i} \Delta \boldsymbol{\varepsilon}_{i}^{\prime} \boldsymbol{Z}_{i}\right] . \]

让 $\boldsymbol{Z}$ 表示堆叠到 $(T-p-1) N \times \ell$ 矩阵中的 $\boldsymbol{Z}_{i}$。 $\alpha$ 的高效 GMM 估计量为

\[ \widehat{\alpha}_{\mathrm{gmm}}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \Omega^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1}\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \Omega^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{Y}\right) . \]

如果错误 $\varepsilon_{i t}$ 是有条件同方差的，那么

\[ \Omega=\mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime} \boldsymbol{H} \boldsymbol{Z}_{i}\right] \sigma_{\varepsilon}^{2} \]

其中 $\boldsymbol{H}$ 在 (17.31) 中给出。在这种情况下设置

\[ \widehat{\Omega}_{1}=\sum_{i=1}^{N} \boldsymbol{Z}_{i}^{\prime} \boldsymbol{H} \boldsymbol{Z}_{i} \]

作为 $\Omega$ 的（缩放）估计。在这些假设下，渐进有效的 GMM 估计量是

\[ \widehat{\alpha}_{1}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1}\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{Y}\right) . \]

估计器 (17.91) 被称为一步 Arellano-Bond GMM 估计器。

假设误差 $\varepsilon_{i t}$ 同方差且序列不相关，$\widehat{\alpha}_{1}$ 的经典协方差矩阵估计量为

\[ \widehat{\boldsymbol{V}}_{1}^{0}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1} \widehat{\sigma}_{\varepsilon}^{2} \]

其中 $\widehat{\sigma}_{\varepsilon}^{2}$ 是单步残差 $\widehat{\boldsymbol{\varepsilon}}_{i}=\Delta \boldsymbol{Y}_{i}-\Delta \boldsymbol{X}_{i} \widehat{\alpha}$ 的样本方差。对于违反这些假设具有鲁棒性的协方差矩阵估计器是

\[ \widehat{\boldsymbol{V}}_{1}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1}\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \widehat{\Omega}_{2} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{1}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1} \]

在哪里

\[ \widehat{\Omega}_{2}=\sum_{i=1}^{N} \boldsymbol{Z}_{i}^{\prime} \widehat{\varepsilon}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \boldsymbol{Z}_{i} \]

是使用一步残差的 $\Omega$ 的（缩放的）集群鲁棒估计器。

允许异方差的渐近有效两步 GMM 估计器是

\[ \widehat{\alpha}_{2}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1}\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{Y}\right) . \]

估计器 (17.94) 被称为两步 Arellano-Bond GMM 估计器。 $\widehat{\alpha}_{2}$ 的适当鲁棒协方差矩阵估计器是

\[ \widehat{\boldsymbol{V}}_{2}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1}\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \widehat{\Omega}_{3} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1} \]

在哪里

\[ \widehat{\Omega}_{3}=\sum_{i=1}^{N} \boldsymbol{Z}_{i}^{\prime} \widehat{\varepsilon}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \boldsymbol{Z}_{i} \]

是使用两步残差 $\widehat{\boldsymbol{\varepsilon}}_{i}=\Delta \boldsymbol{Y}_{i}-\Delta \boldsymbol{X}_{i} \widehat{\alpha}_{2}$ 的 $\Omega$ 的（缩放）集群鲁棒估计器。渐进地，$\widehat{\boldsymbol{V}}_{2}$ 等价于

\[ \widetilde{\boldsymbol{V}}_{2}=\left(\Delta \boldsymbol{X}^{\prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \Delta \boldsymbol{X}\right)^{-1} . \]

GMM 估计器可以迭代直至收敛以产生迭代 GMM 估计器。

Arellano-Bond 估计器相对于 Anderson-Hsiao 估计器的优势在于，当 $T>$ $p+2$ 时，附加（过度识别）矩条件会减少估计器的渐近方差并稳定其性能。缺点是，当 $T$ 很大时，使用全套滞后作为工具可能会导致“许多弱工具”问题。建议的折衷方案是限制用作工具的滞后数量。

一步 Arellano-Bond 估计器的优点是权重矩阵 $\widehat{\Omega}_{1}$ 不依赖于残差，因此比两步权重矩阵 $\widehat{\Omega}_{2}$ 的随机性要低。这可以使单步估计器在小到中等样本中获得更好的性能，特别是当误差近似同方差时。两步估计器的优点是它实现了允许异方差性的渐近效率，因此预计在具有非同方差误差的大样本中表现更好。

总而言之，Arellano-Bond 估计器使用一组可用滞后 $Y_{i, t-2}, Y_{i, t-3}, \ldots$ 作为 $\Delta Y_{i, t-1}, \ldots, \Delta Y_{i, t-p}$ 的工具，将 GMM 应用于一阶微分方程 (17.87)。

Arellano-Bond 估计量可以在 Stata 中使用 xtabond 或 $x t d p d$ 命令获得。默认设置是一步估计器 (17.91) 和非稳健标准误 (17.92)。对于两步估计器和稳健标准误差，请使用两步 vce（稳健）选项。 Stata 中报告的标准误差基于 Windmeijer (2005) 对渐近估计量 (17.96) 的有限样本校正。实现了鲁棒协方差矩阵 (17.95) 和迭代 GMM 估计器。

17.40 弱仪器

Blundell 和 Bond (1998) 指出 Anderson-Hsiao 和 Arellano-Bond 估计器受到工具较弱的影响。这在带有 Anderson-Hsiao 估计器的 AR(1) 模型中最容易看出，该估计器使用 $Y_{i, t-2}$ 作为 $\Delta Y_{i, t-1}$ 的工具。 $\Delta Y_{i t-1}$ 的简化形式方程为

\[ \Delta Y_{i, t-1}=Y_{i, t-2} \gamma+v_{i t} . \]

简化形式系数 $\gamma$ 由投影定义。使用 $\Delta Y_{i, t-1}=(\alpha-1) Y_{i, t-2}+u_{i}+\varepsilon_{i, t-1}$ 和 $\mathbb{E}\left[Y_{i t-2} \varepsilon_{i, t-1}\right]=0$ 我们计算出

\[ \gamma=\frac{\mathbb{E}\left[Y_{i, t-2} \Delta Y_{i, t-1}\right]}{\mathbb{E}\left[Y_{i t-2}^{2}\right]}=(\alpha-1)+\frac{\mathbb{E}\left[Y_{i, t-2} u_{i}\right]}{\mathbb{E}\left[Y_{i, t-2}^{2}\right]} . \]

假设平稳性使得 (17.83) 成立，

\[ \mathbb{E}\left[Y_{i, t-2} u_{i}\right]=\mathbb{E}\left[\left(\frac{u_{i}}{1-\alpha}+\sum_{j=0}^{\infty} \alpha^{j} \varepsilon_{i, t-2-j}\right) u_{i}\right]=\frac{\sigma_{u}^{2}}{1-\alpha} \]

和

\[ \mathbb{E}\left[Y_{i, t-2}^{2}\right]=\mathbb{E}\left[\left(\frac{u_{i}}{1-\alpha}+\sum_{j=0}^{\infty} \alpha^{j} \varepsilon_{i t-2-j}\right)^{2}\right]=\frac{\sigma_{u}^{2}}{(1-\alpha)^{2}}+\frac{\sigma_{\varepsilon}^{2}}{\left(1-\alpha^{2}\right)} \]

其中 $\sigma_{u}^{2}=\mathbb{E}\left[u_{i}^{2}\right]$ 和 $\sigma_{\varepsilon}^{2}=\mathbb{E}\left[\varepsilon_{i t}^{2}\right]$。利用这些表达式和大量代数，Blundell 和 Bond (1998) 发现简化形式系数等于

\[ \gamma=(\alpha-1)\left(\frac{k}{k+\sigma_{u}^{2} / \sigma_{\varepsilon}^{2}}\right) \]

其中 $k=(1-\alpha) /(1+\alpha)$.如果 $\gamma$ 接近于零，则 Anderson-Hsiao 工具 $Y_{i, t-2}$ 很弱。从（17.97）我们看到，当$\alpha=1$（单位根）或$\sigma_{u}^{2} / \sigma_{\varepsilon}^{2}=\infty$（特殊效应相对于个体特定效应较小）时，$\gamma=0$。在任何一种情况下，系数 $\alpha$ 都未被识别。我们从之前对弱工具问题（第 12.36 节）的研究中知道，当 $\gamma$ 接近于零时，$\alpha$ 的识别能力较弱，估计器的表现将会很差。这意味着当自回归系数 $k=(1-\alpha) /(1+\alpha)$ 较大或个体特异性效应主导特殊效应时，这些估计量将难以识别，性能较差，并且传统的推理方法将产生误导。由于 $k=(1-\alpha) /(1+\alpha)$ 的值和相对方差先验未知，这意味着我们应该一般将此类估计量视为弱识别。

第 17.42 节讨论了一种具有改进性能的替代估计器。

17.41 具有预定回归器的动态面板

回归变量严格是外生的假设是有限制性的。一个限制性较小的假设是回归量是预先确定的。可以修改动态面板方法，通过使用滞后量作为工具来处理预定的回归量。

定义 17.2 回归量 $X_{i t}$ 是针对误差 $\varepsilon_{i t}$ 预先确定的，如果

\[ \mathbb{E}\left[X_{i, t-s} \varepsilon_{i t}\right]=0 \]

对于所有 $s \geq 0$。

严格外生回归量和预定回归量之间的区别在于，前者 (17.98) 对所有 $s$ 都成立，而不仅仅是 $s \geq 0$。解释具有预定回归量的回归模型的一种方法是，该模型是对回归量的完整过去历史的投影。

在 (17.98) 下，$X_{i t}$ 的领先可以与 $\varepsilon_{i t}$ 相关，即 $\mathbb{E}\left[X_{i t+s} \varepsilon_{i t}\right] \neq 0$ 与 $s \geq 1$ 相关，或者等效地 $X_{i t}$ 可以与 $\varepsilon_{i j}$ 的滞后相关，即 $\mathbb{E}\left[X_{i t} \varepsilon_{i t-s}\right] \neq 0$ 对于 $数学8$。这意味着 $X_{i t}$ 可以动态响应 $X_{i t}$ 的过去值，例如无限制向量自回归。

考虑差分方程 (17.87)

\[ \Delta Y_{i t}=\alpha_{1} \Delta Y_{i, t-1}+\alpha_{2} \Delta Y_{i, t-2}+\cdots+\alpha_{p} \Delta Y_{i, t-p}+\Delta X_{i t}^{\prime} \beta+\Delta \varepsilon_{i t} . \]

当回归量是预先确定的但不是严格外生的时，$X_{i t}$ 和 $\varepsilon_{i t}$ 不相关，但 $\Delta X_{i t}$ 和 $\Delta \varepsilon_{i t}$ 相关。看到这个，

\[ \begin{aligned} \mathbb{E}\left[\Delta X_{i t} \Delta \varepsilon_{i t}\right] &=\mathbb{E}\left[X_{i t} \varepsilon_{i t}\right]-\mathbb{E}\left[X_{i, t-1} \varepsilon_{i t}\right]-\mathbb{E}\left[X_{i t} \varepsilon_{i, t-1}\right]+\mathbb{E}\left[X_{i, t-1} \varepsilon_{i, t-1}\right] \\ &=-\mathbb{E}\left[X_{i t} \varepsilon_{i, t-1}\right] \neq 0 . \end{aligned} \]

这意味着如果我们将 $\Delta X_{i t}$ 视为外生的，则系数估计将会有偏差。

为了解决相关性问题，我们可以使用 $\Delta X_{i t}$ 的工具。有效的工具是 $X_{i, t-1}$，因为它通常与 $\Delta X_{i t}$ 相关，但与 $\Delta \varepsilon_{i t}$ 不相关。事实上，对于任何 $s \geq 1$

\[ \mathbb{E}\left[X_{i, t-s} \Delta \varepsilon_{i t}\right]=\mathbb{E}\left[X_{i, t-s} \varepsilon_{i t}\right]-\mathbb{E}\left[X_{i, t-s} \varepsilon_{i, t-1}\right]=0 . \]

因此，Arellano 和 Bond (1991) 推荐工具集 $\left(X_{i 1}, X_{i 2}, \ldots, X_{i t-1}\right)$。当时间段数量较多时，建议限制仪器滞后的数量，以避免出现许多弱仪器问题。从代数上来说，GMM 估计与第 17.39 节中描述的估计器相同，只是工具矩阵 (17.89) 被修改为

为了了解模型是如何识别的，我们检查回归量的简化形式方程。对于 $t=p+2$ 并使用第一个滞后作为工具，简化形式为

\[ \Delta X_{i t}=\gamma_{1} Y_{i, t-2}+\Gamma_{2} X_{i, t-1}+\zeta_{i t} . \]

如果 $\Gamma_{2}$ 为满秩，则模型被识别。当 $X_{i t}$ 静止时，这是有效的（通常）。然而，当 $X_{i t}$ 具有单位根时，识别失败。这表明当预定的回归量高度持久时，模型将被弱识别。

该方法概括为处理预定回归量的多个滞后。要看到这一点，请将模型显式编写为

\[ Y_{i t}=\alpha_{1} Y_{i, t-1}+\cdots+\alpha_{p} Y_{i, t-p}+X_{i t}^{\prime} \beta_{1}+\cdots+X_{i, t-q}^{\prime} \beta_{q}+u_{i}+\varepsilon_{i t} . \]

一阶差分模型是

\[ \Delta Y_{i t}=\alpha_{1} \Delta Y_{i, t-1}+\cdots+\alpha_{p} \Delta Y_{i, t-p}+\Delta X_{i t}^{\prime} \beta_{1}+\cdots+\Delta X_{i, t-q}^{\prime} \beta_{q}+\Delta \varepsilon_{i t} . \]

回归器的足够工具集是 $\left(X_{i t-1}, \Delta X_{i, t-1}, \ldots, \Delta X_{i, t-q}\right)$ 或等效的 $\left(X_{i, t-1}, X_{i, t-2}, \ldots, X_{i, t-q-1}\right)$。

在许多情况下，假设 $X_{i t-1}$ 是预先确定的而不是 $X_{i t}$ 更合理，因为 $X_{i t}$ 和 $\varepsilon_{i t}$ 可能是内生的。例如，这是向量自回归中的标准假设。在这种情况下，估计方法被修改为使用工具 $\left(X_{i, t-2}, X_{i, t-3}, \ldots, X_{i, t-q-1}\right)$。虽然这削弱了外生性假设，但它也削弱了工具集，因为现在简化形式使用第二个滞后 $X_{i, t-2}$ 来预测 $\Delta X_{i t}$。

将回归量视为预先确定的（而不是严格外生的）所获得的优点是，它大大放松了动态假设。否则，由于内生性，参数估计将不一致。

将回归量视为预定的主要缺点是，它大大降低了识别的强度，特别是当预定回归量高度持久时。

在 Stata 中，xtabond 命令默认将独立回归量视为严格外生的。要将回归量视为预先确定的，请使用选项 pre。默认情况下，所有回归器滞后都用作工具，但如果指定，可以限制数量。

17.42 布伦德尔债券估计器

Arellano 和 Bover (1995) 以及 Blundell 和 Bond (1998) 引入了一组正交条件，可以减少 $17.40$ 节中讨论的弱仪器问题，并提高有限样本中的性能。

考虑没有回归变量的水平 AR(1) 模型 (17.82)。回想一下，最小二乘（合并）回归是不一致的，因为回归量 $Y_{i, t-1}$ 与误差 $u_{i}$ 相关。这就提出了一个问题：是否有一种工具 $Z_{i t}$ 可以解决这个问题，即 $Z_{i t}$ 与 $Y_{i, t-1}$ 相关但与 $u_{i t}+\varepsilon_{i t}$ 不相关？ Blundell-Bond 提出了工具 $\Delta Y_{i, t-1}$。显然，$\Delta Y_{i, t-1}$ 和 $Y_{i, t-1}$ 相关，因此 $Y_{i, t-1}$ 满足相关条件。此外，当后者串行不相关时，$Y_{i, t-1}$ 与特殊错误$Y_{i, t-1}$ 不相关。因此，布伦德尔-邦德工具的关键在于是否

\[ \mathbb{E}\left[\Delta Y_{i t-1} u_{i}\right]=0 . \]

Blundell 和 Bond (1998) 表明 (17.100) 的充分条件是

\[ \mathbb{E}\left[\left(Y_{i 1}-\frac{u_{i}}{1-\alpha}\right) u_{i}\right]=0 . \]

回想一下，$u_{i} /(1-\alpha)$ 是平稳状态下 $Y_{i t}$ 的条件均值。条件 (17.101) 指出初始条件 $Y_{i 1}$ 与该条件均值的偏差与个体效应 $u_{i}$ 不相关。条件 (17.101) 隐含着平稳性，但稍弱。

为了看出 (17.101) 蕴涵 (17.100)，通过对 (17.87) 应用递归，我们发现

\[ \Delta Y_{i, t-1}=\alpha^{t-3} \Delta Y_{i 2}+\sum_{j=0}^{t-3} \alpha^{j} \Delta \varepsilon_{i, t-1-j} . \]

还，

\[ \Delta Y_{i 2}=(\alpha-1) Y_{i 1}+u_{i}+\varepsilon_{i 2}=(\alpha-1)\left(Y_{i 1}-\frac{u_{i}}{1-\alpha}\right)+\varepsilon_{i 2} . \]

因此

\[ \begin{aligned} \mathbb{E}\left[\Delta Y_{i, t-1} u_{i}\right] &=\mathbb{E}\left[\left(\alpha^{t-3}(\alpha-1)\left(Y_{i 1}-\frac{u_{i}}{1-\alpha}\right)+\alpha^{t-3} \varepsilon_{i 2}+\sum_{j=0}^{t-3} \alpha^{j} \Delta \varepsilon_{i, t-1-j}\right) u_{i}\right] \\ &=\alpha^{t-3}(\alpha-1) \mathbb{E}\left[\left(Y_{i 1}-\frac{u_{i}}{1-\alpha}\right) u_{i}\right] \\ &=0 \end{aligned} \]

如所声称的，根据(17.101)。

现在考虑具有预定回归量的完整模型 (17.81)。考虑回归量与个体效应具有恒定相关性的假设

\[ \mathbb{E}\left[X_{i t} u_{i}\right]=\mathbb{E}\left[X_{i s} u_{i}\right] \]

对于所有 $s$。这意味着

\[ \mathbb{E}\left[\Delta X_{i t} u_{i}\right]=0 \]

这意味着差分预定回归量 $\Delta X_{i t}$ 也可以用作水平方程的工具。

使用 (17.100) 和 (17.102) Blundell 和 Bond 提出以下矩条件进行 GMM 估计

\[ \begin{gathered} \mathbb{E}\left[\Delta Y_{i, t-1}\left(Y_{i t}-\alpha_{1} Y_{i, t-1}-\cdots-\alpha_{p} Y_{i, t-p}-X_{i t}^{\prime} \beta\right)\right]=0 \\ \mathbb{E}\left[\Delta X_{i, t}\left(Y_{i t}-\alpha_{1} Y_{i, t-1}-\cdots-\alpha_{p} Y_{i, t-p}-X_{i t}^{\prime} \beta\right)\right]=0 \end{gathered} \]

为 $t=p+2, \ldots, T$。请注意，这些用于水平（无差分）方程，而 Arellano-Bond (17.90) 矩用于差分方程 (17.87)。如果我们设置$\boldsymbol{Z}_{2 i}=\operatorname{diag}\left(\Delta Y_{i 2}, \ldots, \Delta Y_{i T-1}, \Delta X_{i 3}, \ldots, \Delta X_{i T}\right)$，我们可以用向量表示法写出(17.103)-(17.104)。那么 (17.103)-(17.104) 等于

\[ \mathbb{E}\left[\boldsymbol{Z}_{2 i}\left(\boldsymbol{Y}_{i}-\boldsymbol{X}_{i} \theta\right)\right]=0 . \]

Blundell 和 Bond 提议将 $\ell$ Arellano-Bond 矩与水平矩结合起来。这可以通过叠加力矩条件 (17.90) 和 (17.105) 来完成。回想一下 $17.39$ 节中的变量 $\Delta \boldsymbol{Y}_{i}, \Delta \boldsymbol{X}_{i}$ 和 $\boldsymbol{Z}_{i}$。定义堆叠变量 $\overline{\boldsymbol{Y}}_{i}=\left(\Delta \boldsymbol{Y}_{i}^{\prime}, \boldsymbol{Y}_{i}^{\prime}\right)^{\prime}, \overline{\boldsymbol{X}}_{i}=\left(\Delta \boldsymbol{X}_{i}^{\prime}, \boldsymbol{X}_{i}^{\prime}\right)^{\prime}$ 和 $\overline{\boldsymbol{Z}}_{i}=$ $\operatorname{diag}\left(\boldsymbol{Z}_{i}, \boldsymbol{Z}_{2 i}\right)$。堆积矩条件为

\[ \mathbb{E}\left[\overline{\boldsymbol{Z}}_{i}\left(\overline{\boldsymbol{Y}}_{i}-\overline{\boldsymbol{X}}_{i} \theta\right)\right]=0 . \]

Blundell-Bond 估计量是通过将 GMM 应用于该方程来找到的。他们称之为系统 GMM 估计器。令 $\overline{\boldsymbol{Y}}, \overline{\boldsymbol{X}}$ 和 $\overline{\boldsymbol{Z}}$ 表示堆叠成矩阵的 $\overline{\boldsymbol{Y}}_{i}, \overline{\boldsymbol{X}}_{i}$ 和 $\overline{\boldsymbol{Z}}_{i}$。定义 $\overline{\boldsymbol{H}}=\operatorname{diag}\left(\boldsymbol{H}, \boldsymbol{I}_{T-2}\right)$ 其中 $\boldsymbol{H}$ 来自 (17.31) 并设置

\[ \widehat{\Omega}_{1}=\sum_{i=1}^{N} \overline{\boldsymbol{Z}}_{i}^{\prime} \overline{\boldsymbol{Z Z}}_{i} . \]

Blundell-Bond 一步 GMM 估计量为

\[ \widehat{\theta}_{1}=\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{Y}}\right) . \]

系统残差为 $\widehat{\boldsymbol{\varepsilon}}_{i}=\overline{\boldsymbol{Y}}_{i}-\overline{\boldsymbol{X}}_{i} \widehat{\theta}_{1}$。稳健的协方差矩阵估计器是

\[ \widehat{\boldsymbol{V}}_{1}=\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \widehat{\Omega}_{2} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{1}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1} \]

在哪里

\[ \widehat{\Omega}_{2}=\sum_{i=1}^{N} \overline{\boldsymbol{Z}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \overline{\boldsymbol{Z}}_{i} . \]

Blundell-Bond 两步 GMM 估计量为

\[ \widehat{\theta}_{2}=\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{Y}}\right) . \]

两步系统残差为 $\widehat{\boldsymbol{\varepsilon}}_{i}=\overline{\boldsymbol{Y}}_{i}-\overline{\boldsymbol{X}}_{i} \widehat{\theta}_{2}$。稳健的协方差矩阵估计器是

\[ \widehat{\boldsymbol{V}}_{2}=\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1}\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \widehat{\Omega}_{3} \overline{\boldsymbol{Z}} \widehat{\Omega}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1} \]

在哪里

\[ \widehat{\Omega}_{3}=\sum_{i=1}^{N} \overline{\boldsymbol{Z}}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \overline{\boldsymbol{Z}}_{i} . \]

渐进地，$\widehat{\boldsymbol{V}}_{2}$ 等价于

\[ \widetilde{\boldsymbol{V}}_{2}=\left(\overline{\boldsymbol{X}}^{\prime} \overline{\boldsymbol{Z}} \widehat{\Omega}_{2}^{-1} \overline{\boldsymbol{Z}}^{\prime} \overline{\boldsymbol{X}}\right)^{-1} . \]

GMM 估计器可以迭代直至收敛以产生迭代 GMM 估计器。

Blundell 和 Bond (1998) 报告的模拟实验表明，他们的系统 GMM 估计器的性能明显优于 Arellano-Bond 估计器，特别是当 $\alpha$ 接近 1 或方差比 $\sigma_{u}^{2} / \sigma_{\varepsilon}^{2}$ 很大时。解释是，在这些情况下，正交条件 (17.103) 不会遇到弱仪器问题。

Blundell-Bond 估计器的优点在于，当后者弱识别时，相对于 Arellano-Bond 估计器，添加的正交条件 (17.103) 大大提高了性能。 Blundell-Bond 估计器的缺点是其正交性条件由平稳性条件 (17.101) 证明是合理的，违反后者可能会导致估计偏差。

一步与两步 Blundell-Bond 估计器的优点和缺点与第 17.39 节中描述的 Arellano-Bond 估计器相同。另外，正如那里所描述的，当 $T$ 很大时，可能需要限制用作工具的滞后数量，以避免许多弱工具问题。

Blundell-Bond 估计量可以在 Stata 中使用 xtdpdsys 或 xtdpd 命令获得。默认设置是一步估计器 (17.106) 和非稳健标准误差。对于两步估计器和稳健标准误差，请使用两步 vce（稳健）选项。 Stata 标准误差是 Windmeijer (2005) 对渐近估计 (17.110) 的有限样本修正。实现了鲁棒协方差矩阵估计器 (17.109) 和迭代 GMM 估计器。

17.43 正向正交变换

Arellano 和 Bover (1995) 提出了一种替代变换，它消除了个体特定效应，并且可能在动态面板模型中具有优势。前向正交变换为

\[ Y_{i t}^{*}=c_{i t}\left(Y_{i t}-\frac{1}{T_{i}-t}\left(Y_{i, t+1}+\cdots+Y_{i T_{i}}\right)\right) \]

其中 $c_{i t}^{2}=\left(T_{i}-t\right) /\left(T_{i}-t+1\right)$.这可以应用于除最终观察（丢失）之外的所有观察。本质上，$Y_{i t}^{*}$ 从 $Y_{i t}$ 中减去剩余值的平均值，然后重新调整比例，以便在同方差假设下方差保持不变。变换 (17.111) 最初是由 Hayashi 和 Sims (1983) 针对时间序列观测提出的。

在个人层面，这可以写为 $\boldsymbol{Y}_{i}^{*}=\boldsymbol{A}_{i} \boldsymbol{Y}_{i}$，其中 $\boldsymbol{A}_{i}$ 是 $\left(T_{i}-1\right) \times T_{i}$ 正交偏差算子

\[ \boldsymbol{A}_{i}=\operatorname{diag}\left(\sqrt{\frac{T_{i}-1}{T_{i}}}, \ldots, \sqrt{\frac{1}{2}}\right)\left[\begin{array}{ccccccc} 1 & -\frac{1}{T_{i}-1} & -\frac{1}{T_{i}-1} & \cdots & -\frac{1}{T_{i}-1} & -\frac{1}{T_{i}-1} & -\frac{1}{T_{i}-1} \\ 0 & 1 & -\frac{1}{T_{i}-2} & \cdots & -\frac{1}{T_{i}-2} & -\frac{1}{T_{i}-2} & -\frac{1}{T_{i}-2} \\ \vdots & \vdots & \vdots & & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & 1 & -\frac{1}{2} & -\frac{1}{2} \\ 0 & 0 & 0 & \cdots & 0 & -1 & 1 \end{array}\right] . \]

矩阵 $\boldsymbol{A}_{i}$ 的重要属性是 $\boldsymbol{A}_{i} \mathbf{1}_{i}=0$ （因此它消除了个体影响）、$\boldsymbol{A}_{i}^{\prime} \boldsymbol{A}_{i}=\boldsymbol{M}_{i}$ 和 $\boldsymbol{A}_{i} \boldsymbol{A}_{i}^{\prime}=\boldsymbol{I}_{T_{i}-1}$。这些可以通过直接乘法来验证。

将变换 $\boldsymbol{A}_{i}$ 应用于 (17.81) 我们得到

\[ Y_{i t}^{*}=\alpha_{1} Y_{i, t-1}^{*}+\cdots+\alpha_{p} Y_{i, t-p}^{*}+X_{i t}^{* \prime} \beta+\varepsilon_{i t}^{*} . \]

为 $t=p+1, \ldots, T-1$。当 $T=3$ 时，这相当于一阶差分 (17.87)，但对于 $T>3$ 则不同。

变换方程 (17.112) 的特殊之处在于，假设 $\varepsilon_{i t}$ 是序列不相关且同方差的，则误差向量 $\boldsymbol{\varepsilon}_{i}^{*}$ 具有方差 $\sigma_{\varepsilon}^{2} \boldsymbol{A}_{i} \boldsymbol{A}_{i}^{\prime}=\sigma_{\varepsilon}^{2} \boldsymbol{I}_{T_{i}-1}$。这意味着 $\varepsilon_{i}^{*}$ 具有与 $\varepsilon_{i}$ 相同的协方差结构。因此，正交变换算子消除了固定效应，同时保留了协方差结构。这与 (17.87) 形成对比，(17.87) 具有序列相关误差 $\Delta \varepsilon_{i t}$。

转换后的误差 $\varepsilon_{i t}^{*}$ 是 $\varepsilon_{i t}, \varepsilon_{i t+1}, \ldots, \varepsilon_{i T}$ 的函数。因此有效的工具是 $Y_{i t-1}, Y_{i t-2}, \ldots$。在严格外生回归量的情况下，使用 (17.89) 中的工具矩阵 $Z_{i}$ 或在具有预定回归量的情况下 (17.99)，$\ell$ 矩条件可以使用矩阵符号写为

\[ \mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime}\left(\boldsymbol{Y}_{i}^{*}-\boldsymbol{X}_{i}^{*} \theta\right)\right]=0 . \]

定义 $\ell \times \ell$ 协方差矩阵

\[ \Omega=\mathbb{E}\left[Z_{i}^{\prime} \varepsilon_{i}^{*} \varepsilon_{i}^{* \prime} Z_{i}\right] \]

如果错误 $\varepsilon_{i t}$ 是有条件同方差的，那么 $\Omega=\mathbb{E}\left[\boldsymbol{Z}_{i}^{\prime} \boldsymbol{Z}_{i}\right] \sigma_{\varepsilon}^{2}$ 是同方差的。因此，渐近有效的 GMM 估计器是使用 $Z_{i}$ 作为工具将 2SLS 应用于正交方程。用矩阵表示法来说，

\[ \widehat{\theta}_{1}=\left(\boldsymbol{X}^{* \prime} \boldsymbol{Z}\left(\boldsymbol{Z}^{\prime} \boldsymbol{Z}\right)^{-1} \boldsymbol{Z}^{\prime} \boldsymbol{X}^{*}\right)^{-1} \boldsymbol{Y}^{*} \text {. } \]

这是一步 GMM 估计器。

给定残差 $\widehat{\boldsymbol{\varepsilon}}_{i}=\boldsymbol{Y}_{i}^{*}-\boldsymbol{X}_{i}^{*} \widehat{\theta}_{1}$，对异方差和任意序列相关具有鲁棒性的两步 GMM 估计器为

\[ \widehat{\theta}_{2}=\left(\boldsymbol{X}^{* \prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \boldsymbol{X}^{*}\right)^{-1}\left(\boldsymbol{X}^{* \prime} \boldsymbol{Z} \widehat{\Omega}_{2}^{-1} \boldsymbol{Z}^{\prime} \boldsymbol{Y}^{*}\right) \]

在哪里

\[ \widehat{\Omega}_{2}=\sum_{i=1}^{N} \boldsymbol{Z}_{i}^{\prime} \widehat{\boldsymbol{\varepsilon}}_{i} \widehat{\boldsymbol{\varepsilon}}_{i}^{\prime} \boldsymbol{Z}_{i} . \]

$\widehat{\theta}_{1}$ 和 $\widehat{\theta}_{2}$ 的标准误差可以使用集群稳健方法获得。

前向正交化可能比一阶差分具有优势。首先，(17.112) 中的方程误差在 i.i.d. 下具有标量协方差结构。特殊误差有望提高估计精度。它还意味着一步估计器是 2SLS 而不是 GMM。其次，虽然在正向正交化后尚未对估计量的弱工具属性进行正式分析，但似乎如果 $T>p+2$ 该方法受弱工具的影响小于一阶差分。前向正交化的缺点是它对早期观测值与后期观测值的处理不对称，与一阶差分相比，其研究较少，并且不适用于几种流行的估计方法。

Stata 命令 xtdpd 包括前向正交化作为选项，但当包括水平（Blundell-Bond）工具或数据中存在间隙时则不包括。另一种选择是可下载的 Stata 软件包 $x$ tabond2。

17.44 实证说明

我们用投资模型（17.3）来说明动态面板方法。表 17.3 列出了两个模型的估计值。两者均由 Blundell-Bond 两步 GMM 估计，其中滞后 2 至 6 作为工具、集群鲁棒权重矩阵和集群标准误差。

第一列介绍 AR(2) 模型的估计。估计结果表明，该序列具有适度的正序列相关性，但由于 AR(2) 系数接近于零，因此似乎可以很好地建模为 AR(1)。这种序列相关模式与跨度两年的投资项目的存在是一致的。

第二列介绍了不包括交易指标的投资回归动态版本 (17.3) 的估计。因变量和每个回归量包括两个滞后。与将回归变量视为严格外生的固定效应回归相比，回归变量被视为预先确定的。回归量与因变量不同时，而是滞后一期和两期。这样做是为了使它们成为有效的预定变量。同期变量可能是内生的，因此不应被视为预先确定的。

表 $17.3$ 第二列中的估计值补充了之前的结果。证据表明，投资具有中等程度的序列依赖性，与Q的第一滞后呈正相关，与滞后债务呈负相关。投资似乎与现金流的变化而不是水平呈正相关。因此，$t-1$ 年现金流的增加导致 $t$ 年的投资。表 17.3：动态投资方程的估计

	AR(2)	AR(2) with Regressors
$I_{i t-1}$	$0.3191$	$0.2519$
	$(0.0172)$	$(0.0220)$
$I_{i t-2}$	$0.0309$	$0.0137$
	$(0.0112)$	$(0.0125)$
$Q_{i t-1}$		$0.0018$
		$(0.0007)$
$Q_{i t-2}$		$-0.0000$
		$(0.0003)$
$D_{i t-1}$		$-0.0154$
		$(0.0058)$
$D_{i t-2}$		$-0.0043$
		$(0.0054)$
$C F_{i t-1}$		$0.0400$
		$(0.0091)$
$C F_{i t-2}$		$-0.0290$
		$(0.0051)$

两步 GMM 估计。括号中的集群稳健标准错误。

所有回归都包含时间效应。 GMM 工具包括滞后 2 到 6。

17.45 练习

17.46 练习17.1

显示 (17.11) 和 (17.12)。
显示(17.13)。

练习 17.2 $\mathbb{E}\left[\varepsilon_{i t} \mid X_{i t}\right]=0$ 是否足以使 $\widehat{\beta}_{\mathrm{fe}}$ 对 $\beta$ 无偏？解释为什么能或者为什么不能。

练习17.3 证明$\operatorname{var}\left[\dot{X}_{i t}\right] \leq \operatorname{var}\left[X_{i t}\right]$

练习17.4 显示（17.24）。

练习17.5 显示（17.28）。

练习17.6 证明当$T=2$ 时差分估计量等于固定效应估计量。

练习 17.7 在 $17.14$ 节中，描述了如何使用残差估计个体效应方差 $\sigma_{u}^{2}$。仅使用固定效应误差方差 $\widehat{\sigma}_{\varepsilon}^{2}$ 和水平误差方差 $\widehat{\sigma}_{e}^{2}=n^{-1} \sum_{i=1}^{N} \sum_{t \in S_{i}} \widehat{e}_{i t}^{2}$ 开发 $\sigma_{u}^{2}$ 的替代估计器，其中 $\widehat{e}_{i t}=Y_{i t}-X_{i t}^{\prime} \widehat{\beta}_{\text {fe }}$ 是根据水平变量计算的。

练习17.8 验证(17.37)中定义的$\widehat{\sigma}_{\varepsilon}^{2}$对于(17.18)、(17.25)和(17.26)下的$\sigma_{\varepsilon}^{2}$是无偏的。练习 17.9 为差分估计器 $\widehat{\beta}_{\Delta}$ 开发定理 $17.2$ 的一个版本。你能弱化假设17.2.3吗？陈述一个足以满足渐近正态性的适当版本。

练习 17.10 显示 (17.57)。

17.47 练习$17.11$

对于(17.59)中定义的$\widehat{\sigma}_{i}^{2}$，显示$\mathbb{E}\left[\widehat{\sigma}_{i}^{2} \mid \boldsymbol{X}_{i}\right]=\bar{\sigma}_{i}^{2}$
对于 (17.58) 中定义的 $\widetilde{\boldsymbol{V}}_{\mathrm{fe}}$，显示 $\mathbb{E}\left[\widetilde{\boldsymbol{V}}_{\mathrm{fe}} \mid \boldsymbol{X}\right]=\boldsymbol{V}_{\mathrm{fe}}$。

17.48 练习$17.12$

显示 (17.61).\
显示 (17.62).\
对于 (17.60) 中定义的 $\widetilde{\boldsymbol{V}}_{\mathrm{fe}}$，显示 $\mathbb{E}\left[\widetilde{\boldsymbol{V}}_{\mathrm{fe}} \mid \boldsymbol{X}\right]=\boldsymbol{V}_{\mathrm{fe}}$。

练习17.13 采用固定效应模型$Y_{i t}=X_{i t} \beta_{1}+X_{i t}^{2} \beta_{2}+u_{i}+\varepsilon_{i t}$。研究人员通过首先获得变换后的 $\dot{Y}_{i t}$ 和 $\dot{X}_{i t}$ 内的值，然后在 $\dot{X}_{i t}$ 和 $\dot{X}_{i t}^{2}$ 上回归 $\dot{Y}_{i t}$ 来估计模型。估算方法是否正确？如果不是，请描述正确的固定效应估计器。

练习 17.14 在 $17.33$ 节中，验证在刚刚确定的情况下，2SLS 估计器 $\widehat{\beta}_{2 \text { sls }}$ 按声明进行简化：$\widehat{\beta}_{1}$ 和 $\widehat{\beta}_{2}$ 是固定效应估计器。 $\widehat{\gamma}_{1}$ 和 $\widehat{\gamma}_{2}$ 等于使用 $17.33$ 作为 $17.33$ 工具对 $Z_{1}$ 和 $Z_{2}$ 进行 $\widehat{\boldsymbol{u}}$ 回归的 2SLS 估计器。

练习17.15 在本练习中，您将复制并扩展Arellano 和Bond (1991) 以及Blundell 和Bond (1998) 中报告的实证工作。 Arellano-Bond 从 140 家英国公司的不平衡小组收集了 1976 年至 1984 年期间 1031 个观察结果的数据集，并位于教科书网页上的数据文件 AB1991 中。我们将使用的变量是对数就业 $(N)$、对数实际工资 $(W)$ 和对数资本 $(K)$。有关定义，请参阅描述文件。

使用具有聚类标准误差的 Arellano-Bond 一步 GMM 估计面板 AR(1) $K_{i t}=\alpha K_{i t-1}+u_{i}+v_{t}+\varepsilon_{i t}$。请注意，该模型包括年份固定效应。
使用带有聚类标准误差的 Blundell-Bond 一步 GMM 重新估计。
解释估计值的差异。

练习17.16 本练习使用与上一个问题相同的数据集。 Blundell 和 Bond (1998) 估计了对数就业 $N$ 对对数实际工资 $W$ 和对数资本 $K$ 的动态面板回归。以下规范 ${ }^{1}$ 使用 Arellano-Bond 一步估计器，将 $W_{i, t-1}$ 和 $K_{i, t-1}$ 视为预定值。

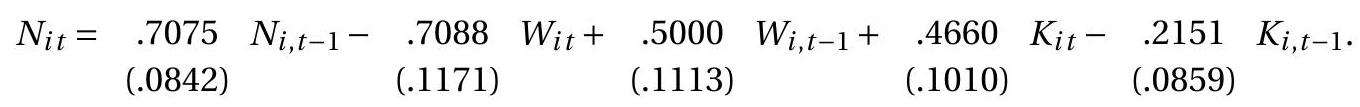
该方程还包括年份虚拟值，并且标准误差是聚集的。

${ }^{1}$ Blundell 和 Bond (1998)，表 4，第 3 栏。 (a) 使用 Arellano-Bond 一步估计器将 $W_{i t}$ 和 $K_{i t}$ 视为严格外生的估计 (17.114)。

估计 (17.114) 将 $W_{i, t-1}$ 和 $K_{i, t-1}$ 视为预定值以验证 (17.114) 中的结果。将回归变量视为严格外生变量与预先确定变量的估计之间有什么区别？
使用 Blundell-Bond 一步系统 GMM 估计器估计方程。
将 (17.114) 的系数估计解释为企业层面的劳动力需求方程。
描述如果您忘记使用聚类，对 (c) 部分中的 Blundell-Bond 估计的标准误差的影响。（您不必列出所有标准误差，但可以描述影响的程度。）

练习17.17 使用课本网页上的数据文件Invest 1993。您将估计面板 AR(1) $D_{i t}=\alpha D_{i, t-1}+u_{i}+\varepsilon_{i t}$ 的 $D=$ 债务/资产（这是数据文件中的 Debeta）。有关定义，请参阅描述文件。

使用具有聚类标准误差的 Arellano-Bond 两步 GMM 估计模型。
使用 Blundell-Bond 两步 GMM 重新估计。
试验您的结果，尝试两步与一步、AR(1) 与 AR(2)、用作工具的滞后数以及经典标准误与鲁棒标准误。是什么使得系数估计值差异最大？对于标准误？

练习17.18 使用课本网页上的数据文件Invest1993。您将估计模型

\[ D_{i t}=\alpha D_{i, t-1}+\beta_{1} I_{i, t-1}+\beta_{2} Q_{i, t-1}+\beta_{3} C F_{i, t-1}+u_{i}+\varepsilon_{i t} . \]

数据文件中的变量为 Debeta、inva、vala 和 $c f a$。有关定义，请参阅描述文件。

使用 Arellano-Bond 两步 GMM 估计上述回归，其中聚类标准误差将所有回归量视为预定值。
使用 Blundell-Bond 两步 GMM 重新估计，将所有回归量视为预定值。
试验您的结果，尝试两步与一步、用作工具的滞后数以及经典与稳健标准误差。是什么使得系数估计值差异最大？对于标准误？

Firm Code Number	Year	\(I_{i t}\)	\(\bar{I}_{i}\)	\(\dot{I}_{i t}\)	\(Q_{i t}\)	\(\bar{Q}_{i}\)	\(\dot{Q}_{i t}\)	\(\widehat{e}_{i t}\)
32	1970	\(0.122\)	\(0.155\)	\(-0.033\)	\(1.17\)	\(0.62\)	\(0.55\)	.
32	1971	\(0.092\)	\(0.155\)	\(-0.063\)	\(0.79\)	\(0.62\)	\(0.17\)	\(-0.005\)
32	1972	\(0.094\)	\(0.155\)	\(-0.061\)	\(0.91\)	\(0.62\)	\(0.29\)	\(-0.005\)
32	1973	\(0.116\)	\(0.155\)	\(-0.039\)	\(0.29\)	\(0.62\)	\(-0.33\)	\(0.014\)
32	1974	\(0.099\)	\(0.155\)	\(-0.057\)	\(0.30\)	\(0.62\)	\(-0.32\)	\(-0.002\)
32	1975	\(0.187\)	\(0.155\)	\(0.032\)	\(0.56\)	\(0.62\)	\(-0.06\)	\(0.086\)
32	1976	\(0.349\)	\(0.155\)	\(0.194\)	\(0.38\)	\(0.62\)	\(-0.24\)	\(0.248\)
32	1977	\(0.182\)	\(0.155\)	\(0.027\)	\(0.57\)	\(0.62\)	\(-0.05\)	\(0.081\)
209	1987	\(0.095\)	\(0.071\)	\(0.024\)	\(9.06\)	\(21.57\)	\(-12.51\)	.
209	1988	\(0.044\)	\(0.071\)	\(-0.027\)	\(16.90\)	\(21.57\)	\(-4.67\)	\(-0.244\)
209	1989	\(0.069\)	\(0.071\)	\(-0.002\)	\(25.14\)	\(21.57\)	\(3.57\)	\(-0.257\)
209	1990	\(0.113\)	\(0.071\)	\(0.042\)	\(25.60\)	\(21.57\)	\(4.03\)	\(-0.226\)
209	1991	\(0.034\)	\(0.071\)	\(-0.037\)	\(31.14\)	\(21.57\)	\(9.57\)	\(-0.283\)

	AR(2)	AR(2) with Regressors
\(I_{i t-1}\)	\(0.3191\)	\(0.2519\)
	\((0.0172)\)	\((0.0220)\)
\(I_{i t-2}\)	\(0.0309\)	\(0.0137\)
	\((0.0112)\)	\((0.0125)\)
\(Q_{i t-1}\)		\(0.0018\)
		\((0.0007)\)
\(Q_{i t-2}\)		\(-0.0000\)
		\((0.0003)\)
\(D_{i t-1}\)		\(-0.0154\)
		\((0.0058)\)
\(D_{i t-2}\)		\(-0.0043\)
		\((0.0054)\)
\(C F_{i t-1}\)		\(0.0400\)
		\((0.0091)\)
\(C F_{i t-2}\)		\(-0.0290\)
		\((0.0051)\)

17 面板数据

17.1 介绍

17.2 时间索引和不平衡面板

17.3 符号

17.4 汇总回归

17.5 单向错误组件模型

17.6 随机效应

17.7 固定效应模型

17.8 转型之内

17.9 固定效应估计器

17.10 差分估计器

17.11 虚拟变量回归

17.12 固定效应协方差矩阵估计

17.13 Stata 中的固定效应估计

17.14 估计器之间

17.15 可行的GLS

17.16 固定效应回归中的截距

17.17 固定效应的估计

17.18 固定效应的 GMM 解释

17.19 固定效应模型中的识别

17.20 固定效应估计量的渐近分布

17.21 不平衡面板的渐近分布

17.22 异方差-鲁棒协方差矩阵估计

17.23 异方差-稳健估计-不平衡情况

17.24 随机效应与固定效应的豪斯曼检验

17.25 随机效应还是固定效应？

17.26 时间趋势

17.27 双向误差分量

17.28 工具变量

17.29 工具变量的识别

17.30 固定效应 2SLS 估计器的渐近分布

17.31 线性高斯模

17.32 使用时不变回归器进行估计

17.33 豪斯曼泰勒模型

17.34 折刀协方差矩阵估计

17.35 面板引导程序

17.36 动态面板模型

17.37 固定效应估计的偏差

17.38 Anderson-Hsiao 估计器

17.39 阿雷拉诺债券估计器

17.40 弱仪器

17.41 具有预定回归器的动态面板

17.42 布伦德尔债券估计器

17.43 正向正交变换

17.44 实证说明

17.45 练习

17.46 练习17.1

17.47 练习\(17.11\)

17.48 练习\(17.12\)