第16章: 非平稳时间序列

16 非平稳时间序列

16.1 引言

在第 14 章的开头我们展示了一组经济时间序列。其中若干序列（实际 GDP、汇率、利率、原油价格）看起来并非平稳。在第 14.23 节我们介绍了非平稳的单位根过程，它是一个自回归过程且其自回归根等于 1。两组模拟例子的图形（图 14.5）展示了与这些经济时间序列类似的“游走”轨迹。这提示或许单位根自回归是描述这些序列的一个合理模型。本章我们将研究非平稳单位根时间序列的计量估计与推断。

16.2 部分和过程与函数型收敛

考虑多元随机游走

\[ Y_{t}=Y_{t-1}+e_{t} \]

其中 \(\left(e_{t}, \mathscr{F}_{t}\right)\) 是具有有限协方差矩阵 \(\Sigma\) 的向量鞅差序列（MDS）。回代可得 \(Y_{t}=Y_{0}+S_{t}\)，其中

\[ S_{t}=\sum_{i=1}^{t} e_{i} \]

是截至时间 \(t\) 的误差累积和。我们称 \(S_{t}\) 为部分和过程（partial sum process）。

时间索引 \(t\) 取自 0 到 \(n\)。写作 \(^{1} t=\lfloor n r\rfloor\)，使其成为样本量 \(n\) 的一部分 \(r\)。这使我们能够把 \(S_{\lfloor n r\rfloor}\) 写成 \(r\) 的函数。用 \(\sqrt{n}\) 进行标准化以稳定方差。由此定义标准化的部分和过程：

\[ S_{n}(r)=\frac{1}{\sqrt{n}} S_{\lfloor n r\rfloor}=\frac{1}{\sqrt{n}} \sum_{t=1}^{\lfloor n r\rfloor} e_{t} . \]

随机过程 \(S_{n}(r)\) 是时间序列 \(Y_{t}\) 的缩放版本，且是样本比例 \(r \in[0,1]\) 的函数。作为随机函数，它在任意有限 \(n\) 下都是具有 \(n\) 个跳点的阶梯函数。

考察 \(n\) 增大时 \(S_{n}(r)\) 的行为。它最大的离散跳跃等于 \(n^{-1 / 2} \max _{1 \leq t \leq n}\left\|e_{t}\right\|\)。定理 6.15 表明该量为 \(o_{p}(1)\)。这提示 \(S_{n}(r)\) 中的跳跃在渐近上消失。我们希望找到其渐近分布。我们预期其极限分布同样是一个随机过程。

^{1} 记号 \(\lfloor x\rfloor\) 表示“向下取整”。为此我们需要定义随机函数的渐近分布。主要工具是函数型中心极限定理（FCLT），它是经验过程理论的一部分（参见《Probability and Statistics for Economists》第 18 章）。事实表明，FCLT 依赖于我们如何度量两个函数之间的差异。最常用的度量是统一度量（uniform metric）。在从 \([0,1]\) 到 \(\mathbb{R}^{m}\) 的函数空间上，它定义为

\[ \rho\left(v_{1}, v_{2}\right)=\sup _{0 \leq r \leq 1}\left\|v_{1}(r)-v_{2}(r)\right\| . \]

随机过程的分布收敛（例如《Probability and Statistics for Economists》的定义 18.6）是相对于特定度量来定义的。虽然这里不重复细节，但关键结论是：连续性是相对于该度量来定义的，这会影响诸如连续映射定理等应用。

函数型中心极限定理（《Probability and Statistics for Economists》的定理 18.9）表明：当且仅当两条条件成立时，\(S_{n}(r) \underset{d}{\longrightarrow} S(r)\)（作为 \(r \in[0,1]\) 上的函数）：

1. \(S_{n}(r)\) 的有限维极限分布与 \(S(r)\) 的对应有限维分布一致；
2. \(S_{n}(r)\) 渐近等度连续（asymptotically equicontinuous）。

第一条意味着对任意固定的 \(r_{1}, \ldots, r_{m}\)，有 \(\left(S_{n}\left(r_{1}\right), \ldots, S_{n}\left(r_{m}\right)\right) \underset{d}{\longrightarrow}\left(S\left(r_{1}\right), \ldots, S\left(r_{m}\right)\right)\)。第二条在技术上要求 \(S_{n}(r)\) 在大样本下关于统一度量近似连续。

接下来刻画 \(S_{n}(r)\) 的极限分布。三个重要性质如下：

1. \(S_{n}(0)=0\)；
2. 对任意 \(r\)，\(S_{n}(r) \underset{d}{\longrightarrow} \mathrm{N}(0, r \Sigma)\)；
3. 当 \(r_{1}<r_{2}\) 时，\(S_{n}\left(r_{1}\right)\) 与 \(S_{n}\left(r_{2}\right)-S_{n}\left(r_{1}\right)\) 渐近独立。

第一条由定义即得。对第二条，令 \(N=\lfloor n r\rfloor\)。当 \(r>0\) 时，\(N \rightarrow \infty\) 随 \(n \rightarrow \infty\)。MDS 的 CLT（定理 14.11）推出

\[ S_{n}(r)=\sqrt{\frac{\lfloor n r\rfloor}{n}} \frac{1}{\sqrt{N}} \sum_{t=1}^{N} e_{t} \underset{d}{\longrightarrow} \sqrt{r} \mathrm{~N}(0, \Sigma)=\mathrm{N}(0, r \Sigma) \]

如所述。对第三条，由 \(e_{t}\) 为 MDS 可知 \(S_{n}\left(r_{1}\right)\) 与 \(S_{n}\left(r_{2}\right)-S_{n}\left(r_{1}\right)\) 不相关。类似的渐近论证可得它们联合渐近正态且协方差为零，因而渐近独立。

上述三个极限性质正是布朗运动定义的渐近版本。定义 16.1 向量布朗运动 \(B(r)\)（\(r \geq 0\)）由以下性质定义：

1. \(B(0)=0\)；
2. 对任意 \(r\)，\(B(r) \sim \mathrm{N}(0, r \Sigma)\)；
3. 对任意 \(r_{1} \leq r_{2}\)，\(B\left(r_{1}\right)\) 与 \(B\left(r_{2}\right)-B\left(r_{1}\right)\) 相互独立。

我们称 \(\Sigma\) 为 \(B(r)\) 的协方差矩阵。若 \(\Sigma=\boldsymbol{I}_{m}\)，则称 \(B(r)\) 为标准布朗运动，记为 \(W(r)\)。此时有 \(B(r)=\Sigma^{1 / 2} W(r)\)。

布朗运动 \(B(r)\) 以概率 1 连续，但处处不可微。在物理学中，布朗运动用于描述粒子的运动。关于悬浮在液体中的粒子所呈现的漂移性质，最早可追溯至罗马诗人卢克莱修（Lucretius，《宇宙的本性》，公元前 55 年）。该名称致敬了植物学家 Robert Brown 的开创性观测研究；数学过程中也常称为 Wiener 过程，以纪念 Norbert Wiener 的工作。

以上讨论表明，部分和过程 \(S_{n}(r)\) 的极限分布与布朗运动 \(B(r)\) 的性质一致。在第 16.22 节我们将证明 \(S_{n}(r)\) 渐近等度连续。结合 FCLT 可得 \(S_{n}(r)\) 按分布收敛到 \(B(r)\)。

定理 16.1 部分和过程的弱收敛 若 \(\left(e_{t}, \mathscr{F}_{t}\right)\) 是严格平稳、遍历的 MDS，且 \(\Sigma=\mathbb{E}\left[e_{t} e_{t}^{\prime}\right]<\infty\)，则作为 \(r \in[0,1]\) 上的函数，有 \(S_{n}(r) \underset{d}{\longrightarrow} B(r)\)，其中 \(B(r)\) 为协方差矩阵为 \(\Sigma\) 的布朗运动。

我们将在第 16.4 节将定理 16.1 推广至存在序列相关的情形。

16.3 Beveridge-Nelson 分解

上一小节聚焦于随机游走过程。更广义地，单位根过程是指具有单一单位根的自回归过程，这意味着差分过程 \(\Delta Y_{t}\) 存在序列相关但平稳。

Beveridge 和 Nelson (1981) 提出了将单位根过程分解为永久（随机游走）分量与暂时（平稳）分量的方法。这使得定理 16.1 能方便地推广以纳入序列相关。

回忆：平稳过程具有 Wold 表示 \(\Delta Y_{t}=\Theta(\mathrm{L}) e_{t}\)，其中 \(\Theta(z)=\sum_{j=0}^{\infty} \Theta_{j} z^{j}\)。假设 16.1：\(\Delta Y_{t}\) 严格平稳、无确定性成分、均值为零，且具有有限协方差矩阵 \(\Sigma\)。其 Wold 表示 \(\Delta Y_{t}=\Theta(\mathrm{L}) e_{t}\) 的系数满足

\[ \sum_{j=0}^{\infty}\left\|\sum_{\ell=j+1}^{\infty} \Theta_{\ell}\right\|<\infty . \]

该条件（16.1）强于绝对可和，但在 \(\Delta Y_{t}\) 由平稳 AR 过程生成时成立。它与自回归 Wold 表示（定理 14.19）所用条件相似。

考虑滞后多项式的分解：

\[ \Theta(z)=\Theta(1)+(1-z) \Theta^{*}(z) \]

其中 \(\Theta(1)=\sum_{\ell=0}^{\infty} \Theta_{\ell}\) 且 \(\Theta^{*}(z)\) 为滞后多项式

\[ \begin{aligned} \Theta^{*}(z) &=\sum_{j=0}^{\infty} \Theta_{j}^{*} z^{j} \\ \Theta_{j}^{*} &=-\sum_{\ell=j+1}^{\infty} \Theta_{\ell} . \end{aligned} \]

本节末我们将验证（16.2）—（16.4）。假设（16.1）与 \(\sum_{j=0}^{\infty}\left\|\Theta_{j}^{*}\right\|<\infty\) 等价，后者意味着 \(U_{t}=\Theta^{*}(\mathrm{~L}) e_{t}\) 收敛、严格平稳且遍历（定理 15.4）。

分解（16.2）意味着

\[ \Delta Y_{t}=\xi_{t}+U_{t}-U_{t-1} . \]

其中 \(\xi_{t}=\Theta(1) e_{t}\)。这把 \(\Delta Y_{t}\) 分解为创新 \(e_{t}\) 与过程 \(U_{t}\) 的一阶差分。对两边求和得

\[ Y_{t}=S_{t}+U_{t}+V_{0} \]

其中 \(S_{t}=\sum_{i=1}^{t} \xi_{t}\)，\(V_{0}=Y_{0}-U_{0}\)。这将单位根过程 \(Y_{t}\) 分解为随机游走 \(S_{t}\)、平稳过程 \(U_{t}\) 与初始条件 \(V_{0}\)。

据此有

\[ \begin{aligned} &\text { 定理 16.2 在假设 16.1 下，（16.2）—（16.4）成立，且 } \\ &\begin{array}{l} \sum_{j=0}^{\infty}\left\|\Theta_{j}^{*}\right\|<\infty \text { 。过程 } \Delta Y_{t} \text { 满足 } \\ \qquad \Delta Y_{t}=\xi_{t}+U_{t}-U_{t-1} \\ \text { 且 } \\ \qquad Y_{t}=S_{t}+U_{t}+V_{0} \end{array} \\ &\text { 其中 } S_{t}=\sum_{i=1}^{t} \xi_{t} \text { 为随机游走，} \xi_{t} \text { 的方差为 } \Theta(1) \Sigma \Theta(1)^{\prime}，\\ &U_{t} \text { 严格平稳，} V_{0} \text { 为初始条件。 } \end{aligned} \]

Beveridge 和 Nelson (1981) 将 \(S_{t}\) 称为 \(Y_{t}\) 的永久（趋势）分量，将 \(U_{t}\) 称为暂时分量。之所以称 \(S_{t}\) 为永久分量，是因为它决定了 \(Y_{t}\) 的长期行为。

例如，取 MA(1) 情形 \(\Delta Y_{t}=e_{t}+\Theta_{1} e_{t-1}\)。其分解为 \(\Delta Y_{t}=\left(\boldsymbol{I}_{m}+\Theta_{1}\right) e_{t}-\Theta_{1}\left(e_{t}-e_{t-1}\right)\)。此时 \(U_{t}=-\Theta_{1} e_{t}\)。

BN 分解是唯一的，但并非唯一的永久/暂时分解方式。BN 分解的特征是：驱动永久与暂时分量 \(S_{t}\) 与 \(U_{t}\) 的创新完全相关。其他分解不必施加该限制。

最后验证（16.2）—（16.4）。注意（16.2）右侧为

\[ \begin{aligned} \sum_{j=0}^{\infty} \Theta_{j}-\sum_{j=0}^{\infty} \sum_{\ell=j+1}^{\infty} \Theta_{\ell} z^{j}(1-z) &=\sum_{j=0}^{\infty} \Theta_{j}-\sum_{j=0}^{\infty} \sum_{\ell=j+1}^{\infty} \Theta_{\ell} z^{j}+\sum_{j=0}^{\infty} \sum_{\ell=j+1}^{\infty} \Theta_{\ell} z^{j+1} \\ &=\Theta_{0}-\sum_{j=1}^{\infty} \sum_{\ell=j+1}^{\infty} \Theta_{\ell} z^{j}+\sum_{j=1}^{\infty} \sum_{\ell=j}^{\infty} \Theta_{\ell} z^{j} \\ &=\Theta_{0}+\sum_{j=1}^{\infty} \Theta_{j} z^{j} \end{aligned} \]

即 \(\Theta(z)\)，如所示。

16.4 函数型 CLT

定理 16.1 表明随机游走过程按分布收敛到布朗运动。现在将该结果扩展到具有相关差分的单位根过程。

在假设 16.1 下，单位根过程可写作 \(Y_{t}=S_{t}+U_{t}+V_{0}\)，其中 \(S_{t}=\sum_{i=1}^{t} \xi_{t}\)。定义缩放过程 \(Z_{n}(r)=n^{-1 / 2} Y_{\lfloor n r\rfloor}\) 与 \(S_{n}(r)=n^{-1 / 2} S_{\lfloor n r\rfloor}\)，则

\[ Z_{n}(r)=S_{n}(r)+\frac{1}{\sqrt{n}} V_{0}+\frac{1}{\sqrt{n}} U_{\lfloor n r\rfloor} . \]

若 \(e_{t}\) 为协方差矩阵为 \(\Sigma\) 的 MDS，则由定理 16.1 有 \(S_{n}(r) \underset{d}{\longrightarrow} B(r)\)，其中 \(B(r)\) 为协方差矩阵 \(\Omega=\Theta(1) \Sigma \Theta(1)^{\prime}\) 的向量布朗运动。初始条件项 \(n^{-1 / 2} V_{0}=o_{p}(1)\)。只要 \(\sup _{1 \leq t \leq n}\left|n^{-1/2} U_{t}\right|=o_{p}(1)\)，第三项 \(n^{-1 / 2} U_{\lfloor n r\rfloor}=o_{p}(1)\)。若 \(U_{t}\) 方差有限，则由定理 6.15 成立。在假设 16.1 下成立：因为 \(\sum_{j=0}^{\infty}\left\|\Theta_{j}^{*}\right\|<\infty\)，从而

\[ \left\|\operatorname{var}\left[U_{t}\right]\right\|=\left\|\sum_{j=0}^{\infty} \Theta_{j}^{*} \Sigma \Theta_{j}^{* \prime}\right\| \leq\|\Sigma\| \sum_{j=0}^{\infty}\left\|\Theta_{j}^{*}\right\|^{2} \leq\|\Sigma\| \max _{j}\left\|\Theta_{j}^{*}\right\| \sum_{j=0}^{\infty}\left\|\Theta_{j}^{*}\right\|<\infty . \]

由此

\[ Z_{n}(r)=S_{n}(r)+o_{p}(1) \underset{d}{\longrightarrow} B(r) . \]

极限过程的协方差矩阵为 \(\Omega=\Theta(1) \Sigma \Theta(1)^{\prime}\)，这就是 \(\Delta Y_{t}\) 的“长期方差”。

定理 16.3 在假设 16.1 且另外 \((e_{t}, \mathscr{F}_{t})\) 为协方差矩阵为 \(\Sigma\) 的 MDS 条件下，作为 \(r \in[0,1]\) 上的函数，有 \(Z_{n}(r) \underset{d}{\rightarrow} B(r)\)，其中 \(B(r)\) 的协方差矩阵为 \(\Omega\)。

我们的推导使用了线性投影误差为 MDS 的假设。但这并非基本结果所必需；FCLT 在多种依赖条件下均成立，可用 mixing 条件表述。

定理 16.4 若 \(\Delta Y_{t}\) 严格平稳、\(\mathbb{E}[\Delta Y_{t}]=0\)，其 mixing 系数为 \(\alpha(\ell)\)，存在某个 \(r>2\) 使得 \(\mathrm{E} \\|\Delta Y_{t}\\|^{r}<\infty\) 且 \(\sum_{\ell=1}^{\infty} \alpha(\ell)^{1-2 / r}<\infty\)，则作为 \(r \in[0,1]\) 上的函数，\(Z_{n}(r) \underset{d}{\longrightarrow} B(r)\)，其中

\[ \Omega=\sum_{\ell=-\infty}^{\infty} \mathbb{E}[\Delta Y_{t} \Delta Y_{t-\ell}] \]

为协方差矩阵的向量布朗运动。

定理 16.4 的假设与定理 14.15（mixing 过程的 CLT）相同。这意味着在不加强假设的情况下获得了更强的结果（FCLT）。

同时可将长期协方差矩阵分解为 \(\Omega=\Sigma+\Lambda+\Lambda^{\prime}\)，其中 \(\Sigma=\operatorname{var}[\Delta Y_{t}]\)，且

\[ \Lambda=\sum_{\ell=1}^{\infty} \mathbb{E}[\Delta Y_{t} \Delta Y_{t-\ell}^{\prime}] . \]

这将 \(\Delta Y_{t}\) 的长期方差分解为静态（一期）方差 \(\Sigma\) 与协方差和 \(\Lambda\)。矩阵 \(\Lambda\) 一般并不对称。

16.5 积分阶数

取单变量序列 \(Y_{t}\)。定理 16.3 和 16.4 表明，若 \(\Delta Y_{t}\) 平稳且均值为零，则水平过程 \(Y_{t}\) 经适当缩放后渐近为方差 \(\omega^{2}\) 的布朗运动。为使该理论有意义，该方差应严格正定。为理解为何这是潜在限制，假设 \(Y_{t}=a(\mathrm{~L}) e_{t}\)，其中 \(a(z)\) 的系数绝对收敛且 \(e_{t}\) 为 i.i.d. \(\left(0, \sigma^{2}\right)\)。则 \(\Delta Y_{t}=b(\mathrm{~L}) e_{t}\)，其中 \(b(z)=(1-z) a(z)\)，故 \(\omega^{2}=b(1)^{2} \sigma^{2}=0\)。即 \(\Delta Y_{t}\) 的长期方差为 0。我们称过程 \(\Delta Y_{t}\) 过度差分，因为 \(Y_{t}\) 严格平稳且无需差分即可达到平稳性。

为有意义地区分需要差分才能达到平稳性的过程，我们使用以下定义。

定义 16.2 积分阶数

1. \(Y_{t} \in \mathbb{R}\) 是 0 阶积分，记作 \(I(0)\)，若 \(Y_{t}\) 弱平稳且具有正长期方差。
2. \(Y_{t} \in \mathbb{R}\) 是 \(d\) 阶积分，记作 \(I(d)\)，若 \(u_{t}=\Delta^{d} Y_{t}\) 为 \(I(0)\)。

\(I(0)\) 过程是平稳过程且非过度差分。\(I(1)\) 过程包括随机游走和单位根过程。\(I(2)\) 过程需要双重差分才能达到平稳性。\(I(-1)\) 过程平稳但其累积和也平稳，因此是过度差分的平稳过程。许多宏观经济时间序列在对数水平上可能是 \(I(1)\) 过程。可能为 \(I(2)\) 的经济时间序列是对数价格指数，因为其一阶差分（通胀率）可能是非平稳过程。本教材聚焦于整数值积分阶数，但分数 \(d\) 也有明确定义。在大多数应用中，经济学家假设经济序列要么是 \(I(0)\) 要么是 \(I(1)\)，并常用”积分”简指 \(I(1)\) 序列。

ARMA 过程的长期方差计算很直接。如我们所见，若 \(\Delta Y_{t}=b(\mathrm{~L}) e_{t}\)，其中 \(e_{t}\) 为方差 \(\sigma^{2}\) 的白噪声，则 \(\omega^{2}=b(1)^{2} \sigma^{2}\)。现假设 \(a(\mathrm{~L}) \Delta Y_{t}=e_{t}\)，其中 \(a(z)\) 可逆。则 \(b(z)=a(z)^{-1}\) 且 \(\omega^{2}=\sigma^{2} / a(1)^{2}\)。对 ARMA 过程 \(a(\mathrm{~L}) \Delta Y_{t}=b(\mathrm{~L}) e_{t}\) 且 \(a(z)\) 可逆，则 \(\omega^{2}=\sigma^{2} b(1)^{2} / a(1)^{2}\)。因此，若 \(\Delta Y_{t}\) 满足 ARMA 过程 \(a(\mathrm{~L}) \Delta Y_{t}=b(\mathrm{~L}) e_{t}\)，则当 \(a(z)\) 可逆且 \(b(1) \neq 0\) 时 \(Y_{t}\) 为 \(I(1)\)。

考虑向量过程。\(\Delta Y_{t}=\Theta(\mathrm{L}) e_{t}\) 的长期协方差矩阵为 \(\Omega=\Theta(1) \Sigma \Theta(1)^{\prime}\)。\(\boldsymbol{A}(\mathrm{L}) \Delta Y_{t}=e_{t}\) 的长期协方差矩阵为 \(\Omega=\boldsymbol{A}(1)^{-1} \Sigma \boldsymbol{A}(1)^{-1 \prime}\)。通常若 \(\Delta Y_{t}\) 的每个元素都是 \(I(0)\) 则称向量 \(\Delta Y_{t}\) 为 \(I(0)\)，但这允许其协方差矩阵奇异。为排除后者，我们引入以下定义。

定义 16.3 若向量过程 \(Y_{t}\) 的长期协方差矩阵 \(\Omega\) 正定，则称其为满秩 \(I(0)\)。

16.6 均值、局部均值与趋势

定理 16.4 表明 \(Z_{n}(r) \underset{d}{\longrightarrow} B(r)\)。连续映射定理表明，若函数 \(f(x)\) 连续 \({ }^{2}\)，则 \(f\left(Z_{n}\right) \underset{d}{\longrightarrow} f(B)\)。这可用于获得许多感兴趣统计量的渐近分布。简单例子有 \(Z_{n}(r)^{2} \underset{d}{\longrightarrow} B(r)^{2}\) 和 \(\int_{0}^{1} Z_{n}(r) d r \underset{d}{\longrightarrow} \int_{0}^{1} B(r) d r\)。后者产生样本均值的渐近分布，如下所示。

令 \(\bar{Y}_{n}=n^{-1} \sum_{t=1}^{n} Y_{t}\) 为样本均值。为简化假设 \(Y_{0}=0\)。注意对 \(r \in\left[\frac{t}{n}, \frac{t+1}{n}\right)\)，

\[ \frac{1}{n^{1 / 2}} Y_{t}=Z_{n}(r)=n \int_{t / n}^{(t+1) / n} Z_{n}(r) d r . \]

对 \(t=0\) 到 \(n-1\) 取平均得

\[ \frac{1}{n^{1 / 2}} \bar{Y}_{n}=\frac{1}{n^{3 / 2}} \sum_{t=0}^{n-1} Y_{t}=\sum_{t=0}^{n-1} \int_{t / n}^{(t+1) / n} Z_{n}(r) d r=\int_{0}^{1} Z_{n}(r) d r . \]

这是 \(Z_{n}(r)\) 在 \([0,1]\) 上的积分（或平均）。

可应用连续映射定理 \({ }^{3}\)。上述表达式按分布收敛到随机变量 \(\int_{0}^{1} B(r) d r\)。这是布朗运动在 \([0,1]\) 上的平均。

\({ }^{2}\) 相对于统一度量 \(\rho\)。

\({ }^{3}\) 积分 \(f(g)=\int_{0}^{1} g(r) d r\) 是 \(g\) 相对于统一度量的连续函数。（\(g\) 的微小变化导致 \(f\) 的微小变化。）

现考虑子样本均值。令 \(\bar{Y}_{1 n}=(n / 2)^{-1} \sum_{t=0}^{n / 2-1} Y_{t}\) 和 \(\bar{Y}_{2 n}=(n / 2)^{-1} \sum_{t=n / 2}^{n-1} Y_{t}\) 分别为样本前半部分和后半部分的样本均值。通过类似全样本均值的分析

\[ \begin{aligned} &\frac{1}{n^{1 / 2}} \bar{Y}_{1 n}=\frac{2}{n^{3 / 2}} \sum_{t=0}^{n / 2-1} Y_{t}=2 \int_{0}^{1 / 2} Z_{n}(r) d r \underset{\mathrm{d}}{\longrightarrow} 2 \int_{0}^{1 / 2} B(r) d r \\ &\frac{1}{n^{1 / 2}} \bar{Y}_{2 n}=\frac{2}{n^{3 / 2}} \sum_{t=n / 2}^{n-1} Y_{t}=2 \int_{1 / 2}^{1} Z_{n}(r) d r \underset{\mathrm{d}}{\longrightarrow} 2 \int_{1 / 2}^{1} B(r) d r \end{aligned} \]

它们是 \(B(r)\) 在区域 \([0,1 / 2]\) 和 \([1 / 2,1]\) 上的平均。这些是不同的随机变量。这导致预测：若 \(Y_{t}\) 为单位根过程，样本均值将不恒定（即使在大样本中）且在不同子样本间变化。

此外，注意极限分布是在除以 \(n^{1 / 2}\) 后获得的。这意味着没有这种标准化，样本均值在概率上不会有限。这暗示样本均值可能（随机地）很大。这导致相当奇特的特性：样本均值将很大、随机且对总体参数无信息。这意味着当序列可能是单位根过程时，解释简单统计量如均值是危险的。

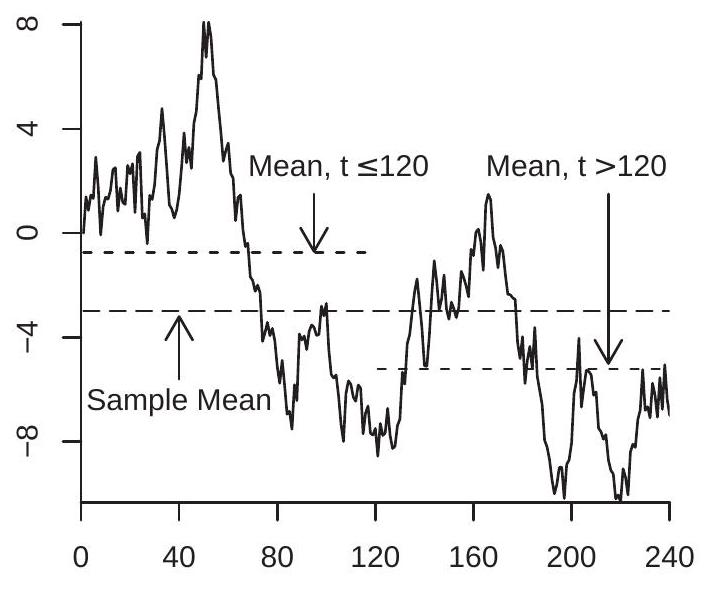
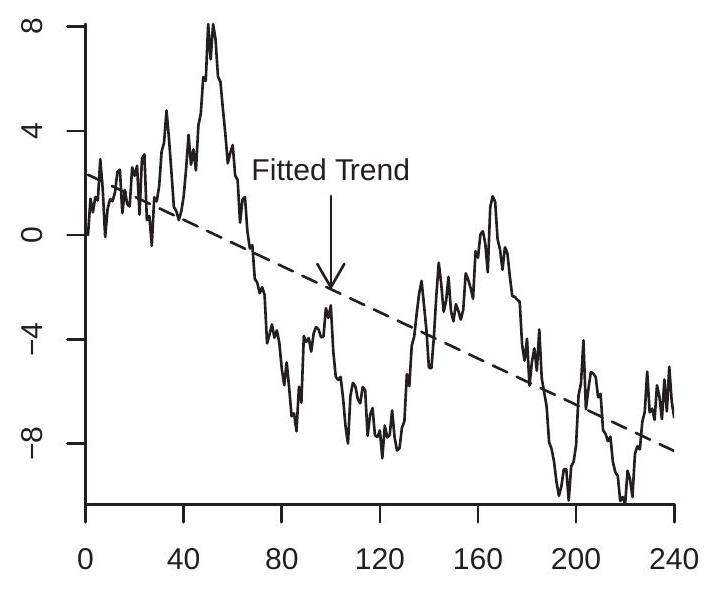
1. 拟合均值

2. 拟合趋势

图 16.1：带拟合均值、子样本均值和趋势的随机游走

为说明，图 16.1(a) 显示了 \(n=240\) 观测值的模拟随机游走。还绘制了样本均值 \(\bar{Y}_{n}=-2.98\)，以及子样本均值 \(\bar{Y}_{1 n}=-0.75\) 和 \(\bar{Y}_{2 n}=-5.21\)。如预测，均值和子样本均值很大、可变且对总体均值无信息。

现考虑 \(Y_{t}\) 对线性时间趋势的线性回归。估计模型为

\[ Y_{t}=\beta_{0}+\beta_{1} t+e_{t}=X_{t}^{\prime} \beta+e_{t} \]

其中 \(X_{t}=(1, t)^{\prime}\)。再次为简化假设 \(Y_{0}=0\)。取最小二乘估计量 \(\widehat{\beta}\)。定理 14.36 表明

\[ \begin{gathered} \frac{1}{n^{2}} \sum_{t=1}^{n} t \rightarrow \int_{0}^{1} r d r=\frac{1}{2} \\ \frac{1}{n^{3}} \sum_{t=1}^{n} t^{2} \rightarrow \int_{0}^{1} r^{2} d r=\frac{1}{3} . \end{gathered} \]

定义 \(D_{n}=\left[\begin{array}{ll}1 & 0 \\ 0 & n\end{array}\right]\)。我们计算

\[ D_{n}^{-1} \frac{1}{n} \sum_{t=1}^{n} X_{t} X_{t}^{\prime} D_{n}^{-1}=\left[\begin{array}{cc} \frac{1}{n} \sum_{t=1}^{n} 1 & \frac{1}{n^{2}} \sum_{t=1}^{n} t \\ \frac{1}{n^{2}} \sum_{t=1}^{n} t & \frac{1}{n^{3}} \sum_{t=1}^{n} t^{2} \end{array}\right] \rightarrow\left[\begin{array}{cc} 1 & \int_{0}^{1} r d r \\ \int_{0}^{1} r d r & \int_{0}^{1} r^{2} d r \end{array}\right]=\int_{0}^{1} X(r) X(r)^{\prime} d r \]

其中 \(X(r)=(1, r)\)。

连续映射定理与定理 16.1 的应用得到

\[ D_{n}^{-1} \frac{1}{n^{3 / 2}} \sum_{t=1}^{n} X_{t} Y_{t}=\int_{0}^{1} X(r) Z_{n}(r) d r \underset{d}{\longrightarrow} \int_{0}^{1} X(r) B(r) d r . \]

综合得到

\[ \begin{aligned} D_{n} n^{-1 / 2} \widehat{\beta} &=D_{n} n^{-1 / 2}\left(\sum_{t=1}^{n} X_{t} X_{t}^{\prime}\right)^{-1}\left(\sum_{t=1}^{n} X_{t} Y_{t}\right) \\ &=\left(D_{n}^{-1} \frac{1}{n} \sum_{t=1}^{n} X_{t} X_{t}^{\prime} D_{n}^{-1}\right)^{-1}\left(D_{n}^{-1} \frac{1}{n^{3 / 2}} \sum_{t=1}^{n} X_{t} Y_{t}\right) \\ & \underset{d}{\longrightarrow}\left(\int_{0}^{1} X(r) X(r)^{\prime} d r\right)^{-1}\left(\int_{0}^{1} X(r) B(r) d r\right) . \end{aligned} \]

这表明估计量 \(\widehat{\beta}\) 的渐近分布是布朗运动 \(B(r)\) 的变换。为简洁，我们常将最终表达式写作 \(\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X B\right)\)。

为说明，图 16.1(b) 显示了面板 (a) 的随机游走以及拟合趋势线。拟合趋势看起来很大且显著。然而它纯粹是随机的，仅是这一特定实现的特征，对潜在参数无信息，且对预测具有危险的误导性。

16.7 去均值与去趋势

时间序列分析中的常见初步步骤是去均值（减去均值）和去趋势（减去线性趋势）。对平稳过程，这不会影响渐近推断。相反，单位根过程的重要特性是这些变换会改变其行为。

取去均值。\(Y_{t}\) 的去均值版本为 \(Y_{t}^{*}=Y_{t}-\bar{Y}_{n}\)。重要观察是 \(Y_{t}^{*}\) 对初始条件 \(Y_{0}\) 不变，故不失一般性我们简单假设 \(Y_{0}=0\)。

标准化过程为

\[ Z_{n}^{*}(r)=\frac{1}{\sqrt{n}} Y_{\lfloor n r\rfloor}-\frac{1}{\sqrt{n}} \bar{Y}_{n}=Z_{n}(r)-Z_{n}(1) \underset{d}{\longrightarrow} B(r)-\int_{0}^{1} B \stackrel{\text { def }}{=} B^{*}(r) . \]

\(B^{*}(r)\) 是去均值布朗运动。它具有性质 \(\int_{0}^{1} B^{*}(r) d r=0\)。

取线性去趋势。基于线性趋势的最小二乘估计，去趋势序列为 \(Y_{t}^{* *}=Y_{t}-X_{t}^{\prime} \widehat{\beta}\)，其中 \(X_{t}=(1, t)^{\prime}\)。与去均值序列类似，去趋势序列对 \(Y_{0}\) 不变。相关标准化过程为

\[ \begin{aligned} & Z_{n}^{* *}(r)=\frac{1}{\sqrt{n}} Y_{\lfloor n r\rfloor}-\frac{1}{\sqrt{n}} X_{\lfloor n r\rfloor}^{\prime} \widehat{\beta} \\ & =Z_{n}(r)-X(\lfloor n r\rfloor / n)^{\prime} D_{n} \frac{1}{\sqrt{n}} \widehat{\beta} \\ & \underset{d}{\longrightarrow} B(r)-X(r)^{\prime}\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X B\right) \stackrel{\text { def }}{=} B^{* *}(r) . \end{aligned} \]

\(B^{* *}(r)\) 是布朗运动 \(B(r)\) 投影到与 \(X(r)=(1, r)^{\prime}\) 正交的连续时间残差。我们称 \(B^{* *}(r)\) 为去趋势布朗运动。

还有通过一阶差分去趋势的另一种方法。假设 \(Y_{t}=\beta_{0}+\beta_{1} t+Z_{t}\)。一阶差分为 \(\Delta Y_{t}=\beta_{1}+\Delta Z_{t}\)。\(\beta_{1}\) 的估计量是 \(\Delta Y_{t}\) 的样本均值：

\[ \overline{\Delta Y}_{n}=\frac{1}{n} \sum_{t=1}^{n} \Delta Y_{t}=\frac{Y_{n}-Y_{0}}{n} . \]

标准化 \(Z_{0}=0\) 意味着 \(Y_{0}=\beta_{0}\)，故 \(\beta_{0}\) 的估计量为 \(Y_{0}\)。\(Y_{t}\) 的去趋势版本为 \(\widetilde{Y}_{t}=Y_{t}-Y_{0}-(t / n)\left(Y_{n}-Y_{0}\right)\)。相关标准化过程为

\[ \widetilde{Z}_{n}(r)=Z_{n}(r)-\frac{\lfloor n r\rfloor}{n} Z_{n}(1) \underset{d}{\longrightarrow} B(r)-r B(1) \stackrel{\text { def }}{=} V(r) . \]

\(V(r)\) 称为布朗桥或绑定的布朗运动。它具有性质 \(V(0)=V(1)=0\)。它也是 \(B(r)\) 的去趋势版本，但与线性去趋势版本 \(B^{*}(r)\) 不同。

我们在以下定理中总结发现。

定理 16.5 在定理 16.3 或定理 16.4 的条件下，当 \(n \rightarrow \infty\) 时

1. \(Z_{n}^{*}(r) \underset{d}{\longrightarrow} B^{*}(r)\)
2. \(Z_{n}^{* *}(r) \underset{d}{\longrightarrow} B^{* *}(r)\)
3. \(\widetilde{Z}_{n}(r) \underset{d}{\longrightarrow} V(r)\)

为说明，图 16.2 显示了图 16.1 序列的两种去趋势版本。面板 (a) 显示线性去趋势序列 \(Y_{t}^{*}\)。面板 (b) 显示一阶差分去趋势序列 \(\widetilde{Y}_{t}\)。它们在视觉上彼此相似且与图 16.1 相似，除了强线性趋势已被移除。

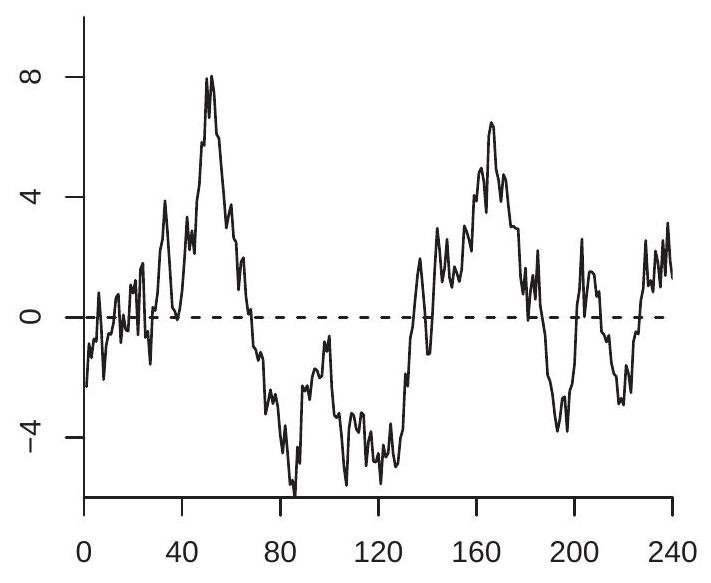
1. 线性去趋势序列

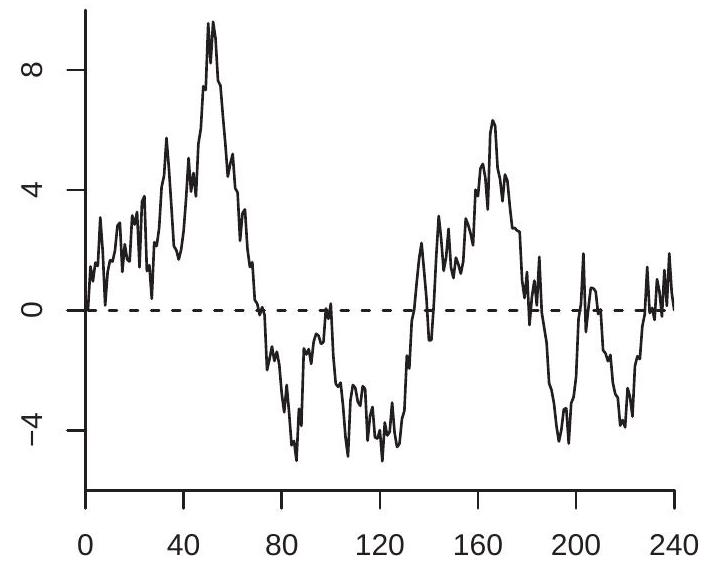
2. 一阶差分去趋势序列

图 16.2：去趋势随机游走

16.8 随机积分

回归模型 \(Y_{t}=X_{t}^{\prime} \beta+e_{t}\) 中最小二乘估计量的分布需要样本矩 \(n^{-1} \sum_{t=1}^{n-1} X_{t} e_{t+1}\) 的分布。当 \(X_{t}\) 非平稳时，极限分布是非标准的且等于随机积分。

回忆 Riemann-Stieltjes 积分的定义可能有助于理解。在区域 \([0,1]\) 上，\(g(x)\) 关于 \(f(x)\) 的积分为

\[ \int_{0}^{1} g(x) d f(x)=\lim _{N \rightarrow \infty} \sum_{i=0}^{N-1} g\left(\frac{i}{N}\right)\left(f\left(\frac{i+1}{N}\right)-f\left(\frac{i}{N}\right)\right) . \]

随机积分是函数 \(f\) 为随机且定义为概率极限的情形。

定义 16.4 向量值 \(X(r)\) 关于向量值 \(Z(r)\) 在 \([0,1]\) 上的随机积分为

\[ \int_{0}^{1} X d Z^{\prime}=\int_{0}^{1} X(r) d Z(r)^{\prime}=\underset{N \rightarrow \infty}{\operatorname{plim}} \sum_{i=0}^{N-1} X\left(\frac{i}{N}\right)\left(Z\left(\frac{i+1}{N}\right)-Z\left(\frac{i}{N}\right)\right)^{\prime} . \]

现考虑以下设定。令 \(\left(X_{t}, e_{t}\right)\) 为向量值序列，其中 \(e_{t}\) 为具有有限协方差的 MDS，\(X_{t}\) 为非平稳。假设对某个缩放序列 \(D_{n}\)，缩放过程 \(X_{n}(r)=D_{n}^{-1} X_{\lfloor n r\rfloor}\) 满足 \(X_{n}(r) \underset{d}{\longrightarrow} X(r)\)，其中 \(X(r)\) 为确定性或随机过程。\(X_{t}\) 序列的例子包括由 \(e_{t}\) 或另一个冲击构造的部分和过程、部分和过程的去趋势版本，或确定性趋势过程。我们期望 \(\sum_{t=1}^{n-1} X_{t} e_{t+1}^{\prime}\) 的渐近分布。定义 \(e_{t}\) 的部分和过程为 \(S_{n}(r)=n^{-1 / 2} \sum_{t=1}^{\lfloor n r\rfloor} e_{t}\)。由定理 16.1，\(S_{n} \underset{d}{\longrightarrow} B\)。我们计算

\[ \frac{1}{\sqrt{n}} D_{n}^{-1} \sum_{t=0}^{n-1} X_{t} e_{t+1}^{\prime}=\sum_{t=0}^{n-1} X_{n}\left(\frac{t}{n}\right)\left(S_{n}\left(\frac{t+1}{n}\right)-S_{n}\left(\frac{t}{n}\right)\right)^{\prime}=\int_{0}^{1} X_{n} d S_{n}^{\prime} . \]

等式成立是因为 \(S_{n}(r)\) 和 \(X_{n}(r)\) 是在 \(r=t / n\) 处跳跃的阶梯函数。由于 \(X_{n}(r)\) 和 \(S_{n}(r)\) 收敛到 \(X(r)\) 和 \(B(r)\)，类比我们期望 \(\int_{0}^{1} X_{n} d S_{n}\) 收敛到 \(\int_{0}^{1} X d B\)。这是正确的，但相当棘手，因为随机积分不是 \(B(r)\) 的连续函数。Kurtz 和 Protter (1991, 定理 2.2) 提供了条件的一般表述。以下是其结果的简化。

定理 16.6 若 \(\left(e_{t}, \mathscr{F}_{t}\right)\) 为鞅差序列，\(\mathbb{E}\left[e_{t} e_{t}^{\prime}\right]=\Sigma<\infty\)，\(X_{t} \in \mathscr{F}_{t}\)，且 \(\left(X_{n}(r), S_{n}(r)\right) \underset{d}{\longrightarrow}(X(r), B(r))\)，则

\[ \int_{0}^{1} X_{n} d S_{n}^{\prime}=\frac{1}{\sqrt{n}} D_{n}^{-1} \sum_{t=1}^{n-1} X_{t} e_{t+1} \underset{d}{\longrightarrow} \int_{0}^{1} X d B^{\prime} \]

其中 \(B(r)\) 为协方差矩阵 \(\Sigma\) 的布朗运动。

定理 16.6 的基本应用是情形 \(X_{n}(r)=S_{n}(r)\)。因此若 \(S_{t}=\sum_{i=1}^{t} e_{t}\) 且 \(e_{t}\) 为协方差矩阵 \(\Sigma\) 的 MDS，则

\[ \frac{1}{n} \sum_{t=1}^{n-1} S_{t} e_{t+1}^{\prime} \underset{d}{\longrightarrow} \int_{0}^{1} B d B^{\prime} . \]

我们可以将此结果扩展到序列相关误差的情形。

定理 16.7 若 \(Z_{t}\) 满足定理 16.4 的条件且 \(S_{t}=\sum_{i=1}^{t} Z_{t}\)，则

\[ \frac{1}{n} \sum_{t=1}^{n-1} S_{t} Z_{t+1}^{\prime} \underset{d}{\longrightarrow} \int_{0}^{1} B d B^{\prime}+\Lambda \]

其中 \(B(r)\) 为协方差矩阵 \(\Omega=\Sigma+\Lambda+\Lambda^{\prime}\) 的布朗运动，\(\Sigma=\mathbb{E}\left[Z_{t} Z_{t}^{\prime}\right]\)，且 \(\Lambda=\sum_{j=1}^{\infty} \mathbb{E}\left[Z_{t-j} Z_{t}^{\prime}\right]\)。

证明见第 16.22 节。

16.9 AR(1) 的估计

考虑模型 \(Y_{t}=\alpha Y_{t-1}+e_{t}\) 中 AR(1) 参数 \(\alpha\) 的最小二乘估计。中心化估计量为 \(\widehat{\alpha}-\alpha=\left(\sum_{t=1}^{n-1} Y_{t}^{2}\right)^{-1}\left(\sum_{t=1}^{n-1} Y_{t} e_{t+1}\right)\)。我们使用缩放

\[ n(\widehat{\alpha}-\alpha)=\frac{\frac{1}{n} \sum_{t=1}^{n-1} Y_{t} e_{t+1}}{\frac{1}{n^{2}} \sum_{t=1}^{n-1} Y_{t}^{2}} . \]

我们在假设 \(\alpha=1\) 下分别检查分母和分子。类似于我们对样本均值的分析，分母可写作积分。因此

\[ \frac{1}{n^{2}} \sum_{t=1}^{n-1} Y_{t}^{2}=\frac{1}{n} \sum_{t=1}^{n-1}\left(\frac{1}{n^{1 / 2}} Y_{t}\right)^{2}=\int_{0}^{1} Z_{n}(r)^{2} d r \underset{d}{\longrightarrow} \int_{0}^{1} B(r)^{2} d r=\sigma^{2} \int_{0}^{1} W(r)^{2} d r \]

收敛由连续映射定理 \({ }^{4}\) 得到。最终等式认识到若 \(B(r)\) 方差为 \(\sigma^{2}\)，则 \(B(r)^{2}=\sigma^{2} W(r)^{2}\)，其中 \(W(r)\) 为标准布朗运动。为简洁，我们常将最终积分写作 \(\int_{0}^{1} W^{2}\)。

对分子我们诉诸定理 16.6。

\[ \frac{1}{n} \sum_{t=1}^{n-1} Y_{t} e_{t+1}=\int_{0}^{1} Z_{n} d S_{n} \underset{d}{\longrightarrow} \int_{0}^{1} B d B=\sigma^{2} \int_{0}^{1} W d W . \]

这个极限随机积分相当著名。它被称为 Itô 积分。

定理 16.8 Itô 积分 \(\int_{0}^{1} W d W=\frac{1}{2}\left(W(1)^{2}-1\right)\)

若你对 Itô 积分不感到惊讶，请再仔细看看。\(\frac{1}{2} W(r)^{2}\) 的导数为 \(W(r) d W(r)\)。因此由标准微积分和 \(W(0)=0\)，你可能期望 \(\int_{0}^{1} W d W=\frac{1}{2} W(1)^{2}\)。额外项 \(-1 / 2\) 的存在令人惊讶。这源于 \(W(r)\) 具有无界变差。

随机变量 \(W(1)^{2}\) 为 \(\chi_{1}^{2}\)，期望为 1。因此随机变量 \(\int_{0}^{1} W d W\) 均值为零但偏斜。

定理 16.8 的证明见第 16.22 节。

回到最小二乘估计问题，我们已证明当 \(\alpha=1\) 时

\[ n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\frac{\sigma^{2}}{2}\left(W(1)^{2}-1\right)}{\sigma^{2} \int_{0}^{1} W^{2}}=\frac{\int_{0}^{1} W d W}{\int_{0}^{1} W^{2}} . \]

定理 16.9 Dickey-Fuller 系数分布 若 \(Y_{t}=\alpha Y_{t-1}+e_{t}\) 且 \(\alpha=1\)，\(\left(e_{t}, \mathscr{F}_{t}\right)\) 为严格平稳、遍历的鞅差序列且具有有限方差，则

\[ n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W d W}{\int_{0}^{1} W^{2}} . \]

定理 16.9 中的极限分布被称为 Dickey-Fuller 分布，源于 Wayne Fuller 和 David Dickey 的工作。定理 16.9 表明最小二乘估计量对 \(\alpha=1\) 一致且以”超一致”速率 \(O_{p}\left(n^{-1}\right)\) 收敛。极限分布是非标准的，写作布朗运动 \(W(r)\) 的函数。该统计量的分布或密度没有闭式表达式。通常通过模拟计算。

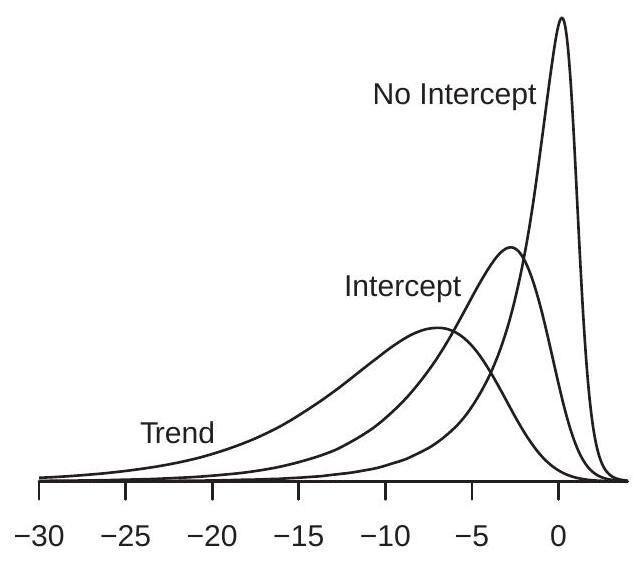
\({ }^{4}\) 函数 \(g(f)=\int_{0}^{1} f(x)^{2} d x\) 相对于统一度量连续。Dickey-Fuller 系数分布的密度在图 16.3(a) 中显示 \({ }^{5}\)，标签为”无截距”。你可以看到密度高度偏斜且具有长左尾。你可以看到分布的大部分概率质量在负区域。这意味着密度具有负均值和负中位数。因此最小二乘估计量的渐近分布向下偏倚。这具有实际含义：当 \(\alpha=1\) 时，最小二乘估计量偏离 1。

我们也可以检查 t 比的极限分布。令 \(\widehat{e}_{t}=Y_{t}-\widehat{\alpha} Y_{t-1}\) 为最小二乘残差，\(\widehat{\sigma}^{2}=n^{-1} \sum \widehat{e}_{t}^{2}\) 为最小二乘方差估计量，\(s(\widehat{\alpha})=\widehat{\sigma} / \sqrt{\sum Y_{t}^{2}}\) 为 \(\widehat{\alpha}\) 的经典标准误。\(\alpha\) 的 t 比为 \(T=(\widehat{\alpha}-1) / s(\widehat{\alpha})\)。

定理 16.10 Dickey-Fuller T 分布 在定理 16.9 的假设下

\[ T=\frac{\widehat{\alpha}-1}{s(\widehat{\alpha})} \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W d W}{\left(\int_{0}^{1} W^{2}\right)^{1 / 2}} . \]

定理 16.10 中的极限分布被称为 Dickey-Fuller T 分布。定理 16.10 表明经典 t 比收敛到非标准渐近分布。分布或密度没有闭式表达式，因此通常使用模拟技术计算。证明见第 16.22 节。

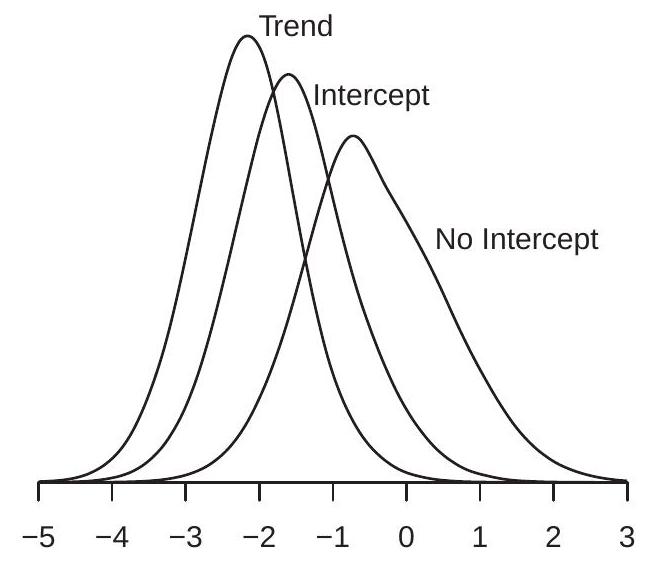
Dickey-Fuller T 分布的密度在图 16.3(b) 中显示，标签为”无截距”。你可以看到密度偏斜但比系数分布偏斜程度小得多。分布似乎是传统学生 t 分布的”更胖”版本。含义是传统推断（置信区间和检验）将不准确。我们在第 16.13 节讨论检验。

16.10 带截距的 AR(1) 估计

假设 \(Y_{t}\) 为随机游走，我们估计带截距的 AR(1) 模型。估计模型为 \(Y_{t}=\mu+\alpha Y_{t-1}+e_{t}\)。由 Frisch-Waugh-Lovell 定理（定理 3.5），\(\alpha\) 的最小二乘估计量 \(\widehat{\alpha}\) 可写作使用去均值序列 \(Y_{t}^{*}\) 的简单回归。即，标准化估计量为

\[ n(\widehat{\alpha}-1)=\frac{\frac{1}{n} \sum_{t=1}^{n-1} Y_{t}^{*} e_{t+1}}{\frac{1}{n^{2}} \sum_{t=1}^{n-1} Y_{t}^{* 2}} \]

其中 \(Y_{t}^{*}=Y_{t}-\bar{Y}\)，\(\bar{Y}=\frac{1}{n} \sum_{t=1}^{n-1} Y_{t}\)。由定理 16.5.1 和 16.6，前一节的计算表明

\[ n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{*} d W}{\int_{0}^{1} W^{* 2}} . \]

\({ }^{5}\) 图 16.3 中的密度由样本量 \(n=10,000\) 的有限样本分布的一百万次模拟抽取估计。密度使用非参数核方法估计（见《Introduction to Econometrics》第 17 章）。

1. Dickey-Fuller 系数密度

2. Dickey-Fuller T 密度

图 16.3：单位根分布

这类似于定理 16.9 中的分布。这被称为包含截距情形的 Dickey-Fuller 系数分布。

类似地，若我们估计带截距和趋势的 AR(1) 模型，估计模型为 \(Y_{t}=\mu+\beta t+\alpha Y_{t-1}+e_{t}\)。由 Frisch-Waugh-Lovell 定理，这等价于对去趋势序列 \(Y_{t}^{* *}\) 的回归。应用定理 16.5.2 和 16.6，我们发现

\[ n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{* *} d W}{\int_{0}^{1} W^{* * 2}} . \]

这被称为包含截距和线性趋势情形的 Dickey-Fuller 系数分布。

t 比也有类似结果。我们在以下定理中总结结果。

定理 16.11 在定理 16.9 的假设下，对带截距的估计 AR(1) 情形

\[ \begin{gathered} n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{*} d W}{\int_{0}^{1} W^{* 2}} \\ T \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{*} d W}{\left(\int_{0}^{1} W^{* 2}\right)^{1 / 2}} . \end{gathered} \]

对带截距和线性时间趋势的估计 AR(1) 情形

\[ \begin{gathered} n(\widehat{\alpha}-1) \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{* *} d W}{\int_{0}^{1} W^{* * 2}} \\ T \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W^{* *} d W}{\left(\int_{0}^{1} W^{* * 2}\right)^{1 / 2}} . \end{gathered} \]

Dickey-Fuller 系数分布的密度在图 16.3(a) 中显示，包含截距情形标记为”截距”，包含截距和线性时间趋势情形标记为”趋势”。包含截距或截距和趋势对分布有显著影响。影响是双重的：(1) 分布大幅左移；(2) 分布大幅加宽。检查”趋势”版本，我们可以看到零上方几乎没有概率质量。这意味着渐近分布不仅向下偏倚，实现几乎总是负的。这具有实际含义：最小二乘估计量几乎肯定小于真实系数值。这是强形式的偏倚。

Dickey-Fuller T 分布的密度在图 16.3(b) 中显示。去趋势对 T 分布的影响与对系数分布的影响大不相同。这里我们看到主要影响是位置移动，对离散度只有轻微影响。强位置移动是渐近 T 分布的偏倚，意味着传统推断将不正确。

16.11 积分和协方差的样本协方差

令 \(\left(X_{t}, u_{t}\right)\) 为序列，其中 \(X_{t}\) 为非平稳，\(u_{t}\) 均值为零且严格平稳。假设对某个缩放序列 \(D_{n}\)，缩放过程 \(X_{n}(r)=D_{n}^{-1} X_{\lfloor n r\rfloor}\) 满足 \(X_{n}(r) \underset{d}{\longrightarrow} X(r)\)，其中 \(X(r)\) 以概率 1 连续。考虑缩放样本协方差

\[ C_{n}=\frac{1}{n} D_{n}^{-1} \sum_{t=1}^{n} X_{t} u_{t} . \]

定理 16.12 假设 \(X_{n}(r)=D_{n}^{-1} X_{\lfloor n r\rfloor} \underset{d}{\longrightarrow} X(r)\)，其中 \(X(r)\) 几乎必然连续。假设 \(u_{t}\) 均值为零、严格平稳、遍历，且 \(\mathbb{E}\left|u_{t}\right|<\infty\)。则当 \(n \rightarrow \infty\) 时 \(C_{n} \underset{p}{\longrightarrow} 0\)。证明见第 16.22 节。

16.12 带单位根的 AR(p) 模型

假设 \(Y_{t}\) 满足 \(a(\mathrm{~L}) \Delta Y_{t}=e_{t}\)，其中 \(a(z)\) 为 \(p-1\) 阶可逆滞后多项式，\(e_{t}\) 为具有有限方差 \(\sigma^{2}\) 的平稳 MDS。则 \(Y_{t}\) 可写作 AR(p) 过程

\[ Y_{t}=a_{1} Y_{t-1}+\cdots+a_{p} Y_{t-p}+e_{t} \]

其中系数满足 \(a_{1}+\cdots+a_{p}=1\)。令 \(\widehat{a}\) 为 \(a=\left(a_{1}, \ldots, a_{p}\right)\) 的最小二乘估计量。我们现在描述其抽样分布。

令 \(B\) 为将 \(\left(Y_{t-1}, \ldots, Y_{t-p}\right)\) 变换为 \(\left(Y_{t-1}, \Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\right)\) 的 \(p \times p\) 矩阵，例如当 \(p=3\) 时 \(B=\left[\begin{array}{ccc}1 & 0 & 0 \\ 1 & -1 & 0 \\ 0 & 1 & -1\end{array}\right]\)。做分割 \(B^{-1 \prime} a=(\rho, \beta)\)，其中 \(\rho \in \mathbb{R}\) 且 \(\beta \in \mathbb{R}^{p-1}\)。则 AR(p) 模型可写作

\[ Y_{t}=\rho Y_{t-1}+\beta^{\prime} X_{t-1}+e_{t} \]

其中 \(X_{t-1}=\left(\Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\right)\)。主导系数为 \(\rho=a_{1}+\cdots+a_{p}=1\)。此变换将回归变量分离为单位根分量 \(Y_{t-1}\) 和平稳分量 \(X_{t-1}\)。

考虑最小二乘估计量 \((\widehat{\rho}, \widehat{\beta})\)。在单位根假设下，它们可写作

\[ \left(\begin{array}{c} n(\widehat{\rho}-1) \\ \sqrt{n}(\widehat{\beta}-\beta) \end{array}\right)=\left(\begin{array}{cc} \frac{1}{n^{2}} \sum_{t=1+p}^{n} Y_{t-1}^{2} & \frac{1}{n^{3 / 2}} \sum_{t=1+p}^{n} Y_{t-1} X_{t-1}^{\prime} \\ \frac{1}{n^{3 / 2}} \sum_{t=1+p}^{n} X_{t-1} Y_{t-1} & \frac{1}{n} \sum_{t=1+p}^{n} X_{t-1} X_{t-1}^{\prime} \end{array}\right)^{-1}\left(\begin{array}{c} \frac{1}{n} \sum_{t=1+p}^{n} Y_{t-1} e_{t} \\ \frac{1}{\sqrt{n}} \sum_{t=1+p}^{n} X_{t-1} e_{t} \end{array}\right) . \]

定理 16.4 和 CMT 表明

\[ \frac{1}{n^{2}} \sum_{t=1+p}^{n} Y_{t-1}^{2} \underset{d}{\rightarrow} \omega^{2} \int_{0}^{1} W^{2} \]

其中 \(\omega^{2}\) 为 \(\Delta Y_{t}\) 的长期方差，等于 \(\omega^{2}=\sigma^{2} / a(1)^{2}>0\)。

定理 16.12 表明

\[ \frac{1}{n^{3 / 2}} \sum_{t=1+p}^{n} X_{t-1} Y_{t-1} \underset{p}{\longrightarrow} 0 . \]

定理 16.4 和 16.6 表明

\[ \frac{1}{n} \sum_{t=1+p}^{n} Y_{t-1} e_{t} \underset{d}{\longrightarrow} \omega \sigma \int_{0}^{1} W d W . \]

平稳过程的 WLLN 和 CLT 表明

\[ \begin{aligned} &\frac{1}{n} \sum_{t=1+p}^{n} X_{t-1} X_{t-1}^{\prime} \rightarrow \boldsymbol{Q} \\ &\frac{1}{\sqrt{n}} \sum_{t=1+p}^{n} X_{t-1} e_{t} \underset{d}{\longrightarrow} \mathrm{N}(0, \Omega) \end{aligned} \]

其中 \(\boldsymbol{Q}=\mathbb{E}\left[X_{t-1} X_{t-1}^{\prime}\right]\) 且 \(\Omega=\mathbb{E}\left[X_{t-1} X_{t-1}^{\prime} e_{t}^{2}\right]\)。综合我们建立了以下结果。

定理 16.13 假设 \(Y_{t}\) 满足 \(a(\mathrm{~L}) \Delta Y_{t}=e_{t}\)，其中 \(a(z)\) 为 \(p-1\) 阶可逆滞后多项式，\(\left(e_{t}, \mathscr{F}_{t}\right)\) 为具有有限方差 \(\sigma^{2}\) 的平稳 MDS。则

\[ \left(\begin{array}{c} n(\widehat{\rho}-1) \\ \sqrt{n}(\widehat{\beta}-\beta) \end{array}\right) \rightarrow\left(\begin{array}{c} a(1) \frac{\int_{0}^{1} W d W}{\int_{0}^{1} W^{2}} \\ \mathrm{~N}(0, V) \end{array}\right) \]

其中 \(V=\boldsymbol{Q}^{-1} \Omega \boldsymbol{Q}^{-1}\)。

此定理为最小二乘估计量提供了渐近分布理论。估计量 \((\widehat{a}, \widehat{\beta})\) 一致，平稳变量上的系数 \(\widehat{\beta}\) 渐近正态，单位根分量上的系数 \(\widehat{a}\) 具有缩放 Dickey-Fuller 分布。

表示 (16.6) 的估计量是线性变换 \(B^{\prime}\left(\widehat{\rho}, \widehat{\beta}^{\prime}\right)^{\prime}\)，因此其渐近分布是 (16.8) 的变换 \(B^{\prime}\)。由于单位根分量以比平稳分量更快的 \(O_{p}\left(n^{-1}\right)\) 速率收敛，它从渐近分布中消失。我们得到

\[ \sqrt{n}(\widehat{a}-a) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{G} V \boldsymbol{G}^{\prime}\right) \]

其中，在 \(p=3\) 情形

\[ \boldsymbol{G}=\left[\begin{array}{cc} 1 & 0 \\ -1 & 1 \\ 0 & -1 \end{array}\right] . \]

渐近协方差矩阵 \(\boldsymbol{G} V \boldsymbol{G}^{\prime}\) 是秩为 \(p-1\) 的亏缺矩阵。因此这只是渐近分布的部分刻画；方程 (16.8) 是完整的一阶刻画。(16.9) 的含义是 (16.6) 的个别系数估计量和标准误具有传统渐近解释。这扩展到不包括系数和的传统假设检验。对大多数目的（除了检验单位根假设）这意味着 (16.6) 系数的渐近推断可基于传统正态近似并忽略单位根的可能存在。

16.13 单位根检验

时间序列过程的渐近性质在单位根 \(\rho=a_{1}+\cdots+a_{p}=1\) 处不连续变化。因此检验单位根假设是标准兴趣。我们通常将其表达为 \(\mathbb{H}_{0}: \rho=1\) 对 \(\mathbb{H}_{1}: \rho<1\) 的检验。我们通常将检验视为单侧，因为我们感兴趣的是序列平稳的备择假设（而不是爆炸性的）。

\(\mathbb{H}_{0}\) 对 \(\mathbb{H}_{1}\) 的检验是 AR(p) 模型 (16.6) 中 \(a_{1}+\cdots+a_{p}=1\) 的 t 统计量。这与重参数化形式 (16.7) 中 \(\rho=1\) 的 t 统计量相同。由于后者是简单 t 比，这是最方便的实现。它通常称为增广 Dickey-Fuller 统计量。它等于

\[ \mathrm{ADF}=\frac{\widehat{\rho}-1}{s(\widehat{\rho})} \]

其中 \(s(\widehat{\rho})\) 为 \(\widehat{\rho}\) 的标准误。此 t 比通常使用经典（同方差）标准误计算，可能是出于历史原因，也可能是因为 ADF 的渐近分布对条件异方差不变。当估计模型为 \(p>1\) 的 AR(p) 模型时，统计量称为 ADF 统计量；当估计模型为 AR(1) 时，通常称为 Dickey-Fuller 统计量。

ADF 的渐近分布依赖于拟合的确定性分量。检验统计量最常在带拟合截距或拟合截距和时间趋势的模型中计算，尽管理论也针对无拟合截距情形提出，并扩展到任何多项式阶趋势。

定理 16.14 假设 \(Y_{t}\) 满足 \(a(\mathrm{~L}) \Delta Y_{t}=e_{t}\)，其中 \(a(z)\) 为 \(p-1\) 阶可逆滞后多项式，\(\left(e_{t}, \mathscr{F}_{t}\right)\) 为具有有限方差 \(\sigma^{2}\) 的平稳 MDS。则

\[ \mathrm{ADF} \underset{d}{\longrightarrow} \frac{\int_{0}^{1} U d W}{\left(\int_{0}^{1} U^{2}\right)^{1 / 2}} \stackrel{\text { def }}{=} \xi \]

其中 \(W\) 为布朗运动。过程 \(U\) 依赖于拟合的确定性分量：

1. 情形 1：无截距或趋势。\(U(r)=W(r)\)。
2. 情形 2：拟合截距（去均值数据）。\(U(r)=W(r)-r \int_{0}^{1} W\)。
3. 情形 3：拟合截距和趋势（去趋势数据）。\(U(r)=W(r)-X(r)^{\prime}\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X W\right)\)，其中 \(X(r)=(1, r)^{\prime}\)。

令 \(Z_{\alpha}\) 满足 \(\mathbb{P}\left[\xi \leq Z_{\alpha}\right]=\alpha\)。检验”若 \(\mathrm{ADF}<Z_{\alpha}\) 则拒绝 \(\mathbb{H}_{0}\)“具有渐近水平 \(\alpha\)。

渐近临界值在表 16.1 的前三列中显示。ADF 是单侧假设检验，因此当检验统计量小于（比）临界值更负时发生拒绝。例如，拟合截距情形的 \(5 \%\) 临界值为 \(-2.86\)。这意味着如果 ADF t 比比 \(-2.86\) 更负（例如 \(\mathrm{ADF}=-3.0\)），则检验拒绝无单位根假设。但如果 ADF t 比大于 \(-2.86\)（例如 ADF \(=-2.0\)），则检验不拒绝单位根假设。

在大多数应用中，ADF 检验至少用拟合截距实现（表中第二列）。许多用拟合线性时间趋势实现（第三列）。选择依赖于备择假设的性质。如果 \(\mathbb{H}_{1}\) 是序列关于常数均值平稳，则拟合截距情形是适当的。此情形的例子序列是失业率和利率。如果 \(\mathbb{M}_{1}\) 是序列关于线性趋势平稳，则拟合趋势情形是适当的。此情形的例子是宏观经济总量的水平或对数水平。

ADF 检验依赖于自回归阶数 \(p\)。\(p\) 的选择问题类似于自回归模型选择。一般而言，如果 \(p\) 太小则模型误设且 ADF 统计量有渐近偏倚。如果 \(p\) 太大则检验系数 \(\widehat{\rho}\) 估计不精确，降低检验功效。由于 \(\widehat{\rho}\) 是水平模型中 \(p\) 个估计 AR 系数的和，不精确性对 \(p\) 的选择可能敏感。合理的选择规则是使用 AIC 选择的 AR 模型。Ng 和 Perron (2001) 研究了改进规则。

我们已论证报告渐近 p 值比”接受/拒绝”更好。对此计算我们需要渐近分布函数但这不是闭式可得的。简单近似是临界值的插值。例如，假设 ADF \(=-3.0\) 且拟合截距。两个最接近的临界值是 \(10 \%(-3.13)\) 和 \(15 \%(-2.94)\)。这些值间的线性插值产生

\[ p=\frac{0.10 \times(3.0-2.94)+0.15 \times(3.13-3.0)}{3.13-2.94}=0.13 . \]

因此渐近 p 值约为 \(13 \%\)。报告 p 值而不是检验的”决策”改善了解释和沟通。

单位根检验在实证实践中应如何使用？答案是微妙的。常见错误是”我们使用单位根检验来发现序列是否有单位根。“这是错误，因为检验不揭示真相。相反，它呈现 \(\mathbb{M}_{0}\) 是否可被拒绝的证据。如果检验未能拒绝 \(\mathbb{H}_{0}\)，这并不意味着”我们发现了单位根”。相反，正确结论是”我们不能拒绝它有单位根的假设”。因此我们不知道。如果检验拒绝 \(\mathbb{H}_{0}\)（如果 p 值很小），则我们可以得出结论序列不太可能是单位根过程；其行为更符合平稳过程。另一个常见错误是采用规则：“如果 ADF 检验拒绝则我们用 \(Y_{t}\) 水平工作；如果 ADF 检验不拒绝则我们用差分序列 \(\Delta Y_{t}\) 工作。”这是错误，因为它将建模规则分配给统计检验的结果，而检验仅设计回答是否存在反对单位根假设的证据的问题。\(Y_{t}\) 对 \(\Delta Y_{t}\) 的选择是模型选择选择而不是假设检验决策。

我相信合理方法是从基于理论和背景的假设开始。经济理论引导你将序列视为平稳还是非平稳？有理由相信序列应该是平稳的——因此在均值上稳定——还是有理由相信序列将表现出增长和变化？如果你对这些问题有明确答案，那应该是你的起点，你的默认。使用单位根检验帮助确认你的假设而不是选择建模方法。如果你的假设是 \(Y_{t}\) 有单位根但单位根检验强烈拒绝，则你应该重新评估你的理论。另一方面，如果你的假设是 \(Y_{t}\) 平稳但单位根检验未能拒绝单位根原假设，不一定偏离你的理论基础。考虑证据程度、样本大小以及点估计。使用所有信息一起基于你的决策。

为说明 ADF 检验的应用，让我们使用水平或对数水平测量的变量对图 14.1-14.2 中显示的八个序列进行检验。变量和变换列在表 16.2 中。对八个序列中的六个（除利率和失业率外的所有）我们取对数变换。我们在每个回归中包含截距和线性时间趋势，并通过在带线性时间趋势的 AR(p) 模型中最小化 AIC 来选择自回归阶数。对季度序列我们检查高达 \(p=8\) 的 AR(p) 模型，对月度序列高达 \(p=12\)。选择的 \(p\) 值在表中显示。点估计 \(\widehat{\rho}-1\)、其标准误、ADF t 统计量及其渐近 p 值显示。我们看到的是八个序列中的七个（除失业率外的所有）p 值远离临界区域，表明未能拒绝单位根原假设。失业率的 p 值为 \(0.01\)，然而，表明拒绝单位根。总体而言，结果与失业率平稳和其他七个变量可能（但不决定性地）为单位根过程的假设一致。

ADF 检验在经济学中因 Nelson 和 Plosser (1982) 的研讨会论文而流行。这些作者将 ADF 应用于一组标准宏观经济变量（类似于表 16.2 中的变量）并发现单位根假设在大多数序列中不能被拒绝。这一实证发现对应用经济时间序列有重大影响。在此论文之前，传统智慧是经济序列是平稳的（可能关于线性时间趋势）。在他们的工作之后，假设经济时间序列更好地描述为自回归单位根过程变得更加被接受。Nelson 和 Plosser (1982) 使用这一实证发现做出进一步更强的声明。他们论证凯恩斯主义宏观经济模型（当时是标准的）暗示经济时间序列是平稳的，而实际商业周期（RBC）模型（当时是新的）暗示经济时间序列是单位根过程。Nelson-Plosser 论证单位根检验不拒绝的实证发现是对 RBC 研究计划的强有力支持。他们的论证有影响力，是推动 RBC 文献兴起的因素。事后看来，我们可以看到 Nelson 和 Plosser (1982) 在后一论证中犯了根本错误。RBC 模型中的单位根行为不是其结构固有的；相反，它是技术过程假设的副产品。（如果外生技术是单位根过程或平稳过程，则宏观经济变量也将分别是单位根过程或平稳过程。）类似地，1970 年代凯恩斯主义模型的平稳行为不是其结构固有的，而是关于不可观测物假设的副产品。从根本上说，单位根/平稳区分对 RBC/凯恩斯主义辩论说得很少。

带拟合截距的 ADF 检验可在 Stata 中通过命令 dfuller y, lags (q) regress 实现。对拟合截距和趋势添加选项 trend。命令中的滞后数”\(q\)“是 (16.7) 中一阶差分的数量，因此 \(q=p-1\)，其中 \(p\) 是自回归阶数。dfuller 命令报告估计回归、ADF 统计量、渐近临界值和近似渐近 p 值。

16.14 KPSS 平稳性检验

Kwiatkowski、Phillips、Schmidt 和 Shin (1992) 开发了原假设为平稳性对备择假设为单位根的检验，被称为 KPSS 检验。许多用户发现这一想法作为 ADF 检验的对立面很有吸引力。

检验从称为局部水平模型的内容推导。这是

\[ \begin{aligned} &Y_{t}=\mu+\theta S_{t}+e_{t} \\ &S_{t}=S_{t-1}+u_{t} \end{aligned} \]

其中 \(e_{t}\) 为均值为零的平稳过程，\(u_{t}\) 为 i.i.d. \(\left(0, \sigma_{u}^{2}\right)\)。当 \(\sigma_{u}^{2}=0\) 时 \(Y_{t}\) 平稳。当 \(\sigma_{u}^{2}>0\) 时 \(Y_{t}\) 为单位根过程。因此平稳性原假设对单位根备择假设的检验是 \(\mathbb{H}_{0}: \sigma_{u}^{2}=0\) 对 \(\mathbb{M}_{1}: \sigma_{u}^{2}>0\) 的检验。添加 \(\left(e_{t}, u_{t}\right)\) 为 i.i.d. 正态的辅助假设。拉格朗日乘数检验可证明对以下大值拒绝 \(\mathbb{H}_{0}\) 支持 \(\mathbb{H}_{1}\)

\[ \frac{1}{n^{2} \widehat{\sigma}^{2}} \sum_{i=1}^{n}\left(\sum_{t=1}^{i} \widehat{e}_{t}\right)^{2} \]

其中 \(\widehat{e}_{t}=Y_{t}-\bar{Y}\) 为原假设下的残差，\(\widehat{\sigma}^{2}\) 为其样本方差。为推广到序列相关 \(e_{t}\) 的情形，KPSS 提出统计量

\[ \mathrm{KPSS}_{1}=\frac{1}{n^{2} \widehat{\omega}^{2}} \sum_{i=1}^{n}\left(\sum_{t=1}^{i} \widehat{e}_{t}\right)^{2} \]

其中

\[ \widehat{\omega}^{2}=\sum_{\ell=-M}^{M}\left(1-\frac{|\ell|}{M+1}\right) \frac{1}{n} \sum_{t=1}^{n} \widehat{e}_{t} \widehat{e}_{t-\ell} \]

是 \(Y_{t}\) 的长期方差 \(\omega^{2}\) 的 Newey-West 估计量。

对允许线性时间趋势的情形，局部水平模型采用形式

\[ Y_{t}=\mu+\beta t+\theta S_{t}+e_{t} \]

其原假设最小二乘估计量为

\[ Y_{t}=\widetilde{\mu}+\widetilde{\beta} t+\widetilde{e}_{t} . \]

注意 \(\widetilde{e}_{t}\) 是线性去趋势的 \(Y_{t}\)。\(\mathbb{H}_{0}\) 对 \(\mathbb{H}_{1}\) 的 KPSS 检验对以下大值拒绝

\[ \mathrm{KPSS}_{2}=\frac{1}{n^{2} \widetilde{\omega}^{2}} \sum_{i=1}^{n}\left(\sum_{t=1}^{i} \widetilde{e}_{t}\right)^{2} \]

其中 \(\widetilde{\omega}^{2}\) 定义为 \(\widehat{\omega}^{2}\) 但使用去趋势残差 \(\widetilde{e}_{t}\)。

定理 16.15 若 \(Y_{t}\) 遵循假设 16.1，则

\[ \operatorname{KPSS}_{1} \underset{d}{\longrightarrow} \int_{0}^{1} V^{2} \]

且

\[ \operatorname{KPSS}_{2} \underset{d}{\longrightarrow} \int_{0}^{1} V_{2}^{2} \]

其中 \(V(r)=W(r)-r W(1)\) 为布朗桥，\(V_{2}(r)=W(r)-\left(\int_{0}^{r} X(s) d s\right)^{\prime}\left(\int_{0}^{1} X X^{\prime}\right)^{\prime} \int_{0}^{1} X d W\)，\(X(s)=(1, s)^{\prime}\)。

定理 16.15 中的渐近分布是非标准的，通常通过模拟计算。过程 \(V_{2}(r)\) 称为二级布朗桥。渐近分布在图 16.4 中显示 \({ }^{6}\)。密度偏斜且具有缓慢衰减的右尾。\(\mathrm{KPSS}_{2}\) 分布与 \(\mathrm{KPSS}_{1}\) 分布相比大幅向原点移动，表明去趋势的显著影响。

渐近临界值在表 16.1 的最后两列中显示。当检验统计量超过临界值时发生拒绝。例如，对带拟合截距和时间趋势的回归，假设统计量等于 \(\mathrm{KPSS}_{2}=0.163\)。这超过 \(4 \%\) 临界值 \(0.157\) 但不超过 \(3 \%\) 临界值 \(0.169\)。因此检验在 \(4 \%\) 水平拒绝但不在 \(3 \%\) 水平。插值 p 值为 \(3.5 \%\)。这将是反对平稳性假设支持非平稳性备择假设的中等证据。

KPSS 统计量依赖于用于估计长期方差 \(\omega^{2}\) 的滞后阶数 \(M\)。这对检验实现是挑战。如果 \(Y_{t}\) 平稳但高度持久（例如，具有大自回归系数的 AR(1)），则滞后截断 \(M\) 需要大以准确估计 \(\omega^{2}\)。然而，在 \(Y_{t}\) 为单位根过程的备择下，估计量 \(\widehat{\omega}^{2}\) 将大致随 \(M\) 线性增长，因此对任何给定样本，通过选择足够大的 \(M\) 可使 KPSS 统计量任意小。

回忆 Andrews (1991) 参考规则 (14.51) 是

\[ M=\left(6 \frac{\rho^{2}}{\left(1-\rho^{2}\right)^{2}}\right)^{1 / 3} n^{1 / 3} \]

其中 \(\rho\) 是 \(Y_{t}\) 的一阶自相关。对 KPSS 检验我们不应将 \(\rho\) 替换为估计量 \(\widehat{\rho}\)，因为后者在 \(\mathbb{H}_{0}\) 下收敛到 1，导致 \(M \rightarrow \infty\) 使检验不一致。相反我们可以

\({ }^{6}\) 由样本量 \(n=10,000\) 的一百万次模拟抽取计算。

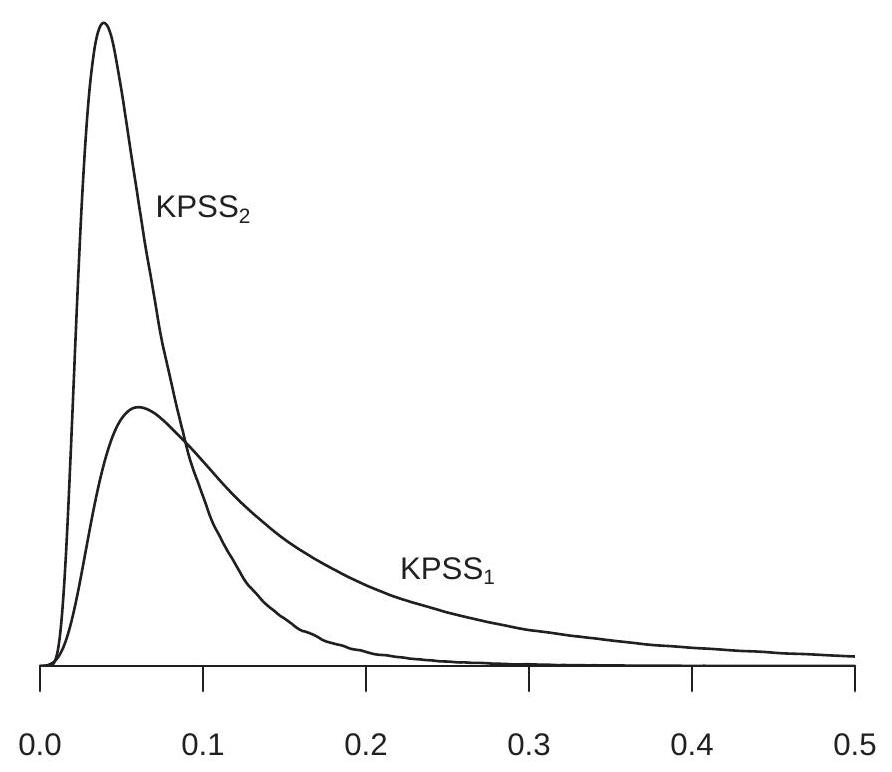
图 16.4：KPSS 分布密度

使用基于合理备择的默认规则。假设我们考虑备择 \(\rho=0.8\)。相关 Andrews 参考规则是 \(M=3.1 n^{1 / 3}\)。这导致简单规则 \(M=3 n^{1 / 3}\)。此选择的解释是当真实是系数 \(0.8\) 的 AR(1) 时它应大致控制检验水平，但对更持久的 AR 过程过度拒绝。

为说明，表 16.2 报告了与前一节检查的相同八个序列的 \(\mathrm{KPSS}_{2}\) 统计量，使用 \(M=3 n^{1 / 3}\)。对前两个季度序列 \(n=228\) 导致 \(M=18\)。对六个月度序列 \(n=684\) 导致 \(M=26\)。对八个序列中的六个（除消费和失业率外的所有）KPSS 统计量等于或超过 \(1 \%\) 临界值，导致拒绝平稳性原假设支持单位根备择。这与对这些序列未能拒绝单位根的 ADF 检验一致。

对消费序列，KPSS 统计量的 p 值为 \(12 \%\)，不拒绝平稳性假设。回忆 ADF 检验未能拒绝单位根假设。因此两个检验都不导致决定性结果；作为一对，两个检验是不确定的。在此背景下我建议坚持经济理论的预测（消费是鞅），因为它不被假设检验拒绝。KPSS 未能拒绝平稳性但这不意味着序列是平稳的。

有趣的情形是失业率序列。它有 \(\mathrm{KPSS}_{2}=0.14\)，p 值为 \(6 \%\)。这对拒绝平稳性是边界显著的。另一方面，回忆 ADF 检验有 \(1 \%\) 的 p 值拒绝单位根假设。这些结果是边界冲突的。为增强我们的信息，我们计算 KPSS \(_{1}\) 检验，因为失业率似乎没有趋势。我们发现 \(\operatorname{KPSS}_{1}=0.19\)，p 值为 \(30 \%\)。这显然在非拒绝区域，未能提供反对平稳性的证据。总体而言，ADF 检验（拒绝单位根）、\(\mathrm{KPSS}_{1}\) 检验（接受平稳性）和 \(\mathrm{KPSS}_{2}\) 检验（边界拒绝平稳性）合起来与失业率是平稳过程的解释一致。

\(\mathrm{KPSS}_{2}\) 检验可在 Stata 中使用命令 \({ }^{7} \mathrm{kpss}\) y, \(\operatorname{maxlag}(\mathrm{q})\) 实现。对 KPSS \(_{1}\) 检验添加选项 notrend。命令报告 \(M=1, \ldots, q\) 的 KPSS 统计量以及渐近临界值。不报告近似渐近 p 值。

16.15 虚假回归

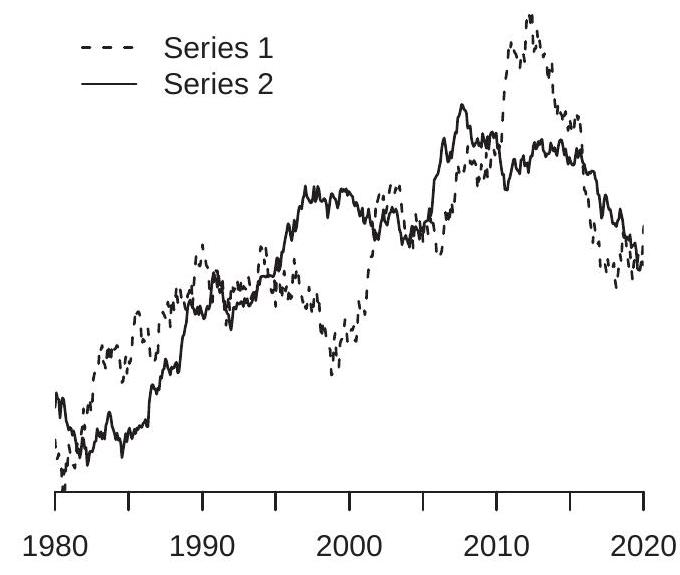
非平稳时间序列理论最实证相关的发现之一是虚假回归现象。这是发现两个统计独立的序列，如果都是单位根过程，可能通过肉眼检查和传统统计检验都显示统计相关来愚弄传统统计分析。现象由 Granger 和 Newbold (1974) 观察 \({ }^{8}\) 并命名，并由 Phillips (1986) 使用非平稳时间序列理论解释。主要教训是容易被非平稳时间序列愚弄，但如果我们适当注意动态规范，问题就消失了。

1. 两个无关随机游走

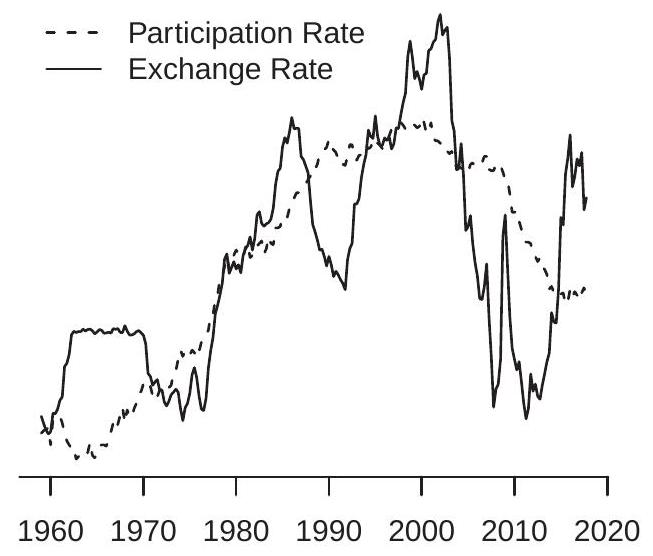
2. 汇率和劳动力参与率

图 16.5：实证序列图

为说明问题，检查图 16.5(a)。显示的是两个时间序列，1980-2018 年月度。图的随意回顾显示两个序列在 1980-2010 年期间总体上升，2000 年左右无增长期，序列在最后十年显示下降趋势。更精细的审视可能似乎揭示序列 2 领先序列 1 约五年，在序列 2 在序列 1 之前约五年达到转折点的意义上。随意观察者可能基于图 16.5(a) 推断两个时间序列强相关。

\({ }^{7}\) 命令 kpss 不是标准包的一部分，但可通过输入 ssc install kpss 安装。

\({ }^{8}\) 在数值模拟中。然而真相是序列 1 和序列 2 是计算机模拟生成的统计独立随机游走，每个标准化为均值为零和单位方差以便视觉比较。两个序列总体上升趋势和”相似”转折点的”事实”是统计意外。随机游走具有愚弄随意分析的不可思议能力。包含时间序列图的报纸（和其他新闻）文章通常受图 16.5(a) 的把戏影响。经济学家也经常被愚弄。

图 16.5(a) 中序列的传统统计检查也可能导致强关系的错误推断。序列 1 对序列 2 的线性回归产生斜率系数 \(0.76\)，经典标准误为 \(0.03\)。零斜率检验的 t 比为 \(T=26\)。方程 \(R^{2}\) 为 \(0.59\)。这些传统统计支持两个序列强相关的错误推断。

这种形式的虚假关系在经济时间序列中很常见。例子显示在图 16.5(b) 中，显示美国劳动力参与率和美加汇率，1960-2018 年季度。作为视觉辅助，两个序列已标准化为均值为零和单位方差。两个序列似乎从 1960-2000 年以相似速率增长，尽管汇率更波动。从 2000-2018 年它们逆转方向，两个序列都下降。视觉证据得到传统统计支持。劳动力参与对汇率的线性回归产生斜率系数 \(0.70\)，经典标准误为 \(0.05\)。零斜率检验的 t 比为 \(T=15\)。方程 \(R^{2}\) 为 \(0.49\)。视觉和统计证据支持两个序列相关的推断。

劳动力参与和汇率相关的这一实证”发现”在经济上没有意义。这是非平稳变量间虚假回归的例子吗？每个序列的视觉检查支持每个都是非平稳且可能很好地刻画为单位根过程的论点。我们在第 16.13 和 16.14 节看到 ADF 和 KPSS 检验支持汇率是单位根过程的假设。对劳动力参与的类似检验达到相同结论。因此两个序列合理地刻画为单位根过程，这两个序列可能是虚假回归的实证例子。

为正式框架假设序列 \(Y_{t}\) 和 \(X_{t}\) 是随机游走过程

\[ \begin{aligned} Y_{t} &=Y_{t-1}+e_{1 t} \\ X_{t} &=X_{t-1}+e_{2 t} \end{aligned} \]

其中 \(\left(e_{1 t}, e_{2 t}\right)\) 是 i.i.d.、均值为零、相互不相关且标准化为单位方差。令 \(Y_{t}^{*}\) 和 \(X_{t}^{*}\) 表示 \(Y_{t}\) 和 \(X_{t}\) 的去均值版本。由 FCLT 它们满足

\[ \left(\frac{1}{\sqrt{n}} Y_{\lfloor n r\rfloor}^{*}, \frac{1}{\sqrt{n}} X_{\lfloor n r\rfloor}^{*}\right) \underset{d}{\longrightarrow}\left(W_{1}^{*}(r), W_{2}^{*}(r)\right) \]

其中 \(W_{1}^{*}(r)\) 和 \(W_{2}^{*}(r)\) 是去均值布朗运动。

应用 CMT，样本相关有渐近分布

\[ \widehat{\rho}=\frac{\frac{1}{n^{2}} \sum_{i=1}^{n} Y_{i}^{*} X_{i}^{*}}{\left(\frac{1}{n^{2}} \sum_{i=1}^{n} Y_{i}^{* 2}\right)^{1 / 2}\left(\frac{1}{n^{2}} \sum_{i=1}^{n} X_{i}^{* 2}\right)^{1 / 2}} \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W_{1}^{*} W_{2}^{*}}{\left(\int_{0}^{1} W_{1}^{* 2}\right)^{1 / 2}\left(\int_{0}^{1} W_{2}^{* 2}\right)^{1 / 2}} . \]

右侧是随机变量。此外它也是非退化的（确实，它以概率 1 非零）。因此样本相关 \(\widehat{\rho}\) 在大样本中保持随机。

为理解量级，图 16.6(a) 显示 \(\widehat{\rho}\) 的渐近分布 \({ }^{9}\)。密度在区间 \([-0.5,0.5]\) 内有大部分概率质量，在该区间上密度基本平坦。这意味着

\({ }^{9}\) 由样本量 \(n=10,000\) 的一百万次模拟抽取计算。样本相关有扩散分布。上面我们看到两个模拟随机游走有样本相关 \({ }^{10}\) \(0.76\)，两个实证序列有样本相关 \(0.70\)。我们现在可以看到这些结果与图 16.6(a) 中显示的分布一致，因此对潜在关系无信息。

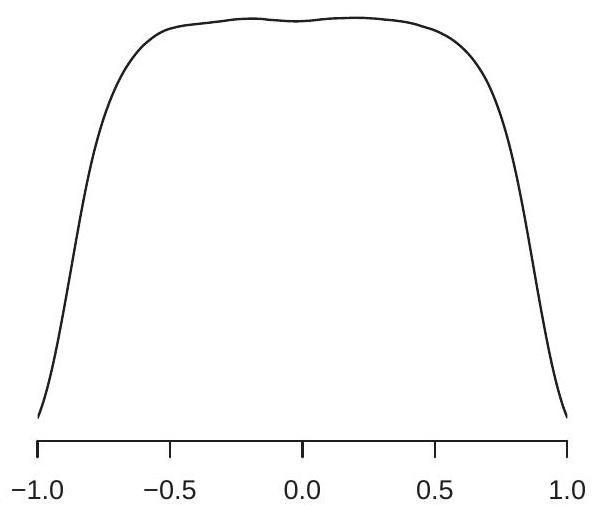
1. 样本相关渐近密度

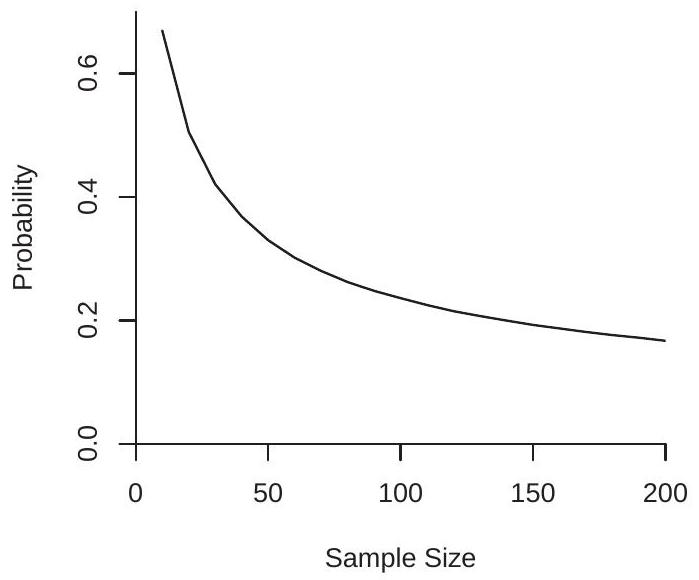
2. 名义 95% 区间覆盖概率

图 16.6：虚假回归性质

我们也可以检查回归估计量。\(Y_{t}\) 对 \(X_{t}\) 回归的斜率系数有渐近分布

\[ \widehat{\beta}=\frac{\frac{1}{n^{2}} \sum_{i=1}^{n} Y_{i}^{*} X_{i}^{*}}{\frac{1}{n^{2}} \sum_{i=1}^{n} X_{i}^{* 2}} \underset{d}{\longrightarrow} \frac{\int_{0}^{1} W_{1}^{*} W_{2}^{*}}{\int_{0}^{1} W_{2}^{* 2}} . \]

这是非退化随机变量。因此斜率估计量在大样本中保持随机且不按概率收敛。

现考虑经典 t 比 \(T\)。它有渐近分布

\[ \frac{1}{n^{1 / 2}} T=\frac{\frac{1}{n^{2}} \sum_{i=1}^{n} Y_{i}^{*} X_{i}^{*}}{\left(\frac{1}{n^{2}} \sum_{i=1}^{n} X_{i}^{* 2}\right)^{1 / 2}\left(\frac{1}{n^{2}} \sum_{i=1}^{n}\left(Y_{i}^{*}-X_{i}^{*} \widehat{\beta}\right)^{2}\right)^{1 / 2}} \underset{d}{\rightarrow} \frac{\int_{0}^{1} W_{1}^{*} W_{2}^{*}}{\left(\int_{0}^{1} W_{2}^{* 2}\right)^{1 / 2}\left(\int_{0}^{1}\left(W_{1}^{*}-W_{2}^{*} \frac{\int_{0}^{1} W_{1}^{*} W_{2}^{*}}{\int_{0}^{1} W_{2}^{* 2}}\right)^{2}\right)^{1 / 2}} . \]

这是非退化的。因此 t 比只有在 \(n^{1 / 2}\) 标准化后才有渐近分布，意味着非标准化 t 比在概率上发散！

为理解经典推断理论的彻底失败，观察回归方程是

\[ Y_{t}=\alpha+\beta X_{t}+\xi_{t} \]

真实值为 \(\alpha=0\) 和 \(\beta=0\)。这意味着误差 \(\xi_{t}=Y_{t}\) 是随机游走。后者比平稳回归理论允许的更强自相关，使传统标准误无效。后者按数量级太小，导致 t 比误导性地大。

\({ }^{10}\) 由于变量已标准化为单位方差，样本相关等于最小二乘斜率系数。这在实践中意味着虚假回归的 t 比是随机且大的，即使没有关系。这解释了模拟序列的大 t 比 \(T=26\) 并显示实证序列的值 \(T=15\) 无信息。大 t 比的原因不是因为序列相关，而是因为序列是单位根过程，所以传统标准误误刻画估计方差。

上述理论的特征之一是它显示 t 比扭曲的幅度随样本大小增加。有趣的是，原始 Granger-Newbold (1974) 分析是模拟研究，将注意力限制在情形 \(n=50\)。Granger-Newbold 发现（当时令人惊讶的）结果，即 t 检验在零系数原假设下大幅过度拒绝。直到 Phillips (1986) 的理论分析才意识到这种扭曲随样本大小增加而恶化。这些结果说明了模拟分析的洞察——和局限性。使用模拟 Granger-Newbold 指出存在问题。但通过将样本大小固定在单一值，他们没有发现样本大小的令人惊讶效应。

t 比随 \(n\) 增加发散的事实意味着经典置信区间的覆盖随 \(n\) 增加而恶化。为校准这种扭曲的幅度，检查图 16.6(b)。这绘制 \({ }^{11}\) 使用学生 \(t\) 临界值的经典名义 \(95 \%\) 置信区间对斜率的有限样本覆盖概率，作为样本大小 \(n\) 的函数绘制。观测值生成为具有正态创新的独立随机游走。你可以看到覆盖范围从 \(0.68\)（对 \(n=10\)）到 \(0.2\)（对 \(n=200\)）。这些覆盖率不可接受地低于名义覆盖水平 \(0.95\)。

上述分析聚焦于经典 t 比和用老式同方差标准误构造的置信区间。这似乎可能是过时的分析，因为我们已经论证老式标准误在当代计量经济学实践中不使用。然而所描述的问题延续到替代标准误构造。常见异方差标准误不根本改变渐近分布。Newey-West 标准误减少覆盖不足但仅部分。它们设计为一致估计平稳序列的长期方差，但当序列非平稳时失败。

此时让我们收集我们学到的。如果我们有两个时间序列，它们是独立单位根过程，则通过时间序列图、相关分析和简单线性回归，容易做出它们相关的错误推断。它们的样本相关和回归斜率估计将是随机的、不一致的且无信息的。

我们的推论是处理潜在非平稳时间序列时使用简单推断技术是不适当的。我们需要更仔细并使用更好的推断方法。

事实证明简单修改通常足以根本改变推断问题。再次，假设我们观察独立序列 (16.10)-(16.11)。线性回归模型是 (16.12)，误差 \(\xi_{t}=Y_{t}\)。我们可以将后者写作 \(\xi_{t}=Y_{t-1}+e_{t}\)。这意味着回归模型的正确动态规范是

\[ Y_{t}=\alpha+\beta X_{t}+\delta Y_{t-1}+e_{t} \]

其中 \(\alpha=\beta=0\) 且 \(\delta=1\)。如果估计方程 (16.13)，误差不再是随机游走，对 \(\beta\) 的推断可以传统进行！在这个简单例子中，解决方案是简单地在估计回归中包含滞后因变量 \(Y_{t-1}\)。更一般地，如果趋势分量缺失或 \(\Delta Y_{t}\) 序列相关，则有必要在估计回归中包含趋势项和/或 \(Y_{t}\) 的足够滞后。

例如，取图 16.5(a) 的模拟随机游走序列。估计模型 (16.13) 我们发现 \(\widehat{\beta}=0.004\)，标准误为 \(0.005\)。因此通过添加滞后因变量

\({ }^{11}\) 在 \(n\) 值网格上通过一百万次模拟重复计算。虚假回归关系已被打破。现在取图 16.5(b) 的实证序列。我们估计 (16.13) 的类似物，用线性趋势增强。此模型中 \(\beta\) 的估计是 \(0.16\)，标准误为 \(0.12\)。再次，虚假回归关系通过简单动态重新调整被打破。

这似乎是直接解决方案。如果是这样，为什么虚假回归问题在应用分析中持续存在 \({ }^{12}\)？原因部分是非专家发现简单回归 (16.12) 容易解释，而动态模型 (16.13) 具有挑战性解释。熟练计量经济学家的任务之一是理解这种推理失败，向同事和用户解释问题，并呈现建设性有用的替代分析方法。

\({ }^{12}\) 一个有趣的练习是浏览报纸/杂志文章中的历史序列时间序列图。更常见的是显示的序列似乎是 \(I(1)\)，更常见的是文章基于肉眼分析和简单相关统计的组合将序列描述为”相关”。

16.16 非平稳 VAR

令 \(Y_{t}\) 为 \(m \times 1\) 时间序列。假设 \(Y_{t}\) 满足一阶差分的 VAR(p-1)，因此 \(\boldsymbol{D}(\mathrm{L}) \Delta Y_{t}=e_{t}\)，其中 \(\boldsymbol{D}(z)\) 可逆且 \(\Sigma=\operatorname{var}\left[e_{t}\right]>0\)。则 \(\Delta Y_{t}\) 具有长期协方差矩阵 \(\Omega=\boldsymbol{D}(1)^{-1} \Sigma \boldsymbol{D}(1)^{-1 \prime}>0\)。在此情形下 \(Y_{t}\) 是向量 \(I(1)\) 过程，在 \(Y_{t}\) 的每个元素都是 \(I(1)\) 且 \(Y_{t}\) 的所有线性组合也都是 \(I(1)\) 的意义上。

模型可写作水平的 VAR

\[ Y_{t}=\boldsymbol{A}_{1} Y_{t-1}+\boldsymbol{A}_{2} Y_{t-2}+\cdots+\boldsymbol{A}_{p} Y_{t-p}+e_{t} \]

其中 \(\boldsymbol{A}_{1}+\boldsymbol{A}_{2}+\cdots+\boldsymbol{A}_{p}=\boldsymbol{I}_{m}\)。它也可写作混合格式

\[ \Delta Y_{t}=\boldsymbol{A} Y_{t-1}+\boldsymbol{D}_{1} \Delta Y_{t-1}+\cdots+\boldsymbol{D}_{p-1} \Delta Y_{t-p+1}+e_{t} \]

其中 \(\boldsymbol{A}=0\)。这些是等价的代数表示。令 \(d=\operatorname{vec}\left(\left(\boldsymbol{D}_{1}, \ldots, \boldsymbol{D}_{p-1}\right)^{\prime}\right)\)。

令 \((\widehat{\boldsymbol{A}}, \widehat{d})\) 为 (16.15) 的多元最小二乘估计量。设 \(X_{t}=\left(\Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\right)\)。

定理 16.16 假设 \(\Delta Y_{t}\) 遵循 \(\operatorname{VAR}(\mathrm{p}-1)\) 过程 \(\boldsymbol{D}(\mathrm{L}) \Delta Y_{t}=e_{t}\)，\(\boldsymbol{D}(z)\) 可逆，\(\mathbb{E}\left[e_{t} \mid \mathscr{F}_{t-1}\right]=0\)，\(\mathbb{E}\left\|e_{t}\right\|^{4}<\infty\)，且 \(\mathbb{E}\left[e_{t} e_{t}^{\prime}\right]=\Sigma>0\)。则当 \(n \rightarrow \infty\) 时

\[ \left(\begin{array}{c} n \widehat{\boldsymbol{A}} \\ \sqrt{n}(\widehat{d}-d) \end{array}\right) \underset{d}{\longrightarrow}\left(\begin{array}{c} \Sigma^{1 / 2} \int_{0}^{1} d W W^{\prime}\left(\int_{0}^{1} W W^{\prime}\right)^{-1} \Omega^{-1 / 2} \\ \mathrm{~N}(0, \boldsymbol{V}) \end{array}\right) \]

其中 \(W(r)\) 为向量布朗运动，且

\[ \begin{aligned} &\boldsymbol{V}=\left(\boldsymbol{I}_{m} \otimes \mathbb{E}\left[X_{t} X_{t}^{\prime}\right]\right)^{-1} \Omega\left(\boldsymbol{I}_{m} \otimes \mathbb{E}\left[X_{t} X_{t}^{\prime}\right]\right)^{-1} \\ &\Omega=\mathbb{E}\left[e_{t} e_{t}^{\prime} \otimes X_{t} X_{t}^{\prime}\right] . \end{aligned} \]

渐近分布的顶部分量是 Dickey-Fuller 系数分布的多元版本。底部分量是传统正态分布。这表明

\({ }^{12}\) 一个有趣的练习是浏览报纸/杂志文章中的历史序列时间序列图。更常见的是显示的序列似乎是 \(I(1)\)，更常见的是文章基于肉眼分析和简单相关统计的组合将序列描述为”相关”。系数估计量 \(\widehat{\boldsymbol{A}}\) 以 \(O_{p}\left(n^{-1}\right)\) 速率一致，收敛到非标准（偏倚且非正态）渐近分布，系数估计量 \(\widehat{d}\) 具有传统渐近正态分布。

感兴趣的参数，包括水平方程 (16.14) 的系数、脉冲响应函数和预测误差分解，是估计量 \((\widehat{\boldsymbol{A}}, \widehat{d})\) 的线性组合。对 \(p \geq 2\) 的 \(\operatorname{VAR}(\mathrm{p})\) 模型，除非感兴趣的线性组合在 \(\widehat{A}\) 的跨度中，否则估计量的渐近分布由 \(O_{p}\left(n^{-1 / 2}\right)\) 分量 \(\widehat{d}\) 主导。因此这些系数估计量具有传统渐近正态分布。因此，对大多数目的，VAR 模型的估计和推断对（多元）单位根的存在是稳健的。

有两个重要例外。首先，对水平系数和 \(A_{1}+A_{2}+\cdots+A_{p}\) 的推断是非标准的，因为该和的估计量具有多元 Dickey-Fuller 系数分布。这包括关于单位根存在的问题和关于序列长期性质的许多问题。其次，长期脉冲矩阵 \(C=A^{-1}=\left(I-A_{1}-A_{2}-\cdots-A_{p}\right)^{-1}\) 是同一和的（非线性）函数，因此通过 Delta 方法渐近是多元 Dickey-Fuller 系数分布的线性变换。这意味着 \(\boldsymbol{C}\) 的最小二乘估计量是非标准的（偏倚且非正态）。由于 \(\boldsymbol{C}\) 是 CIRF 在水平趋于无穷时的极限，这表明 CIRF 在长期水平的估计量在有限样本中是非标准的。因此当 VAR 模型包含可能是单位根过程的变量时，CIRF 在长期水平的传统置信区间不可信。这是一个广泛问题，因为宏观经济学家常规估计带水平宏观经济变量的 VAR 模型（例如，第 15.25 节提出的 Blanchard-Perotti (2002) 模型）。

16.17 协整

一个迷人的主题是协整。这一想法源于 Granger (1981)，由 Engle 和 Granger (1987) 详细阐述。一对单位根过程如果它们的差分（或某个线性组合）是平稳的，则它们是协整的。这意味着这对”长期一起”。

为可视化，检查图 16.7(a)。这显示两个利率序列。实线是十年期美国国债的利率 \({ }^{13}\)（1959-2017 年季度）。虚线是三个月期美国国债的利率 \({ }^{14}\)。在 59 年期间两个序列一起上下移动。十年期利率在大多数时期超过三个月期利率。对某些时期两条线分开但它们总是再次聚在一起。这表明两个时间序列紧密联系在一起。从我们的单位根分析我们已经确定十年期利率与单位根过程一致；相同发现适用于三个月期序列。因此这些似乎是两个单独为单位根过程但联合密切跟踪彼此的时间序列。

为进一步看到这一点，定义利率利差为两个利率的差，长期（十年期）减去短期（三个月期）。该序列绘制在图 16.7(b) 中。序列的均值由虚线显示。我们可以看到利差大致似乎是均值回归的。除了图的前十年可能例外，我们看到利差每个十年多次穿越其均值。波动似乎是平稳的。对利差应用无趋势的 ADF 单位根检验产生 \(\mathrm{ADF}=-4.0\)，小于 \(1 \%\) 临界值，拒绝利差单位根的原假设。因此两个利率的水平似乎是非平稳的，而利差是平稳的。这提示两个利率序列是协整的。

这一概念在以下定义中形式化。

\({ }^{13}\) 来自 FRED-QD，序列 gs10。

\({ }^{14}\) 来自 FRED-QD，序列 tb3ms。

1. 利率

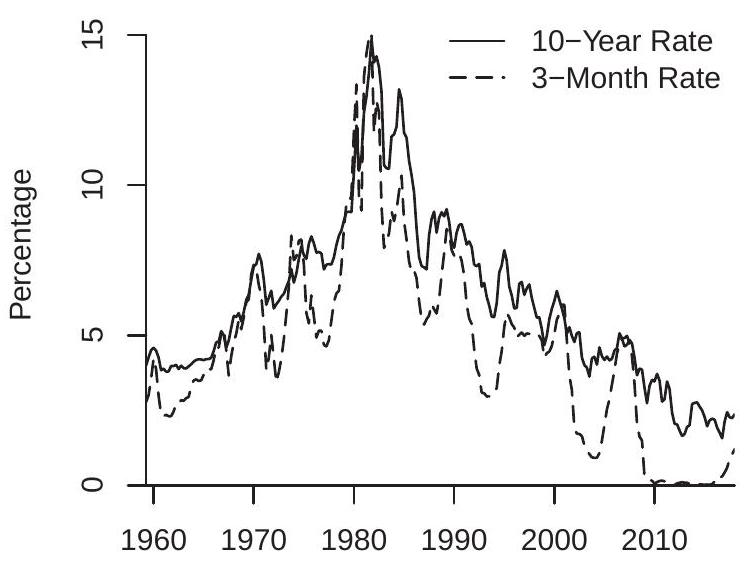
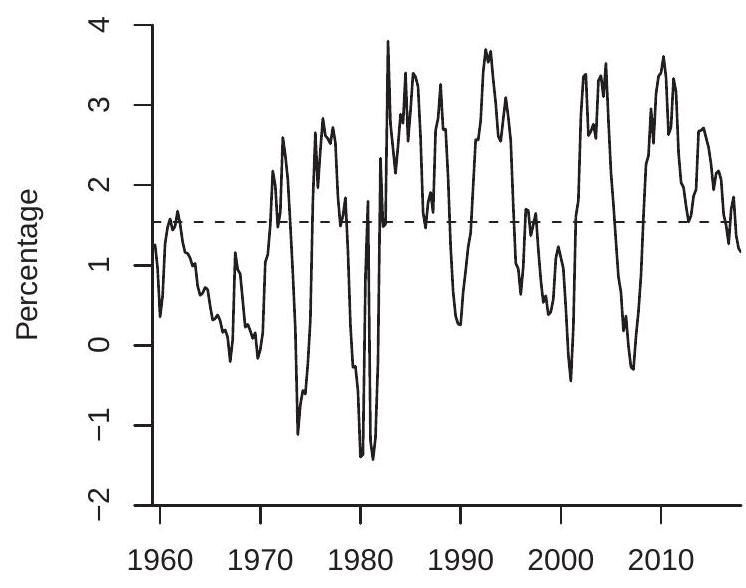
2. 利率利差

图 16.7：协整

定义 16.5 \(m \times 1\) 非确定性序列 \(Y_{t}\) 是协整的，如果存在满秩 \(m \times m\) 矩阵 \(\left[\beta, \beta_{\perp}\right]\) 使得 \(\beta^{\prime} Y_{t} \in \mathbb{R}^{r}\) 和 \(\beta_{\perp}^{\prime} \Delta Y_{t} \in \mathbb{R}^{m-r}\) 是 \(I(0)\)。\(\beta\) 中的 \(r\) 个向量称为协整向量。变量 \(Z_{t}=\beta^{\prime} Y_{t}\) 称为均衡误差。

在图 16.7 的利率例子中，有 \(m=2\) 个序列和 \(r=1\) 个协整关系。我们的讨论假设协整向量是 \(\beta=(1,-1)^{\prime}\)。

协整向量 \(\beta\) 不是单独识别的；只有向量张成的空间被识别，所以 \(\beta\) 通常被标准化。当 \(r=1\) 时，常见标准化是设置一个非零元素等于 1。另一个常见标准化是设置 \(\beta\) 为正交：\(\beta^{\prime} \beta=\boldsymbol{I}_{r}\)。

定理 16.17 Granger 表示定理。如果非确定性 \(Y_{t} \in \mathbb{R}^{m}\) 与 \(m \times r\) 协整向量 \(\beta\) 协整且 (16.1) 成立，则

1. Wold 表示的系数

\[ \Delta Y_{t}=\theta+\Theta(\mathrm{L}) e_{t} \]

满足 \(\Theta(1)=\beta_{\perp} \eta^{\prime}\) 和 \(\theta=\beta_{\perp} \gamma\)，对某个满秩 \(m \times(m-r)\) 矩阵 \(\eta\) 和某个 \((m-r) \times 1\) 向量 \(\gamma\)。

2. \(Y_{t}\) 的 Beveridge-Nelson 分解是

\[ Y_{t}=\beta_{\perp}\left(\gamma t+\eta^{\prime} S_{t}\right)+U_{t}+V_{0} \]

其中 \(S_{t}=\sum_{i=1}^{t} e_{t}\)，\(U_{t}=\Theta^{*}(\mathrm{~L}) e_{t}\) 是平稳线性过程，\(V_{0}=Y_{0}-U_{0}\) 是初始条件。

3. 假设 (a) \(\operatorname{det}(\Theta(z))=0\) 的所有复解要么是 \(z=1\) 要么是 \(|z| \geq 1+\delta\) 对某个 \(\delta>0\)；(b) \(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\) 满秩，其中 \(\eta_{\perp}\) 是满秩 \(m \times r\) 矩阵使得 \(\eta^{\prime} \eta_{\perp}=0\)。则 \(Y_{t}\) 具有（无限阶）收敛 VAR 表示

\[ \boldsymbol{A}(\mathrm{L}) Y_{t}=a+e_{t} \]

其中系数满足 \(\boldsymbol{A}(1)=-\eta_{\perp}\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} \beta^{\prime}\)。\(\operatorname{det}(\boldsymbol{A}(z))=0\) 的所有复解要么是 \(z=1\) 要么是 \(|z| \geq 1+\delta\) 对某个 \(\delta>0\)。

4. 在部分 3 的假设加上 \(\sum_{j=0}^{\infty}\left\|\sum_{k=0}^{\infty} k \Theta_{j+k}\right\|^{2}<\infty\) 下，VAR 表示可写作误差修正形式

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma(\mathrm{L}) \Delta Y_{t-1}+a+e_{t} \]

其中 \(\Gamma(\mathrm{L})\) 是具有绝对可和系数矩阵的滞后多项式，\(\alpha=-\eta_{\perp}\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1}\)。

5. 如果 Wold 表示 (16.16) 中 \(\theta=0\)，则 (16.17) 中 \(\gamma=0\)，所以 (16.17) 中没有线性趋势。(16.18) 和 (16.19) 中的截距等于 \(a=\alpha \mu\)，其中 \(\mu\) 是 \(r \times 1\)。方程 (16.19) 可写作

\[ \Delta Y_{t}=\alpha\left(\beta^{\prime} Y_{t-1}+\mu\right)+\Gamma(\mathrm{L}) \Delta Y_{t-1}+e_{t} . \]

证明见第 16.22 节。Granger 表示定理出现在 Engle 和 Granger (1987) 中。\(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\) 的假设由 Johansen (1995, 定理 4.5) 引入。

部分 1 显示 Wold 表示的系数和等于协整向量零空间中的奇异矩阵。

部分 2 给出 \(Y_{t}\) 的 Beveridge-Nelson 永久-暂时表示。它显示趋势 \(\beta_{\perp}\left(\gamma t+\eta^{\prime} S_{t}\right)\) 位于协整向量的零空间中。因此在协整向量的值空间中无趋势。这表明协整向量 \(Y_{t}\) 可被认为具有 \(r\) 个”单位根和线性趋势”和 \(m-r\) 个”平稳过程”。部分 3 提供 VAR 表示。它显示 VAR 系数和等于协整向量值空间中的奇异矩阵。

部分 4 也许是最著名的结果。它显示协整系统满足方程 (16.19)，称为误差修正表示。误差修正表示是平稳变换中的回归模型，因为变量 \(\Delta Y_{t}\) 和 \(\beta^{\prime} Y_{t-1}\) 是平稳的。方程显示变化 \(\Delta Y_{t}\) 与过去变化 \(\Delta Y_{t-1}\)（如在标准 VAR 中）以及均衡误差 \(\beta^{\prime} Y_{t-1}\) 相关。完整项 \(\alpha \beta^{\prime} Y_{t-1}\) 称为”误差修正项”。它是控制协整关系如何维持的关键分量。

部分 5 检查无线性趋势的情形。条件 \(\theta=0\) 在变量 \(\Delta Y_{t}\) 都均值为零时出现。定理（不令人惊讶地）显示这暗示线性趋势不出现在 Beveridge-Nelson 分解中。更有趣的是定理显示此条件暗示误差修正模型可写作包含截距。

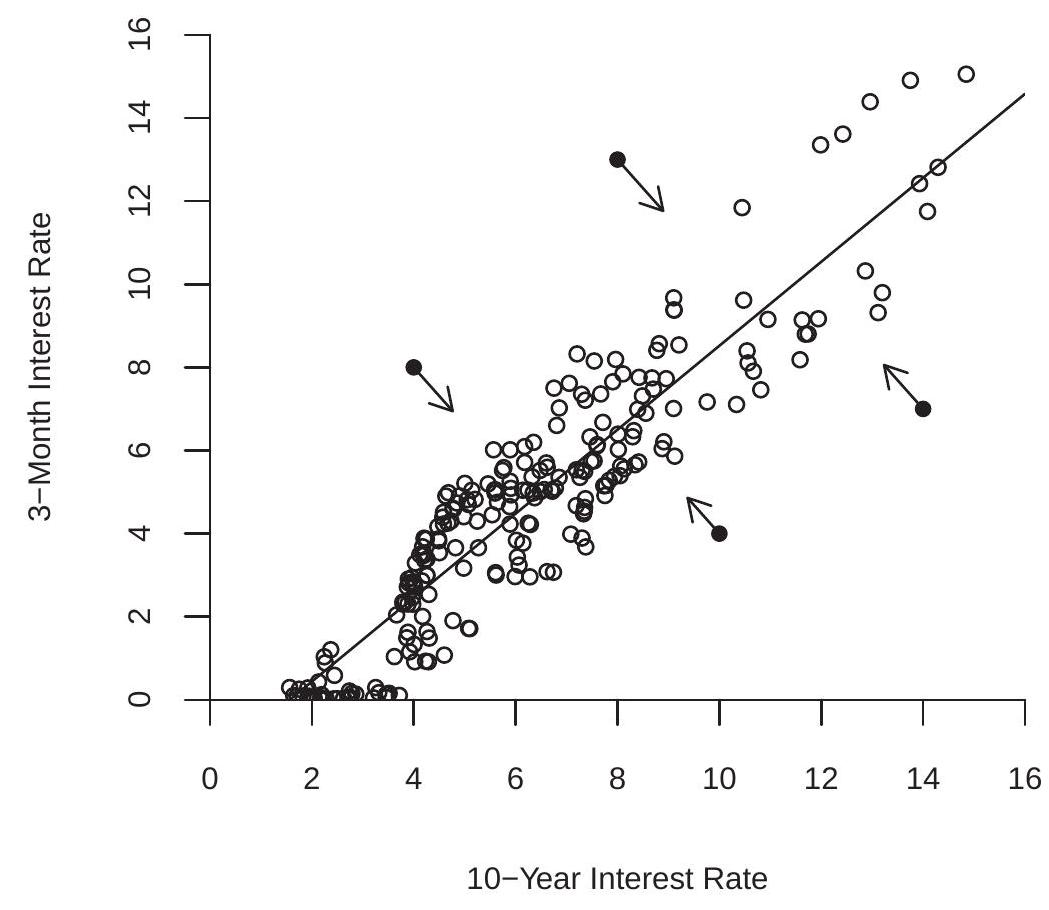
图 16.8：误差修正效应

为理解误差修正效应，检查图 16.8。这显示图 16.7 中两个利率序列的历史值散点图。还绘制了线性关系 \(\beta^{\prime} Y+\mu\) 的估计 \({ }^{15}\)，显示为实线。这是系统的吸引子。对 \(Y\) 在此线上的值 \(\beta^{\prime} Y+\mu=0\)。对东南方的值 \(\beta^{\prime} Y+\mu<0\)，对西北方的值 \(\beta^{\prime} Y+\mu>0\)。\(\alpha\) 的分量决定这些值如何影响 \(\Delta Y\) 的预期方向。箭头指示这些方向 \({ }^{16}\)。当 \(\beta^{\prime} Y+\mu>0\) 时误差修正减少三个月期利率并增加

\({ }^{15}\) 来自表 16.4

\({ }^{16}\) 来自表 16.5 的估计。十年期利率，推动 \(Y\) 朝向吸引线。当 \(\beta^{\prime} Y+\mu<0\) 时误差修正增加三个月期利率并减少十年期利率，再次推动 \(Y\) 朝向吸引线。在此特定例子中两个效应量级相似，所以箭头显示两个变量都响应偏离而朝向吸引子移动。

定理 16.17 显示如果 \(Y_{t}\) 协整则它满足 VECM。反之亦然。

定理 16.18 Granger 表示定理，第二部分。假设 \(Y_{t}\) 满足 \(\operatorname{VAR}(\infty)\) 模型 \(\boldsymbol{A}(\mathrm{L}) Y_{t}=a+e_{t}\) 且具有 VECM 表示

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma(\mathrm{L}) \Delta Y_{t-1}+a+e_{t} \]

其中 \(\beta\) 和 \(\alpha\) 是 \(m \times r\) 且满秩。假设 (a) \(\operatorname{det}(\boldsymbol{A}(z))=0\) 的所有复解要么是 \(z=1\) 要么是 \(|z| \geq 1+\delta\) 对某个 \(\delta>0\)；(b) \(\sum_{j=0}^{\infty}\left\|\Gamma_{j}\right\|<\infty\)；(c) \(\alpha_{\perp}^{\prime}\left(\boldsymbol{I}_{m}-\Gamma(1)\right) \beta_{\perp}\) 满秩，其中 \(\alpha_{\perp}\) 和 \(\beta_{\perp}\) 位于 \(\alpha\) 和 \(\beta\) 的零空间中。则 \(Y_{t}\) 与协整向量 \(\beta\) 协整。

证明见第 16.22 节。有限阶 VAR 的这一结果首次出现在 Johansen (1995, 定理 4.2) 中。

\(\alpha_{\perp}^{\prime} \Gamma(1) \beta_{\perp}\) 满秩的条件是排除系统”多协整”（意味着 \(\beta^{\prime} Y_{t-1}\) 和 \(\Delta Y_{t-1}\) 的线性组合具有降低积分阶数）的（有些病态）可能性的必要条件。综合，定理 16.17 和 16.18 显示 VECM 表示是向量时间序列协整的充要条件。

16.18 截距和趋势的作用

协整 VECM 中截距和趋势的作用产生不同模型。我们列出一些主要选项。

1. 趋势模型 1。此规范无截距或趋势项

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma(\mathrm{L}) \Delta Y_{t-1}+e_{t} . \]

这对教学方便但不相关于实证应用。在 Stata 中使用选项 trend (none)。

2. 趋势模型 2。此规范适用于非趋势序列如利率。在此模型中截距在协整关系中

\[ \Delta Y_{t}=\alpha\left(\beta^{\prime} Y_{t-1}+\mu\right)+\Gamma(\mathrm{L}) \Delta Y_{t-1}+e_{t} . \]

在 Stata 中使用选项 trend (rconstant)。

3. 趋势模型 3。这适用于可能有线性趋势的序列。此模型有无约束截距

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma(\mathrm{L}) \Delta Y_{t-1}+a+e_{t} . \]

在此模型中水平序列 \(Y_{t}\) 是线性时间趋势和单位根过程的和。均衡误差 \(\beta^{\prime} Y_{t}\) 是平稳的，所以消除线性时间趋势和单位根分量。在 Stata 中使用选项 trend (constant)。

4. 趋势模型 4。此模型扩展 VECM 模型以允许协整关系中的线性趋势。此模型是

\[ \Delta Y_{t}=\alpha\left(\beta^{\prime} Y_{t-1}+\mu t\right)+\Gamma(\mathrm{L}) \Delta Y_{t-1}+a+e_{t} . \]

在此模型中水平序列 \(Y_{t}\) 是线性时间趋势和单位根过程的和。均衡误差 \(\beta^{\prime} Y_{t}\) 包含线性时间趋势和平稳过程。因此协整向量 \(\beta\) 只消除单位根，不消除时间趋势分量。在 Stata 中使用选项 trend (rtrend)。

5. 趋势模型 5。这是进一步扩展允许无约束趋势项

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma(\mathrm{L}) \Delta Y_{t-1}+a+b t+e_{t} . \]

在此模型中无约束趋势在水平序列 \(Y_{t}\) 中引入二次时间趋势。这对应用经济时间序列不是典型建模选择。在 Stata 中使用选项 trend (trend)。

16.19 协整回归

如果 \(Y_{t}\) 与单个协整向量 \((r=1)\) 协整，则事实证明 \(\beta\) 可以通过 \(Y_{t}\) 的一个分量对其他分量的最小二乘回归来估计。当主要焦点是协整向量、变量数 \(m\) 小（例如 \(m=2\) 或 \(m=3\)）且已知协整向量数 \(r\) 至多为 1 时，这种方法可能富有成效地使用。

分割 \(Y_{t}=\left(Y_{1 t}, Y_{2 t}\right)\) 并将 \(\beta\) 重新参数化为 \((1,-\beta)\)。因此协整向量的第一个分量已被标准化为 1（这要求真实值非零）且其余乘以 \(-1\)。感兴趣的系数是 \(\beta\)。最小二乘拟合方程

\[ Y_{1 t}=\mu+\beta^{\prime} Y_{2 t}+u_{1 t} \]

（对趋势模型 1 或 2）或方程

\[ Y_{1 t}=\mu+\theta t+\beta^{\prime} Y_{2 t}+u_{1 t} \]

（对趋势模型 3 或 4）。

定义 \(u_{2 t}=\Delta Y_{2 t}\)，\(u_{t}=\left(u_{1 t}, u_{2 t}^{\prime}\right)^{\prime}\)，和长期协方差矩阵 \(\Omega=\Sigma+\Lambda+\Lambda^{\prime}\)，其中 \(\Sigma=\mathbb{E}\left[u_{t} u_{t-\ell}^{\prime}\right]\) 且 \(\Lambda=\sum_{\ell=1}^{\infty} \mathbb{E}\left[u_{t-\ell} u_{t}^{\prime}\right]\)。分割协方差矩阵与 \(Y\) 一致，例如

\[ \Omega=\left[\begin{array}{ll} \Omega_{11} & \Omega_{12} \\ \Omega_{21} & \Omega_{22} \end{array}\right] . \]

定理 16.19 如果 \(u_{t}\) 满足定理 16.4 的条件且 \(\Omega_{22}>0\)，则最小二乘估计量满足

\[ n(\widehat{\beta}-\beta) \underset{d}{\longrightarrow}\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X d B_{1}+\Sigma_{21}+\Lambda_{21}\right) \]

其中 \(B(r)=\left(B_{1}(r), B_{2}(r)\right)\) 是具有协方差矩阵 \(\Omega\) 的向量布朗运动，\(X(r)\) 由模型确定：

趋势模型 1 或 2 通过 \((16.21)\) 估计：\(X=B_{2}^{*}\)（去均值 \(B_{2}(r)\)）。

趋势模型 3 或 4 通过 (16.22) 估计：\(X=B_{2}^{* *}\)（去趋势 \(B_{2}(r)\)）。证明见第 16.22 节。

定理 16.19 显示估计量以超一致 \(O_{p}\left(n^{-1}\right)\) 速率收敛。这由 Stock (1987) 发现，渐近分布由 Park 和 Phillips (1988) 推导。由于序列相关项，渐近分布是非标准的。以我们的实证例子为例。三个月期利率对十年期利率的最小二乘回归产生估计方程 \(\widehat{Y}_{1 t}=1.03 Y_{2 t}-1.71\)。

消除非标准分量的最小二乘估计量修改由 Phillips 和 B. E. Hansen (1990) 以及 Stock 和 Watson (1993) 引入。Phillips-Hansen 估计量，称为完全修正 OLS (FM-OLS)，通过序列相关项的第一阶段估计消除非标准分量。Stock-Watson 估计量，称为动态 OLS (DOLS)，通过估计包含 \(\Delta Y_{2 t}\) 的领先和滞后的增广回归消除非标准分量。

我们经常对检验无协整假设感兴趣：

\[ \begin{aligned} &\mathbb{H}_{0}: r=0 \\ &\mathbb{H}_{1}: r>0 . \end{aligned} \]

在 \(\mathbb{H}_{0}\) 下，\(Z_{t}=\beta^{\prime} Y_{t}\) 是 \(I(1)\)，但在 \(\mathbb{H}_{1}\) 下 \(Z_{t}\) 是 \(I(0)\)。当 \(\beta\) 已知时，\(\mathbb{H}_{0}\) 可通过在 \(Z_{t}\) 上应用单变量 ADF 检验来检验。以利率例子为例。我们已经推测利率利差是平稳的，这与 \(\beta=1\) 是协整系数的假设相同。使用此值我们计算 \(\mathrm{ADF}=-4.0\)，渐近 \(\mathrm{p}\) 值小于 \(0.01\)。因此我们能够拒绝利差中单位根的原假设，或等价地拒绝无协整的原假设。

当 \(\beta\) 未知时，Engle 和 Granger (1987) 提出通过将 ADF 检验应用于来自 (16.21) 或 (16.22) 的最小二乘残差 \(\widehat{u}_{1 t}\) 来检验无协整的原假设。渐近原分布与 Dickey-Fuller 分布不同，因为在 \(\mathbb{M}_{0}\) 下估计回归是虚假的，所以最小二乘估计量不一致。统计量的渐近分布由 Phillips 和 Ouliaris (1990) 通过将虚假回归理论与 Dickey-Fuller 分布理论结合得出。令 \(\mathrm{EG}_{p}\) 表示 Engle-Granger ADF 统计量，在 ADF 回归中有 \(p\) 个自回归滞后。

定理 16.20 假设 \(\left(\Delta Y_{1 t}, \Delta Y_{2 t}\right)\) 满足定理 16.4 的条件且 \(\Omega>0\)。如果 \(p \rightarrow \infty\) 当 \(n \rightarrow \infty\) 时使得 \(p^{3} / n \rightarrow 0\)，则

\[ \mathrm{EG}_{p} \underset{d}{\rightarrow} \frac{\left(\int_{0}^{1} V d V\right)}{\left(\int_{0}^{1} V^{2}\right)^{1 / 2}\left(1+\zeta^{\prime} \zeta^{1 / 2}\right.} \]

其中，\(V(r)=W_{1}^{*}(r)-\zeta^{\prime} W_{2}^{*}(r)\) 且 \(\zeta=\left(\int_{0}^{1} W_{2}^{*} W_{2}^{* \prime}\right)^{-1}\left(\int_{0}^{1} W_{2}^{*} W_{1}^{*}\right)\)，\(W(r)=\left(W_{1}(r), W_{2}(r)\right)\) 是向量标准布朗运动，\(W^{*}(r)\) 是去均值 \(W(r)\)（如果估计 (16.21)）或去趋势 \(W(r)\)（如果估计 (16.22)）。

证明见 Phillips 和 Ouliaris (1990)。

此定理的一个不寻常特征是它要求 \(p \rightarrow \infty\) 当 \(n \rightarrow \infty\) 时，即使真实过程是有限阶 AR 过程，因为第一阶段虚假回归在第一阶段残差中引入序列相关，需要在第二阶段 ADF 检验中处理。另一个不寻常特征是分母中的分量 \(1+\zeta^{\prime} \zeta\)。这是由于方差估计量分量，由于第一阶段虚假回归，它渐近是随机的。

表 16.3：Engle-Granger 协整检验临界值

来源：由样本量 \(n=10,000\) 的一百万次重复模拟计算。

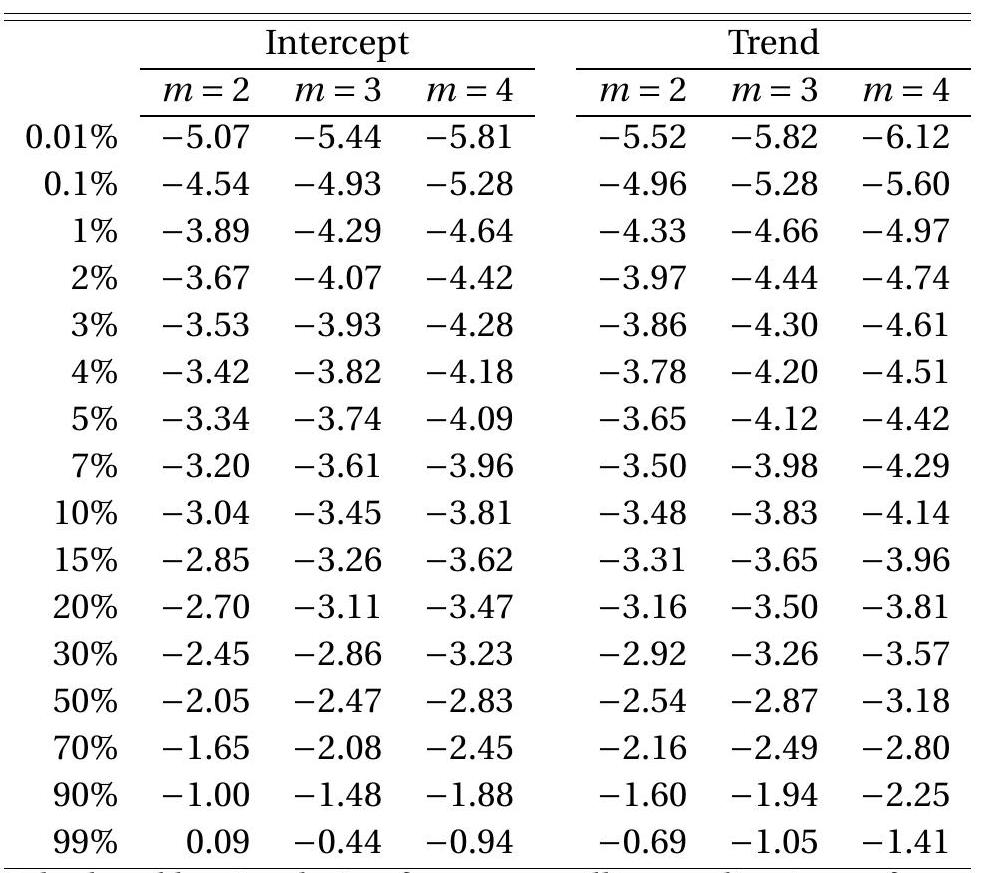
渐近临界值 \({ }^{17}\) 在表 16.3 中显示。EG 检验是单侧的，所以当检验统计量小于（比）临界值更负时发生拒绝。临界值是变量数 \(m\) 和去趋势方法的函数。

让我们总结 Engle-Granger 协整检验：原假设是序列不协整，或等价地均衡误差是 \(I(1)\)。备择假设是协整。回归 (16.21) 或 (16.22) 通过最小二乘估计以获得残差。ADF 检验应用于此残差。这通过拟合 \(\operatorname{AR}(\mathrm{p})\) 模型并检验自回归系数和等于 1 来完成。临界值根据趋势规范（下面讨论）和变量数 \(m\) 从表 16.3 中取。如果 t 统计量小于适当临界值，则无协整的原假设被拒绝，支持协整假设。否则，无协整假设不被拒绝。

一个重要问题是拟合哪个趋势模型。如果观测值无趋势，则应拟合截距回归 (16.21) 并使用”截距”临界值。如果观测值有趋势且无约束，则应拟合趋势回归 (16.22) 并使用”趋势”临界值。在模型 3 的情形中出现复杂性，它允许观测值有趋势但趋势从协整回归中排除。在此情形下有两个选项。一个是将情况视为模型 4：估计回归 (16.22) 并使用相关临界值。另一个选项是估计 (16.21)，因为线性趋势不在协整关系中。在此情形下适当临界值来自表的”趋势”部分，但行对应 \(m-1\)。这是因为回归 (16.22) 中的一个单位根过程由线性趋势主导。例如，如果系统中有 \(m=3\) 个变量且估计 (16.21)，则使用

\({ }^{17}\) 由样本量 \(n=10,000\) 的一百万次模拟抽取计算。“趋势”和 \(m=2\) 的临界值。如果有 \(m=2\) 个变量，则使用表 16.1 的”情形 3”ADF 临界值。

为说明，以利率应用为例。这些变量无趋势，所以我们使用模型 (16.21) 和”截距”临界值。最小二乘残差是 \(\widehat{u}_{1 t}=\widehat{Y}_{1 t}-1.03 Y_{2 t}-1.7\)。应用 \(p=8\) 的 ADF 检验我们获得 \(\mathrm{EG}=-4.0\)。这小于表 16.3 的 \(1 \%\) 渐近临界值 \(-3.9\)。因此我们拒绝无协整假设，支持这对协整的假设。

16.20 VECM 估计

Granger 表示定理（定理 16.17 和 16.18）显示 \(Y_{t}\) 协整当且仅当 \(Y_{t}\) 满足误差修正模型。VECM(p) 模型是

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+\Gamma_{1} \Delta Y_{t-1}+\cdots+\Gamma_{p-1} \Delta Y_{t-p+1}+a+e_{t} . \]

这是第 11.11 节引入的降秩回归。标准估计方法是在 \(e_{t}\) 是 i.i.d. \(\mathrm{N}(0, \Sigma)\) 的辅助假设下的最大似然，在定理 11.7 中描述。我们在此为 VECM 模型重复此结果。

定理 16.21 在 \(e \sim \mathrm{N}(0, \Sigma)\) 下 VECM (16.23) 的 MLE 给出如下。首先，将 \(\Delta Y_{t}\) 和 \(Y_{t-1}\) 对 \(\Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\) 和截距回归以获得残差向量 \(\widehat{u}_{0 t}\) 和 \(\widehat{u}_{1 t}\)，组织为矩阵 \(\widehat{\boldsymbol{U}}_{0}\) 和 \(\widehat{\boldsymbol{U}}_{1}\)。MLE \(\widehat{\beta}\) 等于 \(\frac{1}{n} \widehat{\boldsymbol{U}}_{1}^{\prime} \widehat{\boldsymbol{U}}_{0}\left(\frac{1}{n} \widehat{\boldsymbol{U}}_{0}^{\prime} \widehat{\boldsymbol{U}}_{0}\right)^{-1} \frac{1}{n} \widehat{\boldsymbol{U}}_{0}^{\prime} \widehat{\boldsymbol{U}}_{1}\) 关于 \(\frac{1}{n} \widehat{\boldsymbol{U}}_{1}^{\prime} \widehat{\boldsymbol{U}}_{1}\) 的前 \(r\) 个广义特征向量，对应 \(r\) 个最大特征值 \(\widehat{\lambda}_{j}\)。这使用标准化 \(\widehat{\beta}^{\prime} \frac{1}{n} \widehat{\boldsymbol{U}}_{1}^{\prime} \widehat{\boldsymbol{U}}_{1} \widehat{\beta}=\boldsymbol{I}_{r}\)。其余系数 \(\widehat{\alpha}\)、\(\widehat{\Gamma}_{1}, \ldots, \widehat{\Gamma}_{p-1}\) 和 \(\widehat{a}\) 的 MLE 通过将 \(\Delta Y_{t}\) 对 \(\widehat{\beta}^{\prime} Y_{t-1}\)、\(\Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\) 和截距的最小二乘回归获得。最大化对数似然函数是

\[ \ell_{n}(r)=\frac{m}{2}(n \log (2 \pi)-1)-\frac{n}{2} \operatorname{det}\left(\frac{1}{n} \widehat{\boldsymbol{U}}_{0}^{\prime} \widehat{\boldsymbol{U}}_{0}\right)-\frac{n}{2} \sum_{j=1}^{r} \log \left(1-\widehat{\lambda}_{j}\right) \]

此估计方法由 Johansen \((1988,1991,1995)\) 作为 Anderson (1951) 降秩回归的扩展开发。

VECM 是约束 VAR，所以 VECM 估计可用于 VAR 的任何目的。VECM 估计方法的优势是它提供系统的连贯模型，计算直接，可处理多个协整向量。劣势是当有多个协整向量 \((r>1)\) 时，协整空间（\(\beta\) 张成的空间）的解释困难。

VECM 模型假设 VAR 阶数 \(p\) 和协整秩 \(r\) 已知。在实践中使用基于数据的选择规则。AIC 最小化可用于 \(p\) 的选择。简单方法是通过估计无约束 VAR 模型选择 \(p\)。\(r\) 的选择通常通过检验方法完成；这在下一节中回顾。

我们用已引入的两个利率序列说明。水平 VAR 的 AIC 选择选择 VAR(8)；我们在此报告 VAR(4)，因为它产生相似结果。这暗示具有 3 个动态滞后的 VECM。

表 16.4：VECM 协整向量

	\(\beta\)	s.e.
3-Month	1
10-Year	\(-1.01\)	\(0.07\)
Intercept	\(1.58\)	\(0.46\)

表 16.5：向量误差修正模型

	\(\Delta 3-\) Month \(_{t}\)	\(\Delta 10-\) Year \(_{t}\)
\(Z_{t-1}\)	\(-0.09\)	\(0.07\)
	\((0.04)\)	\((0.03)\)
\(\Delta 3_{-\text {Month }_{t-1}}\)	\(0.37\)	\(0.04\)
	\((0.08)\)	\((0.06)\)
\(\Delta\) 3-Month \(_{t-2}\)	\(-0.20\)	\(-0.08\)
	\((0.08)\)	\((0.06)\)
\(\Delta\) 3-Month \(_{t-3}\)	\(0.28\)	\(0.07\)
	\((0.08)\)	\((0.06)\)
\(\Delta 10-\) Year \(_{t-1}\)	\(0.06\)	\(0.21\)
	\((0.07)\)	\((0.08)\)
\(\Delta 10-\) Year\(_{t-2}\)	\(-0.19\)	\(-0.09\)
	\((0.12)\)	\((0.08)\)
\(\Delta 10\) - Year \(_{t-3}\)	\(0.10\)	\(0.06\)
	\((0.12)\)	\((0.08)\)

由于利率不是趋势序列，我们使用趋势模型 2。估计模型在表 16.4 和 16.5 中报告。

表 16.4 报告估计的协整向量 \(\beta\)。三个月期利率的系数标准化为 1。十年期利率的估计系数接近 \(-1\)，估计截距约为 1.6。后者意味着三个月期利率平均比十年期利率低 1.6 个百分点。估计 VECM 的系数在表 16.5 中报告，每个变量一列。第一个报告的系数是 \(\widehat{\alpha}\)，误差修正项。三个月期利率的系数为负，十年期利率的系数为正，它们量级相似。因此当三个月期利率超过十年期利率超过典型 1.6 时，三个月期利率趋于下降，十年期利率趋于上升，推动两个利率更接近协整关系。以下六个系数是 VECM 的动态系数。我们可以看到每个变量趋于主要响应其自己的滞后变化。三个月期利率的系数比十年期利率大得多，表明它有更强的序列相关。系数的变化符号揭示复杂动态。

VECM 估计量的渐近分布需要协整向量的标准化。流行选择是 \(\beta=\left(\boldsymbol{I}_{r}, \beta^{* \prime}\right)^{\prime}\)。Johansen (1995, 定理 13.5) 显示在误差 \(e_{t}\) 是 i.i.d. 且协方差矩阵 \(\Sigma\) 的假设下，系数估计量 \(\widehat{\theta}=(\widehat{\alpha}, \widehat{\Gamma})\) 满足

\[ \sqrt{n}(\widehat{\theta}-\theta) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \Sigma \otimes \boldsymbol{Q}^{-1}\right) \]

其中 \(\boldsymbol{Q}=\mathbb{E}\left[X_{t} X_{t}^{\prime}\right]\)，\(X_{t}=\left(\beta^{\prime} Y_{t-1}, \Delta Y_{t-1}, \ldots, \Delta Y_{t-p+1}\right)\)，给定 \(\beta\) 的回归变量。这是多元回归的经典（同方差）渐近分布。此结果显示系数 \(\theta\) 的推断可使用传统方法进行。同方差协方差矩阵是由于误差同方差的假设。如果放宽后者假设，则渐近分布推广到无约束协方差矩阵的情形。

Johansen (1995, 定理 13.3) 提出 \(\widehat{\beta}\) 的渐近分布。他显示渐近分布是具有随机协方差矩阵的正态分布。后者称为混合高斯分布。从实际观点看，这意味着我们可以将渐近分布视为正态，因为当用适当标准误缩放时，渐近分布是标准正态。为简洁我们不呈现细节。

在 Stata 中使用命令 vec 估计具有给定协整秩 \(r\) 和 VAR 阶数 \(p\) 的 VECM。

16.21 VECM 中的协整检验

取模型

\[ \Delta Y_{t}=\Pi Y_{t-1}+\Gamma_{1} \Delta Y_{t-1}+\cdots+\Gamma_{p-1} \Delta Y_{t-p+1}+a+e_{t} . \]

Granger 表示定理显示 \(Y_{t}\) 与 \(r\) 个协整向量协整当且仅当 \(\Pi\) 的秩等于 \(r\)。因此协整检验等于检验 \(\Pi\) 秩的假设。将存在 \(r\) 个协整向量的假设写作 \(\mathbb{H}(r): \operatorname{rank}(\Pi)=r\)。

协整是对无约束模型 \(\mathbb{H}(m)\) 的约束。对 \(r\) 个协整向量对无约束备择的检验是 \(\mathbb{H}(r)\) 对 \(\mathbb{H}(m)\) 的检验。\(\mathbb{H}(r)\) 对 \(\mathbb{H}(m)\) 的似然比统计量是

\[ \operatorname{LR}(r)=2\left(\ell_{n}(m)-\ell_{n}(r)\right)=-n \sum_{j=1}^{m} \log \left(1-\hat{\lambda}_{j}\right)+n \sum_{j=1}^{r} \log \left(1-\hat{\lambda}_{j}\right)=-n \sum_{j=r+1}^{m} \log \left(1-\hat{\lambda}_{j}\right) \]

其中 \(\hat{\lambda}_{j}\) 是估计问题 (16.21) 的特征值。检验对 \(\operatorname{LR}(r)\) 的小值接受 \(\mathbb{H}(r)\)；检验对 \(\operatorname{LR}(r)\) 的大值拒绝 \(\mathbb{H}(r)\)。

表 16.6：VECM 协整秩临界值：趋势模型 2

\(m-r\)	1	2	3	4	5	6	7	8	9	10	11	12
\(0.01 \%\)	\(22.4\)	\(37.3\)	\(55.7\)	\(78.5\)	105	135	169	208	250	296	347	402
\(0.1 \%\)	\(17.6\)	\(31.5\)	\(48.8\)	\(70.1\)	\(95.7\)	125	158	196	237	282	332	385
\(1 \%\)	\(12.8\)	\(25.1\)	\(41.3\)	\(61.3\)	\(85.4\)	113	146	182	222	266	314	366
\(2 \%\)	\(11.3\)	\(23.1\)	\(38.7\)	\(58.4\)	\(81.9\)	110	141	177	216	260	308	359
\(3 \%\)	\(10.4\)	\(21.9\)	\(37.2\)	\(56.5\)	\(79.8\)	107	138	174	213	256	304	355
\(4 \%\)	\(9.71\)	\(21.0\)	\(36.1\)	\(55.2\)	\(78.3\)	105	136	171	210	254	301	352
\(5 \%\)	\(9.19\)	\(20.3\)	\(35.2\)	\(54.1\)	\(77.0\)	104	135	170	208	251	298	349
\(7 \%\)	\(8.42\)	\(19.2\)	\(33.8\)	\(52.5\)	\(75.0\)	102	132	167	205	248	295	345
\(10 \%\)	\(7.57\)	\(18.0\)	\(32.3\)	\(50.6\)	\(72.8\)	\(99.0\)	129	163	202	244	290	341
\(15 \%\)	\(6.60\)	\(16.6\)	\(30.4\)	\(48.3\)	\(70.1\)	\(95.9\)	126	159	197	239	285	335
\(20 \%\)	\(5.89\)	\(15.5\)	\(29.0\)	\(46.5\)	\(67.9\)	\(93.4\)	123	156	194	235	281	330
\(30 \%\)	\(4.86\)	\(13.9\)	\(26.8\)	\(43.7\)	\(64.6\)	\(89.5\)	119	151	188	229	274	323
\(50 \%\)	\(3.45\)	\(11.4\)	\(23.4\)	\(39.4\)	\(59.4\)	\(83.4\)	111	143	179	219	263	312
\(70 \%\)	\(2.39\)	\(9.39\)	\(20.4\)	\(35.5\)	\(54.6\)	\(77.6\)	105	136	171	210	253	300
\(90 \%\)	\(1.35\)	\(6.96\)	\(16.7\)	\(30.4\)	\(48.1\)	\(69.9\)	\(95.7\)	125	159	197	239	285

来源：由样本量 \(n=10,000\) 的一百万次重复模拟计算。

渐近分布理论由 Johansen \((1988,1991,1995)\) 开发。

定理 16.22 假设有限滞后 VECM (16.24) 正确指定，定理 16.18 的条件成立，且误差 \(e_{t}\) 是 MDS。在 \(\Pi\) 有秩 \(r\) 的假设下

\[ \operatorname{LR}(r) \underset{d}{\longrightarrow} \operatorname{tr}\left[\left(\int_{0}^{1} d W X^{\prime}\right)\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X d W^{\prime}\right)\right] \]

其中 \(W(r)\) 是 \(m-r\) 维标准布朗运动，\(X(r)\) 是 \(W(r)\) 的函数的随机过程，依赖于趋势模型。

1. 趋势模型 1。\(X(r)=W(r)\)
2. 趋势模型 2。\(X(r)=(W(r), 1)\)
3. 趋势模型 3。\(X(r)=\left(W_{1}^{*}(r), r-1 / 2\right)\)
4. 趋势模型 4。\(X(r)=\left(W^{*}(r), r-1 / 2\right)\)

其中 \(W^{*}(r)=W(r)-\int_{0}^{1} W\) 是去均值 \(W(r)\)，\(W_{1}^{*}(r)\) 是 \(W^{*}(r)\) 的前 \(m-r-1\) 个分量。

定理 16.22 的证明在代数上繁琐。我们在第 16.22 节提供概要。完整细节见 Johansen (1995, 第 11 章)。

表 16.7：VECM 协整秩临界值：趋势模型 3

来源：由样本量 \(n=10,000\) 的一百万次重复模拟计算。

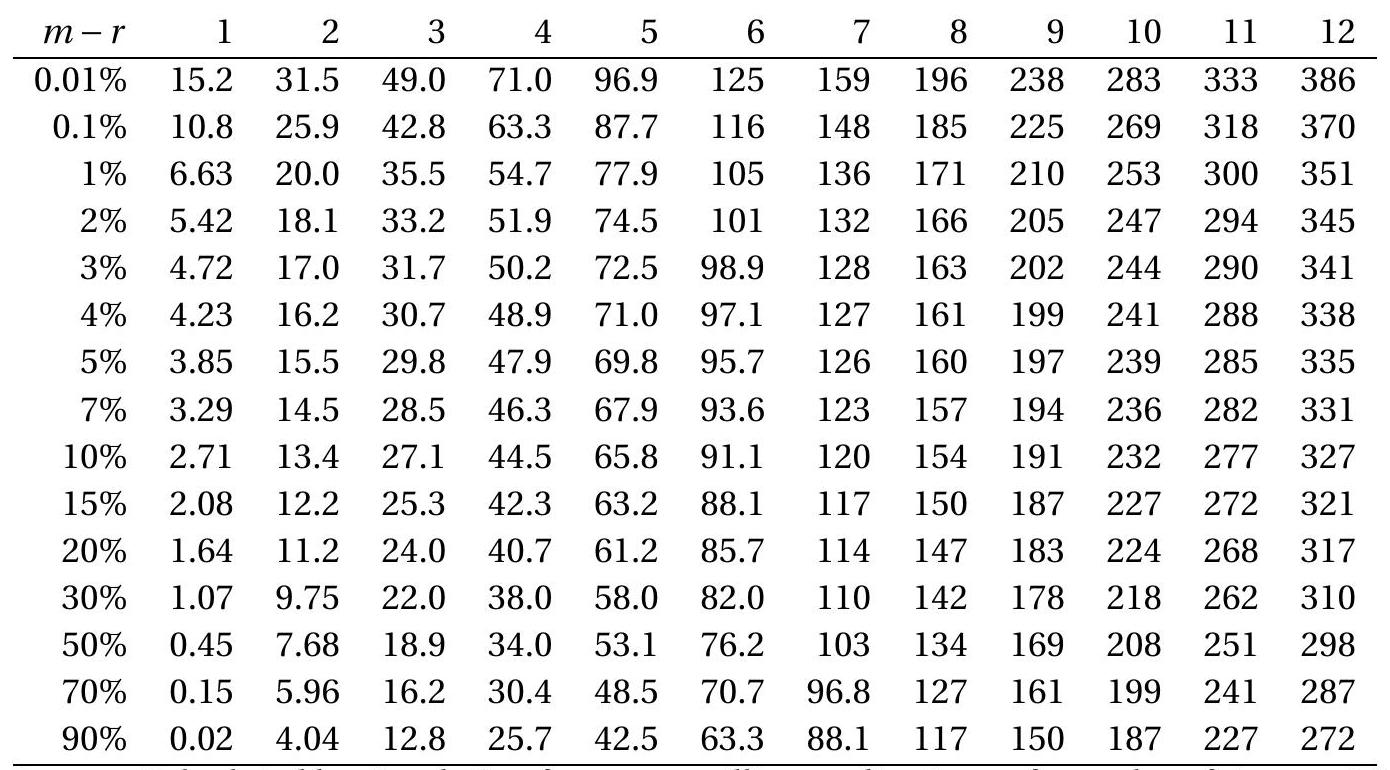
定理 16.22 提供协整秩 LR 检验的渐近分布。由于渐近分布等于多元 Dickey-Fuller 分布的迹，统计量 LR 通常称为”迹检验”或”Johansen 迹检验”。渐近分布是随机过程 \(X(r)\) 的函数，\(X(r)\) 等于 \(Y_{t}\) 的趋势分量（在 \(r\) 个协整向量的假设下）投影到其他回归变量的正交。对趋势模型 2，截距包含在协整关系中，所以它是 \(X(r)\) 的分量。对趋势模型 3，变量有趋势，主导其他分量，所以出现在渐近分布中。由于截距从协整关系中排除，\(X(r)\) 的分量都是去均值的。对趋势模型 4，线性趋势包含在协整关系中，所以它添加到趋势分量中，而截距被排除，所以 \(X(r)\) 过程是去均值的。

渐近分布只是 \(m-r\) 和趋势规范的函数。渐近临界值 \({ }^{18}\) 在表 16.6-16.8 中显示，对趋势模型 2、3 和 4，\(m-r\) 高达 12。这些是上尾检验，所以协整秩为 \(r\) 的原假设在检验统计量大于适当临界值时被拒绝；否则原假设不被拒绝。例如，无协整假设与 \(r=0\) 相同。适当临界值是对应变量数 \(m\) 的列。例如，对趋势模型 2 有 \(m=4\) 个变量，\(5 \%\) 临界值是 54.1。如果 \(\operatorname{LR}(r)>54.1\)，无协整假设被拒绝（暗示序列协整）；否则无协整假设不被拒绝。

检验统计量 \(\operatorname{LR}(r)\) 在实践中如何使用？当协整秩未知时，统计量可用于确定 \(r\)。传统程序是序贯检验。从 \(\mathbb{H}(0)\)（无协整的原假设）和相关的统计量 LR(0) 开始，它有 \(m\) 个自由度。如果检验拒绝（如果 LR(0) 超过行 \(m\) 临界值），这是至少有一个协整向量的证据，或 \(r \geq 1\)。接下来，取 \(\mathbb{\square}(1)\)（一个协整向量的原假设）和相关的统计量 LR(1)，它有 \(m-1\) 个自由度。如果此检验也拒绝（如果 LR(1) 超过行 \(m-1\) 临界值），这是至少有两个协整向量的证据，或 \(r \geq 2\)。继续此检验序列直到一个不拒绝。

例如，当有两个变量 \((m=2)\) 时，将统计量 \(\operatorname{LR}(0)\) 与 \(m=2\) 临界值比较。如果检验拒绝（如果统计量超过临界值），这是序列协整的证据。如果检验不拒绝，推断不确定。

表 16.8：VECM 协整秩临界值：趋势模型 4

\(m-r\)	1	2	3	4	5	6	7	8	9	10	11	12
\(0.01 \%\)	\(27.4\)	\(44.4\)	\(64.6\)	\(90.0\)	117	150	186	226	271	319	372	428
\(0.1 \%\)	\(22.1\)	\(38.1\)	\(57.4\)	\(81.0\)	108	139	175	214	258	305	356	412
\(1 \%\)	\(16.6\)	\(31.2\)	\(49.4\)	\(71.5\)	\(97.6\)	128	162	200	242	288	338	392
\(2 \%\)	\(14.9\)	\(29.0\)	\(46.7\)	\(68.4\)	\(94.0\)	124	157	195	236	282	332	385
\(3 \%\)	\(13.9\)	\(27.6\)	\(45.1\)	\(66.4\)	\(91.8\)	121	154	192	233	278	328	381
\(4 \%\)	\(13.1\)	\(26.7\)	\(43.9\)	\(65.0\)	\(90.1\)	119	152	189	230	275	325	378
\(5 \%\)	\(12.5\)	\(25.9\)	\(42.9\)	\(63.9\)	\(88.8\)	118	151	187	228	273	322	375
\(7 \%\)	\(11.7\)	\(24.7\)	\(41.4\)	\(62.1\)	\(86.7\)	115	148	184	225	270	318	371
\(10 \%\)	\(10.7\)	\(23.3\)	\(39.8\)	\(60.1\)	\(84.4\)	113	145	181	221	266	314	366
\(15 \%\)	\(9.53\)	\(21.7\)	\(37.7\)	\(57.6\)	\(81.5\)	109	141	177	217	261	309	360
\(20 \%\)	\(8.70\)	\(20.5\)	\(36.2\)	\(55.7\)	\(79.2\)	107	138	174	213	257	304	356
\(30 \%\)	\(7.45\)	\(18.7\)	\(33.8\)	\(52.8\)	\(75.7\)	103	134	169	207	250	297	348
\(50 \%\)	\(5.70\)	\(15.9\)	\(30.0\)	\(48.1\)	\(70.2\)	\(96.2\)	126	160	198	240	286	336
\(70 \%\)	\(4.28\)	\(13.5\)	\(26.7\)	\(43.8\)	\(65.0\)	\(90.1\)	119	152	189	231	276	325
\(90 \%\)	\(2.79\)	\(10.5\)	\(22.4\)	\(38.2\)	\(58.0\)	\(81.8\)	110	141	177	217	261	309

来源：由样本量 \(n=10,000\) 的一百万次重复模拟计算。

此检验程序在 \(m\) 小时（例如 \(m \leq 4\)）有吸引力，但对大 \(m\) 吸引力较小。

\({ }^{18}\) 由样本量 \(n=10,000\) 的一百万次模拟抽取计算。对大 \(m\)，程序有几个挑战。序贯检验需要多重检验，难以控制 I 类错误。同时检验可能有低功效，暗示程序可能”识别”不适当低的 \(r\) 值。

替代方法是使用协整检验验证选择的规范。从经济建模开始以激励协整秩 \(r\)。似然比 \(\operatorname{LR}(r)\) 可用于检验此假设对无约束 VAR。如果检验拒绝 \(\mathbb{H}(r)\)，这是提议模型不正确的证据。

我们用利率序列和 \(\operatorname{VAR}(4)\) 和趋势模型 2 说明。我们的起始假设是变量是 \(I(1)\) 且协整，暗示协整秩是 \(r=1\)。LR(0) 的值是 31.6。为计算 \(\mathrm{p}\) 值，我们使用表 16.6 对趋势模型 2 和 \(m-r=2\)。值 \(31.6\) 超过 \(1 \%\) 临界值 \(25.1\)，所以检验的渐近 \(p\)-值是 \(1 \%\)。因此无协整的原假设被强烈拒绝，支持至少一个协整向量。LR(1) 的值是 \(2.8\)。\(\mathrm{p}\) 值使用 \(m-r=1\) 计算。值 \(2.8\) 小于 \(50 \%\) 临界值 \(3.5\)，所以 p 值大于 \(50 \%\)。统计量不拒绝 \(\mathbb{\square}(1)\) 假设。综合，统计量与序列是 \(I(1)\) 且相互协整的建模假设一致。

为更广泛的应用，我们扩展到五个国债利率 \({ }^{19}\)：三个月期、六个月期、一年期、五年期和十年期。我们的起始假设是序列每个都是 \(I(1)\) 且变量系统协整，所以协整秩至少为 1。如果所有四个利差相互平稳，则系统将有四个协整向量，因此 \(r=4\)。但如果利差分布随时间变化，协整秩可能小于四。因此我们期望 \(1 \leq r \leq 4\) 但不确定其精确值。

我们在表 16.9 中报告协整秩的似然比检验。\(r=0\) 的 LR 检验是 120，超过 \(1 \%\) 临界值 \(85.4\)，\(r=1\) 的 LR 检验是 \(68.3\)，超过 \(1 \%\) 临界值 \(61.3\)，所以我们安全拒绝 \(r=0\) 和 \(r=1\) 假设。这提示 \(r \geq 2\)。\(r=2\) 的 LR 检验是 \(33.6\)，p 值为 \(0.07\)，这是边界显著的。\(r=3\) 和 \(r=4\) 的检验不显著。总之，我们不能拒绝模型 \(\mathbb{H}(2)\)、\(\mathbb{H}(3)\) 或 \(\mathbb{H}(4)\)。\(\mathbb{H}(2)\) 是可疑的，但统计证据单独不能区分 \(\mathbb{M}(3)\) 与 \(\mathbb{M}(4)\)。我们在此背景下的建议是使用 \(\mathbb{H}(3)\) 或 \(\mathbb{H}(4)\)。

表 16.9：协整秩检验

	LR(r)	p-value
0	120	\(<0.01\)
1	\(68.3\)	\(<0.01\)
2	\(33.6\)	\(0.07\)
3	\(10.8\)	\(>0.50\)
4	\(2.9\)	\(>0.50\)

在 Stata 中使用 vecrank 计算协整秩的 LR 检验。输出是显示 \(r=0, \ldots, m-1\) 的 \(\mathrm{LR}(\mathrm{r})\) 以及渐近 \(5 \%\) 临界值的表。p 值可从表 16.6-16.8 计算。

\({ }^{19}\) FRED-MD 序列 TB3MS、TB6MS、GS1、GS5 和 GS10。

16.22 技术证明*

定理 16.1 的证明。在正文中我们显示 \(S_{n}\) 的极限分布与 \(B\) 的分布一致。为应用函数型中心极限定理（《经济学家概率与统计》定理 18.3），我们需要验证 \(S_{n}\) 渐近等连续（见《经济学家概率与统计》定义 18.7）。为简单起见我们聚焦于标量情形 \(e_{t} \in \mathbb{R}\)。

假设不失一般性 \(\sigma^{2}=1\)。取任何 \(0<\eta<1\) 和 \(0<\epsilon<1\)。设 \(\delta \leq \epsilon \eta^{4} / 48^{2}\)。注意

\[ \sup _{\left|r_{2}-r_{1}\right| \leq \delta}\left|S_{n}\left(r_{2}\right)-S_{n}\left(r_{1}\right)\right| \leq 2 \sup _{0 \leq j \leq\lfloor 1 / \delta\rfloor} \sup _{0 \leq r \leq \delta}\left|S_{n}(j \delta+r)-S_{n}(j \delta)\right| . \]

则

\[ \begin{aligned} \mathbb{P}\left[\sup _{\left|r_{2}-r_{1}\right| \leq \delta}\left|S_{n}\left(r_{2}\right)-S_{n}\left(r_{1}\right)\right|>\eta\right] & \leq \mathbb{P}\left[\bigcup_{j=0}^{\lfloor 1 / \delta\rfloor} \sup _{0 \leq r \leq \delta}\left|S_{n}(j \delta+r)-S_{n}(j \delta)\right|>\frac{\eta}{2}\right] \\ & \leq \sum_{j=0}^{\lfloor 1 / \delta\rfloor} \mathbb{P}\left[\sup _{0 \leq r \leq \delta}\left|S_{n}(j \delta+r)-S_{n}(j \delta)\right|>\frac{\eta}{2}\right] \\ & \leq\left(\frac{1}{\delta}+1\right) \mathbb{P}\left[\sup _{0 \leq r \leq \delta}\left|S_{n}(r)\right|>\frac{\eta}{2}\right] \\ &=\left(\frac{1}{\delta}+1\right) \mathbb{P}\left[\max _{i \leq\lfloor n \delta\rfloor}\left|\frac{1}{\sqrt{n}} \sum_{t=1}^{i} e_{t}\right|>\frac{\eta}{2}\right] \\ & \leq 2\left(\frac{1}{\delta}+1\right) \mathbb{P}\left[\left|\frac{1}{\sqrt{n}} \sum_{t=1}^{\lfloor n \delta\rfloor} e_{t}\right|>\frac{\eta}{4}\right] . \end{aligned} \]

最终不等式是 Billingsley 的 (B.52)，在假设下成立，因为 \(\delta<\eta / 4 \sqrt{2}\)。我们关于 Billingsley 不等式的陈述 (B.52) 假设 \(e_{t}\) 是 i.i.d. 序列；结果可扩展到 MDS 序列。

CLT 暗示 \(n^{-1 / 2} \sum_{t=1}^{\lfloor n \delta\rfloor} e_{t} \underset{d}{\rightarrow} Z_{\delta} \sim \mathrm{N}(0, \delta)\)。对足够大的 \(n\)，最终行有界

\[ \frac{3}{\delta} \mathbb{P}\left[\left|Z_{\delta}\right|>\frac{\eta}{4}\right]=\frac{3}{\delta} \mathbb{P}\left[Z_{\delta}^{4}>\frac{\eta^{4}}{16^{2}}\right] \leq \frac{3}{\delta} \frac{16^{2}}{\eta^{4}} \mathbb{E}\left[Z^{4}\right]=\frac{48^{2}}{\eta^{4}} \delta=\epsilon . \]

第一个不等式是 Markov 的，以下等式 \(\mathbb{E}\left[Z_{\delta}^{4}\right]=3 \delta^{2}\)，最终等式是假设 \(\delta=\epsilon \eta^{4} / 48^{2}\)。这显示 \(S_{n}\) 满足渐近等连续的定义。

定理 16.7 的证明。\(Z_{t}\) 具有 Wold 分解 \(Z_{t}=\Theta(\mathrm{L}) e_{t}\)。我们添加 \(e_{t}\) 是 MDS 的额外假设以简化证明。通过 Beveridge-Nelson 分解 \(Z_{t}=\xi_{t}+U_{t}-U_{t-1}\)，其中 \(\xi_{t}=\Theta(1) e_{t}\) 且 \(U_{t}=\Theta^{*}(\mathrm{~L}) e_{t}\)。则

\[ \begin{aligned} \frac{1}{n} \sum_{t=1}^{n} S_{t-1} Z_{t}^{\prime} &=\frac{1}{n} \sum_{t=1}^{n} S_{t-1} \xi_{t}^{\prime}+\frac{1}{n} \sum_{t=1}^{n} S_{t-1} U_{t}^{\prime}-\frac{1}{n} \sum_{t=1}^{n} S_{t-1} U_{t-1}^{\prime} \\ &=\frac{1}{n} \sum_{t=1}^{n} S_{t-1} \xi_{t}^{\prime}-\frac{1}{n} \sum_{t=1}^{n-1} Z_{t} U_{t}^{\prime}+o_{p}(1) . \end{aligned} \]

第一项通过定理 16.6 收敛到 \(\int_{0}^{1} B d B^{\prime}\)。布朗运动具有等于 \(Z_{t}\) 长期方差的协方差矩阵，即 \(\Omega\)。第二项按概率收敛到 \(\mathbb{E}\left[Z_{t} U_{t}^{\prime}\right]\)。做替换 \(U_{t}=\xi_{t+1}+U_{t+1}-Z_{t+1}\) 和 \(\mathbb{E}\left[Z_{t} \xi_{t+1}^{\prime}\right]=0\)，这可写作

\[ \begin{aligned} \mathbb{E}\left[Z_{t} U_{t}^{\prime}\right] &=\mathbb{E}\left[Z_{t} \xi_{t+1}^{\prime}\right]+\mathbb{E}\left[Z_{t} U_{t+1}^{\prime}\right]-\mathbb{E}\left[Z_{t} Z_{t+1}^{\prime}\right] \\ &=\mathbb{E}\left[Z_{t} U_{t+1}^{\prime}\right]-\mathbb{E}\left[Z_{t} Z_{t+1}^{\prime}\right] \\ &=\mathbb{E}\left[Z_{t} U_{t+2}^{\prime}\right]-\mathbb{E}\left[Z_{t} Z_{t+2}^{\prime}\right]-\mathbb{E}\left[Z_{t} Z_{t+1}^{\prime}\right] \\ &=\cdots \\ &=-\sum_{j=1}^{\infty} \mathbb{E}\left[Z_{t} Z_{t+j}^{\prime}\right]=-\sum_{j=1}^{\infty} \mathbb{E}\left[Z_{t-j} Z_{t}^{\prime}\right]=-\Lambda . \end{aligned} \]

第三行做替换 \(U_{t+1}=\xi_{t+2}+U_{t+2}-Z_{t+2}\) 和 \(\mathbb{E}\left[Z_{t} \xi_{t+2}^{\prime}\right]=0\)，替换重复直到无穷。我们已显示如声称的结果。

定理 16.8 的证明。通过随机积分的定义

\[ \int_{0}^{1} W d W=\operatorname{plim}_{N \rightarrow \infty} \sum_{i=0}^{N-1} W\left(\frac{i}{N}\right)\left(W\left(\frac{i+1}{N}\right)-W\left(\frac{i}{N}\right)\right) . \]

取任何正整数 \(N\) 和任何 \(j<N\)。观察

\[ W\left(\frac{j+1}{N}\right)=W\left(\frac{j}{N}\right)+\left(W\left(\frac{j+1}{N}\right)-W\left(\frac{j}{N}\right)\right) . \]

平方我们获得

\[ W\left(\frac{j+1}{N}\right)^{2}-W\left(\frac{j}{N}\right)^{2}=2 W\left(\frac{j}{N}\right)\left(W\left(\frac{j+1}{N}\right)-W\left(\frac{j}{N}\right)\right)+\frac{1}{N} \chi_{j N} . \]

其中 \(\chi_{j N}=N\left(W\left(\frac{j+1}{N}\right)-W\left(\frac{j}{N}\right)\right)^{2}\)。注意 \(\chi_{j N}\) 在 \(j\) 上 i.i.d.，分布为 \(\chi_{1}^{2}\)，期望为 1。对 \(j=0\) 到 \(N-1\) 求和我们获得

\[ W(1)^{2}=2 \sum_{i=0}^{N-1} W\left(\frac{i}{N}\right)\left(W\left(\frac{i+1}{N}\right)-W\left(\frac{i}{N}\right)\right)+\frac{1}{N} \sum_{i=0}^{N-1} \chi_{i N}^{2} . \]

重写

\[ \sum_{i=0}^{N-1} W\left(\frac{i}{N}\right)\left(W\left(\frac{i+1}{N}\right)-W\left(\frac{i}{N}\right)\right)=\frac{1}{2}\left(W(1)^{2}-\frac{1}{N} \sum_{i=0}^{N-1} \chi_{i N}^{2}\right) . \]

通过 (16.26)，\(\int_{0}^{1} W d W\) 是右侧的概率极限。通过 WLLN 这是 \(\frac{1}{2}\left(W(1)^{2}-1\right)\)，如声称。

定理 16.10 的证明。

\[ \widehat{\sigma}^{2}=\frac{1}{n} \sum_{t=1}^{n-1} \widehat{e}_{t+t}^{2}=\frac{1}{n} \sum_{t=1}^{n-1} e_{t+t}^{2}-\frac{1}{n} \frac{\left(\frac{1}{n} \sum_{t=1}^{n-1} Y_{t} e_{t+1}\right)^{2}}{\frac{1}{n^{2}} \sum_{t=1}^{n-1} Y_{t}^{2}}=\frac{1}{n} \sum_{t=1}^{n-1} e_{t+t}^{2}+o_{p}(1) \longrightarrow \vec{p}^{2} . \]

则

\[ T=\frac{\frac{1}{n} \sum_{t=1}^{n-1} Y_{t} e_{t+1}}{\left(\frac{1}{n^{2}} \sum_{t=1}^{n-1} Y_{t}^{2}\right)^{1 / 2}} \underset{\widehat{\sigma}}{\longrightarrow} \frac{\sigma^{2} \int_{0}^{1} W d W}{\left(\sigma^{2} \int_{0}^{1} W^{2}\right)^{1 / 2} \sigma}=\frac{\int_{0}^{1} W d W}{\left(\int_{0}^{1} W^{2}\right)^{1 / 2}} \]

定理 16.12 的证明。选择 \(\eta>0\) 和 \(\epsilon>0\)。选择 \(\delta\) 使得

\[ \mathbb{P}\left(\sup _{|r-s| \leq \delta}|X(r)-X(s)|>\epsilon\right) \leq \eta \]

这是可能的，因为 \(X(r)\) 几乎必然连续。设 \(N=\lfloor 1 / \delta\rfloor\) 和 \(t_{k}=k n / N\)。写 \(X_{n t}=D_{n}^{-1} X_{t}\)。则

\[ C_{n}=\frac{1}{n} \sum_{k=0}^{N} \sum_{t=t_{k}}^{t_{k+1}-1} X_{n t} u_{t}=\frac{1}{n} \sum_{k=0}^{N} X_{n, t_{k}} \sum_{t=t_{k}}^{t_{k+1}-1} u_{t}+\frac{1}{n} \sum_{k=0}^{N} \sum_{t=t_{k}}^{t_{k+1}-1}\left(X_{n t}-X_{n, t_{k}}\right) u_{t} \]

且

\[ \left|C_{n}\right| \leq \sup _{0 \leq r \leq 1}\left|X_{n}(r)\right| A_{n}+\sup _{|r-s| \leq \delta}\left|X_{n}(r)-X_{n}(s)\right| B_{n} \]

其中

\[ \begin{aligned} &A_{n}=\frac{N}{n} \max _{k \leq N}\left|\sum_{t=t_{k}}^{t_{k+1}-1} u_{t}\right| \\ &B_{n}=\frac{1}{n} \sum_{t=1}^{n}\left|u_{t}\right| . \end{aligned} \]

由于 \(X_{n} \underset{d}{\longrightarrow} X\) 且 \(X\) 连续，

\[ \sup _{0 \leq r \leq 1}\left|X_{n}(r)\right| \underset{d}{\longrightarrow} \sup _{0 \leq r \leq 1}|X(r)|<\infty \]

几乎必然。因此 \(\sup _{0 \leq r \leq 1}\left|X_{n}(r)\right|=O_{p}(1)\)。由于 \(X_{n} \underset{d}{\longrightarrow} X\)，

\[ \sup _{|r-s| \leq \delta}\left|X_{n}(r)-X_{n}(s)\right| \underset{d}{\longrightarrow} \sup _{|r-s| \leq \delta}|X(r)-X(s)| \leq \epsilon \]

其中不等式通过 (16.27) 以超过 \(1-\eta\) 的概率成立。因此对足够大的 \(n\)，左侧以相同概率有界于 \(2 \epsilon\)，因此是 \(o_{p}(1)\)。

对固定 \(N\)，\(A_{n} \underset{p}{\longrightarrow} 0\) 通过遍历定理。\(\mathbb{E}\left|u_{t}\right|<\infty\) 的假设暗示 \(B_{n}=O_{p}(1)\)。综合，我们已显示

\[ \left|C_{n}\right| \leq O_{p}(1) o_{p}(1)+o_{p}(1) O_{p}(1)=o_{p}(1) \]

如陈述。

定理 16.17 的证明。

部分 1：协整的定义暗示 \(\Delta Y_{t}\) 是平稳的且具有有限协方差矩阵。通过多元 Wold 表示（定理 15.2），\(\Delta Y_{t}=\theta+\Theta(\mathrm{L}) e_{t}\)，误差为白噪声。左乘 \(\beta^{\prime}\) 产生 \(\beta^{\prime} \Delta Y_{t}=\beta^{\prime} \theta+\beta^{\prime} \Theta(\mathrm{L}) e_{t}\)，其具有长期方差 \(\beta^{\prime} \Theta(1) \Sigma \Theta(1)^{\prime} \beta\)，其中 \(\Sigma\) 是 \(e_{t}\) 的协方差矩阵。\(\beta^{\prime} Y_{t}\) 是 \(I(0)\) 的假设暗示 \(\beta^{\prime} \theta=0\)（否则 \(\beta^{\prime} Y_{t}\) 将有时间趋势）。这暗示 \(\theta\) 位于 \(\beta_{\perp}\) 的值空间中，因此对某个 \(\gamma\)，\(\theta=\beta_{\perp} \gamma\)。此外，\(\beta^{\prime} Y_{t}\) 是 \(I(0)\) 的假设暗示 \(\beta^{\prime} \Delta Y_{t}\) 是 \(I(-1)\)，这暗示其长期协方差矩阵等于零。这暗示 \(\beta^{\prime} \Theta(1)=0\)，因此对某个矩阵 \(\eta\)，\(\Theta(1)=\beta_{\perp} \eta^{\prime}\)。\(\beta_{\perp}^{\prime} \Delta Y_{t}\) 是 \(I(0)\) 的假设暗示 \(\beta_{\perp}^{\prime} \Theta(1) \Sigma \Theta(1)^{\prime} \beta_{\perp}>0\)，这暗示 \(\Theta(1)\) 必须具有秩 \(m-r\)，因此矩阵 \(\eta\) 也是如此。

部分 2：Beveridge-Nelson 分解加上 \(\Theta(1)=\beta_{\perp} \eta^{\prime}\) 暗示 \(\Theta(\mathrm{L})=\beta_{\perp} \eta^{\prime}+\Theta^{*}(\mathrm{~L})(1-\mathrm{L})\)。应用于 Wold 表示我们获得 \(\Delta Y_{t}=\beta_{\perp} \gamma+\beta_{\perp} \eta^{\prime} e_{t}+\Theta^{*}(\mathrm{~L}) \Delta e_{t}\)。求和我们发现陈述的表示。

部分 3：不失一般性假设 \(H=\left[\beta, \beta_{\perp}\right]\) 是正交的。也定义正交矩阵 \(H_{\eta}=\left[\eta_{\perp}, \bar{\eta}\right]\)，其中 \(\bar{\eta}=\eta\left(\eta^{\prime} \eta\right)^{-1 / 2}\)。定义 \(X_{t}=H^{\prime} Y_{t}\)。Wold 表示暗示 \(\Delta X_{t}=\left(\begin{array}{l}0 \\ \gamma\end{array}\right)+C(\mathrm{~L}) e_{t}\)，其中使用 Beveridge-Nelson 分解

\[ \boldsymbol{C}(\mathrm{L})=H^{\prime}\left(\beta_{\perp} \eta^{\prime}+\Theta^{*}(\mathrm{~L})(1-\mathrm{L})\right)=\left(\begin{array}{c} \beta^{\prime} \Theta^{*}(\mathrm{~L})(1-\mathrm{L}) \\ \eta^{\prime}+\beta_{\perp}^{\prime} \Theta^{*}(\mathrm{~L})(1-\mathrm{L}) \end{array}\right) \]

分割 \(X_{t}=\left(X_{1 t}, X_{2 t}\right)\) 与 \(H\) 一致。我们看到

\[ \left(\begin{array}{c} \Delta X_{1 t} \\ \Delta X_{2 t} \end{array}\right)=\left(\begin{array}{c} \beta^{\prime} \Theta^{*}(\mathrm{~L})(1-\mathrm{L}) e_{t} \\ \gamma+\eta^{\prime} e_{t}+\beta_{\perp}^{\prime} \Theta^{*}(\mathrm{~L})(1-\mathrm{L}) e_{t} \end{array}\right) . \]

对第一个方程求和我们获得

\[ \left(\begin{array}{c} X_{1 t} \\ \Delta X_{2 t} \end{array}\right)=\left(\begin{array}{c} \mu \\ \gamma \end{array}\right)+\boldsymbol{D}(\mathrm{L}) H_{\eta}^{\prime} e_{t} \]

其中 \(\mu=X_{1,0}-\beta^{\prime} \Theta^{*}(\mathrm{~L}) e_{0}\) 且

\[ \boldsymbol{D}(\mathrm{L})=\left(\begin{array}{c} \beta^{\prime} \Theta^{*}(\mathrm{~L}) \\ \eta^{\prime}+\beta_{\perp}^{\prime} \Theta^{*}(\mathrm{~L})(1-\mathrm{L}) \end{array}\right) H_{\eta}=\left(\begin{array}{cc} \beta^{\prime} \Theta^{*}(\mathrm{~L}) \eta_{\perp} & \beta^{\prime} \Theta^{*}(\mathrm{~L}) \bar{\eta} \\ \beta_{\perp}^{\prime} \Theta^{*}(\mathrm{~L}) \eta_{\perp}(1-\mathrm{L}) & \left(\eta^{\prime} \eta\right)^{1 / 2}+\beta_{\perp}^{\prime} \Theta^{*}(\mathrm{~L}) \bar{\eta}(1-\mathrm{L}) \end{array}\right) . \]

这是可逆矩阵多项式。为看到这一点，首先观察

\[ \boldsymbol{D}(1)=\left(\begin{array}{cc} \beta^{\prime} \Theta^{*}(1) \eta_{\perp} & \beta^{\prime} \Theta^{*}(1) \bar{\eta} \\ 0 & \left(\eta^{\prime} \eta\right)^{1 / 2} \end{array}\right) \]

在 \(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\) 满秩的假设下满秩。这意味着 \(\operatorname{det}(\boldsymbol{D}(z))\) 无单位根。其次，(16.28) 和 \(X_{t}\) 的定义暗示

\[ \boldsymbol{D}(z)=\left(\begin{array}{cc} 1-z & 0 \\ 0 & 1 \end{array}\right) H \Theta(z) H_{\eta} . \]

由于 \(H\) 和 \(H_{\eta}\) 满秩，这暗示 \(\operatorname{det}(\boldsymbol{D}(z))=0\) 的解是 \(\operatorname{det}(\Theta(z))=0\) 的解，因此通过 \(\Theta(z)\) 的假设满足 \(|z| \geq 1+\delta\)（因为 \(z \neq 1\)）。综合我们已显示 \(\boldsymbol{D}(\mathrm{L})\) 可逆。因此 (16.28) 暗示

\[ H_{\eta} \boldsymbol{D}(\mathrm{L})^{-1}\left(\begin{array}{c} X_{1 t} \\ \Delta X_{2 t} \end{array}\right)=a+e_{t} \]

其中

\[ a=H_{\eta} \boldsymbol{D}(1)^{-1}\left(\begin{array}{l} \mu \\ \gamma \end{array}\right) \text {. } \]

(16.29) 是 \(\left(\beta^{\prime} Y_{t}, \beta_{\perp}^{\prime} \Delta Y_{t}\right)\) 的 VAR 表示，所有根满足 \(|z| \geq 1+\delta\)。这暗示 \(Y_{t}\) 的 VAR 表示，即方程 (16.18)，其中

\[ \boldsymbol{A}(z)=H_{\eta} \boldsymbol{D}(z)^{-1}\left(\begin{array}{c} \beta^{\prime} \\ \beta_{\perp}^{\prime}(1-z) \end{array}\right) . \]

通过分块矩阵求逆我们计算

\[ \begin{aligned} \boldsymbol{A}(1) &=H_{\eta} \boldsymbol{D}(1)^{-1}\left(\begin{array}{c} \beta^{\prime} \\ 0 \end{array}\right) \\ &=\left[\eta_{\perp}, \bar{\eta}\right]\left(\begin{array}{cc} \left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} & -\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} \beta^{\prime} \Theta^{*}(1) \eta \\ 0 & \left(\eta^{\prime} \eta\right)^{-1 / 2} \end{array}\right)\left(\begin{array}{c} \beta^{\prime} \\ 0 \end{array}\right) \\ &=\eta_{\perp}\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} \beta^{\prime} \\ &=-\alpha \beta^{\prime} . \end{aligned} \]

如声称。

部分 4。在假设 \(\sum_{j=0}^{\infty}\left\|\sum_{k=0}^{\infty} k \Theta_{j+k}\right\|^{2}<\infty\) 下，定理 15.3 暗示系数 \(\boldsymbol{A}_{k}^{*}=\sum_{j=0}^{\infty} \boldsymbol{A}_{j+k}\) 绝对可和。然后我们可以应用 Beveridge-Nelson 分解 \(\boldsymbol{A}(z)=\boldsymbol{A}(1)+\boldsymbol{A}^{*}(z)(1-z)\)。应用 \(\boldsymbol{A}(1)=-\alpha \beta^{\prime}\) 和一点重写产生

\[ \boldsymbol{A}(z)=\boldsymbol{I}_{m}(1-z)-\alpha \beta^{\prime} z-\left(\boldsymbol{I}_{m}+\alpha \beta^{\prime}-\boldsymbol{A}^{*}(z)\right)(1-z) . \]

应用于 (16.18) 我们获得陈述的结果，其中 \(\Gamma(\mathrm{L})=\boldsymbol{I}_{m}+\alpha \beta^{\prime}-A^{*}(z)\)。\(\Gamma(\mathrm{L})\) 的系数绝对可和，因为系数 \(\boldsymbol{A}_{k}^{*}\) 是。

部分 5。假设 \(\theta=0\) 直接暗示 \(\gamma=0\)。这暗示

\[ \begin{aligned} a &=H_{\eta} \boldsymbol{D}(1)^{-1}\left(\begin{array}{c} \mu \\ 0 \end{array}\right) \\ &=\left[\eta_{\perp}, \bar{\eta}\right]\left(\begin{array}{cc} \left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} & -\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} \beta^{\prime} \Theta^{*}(1) \eta \\ 0 & \left(\eta^{\prime} \eta\right)^{-1 / 2} \end{array}\right)\left(\begin{array}{c} \mu \\ 0 \end{array}\right) \\ &=\eta_{\perp}\left(\beta^{\prime} \Theta^{*}(1) \eta_{\perp}\right)^{-1} \mu \\ &=\alpha \mu \end{aligned} \]

如声称。

定理 16.18 的证明。将 VECM 写作 \(\Gamma^{*}(\mathrm{~L}) \Delta Y_{t}-\alpha \beta^{\prime} Y_{t-1}=a+e_{t}\)，其中 \(\Gamma^{*}(z)=\boldsymbol{I}_{m}-\Gamma(z)\)。设 \(\bar{\alpha}=\alpha\left(\alpha^{\prime} \alpha\right)^{-1 / 2}\) 和正交 \(H=\left[\bar{\alpha}, \alpha_{\perp}\right]\)。假设 \(\left[\beta, \beta_{\perp}\right]\) 正交。定义 \(Z_{t}=\beta^{\prime} Y_{t}\) 和 \(U_{t}=\beta_{\perp}^{\prime} \Delta Y_{t}\)。我们的目标是显示 \(\left(Z_{t}, U_{t}\right)\) 是 \(I(0)\)，这与显示 \(Y_{t}\) 与协整向量 \(\beta\) 协整相同。

左乘 VECM 模型 \(H^{\prime}\) 我们发现系统

\[ H^{\prime}\left(\Gamma^{*}(\mathrm{~L}) \Delta Y_{t}-\alpha \beta^{\prime} Y_{t-1}\right)=H^{\prime} a+H^{\prime} e_{t} . \]

使用恒等式 \(\boldsymbol{I}_{m}=\beta \beta^{\prime}+\beta_{\perp} \beta_{\perp}^{\prime}\) 我们看到 \(\Delta Y_{t}=\beta \Delta Z_{t}+\beta_{\perp} U_{t}\)。做此替换并设 \(\bar{a}=H^{\prime} a v_{t}=H^{\prime} e_{t}\) 我们获得系统

\[ \boldsymbol{D}(\mathrm{L})\left(\begin{array}{c} Z_{t} \\ U_{t} \end{array}\right)=\bar{a}+v_{t} \]

其中

\[ \boldsymbol{D}(z)=\left[\begin{array}{cc} \bar{\alpha}^{\prime} \Gamma^{*}(z) \beta(1-z)-\boldsymbol{I}_{m} & \bar{\alpha}^{\prime} \Gamma^{*}(z) \beta_{\perp} \\ \alpha_{\perp}^{\prime} \Gamma^{*}(z) \beta(1-z) & \alpha_{\perp}^{\prime} \Gamma^{*}(z) \beta_{\perp} \end{array}\right] . \]

我们现在显示这是平稳系统。首先，注意

\[ \boldsymbol{D}(1)=\left[\begin{array}{cc} -\boldsymbol{I}_{m} & \bar{\alpha}^{\prime} \Gamma^{*}(1) \beta_{\perp} \\ 0 & \alpha_{\perp}^{\prime} \Gamma^{*}(1) \beta_{\perp} \end{array}\right] \]

在 \(\alpha_{\perp}^{\prime} \Gamma^{*}(1) \beta_{\perp}\) 满秩的假设下满秩。这意味着 \(\operatorname{det}(\boldsymbol{D}(z))=0\) 无解 \(z=1\)。其次，\(\boldsymbol{D}(z)\) 通过关系与 \(\boldsymbol{A}(z)\) 相关

\[ \boldsymbol{D}(z)=H^{\prime} \boldsymbol{A}(z)\left[\beta, \beta_{\perp}(1-z)\right] . \]

因此解 \(z \neq 1\) 到

\[ \operatorname{det}(\boldsymbol{D}(z))=\operatorname{det}(H) \operatorname{det}(\boldsymbol{A}(z)) \operatorname{det}\left(\left[\beta, \beta_{\perp}(1-z)\right]\right)=0 \]

都是 \(\operatorname{det}(\boldsymbol{A}(z))=0\) 的解，通过假设都满足 \(|z| \geq 1+\delta\)。因此 \(\boldsymbol{D}(z)\) 可逆且具有可和移动平均系数矩阵。这暗示 \(\left(Z_{t}, U_{t}\right)\) 的 VAR 系统是平稳的。

如上面讨论的，这显示 \(\left(Z_{t}, U_{t}\right)\) 是平稳过程，因此 \(Y_{t}\) 与协整向量 \(\beta\) 协整。

定理 16.19 的证明。设 \(Y_{2 t}^{*}=Y_{2 t}-\bar{Y}_{2}\)。估计量满足

\[ n(\widehat{\beta}-\beta)=\left(\frac{1}{n^{2}} \sum_{t=1}^{n} Y_{2 t}^{*} Y_{2 t}^{* \prime}\right)^{-1}\left(\frac{1}{n} \sum_{t=1}^{n} Y_{2 t}^{*} u_{1 t}\right) \]

设 \(S_{t}=\sum_{i=1}^{t} u_{t}\)。定理 16.4 和 16.5 暗示 \(S_{\lfloor n r\rfloor} \underset{d}{\longrightarrow} B(r)\) 且 \(Y_{2\lfloor n r\rfloor}^{*} \underset{d}{\longrightarrow} B_{2}^{*}(r)\)。通过连续映射定理

\[ \frac{1}{n^{2}} \sum_{t=1}^{n} Y_{2 t}^{*} Y_{2 t}^{* \prime} \underset{d}{\longrightarrow} \int_{0}^{1} B_{2}^{*} B_{2}^{* \prime} \text {. } \]

通过定理 16.7 和 WLLN

\[ \frac{1}{n} \sum_{t=1}^{n} Y_{2 t}^{*} u_{1 t}=\frac{1}{n} \sum_{t=1}^{n} Y_{2 t-1}^{*} u_{1 t}+\frac{1}{n} \sum_{t=1}^{n} u_{2 t} u_{1 t}+o_{p}(1) \underset{d}{\longrightarrow} \int_{0}^{1} B_{2}^{*} d B_{1}+\Lambda_{21}+\Sigma_{21} . \]

综合我们获得陈述的结果。

定理 16.22 的证明（概要）。为简单起见从动态和趋势系数抽象，所以无约束模型是

\[ \Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+e_{t} . \]

其中 \(e_{t}\) 是具有协方差矩阵 \(\Sigma\) 的 MDS。我们详细检查两个情形。首先，情形 \(\mathbb{R}(0)\)（相对直接）和其次情形 \(\mathbb{H}(r)\)（代数上更繁琐）。

首先，取 \(\mathbb{H}(0)\)，在此情形下过程是 \(\Delta Y_{t}=e_{t}\)。统计量是

\[ \begin{aligned} \operatorname{LR}(0) &=-n \sum_{j=1}^{m} \log \left(1-\hat{\lambda}_{j}\right) \simeq n \sum_{j=1}^{m} \widehat{\lambda}_{j} \\ &=\operatorname{tr}\left[\left(\frac{1}{n} \sum_{t=1}^{n} Y_{t-1} e_{t}^{\prime}\right)\left(\frac{1}{n} \sum_{t=1}^{n} e_{t} e_{t}^{\prime}\right)^{-1}\left(\frac{1}{n} \sum_{t=1}^{n} e_{t} Y_{t-1}^{\prime}\right)\left(\frac{1}{n^{2}} \sum_{t=1}^{n} Y_{t-1} Y_{t-1}^{\prime}\right)^{-1}\right] \\ & \underset{d}{\rightarrow} \operatorname{tr}\left[\left(\int_{0}^{1} d B B^{\prime}\right)\left(\int_{0}^{1} B B^{\prime}\right)^{-1}\left(\int_{0}^{1} B d B^{\prime}\right)\right] \\ &=\operatorname{tr}\left[\left(\int_{0}^{1} d W W^{\prime}\right)\left(\int_{0}^{1} W W^{\prime}\right)^{-1}\left(\int_{0}^{1} W d W^{\prime}\right)\right] \end{aligned} \]

其中 \(B(r)\) 是具有协方差矩阵 \(\Sigma\) 的布朗运动，\(W(r)=\Sigma^{-1 / 2} B(r)\) 是标准布朗运动。这是陈述的结果。其次，取 \(1<r<m\) 的 \(\mathbb{H}(r)\)。定义 \(Z_{t}=\beta^{\prime} Y_{t}\)。\(\mathbb{H}(r)\) 下的过程是 \(\Delta Y_{t}=\alpha Z_{t-1}+e_{t}\)。标准化 \(\beta\) 使得 \(\mathbb{E}\left[Z_{t} Z_{t}^{\prime}\right]=\boldsymbol{I}_{r}\)。检验统计量对 \(Y_{t}\) 的线性变换不变，所以我们可以重新缩放数据使得 \(\mathbb{E}\left[\Delta Y_{t} \Delta Y_{t}^{\prime}\right]=\boldsymbol{I}_{m}\)。注意 \(\Sigma=\mathbb{E}\left[e_{t} e_{t}^{\prime}\right]=\mathbb{E}\left[\Delta Y_{t} \Delta Y_{t}^{\prime}\right]-\alpha \mathbb{E}\left[Z_{t} Z_{t}^{\prime}\right] \alpha^{\prime}=\boldsymbol{I}_{m}-\alpha \alpha^{\prime}\)。

似然比统计量是

\[ \operatorname{LR}(r)=-n \sum_{j=r+1}^{m} \log \left(1-\widehat{\lambda}_{j}\right) \simeq \sum_{j=r+1}^{m} \widehat{\rho}_{j} \]

其中 \(\widehat{\rho}_{j}=n \widehat{\lambda}_{j}\) 是方程 \(\operatorname{det}(S(\rho))=0\) 的 \(m-r\) 个最小根，其中

\[ S(\rho)=\rho \frac{1}{n^{2}} \sum_{t=1}^{n} Y_{t-1} Y_{t-1}^{\prime}-\frac{1}{n} \sum_{t=1}^{n} Y_{t-1} \Delta Y_{t}^{\prime}\left(\frac{1}{n} \sum_{t=1}^{n} \Delta Y_{t} \Delta Y_{t}^{\prime}\right)^{-1} \frac{1}{n} \sum_{t=1}^{n} \Delta Y_{t} Y_{t-1}^{\prime} . \]

定义满秩矩阵 \(H=\left[\beta, \beta_{\perp}\right]\)，其中 \(\beta^{\prime} \beta_{\perp}=0\)。\(\widehat{\rho}_{j}\) 的根与 \(\operatorname{det}\left(S^{*}(\rho)\right)=0\) 的根相同，其中 \(S^{*}(\rho)=H^{\prime} S(\rho) H\)，将 \(Y_{t-1}\) 替换为 \(\left(Z_{t-1}, X_{t-1}\right)\)，其中 \(X_{t}=\beta_{\perp}^{\prime} Y_{t}\)。我们计算

\[ \begin{aligned} S^{*}(\rho) &=\rho\left[\begin{array}{cc} \frac{1}{n^{2}} \sum_{t=1}^{n} Z_{t-1} Z_{t-1}^{\prime} & \frac{1}{n^{2}} \sum_{t=1}^{n} Z_{t-1} X_{t-1}^{\prime} \\ \frac{1}{n^{2}} \sum_{t=1}^{n} X_{t-1} Z_{t-1}^{\prime} & \frac{1}{n^{2}} \sum_{t=1}^{n} X_{t-1} X_{t-1}^{\prime} \end{array}\right] \\ &-\left[\begin{array}{c} \frac{1}{n} \sum_{t=1}^{n} Z_{t-1} \Delta Y_{t}^{\prime} \\ \frac{1}{n} \sum_{t=1}^{n} X_{t-1} \Delta Y_{t}^{\prime} \end{array}\right]\left(\frac{1}{n} \sum_{t=1}^{n} \Delta Y_{t} \Delta Y_{t}^{\prime}\right)^{-1}\left[\begin{array}{c} \frac{1}{n} \sum_{t=1}^{n} Z_{t-1} \Delta Y_{t}^{\prime} \\ \frac{1}{n} \sum_{t=1}^{n} X_{t-1} \Delta Y_{t}^{\prime} \end{array}\right]^{\prime} . \end{aligned} \]

我们现在对每个分量应用非平稳理论的渐近理论。过程 \(X_{t}=\beta_{\perp}^{\prime} Y_{t}\) 是非平稳的且满足 FCLT \(n^{-1} X_{\lfloor n r\rfloor} \underset{d}{\longrightarrow} X(r) \sim B M\left(\beta_{\perp}^{\prime} \Omega \beta_{\perp}\right)\)，其中 \(\Omega\) 是 \(\Delta Y_{t}\) 的长期协方差矩阵。误差和满足 \(n^{-1 / 2} \sum_{t=1}^{\lfloor n r\rfloor} e_{t} \underset{d}{\longrightarrow} B(r) \sim B M(\Sigma)\)。过程 \(X(r)\) 是 \(B(r)\) 的线性函数。

我们发现 \(\frac{1}{n^{2}} \sum_{t=1}^{n} X_{t-1} X_{t-1}^{\prime} \underset{d}{\longrightarrow} \int_{0}^{1} X X^{\prime}\)，\(\frac{1}{n^{2}} \sum_{t=1}^{n} X_{t-1} e_{t} \underset{d}{\longrightarrow} \int_{0}^{1} X d B^{\prime}\)，\(\frac{1}{n} \sum_{t=1}^{n} Z_{t-1} Z_{t-1}^{\prime} \underset{p}{\longrightarrow} \boldsymbol{I}_{r}\)，\(\frac{1}{n} \sum_{t=1}^{n} \Delta Y_{t} \Delta Y_{t}^{\prime} \underset{p}{\longrightarrow} \boldsymbol{I}_{m}\)，\(\frac{1}{n} \sum_{t=1}^{n} Z_{t-1} \Delta Y_{t}^{\prime} \underset{p}{\longrightarrow} \alpha^{\prime}\)，\(\frac{1}{n} \sum_{t=1}^{n} X_{t-1} Z_{t-1}^{\prime} \underset{d}{\longrightarrow} \zeta\) 对某个随机矩阵通过定理 16.7，且 \(\frac{1}{n} \sum_{t=1}^{n} X_{t-1} \Delta Y_{t}^{\prime} \underset{d}{\longrightarrow} \zeta^{\prime} \alpha^{\prime}+\int_{0}^{1} X d B^{\prime}\)。综合我们发现

\[ S^{*}(\rho) \underset{d}{\longrightarrow} \rho\left[\begin{array}{cc} 0 & \\ 0 & \int_{0}^{1} X X^{\prime} \end{array}\right]-\left[\begin{array}{cc} \alpha^{\prime} \alpha & \alpha^{\prime}\left(\alpha \zeta+\int_{0}^{1} d B X^{\prime}\right) \\ \left(\zeta^{\prime} \alpha^{\prime}+\int_{0}^{1} X d B^{\prime}\right) \alpha & \left(\zeta^{\prime} \alpha^{\prime}+\int_{0}^{1} X d B^{\prime}\right)\left(\alpha \zeta+\int_{0}^{1} d B X^{\prime}\right) \end{array}\right] . \]

因此 \(\operatorname{det}\left(S^{*}(\rho)\right)\) 按分布收敛到右侧的行列式，它等于（使用定理 A.1.5）\(\operatorname{det}\left(\alpha^{\prime} \alpha\right)\) 乘以

\[ \begin{aligned} &\rho \int_{0}^{1} X X^{\prime}-\left(\zeta^{\prime} \alpha^{\prime}+\int_{0}^{1} X d B^{\prime}\right)\left(I_{m}-\alpha\left(\alpha^{\prime} \alpha\right)^{-1} \alpha^{\prime}\right)\left(\alpha \zeta+\int_{0}^{1} d B X^{\prime}\right) \\ &=\rho \int_{0}^{1} X X^{\prime}-\int_{0}^{1} X d B^{\prime} M_{\alpha} \int_{0}^{1} d B X^{\prime} \\ &=\rho \int_{0}^{1} X X^{\prime}-\int_{0}^{1} X d W^{\prime} H_{1}^{\prime} \int_{0}^{1} H_{1} d W X^{\prime} \\ &=\rho \int_{0}^{1} X X^{\prime}-\int_{0}^{1} X d W^{\prime} \int_{0}^{1} d W X^{\prime} \end{aligned} \]

的行列式，其中 \(M_{\alpha}=\boldsymbol{I}_{m}-\alpha\left(\alpha^{\prime} \alpha\right)^{-1} \alpha^{\prime}\) 且

\[ M_{\alpha} B(r) \sim B M\left(M_{\alpha}\left(\boldsymbol{I}_{m}-\alpha \alpha^{\prime}\right) M_{\alpha}\right)=B M\left(M_{\alpha}\right)=H_{1} W(r) \]

其中 \(M_{\alpha}=H_{1} H_{1}^{\prime}\)，\(H_{1}^{\prime} H_{1}=\boldsymbol{I}_{m-r}\) 且 \(W(r) \sim B M\left(\boldsymbol{I}_{m-r}\right)\)。

(16.30) 的行列式有 \(m-r\) 个根，它们的和等于

\[ \operatorname{tr}\left[\left(\int_{0}^{1} d W X^{\prime}\right)\left(\int_{0}^{1} X X^{\prime}\right)^{-1}\left(\int_{0}^{1} X d W^{\prime}\right)\right]=\operatorname{tr}\left[\left(\int_{0}^{1} d W W^{\prime}\right)\left(\int_{0}^{1} W W^{\prime}\right)^{-1}\left(\int_{0}^{1} W d W^{\prime}\right)\right] \]

因为 \(X(r)\) 是 \(W(r)\) 的线性旋转。这是陈述的结果。

16.23 练习

练习 16.1 取 \(S_{t}=S_{t-1}+e_{t}\)，其中 \(S_{0}=0\) 且 \(e_{t}\) i.i.d. \(\left(0, \sigma^{2}\right)\)。

1. 计算 \(\mathbb{E}\left[S_{t}\right]\) 和 \(\operatorname{var}\left[S_{t}\right]\)。

2. 设 \(Y_{t}=\left(S_{t}-\mathbb{E}\left[S_{t}\right]\right) / \sqrt{\operatorname{var}\left[S_{t}\right]}\)。通过构造 \(\mathbb{E}\left[Y_{t}\right]=0\) 且 \(\operatorname{var}\left[Y_{t}\right]=1\)。\(Y_{t}\) 是平稳的吗？

3. 求 \(Y_{\lfloor n r\rfloor}\) 对 \(r \in[\delta, 1]\) 的渐近分布。

练习 16.2 求 \(\Delta Y_{t}=e_{t}+\Theta_{1} e_{t-1}+\Theta_{2} e_{t-2}\) 的 Beveridge-Nelson 分解。

练习 16.3 假设 \(Y_{t}=X_{t}+u_{t}\)，其中 \(X_{t}=X_{t-1}+e_{t}\) 且 \(\left(e_{t}, u_{t}\right) \sim I(0)\)。

1. \(Y_{t}\) 是 \(I(0)\) 还是 \(I(1)\)？

2. 求 \(\mathrm{n}^{-1 / 2} Y_{\lfloor n r\rfloor}\) 的渐近函数型分布。

练习 16.4 设 \(Y_{t}=e_{t}\) 为 i.i.d. 且 \(X_{t}=\Delta Y_{t}\)。

1. 显示 \(Y_{t}\) 是平稳的且 \(I(0)\)。

2. 显示 \(X_{t}\) 是平稳的但不是 \(I(0)\)。

练习 16.5 设 \(U_{t}=U_{t-1}+e_{t}\)，\(Y_{t}=U_{t}+v_{t}\) 且 \(X_{t}=2 U_{t}+w_{t}\)，其中 \(\left(e_{t}, v_{t}, w_{t}\right)\) 是 i.i.d. 序列。求 \(\left(Y_{t}, X_{t}\right)\) 的协整向量。

练习 16.6 取 AR(1) 模型 \(Y_{t}=\alpha Y_{t-1}+e_{t}\)，其中 i.i.d. \(e_{t}\) 和最小二乘估计量 \(\widehat{\alpha}\)。在第 14 章我们学习了当 \(|\alpha|<1\) 时的渐近分布是 \(\sqrt{n}(\widehat{\alpha}-\alpha) \underset{d}{\longrightarrow} \mathrm{N}\left(0,1-\alpha^{2}\right)\)。你如何将此与定理 16.9 调和，特别是对接近 1 的 \(\alpha\)？

练习 16.7 取 VECM(1) 模型 \(\Delta Y_{t}=\alpha \beta^{\prime} Y_{t-1}+e_{t}\)。显示 \(Z_{t}=\beta^{\prime} Y_{t}\) 遵循 AR(1) 过程。

练习 16.8 一位经济学家估计模型 \(Y_{t}=\alpha Y_{t-1}+e_{t}\) 并发现 \(\widehat{\alpha}=0.9\)，\(s(\widehat{\alpha})=0.05\)。他们断言：“检验 \(\alpha=1\) 的 t 统计量是 2，所以 \(\alpha=1\) 被拒绝。”他们的推理有错误吗？

练习 16.9 一位经济学家估计模型 \(Y_{t}=\alpha Y_{t-1}+e_{t}\) 并发现 \(\widehat{\alpha}=0.9\)，\(s(\widehat{\alpha})=0.04\)。他们断言：“\(\alpha\) 的 \(95 \%\) 置信区间是 \([0.82,0.98]\)，不包含 1。所以 \(\alpha=1\) 与数据不一致。”他们的推理有错误吗？

练习 16.10 一位经济学家取 \(Y_{t}\)，去趋势得到去趋势序列 \(Z_{t}\)，对 \(Z_{t}\) 应用 ADF 检验并发现 \(\mathrm{ADF}=-2.5\)。他们断言：“Stata 提供 \(5 \%\) 临界值 \(-1.9\)，p 值小于 \(1 \%\)。因此我们拒绝单位根的原假设。”他们的推理有错误吗？

练习 16.11 一位经济学家想为一位著名政治家的每日推文数量建立自回归模型。对于带截距的模型，他们获得 \(\mathrm{ADF}=-2.0\)。他们断言”推文数量是单位根过程。“他们的推理有错误吗？

练习 16.12 对以下来自 FRED-MD 的月度序列实现 Dickey-Fuller 单位根检验。对每个，你需要考虑 AR 阶 \(p\) 和趋势规范。

1. 对数实际个人收入：\(\log (r p i)\)

2. 工业生产指数：indpro

3. 住房开工：houst

4. 求职指数：hwi

5. 平民劳动力：clf16ov

6. 首次申请：claims

7. 工业生产指数（燃料）：ipfuels

练习 16.13 对前一练习中的每个序列实现 KPSS 平稳性检验。对每个，你需要考虑滞后截断 \(M\) 和趋势规范。

练习 16.14 对以下来自 FRED-MD 的月度对使用 Johansen 迹检验检验无协整假设。对每个，你需要考虑 VAR 阶 \(p\) 和趋势规范。

1. 3 个月国债利率 \((t b 3 m s)\) 和 10 年期国债利率 \((g s 10)\)。注意：在正文中我们在季度序列上实现检验，不是月度。

2. AAA 债券利率 \((a a a)\) 和 BAA 债券利率 \((b a a)\)。

3. \(\log (\) 工业生产耐用消费品) 和 log(工业生产非耐用消费品) (log of ipdcongd 和 ipncongd)。