第25章: 二分类选择
25 二分类选择
25.1 引言
本章以及接下来的两章将讨论所谓的受限因变量。这些变量具有受限的支撑集(实线的一个子集),这种限制对计量经济学建模具有重要影响。本章关注最简单的情况,即 \(Y\) 是二分类的,意味着它取两个值。不失一般性,我们将其设为0和1,因此 \(Y\) 的支撑集为 \(\{0,1\}\)。在计量经济学中,我们通常称这类模型为二分类选择。
二分类因变量的例子包括:购买单一商品;市场进入;参与;申请/专利/贷款的批准。因变量可能记录为是/否、真/假或 \(1/-1\),但总是可以写成 \(1/0\)。
二分类选择分析的目标是在给定一组回归变量 \(X\) 的情况下估计条件概率或响应概率 \(\mathbb{P}[Y=1 \mid X]\)。我们可能对响应概率或其某种变换(如导数——边际效应)感兴趣。二分类选择建模(以及一般的受限因变量模型)的传统方法是参数化的,通过最大似然估计。半参数估计也有大量文献。近年来,应用实践倾向于使用最小二乘法估计的线性概率模型。
更详细的处理请参见 Maddala (1983)、Cameron and Trivedi (2005) 和 Wooldridge (2010)
25.2 二分类选择模型
设 \((Y, X)\) 是随机的,其中 \(Y \in\{0,1\}\) 且 \(X \in \mathbb{R}^{k}\)。\(Y\) 相对于 \(X\) 的响应概率为
\[ P(x)=\mathbb{P}[Y=1 \mid X=x]=\mathbb{E}[Y \mid X=x] . \]
响应概率完全描述了条件分布。边际效应为
\[ \frac{\partial}{\partial x} P(x)=\frac{\partial}{\partial x} \mathbb{P}[Y=1 \mid X=x]=\frac{\partial}{\partial x} \mathbb{E}[Y \mid X=x] . \]
这等于回归导数。经济应用通常关注边际效应。
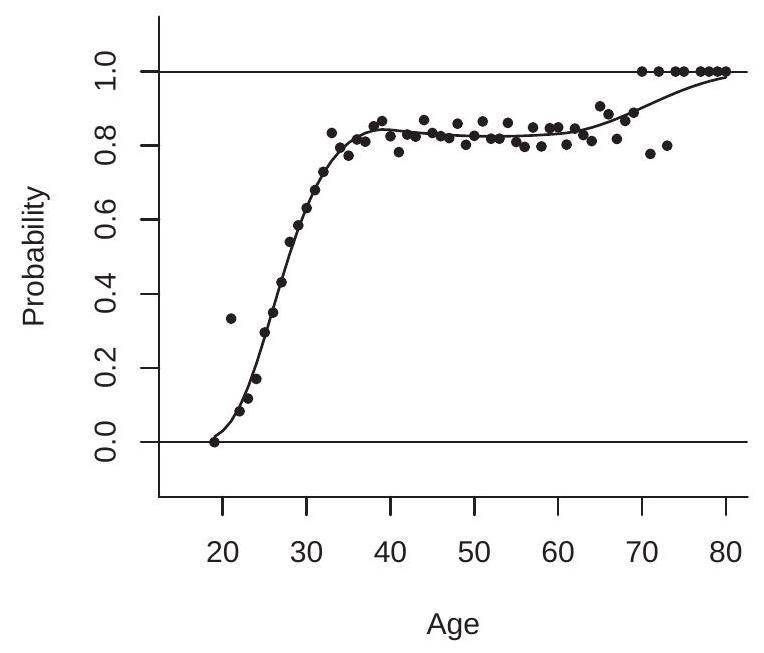
为了说明,考虑给定年龄的结婚概率。我们使用 cps09mar 数据集,取具有大学学位的男性子集(\(n=6441\)),如果个人已婚或丧偶但未分居或离婚则设 \(Y=1\),否则设 \(Y=0\)。回归变量是年龄,取值范围为 \([19,80]\)。
\({ }^{1}\) 婚姻状况等于 \(1,2,3\) 或 4。在图 25.1(a) 中,我们绘制了 \(P(x)\) 的两个估计值。实心圆是非参数估计——每个年龄的实证结婚频率——实线是我们偏好的设定(probit 样条模型,如下所述)。似乎明显的是,年龄 \(=19\) 时结婚概率接近零,线性增加到年龄 \(=35\) 左右约 \(80\%\),在年龄 \(40-65\) 时大致保持在 \(80\%\),在更高年龄时增加。
- 响应概率
- 二分类选择模型
图 25.1:受过大学教育的男性给定年龄的结婚概率
变量满足回归框架
\[ \begin{aligned} Y &=P(X)+e \\ \mathbb{E}[e \mid X] &=0 . \end{aligned} \]
误差 \(e\) 不是”经典的”。它具有两点条件分布
\[ e=\left\{\begin{array}{c} 1-P(X), \quad \text { 概率为 } P(X) \\ -P(X), \quad \text { 概率为 } 1-P(X) . \end{array}\right. \]
它也是高度异方差的,条件方差为
\[ \operatorname{var}[e \mid X]=P(X)(1-P(X)) . \]
二分类 \(Y\) 的回归散点图实际上是无用的,因为 \(Y\) 值不”分散”,而是完全位于直线 \(y=0\) 和 \(y=1\) 上。
25.3 响应概率模型
我们现在描述用于响应概率 \(P(x)\) 的最常见模型。
线性概率模型:\(P(x)=x^{\prime} \beta\),其中 \(\beta\) 是系数向量。在这个模型中,响应概率是回归变量的线性函数。线性概率模型的优点是解释简单。系数 \(\beta\) 等于边际效应(当 \(X\) 不包含非线性变换时)。由于响应概率等于条件均值,这个模型等于线性回归模型。线性意味着估计简单,因为可以使用最小二乘法来估计系数。在更复杂的情况下(例如,具有固定效应的面板数据或具有工具变量的内生变量),可以使用标准估计量。
线性概率模型的缺点是不尊重 \([0,1]\) 边界。来自估计的线性概率模型的拟合值和预测值经常违反这些边界,产生无意义的结果。
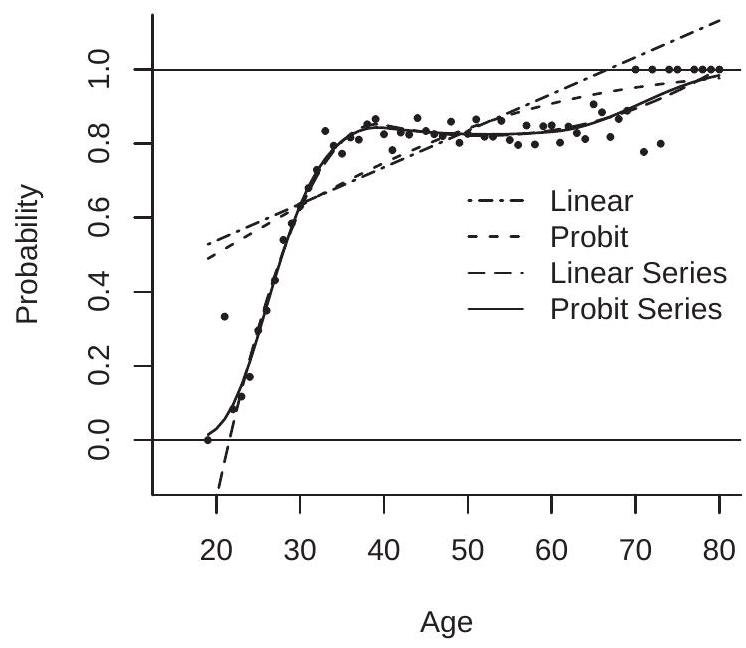
为了说明,在图 25.1(b) 中,我们用虚线绘制了线性概率模型对前一节描述的样本中观测值的拟合。拟合值是对响应概率的较差近似。它们还违反了 67 岁以上男性的 \([0,1]\) 边界。根据模型,80 岁的人结婚概率为 \(113\%\)!
总的来说,线性概率模型对于概率计算是一个糟糕的选择。
指数模型:\(P(x)=G\left(x^{\prime} \beta\right)\),其中 \(G(u)\) 是链接函数,\(\beta\) 是系数向量。这个框架也称为单指数模型,其中 \(x^{\prime} \beta\) 是线性指数函数。在二分类选择模型中,\(G(u)\) 是尊重概率边界 \(0 \leq G(u) \leq 1\) 的分布函数。在经济应用中,\(G(u)\) 通常是正态或逻辑分布函数,两者都关于零对称,因此 \(G(-u)=1-G(u)\)。我们在本章中假设这个对称条件成立。设 \(g(u)=\frac{\partial}{\partial u} G(u)\) 表示 \(G(u)\) 的密度函数。在指数模型中,边际效应函数为
\[ \frac{\partial}{\partial x} P(x)=\beta g\left(x^{\prime} \beta\right) . \]
指数模型仅比线性概率模型稍微复杂一些,但具有尊重 \([0,1]\) 边界的优点。两个最常见的指数模型是 probit 和 logit。
Probit 模型:\(P(x)=\Phi\left(x^{\prime} \beta\right)\),其中 \(\Phi(u)\) 是标准正态分布函数。这是二分类选择分析的传统主力模型。它简单、易用、易解释,并且基于经典正态分布。
Logit 模型:\(P(x)=\Lambda\left(x^{\prime} \beta\right)\),其中 \(\Lambda(u)=(1+\exp (-u))^{-1}\) 是逻辑分布函数。这是二分类选择分析的替代主力模型。逻辑和正态分布函数(适当缩放)具有相似的形状,因此 probit 和 logit 模型通常对响应概率和边际效应产生相似的估计。logit 模型的一个优点是分布函数以封闭形式可用,这加速了计算。
线性级数模型:\(P(x)=x_{K}^{\prime} \beta_{K}\),其中 \(x_{K}=x_{K}(x)\) 是 \(x\) 的变换向量,\(\beta_{K}\) 是系数向量。级数展开能够近似任何连续函数,包括响应概率 \(P(x)\)。线性级数模型的优点是其线性形式允许应用线性计量经济学方法。但是,它不保证尊重边界。
指数级数模型:\(P(x)=G\left(x_{K}^{\prime} \beta_{K}\right)\),其中 \(G(u)\) 是分布函数(在实践中是正态或逻辑),\(x_{K}=x_{K}(x)\) 是 \(x\) 的变换向量,\(\beta_{K}\) 是系数向量。级数展开能够近似任何连续函数,包括变换的响应概率 \(G^{-1}(p(x))\)。这意味着指数级数模型能够近似任何连续响应概率。此外,该模型尊重边界。
为了说明模型的近似能力,查看图 25.1(b),它绘制了四个估计的响应概率函数:(1) 线性;(2) Probit;(3) 线性级数;(4) Probit 级数。前两个模型被指定为年龄的线性。两个级数模型在年龄中使用二次样条,在 40 和 60 处有节点。
如前所述,在这个应用中,线性概率模型拟合特别差。它高估了 30 岁以下和 50 岁以上男性的概率,低估了其他年龄,并违反了 \([0,1]\) 边界。简单的 probit 模型也相当差。它产生的估计响应概率函数在 60 岁以下的年龄与线性概率模型相似。它的优点是对于 60 岁以上的年龄,它不违反 \([0,1]\) 边界。相比之下,两个级数模型产生了优秀的拟合响应概率函数。两个估计在 25 岁以上的年龄几乎相同。估计函数之间的主要区别是 probit 级数模型提供了全局优秀的拟合,而线性级数模型在 25 岁以下的年龄失败,严重违反了 \([0,1]\) 边界。线性级数模型估计 19 岁的人结婚概率为负:\(-27\%\)!
总结一下,probit 级数模型有几个优秀的特征。它简单,基于流行的链接函数,全局近似任何连续响应概率函数,并尊重 \([0,1]\) 边界。线性级数模型也是一个合理的候选,但具有不必然尊重 \([0,1]\) 边界的缺点。
25.4 Probit 和 Logit
probit 和 logit 这些有趣的标签在统计分析中有着悠久的历史。probit 这个术语是由 Chester Bliss 在 1934 年创造的,是”概率单位”的缩写。逻辑函数是由 Pierre François Verhulst 在 1938 年作为修正的指数增长模型引入的。据推测,他使用 logistic 这个术语作为与 logarithmic 的对比。1944 年,Joseph Berkson 提出了基于逻辑分布函数的二分类选择模型。他将逻辑作为正态的便利计算近似。由于他的模型是 probit 的类似物,Berkson 称他的模型为 logit。
25.5 潜变量解释
指数模型可以解释为潜变量模型。考虑
\[ \begin{aligned} Y^{*} &=X^{\prime} \beta+e \\ e & \sim G(e) \\ Y &=\mathbb{1}\left\{Y^{*}>0\right\}=\left\{\begin{array}{cc} 1 & \text { 如果 } Y^{*}>0 \\ 0 & \text { 否则。 } \end{array}\right. \end{aligned} \]
在这个模型中,可观测变量是 \((Y, X)\)。变量 \(Y^{*}\) 是潜在的,在 \(X\) 和误差 \(e\) 中是线性的,后者来自对称分布 \(G\)。观测到的二分类变量 \(Y\) 如果潜变量 \(Y^{*}\) 超过零则等于 1,否则等于 0。
事件 \(Y=1\) 与 \(Y^{*}>0\) 相同,这与
\[ X^{\prime} \beta+e>0 . \]
相同。
这意味着响应概率为
\[ P(x)=\mathbb{P}\left[e>-x^{\prime} \beta\right]=1-G\left(-x^{\prime} \beta\right)=G\left(x^{\prime} \beta\right) . \]
最后的等式使用了 \(G(u)\) 关于零对称的假设。这表明响应概率是 \(P(x)=G\left(x^{\prime} \beta\right)\),这是一个具有链接函数 \(G(u)\) 的指数模型。
这个潜变量模型对应于一个选择模型,其中 \(Y^{*}\) 是个体对选项 \(Y=1\) 和 \(Y=0\) 的相对效用(或利润),个体选择效用更高的选项。我们看到这个结构选择模型与具有等于误差分布的链接函数的指数模型相同。如果误差 \(e\) 是标准正态的,则它是 probit 模型;如果 \(e\) 是逻辑分布的,则它是 logit 模型。
您可能已经注意到,我们讨论了误差 \(e\) 要么是标准正态要么是标准逻辑的情况,也就是说,它们的尺度是固定的。这是因为误差分布的尺度无法识别。要看到这一点,假设 \(e=\sigma \varepsilon\),其中 \(\varepsilon\) 具有单位方差的分布 \(G(u)\)。那么响应概率为
\[ \mathbb{P}[Y=1 \mid X=x]=\mathbb{P}\left[\sigma e>-x^{\prime} \beta\right]=G\left(\frac{x^{\prime} \beta}{\sigma}\right)=G\left(x^{\prime} \beta^{*}\right) \]
其中 \(\beta^{*}=\beta / \sigma\)。这是一个具有系数 \(\beta^{*}\) 的指数模型。这意味着 \(\beta\) 和 \(\sigma\) 不能单独识别;只有比率 \(\beta^{*}=\beta / \sigma\) 被识别。标准解决方案是将 \(\sigma\) 标准化为便利值。probit 和 logit 模型分别使用标准化 \(\sigma=1\) 和 \(\sigma=\pi / \sqrt{3} \simeq 1.8\)。
上述分析的两个后果是:(1) 系数向量 \(\beta\) 的解释不能与误差的尺度分离;(2) probit 和 logit 模型的系数不能在不重新缩放的情况下进行比较。一般来说,最好将 probit 模型的系数解释为 \(\beta / \sigma\),即按结构标准差缩放的结构系数,将 logit 模型的系数解释为 \(\beta / \nu\),即按结构逻辑尺度参数 \(v=\sigma \sqrt{3} / \pi\) 缩放的结构系数。对于 probit 和 logit 系数的粗略比较,将 probit 系数乘以 \(1.8\) 或将 logit 系数除以 \(1.8\)。
虽然系数 \(\beta\) 无法识别,但以下参数是可识别的:
- 缩放系数:\(\beta^{*}=\beta / \sigma\)。
- 系数比率:\(\beta_{1} / \beta_{2}=\beta_{1}^{*} / \beta_{2}^{*}\)。
- 边际效应:\(\frac{\partial}{\partial x} P(x)=\frac{\beta}{\sigma} g\left(\frac{x^{\prime} \beta}{\sigma}\right)=\beta^{*} g\left(x^{\prime} \beta^{*}\right)\)。
这些只依赖于 \(\beta^{*}\),因此是可识别的。
关于识别,如果我们采用更广泛的非参数观点,误差分布 \(G(u)\) 无法识别。要看到这一点,将结构方程非参数地写为 \(Y^{*}=m(X)+e\)。响应概率为
\[ P(x)=1-G(-m(x)) . \]
联合分布识别 \(P(x)\)。如果 \(G(e)\) 和 \(m(x)\) 是非参数的,它们不能从响应概率中单独识别。只有复合函数 (25.4) 被识别。
一个重要的含义是,只要函数 \(m(x)\) 被非参数地处理,将 \(G(u)\) 设置为特定参数分布(如正态)就没有一般性的损失。
\({ }^{2}\) 这只产生粗略的比较,因为这种标准化只是将系数放在相同的尺度上。由于模型不同,它们不相等。
25.6 似然函数
Probit 和 logit 模型通常通过最大似然估计。为了构建似然函数,我们需要单个观测的分布。回顾如果 \(Y\) 是伯努利的,使得 \(\mathbb{P}[Y=1]=p\) 和 \(\mathbb{P}[Y=0]=1-p\),那么 \(Y\) 具有概率质量函数
\[ \pi(y)=p^{y}(1-p)^{1-y}, \quad y=0,1 . \]
在指数模型中 \(\mathbb{P}[Y=1 \mid X]=G\left(X^{\prime} \beta\right)\),\(Y\) 是条件伯努利的,所以它的条件概率质量函数为
\[ \pi(Y \mid X)=G\left(X^{\prime} \beta\right)^{Y}\left(1-G\left(X^{\prime} \beta\right)\right)^{1-Y}=G\left(X^{\prime} \beta\right)^{Y} G\left(-X^{\prime} \beta\right)^{1-Y}=G\left(Z^{\prime} \beta\right) \]
其中
\[ Z=\left\{\begin{array}{cc} X & \text { 如果 } Y=1 \\ -X & \text { 如果 } Y=0 . \end{array}\right. \]
取对数并对观测值求和,我们得到对数似然函数:
\[ \ell_{n}(\beta)=\sum_{i=1}^{n} \log G\left(Z_{i}^{\prime} \beta\right) \]
对于 probit 和 logit 模型,这是
\[ \begin{aligned} \ell_{n}^{\text {probit }}(\beta) &=\sum_{i=1}^{n} \log \Phi\left(Z_{i}^{\prime} \beta\right) \\ \ell_{n}^{\text {logit }}(\beta) &=\sum_{i=1}^{n} \log \Lambda\left(Z_{i}^{\prime} \beta\right) \end{aligned} \]
定义对数分布函数的一阶和(负)二阶导数:\(h(x)=\frac{d}{d x} \log G(x)\) 和 \(H(x)=-\frac{d^{2}}{d x^{2}} \log G(x)\)。对于 logit 模型,这些等于(参见练习 25.5)
\[ \begin{aligned} &h_{\text {logit }}(x)=1-\Lambda(x) \\ &H_{\text {logit }}(x)=\Lambda(x)(1-\Lambda(x)) \end{aligned} \]
对于 probit 模型(参见练习 25.6)
\[ \begin{aligned} h_{\text {probit }}(x) &=\frac{\phi(x)}{\Phi(x)} \stackrel{\text { def }}{=} \lambda(x) \\ H_{\text {probit }}(x) &=\lambda(x)(x+\lambda(x)) . \end{aligned} \]
函数 \(\lambda(x)=\phi(x) / \Phi(x)\) 被称为逆 Mills 比率。
logit 和 probit 都具有 \(H(x)>0\) 的性质。这在 logit 情况下很容易看到,因为它是分布函数与其补集的乘积,但在 probit 情况下不太明显。这里我们利用对数凹函数 \({ }^{3}\) 的便利性质:如果密度 \(f(x)\) 是对数凹的,那么分布函数 \(F(x)\) 是对数凹的。标准正态密度 \(\phi(x)\) 是对数凹的 \({ }^{4}\),意味着 \(\Phi(x)\) 是对数凹的,意味着 \(H_{\text {probit }}(x)>0\) 如期望的那样。
\({ }^{3}\) 函数 \(f(x)\) 是对数凹的,如果 \(\log f(x)\) 是凹的。
\({ }^{4} \log \phi(x)=-\log (2 \pi)-x^{2} / 2\) 是凹的。似然得分和 Hessian 矩阵为
\[ \begin{gathered} S_{n}(\beta)=\frac{\partial}{\partial \beta} \ell_{n}(\beta)=\sum_{i=1}^{n} Z_{i} h\left(Z_{i}^{\prime} \beta\right) \\ \mathscr{H}_{n}(\beta)=-\frac{\partial^{2}}{\partial \beta \partial \beta^{\prime}} \ell_{n}(\beta)=\sum_{i=1}^{n} X_{i} X_{i}^{\prime} H\left(Z_{i}^{\prime} \beta\right) . \end{gathered} \]
检查 (25.7),我们可以看到 \(H(x)>0\) 意味着 \(\mathscr{H}_{n}(\beta)>0\) 在 \(\beta\) 中全局成立。这反过来意味着对数似然 \(\ell_{n}(\beta)\) 在 \(\beta\) 中全局凹。由于 \(H_{\operatorname{logit}}(x)>0\) 和 \(H_{\text {probit }}(x)>0\) 都成立,我们推断 probit 和 logit 对数似然函数 \(\ell_{n}^{\text {probit }}(\beta)\) 和 \(\ell_{n}^{\operatorname{logit}}(\beta)\) 在 \(\beta\) 中全局凹。
MLE 是使 \(\ell_{n}(\beta)\) 最大化的值。我们将其写为
\[ \begin{aligned} \widehat{\beta}^{\text {probit }} &=\underset{\beta}{\operatorname{argmax}} \ell_{n}^{\text {probit }}(\beta) \\ \widehat{\beta}^{\text {logit }} &=\underset{\beta}{\operatorname{argmax}} \ell_{n}^{\text {logit }}(\beta) . \end{aligned} \]
由于 probit 和 logit 对数似然是全局凹的,\(\widehat{\beta}^{\text {probit }}\) 和 \(\widehat{\beta}^{\text {logit }}\) 是唯一的。没有显式解,所以需要数值求解。由于对数似然是光滑的、凹的,具有已知的一阶和二阶导数,数值优化是直接的。
在 Stata 中,使用命令 probit 和 logit 来获得 MLE。在 R 中,使用命令
\[ \begin{aligned} &\operatorname{glm}\left(Y^{\sim} X, f a m i l y=b i n o m i a l(\text { ink="probit")) }\right. \\ &\operatorname{glm}\left(Y^{\sim} X,\right. \text { family=binomial (link="logit")). } \end{aligned} \]
25.7 伪真值
期望对数质量函数为
\[ \ell(\beta)=\mathbb{E}\left[\log G\left(Z^{\prime} \beta\right)\right] . \]
如果存在系数 \(\beta_{0}\) 使得 \(\mathbb{P}[Y=1 \mid X]=G\left(X^{\prime} \beta_{0}\right)\),则模型被正确设定。当这成立时,\(\beta_{0}\) 具有使 \(\ell(\beta)\) 最大化的性质,因此满足
\[ \beta_{0}=\underset{\beta}{\operatorname{argmax}} \ell(\beta) . \]
如果没有 \(\beta\) 使得 \(\mathbb{P}[Y=1 \mid X]=G\left(X^{\prime} \beta\right)\),我们说模型被错误设定。在这种情况下,我们将模型 \(G\left(X^{\prime} \beta\right)\) 视为响应概率的近似,并定义伪真系数 \(\beta_{0}\) 为满足 (25.8) 的值。通过构造,(25.8) 在模型正确设定时等于真系数,否则产生相对于期望 \(\log\) 质量函数的最佳拟合模型。
当分布函数 \(G(x)\) 是对数凹的(如 probit 和 logit 模型的情况)时,\(\ell(\beta)\) 是全局凹的。要看到这一点,定义
\[ \boldsymbol{Q}(\beta)=-\frac{\partial^{2}}{\partial \beta \partial \beta^{\prime}} \ell(\beta)=\mathbb{E}\left[X X^{\prime} H\left(Z^{\prime} \beta\right)\right] \]
并观察到 \(H(x)>0\)(通过对数凹性),这意味着 \(\boldsymbol{Q}(\beta) \geq 0\),这意味着 \(\ell(\beta)\) 是全局凹的。此外,在满秩条件下,最小化器 (25.8) 是唯一的
\[ \mathbb{E}\left[X X^{\prime} H\left(X^{\prime} \beta_{0}\right)\right]>0 . \]
重要的是要注意 \(\ell(\beta)\) 的凹性和最大化器 \(\beta_{0}\) 的唯一性是模型 \(G\left(X^{\prime} \beta\right)\) 的性质,而不是真分布的性质。
为了具体性,对于 probit 和 logit 模型,定义总体准则
\[ \begin{aligned} \ell^{\operatorname{probit}^{\prime}(\beta)} &=\mathbb{E}\left[\log \Phi\left(Z^{\prime} \beta\right)\right] \\ \ell^{\operatorname{logit}}(\beta) &=\mathbb{E}\left[\log \Lambda\left(Z^{\prime} \beta\right)\right] \end{aligned} \]
和伪真值
\[ \begin{aligned} \beta^{\text {probit }} &=\underset{\beta}{\operatorname{argmax}} \ell^{\text {probit }}(\beta) \\ \beta^{\text {logit }} &=\underset{\beta}{\operatorname{argmax}} \ell^{\text {logit }}(\beta) . \end{aligned} \]
我们现在描述 logit 和 probit 模型的满秩条件 (25.9)。对于 probit 模型 \(H_{\text {logit }}(-x)=H_{\text {logit }}(x)\) 关于零对称,所以 \(H_{\text {logit }}\left(Z^{\prime} \beta\right)=H_{\text {logit }}\left(X^{\prime} \beta\right)=\Lambda\left(X^{\prime} \beta\right)\left(1-\Lambda\left(X^{\prime} \beta\right)\right)\)。我们推断 (25.9) 与
\[ \boldsymbol{Q}_{\text {logit }} \stackrel{\text { def }}{=} \mathbb{E}\left[X X^{\prime} \Lambda\left(X^{\prime} \beta^{\text {logit }}\right)\left(1-\Lambda\left(X^{\prime} \beta^{\text {logit }}\right)\right)\right]>0 . \]
相同。
对于 probit 模型,条件 (25.9) 为
\[ \boldsymbol{Q}_{\text {probit }} \stackrel{\text { def }}{=} \mathbb{E}\left[X X^{\prime} H_{\text {probit }}\left(Z^{\prime} \beta^{\text {probit }}\right)\right]>0 . \]
当 (25.10) 和/或 (25.11) 成立时,总体最小化器 \(\beta^{\text {probit }}\) 和/或 \(\beta^{\text {logit }}\) 是唯一的。
25.8 渐近分布
我们首先提供一致估计的条件。设 \(B\) 为 \(\beta\) 的参数空间。
定理 25.1 Logit 估计的一致性。如果 (1) \(\left(Y_{i}, X_{i}\right)\) 是独立同分布的;(2) \(\mathbb{E}\|X\|<\infty\);(3) \(\boldsymbol{Q}_{\text {logit }}>0\);以及 (4) B 是紧的;那么 \(\widehat{\beta}^{\operatorname{logit}} \underset{p}{\longrightarrow} \beta^{\operatorname{logit}}\) 当 \(n \rightarrow \infty\) 时。
定理 25.2 Probit 估计的一致性。如果 (1) \(\left(Y_{i}, X_{i}\right)\) 是独立同分布的;(2) \(\mathbb{E}\|X\|^{2}<\infty\);(3) \(\boldsymbol{Q}_{\text {probit }}>0\);以及 (4) B 是紧的;那么 \(\widehat{\beta}^{\text {probit }} \underset{p}{\longrightarrow} \beta^{\text {probit }}\) 当 \(n \rightarrow \infty\) 时。
证明在第 25.14 节中。为了推导渐近分布,我们求助于定理 22.4 关于 m-估计量,它表明渐近分布是正态的,协方差矩阵为 \(V=\) \(\boldsymbol{Q}^{-1} \Omega \boldsymbol{Q}^{-1}\),其中 \(\boldsymbol{Q}\) 在 (25.10) 中为 logit 模型定义,在 (25.11) 中为 probit 模型定义。得分的方差为 \(\Omega=\mathbb{E}\left[X X^{\prime} h\left(Z^{\prime} \beta\right)^{2}\right]\)。在 logit 模型中,我们有简化
\[ \Omega_{\text {logit }}=\mathbb{E}\left[X X^{\prime}\left(Y-\Lambda\left(X^{\prime} \beta^{\text {logit }}\right)\right)^{2}\right] \]
(如下所述)。对于 probit 模型,我们没有类似的简化(除了在正确设定下,如下所述),因此定义
\[ \Omega_{\text {probit }}=\mathbb{E}\left[X X^{\prime} \lambda\left(Z^{\prime} \beta^{\text {probit }}\right)^{2}\right] . \]
要看到 (25.12),通过一些代数运算,您可以证明
\[ h\left(Z^{\prime} \beta\right)^{2}=\frac{g\left(X^{\prime} \beta\right)^{2}}{G\left(X^{\prime} \beta\right)^{2}} Y+\frac{g\left(X^{\prime} \beta\right)^{2}}{\left(1-G\left(X^{\prime} \beta\right)\right)^{2}}(1-Y)=\frac{g\left(X^{\prime} \beta\right)^{2}\left(Y-G\left(X^{\prime} \beta\right)\right)^{2}}{G\left(X^{\prime} \beta\right)^{2}\left(1-G\left(X^{\prime} \beta\right)\right)^{2}} . \]
在 logit 模型中,右侧简化为 \(\left(Y-\Lambda\left(X^{\prime} \beta\right)\right)^{2}\)。这意味着
\[ \Omega_{\text {logit }}=\mathbb{E}\left[X X^{\prime} h_{\text {logit }}\left(Z^{\prime} \beta\right)^{2}\right]=\mathbb{E}\left[X X^{\prime}\left(Y-\Lambda\left(X^{\prime} \beta^{\text {logit }}\right)\right)^{2}\right] \]
如所声称的。
定理 25.3 如果定理 25.1 的条件成立,加上 \(\mathbb{E}\|X\|^{4}<\infty\) 和 \(\beta^{\text {logit }}\) 在 \(B\) 的内部;那么当 \(n \rightarrow \infty\) 时
\[ \sqrt{n}\left(\widehat{\beta}^{\text {logit }}-\beta^{\text {logit }}\right) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{V}_{\text {logit }}\right) \]
其中 \(V_{\text {logit }}=Q_{\text {logit }}^{-1} \Omega_{\text {logit }} Q_{\text {logit }}^{-1}\)
定理 25.4 如果定理 25.2 的条件成立,加上 \(\mathbb{E}\|X\|^{4}<\infty\) 和 \(\beta^{\text {probit }}\) 在 \(B\) 的内部;那么当 \(n \rightarrow \infty\) 时
\[ \sqrt{n}\left(\widehat{\beta}^{\text {probit }}-\beta^{\text {probit }}\right) \underset{d}{\longrightarrow} \mathrm{N}\left(0, \boldsymbol{V}_{\text {probit }}\right) \]
其中 \(\boldsymbol{V}_{\text {probit }}=\boldsymbol{Q}_{\text {probit }}^{-1} \Omega_{\text {probit }} \boldsymbol{Q}_{\text {probit }}^{-1}\)
证明在第 25.14 节中。
在正确设定下,信息矩阵等式意味着简化 \(\boldsymbol{V}_{\text {logit }}=\boldsymbol{Q}_{\operatorname{logit}}^{-1}\) 和 \(\boldsymbol{V}_{\text {probit }}=\boldsymbol{Q}_{\text {probit }}^{-1}\)。我们还有简化
\[ \Omega_{\text {probit }}=\boldsymbol{Q}_{\text {probit }}=\mathbb{E}\left[X X^{\prime} \lambda\left(X^{\prime} \beta^{\text {probit }}\right) \lambda\left(-X^{\prime} \beta^{\text {probit }}\right)\right] . \]
这来自 (25.14),对于 probit 模型可以写为
\[ \lambda\left(Z^{\prime} \beta\right)^{2}=\lambda\left(X^{\prime} \beta\right) \lambda\left(-X^{\prime} \beta\right) \frac{\left(Y-\Phi\left(X^{\prime} \beta\right)\right)^{2}}{\Phi\left(X^{\prime} \beta\right)\left(1-\Phi\left(X^{\prime} \beta\right)\right)} . \]
在正确设定下 \(\mathbb{E}[Y \mid X]=\Phi\left(X^{\prime} \beta\right)\) 和 \(\mathbb{E}\left[\left(Y-\Phi\left(X^{\prime} \beta\right)\right)^{2} \mid X\right]=\Phi\left(X^{\prime} \beta\right)\left(1-\Phi\left(X^{\prime} \beta\right)\right)\)。给定 \(X\) 取期望,上述表达式简化为 \(\lambda\left(X^{\prime} \beta\right) \lambda\left(-X^{\prime} \beta\right)\)。代入 (25.13) 得到 (25.15)。
25.9 协方差矩阵估计
对于 logit 模型,定义 \(\widehat{\Lambda}_{i}=\Lambda\left(X_{i}^{\prime} \widehat{\beta}^{\text {logit }}\right)\) 和
\[ \begin{aligned} &\widehat{\boldsymbol{Q}}_{\text {logit }}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X_{i}^{\prime} \widehat{\Lambda}_{i}\left(1-\widehat{\Lambda}_{i}\right) \\ &\widehat{\Omega}_{\text {logit }}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X_{i}^{\prime}\left(Y_{i}-\widehat{\Lambda}_{i}\right)^{2} \end{aligned} \]
\(\boldsymbol{V}_{\text {logit }}\) 的三明治协方差矩阵估计量为 \(\widehat{\boldsymbol{V}}_{\text {logit }}=\widehat{\boldsymbol{Q}}_{\text {logit }}^{-1} \widehat{\Omega}_{\text {logit }} \widehat{\boldsymbol{Q}}_{\text {logit }}^{-1}\)。在正确设定假设下,我们也可以使用 \(\widehat{\boldsymbol{V}}_{\text {logit }}^{0}=\widehat{\boldsymbol{Q}}_{\operatorname{logit}}^{-1}\)。
对于 probit 模型,定义 \(\widehat{\mu}_{i}=Z_{i}^{\prime} \widehat{\beta}^{\text {probit }}, \widehat{\lambda}_{i}=\lambda\left(\widehat{\mu}_{i}\right)\),和
\[ \begin{aligned} &\widehat{\boldsymbol{Q}}_{\text {probit }}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X_{i}^{\prime} \widehat{\lambda}_{i}\left(\widehat{\mu}_{i}+\widehat{\lambda}_{i}\right) \\ &\widehat{\Omega}_{\text {probit }}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X_{i}^{\prime} \widehat{\lambda}_{i}^{2} . \end{aligned} \]
\(\boldsymbol{V}_{\text {probit }}\) 的三明治协方差矩阵估计量为 \(\widehat{\boldsymbol{V}}_{\text {probit }}=\widehat{\boldsymbol{Q}}_{\text {probit }}^{-1} \widehat{\Omega}_{\text {probit }} \widehat{\boldsymbol{Q}}_{\text {probit }}^{-1}\)。在正确设定假设下,我们也可以使用
\[ \widehat{\boldsymbol{Q}}_{\mathrm{probit}}^{0}=\frac{1}{n} \sum_{i=1}^{n} X_{i} X_{i}^{\prime} \lambda\left(X^{\prime} \widehat{\beta}^{\text {probit }}\right) \lambda\left(-X^{\prime} \widehat{\beta}^{\text {probit }}\right) \]
和 \(\widehat{\boldsymbol{V}}_{\text {probit }}^{0}=\left(\widehat{\boldsymbol{Q}}^{0}\right)^{-1}\)。
在 Stata 和 R 中,默认协方差矩阵和标准误差通过 \(\widehat{\boldsymbol{V}}_{\text {logit }}^{0}\) 和 \(\widehat{\boldsymbol{V}}_{\text {probit }}^{0}\) 计算。对于稳健协方差矩阵估计和标准误差 \(\widehat{\boldsymbol{V}}_{\text {logit }}\) 和 \(\widehat{\boldsymbol{V}}_{\text {probit }}\),在 Stata 中使用选项 vce(robust)。在 R 中使用 sandwich 包,它有 HC0、HC1 和 HC2(以及其他)协方差矩阵估计量的选项。
25.10 边际效应
正如我们之前提到的,通常关注边际效应而不是系数,因为后者难以解释。在本节中,我们更详细地描述边际效应并描述常见的估计量。
取指数模型 \(\mathbb{P}[Y=1 \mid X=x]=G\left(x^{\prime} \beta\right)\),当 \(x\) 不包含非线性变换时。在这种情况下,边际效应为
\[ \delta(x)=\frac{\partial}{\partial x} P(x)=\beta g\left(x^{\prime} \beta\right) . \]
这随 \(x\) 变化。例如,在图 25.1 中,我们看到年龄对结婚概率的边际效应在 20-30 岁之间每年约为 \(0.06\),但在 40 岁以上时接近零。
对于报告,通常计算”平均”值。有多种方法可以做到这一点。最常见的是平均边际效应
\[ \mathrm{AME}=\mathbb{E}[\delta(X)]=\beta \mathbb{E}\left[g\left(X^{\prime} \beta\right)\right] . \]
\(\delta(x)\) 的估计量为 \(\widehat{\delta}(x)=\widehat{\beta} g\left(x^{\prime} \widehat{\beta}\right)\)。AME 的估计量为
\[ \widehat{\mathrm{AME}}=\frac{1}{n} \sum_{i=1}^{n} \widehat{\delta}\left(X_{i}\right)=\widehat{\beta} \frac{1}{n} \sum_{i=1}^{n} g\left(X_{i}^{\prime} \widehat{\beta}\right) . \]
当向量 \(X\) 包含非线性变换时,边际效应需要仔细定义。例如,在模型 \(\mathbb{P}[Y=1 \mid X=x]=G\left(\beta_{0}+\beta_{1} x+\cdots+\beta_{p} x^{p}\right)\) 中,边际效应为
\[ \delta(x)=\left(\beta_{1}+\cdots+p \beta_{p} x^{p-1}\right) g\left(\beta_{0}+\beta_{1} x+\cdots+\beta_{p} x^{p}\right) . \]
\(\delta(x)\) 的估计量为
\[ \widehat{\delta}(x)=\left(\widehat{\beta}_{1}+\cdots+p \widehat{\beta}_{p} x^{p-1}\right) g\left(\widehat{\beta}_{0}+\widehat{\beta}_{1} x+\cdots+\widehat{\beta}_{p} x^{p}\right) . \]
AME 的估计量为 \(\widehat{\mathrm{AME}}=\frac{1}{n} \sum_{i=1}^{n} \widehat{\delta}\left(X_{i}\right)\)
在 Stata 中,边际效应可以用 margins , \(\mathrm{dydx}(*)\) 估计。
25.11 应用
我们用一个关于结婚概率的应用来说明,使用 cps09mar 数据集。我们使用年龄不超过 35 岁的男性子样本(\(n=9137\))。我们包括作为回归变量的个人年龄、教育程度,以及黑人、亚洲人、西班牙裔和三个地区的指标。我们估计线性 logit 和线性 probit 模型,计算系数和平均边际效应,并报告稳健标准误差。结果在表 25.1 中报告。
阅读表格,您会看到 logit 和 probit 系数估计都具有相同的符号,但 logit 系数在幅度上更大。我们看到结婚概率随年龄增加,黑人个体较低,并且在地理区域间变化。系数本身难以解释,所以最好关注估计的边际效应。这样做,我们看到 logit 和 probit 估计基本相同。这在经验应用中是一个常见发现,当两者都提供对响应概率的良好近似时。进一步检查系数,我们看到结婚概率每年增加约 \(4.5\%\)。教育影响的点估计为每年教育 \(0.3\%\),这是一个小的幅度。黑人男性相对于省略类别(非黑人、非亚洲人、非西班牙裔男性)的结婚概率降低了 \(15\%\)。亚洲和西班牙裔男性的估计边际效应相对于省略类别较小(分别为 \(1\%\) 和 \(-2\%\))。比较地区,我们看到中西部、南部和西部的结婚率相对于东北部(省略类别)高约 6-8%。等价地,东北部的男性相对于该国其他地区结婚概率降低了约 \(7\%\)。
从这个应用中的两个信息是 logit 与 probit 的选择不重要,以及关注边际效应比系数更好。一个隐藏的信息是(如所有计量经济学应用)模型设定至关重要。表 25.1 中的估计是针对 19-35 岁的男性。这个选择是为了响应概率可以用年龄的单个线性项很好地建模。如果相反,估计是在全样本上计算的(仍然使用线性设定),那么年龄的估计边际效应将是每年 \(1\%\) 而不是 \(4.5\%\),这是年龄对结婚概率影响的大误估计。
25.12 半参数二分类选择
半参数二分类选择模型为
\[ \mathbb{P}[Y=1 \mid X]=G\left(X^{\prime} \beta\right) \]
表 25.1:结婚的二分类选择回归
| Logit | Probit | |||
|---|---|---|---|---|
| 系数 | AME | 系数 | AME | |
| age | \(0.217\) | \(0.044\) | \(0.132\) | \(0.045\) |
| \((0.006)\) | \((0.001)\) | \((0.003)\) | \((0.001)\) | |
| education | \(0.014\) | \(0.003\) | \(0.009\) | \(0.003\) |
| \((0.010)\) | \((0.002)\) | \((0.006)\) | \((0.002)\) | |
| Black | \(-0.767\) | \(-0.156\) | \(-0.454\) | \(-0.153\) |
| \((0.092)\) | \((0.018)\) | \((0.054)\) | \((0.018)\) | |
| Asian | \(0.033\) | \(0.007\) | \(0.025\) | \(0.008\) |
| \((0.103)\) | \((0.021)\) | \((0.063)\) | \((0.021)\) | |
| Hispanic | \(-0.084\) | \(-0.017\) | \(-0.048\) | \(-0.017\) |
| \((0.063)\) | \((0.013)\) | \((0.038)\) | \((0.013)\) | |
| MidWest | \(0.272\) | \(0.056\) | \(0.165\) | \(0.056\) |
| \((0.074)\) | \((0.011)\) | \((0.045)\) | \((0.015)\) | |
| South | \(0.338\) | \(0.069\) | \(0.203\) | \(0.069\) |
| \((0.070)\) | \((0.014)\) | \((0.043)\) | \((0.014)\) | |
| West | \(0.383\) | \(0.078\) | \(0.228\) | \(0.077\) |
| \((0.072)\) | \((0.015)\) | \((0.044)\) | \((0.015)\) | |
| Intercept | \(-6.45\) | \(-3.93\) | ||
| \((0.21)\) | \((0.12)\) |
其中 \(G(x)\) 是未知的。兴趣通常集中在系数 \(\beta\) 上。
在潜变量框架中,\(G(x)\) 是潜误差 \(e\) 的分布函数。由于分布 \(G(x)\) 已知是不可信的,半参数模型将 \(G(x)\) 视为未知。目标是在对 \(G(x)\) 不可知的情况下估计系数 \(\beta\)。
这个文献有很多贡献。其中两个最有影响力的是 Manski (1975) 和 Klein and Spady (1993)。两者都使用潜变量框架 \(Y^{*}=X^{\prime} \beta+e\)。
Manski (1975) 表明,如果 med \([e \mid X]=0\),则 \(\beta\) 在尺度上可识别。他提出了一个巧妙的最大得分估计量,在这个弱条件下对 \(\beta\) 在尺度上是一致的。然而,他的方法不允许估计响应概率或边际效应,因为他的假设不足以识别 \(G(x)\)。
Klein and Spady (1993) 添加了 \(e\) 独立于 \(X\) 的假设,这意味着 \(G(x)\) 的识别。他们提出了基于以下两个性质的 \(\beta\) 和 \(G(x)\) 的联合估计:(1) 如果 \(G(x)\) 已知,则 \(\beta\) 可以通过最大似然估计;(2) 如果 \(\beta\) 已知,则 \(G(x)\) 可以通过 \(Y\) 对 \(X^{\prime} \beta\) 的非参数回归估计。将这两个性质结合到一个嵌套准则中,他们产生了一个一致的、渐近正态的、有效的 \(\beta\) 估计量。
虽然 Manski 和 Klein-Spady 的想法相当巧妙,但问题是模型 \(G\left(x^{\prime} \beta\right)\) 依赖于参数线性指数假设。假设我们将后者放宽为非参数函数 \(m(x)\) 但假设 \(e\) 独立于 \(X\)。那么响应概率为 \(1-G(-m(x))\)。在这种情况下,\(G(x)\) 和 \(m(x)\) 都无法识别;只有复合函数 \(G(-m(x))\) 被识别。这意味着在对 \(G(x)\) 不可知的情况下估计 \(m(x)\) 是不可能的,除非对 \(m(x)\) 有参数假设。因此,现代观点是将 \(P(x)=\mathbb{P}[Y=1 \mid X=x]\) 视为非参数识别的。可以通过级数近似实现一致估计,使用线性、probit 或 logit 链接。从这个观点来看,限制到函数形式 \(G\left(x^{\prime} \beta\right)\) 没有收益,因此半参数方法没有收益。
25.13 内生 Probit
潜变量结构方程模型为
\[ \begin{aligned} Y_{1}^{*} &=X^{\prime} \beta_{1}+Y_{2} \beta_{2}+e_{1} \\ Y_{2} &=X^{\prime} \gamma_{1}+Z^{\prime} \gamma_{2}+e_{2} \\ Y_{1} &=\mathbb{1}\left\{Y_{1}^{*}>0\right\} . \end{aligned} \]
在这个模型中,\(Y_{2}\) 是标量、内生的、连续分布的,\(X\) 是包含的外生回归变量,\(Z\) 是排除的外生工具。
标准估计方法是基于误差联合正态假设的最大似然
\[ \left(\begin{array}{l} e_{1} \\ e_{2} \end{array}\right) \mid(X, Z) \sim \mathrm{N}\left(\left(\begin{array}{l} 0 \\ 0 \end{array}\right),\left(\begin{array}{cc} 1 & \sigma_{12} \\ \sigma_{21} & \sigma_{2}^{2} \end{array}\right)\right) . \]
似然推导如下。\(e_{1}\) 对 \(e_{2}\) 的回归等于
\[ \begin{aligned} e_{1} &=\rho e_{2}+\varepsilon \\ \rho &=\frac{\sigma_{12}}{\sigma_{2}^{2}} \\ \varepsilon & \sim \mathrm{N}\left(0, \sigma_{\varepsilon}^{2}\right) \\ \sigma_{\varepsilon}^{2} &=1-\frac{\sigma_{12}^{2}}{\sigma_{2}^{2}} . \end{aligned} \]
使用这些关系,我们可以将结构方程写为
\[ \begin{aligned} Y_{1}^{*} &=\mu(\theta)+\varepsilon \\ \mu(\theta) &=X^{\prime} \beta_{1}+Y_{2} \beta_{2}+\rho\left(Y_{2}-X^{\prime} \gamma_{1}-Z^{\prime} \gamma_{2}\right) . \end{aligned} \]
误差 \(\varepsilon\) 独立于 \(e_{2}\) 因此独立于 \(Y_{2}\)。因此 \(Y_{1}^{*}\) 的条件分布为 \(\mathrm{N}\left(\mu(\theta), \sigma_{\varepsilon}^{2}\right)\)。因此 \(\left(Y_{1}, Y_{2}\right)\) 的联合密度为
\[ \Phi\left(\frac{\mu(\theta)}{\sigma_{\varepsilon}}\right)^{Y_{1}}\left(1-\Phi\left(\frac{\mu(\theta)}{\sigma_{\varepsilon}}\right)\right)^{1-Y_{1}} \frac{1}{\sigma_{2}} \phi\left(\frac{Y_{2}-X^{\prime} \gamma_{1}-Z^{\prime} \gamma_{2}}{\sigma_{2}}\right) . \]
参数向量为 \(\theta=\left(\beta_{1}, \beta_{2}, \gamma_{1}, \gamma_{2}, \rho, \sigma_{\varepsilon}^{2}, \sigma_{2}^{2}\right)\)。
随机样本 \(\left\{Y_{1 i}, Y_{2 i}, X_{i}, Z_{i}\right\}\) 的联合对数似然为
\[ \begin{aligned} \ell_{n}(\theta) &=\sum_{i=1}^{n}\left[Y_{1 i} \log \Phi\left(\frac{\mu_{i}(\theta)}{\sigma_{\varepsilon}}\right)+\left(1-Y_{1 i}\right) \log \left(1-\Phi\left(\frac{\mu_{i}(\theta)}{\sigma_{\varepsilon}}\right)\right)\right] \\ &-\frac{n}{2} \log (2 \pi)-\frac{n}{2} \log \sigma_{2}^{2}-\frac{1}{2 \sigma_{2}^{2}} \sum_{i=1}^{n}\left(Y_{2 i}-X_{i}^{\prime} \gamma_{1}-Z_{i}^{\prime} \gamma_{2}\right)^{2} \end{aligned} \]
最大似然估计量 \(\widehat{\theta}\) 通过数值最大化 \(\ell_{n}(\theta)\) 找到。
probit 假设(将 \(\left(e_{1}, e_{2}\right)\) 视为联合正态)对这个推导很重要,因为它允许将联合分布简单分解为给定 \(Y_{2}\) 的 \(Y_{1}\) 的条件分布和 \(Y_{2}\) 的边际分布。在 logit 框架中不容易实现类似的分解。
在 Stata 中,这个估计量可以用 ivprobit 命令实现。
25.14 二分类面板数据
二分类选择面板模型通常写为
\[ \begin{aligned} &Y_{i t}^{*}=X_{i t}^{\prime} \beta+u_{i}+e_{i t} \\ &Y_{i t}=\mathbb{1}\left\{Y_{i t}^{*}>0\right\} . \end{aligned} \]
这里,观测值为 \(\left(Y_{i t}, X_{i t}\right)\),其中 \(i=1, \ldots, n\) 和 \(t=1, \ldots, T\),\(Y_{i t}\) 是二分类的。例如,\(Y_{i t}\) 可以表示个体 \(i\) 在时期 \(t\) 的购买决策。个体效应 \(u_{i}\) 旨在捕捉某些个体 \(i\) 比回归变量能解释的更频繁(或更少)购买的特征。
与线性模型一样,在将个体效应 \(u_{i}\) 视为随机(意味着它独立于回归变量)或固定(意味着它与回归变量相关)之间存在区别。
在随机效应假设下,模型可以通过最大似然估计。这被称为随机效应 probit 或随机效应 logit,取决于误差分布。
允许固定效应更复杂。个体效应不能通过线性操作消除,因为 \(Y_{i t}\) 是 \(u_{i}\) 的非线性函数。例如,变换
\[ \Delta Y_{i t}=\mathbb{1}\left\{Y_{i t}^{*}>0\right\}-\mathbb{1}\left\{Y_{i, t-1}^{*}>0\right\} \]
不消除 \(u_{i}\)。
因此,probit 模型没有固定效应估计量。然而,对于 logit 模型,Chamberlain \((1980,1984)\) 基于条件似然开发了固定效应估计量。他表明逻辑分布的一个特征是个体效应可以通过优势比消除,允许计算给定因变量和的条件似然。
我们说明 \(T=2\) 情况的似然构建。设 \(Y_{i 1}, Y_{i 2}\) 表示结果,\(N_{i}=Y_{i 1}+Y_{i 2}\) 表示它们的和。我们计算给定 \(N_{i}\) 的 \(\left(Y_{i 1}, Y_{i 2}\right)\) 的条件分布。这是给定总选择数的选择分布。
当 \(N_{i}=0\) 或 \(N_{i}=2\) 时,似然是平凡的。即,
\[ \begin{aligned} &\mathbb{P}\left[Y_{i t}=0 \mid N_{i}=0\right]=0 \\ &\mathbb{P}\left[Y_{i t}=1 \mid N_{i}=2\right]=1 . \end{aligned} \]
这不依赖于 \(\beta\),所以不影响估计。因此我们专门关注 \(N_{i}=1\) 的情况。
选择概率为
\[ \begin{aligned} &\mathbb{P}\left[Y_{i t}=0\right]=\frac{\exp \left(-X_{i t}^{\prime} \beta-u_{i}\right)}{1+\exp \left(-X_{i t}^{\prime} \beta-u_{i}\right)} \\ &\mathbb{P}\left[Y_{i t}=1\right]=\frac{1}{1+\exp \left(-X_{i t}^{\prime} \beta-u_{i}\right)} . \end{aligned} \]
它们的比率为
\[ \frac{\mathbb{P}\left[Y_{i t}=0\right]}{\mathbb{P}\left[Y_{i t}=1\right]}=\exp \left(-X_{i t}^{\prime} \beta-u_{i}\right) . \]
对 \(t=1\) 和 \(t=2\) 取进一步比率,我们得到
\[ \frac{\mathbb{P}\left[Y_{i 1}=0\right]}{\mathbb{P}\left[Y_{i 1}=1\right]} \frac{\mathbb{P}\left[Y_{i 2}=1\right]}{\mathbb{P}\left[Y_{i 2}=0\right]}=\frac{\exp \left(-X_{1 t}^{\prime} \beta-u_{i}\right)}{\exp \left(-X_{2 t}^{\prime} \beta-u_{i}\right)}=\exp \left(\left(X_{2 t}-X_{1 t}\right)^{\prime} \beta\right) . \]
这不依赖于固定效应 \(u_{i}\)。它只是回归变量变化 \(\Delta X_{i}=\) \(X_{i 2}-X_{i 1}\) 的函数
这实际上是一个非线性内部变换。这个优势比由于逻辑分布的指数结构消除了对个体效应的依赖。这对 logit 模型是特殊的,允许构建不依赖于 \(u_{i}\) 的条件似然函数。
考虑给定 \(N_{i}=1\) 的时期 1 的选择概率。它是
\[ \begin{aligned} \mathbb{P}\left[Y_{i 1}=1 \mid N_{i}=1\right] &=\frac{\mathbb{P}\left[Y_{i 1}=1, Y_{i 2}=0\right]}{\mathbb{P}\left[Y_{i 1}=1, Y_{i 2}=0\right]+\mathbb{P}\left[Y_{i 1}=0, Y_{i 2}=1\right]} \\ &=\frac{\mathbb{P}\left[Y_{i 1}=1\right] \mathbb{P}\left[Y_{i 2}=0\right]}{\mathbb{P}\left[Y_{i 1}=1\right] \mathbb{P}\left[Y_{i 2}=0\right]+\mathbb{P}\left[Y_{i 1}=0\right] \mathbb{P}\left[Y_{i 2}=1\right]} \\ &=\frac{1}{1+\frac{\mathbb{P}\left[Y_{i 1}=0\right]}{\mathbb{P}\left[Y_{i 1}=1\right]} \frac{\mathbb{P}\left[Y_{i 2}=1\right]}{\mathbb{P}\left[Y_{i 2}=0\right]}} \\ &=\frac{1}{1+\exp \left(\Delta X_{i}^{\prime} \beta\right)} \\ &=1-\Lambda\left(\Delta X_{i}^{\prime} \beta\right) . \end{aligned} \]
类似地 \(\mathbb{P}\left[Y_{i 1}=0 \mid N_{i}=1\right]=\Lambda\left(\Delta X_{i}^{\prime} \beta\right)\)。一起,对数似然函数为
\[ \ell_{n}(\beta)=\sum_{i=1}^{n} \mathbb{1}\left\{N_{i}=1\right\}\left[\left(1-Y_{i 1}\right) Y_{2 i} \log \Lambda\left(\Delta X_{i}^{\prime} \beta\right)+Y_{i 1}\left(1-Y_{i 2}\right) \log \left(1-\Lambda\left(\Delta X_{i t}^{\prime} \beta\right)\right)\right] . \]
这个条件似然不依赖于个体效应。由于条件似然可以计算,它可以被最大化以获得条件似然估计量。
为了使似然成为 \(\beta\) 的非退化函数,必须有切换者个体(在一个时期选择 \(Y=0\),在另一个时期选择 \(Y=1\)),并且切换者有随时间变化的回归变量。时不变回归变量的系数无法识别。
我们的推导专注于 \(T=2\)。扩展到 \(T>2\) 是类似的,但在代数上更复杂。
在 Stata 中,随机效应 probit 用 xtoprobit 实现,随机效应 logit 用 xtologit 实现。固定效应 probit 可以用 xtologit, fe 或 clogit 实现。
25.15 技术证明*
定理 25.1 的证明:MLE \(\widehat{\beta}^{\text {logit }}\) 是一个 m-估计量,所以我们求助于定理 22.3,它表明 \(\widehat{\beta}^{\text {logit }}\) 在五个条件下是一致的。条件 1 和 4 由假设成立。条件 5(\(\beta^{\text {logit }}\) 唯一最小化 \(\left.\ell^{\text {logit }}(\beta)\right)\) 在假设 \(\boldsymbol{Q}_{\text {logit }}>0\) 下成立。对数似然分量 \(\log \Lambda\left(Z^{\prime} \beta\right)\) 在任何紧集 \(B\) 上连续,所以条件 2 成立。最后,
\[ |\log \Lambda(t)|=-\log \Lambda(t)=\log (1+\exp (-t)) \leq \log (1+\exp (|t|)) \leq \log (2)+|t| \]
因此
\[ \left|\log \Lambda\left(Z^{\prime} \beta\right)\right| \leq \log (2)+\left|X^{\prime} \beta\right| \leq \log (2)+\|\beta\|\|X\| \leq \log (2)+\bar{\beta}\|X\| \]
其中 \(\bar{\beta}=\sup _{\beta \in B}\|\beta\|\)。右侧有有限期望,因为 \(\mathbb{E}\|X\|<\infty\) 由假设。这建立了条件 3。总之,定理 22.3 的条件得到满足。
定理 25.2 的证明:遵循定理 25.1 的证明,我们需要证明 \(\left|\log \Phi\left(Z^{\prime} \beta\right)\right| \leq G(Z)\) 且 \(\mathbb{E}|G(Z)|<\infty\)。
《经济学家的概率与统计》定理 5.7.6 表明
\[ |\frac{d}{d t} \log \Phi(t)=\lambda(t)=\frac{\phi(t)}{\Phi(t)} \leq 1+|t| . \]
这意味着
\[ |\log \Phi(t)|=-\log \Phi(t) \leq \log (\sqrt{2 \pi})+\frac{t^{2}}{2}+\log (1+|t|) \leq \log (\sqrt{2 \pi})+\frac{t^{2}}{2}+|t| \]
使用 Schwarz (B.12) 不等式
\[ \left|\log \Phi\left(Z^{\prime} \beta\right)\right| \leq \log (\sqrt{2 \pi})+\frac{1}{2}\left|X^{\prime} \beta\right|^{2}+\left|X^{\prime} \beta\right| \leq 2 \log (\sqrt{2 \pi})+\frac{1}{2} \bar{\beta}^{2}\|X\|^{2}+\bar{\beta}\|X\| \]
其中 \(\bar{\beta}=\sup _{\beta \in B}\|\beta\|\)。右侧有有限期望,因为 \(\mathbb{E}\|X\|^{2}<\infty\)。
定理 25.3 的证明:由于 \(\widehat{\beta}^{\text {logit }}\) 是一个 m-估计量,我们验证定理 22.4 的五个条件。条件 2 和 5 由假设成立。
由于 \(\left|h_{\text {logit }}(t)\right| \leq 1\),我们看到 \(\mathbb{E}\left[\left\|Z h_{\text {logit }}\left(Z^{\prime} \beta^{\text {logit }}\right)\right\|^{2}\right] \leq \mathbb{E}\|X\|^{2}<\infty\)。因此条件 1 成立。
函数 \(\boldsymbol{Q}_{\text {logit }}(\beta)\) 有界且 \(\Lambda(x)\) 连续。因此 \(\boldsymbol{Q}_{\operatorname{logit}}(\beta)\) 在 \(\beta\) 中连续,条件 3 成立。
如练习 25.5(d) 所示,\(\left|H_{\text {logit }}(t)\right| \leq 1\)。那么
\[ \mathbb{E}\left[\sup _{\beta}\left\|\frac{\partial}{\partial \beta} Z h_{\text {logit }}\left(X^{\prime} \beta\right)\right\|^{2}\right] \leq \mathbb{E}\|X\|^{4} \sup _{t}\left|H_{\text {logit }}(t)\right|<\infty \]
这意味着条件 4。
我们已经验证了定理 22.4 所需的五个条件。
定理 25.4 的证明:证明遵循与定理 25.3 相同的路线,通过验证定理 22.4 的条件 1、3 和 4。
使用 (25.17)
\[ \mathbb{E}\left\|Z \lambda\left(Z^{\prime} \beta^{\text {probit }}\right)\right\|^{2} \leq \mathbb{E}\left(\|X\|\left(1+\left|X^{\prime} \beta^{\text {probit }}\right|\right)\right)^{2} \leq \mathbb{E}\|X\|^{2}+\left\|\beta^{\text {probit }}\right\|^{2} \mathbb{E}\|X\|^{4}<\infty \]
意味着条件 1。
函数 \(\boldsymbol{Q}_{\text {probit }}(\beta)\) 有界且 \(H_{\text {probit }}(x)\) 连续。因此 \(\boldsymbol{Q}_{\text {probit }}(\beta)\) 在 \(\beta\) 中连续,条件 3 成立。
《经济学家的概率与统计》定理 5.7.7 表明 \(\left|H_{\text {probit }}(t)\right| \leq 1\)。因此通过定理 25.3 证明中的相同论证,我们可以验证条件 4。
我们已经验证了定理 22.4 所需的条件。
25.16 练习题
练习 25.1 Emily 估计一个 probit 回归,将她的因变量设为 \(Y=1\) 表示购买,\(Y=0\) 表示不购买。使用相同的数据和回归变量,Jacob 估计一个 probit 回归,将因变量设为 \(Y=1\) 表示不购买,\(Y=0\) 表示购买。他们估计的斜率系数有什么差异?
练习 25.2 Jackson 估计一个 logit 回归,其中主要回归变量以美元为单位测量。Julie 使用相同的样本和因变量估计 logit 回归,但以千美元为单位测量主要回归变量。估计的斜率系数有什么差异?
练习 25.3 证明 (25.1) 和 (25.2)。
练习 25.4 验证 (25.5),即 \(\pi(Y \mid X)=G\left(Z^{\prime} \beta\right)\)。
练习 25.5 对于逻辑分布 \(\Lambda(x)=(1+\exp (-x))^{-1}\),验证 (a) \(\frac{d}{d x} \Lambda(x)=\Lambda(x)(1-\Lambda(x))\) (b) \(h_{\operatorname{logit}}(x)=\frac{d}{d x} \log \Lambda(x)=1-\Lambda(x)\)。 (c) \(H_{\operatorname{logit}}(x)=-\frac{d^{2}}{d x^{2}} \log \Lambda(x)=\Lambda(x)(1-\Lambda(x))\)。 (d) \(\left|H_{\operatorname{logit}}(x)\right| \leq 1\)。
练习 25.6 对于正态分布 \(\Phi(x)\),验证 (a) \(h_{\text {probit }}(x)=\frac{d}{d x} \log \Phi(x)=\lambda(x)\),其中 \(\lambda(x)=\phi(x) / \Phi(x)\)。 (b) \(H_{\text {probit }}(x)=-\frac{d^{2}}{d x^{2}} \log \Phi(x)=\lambda(x)(x+\lambda(x))\)
练习 25.7
验证方程 (25.6) 和 (25.7)。
验证 \(H(x)>0\) 意味着 \(\mathscr{H}_{n}(\beta)>0\) 在 \(\beta\) 中全局成立的断言。
验证部分 (b) 意味着 \(\ell_{n}(\beta)\) 在 \(\beta\) 中全局凹的断言。
练习 25.8 从总体最大化问题 (25.8) 中找到 \(\beta_{0}\) 的一阶条件。
练习 25.9 找到 logit MLE \(\widehat{\beta}^{\text {logit }}\) 的一阶条件。
练习 25.10 找到 probit MLE \(\widehat{\beta}^{\text {probit }}\) 的一阶条件。
练习 25.11 证明 (25.14)。在 logit 模型中,证明 (25.14) 的右侧简化为 \(\left(Y-\Lambda\left(X^{\prime} \beta\right)\right)^{2}\)
练习 25.12 说明如何使用 NLLS 估计 probit 模型。
练习 25.13 取第 25.12 节的内生 probit 模型。
验证方程 (25.16)。
解释为什么 \(\varepsilon\) 独立于 \(e_{2}\) 和 \(Y_{2}\)。
验证 \(Y_{1}^{*}\) 的条件分布是 \(\mathrm{N}\left(\mu(\theta), \sigma_{\varepsilon}^{2}\right)\)。
练习 25.14 取异方差非参数二分类选择模型
\[ \begin{aligned} &Y^{*}=m(X)+e \\ &e \mid X \sim \mathrm{N}\left(0, \sigma^{2}(X)\right) \\ &Y=Y^{*} \mathbb{1}\left\{Y^{*}>0\right\} . \end{aligned} \]
可观测变量是 \(\left\{Y_{i}, X_{i}: i=1, \ldots, n\right\}\)。函数 \(m(x)\) 和 \(\sigma^{2}(x)\) 是非参数的。
找到响应概率的公式。
\(m(x)\) 和 \(\sigma^{2}(x)\) 都被识别吗?解释。
找到一个实现识别的标准化。
根据您对部分 (c) 的回答,在二分类选择模型中”允许异方差”有意义吗?解释?
练习 25.15 使用 cps09mar 数据集和男性子集。如果个人是工会成员(union=1)则设 \(Y=1\),否则设 \(Y=0\)。估计一个 probit 模型,作为年龄、教育程度以及黑人和西班牙裔个体指标的线性函数。报告系数估计和标准误差。解释结果。
练习 25.16 复制前面的练习,但使用女性子集。解释结果。
练习 25.17 使用 cps09mar 数据集和具有大学学位的女性子集。如果婚姻状况等于 1、2 或 3,则设 \(Y=1\),否则设 \(Y=0\)。估计 \(Y\) 的二分类选择模型,作为年龄的可能非线性函数。描述您使用模型的动机。绘制估计的响应概率。估计与图 25.1 中男性的估计相比如何?
练习 25.18 使用 cps09mar 数据集和男性子集。按前一问题设置 \(Y\)。估计 \(Y\) 的二分类选择模型,作为年龄的可能非线性函数、教育的线性函数,并包括黑人和西班牙裔个体的指标。报告系数估计和标准误差。解释结果。
练习 25.19 复制前面的练习,但使用女性子集。解释结果。