| staff | salary | sale | score | race |
|---|---|---|---|---|
| Zhang | 25 | 140 | 2 | yellow |
| Tom | 35 | 195 | 3 | white |
| Lee | 27 | 184 | 1 | yellow |
| Jeff | 42 | 256 | 5 | white |
| Kevin | 38 | 207 | 4 | black |
8 虚拟变量回归
8.1 实验目的及要求
目的:掌握虚拟变量模型的设置和分析方法。
要求:熟悉虚拟变量的设置方法;理解定性变量和定量变量模型的内涵;熟练加法模型和乘法模型的运用原理。
8.2 实验原理
计量经济学建模分析中,我们常常需要把一些定性变量(Qualitative variables)(如性别、地区、党派等)作为自变量放入回归模型中。从变量层次(Variable Scale)来看,这些变量没有具体的取值,只有特定属性类别。例如,性别变量的具体取值往往为男或女。显然,诸如此类的变量如果直接放到线性回归模型中,将会产生一系列的参数估计、模型解释等问题。
区域经理年薪案例中(见 表 8.1 ),公司有五名区域经理,分别负责不同的国际市场。定量变量\(salary\)表示区域经理的年薪(万元);变量\(sale\)表示负责市场的销售额;变量\(score\)表示客户对区域经理的评价(1表示很不满意,2表示不满意,3表示一般,4表示很满意,5表示非常满意);变量\(race\)表示区域市场主要消费群体的肤色(yellow表示黄色消费群体、white表示白色消费群体,black表示黑色消费群体)。
定义 8.1 (变量类型) 定量变量(Quantitative variable)一般也称为连续变量,是由测量或计数、统计所得到的量,可以通过数值表达,并具有直接的数值含义。
定性变量(Qualitative variable)一般也称为分类变量,主要用于区分事物性质差异,往往用语义类别表达,没有直接的数值含义。
定义 8.2 (变量尺度) 变量尺度(Variable scale)刻画的是变量的数值含义或数值关系。它将意味着在数值含义和关系上,变量是有层次级别的差异性。根据变量层级不同,具体可以分为由低到高的4个层级:
名义尺度(nominal scale)变量:这类变量只用于属性分类,不具备任何数值含义或数值关系,也即不能加、减、乘、除,也不能比较大小。 序数尺度(order scale)变量:这类变量具备很少的数值含义或数值关系,它可以比较大小,但不能进行加、减、乘、除。 区间尺度(interval scale)变量:这类变量具备一定的数值含义或数值关系,它可以比较大小,也可以进行加、减,但不能进行乘、除。 比率尺度(ratio scale)变量:这类变量具备最多的数值含义或数值关系,它可以比较大小,也可以进行加、减、乘、除。
根据以上定义,区域经理年薪案例中,可以认为年薪\(salary\)、销售额\(sale\),以及客户评价\(score\)为定量变量,消费群体主要肤色\(race\)为定性变量。其中,从变量的度量尺度来看:
- 年薪\(salary\)和销售额\(sale\)两个变量为比率尺度变量
- 客户评价\(score\)变量为序数尺度变量
- 消费群体主要肤色\(race\)为名义尺度变量
8.2.1 如何把定性变量转换为虚拟变量?
一个定性变量的不同数据取值,称为该定性变量的属性。定性变量的任一属性,都可以设置为一个虚拟变量。实际上,我们可以用一套虚拟变量体系来完全表达一个定性变量。然后按照一定的规则构建虚拟变量回归模型,从而避免参数估计、模型解释等问题的出现。
定义 8.3 (虚拟变量) 对于某定性变量的任一特定属性,可以构造出一个虚拟变量(记为D),使得该虚拟变量能够表达这一属性。同时,给该虚拟变量D赋值为1,记为具备这一属性;给该虚拟变量赋值为0,记为不具备该属性。正式地,假设定性变量\(X\)具有\(m\)个属性\(a_1,a_2,\cdots,a_m\),对于任意属性\(k,(k\in{1,2,\cdots,m})\),可以定义如下的虚拟变量\(D_k\): \[\begin{aligned} D_k= \begin{cases} 1, & \text{if } a_k\\ 0, & \text{if not } a_k \end{cases} \end{aligned}\]
定义 8.4 (虚拟变量体系) 完整表达某个定性变量全部信息的一组虚拟变量。正式地,假设定性变量\(X\)具有\(m\)个属性\(a_1,a_2,\cdots,a_m\),可以用如下一组虚拟变量\(D_1,\cdots,D_k,\cdots,D_m\)完全表达该定性变量:
\[ \begin{aligned} X\{a_1,a_2,\cdots,a_m\} \Rightarrow \begin{cases} D_1 = \begin{cases} 1, & \text{if } a_1\\ 0, & \text{if not } a_1 \end{cases} \\ \vdots \\ D_k = \begin{cases} 1, & \text{if } a_k\\ 0, & \text{if not } a_k \end{cases} \\ \vdots\\ D_m = \begin{cases} 1, & \text{if } a_m\\ 0, & \text{if not } a_m \end{cases} \end{cases} \end{aligned} \]
区域经理年薪案例中,定性变量肤色(\(race\))具有3个属性(\(m=3\)),具体为\(X\{a_1=yellow,a_2=white,a_3=black\}\),则可以构造出如下的虚拟变量体系1。
\[\begin{aligned} race\{a_1=\text{yellow},a_2=\text{white},a_3=\text{black}\} \\ \Longrightarrow \begin{cases} race\_yellow = \begin{cases} 1, & \text{yellow}\\ 0, & \text{not yellow} \end{cases} \\ race\_white = \begin{cases} 1, & \text{white}\\ 0, & \text{not white} \end{cases} \\ race\_black = \begin{cases} 1, & \text{black}\\ 0, & \text{not black} \end{cases} \end{cases} \end{aligned}\]
实际数据操作中,一般需要对定性变量\(race\)进行重新编码(recode),生成三个对应的虚拟变量(见 表 8.2 )。
| staff | race | race_black | race_white | race_yellow |
|---|---|---|---|---|
| Zhang | yellow | 0 | 0 | 1 |
| Tom | white | 0 | 1 | 0 |
| Lee | yellow | 0 | 0 | 1 |
| Jeff | white | 0 | 1 | 0 |
| Kevin | black | 1 | 0 | 0 |
8.2.2 如何理解虚拟变量回归模型?
区域经理薪水案例中,如果不区分变量类型和特征,建议如下的回归模型(见方程 式 8.1 ),则回归分析结果将会带来严重的问题。
\[ \begin{aligned} salary={\alpha}_1+{\alpha}_2race+{\alpha}_3sale+u \end{aligned} \tag{8.1}\]
事实上,应该将上述模型转换为虚拟变量回归模型(如方程 式 8.2 )。这类模型往往又被称为方差分析模型,其模型本质上是对不同“类型”或不同“分组”的均值水平(期望水平)进行比较和检验。
\[ \begin{aligned} salary={\beta}_1+{\beta}_2race\_yellow+{\beta}_3race\_white+{\beta}_4sale+u \end{aligned} \tag{8.2}\]
很显然,在总体回归模型 式 8.2 下,可以得到所有3类“分组”情形下的期望年薪水平:
\[ \begin{aligned} E(Y|race\_yellow=1,race\_white=0,sale)&=\beta_1+\beta_2+\beta_4sale &&\text{(market yellow)} \\ E(Y|race\_yellow=0,race\_white=1,sale)&=\beta_1+\beta_3 +\beta_4sale &&\text{(market white)} \\ E(Y|race\_yellow=0,race\_white=0,sale)&=\beta_1+\beta_4sale &&\text{(market black)} \end{aligned} \tag{8.3}\]
对于模型 式 8.2 ,我们称其为有截距的含有虚拟变量的、加法形式的回归模型。显然,虚拟变量\(race\_{black}\)没有进入模型 式 8.2 中,且模型 式 8.2 设置有截距项\(\beta_1\)。在这种设定下,我们称:
同时,我们称:
有序变量\(rank\)为协变量(covariates)或控制变量(control variable)
\(\beta_1\)为截距系数,代表基础组的期望水平
\(\beta_2,\beta_3\)为极差系数,代表的是比较组与基础组期望水平的差距
\(\beta_4\)为平行斜率系数,代表协变量的影响效应
8.2.3 虚拟变量回归模型有哪些形式?
一个线性回归模型,只要回归元中包含了虚拟变量,这种模型就被称为虚拟变量回归模型,也可以称为方差分析模型 (Analysis of variance, ANOVA)2。
根据回归元包含定量变量和虚拟变量的数量关系,可以将虚拟变量回归模型分为:
只含有虚拟变量的回归模型:全部解释变量都是由虚拟变量构成
同时含有虚拟变量和定量变量的回归模型:解释变量同时含有虚拟变量和定量变量
根据虚拟变量引入模型方式的不同,可以划分为:
加法模型:虚拟变量以独立项的形式出现在方程中
乘法模型:虚拟变量以交叉项的形式出现在方程中
混合模型:虚拟变量以独立项和/或交叉项的形式出现在方程中3。包括完全混合模型,以及部分混合模型。
根据虚拟变量模型是否参照基础组,可以划分为4:
有截距模型:此时模型解释中将有明确的基础组,其他组可以直接与之参照对比。
无截距模型:此时模型解释中将没有明确的基础组,各组间将不直接参照对比。
根据模型中的因变量\(Y\)是否取对数,可以划分为5:
经典线性模型:因变量为\(Y\)
半对数模型:因变量为\(ln(Y)\)
根据虚拟变量模型应用情景的不同,可以划分为:
截面数据虚拟变量回归模型:此时虚拟变量用于表达回归元为定性变量的情形
时间序列季节虚拟变量回归模型:此时虚拟变量用于表达季节周期(具体请参看 小节 8.5.6)
分段线性虚拟变量回归模型:此时虚拟变量用于表达阀值分段(具体请参看 小节 8.5.7)
对于具体的实证分析案例,我们往往需要根据变量的属性和特征,构建不同类型的虚拟变量回归模型,比较不同模型的回归分析结果,甄选并得到其中相对理想的模型。显然,不同类型的虚拟变量模型设置,具有不同的经济学含义。甚至回归方程系数解读的直观性,模型构建意图表达的直接性等,也存在较大差异,都需要对各种备选的、可行的模型进行反复测试和甄选。
例如,仅是考虑基础组的有截距模型,可能用到的各类备选组合模型至少包括(具体回归方程设置见 小节 8.5.4 和 小节 8.5.5 ):
只含有虚拟变量的、加法形式的经典回归模型
只含有虚拟变量的、加法形式的半对数回归模型
只含有虚拟变量的、乘法形式的经典回归模型
只含有虚拟变量的、乘法形式的半对数回归模型
\(\cdots\)
同时含有虚拟变量和定量变量的、加法形式的经典回归模型
同时含有虚拟变量和定量变量的、加法形式的半对数回归模型
同时含有虚拟变量和定量变量的、乘法形式的经典回归模型
同时含有虚拟变量和定量变量的、乘法形式的半对数回归模型
\(\cdots\)
8.3 实验内容
(1)将定性变量都处理成完全虚拟变量体系(也即定性变量有m个属性,则设置m个虚拟变量)
(2)分析只含有虚拟变量的回归模型(有截距)
只含有虚拟变量的、加法形式的经典回归模型
只含有虚拟变量的、加法形式的半对数回归模型
只含有虚拟变量的、乘法形式的经典回归模型
只含有虚拟变量的、乘法形式的半对数回归模型
(3)分析同时含有虚拟变量和定量变量的回归模型(有截距):
同时含有虚拟变量和定量变量的、加法形式的经典回归模型
同时含有虚拟变量和定量变量的、加法形式的半对数回归模型
同时含有虚拟变量和定量变量的、乘法形式的经典回归模型
同时含有虚拟变量和定量变量的、乘法形式的半对数回归模型
(4)分析时间序列季节虚拟变量模型
(5)分析分段线性回归模型(piecewise linear regression)
8.4 实验准备
8.4.1 实验软件
本次实验需要提前准备好如下软件:
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或 360极速浏览器9.5版本及以上
8.4.2 实验材料
印度工人工资:本次实验将使用 表 8.3 给出的114位印度工人在wage工人工资,age年龄,edu教育水平,dpt合同类型,sex性别等方面的数据。
| obs | wage | age | edu | dpt | sex |
|---|---|---|---|---|---|
| 1 | 117 | 26 | pri | per | f |
| 2 | 375 | 42 | pri | per | f |
| 3 | 175 | 33 | pri | per | f |
| 4 | 100 | 33 | pri | per | f |
| 5 | 162 | 30 | pri | per | f |
| 110 | 25 | 18 | ill | tem | m |
| 111 | 25 | 11 | ill | tem | m |
| 112 | 75 | 45 | ill | tem | m |
| 113 | 54 | 14 | ill | tem | m |
| 114 | 50 | 26 | ill | tem | m |
变量说明见 表 8.4:
| variable | label | remark |
|---|---|---|
| obs | 工人编号 | 序号(observations) |
| wage | 工人工资 | 美元/周($/week) |
| age | 年龄 | 岁(year) |
| edu | 教育水平 | ill=文盲(illiteracy);pri=初等教育(primary);mid=中等教育(middle);hig=高等教育(higher) |
| dpt | 合同类型 | tem=短期合同(temporary);per=长期合同(permanent) |
| sex | 性别 | f=女(female);m=男(male) |
8.4.3 实验规则
8.4.3.1 模型及参数命名规则
本次实验将对不同组合下的多个模型进行比较分析,我们对这些不同模型及参数做如下约定:
不同虚拟变量体系命名,依次以希腊字母体系\(\{\alpha_1,\alpha_2,\cdots\};\{\beta_1,\beta_2,\cdots\};\{\gamma_1,\gamma_2,\cdots\};\cdots\)表达
定量变量参数的命名,依次以希腊字母\(\delta_1;\delta_2;\cdots\)表达
虚拟变量交叉项的参数命名,依次以希腊字母\(\lambda_1;\lambda_2;\cdots\)表达
例如,同时含有虚拟变量和定量变量的、乘法形式的、经典线性的、完全变量引入回归模型( eq_both_pro_ord_full)
eq_both_pro_ord_full)
\[ \begin{aligned} \begin{split} wage_i & =\alpha_1+\alpha_2edu_{D2,i}+\alpha_3edu_{D3,i}+\alpha_4edu_{D4,i}+\beta_2 dpt_{D2,i}+\gamma_2sex_{D2,i}+\delta age_i \\ & +\lambda_2edu_{D2,i} \ast dpt_{D2,i}+\lambda_3edu_{D3,i}\ast dpt_{D2,i} +\lambda_4edu_{D4,i}\ast dpt_{D2,i}+u_i \end{split} \end{aligned} \]
8.4.3.2 Eviews对象命名规则
因为案例模型涉及到多个定性变量和定量变量,同时还考虑对不同组合下的多个模型进行比较分析,为了记忆和分析方便,我们约定如下的Eviews对象命名规则:
(1)虚拟变量序列对象(Series) 的命名规则:
的命名规则:
定性变量的属性命名:确定基础组,例如本例中的基础组为{文盲,短期合同,女性}(也即{illiteracy,temporary,female}),并将各个定性变量的基础组属性都命名为\(D_1\)虚拟变量,其他比较组属性则依次命名为\(D_2,D_3,\cdots\)。
虚拟变量体系命名:对于一个定性变量,应完全表达为虚拟变量体系,且以定性变量名+虚拟变量记号的方式命名。
例如:教育水平定性变量\(edu(m=4)\),应设置为4个虚拟变量定性
edu_D1、
edu_D2、
edu_D3、
edu_D4。
(2)方程对象(Equation) 的命名规则:
的命名规则:
only,表示只含有虚拟变量的回归方程both,表示同时含有虚拟变量和定量变量的回归方程plus,表示加法形式(plus)的回归方程prod,表示乘法形式(product)的回归方程ord,表示因变量为普通形态\(Y\)的回归方程log,表示因变量为对数形态\(ln(Y)\)的回归方程full,表示一个定性变量的虚拟变量与另一个变量的全部交叉项,以及该定性变量的虚拟变量的独立项,全部进入回归方程。
例如:有截距模型下(考虑基础组),教育水平定性变量\(edu(m=4)\)与工作类型定性变量\(dpt(m=2)\)的交叉项\(edu_{D2}*dpt_{D2}\)、\(edu_{D3}*dpt_{D2}\)和\(edu_{D4}*dpt_{D2}\),以及独立项\(edu_{D2}\)、\(edu_{D3}\)和\(edu_{D4}\),全部进入回归方程。
part,表示一个定性变量的虚拟变量与另一个变量的全部交叉项进入回归方程,但是该定性变量的虚拟变量的独立项不进入回归方程。例如,有截距模型下(考虑基础组),教育水平定性变量\(edu(m=4)\)与工作类型定性变量\(dpt(m=2)\)的交叉项\(edu_{D2}*dpt_{D2}\)、\(edu_{D3}*dpt_{D2}\)和\(edu_{D4}*dpt_{D2}\)进入回归方程,但其独立项\(edu_{D2}\)、\(edu_{D3}\)和\(edu_{D4}\)并不引入回归方程中。
例如:方程对象
eq_only_plus_log_full,代表只含有虚拟变量的、加法形式的、对数化的、全部变量进入的回归方程。
8.5 主要实验步骤
8.5.1 导入数据并进行预处理
目标:构建工作文件并正确导入数据
思路:数据结构为unstructured/undatede
新建Eviews工作文件(见 图 8.1 )
Eviews菜单操作:
(1)依次操作:File\(\Rightarrow\)New\(\Rightarrow\)Workfile
(2)进行workfile create引导设置:
workfile structure type:
unstructured/undatededata range:114
workfile names(optional): 建议命名如下
- WF: `worker`(**建议命名**)
- Page: `indian`(**建议命名**) Eviews导入数据的菜单操作(Excel和Eviews)步骤如下:
提示:Excel数据,每个同学的Y数据都不同,找到自己学号对应下的Y数据(X数据所有同学都一样)
Excel找到数据。Excel表格中仅保留自己需要的数据(obswageageedudptsex)
Eviews导入数据。File \(\Rightarrow\) Import \(\Rightarrow\) Import From File:
d:/econometrics/data/Lab8-indian-wage.xlsx
8.5.2 把定性变量设置成虚拟变量体系
目标:学会用一套虚拟变量体系来完整表达一个定性变量
思路:按照完备、互斥的法则设置虚拟变量;如果要设置有截距模型,应统筹、优先考虑基础组的虚拟变量设置。
Eviews操作:
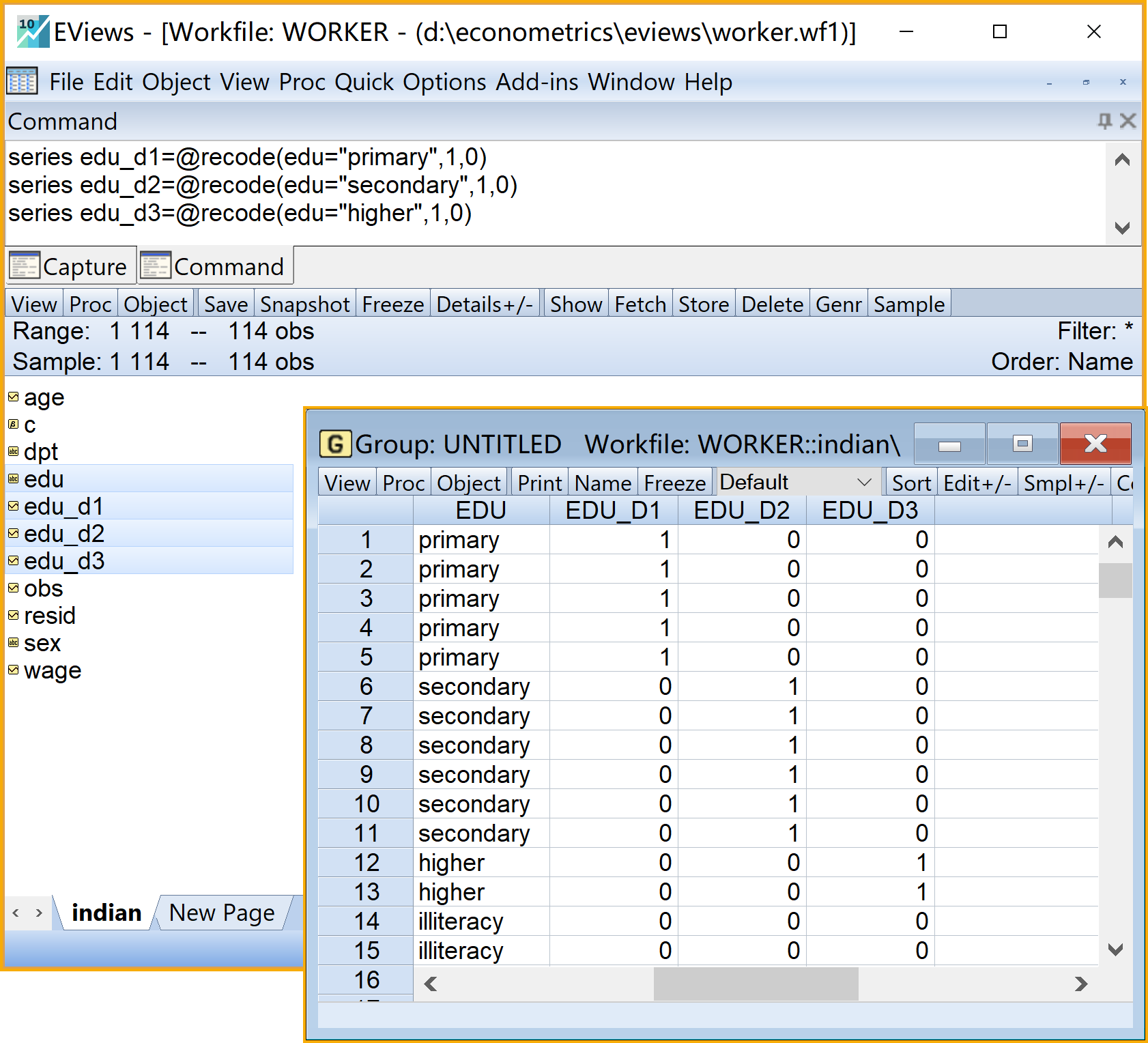
(1)把定性变量教育水平edu(m=4)设置成虚拟变量体系。(具体操作见 图 8.2)
- 命令视窗(Command)依次输入如下命令(建议分别命名为edu_ill、edu_pri、edu_mid和edu_hig)
- `series edu_ill=@recode(edu="ill",1,0)'`
- `series edu_pri=@recode(edu="pri",1,0)'`
- `series edu_mid=@recode(edu="mid",1,0)`
- `series edu_hig=@recode(edu="hig",1,0)'`运行命令:命令行中按Enter键
查看结果(以组group的形式查看):具体步骤如下
按住键盘Ctrl+依次点击

edu、
edu_ill、
edu_pri、
edu_mid、
edu_hig点击鼠标右键\(\Rightarrow\) Open \(\Rightarrow\) as Group
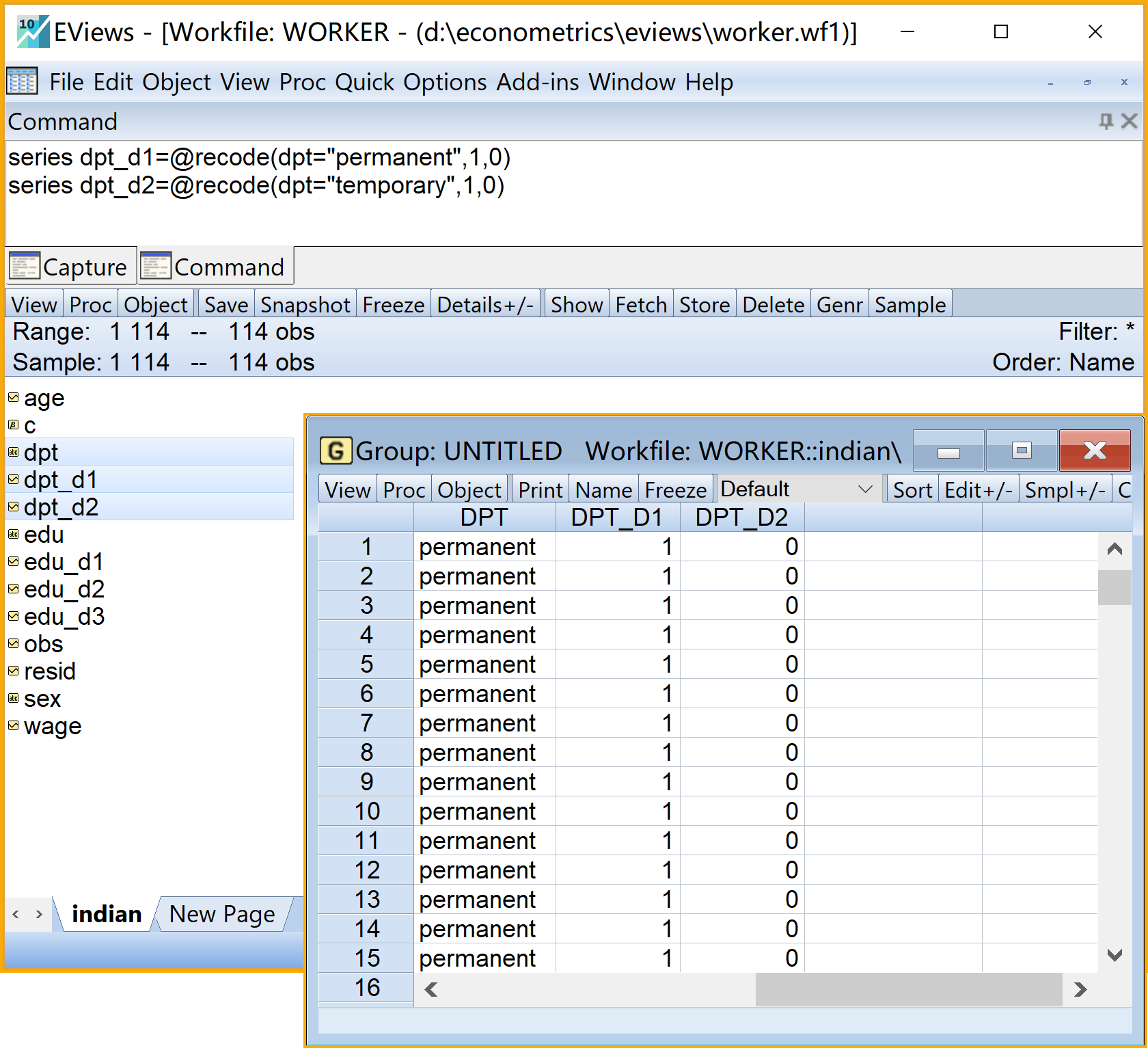
(2)把定性变量合同类型dpt(m=2)设置成虚拟变量体系。(具体操作见 图 8.3)
- 命令视窗(Command)依次输入如下命令(建议分别命名为dpt_tem和dpt_per)
`series dpt_tem=@recode(dpt="tem",1,0)'`
`series dpt_per=@recode(dpt="per",1,0)`运行命令:命令行中按Enter键
查看结果(以组group的形式查看):具体步骤如下
按住键盘Ctrl+依次点击

dpt、
dpt_tem、
dpt_per点击鼠标右键\(\Rightarrow\) Open \(\Rightarrow\) as Group
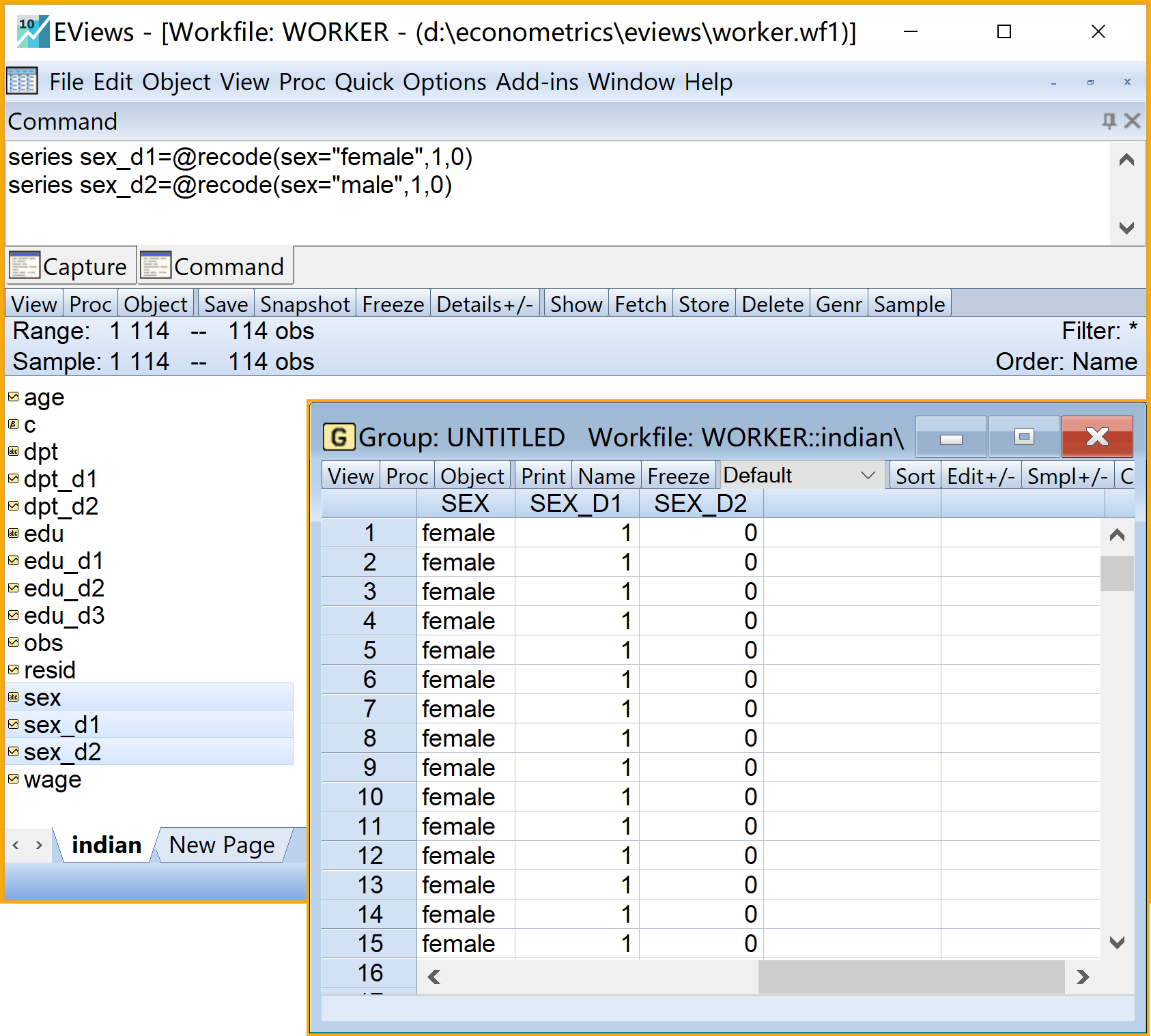
(3)把定性变量性别sex(m=2)设置成虚拟变量体系。(具体操作见 图 8.4)
- 命令视窗(Command)依次输入如下命令(建议分别命名为sex_f和sex_m)
series sex_f=@recode(sex="f",1,0)
series sex_m=@recode(sex="m",1,0)运行命令:命令行中按Enter键
查看结果(以组group的形式查看):具体步骤如下
按住键盘Ctrl+依次点击

sex、
sex_f、
sex_m点击鼠标右键\(\Rightarrow\) Open \(\Rightarrow\) as Group
(4)Eviews代码行的解读
代码
series edu_ill=@recode(edu="ill",1,0)表示给创建一个序列(Series)对象
edu_ill,并对定性变量对象
edu进行重新编码处理(recode),并把重新编码处理后的数值赋值给序列(Series)对象
edu_ill。代码
@recode(edu="ill",1,0)表示对定性变量对象
edu进行重新编码处理。具体做法是,如果edu的取值为ill,则相应赋值为1,或者就相应赋值为0。
8.5.3 操作解读
实际操作中,我们首先要对定性变量进行重新编码,设置成各自的虚拟变量体系。Eviews中对定性变量重新编码为虚拟变量的代码函数为@recode()。我们可以事先将一个定性变量完全地进行虚拟变量编码6。也就是说,如果一个定性变量有m个属性,我们可以直接设置m个虚拟变量。
此外,便于后续多个模型的分析甄选,我们还应该进一步统一设计虚拟变量的名称、命名的顺序等。例如,假设后续的备选模型中将基础组设定为{文盲,临时工,女性}(也即{illiteracy,temporary,female})7。则可以将全部定性变量的基础组属性{illiteracy,temporary,female}分别设置为虚拟变量edu_ill(见 表 8.5)、dpt_tem(见 表 8.6)和sex_f(见 表 8.7)。
| obs | edu | edu_ill | edu_pri | edu_mid | edu_hig | |
|---|---|---|---|---|---|---|
| 1 | 1 | pri | 0 | 1 | 0 | 0 |
| 2 | 2 | pri | 0 | 1 | 0 | 0 |
| 6 | 6 | mid | 0 | 0 | 1 | 0 |
| 7 | 7 | mid | 0 | 0 | 1 | 0 |
| 92 | 92 | hig | 0 | 0 | 0 | 1 |
| 93 | 93 | hig | 0 | 0 | 0 | 1 |
| 113 | 113 | ill | 1 | 0 | 0 | 0 |
| 114 | 114 | ill | 1 | 0 | 0 | 0 |
| obs | dpt | dpt_tem | dpt_per | |
|---|---|---|---|---|
| 1 | 1 | per | 0 | 1 |
| 2 | 2 | per | 0 | 1 |
| 3 | 3 | per | 0 | 1 |
| 4 | 4 | per | 0 | 1 |
| 111 | 111 | tem | 1 | 0 |
| 112 | 112 | tem | 1 | 0 |
| 113 | 113 | tem | 1 | 0 |
| 114 | 114 | tem | 1 | 0 |
| obs | sex | sex_f | sex_m | |
|---|---|---|---|---|
| 1 | 1 | f | 1 | 0 |
| 2 | 2 | f | 1 | 0 |
| 3 | 3 | f | 1 | 0 |
| 4 | 4 | f | 1 | 0 |
| 111 | 111 | m | 0 | 1 |
| 112 | 112 | m | 0 | 1 |
| 113 | 113 | m | 0 | 1 |
| 114 | 114 | m | 0 | 1 |
8.5.4 仅含有虚拟变量
目标:把定性变量的虚拟变量以独立项的形式引入模型方程,解释回归报告
思路:确定基础组,设置总体回归模型(PRM),进行OLS估计,得到Eviews分析报告
8.5.4.1 加法-经典模型
只含有虚拟变量的、加法形式的经典回归模型见方程 式 8.4
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i\\&+\beta_{4}edu\_hig_i+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+u_i \end{split} \end{aligned} \tag{8.4}\]
只含有虚拟变量的、加法形式的经典回归模型见方程 式 8.4 ,菜单操作实现具体见 图 8.5。具体步骤如下:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型

edu_ill
dpt_tem
sex_f
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
wage c edu_pri edu_mid edu_hig dpt_per sex_mEstimation settings:具体设置如下
Method: 下拉选择LS - Least Squares (NLS and ARMA)
Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_only_plus)查看结果:双击

eq_only_plus
具体Eviews报告见@ref(fig:only-plus-report):
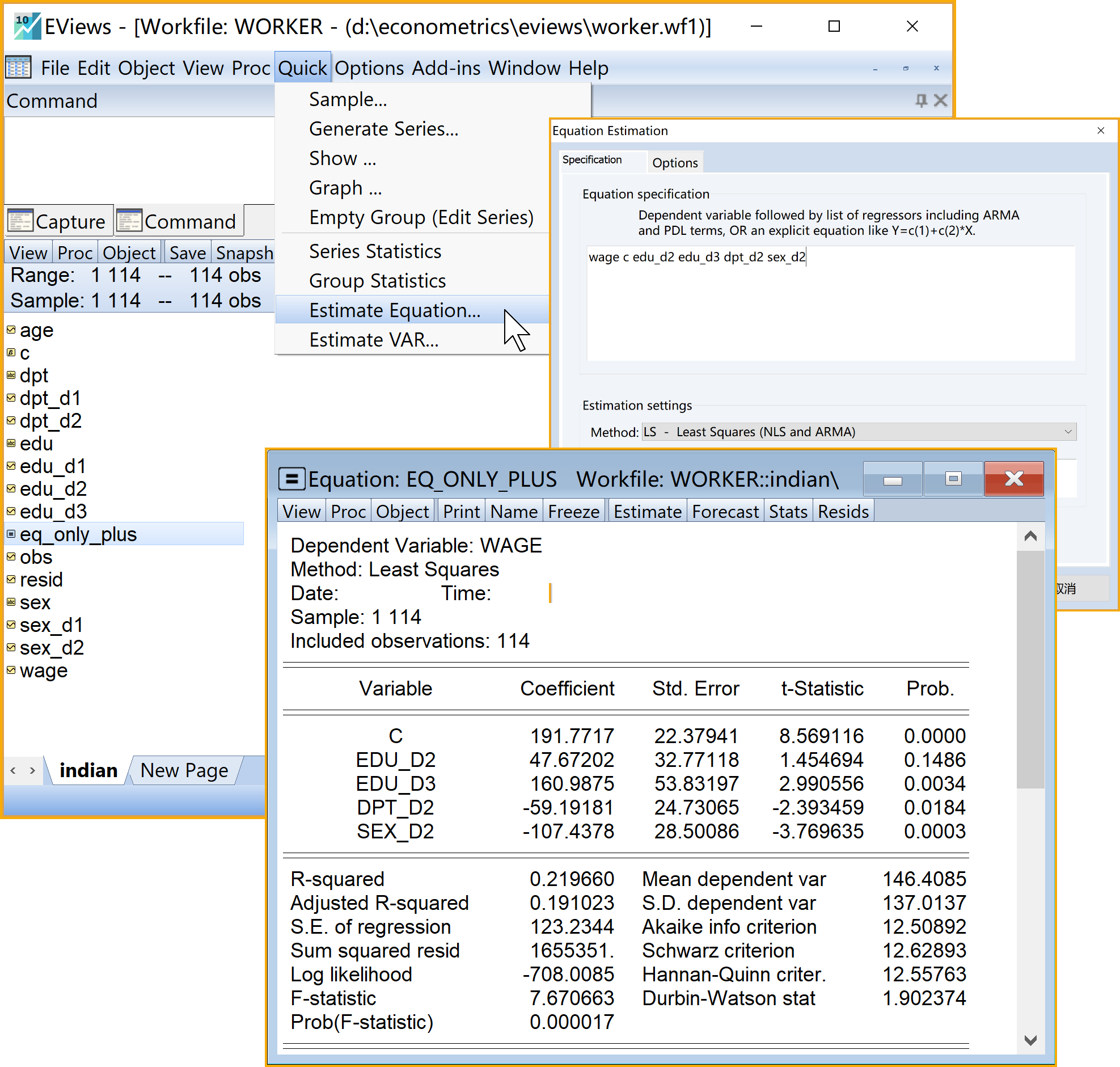
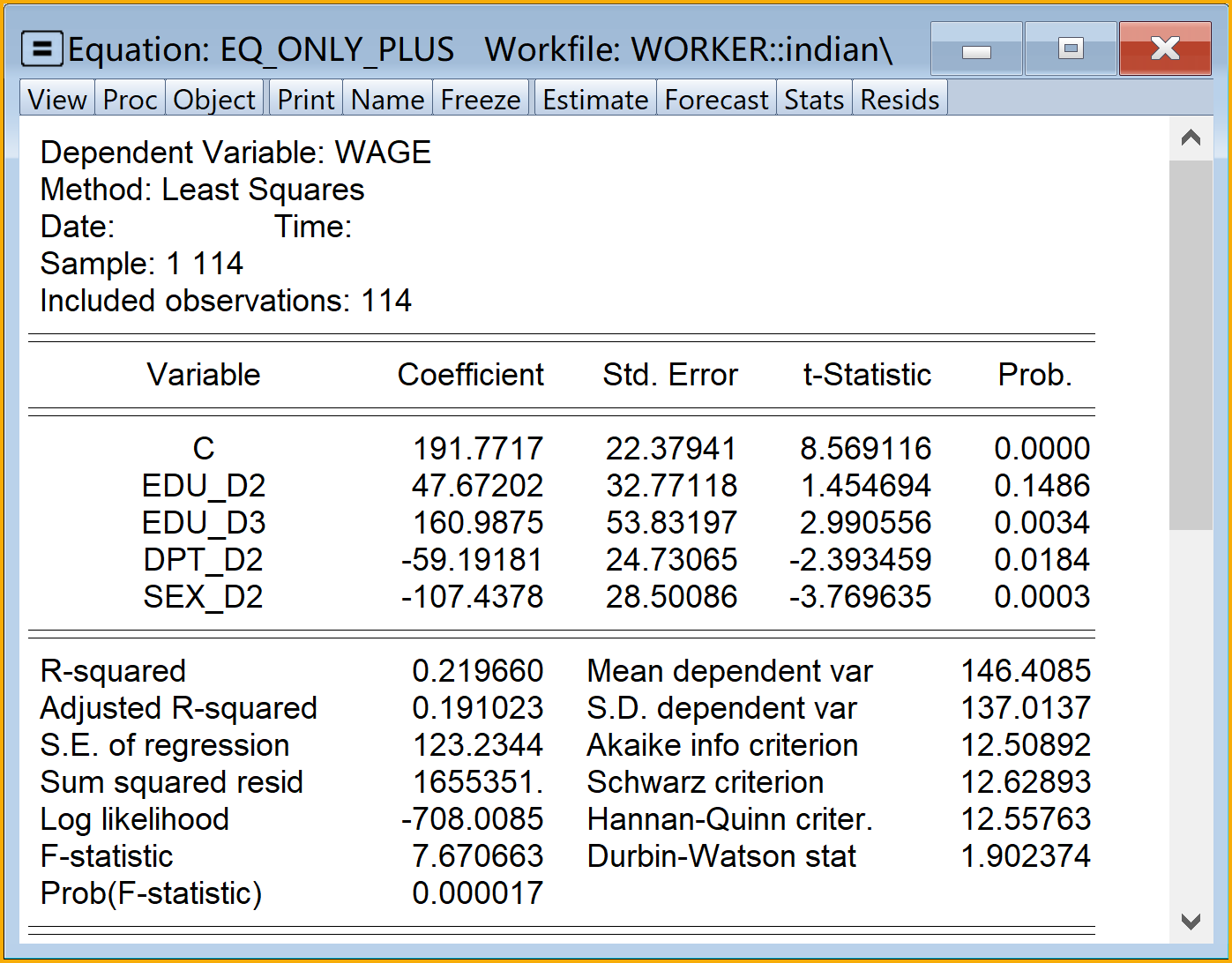
只含虚拟变量的、加法形式的经典回归模型Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+u_i \end{split} \end{aligned} \tag{8.5}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+130.36&&+10.47edu\_pri_i&&+49.71edu\_mid_i\\ &(s)&&(17.7609)&&(33.4850)&&(33.5470)\\ &(t)&&(+7.34)&&(+0.31)&&(+1.48)\\ &(cont.)&&+162.59edu\_hig_i&&+59.37dpt\_per_i&&-106.49sex\_m_i\\ &(s)&&(54.2989)&&(24.8399)&&(28.7784)\\ &(t)&&(+2.99)&&(+2.39)&&(-3.70)\\ &(over)&&n=114&&\hat{\sigma}=123.7476 &&\\ &(fit)&&R^2=0.2204&&\bar{R}^2=0.1843 &&\\ &(Ftest)&&F^*=6.11&&p=0.0001 && \end{split} \end{alignedat} \tag{8.6}\]
此时,根据总体回归模型 式 8.5 和样本回归方程 式 8.6 我们可以得到:
(1)基础组(文盲 & 短期合同 & 女性),也即(illiteracy & temporary & female)的期望工资收入见 式 8.7,拟合的期望工资收入见 式 8.8:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(0)\\ =&\beta_{1} \end{split} \end{aligned} \tag{8.7}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(0)\\ =&+[130.36]\cdot (1)+[10.47]\cdot (0)+[49.71]\cdot (0)+[162.59]\cdot (0)\\&+[59.37]\cdot (0)-[106.49]\cdot (0)\\ =&130.36 \end{split} \end{aligned} \tag{8.8}\]
(2)比较组1(文盲 & 短期合同 & 男性),也即(illiteracy & temporary & male)的期望工资收入见 式 8.9,拟合的期望工资收入见 式 8.10:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=1)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(1)\\ =&\beta_{1} + \beta_{6} \end{split} \end{aligned} \tag{8.9}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=1)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(1)\\ =&+[130.36]\cdot (1)+[10.47]\cdot (0)+[49.71]\cdot (0)+[162.59]\cdot (0)\\&+[59.37]\cdot (0)-[106.49]\cdot (1)\\ =&23.87 \end{split} \end{aligned} \tag{8.10}\]
(3)比较组2(高等教育 & 长期合同 & 男性),也即(higher & permanent & male)的期望工资收入见 式 8.11,拟合的期望工资收入见 式 8.12:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=1)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(1)\\&+\beta_{5}(1) +\beta_{6}(1)\\ =&\beta_{1} + \beta_{4} + \beta_{5} + \beta_{6} \end{split} \end{aligned} \tag{8.11}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=1)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(1)\\&+\hat{\beta}_{5}(1) +\hat{\beta}_{6}(1)\\ =&+[130.36]\cdot (1)+[10.47]\cdot (0)+[49.71]\cdot (0)+[162.59]\cdot (1)\\&+[59.37]\cdot (1)-[106.49]\cdot (1)\\ =&245.82 \end{split} \end{aligned} \tag{8.12}\]
8.5.4.2 加法-半对数模型
只含有虚拟变量的、加法形式的半对数回归模型见方程 式 8.13
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+u_i \end{split} \end{aligned} \tag{8.13}\]
只含有虚拟变量的、加法形式的半对数回归模型见方程 式 8.13 ,菜单操作实现具体见 图 8.7。具体步骤如下:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型

edu_ill
dpt_tem
sex_f
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
log(wage) c edu_pri edu_mid edu_hig dpt_per sex_mEstimation settings。
- Method: 下拉选择LS - Least Squares (NLS and ARMA)
- Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_only_plus_log)查看结果:双击

eq_only_plus_log
具体Eviews报告见@ref(fig:only-plus-log-report):
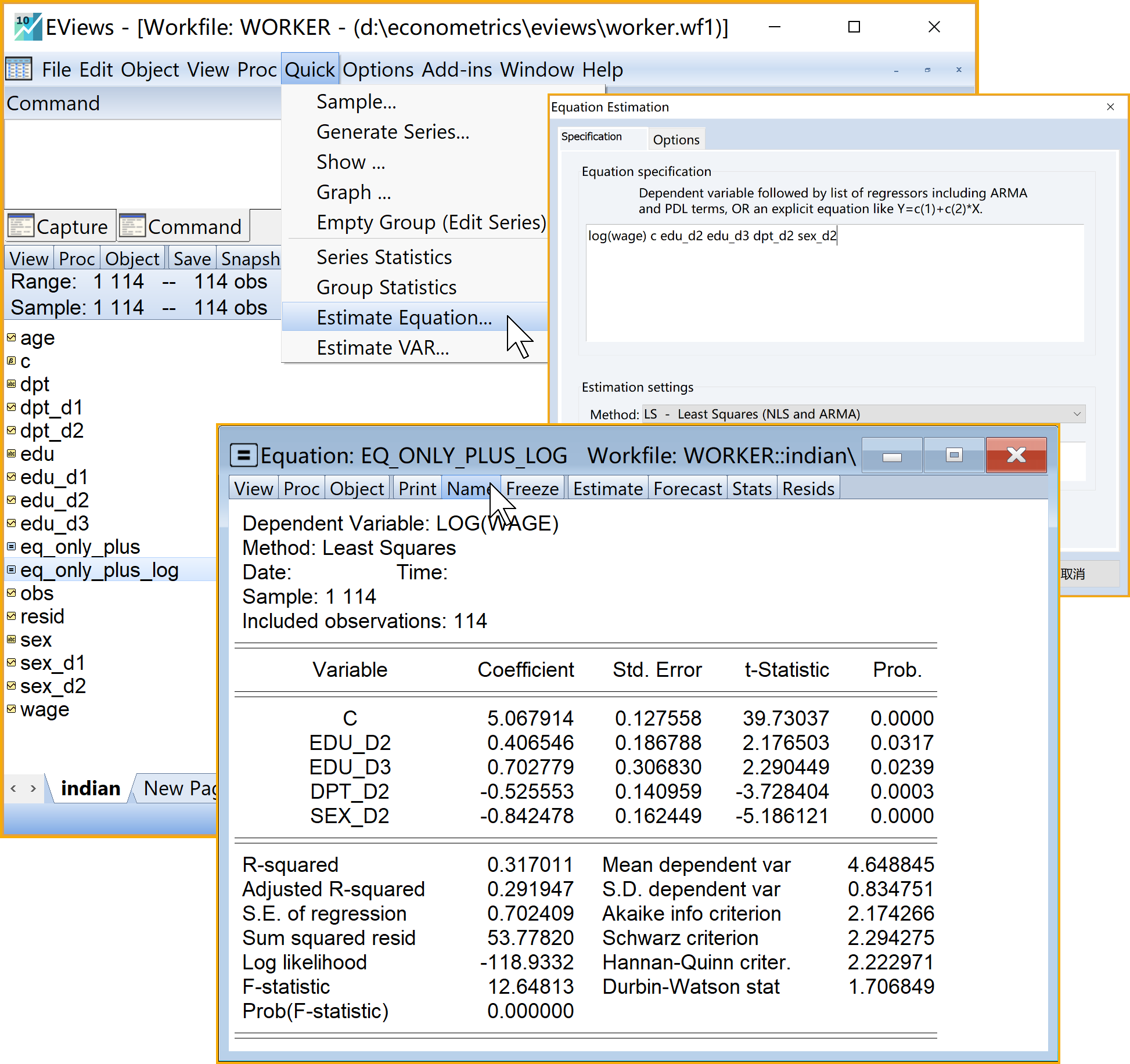

作为对比,只含虚拟变量的、加法形式的半对数回归模型Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+u_i \end{split} \end{aligned} \tag{8.14}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{log(wage)}=&&+4.53&&+0.06edu\_pri_i&&+0.42edu\_mid_i\\ &(s)&&(0.1012)&&(0.1909)&&(0.1912)\\ &(t)&&(+44.75)&&(+0.30)&&(+2.19)\\ &(cont.)&&+0.71edu\_hig_i&&+0.53dpt\_per_i&&-0.84sex\_m_i\\ &(s)&&(0.3095)&&(0.1416)&&(0.1640)\\ &(t)&&(+2.30)&&(+3.72)&&(-5.10)\\ &(over)&&n=114&&\hat{\sigma}=0.7054 &&\\ &(fit)&&R^2=0.3176&&\bar{R}^2=0.2860 &&\\ &(Ftest)&&F^*=10.05&&p=0.0000 && \end{split} \end{alignedat} \tag{8.15}\]
8.5.4.3 乘法-经典模型(完全)
只含有虚拟变量的、乘法形式的经典回归模型(完全交叉项)见方程 式 8.16 ;
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri_i\\&+\beta_{4}edu\_mid_i+\beta_{5}edu\_hig_i+\beta_{6}dpt\_per_i\\&+\beta_{7}edu\_pri \times dpt\_per_i+\beta_{8}edu\_mid \times dpt\_per_i+\beta_{9}edu\_hig \times dpt\_per_i+u_i \end{split} \end{aligned} \tag{8.16}\]
只含有虚拟变量的、乘法形式的经典回归模型见方程 式 8.16 ,菜单操作实现具体见 图 8.9:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型

edu_d1
dpt_d1
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
wage c edu_d2 edu_d3 edu_d4 dpt_d2 sex_d2 edu_d2*dpt_d2 edu_d3*dpt_d2 edu_d4*dpt_d2Estimation settings:
- Method: 下拉选择LS - Least Squares (NLS and ARMA)
- Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_only_prod)查看结果:双击

eq_only_prod
具体Eviews报告见@ref(fig:only-prod-report):
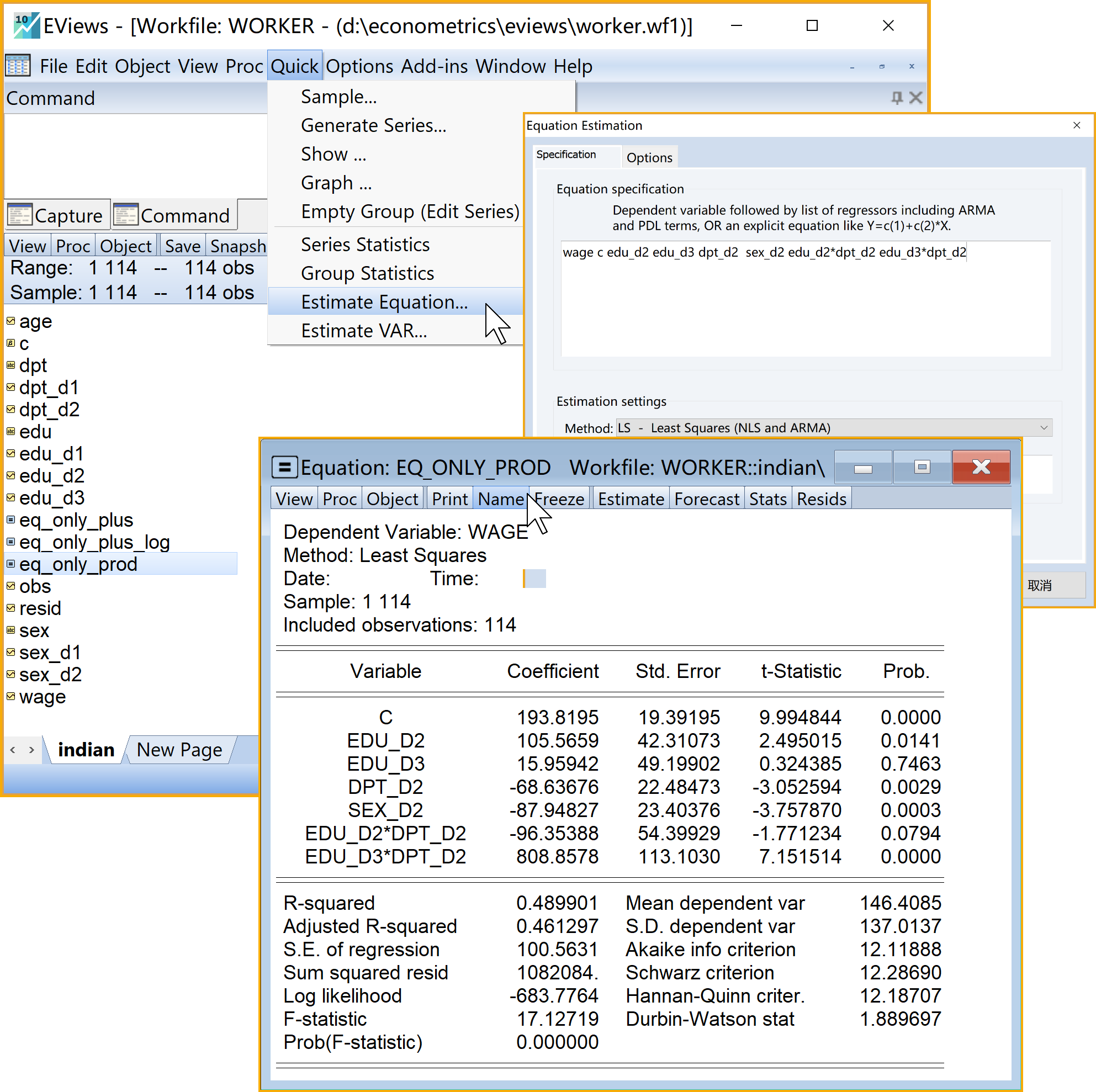
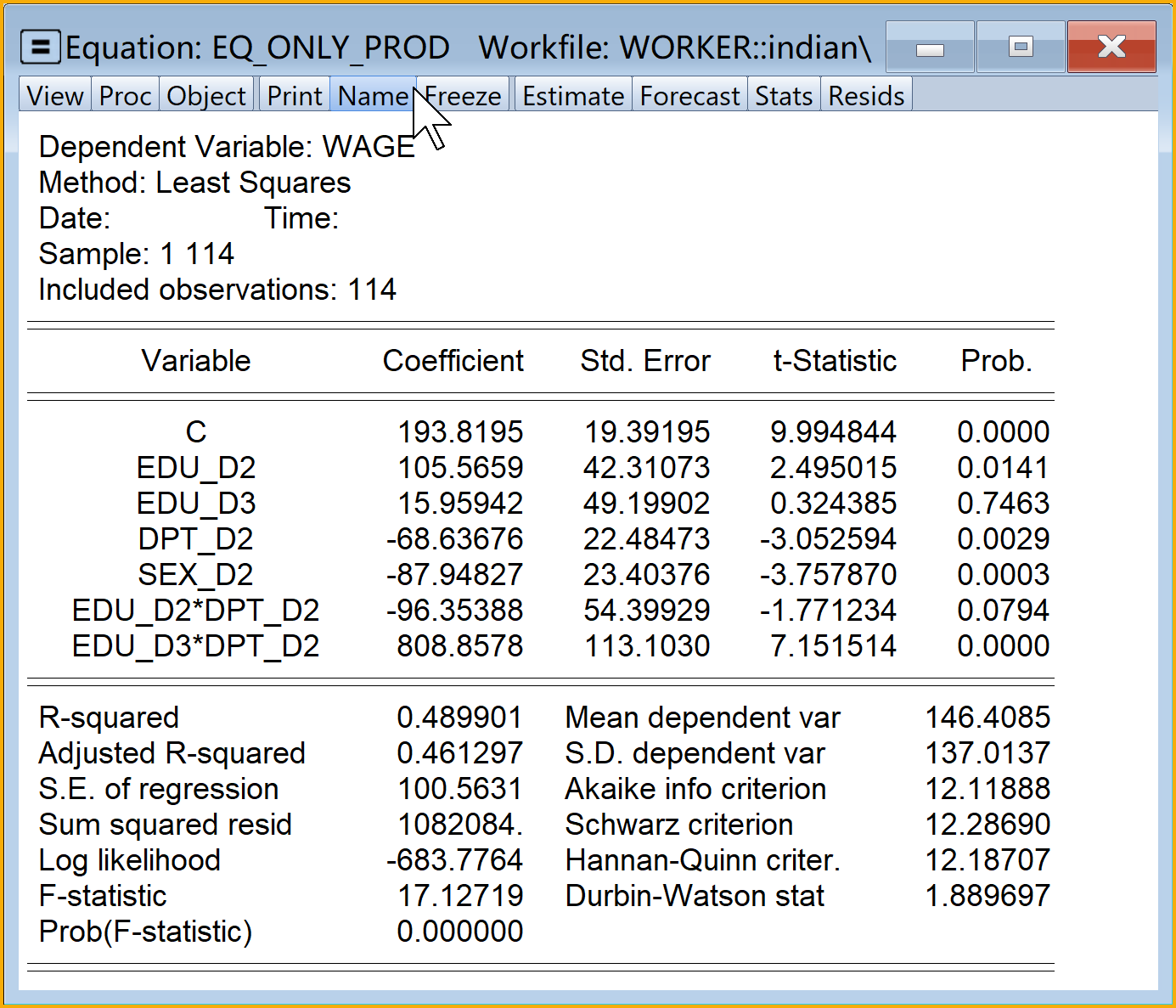
只含虚拟变量的、乘法形式的经典回归模型(全部变量进入,见 式 8.17)Eviews结果简要报告如下(见 式 8.18):
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri_i\\&+\beta_{4}edu\_mid_i+\beta_{5}edu\_hig_i+\beta_{6}dpt\_per_i\\&+\beta_{7}edu\_pri \times dpt\_per_i+\beta_{8}edu\_mid \times dpt\_per_i+\beta_{9}edu\_hig \times dpt\_per_i+u_i \end{split} \end{aligned} \tag{8.17}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+120.70&&-88.19sex\_m_i&&+23.03edu\_pri_i\\ &(s)&&(15.2625)&&(23.8515)&&(32.6264)\\ &(t)&&(+7.91)&&(-3.70)&&(+0.71)\\ &(cont.)&&+13.72edu\_mid_i&&+829.30edu\_hig_i&&+74.78dpt\_per_i\\ &(s)&&(35.2241)&&(102.4020)&&(25.0404)\\ &(t)&&(+0.39)&&(+8.10)&&(+2.99)\\ &(cont.)&&-32.62edu\_pri:dpt\_per_i&&+90.22edu\_mid:dpt\_per_i&&-814.86edu\_hig:dpt\_per_i\\ &(s)&&(59.7485)&&(55.7896)&&(114.2653)\\ &(t)&&(-0.55)&&(+1.62)&&(-7.13)\\ &(over)&&n=114&&\hat{\sigma}=101.2582 &&\\ &(fit)&&R^2=0.4925&&\bar{R}^2=0.4538 &&\\ &(Ftest)&&F^*=12.74&&p=0.0000 && \end{split} \end{alignedat} \tag{8.18}\]
此时,根据总体回归模型 式 8.17 和样本回归方程 式 8.18 我们可以得到:
(1)基础组(文盲 & 短期合同 & 女性),也即(illiteracy & temporary & female)的期望工资收入见 式 8.19,拟合的期望工资收入见 式 8.20:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0)\\&+\beta_{4}(0) +\beta_{5}(0) +\beta_{6}(0)\\&+\beta_{7}(0)\cdot(0) +\beta_{8}(0)\cdot(0) +\beta_{9}(0)\cdot(0)\\ =&\beta_{1} \end{split} \end{aligned} \tag{8.19}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0)\\&+\hat{\beta}_{4}(0) +\hat{\beta}_{5}(0) +\hat{\beta}_{6}(0)\\&+\hat{\beta}_{7}(0)\cdot(0) +\hat{\beta}_{8}(0)\cdot(0) +\hat{\beta}_{9}(0)\cdot(0)\\ =&+[120.70]\cdot (1)-[88.19]\cdot (0)+[23.03]\cdot (0)\\&+[13.72]\cdot (0)+[829.30]\cdot (0)+[74.78]\cdot (0)\\&-[32.62]\cdot (0)\cdot(0)+[90.22]\cdot (0)\cdot(0)-[814.86]\cdot (0)\cdot(0)\\ =&120.70 \end{split} \end{aligned} \tag{8.20}\]
(2)比较组1(文盲 & 长期合同 & 女性),也即(illiteracy & temporary & male)的期望工资收入见 式 8.21,拟合的期望工资收入见 式 8.22:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=1; sex\_m=0)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0)\\&+\beta_{4}(0) +\beta_{5}(0) +\beta_{6}(1)\\&+\beta_{7}(0)\cdot(1) +\beta_{8}(0)\cdot(1) +\beta_{9}(0)\cdot(1)\\ =&\beta_{1} + \beta_{6} \end{split} \end{aligned} \tag{8.21}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=1; sex\_m=0)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0)\\&+\hat{\beta}_{4}(0) +\hat{\beta}_{5}(0) +\hat{\beta}_{6}(1)\\&+\hat{\beta}_{7}(0)\cdot(1) +\hat{\beta}_{8}(0)\cdot(1) +\hat{\beta}_{9}(0)\cdot(1)\\ =&+[120.70]\cdot (1)-[88.19]\cdot (0)+[23.03]\cdot (0)\\&+[13.72]\cdot (0)+[829.30]\cdot (0)+[74.78]\cdot (1)\\&-[32.62]\cdot (0)\cdot(1)+[90.22]\cdot (0)\cdot(1)-[814.86]\cdot (0)\cdot(1)\\ =&195.48 \end{split} \end{aligned} \tag{8.22}\]
(3)比较组2(高等教育 & 长期合同 & 女性),也即(higher & permanent & male)的期望工资收入见 式 8.23,拟合的期望工资收入见 式 8.24:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=0)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0)\\&+\beta_{4}(0) +\beta_{5}(1) +\beta_{6}(1)\\&+\beta_{7}(0)\cdot(1) +\beta_{8}(0)\cdot(1) +\beta_{9}(1)\cdot(1)\\ =&\beta_{1} + \beta_{5} + \beta_{6} + \beta_{9} \end{split} \end{aligned} \tag{8.23}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=0)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0)\\&+\hat{\beta}_{4}(0) +\hat{\beta}_{5}(1) +\hat{\beta}_{6}(1)\\&+\hat{\beta}_{7}(0)\cdot(1) +\hat{\beta}_{8}(0)\cdot(1) +\hat{\beta}_{9}(1)\cdot(1)\\ =&+[120.70]\cdot (1)-[88.19]\cdot (0)+[23.03]\cdot (0)\\&+[13.72]\cdot (0)+[829.30]\cdot (1)+[74.78]\cdot (1)\\&-[32.62]\cdot (0)\cdot(1)+[90.22]\cdot (0)\cdot(1)-[814.86]\cdot (1)\cdot(1)\\ =&209.92 \end{split} \end{aligned} \tag{8.24}\]
8.5.4.4 乘法-经典模型(部分交叉)
只含有虚拟变量的、乘法形式的经典回归模型(部分交叉项)见方程 式 8.25 ;
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}dpt\_per_i+\beta_{4}dpt\_per \times edu\_pri_i\\&+\beta_{5}dpt\_per \times edu\_mid_i+\beta_{6}dpt\_per \times edu\_hig_i+u_i \end{split} \end{aligned} \tag{8.25}\]
只含虚拟变量的、乘法形式的经典回归模型(部分变量进入)Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}dpt\_per_i+\beta_{4}dpt\_per \times edu\_pri_i\\&+\beta_{5}dpt\_per \times edu\_mid_i+\beta_{6}dpt\_per \times edu\_hig_i+u_i \end{split} \end{aligned} \tag{8.26}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+139.60&&-97.26sex\_m_i&&+58.78dpt\_per_i&&-12.48dpt\_per:edu\_pri_i\\ &(s)&&(15.9406)&&(29.8761)&&(29.8391)&&(63.0830)\\ &(t)&&(+8.76)&&(-3.26)&&(+1.97)&&(-0.20)\\ &(cont.)&&+102.33dpt\_per:edu\_mid_i&&+16.98dpt\_per:edu\_hig_i && &&\\ &(s)&&(54.6840)&&(62.9130) && &&\\ &(t)&&(+1.87)&&(+0.27) && &&\\ &(over)&&n=114&&\hat{\sigma}=127.2802 && &&\\ &(fit)&&R^2=0.1752&&\bar{R}^2=0.1370 && &&\\ &(Ftest)&&F^*=4.59&&p=0.0008 && && \end{split} \end{alignedat} \tag{8.27}\]
8.5.4.5 乘法-半对数模型(部分交叉)
只含有虚拟变量的、乘法形式的半对数回归模型(部分交叉项)见方程 式 8.28
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}dpt\_per_i+\beta_{4}dpt\_per \times edu\_pri_i\\&+\beta_{5}dpt\_per \times edu\_mid_i+\beta_{6}dpt\_per \times edu\_hig_i+u_i \end{split} \end{aligned} \tag{8.28}\]
只含有虚拟变量的、乘法形式的半对数回归模型见方程 式 8.28 ,菜单操作实现具体见 图 8.11:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型

edu_d1
dpt_d1
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
log(wage) c dpt_d2 sex_d2 edu_d2*dpt_d2 edu_d3*dpt_d2 edu_d4*dpt_d2Estimation settings:
- Method: 下拉选择LS - Least Squares (NLS and ARMA)
- Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_only_prod_log_part)查看结果:双击

eq_only_prod_log_part
具体Eviews报告见@ref(fig:only-prod-log-part-report):
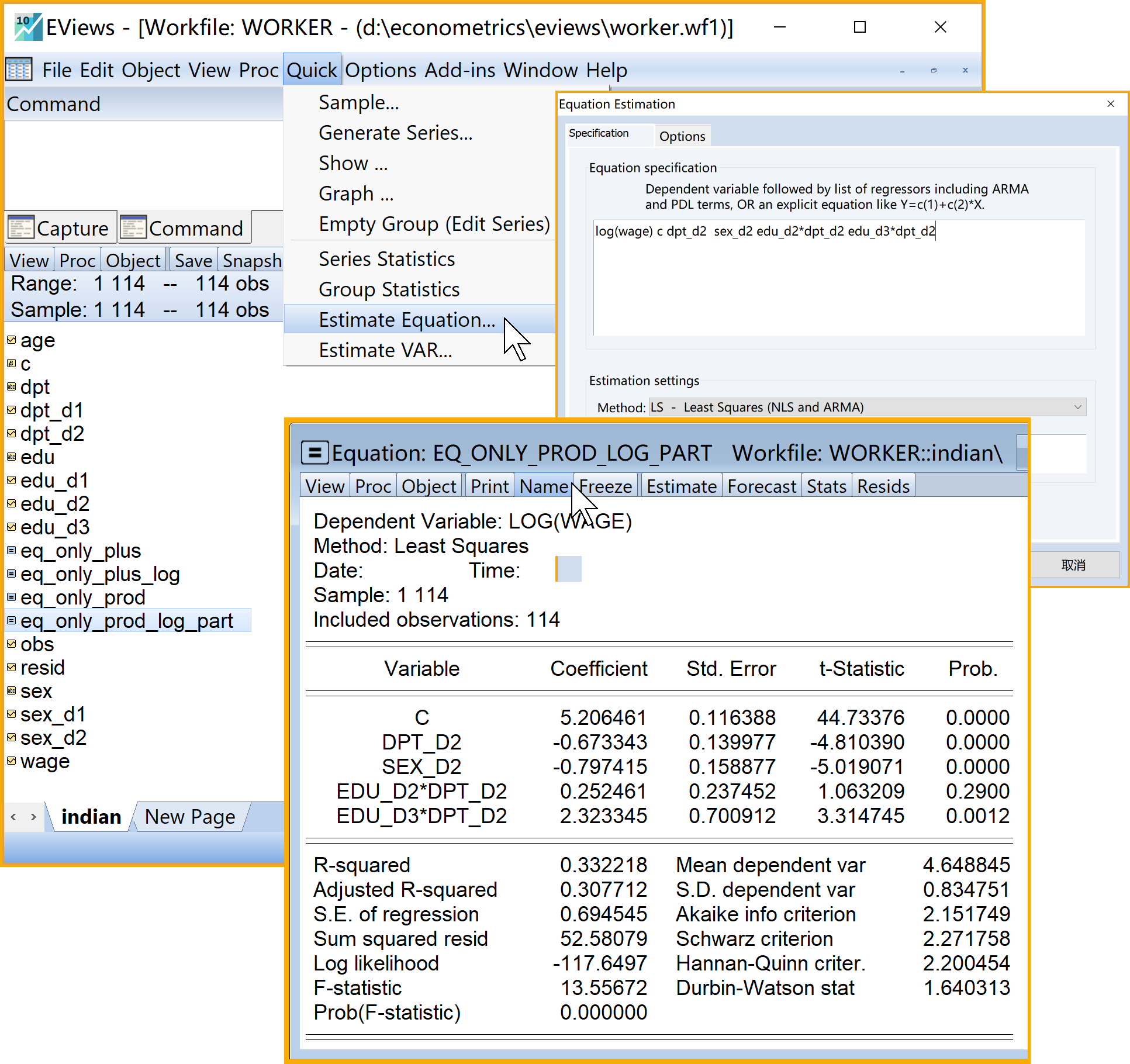
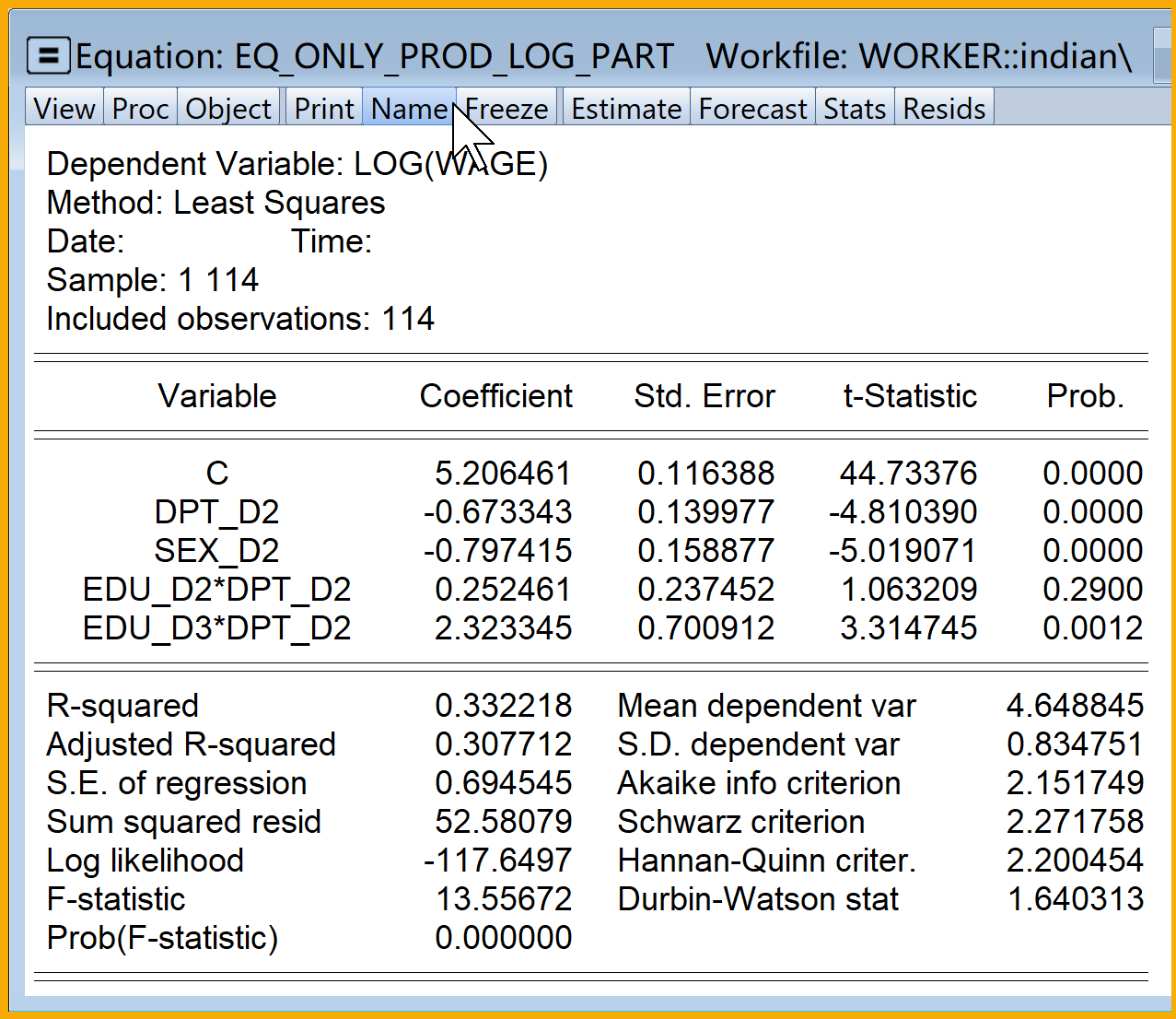
只含虚拟变量的、乘法形式的半对数回归模型(部分变量进入)Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}dpt\_per_i+\beta_{4}dpt\_per \times edu\_pri_i\\&+\beta_{5}dpt\_per \times edu\_mid_i+\beta_{6}dpt\_per \times edu\_hig_i+u_i \end{split} \end{aligned} \tag{8.29}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{log(wage)}=&&+4.61&&-0.82sex\_m_i&&+0.45dpt\_per_i&&+0.06dpt\_per:edu\_pri_i\\ &(s)&&(0.0899)&&(0.1685)&&(0.1683)&&(0.3559)\\ &(t)&&(+51.21)&&(-4.89)&&(+2.67)&&(+0.16)\\ &(cont.)&&+0.64dpt\_per:edu\_mid_i&&+0.38dpt\_per:edu\_hig_i && &&\\ &(s)&&(0.3085)&&(0.3549) && &&\\ &(t)&&(+2.09)&&(+1.08) && &&\\ &(over)&&n=114&&\hat{\sigma}=0.7181 && &&\\ &(fit)&&R^2=0.2928&&\bar{R}^2=0.2600 && &&\\ &(Ftest)&&F^*=8.94&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.30}\]
8.5.5 同时含有虚拟变量和定量变量
8.5.5.1 加法-经典模型
同时含有虚拟变量和定量变量的、加法形式的经典回归模型见方程 式 8.31
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.31}\]
同时含有虚拟变量和定量变量的、加法形式的经典回归模型见方程 式 8.31 ,菜单操作实现具体见 图 8.12):
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型

edu_d1
dpt_d1
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
wage c edu_d2 edu_d3 edu_d4 dpt_d2 sex_d2 ageEstimation settings:
具体设置为: - Method: 下拉选择LS - Least Squares (NLS and ARMA) - Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_both_plus)查看结果:双击

eq_both_plus
具体Eviews报告见@ref(fig:both-plus-report):
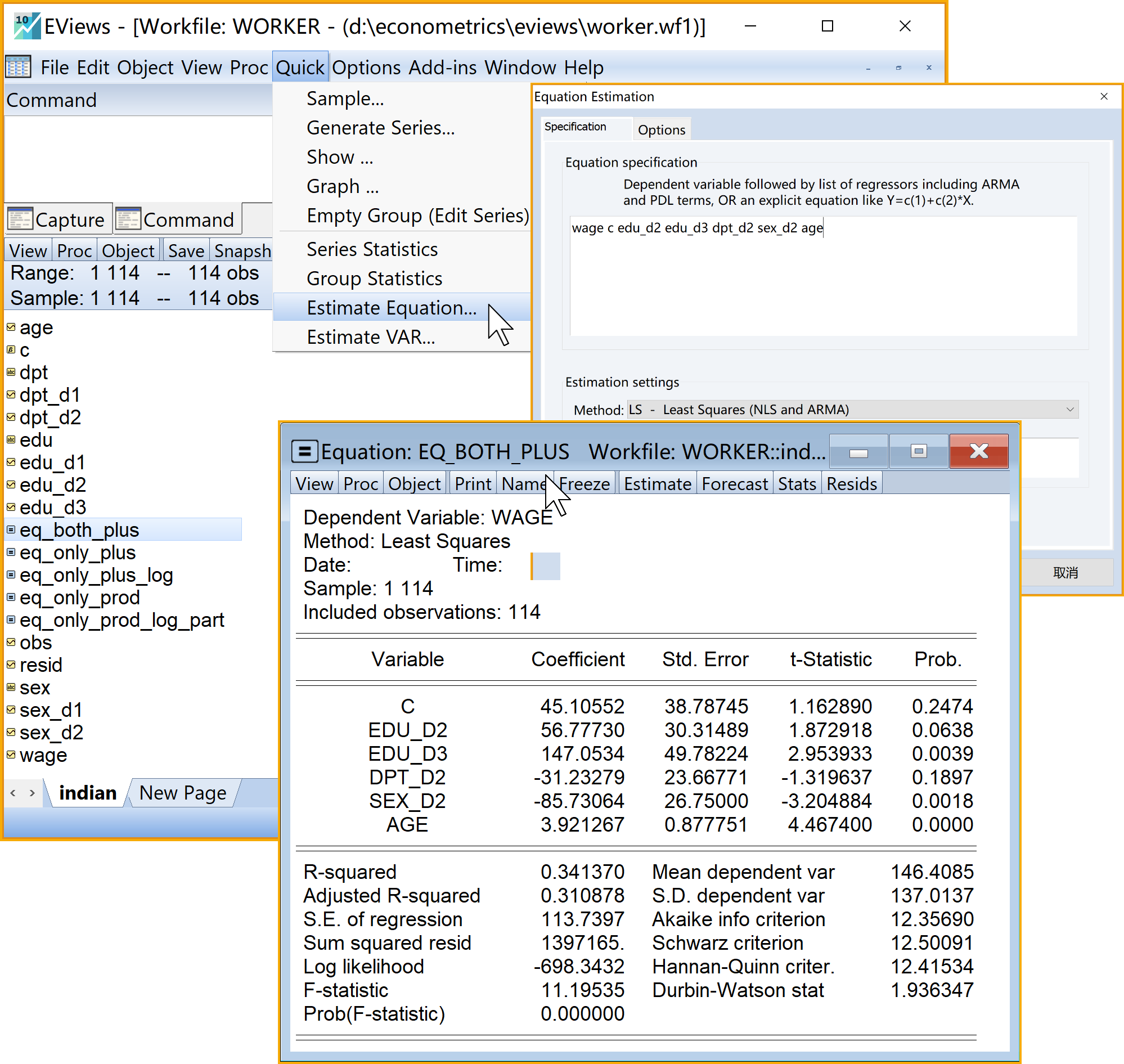
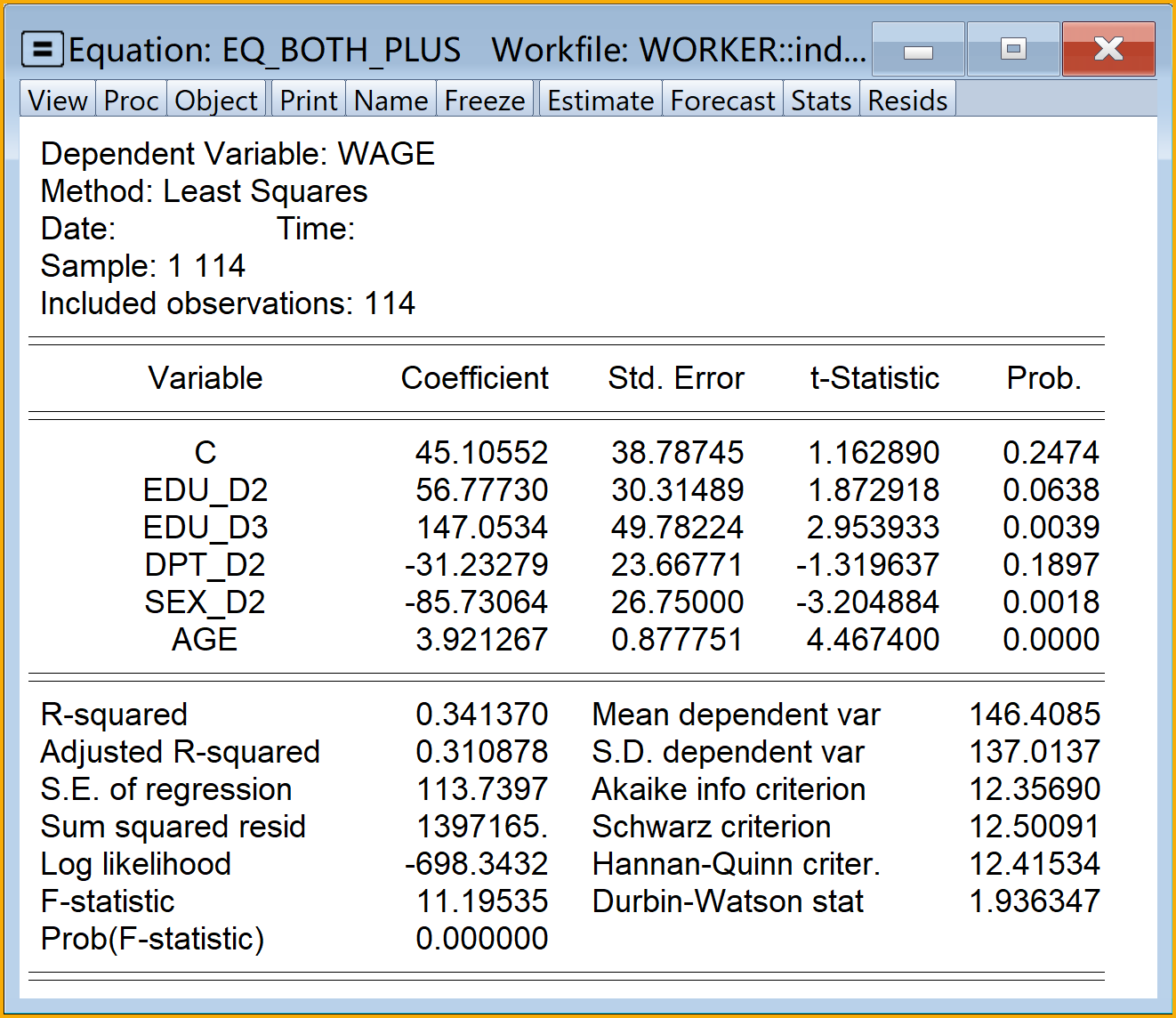
同时含虚拟变量和定量变量的、加法形式的经典回归模型Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.32}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+6.79&&+23.96edu\_pri_i&&+61.59edu\_mid_i&&+150.49edu\_hig_i\\ &(s)&&(31.8931)&&(30.9789)&&(31.0035)&&(50.0725)\\ &(t)&&(+0.21)&&(+0.77)&&(+1.99)&&(+3.01)\\ &(cont.)&&+31.16dpt\_per_i&&-83.20sex\_m_i&&+3.99age_i &&\\ &(s)&&(23.7120)&&(26.9981)&&(0.8835) &&\\ &(t)&&(+1.31)&&(-3.08)&&(+4.51) &&\\ &(over)&&n=114&&\hat{\sigma}=113.9518 && &&\\ &(fit)&&R^2=0.3450&&\bar{R}^2=0.3083 && &&\\ &(Ftest)&&F^*=9.39&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.33}\]
此时,根据总体回归模型 式 8.32 和样本回归方程 式 8.33 我们可以得到:
(1)基础组(文盲 & 短期合同 & 女性),也即(illiteracy & temporary & female),并给定年龄为30岁,其期望工资收入见 式 8.34,拟合的期望工资收入见 式 8.35:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(0) +\beta_{7}(30.00)\\ =&\beta_{1} + 30.00\beta_{7} \end{split} \end{aligned} \tag{8.34}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(0) +\hat{\beta}_{7}(30.00)\\ =&+[6.79]\cdot (1)+[23.96]\cdot (0)+[61.59]\cdot (0)+[150.49]\cdot (0)\\&+[31.16]\cdot (0)-[83.20]\cdot (0)+[3.99]\cdot (30.00)\\ =&126.41 \end{split} \end{aligned} \tag{8.35}\]
(2)比较组1(文盲 & 短期合同 & 男性),也即(illiteracy & temporary & male),并给定年龄为30岁,其期望工资收入见 式 8.36,拟合的期望工资收入见 式 8.37:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=1; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(1) +\beta_{7}(30.00)\\ =&\beta_{1} + \beta_{6} + 30.00\beta_{7} \end{split} \end{aligned} \tag{8.36}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=1; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(1) +\hat{\beta}_{7}(30.00)\\ =&+[6.79]\cdot (1)+[23.96]\cdot (0)+[61.59]\cdot (0)+[150.49]\cdot (0)\\&+[31.16]\cdot (0)-[83.20]\cdot (1)+[3.99]\cdot (30.00)\\ =&43.21 \end{split} \end{aligned} \tag{8.37}\]
(2)比较组2(高等教育 & 长期合同 & 男性),也即(higher & permanent & male),且给定年龄为30岁,其期望工资收入见 式 8.38,拟合的期望工资收入见 式 8.39:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=1; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(1)\\&+\beta_{5}(1) +\beta_{6}(1) +\beta_{7}(30.00)\\ =&\beta_{1} + \beta_{4} + \beta_{5} + \beta_{6} + 30.00\beta_{7} \end{split} \end{aligned} \tag{8.38}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=1; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(1)\\&+\hat{\beta}_{5}(1) +\hat{\beta}_{6}(1) +\hat{\beta}_{7}(30.00)\\ =&+[6.79]\cdot (1)+[23.96]\cdot (0)+[61.59]\cdot (0)+[150.49]\cdot (1)\\&+[31.16]\cdot (1)-[83.20]\cdot (1)+[3.99]\cdot (30.00)\\ =&224.86 \end{split} \end{aligned} \tag{8.39}\]
8.5.5.2 加法-半对数模型
同时含有虚拟变量和定量变量的、加法形式的半对数回归模型见方程 式 8.40
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.40}\]
同时含有虚拟变量和定量变量的、加法形式的半对数回归模型见方程 式 8.40 ,菜单操作实现具体见 图 8.14:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型 a. 
edu_d1 b. 
dpt_d1 c. 
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
log(wage) c edu_d2 edu_d3 edu_d4 dpt_d2 sex_d2 ageEstimation settings:
具体设置为: - Method: 下拉选择LS - Least Squares (NLS and ARMA) - Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_both_plus_log)查看结果:双击

eq_both_plus_log
具体Eviews报告见@ref(fig:both-plus-log-report):
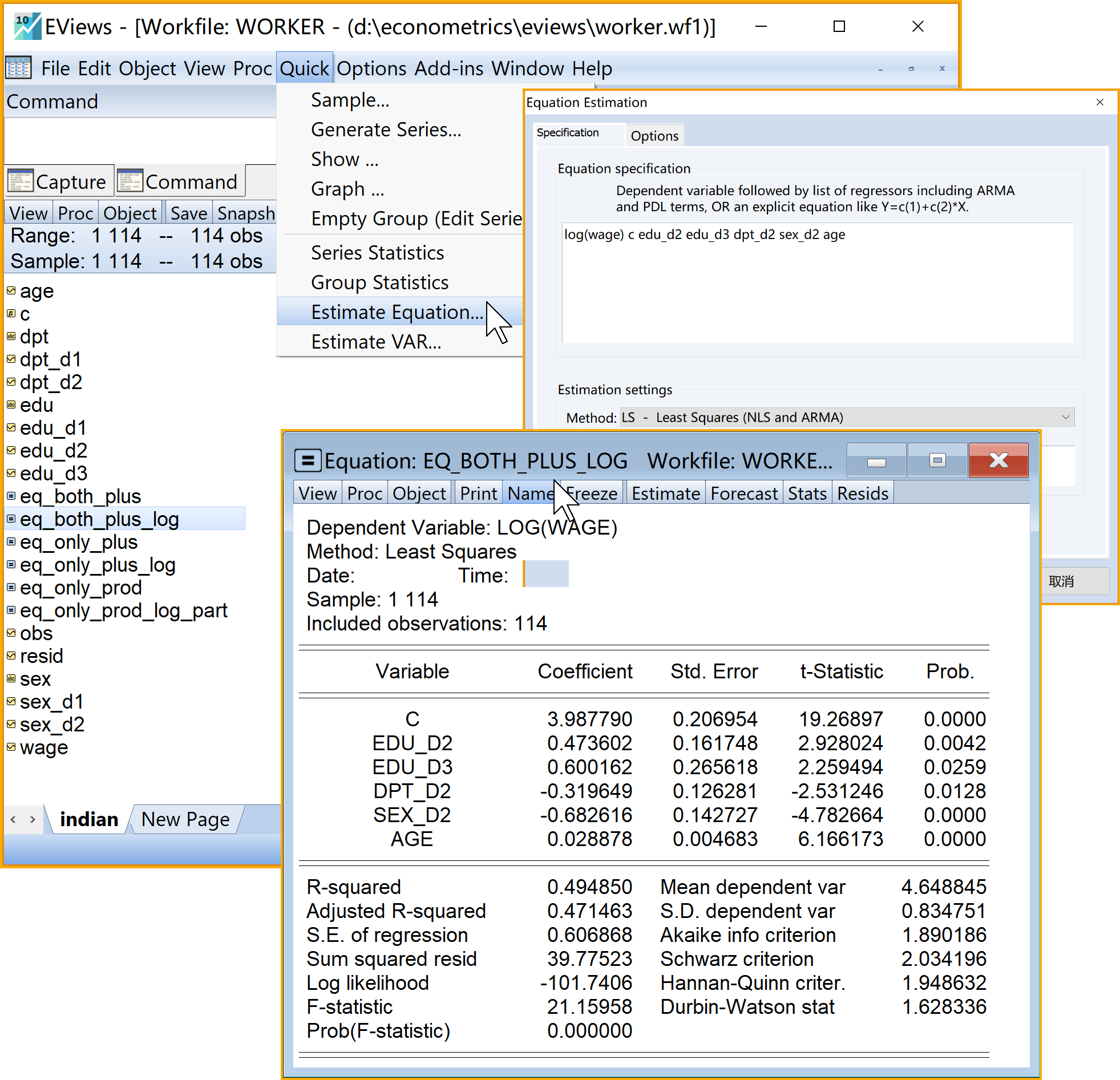
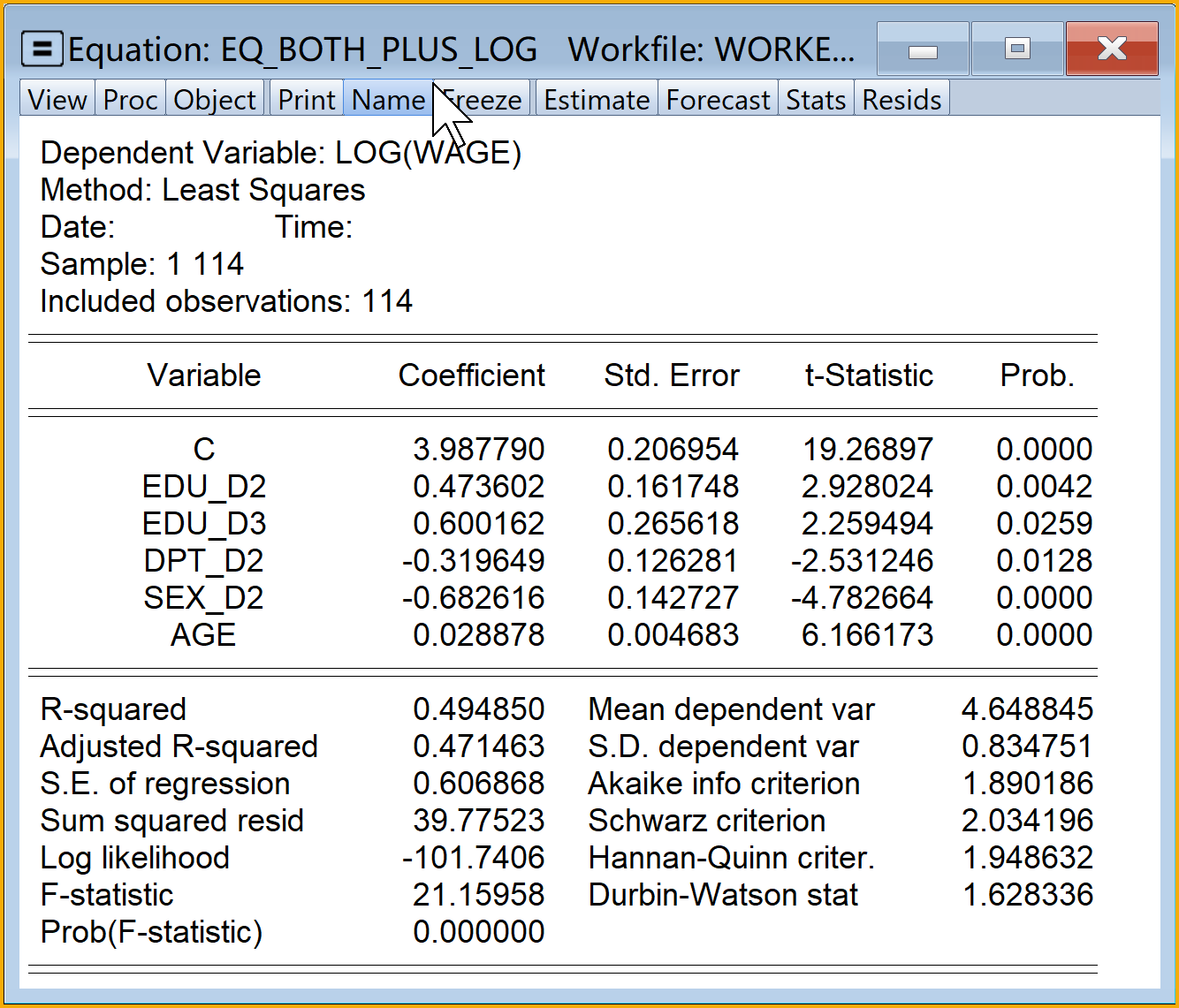
同时含虚拟变量和定量变量的、加法形式的半对数回归模型Eviews结果简要报告如下:
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}edu\_pri_i+\beta_{3}edu\_mid_i+\beta_{4}edu\_hig_i\\&+\beta_{5}dpt\_per_i+\beta_{6}sex\_m_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.41}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{log(wage)}=&&+3.62&&+0.16edu\_pri_i&&+0.51edu\_mid_i&&+0.62edu\_hig_i\\ &(s)&&(0.1699)&&(0.1651)&&(0.1652)&&(0.2668)\\ &(t)&&(+21.31)&&(+0.95)&&(+3.06)&&(+2.33)\\ &(cont.)&&+0.32dpt\_per_i&&-0.67sex\_m_i&&+0.03age_i &&\\ &(s)&&(0.1263)&&(0.1438)&&(0.0047) &&\\ &(t)&&(+2.53)&&(-4.63)&&(+6.23) &&\\ &(over)&&n=114&&\hat{\sigma}=0.6071 && &&\\ &(fit)&&R^2=0.4991&&\bar{R}^2=0.4710 && &&\\ &(Ftest)&&F^*=17.77&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.42}\]
8.5.5.3 乘法-经典模型(完全)
同时含有虚拟变量和定量变量的、乘法形式的经典回归(完全)模型见方程 式 8.43
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri_i+\beta_{4}edu\_mid_i\\&+\beta_{5}edu\_hig_i+\beta_{6}dpt\_per_i+\beta_{7}edu\_pri \times dpt\_per_i+\beta_{8}edu\_mid \times dpt\_per_i\\&+\beta_{9}edu\_hig \times dpt\_per_i+\beta_{10}age_i+u_i \end{split} \end{aligned} \tag{8.43}\]
同时含有虚拟变量和定量变量的、乘法形式的经典回归模型见方程 式 8.43 ,菜单操作实现具体见 图 8.16:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型 a. 
edu_d1 b. 
dpt_d1 c. 
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
wage c edu_d2 edu_d3 edu_d4 dpt_d2 sex_d2 age edu_d2*dpt_d2 edu_d3*dpt_d2 edu_d4*dpt_d2Estimation settings:
具体设置为: - Method: 下拉选择LS - Least Squares (NLS and ARMA) - Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_both_prod)查看结果:双击

eq_both_prod
具体Eviews报告见@ref(fig:both-prod-report):
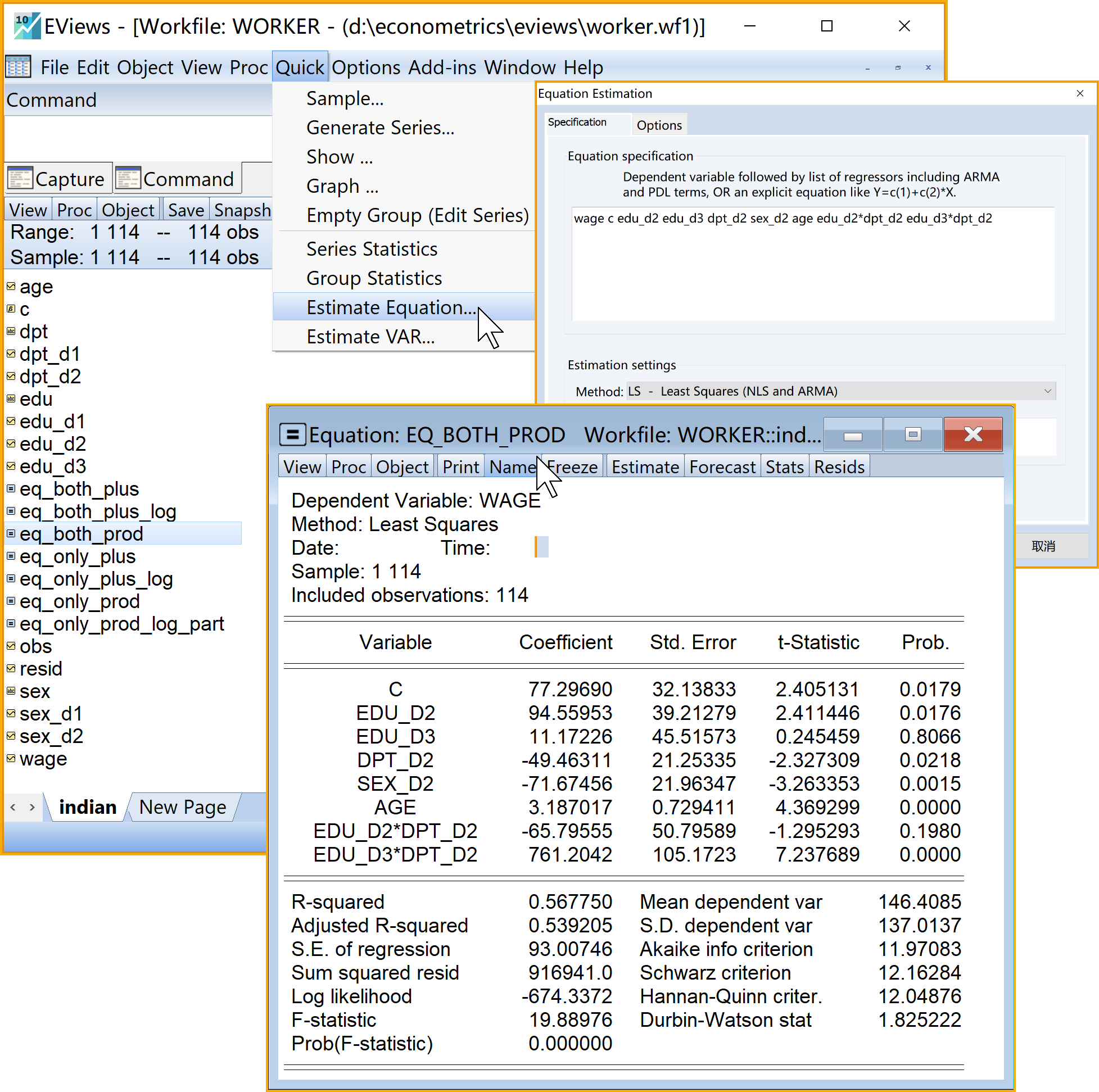
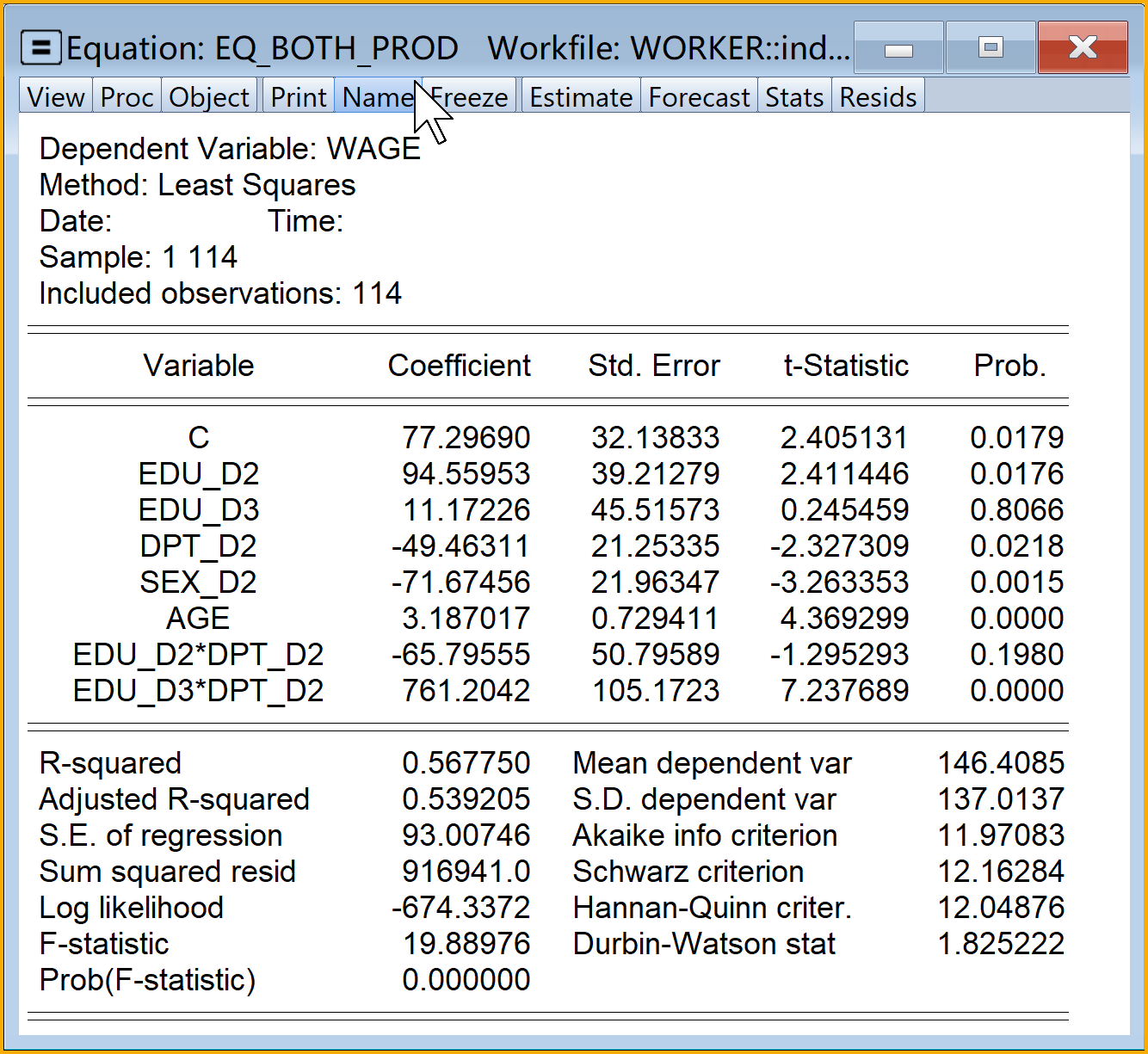
同时含虚拟变量和定量变量的、乘法形式的经典回归模型(见 式 8.44)(全部变量进入)Eviews结果简要报告(见 式 8.45)如下:
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri_i+\beta_{4}edu\_mid_i\\&+\beta_{5}edu\_hig_i+\beta_{6}dpt\_per_i+\beta_{7}edu\_pri \times dpt\_per_i+\beta_{8}edu\_mid \times dpt\_per_i\\&+\beta_{9}edu\_hig \times dpt\_per_i+\beta_{10}age_i+u_i \end{split} \end{aligned} \tag{8.44}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+19.43&&-70.34sex\_m_i&&+32.29edu\_pri_i&&+35.59edu\_mid_i\\ &(s)&&(26.9248)&&(22.3647)&&(30.1607)&&(32.8591)\\ &(t)&&(+0.72)&&(-3.15)&&(+1.07)&&(+1.08)\\ &(cont.)&&+777.93edu\_hig_i&&+54.46dpt\_per_i&&+3.25age_i&&-26.81edu\_pri:dpt\_per_i\\ &(s)&&(95.1488)&&(23.5466)&&(0.7361)&&(55.1151)\\ &(t)&&(+8.18)&&(+2.31)&&(+4.41)&&(-0.49)\\ &(cont.)&&+59.80edu\_mid:dpt\_per_i&&-766.28edu\_hig:dpt\_per_i && &&\\ &(s)&&(51.9083)&&(105.9477) && &&\\ &(t)&&(+1.15)&&(-7.23) && &&\\ &(over)&&n=114&&\hat{\sigma}=93.3791 && &&\\ &(fit)&&R^2=0.5725&&\bar{R}^2=0.5355 && &&\\ &(Ftest)&&F^*=15.48&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.45}\]
此时,根据上述总体回归模型 式 8.44 和样本回归方程 式 8.45 我们可以得到:
(1)基础组为:文盲 & 短期合同 & 女性(也即illiteracy & temporary & female),并给定年龄为30岁(\(age=30\)),则其期望工资收入见 式 8.46,拟合的期望工资收入见 式 8.47:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(0) +\beta_{7}(0)\cdot(0) +\beta_{8}(0)\cdot(0)\\&+\beta_{9}(0)\cdot(0) +\beta_{10}(30.00)\\ =&\beta_{1} + 30.00\beta_{10} \end{split} \end{aligned} \tag{8.46}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=0; sex\_m=0; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(0) +\hat{\beta}_{7}(0)\cdot(0) +\hat{\beta}_{8}(0)\cdot(0)\\&+\hat{\beta}_{9}(0)\cdot(0) +\hat{\beta}_{10}(30.00)\\ =&+[19.43]\cdot (1)-[70.34]\cdot (0)+[32.29]\cdot (0)+[35.59]\cdot (0)\\&+[777.93]\cdot (0)+[54.46]\cdot (0)-[26.81]\cdot (0)\cdot(0)+[59.80]\cdot (0)\cdot(0)\\&-[766.28]\cdot (0)\cdot(0)+[3.25]\cdot (30.00)\\ =&116.86 \end{split} \end{aligned} \tag{8.47}\]
(2)比较组1为:文盲 & 长期合同 & 女性也即(illiteracy & permanent & female),并给定年龄为30岁(\(age=30\)),则其期望工资收入见 式 8.48,拟合的期望工资收入见 式 8.49:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=1; sex\_m=0; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(0) +\beta_{6}(1) +\beta_{7}(0)\cdot(1) +\beta_{8}(0)\cdot(1)\\&+\beta_{9}(0)\cdot(1) +\beta_{10}(30.00)\\ =&\beta_{1} + \beta_{6} + 30.00\beta_{10} \end{split} \end{aligned} \tag{8.48}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=0; dpt\_per=1; sex\_m=0; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(1) +\hat{\beta}_{7}(0)\cdot(1) +\hat{\beta}_{8}(0)\cdot(1)\\&+\hat{\beta}_{9}(0)\cdot(1) +\hat{\beta}_{10}(30.00)\\ =&+[19.43]\cdot (1)-[70.34]\cdot (0)+[32.29]\cdot (0)+[35.59]\cdot (0)\\&+[777.93]\cdot (0)+[54.46]\cdot (1)-[26.81]\cdot (0)\cdot(1)+[59.80]\cdot (0)\cdot(1)\\&-[766.28]\cdot (0)\cdot(1)+[3.25]\cdot (30.00)\\ =&171.32 \end{split} \end{aligned} \tag{8.49}\]
(3)比较组2为:高等教育 & 长期合同 & 女性(也即higher & permanent & female),并给定年龄为30岁(\(age=30\))。则其期望工资收入见 式 8.50,拟合的期望工资收入见 式 8.51:
\[ \begin{aligned} \begin{split} &E(wage|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=0; age=30)\\ =&+\beta_{1}(1) +\beta_{2}(0) +\beta_{3}(0) +\beta_{4}(0)\\&+\beta_{5}(1) +\beta_{6}(1) +\beta_{7}(0)\cdot(1) +\beta_{8}(0)\cdot(1)\\&+\beta_{9}(1)\cdot(1) +\beta_{10}(30.00)\\ =&\beta_{1} + \beta_{5} + \beta_{6} + \beta_{9} + 30.00\beta_{10} \end{split} \end{aligned} \tag{8.50}\]
\[ \begin{aligned} \begin{split} &(\widehat{wage}|edu\_pri=0; edu\_mid=0; edu\_hig=1; dpt\_per=1; sex\_m=0; age=30)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(0)\\&+\hat{\beta}_{5}(1) +\hat{\beta}_{6}(1) +\hat{\beta}_{7}(0)\cdot(1) +\hat{\beta}_{8}(0)\cdot(1)\\&+\hat{\beta}_{9}(1)\cdot(1) +\hat{\beta}_{10}(30.00)\\ =&+[19.43]\cdot (1)-[70.34]\cdot (0)+[32.29]\cdot (0)+[35.59]\cdot (0)\\&+[777.93]\cdot (1)+[54.46]\cdot (1)-[26.81]\cdot (0)\cdot(1)+[59.80]\cdot (0)\cdot(1)\\&-[766.28]\cdot (1)\cdot(1)+[3.25]\cdot (30.00)\\ =&182.97 \end{split} \end{aligned} \tag{8.51}\]
8.5.5.4 乘法-经典模型(部分)
同时含有虚拟变量和定量变量的、乘法形式的经典回归(部分)模型见方程 式 8.52
\[ \begin{aligned} \begin{split} wage_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri \times dpt\_per_i+\beta_{4}edu\_mid \times dpt\_per_i\\&+\beta_{5}edu\_hig \times dpt\_per_i+\beta_{6}dpt\_per_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.52}\]
同时含虚拟变量和定量变量的、乘法形式的经典回归模型(部分变量进入)Eviews结果简要报告(见 式 8.53)如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{wage}=&&+23.30&&-76.57sex\_m_i&&+29.97dpt\_per_i&&+3.88age_i\\ &(s)&&(31.0993)&&(28.1834)&&(28.5419)&&(0.9127)\\ &(t)&&(+0.75)&&(-2.72)&&(+1.05)&&(+4.25)\\ &(cont.)&&+5.31edu\_pri:dpt\_per_i&&+92.00edu\_mid:dpt\_per_i&&+13.83edu\_hig:dpt\_per_i &&\\ &(s)&&(58.7653)&&(50.8699)&&(58.4628) &&\\ &(t)&&(+0.09)&&(+1.81)&&(+0.24) &&\\ &(over)&&n=114&&\hat{\sigma}=118.2676 && &&\\ &(fit)&&R^2=0.2945&&\bar{R}^2=0.2549 && &&\\ &(Ftest)&&F^*=7.44&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.53}\]
8.5.5.5 乘法-半对数模型(部分)
同时含有虚拟变量和定量变量的、乘法形式的半对数回归(部分)模型见方程 式 8.54
\[ \begin{aligned} \begin{split} log(wage)_i=&+\beta_{1}+\beta_{2}sex\_m_i+\beta_{3}edu\_pri \times dpt\_per_i+\beta_{4}edu\_mid \times dpt\_per_i\\&+\beta_{5}edu\_hig \times dpt\_per_i+\beta_{6}dpt\_per_i+\beta_{7}age_i+u_i \end{split} \end{aligned} \tag{8.54}\]
同时含有虚拟变量和定量变量的、乘法形式的半对数回归模型见方程 式 8.54 ,菜单操作实现具体见图@ref(fig:both-prod-part-graph:
(1)确定基础组为[文盲&短期合同&女性],则如下虚拟变量将不进入回归模型 a. 
edu_d1 b. 
dpt_d1 c. 
sex_d1
(2)设置回归模型。进入引导设置Equation Estimation \(\Rightarrow\) specification
Equation specification:输入命令
log(wage) c dpt_d2 sex_d2 age edu_d2*dpt_d2 edu_d3*dpt_d2 edu_d4*dpt_d2Estimation settings:
具体设置为: - Method: 下拉选择LS - Least Squares (NLS and ARMA) - Sample: (默认设置)
点击完成:OK
命名保存方程对象
 :(建议命名为
:(建议命名为eq_both_prod_log_part)查看结果:双击

eq_both_prod_log_part
具体Eviews报告见@ref(fig:both-prod-part-log-report):
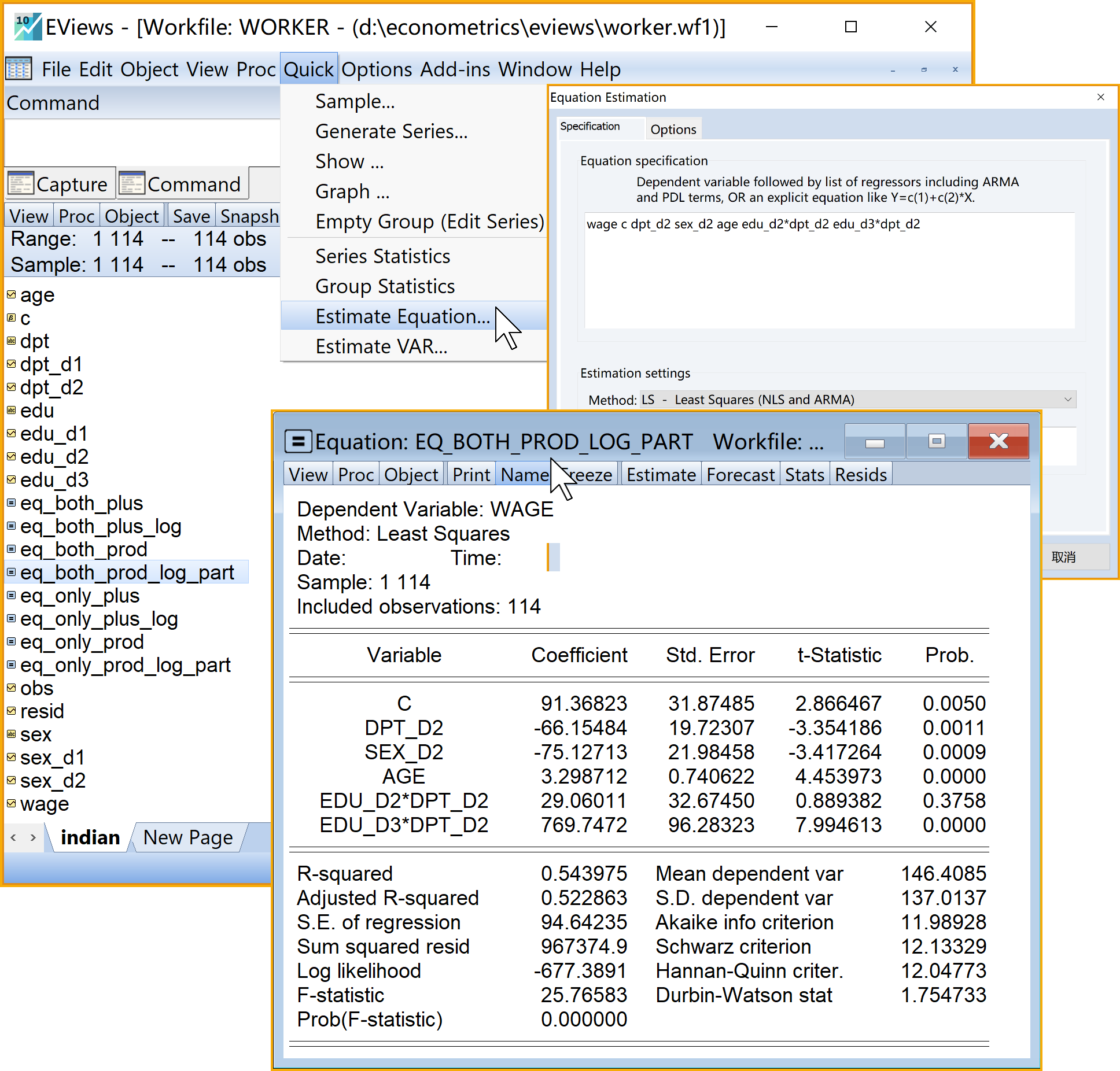
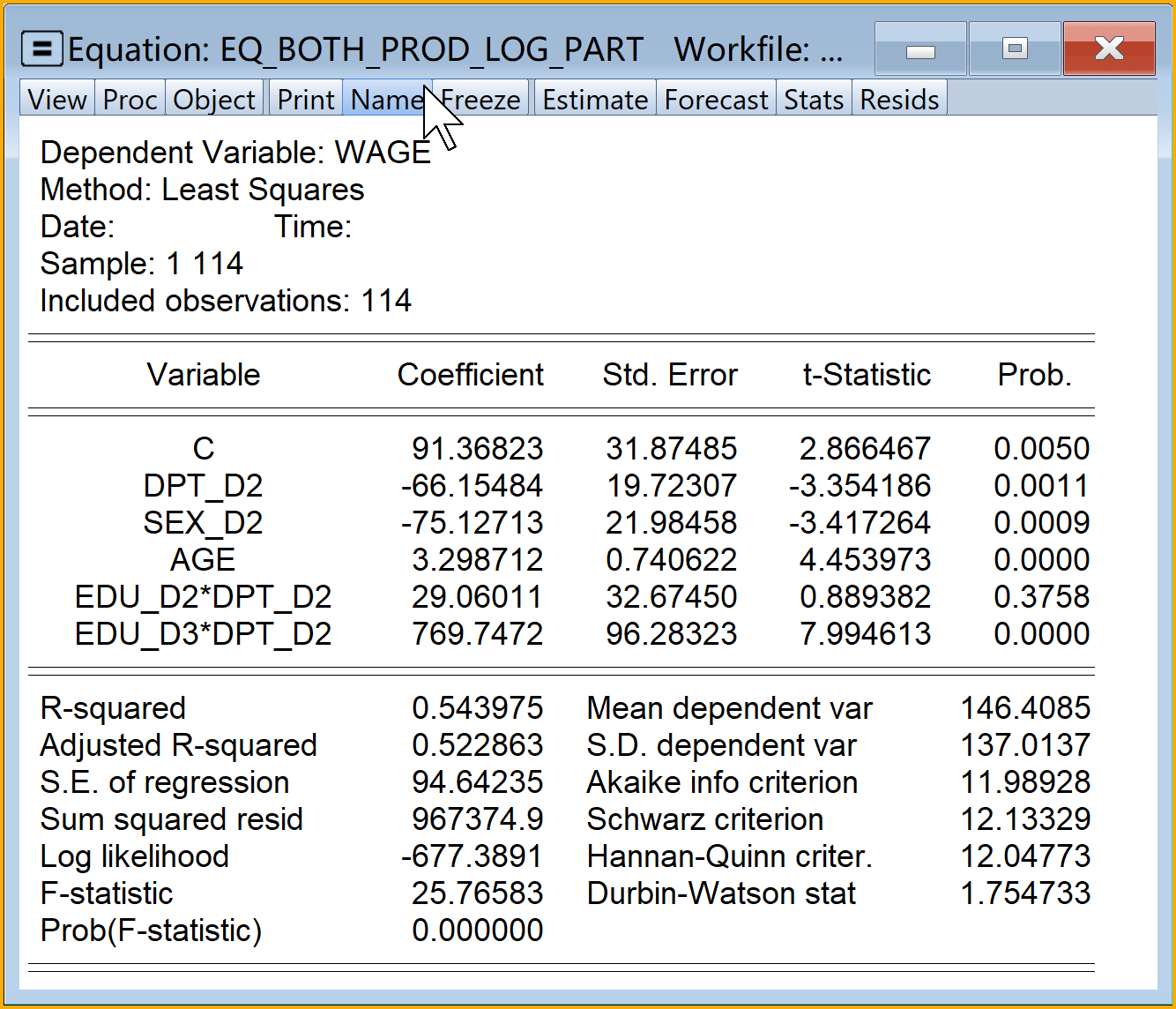
同时含虚拟变量和定量变量的、乘法形式的半对数回归模型(部分变量进入)Eviews结果简要报告(见 式 8.55)如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{log(wage)}=&&+3.76&&-0.67sex\_m_i&&+0.24dpt\_per_i&&+0.03age_i\\ &(s)&&(0.1655)&&(0.1500)&&(0.1519)&&(0.0049)\\ &(t)&&(+22.73)&&(-4.49)&&(+1.58)&&(+5.79)\\ &(cont.)&&+0.18edu\_pri:dpt\_per_i&&+0.57edu\_mid:dpt\_per_i&&+0.36edu\_hig:dpt\_per_i &&\\ &(s)&&(0.3128)&&(0.2707)&&(0.3112) &&\\ &(t)&&(+0.59)&&(+2.10)&&(+1.16) &&\\ &(over)&&n=114&&\hat{\sigma}=0.6295 && &&\\ &(fit)&&R^2=0.4616&&\bar{R}^2=0.4314 && &&\\ &(Ftest)&&F^*=15.29&&p=0.0000 && && \end{split} \end{alignedat} \tag{8.55}\]
8.5.6 时间序列季节虚拟变量模型
目的:通过学习时间序列季节虚拟变量模型,进一步深入理解虚拟变量回归模型的多种形式及应用
思路:设置并引入季节虚拟变量,构建时间序列季节虚拟变量模型,Eviews估计回归结果
定义 8.5 (季节模式和季节调整)
季节模式(seasonal pattern):大多数时间序列经济变量,通常表现出来的季节性往复行为或现象。
季节调整(seasonal adjusted):将时间序列经济变量的季节性变化成分去除,从而得到一个新的变量序列的处理过程。
事实上,一个时间序列经济变量往往同时存在四个成分,分别是季节成分(seasonal component)、周期成分(cyclical component)、趋势成分(trend component)和严格随机成分(strictly random component)。
根据基础组的有无,可以构建以第一季度为基础组的时间序列季节虚拟变量模型 式 8.56 和无基础组的时间序列季节虚拟变量模型 式 8.57 。其中,\(X_t\)为定量变量。
\[ \begin{aligned} Y_t=\beta_1+\beta_2X_t+\lambda_2D2_t+\lambda_3D3_t+\lambda_4D4_t+u_t \end{aligned} \tag{8.56}\]
\[ \begin{aligned} Y_t=\beta_2X_t+\lambda_1D1_t+\lambda_2D2_t+\lambda_3D3_t+\lambda_4D4_t+u_t \end{aligned} \tag{8.57}\]
Eviews操作(此处略)
8.5.7 分段线性回归模型
目的:通过学习分段式线性回归模型,进一步深入理解虚拟变量回归模型的多种形式及应用
思路:设置并引入虚拟变量,构建分段线性回归模型,Eviews估计回归结果
定义 8.6 (分段线性回归)
分段现象:在经济关系中,当解释变量\(X\)的值达到某一水平/阀值\(X^\ast\)之前,与被解释变量之间存在某种线性关系;当解释变量X的值达到或者超过水平/阀值\(X^\ast\)以后,与被解释变量的关系就会发生变化。因而总体看来,似乎被明显“分段”了。
分段线性回归模型(piecewise linear regression):是指用虚拟变量估计不同水平/阀值的解释变量\(X\)对被解释变量\(Y\)的影响的一类线性回归模型。
一个阀值的分段线性回归模型 式 8.58
\[ \begin{aligned} Y_i & =\beta_1+\beta_2X_i+\lambda(X_i-X^{\ast})D_i+u_i \end{aligned} \tag{8.58}\]
两个阀值的分段线性回归模型 式 8.59
\[ \begin{aligned} Y_i & =\beta_1+\beta_2X_i+\lambda_1(X_i-X^{\ast}_1)D1_i+\lambda_2(X_i-X^{\ast}_2)D2_i+u_i \end{aligned} \tag{8.59}\]
Eviews操作(此处略)
8.6 作业题
印度工人工资: 表 8.8 给出给出了114位印度工人在wage工人工资,age年龄,edu教育水平,dpt合同类型,sex性别等方面的数据。
| obs | wage | age | edu | dpt | sex |
|---|---|---|---|---|---|
| 1 | 117 | 26 | primary | permanent | female |
| 2 | 375 | 42 | primary | permanent | female |
| 3 | 175 | 33 | primary | permanent | female |
| 4 | 100 | 33 | primary | permanent | female |
| 5 | 162 | 30 | primary | permanent | female |
| 110 | 25 | 18 | illiteracy | temporary | male |
| 111 | 25 | 11 | illiteracy | temporary | male |
| 112 | 75 | 45 | illiteracy | temporary | male |
| 113 | 54 | 14 | illiteracy | temporary | male |
| 114 | 50 | 26 | illiteracy | temporary | male |
变量说明见 表 8.9 :
| variable | label | remark |
|---|---|---|
| obs | 工人编号 | 序号 |
| wage | 工人工资 | 美元/周 |
| age | 年龄 | 岁 |
| edu | 教育水平 | illiteracy=文盲;primary=初等教育;secondary=中等教育;higher=高等教育 |
| dpt | 合同类型 | temporary=短期合同;permanent=长期合同 |
| sex | 性别 | female=女;male=男 |
请回答如下问题:
(1)请对数据 表 8.8 进行数据处理,将定性变量都处理成完全虚拟变量体系(也即定性变量有m个属性,则设置m个虚拟变量)。
要求:定性变量edu的虚拟变量设置为edu_D1,edu_D2,\(\cdots\);定性变量dpt的虚拟变量设置为dpt_D1,\(\cdots\);定性变量sex的虚拟变量设置为sex_D1,\(\cdots\)。虚拟变量的下标请与变量说明 表 8.9 的保持一致。
(2)使用全部变量,并提出一个加法形式的有截距虚拟变量回归模型,用以预测工人工资。要求基础组设置为(文盲&短期合同&女性)的工人组。
- 请写出加法形式的有截距虚拟变量回归模型(PRM)
- 请利用你自己构建的模型,进行eviews分析,得到分析报告。
要求:将报告截图过来,并写出相应的简要报告形式——三行式或四行式)
- 根据回归分析结果,请预测如下几类工人的工资水平:
(**文盲&短期合同&女性&50岁**)的工人
(**高等教育&长期合同&男性&50岁**)的工人
(**初等教育&短期合同&男性&30岁**)的工人
(**初等教育&长期合同&女性&30岁**)的工人要求:分别写出理论表达式,以及数据分析的预测值)
(3)使用全部变量,并提出一个乘法形式的有截距虚拟变量回归模型,用以预测工人工资。要求基础组设置为(文盲&短期合同&女性)的工人组,且要求教育程度edu的虚拟变量(edu_D1,edu_D2,\(\cdots\))与合同类型dpt的虚拟变量(dpt_D1,\(\cdots\))进行乘法交互。
- 请写出该乘法形式的有截距虚拟变量回归模型(PRM)
- 请利用你自己构建的模型,进行eviews分析,得到分析报告。
要求:将报告截图过来,并写出相应的简要报告形式——三行式或四行式)
- 根据回归分析结果,请预测如下几类工人的工资水平:
- (**文盲&短期合同&女性&50岁**)的工人
- (**高等教育&长期合同&男性&50岁**)的工人
- (**初等教育&短期合同&男性&30岁**)的工人
- (**初等教育&长期合同&女性&30岁**)的工人要求:分别写出理论表达式,以及数据分析的预测值)
(4)使用全部变量,对因变量ln(wage)提出一个乘法形式的有截距虚拟变量回归模型,用以预测工人工资。要求基础组设置为(文盲&短期合同&女性)的工人组,且要求性别sex的虚拟变量(sex_D1,\(\cdots\))与合同类型dpt的虚拟变量(dpt_D1,\(\cdots\))进行乘法交互。
- 请写出该乘法形式的有截距虚拟变量回归模型(PRM)
- 请利用你自己构建的模型,进行eviews分析,得到分析报告,并回答如下问题。
- 你认为这些新引入的交互项看上去有显著的交互影响吗?
- 男性工人与女性工人相比,收入存在明显差异吗?请给出你的理由。
- 长期合同的男性工人与长期合同的女性工人,收入存在明显差异吗?请给出你的理由。
- 短期合同的男性工人与长期合同的女性工人,收入存在明显差异吗?请给出你的理由。
要求:将报告截图过来,并写出相应的简要报告形式——三行式或四行式
- 根据回归分析结果,请预测如下几类工人的工资水平:(要求分别写出理论表达式,以及数据分析的预测值)
- (文盲&短期合同&女性&50岁)的工人
- (高等教育&长期合同&男性&50岁)的工人
- (初等教育&短期合同&男性&30岁)的工人
- (初等教育&长期合同&女性&30岁)的工人
- 使用除教育edu变量之外的其他全部变量,对因变量ln(wage)提出一个乘法形式的有截距虚拟变量回归模型,用以预测工人工资。要求基础组设置为(文盲&短期合同&女性)的工人组,且要求教育程度edu的虚拟变量(edu_D1,edu_D2,\(\cdots\))与合同类型dpt的虚拟变量(dpt_D1,\(\cdots\))进行乘法交互。
- 请写出该乘法形式的有截距虚拟变量回归模型(PRM)
- 你认为这些新引入的交互项看上去有显著的交互影响吗?
- 男性工人与女性工人相比,收入存在明显差异吗?请给出你的理由。
- 长期合同的男性工人与长期合同的女性工人,收入存在明显差异吗?请给出你的理由。
- 短期合同的男性工人与长期合同的女性工人,收入存在明显差异吗?请给出你的理由。
- 请利用你自己构建的模型,进行eviews分析,得到分析报告,并回答如下问题。(要求将报告截图过来,并写出相应的简要报告形式——三行式或四行式)
- 你认为这些新引入的交互项看上去有显著的交互影响吗?
- 高等数育的工人与初等教育的工人,收入存在明显差异吗?请给出你的理由。
- [高等教育的长期合同工人]与[高等教育的短期合同工人],收入存在明显差异吗?请给出你的理由。
- [高等教育的短期合同工人]与[初等教育的长期合同工人],收入存在明显差异吗?请给出你的理由。
- 根据回归分析结果,请预测如下几类工人的工资水平:
- (文盲&短期合同&女性&50岁)的工人
- (高等教育&长期合同&男性&50岁)的工人
- (初等教育&短期合同&男性&30岁)的工人
- (初等教育&长期合同&女性&30岁)的工人
要求:分别写出理论表达式,以及数据分析的预测值
一个定性变量如果有m个属性,那么可以用m个虚拟变量完全表达该定性变量,也可以用\((m-1)\)个虚拟变量充分表达该定性变量。↩︎
方差分析模型(Analysis of variance, ANOVA)常用来分析定量化的因变量\(Y\)与定性回归元或虚拟变量之间的统计显著性关系。一般是通过比较不同类别或不同组的均值差,例如采用t检验可以判断两组均值是否有显著的差异↩︎
有时候模型设置中,某个虚拟变量体系(用来表达某个定性变量)的独立项可以完全不出现在方程中(也即没有它们的加法形式),而却可以出现它们与其他变量的交叉项(也即可以出现它们与其他变量的乘法形式)。↩︎
如果理论要求与基础组对比,则理论模型必须设置为有截距回归模型;否则,理论模型需要设置无截距回归模型。↩︎
半对数或对数模型将蕴含着弹性和斜率的经济学含义,在解释虚拟变量回归模型中往往很有现实意义。↩︎
此时我们可以完全不用关心模型是否有截距(意味着是否有对照比较的基础组)↩︎
理论上,基础组如何选择并不会从根本上改变模型的实际经济学意义,只是一旦选定一个基础组,也就意味着确定了一个相互比较的“基础参照系”。↩︎