| 平方和 | 代数公式 | 矩阵公式 | 自由度df | 均方和MSS |
|---|---|---|---|---|
| 总平方和TSS | \(\sum{y_i^2}\) | \(\mathbf{y'y}-n\bar{Y}^2\) | \(df_{TSS}=n-1\) | \(MSS_{TSS}=TSS/df_{TSS}\) |
| 残差平方和RSS | \(\sum{e_i^2}\) | \(\mathbf{yy'-\hat{\beta}'X'y}\) | \(df_{RSS}=n-k\) | \(MSS_{RSS}=RSS/df_{RSS}\) |
| 回归平法和ESS | \(\sum{\hat{y}_i^2}\) | \(\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2\) | \(df_{ESS}=k-1\) | \(MSS_{ESS}=TSS/df_{ESS}\) |
4 多元线性回归
4.1 实验目的及要求
目的:掌握多元线性回归模型的估计、检验。
要求:在老师指导下完成多元线性回归模型的建立、估计、统计检验,得到正确的分析结果;能运用矩阵方法实现前述操作。
4.2 实验原理
当多元线性回归模型在满足线性模型古典假设的前提下,最小二乘估计结果具有无偏性、有效性等性质,在此基础上进一步对估计所得的模型进行经济意义检验及统计检验。
4.2.1 基本模型和重要概念的矩阵表达
对于如下的k变量线性回归模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{4.1}\]
如果样本数为n,则可以将上述PRM模型表达为矩阵形式:
\[ \begin{aligned} \begin{bmatrix} Y_1 \\ Y_2 \\ \cdots \\ Y_n \\ \end{bmatrix} = \begin{bmatrix} 1 & X_{21} & X_{31} & \cdots & X_{k1} \\ 1 & X_{22} & X_{32} & \cdots & X_{k2} \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 1 & X_{2n} & X_{3n} & \cdots & X_{kn} \end{bmatrix} \begin{bmatrix} \beta_1 \\ \beta_2 \\ \vdots \\ \beta_k \\ \end{bmatrix}+ \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \\ \end{bmatrix} \end{aligned} \tag{4.2}\]
进一步地,可以得到精简化的PRM矩阵形式:
\[ \begin{alignedat}{999} \begin{split} \mathbf{y} &= &&\mathbf{X}\mathbf{\beta}&&+&&\mathbf{u}\\ (n \times 1) & &&{(n \times k)} {(k \times 1)}&& &&{(n \times 1)} \end{split} \end{alignedat} \tag{4.3}\]
其中:
向量(默认为列向量)用加粗体的小写字母表达
矩阵用大写粗体字母表达
矩阵或向量的维度需要注意标明
进一步地,我们可以用矩阵方法表达正态经典线性回归模型假设(N-CLRM):
多元回归情形下,自变量\(X\)间无完全共线性。可记为\(\rho(\mathbf{X})=k\),也即矩阵\(\mathbf{X}\)为列满秩
随机干扰项期望为0。可记为\(E(\mathbf{u})=\mathbf{0}\)
随机干扰项同方差且无自相关。可记为\(E(\mathbf{uu'})=\sigma^2\mathbf{I}\)
在正态性假设下,关于随机干扰项的全部假设可以记为\(\mathbf{u} \sim N(\mathbf{0},\sigma^2\mathbf{I})\)
随机干扰项的方差协方差矩阵为:
\[ \begin{aligned} var-cov(\mathbf{u})&=E(\mathbf{uu'})\\ &=E \begin{bmatrix} u_1\\ u_2\\ \vdots \\ u_n \end{bmatrix} \begin{bmatrix} u_1 & u_2& \cdots & u_n \end{bmatrix}\\ &=E \begin{bmatrix} u_1^2 & u_1u_2 &\cdots &u_1u_n\\ u_2u_1 & u_2^2 &\cdots &u_2u_n\\ \vdots & \vdots &\vdots &\vdots \\ u_nu_1 & u_nu_2 &\cdots &u_n^2\\ \end{bmatrix}\\ &= \begin{bmatrix} E(u_1^2) & E(u_1u_2) &\cdots &E(u_1u_n)\\ E(u_2u_1) & E(u_2^2) &\cdots &E(u_2u_n)\\ \vdots & \vdots &\vdots &\vdots \\ E(u_nu_1) &E(u_nu_2) &\cdots &E(u_n^2)\\ \end{bmatrix} \end{aligned} \]
如果满足N-CLRM假设,则随机干扰项的方差协方差矩阵进一步可以写成:
\[ \begin{aligned} var-cov(\mathbf{u})&=E(\mathbf{uu'})\\ &= \begin{bmatrix} \sigma_1^2 & \sigma_{12}^2 &\cdots &\sigma_{1n}^2\\ \sigma_{21}^2 & \sigma_2^2 &\cdots &\sigma_{2n}^2\\ \vdots & \vdots &\vdots &\vdots \\ \sigma_{n1}^2 & \sigma_{n2}^2 &\cdots &\sigma_n^2\\ \end{bmatrix} && \leftarrow (E{(u_i)}=0)\\ &= \begin{bmatrix} \sigma^2 & \sigma_{12}^2 &\cdots &\sigma_{1n}^2\\ \sigma_{21}^2 & \sigma^2 &\cdots &\sigma_{2n}^2\\ \vdots & \vdots &\vdots &\vdots \\ \sigma_{n1}^2 & \sigma_{n2}^2 &\cdots &\sigma^2\\ \end{bmatrix} && \leftarrow (var{(u_i)}=\sigma^2)\\ &= \begin{bmatrix} \sigma^2 & 0 &\cdots &0\\ 0 & \sigma^2 &\cdots &0\\ \vdots & \vdots &\vdots &\vdots \\ 0 & 0 &\cdots &\sigma^2\\ \end{bmatrix} && \leftarrow (cov{(u_i,u_j)}=0,i \neq j)\\ &=\sigma^2 \begin{bmatrix} 1 & 0 &\cdots &0\\ 0 & 1 &\cdots &0\\ \vdots & \vdots &\vdots &\vdots \\ 0 & 0 &\cdots &1\\ \end{bmatrix}\\ &=\sigma^2\mathbf{I} \end{aligned} \]
4.2.2 OLS估计及BLUE性质的矩阵表达
给定如下的样本回归模型(SRM): \[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{4.4}\]
最小二乘方法将求解最小化过程:
\[ \begin{aligned} \begin{split} Q&=\sum{e_i^2}\\ &=\mathbf{e'e}\\ &=\mathbf{(y-X\hat{\beta})'(y-X\hat{\beta})}\\ &=\mathbf{y'y-2\hat{\beta}'X'y+\hat{\beta}'X'X\hat{\beta}} \end{split} \end{aligned} \tag{4.5}\]
进一步可以得到:
\[ \begin{aligned} \frac{\partial Q}{\partial \mathbf{\hat{\beta}}}&=0\\ \frac{\partial(\mathbf{y'y-2\hat{\beta}'X'y+\hat{\beta}'X'X\hat{\beta}})}{\partial \mathbf{\hat{\beta}}}&=0\\ -2\mathbf{X'y}+2\mathbf{X'X\hat{\beta}}&=0\\ -\mathbf{X'y}+\mathbf{X'X\hat{\beta}}&=0\\ \mathbf{X'X\hat{\beta}} &=\mathbf{X'y} \end{aligned} \]
如果矩阵\(\mathbf{X'X}\)的逆矩阵存在,则两边同时左乘\(\mathbf{(X'X)^{-1}}\),得到OLS估计量:
\[ \begin{aligned} \mathbf{\hat{\beta}} &=\mathbf{(X'X)^{-1}X'y} \end{aligned} \tag{4.6}\]
对于回归系数的OLS估计量\(\mathbf{\hat{\beta}}\),进一步讨论其方差和协方差矩阵\(var-cov(\mathbf{\hat{\beta}})\),一般记为:
\[ \begin{aligned} var-cov(\mathbf{\hat{\beta}}) &=E\left( \left(\hat{\beta}-E(\hat{\beta}) \right) \left( \hat{\beta}-E(\hat{\beta}) \right )' \right)\\ &= \begin{bmatrix} var(\hat{\beta_1}) & cov(\hat{\beta_1},\hat{\beta_2}) &\cdots &cov(\hat{\beta_1},\hat{\beta_k})\\ cov(\hat{\beta_2},\hat{\beta_1}) & var(\hat{\beta_2}) &\cdots &cov(\hat{\beta_2},\hat{\beta_k})\\ \vdots & \vdots &\vdots &\vdots \\ cov(\hat{\beta_k},\hat{\beta_1}) & cov(\hat{\beta_k},\hat{\beta_2}) &\cdots &var(\hat{\beta_k})\\ \end{bmatrix} \end{aligned} \]
如果满足N-CLRM假设,则回归系数的OLS估计量\(\mathbf{\hat{\beta}}\)的方差和协方差矩阵\(var-cov(\mathbf{\hat{\beta}})\)可以进一步可以写成:
\[ \begin{aligned} var-cov(\mathbf{\hat{\beta}}) &=\mathbf{E\left( \left(\hat{\beta}-E(\hat{\beta}) \right) \left( \hat{\beta}-E(\hat{\beta}) \right )' \right)}\\ &=\mathbf{E\left( \left(\hat{\beta}-{\beta} \right) \left( \hat{\beta}-\beta \right )' \right)} \\ &=\mathbf{E\left( \left((X'X)^{-1}X'u \right) \left( (X'X)^{-1}X'u \right )' \right)} \\ &=\mathbf{E\left( (X'X)^{-1}X'uu'X(X'X)^{-1} \right)} \\ &= \mathbf{(X'X)^{-1}X'E(uu')X(X'X)^{-1}} \\ &= \mathbf{(X'X)^{-1}X'}\sigma^2\mathbf{IX(X'X)^{-1}} \\ &= \sigma^2\mathbf{(X'X)^{-1}X'X(X'X)^{-1}} \\ &= \sigma^2\mathbf{(X'X)^{-1}} \end{aligned} \tag{4.7}\]
此外,很用以证明OLS方法下,利用样本回归模型 式 4.4 得到的估计量\(\hat{\sigma}^2\),是对总体回归模型 式 4.1 参数\({\sigma}^2\)的无偏估计,也即:
\[ \begin{aligned} \hat{\sigma}^2&=\frac{\sum{e_i^2}}{n-k}=\frac{\mathbf{e'e}}{n-k} \\ E(\hat{\sigma}^2)&=\sigma^2 \end{aligned} \tag{4.8}\]
那么,可以很快得到回归系数的OLS估计量\(\mathbf{\hat{\beta}}\)的样本方差和协方差矩阵\(S^2_{ij}(\mathbf{\hat{\beta}})\)
\[ \begin{aligned} S^2_{ij}(\mathbf{\hat{\beta}}) &= \hat{\sigma}^2\mathbf{(X'X)^{-1}} \\ &= \frac{\mathbf{e'e}}{n-k}\mathbf{(X'X)^{-1}} \\ \end{aligned} \tag{4.9}\]
下面我们将证明高斯-马尔可夫定理(Gauss-Markov Theorem):在正态经典线性回归模型假设(N-CLRM)下,采用普通最小二乘法(OLS),得到的估计量\(\hat{\beta}\),是真实参数\(\beta\)最优的、线性的、无偏估计量(BLUE)。记为:
\[ \begin{aligned} \xrightarrow[\text{N-CLRM}]{\text{OLS}}\mathbf{\hat{\beta}} \xrightarrow[\text{}]{\text{BLUE}} \mathbf{\beta} \end{aligned} \]
证明 (线性性). 因为模型参数的OLS估计为:
\[ \begin{aligned} \mathbf{\hat{\beta}} &=\mathbf{(X'X)^{-1}X'y} \end{aligned} \]
又因为矩阵\(\mathbf{X}\)为列满秩,也即\(\rho(\mathbf{X})=k\),所以\(\mathbf{\hat{\beta}}\)关于\(\mathbf{y}\)是线性的。
证明 (无偏性). 根据模型参数OLS估计,容易得到如下过程:
\[ \begin{aligned} \mathbf{\hat{\beta}} &=\mathbf{(X'X)^{-1}X'y} \\ &=\mathbf{(X'X)^{-1}X'(X\beta+u)} \\ &=\mathbf{(X'X)^{-1}X'X\beta+(X'X)^{-1}X'u} \\ &=\mathbf{\beta+(X'X)^{-1}X'u} \\ \end{aligned} \]
进一步可证明
\[ \begin{aligned} E(\mathbf{\hat{\beta}}) &=E(\mathbf{\beta+(X'X)^{-1}X'u}) \\ &=\mathbf{E(\beta)+(X'X)^{-1}X'E(u)} \\ &=\mathbf{\beta} \end{aligned} \]
因此,\(\mathbf{\hat{\beta}}\)是参数\(\mathbf{\beta}\)的无偏估计量得证。
证明 (方差最小/最优性). 假设存在用其他方法估计的线性无偏估计量\(\mathbf{\beta^{\ast}}\),则要求\(\mathbf{C}\)满足如下条件:
\[ \begin{aligned} \mathbf{CX} &=0 \end{aligned} \]
从而保证如下式子成立:
\[ \begin{aligned} \mathbf{\beta^{\ast}} &=\mathbf{\left((X'X)^{-1}X'+C \right)y} \\ &=\mathbf{\left((X'X)^{-1}X'+C \right)(X\beta+u)} \\ &=\mathbf{\beta+CX\beta+(X'X)^{-1}X'u+Cu} \\ &=\mathbf{\beta+(X'X)^{-1}X'u+Cu} \\ \end{aligned} \]
进一步得到:
\[ \begin{aligned} \mathbf{\beta^{\ast}-\beta} &=\mathbf{(X'X)^{-1}X'u+Cu} \end{aligned} \]
根据方差定义,有:
\[ \begin{aligned} var-cov(\mathbf{\beta^{\ast}}) &=\mathbf{E\left( (\beta^{\ast}-\beta)(\beta^{\ast}-\beta)'\right)}\\ &=\mathbf{E\left( \left((X'X)^{-1}X'u+Cu\right)\left((X'X)^{-1}X'u+Cu\right)'\right)}\\ &=\mathbf{\sigma^2(X'X)^{-1}+\sigma^2CC'}\\ &=var-cov(\mathbf{\hat{\beta}})+\mathbf{\sigma^2CC'} \end{aligned} \]
其中,我们可以证明\(\mathbf{\sigma^2CC'}\)是半正定矩阵,矩阵对角线元素\(\geq 0\),因此有:
\[ \begin{aligned} var-cov(\mathbf{\beta^{\ast}}) & \geq var-cov(\mathbf{\hat{\beta}}) \end{aligned} \]
从而表明N-CLRM假设下,OLS方法估计得到的\(\mathbf{\hat{\beta}}\),方差最小。
4.2.3 平方和分解与拟合优度的矩阵表达
对于多元回归模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)}\\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)}\\ \hat{Y}_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki} && \text{(SRF)} \end{aligned} \]
通过对\(Y_i\)的变异及其来源的分解,可以得到:
\[ \begin{aligned} (Y_i-\bar{Y_i}) &= (\hat{Y_i}-\bar{Y_i}) +(Y_i-\bar{Y_i}) \end{aligned} \tag{4.10}\]
\[ \begin{aligned} y_i &=\hat{y_i}+ e_i \end{aligned} \tag{4.11}\]
\[ \begin{aligned} \sum{y_i^2} &= \sum{\hat{y_i}^2} +\sum{e_i^2} \end{aligned} \tag{4.12}\]
\[ \begin{aligned} TSS&=ESS+RSS \end{aligned} \tag{4.13}\]
其中TSS表示总离差平方和,ESS表示回归平法和,RSS表示残差平方和。它们分别可以用矩阵表达为:
\[ \begin{aligned} TSS&=\mathbf{y'y}-n\bar{Y}^2 \end{aligned} \tag{4.14}\]
\[ \begin{aligned} RSS&=\mathbf{ee'}=\mathbf{yy'-\hat{\beta}'X'y} \end{aligned} \tag{4.15}\]
\[ \begin{aligned} ESS&=\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2 \end{aligned} \tag{4.16}\]
进一步地,可以得到方差分析表(ANOVA):
根据拟合优度的定义 定义 2.10 ,判定系数\(R^2\)的矩阵计算公式为:
\[ \begin{aligned} R^2&=\frac{ESS}{TSS}\\ &=\frac{\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2}{\mathbf{y'y}-n\bar{Y}^2} \end{aligned} \tag{4.17}\]
4.2.4 回归系数显著性检验(t检验)的矩阵方法实现
根据回归系数显著性检验的定义 定义 2.11 ,利用矩阵方法实现t检验的过程如下:
对于多元回归模型
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i \end{aligned} \tag{4.18}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\beta}+\mathbf{u} && \text{(PRM)} \end{aligned} \tag{4.19}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\hat{\beta}}+\mathbf{e} && \text{(SRM)} \end{aligned} \tag{4.20}\]
在N-CLRM假设下,采用OLS估计方法,可以证明:
\[ \begin{aligned} \mathbf{u}&\sim N(\mathbf{0},\sigma^2\mathbf{I}) \end{aligned} \tag{4.21}\]
\[ \begin{aligned} \mathbf{\hat{\beta}} &\sim N\left(\mathbf{\beta},\sigma^2\mathbf{X'X}^{-1} \right) \end{aligned} \tag{4.22}\]
从而可以构造t统计量
\[ \begin{aligned} \mathbf{t_{\hat{\beta}}}&=\mathbf{\frac{\hat{\beta}-\beta}{S_{\hat{\beta}}}} \sim \mathbf{t(n-k)} \end{aligned} \tag{4.23}\]
对于总体回归模型 式 4.18 的任一参数\(\mathbf{\beta_j}, j \in (1,2,\cdots,k)\)提出假设:
\[ \begin{aligned} \mathbf{\beta_j}: \begin{cases} H_0:\mathbf{\beta_j}=0\\ H_1:\mathbf{\beta_j}\neq 0 \end{cases} \end{aligned} \]
根据原假设\(H_0\),可以得到:
\[\begin{aligned} \mathbf{t_{\hat{\beta}}^{\ast}}&=\frac{\mathbf{\hat{\beta}}}{\mathbf{\sqrt{S^2_{ij}(\hat{\beta}_{kk})}}} \end{aligned} \tag{4.24}\]
其中\(\mathbf{S^2_{ij}(\hat{\beta_{kk}})}\)表示,由\(\mathbf{\hat{\beta}}\)的样本方差和协方差矩阵\(S^2_{ij}(\mathbf{\hat{\beta}})\)的对角线元素组成的列向量,即
\[S^2_{ij}(\hat{\beta}_{kk})=[s^2_{\hat{\beta}_1},s^2_{\hat{\beta}_2},\cdots,s^2_{\hat{\beta}_k}]'\]
若给定显著性水平\(\alpha\)和自由度\((n-k)\),很快可以得到t分布的查表t值,也即\(t_{(1-\alpha/2)}(n-k)\)。然后比较样本t统计量\(\mathbf{t_{\hat{\beta}}^{\ast}}\)与理论t分布查的表t值\((t_{(1-\alpha/2)}(n-2))\)的关系。根据如下法则做出参数\(\beta_2\)的显著性检验结论:
- 如果列向量\(\mathbf{t_{\hat{\beta}}^{\ast}}\)的第\(k\)个元素\(t_{\hat{\beta_k}}^{\ast}>t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_k\)的t检验在\(\alpha\)水平下是显著的,也即显著地拒绝\(H_0:\beta_k=0\),从而接受\(H_1:\beta_k\neq 0\)。
- 如果列向量\(\mathbf{t_{\hat{\beta}}^{\ast}}\)的第\(k\)个元素\(t_{\hat{\beta_k}}^{\ast} \leq t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_k\)的t检验在\(\alpha\)水平下是不显著的,也即不能显著地拒绝\(H_0:\beta_k=0\),从而只能暂时接受\(H_0:\beta_2=0\)。
4.2.4.1 模型整体显著性检验(F检验)的矩阵方法实现
对于多元回归模型
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(U-PRM)} \end{aligned} \tag{4.25}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta_3}X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(U-SRM)} \end{aligned} \tag{4.26}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\beta}+\mathbf{u} && \text{(PRM)} \end{aligned} \tag{4.27}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\hat{\beta}}+\mathbf{e} && \text{(SRM)} \end{aligned} \tag{4.28}\]
我们称总体回归模型 式 4.25 和对应的样本回归模型 式 4.26 为为无约束模型(unrestricted model)。
对于总体回归模型 式 4.25 的斜率参数\(\mathbf{\beta_j}, j \in (2,\cdots,k)\)提出如下联合假设(joint hypothesis):
\[ \begin{aligned} \mathbf{\beta_j}: \begin{cases} H_0:\beta_2=\beta_3=\cdots=\beta_k=0\\ H_1:\beta_j \text{ not all }0, \text{ for } j \in (2,\cdots,k) \end{cases} \end{aligned} \]
在原假设\(H_0:\beta_2=\beta_3=\cdots=\beta_k=0\)下,我们可以得到如下模型:
\[ \begin{aligned} Y_i&=\beta_1+u_i && \text{(R-PRM)} \end{aligned} \tag{4.29}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+e_i && \text{(R-SRM)} \end{aligned} \tag{4.30}\]
此时,我们称总体回归模型 式 4.29 和对应的样本回归模型 式 4.30 为受约束模型(restricted model)。
在备择假设\(H_1:\beta_j\)不全为0,\(j \in (2,\cdots,k)\)下,我们可以得到该假设下的一种特殊回归模型1(如\(\beta_j \neq 0, j \in (2,\cdots,k)\)),也即无约束总体回归模型 式 4.25 和无约束样本回归模型 式 4.26 。
定义 4.1 (受约束模型) 一般也称为参数约束回归模型(restricted model),是指总体参数满足某种约束条件的一类回归模型。
定义 4.2 (无约束模型) 一般也称为参数无约束回归模型(unrestricted model),是指总体参数没有被指定满足某种约束条件的一类回归模型。
根据回归系数显著性检验的定义,利用矩阵方法实现F检验的过程如下:
在N-CLRM假设下,采用OLS估计方法,容易证明:
对于无约束总体回归模型 式 4.25 有
\[ \begin{aligned} \begin{split} u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&\sim i.i.d \ N(\beta_1+\beta_2X_i+\cdots+\beta_kX_i,\sigma^2)\\ RSS_U&=\sum{(Y_i-\hat{Y_i})^2} \sim \chi^2(n-k) \\ \end{split} \end{aligned} \tag{4.31}\]
对于受约束总体回归模型 式 4.29 有
\[ \begin{aligned} \begin{split} u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&\sim i.i.d \ N(\beta_1,\sigma^2)\\ RSS_R&=\sum{(Y_i-\hat{Y_i})^2} \sim \chi^2(n-1) \end{split} \end{aligned} \tag{4.32}\]
然后我们可以构造得到一个F统计量:
\[ \begin{aligned} F^{\ast}&=\frac{(RSS_R-RSS_U)/(k-1)}{RSS_U/(n-k)} \\ &=\frac{ESS_U/df_{ESS_U}}{RSS_U/df_{RSS_U}} \\ &\sim F(df_{ESS_U},df_{RSS_U}) \end{aligned} \tag{4.33}\]
若给定显著性水平\(\alpha\)和样本数\((n)\),很快可以得到F分布的查表F值,也即\(F_{(1-\alpha)}(k-1,n-k)\),然后比较其与样本F统计量\(F^{\ast}\)的关系。
根据如下法则做出总体回归模型整体显著性检验结论:
如果\(F^{\ast}>F_{(1-\alpha)}(k-1,n-k)\),则表明总体回归模型的F检验在\(\alpha\)水平下是显著的,也即显著地拒绝\(H_0:\beta_2=\beta_3=\cdots=\beta_k=0\),从而接受\(H_1:\beta_j\)不全为0,\(j \in (2,\cdots,k)\),认为模型 式 4.25 整体统计上是有意义的!
如果\(F^{\ast} \leq F_{(1-\alpha)}(k-1,n-k)\),则表明总体回归模型的F检验在\(\alpha\)水平下是不显著的,也即不能显著地拒绝\(H_0:\beta_2=\beta_3=\cdots=\beta_k=0\),从而只能暂时接受\(H_0:\beta_2=0\),认为模型 式 4.25 整体在统计上是无意义的!
具体第,计算\(F^{\ast}\)的矩阵公式为
\[ \begin{aligned} F^{\ast}&=\frac{ESS_U/df_{ESS_U}}{RSS_U/df_{RSS_U}} =\frac{\left(\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2 \right)/{(k-1)}}{\left(\mathbf{yy'-\hat{\beta}'X'y}\right)/{(n-k)}} \end{aligned} \]
此外,我们还可以通过拟合优度\(R^2\),计算得到\(F^{\ast}\)
\[ \begin{aligned} F^{\ast}&=\frac{ESS_U/df_{ESS_U}}{RSS_U/df_{RSS_U}} =\frac{R^2_U/{(k-1)}}{\left(1-R^2_U\right)/{(n-k)}} \end{aligned} \tag{4.34}\]
4.2.5 样本外预测的矩阵方法实现
根据一元线性回归样本外预测(节@ref(out-sample-forecast))的知识内容,下面将用矩阵方法实现样本外均值预测\(\mathbf{E(Y_0|X_0)}\)和样本外个值预测\(\mathbf{(Y_0|X_0)}\)。其中,给定样本外数据\(\mathbf{X_0}=[1,X_{20},X_{30},\cdots,X_{k0}]'\)(列向量)。
对于多元回归模型
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i \\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta_3}X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i \\ \mathbf{y} &= \mathbf{X}\mathbf{\beta}+\mathbf{u} \\ \mathbf{y} &= \mathbf{X}\mathbf{\hat{\beta}}+\mathbf{e} \\ \mathbf{\hat{y}} &= \mathbf{X}\mathbf{\hat{\beta}} \end{aligned} \tag{4.35}\]
对于样本外均值预测\(\mathbf{E(Y_0|X_0)}\),矩阵实现步骤如下:
\[ \begin{aligned} E(\hat{Y}_0)&=E\mathbf{(X_0\hat{\beta})}=\mathbf{X_0\beta}=E\mathbf{(Y_0)}\\ var(\hat{Y}_0)&=E\mathbf{(X_0\hat{\beta}-X_0\beta)}^2\\ &=E\mathbf{\left( X_0(\hat{\beta}-\beta)(\hat{\beta}-\beta)'X_0' \right)}\\ &=E\mathbf{X_0\left( (\hat{\beta}-\beta)(\hat{\beta}-\beta)' \right)X_0'}\\ &=\sigma^2\mathbf{X_0\left( X'X \right)^{-1}X_0'}\\ \end{aligned} \]
\[ \begin{aligned} S^2(\hat{Y}_0)&=\hat{\sigma}^2\mathbf{X_0(X'X)^{-1}X_0'} \end{aligned} \]
因此\(\mathbf{\hat{Y}_0}\)服从如下正态分布:
\[ \begin{aligned} \hat{Y}_0& \sim N(\mu_{\hat{Y}_0},\sigma^2_{\hat{Y}_0})\\ \hat{Y}_0& \sim N\left(E(Y_0|X_0), \sigma^2\mathbf{X_0(X'X)^{-1}X_0'}\right) \end{aligned} \tag{4.36}\]
因此可以构造t统计量:
\[ \begin{aligned} t_{\hat{Y}_0}& =\frac{\hat{Y}_0-E(Y|X_0)}{S_{\hat{Y}_0}} &\sim t(n-k) \end{aligned} \tag{4.37}\]
其中:
\[ \begin{aligned} \mathbf{S_{\hat{Y}_0}} &=\sqrt{\hat{\sigma}^2X_0(X'X)^{-1}X_0'} \end{aligned} \tag{4.38}\]
\[ \begin{aligned} \hat{\sigma}^2&=\frac{\mathbf{ee'}}{(n-k)} \end{aligned} \tag{4.39}\]
给定显著性水平\(\alpha\)的情况下,可以查表得到理论t值\(t_{1-\alpha/2}(n-k)\),从而可以计算得到均值预测的置信区间:
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \leq E(Y|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \end{aligned} \tag{4.40}\]
对于多元线性回归模型 式 4.35 ,样本外个值预测\(\mathbf{(Y_0|X_0)}\)的矩阵实现步骤如下:
因为有
\[ \begin{aligned} e_0&=Y_0-\hat{Y}_0 \end{aligned} \tag{4.41}\]
所以\(e_0\)的期望为:
\[ \begin{aligned} E(e_0)&=E(Y_0-\hat{Y}_0)\\ &=E(\mathbf{X_0\beta}+u_0-\mathbf{X_0\hat{\beta}})\\ &=E\left(u_0-\mathbf{X_0 (\hat{\beta}- \beta)} \right)\\ &=E\left(u_0-\mathbf{X_0 (X'X)^{-1}X'u} \right)\\ &=0 \end{aligned} \]
同时,\(e_0\)的方差为:
\[ \begin{aligned} var(e_0)&=E(Y_0-\hat{Y}_0)^2\\ &=E(e_0^2)\\ &=E\left(u_0-\mathbf{X_0 (X'X)^{-1}X'u} \right)^2\\ &=\sigma^2\left( 1+ \mathbf{X_0(X'X)^{-1}X_0'}\right) \end{aligned} \]
进一步地,\(e_0\)服从如下正态分布:
\[ \begin{aligned} e_0& \sim N(\mu_{e_0},\sigma^2_{e_0})\\ e_0& \sim N\left(0, \sigma^2\left(1+\mathbf{X_0(X'X)^{-1}X_0'}\right)\right) \end{aligned} \tag{4.42}\]
因此可以构造t统计量:
\[ \begin{aligned} t_{e_0}& =\frac{\hat{Y}_0-Y_0}{S_{e_0}} \sim t(n-k) \end{aligned} \tag{4.43}\]
其中:
\[ \begin{aligned} S_{Y_0-\hat{Y}_0}=S_{e_0} &=\sqrt{\hat{\sigma}^2 \left( 1+X_0(X'X)^{-1}X_0' \right) } \end{aligned} \tag{4.44}\]
\[ \begin{aligned} \hat{\sigma}^2&=\frac{\mathbf{ee'}}{(n-k)} \end{aligned} \tag{4.45}\]
给定显著性水平\(\alpha\)的情况下,可以查表得到理论t值\(t_{1-\alpha/2}(n-k)\),从而可以计算得到均值预测的置信区间:
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0} \leq (Y_0|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0} \end{aligned} \tag{4.46}\]
4.3 实验内容
在Eviews中运用矩阵方法,计算如下步骤:
计算直线回归方程的回归系数向量(\(\mathbf{\hat{\beta}}\)),并写出样本回归模型(\(SRM\))。
计算回归误差方差(\(\hat{\sigma}^2\))和回归误差标准差(\(\hat{\sigma}\))。
计算回归系数的样本方差协方差矩阵(\(\widehat{var}\_\widehat{cov}\))。
得出回归系数的样本标准差向量(\(S_{\hat{\beta}}\))。
进行平方和分解,计算\(TSS\)、\(ESS\)和\(RSS\)。
计算判定系数\(R^2\),调整判定系数(\(\hat{R}^2\))。
计算样本t统计量(\(\mathbf{t^{\ast}_{\beta}}\)),并进行t假设检验。
对回归方程的进行样本外均值预测\(E(Y\mid X=X_0)\)
对回归方程的进行样本外个值预测\((Y_0\mid X=X_0)\)
4.4 实验准备
4.4.1 实验软件
本次实验需要提前准备好如下软件:
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或 360极速浏览器9.5版本及以上
4.4.2 实验材料
玫瑰的需求: 表 4.1 给出美国底特律市区对玫瑰的季度需求数据。
| YEAR | Q | X2 | X3 | X4 | X5 |
|---|---|---|---|---|---|
| 1971 | 11484 | 2.3 | 3.5 | 158 | 1 |
| 1971 | 9348 | 2.5 | 2.8 | 173 | 2 |
| 1972 | 8429 | 3.1 | 4.1 | 165 | 3 |
| 1972 | 10079 | 2.9 | 3.6 | 173 | 4 |
| 1972 | 9240 | 2.7 | 3.2 | 178 | 5 |
| 1972 | 8862 | 2.8 | 3.7 | 199 | 6 |
| 1973 | 6216 | 3.6 | 3.8 | 186 | 7 |
| 1973 | 8253 | 3.2 | 3.5 | 189 | 8 |
| 1973 | 8038 | 2.6 | 3.1 | 180 | 9 |
| 1973 | 7476 | 2.9 | 3.2 | 183 | 10 |
| 1974 | 5911 | 3.8 | 3.6 | 182 | 11 |
| 1974 | 7950 | 3.6 | 3.6 | 185 | 12 |
| 1974 | 6134 | 2.8 | 2.9 | 184 | 13 |
| 1974 | 5868 | 3.0 | 3.1 | 188 | 14 |
| 1975 | 3160 | 4.2 | 3.6 | 176 | 15 |
| 1975 | 5872 | 3.7 | 3.5 | 188 | 16 |
变量说明见 表 4.2 :
| variable | label |
|---|---|
| YEAR | 年份.季度 |
| Q | 玫瑰销售量(打) |
| X2 | 玫瑰批发价格(\(/打) | |X3 |石竹的平均批发价格(\)/打) |
| X4 | 家庭可支配收入($/周) |
| X5 | 时间趋势 |
请考虑如下两个需求函数:
\[ \begin{aligned} Y_t&=\hat{\alpha}_1+\hat{\alpha}_2X_{2t}+\hat{\alpha}_3X_{3t}+ \hat{\alpha}_4X_{4t}+\hat{\alpha}_5X_{5t}+e_{1t} \end{aligned} \tag{4.47}\]
\[ \begin{aligned} ln(Y_t)&=\hat{\beta}_1+\hat{\beta}_2ln(X_{2t})+\hat{\beta}_3ln(X_{3t})+\hat{\beta}_4ln(X_{4t})+\hat{\beta}_5X_{5t}+e_{2t} \end{aligned} \tag{4.48}\]
4.4.3 实验规则
本次实验将利用矩阵方法进行计算,我们对计算过程中的Eviews对象做如下命名约定:
| name_chn | cat_eng | math | name_eviews |
|---|---|---|---|
| 序列Y | series | \(Y\) | q |
| 组X | group | \(X\) | xg |
| 矩阵\(\mathbf{y}\) | matrix | \(\mathbf{y}\) | y |
| 矩阵\(\mathbf{X}\) | matrix | \(\mathbf{X}\) | x |
| 矩阵\(\mathbf{(X'X)}\) | matrix | \(\mathbf{(X'X)}\) | xtx |
| 矩阵\(\mathbf{{(X'X)}^{-1}}\) | matrix | \(\mathbf{{(X'X)}^{-1}}\) | xtxi |
| 矩阵\(\mathbf{X'y}\) | matrix | \(\mathbf{X'y}\) | xty |
| 矩阵\(\mathbf{\hat{\beta}}\) | matrix | \(\mathbf{\hat{\beta}}\) | beta_hat |
| 回归误差方差 | scalar | \(\hat{\sigma}^2\) | sigma2_hat |
| 回归误差标准差 | scalar | \(\hat{\sigma}\) | sigma_hat |
| \(\hat{\beta}\)样本方差协方差矩阵 | matrix | \(\mathrm{var}-\mathrm{cov}{(\mathbf{\hat{\beta}})}\) | s2_varcov_beta_hat |
| \(\hat{\beta}\)样本方差矩阵 | matrix | \(\mathbf{S_{\hat{\beta}}^2}\) | s2_beta_hat |
| \(\hat{\beta}\)样本标准差矩阵 | matrix | \(\mathbf{S_{\hat{\beta}}}\) | s_beta_hat |
| 均值修正值 | scalar | \(n\bar{Y}^2\) | mean_adj |
| 总平方和 | scalar | \(TSS\) | tss |
| 残差平方和 | scalar | \(RSS\) | rss |
| 回归平方和 | scalar | \(ESS\) | ess |
| 判定系数 | scalar | \(R^2\) | r2 |
| 调整判定系数 | scalar | \(\bar{R}^2\) | r2_adj |
| 矩阵t统计量 | matrix | \(\mathbf{t}^{\ast}_{\mathbf{\beta}}\) | t_str_beta_hat |
| 理论t值 | scalar | \(t_{1-\alpha/2}(n-k)\) | t_value |
| F统计量 | scalar | \(F^{\ast}\) | f_str |
| 理论F值 | scalar | \(F_{1-\alpha}(k-1,n-k)\) | f_value |
| 样本外X0 | matrix | \(X_0\) | x0 |
| 样本外回归值\(\hat{Y}_0\) | scalar | \(\hat{Y}_0\) | y0_hat |
| 均值预测 | scalar | \(E(Y\mid X=X_0)\) | forecast_exp |
| \(\hat{Y}_0\)的样本标准差 | scalar | \(S_{\hat{Y}_0}\) | s_y0h |
| 均值区间预测的左界 | scalar | \(E(Y\mid X=X_0)_L\) | y_exp_lft |
| 均值区间预测的右界 | scalar | \(E(Y\mid X=X_0)_R\) | y_exp_rht |
| 个值预测 | scalar | \((Y_0\mid X=X_0)\) | forecast_ind |
| \((\hat{Y}_0-{Y_0})\)的样本标准差 | scalar | \(S_{(\hat{Y}_0-Y_0)}\) | s_y0h_mns_y0 |
| 个值区间预测的左界 | scalar | \((Y_0\mid X=X_0)_L\) | y_ind_lft |
| 个值区间预测的右界 | scalar | \((Y_0\mid X=X_0)_R\) | y_ind_rht |
4.5 主要实验步骤——以对数模型为例 式 4.58
4.5.1 新建工作文件并导入数据
Eviews操作目标:构建工作文件,成功导入数据
Eviews操作思路:利用EViews代码创建工作文件并导入数据。
在命令视窗中依次输入并运行如下EViews代码:
'创建工作文件(工作文件名=rose,子页命名=sale),无结构无日期,样本数为16
wfcreate(wf=rose,page=sale) u 16
'导入外部数据,路径为d:\github\books\data\Lab3-family-spends.xlsx
import d:\github\books\data\lab4-rose-demand-origin.xlsx在工作文件视窗下,可以看到创建的工作文件和导入的数据,可以双击查看(见 图 4.1 ):
上述过程也可以通过菜单操作实现:
(1)创建工作文件:
(a)EViews主窗口上依次点击\(\Rightarrow\) File\(\Rightarrow\) New\(\Rightarrow\) Workfile
(b)进行workfile create引导设置:
workfile structure type:
unstructured/undatededata range:
workfile names(optional):
WF:
rosePage:
sale_log(建议命名sale_log)
(2)导入外部数据:
- EViews主窗口上依次点击\(\Rightarrow\)
File\(\Rightarrow\)Import\(\Rightarrow\)Import from file ...
4.5.2 进行对数模型的Eviews回归分析
Eviews操作目标:得到回归方程,查看回归结果
Eviews操作思路:构建回归方程对象。回归模型为:
\[ \begin{aligned} \begin{split} log(Q)_i=&+\beta_{1}+\beta_{2}log(X2)_i\\&+\beta_{3}log(X3)_i+\beta_{4}log(X4)_i\\&+\beta_{5}X5_i+u_i \end{split} \end{aligned} \tag{4.49}\]
在命令视窗中依次输入并运行如下EViews代码:
'生成线性回归模型的方程对象
equation eq_log.ls log(q) c log(x2) log(x3) log(x4) x5 '对数模型在工作文件视窗下,可以看到如下新生成的方程对象,可以双击查看 eq_log(见 图 4.2 ):
eq_log(见 图 4.2 ):
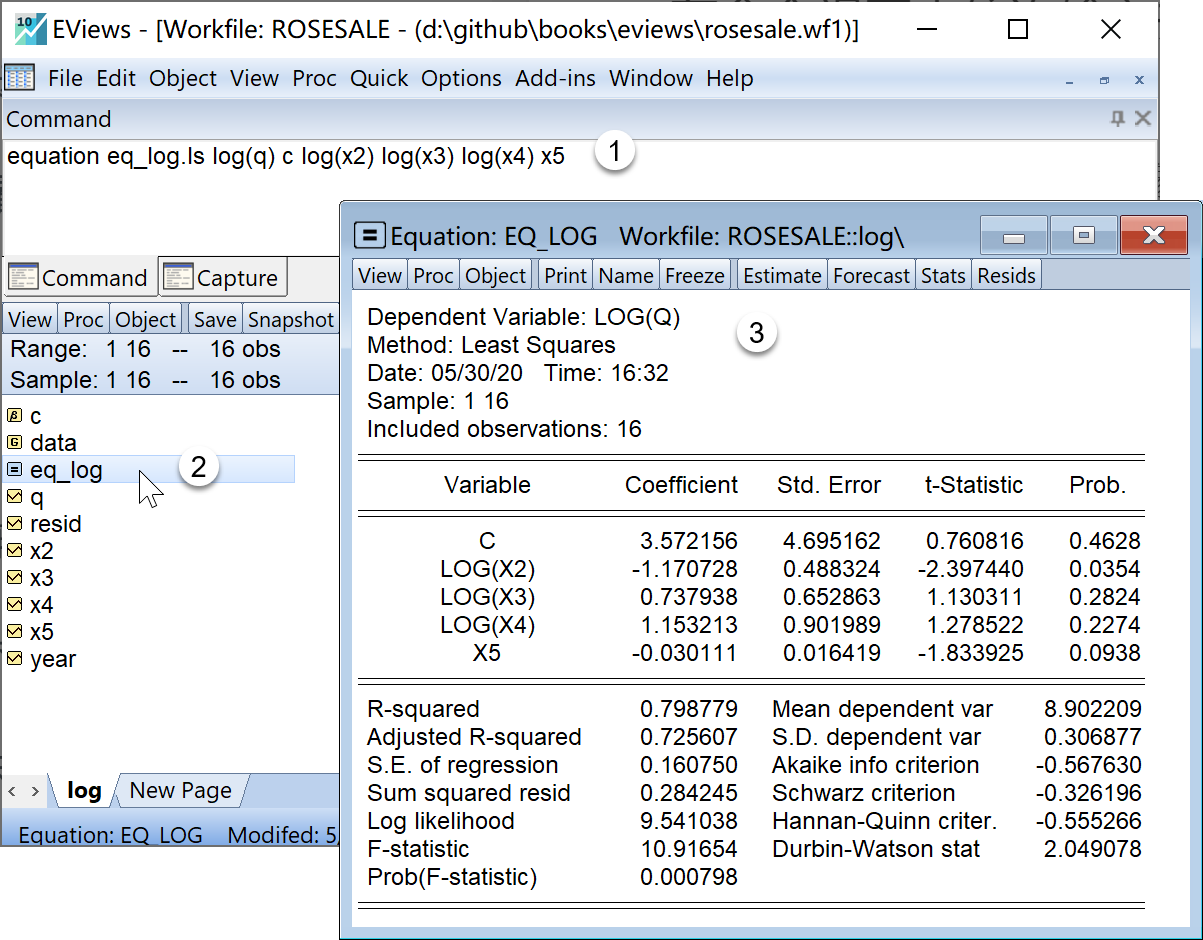
上述过程也可以通过菜单操作实现:
(1)进入方程估计的引导界面。
- EViews主窗口上依次点击点
Quick\(\Rightarrow\)Estimation Equation
(2)完成方程估计的引导设置。
设置方程。
Equation Estimation\(\Rightarrow\)Specification\(\Rightarrow\)Equation specification中依次输入变量log(q) c log(x2) log(x3) log(x4) x5(注意变量之间的空格,以及截距c)选择估计方程。
Estimation settings中的Method下拉框 \(\Rightarrow\) 下拉选择LS - Least Squares (NLS and ARMA)完成设置,点击
OK
(3)命名并保存回归方程。
- 在未命名的方程对象
 UNTITLED视窗下,点击菜单栏
UNTITLED视窗下,点击菜单栏Name\(\Rightarrow\) 输入命名eq_log(建议命名) \(\Rightarrow\) 完成命名,点击Ok
回归方程结果见 图 4.3 :
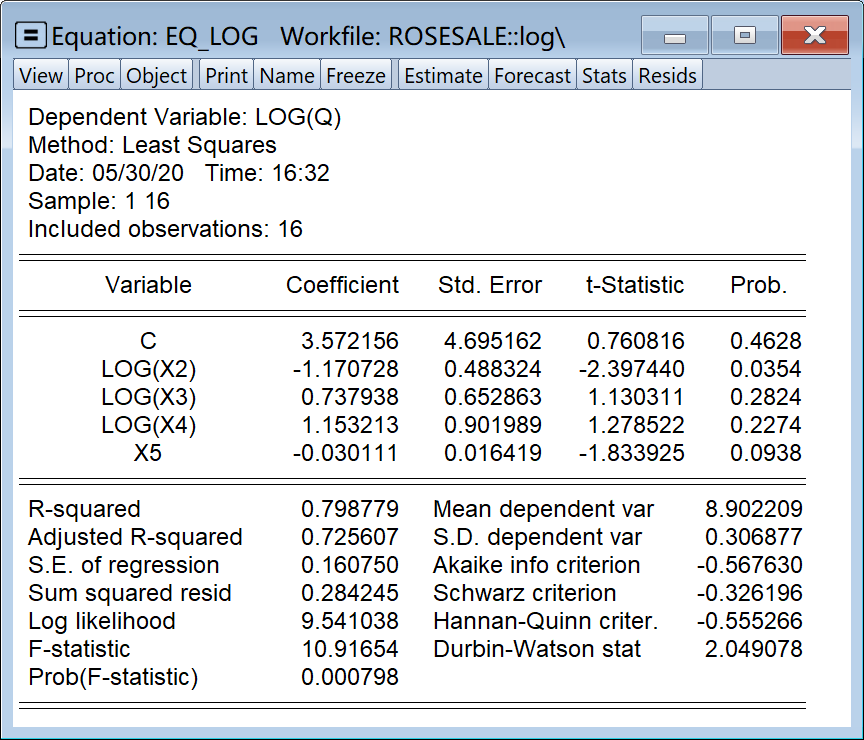
玫瑰销售的对数模型的简要回归报告如下:
\[ \begin{aligned} \begin{split} \widehat{log(Q)}_i=&+\hat{\beta}_{1}+\hat{\beta}_{2}log(X2)_i\\&+\hat{\beta}_{3}log(X3)_i+\hat{\beta}_{4}log(X4)_i\\&+\hat{\beta}_{5}X5_i \end{split} \end{aligned} \tag{4.50}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{log(Q)}=&&+3.57&&-1.17ln(X2)_i&&+0.74ln(X3)_i\\ &(s)&&(4.6952)&&(0.4883)&&(0.6529)\\ &(t)&&(+0.76)&&(-2.40)&&(+1.13)\\ &(cont.)&&+1.15ln(X4)_i&&-0.03X5_i &&\\ &(s)&&(0.9020)&&(0.0164) &&\\ &(t)&&(+1.28)&&(-1.83) &&\\ &(over)&&n=16&&\hat{\sigma}=0.1607 &&\\ &(fit)&&R^2=0.7988&&\bar{R}^2=0.7256 &&\\ &(Ftest)&&F^*=10.92&&p=0.0008 && \end{split} \end{alignedat} \tag{4.51}\]
4.5.3 构建几个重要变量对象
Eviews操作目标:构造几个重要EViews对象,便于后面分析使用
Eviews操作思路:样本数n,构造常数序列,构造组对象
在命令视窗中依次输入并运行如下EViews代码:
'构造几个重要变量对象
scalar n=@obs(x2) '样本数n(标量)
series cst=1 '新建元素全为1的序列对象(用于构造矩阵X)
group xg cst log(x2) log(x3) log(x4) x5 '构造为group,便于观察在工作文件视窗下,可以看到如下新生成的对象,可以双击查看(见 图 4.4 ):
样本数n的标量对象
 n
n元素全为1的常数序列对象
 cst
cst组对象xg
 xg
xg
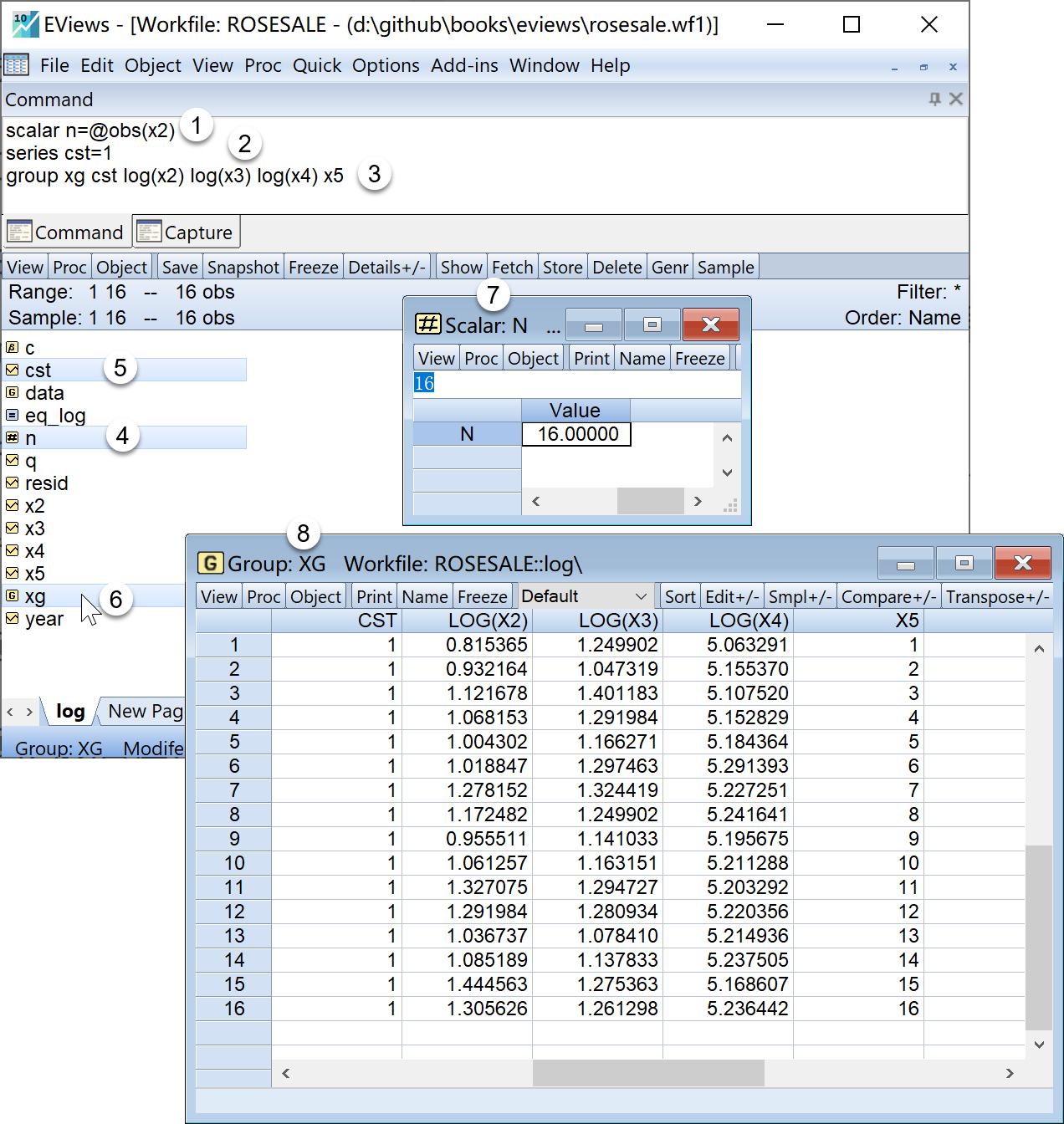
4.5.4 构造X矩阵和Y矩阵对象
Eviews操作目标:构造X矩阵和Y矩阵对象,便于后面分析使用
Eviews操作思路:把组对象转换成X矩阵;利用log()函数构造Y矩阵
在命令视窗中依次输入并运行如下EViews代码:
'构造X矩阵和Y矩阵对象。
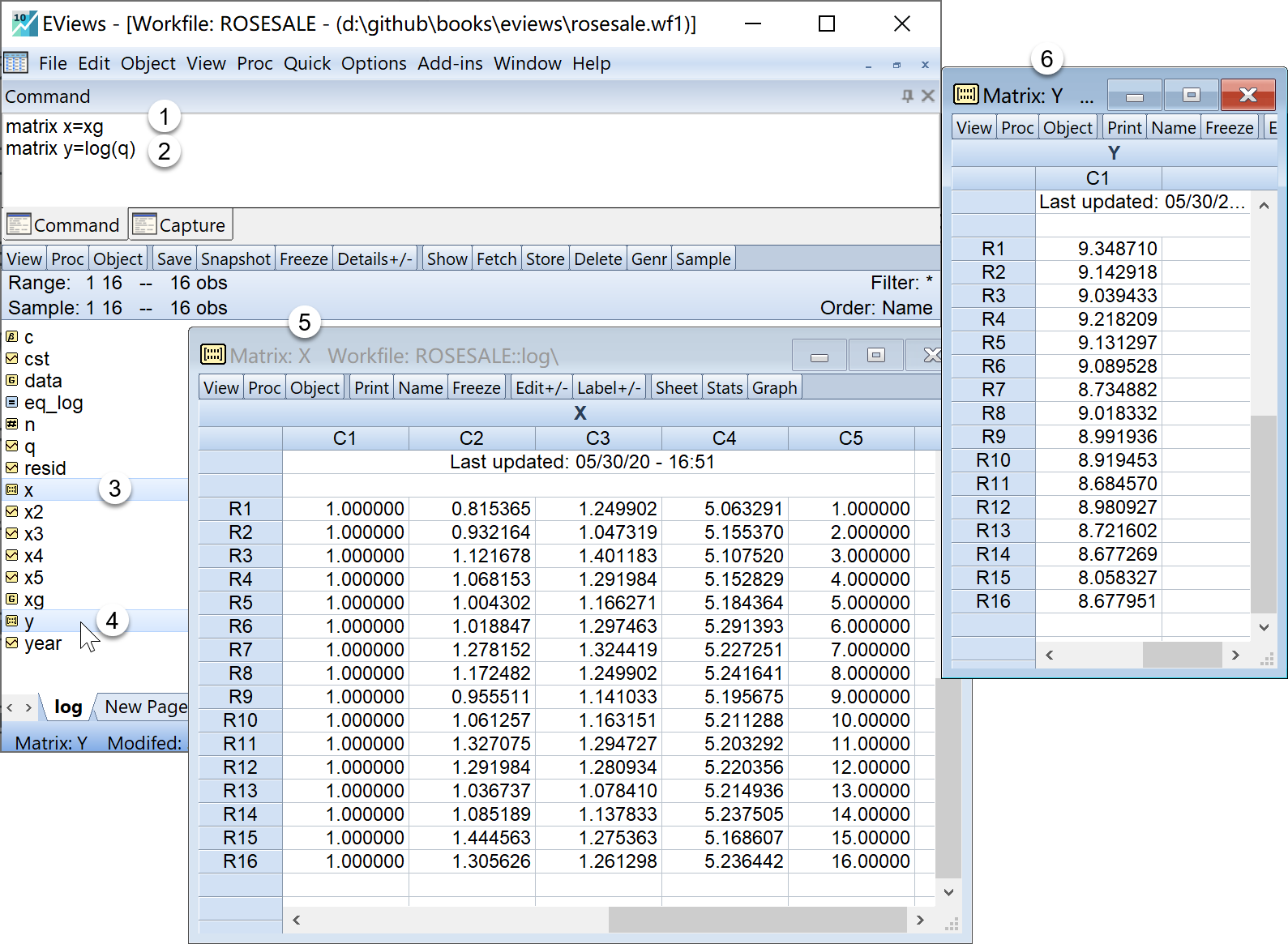
matrix x=xg '转换为X矩阵对象
matrix y=log(q) '构造Y矩阵对象在工作文件视窗下,可以看到如下新生成的对象,可以双击查看(见 图 4.5 ):
矩阵\(\mathbf{X}\)的矩阵对象
 x
x矩阵\(\mathbf{y}\)的矩阵对象
 y
y
4.5.5 计算回归方程的回归系数向量
Eviews操作目标:计算得到回归方程的回归系数向量(包含5个系数估计值)。
Eviews操作思路:利用理论公式,先计算得到几个重要矩阵(后面分析还要用到),最后利用矩阵运算计算得出回归系数向量。理论计算公式为:
\[ \begin{aligned} \mathbf{\hat{\beta}}=\mathbf{{(X'X)}^{-1}X'y} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'计算回归方程的回归系数向量
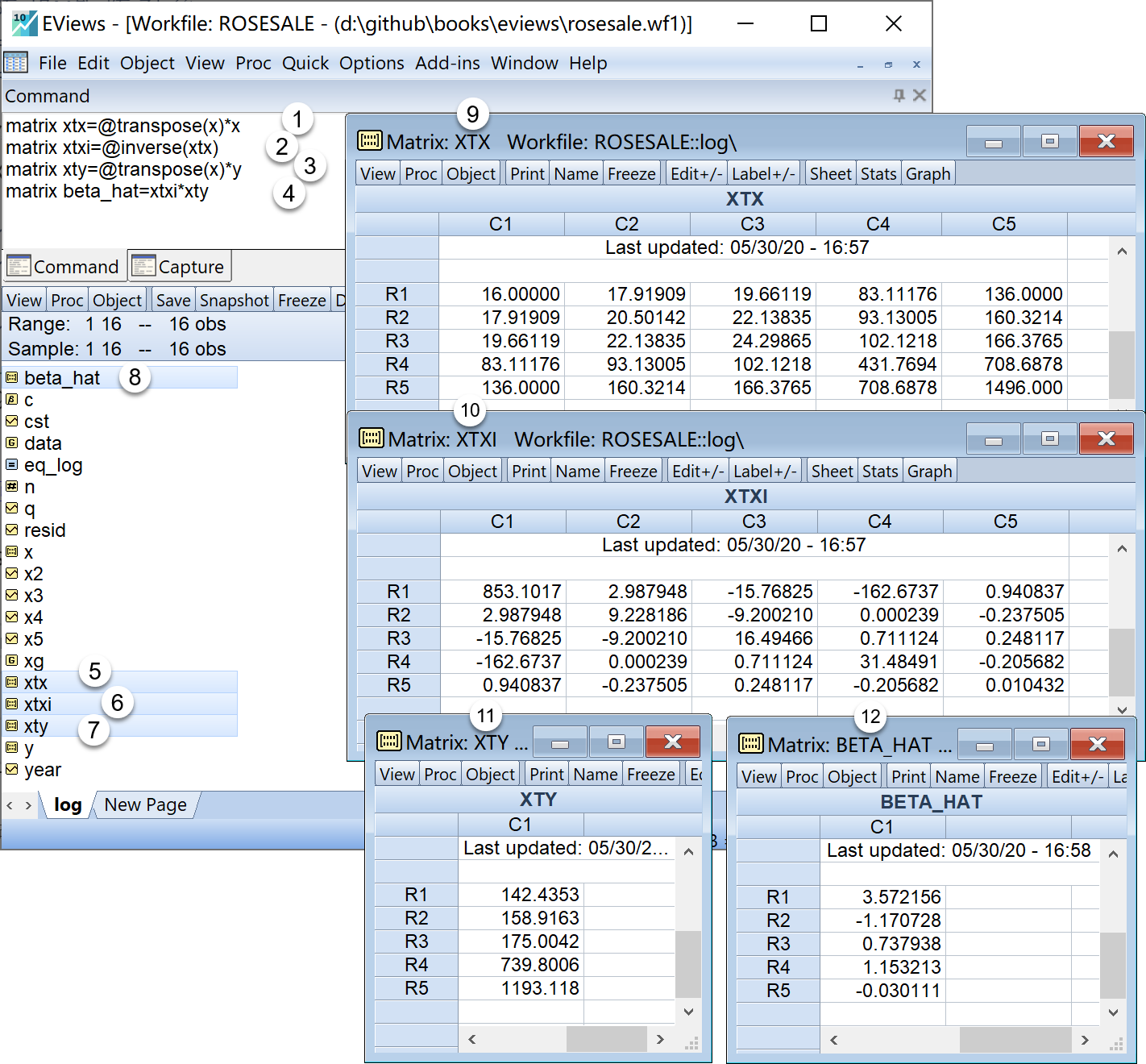
matrix xtx=@transpose(x)*x '得到重要矩阵X'X
matrix xtxi=@inverse(xtx) '得到重要矩阵(X'X)^(-1)
matrix xty=@transpose(x)*y '得到重要矩阵X'y
matrix beta_hat=xtxi*xty '得到回归系数矩阵在工作文件视窗下,可以看到如下新生成的矩阵对象,可以双击查看(见 图 4.6 ):
重要矩阵\(\mathbf{X'X}\)的矩阵对象
 xtx
xtx重要矩阵\(\mathbf{{(X'X)}^{-1}}\)的矩阵对象
 xtxi
xtxi重要矩阵\(\mathbf{(X'y)}\)的矩阵对象
 xty
xty回归系数向量\(\mathbf{\hat{\beta}={(X'X)}^{-1}X'y}\)的矩阵对象
 beta_hat
beta_hat
4.5.6 计算回归方程的误差方差及标准差
Eviews操作目标:计算回归方程的误差方差及标准差(标量),与主回归结果进行核验。
Eviews操作思路:利用理论公式
回归误差方差(\(\hat{\sigma}^2\))和回归误差标准差(\(\hat{\sigma}\))的理论计算公式分别为:
\[ \begin{aligned} \hat{\sigma}^2&=\frac{\sum{e_i^2}}{n-k}=\frac{\mathbf{y'y-\hat{\beta}'X'y}}{n-k}\\ \hat{\sigma}&=\sqrt{\frac{\sum{e_i^2}}{n-k}}=\sqrt{\frac{\mathbf{yy'-\hat{\beta}'X'y}}{n-k}} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'计算回归误差方差及标准差
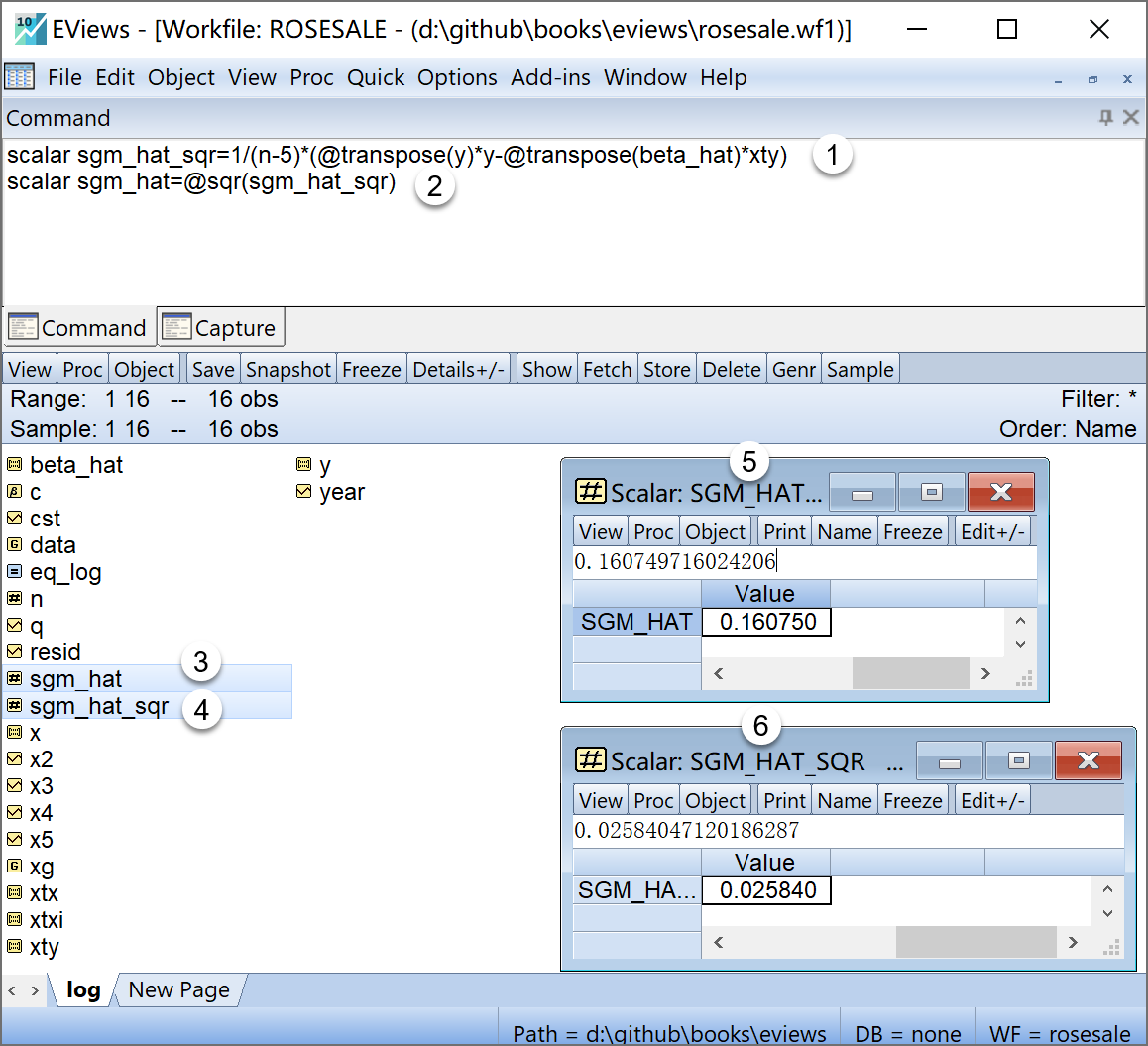
scalar sgm_hat_sqr=1/(n-5)*(@transpose(y)*y-@transpose(beta_hat)*xty) '回归误差方差
scalar sgm_hat=@sqr(sgm_hat_sqr) 在工作文件视窗下,可以看到如下的标量对象,可以双击查看(见 图 4.7 ):
回归误差方差\(\hat{\sigma}^2\)的标量对象
 sgm_hat_sqr
sgm_hat_sqr回归误差标准差\(\hat{\sigma}\)的标量对象
 sgm_hat
sgm_hat
4.5.7 计算回归系数的方差协方差矩阵、系数的样本方差和标准差(列向量)
Eviews操作目标:计算回归方程的方差协方差矩阵,得到系数的样本方差和标准差。
Eviews操作思路:先得到方差协方差矩阵,再提取对角线元素,利用理论公式
\[ \begin{aligned} &\widehat{var}\_\widehat{cov}(\mathbf{\hat{\beta}})=\hat{\sigma}^2\mathbf{(X'X)^{-1}}\\ &\mathbf{S^2_{\hat{\beta}}}\\ &\mathbf{S_{\hat{\beta}}}=\sqrt{S^2_{\hat{\beta}}} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'计算回归系数的方差协方差矩阵、系数的样本方差和标准差(列向量)
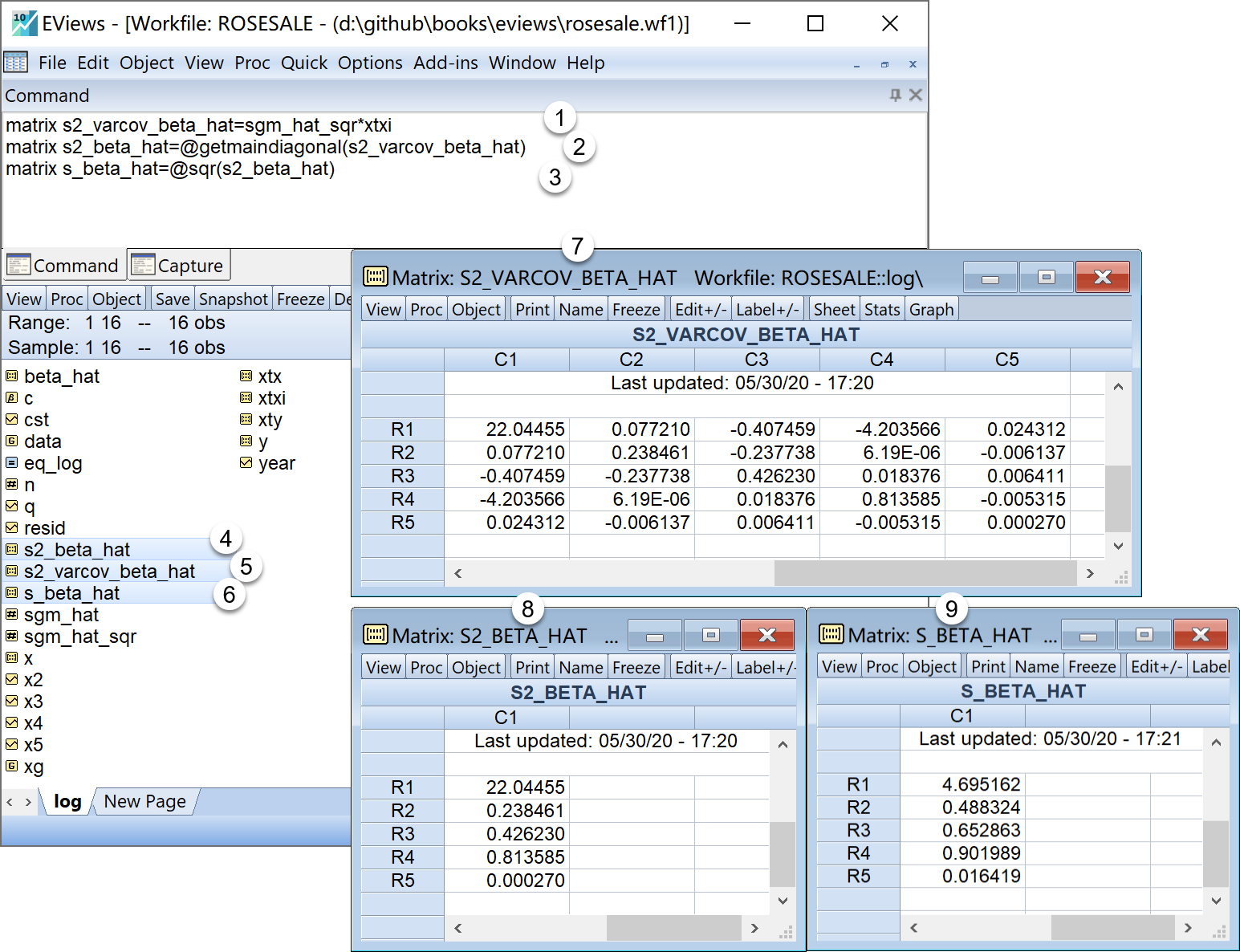
matrix s2_varcov_beta_hat=sgm_hat_sqr*xtxi '回归系数的样本方差协方差矩阵
matrix s2_beta_hat=@getmaindiagonal(s2_varcov_beta_hat) '回归系数的样本方差
matrix s_beta_hat=@sqr(s2_beta_hat) '回归系数的样本标准差在工作文件视窗下,可以看到如下EViews对象,可以双击查看(见 图 4.8 ):
回归系数的样本方差协方差矩阵\(\widehat{var}\_\widehat{cov}(\mathbf{\hat{\beta}})\)的矩阵 对象
 s2_varcov_beta_hat
s2_varcov_beta_hat回归系数的样本方差\(\mathbf{S^2_{\hat{\beta}}}\)的矩阵对象
 s2_beta_hat
s2_beta_hat回归系数的样本标准差\(\mathbf{S_{\hat{\beta}}}\)的矩阵对象
 s_beta_hat
s_beta_hat
4.5.8 进行平方和分解,计算TSS、ESS和RSS,以及各自的自由度(标量)
Eviews操作目标:进行平方和分解,得到方差分析表(ANOVA)。
Eviews操作思路:掌握自由度的计算,利用理论公式
\[ \begin{aligned} &n\bar{Y}^2 \\ TSS &=\mathbf{y'y}-n\bar{Y}^2 \\ RSS &=\mathbf{e'e}=\mathbf{y'y-\hat{\beta}'X'y} \\ ESS &=\mathbf{\hat{y}'\hat{y}}=\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2 \\ df_{TSS} &= n-1 \\ df_{RSS} &= n-k \\ df_{ESS} &=k-1 \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'进行平方和分解,计算TSS、ESS和RSS,以及各自的自由度(标量)
scalar mean_adj=16*(@mean(log(q)))^2 '均值修正值
scalar tss=@transpose(y)*y-mean_adj '总平方和TSS
scalar rss=@transpose(y)*y-@transpose(beta_hat)*xty '剩余平方和RSS
scalar ess=@transpose(beta_hat)*xty-mean_adj '回归平方和ESS
scalar df_tss=n-1 ' TSS的自由度
scalar df_rss=n-5 'RSS的自由度
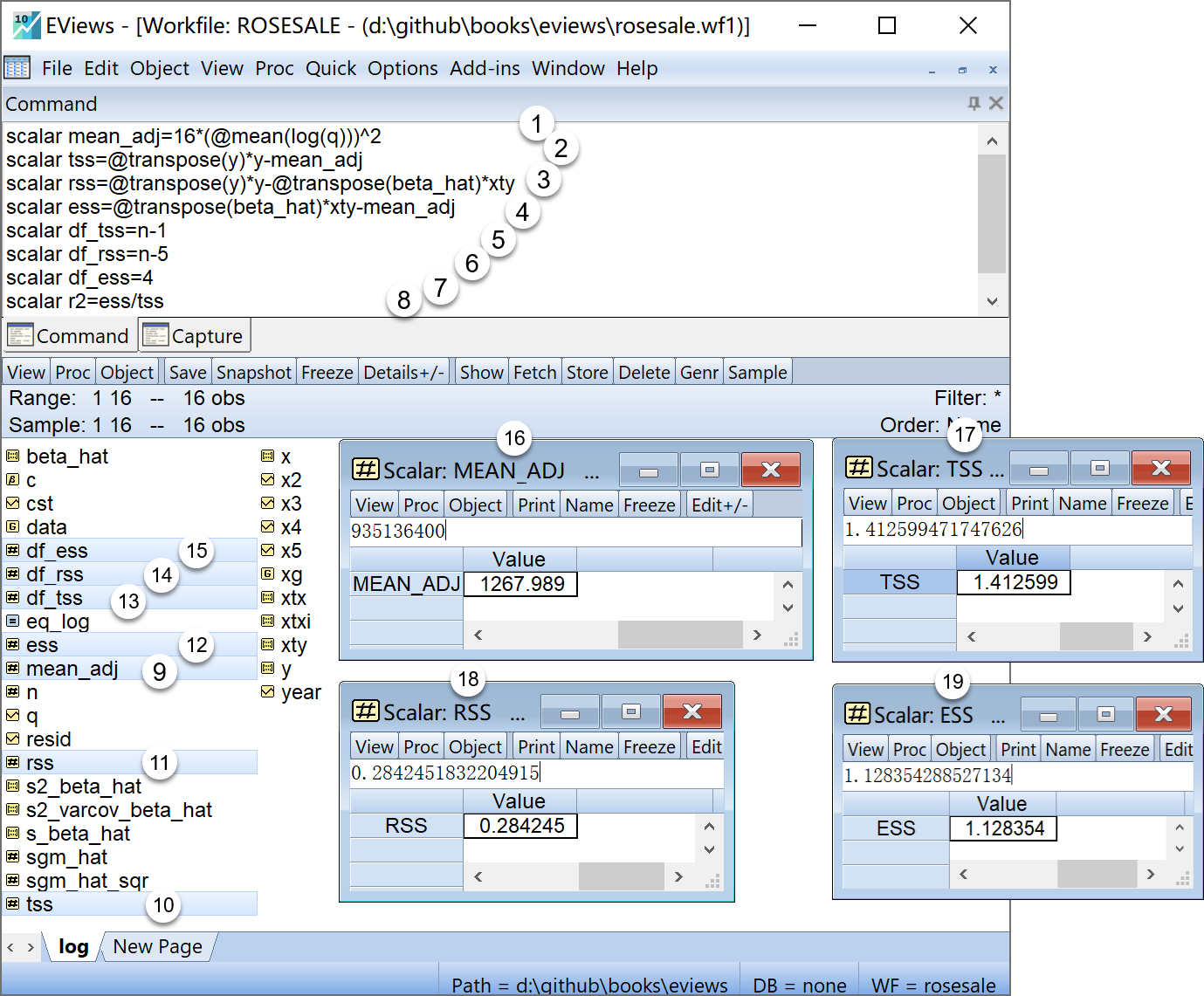
scalar df_ess=4 'ESS的自由度在工作文件视窗下,可以看到如下的标量对象,可以双击查看(见 图 4.9 ):
总平方和\(TSS\)的标量对象
 tss
tss残差平方和\(RSS\)的标量对象
 rss
rss回归平方和\(ESS\)的标量对象
 ess
ess总平方和的自由度\(df_{TSS}\)的标量对象
 df_tss
df_tss残差平方和的自由度\(df_{RSS}\)的标量对象
 df_rss
df_rss回归平方和的自由度\(df_{ESS}\)的标量对象
 df_ess
df_ess
4.5.9 计算自变量的相关系数表格、回归方程的判定系数和调整判定系数
Eviews操作目标:得到自变量的相关系数表,计算方程的判定系数和调整判定系数。
Eviews操作思路:构建自变量组对象,得到相关系数表;利用方差分析表结果计算判定系数和调整判定系数。利用理论公式
\[ \begin{aligned} R^2&=\frac{ESS}{TSS} \\ &=\frac{\mathbf{\hat{\beta}'X'y}-n\bar{Y}^2}{\mathbf{y'y}-n\bar{Y}^2} \\ \bar{R}^2 &=1-\frac{RSS/{f_{RSS}}}{TSS/{f_{TSS}}} \\ &=1-\frac{\mathbf{y'y-\hat{\beta}X'y}/{n-k}}{{(\mathbf{y'y}-n\bar{Y}^2)}/{n-1}} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'计算自变量的相关系数表格、回归方程的判定系数和调整判定系数
group varx x2 x3 x4 x5 ' 构建只含X的group
freeze(tab_cor) varx.cor '把group的相关系数矩阵表视图保存为表格
scalar r2=ess/tss '回归方程的判定系数
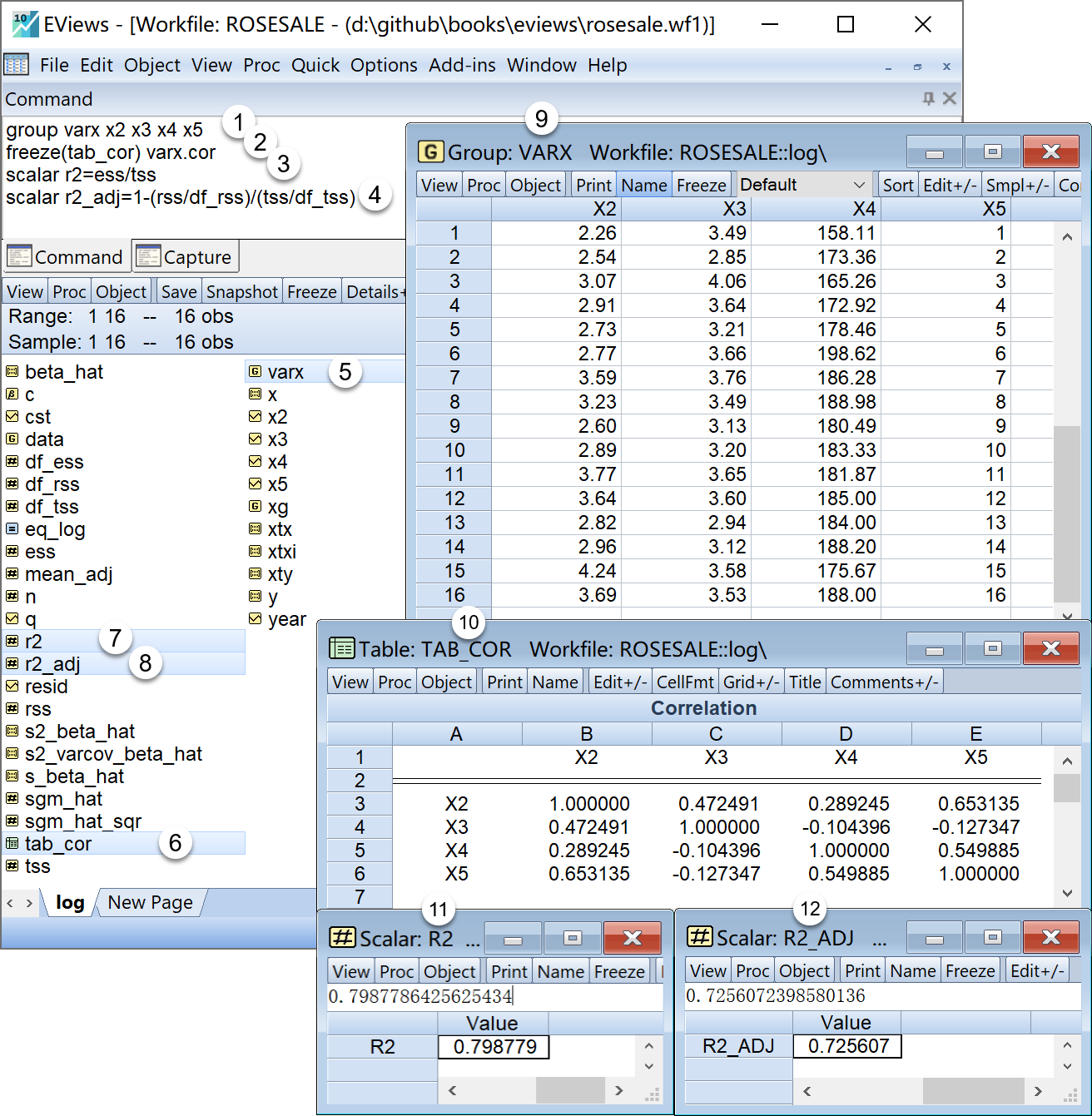
scalar r2_adj=1-(rss/df_rss)/(tss/df_tss) '回归方程的调整判定系数在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 4.10 ):
只含回归元变量(X2、X3、X4、X5)的组对象
 varx
varx回归元变量间相关系数的表格对象
 tab_cor
tab_cor回归方程判定系数\(R^2\)的标量对象
 r2
r2回归方程调整判定系数\(\bar{R}^2\)的标量对象
 r2_adj
r2_adj
4.5.10 对回归方程的回归系数进行显著性t检验
目标:检验各个回归系数是否显著
思路:根据理论的矩阵公式,计算样本t统计量;计算给定显著性水平下的理论t值;进行t假设检验。
回归系数的样本t统计量以及给定显著性水平下的理论t值的计算公式为:
\[ \begin{aligned} \mathbf{t^{\ast}_{\beta}} &=\mathbf{\frac{\hat{\beta}}{S_{\hat{\beta}}}} \\ t_{1-\alpha/2}(n-k) &=t_{0.975}(11) \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'对回归方程的回归系数进行显著性t检验
matrix t_str_beta_hat=@ediv(beta_hat,s_beta_hat) '计算得到回归系数的样本t统计量
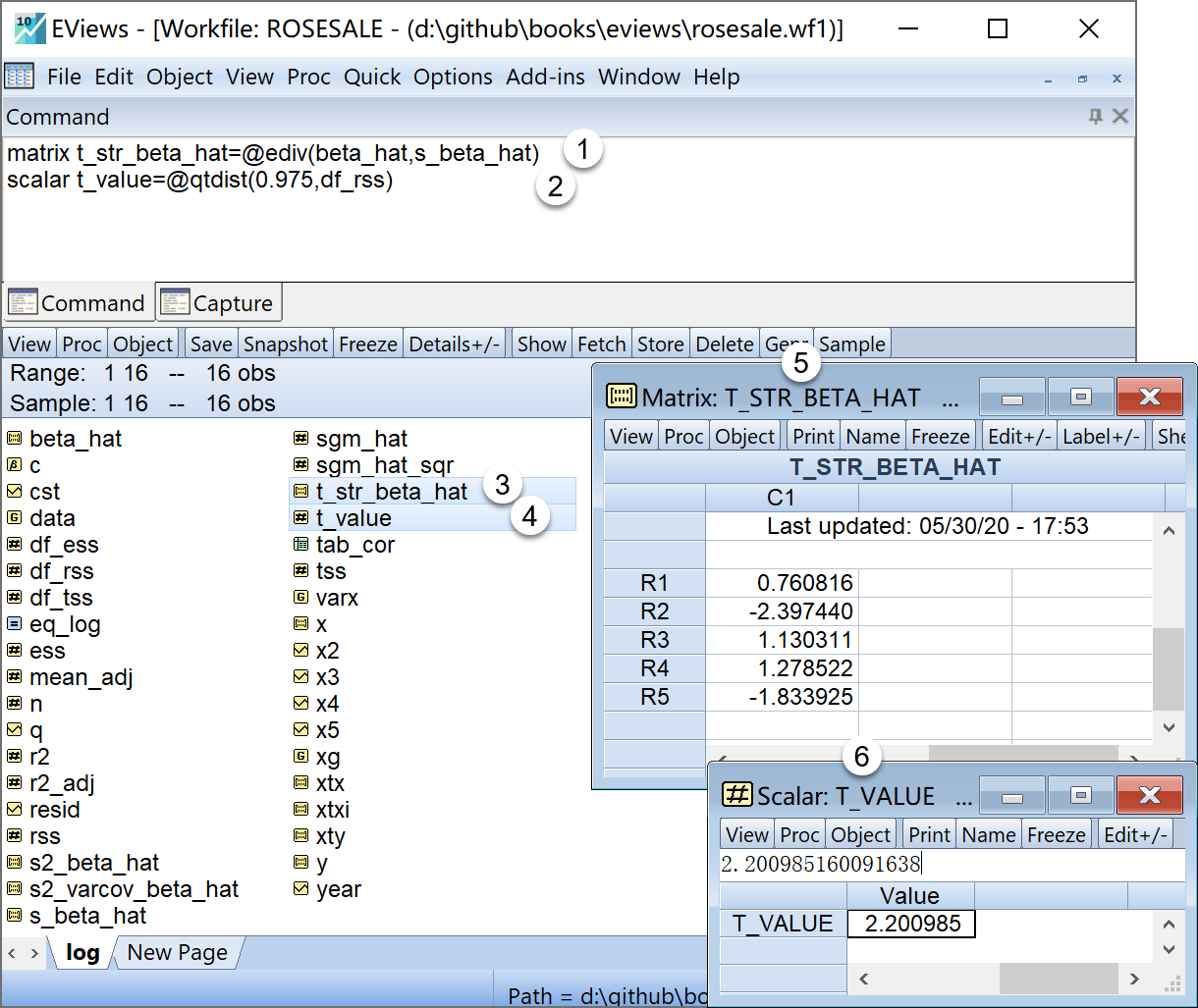
scalar t_value=@qtdist(0.975,df_rss) '给定α=0.05 水平下的理论t值(右侧正值在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 4.11 ):
回归系数的样本t统计量\(\mathbf{t^{\ast}_{\beta}}\)的矩阵对象
 t_str_beta_hat
t_str_beta_hat给定\(\alpha=0.05\)水平下的理论t值(右侧正值)\(t_{1-\alpha/2}(n-k)\)的标量对象
 t_value
t_value
4.5.11 对回归方程的整体显著性进行F假设检验
目标:进行回归方程的整体显著性进行F假设检验
思路:根据理论的矩阵公式,计算样本F统计量;给定显著性水平下,计算得到理论F值;完成模型整体显著性F检验过程。
回归方程的样本F统计量,以及给定显著性水平下理论F值的计算公式为:
\[ \begin{aligned} F^{\ast} &=\frac{ESS/{f_{ESS}}}{RSS/{f_{RSS}}} =\frac{MSS_{ESS}}{MSS_{RSS}} \\ &=\frac{(\mathbf{\hat{\beta}X'y}-n\bar{Y}^2)/{k-1}}{{(\mathbf{y'y-\hat{\beta}'X'y})}/{n-k}} \\ F_{1-\alpha}(k-1,n-k) &=F_{0.95}(4,11) \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 对回归方程的整体显著性进行F假设检验
scalar f_str=(ess/df_ess)/(rss/df_rss) '计算回归方程的样本F统计量
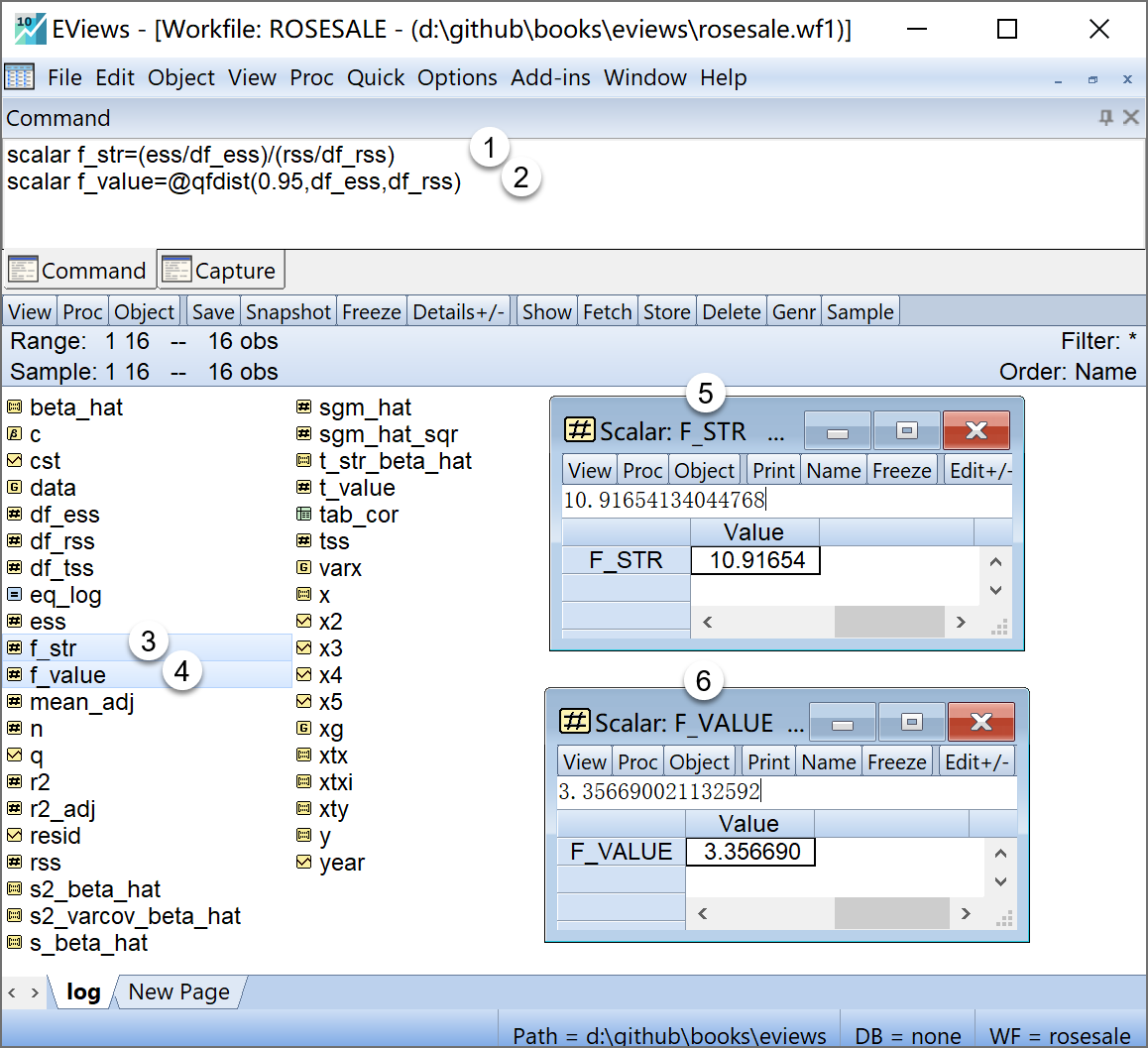
scalar f_value=@qfdist(0.95,df_ess,df_rss) '计算给定 α=0.05 水平下的查表的理论F值在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 4.12 ):
回归方程的样本F统计量\(F^{\ast}\)的标量对象
 f_str
f_str给定\(\alpha=0.05\)水平下的理论F值(右侧大值)\(F_{1-\alpha}(n-1,n-k)\)的标量对象
 f_value
f_value
4.5.12 进行样本外的均值预测、个值预测,并计算置信区间
目标:样本外的均值预测、个值预测,计算得到置信区间(给定显著性水平)
思路:构建样本外\(\mathbf{X_0}\)矩阵;计算得到回归估计值\(\hat{Y}_0\);构造分别计算得到均值预测的t分布样本标准差\(\mathbf{S_{\hat{Y}_0}}\)和个值预测的t分布样本标准差\(\mathbf{S_{Y_0-\hat{Y}_0}}\);给定显著性水平下,计算得到理论t值;利用公式分别计算均值预测和个值预测的置信区间。
相关参考计算公式为:
\[ \begin{aligned} \mathbf{\hat{Y_0}=X_0\hat{\beta}} \end{aligned} \]
\[ \begin{aligned} \mathbf{S_{\hat{Y}_0}} &=\sqrt{\hat{\sigma}^2X_0(X'X)^{-1}X_0'} \end{aligned} \tag{4.52}\]
\[ \begin{aligned} S_{Y_0-\hat{Y}_0}=S_{e_0} &=\sqrt{\hat{\sigma}^2 \left( 1+X_0(X'X)^{-1}X_0' \right) } \\ \end{aligned} \tag{4.53}\]
\[ \begin{aligned} \hat{\sigma}^2&=\frac{\mathbf{ee'}}{(n-k)} \end{aligned} \tag{4.54}\]
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \leq E(Y|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \end{aligned} \tag{4.55}\]
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0} \leq (Y_0|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0} \end{aligned} \tag{4.56}\]
在命令视窗中依次输入并运行如下EViews代码:
' 进行样本外的均值预测、个值预测,并计算置信区间
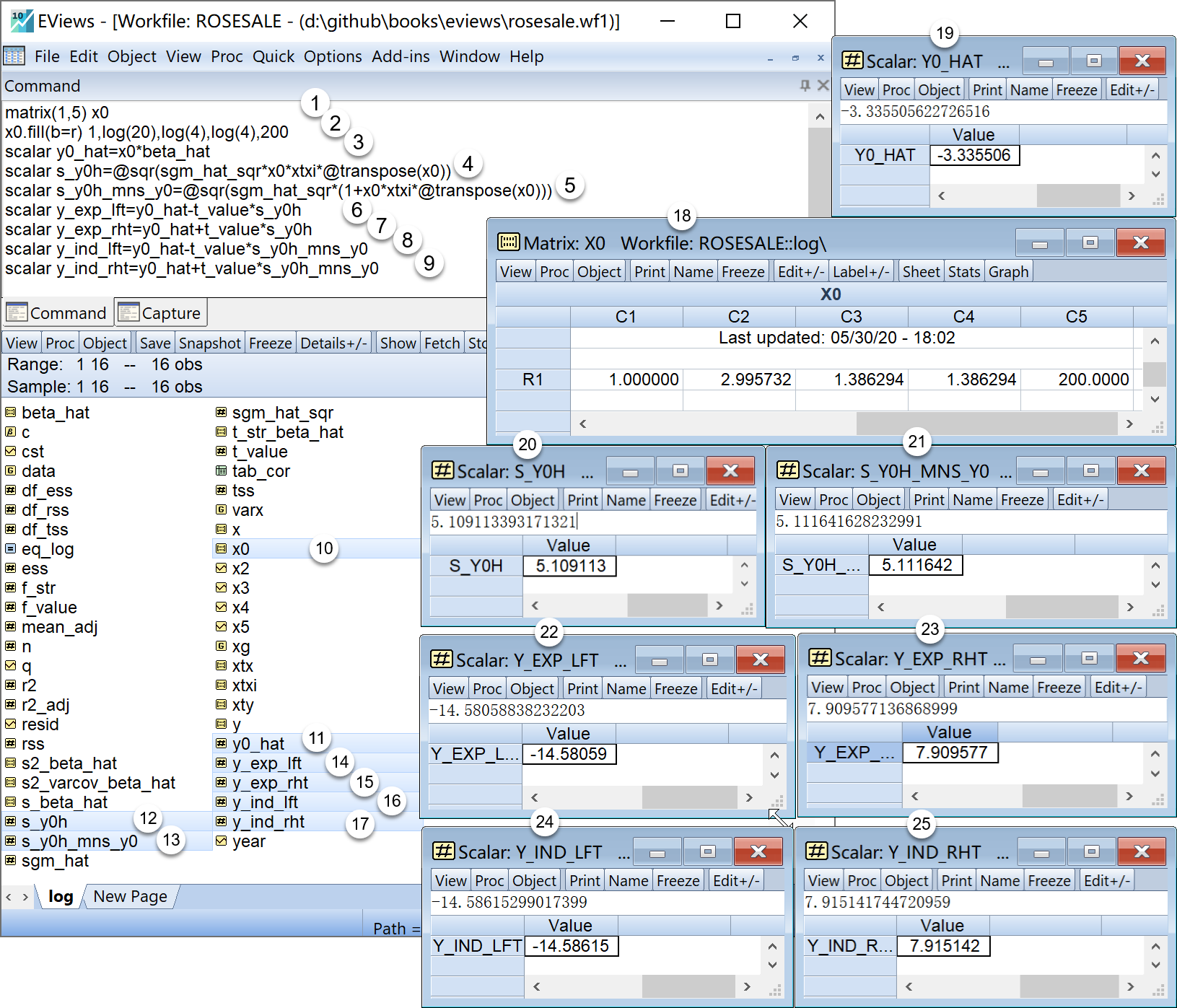
matrix(1,5) x0 '产生1行*5列的空矩阵
x0.fill(b=r) 1,log(20),log(4),log(4),200 '样本外X值为(x2=log(20), x3=log(4), x4=log(4), x5=200)
scalar y0_hat=x0*beta_hat '样本外估计Y值
scalar s_y0h=@sqr(sgm_hat_sqr*x0*xtxi*@transpose(x0)) '均值预测的样本标准差
scalar s_y0h_mns_y0=@sqr(sgm_hat_sqr*(1+x0*xtxi*@transpose(x0))) '个值预测的样本标准差
scalar y_exp_lft=y0_hat-t_value*s_y0h '均值预测的置信区间的左界值
scalar y_exp_rht=y0_hat+t_value*s_y0h '均值预测的置信区间的右界值
scalar y_ind_lft=y0_hat-t_value*s_y0h_mns_y0 '个值预测的置信区间的左界值
scalar y_ind_rht=y0_hat+t_value*s_y0h_mns_y0 '个值预测的置信区间的右界值在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 4.13 ):
样本外\(\mathbf{X_0}\)矩阵(元素为1,x2=log(20), x3=log(4), x4=log(4), x5=200)的矩阵对象
 x0
x0样本外估计\(\hat{Y_0}\)值的标量对象
 y0_hat
y0_hat均值预测的样本标准差\(S_{\hat{Y}_0}\)的标量对象
 s_y0h
s_y0h个值预测的样本标准差\(S_{Y_0-\hat{Y}_0}\)的标量对象
 s_y0h_mns_y0
s_y0h_mns_y0均值预测的置信区间的左界值\(\hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0}\)的标量对象
 y_exp_lft
y_exp_lft均值预测的置信区间的右界值\(\hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0}\)的标量对象
 y_exp_rht
y_exp_rht个值预测的置信区间的左界值\(\hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0}\)的标量对象
 y_ind_lft
y_ind_lft个值预测的置信区间的右界值\(\hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0}\)的标量对象
 y_ind_rht
y_ind_rht
4.6 附录:prg源代码
实际操作中,在EViews命令视窗中逐条输入代码,既容易出错,又不便于维护这些代码,还不能进行代码的重复使用(在第一章的节@ref(command-system)中已经论述)。
因此,读者可以创建一个.prg编程文件 ,并在其中编写EViews代码,进行管理、维护、运行和分析。下面代码按本章主要实验步骤编写,读者可以用于本章的EViews编程参考,进行实验练习。
,并在其中编写EViews代码,进行管理、维护、运行和分析。下面代码按本章主要实验步骤编写,读者可以用于本章的EViews编程参考,进行实验练习。
'=========================================================================================================
'说明:以下为EViews编程文件rosesale.prg的代码
'将展示第三章中“英国家庭食物支出案例”主要分析步骤的“批量式命令驱动”实现方法(::
'其中,符号'起始的行,为注释行,其他为EViews命令行。
'=========================================================================================================
'创建工作文件(工作文件名=rose,子页命名=sale),无结构无日期,样本数为16
wfcreate(wf=rose,page=sale) u 16
'导入外部数据,路径为d:\github\books\data\Lab3-family-spends.xlsx
import d:\github\books\data\lab4-rose-demand-origin.xlsx
'生成线性回归模型的方程对象
equation eq_main.ls log(q) c log(x2) log(x3) log(x4) x5 '对数模型
'构造几个重要变量对象
scalar n=@obs(x2) '样本数n(标量)
series cst=1 '新建元素全为1的序列对象(用于构造矩阵X)
group xg cst log(x2) log(x3) log(x4) x5 '构造为group,便于观察
'构造X矩阵和Y矩阵对象。
matrix x=xg '转换为X矩阵对象
matrix y=log(q) '构造Y矩阵对象
'计算回归方程的回归系数向量
matrix xtx=@transpose(x)*x '得到重要矩阵X'X
matrix xtxi=@inverse(xtx) '得到重要矩阵(X'X)^(-1)
matrix xty=@transpose(x)*y '得到重要矩阵X'y
matrix beta_hat=xtxi*xty '得到回归系数矩阵
'计算回归误差方差及标准差
scalar sgm_hat_sqr=1/(n-5)*(@transpose(y)*y-@transpose(beta_hat)*xty) '回归误差方差
scalar sgm_hat=@sqr(sgm_hat_sqr) '回归误差标准差
'计算回归系数的方差协方差矩阵、系数的样本方差和标准差(列向量)
matrix s2_varcov_beta_hat=sgm_hat_sqr*xtxi '回归系数的方差协方差矩阵
matrix s2_beta_hat=@getmaindiagonal(s2_varcov_beta_hat) '回归系数的样本方差
matrix s_beta_hat=@sqr(s2_beta_hat) '回归系数的样本标准差
'进行平方和分解,计算TSS、ESS和RSS,以及各自的自由度(标量)
scalar mean_adj=16*(@mean(q))^2 '均值修正值
scalar tss=@transpose(y)*y-mean_adj '总平方和TSS
scalar rss=@transpose(y)*y-@transpose(beta_hat)*xty '剩余平方和RSS
scalar ess=@transpose(beta_hat)*xty-mean_adj '回归平方和ESS
scalar df_tss=n-1 ' TSS的自由度
scalar df_rss=n-5 'RSS的自由度
scalar df_ess=4 'ESS的自由度
'计算自变量的相关系数表格、回归方程的判定系数和调整判定系数
group varx x2 x3 x4 x5 ' 构建只含X的group
freeze(tab_cor) varx.cor '把group的相关系数矩阵表视图保存为表格
scalar r2=ess/tss '回归方程的判定系数
scalar r2_adj=1-(rss/df_rss)/(tss/df_tss) '回归方程的调整判定系数
'对回归方程的回归系数进行显著性t检验
matrix t_str_beta_hat=@ediv(beta_hat,s_beta_hat) '计算得到回归系数的样本t统计量
scalar t_value=@qtdist(0.975,df_rss) '给定α=0.05 水平下的理论t值(右侧正值)
' 对回归方程的整体显著性进行F假设检验
scalar f_str=(ess/4)/(rss/11) '计算回归方程的样本F统计量
scalar t_value=@qfdist(0.95,df_ess,df_rss) '计算给定 α=0.05 水平下的查表的理论F值
' 进行样本外的均值预测、个值预测,并计算置信区间
matrix(1,5) x0 '产生1行*5列的空矩阵
x0.fill(b=r) 1,log(20),log(4),log(4),200 '样本外X值为(x2=log(20), x3=log(4), x4=log(4), x5=200)
scalar y0_hat=x0*beta_hat '样本外估计Y值
scalar s_y0h=@sqr(sgm_hat_sqr*x0*xtxi*@transpose(x0)) '均值预测的样本标准差
scalar s_y0h_mns_y0=@sqr(sgm_hat_sqr*(1+x0*xtxi*@transpose(x0))) '个值预测的样本标准差
scalar y_exp_lft=y0_hat-t_value*s_y0h '均值预测的置信区间的左界值
scalar y_exp_rht=y0_hat+t_value*s_y0h '均值预测的置信区间的右界值
scalar y_ind_lft=y0_hat-t_value*s_y0h_mns_y0 '个值预测的置信区间的左界值
scalar y_ind_rht=y0_hat+t_value*s_y0h_mns_y0 '个值预测的置信区间的右界值
' ===========================================================================
4.7 实验作业
玫瑰的需求: 表 4.4 给出美国底特律市区对玫瑰的季度需求数据。
| X1 | YEAR | X2 | X3 | X4 | X5 | Ydata1 | Ydata2 | Ydata3 | Ydata4 |
|---|---|---|---|---|---|---|---|---|---|
| id | YEAR | X2 | X3 | X4 | X5 | 2015014495 | 2016010317 | 2016011222 | 2016013000 |
| name | YEAR | X2 | X3 | X4 | X5 | 刘琳 | 王雪明 | 韩双瑞 | 任畅 |
| class | YEAR | X2 | X3 | X4 | X5 | 保险1601 | 保险1601 | 保险1601 | 保险1601 |
| n1 | 1971.3 | 2.2599999999999998 | 3.49 | 158.11000000000001 | 1 | 11483.44 | 11483.77 | 11485.56 | 11484.07 |
| n2 | 1971.4 | 2.54 | 2.85 | 173.36 | 2 | 9348.0499999999993 | 9348.92 | 9350.0499999999993 | 9347.51 |
| n11 | 1974.1 | 3.77 | 3.65 | 181.87 | 11 | 5910.48 | 5910.71 | 5911.4 | 5910.45 |
| n12 | 1974.2 | 3.64 | 3.6 | 185 | 12 | 7949.9 | 7949.92 | 7951.02 | 7950.71 |
| n13 | 1974.3 | 2.82 | 2.94 | 184 | 13 | 6134.28 | 6134.14 | 6133.92 | 6136.16 |
变量说明见 表 4.5 :
| variable | label |
|---|---|
| YEAR | 年份.季度 |
| Q | 玫瑰销售量(打) |
| X2 | 玫瑰批发价格(\(/打) | |X3 |石竹的平均批发价格(\)/打) |
| X4 | 家庭可支配收入($/周) |
| X5 | 时间趋势 |
请考虑如下两个需求函数:
\[ \begin{aligned} Y_t=\hat{\alpha}_1+\hat{\alpha}_2X_{2t}+\hat{\alpha}_3X_{3t}+ \hat{\alpha}_4X_{4t}+\hat{\alpha}_5X_{5t}+e_{1t} \end{aligned} \tag{4.57}\]
\[ \begin{aligned} ln(Y_t)=\hat{\beta}_1+\hat{\beta}_2ln(X_{2t})+\hat{\beta}_3ln(X_{3t})+\hat{\beta}_4ln(X_{4t})+\hat{\beta}_5X_{5t}+e_{2t} \end{aligned} \tag{4.58}\]
请回答如下问题:
(1)关于线性模型 式 4.57 ,运用菜单操作,得到回归分析报告。
(2)关于线性模型 式 4.57 ,在Eviews中运用矩阵方法,计算如下步骤:
计算直线回归方程的回归系数向量(\(\mathbf{\hat{\beta}}\)),并写出样本回归模型(\(SRM_2\))。
计算回归误差方差(\(\hat{\sigma}^2\))和回归误差标准差(\(\hat{\sigma}\))。
计算回归系数的样本方差协方差矩阵(\(\widehat{var}\_\widehat{cov}(\mathbf{\hat{\beta}})\))。
得出回归系数的样本标准差向量(\(\mathbf{S_{\hat{\beta}}}\))。
进行平方和分解,计算\(TSS\)、\(ESS\)和\(RSS\)。
计算判定系数\(R^2\),调整判定系数(\(\hat{R}^2\))。
计算样本t统计量(\(\mathbf{t^{\ast}_{\beta}}\)),并进行t假设检验。
对回归方程的整体显著性进行F假设检验。
对回归方程的进行样本外均值预测\(E(Y\mid X=X_0)\)。
对回归方程的进行样本外个值预测\((Y_0\mid X=X_0)\)。
(3)关于对数线性模型 式 4.58 ,运用菜单操作,得到回归分析报告。
(4)关于对数线性模型 式 4.58 ,在Eviews中运用矩阵方法,计算如下步骤:
算直线回归方程的回归系数向量(\(\mathbf{\hat{\beta}}\)),并写出样本回归模型(\(SRM_2\))
计算回归误差方差(\(\hat{\sigma}^2\))和回归误差标准差(\(\hat{\sigma}\))。
计算回归系数的样本方差协方差矩阵(\(\widehat{var}\_\widehat{cov}(\mathbf{\hat{\beta}})\))。
得出回归系数的样本标准差向量(\(\mathbf{S_{\hat{\beta}}}\))。
进行平方和分解,计算\(TSS\)、\(ESS\)和\(RSS\)。
计算判定系数\(R^2\),调整判定系数(\(\hat{R}^2\))。
计算样本t统计量(\(\mathbf{t^{\ast}_{\beta}}\)),并进行t假设检验。
对回归方程的整体显著性进行F假设检验。
对回归方程的进行样本外均值预测\(E(Y\mid X=X_0)\)。
对回归方程的进行样本外个值预测\((Y_0\mid X=X_0)\)。
(5)根据对数模型特征,可知\(\hat{\beta_2}\)、\(\hat{\beta_3}\)和\(\hat{\beta_4}\)分别为玫瑰需求的自价格弹性,交叉价格弹性和收入弹性。 它们的先验符号是什么?你的结果同先验预期相符吗?
(6)根据你的分析,你会选择哪个模型(如果可选)? 为什么?
(7)仅考虑对数设定形式模型 式 4.58 :
所估计的需求自价格弹性 (即对玫瑰价格的弹性)是什么?
它是统计显著的吗?
如果是,它是否在统计上异于1?(此题为选作)
理论上,你对\(\hat{\beta_3}\)和\(\hat{\beta_4}\)的预期符号是什么?eviews结果和这些预期相符吗?
如果\(\hat{\beta_3}\)和\(\hat{\beta_4}\)的系数在统计意义上不显著,可能是什么原因?
实际上在假设{\(H_1:\beta_j\)不全为0,\(j \in (2,\cdots,k)\)}下,回归模型的形式有很多种,但对于这里所要说明的F检验而言,这些不同的模型形式已经不再重要↩︎