7 自相关问题
7.1 实验目的及要求
目的：掌握自相关问题的检验与处理方法。
要求：在老师指导下完成计量经济模型的自相关检验，并对存在自相关的模型进行修正，最终得到正确的分析结果。
7.2 实验原理
使用时间序列数据建模时，我们往往会面临时间序列数据自相关的现实问题。如果存在自相关问题，则可能对模型及分析结论的科学性产生一定程度影响。
7.2.1 什么时候模型会出现自相关问题？
对于总体回归模型（PRM）：
\[ \begin{aligned} Y_t=\beta_1+\beta_2X_{2t}+\cdots+\beta_kX_{kt}+u_t \end{aligned} \tag{7.1}\]
随机干扰项\(u_t\)可能与其滞后变量存在自相关现象，我们定义如下：
定义 7.1 (随机干扰项p阶自相关) 对于给定的滞后阶数\(p(p \subset \mathcal{N})\)下，随机干扰项\(u_t\)与其滞后变量\(u_{t-p}\)之间存在\(cov(u_t,u_{t-p}) \neq0\)。
在经典线性回归模型假设（CLRM）下，我们假设主模型 式 7.1 随机误差项\(u_t\)是无自相关的，也即\(u_t\)与\(u_{t-1}\)或任意其他滞后变量\(u_{t-p},\ \ p\in (1,2,\cdots)\)都不存在线性相关关系。如果这一假设不能得到保证，我们认为模型将出现自相关问题。
定义 7.2 (模型出现自相关问题) 对于主回归模型，如果给定任意的滞后阶数\(p \in (1,2,\cdots)\)，只要随机干扰项\(u_t\)与其滞后变量\(u_{t-p}\)之间存在\(cov(u_t,u_{t-p}) \neq 0\)的现象。
此时，模型 式 7.1 出现自相关问题也可以表达为方差-协方差的矩阵形式：
\[ \begin{aligned} E(\mathbf{uu'|X})&= \begin{bmatrix} E(u^2_1) & E(u_1u_2) & \cdots & E(u_1u_n) \\ E(u_2u_1) & E(u^2_2) & \cdots & E(u_2u_n) \\ \cdots & \cdots & \cdots & \cdots \\ E(u_nu_1) & \cdots & \cdots & E(u_nu_n) \\ \end{bmatrix} \end{aligned} \tag{7.2}\]
\[ \begin{aligned} E(\mathbf{uu'|X})&= \begin{bmatrix} \sigma^2 & \sigma^2_{12} & \cdots & \sigma^2_{1n} \\ \sigma^2_{21} & \sigma^2 & \cdots & \sigma^2_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ \sigma^2_{n1} & \cdots & \cdots & \sigma^2 \end{bmatrix} \end{aligned} \tag{7.3}\]
其中，方差-协方差矩阵（见公式 式 7.2 ）的协方差部分（矩阵下三角）元素将不全为0（见公式 式 7.3 ）。
简而言之，只要的随机干扰项\(u_t\)出现了任何形式的p阶自相关，我们都称模型 式 7.1 出现自相关问题。一种简单的情形就是马尔科夫1阶自相关：
\[ \begin{aligned} \begin{split} Y_t&=\beta_1+\beta_2X_{2t}+\cdots+\beta_kX_{kt}+u_t \notag \\ u_t&=\rho u_{t-1}+\varepsilon_t \\ \varepsilon_t &\sim \text{i.i.d} \ \ N(0,\sigma^2) \end{split} \end{aligned} \tag{7.4}\]
当然，模型自相关的情形还有其他更加多样和复杂的形态，例如：
\[ \begin{aligned} \begin{split} u_t&=\rho_1 u_{t-1}+\rho_2 u_{t-2}+\varepsilon_t \\ u_t&=\rho_2 u_{t-2}+\varepsilon_t \\ &\cdots\\ \varepsilon_t &\sim \text{i.i.d} \ \ N(0,\sigma^2) \end{split} \end{aligned} \tag{7.5}\]
7.2.2 随机干扰项自相关有哪些表现形态？
对于马尔科夫1阶自相关情形（见公式 式 7.4 ），如果自相关系数\(-1<\rho<0\)，则随机干扰项\(u_t\)及其一阶滞后变量具有某种图形模式（见 图 7.1）：其中\(u_t\)的时序图表现为正弦波形态，而\(u_t\)与\(u_{t-1}\)的散点图表现为正的线性相关关系。
7.2.3 自相关问题模型会有什么后果？
模型出现自相关问题时时，主要的影响包括：
普通最小二乘法（OLS）估计量仍是线性的、无偏的和一致性的
普通最小二乘法（OLS）估计量将不再是有效的(亦即最小方差)
模型参数的显著性检验失去意义
模型的预测将失效
模型的异方差检验流程也会变得不可靠
我们可以对马尔科夫一阶自相关情形做简要的证明：
Proof (马尔科夫1阶自相关下的理论后果). 已知模型存在马尔科夫一阶自相关情形，则有：
\[ \begin{aligned} Y_t&=\beta_1+\beta_2X_{2t}+\cdots+\beta_kX_{kt}+u_t \\ u_t&=\rho u_{t-1}+\varepsilon_t \\ \varepsilon_t &\sim \text{i.i.d} \ \ N(0,\sigma^2_\varepsilon) \end{aligned} \]
在经典线性回归模型假设下（CLRM），执意采用普通最小二乘法（OLS），我们容易可以得到斜率参数的点估计值\(\hat{\beta}_2\)及其方差\(\mathrm{var}(\hat{\beta}_2)\)：
\[ \begin{aligned} \hat{\beta}_2 &=\frac{\sum{x_ty_t}}{\sum{x^2_t}}\\ E(\hat{\beta}_2) & =\beta_2 \\ \mathrm{var}(\hat{\beta}_2)^{OLS}_{CLRM} &=\frac{\sigma^2}{\sum{x^2_t}} \end{aligned} \]
反之，如果我们考虑到一阶自相关问题已经违背了经典线性回归模型假设（CLRM），但仍采用普通最小二乘法（OLS），则斜率参数的点估计值\(\hat{\beta}_2\)及其方差\(\mathrm{var}(\hat{\beta}_2)\)的理论计算结果应该为：
\[ \begin{aligned} \begin{split} \hat{\beta}_2 & =\frac{\sum{x_ty_t}}{\sum{x^2_t}} \\ E(\hat{\beta}_2) & =\beta_2 \\ \mathrm{var}(\hat{\beta}_2)^{OLS}_{AR1} &=\frac{\sigma^2}{\sum{x^2_t}}+\frac{2\sigma^2}{\sum{x^2_t}} \\ &\cdot \left [\rho\frac{\sum_{t=1}^{n-1}{x_tx_{t+1}}}{\sum_{t=1}^n{x^2_t}}+\rho^2\frac{\sum_{t=1}^{n-2}{x_tx_{t+2}}}{\sum_{t=1}^n{x^2_t}}+\cdots+\rho^{n-1}\frac{{x_1x_n}}{\sum_{t=1}^n{x^2_t}} \right ]\\ &\simeq \frac{\sigma^2}{\sum{x^2_t}} \left ( \frac{1+r\rho}{1-r\rho} \right ) \end{split} \end{aligned} \]
其中，\(r\)为简单相关系数。因此，我们可以发现：
\[ \begin{aligned} \mathrm{var}(\hat{\beta}_2)^{OLS}_{AR1} &\simeq \frac{\sigma^2}{\sum{x^2_t}} \left ( \frac{1+r\rho}{1-r\rho} \right )\\ &=\mathrm{var}(\hat{\beta}_2)^{OLS}_{CLRM}\cdot \left ( \frac{1+r\rho}{1-r\rho} \right ) \end{aligned} \]
从而证明了\(\mathrm{var}(\hat{\beta}_2)^{OLS}_{AR1}\)与\(\mathrm{var}(\hat{\beta}_2)^{OLS}_{CLRM}\)是不相等的，也即表明当模型存在一阶自相关问题时，普通最小二乘法估计量仍是线性和无偏的，但却不再是方差最小的。1
7.2.4 如何诊断模型存在自相关问题？
显然，模型如果存在自相关问题，应该努力侦察随机干扰项\(u_t\)及其滞后变量\(u_{t-1},\cdots,u_{t-p} \ \ (p\in \mathcal{N})\)的行为模式。
对于总体回归模型存在一阶马尔科夫自回归情形：
\[ \begin{aligned} \begin{split} Y_t&=\beta_1+\beta_2X_{2t}+\cdots+\beta_kX_{kt}+u_t \\ u_t&=\rho u_{t-1}+\varepsilon_t \\ \varepsilon_t &\sim \text{i.i.d} \quad N(0,\sigma^2_\varepsilon) \end{split} \text(PRM-AR1) \end{aligned} \tag{7.6}\]
我们也有理由认为，样本回归模型（SRM）也会继承总体回归模型（PRM）的特征，从而有：
\[ \begin{aligned} \begin{split} Y_t&=\hat{\beta}_1+\hat{\beta}_2X_{2t}+\cdots+\hat{\beta}_kX_{kt}+e_t \\ e_t&=\hat{\rho} e_{t-1}+v_t \\ v_t &\sim \text{i.i.d} \ \ N(0,\sigma^2_v) \end{split} \text(SRM-AR1) \end{aligned} \tag{7.7}\]
鉴于样本回归模型（SRM）的残差\(e_t\)及其滞后变量\(e_{t-1},\cdots,e_{t-p} \ \ (p\in \mathcal{N})\)是可观测的，因此诊断模型是否存在自相关问题往往就转化为侦察残差\(e_t\)及其滞后变量\(e_{t-1},\cdots,e_{t-p} \ \ (p\in \mathcal{N})\)的行为模式。总体来看，诊断模型是否存在自相关问题，主要包括两大类方法：
（1）图形观察法：
残差序列观察法（描点图法）：绘制\(e_t\)序列的描点图（dot plot）
残差序列观察法（描点图法）：确定滞后阶数并分别绘制\(e_t\)序列与\({e_{t-1},e_{t-2},\cdots}\)序列的散点图（scatter plot）
（2）定量分析法：
辅助回归法：构建残差\(e_t\)序列对\({e_{t-1},e_{t-2},\cdots}\)序列的辅助回归方程
自相关和偏相关分析法：Eviews菜单操作对残差\(e_t\)序列进行自相关和偏相关分析
Durbin-Watson检验法：分析Eviews报告中的D-W统计量
拉格朗日检验法（LM-test）：Eviews菜单操作进行布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)
显然，模型无自相关是一种假设的理想状态。而事实是，模型只要存在任何一种情形的自相关模式，我们都称模型出现了自相关问题。因此，我们使用以上任一诊断方法，只要发现了自相关的明显证据，则都应该引起重视。
辅助回归方程诊断法：分析主回归模型 式 7.9 ，然后或者通过图形观察，或者通过猜测和尝试，再对残差及其滞后变量进行辅助回归 式 7.10 的建模分析：
\[ \begin{aligned} Y_t&={\beta}_1+{\beta}_2X_{2t}+\cdots+{\beta}_kX_{kt}+u_t &&\text{(PRM)} \end{aligned} \tag{7.8}\]
\[ \begin{aligned} Y_t&=\hat{\beta}_1+\hat{\beta}_2X_{2t}+\cdots+\hat{\beta}_kX_{kt}+e_t &&\text{(SRM)} \end{aligned} \tag{7.9}\]
\[ \begin{aligned} e_t&=\hat{\rho}_1e_{t-1}+\hat{\rho}_2e_{t-2}+\cdots+\hat{\rho}_pe_{t-p}+\varepsilon_t &&\text{(auxiliary equation)} \end{aligned} \tag{7.10}\]
其中，\(p=1,2,\cdots,t-1\)。实际上，具体的辅助诊断模型 式 7.10 往往需要多次尝试，由简单模型逐渐到扩展模型。为简单起见，我们可以先做AR(1)辅助方程（也即\(e_t\)对\(e_{t-1}\)的回归）或AR(2)辅助方程（也即\(e_t\)对\(e_{t-1}\)和\(e_{t-2}\)的辅助回归）。
辅助回归方程诊断法的诊断标准是：
7.2.5 如何矫正存在自相关问题模型？
对于存在自相关问题的模型，我们的最终目标应该是矫正并得到一个替代的新模型，使得该新模型能满足经典线性回归模型假设（CLRM），从而可以继续采用普通最小二乘法（OLS），最终估计并获得总体参数的最优线性无偏估计量（BLUE）。
自相关问题模型矫正的前提，首要工作是判明问题模型的自相关形式。它可以是简单的马尔科夫一阶自相关（见公式 式 7.6 ），也可以是更复杂的高阶自相关形式。然后再采用针对性的方法，把自相关问题模型处理为无自相关问题的新模型。从模型矫正的操作方法来看，这些针对性的矫正方法可以分为广义差分方程法（General difference equation，GDE ）2和一致标准误校正法（Heteroscedasticity and autocorrelation consistent standard error，HAC）3。当然，从实际矫正操作流程来看，矫正方法也可以划分为如下两大类：
（1）广义差分方程两步法（Two-steps）：
广义最小二乘法(GLS)：一阶差分法变换
广义最小二乘法(GLS)：基于残差辅助方程近似得到\(\rho\)
广义最小二乘法(GLS)：基于D-W统计量近似计算得到\(\rho\)
广义最小二乘法(GLS)：基迭代法近似计算得到\(\rho\)
（2）标准误校正一步法（One-steps）：
- 一致标准误校正法（HAC）：尼威-威斯特(Newey-West)校正法
7.3 实验内容
（1）采用最小二乘法建立主回归模型
（2）自相关问题模型的侦察方法
残差序列观察法（描点图法）：绘制\(e_t\)序列的描点图（dot plot）
残差序列观察法（描点图法）：确定滞后阶数并分别绘制\(e_t\)序列与\({e_{t-1},e_{t-2},\cdots}\)序列的散点图（scatter plot）
辅助回归法：构建残差\(e_t\)序列对\({e_{t-1},e_{t-2},\cdots}\)序列的辅助回归方程
自相关和偏相关分析法：Eviews菜单操作对残差\(e_t\)序列进行自相关和偏相关分析（注意滞后阶数的选择）
Durbin-Watson检验法：分析Eviews报告中的D-W统计量
拉格朗日检验法（LM-test）：Eviews菜单操作进行布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)
（3）自相关问题模型的矫正方法：
广义最小二乘法(GLS)：一阶差分法变换
广义最小二乘法(GLS)：基于残差辅助方程近似得到\(\rho\)
广义最小二乘法(GLS)：基于D-W统计量近似计算得到\(\rho\)
广义最小二乘法(GLS)：基迭代法近似计算得到\(\rho\)
一致标准误校正法（HAC）：尼威-威斯特(Newey-West)校正法
7.4 实验准备
7.4.1 实验软件
本次实验需要提前准备好如下软件：
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或 360极速浏览器9.5版本及以上
7.4.2 实验材料
商业部门的工资水平与生产率： 表 7.1 给出给出了美国46个商业部门Y部门工资水平，X部门生产率等方面的数据。
| obs | Y | X |
|---|---|---|
| 1960 | 61 | 49 |
| 1961 | 62 | 51 |
| 1962 | 65 | 53 |
| 1963 | 66 | 55 |
| 1964 | 68 | 57 |
| 2001 | 114 | 119 |
| 2002 | 116 | 124 |
| 2003 | 118 | 129 |
| 2004 | 119 | 133 |
| 2005 | 120 | 136 |
变量说明见 表 7.2：
| variable | label |
|---|---|
| obs | 年份 |
| Y | 部门工资水平 |
| X | 部门生产率 |
请考虑如下样本回归模型：
\[ \begin{aligned} log(Y_t)=\hat{\beta}_1+\hat{\beta}_2log(X_{2t})+e_{t} \end{aligned} \tag{7.11}\]
7.4.3 实验规则
本实验将要求保留Eviews操作过程的相关结果，因此对Eviews对象命名规则设计如下：
（1）方程对象（Equation）
的命名规则：
主回归方程对象保存命名为
eq_m0自相关问题诊断中的辅助回归方程，根据具体诊断类型，酌情保存并命名为：残差AR1辅助方程诊断法：
eq_ar1_test；\(\cdots\)自相关问题GLS矫正后的回归方程，根据具体矫正类型，酌情保存并命名为：
Tip
基于残差辅助方程结果进行1阶广义差分（GLS）矫正：
eq_adj_ar1基于D-W统计量结果进行广义差分（GLS）矫正：
eq_adj_dw自相关问题可行广义最小二乘法(FGLS)矫正后的回归方程，根据具体矫正类型，酌情保存并命名为：
基于科克伦-奥克特迭代法(Cochrane-Orcutt iterative procedure)：
eq_adj_co
- 自相关问题一致性标准误校正法（HAC），也即尼威-威斯特(Newey-West)校正法矫正后的回归方程，保存并命名为：eq_adj_nw
（2）序列对象（Series）
的命名规则：
（主回归方程的）残差序列，保存并命名为
et（主回归方程的）标准化残差序列，保存并命名为
et_sd（主回归方程的）倍数放大（或缩小）的残差序列（此处为放大100倍，具体应视案例而定），保存并命名为
et_100
-（主回归方程的）残差滞后序列，酌情分别保存并命名为：et_l1；et_l2；\(\cdots\)。
（3）图形对象（Graph）
的命名规则：
残差\(e_t\)、标准化残差\(e_t^{\ast}\)、倍数放大残差\(\hat{e}_t\)的描点图（dot plot），绘制成一张图，保存并命名为并命名为：
dot_resid残差\(e_t\)相对于残差一阶滞后变量\(e_{t-1}\)的散点图（scatter）,保存并命名为并命名为：
scatter_et
（4）表格对象（Table）
的命名规则：
自相关问题的自相关和偏相关诊断法，另存并命名为：
tab_corrl_test自相关问题的拉格朗日诊断法（LM-test），另存并命名为：
tab_LM_test
（5）标量对象（Scalar）
的命名规则。自相关问题模型矫正的不同方法中，可能会计算得到\(\rho\)的近似\(\hat{\rho}\)，具体命名视不同矫正方法：
基于残差辅助方程结果进行1阶广义差分（GLS）矫正：
rho_ar1基于D-W统计量结果进行广义差分（GLS）矫正：
rho_dw基于科克伦-奥克特迭代法的可行广义最小二乘法(FGLS)矫正：
rho_co
7.5 主要实验步骤
7.5.1 导入数据并进行预处理
新建Eviews工作文件（见 图 7.2）。Eviews菜单操作如下：
依次操作：File\(\Rightarrow\)New\(\Rightarrow\)Workfile
进行workfile create引导设置：
Tip
具体设置如下：
a）workfile structure type: unstructured/undatede
b）data range：46
c）workfile names(optional):
WF:
wage（建议命名）Page:
corrl（建议命名）
Eviews导入数据。菜单操作（Excel和Eviews）步骤如下：
提示：Excel数据，每个同学的Y数据都不同，找到自己学号对应下的Y数据（X数据所有同学都一样）
Excel找到数据。Excel表格中仅保留自己需要的数据（obsYX）
Eviews导入数据。File\(\Rightarrow\)Import\(\Rightarrow\)Import From File：
d:/econometrics/data/Lab7-wage.xlsx
7.5.2 采用最小二乘法建立主回归模型
主回归模型为
\[log(Y_t)=\hat{\beta}_1+\hat{\beta}_2log(X_{2t})+e_{t}\]
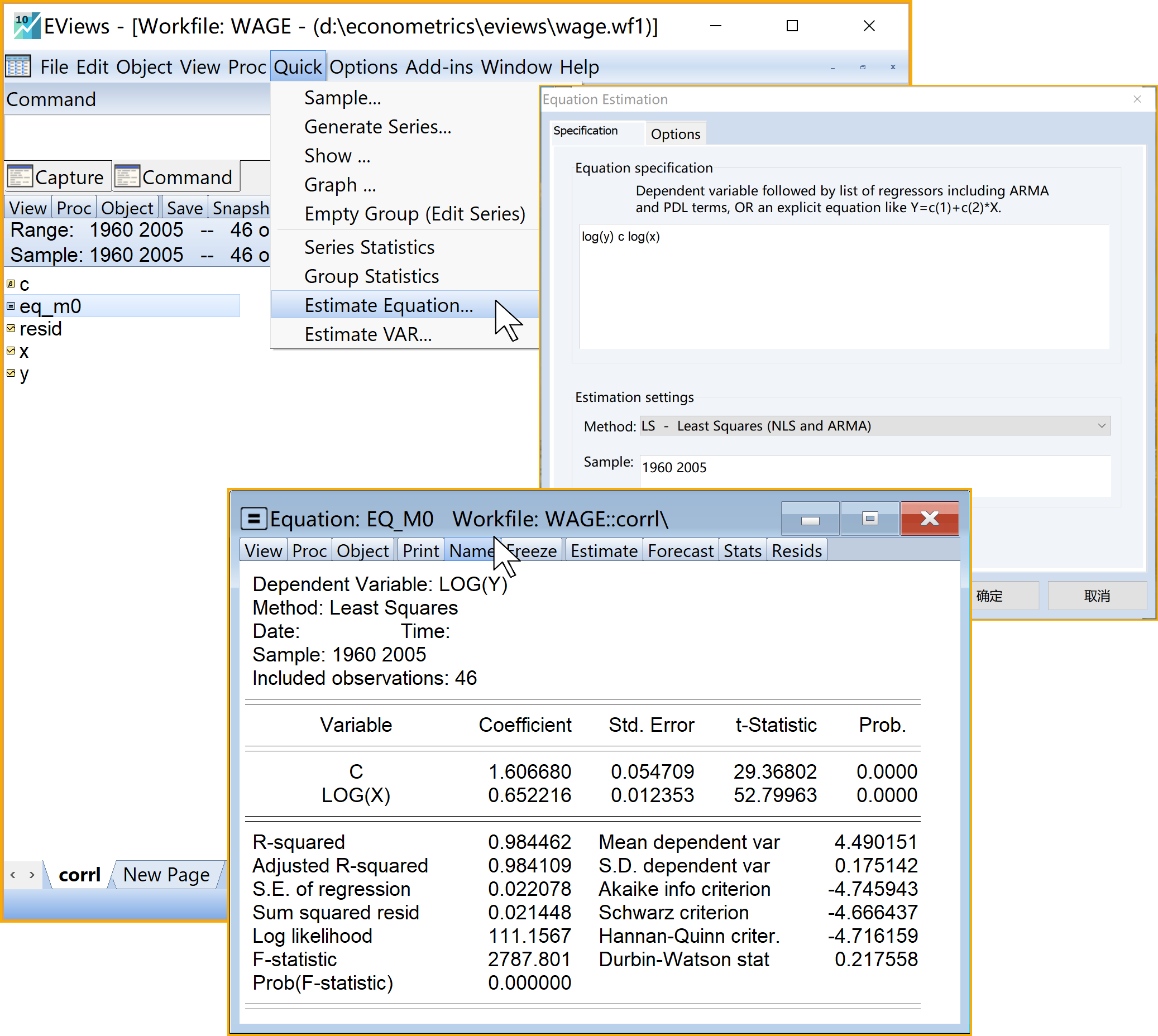
Eviews菜单操作（见 图 7.3）：
（1）依次选择\(\Rightarrow\)Quick\(\Rightarrow\)Estimation Equation
（2）引导设置Equation Estimation\(\Rightarrow\)specification
Tip
具体设置如下
a）Equation specification：
- 输入命令 log(Y) c log(X)
b）Estimation settings：
- Method: 下拉选择
LS - Least Squares (NLS and ARMA) - Sample: 默认设置
c）点击OK
（3）模型命名：建议为eq_m0
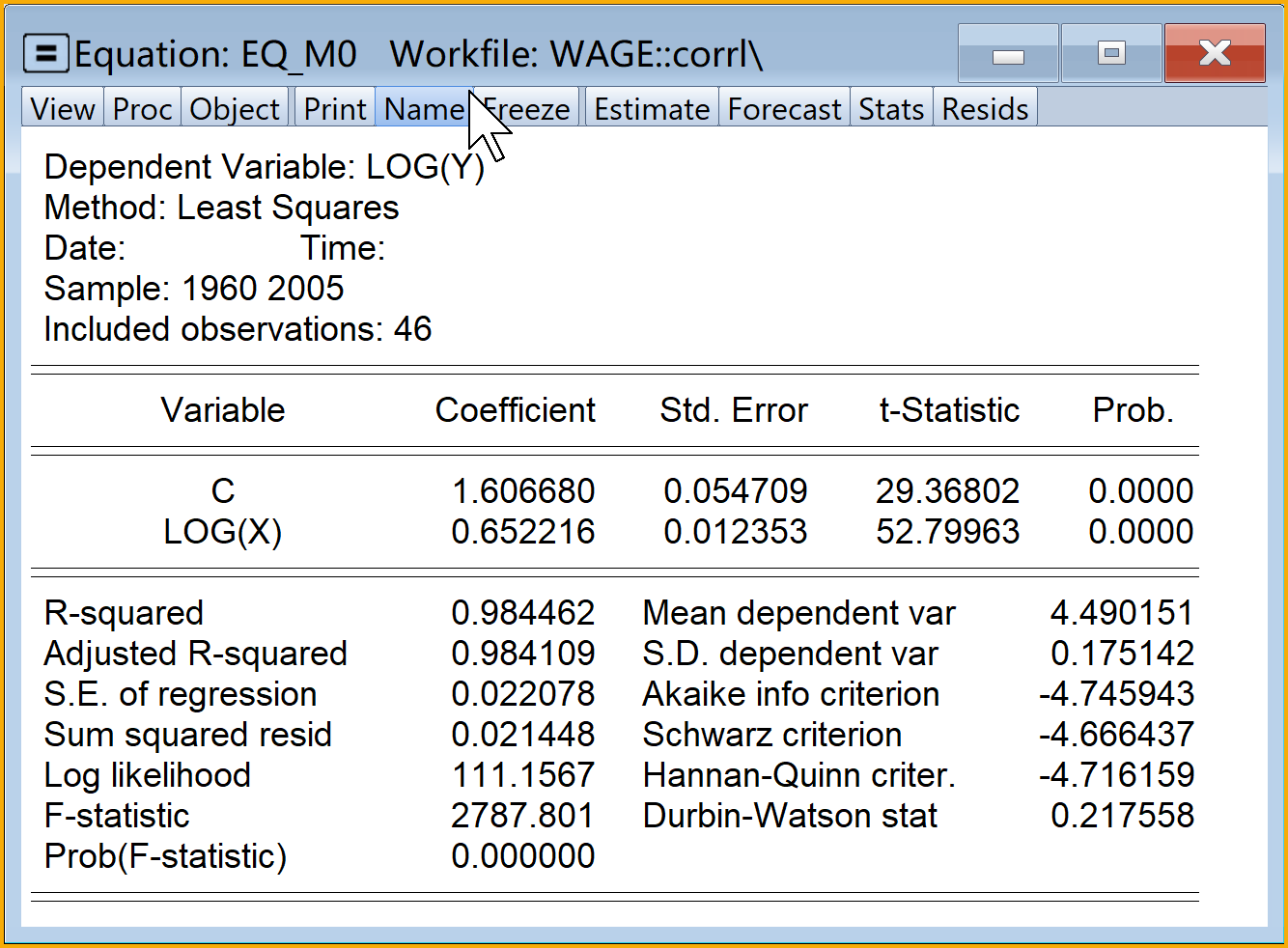
主回归分析结果见 图 7.4：
7.5.3 侦查模型是否存在自相关问题
诊断方法包括残差观察法、辅助回归法、自相关和偏相关分析法、Durbin-Watson检验法、拉格朗日检验法（LM-test）等。分析Eviews诊断报告，与相关参考标准进行比较，得到相关结论
7.5.3.1 残差观察法
目标：观察残差序列、标准化残差序列，以及残差滞后序列之间的图形模式和图形关系的图形模式
思路：判定\(e_t,e^{\ast}_t,e_{t-1},\cdots,e_{t-s}\)等的图形模式和关系
Tip
提示：
描点图（dot plot）是分析一个变量的图形模式。例如残差\(e_t\)或标准化残差\(e^{\ast}_t\)（做纵轴）相对于时间\(t\)（做横轴）的图形关系
散点图（scatter plot）是分析两个变量之间的图形模式。例如\(e_t\)（做纵轴），相对于\(e_{t-1}\)或\(e_{t-2}\)或\(e_{t-s}\)的图形关系。
Eviews菜单操作：
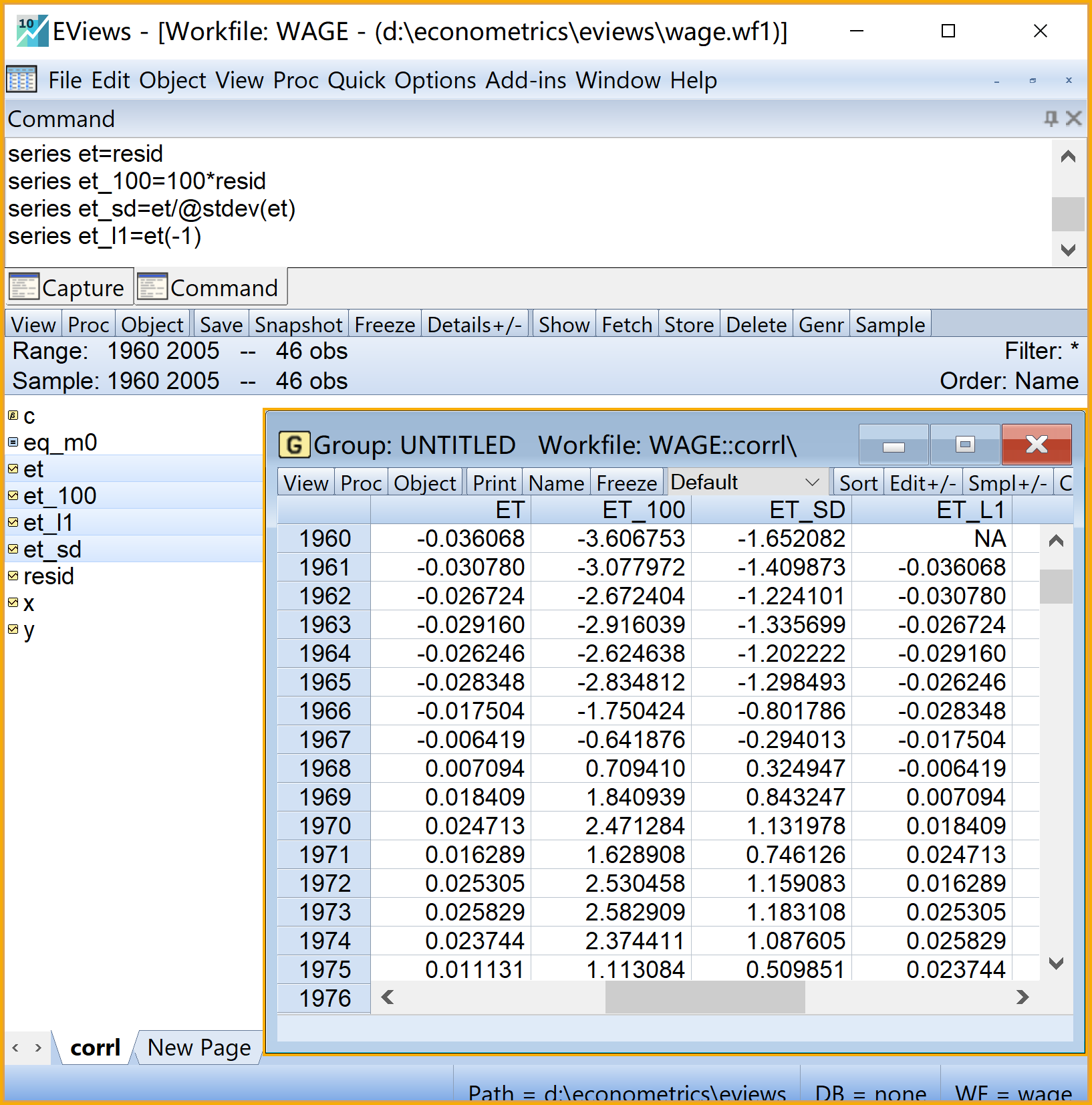
（1）分别生成残差序列\(e_t\)、放大100倍的残差（请根据实际情况酌情考虑调整倍数，目的是便于与标准化残差做比较）、标准化残差序列\(e^{\ast}_t\)和滞后一阶变量\(e_{t-1}\)序列（见 图 7.5）
- 命令视窗（Command）依次输入命令（建议分别命名为
et、et_100、et_sd和et_l1）
series et=resid
series et_100=100*resid
series et_sd=et/@stdev(et)
series et_l1=et(-1)- 运行命令：命令行中按Enter键，并可以查看运行结果
Tip
查看运行结果：
双击
et双击
et_100双击
et_sd双击
et_l1
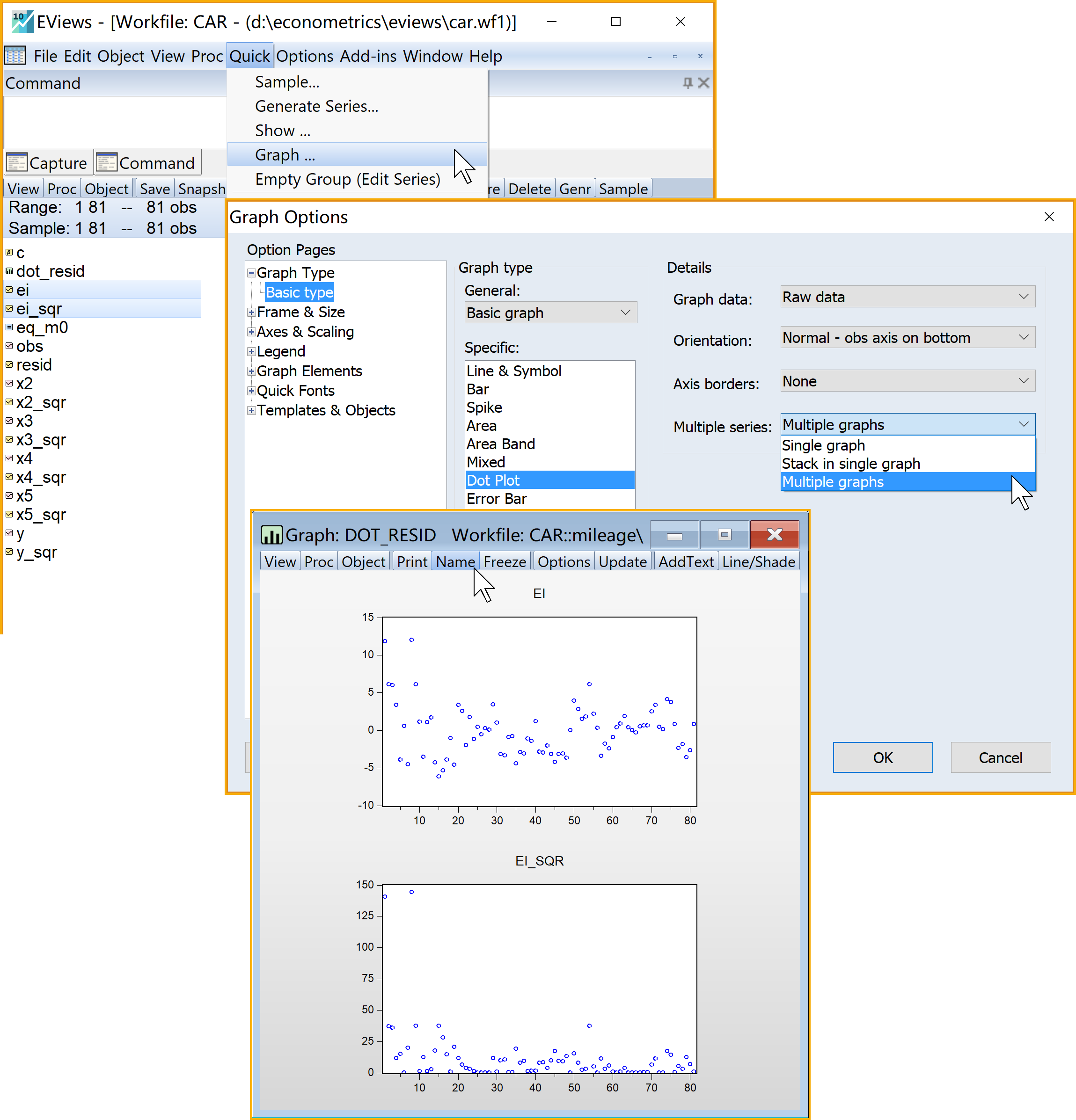
（2）绘制残差\(e_t\)和标准化残差\(e^{\ast}_t\)序列的描点图（dot plot）（见 图 7.6）
选择序列对象：键盘Ctrl键+依次单击选择序列
et和et_sd进入引导菜单：\(\Rightarrow\) Quick \(\Rightarrow\) Graph
Tip
具体设置细节：
选择绘图类型(Graph type)：Dot plot
选择绘图细节(Detail)：\(\Rightarrow\) Multiple series \(\Rightarrow\) 下拉选择 Multiple graphs
点击完成：OK
命名并保存绘图（graph）对象
：建议命名为dot_resid查看结果：双击
dot_resid（见 图 7.7）
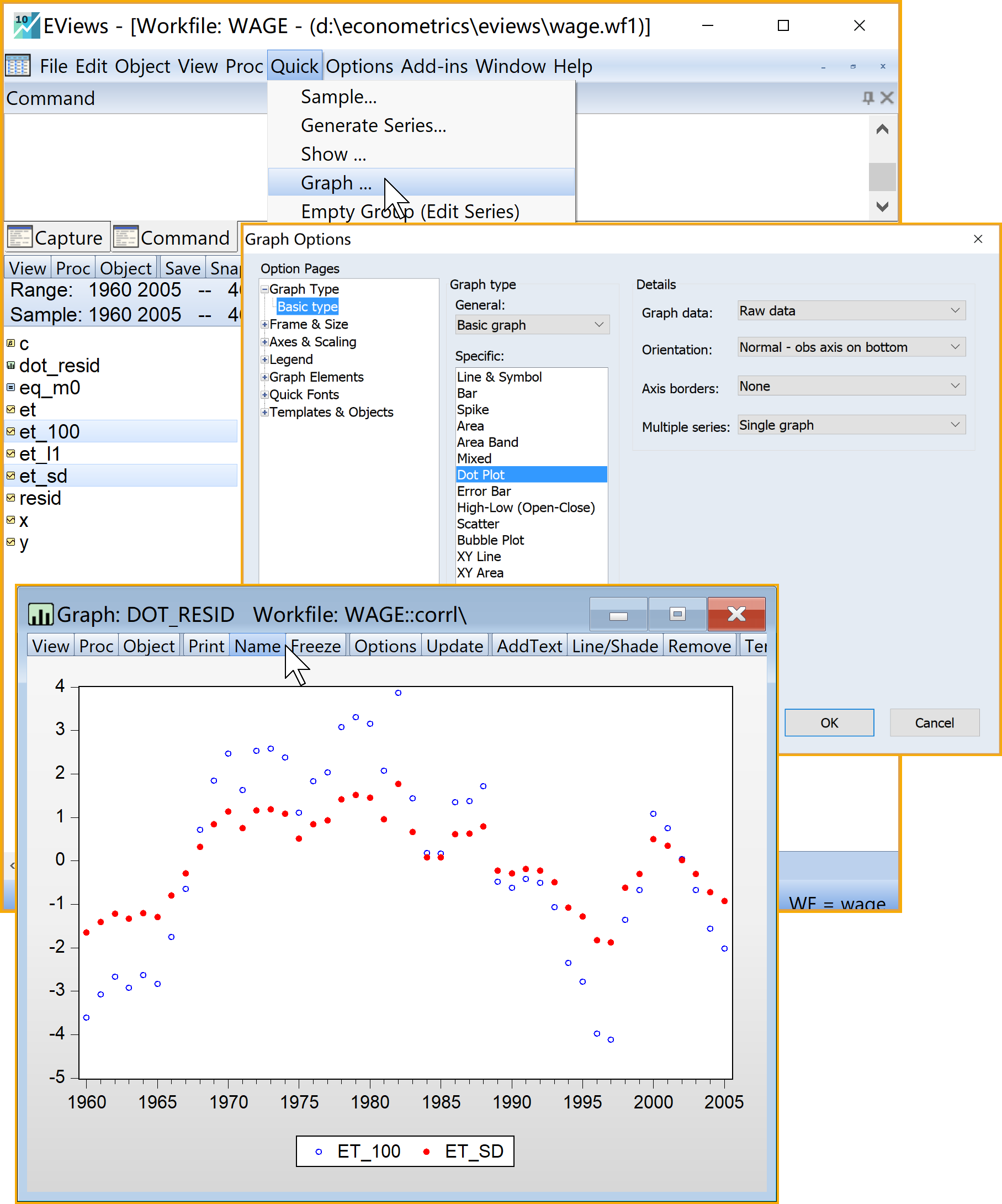
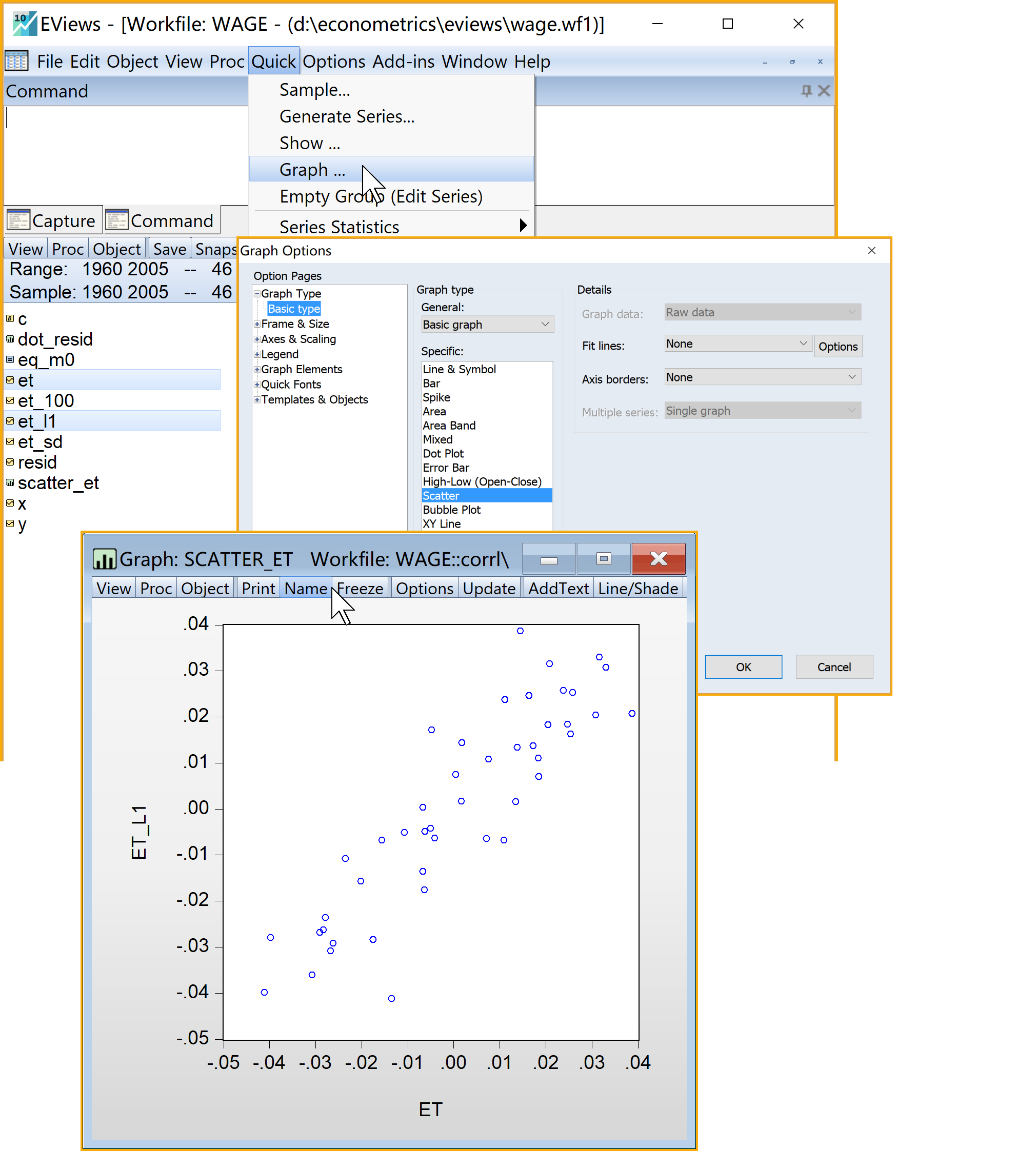
（3）绘制\(e_t\)序列对\(e_{t-1}\)的散点图（scatter plot）（见 图 7.8）
选择序列对象：键盘Ctrl键+依次单击选择序列
et；et_l1进入引导菜单：\(\Rightarrow\) Quick \(\Rightarrow\) Graph
Tip
具体设置细节：
选择绘图类型(Graph type)：Scatter
选择绘图细节(Detail)：默认设置
点击完成：OK
命名并保存绘图（graph）对象
：建议命名为scatter_et查看结果：双击
scatter_et（见 图 7.8）
7.5.3.2 辅助回归法
目标：根据残差图模式，构建残差辅助回归方程，得到你的初步结论
思路：分析残差\(e_t\)序列对\(e_{t-1},e_{t-2},\cdots\)序列的辅助回归方程 式 7.10 的Eviews报告
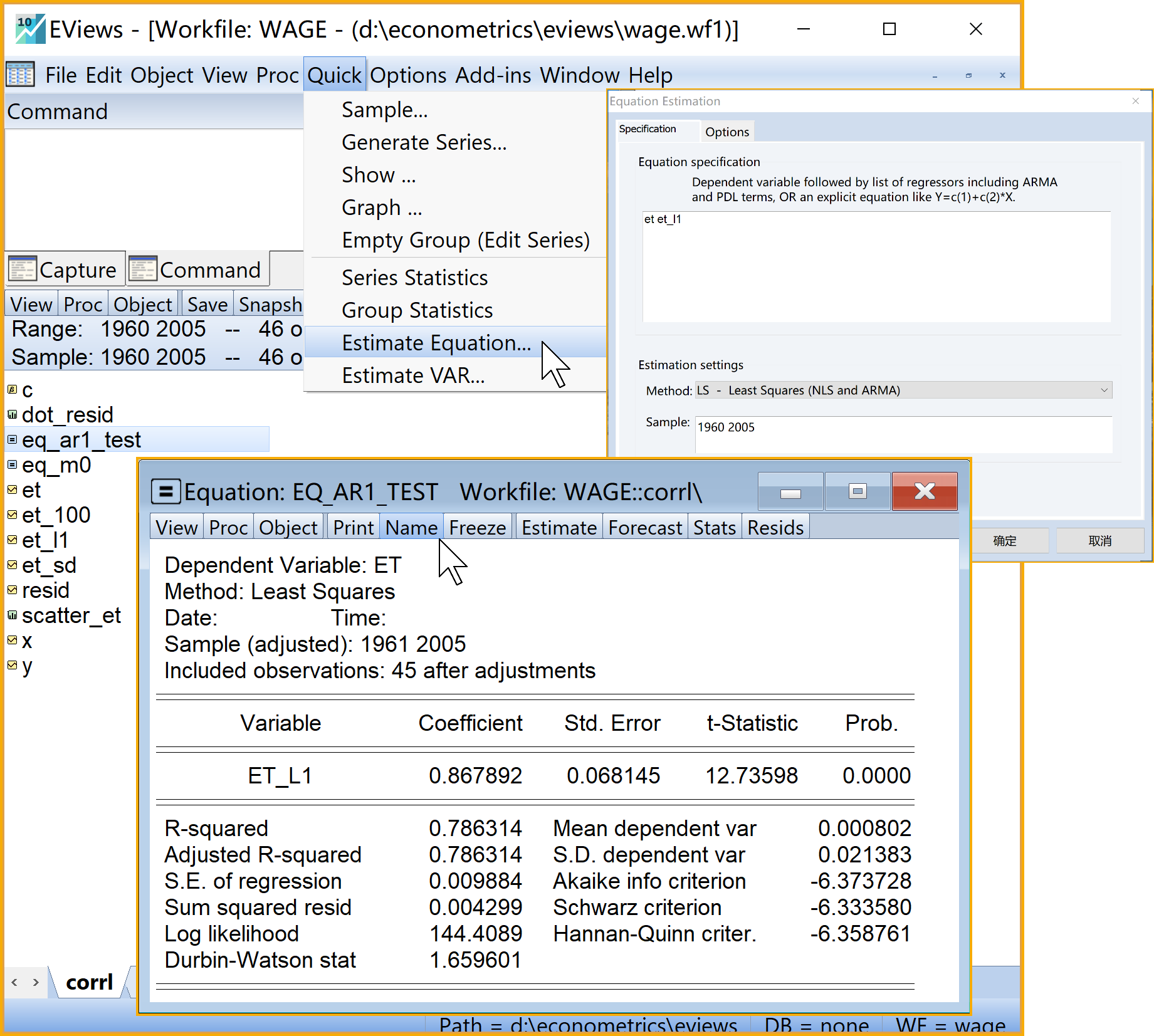
Eviews操作（此处仅展示AR(1)辅助回归方程的情形，菜单操作实现具体见 图 7.9）：
（1）依次选择\(\Rightarrow\) Quick \(\Rightarrow\) Estimation Equation
（2）引导设置Equation Estimation \(\Rightarrow\) specification
- Equation specification：输入命令et et_l1
Estimation settings：a）Method: 下拉选择LS - Least Squares (NLS and ARMA)；b）Sample: （默认设置）
点击完成：OK
命名保存方程对象
：（建议命名为eq_ar1_test）查看结果：双击
eq_ar1_test
具体Eviews报告见 图 7.10：
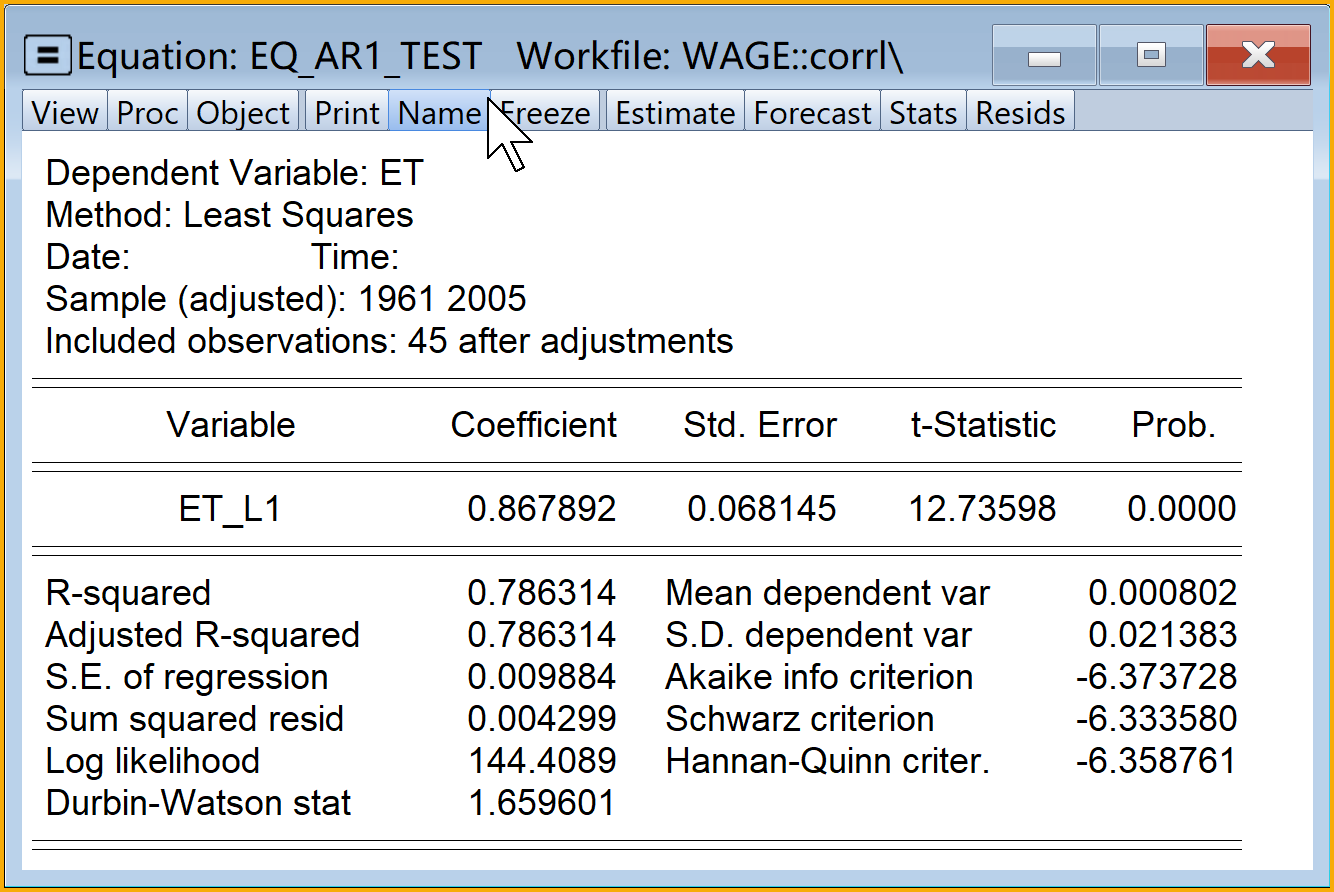
7.5.3.3 自相关和偏相关分析法
目标：根据残差自相关和偏相关图表结果，得到你的初步结论
思路：分析残差\(e_t\)序列对\(e_{t-1},e_{t-2},\cdots\)序列的自相关和偏相关Eviews报告（注意滞后阶数的选择）
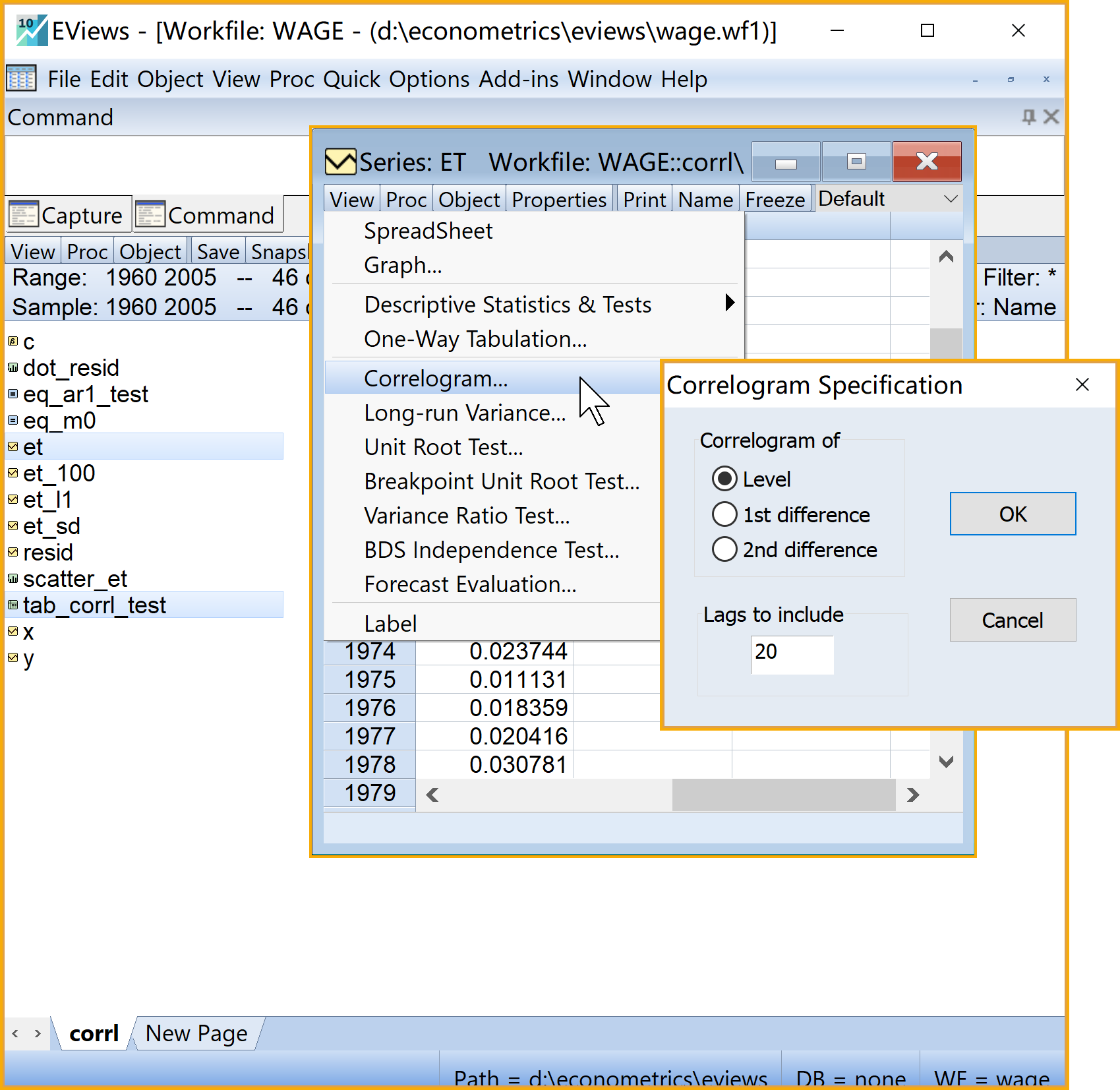
Eviews操作（菜单操作实现，具体见 图 7.11）：
（1）打开残差序列：双击序列（Series）对象et
（2）进入引导菜单：\(\Rightarrow\) View \(\Rightarrow\) Correlogram \(\Rightarrow\) Correlogram Specification
设置诊断序列（Correlogram of）: 点击选择Level
设置诊断阶数（Lags to include）：默认设置
（3）完成设置：点击Ok
（4）命名并保存表格（table）对象
另存为表格（table）对象：点击Freeze
命名并保存表格（talbe）对象：点击name(建议为tab_corrl_test)
查看结果：双击
tab_corrl_test
具体Eviews报告见 图 7.12：
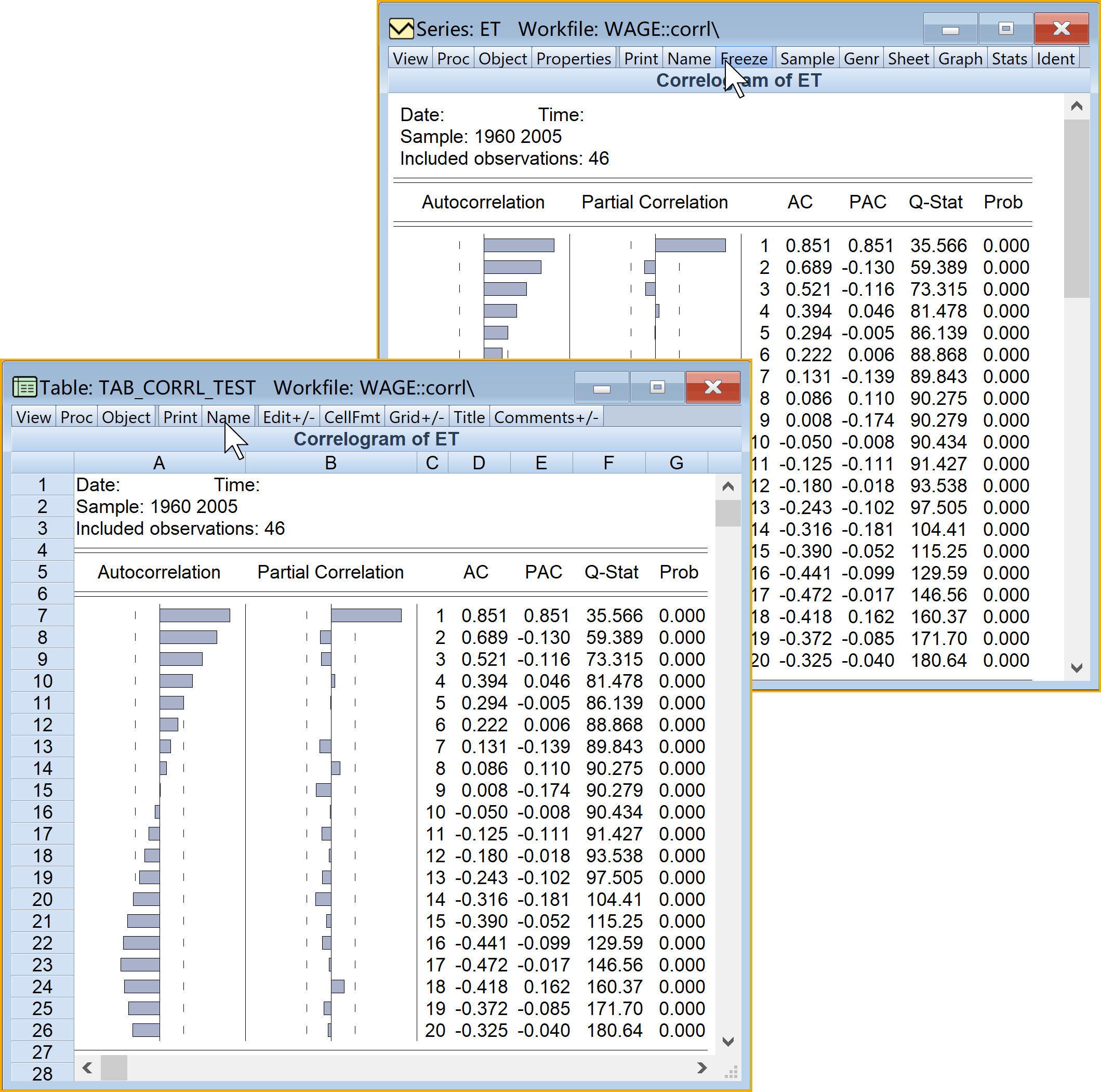
7.5.3.4 Durbin-Watson检验法
目标：观察主回归方程分析报告的D-W统计量，根据诊断标准，得出初步结论
思路：得到Durbin-Watson的d统计量，并查表得到理论\(\chi^2(n,k,\alpha)\)分布标准值\(d_L\)和\(d_U\)，进行比较
理论提示：
Durbin-Watson统计量服从\(\chi^2(n,k,\alpha)\)分布。具体可以参看Eviews在线帮助文档网址
\(d_L\)和\(d_U\)的理论值使用bootstrap方法仿真计算得到，与\((n,k,\alpha)\)有关
判定准则：
分析结论：根据主回归报告（见 图 7.4），Durbin-Watson的d统计量为\(d=0.22\)。 查表可知在当\((n='r n ',k=3,\alpha=0.05)\)时，\(d_L=1.475,d_U=1.566\)，表明\(0<d<d_L\)，因此认为主模型 式 7.11 可能存在的一阶正自相关问题。
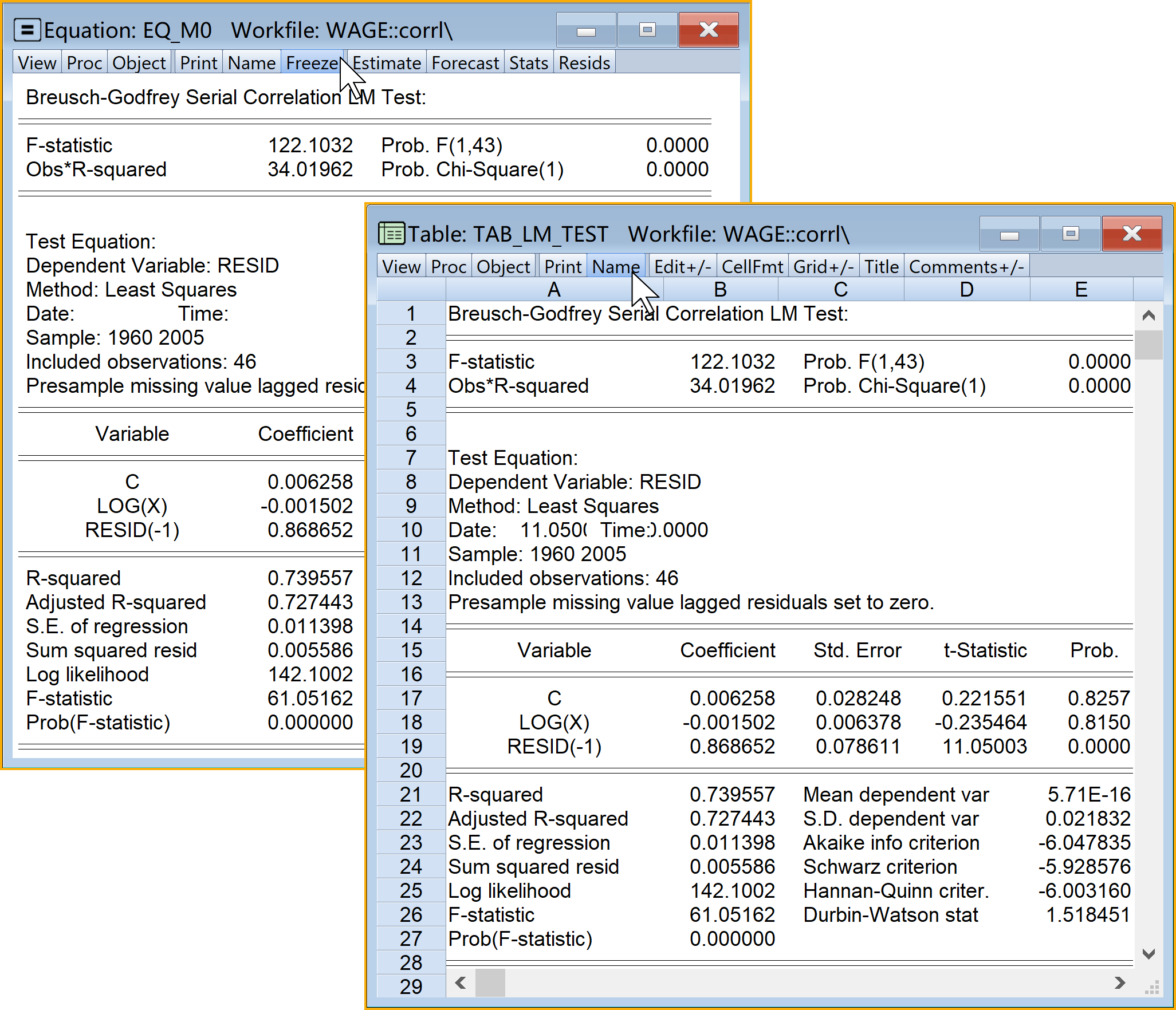
7.5.3.5 拉格朗日检验法（LM-test）
目标：对主回归方程进行布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)，根据诊断标准，得出初步结论
思路：利用Eviews菜单操作Residual Diagnostics \(\Rightarrow\) Serial Correlation LM Test
理论提示：
布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)可以检验高阶自相关的情形（见模型 式 7.12 ）
布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)将计算得到一个服从\(\chi^2\)分布的LM统计量，具体为\(LM=(n-p)R^2~\chi^2_p\)
\[ \begin{aligned} u_t=\rho_1e_{t-1}+\rho_2e_{t-2}+\cdots+\rho_pe_{t-p}+\varepsilon_t \end{aligned} \tag{7.12}\]
诊断标准：
如果LM检验不显著，也即\(LM<\chi^2(p,\alpha)\)，则表明主模型 式 7.11 不存在的p阶自相关问题
如果LM检验显著，也即\(LM>\chi^2(p,\alpha)\)，则表明主模型 式 7.11 存在的p阶自相关问题
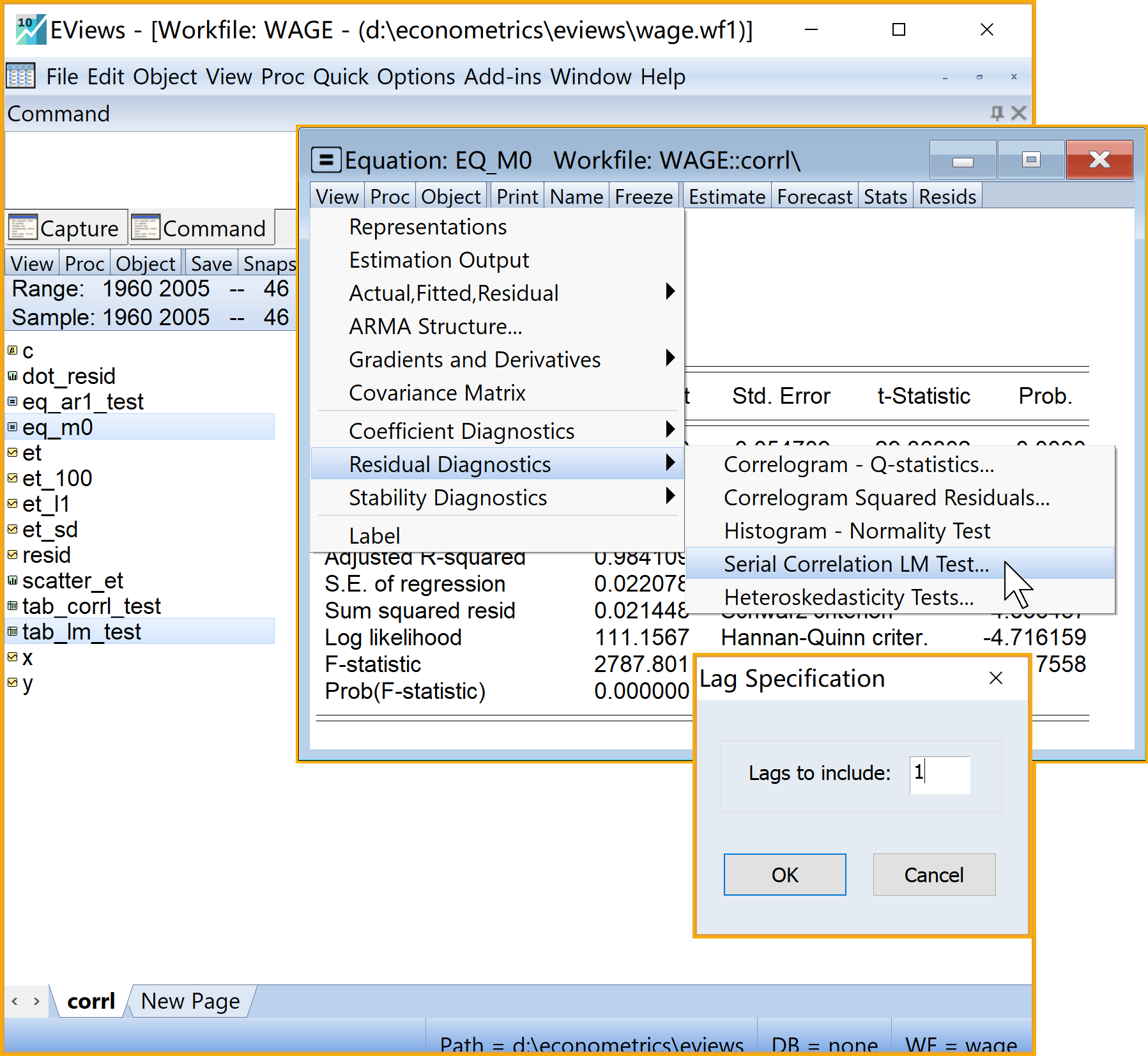
Eviews的菜单操作实现，具体见 图 7.13）：
（1）打开主方程：双击方程（equation）对象eq_m0
（2）进入引导菜单：\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Serial Correlation LM Test
（3）设置检验阶数（Lag Specification）: 输入滞后阶数1（酌情尝试）
（4）完成设置：点击Ok
（5）命名并保存表格（table）对象
另存为表格（table）对象：点击Freeze
命名并保存表格（table）对象：点击name(建议为tab_LM_test)
查看结果：双击
tab_LM_test
具体Eviews报告见 图 7.14：
7.5.4 自相关问题模型的矫正
自相关问题模型的矫正主要包括三类方法，分别是广义最小二乘法(GLS)、可行广义最小二乘法(FGLS)、一致性标准误校正法（HAC）。其中，广义最小二乘法(GLS)又包括了广义差分法变换、基于残差辅助方程近似估计法、以及基于D-W统计量近似计算法。下面我们将依次进行操作说明。
7.5.4.1 广义差分法变换（自相关系数已知）
目标：对主回归方程进行合适的广义差分变换，使得变换以后的新模型不再有自相关问题
思路：如果主模型随机干扰项的自相关系数已知（见模型 式 7.14 ），则可以直接用差分变换得到新模型（见模型 式 7.16 ），容易证明新模型将不再有自相关问题（见模型 式 7.17 ）。
理论提示：如下将展示一阶自相情形下的广义差分变换的理论过程
\[ \begin{aligned} Y_t & =\beta_1+\beta_2X_{2t}+u_{t} && \text{(PRM)} \end{aligned} \tag{7.13}\]
\[ \begin{aligned} u_t & =\rho u_{t-1}+\varepsilon_t && \text{(AR1)} \end{aligned} \tag{7.14}\]
\[ \begin{aligned} \rho Y_{t-1} & =\rho \beta_1+\beta_2\rho X_{2t-1}+\rho u_{t-1} && \text{(Lag 1 Model)} \end{aligned} \tag{7.15}\]
\[ \begin{aligned} (Y_t-\rho Y_{t-1}) & =\beta_1(1-\rho)+\beta_2(X_{2t}-\rho X_{2t-1})+(u_t-\rho u_{t-1}) && \Delta\text{(Model)} \end{aligned} \tag{7.16}\]
\[ \begin{aligned} Y^{\ast}_t & =\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2t}+\varepsilon_{t} && \text{(Adjusted Model)} \end{aligned} \tag{7.17}\]
其中，AR(1)模型 式 7.14 中的\(\varepsilon_t\sim i.i.d\ \ N(0,\sigma^2_{\varepsilon})\)。
7.5.4.2 基于残差辅助方程近似估计得到\(\rho\)（自相关系数未知）
目标：对主回归方程进行合适的广义差分变换，使得变换以后的新模型不再有自相关问题
思路：如果主模型随机干扰项的自相关系数未知（见模型 式 7.19 ），则可以直接用基于残差辅助方程估计得到\(\hat{\rho}\)，再根据\(\rho\simeq\hat{\rho}\)用广义差分变换得到新模型（见模型 式 7.23 ），容易证明新模型将不再有自相关问题（见模型 式 7.24 ）。
理论提示：如下将展示一阶自相关情形下的广义差分变换的理论过程
\[ \begin{aligned} Y_t & =\beta_1+\beta_2X_{2t}+u_{t} && \text{(PRM)} \end{aligned} \tag{7.18}\]
\[ \begin{aligned} u_t & =\rho u_{t-1}+\varepsilon_t && \text{(AR1)} \end{aligned} \tag{7.19}\]
\[ \begin{aligned} Y_t & =\hat{\beta}_1+\hat{\beta}_2X_{2t}+e_{t} && \text{SRM} \end{aligned} \tag{7.20}\]
\[ \begin{aligned} e_t & =\hat{\rho}e_{t-1}+v_t && \text{(Auxiliary Model)} \end{aligned} \tag{7.21}\]
\[ \begin{aligned} \rho & \simeq \hat{\rho} \notag \\ \rho Y_{t-1} & =\rho \beta_1+\beta_2\rho X_{2t-1}+\rho u_{t-1} && \text{(Lag 1 Model)} \end{aligned} \tag{7.22}\]
\[ \begin{aligned} (Y_t-\rho Y_{t-1}) & =\beta_1(1-\rho)+\beta_2(X_{2t}-\rho X_{2t-1})+(u_t-\rho u_{t-1}) && \Delta1\text{ (Model)} \end{aligned} \tag{7.23}\]
\[ \begin{aligned} Y^{\ast}_t & =\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2t}+\varepsilon_{t} && \text{(Adjusted Model)} \end{aligned} \tag{7.24}\]
其中，AR(1)模型 式 7.19 中的\(\varepsilon_t\sim i.i.d\ \ N(0,\sigma^2_{\varepsilon})\)。
Eviews菜单操作：
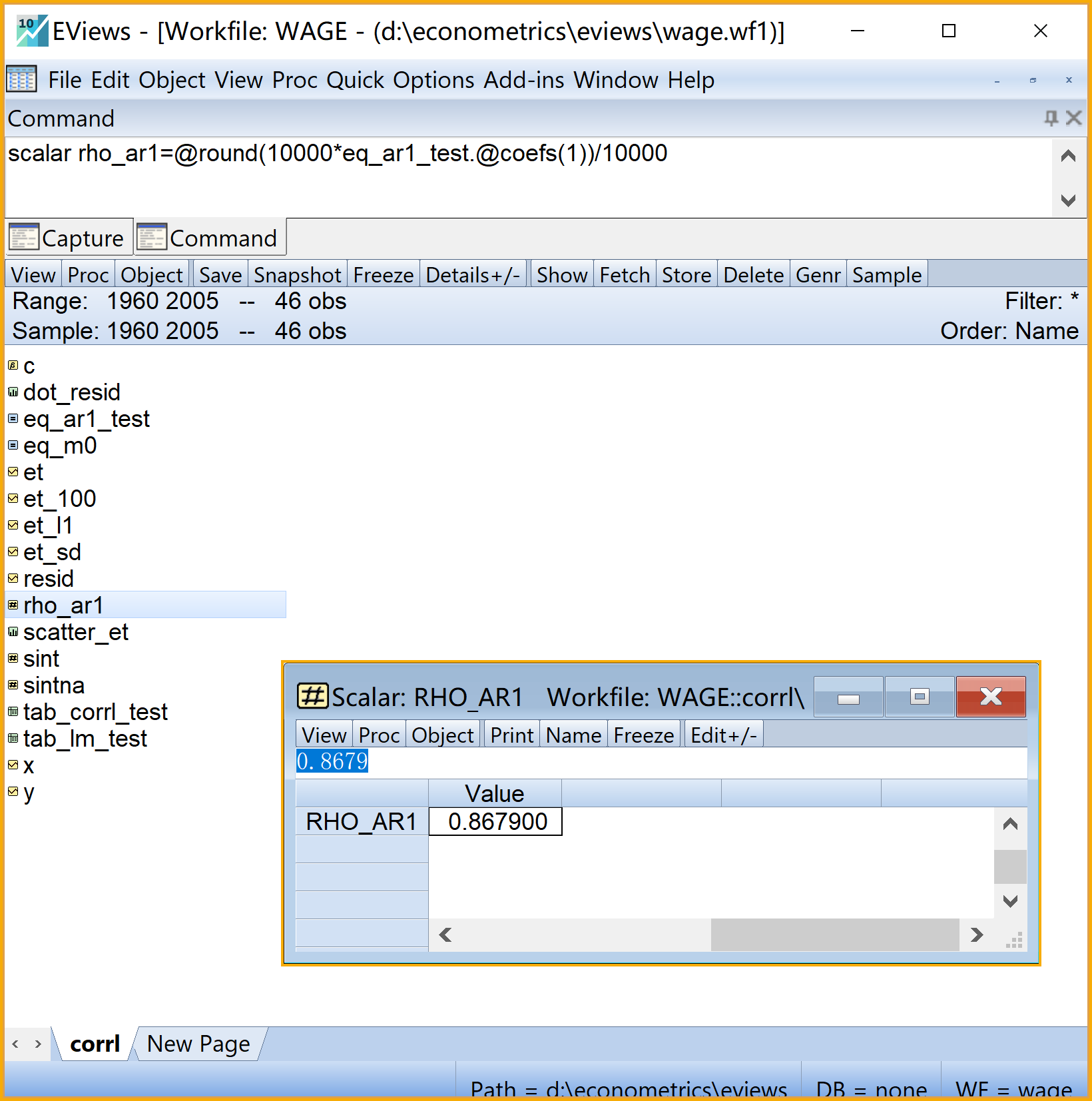
（1）提取辅助回归方程的回归系数。构建一个标量（Scalar）对象rho_ar1，并将辅助回归方程的回归系数赋值给这个标量对象rho_ar1。具体过程参看 图 7.15
命令视窗（Command）输入命令 ：
scalar rho_ar1=@round(10000*eq_ar1_test.@coefs(1))/10000运行命令：命令行中按Enter键
查看结果：双击
rho_ar1
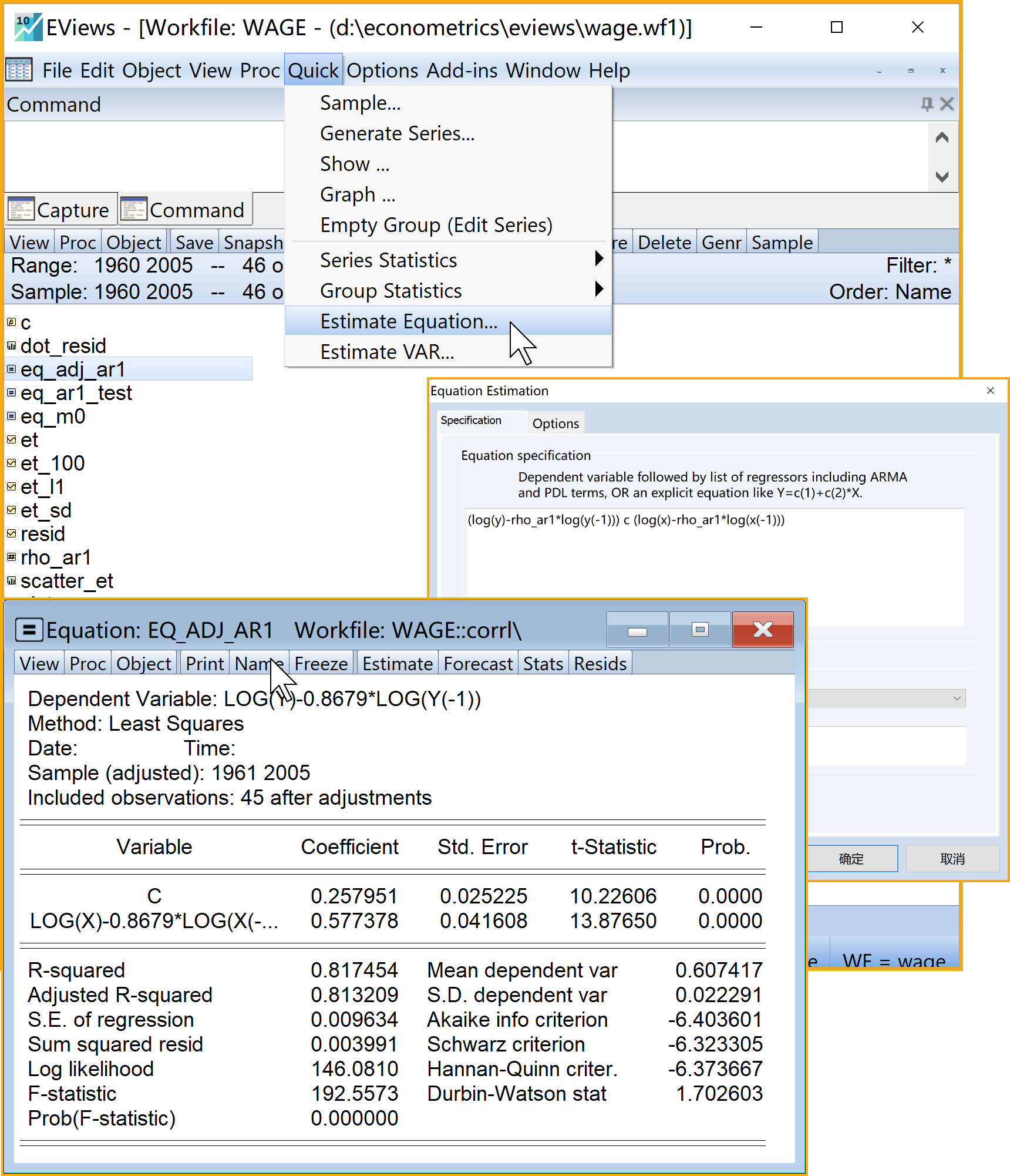
（2）进行一阶广义差分变换，并估计新模型。依次选择\(\Rightarrow\)Quick\(\Rightarrow\)Estimation Equation\(\Rightarrow\)specification。具体过程参看 图 7.16
Equation specification：输入命令
(log(y)-rho_ar1*log(y(-1))) c (log(x)-rho_ar1*log(x(-1)))Estimation settings：具体设置如下
Tip
具体设置：
Method: 下拉选择
LS - Least Squares (NLS and ARMA)Sample: 默认设置
点击
OK模型命名：建议为
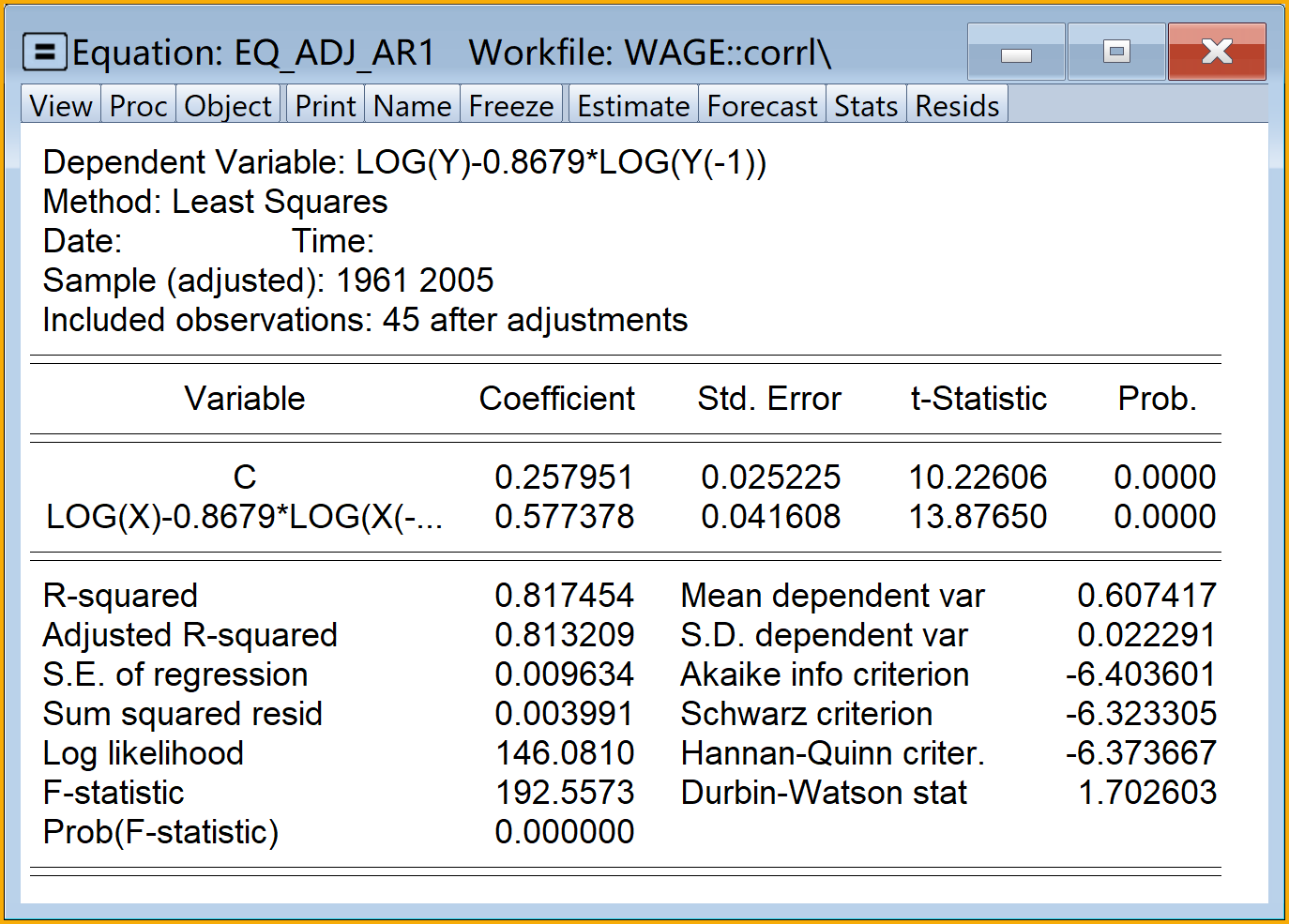
eq_adj_ar1查看结果：双击
eq_adj_ar1
（3）说明（Eviews代码行的解读。
具体细节请参看Eviews在线帮助文档。
代码
scalar rho_ar1=@round(10000*eq_ar1_test.@coefs(1))/10000表示给创建一个标量（Scalar）对象rho_ar1,并把辅助模型 式 7.10 的回归系数的第一个值提取出来，并赋值给这个名为rho_ar1的标量对象，同时保留四位小数。代码
eq_ar1_test.@coefs(1)表示提取方程（equation）对象eq_ar1_test的回归系数的第一个值。代码
@round(10000*( ))/10000表示对数据保留4为小数。
7.5.4.3 基于D-W统计量近似计算得到\(\rho\)（自相关系数未知）
目标：对主回归方程进行合适的广义差分变换，使得变换以后的新模型不再有自相关问题
思路：如果主模型随机干扰项的自相关系数未知（见模型 式 7.26 ），则可以基于Durbin-Waston检验的d统计量计算得到\(\hat{\rho}\)（见模型 式 7.27 和模型 式 7.28 ），再根据\(\rho\simeq\hat{\rho}\)用广义差分变换得到新模型（见模型 式 7.30 ），容易证明新模型将不再有自相关问题（见模型 式 7.31 ）。
理论提示：如下将展示一阶自相情形下的广义差分变换的理论过程
\[ \begin{aligned} Y_t & =\beta_1+\beta_2X_{2t}+u_{t} && \text{(PRM)} \end{aligned} \tag{7.25}\]
\[ \begin{aligned} u_t & =\rho u_{t-1}+\varepsilon_t && \text{(AR1)} \end{aligned} \tag{7.26}\]
\[ \begin{aligned} d & \simeq2(1-\hat{\rho}) && \text{(Durbin-Waston)} \end{aligned} \tag{7.27}\]
\[ \begin{aligned} \hat{\rho} & \simeq 1-d/2 \end{aligned} \tag{7.28}\]
\[ \begin{aligned} \rho & \simeq \hat{\rho} \notag \\ \rho Y_{t-1} & =rho \beta_1+\beta_2\rho X_{2t-1}+\rho u_{t-1} && \text{(Lag 1 Model)} \end{aligned} \tag{7.29}\]
\[ \begin{aligned} (Y_t-\rho Y_{t-1}) & =\beta_1(1-\rho)+\beta_2(X_{2t}-\rho X_{2t-1})+(u_t-\rho u_{t-1}) && \Delta1\text{ (Model)} \end{aligned} \tag{7.30}\]
\[ \begin{aligned} Y^{\ast}_t & =\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2t}+\varepsilon_{t} && \text{(Adjusted Model)} \end{aligned} \tag{7.31}\]
其中，AR(1)模型 式 7.26 中的\(\varepsilon_t\sim i.i.d\ \ N(0,\sigma^2_{\varepsilon})\)。
Eviews菜单操作：
（1）提取并得到Durbin-Waston统计量。构建一个标量（Scalar）对象，建议命名为dw。具体过程参看 图 7.18
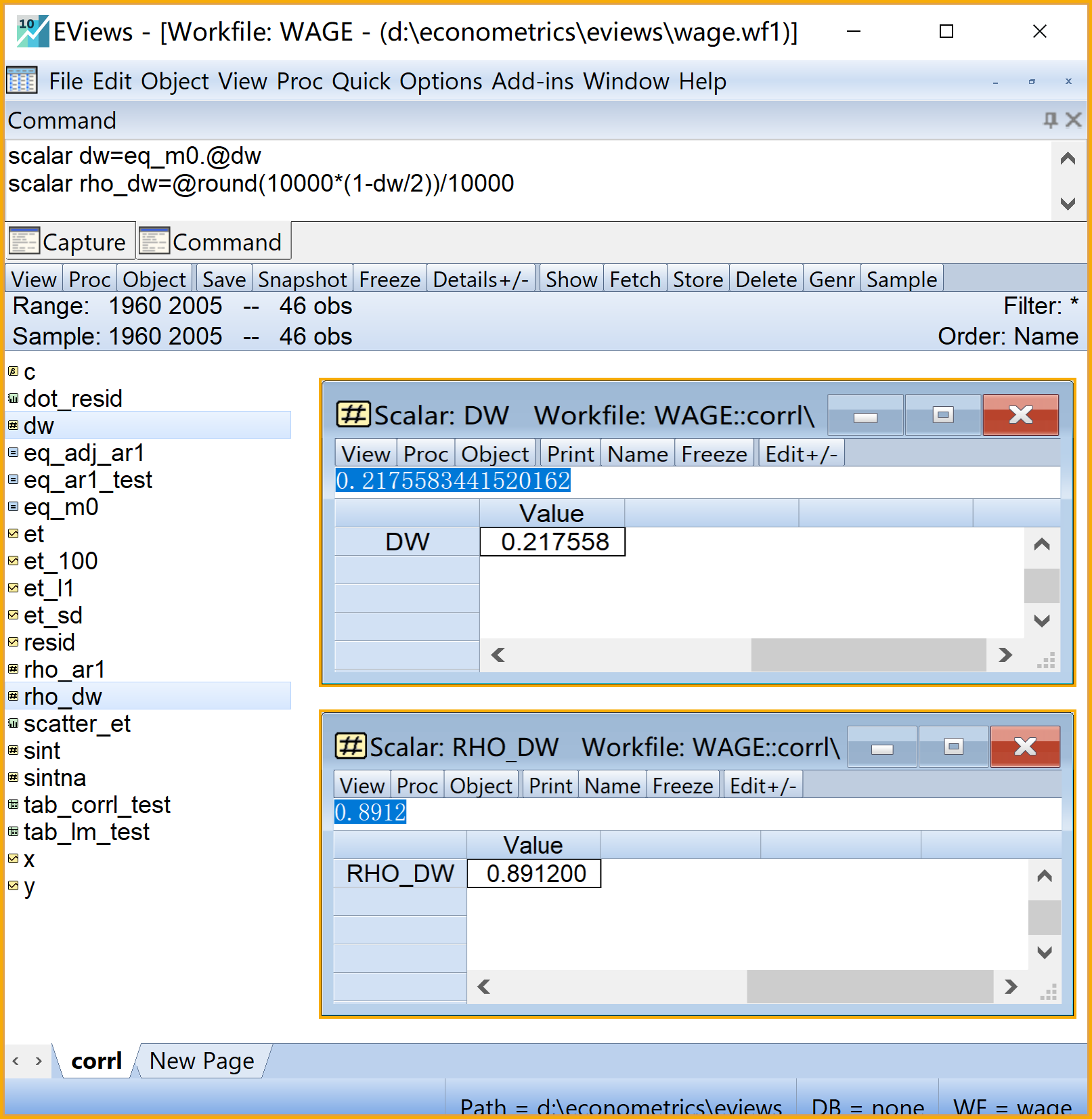
命令视窗（Command）输入命令 ：
scalar dw=eq_m0.@dw运行命令：命令行中按Enter键
查看结果：双击
rho_dw
（2）计算得到自相关系数的近似值\(\rho \simeq\hat{\rho}=1-d/2\)。构建一个标量（Scalar）对象，建议命名为rho_dw。具体过程参看 图 7.18 。
命令视窗（Command）输入命令 ：
scalar rho_dw=@round(10000*(1-dw/2))/10000运行命令：命令行中按Enter键
查看结果：双击
rho_dw
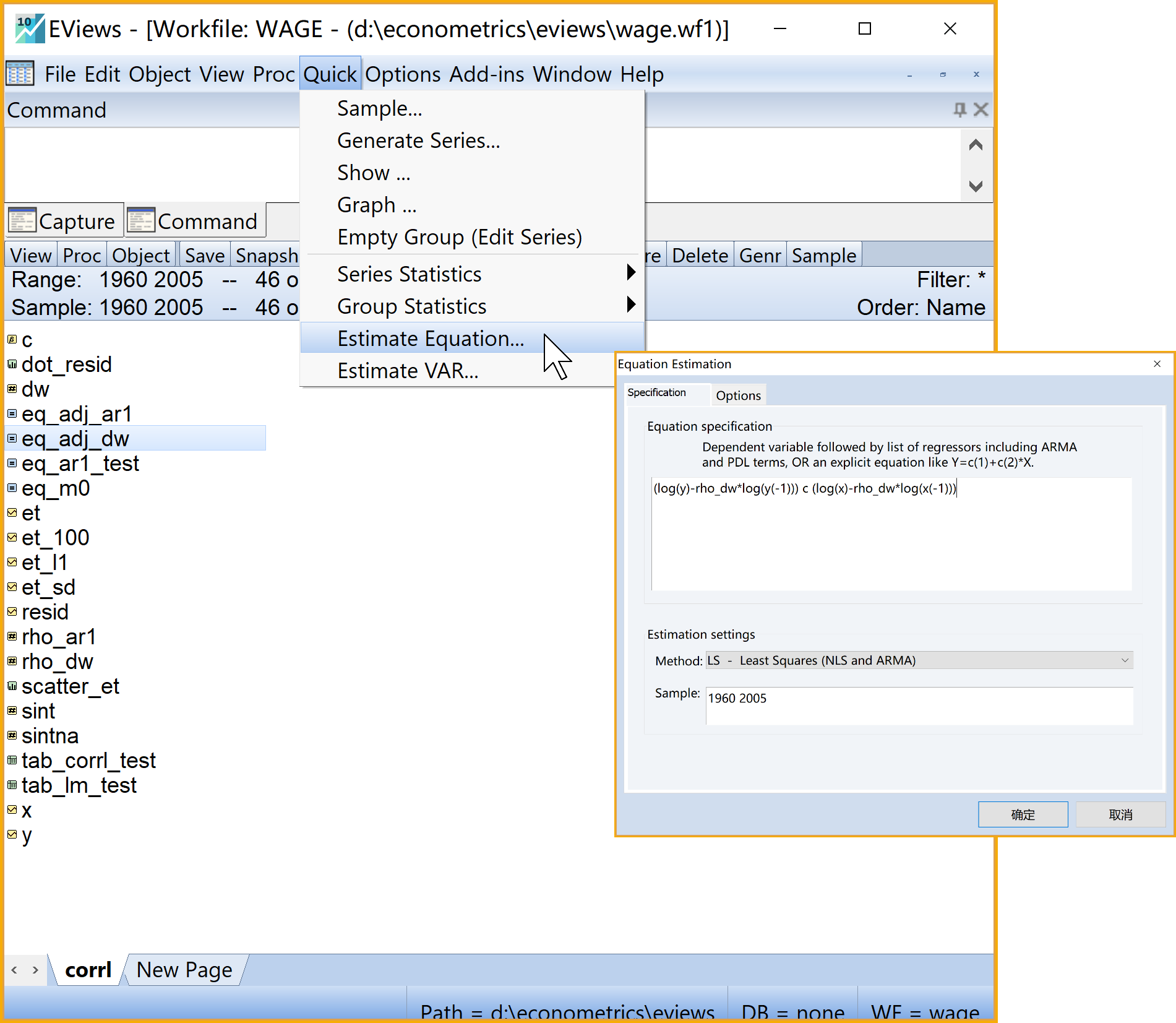
（3）进行一阶广义差分变换，并估计新模型。依次选择\(\Rightarrow\)Quick\(\Rightarrow\)Estimation Equation\(\Rightarrow\)specification。具体过程参看 图 7.19
Equation specification：输入命令
(log(y)-rho_dw*log(y(-1))) c (log(x)-rho_dw*log(x(-1)))Estimation settings：设置如下
Tip
具体设置：
Method: 下拉选择
LS - Least Squares (NLS and ARMA)Sample: 默认设置
点击
OK模型命名：建议为
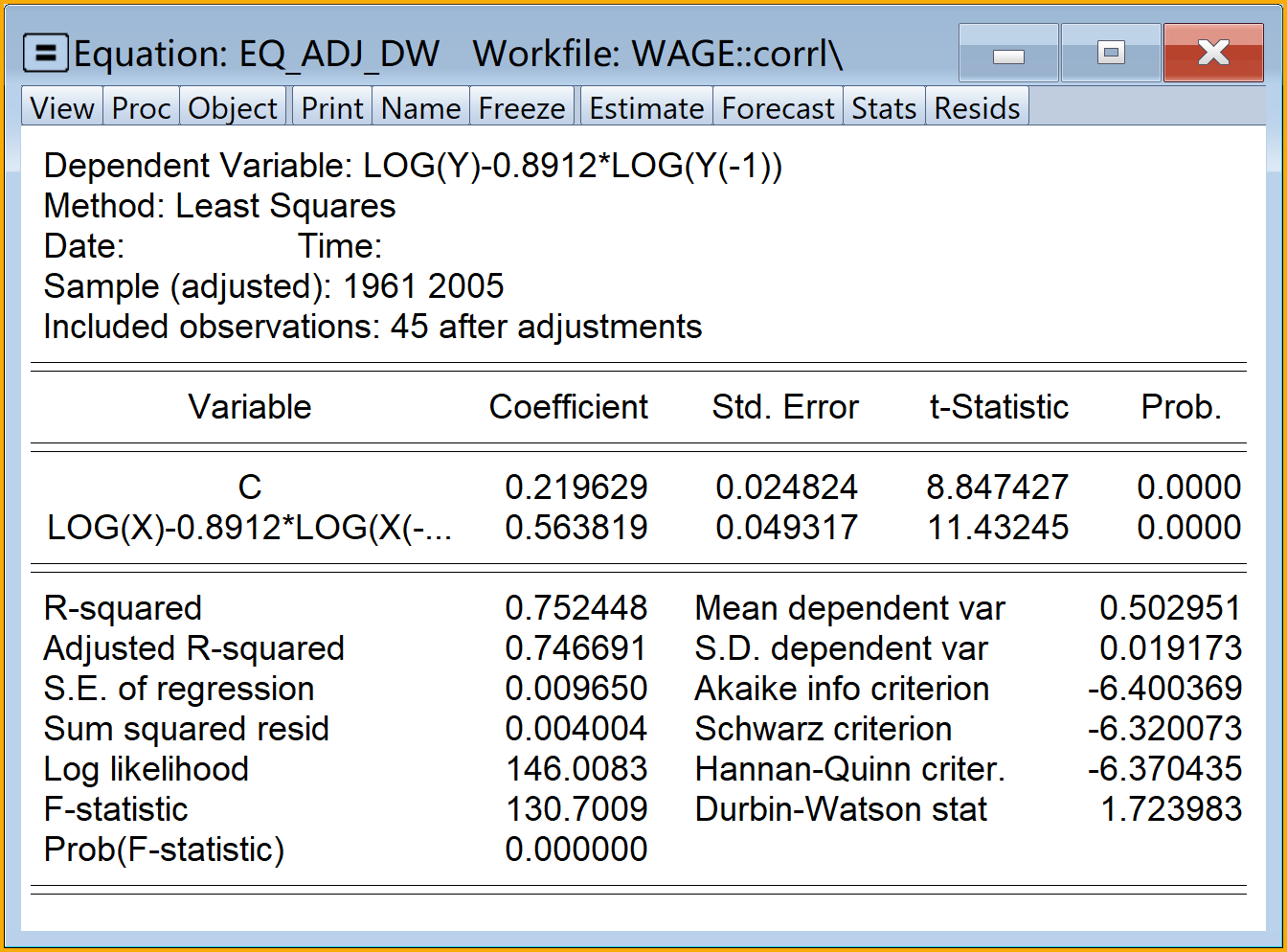
eq_adj_dw查看结果：双击
eq_adj_dw
（4）Eviews代码行的解读：
代码
scalar d=eq_m0.@dw表示给创建一个标量（Scalar）对象dw,并把主模型 式 7.11 的Durbin-Waston统计量值提取出来，并赋值给这个名为dw的标量对象。代码
scalar rho_dw=@round(10000*(1-dw/2))/10000计算得到标量（Scalar）对象rho_dw，并对数据取4位小数。
7.5.4.4 基迭代法近似计算得到\(\rho\)（自相关系数未知）
目标：基迭代法近似计算的方法被称为可行广义最小二乘法(FGLS)。对主回归方程进行合适的广义差分变换，使得变换以后的新模型不再有自相关问题
思路：
如果主模型随机干扰项的自相关系数未知，而且存在高阶自相关情形，则可以使用基于迭代的可行广义最小二乘法(FGLS)计算得到\(\hat{\rho_1},\hat{\rho_2},\cdots,\hat{\rho_p}\ \ p\in(1,2,\cdots)\)，再根据\(\rho\simeq\hat{\rho}\)用广义差分变换得到新模型（见模型 式 7.30 ），容易证明新模型将不再有自相关问题（见模型 式 7.31 ）。
这些迭代方法主要包括科克伦-奥克特迭代法(Cochrane-Orcutt iterative procedure) ;科克伦-奥克特两步法(Cochrane-Orcutt two-step procedure) ;德宾两步法(Durbin two-step procedure) ;希尔德雷思-卢扫描或搜寻程序(Hildreth-Lu scanning or search procedure) 等
理论提示：如下将展示科克伦-奥克特迭代法下对二阶自相关（\(AR(p),p=2\)）情形下的广义差分变换的理论过程
\[ \begin{aligned} Y_t & =\beta_1+\beta_2X_{2t}+u_{t} && \text{(PRM)} \end{aligned} \tag{7.32}\]
\[ \begin{aligned} u_t & =\rho_1u_{t-1}+\rho_2u_{t-2}+\varepsilon_t && \text{(AR2)} \end{aligned} \tag{7.33}\]
\[ \begin{aligned} \cdots & \text{Cochrane-Orcutt iterative procedure} \notag \\ \rho_p & \simeq \hat{\rho_p} \notag \\ \rho_1Y_{t-1} & =\rho_1\beta_1+\beta_2\rho_1X_{2t-1}+\rho_1u_{t-1} && \text{Lag 1 Model} \end{aligned} \tag{7.34}\]
\[ \begin{aligned} \rho_2Y_{t-2} & =\rho_2\beta_1+\beta_2\rho_2X_{2t-2}+\rho_2u_{t-2} && \text{Lag 2 Model} \end{aligned} \tag{7.35}\]
\[\begin{aligned} \begin{split} (Y_t-\rho_1Y_{t-1}-\rho_2Y_{t-2}) & =\beta_1(1-\rho_1-\rho_2)\\ & +\beta_2(X_{2t}-\rho_1X_{2t-1}-\rho_2X_{2t-2}) \\ & +(u_t-\rho_1u_{t-1}-\rho_2u_{t-2}) \end{split} && (\Delta2 \quad \text{Model}) \end{aligned} \tag{7.36}\]
\[ \begin{aligned} Y^{\ast}_t &=\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2t}+\varepsilon_{t} && \text{(Adjusted Model)} \end{aligned} \tag{7.37}\]
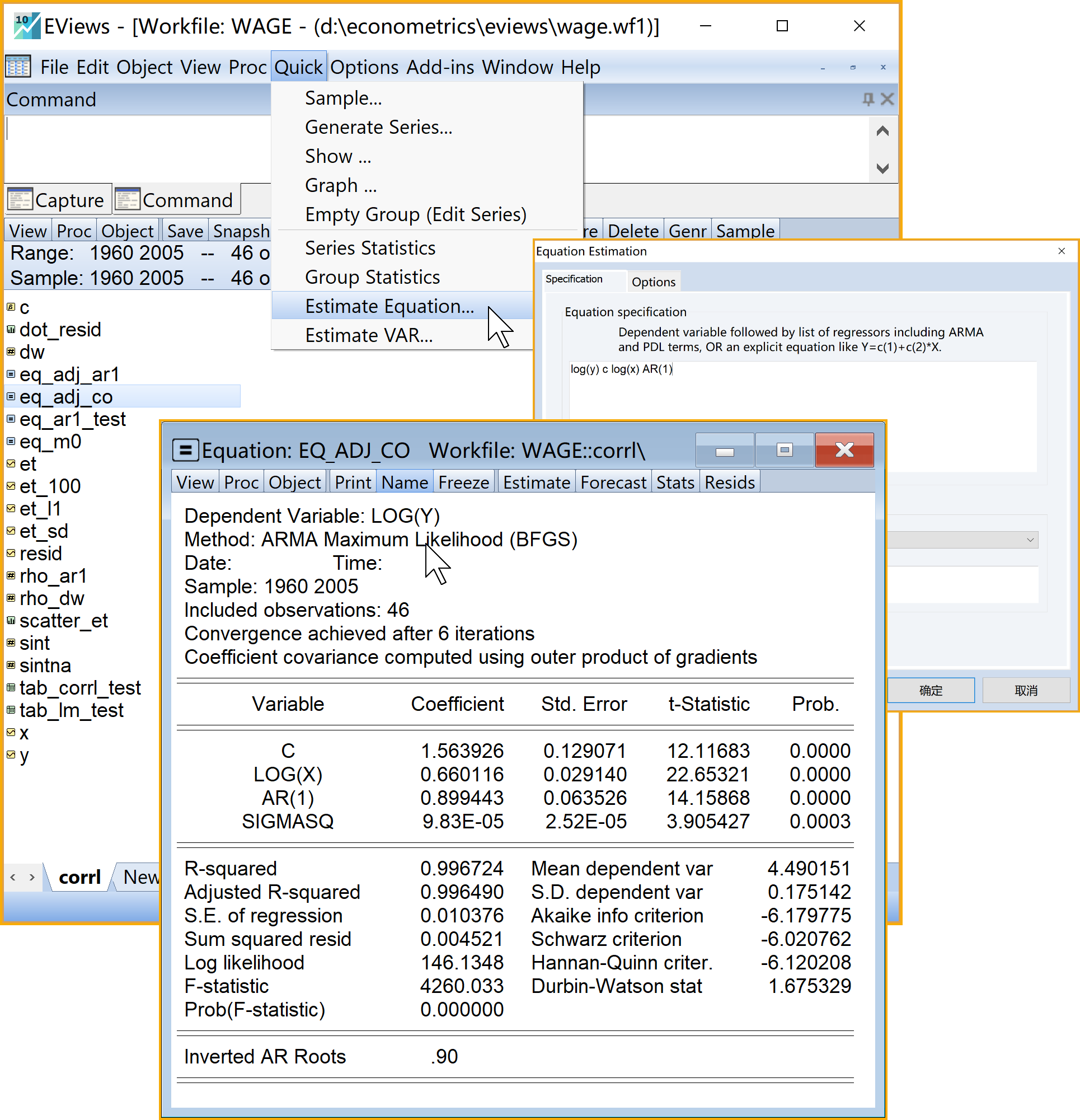
Eviews菜单操作（此处展示的是AR(1)的自相关情形，见 图 7.21）：
（1）依次选择\(\Rightarrow\)Quick\(\Rightarrow\)Estimation Equation
（2）引导设置Equation Estimation\(\Rightarrow\)specification
- Equation specification：输入命令log(Y) c log(X) AR(1)
- Estimation settings：具体设置如下
Method: 下拉选择`LS - Least Squares (NLS and ARMA)`
Sample: **默认设置**
- 点击
OK
（3）模型命名：建议为eq_adj_CO
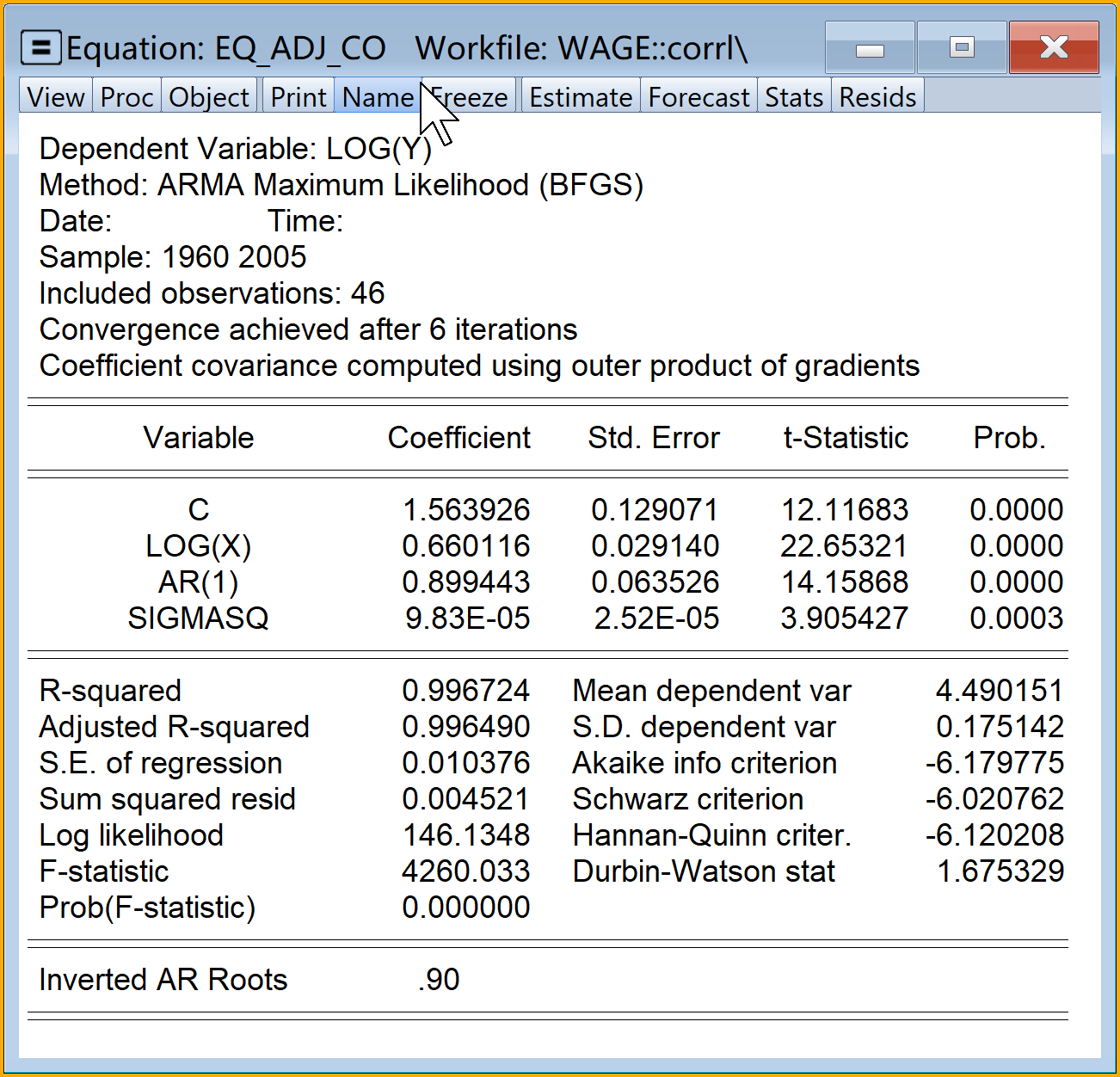
- 主回归分析结果见 图 7.22：
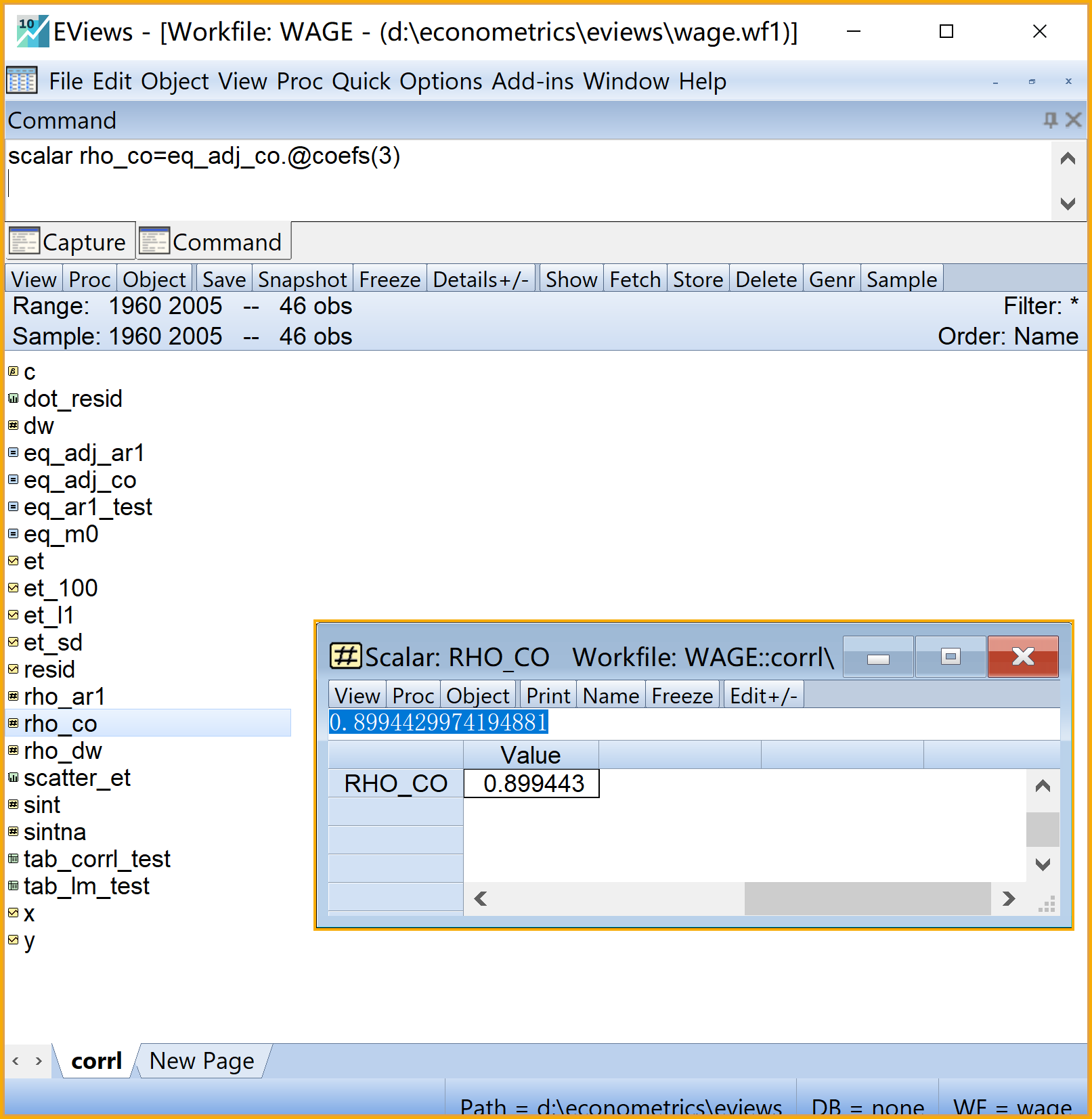
（4）提取并得到科克伦-奥克特迭代法下近似的残差自相关系数\(\rho\)。构建一个标量（Scalar）对象，建议命名为rho_co。具体过程参看 图 7.23
命令视窗（Command）输入命令 ：
scalar rho_co=eq_adj_co.@coefs(3)运行命令：命令行中按Enter键
查看结果：双击
rho_co
（5）Eviews代码行的解读：
- 代码
scalar rho_co=eq_adj_co.@coefs(3)表示给创建一个标量（Scalar）对象rho_co,并把方程（Equation）对象eq_adj_co的第三个回归系数提取出来，赋值给这个标量对象rho_co。
7.5.4.5 尼威-威斯特(Newey-West)一致性标准误矫正法
目标：直接用尼威-威斯特(Newey-West)一致性标准误矫正流程方法，构建回归分析模型，此时模型的自相关问题将会有所缓解。
思路：利用Eviews菜单操作，进行基于尼威-威斯特(Newey-West)一致性标准误矫正程序的建模分析。
理论提示：（数学表达和证明过程略）
异方差-自相关一致性标准误（heteroscedasticity-autocorralation consistent standard errors，HAC）也被简称为尼威-威斯特一致性标准误(Newey-West consistent standard errors)
尼威-威斯特(Newey-West)一致性标准误矫正程序或菜单，在主流的统计软件里都会配置
尼威-威斯特(Newey-West)一致性标准误矫正程序，严格意义上对于大样本数据是有效的，因此不太适合于小样本数据的情形。
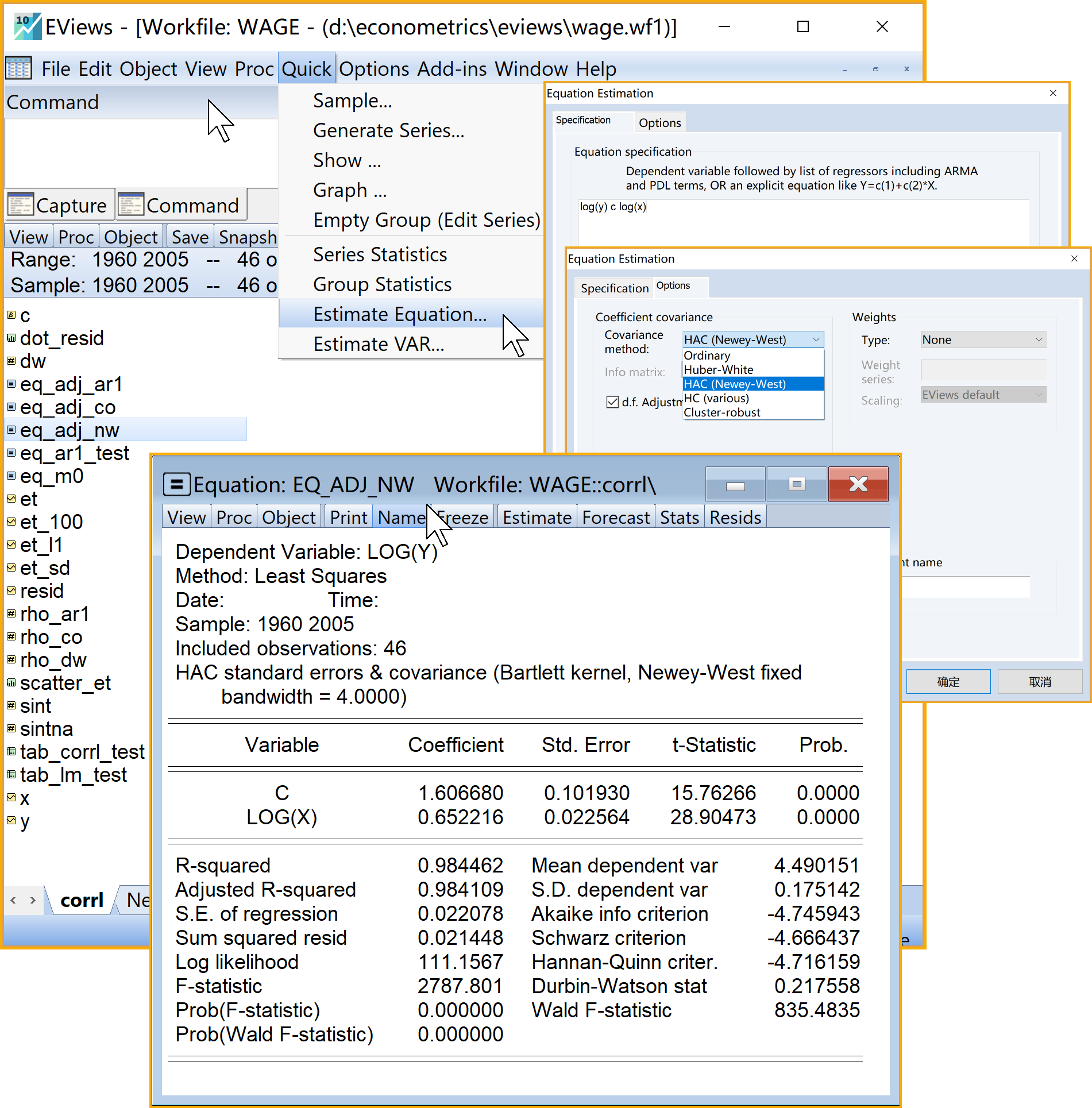
Eviews操作（见 图 7.24）
（1）依次选择\(\Rightarrow\) Quick \(\Rightarrow\) Estimation Equation
（2）引导设置Equation Estimation \(\Rightarrow\) Specification
- 方程设置（Equation Specification）： 输入变量log(Y) c log(X)
- 估计方法（Estimation settings）：具体如下
* Method：选择`LS - Least Squares(NLS and ARMA)`
* Sample： **默认设置**（3）引导设置Equation Estimation \(\Rightarrow\) Options
- 系数协方差设置（Coefficient covariance）：具体如下
* 协方差方法（Coefficient method）：下拉选择HAC (Newey-West)权重设置（Weights）：默认设置
最优化设置（Optimization）：默认设置
完成设置：点击
OK
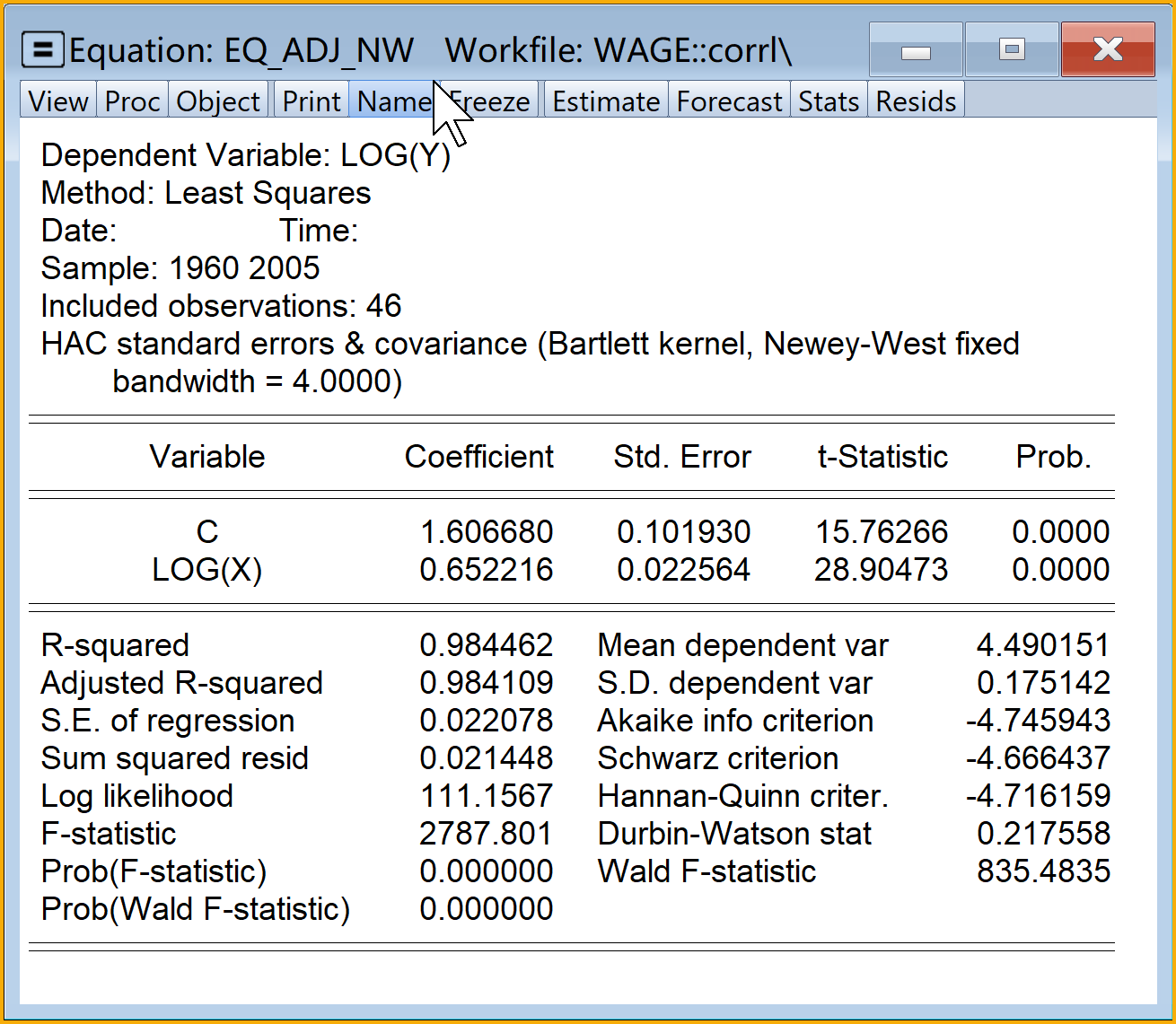
（4）模型命名：建议为eq_adj_NW
（5）查看分析报告（见 图 7.25）
7.6 作业题：存货案例
存货案例： 表 7.3 给出给出了41年的Y存货（百万美元），X2销售额（百万美元）等方面数据。
| Year | Y | X2 |
|---|---|---|
| 1950 | 84646 | 46486 |
| 1951 | 90560 | 50229 |
| 1952 | 98145 | 53501 |
| 1953 | 101599 | 52805 |
| 1954 | 102567 | 55906 |
| 1986 | 423082 | 326227 |
| 1987 | 408226 | 334616 |
| 1988 | 439821 | 359081 |
| 1989 | 479106 | 394615 |
| 1990 | 509902 | 411663 |
变量说明见 表 7.4：
| variable | label |
|---|---|
| Year | 年份 |
| Y | 存货（百万美元） |
| X2 | 销售额（百万美元） |
请考虑如下样本回归模型：
\[ \begin{aligned} Y_t & =\beta_1+\beta_2X_{2t}+u_{t} &&\text{(classic)} \end{aligned} \tag{7.38}\]
\[ \begin{aligned} ln(Y_t) & =\beta_1+\beta_2ln(X_{2t})+u_{t} &&\text{(log)} \end{aligned} \tag{7.39}\]
请回答如下问题:
（1）根据总体回归模型 式 7.38 ，请对模型参数的理论预期（符号、大小、关系）进行说明。
（2）利用Eviews对模型 式 7.38 进行回归分析（将报告截图过来，并写出相应的简要报告形式——三行式或四行式）。参数估计结果符合你的理论预期么？
（3）回归模型 式 7.38 存在自相关问题的证据吗？请按照下列方法分别进行诊断，并分别得到分析结论（要求截图过来并进行简要说明）：
\[ \begin{aligned} e_t=\hat{\rho}_1e_{t-1}+\hat{\rho}_2e_{t-2}+\cdots+v_t \end{aligned} \]
- 残差序列观察法（描点图法）：绘制\(e_t\)序列的描点图（dot plot），得到你的初步结论。
- 残差序列观察法（描点图法）：根据前述观察，确定滞后阶数并分别绘制\(e_t\)序列与\(e_{t-1},e_{t-2},\cdots\)序列的散点图（scatter plot），得到你的初步结论
- 辅助回归法：构建残差\(e_t\)序列对\(e_{t-1},e_{t-2},\cdots\)序列的辅助回归方程 式 7.10 ，得到你的初步结论
- 自相关和偏相关分析法：Eviews菜单操作对残差\(e_t\)序列进行自相关和偏相关分析（注意滞后阶数的选择）
- Durbin-Watson检验法：分析Eviews报告中的D-W统计量
- 拉格朗日检验法（LM-test）：Eviews菜单操作进行布罗施-戈弗雷(Breusch-Goldfrey)的拉格朗日检验(B-G LM test)
（4）若发现回归模型 式 7.38 存在自相关问题，你如何对该模型进行矫正？请按照下列方法分别进行诊断，并分别得到分析结论（要求截图过来并进行简要说明）：
- 广义最小二乘法(GLS)：一阶差分法变换
- 广义最小二乘法(GLS)：基于残差辅助方程 式 7.10 中估计出来的\(\hat{\rho}\)近似得到\(\rho\)
- 广义最小二乘法(GLS)：基于D-W统计量近似计算得到\(\rho\)
- 广义最小二乘法(GLS)：基迭代法近似计算得到\(\rho\)
- 一致标准误校正法（HAC）：尼威-威斯特(Newey-West)校正法
- 对数变换法：对数模型 式 7.39 进行Eviews回归分析
（5）如果模型 式 7.38 与上面各种方法修正的结果相差较大，你认为哪一个方法要相对较好，为什么？