2 一元线性回归
2.1 实验目的及要求
目的:熟悉一元回归建模和分析的基本原理。
要求:熟练利用EViews软件进行一元回归分析,并进行计量经济检验;能快速看懂EViews分析报告,并理解报告内容的内部关系。
2.2 实验原理
经济建模要点
参数估计
参数推断
拟合优度(判定系数)
模型检验(经济学检验、统计学检验_t检验和F检验)
2.2.1 回归的本质是什么?
回归是对个体值\(Y_i\)有“回归”到的条件期望值\((Y|X_i)\)这一现象的形象表达,这也是回归的本质。
一般所说的线性回归,是指条件期望值\((Y|X_i)\)的轨迹表现为直线的情形,也就意味着在给定不同的\(X_i\),个体值\(Y_i\)有“回归”到一条直线的趋势。
此外,回归分析在根本上是对宏大的、规则化的、超现实的总体真实规律的探索和认知,但实际上我们只能通过局部的、破碎的、现实的样本来对其加以猜测和推断。这一“故事主线”是始终贯穿于回归分析全部过程中。
定义 2.1 (回归) 通过解释变量\(X_i\)(在重复抽样中)的已知或设定值,去估计和(或)预测应变量\(Y_i\)的总体均值。
定义 2.2 (概率) 注意区分两种概率定义:
无条件概率:不受\(X_i\)变量取值影响下,\(Y_i\)出现的可能性,记为: \(p(Y_i)\)
条件概率:给定变量\(X_i\)的取值条件下,\(Y_i\)出现的可能性,记为: \(p(Y_i|X_i)\)
定义 2.3 (期望) 注意区分两种期望定义:
无条件期望:不受\(X_i\)变量取值影响下,变量\(Y_i\)的期望值。
离散变量情形下记为: \(E(Y)=\sum_{i=1}^{N}{Y_i}\cdot p(Y_i)\)
连续变量情形下记为:\(E(Y)=\int{Y}\cdot g(Y)dY\)
条件期望:在给定变量\(X_i\)的取值条件下,变量\(Y_i\)的期望值。
离散变量情形下记为: \(E(Y|X_i)=\sum_{i=1}^{N}{(Y_i|X_i)}\cdot p(Y_i|X_i)\)
连续变量情形下记为:\(E(Y|X)=\int{(Y|X)}\cdot g(Y|X)dY\)
定义 2.4 (总体回归线) 总体回归线(PRC):是给定变量\(X_i\)值时\(Y_i\)的条件期望值的轨迹。
定义 2.5 (总体回归函数) 总体回归函数(PRF):是用来刻画总体回归线的数学函数。
一般地可以表达为:\(E(Y|X_i)=f(X_i)\)。
如果总体回归线表现为直线,则可以用如下函数表达:\(E(Y|X_i)=f(X_i)=\beta_1+\beta_2X_i\)
定义 2.6 (样本回归线) 样本回归线(SRC):是通过对样本数据拟合后得到的一条抽象化的曲线。
定义 2.7 (样本回归函数) 样本回归函数(SRF)是样本回归曲线的数学函数形式。
- 一般地可以表达为:\(\hat{Y_i}=f(X_i)\)。
- 如果样本回归曲线表现为直线,则可以用如下函数表达:\(\hat{Y_i}=f(X_i)=\hat{\beta}_1+\hat{\beta}_2X_i\)
定义 2.8 (随机干扰项和总体回归模型) 随机干扰项:是总体回归函数SRF中忽略掉的,但又影响着\(Y_i\)的其他全部变量的替代物。它是\(Y_i\)与其条件期望的离差,也即\(u_i=Y_i-E(Y|X_i)\)。
总体回归模型(PRM):用确定性的总体回归函数和非系统性的随机干扰项共同来刻画变量\(Y_i\)的一种假象模型。
- 如果没有明确的总体回归函数,一般表达为:\(Y_i=E(Y|X_i)+u_i\)
- 如果总体回归函数为直线形式,则表达为:\(Y_i=\beta_1+\beta_2X_i+u_i\)
定义 2.9 (残差和样本回归模型) 残差:是样本回归函数忽略掉的,但又影响着\(Y_i\)的全部其他变量的替代物。它是样本观测值\(Y_i\),与样本回归线上的点的取值\(\hat{Y_i}\)之间的离差,也即:\(e_i=Y_i-\hat{Y}_i\)
样本回归模型(SRM):用拟合的样本回归函数和未能拟合的残差共同来刻画样本观测值\(Y_i\)的一种假象模型。
- 如果无明确拟合的样本回归函数,一般表达为:\(Y_i=f(X_i)+e_i\)
- 如果拟合样本回归函数为直线形式,则表达为:\(Y_i=\hat{\beta}_1+\hat{\beta}_2X_i+e_i\)
如果说回归的本质是对总体规律的认知,那么人们脑海中马上浮出的问题往往还有:
- 什么情况下我们认为总体是能被认知的?
- 以及怎样才能说我们完全知悉了总体规律?
看来用样本数据推断总体参数,必须首先交代“故事背景”:
对于线性总体回归模型:
\[ \begin{aligned} Y_i=\beta_1+\beta_2X_i+u_i \end{aligned} \tag{2.1}\]
显然,模型 式 2.1 等式左边的因变量\(Y_i\)背后的决定规律是一个谜团,研究者希望破解和揭晓它。然而,计量分析活动的前提是\(Y_i\)要“能被认知”。我们一般认为\(Y_i\)“能被认知”,至少需要进行下面几个步骤的理解:
\(Y_i\)是一个客观存在物,不以研究者主观意志而改变
\(Y_i\)是一个随机变量,它背后有值得探索的规律和秘密
一个随机变量只有通过概率分布,才能够被人们所理解和认知
一个随机变量的概率分布,可以用参数进行充分的、抽象的表达
如果概率分布及其参数都知道了,这个随机变量的规律也被揭晓了。
那么,模型 式 2.1 等式右边就是研究者的主观化的构建,期望通过它实现对等式左边的客观存在物\(Y_i\)的规律破解。它是计量经济学“建模”的核心,需要注意的是:
2.2.2 怎样用样本数据推断总体参数?
用样本数据估计总体参数,有三种指导理念完全不同方法:
最小二乘法(Least Square,LS):随机抽样情形下,使得拟合的样本回归线与样本观测点之间的欧几里得空间距离最小化,那么就有理由认为基于这次样本拟合得到的参数估计值是对真实参数的一个可信推断。
极大似然法(Maximum Likelihood,ML):随机抽样情形下,如果一次实验样本在下次抽样的时候(假想的)能最大可能再次出现(似然函数值最大),那么就有理由认为基于这次实验样本得到的参数估计值是对真实参数的一个可信推断。
矩估计法(Method of Moment,MM):随机抽样情形下,如果样本能很好的继承总体特征,那么就有理由认为通过样本矩等于总体矩3,求解得到的参数估计值是对真实参数的一个可信推断。
下面重点介绍最小二乘法(LS)在线性回归模型中的使用。
对于如下线性模型:
\[ \begin{aligned} Y_i &=\beta_1+\beta_2X_i+u_i && \text{(PRM)} \end{aligned} \tag{2.2}\]
其中:
\[ u_i \sim N(0,\sigma^2) \]
\[ \begin{aligned} Y_i &=\hat{\beta}_1+\hat{\beta}_2X_i+e_i && \text{(SRM)} \end{aligned} \tag{2.3}\]
对模型 式 2.3 求解如下最小化过程:
\[ \begin{aligned} Min(Q) &=\sum{(Y_i-\hat{Y}_i)^2}\\ &=\sum{\left ( Y_i-(\hat{\beta}_1+\hat{\beta}_2X_i) \right )^2}\\ &=f(\hat{\beta}_1,\hat{\beta}_2) \end{aligned} \]
可以得到模型 式 2.2 的回归参数估计值:
\[ \begin{aligned} \begin{split} \hat{\beta}_2 &=\frac{n\sum{X_iY_i}-\sum{X_i}\sum{Y_i}}{n\sum{X_i^2}-\left ( \sum{X_i} \right)^2}\\ \hat{\beta_1} &=\frac{n\sum{X_i^2Y_i}-\sum{X_i}\sum{X_iY_i}}{n\sum{X_i^2}-\left ( \sum{X_i} \right)^2} \end{split} &&\text{(FF solution)} \end{aligned} \tag{2.4}\]
以上求解公式也称为公式(Favorite Five,FF)。 此外我们也可以得到如下的离差公式(favorite five,ff):
\[ \begin{aligned} \begin{split} \hat{\beta}_2 &=\frac{\sum{x_iy_i}}{\sum{x_i^2}}\\ \hat{\beta_1} &=\bar{Y}_i-\hat{\beta}_2\bar{X}_i \end{split} && \text{(ff solution)} \end{aligned} \tag{2.5}\]
进一步地,可以计算得到随机干扰项\(u_i\)的真是方差\(\sigma^2\)的LS估计量\(\hat{\sigma}^2\):
\[ \begin{aligned} \hat{Y}_i &=\hat{\beta}_1+\hat{\beta}_2X_i \end{aligned} \tag{2.6}\]
\[ \begin{aligned} \hat{\sigma}^2 &=\frac{\sum{e_i^2}}{n-1}=\frac{\sum{(Y_i-\hat{Y}_i)^2}}{n-1} \end{aligned} \tag{2.7}\]
2.2.3 最小二乘法有哪些优点?
在正态经典线性回归模型假设(N-CLRM)下,回归斜率系数\(\hat{\beta}_2\)最小二乘估计量的总体方差/标准差,及其样本方差/标准差公式如下:
\[ \begin{aligned} var(\hat{\beta}_2) =\sigma_{\hat{\beta}_2}^2&=\frac{1}{\sum{x_i^2}}\cdot\sigma^2&&\text{} \end{aligned} \tag{2.8}\]
\[ \begin{aligned} s.e.(\hat{\beta}_2) =\sigma_{\hat{\beta}_2} &=\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\sigma &&\text{} \end{aligned} \tag{2.9}\]
\[ \begin{aligned} S_{\hat{\beta}_2}^2 &=\frac{1}{\sum{x_i^2}}\cdot\hat{\sigma}^2 &&\text{} \end{aligned} \tag{2.10}\]
\[ \begin{aligned} S_{\hat{\beta}_2} &=\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\hat{\sigma} &&\text{} \end{aligned} \tag{2.11}\]
在正态经典线性回归模型假设(N-CLRM)下,回归截距系数\(\hat{\beta}_1\)最小二乘估计量的总体方差/标准差,及其样本方差/标准差公式如下:
\[ \begin{aligned} var(\hat{\beta}_1) =\sigma_{\hat{\beta}_1}^2 &=\frac{\sum{X_i^2}}{n\sum{x_i^2}}\cdot\sigma^2 \end{aligned} \tag{2.12}\]
\[ \begin{aligned} s.e.(\hat{\beta}_1) =\sigma_{\hat{\beta}_1} &=\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\sigma \end{aligned} \tag{2.13}\]
\[ \begin{aligned} S_{\hat{\beta}_1}^2 &=\frac{\sum{X_i^2}}{n\sum{x_i^2}}\cdot\hat{\sigma}^2 \end{aligned} \tag{2.14}\]
\[ \begin{aligned} S_{\hat{\beta}_1} &=\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\hat{\sigma} \end{aligned} \tag{2.15}\]
定理 2.1 (高斯-马尔可夫定理(Gauss-Markov Theorem)) 在正态经典线性回归模型假设(N-CLRM)下,采用普通最小二乘法(OLS),得到的估计量\(\hat{\beta}\),是真实参数\(\beta\)最优的、线性的、无偏估计量(BLUE)。记为:
\[ \begin{aligned} \xrightarrow{\text{N-CLRM}} {\text{OLS}}(\hat{\beta})\xrightarrow[\text{}]{\text{BLUE}}\beta \end{aligned} \]
证明 (线性性). 根据离差公式,可以得到:
\[\hat{\beta}_2=\frac{\sum{x_iy_i}}{\sum{x_i^2}}=\sum{k_iY_i}\]
其中,\(k_i=\frac{x_i}{\sum{x_i^2}}\)。
容易证明,\(\frac{x_i}{\sum{x_i^2}}\)不全为0, 所以\(\hat{\beta}_2\)是线性的。
同理可以证明:
\[\hat{\beta}_1=\bar{Y_i}-\hat{\beta}_2\bar{X_i}=\sum{w_iY_i}\]
其中,\(w_i=\frac{1}{n}-\bar{X_i}k_i\)。
容易证明,\(\frac{1}{n}-\bar{X_i}k_i\)不全为0。
所以\(\hat{\beta}_1\)是线性的。
证明 (无偏性). 根据离差公式,可以得到:
\[ \begin{aligned} \hat{\beta}_2 &=\sum{k_iY_i}\\ &=\sum{k_i(\beta_1+\beta_2X_i+u_i)}\\ &=\beta_2+\sum{k_iu_i} \end{aligned} \]
其中,\(k_i=\frac{x_i}{\sum{x_i^2}}\),且可以证明,\(\sum{k_i}=0\)。
因此有:
\[ \begin{aligned} E(\hat{\beta}_2)&=\beta_2+E(\sum{k_iu_i})\\ &=\beta_2+\sum{k_iE(u_i)}\\ &=\beta_2 \end{aligned} \]
同理可以证明: \[ \begin{aligned} E(\hat{\beta}_1)&=\beta_1+E(\sum{w_iu_i})\\ &=\beta_1+\sum{w_iE(u_i)}\\ &=\beta_1 \end{aligned} \] 其中,\(w_i=\frac{1}{n}-\bar{X_i}k_i\)。
证明 (方差最小/最优性). 已知:
\[ \begin{aligned} var(\hat{\beta}_2) =\sigma_{\hat{\beta}_2}^2&=\frac{1}{\sum{x_i^2}}\cdot\sigma^2 var(\hat{\beta}_1) =\sigma_{\hat{\beta}_1}^2 &=\frac{\sum{X_i^2}}{n\sum{x_i^2}}\cdot\sigma^2 \end{aligned} \]
假设存在用其他方法估计的线性无偏估计量:
\[ \begin{aligned} \hat{\beta}^\ast_2 &=\sum{(k_i+d_i)Y_i} &&=\sum{c_iY_i}\\ \hat{\beta}^\ast_1 &=\sum{(w_i+g_i)Y_i} &&=\sum{h_iY_i}\\ \end{aligned} \]
其中,\(d_i\)和\(g_i\)是不全为0的常数,则可以证明:
\[ \begin{aligned} var(\hat{\beta}_2^\ast) &\geq var(\hat{\beta}_2)\\ var(\hat{\beta}_1^\ast) &\geq var(\hat{\beta}_1)\\ \end{aligned} \]
2.2.4 如何对模型进行统计检验?
在经典回归模型假设(CLRM)下,采用最小二乘法(LS),对样本数据进行拟合,得到的样本回归线,已经是最优的了(残差平方和最小),并且样本回归系数理论上也是总体参数的最优线性无偏估计量(BLUE)。为什么我们还需要对回归模型进行统计检验?
一个直接的回答是:样本数据来自于总体,样本是随机抽样得到的。对于一份特定的抽样数据,最小二乘法(LS)拟合的样本回归线此时确实是最优的,其回归系数也确实是总体参数的最优线性无偏估计量(BLUE)。但是,这一份随机样本数据得到的全部结论,究竟能多大程度地“推断”或“证实”模型的真实参数?这一问题仍旧悬而未决。
2.2.4.1 平方和分解及拟合优度
首先需要确定的工作是,采用最小二乘法(LS),样本回归线对这一组数据拟合得有多好?
通过对\(Y_i\)的变异及其来源的分解,我们可以得到有关拟合优度评价的启发。其中TSS表示总离差平方和,ESS表示回归平法和,RSS表示残差平方和。
\[ \begin{aligned} (Y_i-\bar{Y_i}) &= (\hat{Y_i}-\bar{Y_i}) +(Y_i-\bar{Y_i}) \end{aligned} \tag{2.16}\]
\[ \begin{aligned} y_i &=\bar{y_i}+ e_i \end{aligned} \tag{2.17}\]
\[ \begin{aligned} \sum{y_i^2} &= \sum{\hat{y_i}^2} +\sum{e_i^2} \end{aligned} \tag{2.18}\]
\[ \begin{aligned} TSS&=ESS+RSS \end{aligned} \tag{2.19}\]
进一步地,可以得到方差分析表(ANOVA):
| 变异来源 | 平方和符号SS | 平方和计算公式 | 自由度df | 均方和符号MSS | 均方和计算公式 |
|---|---|---|---|---|---|
| 回归平方和 | \(ESS\) | \(\sum{(\hat{Y}_i-\bar{Y}_i)^2}=\sum{\hat{y}_i^2}\) | \(1\) | \(MSS_{ESS}\) | \(ESS/df_{ESS}=\hat{\beta}_2^2\sum{x_i^2}\) |
| 残差平方和 | \(RSS\) | \(\sum{(Y_i-\hat{Y_i})^2}=\sum{e_i^2}\) | \(n-2\) | \(MSS_{RSS}\) | \(RSS/df_{RSS}=\frac{\sum{e_i^2}}{n-2}\) |
| 总平方和 | \(TSS\) | \(\sum{(Y_i-\bar{Y_i})^2}=\sum{y_i^2}\) | \(n-1\) | \(MSS_{TSS}\) | \(TSS/df_{TSS}=\frac{\sum{y_i^2}}{n-1}\) |
定义 2.10 (拟合优度) 评价样本回归线对一组数据拟合程度的指标,称为拟合优度(goodness of fit)。其中最常用的指标是判定系数(coefficient of determination),记为\(r^2\)(一元回归中)或\(R^2\)(多元回归中)。
根据拟合优度的定义 定义 2.10 ,判定系数\(r^2\)可以通过如下几个公式计算得到:
\[ \begin{aligned} r^2 &=\frac{ESS}{TSS}=\frac{\sum{(\hat{Y_i}-\bar{Y})^2}}{\sum{(Y_i-\bar{Y})^2}}\\ &=1-\frac{RSS}{TSS}=1-\frac{\sum{(Y_i-\hat{Y_i})^2}}{\sum{(Y_i-\bar{Y})^2}} \end{aligned} \]
\[ \begin{aligned} r^2 &=\frac{ESS}{TSS}=\frac{\sum{\hat{y}_i^2}}{\sum{y_i^2}} =\frac{(\hat{\beta_2}x_i)^2}{\sum{y_i^2}} =\hat{\beta}_2^2\left(\frac{\sum{x_i^2}}{\sum{y_i^2}}\right) =\hat{\beta}_2^2\frac{S_X^2}{S_Y^2} \end{aligned} \]
\[ \begin{aligned} r^2 &=\hat{\beta}_2^2\left(\frac{\sum{x_i^2}}{\sum{y_i^2}}\right) =\left(\frac{\sum{x_iy_i}}{\sum{y_i^2}}\right)^2\left(\frac{\sum{x_i^2}}{\sum{y_i^2}}\right) =\frac{(\sum{x_iy_i})^2}{\sum{x_i^2}\sum{y_i^2}} \end{aligned} \]
需要注意的是,一元回归分析中判定系数\(r^2\)与简单相关系数\(r_{X_i,Y_i}\)存在某种联系(\(\rho_{X_i,Y_i}\)为总体相关系数):
\[ \begin{aligned} \rho_{X_i,Y_i}&=\frac{cov(X_i,Y_i)}{\sqrt{var(X_i)var(Y_i)}} =\frac{E\left((X_i-EX_i)(Y_i-EY_i) \right)}{\sqrt{E(X_i-EX_i)^2E(Y_i-EY_i)^2}} \end{aligned} \tag{2.20}\]
\[ \begin{aligned} r_{X_i,Y_i}&=\frac{Cov(X_i,Y_i)}{S_{X_i}\cdot S_{Y_i}} = \frac{\sum{(X_i-\bar{X})(Y_i-\bar{Y})}}{\sqrt{\sum{(X_i-\bar{X}})^2\sum{(Y_i-\bar{Y})^2}}} \end{aligned} \tag{2.21}\]
\[ \begin{aligned} \left[r_{(X_i,Y_i)}\right]^2 &\simeq r^2 \end{aligned} \tag{2.22}\]
2.2.4.2 回归系数的显著性检验——t检验
定义 2.11 (回归系数的显著性检验) 对于总体线性回归模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i \end{aligned} \]
利用OLS方法,通过样本数据回归,推断回归参数是否是否等于0的一种统计学检验。
在正态经典线性回归模型假设(N-CLRM)下,由于随机干扰项服从\(u_i \sim i.i.d \ N(0,\sigma^2)\),使得\(\hat{\beta_2}\sim N(\beta_2,\sigma^2_{\hat{\beta_2}})\)和\(\hat{\beta_1}\sim N(\beta_1,\sigma^2_{\hat{\beta_1}})\)。因此,我们可以借助这一概率分布特征,对最小二乘法参数估计量\((\hat{\beta_2},\hat{\beta_1})\)进行统计学检验(显著性检验)。具体的做法是:
列明模型环境
提出理论假设
构造出一个可以计算得到的样本统计量(t统计量)
借助假设检验流程进行分析、计算、比较,并得出显著性检验结论
因为:
\[ \begin{aligned} u_i \sim i.i.d \ N(0,\sigma^2) \end{aligned} \tag{2.23}\]
可以证明:
\[ \begin{aligned} \hat{\beta_2} &\sim N(\beta_2,\sigma^2_{\hat{\beta_2}}) \end{aligned} \tag{2.24}\]
\[ \begin{aligned} \hat{\beta_1} &\sim N(\beta_1,\sigma^2_{\hat{\beta_1}}) \end{aligned} \tag{2.25}\]
又因为:
\[ \begin{aligned} \sigma_{\hat{\beta}_2} &=\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\sigma \end{aligned} \tag{2.26}\]
\[ \begin{aligned} \sigma_{\hat{\beta}_1} &=\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\sigma \end{aligned} \tag{2.27}\]
容易证明:
\[ \begin{aligned} Z_{\hat{\beta_2}}&=\frac{\hat{\beta_2}-\beta_2}{\sigma_{\hat{\beta_2}}} \sim Z(0,1) \end{aligned} \tag{2.28}\]
\[ \begin{aligned} Z_{\hat{\beta_1}}&=\frac{\hat{\beta_1}-\beta_1}{\sigma_{\hat{\beta_1}}} \sim Z(0,1) \end{aligned} \tag{2.29}\]
同时,又因为:
\[ \begin{aligned} S_{\hat{\beta}_2} &=\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\hat{\sigma} \end{aligned} \tag{2.30}\]
\[ \begin{aligned} S_{\hat{\beta}_1} &=\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\hat{\sigma} \end{aligned} \tag{2.31}\]
所以进一步可以证明:
\[ \begin{aligned} t_{\hat{\beta_2}}^{\ast}&=\frac{\hat{\beta_2}-\beta_2}{S_{\hat{\beta_2}}} \sim t(n-2) \end{aligned} \tag{2.32}\]
\[ \begin{aligned} t_{\hat{\beta_1}}^{\ast}&=\frac{\hat{\beta_1}-\beta_1}{S_{\hat{\beta_1}}} \sim t(n-2) \end{aligned} \tag{2.33}\]
对于模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_i+e_i \end{aligned} \]
对总体参数\(({\beta_2},{\beta_1})\)分别提出如下的假设:
\[ \begin{aligned} \beta_2: \begin{cases} H_0:\beta_2=0\\ H_1:\beta_2\neq 0 \end{cases}\\ \beta_1: \begin{cases} H_0:\beta_1=0\\ H_1:\beta_1\neq 0 \end{cases} \end{aligned} \]
根据原假设\(H_0\),可以得到:
\[ \begin{aligned} t_{\hat{\beta_2}}^{\ast}&=\frac{\hat{\beta_2}-\beta_2}{S_{\hat{\beta_2}}} =\frac{\hat{\beta_2}}{S_{\hat{\beta_2}}} =\frac{\hat{\beta_2}}{\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\hat{\sigma}} \sim t(n-2) \end{aligned} \tag{2.34}\]
\[ \begin{aligned} t_{\hat{\beta_1}}^{\ast}&=\frac{\hat{\beta_1}-\beta_1}{S_{\hat{\beta_1}}} =\frac{\hat{\beta_1}}{S_{\hat{\beta_1}}} =\frac{\hat{\beta_1}}{\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\hat{\sigma}} \sim t(n-2) \end{aligned} \tag{2.35}\]
若给定显著性水平\(\alpha=0.01\)和自由度\((n-2)\),很快可以得到t分布的查表t值,也即\(t_{(1-\alpha/2)}(n-2)\)。然后比较样本t统计量\((t_{\hat{\beta_2}}^{\ast},t_{\hat{\beta_1}}^{\ast})\)与理论t分布查的表t值\((t_{(1-\alpha/2)}(n-2))\)的关系。
根据如下法则做出参数\(\beta_2\)的显著性检验结论:
如果\(t_{\hat{\beta_2}}^{\ast}>t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_2\)的t检验在\(\alpha=0.01\)水平下是显著的,也即显著地拒绝\(H_0:\beta_2=0\),从而接受\(H_1:\beta_2\neq 0\)。
如果\(t_{\hat{\beta_2}}^{\ast}\leq t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_2\)的t检验在\(\alpha=0.01\)水平下是不显著的,也即不能显著地拒绝\(H_0:\beta_2=0\),从而只能暂时接受\(H_0:\beta_2=0\)。
同样地,根据如下法则做出参数\(\beta_1\)的显著性检验结论:
如果\(t_{\hat{\beta_1}}^{\ast}>t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_1\)的t检验在\(\alpha=0.01\)水平下是显著的,也即显著地拒绝\(H_0:\beta_1=0\),从而接受\(H_1:\beta_1\neq 0\)。
如果\(t_{\hat{\beta_1}}^{\ast}\leq t_{(1-\alpha/2)}(n-2)\),则表明参数\(\beta_2\)的t检验在\(\alpha=0.01\)水平下是不显著的,也即不能显著地拒绝\(H_0:\beta_1=0\),从而只能暂时接受\(H_0:\beta_1=0\)。
2.2.4.3 模型整体显著性检验——F检验
2.2.4.4 模型整体显著性检验
对于总体线性回归模型, \[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ \end{aligned} \]
利用LS方法,通过样本数据回归,推断模型的线性关系是否成立的一种统计学检验。
在正态经典线性回归模型假设(N-CLRM)下,随机干扰项服从\(u_i \sim i.i.d \ N(0,\sigma^2)\)。因此,我们可以借助这一概率分布特征,利用最小二乘法参数估计量\((\hat{\beta_2},\hat{\beta_1})\)结果,对总体回归模型进行整体显著性检验——F检验。具体的做法是:
列明模型环境
提出理论假设
构造出一个可以计算得到的样本统计量(F统计量)
借助假设检验流程进行分析、计算、比较,并得出显著性检验结论
因为:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ u_i &\sim i.i.d \ N(0,\sigma^2)\\ \end{aligned} \]
在N-CLRM下容易证明:
\[ \begin{aligned} Y_i&\sim i.i.d \ N(\beta_1+\beta_2X_i,\sigma^2)\\ \end{aligned} \]
进一步可以证明:
\[ \begin{aligned} ESS&=\sum{(\hat{Y_i}-\bar{Y})^2} \sim \chi^2(df_{ESS}) \end{aligned} \tag{2.36}\]
\[ \begin{aligned} RSS&=\sum{(Y_i-\hat{Y_i})^2} \sim \chi^2(df_{RSS}) \end{aligned} \tag{2.37}\]
从而得到:
\[ \begin{aligned} F^{\ast}&=\frac{ESS/df_{ESS}}{RSS/df_{RSS}}=\frac{MSS_{ESS}}{MSS_{RSS}} \\ &=\frac{\sum{(\hat{Y_i}-\bar{Y})^2}/df_{ESS}}{\sum{(Y_i-\hat{Y_i})^2}/df_{RSS}} \\ &\sim F(df_{ESS},df_{RSS}) \end{aligned} \tag{2.38}\]
对于模型: \[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_i+e_i \end{aligned} \]
对线性模型的斜率参数\({\beta_2}\)提出如下的假设:
\[ \begin{aligned} \beta_2: \begin{cases} H_0:\beta_2=0\\ H_1:\beta_2\neq 0 \end{cases}\\ \end{aligned} \]
根据原假设\(H_0\),可以得到:
\[ \begin{aligned} F^{\ast}&=\frac{ESS/df_{ESS}}{RSS/df_{RSS}}=\frac{MSS_{ESS}}{MSS_{RSS}}\\ &=\frac{\sum{(\hat{Y_i}-\bar{Y})^2}/df_{ESS}}{\sum{(Y_i-\hat{Y_i})^2}/df_{RSS}} \\ &=\frac{\hat{\beta_2}^2\sum{x_i^2}}{\sum{e_i^2}/{(n-2)}}\\ &=\frac{\hat{\beta_2}^2\sum{x_i^2}}{\hat{\sigma}^2} \end{aligned} \]
若给定显著性水平\(\alpha=0.01\)和样本数\((n)\),很快可以得到F分布的查表F值,也即\(F_{(1-\alpha)}(1,n-2)\),然后比较其与样本F统计量\(F^{\ast}\)的关系。
根据如下法则做出总体回归模型整体显著性检验结论:
如果\(F^{\ast}>F_{(1-\alpha)}(1,n-2)\),则表明总体回归模型的F检验在\(\alpha=0.01\)水平下是显著的,也即显著地拒绝\(H_0:\beta_2=0\),从而接受\(H_1:\beta_2\neq 0\)。
\(F^{\ast} \leq F_{(1-\alpha)}(1,n-2)\),则表明总体回归模型的F检验在\(\alpha=0.01\)水平下是不显著的,也即不能显著地拒绝\(H_0:\beta_2=0\),从而只能暂时接受\(H_0:\beta_2=0\)。
2.2.5 如何进行样本外预测?
样本外预测包括均值预测(mean prediction)和个值预测(individual prediction)两个内容。
定义 2.12 (均值预测) 均值预测(mean prediction),是一种对样本外条件均值的预测。正式地,给定\(X_0\),预测\(Y_i\)的条件均值,也即\(E(Y|X=X_0)\)
定义 2.13 (个值预测) 个值预测(individual prediction),是一种对样本外个体值的预测。正式地,给定\(X_0\),预测\(Y_i\)的个别值,也即\((Y_0|X=X_0)\)
定义 2.14 (点预测) 是通过一次性的样本数据拟合结果,得到的关于样本外因变量的、可信的单一个值预测(point forecast)。
定义 2.15 (区间预测) 是利用随机变量的分布特性,借助于一次性的样本数据拟合结果,得到的关于样本外因变量的、可信的取值范围预测(interval forecast)。
事实上,无论是进行均值预测还是个值预测,关键思路是我们将能够证明:
样本回归函数的拟合值\(\hat{Y}_0\)很独特,它既是条件均值\(E(Y|X=X_0)\)的无偏估计,也是个值\((Y_0|X=X_0)\)的无偏估计。也就意味着\(\hat{Y}_0\)是它们二者的无偏的点预测值。
随机变量\(\hat{Y}_0\)和\(Y_0\)都服从正态分布,并且基于此我们可以构造并计算出均值预测的置信区间和个值预测的置信区间
2.2.5.1 样本外均值预测
对于模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_i+e_i \end{aligned} \]
容易证明随机变量\(\hat{Y}_0\)的期望和方差分别为:
\[ \begin{aligned} \mu_{\hat{Y}_0}&=E(\hat{Y}_0)\\ &=E(\hat{\beta}_1+\hat{\beta}_2X_0)\\ &=\beta_1+\beta_2X_0\\ &=E(Y|X_0) \end{aligned} \tag{2.39}\]
\[ \begin{aligned} var(\hat{Y}_0)&=\sigma^2_{\hat{Y}_0}\\ &=E(\hat{\beta}_1+\hat{\beta}_2X_0)\\ &=\sigma^2 \left( \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right) \end{aligned} \tag{2.40}\]
而且服从如下正态分布:
\[ \begin{aligned} \hat{Y}_0& \sim N(\mu_{\hat{Y}_0},\sigma^2_{\hat{Y}_0})\\ \hat{Y}_0& \sim N \left(E(Y|X_0), \sigma^2 \left( \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right) \right) \end{aligned} \tag{2.41}\]
进一步地,可以构造t统计量:
\[ \begin{aligned} t_{\hat{Y}_0}& =\frac{\hat{Y}_0-E(Y|X_0)}{S_{\hat{Y}_0}} \sim t(n-2) \end{aligned} \tag{2.42}\]
其中:
\[ \begin{aligned} S_{\hat{Y}_0}& = \sqrt{\hat{\sigma}^2 \left( \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right)} \end{aligned} \tag{2.43}\]
给定显著性水平\(\alpha\)的情况下,可以查表得到理论t值\(t_{1-\alpha/2}(n-2)\),从而可以计算得到均值预测的置信区间:
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \leq E(Y|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0} \end{aligned} \tag{2.44}\]
2.2.5.2 样本外个值预测
对于模型:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_i+u_i\\ u_i &\sim i.i.d \ N(0,\sigma^2)\\ Y_i&=\hat{\beta}_1+\hat{\beta}_2X_i+e_i \end{aligned} \]
容易证明随机变量\(Y_0\)服从如下的正态分布:
\[ \begin{aligned} Y_0& \sim N(\mu_{Y_0},\sigma^2_{Y_0})\\ Y_0& \sim N \left( \beta_1+\beta_2X_0,\sigma^2 \right) \end{aligned} \tag{2.45}\]
因为已经证明了:
\[ \begin{aligned} \hat{Y}_0& \sim N(\mu_{\hat{Y}_0},\sigma^2_{\hat{Y}_0})\\ \hat{Y}_0& \sim N \left(E(Y|X_0), \sigma^2 \left( \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right) \right) \end{aligned} \tag{2.46}\]
因此我们可以构造一个新的正态随机变量\((Y_0-\hat{Y}_0)\):
\[ \begin{aligned} (Y_0-\hat{Y}_0)& \sim N \left(\mu_{(Y_0-\hat{Y}_0)},\sigma^2_{(Y_0-\hat{Y}_0)} \right)\\ (Y_0-\hat{Y}_0)& \sim N \left(0, \sigma^2 \left(1+ \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right) \right) \end{aligned} \tag{2.47}\]
进一步地,可以构造t统计量:
\[ \begin{aligned} t_{(Y_0-\hat{Y}_0)}& =\frac{(Y_0-\hat{Y}_0)}{S_{(Y_0-\hat{Y}_0)}} \sim t(n-2) \end{aligned} \tag{2.48}\]
其中:
\[ \begin{aligned} S_{(Y_0-\hat{Y}_0)}& = \sqrt{\hat{\sigma}^2 \left(1+ \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right)} \end{aligned} \tag{2.49}\]
给定显著性水平\(\alpha\)的情况下,可以查表得到理论t值\(t_{1-\alpha/2}(n-2)\),从而可以计算得到个值预测的置信区间:
\[ \begin{aligned} \hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{(Y_0-\hat{Y}_0)} \leq (Y_0|X_0) \leq \hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{(Y_0-\hat{Y}_0)} \end{aligned} \tag{2.50}\]
2.2.6 怎样看懂EViews回归分析报告结果?
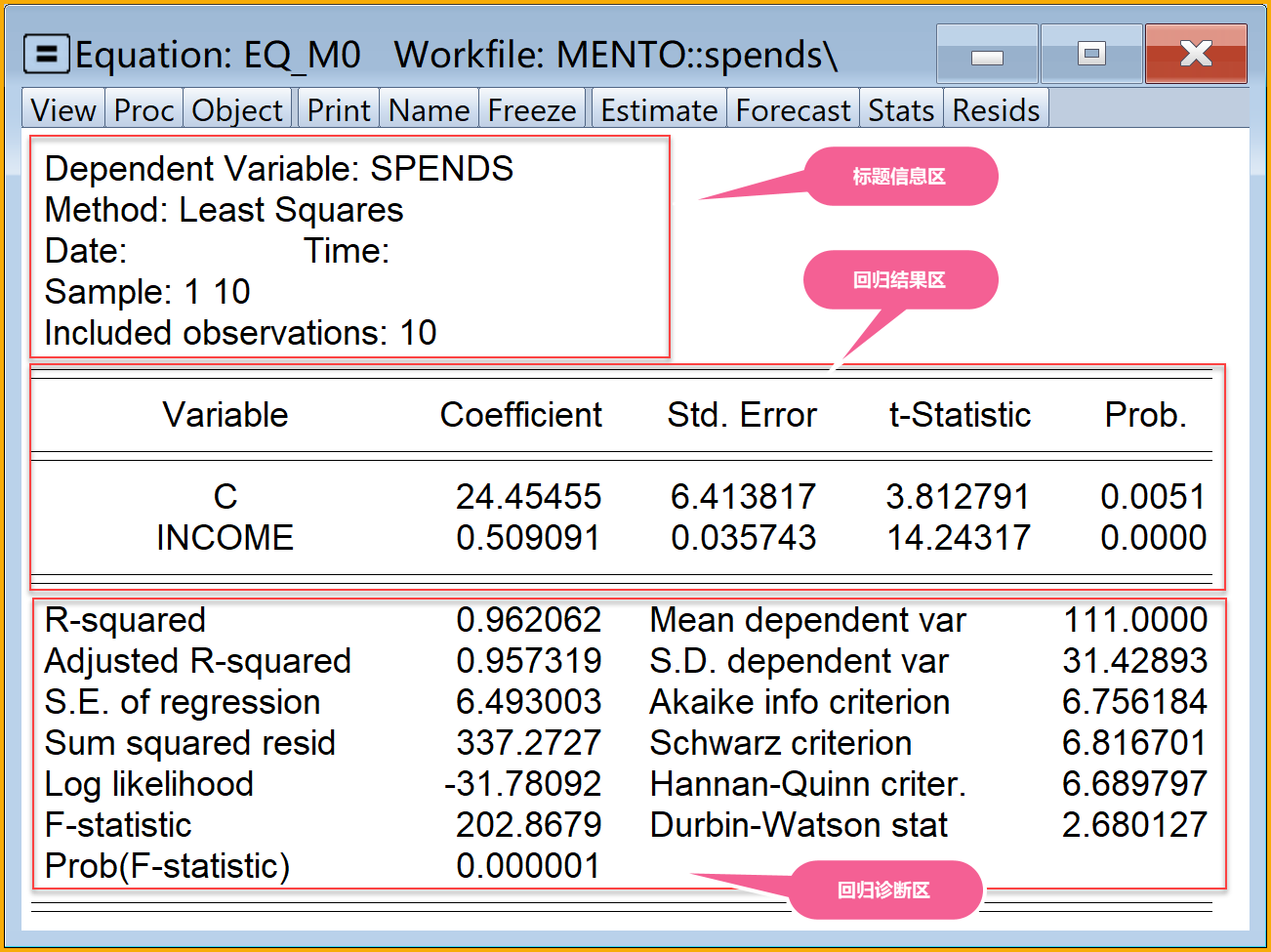
| row | content | mark |
|---|---|---|
| 第1行 | Dependent Variable: SPENDS | 因变量 |
| 第2行 | Method: Least Squares | 方法 |
| 第3行 | Date: Time: | 日期、时间 |
| 第4行 | Sample: 1 10 | 样本框 |
| 第5行 | Included observations: 10 | 样本数 |
| row | column | content | mark | math |
|---|---|---|---|---|
| 第1行 | 第1列 | Variable | 方程变量 | |
| 第2行 | 第1列 | C | 回归方程的截距 | |
| 第3行 | 第1列 | INCOME | 回归方程的变量X | |
| 第1行 | 第2列 | Coefficient | 系数(回归参数的点估计值) | |
| 第2行 | 第2列 | … | 截距系数 | \(\hat{\beta}_1\) |
| 第3行 | 第2列 | … | 斜率系数 | \(\hat{\beta}_2\) |
| 第1行 | 第3列 | Std. Error | 系数的样本标准差 | |
| 第2行 | 第3列 | … | 截距系数的样本标准差 | \(S_{\hat{\beta}_1}\) |
| 第3行 | 第3列 | … | 斜率系数的样本标准差 | \(S_{\hat{\beta}_2}\) |
| 第1行 | 第4列 | t-Statistic | 系数的样本t值 | |
| 第2行 | 第4列 | … | 截距系数的样本t值 | \(t^{\ast}_{\hat{\beta}_1}\) |
| 第3行 | 第4列 | … | 斜率系数的样本t值 | \(t^{\ast}_{\hat{\beta}_2}\) |
| 第1行 | 第5列 | Prob. | 系数的样本t值对应的概率值p | |
| 第2行 | 第5列 | … | 截距系数的样本t值对应的概率值p | \(p(\alpha/2, t^{\ast}_{\hat{\beta}_1}, f)\) |
| 第3行 | 第5列 | … | 斜率系数的样本t值对应的概率值p | \(p(\alpha/2, t^{\ast}_{\hat{\beta}_2}, f)\) |
| row | column | content | mark | math |
|---|---|---|---|---|
| 第1行 | 第1列 | R-squared | 判定系数 | \(R^2\) |
| 第2行 | 第1列 | Adjusted R-squared | 调整判定系数 | \(\bar{R}^2\) |
| 第3行 | 第1列 | S.E. of regression | 回归标准误 | \(\hat{\sigma}\) |
| 第4行 | 第1列 | Sum squared resid | 残差平方和 | \(RSS=\sum{e_i^2}\) |
| 第5行 | 第1列 | Log likelihood | 对数似然值 | |
| 第6行 | 第1列 | F-statistic | 回归方程的F统计量值 | \(F^{\ast}\) |
| 第7行 | 第1列 | Prob(F-statistic) | F统计量值对应的概率值p | \(p(\alpha, F^{\ast}, f_1,f_2)\) |
| 第1行 | 第3列 | Mean dependent var | 因变量的均值 | \(\bar{Y}\) |
| 第2行 | 第3列 | S.D. dependent var | 应变量的标准差 | \(S_{Y_i}=\sqrt{\frac{\sum{(Y_i-\bar{Y})^2}}{(n-1)}}\) |
| 第3行 | 第3列 | Akaike info criterion | AIC指数 | |
| 第4行 | 第3列 | Schwarz criterion | SC指数 | |
| 第5行 | 第3列 | Hannan-Quinn criter. | HQ指数 | |
| 第6行 | 第3列 | Durbin-Watson stat | DW统计量 | 德宾沃森统计量 |
2.3 实验内容
(1)利用eviews菜单(Quick \(\Rightarrow\) Estimate Equation)进行线性回归模型分析,学会读懂回归报告结果。
(2)利用EViews命令代码编程,回归理论知识点,验证回归分析的全部细节步骤。
计算直线回归方程的回归系数\(\hat{\beta}_1\)、\(\hat{\beta}_2\)
计算回归误差方差(\(\hat{\sigma}^2\))其标准差(\(\hat{\sigma}\))
计算回归截距系数的样本方差 (\(S_{\hat{\beta}_1}^2\))及其样本标准差( \(S_{\hat{\beta}_1}\));计算回归斜率系数的样本方差(\(S_{\hat{\beta}_2}^2\))及其样本标准差( \(S_{\hat{\beta}_2}\))
计算平方和分解式(\(TSS\)、\(ESS\)、\(RSS\))及其相对应的自由度(\(df_{TSS}\),\(df_{ESS}\),\(df_{RSS}\) ),并写出方差分析表(ANOV table)
计算得到两个变量的样本相关系数\(r\),以及回归方程的判定系数\(r^2\),并比较相关系数与判定系数的关系(数量关系)
计算回归系数的样本t值(\(t^{\ast}_{\hat{\beta}_2}\)和\(t^{\ast}_{\hat{\beta}_1}\))
用eviews命令计算得到理论t值(\(t_{1-\alpha/2}(n-2)\),给定\(\alpha=0.05\)),并对回归系数显著性进行假设检验。
计算回归方程整体显著性检验的的样本F值(\(F_{\ast}\))
用eviews命令计算得到理论F值(\(F_{1-\alpha}(df_1,df_2)=F_{1-\alpha}(df_{ESS},df_{RSS})\),给定\(\alpha=0.05\) ),并对模型整体显著性进行假设检验
给定样本外的\(X_0\) ,计算点预测值\(\hat{Y}_0\)
计算均值预测下的样本标准差\(S_{(\hat{Y}_0)}\)
计算均值预测的置信区间\(\hat{Y}_0-t_{1-\alpha/2}(n-2)\cdot S_{\hat{Y}_0}\leq E(Y\mid X=X_0)\leq \hat{Y}_0+t_{1-\alpha/2}(n-2)\cdot S_{\hat{Y}_0}\)
计算个值预测下的样本标准差\(S_{(Y_0-\hat{Y}_0)}\)
计算个值预测的置信区间\(\hat{Y}_0-t_{\alpha/2}(n-2)\cdot S_{Y_0-\hat{Y}_0}\leq E(Y\mid X=X_0)\leq \hat{Y}_0+t_{\alpha/2}(n-2)\cdot S_{Y_0-\hat{Y}_0}\)
2.4 实验准备
2.4.1 实验软件
本次实验需要提前准备好如下软件:
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或 360极速浏览器9.5版本及以上
2.4.2 实验材料
蒙特卡洛模拟数据: 表 2.5 给出给出了10个家庭在spends家庭支出,income家庭收入等方面的数据。
| obs | spends | income |
|---|---|---|
| 1 | 70 | 80 |
| 2 | 65 | 100 |
| 3 | 90 | 120 |
| 4 | 95 | 140 |
| 5 | 110 | 160 |
| 6 | 115 | 180 |
| 7 | 120 | 200 |
| 8 | 140 | 220 |
| 9 | 155 | 240 |
| 10 | 150 | 260 |
变量说明见 表 2.6 :
| variable | label |
|---|---|
| obs | 样本编号 |
| spends | 家庭支出 |
| income | 家庭收入 |
上机数据说明:
所有同学的\(X\)数据(家庭收入\(income\))都一样!
每个同学的\(Y\)数据(家庭支出\(spends\))都不一样!
请下载数据表后,找到自己的两列,并进行Excel预处理(以便导入到Eviews!)
如果消费和收入之间可以构造如下一元线性回归模型:
\[ \begin{aligned} Y_i & =\hat{\beta}_1+\hat{\beta}_2X_i+e_i && \text{(SRM)} \end{aligned} \tag{2.51}\]
\[ \begin{aligned} \hat{Y}_i & =\hat{\beta}_1+\hat{\beta}_2X_i && \text{(SRF)} \end{aligned} \tag{2.52}\]
2.4.3 实验规则
Eviews操作会得到各种计算结果,我们需要把计算结果以对象的形式保存在Eviews的工作文件内。因此我们提前设计好了各种对象保存命名规则,以便计算过程中的连续性、一致性调用。 表 2.7 给出了记号、含义、对应英文词和示例。
| remark | mean | word | example |
|---|---|---|---|
| upr | 字母大写 | uper | 样本序列\(Y_i\),可记为y_upr |
| lwr | 字母小写 | lower | 离差序列\(y_i\),可记为y_lwr |
| avr | 均值 | average | 样本均值\(\bar{X}\),可记为x_avr |
| sqr | 平方 | square | 样本序列\(Y^2_i\),可记为y_upr_sqr |
| hat | 估计值 | hat | \(\hat{\beta}_2\)和\(\hat{Y}_i\),可分别记为b2_hat和y_upr_hat |
| str | 星号 | star | 斜率系数的样本t值\(t^{\ast}_{\hat{\beta}_2}\),可记为t_str_b2_hat |
| scl | 标量 | scalar | 样本均值\(\bar{X}\)作为标量,可记为x_avr_scl |
| ser | 序列 | series | 样本均值\(X_i\)可作为有 n个数值的序列,可记为x_avr_ser |
| sgm | 方差参数 | sigma | 回归误差方差\(\hat{\sigma}^2\),可记为sgm_hat_sqr |
| b | 回归参数 | beta | 斜率参数\(\beta_2\),可记为b2 |
| mns | 减号 | minus | 样本标准差\(S_{(\hat{Y}_0-Y_0)}\),可记为s_y0h_mns_y0 |
| fst | 预测 | forecast | 均值预测值\(E(Y{\mid}X=X_0)\),可记为fst_exp |
| exp | 期望值 | expect | 均值预测值\(E(Y{\mid}X=X_0)\),可记为fst_exp |
| ind | 个值 | individual | 个值预测值\((Y_0{\mid}X=X_0)_L\),可记为fst_ind |
| lft | 左界 | left | 均值区间预测的左界值\(E(Y{\mid}X=X_0)_L\),可记为y_exp_lft |
| rht | 右界 | right | 均值区间预测的右界值\(E(Y{\mid}X=X_0)_R\),可记为y_exp_rht |
| name_chn | cat_eng | math | name_eviews |
|---|---|---|---|
| 自变量X序列 | series | \(X_i\) | x_upr |
| 因变量Y序列 | series | \(Y_i\) | y_upr |
| X均值标量 | scalar | \(\bar{X}\) | x_avr_scl |
| Y均值标量 | scalar | \(\bar{Y}\) | y_avr_scl |
| X均值序列 | series | \(\bar{X}_i\) | x_avr_ser |
| Y均值序列 | series | \(\bar{Y}_i\) | y_avr_ser |
| 样本数n | scalar | \(n\) | n |
| X平方序列 | series | \(X_i^2\) | x_upr_sqr |
| Y平方序列 | series | \(Y_i^2\) | y_upr_sqr |
| XY序列 | series | \(X_iY_i\) | xy_upr |
| 离差x序列 | series | \(x_i\) | x_lwr |
| 离差y序列 | series | \(y_i\) | y_lwr |
| 离差x平方序列 | series | \(x_i^2\) | x_lwr_sqr |
| 离差y平方序列 | series | \(y_i^2\) | y_lwr_sqr |
| 离差xy序列 | series | \(x_iy_i\) | xy_lwr |
| 斜率估计值 | scalar | \(\hat{\beta}_2\) | b2_hat |
| 截距估计值 | scalar | \(\hat{\beta}_1\) | b1_hat |
| 回归预测值Y帽序列 | series | \(\hat{Y}_i\) | y_upr_hat |
| 回归预测值的离差y帽序列 | series | \(\hat{y}_i\) | y_lwr_hat |
| 残差序列 | series | \(e_i\) | ei |
| 残差平方序列 | series | \(e_i^2\) | ei_sqr |
| 回归误差方差 | scalar | \(\hat{\sigma}^2\) | sgm_hat_sqr |
| 回归误差标准差 | scalar | \(\hat{\sigma}\) | sgm_hat |
| 斜率的样本方差 | scalar | \(S^2_{\hat{\beta}_2}\) | ss_b2_hat |
| 斜率的样本标准差 | scalar | \(S_{\hat{\beta}_2}\) | s_b2_hat |
| 截距的样本方差 | scalar | \(S^2_{\hat{\beta}_1}\) | ss_b1_hat |
| 截距的样本标准差 | scalar | \(S_{\hat{\beta}_1}\) | s_b1_hat |
| 总平方和 | scalar | \(TSS\) | tss |
| 残差平方和 | scalar | \(RSS\) | rss |
| 回归平方和 | scalar | \(ESS\) | ess |
| 总平方和的自由度 | scalar | \(df_{TSS}\) | df_tss |
| 残差平方和的自由度 | scalar | \(df_{RSS}\) | df_rss |
| 回归平方和的自由度 | scalar | \(df_{ESS}\) | df_ess |
| 简单相关系数 | scalar | \(r\) | r |
| 判定系数 | scalar | \(R^2\) | r_sqr |
| 斜率系数的t统计量 | scalar | \(t^{\ast}_{\hat{\beta}_2}\) | t_str_b2_hat |
| 截距系数的t统计量 | scalar | \(t^{\ast}_{\hat{\beta}_1}\) | t_str_b1_hat |
| 理论t值 | scalar | \(t_{1-\alpha/2}(n-k)\) | t_value |
| 回归方程的F统计量 | scalar | \(F^{\ast}\) | f_str |
| 理论F值 | scalar | \(F_{1-\alpha}(k-1,n-k)\) | f_value |
| 样本外数据 | scalar | \(X_0\) | x0 |
| 样本外回归值 | scalar | \(\hat{Y}_0\) | y0_hat |
| 均值预测 | scalar | \(E(Y{\mid}X=X_0)\) | fst_exp |
| \(\hat{Y}_0\)的样本标准差 | scalar | \(S_{\hat{Y}_0}\) | s_y0h |
| 均值区间预测的左界 | scalar | \(E(Y{\mid}X=X_0)_L\) | y_exp_lft |
| 均值区间预测的右界 | scalar | \(E(Y{\mid}X=X_0)_R\) | y_exp_rht |
| 个值预测 | scalar | \((Y_0{\mid}X=X_0)\) | fst_ind |
| \(\hat{Y}_0-Y_0\)的样本标准差 | scalar | \(S_{(\hat{Y}_0-Y_0)}\) | s_mns |
| 个值区间预测的左界 | scalar | \((Y_0{\mid}X=X_0)_L\) | y_ind_lft |
| 个值区间预测的右界 | scalar | \((Y_0{\mid}X=X_0)_R\) | y_ind_rht |
2.5 主要实验步骤
2.5.1 新建工作文件并导入数据
Eviews操作目标:构建工作文件,成功导入数据。
Eviews操作思路:利用EViews代码创建工作文件并导入数据。
在命令视窗中依次输入并运行如下EViews代码:
'创建工作文件(工作文件名=mento,子页命名=spend),无结构无日期,样本数为10
wfcreate(wf=mento,page=spend) u 10
'导入外部数据,路径为d:\github\books\data\lab2-mento-demon.xlsx
import d:\github\books\data\lab2-mento-demon.xlsx
在工作文件视窗下,可以看到创建的工作文件和导入的数据,可以双击查看(见 图 2.2 ):
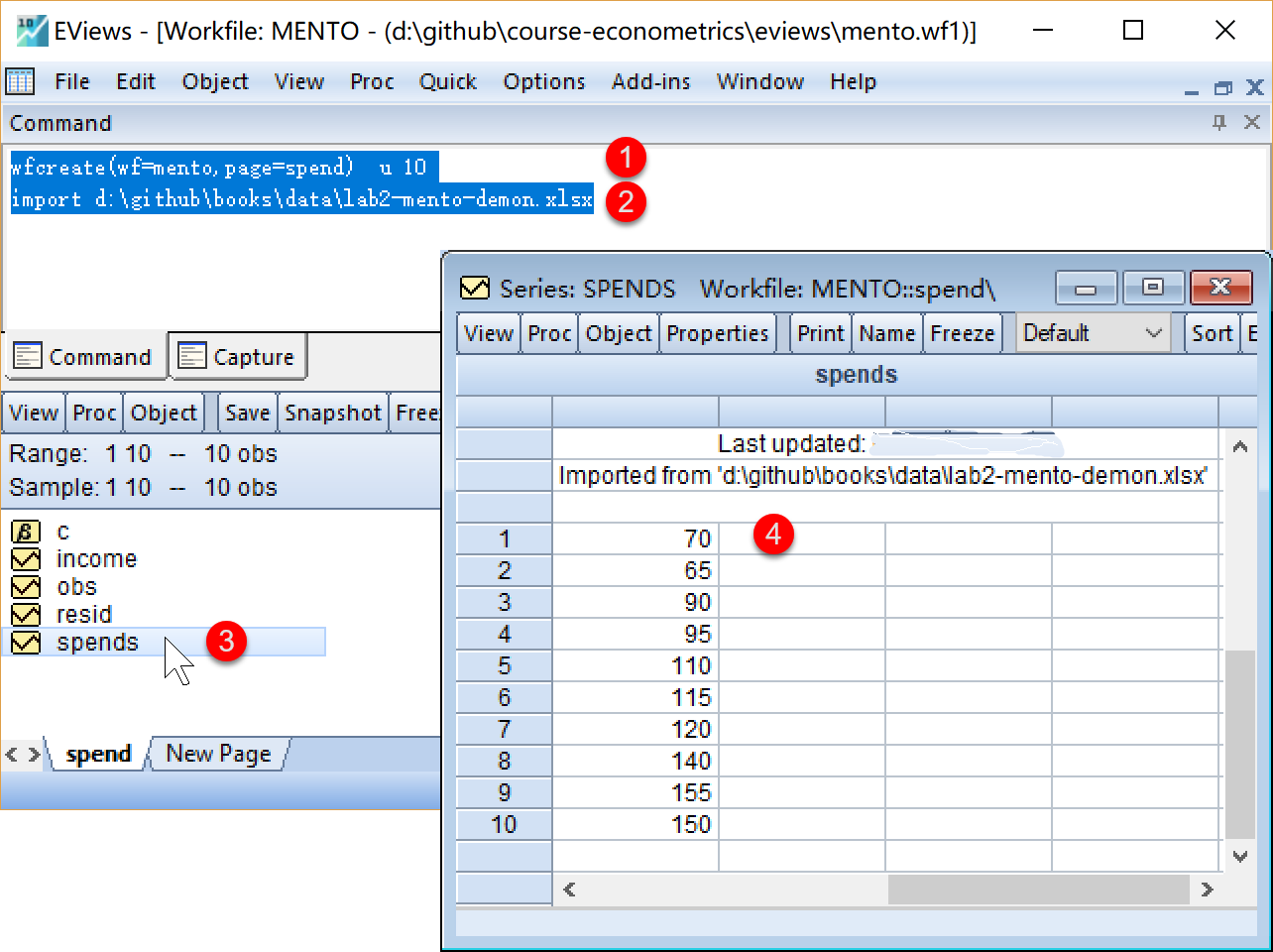
上述过程也可以通过菜单操作实现:
创建工作文件:
(1)EViews主窗口上依次点击\(\Rightarrow\) File\(\Rightarrow\) New\(\Rightarrow\) Workfile
(2)进行workfile create引导设置:
workfile structure type:
unstructured/undatededata range:默认设置
workfile names(optional):
- WF:
mento - Page:
spends(建议命名spends)
- WF:
导入外部数据:EViews主窗口上依次点击\(\Rightarrow\) File \(\Rightarrow\) Import \(\Rightarrow\) Import from file ...
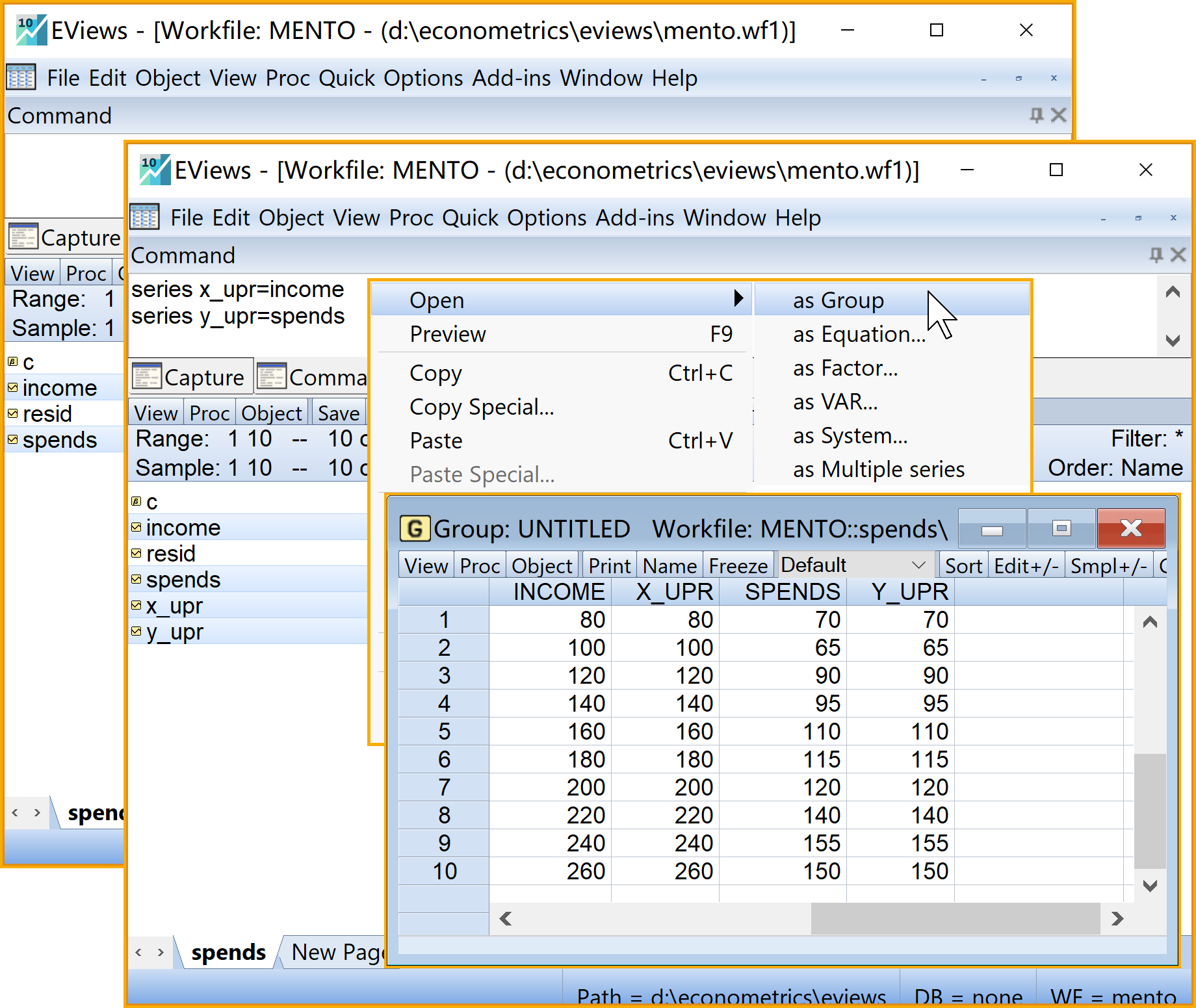
2.5.2 进行Eviews回归分析
Eviews操作目标:得到回归方程,查看回归结果
Eviews操作思路:构建回归方程对象。回归方程为:
\[ \begin{aligned} \begin{split} spends_i=&+\beta_{1}+\beta_{2}income_i+u_i \end{split} \end{aligned} \tag{2.53}\]
在命令视窗中依次输入并运行如下EViews代码:
' 生成线性回归方程对象eq_main
equation eq_m0.ls spends c income
在工作文件视窗下,可以看到如下新生成的方程对象,可以双击查看 eq_m0(见 图 2.4 ):
eq_m0(见 图 2.4 ):
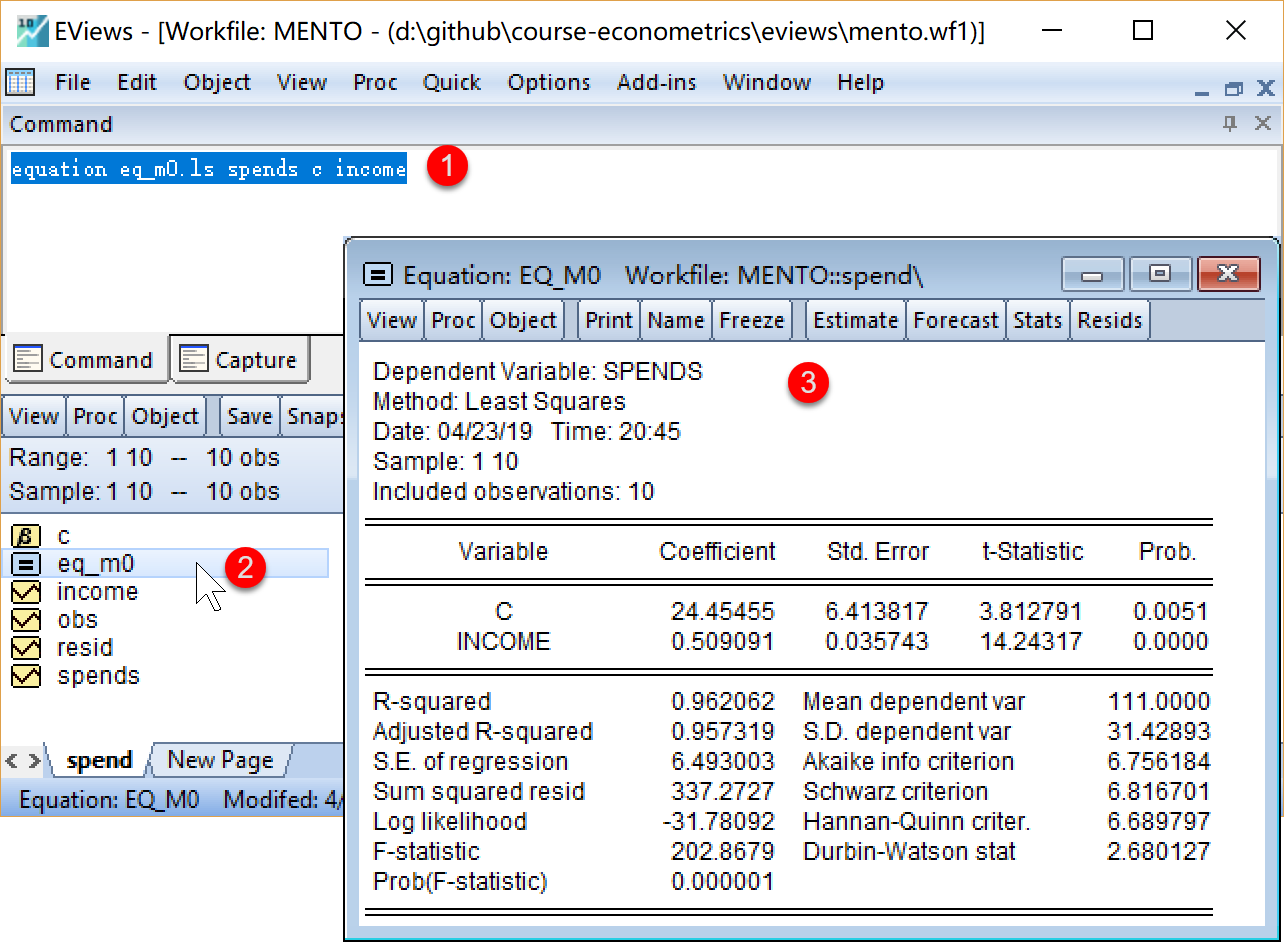
上述过程也可以通过菜单操作实现:
(1)进入方程估计的引导界面:
- EViews主窗口上依次点击点
Quick\(\Rightarrow\)Estimation Equation
(2)完成方程估计的引导设置。
设置方程。
Equation Estimation\(\Rightarrow\)Specification\(\Rightarrow\)Equation specification中依次输入变量spend c income(注意变量之间的空格,以及截距c)选择估计方法。
Estimation settings中的Method下拉框 \(\Rightarrow\) 下拉选择LS - Least Squares (NLS and ARMA)完成设置,点击
OK
(3)命名并保存回归方程:
- 在未命名的方程对象
 UNTITLED视窗下,点击菜单栏
UNTITLED视窗下,点击菜单栏Name\(\Rightarrow\) 输入命名eq_m0(建议命名) \(\Rightarrow\) 完成命名,点击Ok
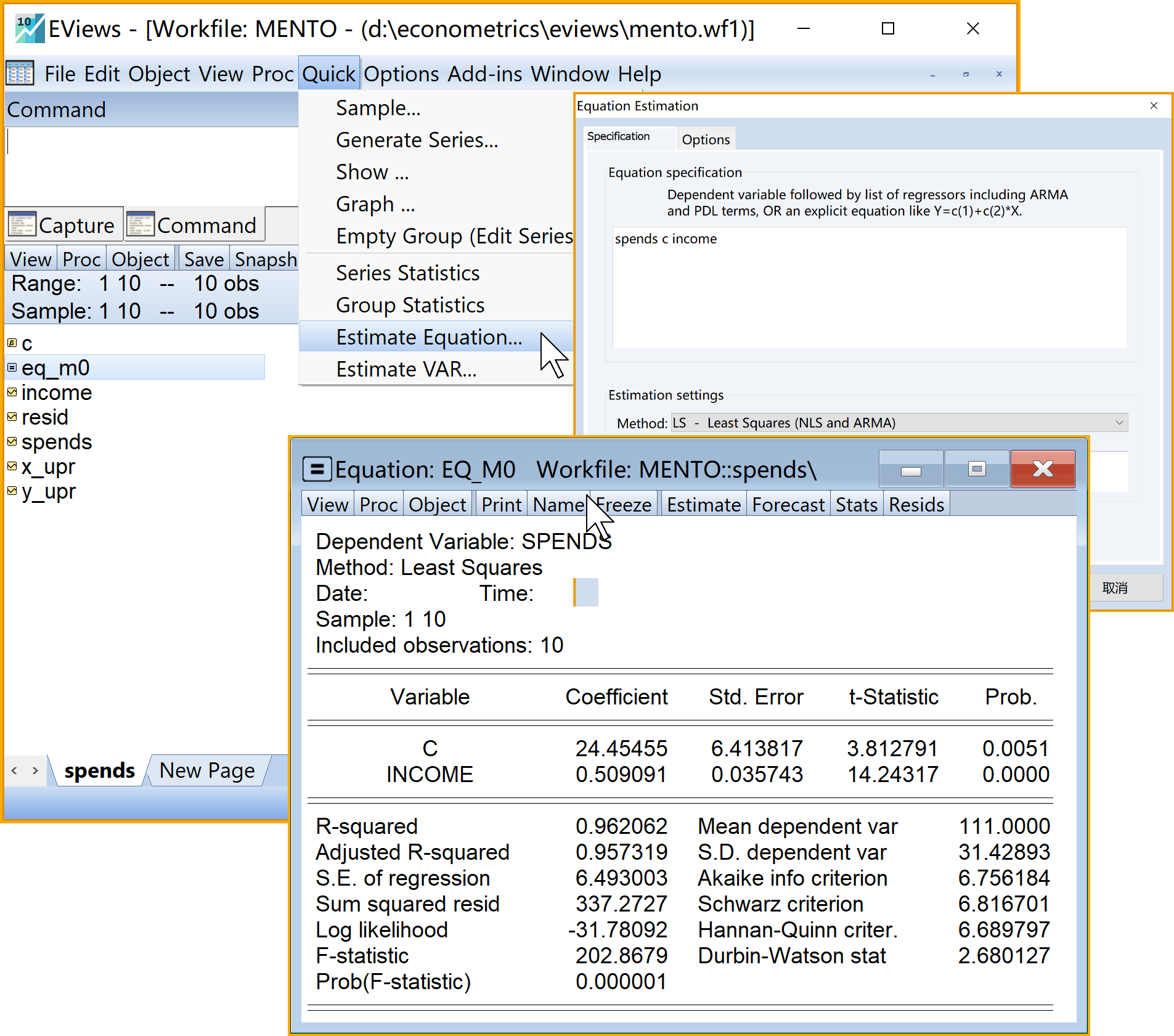
回归方程结果见 图 2.6 :
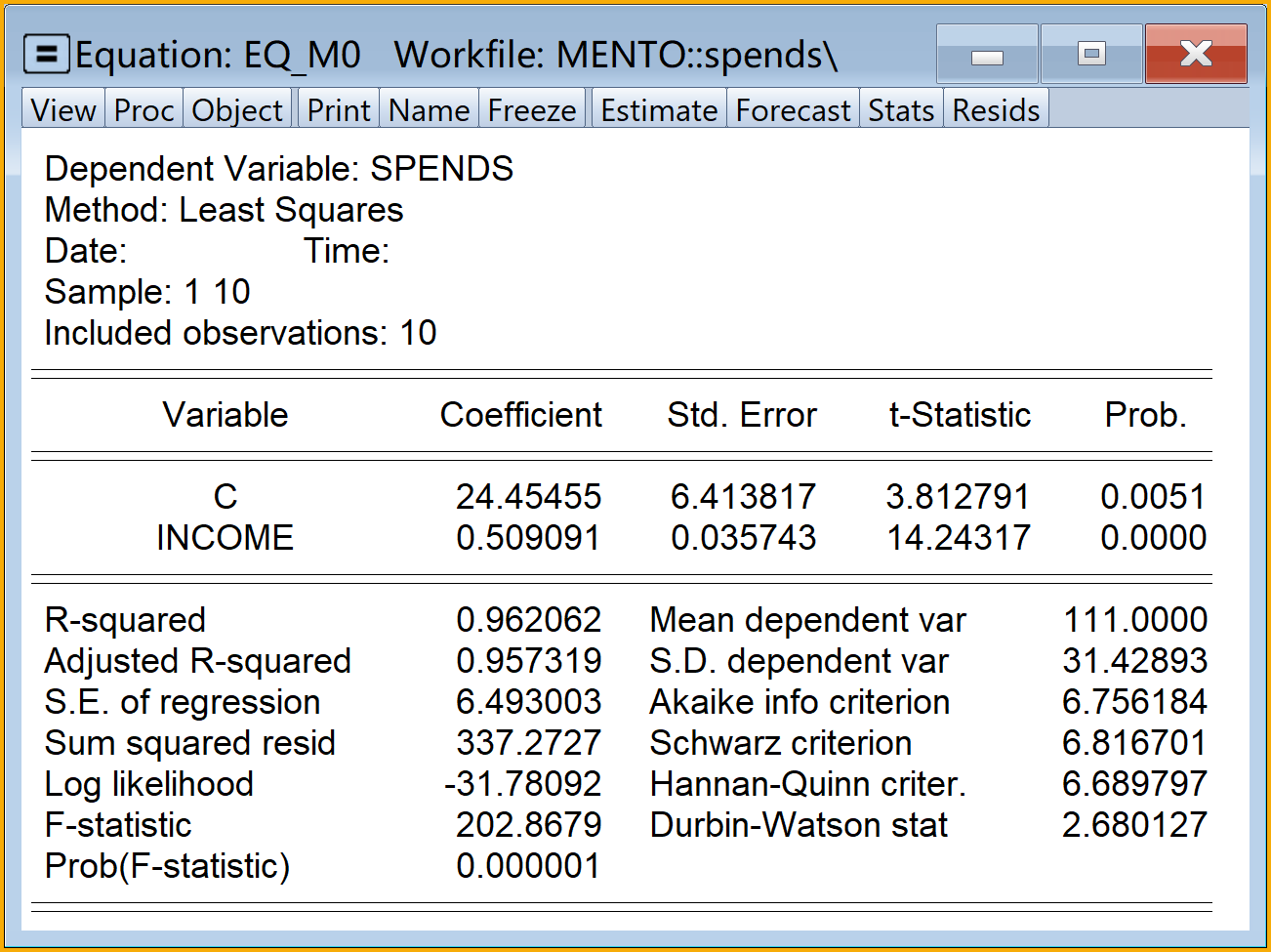
家庭消费支出回归模型的简要回归报告如下:
\[ \begin{aligned} \begin{split} \widehat{spends}_i=&+\hat{\beta}_{1}+\hat{\beta}_{2}income_i \end{split} \end{aligned} \tag{2.54}\]
\[ \begin{alignedat}{999} \begin{split} &\widehat{spends}=&&+24.45&&+0.51income_i\\ &(s)&&(6.4138)&&(0.0357)\\ &(t)&&(+3.81)&&(+14.24) \end{split} \end{alignedat} \tag{2.55}\]
2.5.3 构建几个重要变量对象
Eviews操作目标:构造几个重要EViews对象,便于后面分析使用
Eviews操作思路:转换变量名;均值\(\bar{X}\)和\(\bar{Y}\)的标量对象;样本数n的标量对象;均值\(\bar{X}\)和\(\bar{Y}\)的序列对象
\[ \begin{aligned} \bar{X}=\frac{\sum_{X_i}}{n}\\ \bar{Y}=\frac{\sum_{Y_i}}{n} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 转换变量名
series x_upr=x '序列X
series y_upr=y '序列Y
'计算三个重要标量
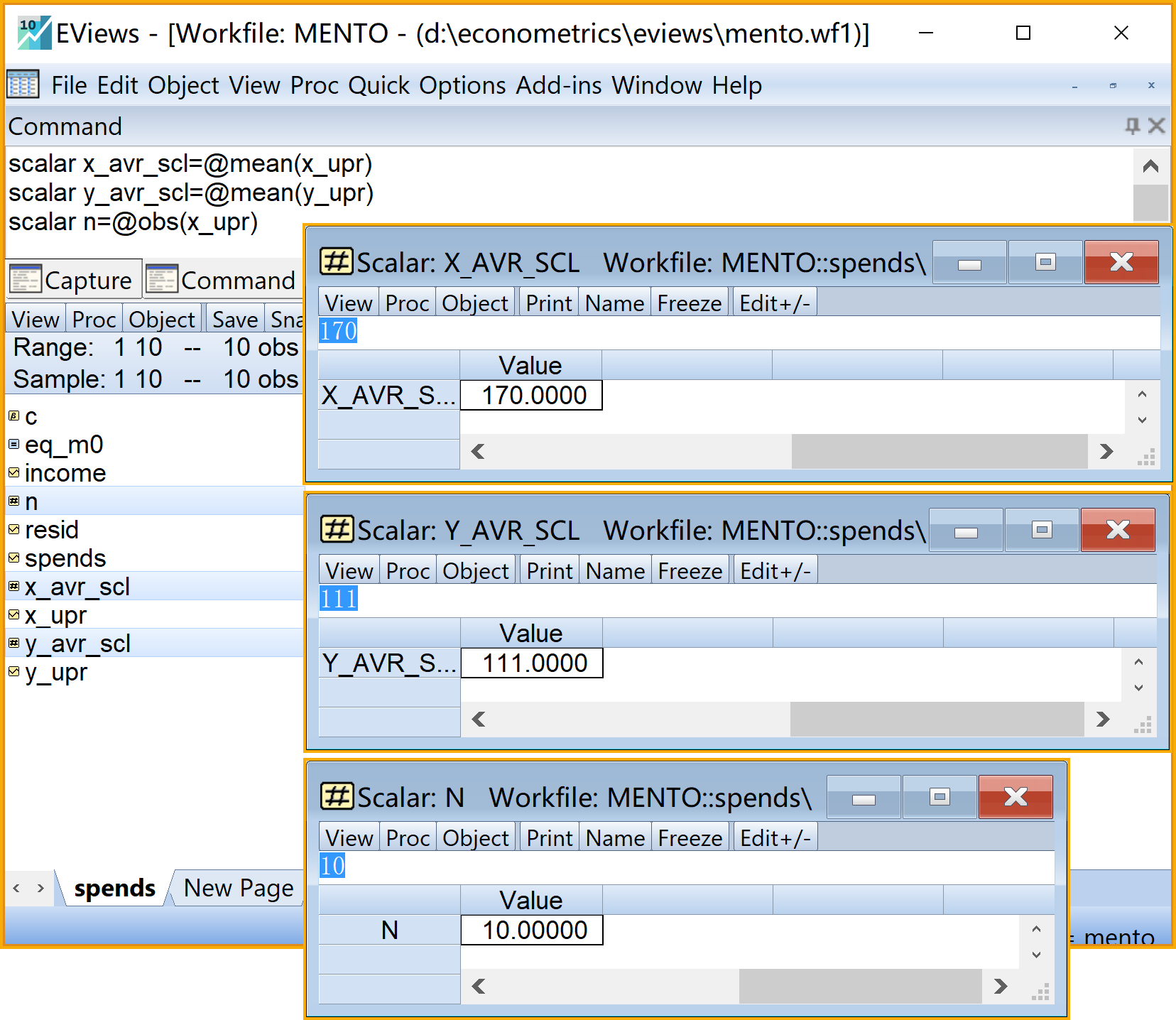
scalar x_avr_scl=@mean(x_upr) 'X的均值(标量)
scalar y_avr_scl=@mean(y_upr) 'Y的均值(标量)
scalar n=@obs(x_upr) '样本数n(标量)
'计算均值序列
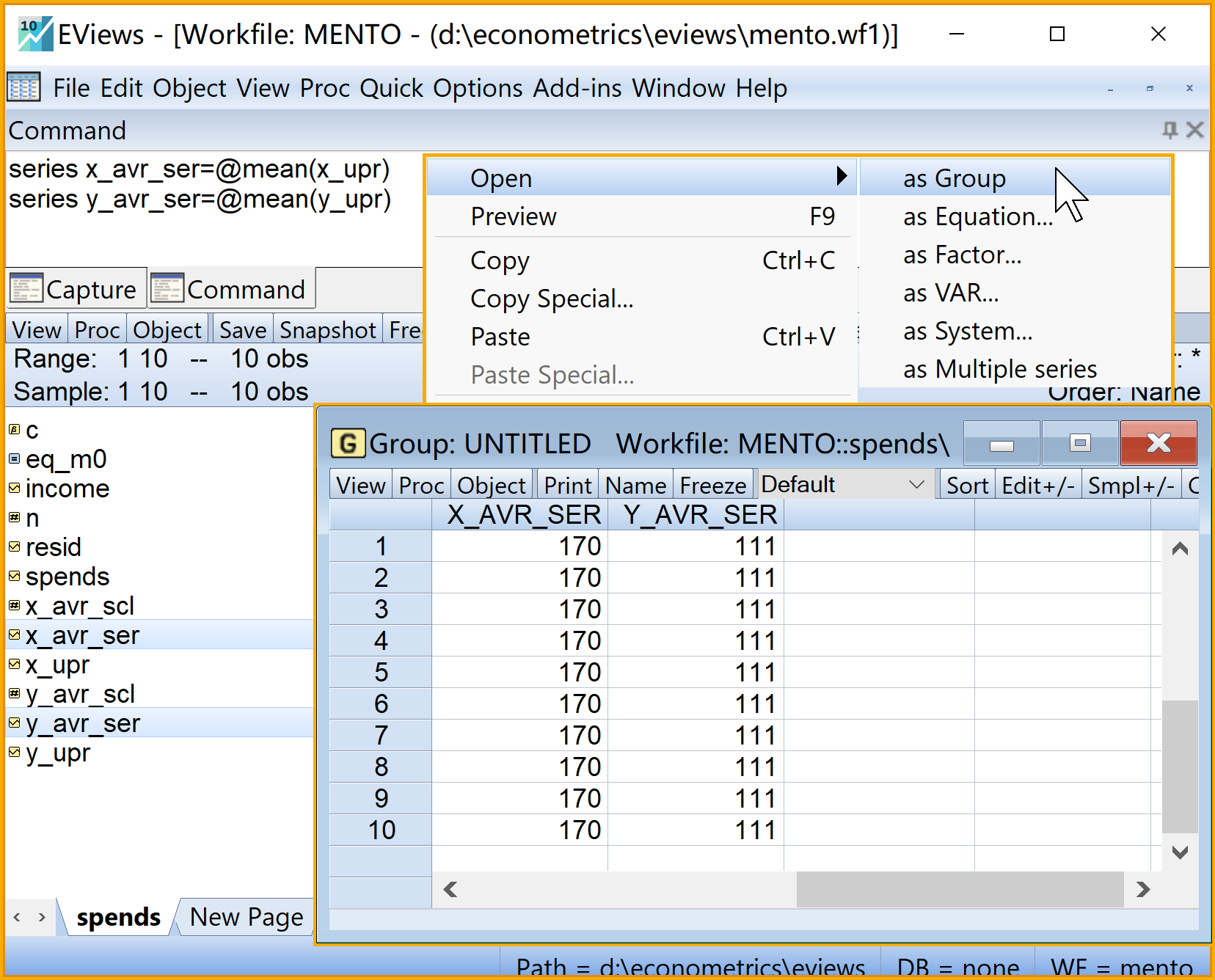
series x_avr_ser=@mean(x_upr) 'X的均值(序列)
series y_avr_ser=@mean(y_upr) 'Y的均值(序列)
在工作文件视窗下,可以看到如下新生成的对象,可以双击查看(见 图 2.7 和 图 2.8 ):
\(X_i\)的序列对象
 x_upr
x_upr\(Y_i\)的序列对象
 y_upr
y_upr均值\(\bar{X}\)的标量对象
 x_avr_scl
x_avr_scl均值\(\bar{Y}\)的标量对象
 y_avr_scl
y_avr_scl样本数n的标量对象
 n
n均值\(\bar{X}\)的标量对象
 x_ser_scl
x_ser_scl均值\(\bar{Y}\)的标量对象
 y_ser_scl
y_ser_scl
2.5.4 计算FF原序列(5个序列series)
目标:得到FF原序列(5个序列series)
思路:分别计算得到\(X_i; Y_i; X^2_i; Y^2_i; X_iY_i\)五个序列,并以组对象的形式保存
在命令视窗中依次输入并运行如下EViews代码:
'计算FF,并以group形式打开
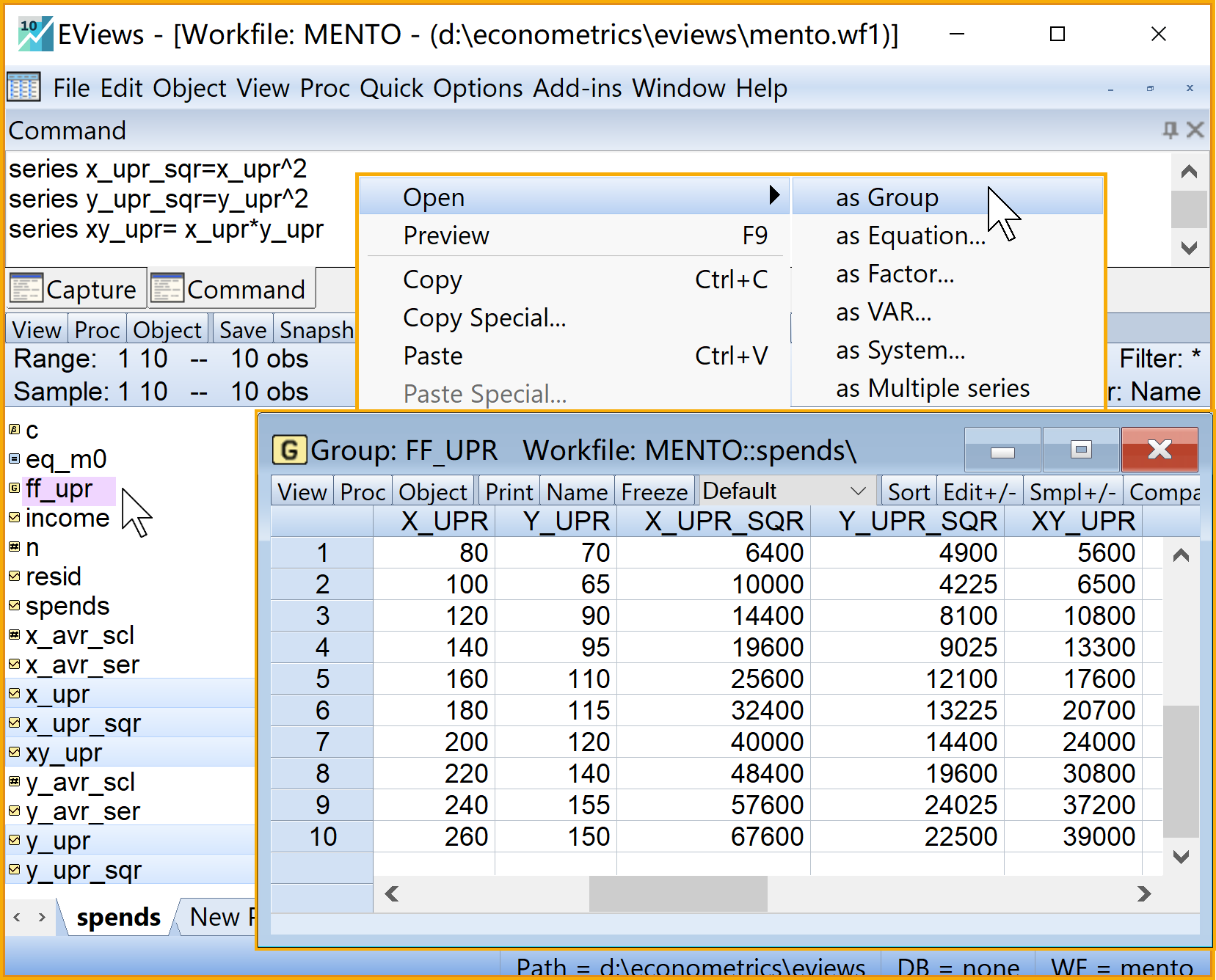
series x_upr_sqr=x_upr^2 '序列X^2
series y_upr_sqr=y_upr^2 '序列Y^2
series xy_upr= x_upr*y_upr '序列XY
group ff_upr x_upr y_upr x_upr_sqr y_upr_sqr xy_upr '构建FF序列组(group)
在工作文件视窗下,可以看到如下新生成的对象,可以双击查看(见 图 2.9 ):
- \(X^2_i\)的序列对象
 x_upr_sqr
x_upr_sqr - \(Y^2_i\)的序列对象
 y_upr_sqr
y_upr_sqr - \(X_iY_i\)的序列对象
 xy_upr
xy_upr - FF\((X_i; Y_i; X^2_i;Y^2_i,X_iY_i)\)的组对象
 ff_upr
ff_upr
Eviews操作:(Eviews具体操作过程见 图 2.9)
2.5.5 计算ff离差序列(5个序列series)
目标:得到FF原序列(5个序列series)
思路:分别计算得到\((x_i; y_i; x^2_i;y^2_i,x_iy_i)\)五个序列,并以组对象的形式保存。
\[ \begin{aligned} x_i & =(X_i-\bar{X}) \\ y_i & =(Y_i-\bar{Y}) \\ x_i^2 & =(X_i-\bar{X})^2 \\ y_i^2 & =(Y_i-\bar{Y})^2 \\ x_iy_i & =(X_i-\bar{X})(Y_i-\bar{Y}) \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
'计算ff离差series,并构建group
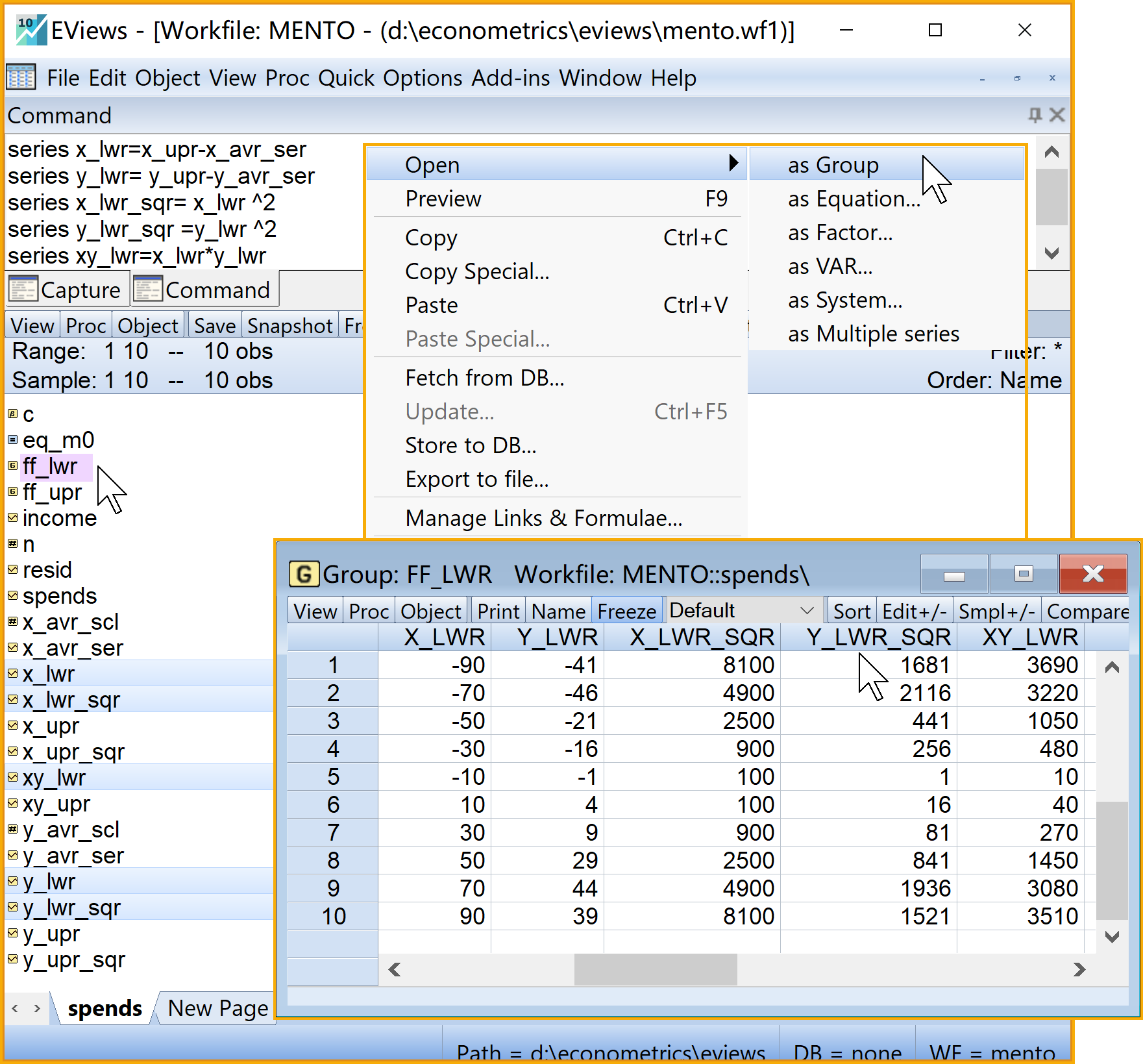
series x_lwr=x_upr-x_avr_ser '离差序列x
series y_lwr= y_upr-y_avr_ser '离差序列y
series x_lwr_sqr= x_lwr ^2 '离差序列x^2
series y_lwr_sqr =y_lwr ^2 '离差序列y^2
series xy_lwr=x_lwr*y_lwr '离差序列xy
group ff_lwr x_lwr y_lwr x_lwr_sqr y_lwr_sqr xy_lwr '构建ff离差序列组(group)
在工作文件视窗下,可以看到如下新生成的对象,可以双击查看(见 图 2.10 ):
\(x_i\)离差的序列对象
 x_lwr
x_lwr\(y_i\)离差的序列对象
 y_lwr
y_lwr\(x^2_i\)离差的序列对象
 x_lwr_sqr
x_lwr_sqr\(y^2_i\)离差的序列对象
 y_lwr_sqr
y_lwr_sqr\(x_iy_i\)离差的序列对象
 xy_lwr
xy_lwrff\((x_i; y_i; x^2_i;y^2_i,x_iy_i)\)的组对象
 ff_lwr
ff_lwr
2.5.6 计算回归系数的估计值:
Eviews操作目标:计算得到回归方程的回归系数(包含2个系数估计值)。
Eviews操作思路:根据FF或ff,利用理论公式,计算得出方程的斜率系数和截距系数。理论计算公式为:
\[ \begin{aligned} \hat{\beta}_2 &=\frac{\sum{x_iy_i}}{\sum{x_i^2}} &&\text{(b2\_hat)} \\ \hat{\beta}_1 &= \bar{Y}-\hat{\beta}_2\bar{X} &&\text{(b1\_hat)} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 计算回归系数scalar:b2和b1
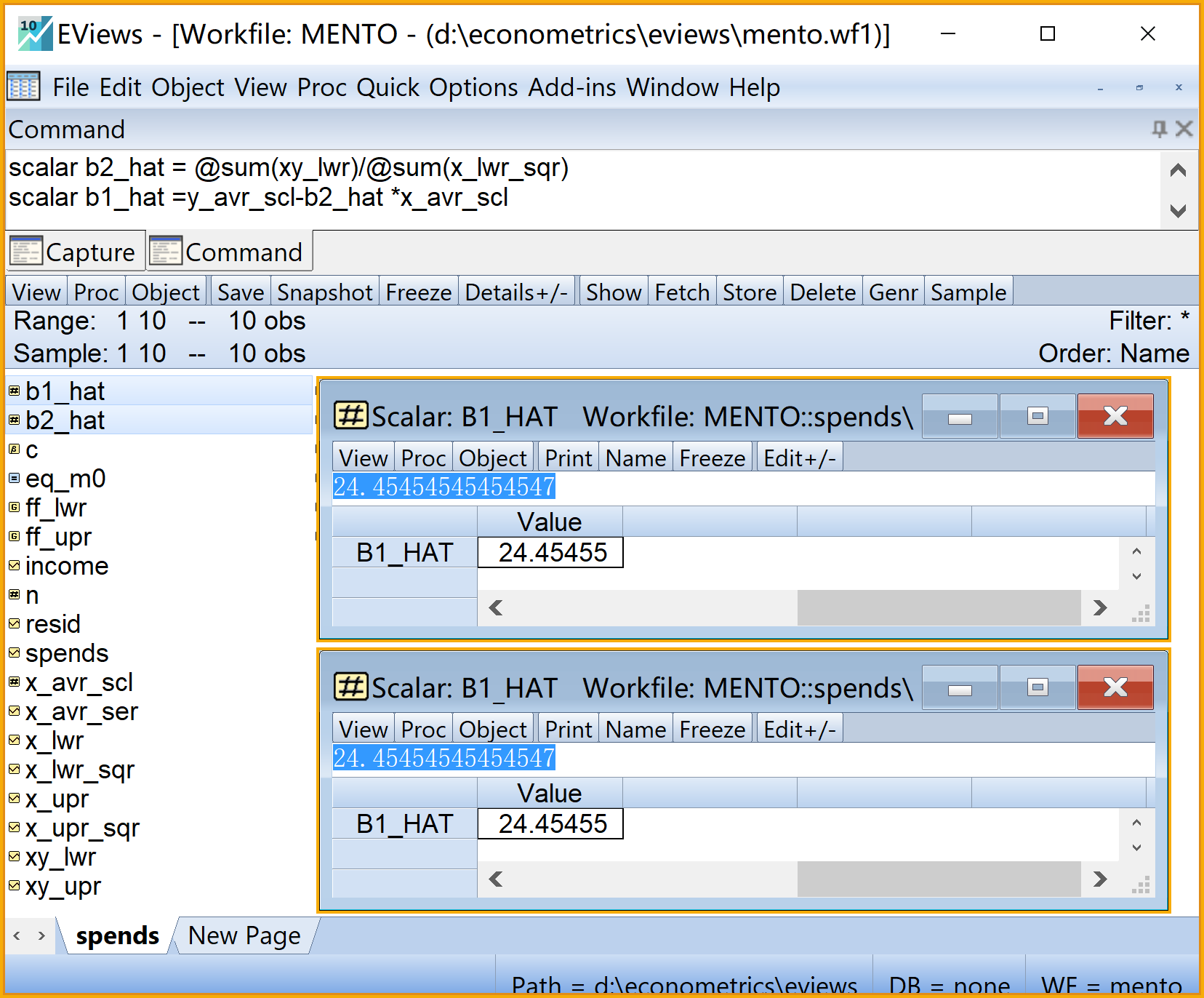
scalar b2_hat = @sum(xy_lwr)/@sum(x_lwr_sqr) '斜率系数
scalar b1_hat =y_avr_scl-b2_hat *x_avr_scl '截距系数
在工作文件视窗下,可以看到如下新生成的标量对象,可以双击查看(见 图 2.11 ):
回归方程斜率系数\(\hat{\beta}_2\)的标量对象
 b2_hat
b2_hat回归方程截距系数\(\hat{\beta}_1\)的标量对象
 b1_hat
b1_hat
2.5.7 计算回归拟合值、拟合值的离差、回归残差和残差平方序列(series):
目标:得到回归拟合值\(\hat{Y_i}\)、拟合值的离差\(\hat{y_i}\)、回归残差\(e_i\)和回归残差平方\(e^2_i\)等五个序列对象,用于后续分析
思路:借助回归方程和回归系数值,先计算回归拟合值及其离差,再计算残差和残差平方序列
\[ \begin{aligned} \hat{Y_i} &=\hat{\beta}_1+\hat{\beta}_2\ast X_i \\ \hat{y}_i &=\hat{Y}_i-\bar{Y}\\ e_i &=Y_i-\hat{Y_i}\\ e^2_i&={(e_i)}^2 \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 计算回归预测值及其离差series
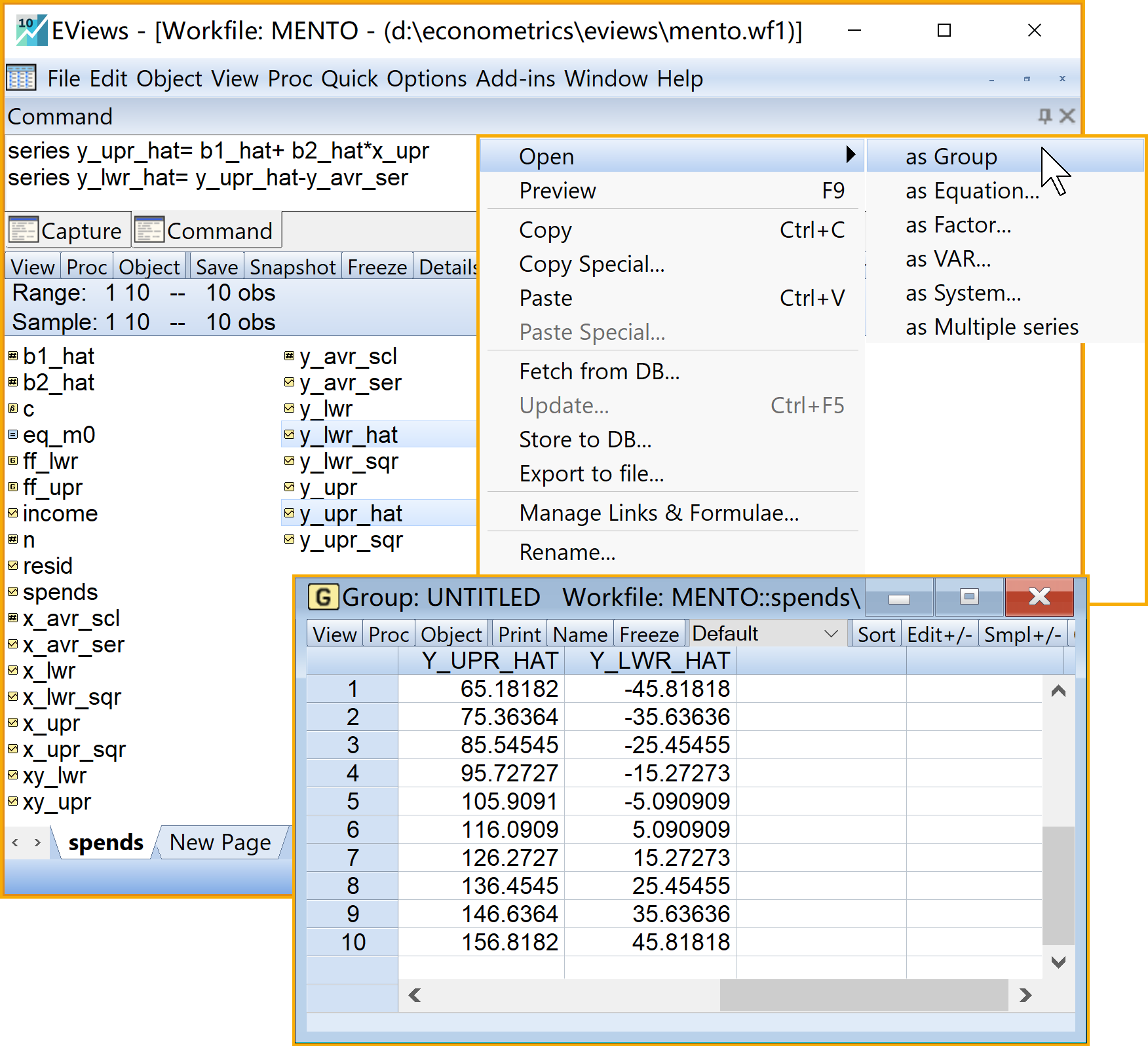
series y_upr_hat= b1_hat+ b2_hat*x_upr '回归预测值
series y_lwr_hat= y_upr_hat-y_avr_ser '回归预测的离差值
' 计算残差及残差平方series
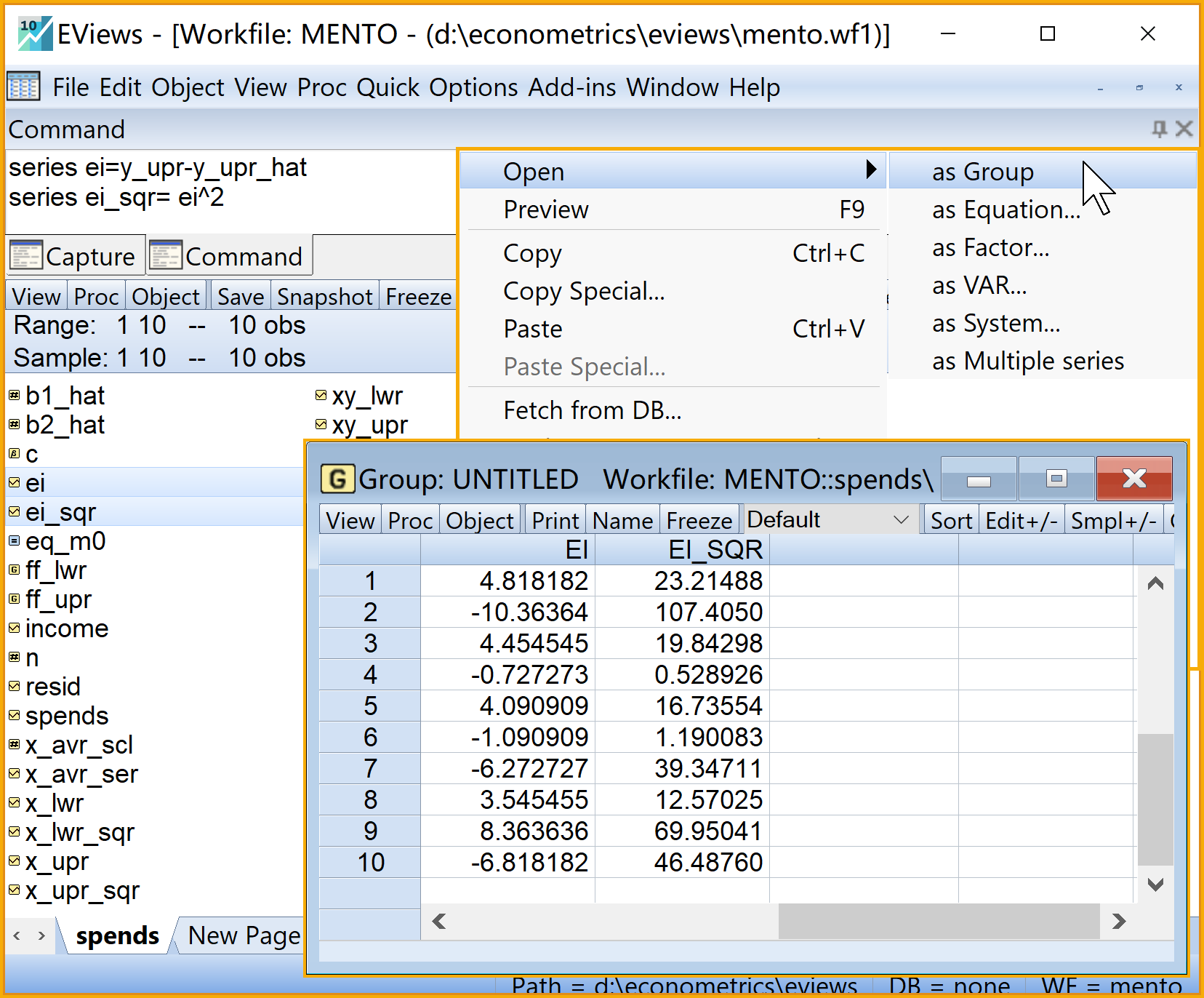
series ei=y_upr-y_upr_hat '残差序列
series ei_sqr= ei^2 '残差平方序列
在工作文件视窗下,可以看到如下新生成的序列对象,可以双击查看(见 图 2.12 和 图 2.13 ):
回归拟合值\(\hat{Y_i}\)的序列对象
 y_upr_hat
y_upr_hat回归拟合值离差\(\hat{y_i}\)的序列对象
 y_lwr_hat
y_lwr_hat回归残差\(e_i\)的序列对象
 ei
ei回归残差平方\(e^2_i\)的序列对象
 ei_sqr
ei_sqr
2.5.8 计算回归方程的误差方差及标准差
Eviews操作目标:计算回归方程的误差方差\(\hat{\sigma}^2\)及标准差\(\hat{\sigma}\)(标量),与主回归结果进行核验。
Eviews操作思路:利用残差序列对象,并参考如下公式
\[ \begin{aligned} \hat{\sigma}^2 &=\frac{\sum{e_i^2}}{n-2} \\ \hat{\sigma} & =\sqrt{\frac{\sum{e_i^2}}{n-2}} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 计算回归误差方差及其标准差scalar
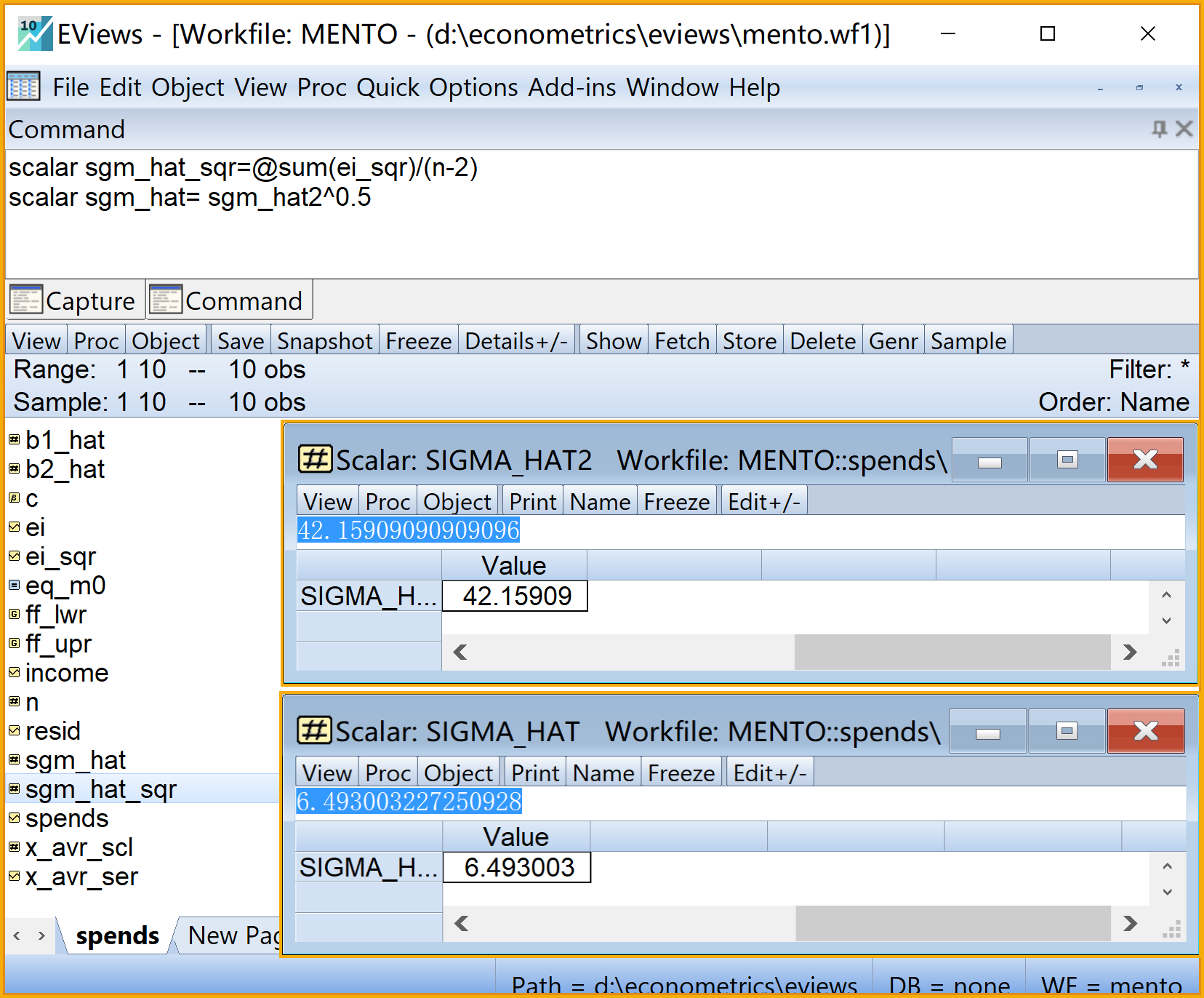
scalar sgm_hat_sqr=@sum(ei_sqr)/(n-2) '方程的回归误差方差
scalar sgm_hat= sgm_hat_sqr^0.5 '方程的回归误差标准差
在工作文件视窗下,可以看到如下的标量对象,可以双击查看(见 图 2.14 ):
回归误差方差\(\hat{\sigma}^2\)的标量对象
 sgm_hat_sqr
sgm_hat_sqr回归误差标准差\(\hat{\sigma}\)的标量对象
 sgm_hat
sgm_hat
2.5.9 计算回归系数的样本方差和标准差:
目标:分别得到斜率系数的样本方差和标准差(\(S_{\hat{\beta}_2}^2\)、\(S_{\hat{\beta}_2}^2\)),以及截距系数的样本方差和标准差(\(S_{\hat{\beta}_1}\)、\(S_{\hat{\beta}_1}\))
思路:借助如下的计算公式:
\[ \begin{aligned} S_{\hat{\beta}_2}^2 &=\frac{\hat{\sigma}^2}{\sum{x_i^2}} \\ S_{\hat{\beta}_2} &=\sqrt{\frac{\hat{\sigma}^2}{\sum{x_i^2}}} \\ S_{\hat{\beta}_1}^2 &=\frac{\hat{\sigma}^2}{\sum{x_i^2}}\ast \frac{\sum{X^2_i}}{n} \\ S_{\hat{\beta}_1} &=\sqrt{\frac{\hat{\sigma}^2}{\sum{x_i^2}}\ast \frac{\sum{X^2_i}}{n}} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 计算回归系数的样本方差和标准差scalar
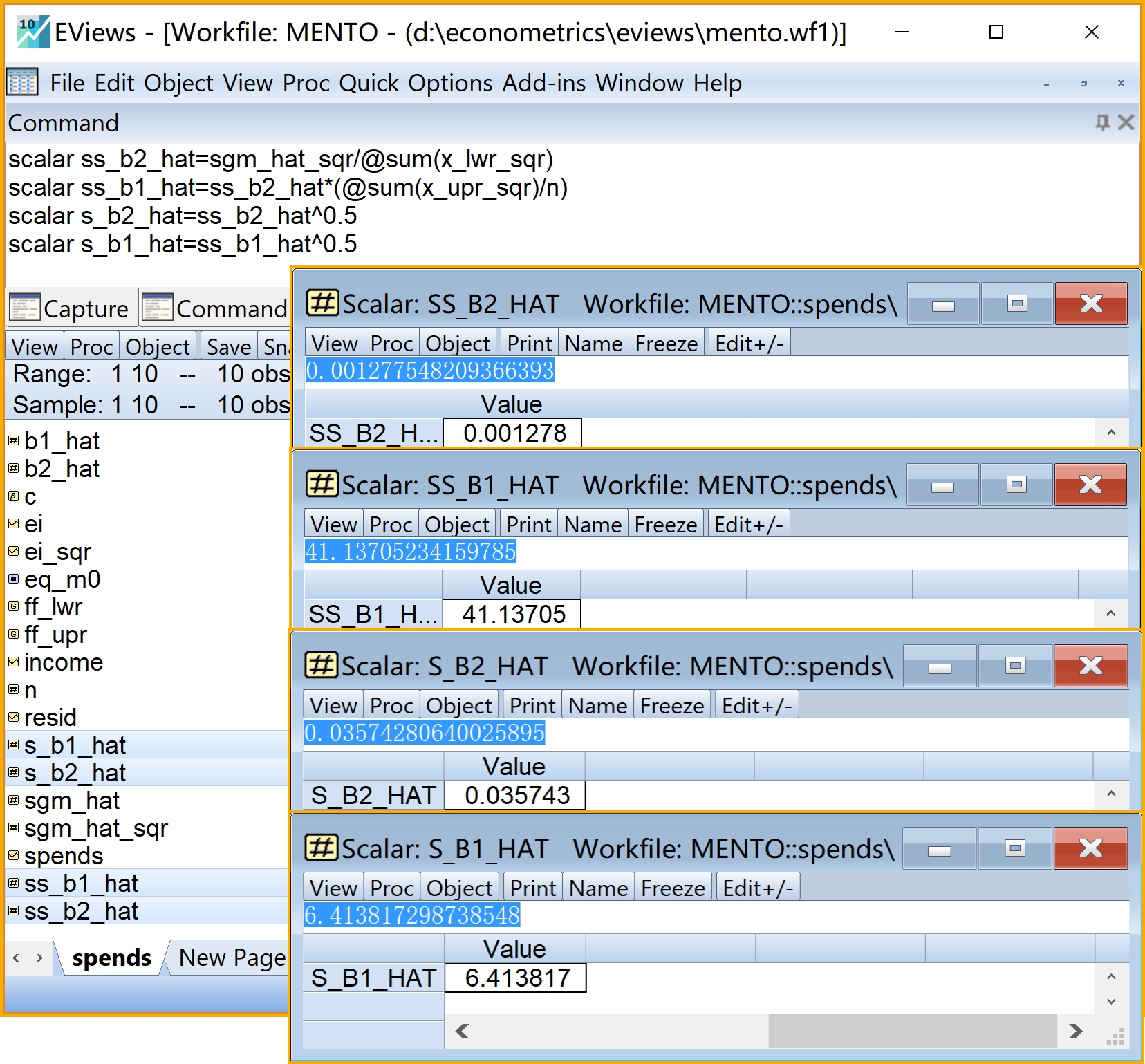
scalar ss_b2_hat=sgm_hat_sqr/@sum(x_lwr_sqr) '斜率系数的样本方差
scalar ss_b1_hat=ss_b2_hat*(@sum(x_upr_sqr)/n) '截距系数的样本方差
scalar s_b2_hat=ss_b2_hat^0.5 '斜率系数的样本标准差
scalar s_b1_hat=ss_b1_hat^0.5 '截距系数的样本标准差
在工作文件视窗下,可以看到如下EViews对象,可以双击查看(见 图 2.15 ):
斜率系数样本方差\(S_{\hat{\beta}_2}^2\)的标量对象
 ss_b2_hat
ss_b2_hat截距系数样本方差\(S_{\hat{\beta}_1}^2\)的标量对象
 ss_b1_hat
ss_b1_hat斜率系数样本标准差\(S_{\hat{\beta}_2}\)的标量对象
 s_b2_hat
s_b2_hat截距系数样本标准差\(S_{\hat{\beta}_1}\)的标量对象
 s_b1_hat
s_b1_hat
2.5.10 进行平方和分解,计算TSS、ESS和RSS,以及各自的自由度(标量)
Eviews操作目标:进行平方和分解,得到方差分析表(ANOVA)。
Eviews操作思路:掌握自由度的计算,利用理论公式
\[ \begin{aligned} TSS &=\sum{y_i^2}=\sum{(Y_i-\bar{Y})^2} \\ RSS &=\sum{e^2_i}=\sum{(Y_i-\hat{Y}_i)^2} \\ ESS &=\sum{\hat{y}_i^2}=\sum{(\hat{Y_i}-\bar{Y})^2}\\ TSS &=RSS+ESS\\ df_{TSS} &=n-1 \\ df_{RSS} &=n-k \\ df_{ESS} &=k-1 \\ df_{TSS} &=df_{RSS}+df_{ESS} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
' 进行平方和分解并得到相应自由度(标量scalar)
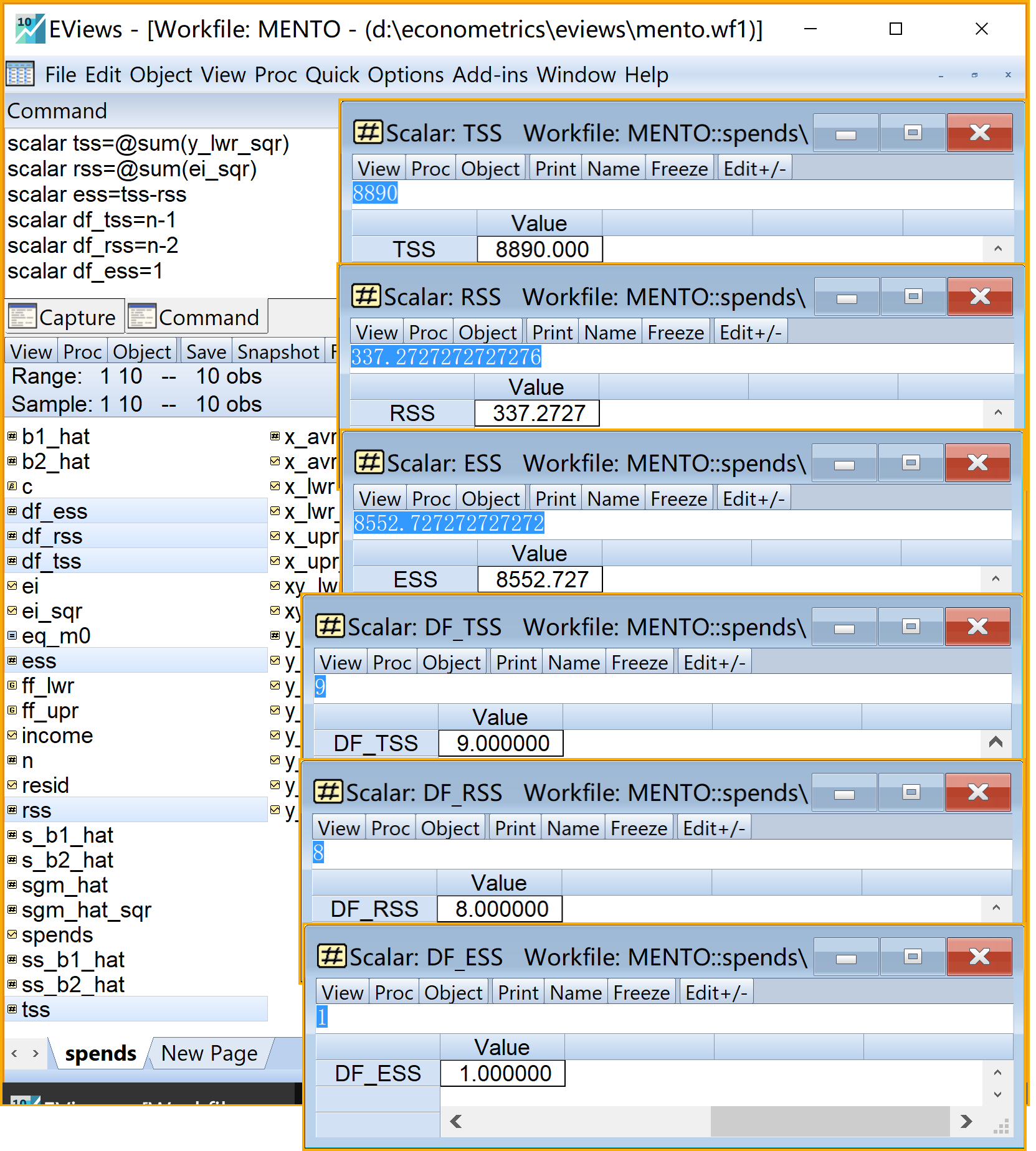
scalar tss=@sum(y_lwr_sqr) '总平方和TSS
scalar rss=@sum(ei_sqr) '残差平方和RSS
scalar ess=tss-rss '回归平方和ESS
scalar df_tss=n-1 ' TSS的自由度
scalar df_rss=n-2 ' RSS的自由度
scalar df_ess=1 ' ESS的自由度
在工作文件视窗下,可以看到如下的标量对象,可以双击查看(见 图 2.16 ):
总平方和\(TSS\)的标量对象
 tss
tss残差平方和\(RSS\)的标量对象
 rss
rss回归平方和\(ESS\)的标量对象
 ess
ess总平方和的自由度\(df_{TSS}\)的标量对象
 df_tss
df_tss残差平方和的自由度\(df_{RSS}\)的标量对象
 df_rss
df_rss回归平方和的自由度\(df_{ESS}\)的标量对象
 df_ess
df_ess
2.5.11 计算相关系数\(r\)和判定系数\(r^2\)(标量scalar):
Eviews操作目标:得到自变量\(X_i\)与因变量\(Y_i\)的相关系数,计算回归方程的判定系数。
Eviews操作思路:借助方差分析表结果计算判定系数。利用理论公式
\[ \begin{aligned} r &=\frac{Cov(X,Y)}{S_X\ast S_Y}=\frac{\sum{(X_i-\bar{X})(Y_i-\bar{Y})}}{\sqrt{\sum{(X_i-\bar{X}})^2\sum{(Y_i-\bar{Y})^2}}}\\ r^2 &=\frac{ESS}{TSS} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
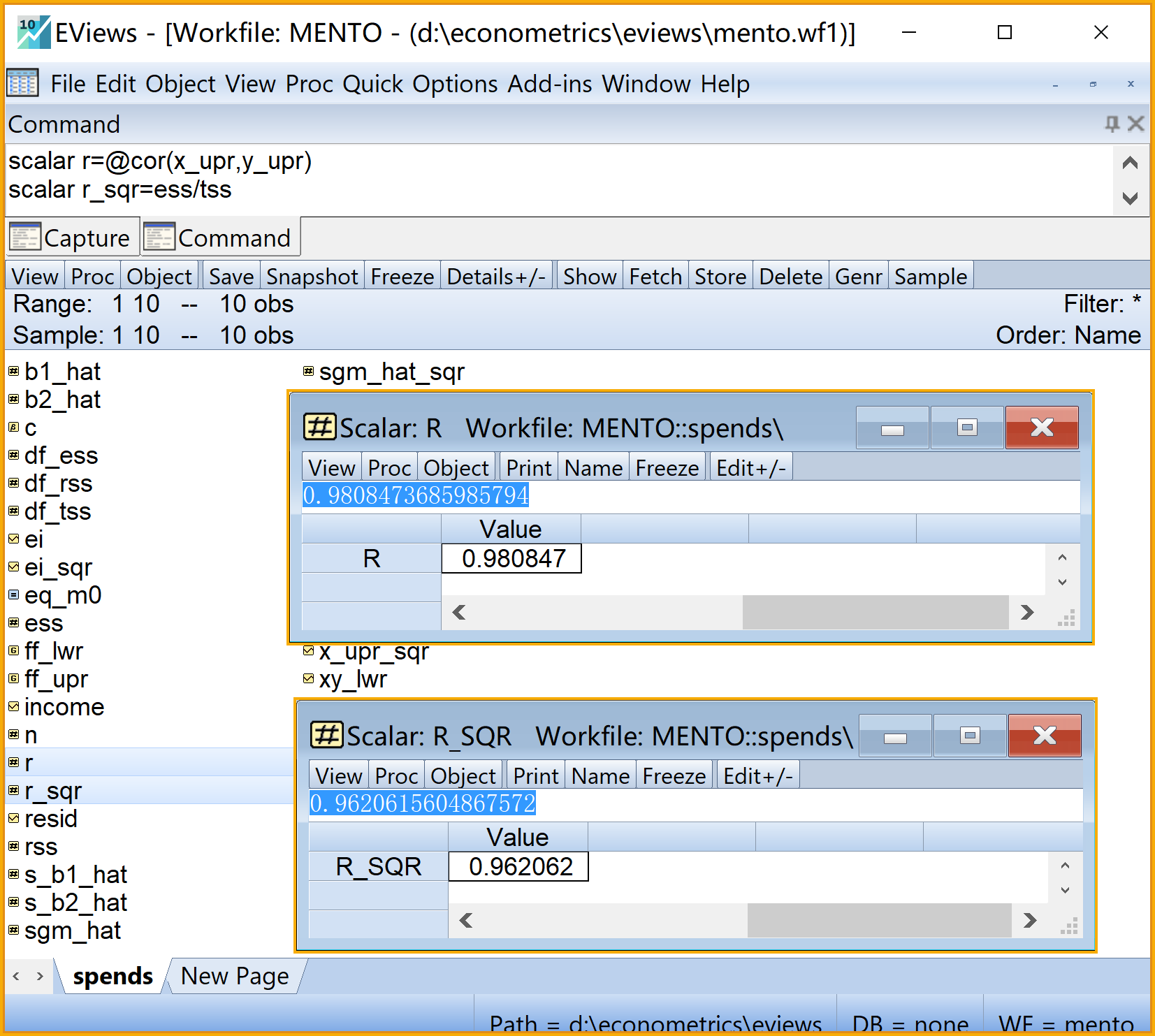
' 计算相关系数r和判定系数(标量scalar)
scalar r=@cor(x_upr,y_upr) 'X和Y变量的相关系数
scalar r_sqr=ess/tss '回归方程的判定系数
在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 2.17 ):
自变量\(X_i\)与因变量\(Y_i\)相关系数的标量对象
 r
r回归方程判定系数\(R^2\)的标量对象
 r_sqr
r_sqr
2.5.12 回归系数的t检验
目标:检验各个回归系数是否显著
思路:根据理论的矩阵公式,计算样本t统计量;计算给定显著性水平下的理论t值;进行t假设检验。
回归系数的样本t统计量以及给定显著性水平下的理论t值的计算公式为:
\[ \begin{aligned} t^{\ast}_{\hat{\beta}_2} &=\frac{\hat{\beta}_2}{S_{\hat{\beta}_2}}\\ t^{\ast}_{\hat{\beta}_1} &=\frac{\hat{\beta}_1}{S_{\hat{\beta}_1}}\\ t_{rht}&=t_{(1-\alpha)/2}(df_{RSS})=t_{0.975}(8)\\ t_{lft}&=t_{\alpha/2}(df_{RSS})=t_{0.025}(8) \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
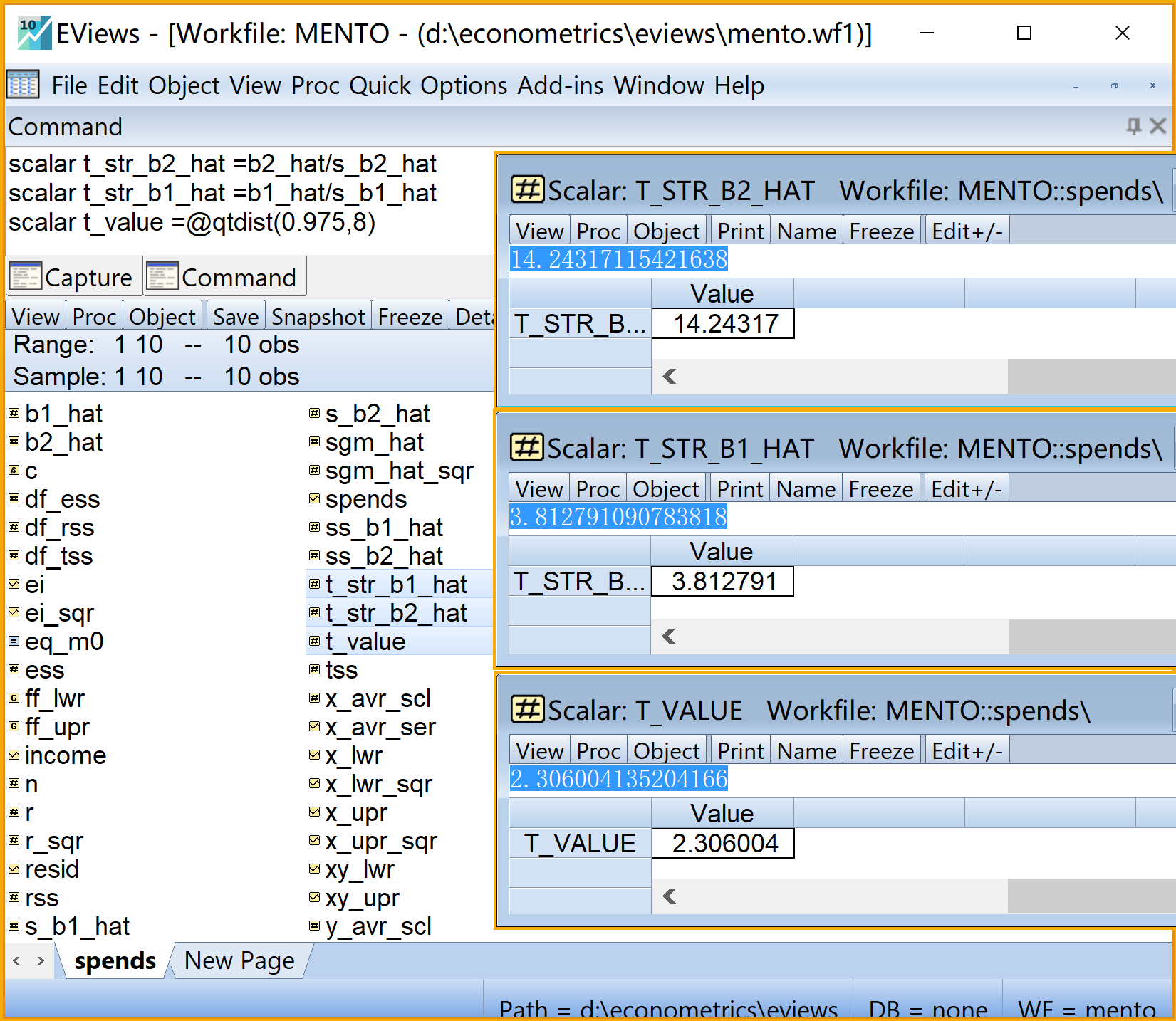
' 回归系数的t检验
scalar t_str_b2_hat =b2_hat/s_b2_hat '斜率的t统计量
scalar t_str_b1_hat =b1_hat/s_b1_hat '截距的t统计量
scalar t_value =@qtdist(0.975,8) 'a=0.05下的t查表值(右侧正值)
scalar t_value2 =@qtdist(0.025,8) 'a=0.05下的t查表值(左侧负值)在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 2.18 ):
斜率系数样本t统计量\({t^{\ast}_{\beta_2}}\)的标量对象
 t_str_b2_hat
t_str_b2_hat截距系数样本t统计量\({t^{\ast}_{\beta_1}}\)的标量对象
 t_str_b1_hat
t_str_b1_hat给定\(\alpha=0.05\)水平下的理论t值(右侧正值)\(t_{1-\alpha/2}(n-k)\)的标量对象
 t_value
t_value给定\(\alpha=0.05\)水平下的理论t值(左侧负值)\(t_{\alpha/2}(n-k)\)的标量对象
 t_value2
t_value2
2.5.13 对回归方程的整体显著性进行F假设检验
目标:进行回归方程的整体显著性进行F假设检验
思路:根据理论公式,计算回归方程的样本F统计量;给定显著性水平下,计算得到理论F值;完成模型整体显著性F检验过程。
回归方程的样本F统计量,以及给定显著性水平下理论F值的计算公式为:
\[ \begin{aligned} F^\ast & ={\frac{MSS_{ESS}}{MSS_{RSS}}=\frac{ESS/df_{ESS}}{RSS/df_{RSS}}}\\ F_{rht} & =F_{1-\alpha}(df_{ESS},df_{RSS})=F_{0.95}(1,8)\\ F_{lft} & =F_{\alpha}(df_{ESS},df_{RSS})=F_{0.05}(1,8) \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
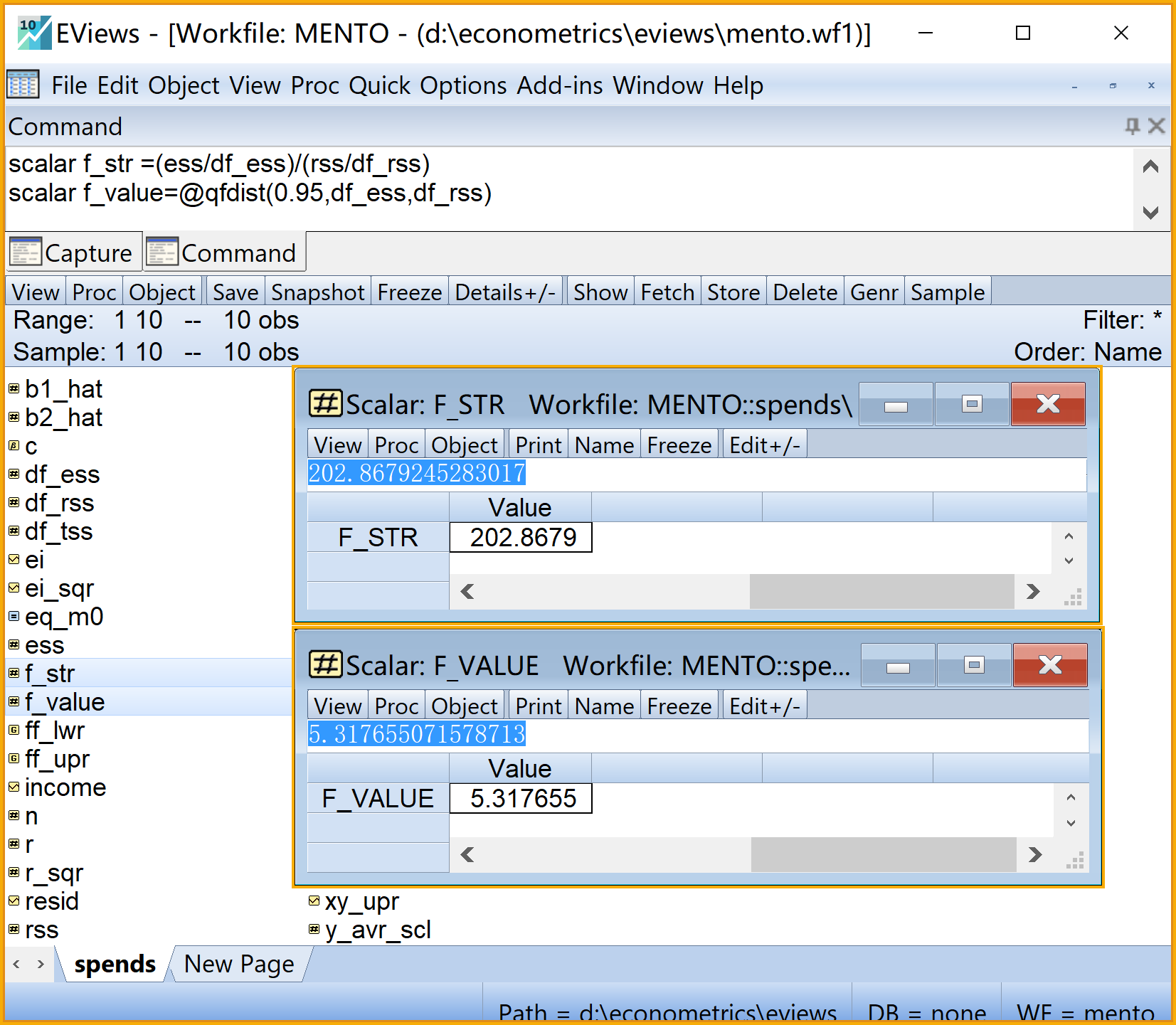
' 回归方程的F检验
scalar f_str =(ess/df_ess)/(rss/df_rss) '回归方程的F统计量值
scalar f_value=@qfdist(0.95,df_ess,df_rss) 'a=0.05下的t查表值(右侧大值)
scalar f_value2=@qfdist(0.05,df_ess,df_rss) 'a=0.05下的t查表值(左侧小值)
在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 2.19 ):
回归方程的样本F统计量\(F^{\ast}\)的标量对象
 f_str
f_str给定\(\alpha=0.05\)水平下的理论F值(右侧大值)\(F_{1-\alpha}(n-1,n-k)\)的标量对象
 f_value
f_value给定\(\alpha=0.05\)水平下的理论F值(左侧小值)\(F_{\alpha}(n-1,n-k)\)的标量对象
 f_value2
f_value2
2.5.14 进行样本外的均值预测、个值预测,并计算置信区间
目标:样本外的均值预测、个值预测,计算得到置信区间(给定显著性水平)
思路:构建样本外\({X_0}\);计算得到回归估计值\(\hat{Y}_0\);构造分别计算得到均值预测的t分布样本标准差\(S_{\hat{Y}_0}\)和个值预测的t分布样本标准差\(S_{Y_0-\hat{Y}_0}\);给定显著性水平下,计算得到理论t值;利用公式分别计算均值预测和个值预测的置信区间。
相关参考计算公式为:
\[ \begin{aligned} X_0 &=280 \\ \hat{Y_0} &=\hat{\beta_1}+\hat{\beta}_2\ast{X_0} \\ S_{\hat{Y}_0}&=\sqrt{\hat{\sigma}^2\left(\frac{1}{n}+\frac{(X_0-\bar{X})}{\sum{x_i^2}}\right)} \\ S_{Y_0-\hat{Y}_0} & =\sqrt{{\hat{\sigma}^2}{\left(1+\frac{1}{n}+\frac{{(X_0-\bar{X})}^2}{\sum{x^2_i}} \right)}} \\ \hat{\sigma}^2&=\frac{\sum{e^2_i}}{(n-k)} \\ E(Y|X=X_0)_{left} &=\hat{Y}_0-t_{1-\alpha/2}(df_{RSS}) \ast S_{\hat{Y}_0} \\ E(Y|X=X_0)_{right} &=\hat{Y}_0+t_{1-\alpha/2}(df_{RSS}) \ast S_{\hat{Y}_0} \\ (Y_0| X=X_0)_{left} & =\hat{Y}_0-t_{(1-\alpha/2)}(df_{RSS}) \ast S_{Y_0-\hat{Y}_0} \\ (Y_0| X=X_0)_{right} &=\hat{Y}_0+t_{(1-\alpha/2)}(df_{RSS}) \ast S_{Y_0-\hat{Y}_0} \end{aligned} \]
在命令视窗中依次输入并运行如下EViews代码:
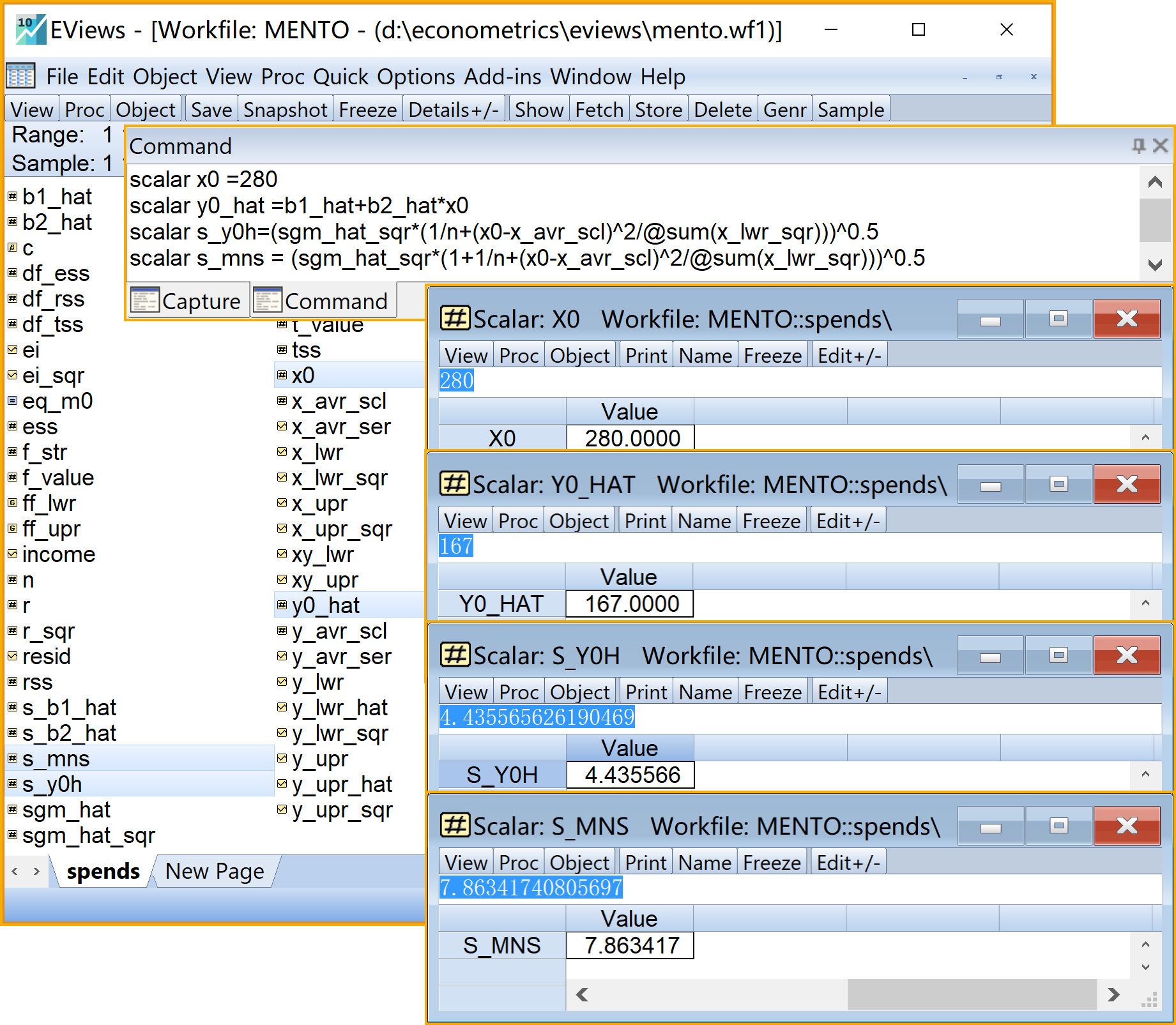
' 计算样本外预测(标量scalar)
scalar x0 =280 '样本外X值
scalar y0_hat =b1_hat+b2_hat*x0 '样本外估计Y值
scalar s_y0h=(sgm_hat_sqr*(1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr)))^0.5 '均值预测的样本标准差
scalar s_mns = (sgm_hat_sqr*(1+1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr) ))^0.5 '个值预测的样本标准差
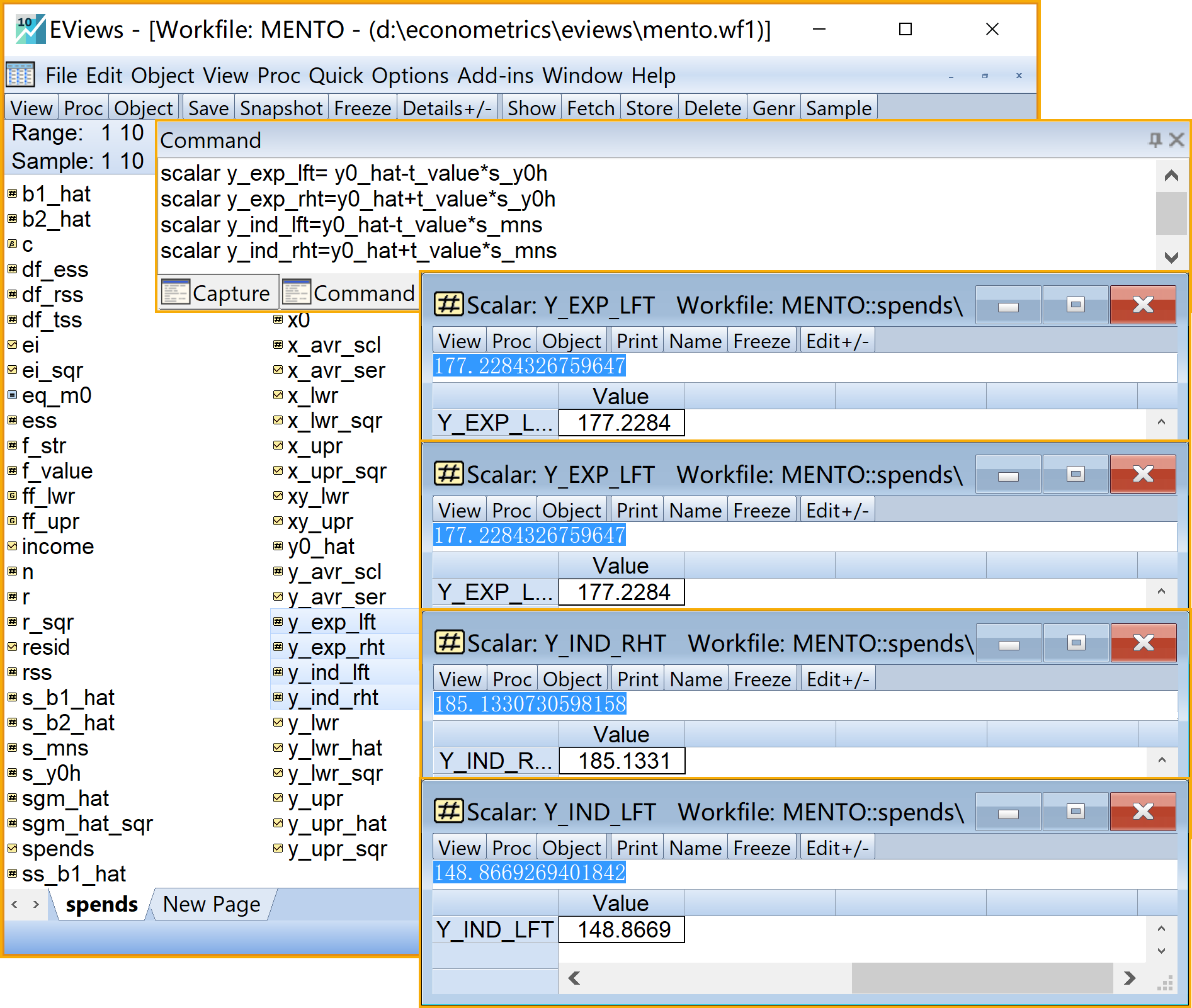
scalar y_exp_lft= y0_hat-t_value*s_y0h '均值预测的置信区间的左界值
scalar y_exp_rht= y0_hat+t_value*s_y0h '均值预测的置信区间的右界值
scalar y_ind_lft= y0_hat-t_value*s_mns '个值预测的置信区间的左界值
scalar y_ind_rht= y0_hat+t_value*s_mns '个值预测的置信区间的右界值
在工作文件视窗下,可以看到如下的EViews对象,可以双击查看(见 图 2.20 和 图 2.21 ):
样本外\({X_0}=280\)的标量对象
 x0
x0样本外估计\(\hat{Y_0}\)值的标量对象
 y0_hat
y0_hat均值预测的样本标准差\(S_{\hat{Y}_0}\)的标量对象
 s_y0h
s_y0h个值预测的样本标准差\(S_{Y_0-\hat{Y}_0}\)的标量对象
 s_y0h_mns_y0
s_y0h_mns_y0均值预测的置信区间的左界值\(\hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0}\)的标量对象
 y_exp_lft
y_exp_lft均值预测的置信区间的右界值\(\hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{\hat{Y}_0}\)的标量对象
 y_exp_rht
y_exp_rht个值预测的置信区间的左界值\(\hat{Y}_0-t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0}\)的标量对象
 y_ind_lft
y_ind_lft个值预测的置信区间的右界值\(\hat{Y}_0+t_{1-\alpha/2}(n-2) \cdot S_{Y_0-\hat{Y}_0}\)的标量对象
 y_ind_rht
y_ind_rht
2.6 附录:prg源代码
实际操作中,在EViews命令视窗中逐条输入代码,既容易出错,又不便于维护这些代码,还不能进行代码的重复使用(在第一章 中已经论述)。
因此,读者可以创建一个.prg编程文件 ,并在其中编写EViews代码,进行管理、维护、运行和分析。下面代码按本章主要实验步骤编写,读者可以用于本章的EViews编程参考,进行实验练习。
,并在其中编写EViews代码,进行管理、维护、运行和分析。下面代码按本章主要实验步骤编写,读者可以用于本章的EViews编程参考,进行实验练习。
'=========================================================================================================
'说明:以下为EViews编程文件mento.prg的代码
'将展示第二章中“蒙特卡洛模拟数据案例”主要分析步骤的“批量式命令驱动”实现方法(::
'其中,符号'起始的行,为注释行,其他为EViews命令行。
'=========================================================================================================
'创建工作文件(工作文件名=mento,子页命名=spend),无结构无日期,样本数为10
wfcreate(wf=mento,page=spend) u 10
'导入外部数据,路径为d:\github\books\data\lab1-basic-development.xlsx
import d:\github\books\data\lab2-mento-demon.xlsx
' 命令行1:生成线性回归方程对象eq_main
equation eq_main.ls y c x
' 转换变量名
series x_upr=x '序列X
series y_upr=y '序列Y
'计算三个重要标量
scalar x_avr_scl=@mean(x_upr) 'X的均值(标量)
scalar y_avr_scl=@mean(y_upr) 'Y的均值(标量)
scalar n=@obs(x_upr) '样本数n(标量)
'计算均值序列
series x_avr_ser=@mean(x_upr)
series y_avr_ser=@mean(y_upr)
series xy_upr= x_upr*y_upr
'计算FF,并以group形式打开
series x_upr_sqr=x_upr^2 '序列X^2
series y_upr_sqr=y_upr^2 '序列Y^2
series xy_upr= x_upr*y_upr '序列XY
group ff_upr x_upr y_upr x_upr_sqr y_upr_sqr xy_upr '构建FF序列组(group)
'计算ff离差series,并构建group
series x_lwr=x_upr-x_avr_ser '离差序列x
series y_lwr= y_upr-y_avr_ser '离差序列y
series x_lwr_sqr= x_lwr ^2 '离差序列x^2
series y_lwr_sqr =y_lwr ^2 '离差序列y^2
series xy_lwr=x_lwr*y_lwr '离差序列xy
group ff_lwr x_lwr y_lwr x_lwr_sqr y_lwr_sqr xy_lwr '构建ff离差序列组(group)
' 计算回归系数scalar:b2和b1
scalar b2_hat = @sum(xy_lwr)/@sum(x_lwr_sqr) '斜率系数
scalar b1_hat =y_avr_scl-b2_hat *x_avr_scl '截距系数
' 计算回归预测值及其离差series
series y_upr_hat= b1_hat+ b2_hat*x_upr '回归预测值
series y_lwr_hat= y_upr_hat-y_avr_ser '回归预测的离差值
' 计算残差及残差平方series
series ei=y_upr-y_upr_hat '残差序列
series ei_sqr= ei^2 '残差平方序列
' 计算回归误差方差及其标准差scalar
scalar sgm_hat_sqr=@sum(ei_sqr)/(n-2) '方程的回归误差方差
scalar sgm_hat= sgm_hat_sqr^0.5 '方程的回归误差标准差
' 计算回归系数的样本方差和标准差scalar
scalar ss_b2_hat=sgm_hat_sqr/@sum(x_lwr_sqr) '斜率系数的样本方差
scalar ss_b1_hat=ss_b2_hat*(@sum(x_upr_sqr)/n) '截距系数的样本方差
scalar s_b2_hat=ss_b2_hat^0.5 '斜率系数的样本标准差
scalar s_b1_hat=ss_b1_hat^0.5 '截距系数的样本标准差
' 进行平方和分解并得到相应自由度(标量scalar)
scalar tss=@sum(y_lwr_sqr) '总平方和TSS
scalar rss=@sum(ei_sqr) '残差平方和RSS
scalar ess=tss-rss '回归平方和ESS
scalar df_tss=n-1 ' TSS的自由度
scalar df_rss=n-2 ' RSS的自由度
scalar df_ess=1 'ESS的自由度
' 计算相关系数r和判定系数(标量scalar)
scalar r=@cor(x_upr,y_upr) 'X和Y变量的相关系数
scalar r_sqr=ess/tss '回归方程的判定系数
' 回归系数的t检验
scalar t_str_b2_hat =b2_hat/s_b2_hat '斜率的t统计量
scalar t_str_b1_hat =b1_hat/s_b1_hat '截距的t统计量
scalar t_value =@qtdist(0.975,8) 'a=0.05下的t查表值(右侧正值)
scalar t_value2 =@qtdist(0.025,8) 'a=0.05下的t查表值(左侧负值)
' 回归方程的F检验
scalar f_str =(ess/df_ess)/(rss/df_rss) '回归方程的F统计量值
scalar f_value=@qfdist(0.95,df_ess,df_rss) 'a=0.05下的t查表值(右侧大值)
scalar f_value2=@qfdist(0.05,df_ess,df_rss) 'a=0.05下的t查表值(左侧小值)
' 计算样本外预测(标量scalar)
scalar x0 =280 '样本外X值
scalar y0_hat =b1_hat+b2_hat*x0 '样本外估计Y值
scalar s_y0h=(sgm_hat_sqr*(1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr)))^0.5 '均值预测的样本标准差
scalar s_mns = (sgm_hat_sqr*(1+1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr) ))^0.5 '个值预测的样本标准差
scalar y_exp_lft= y0_hat-t_value*s_y0h '均值预测的置信区间的左界值
scalar y_exp_rht= y0_hat+t_value*s_y0h '均值预测的置信区间的右界值
scalar y_ind_lft= y0_hat-t_value*s_mns '个值预测的置信区间的左界值
scalar y_ind_rht= y0_hat+t_value*s_mns '个值预测的置信区间的右界值
' ===========================================================================
2.7 作业题
蒙特卡洛模拟数据: 表 2.9 给出给出了7个家庭在收入和支出方面的数据。
| obs | income | spends |
|---|---|---|
| 1 | 80 | 55 |
| 2 | 100 | 88 |
| 3 | 120 | 90 |
| 4 | 140 | 80 |
| 5 | 160 | 118 |
| 6 | 180 | 120 |
| 7 | 200 | 145 |
| 8 | 220 | 135 |
| 9 | 240 | 145 |
| 10 | 260 | 175 |
变量说明见 表 2.10 :
| variable | label |
|---|---|
| obs | 样本编号 |
| spends | 家庭支出 |
| income | 家庭收入 |
如果消费和收入之间可以构造如下一元线性回归模型:
\[ \begin{aligned} Y_i & =\hat{\beta}_1+\hat{\beta}_2X_i+e_i && \text{SRM}\\ \hat{Y}_i & =\hat{\beta}_1+\hat{\beta}_2X_i && \text{SRF} \end{aligned} \]
请在Eviews中对模型进行计算(手动计算),要求回答如下问题:
运用eviews菜单(Quick \(\Rightarrow\) Estimate Equation),对上述模型进行回归分析,分别列出主要的回归报告,并比较与你在a题中手动计算的结果是否一致。
利用eviews将(X,Y)数据绘制散点图(scatter),并对残差序列绘制线图(line plot)。
1.将数据导入Eviews,并计算出FF序列\(\bar{X}\)、\(\bar{Y}\)、\(X^2\)、\(Y^2\)、\(XY\),以及ff序列\(x\)、\(y\)、\(x^2\)、\(y^2\)、\(xy\),并以Group形式保存并截图过来。
2.根据所给数据,计算直线回归方程的回归系数\(\hat{\beta}_1\)、\(\hat{\beta}_2\)(写出公式、主要计算过程和结果)。
3.分别写出样本回归方程(SRF)和样本回归模型(SRM)(根据计算结果写出实际方程和模型)。
4.计算回归误差方差(\(\hat{\sigma}^2\))其标准差(以及\(\hat{\sigma}\))。(写出公式、主要计算过程和结果)。
5.计算得到回归截距系数的样本方差(\(S_{\hat{\beta}_1}^2\))及其样本标准差(\(S_{\hat{\beta}_1}\));计算回归斜率系数的样本方差(\(S_{\hat{\beta}_2}^2\))及其样本标准差(\(S_{\hat{\beta}_2}\))。(写出公式及主要计算结果)。
6.计算得到两个模型的平方和分解式(\(TSS\)、\(ESS\)、\(RSS\))及其相对应的自由度(\(df_{TSS}\),\(df_{ESS}\),\(df_{RSS}\) ),并写出方差分析表(ANOV table)。
7.计算得到两个变量的样本相关系数\(r\) ,以及回归方程的判定系数\(r^2\),并比较相关系数与判定系数的关系(数量关系)。(写出公式及主要计算过程)。
8.计算两个回归系数的样本t值(\(t^{\ast}_{\hat{\beta}_2}\)和\(t^{\ast}_{\hat{\beta}_1}\))。
9.用eviews命令计算得到理论t值(\(t_{1-\alpha/2}(n-2)\),给定\(\alpha=0.05\) ),并对回归系数显著性进行假设检验。
10.计算回归方程整体显著性检验的的样本F值( \(F_{\ast}\))。
11.用eviews命令计算得到理论F值(\(F_{1-\alpha}(df_1,df_2)=F_{1-\alpha}(df_{ESS},df_{RSS})\),给定\(\alpha=0.05\) ),并对模型整体显著性进行假设检验。
12.给定样本外的\(X_0=280\) ,计算点预测值\(\hat{Y}_0\) 。
13.计算均值预测下的样本标准差\(S_{(\hat{Y}_0)}\)。
14.计算均值预测的置信区间\(\hat{Y}_0-t_{1-\alpha/2}(n-2)\cdot S_{\hat{Y}_0}\leq E(Y\mid X=X_0)\leq \hat{Y}_0+t_{1-\alpha/2}(n-2)\cdot S_{\hat{Y}_0}\)。
均值预测\(E(Y|X=X_0)=\)
均值区间预测的左界\(E(Y|X=X_0)_L=\)
均值区间预测的右界\(E(Y|X=X_0)_L=\)
15.计算个值预测下的样本标准差\(S_{(Y_0-\hat{Y}_0)}\)。
16.计算个值预测的置信区间\(\hat{Y}_0-t_{\alpha/2}(n-2)\cdot S_{Y_0-\hat{Y}_0}\leq E(Y\mid X=X_0)\leq \hat{Y}_0+t_{\alpha/2}(n-2)\cdot S_{Y_0-\hat{Y}_0}\)。
个值预测\((Y_0|X=X_0)\)
个值区间预测的左界\((Y_0|X=X_0)_L\)
个值区间预测的右界\((Y_0|X=X_0)_R\)