| year | quarter | GDP | PCE | Investment | Government |
|---|---|---|---|---|---|
| 1980 | Q1 | 5903 | 3797 | 778 | 1365 |
| 1980 | Q2 | 5782 | 3710 | 708 | 1370 |
| 1980 | Q3 | 5772 | 3750 | 654 | 1351 |
| 1980 | Q4 | 5878 | 3800 | 721 | 1349 |
| 1981 | Q1 | 6001 | 3821 | 792 | 1367 |
| 2011 | Q1 | 13228 | 9377 | 1751 | 2514 |
| 2011 | Q2 | 13272 | 9393 | 1778 | 2508 |
| 2011 | Q3 | 13332 | 9434 | 1784 | 2508 |
| 2011 | Q4 | 13429 | 9482 | 1876 | 2481 |
| 2012 | Q1 | 13502 | 9550 | 1903 | 2462 |
1 EViews入门
1.1 为何选择EViews?
EViews全称为Econometrics Views,是计量经济分析的常用软件之一。1981年David Lilien开发一款名为MicroTSP(Time Series Processor)分析工具,主要用于大型计算机进行时间序列数据分析。1994年QMS(Quantitative Micro Software)公司用C++语言对MicroTSP进行重新设计,成功开发出EViews,使其广泛适用于Windows操作系统。2010年QMS公司被IHS公司收购1。
实际上,计量经济分析软件类型多样,功能特征各有侧重,不同使用群体根据自身情况可以灵活选择。常用的计量经济分析软件就包括SPSS、EViews、Stata、SAS、Matlab等,它们也是各有优势和不足。作为参考,不同任务情形和学习阶段应选择合适的软件:
(1)计量经济初级学习者往往以菜单驱动型操作为主,适合的软件包括:
EViews:属于商业软件,基于C++语言
SPSS:属于商业软件,基于Java语言
Stata:属于商业软件,基于C语言
\(\cdots\)
(2)计量经济中高级学习者则追求更多灵活的命令编程设计和操作,适合的软件包括:
Matlab:属于商业软件,基于C++、Java、MATLAB语言
SAS:属于商业软件,基于C语言
R:属于开源软件,基于C、Fortran、R语言
Python:属于开源软件
\(\cdots\)
计量经济学课程中使用到的数据类型主要包括截面数据(cross-section data)、时间序列数据(time series data)和面板数据(pannel data)。EViews软件因为继承了其前身软件MicroTSP的主要特征,在计量经济分析中能满足基本功能分析需求,并且拥有十分全面的时间序列分析工具。此外,EViews软件同时支持菜单型操作和命令代码操作,很适合计量经济学初学者使用,学习门槛相对较低,使用者可以集中于关注计量建模分析的理论应用与验证。而对于中高级使用者,EViews也可以进行代码编程实现各种定制化的计量分析需求,从而保证软件使用的连贯性和一致性。
1.2 怎样理解Eviews的运作逻辑?
(1)使用者通过菜单操作基本就可以实现大部分的EViews功能
主要的统计和计量分析工具都被菜单化设计到EViews软件中。
鼠标+键盘的操作符合使用者的直观化学习习惯。
意味着使用者要熟记各类统计和计量分析操作的准确菜单位置,这一定程度上增加了使用者的记忆负担。
(2)使用者也可以通过运行命令来实现各种EViews功能
单独编写命令行,独立运行每一行命令。适用于简单分析任务,与菜单操作进行配合使用。
批量编写命令代码,整体运行代码文件。适合于复杂的或个性化的分析任务,便于命令代码维护,而且代码可重复使用,可以灵活开发出使用者定制化的分析流程(往往是EViews常用分析流程不能满足需求)。
EViews具有独树一帜命令代码编写体系,使用者需要理解EViews代码规则,避免与其他统计软件代码编写规则的混淆使用。
(3)EViews是以对象(Object)方式来进行操作结果的管理和维护
所有的数据(data)、表格(table)、图片(graph)、方程(equation)等都将保存为对象(Object)。
所有的对象(Object)都存放在一个工作文件(workfile)中。
所有对象都可以进行复制(copy)、粘贴(paste)、保存(save)、重命名(rename)等操作。
1.3 如何获取Eviews官方帮助?
作为一款商业软件,EViews能得到商业公司持续的软件维护和版本更新,不同EViews版本的界面、功能、特性等会有一定的改进和变化。2010年以后,IHS公司拥有EViews软件的商标和版权,目前发布的最新版本为EViews 10。本书所用示例均以EViews 10版本进行运行和演示,使用者应注意实际使用版本下可能细节上的变化和差异2。
如果正确安装EViews 10,使用者将得到IHS公司官方提供的详尽帮助手册和在线文档。菜单操作的具体获取办法是:运行EViews 10 \(\Rightarrow\) 点击Help \(\Rightarrow\) 下拉选择相应帮助手册或文档。
(1)快速帮助手册
Object Reference
Basic Command Reference
Function Reference
Matrix Reference
Programming Reference
Online Tutorials
(2)pdf帮助文档
User Guide I.pdf
User Guide II.pdf
Command & Programming Ref.pdf
Object Reference.pdf
Eviews Illustrated.pdf
1.4 实验内容
利用EViews软件进行如下操作:
EViews 软件的启动;
数据的输入、编辑与序列生成;
图形分析与描述统计分析;
数据文件的存贮、调用。
1.5 实验准备
1.5.1 实验软件
本次实验需要提前准备好如下软件:
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或360极速浏览器9.5版本及以上
1.5.2 实验材料
1.5.3 实验规则
1.6 EViews快速入门
宏观经济数据:表 1.1 给出给出了一国1980年第1季度到2012年第1季度间共计129个季度,关于quarter季度,GDP国内生产总值(10亿美元),PCE人均消费支出(美元),Investment投资(10亿美元),Government政府支出(10亿美元)等方面的数据。
变量定义和说明见 表 1.2 :
| variable | label |
|---|---|
| year | 年 |
| quarter | 季度 |
| GDP | 国内生产总值(10亿美元) |
| PCE | 人均消费支出(美元) |
| Investment | 投资(10亿美元) |
| Government | 政府支出(10亿美元) |
使用EViews软件分析该国宏观经济发展情况,一般需要事先将相关经济变量收集和整理成规范化的数据表(见 表 1.1 )。其中,每列代表变量(variables),每行代表样本(observations),数据文件格式为电子表格文件(.xlsx)等。
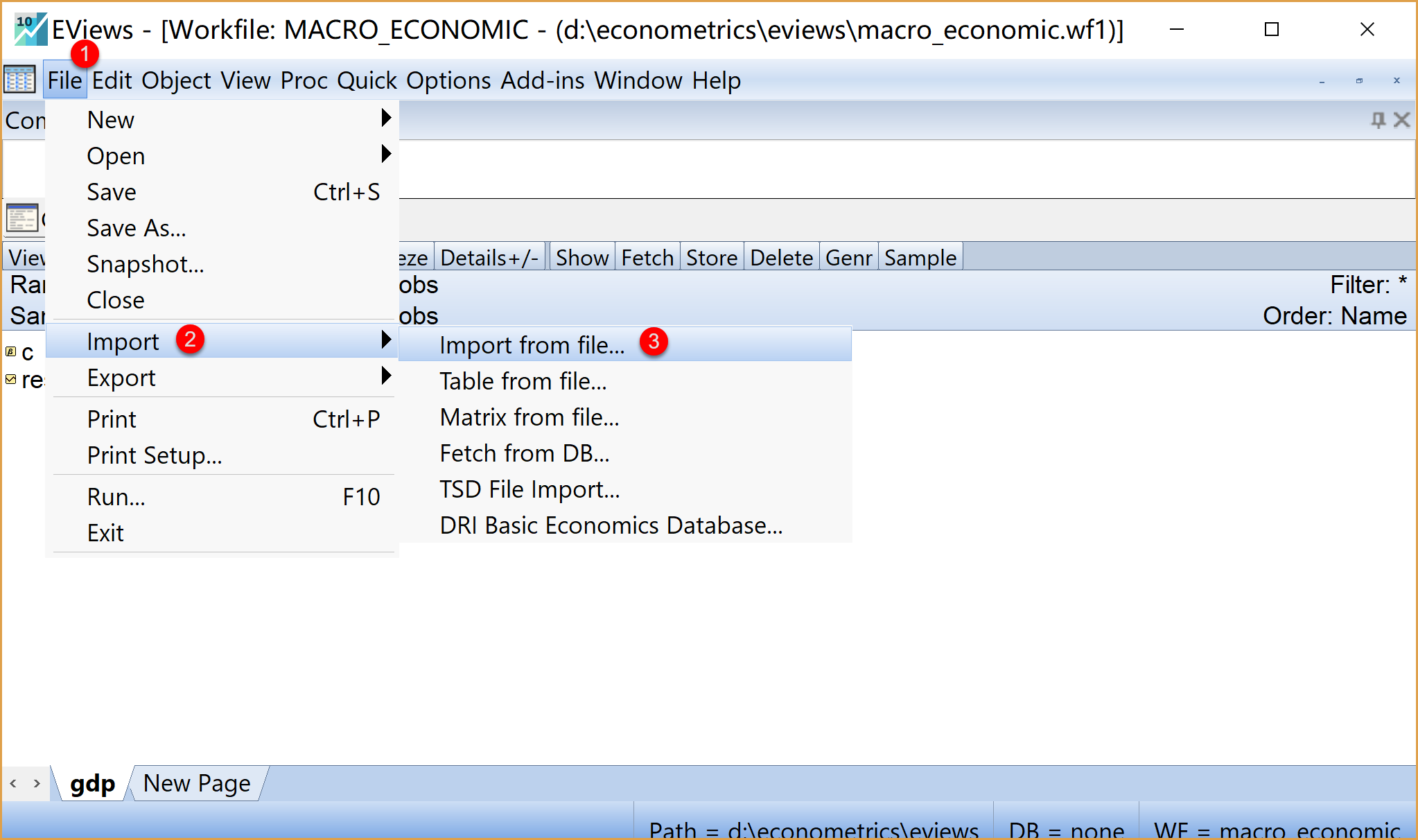
利用数据导入菜单,可以把预备好的电子表格文件(.xlsx)导入到EViews工作文件(workfile)中。导入数据后的EViews界面见 图 1.1 :
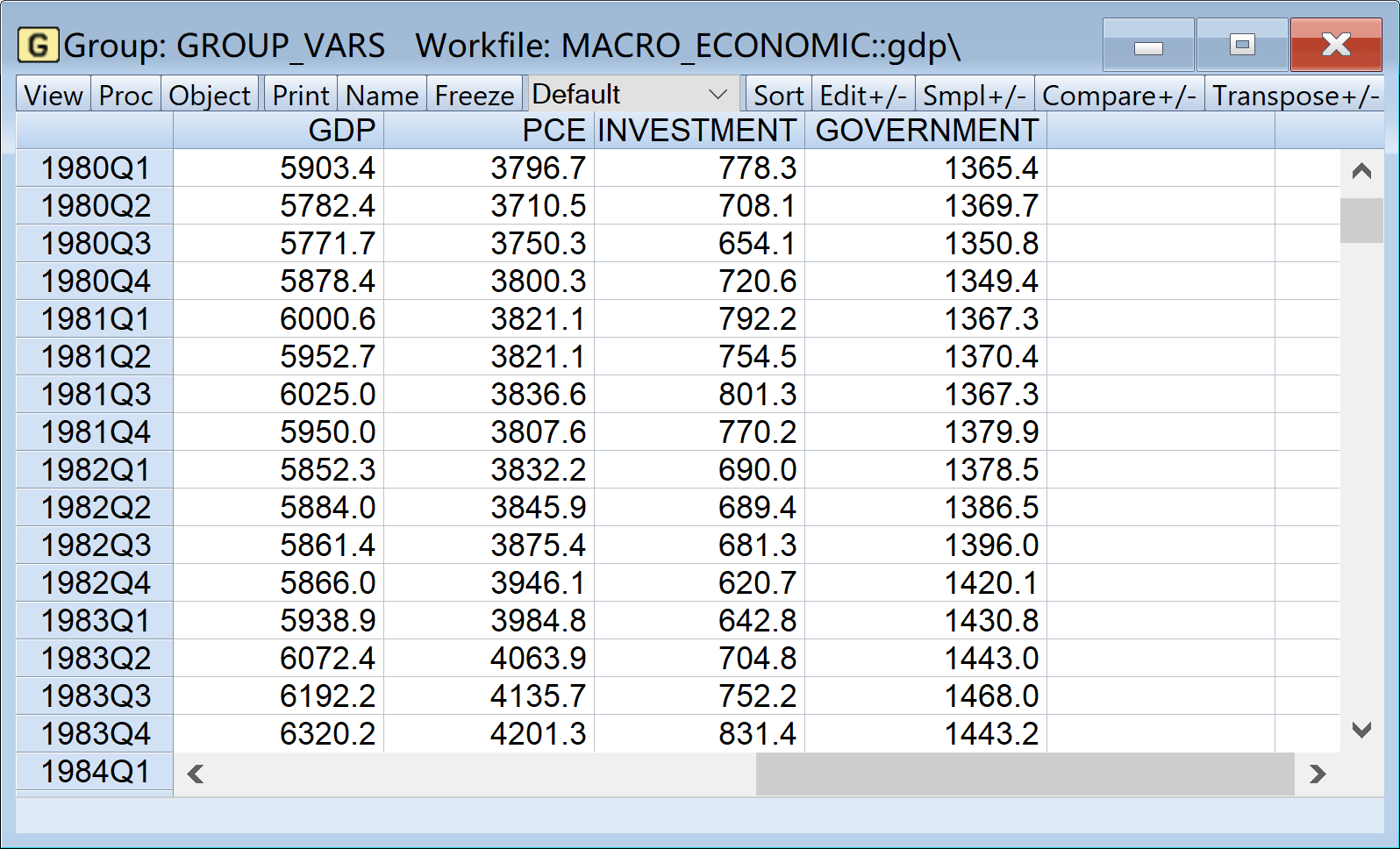
为了掌握宏观经济的样本数据特征,可以进行EViews基本的描述性统计分析。描述性统计分析结果见 图 1.2 :
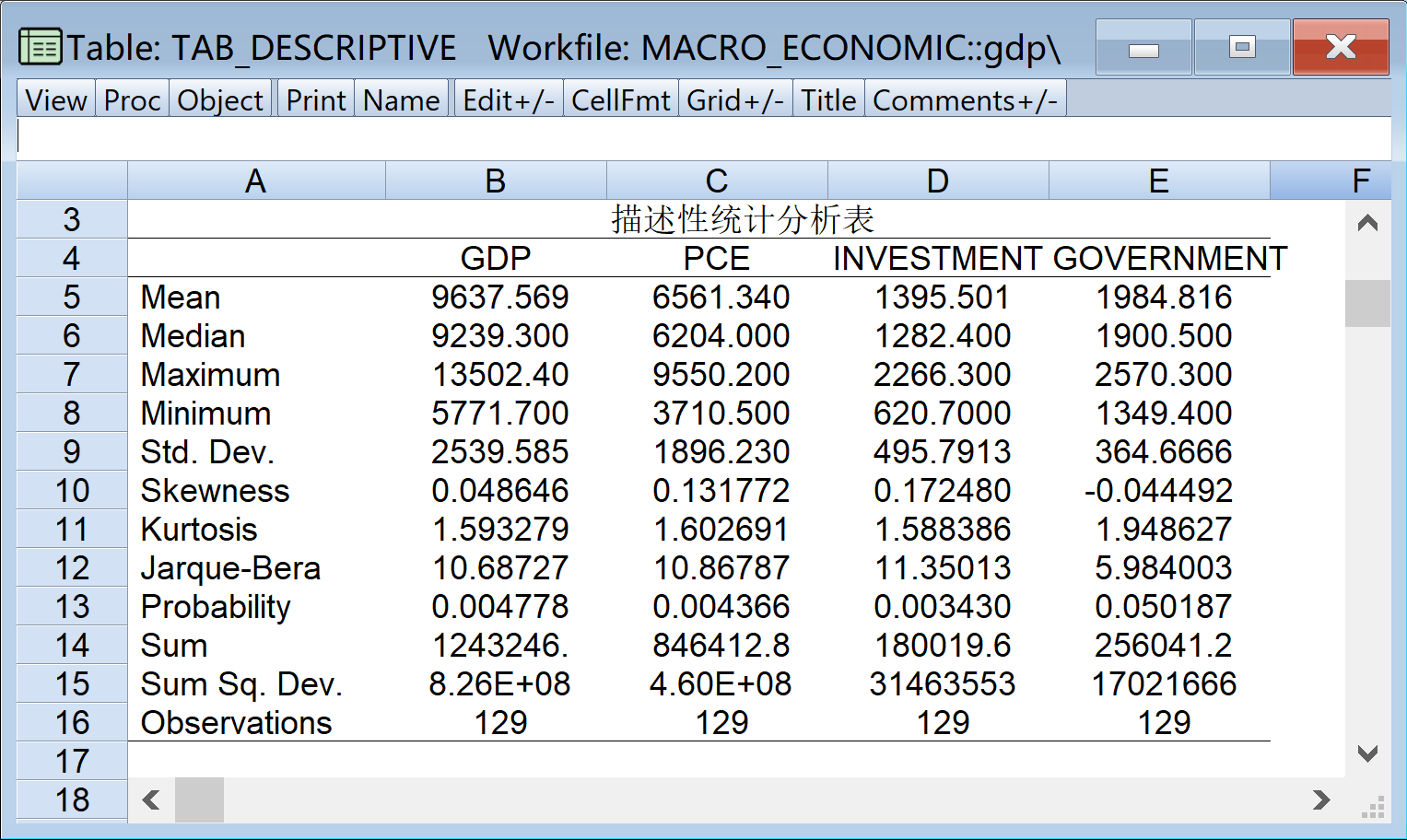
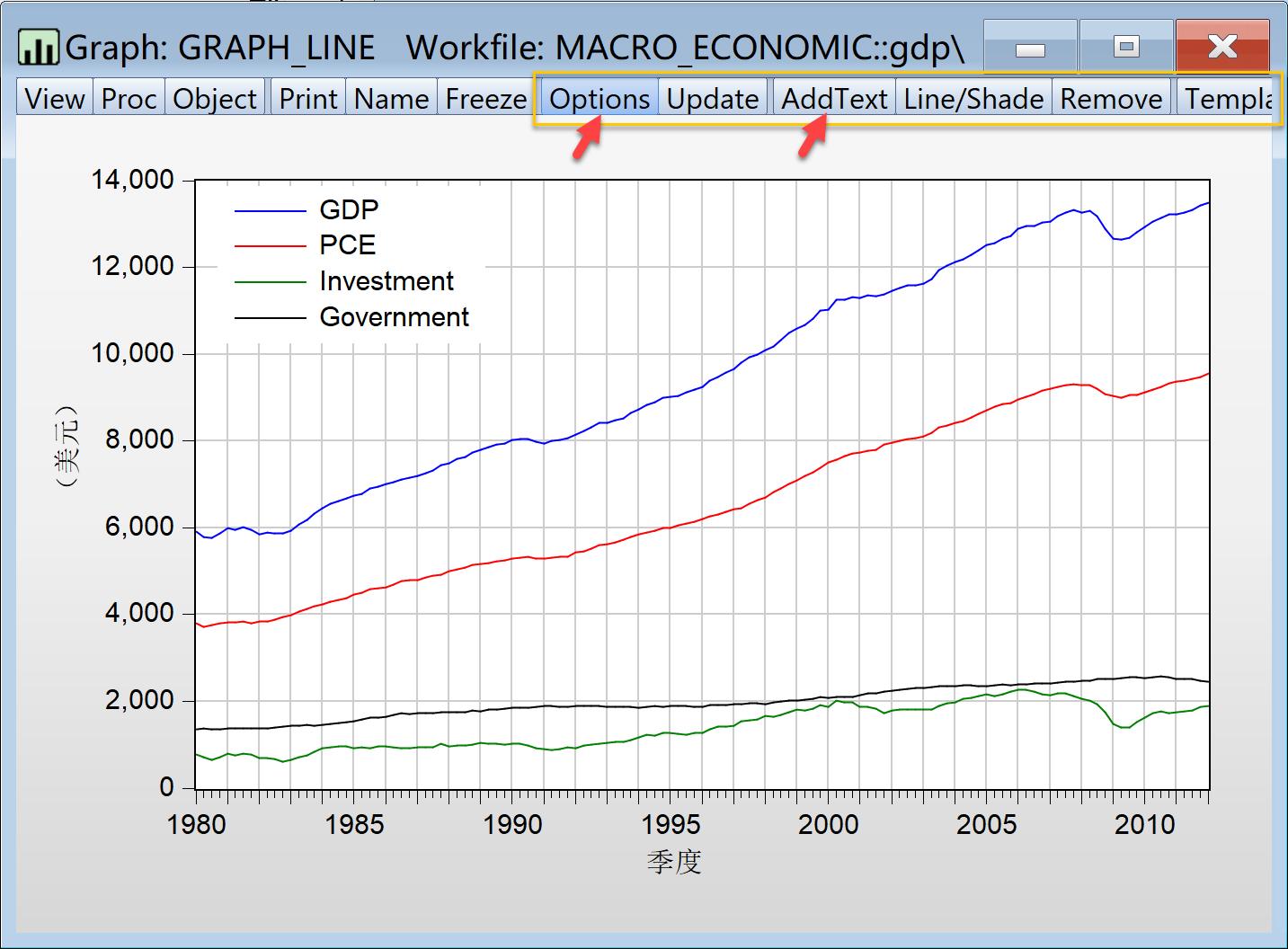
进一步地,利用绘图操作,可以得到4个主要变量的多线图(见 图 1.3 )
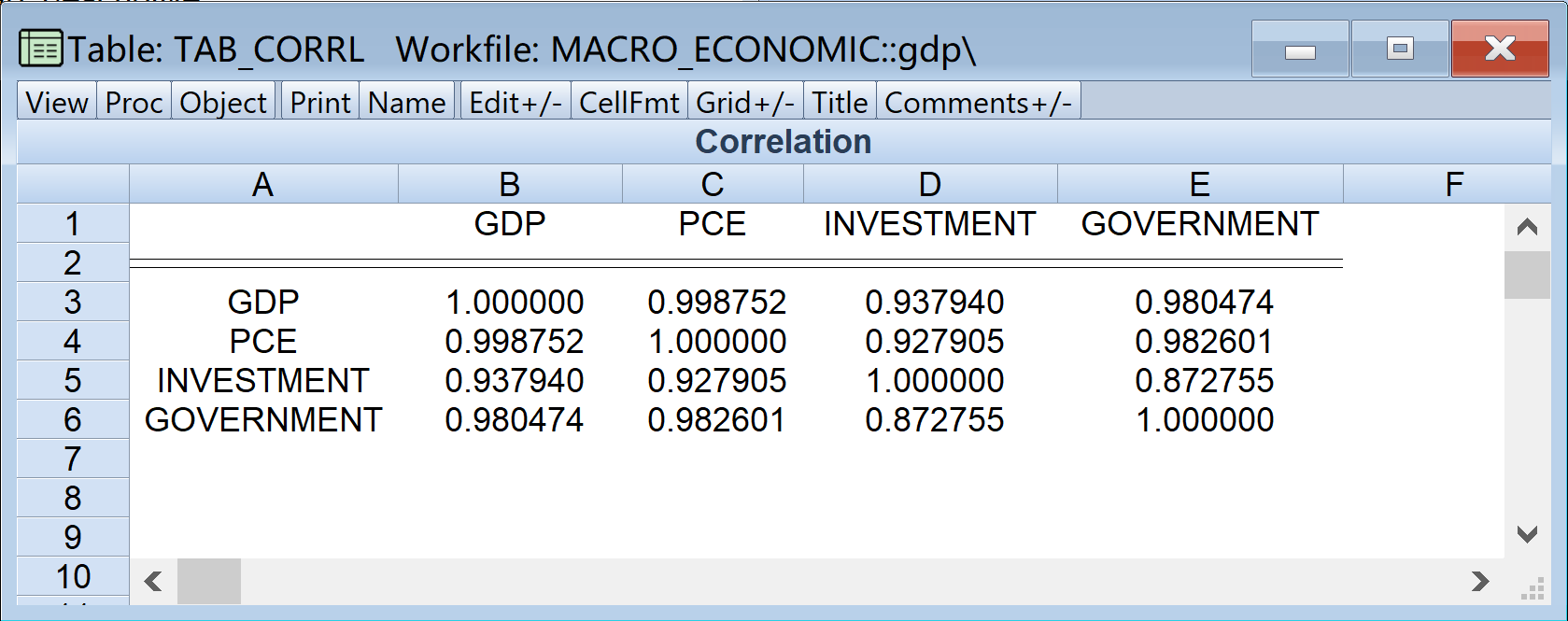
同时,还可以绘制对数化的国内生产总值GDP与其他变量(PCE,Investment,Government)之间的相关系数表(见 图 1.4 )。
一个重要的工作还包括进行回归建模分析,可以尝试如下的回归模型:
\[ \begin{aligned} GDP&=\beta_1+\beta_2PCE+\beta_3Investment+\beta_4Government+u_i \end{aligned} \tag{1.1}\]
\[ \begin{aligned} GDP&=\hat{\beta}_1+\hat{\beta}_2PCE+\hat{\beta}_3Investment+\hat{\beta}_4Government+e_i \end{aligned} \tag{1.2}\]
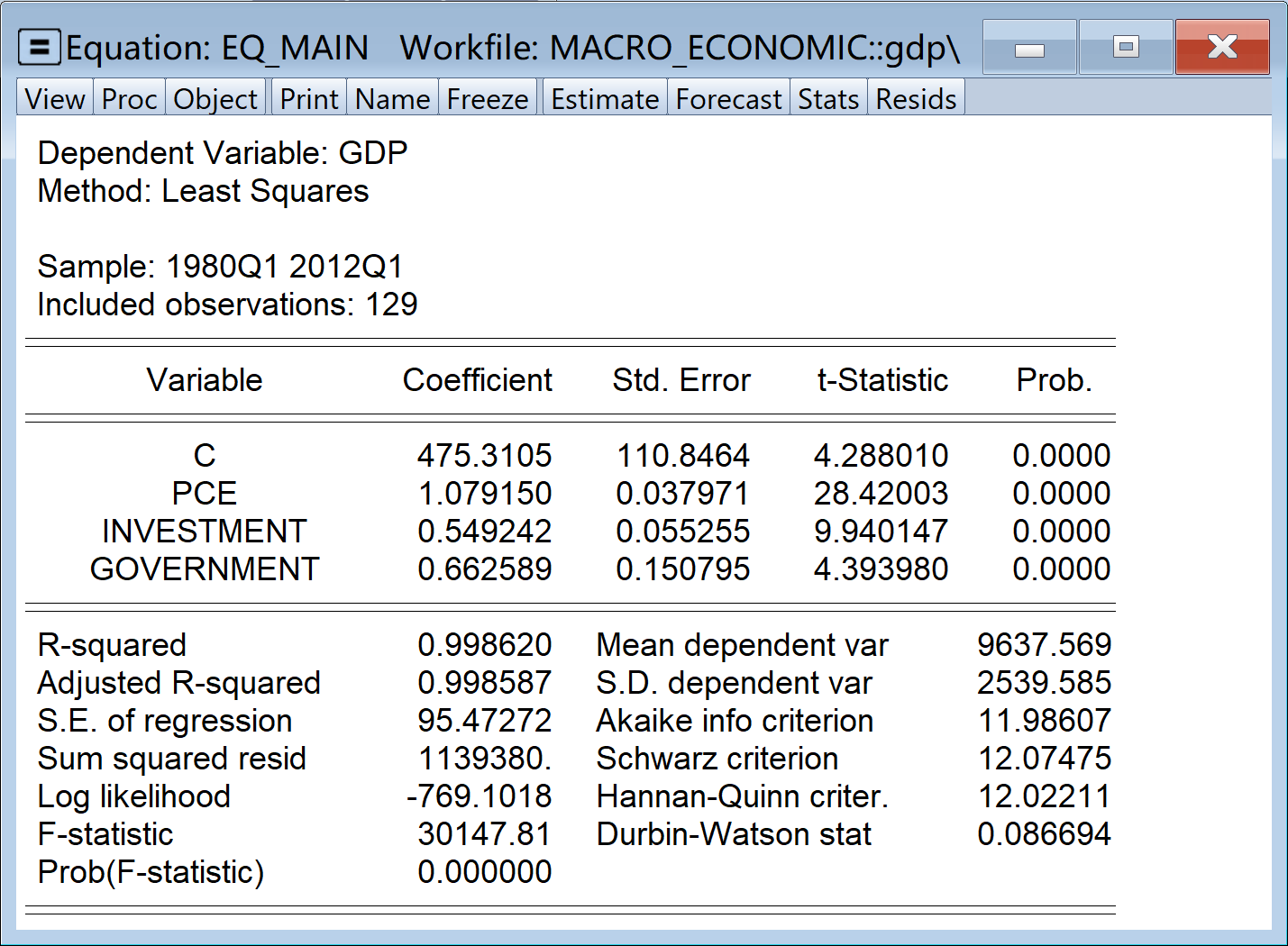
利用EViews回归分析操作,可以得到如下的回归分析报告结果(见 图 1.5 )
1.7 EViews菜单操作流程
上述的快速案例速览,简要列出了使用EViews进行一次样本数据实证分析的主要步骤过程,是典型的实践操作流程。我们基本可以总结为如下6个步骤:
准备数据(data preparing)
构建工作文件(workfile creating)
构造对象(objects generating)
探索性分析(exploratory analyzing)
线性回归分析(linear regression analyzing)
报告结果输出(output reporting)
下面将逐条进行简要说明。
1.7.1 准备数据(data preparing)
准备数据(data preparing)属于前期准备工作,包括数据收集、清洗、整理等环节。目标是获得规范的数据表,要求每列都代表变量(variables),每行都代表样本(observations)。在进行正式EViews分析之前,提前准备一份规范的数据表是极为重要的。需要做的准备工作包括:
数据收集:根据研究目的设计理论模型,模型中的理论变量需要找到对应的现实数据变量。一般情况下,一个理论变量可以对应多个数据变量,但由于实际情况制约(如人力、资金、技术等条件约束),数据变量并不总是可以收集得到。
数据清洗:收集得到的数据并不总是完美和理想,比如常常有数据缺失、虚假数据、错误数据等,从而需要进行数据替换、删减、调整等操作。
数据整理:清洗后的数据,还需要以某种形式呈现出来。数据整理就是把数据的统计结构(变量和样本)与物理结构(行和列)进行某种匹配整合。
规范的数据表要求具有下面的结构形式(Hadley 2016):
每列都代表变量(variables)
每行都代表样本(observations)
规范的数据表可以称为坐标型数据(Cartesian data),数据的统计结构和物理结构是严格对应的,也即每列代表变量,每行都代表样本,数据点通过行坐标和列坐标一起定位得到。
大部分不规范的数据表则可以称为索引型数据(indexed data),数据的统计结构和物理结构并不是严格对应的,数据点往往是通过查询索引序号而得到(有点像通过偏旁部首查字典的方式)。
一份规范化的数据数据表,具有属于坐标型数据的形式,以 表 1.3 为例:
每一行都代表一个观测样本(observation),分别从1980年Q1季度到2012年Q1季度,共有129行(也即129个季度);
每一列都代表一个变量(variable),分别是year年、quarter季度、GDP国内生产总值(10亿美元)、PCE人均消费支出(美元)、Investment投资(10亿美元)、Government政府支出(10亿美元),共有6列(也即6个变量)。
数据表的维度为(行数=129;列数=6),统计结构和物理结构严格对应。
| year | quarter | GDP | PCE | Investment | Government | |
|---|---|---|---|---|---|---|
| 1 | 1980 | Q1 | 5903 | 3797 | 778 | 1365 |
| 2 | 1980 | Q2 | 5782 | 3710 | 708 | 1370 |
| 3 | 1980 | Q3 | 5772 | 3750 | 654 | 1351 |
| 4 | 1980 | Q4 | 5878 | 3800 | 721 | 1349 |
| 5 | 1981 | Q1 | 6001 | 3821 | 792 | 1367 |
| 125 | 2011 | Q1 | 13228 | 9377 | 1751 | 2514 |
| 126 | 2011 | Q2 | 13272 | 9393 | 1778 | 2508 |
| 127 | 2011 | Q3 | 13332 | 9434 | 1784 | 2508 |
| 128 | 2011 | Q4 | 13429 | 9482 | 1876 | 2481 |
| 129 | 2012 | Q1 | 13502 | 9550 | 1903 | 2462 |
而糟糕的数据表往往有很多种形式,下面列出三种形式(见 表 1.4 、 表 1.5 和 表 1.6 )。它们都属于索引型数据形式,其中:
对于 表 1.4 :统计结构中,我们所关心的变量被分散在第2列所对应的各行中,而观测样本则被割裂在第一列对应的各行(表示年份)和第3列到第4列(表示季度)。整个数据表的维度为(行数=132;列数=6),统计结构和物理结构不能一一对应,而是通过索引指标才能查到数据点。
对于 表 1.5 :统计结构中,我们所关心的变量与观测样本糅合在一起,除第1列之外,其他列都是这样的混合体,如GDP_Q1GDP_Q2GDP_Q3表示国内生产总值GDP分别与Q1~Q4季度的混合。同时,观测样本(如1980年Q1季度)也是被割裂开来了。整个数据表的维度为(行数=33;列数=17),统计结构和物理结构不能一一对应,而是通过索引指标才能查到数据点。
对于 表 1.6 :该形式的数据表属于典型的索引型数据形式。其中,我们所关系的变量全部作为索引指标之一,出现在第3列(variable);而数据值则全部出现在第4列(value)。数据值必须通过观测样本索引指标(第1列的year和第2列的quarter)与变量索引指标(第3列的variable)才能查询得到。该数据表的维度为(行数=516;列数=4),统计结构和物理结构不能一一对应,而是通过索引指标才能查到数据点。
| year | variable | Q1 | Q2 | Q3 | Q4 | |
|---|---|---|---|---|---|---|
| 1 | 1980 | GDP | 5903 | 5782 | 5772 | 5878 |
| 2 | 1980 | PCE | 3797 | 3710 | 3750 | 3800 |
| 3 | 1980 | Investment | 778 | 708 | 654 | 721 |
| 4 | 1980 | Government | 1365 | 1370 | 1351 | 1349 |
| 5 | 1981 | GDP | 6001 | 5953 | 6025 | 5950 |
| 125 | 2011 | GDP | 13228 | 13272 | 13332 | 13429 |
| 126 | 2011 | PCE | 9377 | 9393 | 9434 | 9482 |
| 127 | 2011 | Investment | 1751 | 1778 | 1784 | 1876 |
| 128 | 2011 | Government | 2514 | 2508 | 2508 | 2481 |
| 129 | 2012 | GDP | 13502 | |||
| 130 | 2012 | PCE | 9550 | |||
| 131 | 2012 | Investment | 1903 | |||
| 132 | 2012 | Government | 2462 |
| year | GDP_Q1 | GDP_Q2 | GDP_Q3 | GDP_Q4 | Government_Q3 | Government_Q4 | |
|---|---|---|---|---|---|---|---|
| 1 | 1980 | 5903 | 5782 | 5772 | 5878 | 1351 | 1349 |
| 2 | 1981 | 6001 | 5953 | 6025 | 5950 | 1367 | 1380 |
| 3 | 1982 | 5852 | 5884 | 5861 | 5866 | 1396 | 1420 |
| 4 | 1983 | 5939 | 6072 | 6192 | 6320 | 1468 | 1443 |
| 5 | 1984 | 6443 | 6554 | 6618 | 6672 | 1500 | 1532 |
| 29 | 2008 | 13267 | 13310 | 13187 | 12884 | 2511 | 2520 |
| 30 | 2009 | 12663 | 12641 | 12694 | 12814 | 2554 | 2548 |
| 31 | 2010 | 12938 | 13058 | 13140 | 13216 | 2570 | 2552 |
| 32 | 2011 | 13228 | 13272 | 13332 | 13429 | 2508 | 2481 |
| 33 | 2012 | 13502 |
| year | quarter | variable | value | |
|---|---|---|---|---|
| 1 | 1980 | Q1 | GDP | 5903 |
| 2 | 1980 | Q2 | GDP | 5782 |
| 3 | 1980 | Q3 | GDP | 5772 |
| 4 | 1980 | Q4 | GDP | 5878 |
| 5 | 1981 | Q1 | GDP | 6001 |
| 6 | 1981 | Q2 | GDP | 5953 |
| 510 | 2010 | Q3 | Government | 2570 |
| 511 | 2010 | Q4 | Government | 2552 |
| 512 | 2011 | Q1 | Government | 2514 |
| 513 | 2011 | Q2 | Government | 2508 |
| 514 | 2011 | Q3 | Government | 2508 |
| 515 | 2011 | Q4 | Government | 2481 |
| 516 | 2012 | Q1 | Government | 2462 |
简单地总结起来就是:
1.7.2 构建工作文件(workfile creating)
工作文件(workfile)是EViews所有操作结果的“大容器”,操作结果将“分门别类”地以各种对象(objects)形式留存在这个“大容器”里。工作文件(workfile)的构建跟数据类型(截面数据、时间序列数据、面板数据)很有关系,一般都需要提前设置(当然也可以事后修改)。
1.7.2.1 启动EViews软件
在电脑操作系统中,找到EViews安装程序,点击运行后将显示EViews软件界面(见 图 1.6 )
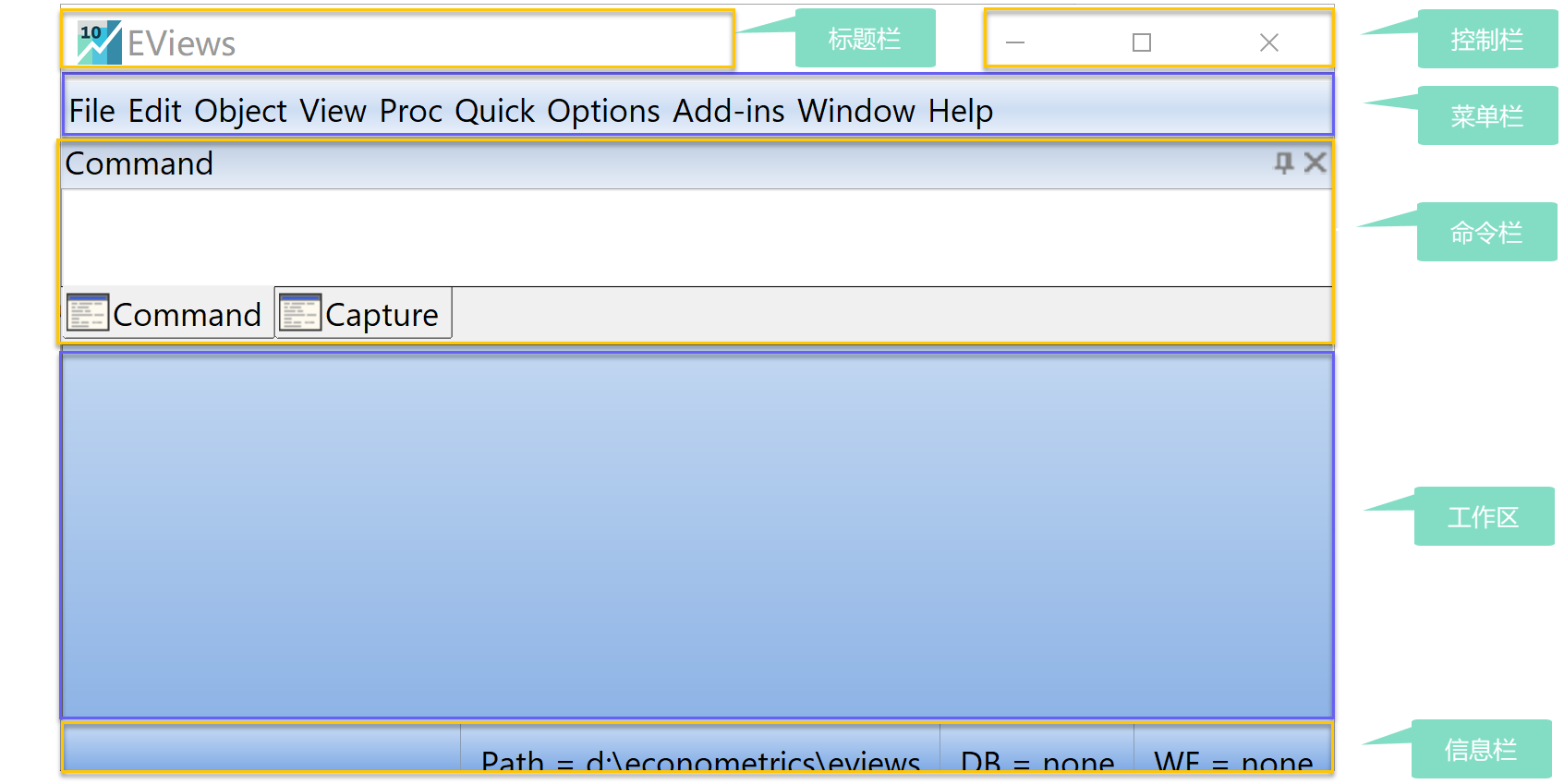
其中界面分块情况如下:
标题栏:用于显示EViews任务的标题信息,并控制窗口状态。
菜单栏:菜单栏中排列着按照功能划分的10个主菜单选项,用鼠标单击任意选项会出现不同的下拉菜单,显示该部分的具体功能。
命令窗口:用户可在光标位置用键盘输入各种Eviews命名,并按回车键执行该命令。
工作区窗口:操作过程中打开的各子窗口在工作区内显示。
状态栏:Eviews主窗口的底部是状态栏,从左到右分别为:信息框、路径框、当前数据库框和当前工作文件框。
1.7.2.2 创建工作文件(workfile)
进入EViews软件后的第一件工作应从创建新的或调入原有的工作文件(workfile)开始。只有新建或调入原有工作文件,EViews才允许用户输入开始进行数据处理。
EViews工作文件(workfile)的创建需要提前考虑如下几个方面:
(1)工作文件的结构类型(workfile structure type),一般包括截面数据、时间序列数据、面板数据三种类型
对于截面数据,可以选择非结构型/非日期型(Unstructured/Undated)
对于时间序列数据,可以选择有规则日期型(Data-regular frequency)
对于面板数据,可以选择平衡面板(Balanced Panel)
(2)数据长度或起止时间(data specification),依据数据类型而不同
对于截面数据,需要设置观测样本数(observations)
对于时间序列数据,需要设置数据频率(frequency)和起止时间(start date 和end date)
对于面板数据,需要设置数据频率(frequency)、起止时间(start date 和end date)和截面单元数(number of cross sections)
(3)工作文件的命名(workfile names),而且在一个工作文件下可以开展多个分析任务。不同分析任务可以设置不同的子页(page),并可以对子页进行命名以便区分
(4)工作文件的存放地址(path),可以决定存放在电脑本地的具体文件夹位置
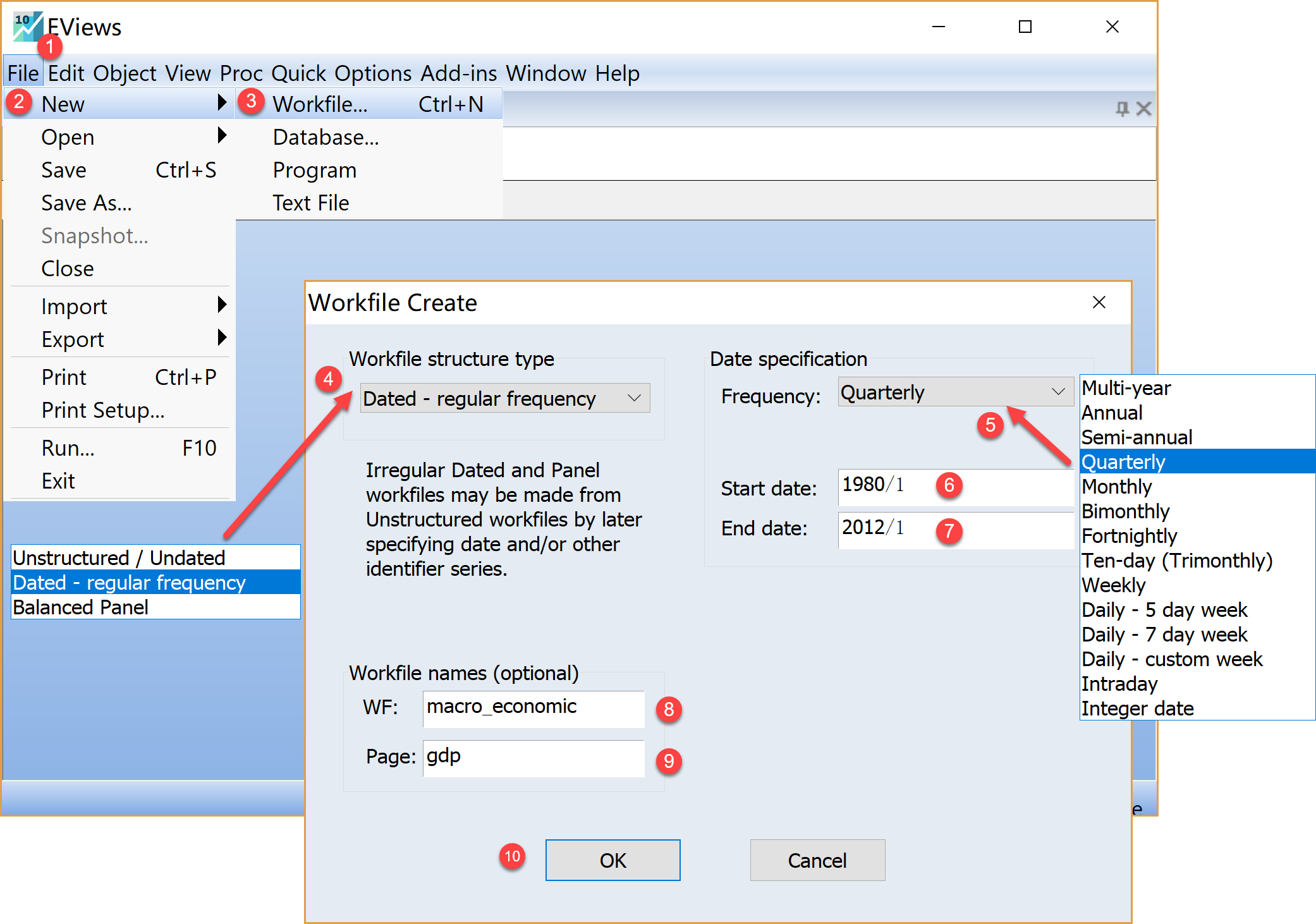
此次实验演示的宏观经济发展案例为时间序列数据,我们将构建一个工作文件(workfile)和一个子页(page),具体步骤是(见 图 1.7 和 图 1.8 ):
(1)启动EViews软件并新建workfile - 在菜单上依次点击\(\Rightarrow\) File\(\Rightarrow\) New\(\Rightarrow\) Workfile - 设置工作文件的结构类型(workfile structure type) - 点击选择有规则日期型(Data-regular frequency)
(2)设置数据长度或起止时间(data specification) - 设置数据频率(frequency):点击选择季度(Quarterly) - 设置起始时间(start date):手工输入1980/1 - 设置结束时间(end date):手工输入2012/1
(3)设置工作文件的命名(workfile names) - WF:手工输入macro_economic(建议命名) - page:手工输入gdp(建议命名)
(4)完成设置,查看工作文件,并保存到指定本地地址。
\(\Rightarrow\) 点击Ok。
此时可以看到已经建好的工作文件视窗。
保存工作文件到指定的本地地址(如
D:\econometrics\eviews\macro_economic.wf1)。方法1(快捷保存):在工作文件视窗下,同时按键盘Ctrl+S \(\Rightarrow\) 选择本地路径地址 \(\Rightarrow\) 点击确认
方法2(菜单保存):在工作文件视窗下,点击菜单栏中的Save \(\Rightarrow\) 选择本地路径地址 \(\Rightarrow\) 点击确认
1.7.2.3 导入数据
建立或调入工作文件以后,可以输入和编辑数据。 输入数据的基本方法有三种:
(1)方式1:通过菜单操作导入(import)数据
直接导入(import)外部数据(最为常用),支持的外部数据文件格式包括:表格文件excel(最为常用的.xls、.xlsx);文本文件text(较为常用的.txt、.csv、.dat) ;其他文件\(\cdots\)。
从EViews数据库中抓取(fetch)数据(较为常用)
其他方式的导入\(\cdots\)
(2)方式2:在工作文件下手工输入数据(较少使用)
手工一个一个数据输入(重复且单调)
复制粘贴数据,利用操作系统的剪贴板功能把外部数据复制并粘贴过来(对外部数据格式有一定要求,出错率较高)
(3)方式3:在命令窗口下,使用EViews代码输入数据(较少使用,此处细节略过)
此次实验演示的宏观经济发展案例,我们采取方式1,直接导入已经规范化的外部表格数据(.xlsx)文件,具体操作过程为:
(1)通过菜单操作读取外部文件(见 图 1.9 ):
在菜单上依次点击:\(\Rightarrow\) File \(\Rightarrow\) Import \(\Rightarrow\) Import from file …
选择本地数据文件:选择文件路径
d:/econometrics/eviews/macro_economic.xlsx(根据文件位置而定)
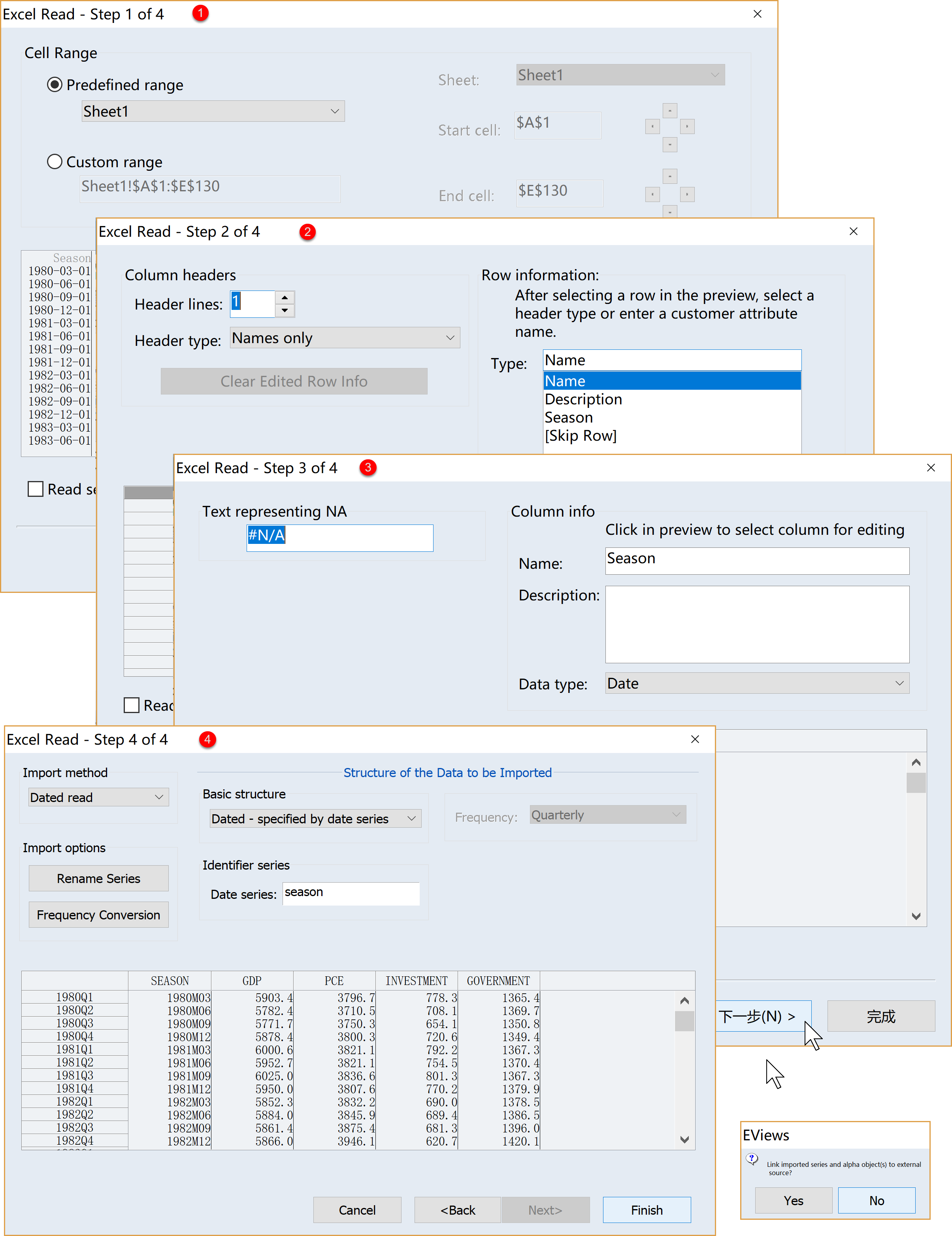
(2)设置数据导入的引导界面:(如果数据足够规范,基本无需调整各项默认设置,见 图 1.10 )。
step 1 of 4:设置并确认数据读取范围
step 2 of 4:设置并确认变量名和行数据说明
step 3 of 4:设置并确认缺失值和列数据说明
step 4 of 4:设置并确认导入方法、选项、数据结构等
完成导入:点击finish
(3) 检查数据是否正确导入,以序列对象形式查看个别数据。在工作文件视窗下:
- 双击打开并查看序列对象
 gdp
gdp
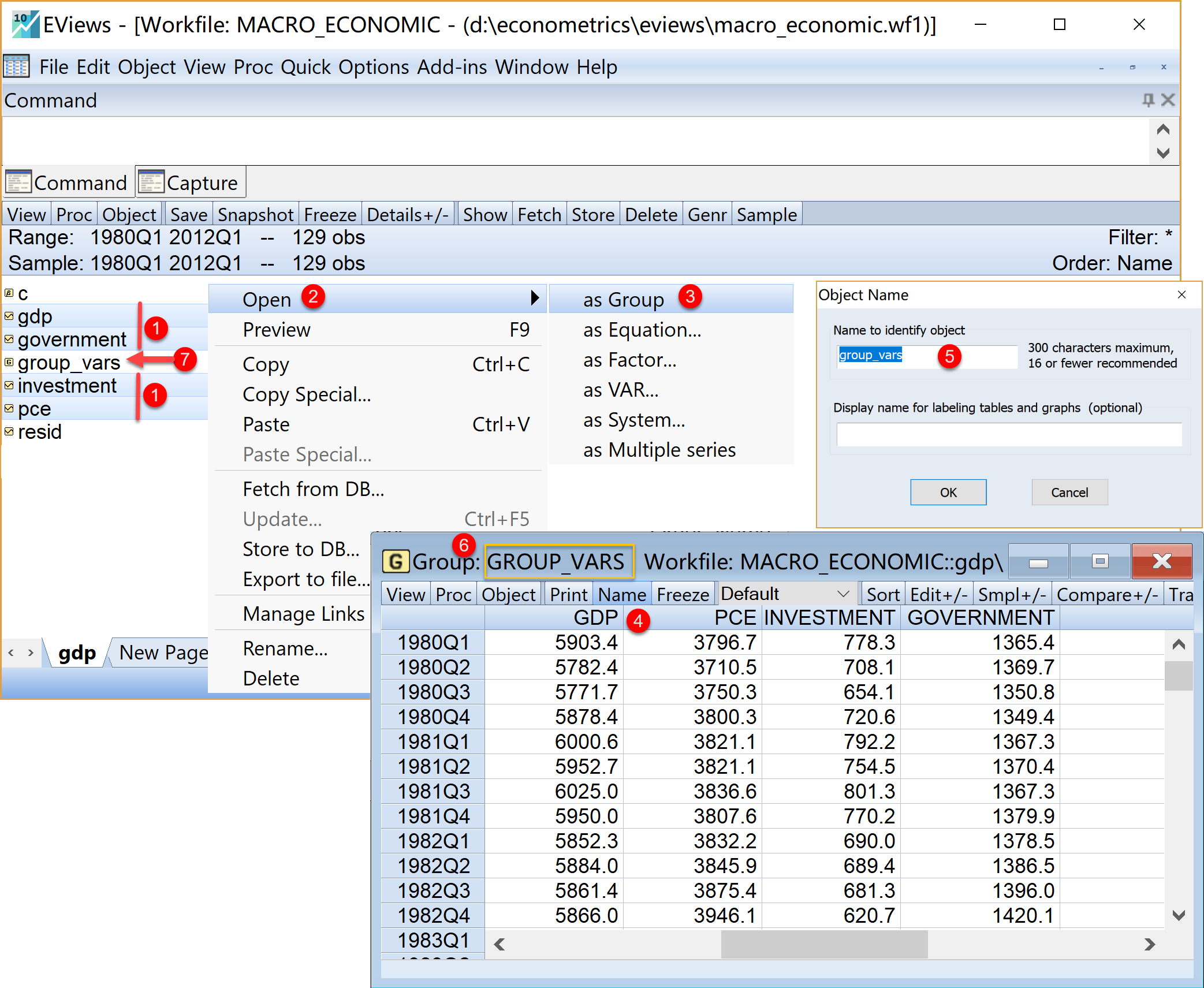
(4) 检查数据是否正确导入,以组对象形式查看全部数据(见 图 1.11 )。
选择4个主要变量。工作文件视窗中:按住键盘CTRL键,鼠标左键依次点击选择对象
 gdp、
gdp、 pce、
pce、 investment、
investment、 government
government构造组对象。在工作文件的选定区(有底域阴影)上:
点击右键\(\Rightarrow\) 选择
Open\(\Rightarrow\) 选择as Group得到未命名组对象
 UNTITLED
UNTITLED
命名组对象并保存。在未命名组对象
 UNTITLED视窗下
UNTITLED视窗下点击菜单栏中的
Name输入命名
group_vars(建议命名)点击
Ok
查看组对象。在工作文件视窗中,双击查看已经命名的组对象
 group_vars
group_vars
1.7.3 构造对象(objects generating)
既然EViews是以对象(Object)方式来进行操作结果的管理和维护,那么所有的EViews操作过程几乎都会“凡走过必留下痕迹”,这些可见的“痕迹”就是EViews对象(object)。简言之,EViews操作中的所有信息都存放在对象(object)里。同时,构造对象(objects generating)是一系列EViews操作过程的副产品:
随着分析操作环节的增加,各种对象都会相应产生,如表格(table)、图片(graph)、方程(equation)等。
如有必要,可能还会基于某个对象产生另一个新对象,如从方程(equation)对象中提取得到系数(beta)对象;或基于X变量的序列对象(series)生成新的ln(X)序列(series)对象。
1.7.3.1 EViews对象(object)的“全家福”
对于EViews初学者,很有必要系统地了解EViews对象(object)都有哪些3。其中,尤其需要关注那些最为常用的(对于初级或中级使用者而言)EViews对象:
| star | icon | name_eng | name_chn | role |
|---|---|---|---|---|
| \(4^{\ast}\) |  |
Alpha | 字母数字(序列型) | 表达包含字母数字的变量 |
| \(4^{\ast}\) |  |
Coef | 系数(向量型) | 表示方程(Equation)或系统(System)的参数 |
| \(5^{\ast}\) |  |
Equation | 方程 | 表示方程的估计、检验或预测 |
| \(5^{\ast}\) |  |
Graph | 图形 | 表示图形输出结果 |
| \(5^{\ast}\) |  |
Group | 组 | 表示序列型对象(包括Series/Alpha等)的一个集合体 |
| \(4^{\ast}\) |  |
Matrix | 矩阵 | 表示矩阵(二维数组) |
| \(4^{\ast}\) |  |
Scalar | 标量 | 表示标量(也即一个数值) |
| \(5^{\ast}\) |  |
Series | 序列(数值型) | 表示时间序列变量,其元素需为数值 |
| \(5^{\ast}\) |  |
Table | 表格 | 表示表格输出结果 |
| \(4^{\ast}\) |  |
Vector | 列向量(数值) | 表示数值类型的列向量 |
其他一些不太常用(对于初级或中级使用者而言)EViews对象包括:
| star | icon | name_eng | name_chn | role |
|---|---|---|---|---|
 |
Factor | 因子 | 表示因子分析结果 | |
 |
Logl | 对数似然 | 表示对数似然分析结果 | |
 |
Model | 模型 | 表示联立方程的预测、模拟等 | |
| \(3^{\ast}\) |  |
Pool | 数据池 | 表示面板数据(同时含有时间和截面单元) |
 |
Rowvector | 行向量 | 表示行向量(一维数组) | |
| \(3^{\ast}\) |  |
Sample | 样本 | 表示观测样本的集合体 |
 |
Spool | 对象池 | 表示包含各种输出对象的容器池 | |
 |
Sspace | 设置状态空间模型 | 表示状态空间模型分析结果 | |
 |
String | 字符串 | 表示标准字符串表达式(不同于字符串值) | |
 |
Svector | 列向量(字符串) | 表示字符串类型的向量 | |
| \(2^{\ast}\) |  |
Sym | 对称矩阵 | 表示对称矩阵 |
 |
System | 系统 | 表示估计方程的系统(与Model类似,但不能用于模拟仿真分析) | |
 |
Text | 文本 | 表示任意文本信息 | |
 |
Userobj | 自定义对象 | 用于用户自主设置的对象 | |
| \(2^{\ast}\) |  |
Valmap | 值映射 | 表示映射关系,给序列型对象(Series/Alpha)的值赋予标签 |
 |
Var | 向量自回归 | 表示向量自回归和误差矫正模型分析结果 |
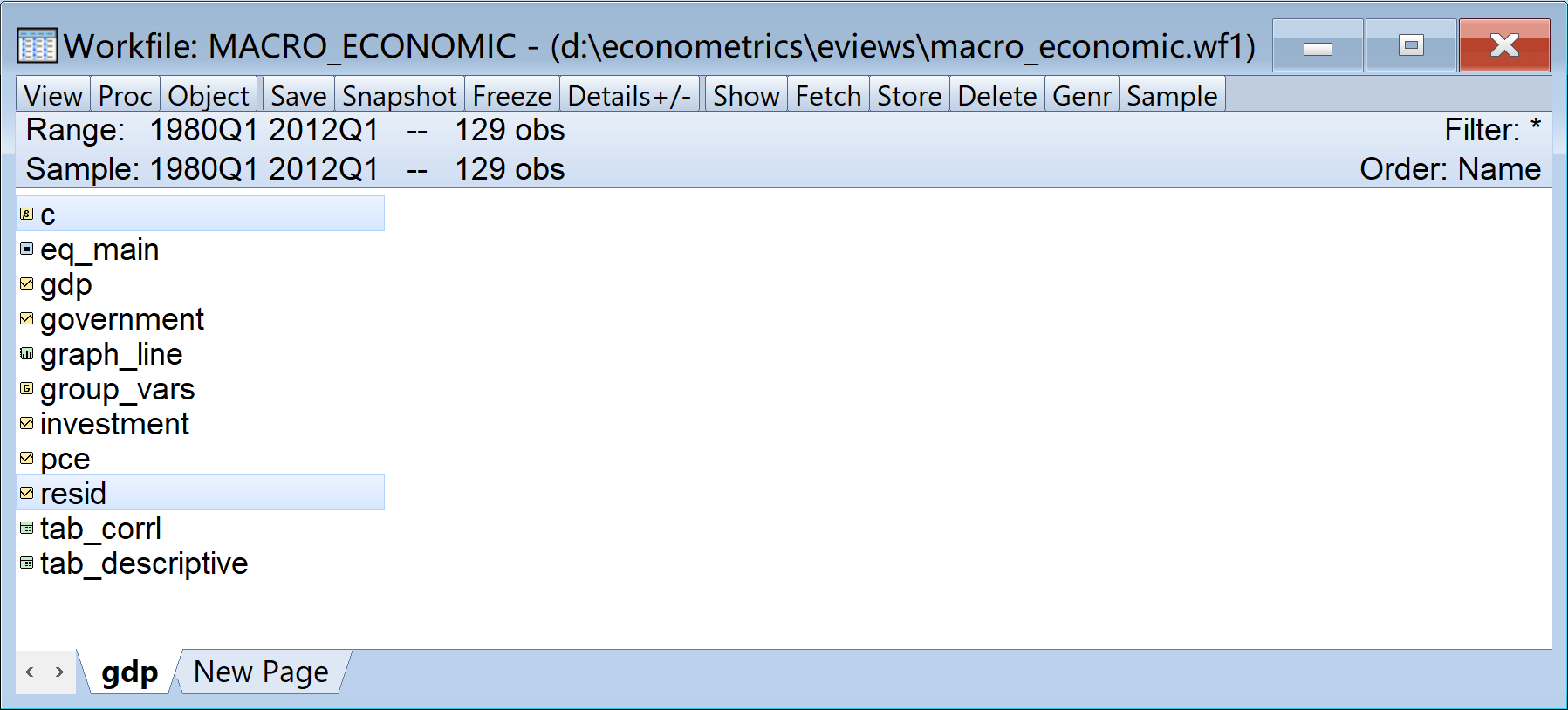
在宏观经济发展模型案例中,我们就可以看到这些常见EViews对象的容貌(参看 小节 1.6 中的快速案例,以及 图 1.12 ):
(1)序列(Series)对象: GDP、
GDP、 PCE、
PCE、 Government、
Government、 Investment、\(\cdots\)
Investment、\(\cdots\)
(2)组(Group)对象: group_vars
group_vars
(3)表格(Table)对象: tab_descriptive、
tab_descriptive、 tab_corrl
tab_corrl
(4)图形(Graph)对象: graph_line
graph_line
(5)方程(Equation)对象: eq_gdp
eq_gdp
(6)系统保留对象(一旦建立工作文件,就会自动产生的对象):
用来装载回归方程系数的系数(Coef)对象:
 C
C用来装载回归方程残差的序列(Series)对象:
 resid
resid
1.7.3.2 EViews分析中常用的对象构造情形
给定特定的数据分析案例,所有的EViews操作过程要么会直接产生特定对象,要么迫于分析工作要求而需要手动生成特定对象。这些常见的对象构造情形可以初步概括为:
第一,自动生成新对象。每一个具体的EViews分析操作,都会自动生成新对象。
回归方程的分析操作,会直接生成一个方程对象
 。
。探索性分析的绘图操作,会直接生成一个图形对象
 。
。探索性分析的相关系数表计算,会生成得到一个表格对象
 。
。数据的矩阵运算,会直接生成一个矩阵对象
 。
。\(\cdots\)
第二,手动生成新对象。根据分析任务需要,生成某些有助于分析工作进行的新对象。
(1)通过功能菜单操作,直接生成新对象。
直接生成新对象是较为常用的,使用情形包括:直接手动构造一个新序列
 用于更灵活的建模分析;手动构造一个空白向量
用于更灵活的建模分析;手动构造一个空白向量 ,用于后续提取并存放重要数值(如若干个对比模型的弹性系数);\(\cdots\)
,用于后续提取并存放重要数值(如若干个对比模型的弹性系数);\(\cdots\)例如,宏观经济发展案例中,在导入Excel数据后,我们可能还需要额外增加一个序列对象(series)
时间趋势trend来调整样本回归模型 式 1.2 ,其中变量trend的取值为\(trend \in \{0,1,2,\cdots,128\}\)。因为原数据表.xlsx中并没有该数据,需要手动产生一个新的序列对象 trend(变量名可以自己设置)
trend(变量名可以自己设置)
(2)通过某些形式的公式运算,生成新对象。
常用的公式运算情形包括:对数变换
log();倒数变换1/X;差分变换d();滞后变量运算x(-1);\(\cdots\)例如,宏观经济发展案例中,在导入Excel数据后,可能还需要使用
对数化国内生产总值log(GDP)变量来调整样本回归模型 式 1.2 或用于其他目的的分析。因此需要通过公式变换\(ln\_gdp=log(gdp)\),从而产生一个新的序列对象 log_gdp(变量名可以自己设置)
log_gdp(变量名可以自己设置)
(3)通过提取已存在对象的部分或全部信息,生成新对象。
常用的信息提取情形包括:提取回归报告中的某些系数
 ;提取方差协方差矩阵
;提取方差协方差矩阵 ;\(\cdots\)
;\(\cdots\)例如,宏观经济发展案例中,为了在撰写报告时使用样本回归模型 式 1.2 中的*政府支出的产出弹性,常常需要提取回归方程
 eq_gdp中的系数值
eq_gdp中的系数值
对于大部分常用Eviews对象(如 图 1.13 )的创建工作,可以通过菜单操作来实现:
(1)打开对象创建引导界面:
依次点击\(\Rightarrow\) Object \(\Rightarrow\) New object…
选择并设置对象:
手动选择对象类型:复选框(Type of object)选择
命名对象:文本框(Name for object)输入
完成操作:点击OK
(2)编辑对象数值或属性
(3)工作文件窗口中查看结果
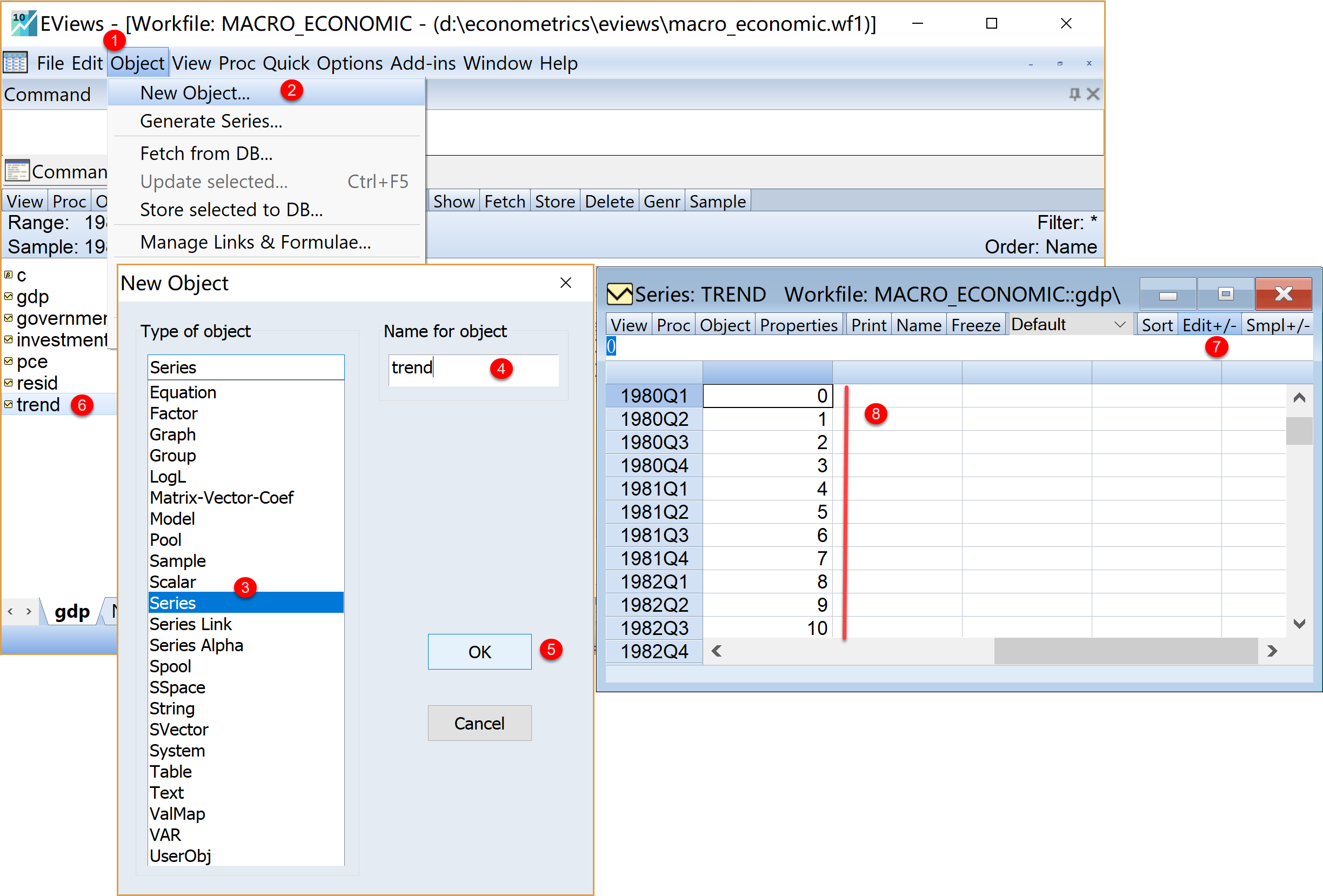
下面将展示宏观经济发展案例中,新增创建一个序列对象(series)时间趋势trend(取值为\(trend \in \{0,1,2,\cdots,128\}\))的基本步骤(见 图 1.13 )。
(1)打开对象创建引导界面。在工作视窗下:
- 依次点击菜单栏,\(\Rightarrow\) Object \(\Rightarrow\) New object…
(2)选择并设置对象。在对象创建引导视图下:
手动选择对象类型:复选框(Type of object)选择
Series命名对象:文本框(Name for object)输入
trend完成操作:点击OK
(3)查看并编辑对象数值。在序列对象视窗下:
点击菜单栏中的Edit+/-
双击单元格
手动填写或编辑数值
保存编辑操作,按键盘快捷组合键Ctrl+S
1.7.4 探索性分析(exploratory analyzing)
探索性分析(exploratory analyzing)是借助统计学基本原理对研究问题进行探索性分析。分析用到的一些统计学基本概念包括均值、中位数、众数、极大值、极小值、标准差、正态性、偏度、峰度、显著度等。探索性分析一般以形象化的数据可视化(data visualization)方式呈现数据特征,主要是通过表格(table)或图形(graph)的形式展现变量之间的特征、趋势、和关系。
1.7.4.1 图表可视化的一般性原则
常用的表格形式包括:描述性统计表、相关系数表等。
绘制表格主要的目的是展示确定的数值大小、汇总统计关系等
原始数据可以构造形成一张表格
计算得到的统计量也可以构造形成一张表格
特定的分析操作,往往意味着可以得到特定的表格。例如,回归分析能得到回归分析报告表;自相关分析就能得到自相关表;\(\cdots\)
常用的图形形式包括:线形图(line)、描点图(dot)、柱状图(bar)、散点图(scatter)、箱线图(boxplot)等。图形可视化的关键在于——以合适的形式,合理地呈现必要的信息!。因此,选择合适的图形形式至为重要,而数据的类型、变量的多少等都会影响图形类型的选择。
图形设计需要考虑的一些基本原则有:图中要展示多少个变量?每个变量要展示多少数据点?数据点是否以时间、项目或分组的方式呈现?
根据不同的图形绘制目标,具体图形选择应视需要而定(见 表 1.7 ):
分析数据比较(Data Comparison)时,可选择循环面积图(Circular Area Chart)、折线图(Line Chart)、柱状图(Column Chart)、簇状-折线图(Line Chart)、不等宽柱状图(Variable Width Column Chart)、表格型嵌图(Table with Embedded Charts)、簇状-条形图(Bar Chart)、簇状-柱状图(Column Chart)等图形
分析数据构成(Data Composition)时,可选择饼形图(Pie Chart)、瀑布图(Waterfall Chart)、百分比多层构成图(Components of Components)、堆栈百分比柱状图(Stacked 100% column chart)、堆栈柱状图(Stacked Column Chart)、堆栈百分比面积图(Stacked 100% Area Chart)、堆栈面积图(Stacked Area Chart)等图形
分析数据分布(Data Distribution)时,可选择柱状直方图(Column Histogram)、线状直方图(Line Histogram)、散点图(Scatter Chart)等图形
分析数据关系(Data Relationship)时,可选择3D面积图(3D Area Chart)、散点图(Scatter Chart)、泡泡图(Bubble chart)等图形
| id | purpose | icon | name | characters |
|---|---|---|---|---|
| 1 | 数据比较 |  |
循环面积图(Circular Area Chart) | 时期间比较->时期数较多->周期性时期 |
| 2 | 数据比较 |  |
折线图(Line Chart) | 时期间比较->时期数较多->非周期性时期 |
| 3 | 数据比较 |  |
柱状图(Column Chart) | 时期间比较->时期数较少->分组较少 |
| 4 | 数据比较 |  |
簇状-折线图(Line Chart) | 时期间比较->时期数较少->分组较多 |
| 5 | 数据比较 |  |
不等宽柱状图(Variable Width Column Chart) | 条目间比较->每个条目有两个变量-> |
| 6 | 数据比较 |  |
表格型嵌图(Table with Embedded Charts) | 条目间比较->每个条目有一个变量->分组较多 |
| 7 | 数据比较 |  |
簇状-条形图(Bar Chart) | 条目间比较->每个条目有一个变量->分组较少->条目较多 |
| 8 | 数据比较 |  |
簇状-柱状图(Column Chart) | 条目间比较->每个条目有一个变量->分组较少->条目较少 |
| 1 | 数据构成 |  |
饼形图(Pie Chart) | 构成无时期变化->简单占比构成 |
| 2 | 数据构成 |  |
瀑布图(Waterfall Chart) | 构成无时期变化->累积构成或落差构成 |
| 3 | 数据构成 |  |
百分比多层构成图(Components of Components) | 构成无时期变化->多层次子类的百分比构成 |
| 4 | 数据构成 |  |
堆栈百分比柱状图(Stacked 100% column chart) | 构成有时期变化->时期较少->仅关心成分之间的相对差异 |
| 5 | 数据构成 |  |
堆栈柱状图(Stacked Column Chart) | 构成有时期变化->时期较少->仅关心成分之间的绝对差异 |
| 6 | 数据构成 |  |
堆栈百分比面积图(Stacked 100% Area Chart) | 构成有时期变化->时期较多->仅关心成分之间的相对差异 |
| 7 | 数据构成 |  |
堆栈面积图(Stacked Area Chart) | 构成有时期变化->时期较多->仅关心成分之间的绝对差异 |
| 1 | 数据分布 |  |
柱状直方图(Column Histogram) | 一个变量的分布->数据点较少 |
| 2 | 数据分布 |  |
线状直方图(Line Histogram) | 一个变量的分布->数据点较多 |
| 3 | 数据分布 |  |
散点图(Scatter Chart) | 两个变量的分布 |
| 1 | 数据关系 |  |
3D面积图(3D Area Chart) | 三个变量间的分布 |
| 2 | 数据关系 |  |
散点图(Scatter Chart) | 两个变量间的关系 |
| 3 | 数据关系 |  |
泡泡图(Bubble chart) | 三个变量间的关系 |
1.7.4.2 EViews图表可视化工具集
EViews软件中的表格可视化,大多数“隐藏”在每一项分析操作的背后。这就意味着:表格可视化应该更加重视特定的数据分析操作(例如序列自相关分析、或者异方差分析等);然后,根据分析结果,获得一份粗糙的原始表格 ;最后,根据需要进行表格的细节修改和完善。
与表格可视化不同,EViews软件提供了丰富的图形可视化工具箱(见 表 1.8 ),与上述图形选择的一般性原则一致,需要综合考虑图形绘制目的、变量数据特征(变量个数、变量类型、数据分组、数据趋势、时期关系\(\cdots\))等。
EViews软件中图形可视化的基本操作过程包括:
(1)选择变量数据(包括选择变量、数据分组、样本区间等)
- 一般是选择工作文件中的组(Group)对象或序列(Series)对象
(2)选择图形类型(选定什么样的数据,就会给出怎样的工具箱)
根据选择变量数据的不同,图形工具箱的界面会有差异
EViews给出可选的图形包括:饼图(Pie)、不等宽柱状图(XY Bar)、带形图(Area Band)、点图(Dot Plot)、钉形图(Spike)、二维面积图(XY Area)、高低图(High-Low)、混合图(Mixed)、季节图(Seasonal Graph)、路径图(XY Line)、密度图(Distribution)、面积图(Area)、泡泡图(Bubble Plot)、散点图(Scatter)、条形图(Bar)、误差图(Error Plot)、线图(line & Symbol)、箱线图(Boxplot)、正态图(Quantile-Quantile)等
(3)设置图形细节
设置图形的颜色、尺寸、边框等
设置图形的坐标轴、网格线等
设置图例
设置图形要素
设置字体
……
(4)保存或输出图形对象
命名图形对象
保存到本地文件或数据库
导出为其他格式(.png/.jpg/.pdf/\(\cdots\))
| id | name_eng | name_chn | icon | mark |
|---|---|---|---|---|
| 1 | line & Symbol | 线图 |  |
表现变化趋势,包含1个序列对象,数据点较多 |
| 1 | line & Symbol | 线图 | 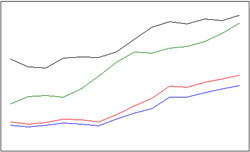 |
表现变化趋势,包含4个序列对象,数据点较多 |
| 2 | Bar | 条形图 | 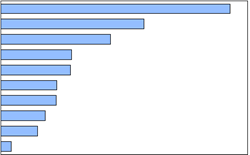 |
表现分组差异,水平条形,包含1个序列对象,数据分组较少 |
| 2 | Bar | 条形图 | 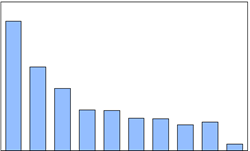 |
表现分组差异,垂直条形,包含1个序列对象,数据分组较少 |
| 2 | Bar | 条形图 | 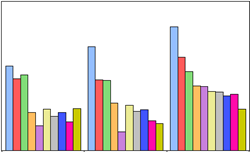 |
表现分组差异,垂直条形,包含若干序列对象,数据分组较少 |
| 3 | Spike | 钉形图 | 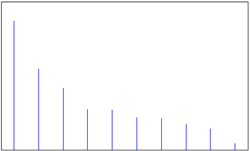 |
表现数值大小,包含1个序列对象,数据分组较少 |
| 4 | Area | 面积图 | 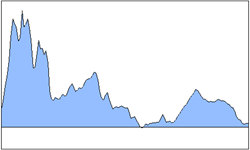 |
表现覆盖面积,包含1个序列对象,数据点较多 |
| 4 | Area | 面积图 | 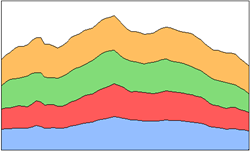 |
表现覆盖面积,包含4个序列对象,数据点较多 |
| 5 | Area Band | 带形图 | 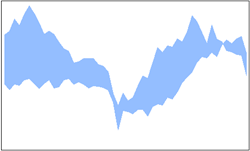 |
表现面积差异,包含2个序列对象,数据点较多 |
| 6 | Mixed | 混合图 | 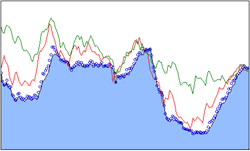 |
表现多样信息,包含多个序列对象,数据点较多 |
| 7 | Dot Plot | 点图 | 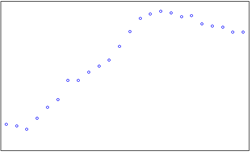 |
表现数值大小,包含1个序列对象,数据点较多 |
| 8 | Error Plot | 误差图 | 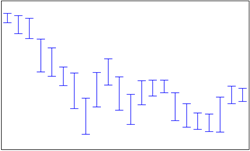 |
表现数值差异,包含2个序列对象,数据点较少 |
| 8 | Error Plot | 误差图 | 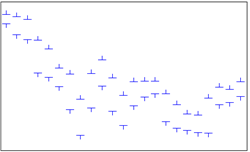 |
表现数值差异,包含3个序列对象,数据点较少 |
| 9 | High-Low | 高低图 | 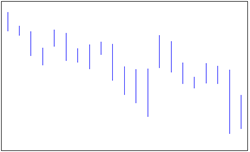 |
表现数值位置关系,包含2个序列对象(最高价、最低价),数据点较少 |
| 9 | High-Low | 高低图 | 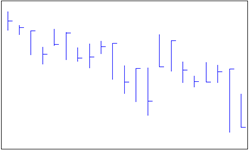 |
表现数值位置关系,包含3个序列对象(开盘价、最高价、最低价),数据点较少 |
| 10 | Scatter | 散点图 | 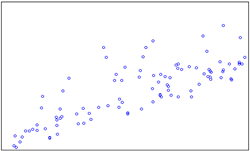 |
表现变量关系,包含2个序列对象,数据点较多 |
| 10 | Scatter | 散点图 | 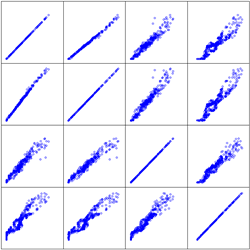 |
表现变量关系,包含多个序列对象,数据点较多 |
| 11 | Bubble Plot | 泡泡图 |  |
表现变量关系,包含3个序列对象,数据点较多 |
| 12 | XY Line | 路径图 |  |
表现数据变化路径,包含2个序列对象,数据点较多 |
| 13 | XY Area | 二维面积图 |  |
表现2D覆盖面积,包含个序列对象,数据点较多 |
| 14 | XY Bar | 不等宽柱状图 |  |
表现分组差异,垂直条形,包含若干个序列对象,数据分组较少 |
| 15 | Pie | 饼图 |  |
表现数据构成关系,包含1个序列对象,数据分组较少 |
| 16 | Distribution | 密度图 |  |
表现数据分布密度,直方图,包含1个序列对象,数据点较多(自动分组) |
| 17 | Quantile-Quantile | 正态图 | 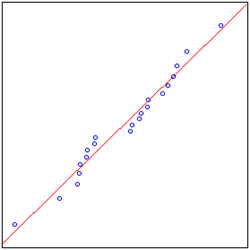 |
表现数据分布密度,正态QQ图,包含1个序列对象,数据点较多 |
| 18 | Boxplot | 箱线图 | 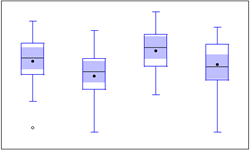 |
表现数据分布形态,包含若干序列对象,数据点较多 |
| 19 | Seasonal Graph | 季节图 | 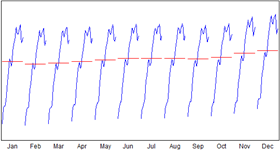 |
表现数据循环关系,包含1个序列对象,数据点较多,分组较少(在同一月份不同年份上的变化) |
| 19 | Seasonal Graph | 季节图 | 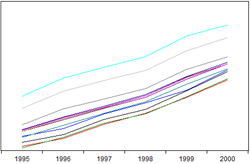 |
表现数据循环关系,包含1个序列对象,数据点较多,分组较少(在同一年份不同月份上的变化) |
下面将利用EViews菜单操作,对宏观经济发展案例进行简要的探索性分析。该部分内容将有助于快速了解EViews图表可视化的基本操作思路和流程。无论是表格可视化,还是图形可视化,如下的简要案例操作及过程都具有普遍的代表性,读者可以照此举一反三,而要达到熟练地推而广之则必须经历更多的实战摸索和训练。
1.7.4.3 EViews表格可视化:描述性统计分析表的制作
首先,对宏观经济发展案例中的主要变量(GDP国内生产总值(10亿美元)、PCE人均消费支出(美元)、Investment投资(10亿美元)、Government政府支出(10亿美元))进行基本描述性统计分析,并得到表格(table)对象形式的描述性统计分析表。然后,对表格(table)对象形式的描述性统计分析表进行美学设计,修改表格细节,实现指定要求的三线表形式。
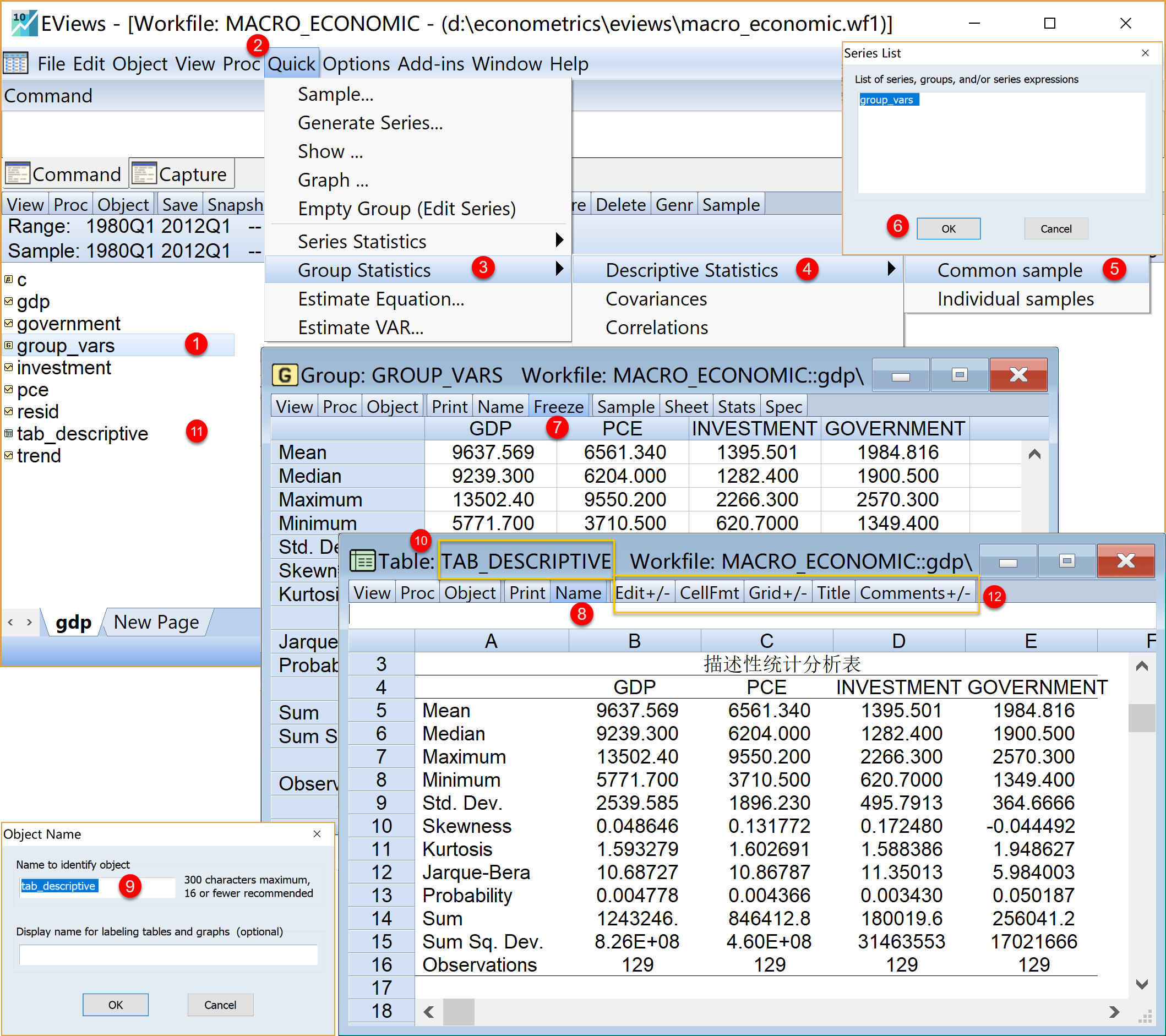
进行基本描述性统计分析(EViews操步作骤见 图 1.14 ):
(1)在工作文件视窗中,单击选择已经命名的组对象 group_vars
group_vars
(2)在工作文件视窗中,点击菜单栏中的Quick \(\Rightarrow\) 选择Group Statistics \(\Rightarrow\) 选择Descriptive Statistics \(\Rightarrow\) 选择Common sample
(3)确认变量对象,\(\Rightarrow\) 点击Ok
(4)得到Group描述性统计分析视窗 group_vars
group_vars
(5)将描述性分析结果转换成表格。在Group描述性统计分析视窗 group_vars下,\(\Rightarrow\) 点击
group_vars下,\(\Rightarrow\) 点击Freeze\(\Rightarrow\) 得到表格对象视窗 UNTITLED
UNTITLED
给表格对象命名。在表格对象视窗
 UNTITLED视窗下,\(\Rightarrow\) 点击
UNTITLED视窗下,\(\Rightarrow\) 点击Name填写表格对象名称。在Object Name窗口中,\(\Rightarrow\) 输入
tab_descriptive(建议命名)\(\Rightarrow\) 点击Ok查看保存的表格对象。在工作文件视窗中,确认可以看到已经保存的表格对象
 tab_descriptive
tab_descriptive
进行美学设计,修改表格细节,实现三线表形式的表格要求。(此处要求把初始表格调整为三线表,具体细节修改过程略。)。
工作文件视窗中,双击打开表格对象
 tab_descriptive
tab_descriptive点击菜单
Edit+/-,可以编辑修改单元格的内容点击菜单
CellFmt,可以调整单元格的大小、颜色、边框等点击菜单
Title,可以填写表格标题点击菜单
Grid+/-,可以显示/隐藏网格线\(\cdots\)
1.7.4.4 EViews图形可视化:多线图(Line-Symbol)的绘制
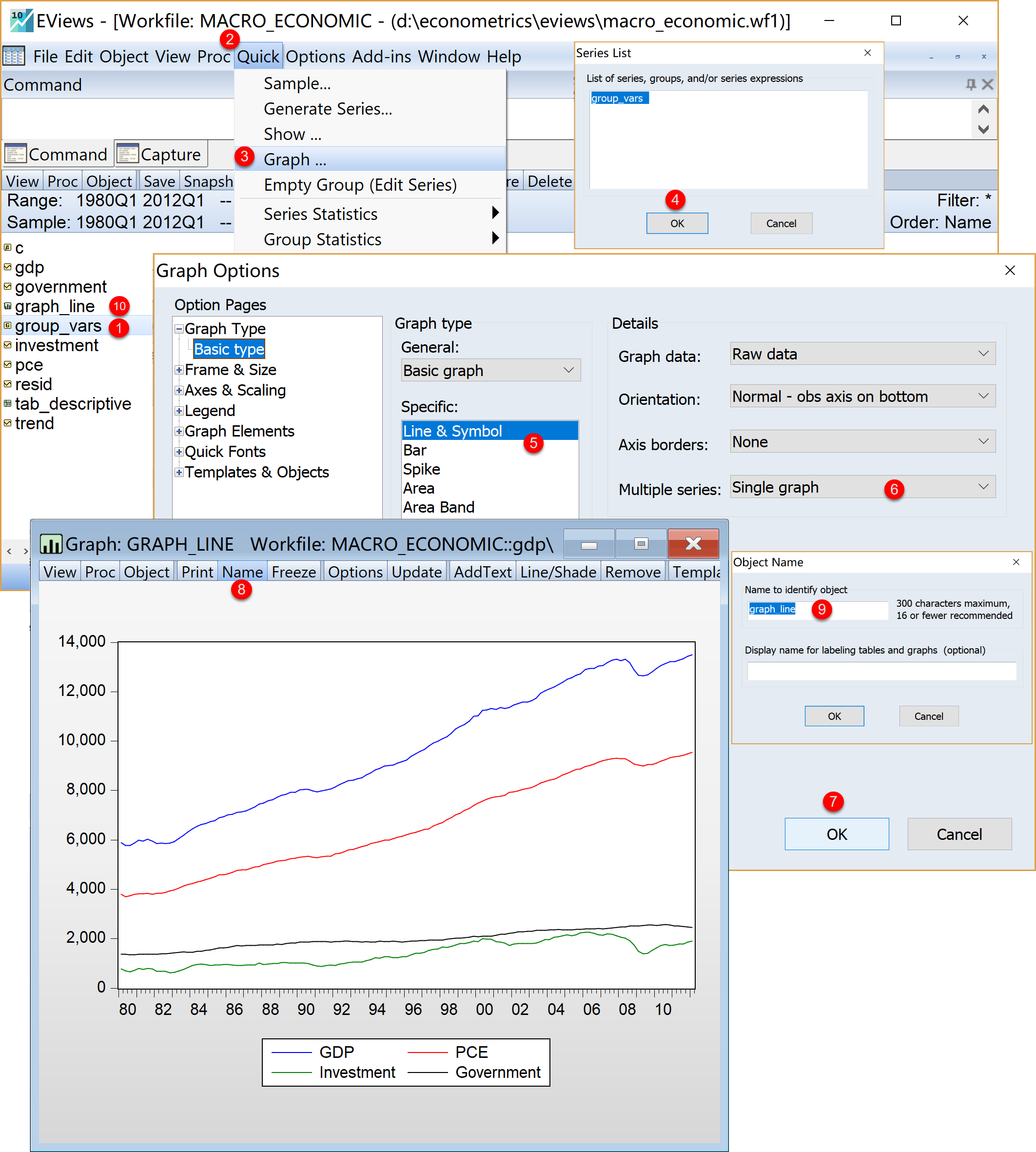
下面将展示EViews软件在多变量下的线图(Line-Symbol)的绘制过程。对宏观经济发展案例中的主要变量(GDP国内生产总值(10亿美元)、PCE人均消费支出(美元)、Investment投资(10亿美元)、Government政府支出(10亿美元))进行简单的图形可视化,绘制简单的(标准化的)多变量线图(Line-Symbol)的主要过程如下:(见 图 1.15 )
选择组(Group)对象。在工作文件视窗下,
鼠标单击选择已经命名的组对象
 group_vars。
group_vars。点击菜单栏中的
Quick\(\Rightarrow\) 选择Graph确认变量对象,点击
Ok
设置图形引导界面。在引导窗口的目录Graph Options 中,分别点击设置如下子选项页:
(1)Graph type(图类型)子选项页,主要用于修改图形类型
General(通用)下拉框:下拉选择Basic graph
Specific(设置)复选框(比较常用的选项设置) :点击选择Line-Symbol
Detail(细节)选项区,有多个设置下拉框选择
Graph data(图形数据)下拉框:默认设置
Orientation(方向)下拉框:默认设置
Axis Borders(坐标轴边框)下拉框:默认设置
Multiple series(多序列)下拉框:下拉选择Single graph
(2)Frame & Size(图框和大小)子选项页,主要用于设置图形的颜色/边框、大小/缩进等:默认设置
(3)Axes & Scaling(图轴和度量)子选项页,主要用于设置数据尺度、数轴标签、网格线等:默认设置
(4)Lgend(图例)子选项,主要用于设置图例相关选项 :默认设置
(5)Graph Element(图形元素)子选项,主要用于设置线型/符号、填充块等:默认设置
(6)Quick Fonts(快速字体)子选项页,用于调整字体:默认设置
(7)Templates & Objects(样式和对象),用于套用样式等:默认设置
(8)Graph Updating(图形更新)子选项页,用于更新修改:默认设置
(9)完成设置。点击Ok。将得到未命名图形对象 UNTITLED
UNTITLED
命名并保存图形对象。在未命名图形对象 UNTITLED窗口中
UNTITLED窗口中
点击菜单栏
Name\(\Rightarrow\) 输入命名graph_line\(\Rightarrow\) 点击Ok可以看到工作文件中,将出现已命名并保存的图形对象
 graph_line
graph_line
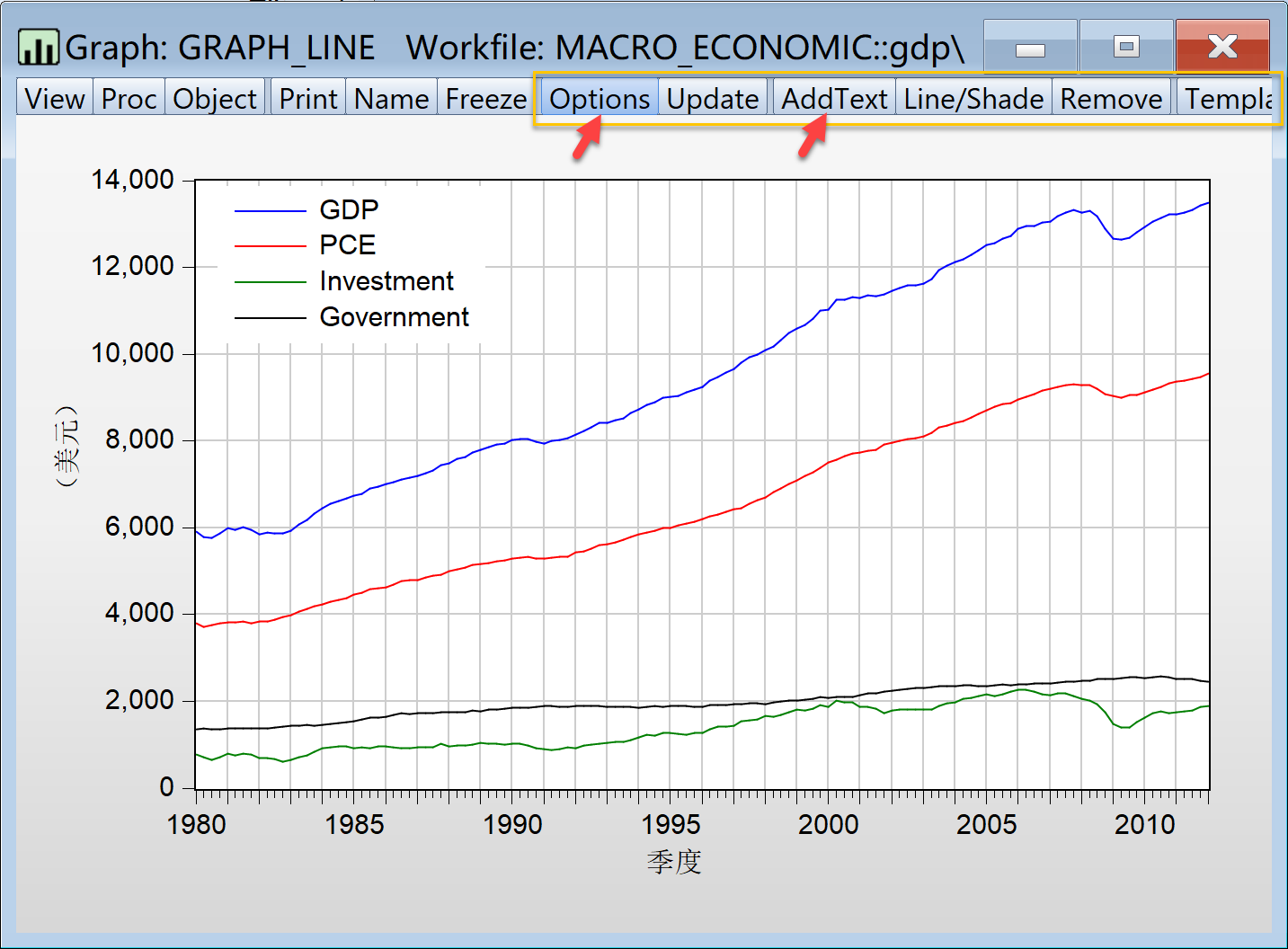
此外,根据研究报告撰写的特定要求,可以对图形进行个性化美学设计。美化图形,修改细节,使其满足个性化美学要求(见 图 1.15 ,具体步骤此处略)。
(1)工作文件中,双击打开已保存的图形对象 graph_line
graph_line
(2)操作并编辑各种图表细节,在图形对象 graph_line视窗中:
graph_line视窗中:
点击菜单
name,可以修改图形对象命名点击菜单
Freeze,可以设置图形是否冻结或可更新(如手工调整样本区间等)点击菜单
Options,可以修改各种图形元素(这是最常用的细节修改内容)
Graph Type,用于修改图形类型Frame & Size,用于修改图形大小、边框等Axes & Scaling,用于修改图形坐标轴、网格线、标尺等Legend,用于修改图形的图例Graph Elements,用于修改图形的数值标签、线型、符号等Quick Font,用于修改图形的字体Templates & Objects,用于快速套用图形样式Graph Updating,用于图形修改更新
点击菜单
Update,可以更新图形修改结果点击菜单
AddTex,可以给图形添加文本\(\cdots\)
1.7.5 线性回归分析(linear regression analyzing)
线性回归分析(linear regression analyzing)是用来探究现象之间因果作用关系的最重要工具之一。线性回归分析属于一类有助于直观地理解复杂问题的理想化分析工具,一般需要较严苛的假设条件。
EViews进行线性回归分析中需要考虑的问题可繁可简,取决于问题的复杂程度、研究的细致程度、条件的满足程度等等。一般而言,线性回归分析都需要进行:模型选择和调试、统计学检验(如t检验、F检验等)、计量经济学检验(如多重共线性、异方差、自相关等检验)、预测性检验、稳健性检验等。
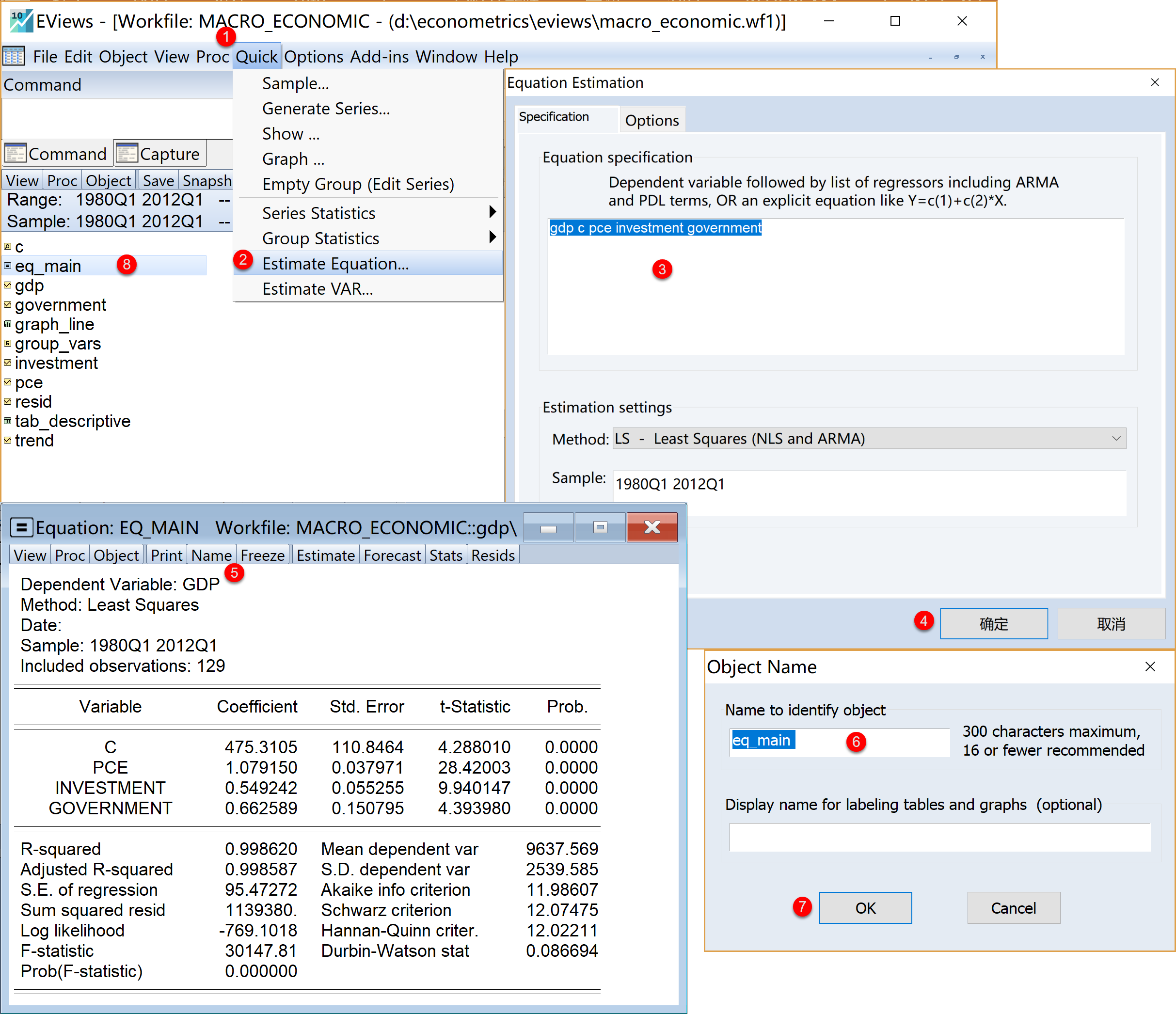
为了简便起见,下面将对宏观经济发展案例中的对数模型(见节 小节 1.6 中的样本回归模型 式 1.2 )进行EViews线性回归分析。Eviews菜单操作的具体步骤为(见 图 1.17 ):
(1)进入方程分析的设置菜单。
- 在工作文件视窗下,点击菜单栏中的
Quick\(\Rightarrow\)Estimation Equation\(\Rightarrow\) 将看到方程估计的引导界面
(2)完成引导设置。方程估计的引导界面Equation Estimation下,进行如下设置:
(a)设置方程。Equation Estimation \(\Rightarrow\) Specification
方程设置
Equation specification:依次输入变量 gdp c pce investment government(注意变量之间的空格,以及截距c)估计方法
Estimation settings:方法
Method: 下拉选择LS - Least Squares (NLS and ARMA)样本
Sample: 默认设置
(b)设置细节选项。Equation Estimation \(\Rightarrow\) Options
协方差设置
Coefficient Covariance\(\Rightarrow\) (细节略)权重设置
Weights\(\Rightarrow\) (细节略)优化算子设置
Optimization\(\Rightarrow\) (细节略)
(c)完成设置,点击OK \(\Rightarrow\) 将得到未命名的方程对象 UNTITLED
UNTITLED
(3)命名并保存回归方程。
在未命名的方程对象
 UNTITLED视窗下,点击菜单栏
UNTITLED视窗下,点击菜单栏Name\(\Rightarrow\) 输入命名eq_main(建议命名) \(\Rightarrow\) 完成命名,点击Ok此时,在工作文件视窗下可以看到已经保存命名的方程对象
 eq_main
eq_main
构建并比较多个类似方程时,可以复制、粘贴、重命名多个方程对象

可以随时修改方程的属性,在方程对象
 视窗下,点击菜单栏中的
视窗下,点击菜单栏中的Estimate\(\Rightarrow\) 重新设置Equation Estimation
1.7.6 报告结果输出(output reporting)
Eviews操作结果是以对象(object)形式存储在工作文件(workfile)中,在撰写研究报告时,往往需要呈现这些分析结果和主要结论。报告结果输出(output reporting)是指把EViews分析的结果导出或呈现在研究报告中的过程或操作。根据研究报告内容的实际需要,EViews的对象可能需要完整输出,也可能只是提取对象中的部分元素。但无论如何,进行合理的选取、整合、呈现、展示是极为必要的。例如:
调整图形(graph)和表格(table)的各种美学细节以符合论文或报告的格式要求,如字体、颜色、线条、形状、图例、坐标等
选取并整合成新的表格,如三线表、多模型对比表
把一个EViews原始的回归分析报告(raw report),处理成简要报告(simple report),一般表达为三行或四行,包括样本回归方程(第一行)、回归系数的标准误(第二行)、t值(第三行)、拟合情况(第四行,包括拟合优度\(R^2\),F检验值、DW检验值等)
\(\cdots\)
对于如下的回归方程:
\[ \begin{aligned} \begin{split} GDP_i=&+\beta_{1}+\beta_{2}PCE_i+\beta_{3}Government_i+\beta_{4}Investment_i+u_i \end{split} \end{aligned} \tag{1.3}\]
其回归报告,可以简要写成:
\[ \begin{alignedat}{999} \begin{split} &\widehat{GDP}=&&+475.31&&+1.08PCE_i\\ &(s)&&(110.8464)&&(0.0380)\\ &(t)&&(+4.29)&&(+28.42)\\ &(cont.)&&+0.66Government_i&&+0.55Investment_i\\ &(s)&&(0.1508)&&(0.0553)\\ &(t)&&(+4.39)&&(+9.94)\\ &(over)&&n=129&&\hat{\sigma}=95.4727\\ &(fit)&&R^2=0.9986&&\bar{R}^2=0.9986\\ &(Ftest)&&F^*=30147.81&&p=0.0000 \end{split} \end{alignedat} \tag{1.4}\]
1.8 Eviews编程体系及语法
1.8.1 命令运行方式
EViews提供了菜单和命令两种方式进行数据分析和处理。事实上,只要能够通过窗口菜单完成的功能,就都可以通过命令窗口中输入相应编程命令来执行实现。根据任务的复杂性、重复性、繁重性等的不同,EViews可以通过如下方式完成分析任务:
(1)方式1:完全窗口菜单驱动,也即通过选择特定菜单栏功能进行分析操作
适合于简单的、一次性的、工作量小的分析任务
适合于EViews软件初学者,可以更加集中于统计分析和计量分析本身
方式1的优缺点:
优点:图形用户界面使得操作十分直观,常用对象窗口和菜单相对固定,简单的几次反复练习后便会形成稳定的“记忆路径”
不足:操作效率较低,难以在底层上实现“掌控一切”的状态
(2)方式2:完全程序命令驱动,也即通过执行特定编程命令来进行分析操作,具体又可分为两种情形:
方式2.1:交互式命令驱动,也即在命令视窗中逐条地编写程序代码,逐条运行各个编程命令
类似于“看一步走一步”的模式,命令编程不需要十分严格的逻辑安排
只要有特定分析需要,就随时编写命令,随时执行编程命令,得到想要的分析结果
适合于相对复杂、有一定重复性,但又不太繁重的分析任务
方式2.1的优缺点:
优点:灵活、自由,可以与菜单操作(方式1)互相结合——只要需要就可随时登台“串场”发挥作用!
不足:代码管理困难,条理性较差,需要繁琐的手工编写和操作
方式2.2:批量式命令驱动,也即在程序文件中系统地编写程序代码,自动运行全部编程命令
EViews程序文件为.prg文件后缀,是一类通用文本文件,所有代码都以文本形式进行编写、组织和管理。
类似于“照着剧本演戏”的模式,所有“剧本”内容(程序代码)都是经过精心设计和安排的
一开始分析任务就极为明确,程序命令有整体“剧情”,各命令间的联系、顺序等逻辑性较强
适合于较为复杂、重复性较高、极为繁重的分析任务
方式2.2的优缺点:
优点:代码管理方便,代码可重复使用,代码逻辑性强,分析操作过程的条理性很清晰
不足:需要系统掌握EViews编程语言,学习使用成本较大;需要较强的代码管理和统计分析逻辑,容易出现各类运行报错。
(3)方式3:菜单窗口和程序命令并行驱动,也即同时结合了功能菜单和编程命令来开展相关分析工作,往往都是菜单驱动加上视窗命令
方式3的优缺点:
菜单驱动的优点是简单直观(类似于“所见即所得”),不足是功能菜单的操作效率较为低下
命令视窗的优点是底层操作(类似于“我思故我在”),不足是命令语法的学习曲线较为陡峭,记忆负担大,代码写作要求较高
1.8.1.1 菜单窗口和程序命令并行驱动
如前所述,菜单窗口和程序命令并行驱动,同时结合了功能菜单和编程命令来开展相关分析工作,是数据分析实践中最常用到的、最受初学者欢迎的操作方式之一。这种操作方式,首先需要掌握功能菜单驱动的数据分析操作,同时还要求了解并使用最基本的EViews编程语言进行简单代码编写和运行分析。总体看来,这种操作方式下,以功能菜单操作为主,以视窗命令操作为辅——数据分析者将主要利用菜单操作完成主要的常规性分析任务,而一些非常规的、需要定制化的分析任务则交给视窗命令去执行。
下面通过宏观经济发展案例演示基本操作步骤,将展示“功能菜单操作-视窗命令操作”的交互执行。其中数据分析的目标任务有两个:一是得到一个向量(Vector)对象 ,用于存放判定系数\(R^2\)和调整判定系数;二是得到一个标量(Scalar)对象
,用于存放判定系数\(R^2\)和调整判定系数;二是得到一个标量(Scalar)对象 ,用于存放给定显著性水平\(\alpha=0.05\),且自由度为\(f=128\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(128)\)。
,用于存放给定显著性水平\(\alpha=0.05\),且自由度为\(f=128\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(128)\)。
假设前期已完成如下菜单操作工作:
(见 小节 1.7.2 )已经成功创建了工作文件
 macro_economic
macro_economic(见 小节 1.7.2 )已经成功导入数据
(见 小节 1.7.5 )已经通过菜单操作进行双对数回归分析,并得到方程对象
 eq_main
eq_main双击方程对象
 eq_main可以查看EViews给出的回归分析报告。可以看到,回归方程拟合优度中的判定系数\(R^2=0.998620\),调整判定系数判定系数\(\bar{R}^2=\)
eq_main可以查看EViews给出的回归分析报告。可以看到,回归方程拟合优度中的判定系数\(R^2=0.998620\),调整判定系数判定系数\(\bar{R}^2=\)
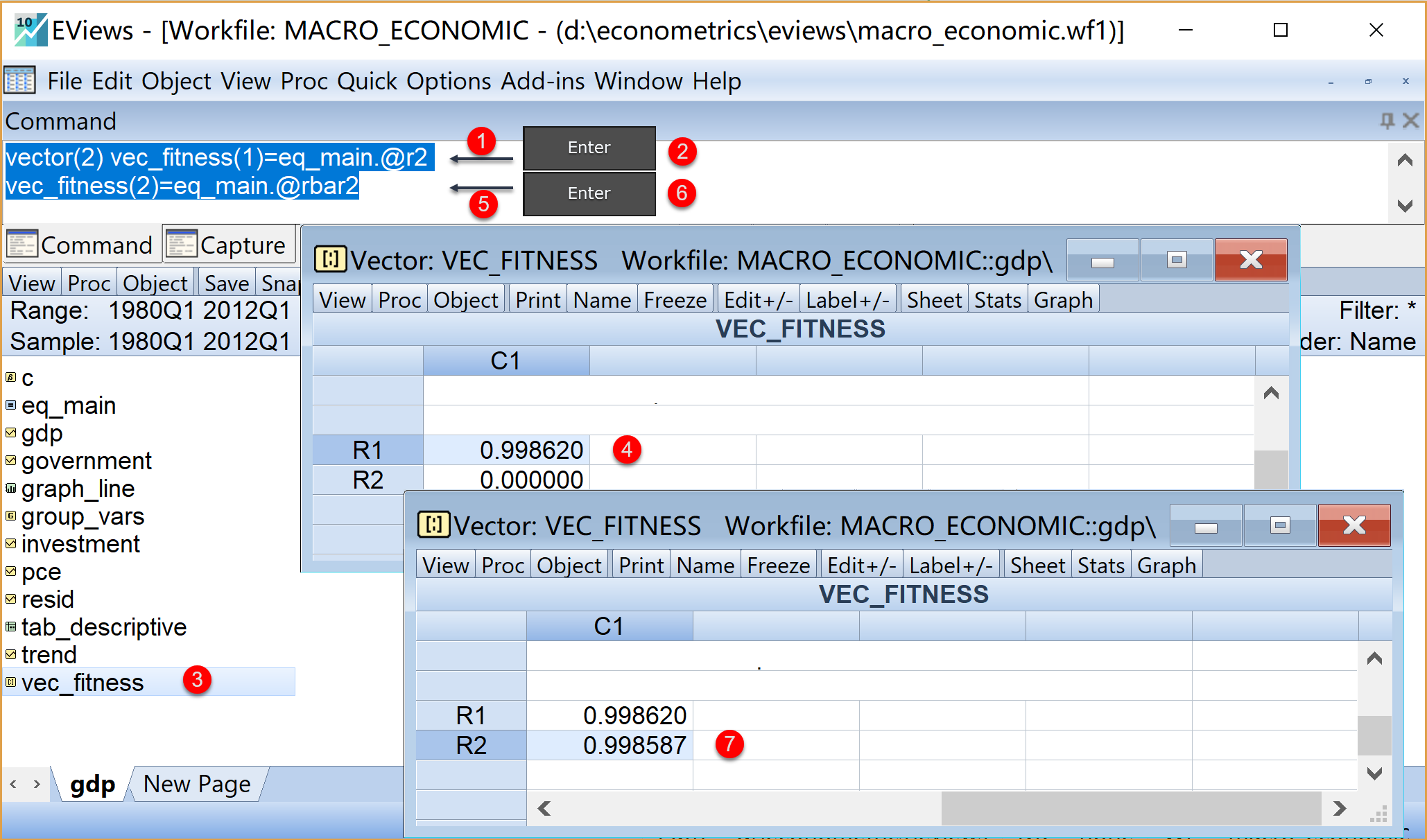
目标任务1(见 图 1.18 ):通过视窗命令操作,提取出双对数回归方程中的判定系数\(R^2\)和调整判定系数\(\bar{R}^2\),并将这两个数值分别存放在一个向量(Vector)对象 vec_fitness中。
vec_fitness中。
(1)在命令视窗中:
输入代码行
vector(2) vec_fitness(1)=eq_main.@r2鼠标光标停留在该代码行上 \(\Rightarrow\) 然后按Enter键,便可以运行该代码行!
(2)在工作文件视窗下:
将看到生成了一个向量对象
 fitness
fitness双击查看
 fitness,发现该向量含有两个元素,其中第一个元素为0.998620(也即回归方程的判定系数\(R^2\)值),第二个元素为0.000000
fitness,发现该向量含有两个元素,其中第一个元素为0.998620(也即回归方程的判定系数\(R^2\)值),第二个元素为0.000000
(3)在命令视窗中:
输入代码行
vec_fitness(2)=eq_main.@rbar2鼠标光标停留在该代码行上 \(\Rightarrow\) 然后按Enter键,便可以运行该代码行!
(4)在工作文件视窗下:
- 双击查看
 vector_fitness,发现该向量含有两个元素,其中第一个元素为0.998620(也即回归方程的判定系数\(R^2\)值),第二个元素为0.998587(也即回归方程的调整判定系数\(\bar{R}^2\)值)
vector_fitness,发现该向量含有两个元素,其中第一个元素为0.998620(也即回归方程的判定系数\(R^2\)值),第二个元素为0.998587(也即回归方程的调整判定系数\(\bar{R}^2\)值)
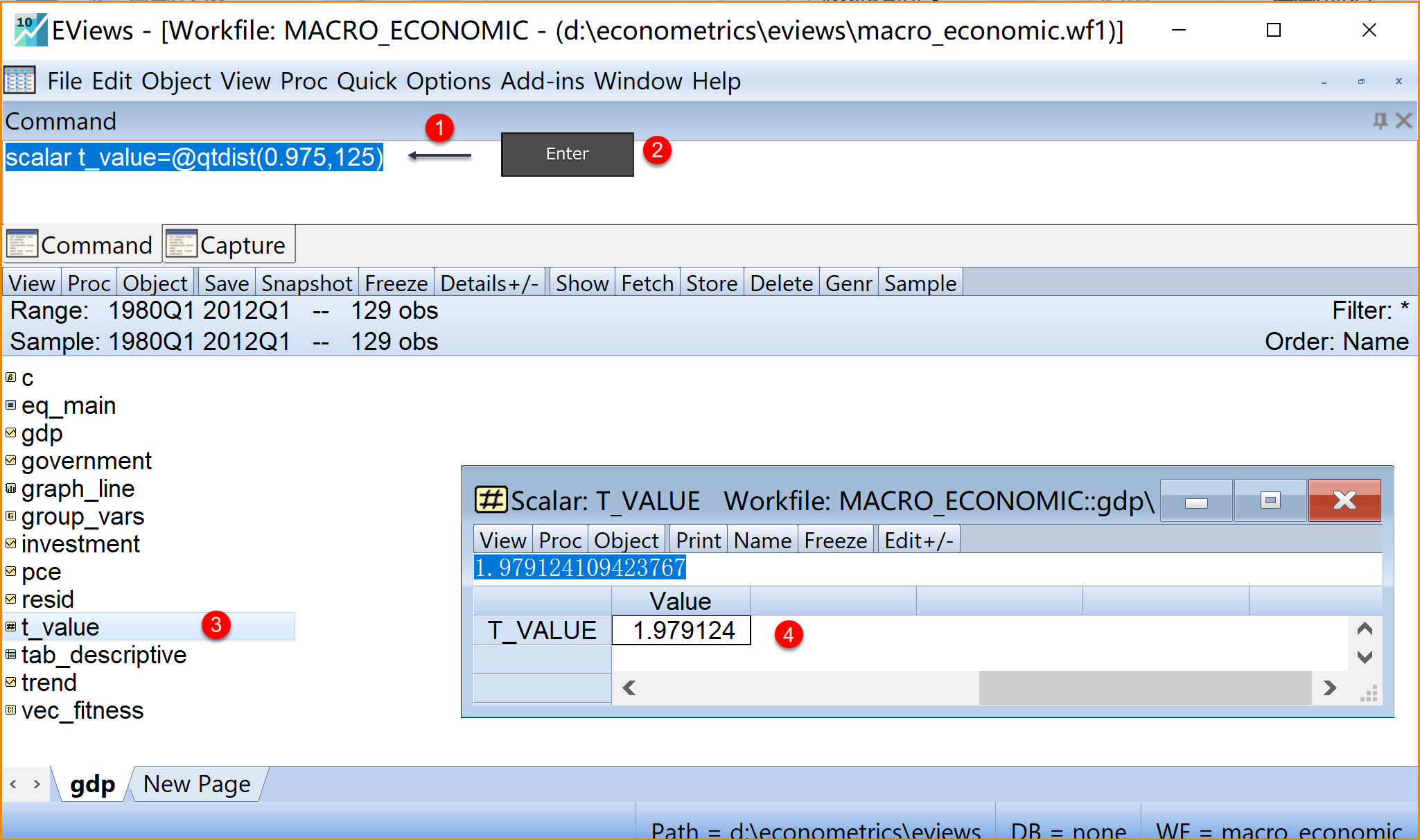
目标任务2(见 图 1.19 ):通过视窗命令操作,得到一个标量(Scalar)对象 t_value,用于存放给定显著性水平\(\alpha=0.05\),且自由度为\(f=125\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(125)\)。
t_value,用于存放给定显著性水平\(\alpha=0.05\),且自由度为\(f=125\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(125)\)。
(1)在命令视窗中:
输入代码行
scalar t_value=@qtdist(0.975,125)在该代码行上按Enter键
(2)在工作文件视窗下中:
将看到生成了一个标量对象
 t_value
t_value双击查看
 t_value,发现该标量含有一个元素,其数值为2(也即计算表明,在给定显著性水平\(\alpha=0.05\),且自由度为\(f=125\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(125)=2\))
t_value,发现该标量含有一个元素,其数值为2(也即计算表明,在给定显著性水平\(\alpha=0.05\),且自由度为\(f=125\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(125)=2\))
1.8.1.2 批量式命令驱动
下面将简要介绍(方式2.2)批量式命令驱动运行模式的基本操作。作为EViews高级学习技巧,很有必要理解EViews程序文件 (文件后缀名为.prg)的创建和运行操作:
(文件后缀名为.prg)的创建和运行操作:
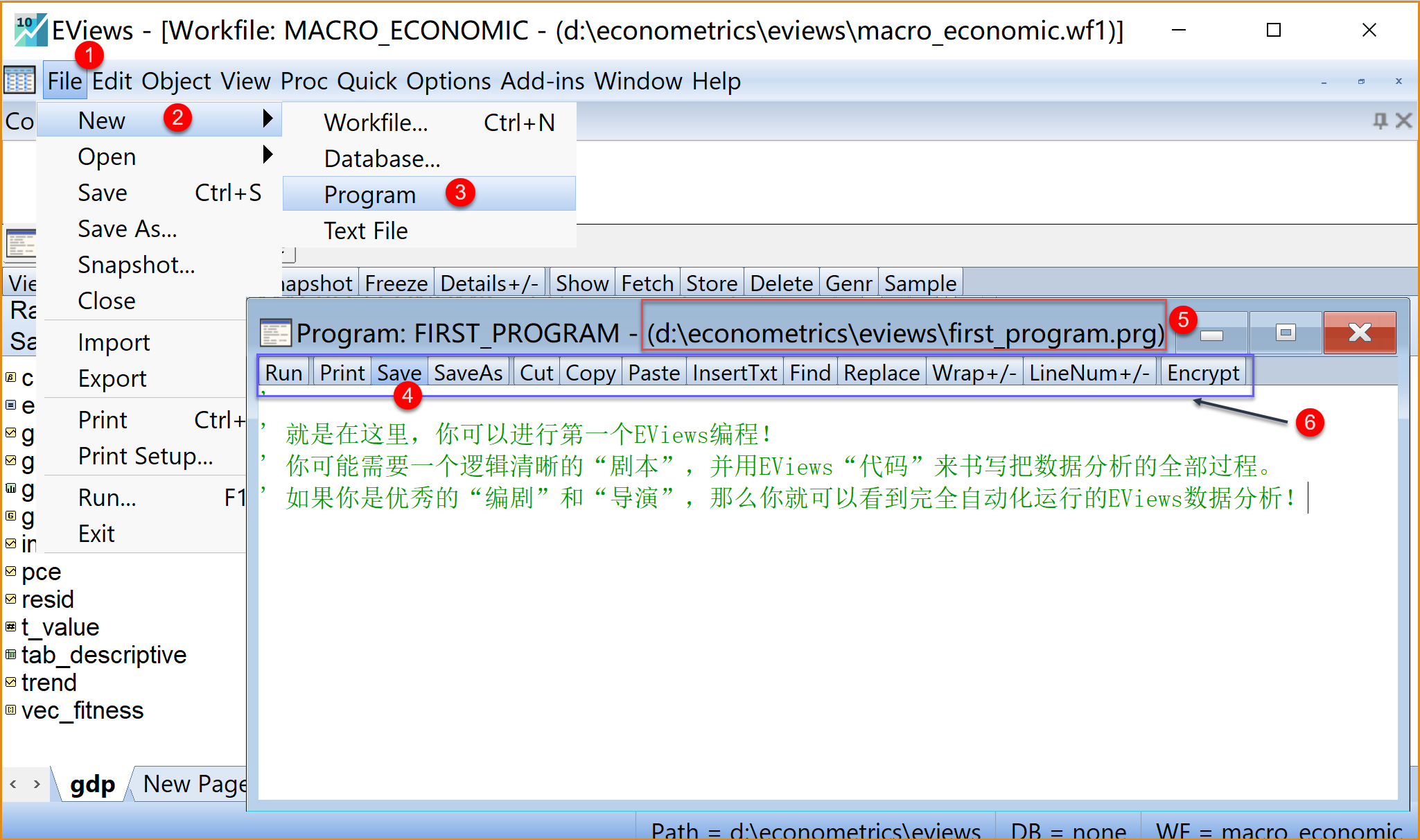
(1)创建程序文件(见 图 1.20 )。
在工作文件视窗下,依次点击选择菜单栏File \(\Rightarrow\) New \(\Rightarrow\) Program。
命名并保存程序文件。在程序文件视窗下,点击菜单栏Save \(\Rightarrow\) 确定文件存放地址(如本地文件夹”d:\econometrics\eviews”下),输入文件名
first_program(建议命名,可修改)\(\Rightarrow\) 完成,点击OK查看已保存的程序文件
 并双击打开。 在本地文件夹下(如”d:\econometrics\eviews”)可以看到程序文件
并双击打开。 在本地文件夹下(如”d:\econometrics\eviews”)可以看到程序文件 first_program.prg,可双击打开
first_program.prg,可双击打开
(2)使用程序文件视窗的功能菜单。
在程序文件视窗(Program:first_grogram)下,可以看到如下功能菜单
运行菜单(Run):用于运行全部代码
打印菜单(Pringt)
保存菜单(Save)和另存菜单(SaveAs)
剪切菜单(Cut)、拷贝菜单(Copy)和粘贴菜单(Paste)
插入文本菜单(InsertTxt)
查找菜单(Find)和替换菜单(Replace)
打包命令菜单(Wrap+/-):用于封装命令
代码行号菜单(LineNum+/-):用于显示或隐藏代码行号
加密菜单(Encrypt):用于给程序文件加密
(3)在程序文件 中编写、管理和运行EViews代码。
中编写、管理和运行EViews代码。
根据EViews编程语言规则(见 小节 1.8.2 ),直接以文本形式编写程序代码。
执行整个程序文件。在检查确认整个程序文件的全部代码后,可以直接运行整个程序文件。在程序文件视窗(Program:first_grogram)下,点击菜单栏中的Run
执行部分代码行。选中已经编写的代码命令行,点击鼠标右键,选择Run Selected。选中已经编写的代码命令行,点击鼠标右键,还可以看到其他一些常用的快捷菜单。
下面所示为EViews程序文件 my_first_program.prg的代码文本,运行该EViews程序文件,将可以完全地、自动地再现第一章中“宏观经济发展案例”主要分析步骤,包括:
my_first_program.prg的代码文本,运行该EViews程序文件,将可以完全地、自动地再现第一章中“宏观经济发展案例”主要分析步骤,包括:
(1)创建工作文件。(工作文件名=development,子页命名=gdp)(效果与 小节 1.7.2.2 相同)
(2)导入外部数据。(效果与 小节 1.7.2.3 相同)
(3)构造组(Group)对象 group_vars。(效果与 小节 1.7.4.3 相同)
group_vars。(效果与 小节 1.7.4.3 相同)
(4)得到描述性分析的表格(Table)对象 tab_descriptive。(效果与 小节 1.7.4.3 相同)
tab_descriptive。(效果与 小节 1.7.4.3 相同)
(5)得到堆栈多线图(Line-Symbol)的图形对象 graph_line。(效果与 小节 1.7.4.3 相同)
graph_line。(效果与 小节 1.7.4.3 相同)
(6)进行双对数线性回归模型分析,得到方程(Equation)对象 eq_main。(效果与 小节 1.7.5 相同)
eq_main。(效果与 小节 1.7.5 相同)
(7)提取出双对数回归方程中的判定系数\(R^2\)和调整判定系数\(\bar{R}^2\),并将这两个数值分别存放在一个向量(Vector)对象 vec_fitness中。(效果与 小节 1.8.1.1 相同)
vec_fitness中。(效果与 小节 1.8.1.1 相同)
(8)计算得到给定显著性水平\(\alpha=0.05\),且自由度为\(f=125\)时,理论查表t值\(t_{1-\alpha/2}(f)=t_{0.975}(125)\),并将这个计算值存放到一个标量(Scalar)对象 t_value中。(效果与 小节 1.8.1.1 相同)
t_value中。(效果与 小节 1.8.1.1 相同)
'=================================================================================
'说明:以下为EViews编程文件my_first_program.prg的代码
' 将展示第一章中“宏观经济发展案例”主要分析步骤的“批量式命令驱动”实现方法:
' 其中符号'起头的行为注释行,其他为EViews命令行。
'=================================================================================
'[命令行1]:创建工作文件(工作文件名=development,子页命名=gdp)。
' 其中数据为季度数据,起始于1980年1季度,结束于2012年1季度。
wfcreate(wf=development,page=gdp) q 1980/1 2012/1
'[命令行2]:导入外部数据,路径为d:\economitrics\macro-economic.xlsx。
import d:\economitrics\macro-economic.xlsx
'[命令行3]:构造组对象,名为group_vars,由序列gdp; pce; investment; government构成。
group group_vars gdp pce investment government
'[命令行4]:得到表格(表格命名为tab_descriptive),
' <--组对象group_vars进行描述性统计分析(Descriptive statistics)。
freeze(tab_descriptive) group_vars.stats
'[命令行5]:进行绘图,图形名为graph_line线图(堆栈图)<--对组对象group_vars
graph graph_line.line(s) group_vars
'[命令行6]:构建方程,给方程命名为eq_main执行线性回归
' 其中,线性方程为 gdp ~ c+ pce+ investment+ government
equation eq_main.ls gdp c pce investment government
'构造向量(含有2个元素),并将向量命名为vec_fitness,其中:
' [命令行7]:向量的第1个元素将用于提取并存放方程eq_main中的判定系数$R^2$
' [命令行8]:向量的第1个元素将用于提取并存放方程eq_main中的调整判定系数$\bar{R}^2$
vector(2) vec_fitness(1)=eq_main.@r2
vec_fitness(2)=eq_main.@rbar2
'[命令行9]:构造标量,标量命名为t_value,
' 利用函数@qtdist(p,f)计算理论t值(a=0.05,f=125)
scalar t_value=@qtdist(0.975,125)
'===================================================================================通过以上EViews程序文件 my_first_program.prg,可以初步对EViews编程语言及命令体系有一个直观的认知,并可以利用数据进行实证练习。当然,里面的很多EViews编程命令与代码,会令初学者不知所以然(尽管只需要修改外部数据文件路径,就能完全再现实验分析结果)。因此,本章后续内容将会帮助梳理和总结EViews编程的命令语法结构,以及常用命令及函数。
my_first_program.prg,可以初步对EViews编程语言及命令体系有一个直观的认知,并可以利用数据进行实证练习。当然,里面的很多EViews编程命令与代码,会令初学者不知所以然(尽管只需要修改外部数据文件路径,就能完全再现实验分析结果)。因此,本章后续内容将会帮助梳理和总结EViews编程的命令语法结构,以及常用命令及函数。
1.8.2 命令语法结构
实际上EViews编程语言源自于一种比较古老的编程语言,最早于1965年由Robert Hall开发而成。EViews编程语言有其自身的体系性和逻辑性。如果具备一定的编程基础,可以很快掌握基本的EViews编程技巧。总体来看,学习EViews编程语言需要把握如下几个基本原则:
(1)Eviews编程的“前台”是各种EViews工作文件对象(workfile object,见 小节 1.7.3.1 ),这些都是在“前台”——工作文件视窗下——“可见的”。
这些EViews工作文件对象(workfile object)包括:序列(Series)对象
 、方程(Equation)对象
、方程(Equation)对象 、表格(Table)对象
、表格(Table)对象 、图形(Graph)对象
、图形(Graph)对象 、标量(Scalar)对象
、标量(Scalar)对象 等
等大部分Eviews编程代码都会直接作用于或指向这些EViews工作文件对象(workfile object)
Eviews编程代码直接产生的各种EViews工作文件对象,也往往就是数据分析的直接成果,将用于报告撰写,也是数据分析的最重要目标之一。
(2)Eviews编程的“后台”是命令视窗或者编程文件.prg ,所有EViews命令代码在这里被编写、管理和运行。
,所有EViews命令代码在这里被编写、管理和运行。
其中的一些EViews命令代码,可能只是辅助性地帮助实现前台的结果——这些命令代码本身并不会直接“可见的”,也即不会直接作用或直接指向“EViews工作文件对象”。
EViews开发有一系列编程变量(programming variables),它们大多只是在“后台”发挥桥梁或表征作用,从不直接在“前台”现身。
编程变量(programming variables)示例:
控制变量(control variables),用以代表数值型的变量,用感叹号!做前缀表达。例如,编写并运行命令
!x=7,表示生成一个数值型变量x,其值为7。然而即便运行此命令行,在工作文件视窗下,也不会产生任何EViews工作文件对象——但控制变量x确确实实是隐身在后台,并可以发挥作用的!字符变量(string variables),用以代表字符型的变量,用百分号%做前缀表达。例如,编写并运行命令
%model="gdp~ c + investment + pce + government",表示生成一个字符型变量model,其值为"gdp~ c + investment + pce + government"。同理,即便运行此命令行,在工作文件视窗下,也不会产生任何EViews工作文件对象——也即字符变量model是隐身在后台发挥作用的!
(3)作为初级或中级Eviews编程学习者,应该重点关注数据分析目标的实现而不是程序运行效率的提高。也就是说:
紧密围绕“可见的”工作文件对象(object)进行EViews代码编程,直接得到可见的分析结果
为了提高编程代码的运行效率,或者为了改善编程代码的简洁性(很多编程者都会被认为有“代码洁癖”倾向),或者为了数据分析的代码可重复性使用,诸如此类目标的实现往往都需要对代码进行“费尽心机”的后台安排和管理。如果这些目标并不那么重要,这些“令人尊敬”的编程努力也就完全有理由可以暂时放弃。
因此,假定Eviews编程学习者关注的重点是数据分析目标的实现,下面将展示EViews编程语言中基于对象(object)的一种标准语法结构(注意空格的使用):
action(action_opt) object_name.view_or_proc(options_list)该语法结构的大意是:将会执行一项动作(action),这项动作的执行必须按照若干标准(action_opt),这项动作将会施加在一个对象(名为object_name)的某种可执行状态上(view_or_proc),对象上的这种可执行状态可以是对象的视图(view)或者程序(proc),并且可能会要求提供这种状态下的具体要求(options_list),而这种状态(view_or_proc)的出现或执行也需要具体的参数条件。其中:
(1)action表示动作(action Commands)命令,包括:
show表示显示结果
do表示执行指定程序
freeze表示从对象视窗中生成表格或图形
print表示打印对象视窗
(2)action_opt表示动作(action Commands)命令的各种选项设置(options)
(3)object_name表示EViews的对象名(object name),例如: - 名为eq_main的方程对象 eq_main - 名为gdp的序列对象
eq_main - 名为gdp的序列对象 gdp - 名为graph_line的图形对象
gdp - 名为graph_line的图形对象 graph_line
graph_line
(4)view_or_proc表示对象可用于执行的视窗或程序命令(View and Procedure Commands)。对于不同的对象(object),其可用于执行的视窗或程序命令,都不尽相同。例如,序列(Series)对象 ser01可用于执行的视窗(View)命令包括:
ser01可用于执行的视窗(View)命令包括:
显示为表单和描述性统计,分别是:ser01.sheet;ser01.stats
显示为图形,包括:ser01.line;ser01.bar;ser01.hist
显示为表单,包括:ser01.freq;ser01.correl;ser01.lrvar;ser01.uroot;ser01.vratio 2 4 8;ser01.bdstest;\(\cdots\)
\(\cdots\)
(5)(options_list)表示对象可用于执行视窗或程序命令(View and Procedure Commands)的各种选项设置(options)
(6)arg_list表示视窗或程序命令下的语法参数(arguments)
- 例如,方程对象
 eq_main的线性回归程序表达为
eq_main的线性回归程序表达为eq_main.ls,就需要提供线性回归方程参数:gdp c investment pce government,也即方程\(gdp=\hat{\beta_1}+\hat{\beta_2}investment+\hat{\beta_3}pce+\hat{\beta_4}government+e_i\)
下面将展示3条典型的EViews编程命令行,它们的语法结构类似,但运行结果则迥然不同:
'说明:以下三个EViews命令行,将简要展示EViews编程的语法结构及其特征。
' 其中,符号'起头的行,为注释行,其他为EViews命令行。
' ===========================================================================
' 命令行1:生成线性回归方程对象eq_main01
equation eq_main01.ls gdp c investment pce government
' 命令行2:生成并打开线性回归方程对象eq_main02
show eq_main02.ls gdp c investment pce government
' 命令行3:生成线性回归方程对象eq_main03,并将回归报告保存为表格对象tab_output
freeze(tab_output) eq_main03.ls gdp c investment pce government
' ===========================================================================以上3条EViews编程命令行的具体解读如下:
命令行1解读:将生成线性回归方程对象 eq_main01
eq_main01
equation表示声明(declare)一个方程对象
eq_main01表示对象名(object_name).ls表示对方程对象执行一个叫ls(也即线性回归分析)的程序(proc)gdp c investment pce government表示执行ls(也即线性回归分析)程序(proc)需要调用的参数(此处为设定回归方程)
命令行2解读:将生成并打开线性回归方程对象 eq_main02
eq_main02
show表示执行一个名为show(也即展示结果)的动作(action)eq_main02表示对象名(object_name).ls表示对方程对象执行一个叫ls(也即线性回归分析)的程序(proc)gdp c investment pce government表示执行ls(也即线性回归分析)程序(proc)需要调用的参数(此处为设定回归方程)
命令行3解读:将生成线性回归方程对象 eq_main03,并将回归报告保存为表格对象
eq_main03,并将回归报告保存为表格对象 tab_output
tab_output
freeze(tab_output)表示执行一个名为freeze(此处为保存表格)的动作(action);括号内的tab_output为执行该动作的选项设置(action_opt),此处表示保存的表格命名为tab_outputeq_main03表示对象名(object_name).ls表示对方程对象执行一个叫ls(也即线性回归分析)的程序(proc)gdp c investment pce government表示执行ls(也即线性回归分析)程序(proc)需要调用的参数(此处为设定回归方程)
总体而言,以上演示只是一种常用的典型语法结构,是基于对象(object)进行操作。实际上,EViews编程语法结构有多种多样,有的是标准化语法结构,有的是简化语法结构,还有更多的约定式语法结构,深入掌握的话需要进行大量记忆,或者查看EViews官方的命令参考书(IHS 2017)。无论如何,围绕对象(object)进行EViews编程是一条切实有效的学习途径,而EViews官方在线帮助文档4提供了全面的对象参考(object reference),并分类列出了全部的相关命令,对EViews编程很有帮助:
对象的声明(Declaration)
对象的方法(Methods)
对象的视窗(Views)
对象的可执行程序(Procs)
对象的可返回数据(Data Members)
1.8.3 常用命令及函数
本书后续章节相关部分还将涉及EViews编程的初级或中级技能。为了便于后续内容的学习,本书总结和梳理了常用的EViews函数命令(见 表 1.9 ),可以更好地配合EViews代码编写和运行,帮助完成计量经济学实证分析任务。
| 序号 | 分类 | 函数命令 | 作用 | 说明 |
|---|---|---|---|---|
| 1 | 运算符 | + |
加 | |
| 2 | 运算符 | - |
减 | |
| 3 | 运算符 | * |
乘 | |
| 4 | 运算符 | / |
除 | |
| 5 | 运算符 | ^ |
幂次 | |
| 6 | 运算符 | = |
等于 | |
| 7 | 常数 | @pi |
圆周率\(\pi\) | \(3.14159 \cdots\) |
| 8 | 基础数学函数 | @abs(x) |
绝对值 | \(\mid{X}\mid\) |
| 9 | 基础数学函数 | @exp(x) |
自然数e的幂次 | \(e^X\) |
| 10 | 基础数学函数 | @inv(x) |
倒数 | \(1/X\) |
| 11 | 基础数学函数 | @log(x) |
自然对数 | \(log_e(X)\) |
| 12 | 基础数学函数 | @log10(x) |
10为底的对数 | \(log_{10}(X)\) |
| 13 | 基础数学函数 | @recode() |
重新编码 | |
| 14 | 基础数学函数 | @round(x) |
取整 | |
| 15 | 基础数学函数 | @sqrt(x) |
平方根 | \(\sqrt{X}\) |
| 16 | 时间序列函数 | @d(x) |
一阶差分 | \(\Delta\) |
| 17 | 时间序列函数 | @lag(x,n) |
n阶滞后 | \(X_{t-n}\) |
| 18 | 时间序列函数 | @trend() |
构造趋势序列 | \({0,1,2,\cdots}\) |
| 19 | 描述性统计函数 | @cor(x,y) |
相关系数 | \(r\) |
| 20 | 描述性统计函数 | @cov(x,y) |
协方差 | \(Cov(X,Y)\) |
| 21 | 描述性统计函数 | @gmean(x) |
几何平均数 | \(\bar{X}_G\) |
| 22 | 描述性统计函数 | @hmean(x) |
调和平均数 | \(\bar{X}_H\) |
| 23 | 描述性统计函数 | @max(x) |
极大值 | Max |
| 24 | 描述性统计函数 | @mean(x) |
简单平均数 | \(\bar{X}\) |
| 25 | 描述性统计函数 | @median(x) |
中位数 | \(M_e\) |
| 26 | 描述性统计函数 | @min(x) |
极小值 | Min |
| 27 | 描述性统计函数 | @obs(x) |
样本数 | \(n\) |
| 28 | 描述性统计函数 | @quantile(x,q) |
分位数 | \(Q_1; Q_3\) |
| 29 | 描述性统计函数 | @skew(x) |
偏度 | |
| 30 | 描述性统计函数 | @stdev(x) |
标准差 | \(S\) |
| 31 | 描述性统计函数 | @sum(x) |
求和 | \(\sum{X_i}\) |
| 32 | 描述性统计函数 | @sumsq(x) |
平方和 | \(\sum{X_i^2}\) |
| 33 | 描述性统计函数 | @var(x) |
方差 | \(S^2\) |
| 34 | 密度;概率函数 | @cchisq(x,f) |
累积卡方分布函数 | \(G_{\chi^2}(X,f)\) |
| 35 | 密度;概率函数 | @dchisq(x,f) |
卡方分布的密度函数 | \(g_{\chi^2}(X,f)\) |
| 36 | 密度;概率函数 | @qchisq(p,f) |
卡方值 | 右侧大值\(\chi^2_{(1-\alpha)}(p,f)\) |
| 37 | 密度;概率函数 | @cfdist(x,f1,f2) |
累积F分布函数 | \(G_{F}(X,f1,f2)\) |
| 38 | 密度;概率函数 | @dfdist(x,f1,f2) |
F分布的密度函数 | \(g_{F}(X,f1,f2)\) |
| 39 | 密度;概率函数 | @qfdist(p,f1,f2) |
F值 | 右侧大值\(F_{(1-\alpha)}(p,f1,f2)\) |
| 40 | 密度;概率函数 | @ctdist(x,f) |
累积t分布函数 | \(G_{t}(X,f)\) |
| 41 | 密度;概率函数 | @dtdist(x,f) |
t分布的密度函数 | \(g_{t}(X,f)\) |
| 42 | 密度;概率函数 | @qtdist(p,f) |
t值 | 右侧正值\(t_{(1-\alpha/2)}(p,f)\) |
| 43 | 密度;概率函数 | @cnorm(x) |
累积t分布函数 | \(G_{N}(X)\) |
| 44 | 密度;概率函数 | @dnorm(x) |
t分布的密度函数 | \(g_{N}(X)\) |
| 45 | 密度;概率函数 | @qnorm(p) |
t值 | 右侧正值\(N_{(1-\alpha/2)}(p)\) |
| 46 | 特定表达式 | ar |
自回归误差设置项 | p阶自回归\(AR(p)\) |
| 47 | 特定表达式 | ma |
移动平均误差设置项 | q阶移动平均\(MA(q)\) |
| 48 | 特定表达式 | @expand |
自动产生的虚拟变量 | \(Edu_{D1};Edu_{D2};\cdots\) |
| 49 | 矩阵函数 | @ones(n,k) |
生成元素全为1的\(n*k\)维矩阵 | \(\mathbf{1}_{n,k}\) |
| 50 | 矩阵函数 | @identity(n,n) |
生成\(n*n\)维单位矩阵 | \(\mathbf{I}_{n,n}\) |
| 51 | 矩阵函数 | @transpose(X) |
对矩阵\(\mathbf{X}\)进行转置 | \(\mathbf{X'}\) |
| 52 | 矩阵函数 | @det(X) |
得到方阵\(\mathbf{X}\)的行列式 | \(\mathbf{\mid{X}\mid}\) |
| 53 | 矩阵函数 | @eigenvalues(X) |
得到对称矩阵的特征值向量 | |
| 54 | 矩阵函数 | @inverse(X) |
对方阵\(\mathbf{X}\)求逆 | \(\mathbf{X}^{-1}\) |
| 55 | 矩阵函数 | @ediv(X,Y) |
两个矩阵对应元素点除 | \(X_{ij}/Y_{ij}\) |
| 56 | 矩阵函数 | @getmaindiagonal(X) |
得到矩阵\(\mathbf{X}\)的主对角线元素(向量) |
参阅IHS官方网站:http://www.eviews.com/general/about_us.html↩︎
需要注意的是,目前EViews1-6将不再兼容Windows 10操作系统↩︎
可以参考在线帮助文档Object View And Procedure Reference↩︎
http://www.eviews.com/help/helpintro.html#page/content%2Fcobjpreface.html%23↩︎