| obs | Y | X2 | X3 | X4 | X5 |
|---|---|---|---|---|---|
| 1 | 65 | 96 | 49 | 89 | 18 |
| 2 | 56 | 97 | 55 | 92 | 20 |
| 3 | 56 | 97 | 55 | 92 | 20 |
| 4 | 49 | 105 | 70 | 92 | 20 |
| 5 | 46 | 96 | 53 | 92 | 20 |
| 77 | 18 | 165 | 322 | 50 | 45 |
| 78 | 17 | 140 | 238 | 115 | 45 |
| 79 | 17 | 147 | 263 | 50 | 45 |
| 80 | 17 | 157 | 295 | 119 | 45 |
| 81 | 13 | 130 | 236 | 107 | 55 |
6 异方差问题
6.1 实验目的及要求
目的:掌握异方差问题的检验与处理方法。
要求:在老师指导下完成计量经济模型的异方差检验,并对存在异方差的模型进行修正,最终得到正确的分析结果。
6.2 实验原理
对于不同的样本点,随机误差项的方差不再是常数,则认为模型出现了异方差问题。
异方差的实质表现为随机误差项的方差随着解释变量(引起异方差的解释变量)观测值的变化而变化。
对于出现异方差的原模型主要采用校正其异方差,再对校正后的模型采用普通最小二乘法估计。
6.2.1 什么是模型异方差问题?
对于模型
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{6.1}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{6.2}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\beta}+\mathbf{u} && \text{(PRM-matrix)} \end{aligned} \tag{6.3}\]
\[ \begin{aligned} \mathbf{y} &= \mathbf{X}\mathbf{\hat{\beta}}+\mathbf{e} && \text{(SRM-matrix)} \end{aligned} \tag{6.4}\]
在正态经典线性回归模型假设(N-CLRM)下,随机干扰项\(u_i\)假设为同方差:
\[ \begin{aligned} var-cov(\mathbf{u})&=E(\mathbf{uu'})\\ &= \begin{bmatrix} E(u_1^2) & E(u_1u_2) &\cdots &E(u_1u_n)\\ E(u_2u_1) & E(u_2^2) &\cdots &E(u_2u_n)\\ \vdots & \vdots &\vdots &\vdots \\ E(u_nu_1) &E(u_nu_2) &\cdots &E(u_n^2)\\ \end{bmatrix} \\ &= \begin{bmatrix} \sigma_1^2 & \sigma_{12}^2 &\cdots &\sigma_{1n}^2\\ \sigma_{21}^2 & \sigma_2^2 &\cdots &\sigma_{2n}^2\\ \vdots & \vdots &\vdots &\vdots \\ \sigma_{n1}^2 & \sigma_{n2}^2 &\cdots &\sigma_n^2\\ \end{bmatrix} \\ &=\sigma^2 \begin{bmatrix} 1 & 0 &\cdots &0\\ 0 & 1 &\cdots &0\\ \vdots & \vdots &\vdots &\vdots \\ 0 & 0 &\cdots &1\\ \end{bmatrix}\\ &=\sigma^2\mathbf{I} \end{aligned} \]
定义 6.1 (异方差) 如果回归模型不再满足N-CLRM假设中关于随机干扰项是同方差的条件,那么我们称模型存在异方差(heteroskedasticity)问题。正式地,对于回归模型 式 6.1 ,如果随机干扰项\(u_i\)表现为:
\[ \begin{aligned} var-cov(\mathbf{u})&=E(\mathbf{uu'})\\ &= \begin{bmatrix} E(u_1^2) & E(u_1u_2) &\cdots &E(u_1u_n)\\ E(u_2u_1) & E(u_2^2) &\cdots &E(u_2u_n)\\ \vdots & \vdots &\vdots &\vdots \\ E(u_nu_1) &E(u_nu_2) &\cdots &E(u_n^2)\\ \end{bmatrix} && \leftarrow (E{(u_i)}\equiv 0)\\ &= \begin{bmatrix} \sigma_1^2 & \sigma_{12}^2 &\cdots &\sigma_{1n}^2\\ \sigma_{21}^2 & \sigma_2^2 &\cdots &\sigma_{2n}^2\\ \vdots & \vdots &\vdots &\vdots \\ \sigma_{n1}^2 & \sigma_{n2}^2 &\cdots &\sigma_n^2\\ \end{bmatrix} && \leftarrow (var{(u_i)} \equiv \sigma_i^2;cov(u_i,u_j)\equiv\sigma_{ij}^2,i\neq j)\\ &= \begin{bmatrix} \sigma_1^2 & 0 &\cdots &0\\ 0 & \sigma_2^2 &\cdots &0\\ \vdots & \vdots &\vdots &\vdots \\ 0 & 0 &\cdots &\sigma_n^2\\ \end{bmatrix} && \leftarrow (cov{(u_i,u_j)}\equiv 0,i \neq j)\\ \end{aligned} \]
则称回归模型 式 6.1 存在异方差问题。
异方差问题的来源很多,包括但不限于:
回归模型的设定偏误,比如忽略了重要的解释变量
数据采集技术的不同和发展
样本数据异常值(outliers)的出现
截面数据往往更容易出现异方差问题
一个或多个回归元的分布呈偏态(skewness)
值得注意的是:
为了分析的简单和方便,上述定义中随机干扰项\(u_i\)表现为异方差(\(var(u_i)=\sigma^2_i\)),但仍旧保证均值为0(\(E(u_i)=0\)),协方差为0(\(cov(u_i,u_j)=0,i \neq j\))
同方差是一种理想化情形(\(var(u_i)=\sigma^2\)),但异方差(\(var(u_i)=\sigma^2_i\))则是更为普遍的存在,而且异方差的具体表现形式有多种多样!
只要出现了任何一种异方差(\(var(u_i)=\sigma^2_i\))形式,都认为模型 式 6.1 存在异方差问题!
其他假定不变,同方差性假定不成立时,OLS估计量通常不再是最优线性无偏估计量(BLUE)。此时,OLS估计量仍然是线性的和无偏的(因这两条性质都与方差无关),但是,不再是“最优的”或“有效的”,也即还是线性无偏估计量(LUE)。
6.2.2 如何诊断模型异方差问题?
异方差诊断是下一步模型矫正的基础,诊断工作的要点有:
(1)根据异方差定义 定义 6.1 ,异方差问题刻画的是总体回归模型 式 6.1 中随机干扰项\(u_i\)的方差为异方差。然而总体回归模型 式 6.1 中随机干扰项\(u_i\)的行为不能直接观测得到,我们只好间接观测对应样本回归模型 式 6.2 中残差\(e_i\),通过观察残差\(e_i\)的表现来间接认识随机干扰项\(u_i\)的特征。因此,下面的异方差问题诊断方法,始终围绕样本回归模型中残差\(e_i\)的表现特征来展开。
(2)异方差问题在理论上可以有很多种形式1,因此在诊断之前我们只能先猜测模型可能有哪一种(或哪几种)异方差形式。而且不同的异方差诊断工具只能识别特定的异方差形式,所以实践操作中可能需要尝试多种诊断工具。一旦诊断出有任何一种(或多种)异方差模式,我们都认为模型 定义 6.1 存在异方差问题。
(3)诊断工作不仅仅只是诊断得到是否存在异方差问题的结论,而且往往还需要诊断出属于哪一种异方差形式,因为后面的异方差问题的模型矫正中(如WLS矫正法)还需要利用这一有价值的信息!
6.2.3 图形识别检验法
通过观察残差\(e_i\)的表现来间接认识随机干扰项\(u_i\)的特征,最直观的是观察残差\(e_i\)的图形模式:
(1)残差描点图(dot plot)
残差\(e_i\)的描点图(dot plot)
标准化残差\(e_i^{\ast}=\frac{e_i}{S_{e_i}}\)的描点图(dot plot)
\(e_i^2\)的描点图(dot plot)
(2)残差散点图(scatter plot)
\(e_i^2\)与\(Y_i\)的散点图(scatter plot)
\(e_i^2\)与\(Y_i^2\)的散点图(scatter plot)
\(e_i^2\)分别与\((X_{2i},X_{3i},\cdots,X_{ki})\)的散点图(scatter plot)
\(e_i^2\)分别与\((X_{2i}^2,X_{3i}^2,\cdots,X_{ki}^2)\)的散点图(scatter plot)
图形识别检验法的判断准则是,一旦发现存在我们所知的系统模式,则认为模型很可能存在异方差问题。例如:
残差\(e_i^2\)的描点图(dot plot),如果表现为线性增加的图形模式,则表明随机干扰项的方差单调增加。
\(e_i^2\)与\(Y_i\)的散点图(scatter plot),如果表现为近似直线模式,则表明随机干扰项的方差单调增加。
\(e_i^2\)与\(X_{3i}^2\)的散点图(scatter plot),如果表现为近似下开口抛物线模式,则表明随机干扰项的方差先增加,后减小
\(\cdots\)
6.2.4 正式检验方法:Park检验法
Park检验方法针对的异方差情形是:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{6.5}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{6.6}\]
\[ \begin{aligned} var(u_i)&\equiv \sigma^2_i=e^{(\mathbf{Z_t'\alpha})} && \text{(type-Park)} \end{aligned} \tag{6.7}\]
其中,\(e\)表示自然底数,也即e=2.71828182845905,\(\mathbf{\alpha}\)表示参数,\(\mathbf{Z_t}\)表示由独立变量组成的向量,一般由主回归方程的回归元组成,但又不是必须由它们组成。
Park检验方法的基本步骤是:
(1)先对样本回归模型 式 6.6 进行回归分析,得到残差序列\(e_i\)和\(e_i^2\)
(2)再对辅助回归模型 式 6.8 进行回归分析
\[ \begin{aligned} ln(e^2_i)&=\hat{\alpha}_1+\hat{\alpha}_2ln(X_{2i})+\cdots+\hat{\alpha}_kln(X_{ki})+v_i && \text{(Auxiliary-Park)} \end{aligned} \tag{6.8}\]
(3)根据辅助回归方程结果得到异方差诊断结论
6.2.5 正式检验方法:Glejser检验法
Glejser检验方法针对的异方差情形是:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{6.9}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{6.10}\]
\[ \begin{aligned} \begin{split} var(u_i)&\equiv \sigma^2_i \\ \sigma^2_i&={(\sigma^2+\mathbf{Z_t'\alpha})}^{\gamma}\\ \gamma &=1,2 \end{split} && \text{(type-Glejser)} \\ \end{aligned} \tag{6.11}\]
其中,\(\mathbf{\alpha}\)表示参数,\(\mathbf{Z_t}\)表示由独立变量组成的向量,一般由主回归方程的回归元组成,但又不是必须由它们组成。
Glejser检验方法的基本步骤是:
(1)先对样本回归模型 式 6.10 进行回归分析,得到残差序列\(e_i\)和\(|e_i|\)
(2)再对如下多种形式的辅助回归模型 式 6.8 进行回归分析2
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_mX_{mi}+v_i &&\text{(Glejser1)} \end{aligned} \tag{6.12}\]
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\sqrt{X_{2i}}+\cdots+\hat{\alpha}_m\sqrt{X_{mi}}+v_i &&\text{(Glejser2)} \end{aligned} \tag{6.13}\]
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\frac{1}{X_{2i}}+\cdots+\hat{\alpha}_m\frac{1}{X_{mi}}+v_i &&\text{(Glejser3)} \end{aligned} \tag{6.14}\]
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\frac{1}{\sqrt{X_{2i}}}+\cdots+\hat{\alpha}_m\frac{1}{\sqrt{X_{mi}}}+v_i &&\text{(Glejser4)} \end{aligned} \tag{6.15}\]
\[ \begin{aligned} |e_i| & =\sqrt{\hat{\alpha}_1+\hat{\alpha}_2{X_{2i}}+\cdots+\hat{\alpha}_m{X_{mi}}}+v_i &&\text{(Glejser5)} \end{aligned} \tag{6.16}\]
\[ \begin{aligned} |e_i| & =\sqrt{\hat{\alpha}_1+\hat{\alpha}_2{X_{2i}^2}+\cdots+\hat{\alpha}_m{X_{mi}^2}}+v_i &&\text{(Glejser6)} \end{aligned} \tag{6.17}\]
(3)根据辅助回归方程结果得到异方差诊断结论
6.2.6 正式检验方法:BPG检验法
BPG检验方法针对的异方差情形是:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{6.18}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{6.19}\]
\[ \begin{aligned} \begin{split} var(u_i)&\equiv \sigma^2_i\\ &=\sigma^2\cdot f(\mathbf{Z_t'\alpha})\\ &=\sigma^2\cdot{f\left(\alpha_1+\alpha_2X_{2i} +\cdots+\alpha_mX_{mi}\right)} \end{split} && \text{(type-BPG)} \\ \end{aligned} \tag{6.20}\]
其中,\(f(\cdot)\)表示函数,\(\mathbf{\alpha}\)表示参数,\(\mathbf{Z_t}\)表示由独立变量组成的向量,一般由主回归方程的回归元组成,但又不是必须由它们组成,\(m \in (1,k]\)。
BPG检验方法的基本步骤是:
(1)先对样本回归模型 式 6.19 进行回归分析,得到残差序列\(e_i\)和\(e_i^2\)
(2)再对辅助回归模型 式 6.32 进行回归分析
\[ \begin{aligned} e^2_i&=\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_mX_{mi}+v_i && \text{(Auxiliary-BPG)} \end{aligned} \tag{6.21}\]
(3)计算并得到ESS(解释的平方和),进一步定义有
\[ \begin{aligned} {\chi^2}^{\ast}=\frac{ESS^{\ast}}{2} \sim \chi^2(m-1) \end{aligned} \]
(4)根据辅助回归方程结果得到异方差诊断结论
6.2.7 正式检验方法:White检验法
White检验方法针对的异方差情形是:
\[ \begin{aligned} Y_i&=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\cdots+\beta_kX_{ki}+u_i && \text{(PRM)} \end{aligned} \tag{6.22}\]
\[ \begin{aligned} Y_i&=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\cdots+\hat{\beta}_kX_{ki}+e_i && \text{(SRM)} \end{aligned} \tag{6.23}\]
\[ \begin{aligned} \begin{split} var(u_i)&\equiv \sigma^2_i\\ &=\sigma^2\cdot f(\mathbf{Z_t'\alpha})\\ &=\sigma^2\cdot{f\left(X_{pi},X^2_{pi},X_{pi}X_{qi}\right)} \\ &p,q \in (1,k];p \neq q \end{split} && \text{(type-White)} \end{aligned} \tag{6.24}\]
其中,\(f(\cdot)\)表示函数,\(\mathbf{\alpha}\)表示参数,\(\mathbf{Z_t}\)表示由独立变量组成的向量,一般由主回归方程的回归元、平方项或交叉项组成,但又不是必须由它们组成,\(m \in (1,k]\)。
White检验方法的基本步骤是:
(1)先对样本回归模型 式 6.23 进行回归分析,得到残差序列\(e_i\)和\(e_i^2\)
(2)再对如下两种辅助回归模型进行回归分析,其中辅助回归模型 式 6.25 只含有回归元及其平方项,辅助回归模型 式 6.26 则还包含了回归元的交叉项。
\[ \begin{aligned} \begin{split} e^2_i&=\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_mX_{mi}+\hat{\lambda}_2X^2_{2i}+\cdots+\hat{\lambda}_mX^2_{mi}+v_i \end{split} && \text{(square-White)} \end{aligned} \tag{6.25}\]
\[ \begin{aligned} \begin{split} e^2_i&=\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_mX_{mi}+\hat{\lambda}_2X^2_{2i}+\cdots+\hat{\lambda}_mX^2_{mi}\\ &+\hat{\delta}_2X_{2i}X_{3i}+\cdots+\hat{\delta}_pX_{pi}X_{qi}+v_i \\ &p,q \in (1,k];p \neq q \end{split} && \text{(cross-White)} \end{aligned} \tag{6.26}\]
(3)计算并得到辅助回归方程的判定系数\(R^2\)(解释的平方和),进一步定义有
\[ \begin{aligned} n{R^2} \sim \chi^2_{df} \end{aligned} \]
(4)对于辅助回归方程 式 6.25 ,诊断结论为:
辅助回归方程 式 6.25 不包含交叉项,则纯粹用于诊断主模型是否含有异方差问题。
如果辅助回归方程 式 6.25 的\(\chi^2\)检验不显著(对应的概率值P>0.1),则表明主模型 式 6.22 是同方差。
如果辅助回归方程 式 6.25 的\(\chi^2\)检验显著(对应的概率值P<0.1),则表明主模型 式 6.22 是异方差。
(5)对于辅助回归方程 式 6.26 ,诊断结论为:
6.2.8 如何矫正模型异方差问题?
如前所述,如果诊断出任何一种形式的异方差问题,我们都认为模型存在异方差问题。异方差问题较严重的话,则需要对模型进行校正,以尽量缓解异方差问题的影响。矫正模型异方差问题的思路主要有两条:
(1)使用稳健标准误(robust standard errors)来矫正异方差。这里我们将主要采用White (1980)提出的异方差一致性矫正法 (heteroskedasticity consistent covariance)进行模型处理3。
(2)使用加权最小二乘法(WLS)矫正异方差问题。针对异方差问题的不同形式,可以借助权重处理的办法,尽可能地将异方差问题转换成同方差。加权最小二乘法(WLS)的操作,本质上是两阶段最小二乘方法(two-stage least squares)。先对原模型进行权重处理,时期转换为同方差模型,然后再用最小二乘法进行回归估计。
使用加权最小二乘法(WLS)矫正异方差问题,具体操作选择有:
(1)异方差情形:如果方差\(\sigma^2_i\)已知且等于样本方差\(S^2\)
- 广义最小二乘法(WLS)处理:对主模型两边同时除以\(S_i\)
(2)异方差情形:如果方差\(\sigma^2_i\)正比于\(X^2_i\)
- 加权最小二乘法(WLS)处理:对主模型两边同时除以\(X_i\)
(3)异方差情形:如果方差\(\sigma^2_i\)正比于\(X_i\)
- 加权最小二乘法(WLS)处理:对主模型两边同时除以\(\sqrt{X_i}\)
(4)异方差情形:如果方差\(\sigma^2_i\)正比于\(\hat{Y_i}^2\)
- 加权最小二乘法(WLS)处理:对主模型两边同时除以\(\hat{Y_i}\)
(5)异方差情形:如果方差\(\sigma^2_i\)未知
- 加权最小二乘法(WLS)处理:对主模型两边同时取对数\(ln()\)
6.3 实验内容
(1)采用最小二乘法建立主回归模型
(2)侦查模型是否存在异方差问题
非正式检验方法(图形检验法):残差趋势图(dot plot)、残差散点图(scatter plot)
正式检验方法:Park检验法、Glejser检验法、BPG检验法、White检验法
(3)在发现存在异方差的基础上,对原模型进行异方差问题的处理:使用加权最小二乘法校正异方差;使用White校正法解决异方差。
6.4 实验准备
6.4.1 实验软件
本次实验需要提前准备好如下软件:
统计分析软件Eviews 9.0版本及以上
公式编辑软件Mathtype 6.0版本及以上
写作编辑软件Office Word/Excel 2010版本及以上
浏览器软件chrome 66.0版本及以上或360极速浏览器9.5版本及以上
6.4.2 实验材料
汽车油耗: 表 6.1 给出给出了81辆汽车在Y单位油耗的行驶里程数(英里/加仑),X2最高时速(英里/小时),X3发动机马力,X4汽车空间(立方英尺),X5车身重量(百磅)等方面的数据。
变量说明见 表 6.2 :
| variable | label |
|---|---|
| obs | 汽车品牌序号 |
| Y | 单位油耗的行驶里程数(英里/加仑) |
| X2 | 最高时速(英里/小时) |
| X3 | 发动机马力 |
| X4 | 汽车空间(立方英尺) |
| X5 | 车身重量(百磅) |
请考虑如下样本回归模型:
\[ \begin{aligned} Y_i=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\beta_4X_{4i}+\beta_5X_{5i}+e_{i} \end{aligned} \tag{6.27}\]
6.4.3 实验规则
本实验将要求保留Eviews操作过程的相关结果,因此对Eviews对象命名规则设计如下:
(1)方程对象(Equation) 的命名规则:
的命名规则:
主回归方程对象保存命名为
 eq_m0
eq_m0异方差问题WLS矫正后的回归方程,根据具体矫正类型,酌情保存并命名为:
 eq_adj_type1
eq_adj_type1 eq_adj_type2
eq_adj_type2- \(\cdots\)
异方差问题White一致标准误矫正后的回归方程,保存并命名为:
 eq_adj_white
eq_adj_white
(2)序列对象(Series) 的命名规则:
的命名规则:
(主回归方程的)残差序列,保存并命名为
 ei
ei(主回归方程的)残差平方序列,保存并命名为
 ei_sqr
ei_sqr各变量的平方序列,分别保存并命名为:
 Y_sqr
Y_sqr X2_sqr
X2_sqr X3_sqr
X3_sqr X4_sqr
X4_sqr X5_sqr
X5_sqr
(3)图形对象(Graph) 的命名规则:
的命名规则:
残差及残差平方的描点图(dot plot),绘制成一张图,保存并命名为并命名为:
 dot_resid
dot_resid全部变量对残差的散点图(scatter),绘制成一张图,保存并命名为并命名为:
 scatter_ei
scatter_ei
(4)表格对象(Table) 的命名规则:
的命名规则:
异方差的Park检验结果,另存为并命名为:
 tab_park
tab_park异方差的Glejser检验结果(前三类情形),分别另存为并命名为:
 G1
G1 G2
G2 G3
G3
异方差的BPG检验结果,另存为并命名为:
 tab_bpg
tab_bpg异方差的White检验结果,另存为并命名为:
 tab_white
tab_white
6.5 主要实验步骤
6.5.1 导入数据并进行预处理
(1)新建Eviews工作文件(见 图 6.1 )。Eviews菜单操作如下:
依次操作:File\(\Rightarrow\)New\(\Rightarrow\)Workfile
进行workfile create引导设置:
提示:Excel数据,每个同学的Y数据都不同,找到自己学号对应下的Y
具体引导设置如下:
workfile structure type:
unstructured/undatededata range:81
workfile names(optional):
- WF:
car(建议命名) - Page:
mileage(建议命名)
- WF:
(2)Eviews导入数据。菜单操作(Excel和Eviews)如下:
Excel找到数据。Excel表格中仅保留自己需要的数据(obsYX2X3X4X5)
Eviews导入数据。File\(\Rightarrow\)Import\(\Rightarrow\)Import From File:
d:/econometrics/data/Lab6-car.xlsx
6.5.2 采用最小二乘法建立主回归模型
主回归模型为:
\[Y_t=\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+\hat{\beta}_4X_{4i}+\hat{\beta}_5X_{5i}+e_{i}\]
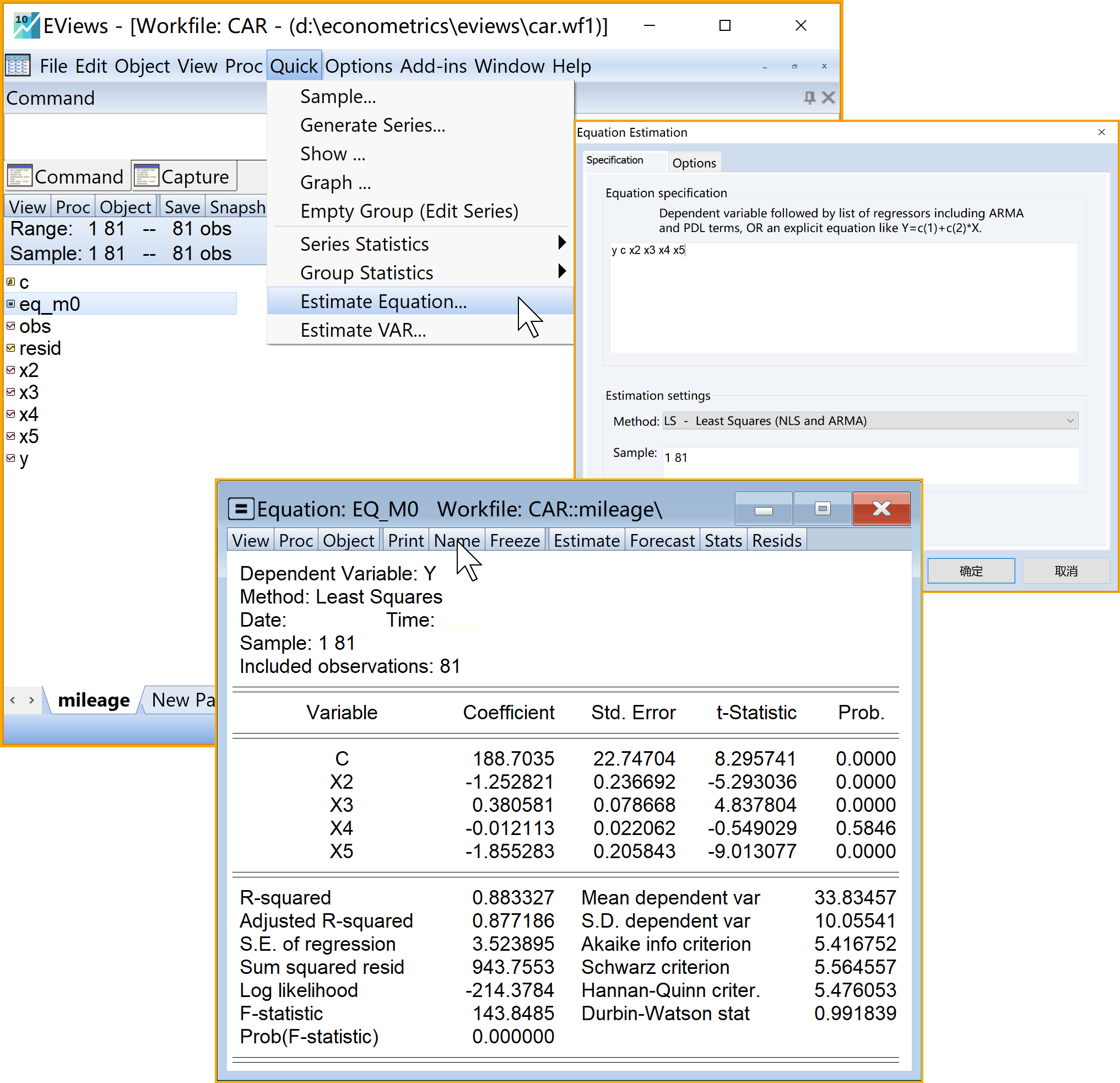
Eviews菜单操作(见 图 6.2 ):
(1)依次选择\(\Rightarrow\)Quick\(\Rightarrow\)Estimation Equation
(2)引导设置Equation Estimation\(\Rightarrow\)specification
Equation specification:输入命令 Y c X2 X3 X4 X5
Estimation settings:
- Method: 下拉选择
LS - Least Squares (NLS and ARMA) - Sample: 默认设置
- Method: 下拉选择
点击
OK
(3)模型命名:建议为eq_m0
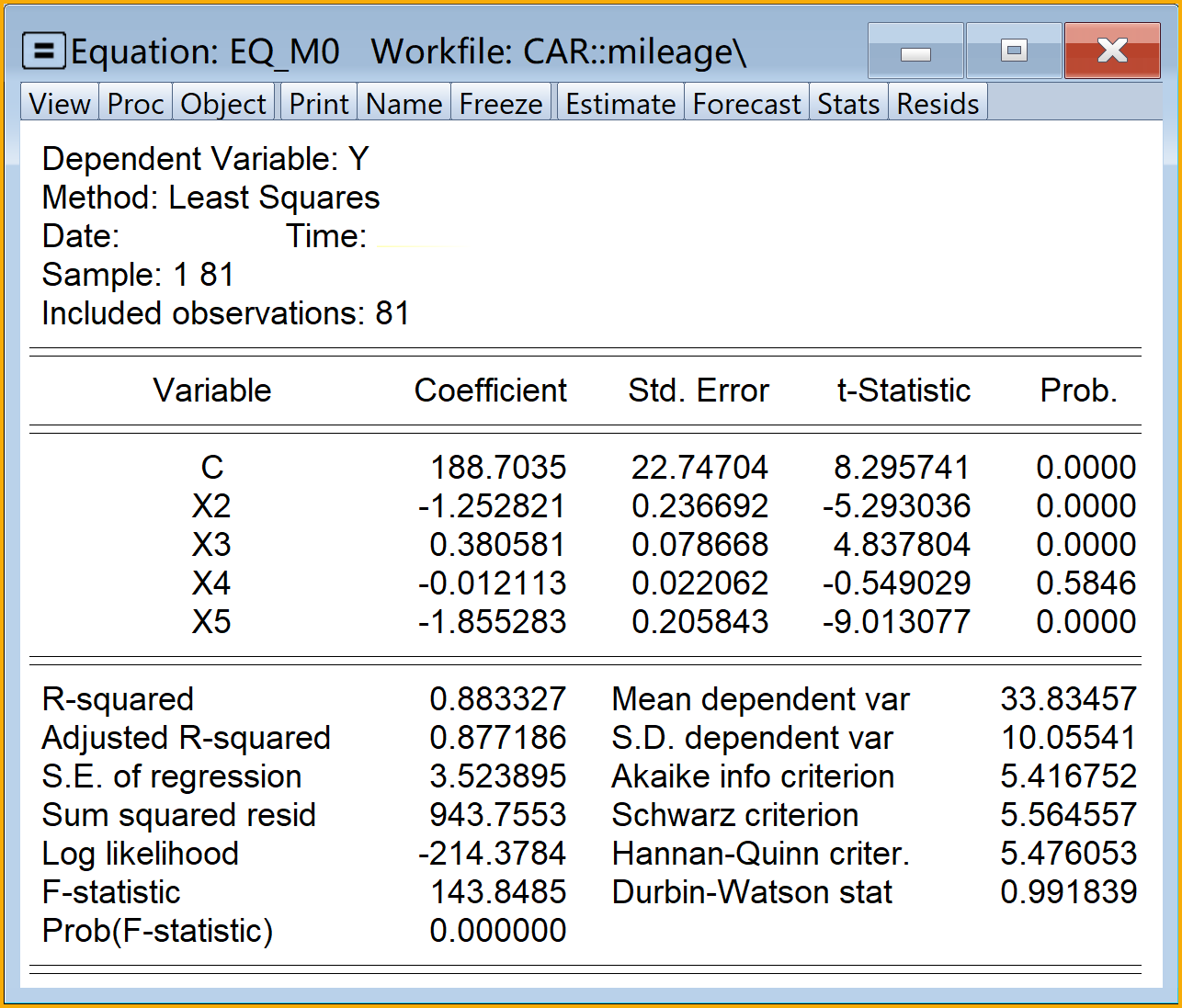
主回归分析结果见 图 6.3 :
6.5.3 侦查模型是否存在异方差
6.5.3.1 初步观察法(观察主回归方程)
目标:观察主回归方程分析报告,分析回归报告结果,得出初步结论
思路:观察\(t^{\ast}\)检验,判定系数\(R^2\),\(F^{\ast}\)检验的关系
提示:模型使用的数据是否是截面数据;主回归分析报告的\(R^2\)值;模型整体\(F^{\ast}\)检验结果;斜率系数的\(t^\ast\)检验结果。
分析结论:根据主回归报告(见 图 6.3 ),表明模型可能存在严重的异方差问题。
6.5.3.2 非正式检验法(图示法)
目标:观察\(e_i\)或\(e^2_i\)的图形模式
思路:判定\(e_i\)或\(e^2_i\)与\(i\)、\(X_i\)、\(X^2_i\)、\(Y_i\)、\(Y^2_i\)等的图形关系
提示:
描点图(dot plot)是分析一个变量的图形模式。例如\(e_i\)或\(e^2_i\)(做纵轴)相对于\(i\)(做横轴)的图形关系
散点图(scatter plot)是分析两个变量之间的图形模式。例如\(e_i\)或\(e^2_i\)(做纵轴),相对于\(X_i\)或\(X^2_i\)或\(Y_i\)或\(Y^2_i\)的图形关系。
Eviews菜单操作:
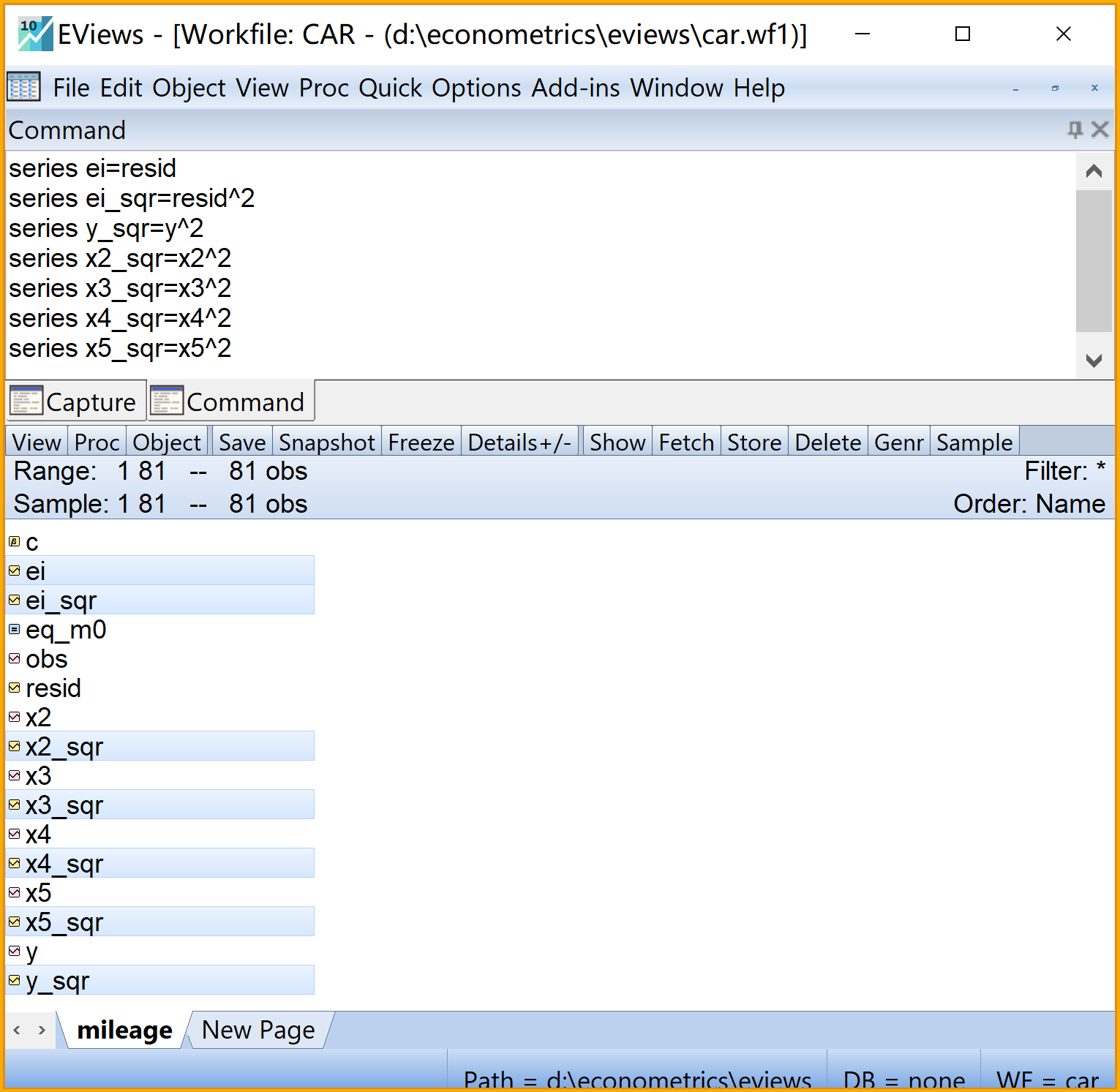
(1)分别生成新序列\(e_i\)、\(e^2_i\)、\(Y^2_i\)和\(X^2_i\)(见 图 6.4 )
生成残差\(e^2_i\)和\(e^2_i\)序列(建议分别命名为ei和ei_sqr)
- 命令视窗(Command)输入命令 :
series ei=resid - 命令视窗(Command)输入命令 :
series ei_sqr=resid^2 - 运行命令:命令行中按Enter键
- 命令视窗(Command)输入命令 :
生成残差\(Y^2_i\)序列(建议命名为Y_sqr)
- 命令视窗(Command)输入命令 :
series Y_sqr=Y^2 - 运行命令:命令行中按Enter键
- 命令视窗(Command)输入命令 :
- 生成残差\(X^2_i\)序列(建议分别命名为X2_sqr,X3_sqr,X4_sqr,X5_sqr)
- 命令视窗(Command)输入命令 :
series X2_sqr=X2^2 - 命令视窗(Command)输入命令 :
series X3_sqr=X3^2 - 命令视窗(Command)输入命令 :
series X4_sqr=X4^2 - 命令视窗(Command)输入命令 :
series X5_sqr=X5^2 - 运行命令:上述命令行中依次按Enter键
- 命令视窗(Command)输入命令 :
查看结果:
- 双击

ei - 双击

ei_sqr - 双击

Y_sqr - 双击

X2_sqr - 双击

X3_sqr - 双击

X4_sqr - 双击

X5_sqr
- 双击
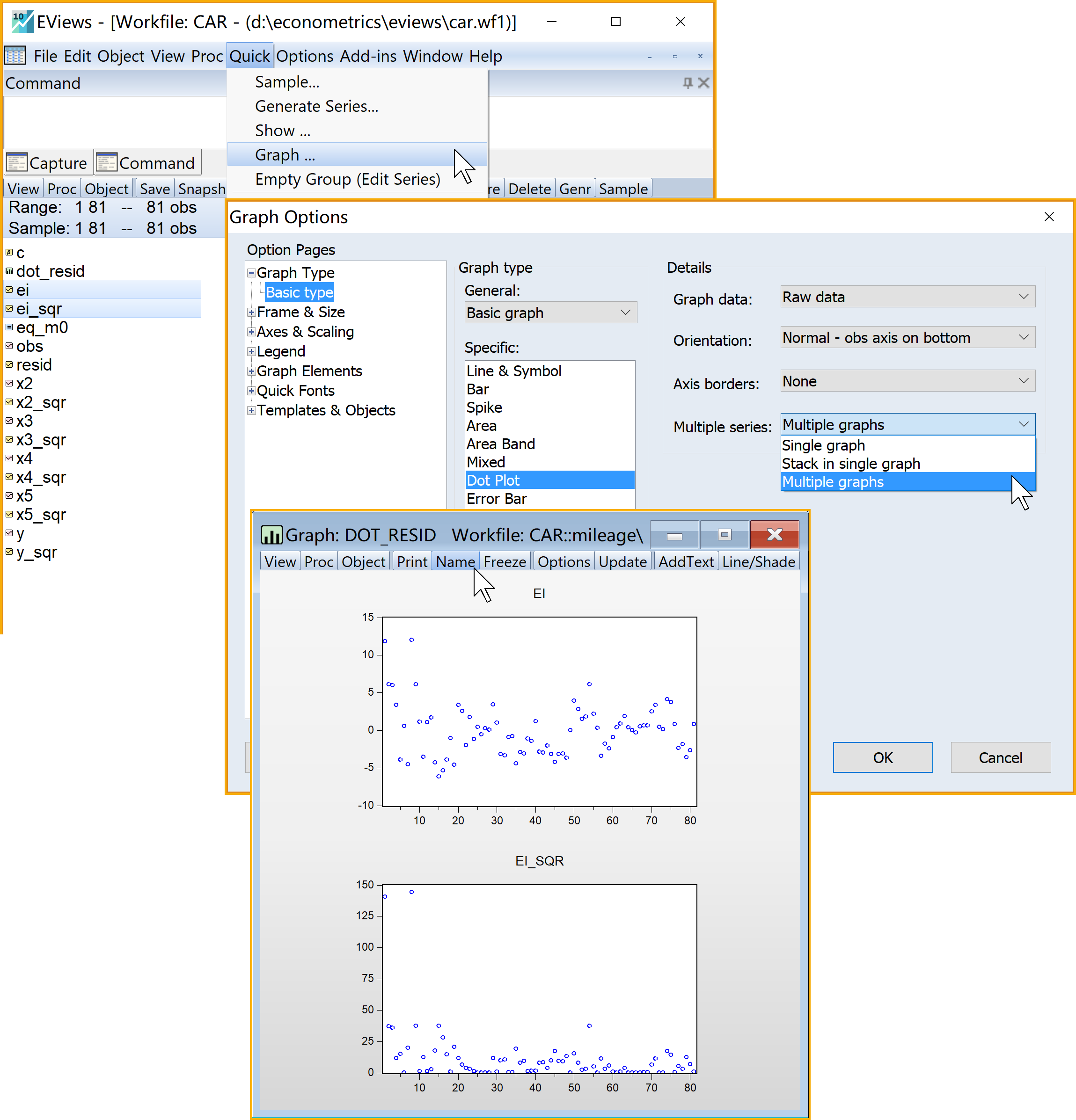
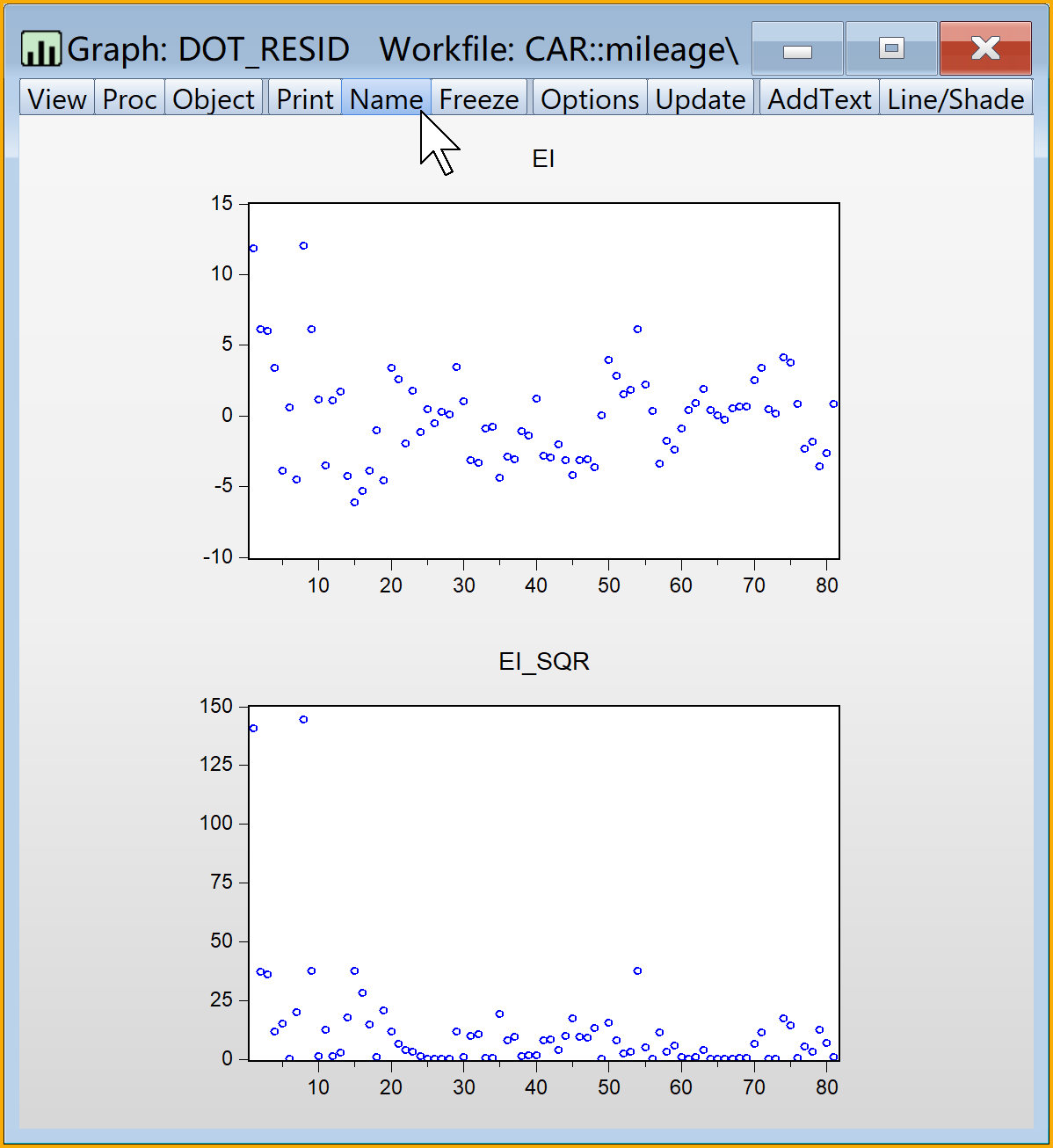
(2)绘制\(e_i\)和\(e^2_i\)序列的描点图(dot plot)(见 图 6.5 )
选择序列对象:键盘Ctrl键+依次单击选择序列

ei和
ei_sqr进入引导菜单:\(\Rightarrow\) Quick \(\Rightarrow\) Graph
- 选择绘图类型(Graph type):Dot plot
- 选择绘图细节(Detail):\(\Rightarrow\) Multiple series \(\Rightarrow\) 下拉选择 Multiple graphs
点击完成:OK
命名并保存绘图(graph)对象
 :建议命名为dot_resid
:建议命名为dot_resid查看结果:双击
 dot_resid(见 图 6.6 )
dot_resid(见 图 6.6 )
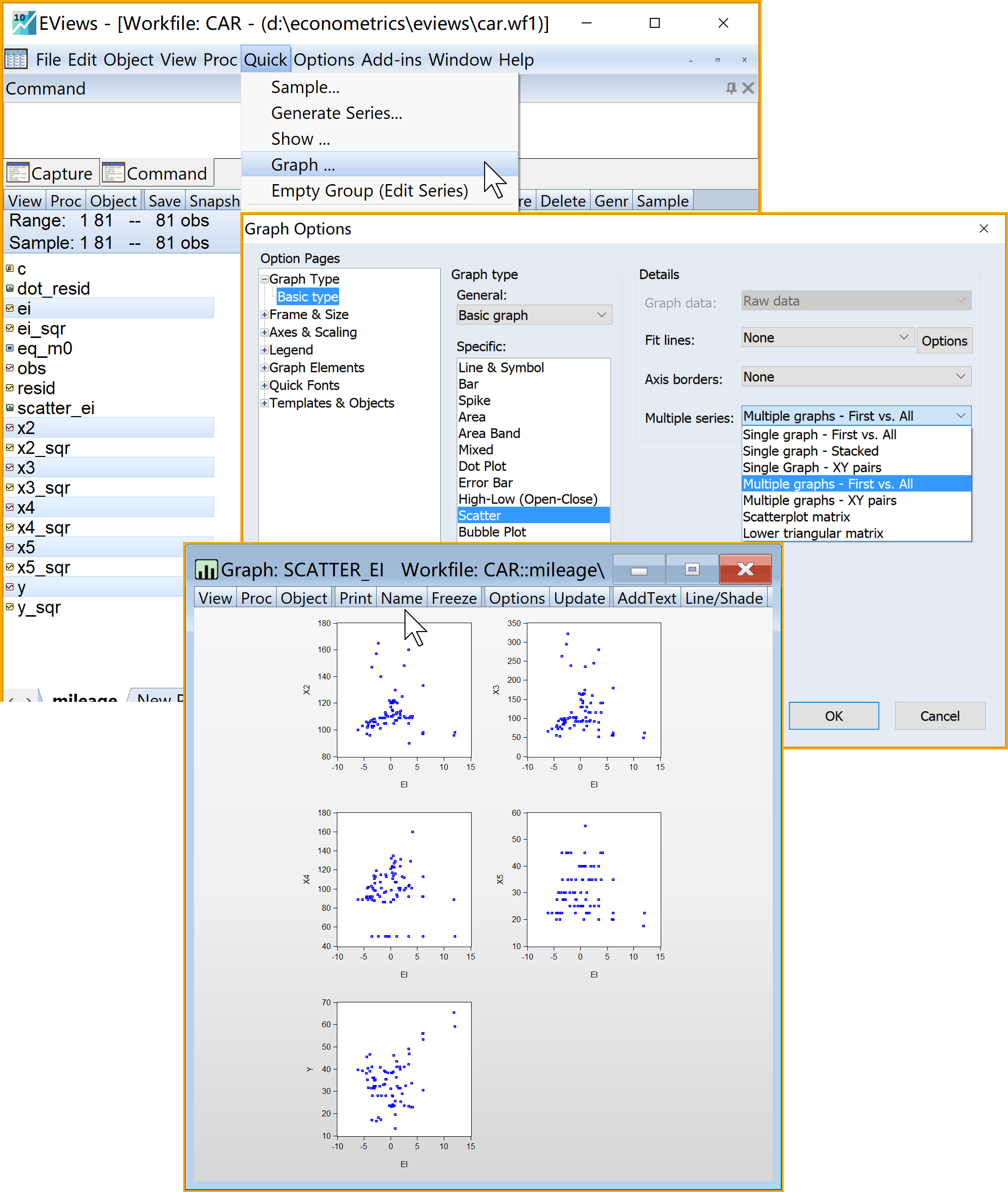
(3)绘制\(e_i\)序列对\(Y_i\); \(X_{1 i};X_{2 i};X_{3 i};X_{4 i}\)的散点图(scatter plot)(见 图 6.7 )
选择序列对象:键盘Ctrl键+依次单击选择序列
 ei;
ei; Y;
Y; X2;
X2; X3;
X3; X4;
X4; X5
X5进入引导菜单:\(\Rightarrow\) Quick \(\Rightarrow\) Graph
- 选择绘图类型(Graph type):Scatter
- 选择绘图细节(Detail):\(\Rightarrow\) Multiple series \(\Rightarrow\) 下拉选择 Multiple graphs - First vs. all
点击完成:OK
命名并保存绘图(graph)对象
 :建议命名为scatter_ei
:建议命名为scatter_ei查看结果:双击
 scatter_ei(见 图 6.7 )
scatter_ei(见 图 6.7 )
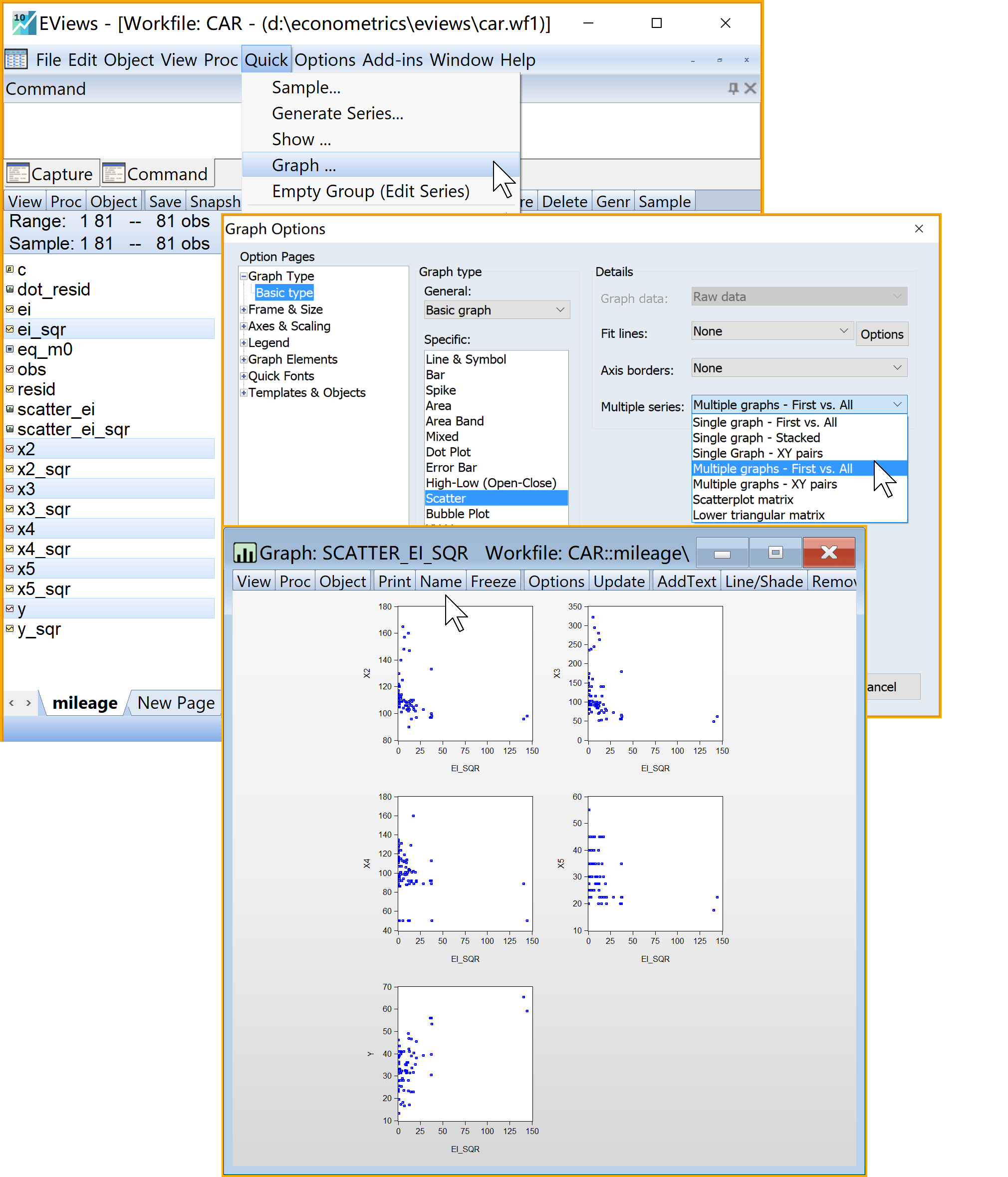
(4)绘制\(e^2_i\)序列对\(Y_i\); \(X_{1 i};X_{2 i};X_{3 i};X_{4 i}\)的散点图(scatter plot)(见 图 6.8 )
选择序列对象:键盘Ctrl键+依次单击选择序列
 ei_sqr;
ei_sqr; Y;
Y; X2;
X2; X3;
X3; X4;
X4; X5
X5进入引导菜单:\(\Rightarrow\) Quick \(\Rightarrow\) Graph
- 选择绘图类型(Graph type):Scatter
- 选择绘图细节(Detail):\(\Rightarrow\) Multiple series \(\Rightarrow\) 下拉选择 Multiple graphs - First vs. all
点击完成:OK
命名并保存绘图(graph)对象
 :建议命名为scatter_ei_sqr
:建议命名为scatter_ei_sqr查看结果:双击
 scatter_ei_sqr(见 图 6.8 )
scatter_ei_sqr(见 图 6.8 )
6.5.3.3 正式检验法
目标:利用Eviews的异方差诊断菜单,分别对主回归模型 式 6.27 进行 进行异方差诊断。
思路:诊断方法包括Park检验、Glejser检验、BPG检验和White检验等。根据辅助诊断方程的理论假设,分析Eviews诊断报告,与相关参考标准进行比较,得到相关结论
定义 6.2 (主回归模型和辅助诊断模型) 主回归模型(Main Model)是指Y变量对全部X变量的线性回归(如主模型 式 6.27 )
辅助诊断模型(Auxiliary Model)是指利用主回归模型的残差序列\(e_i\)对X变量进行特定的线性回归(具体的辅助诊断模型有多个)
6.5.3.4 Park检验法
诊断辅助方程:
\[ \begin{aligned} ln(e^2_i)=\hat{\alpha}_1+\hat{\alpha}_2ln(X_{2i})+\cdots+\hat{\alpha}_kln(X_{ki})+v_i \end{aligned} \tag{6.28}\]
诊断标准:
Eviews说明:Eviews没有Park异方差检验的诊断菜单,但可以通过选择Harvey异方差菜单,并修改相关变量设置来得到Park检验报告。
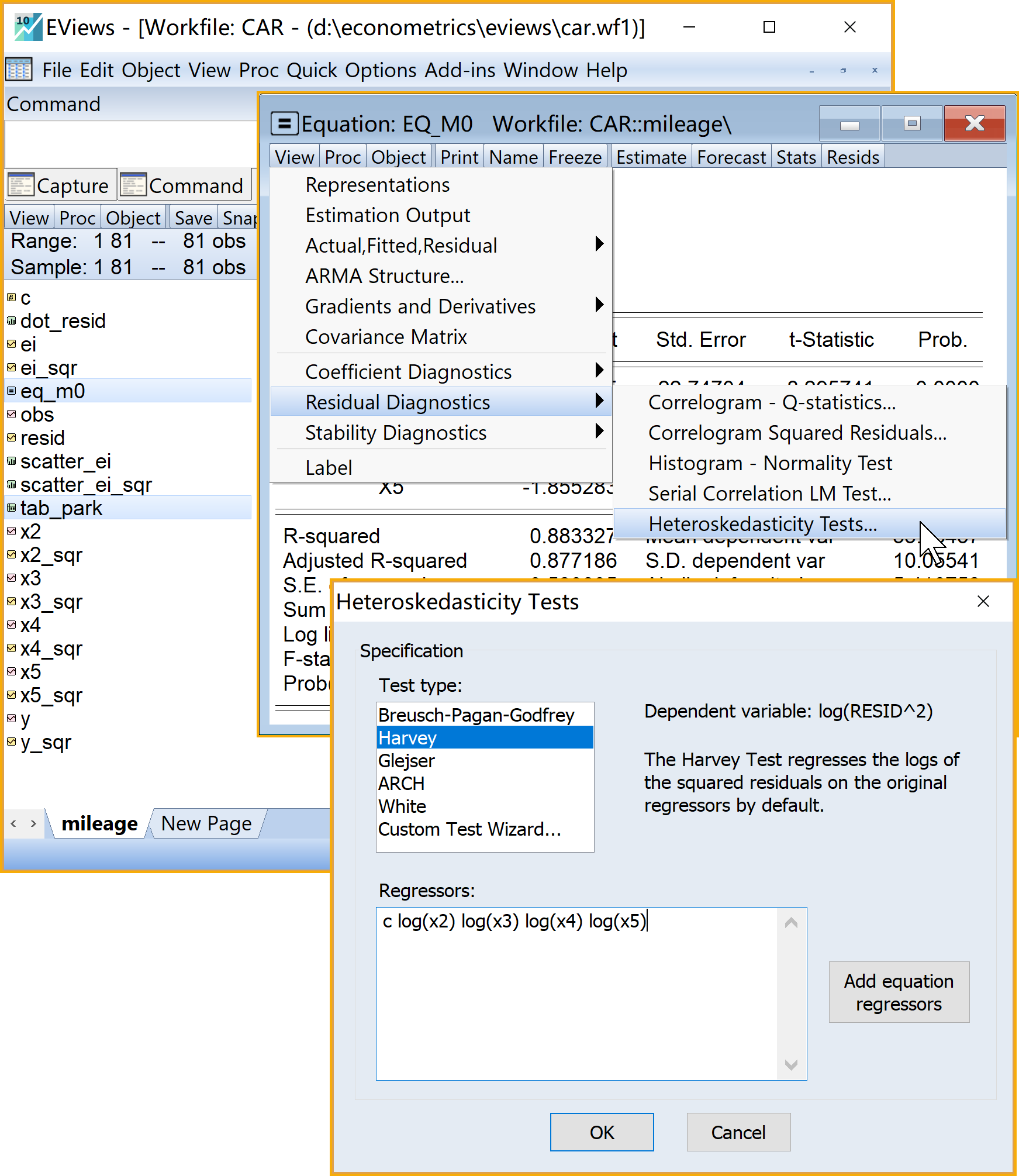
Eviews操作(菜单操作实现,具体见 图 6.9 )。具体操作步骤如下:
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
设置诊断方法(Test type): 点击选择Harvey
设置诊断方程(Regressors):输入c log(X2) log(X3) log(X4) log(X5)
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(talbe)对象:点击name(建议为tab_park)
查看结果:双击
 tab_park
tab_park
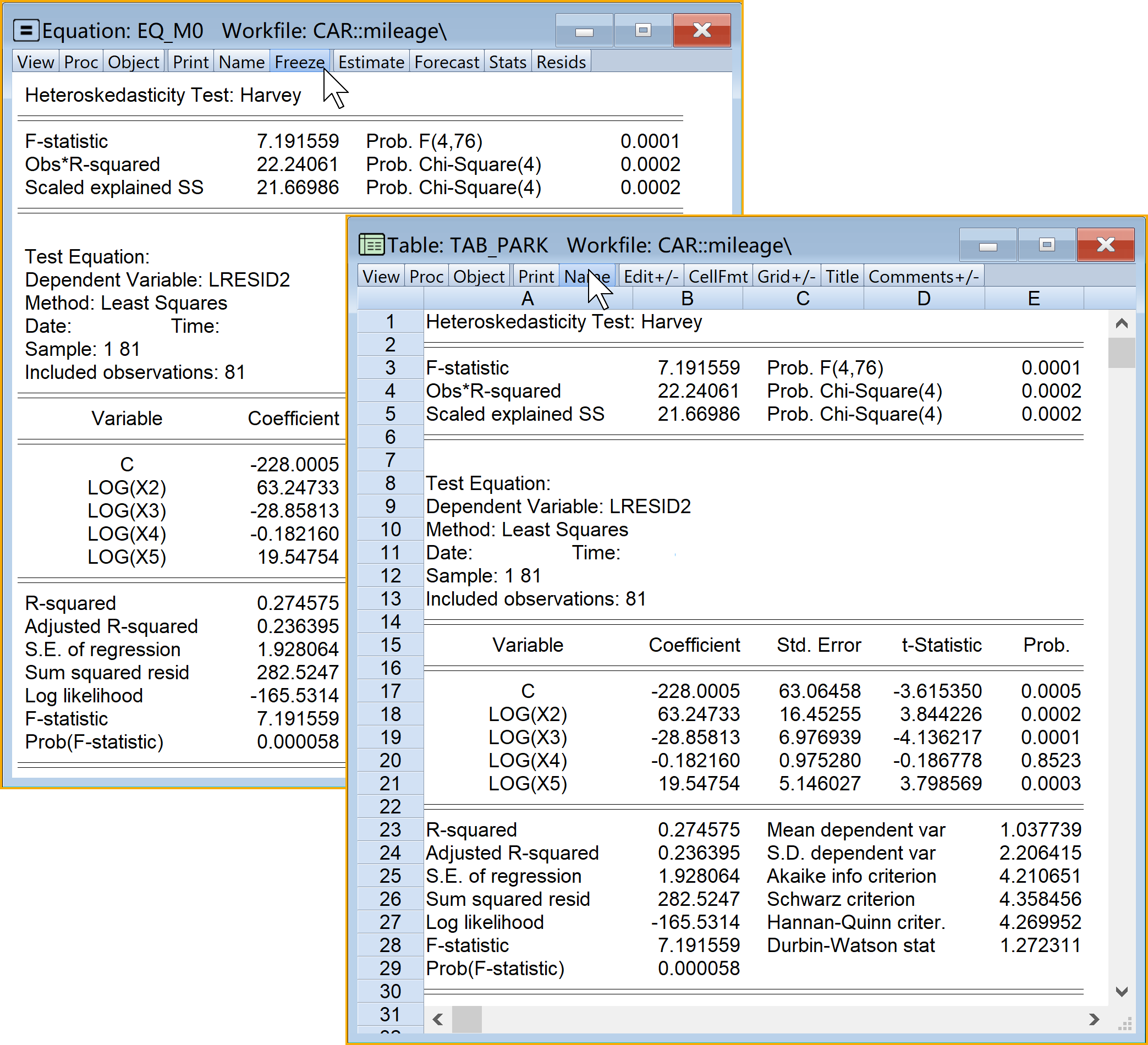
具体Eviews报告见 图 6.10 :
6.5.3.5 Glejser检验法
诊断辅助方程:
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_kX_{ki}+v_i &&\text{G1} \end{aligned} \tag{6.29}\]
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\sqrt{X_{2i}}+\cdots+\hat{\alpha}_k\sqrt{X_{ki}}+v_i &&\text{G2} \end{aligned} \tag{6.30}\]
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\frac{1}{X_{2i}}+\cdots+\hat{\alpha}_k\frac{1}{X_{ki}}+v_i &&\text{G3} \end{aligned} \tag{6.31}\]
诊断标准:
Eviews操作1(Glejser辅助方程 式 6.29 ,具体见 图 6.13 ):
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
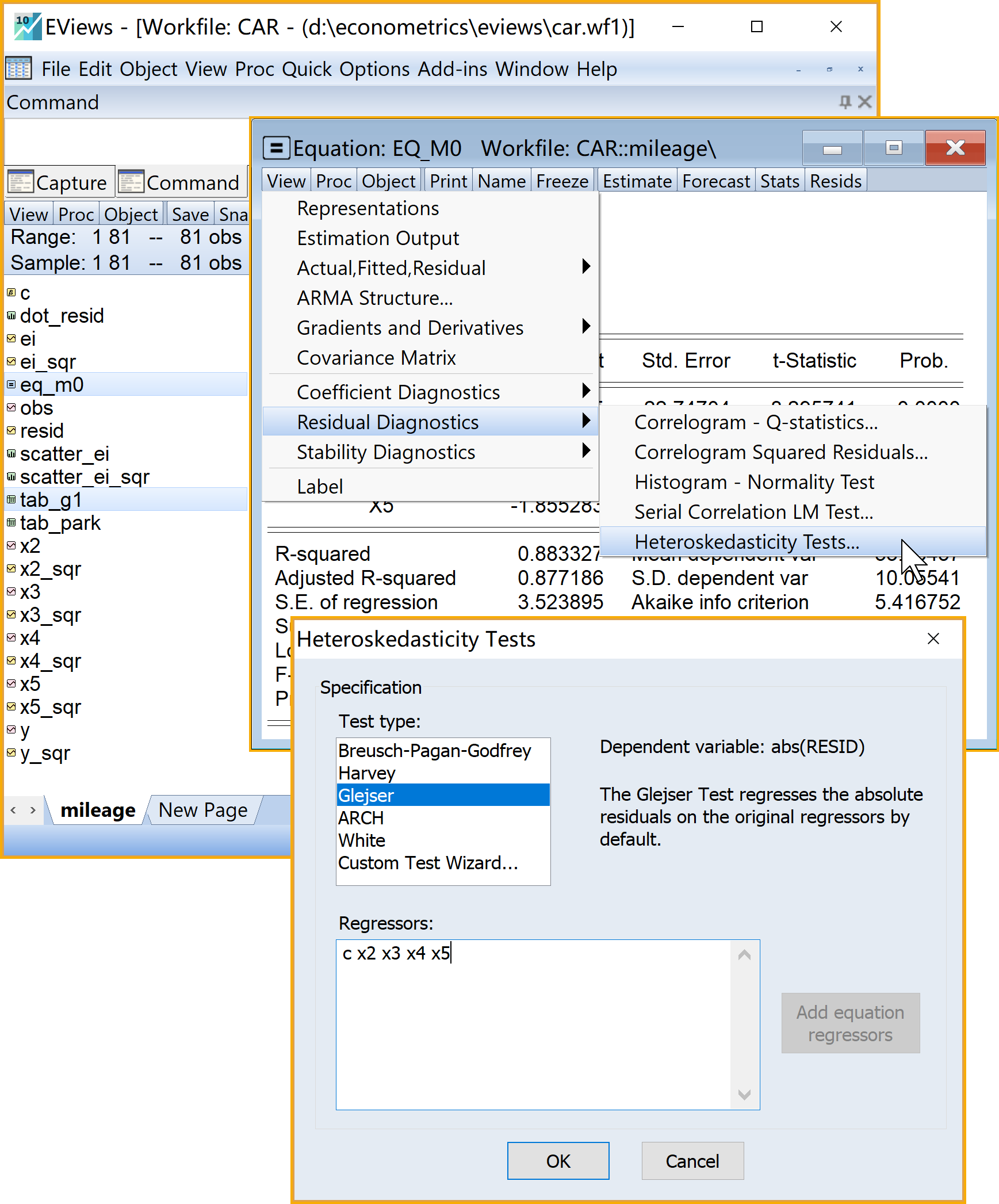
设置诊断方法(Test type): 点击选择Glejser
设置诊断方程(Regressors):输入c X2 c X3 c X4 c X5
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(table)对象:点击name(建议为tab_G1)
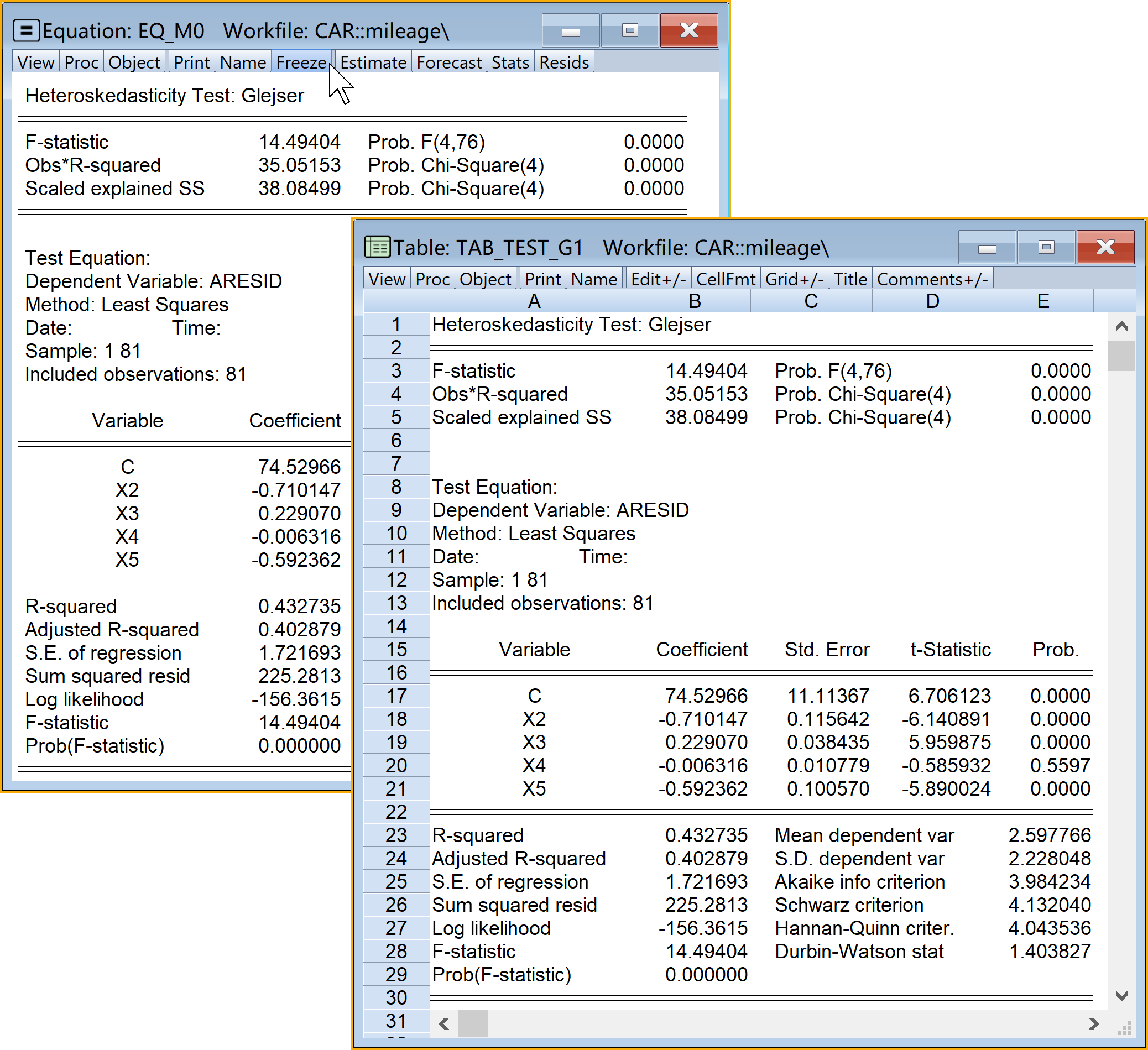
查看结果:双击
 tab_G1
tab_G1
具体Eviews报告见 图 6.14 :
Eviews操作2(Glejser辅助方程 式 6.30 ,具体见 图 6.15 ):
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
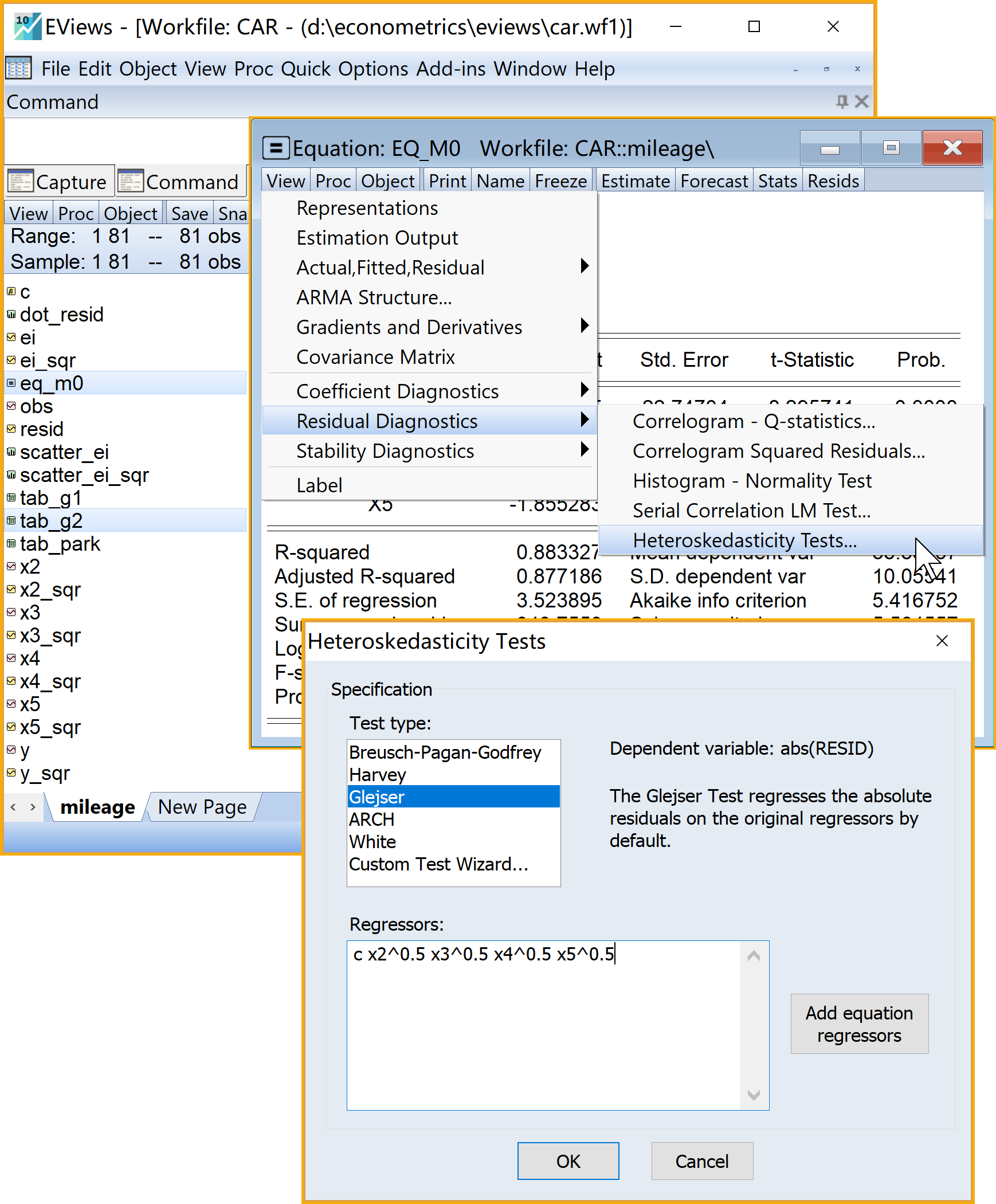
设置诊断方法(Test type): 点击选择Glejser
设置诊断方程(Regressors):输入c X2^0.5 X3^0.5 X4^0.5 X5^0.5
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(table)对象:点击name(建议为tab_G2)
查看结果:双击
 tab_G2
tab_G2
具体Eviews报告见 图 6.16 :
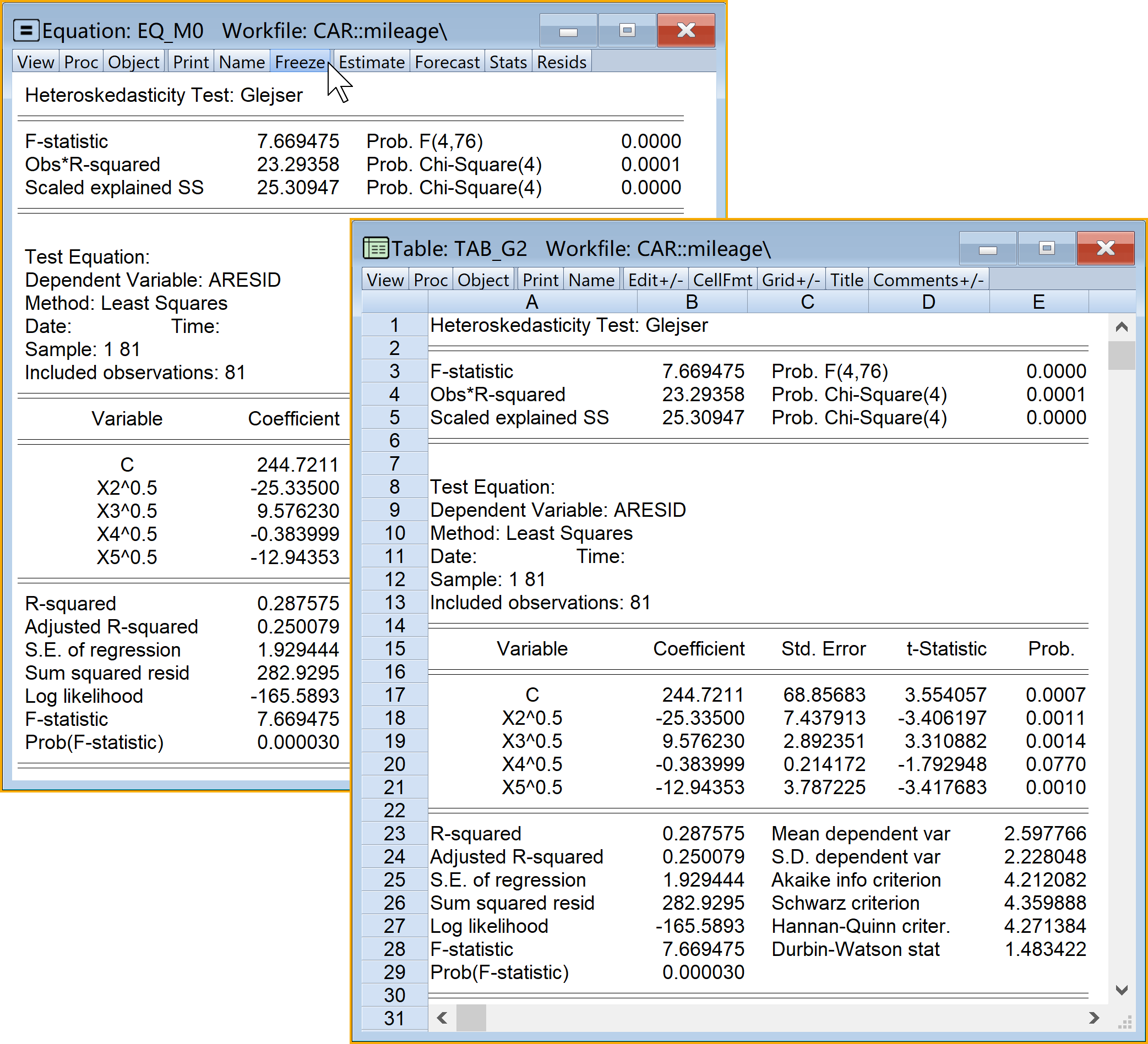
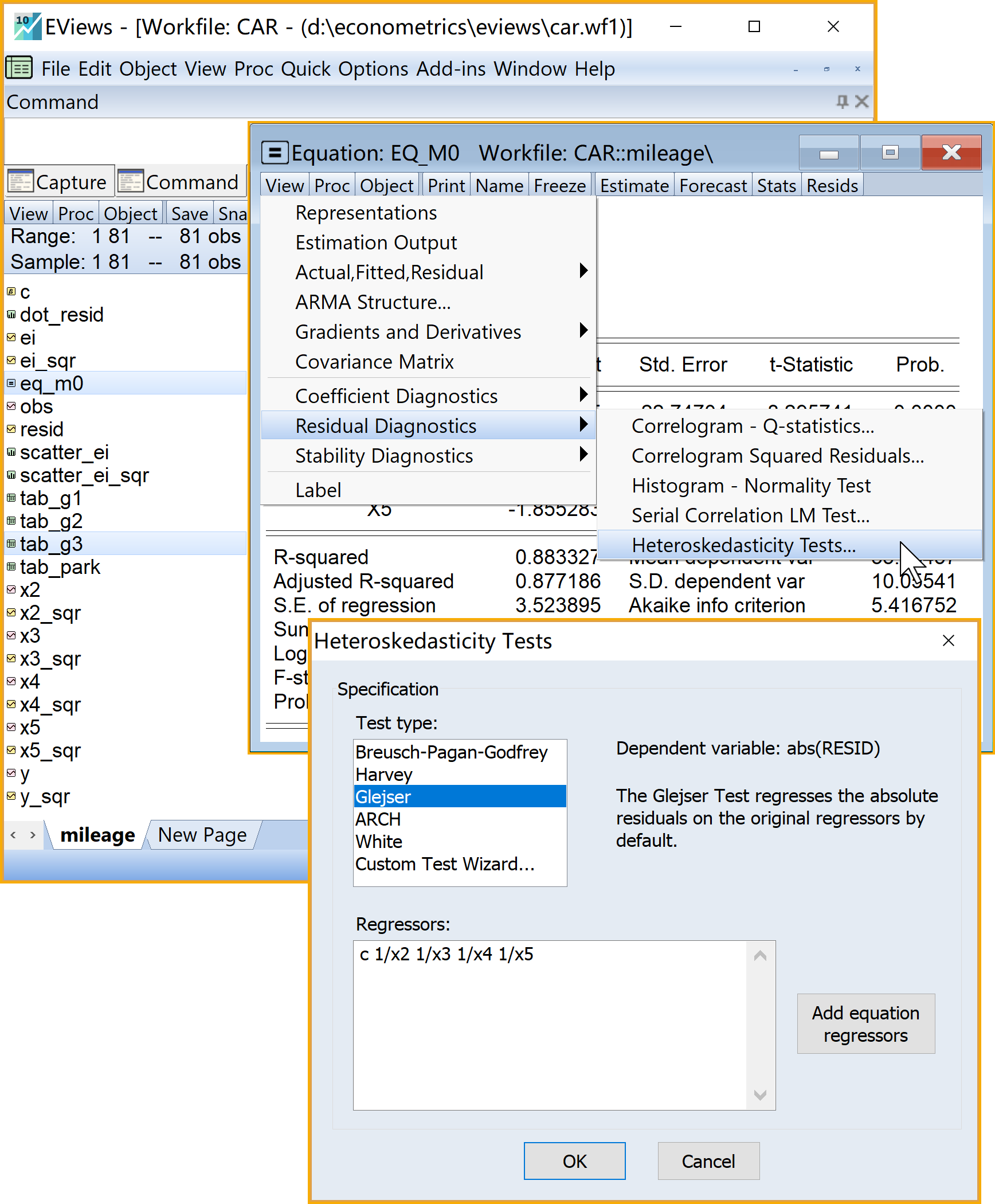
Eviews操作3(Glejser辅助方程 式 6.31 ,具体见 图 6.17 ):
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
设置诊断方法(Test type): 点击选择Glejser
设置诊断方程(Regressors):输入c 1/ X2 1/ X3 1/ X4 1/ X5
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(table)对象:点击name(建议为tab_G3)
查看结果:双击
 tab_G3
tab_G3
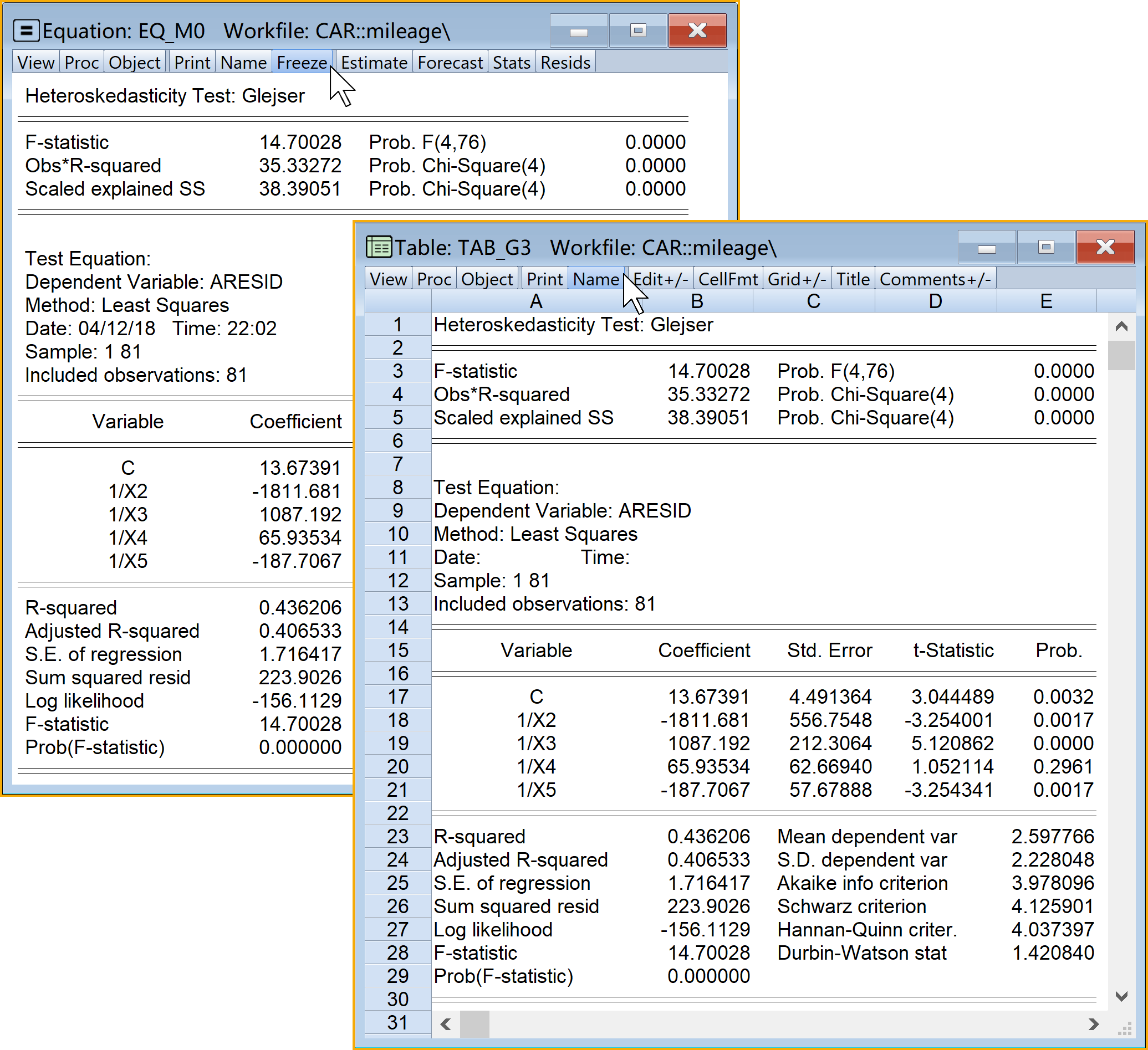
具体Eviews报告见 图 6.18 :
6.5.3.6 BPG检验法
诊断辅助方程:
\[ \begin{aligned} e^2_i=\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_kX_{ki}+v_i \end{aligned} \tag{6.32}\]
诊断标准:
如果诊断辅助方程 式 6.32 的\(\chi^2\)检验(
scaled explained SS)不显著(对应的概率值P>0.1),则表明主模型 式 6.27 是同方差如果诊断辅助方程 式 6.32 的\(\chi^2\)检验(
scaled explained SS)显著(对应的概率值P<0.1),则表明主模型 式 6.27 是异方差。
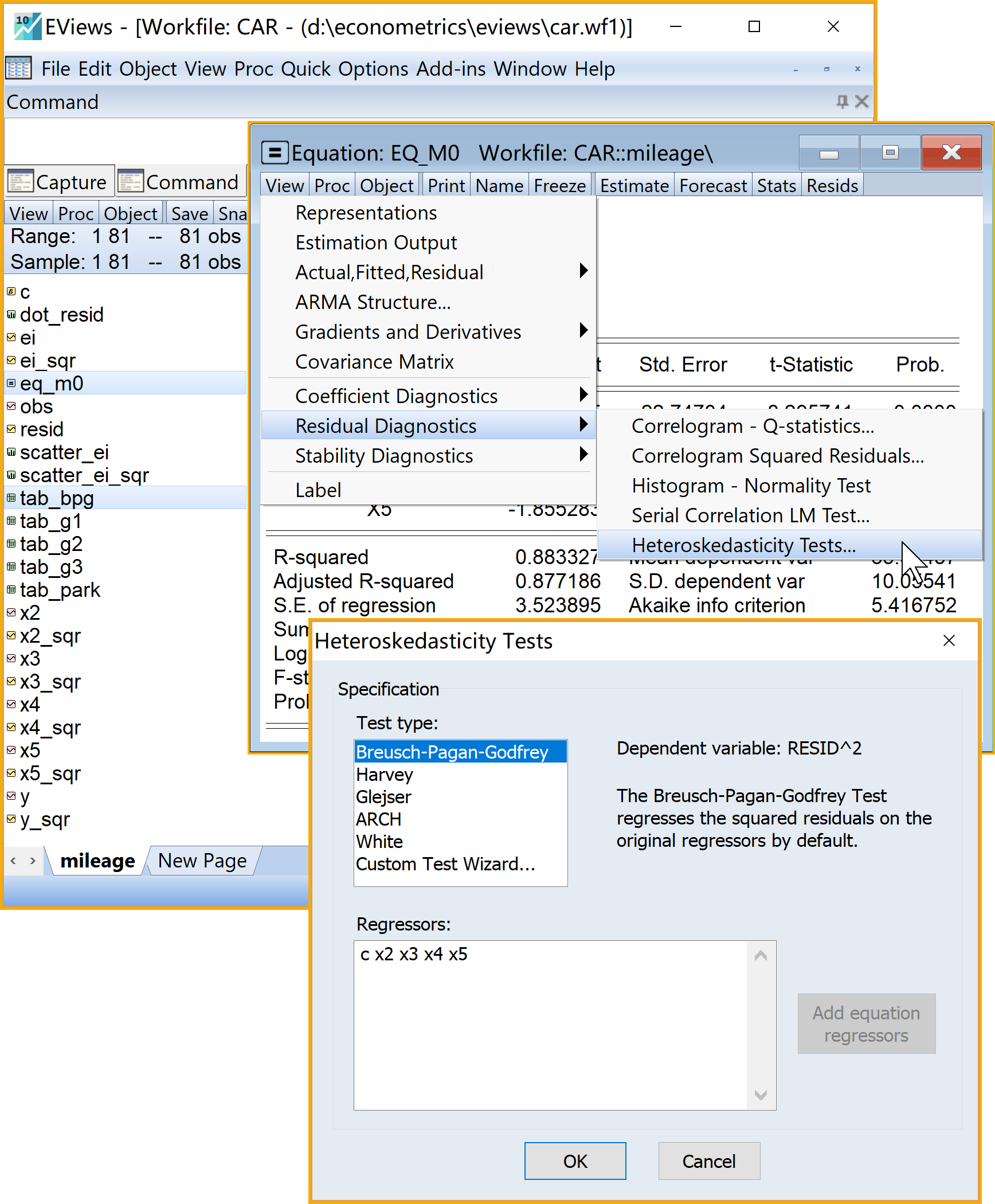
Eviews操作(菜单操作实现,具体见 图 6.19 ):
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
设置诊断方法(Test type): 点击选择Breusch-Pagan-Godfrey
设置诊断方程(Regressors):输入c X2 X3 X4 X5
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(table)对象:点击name(建议为tab_bpg)
查看结果:双击
 tab_bpg
tab_bpg
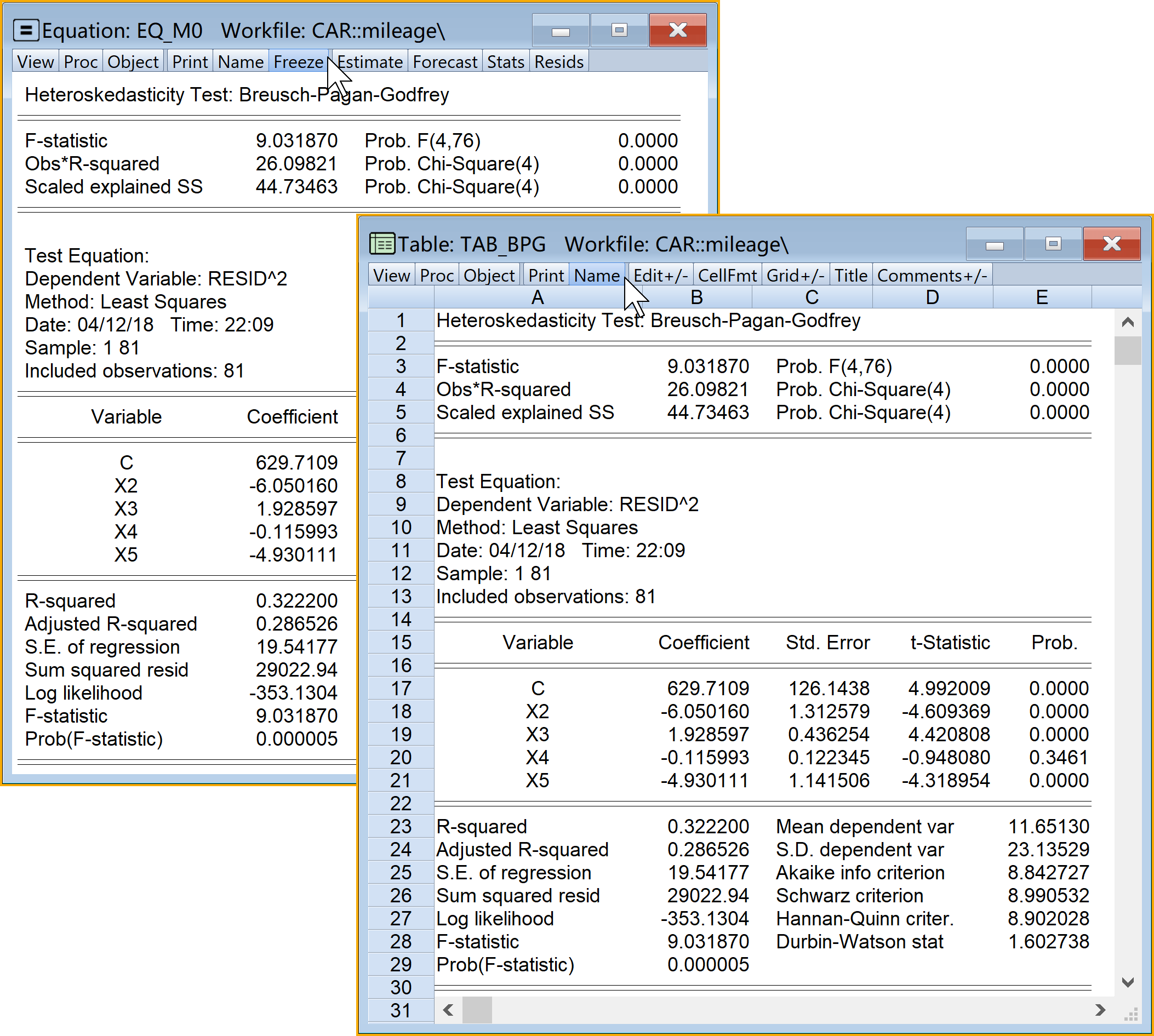
具体Eviews报告见 图 6.20 :
6.5.3.7 White检验法
诊断辅助方程:
\[ \begin{aligned} Y_t & =\hat{\beta}_1+\hat{\beta}_2X_{2i}+\hat{\beta}_3X_{3i}+e_{i} \end{aligned} \tag{6.33}\]
\[ \begin{aligned} e^2_i & =\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\hat{\alpha}_3X_{3i}+\hat{\alpha}_4X^2_{2i}+\hat{\alpha}_5X^2_{3i}+\hat{\alpha}_6X_{2i}X_{3i}+v_i \end{aligned} \tag{6.34}\]
诊断标准:
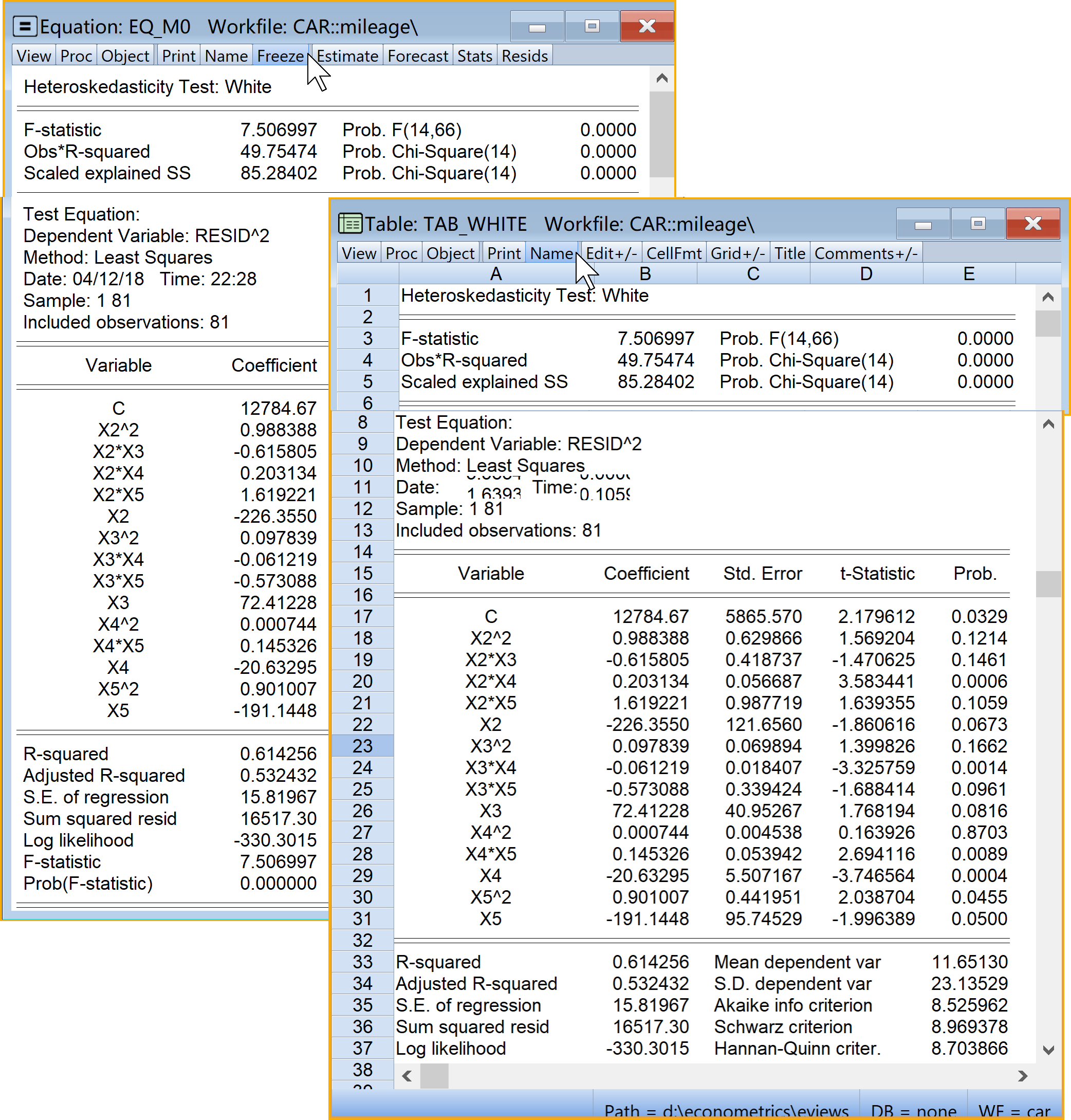
如果诊断辅助方程 式 6.34 的\(\chi^2\)检验(
scaled explained SS)不显著(对应的概率值P>0.1),则表明主模型 式 6.33 是同方差如果诊断辅助方程 式 6.34 的\(\chi^2\)检验(
scaled explained SS)显著(对应的概率值P<0.1),则表明主模型 式 6.33 是异方差。
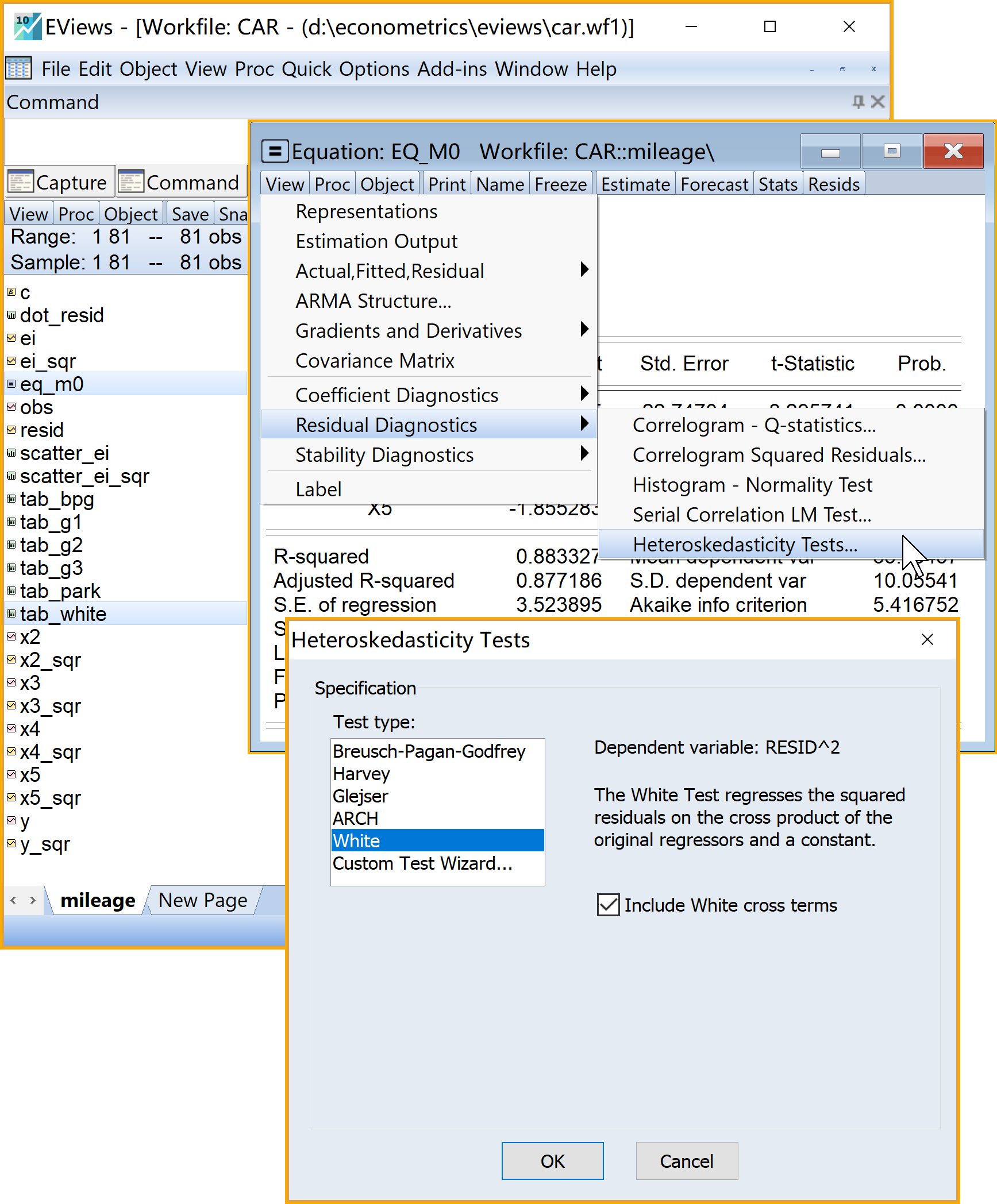
Eviews操作(菜单操作实现,具体见 图 6.21 ):
(1)打开主方程:双击方程(equation)对象 eq_m0
eq_m0
(2)进入引导菜单:\(\Rightarrow\) View \(\Rightarrow\) Residual Diagnostics \(\Rightarrow\) Heteroskedasticity Test \(\Rightarrow\) Specification
设置诊断方法(Test type): 点击选择White
设置诊断方程(下面两类方程自行选择其一):
交叉项方程:勾选 Include White cross term
非交叉项方程:不勾选 Include White cross term
(3)完成设置:点击Ok
(4)命名并保存表格(table)对象
另存为表格(table)对象:点击Freeze
命名并保存表格(table)对象:点击name(建议为tab_white)
查看结果:双击
 tab_white
tab_white
具体Eviews报告见 图 6.22 :
6.5.4 使用加权最小二乘法(WLS)矫正异方差问题
6.5.4.1 方差\(\sigma^2_i\)已知且等于样本方差\(S^2\)
如果主模型 式 6.27 存在异方差问题,且假设方差正比于样本方差\(S^2_i\),则有:
\[ \begin{aligned} var(u_i)=E(u^2_i)=\sigma^2_i=\sigma^2S^2_i \end{aligned} \tag{6.35}\]
对主模型 式 6.27 两边同时除以\(S_i\),得到:
\[ \begin{aligned} \frac{Y_i}{S_i} &=\frac{\hat{\beta}_1}{S_i}+\hat{\beta}_2\frac{X_{2i}}{S_i}+\hat{\beta}_3\frac{X_{3i}}{S_i}+\hat{\beta}_4\frac{X_{4i}}{S_i}+\hat{\beta}_5\frac{X_{5i}}{S_i}+\frac{e_{i}}{S_i} \end{aligned} \tag{6.36}\]
\[ \begin{aligned} Y^{\ast}_i &=\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2i}+\beta^{\ast}_3X^{\ast}_{3i}+\beta^{\ast}_4X^{\ast}_{4i}+\beta^{\ast}_5X^{\ast}_{5i}+v_{i} \end{aligned} \tag{6.37}\]
6.5.4.2 方差\(\sigma^2_i\)正比于\(X^2_i\)
如果主模型 式 6.27 存在异方差问题,且假设方差正比于\(X^2_i\),则有:
\[ \begin{aligned} var(u_i)=E(u^2_i)=\sigma^2_i=\sigma^2X^2_i \end{aligned} \tag{6.38}\]
对主模型 式 6.27 两边同时除以\(X_i\),得到:
\[ \begin{aligned} \frac{Y_i}{X_{2i}} &=\frac{\hat{\beta}_1}{X_{2i}}+\hat{\beta}_2+\hat{\beta}_3\frac{X_{3i}}{X_{2i}}+\hat{\beta}_4\frac{X_{4i}}{X_{2i}}+\hat{\beta}_5\frac{X_{5i}}{X_{2i}}+\frac{e_{i}}{X_{2i}} \end{aligned} \tag{6.39}\]
\[ \begin{aligned} Y^{\ast}_i &=\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2i}+\beta^{\ast}_3X^{\ast}_{3i}+\beta^{\ast}_4X^{\ast}_{4i}+\beta^{\ast}_5X^{\ast}_{5i}+v_{i} \end{aligned} \tag{6.40}\]
6.5.4.3 方差\(\sigma^2_i\)正比于\(X_i\)
如果主模型 式 6.27 存在异方差问题,且假设方差正比于\(X_i\),则有:
\[ \begin{aligned} var(u_i)=E(u^2_i)=\sigma^2_i=\sigma^2X_i \end{aligned} \tag{6.41}\]
对主模型 式 6.27 两边同时除以\(\sqrt{X_i}\),得到:
\[ \begin{aligned} \frac{Y_i}{\sqrt{X_i}} & =\frac{\hat{\beta}_1}{\sqrt{X_i}}+\hat{\beta}_2\sqrt{X_i}+\hat{\beta}_3\frac{X_{3i}}{\sqrt{X_i}}+\hat{\beta}_4\frac{X_{4i}}{\sqrt{X_i}}+\hat{\beta}_5\frac{X_{5i}}{\sqrt{X_i}}+\frac{e_{i}}{\sqrt{X_i}} \end{aligned} \tag{6.42}\]
\[ \begin{aligned} Y^{\ast}_i &=\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2i}+\beta^{\ast}_3X^{\ast}_{3i}+\beta^{\ast}_4X^{\ast}_{4i}+\beta^{\ast}_5X^{\ast}_{5i}+v_{i} \end{aligned} \tag{6.43}\]
6.5.4.4 方差\(\sigma^2_i\)正比于\(\hat{Y_i}^2\)
如果主模型 式 6.27 存在异方差问题,且假设方差正比于\(\hat{Y_i}^2\),则有:
\[ \begin{aligned} var(u_i)=E(u^2_i)=\sigma^2_i=\sigma^2\hat{Y_i}^2 \end{aligned} \tag{6.44}\]
对主模型 式 6.27 两边同时除以\(\hat{Y_i}\),得到:
\[ \begin{aligned} \frac{Y_i}{\hat{Y_i}} &=\frac{\hat{\beta}_1}{\hat{Y_i}}+\hat{\beta}_2\frac{X_{2i}}{\hat{Y_i}}+\hat{\beta}_3\frac{X_{3i}}{\hat{Y_i}}+\hat{\beta}_4\frac{X_{4i}}{\hat{Y_i}}+\hat{\beta}_5\frac{X_{5i}}{\hat{Y_i}}+\frac{e_{i}}{\hat{Y_i}} \end{aligned} \tag{6.45}\]
\[ \begin{aligned} Y^{\ast}_i &=\beta^{\ast}_1+\beta^{\ast}_2X^{\ast}_{2i}+\beta^{\ast}_3X^{\ast}_{3i}+\beta^{\ast}_4X^{\ast}_{4i}+\beta^{\ast}_5X^{\ast}_{5i}+v_{i} \end{aligned} \tag{6.46}\]
6.5.4.5 方差\(\sigma^2_i\)未知
如果主模型 式 6.27 存在异方差问题,且假设方差正比于\(\hat{Y_i}^2\),则有:
\[ \begin{aligned} var(u_i)=E(u^2_i)=\sigma^2_i=\sigma^2\hat{Y_i}^2 \end{aligned} \tag{6.47}\]
对主模型 式 6.27 两边同时取对数\(ln()\),得到:
\[ \begin{aligned} ln{Y_t} =\hat{\beta}_1+\hat{\beta}_2ln{X_{2i}}+\hat{\beta}_ln{3X_{3i}}+\hat{\beta}_4ln{X_{4i}}+\hat{\beta}_5ln{X_{5i}}+e_{i} \end{aligned} \tag{6.48}\]
6.5.5 使用White校正法矫正异方差问题
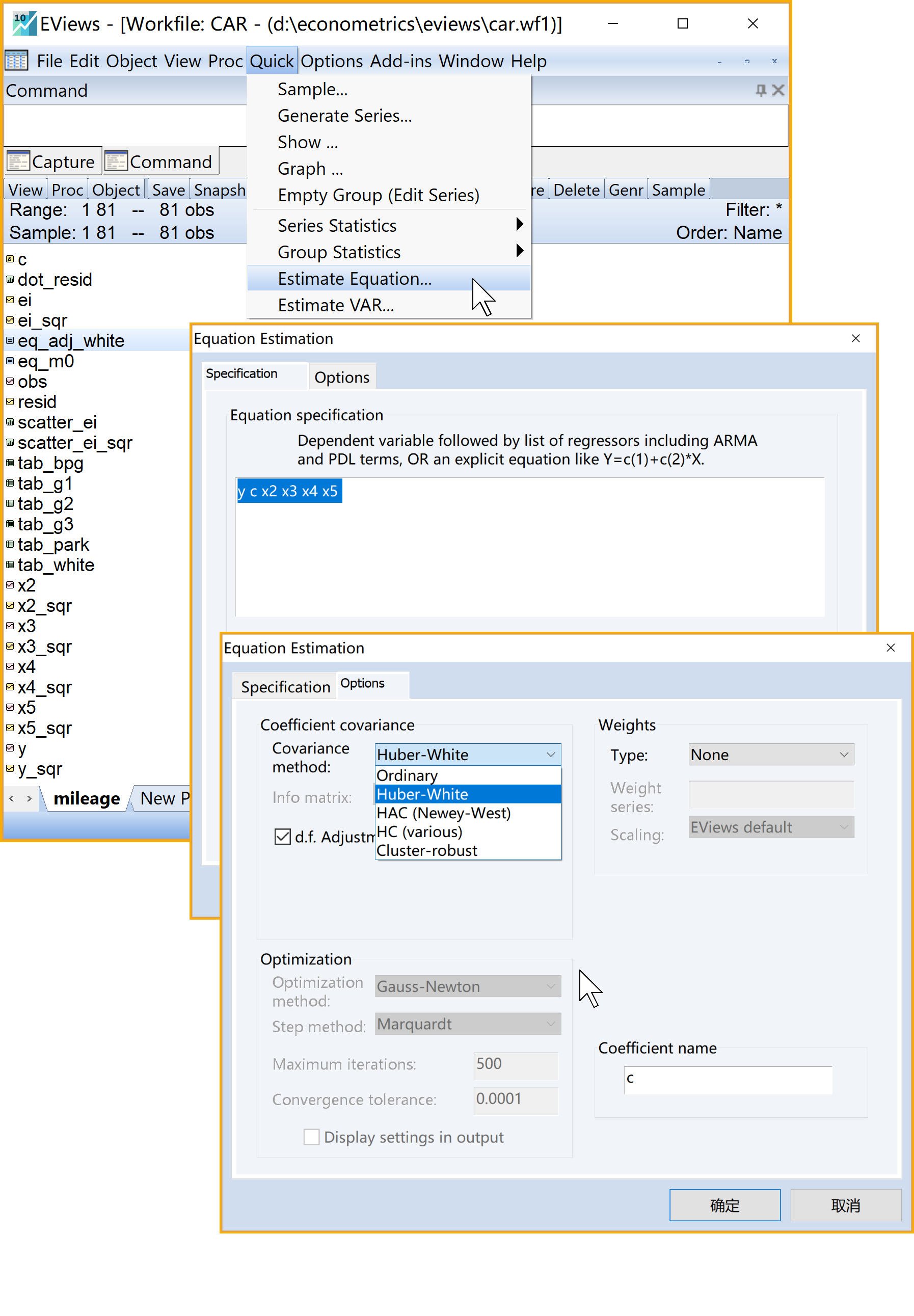
Eviews操作(见 图 6.23 )
(1)依次选择\(\Rightarrow\) Quick \(\Rightarrow\) Estimation Equation
(2)引导设置Equation Estimation \(\Rightarrow\) Specification
- 方程设置(Equation Specification): 输入变量Y c X2 X3 X4 X5
估计方法(Estimation settings):
- Method:选择
LS - Least Squares(NLS and ARMA) - Sample: 默认设置
- Method:选择
(3)引导设置Equation Estimation \(\Rightarrow\) Options
系数协方差设置(Coefficient covariance)
- 协方差方法(Coefficient method):下拉选择Huber-White
权重设置(Weights):默认设置
最优化设置(Optimization):默认设置
完成设置:点击
OK
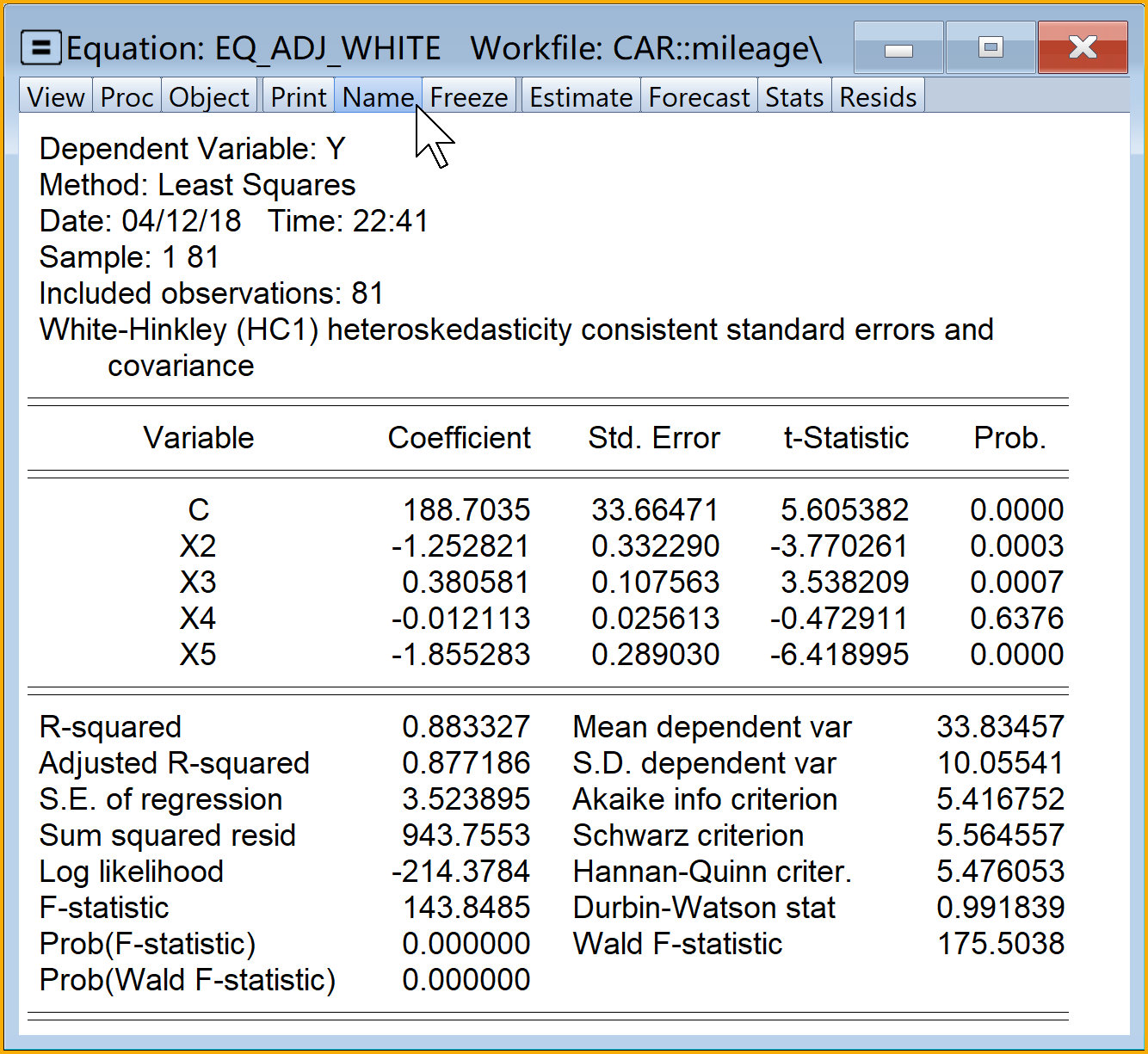
(4)模型命名:建议为eq_adj_white
查看分析报告(见 图 6.24 ):
6.6 作业题
财富500强企业高管薪水数据: 表 6.3 给出给出了447辆汽车在Y高管薪水及分红,X2担任 CEO年数(不足6个月视为的0),X3总裁CEO的年龄,X4企业的总销售收入,X5企业的利润,X6企业的总资产等方面的数据。
| obs | Y | X2 | X3 | X4 | X5 | X6 |
|---|---|---|---|---|---|---|
| 1 | 3030 | 7 | 61 | 161315 | 2956 | 257389 |
| 2 | 6050 | 0 | 51 | 144416 | 22071 | 237545 |
| 3 | 3571 | 11 | 63 | 139208 | 4430 | 49271 |
| 4 | 3300 | 6 | 60 | 100697 | 6370 | 92630 |
| 5 | 10000 | 18 | 63 | 100469 | 9296 | 355935 |
| 443 | 1866 | 10 | 59 | 2934 | 375 | 35800 |
| 444 | 906 | 6 | 59 | 2933 | 194 | 4986 |
| 445 | 2300 | 9 | 57 | 2910 | 183 | 2739 |
| 446 | 875 | 7 | 50 | 2905 | 132 | 5009 |
| 447 | 1758 | 5 | 62 | 2896 | 17 | 2855 |
变量说明见 表 6.4 :
| variable | label |
|---|---|
| obs | TOP500公司序号 |
| Y | 高管薪水及分红 |
| X2 | 担任 CEO年数(不足6个月视为的0) |
| X3 | 总裁CEO的年龄 |
| X4 | 企业的总销售收入 |
| X5 | 企业的利润 |
| X6 | 企业的总资产 |
请考虑如下样本回归模型:
\[ \begin{aligned} Y_i=\beta_1+\beta_2X_{2i}+\beta_3X_{3i}+\beta_4X_{4i}+\beta_5X_{5i}+\beta_6X_{6i}+e_{i} \end{aligned} \tag{6.49}\]
请回答如下问题:
(1)根据回归模型 式 6.49 ,写出总体回归模型(PRM),并对参数的理论预期(符号、大小、关系)进行说明。
(2)利用Eviews对样本回归模型 式 6.49 进行回归分析(将报告截图过来,并写出相应的简要报告形式——三行式或四行式)。参数估计结果符合你的理论预期么?
(3)回归模型 式 6.49 存在异方差问题的证据吗?请以此按照下列方法进行诊断,并分别得到分析结论(要求截图过来并进行简要说明):
(a)非正式检验法(图解法):
绘制\(e_i\)序列和\(e^2_i\)序列的描点图(dot plot),得到你的初步结论。
分别绘制\(e_i\)序列分别与\(Y_i\)、\(X_i(i=2,\cdots,6\)序列的散点图(scatter plot),得到你的初步结论
分别绘制\(e^2_i\)与\(Y^2_i\)、\(X^2_i(i=2,\cdots,6\)序列的散点图(scatter plot),得到你的初步结论
(b)正式检验法
利用Park检验法,并得出你的初步结论(要求写出park诊断方程,并将park检验结果截图过来)
利用Glejser检验法,并得出你的初步结论(请确定X,并做三个类型的辅助回归。分别将Glejser检验结果截图过来)
\[ \begin{aligned} |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2X_{2i}+\cdots+\hat{\alpha}_kX_{ki}+v_i &&\text{G1} \\ |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\sqrt{X_{2i}}+\cdots+\hat{\alpha}_k\sqrt{X_{ki}}+v_i &&\text{G2} \\ |e_i| & =\hat{\alpha}_1+\hat{\alpha}_2\frac{1}{X_{2i}}+\cdots+\hat{\alpha}_k\frac{1}{X_{ki}}+v_i &&\text{G3} \end{aligned} \]
利用BPG检验法,并得出你的初步结论(要求写出BPG诊断方程,并将BPG检验结果截图过来)
利用White检验法(注意交叉项的使用),并得出你的初步结论(要求写出White诊断方程,并将White检验结果截图过来)
(4)若发现存在异方差问题,你如何进行纠正主模型 式 6.49 ?
(a)使用White校正法纠正异方差问题,并比较与主模型 式 6.49 的差别。(要求分别截图两个回归方程的Eviews报告,进行对照分析并得到结论)
(b)使用加权最小二乘法纠正异方差问题(提醒:根据前述分析,几种处理方法选择一种合适的处理方法,进行模型矫正分析。请说明你选择这种处理办法的理由,并得到分析结论!)
(5)现在做以 \(ln(Y_i)\)为因变量的第二个模型。异方差性有所改善吗?(要求截图相关Eviews报告,并简要陈述理由)。