计算题：工资案例

虚拟变量回归模型+约束回归

工资案例，虚拟变量回归模型+约束回归
计算题
虚拟变量
2023fall
作者

胡华平

发布于

2025年12月22日

1 案例分析题

薪资案例：一项实证研究关注薪资问题及其相关影响因素，相关变量的具体定义见 表 1 ：

表 1: 变量定义及说明
变量 定义 取值
Obs 序号 样本编号
Hwage 工资 定量变量，时均工资
Educ 受教育年数 定量变量，年数educ
Exper 工作年数 定量变量，年数exper
Exper2 工作年数平方 定量变量，年数平方exper^2
Gender 性别 定性变量，f表示女性，m表示男性
Gender_f 女性 虚拟变量，1表示女性；0表示其他
Gender_m 男性 虚拟变量，1表示男性；0表示其他
Union 工会身份 定性变量，y表示是工会成员，n表示不是工会成员
Union_y 工会成员 虚拟变量，1表示是工会成员；0表示其他
Union_n 非工会成员 虚拟变量，1表示不是工会成员；0表示其他

为了便于开展分析，研究人员首先把定性变量处理成虚拟变量，其中：定性变量性别 \(Gender\) 处理为2个虚拟变量（\(Gender\_f\)和\(Gender\_m\)）；定性变量 工会身份 \(Union\) 处理为2个虚拟变量（\(Union\_y\)和\(Union\_n\)）。

\[ \begin{aligned} Gender\{m,f\} \Longrightarrow \begin{cases} Gender\_f = \begin{cases} 1, & \text{女性}\\ 0, & \text{其他} \end{cases} \\ Gender\_m = \begin{cases} 1, & \text{男性}\\ 0, & \text{其他} \end{cases} \end{cases} \end{aligned} \]

\[ \begin{aligned} Union\{y,n\} \Longrightarrow \begin{cases} Union\_y = \begin{cases} 1, & \text{是工会成员}\\ 0, & \text{其他} \end{cases} \\ Union\_n = \begin{cases} 1, & \text{不是工会成员}\\ 0, & \text{其他} \end{cases} \end{cases} \end{aligned} \]


该实证研究共收集了样本数n=46943的就业人群数据集，部分数据集见 图 1 ：

图 1: 薪资案例数据集部分示例（总样本数n=46943）

A同学构建了 式 1 所示的虚拟变量回归模型：

\[ \begin{aligned} \begin{split} Hwage_i=&+\beta_{1}+\beta_{2}Educ_i+\beta_{3}Exper_i+\beta_{4}Exper2_i+\beta_{5}Gender\_f_i\\&+\beta_{6}Union\_y*Gender\_f_i+\beta_{7}Union\_y*Gender\_m_i+u_i \end{split} \quad \text{(A模型)}\quad \end{aligned} \tag{1}\]

B同学构建了 式 2 所示的虚拟变量回归模型：

\[ \begin{aligned} \begin{split} Hwage_i=&+\alpha_{1}+\alpha_{2}Educ_i+\alpha_{3}Exper_i+\alpha_{4}Exper2_i+\alpha_{5}Gender\_f_i+u_i \end{split} \quad \text{(B模型)}\quad \end{aligned} \tag{2}\]


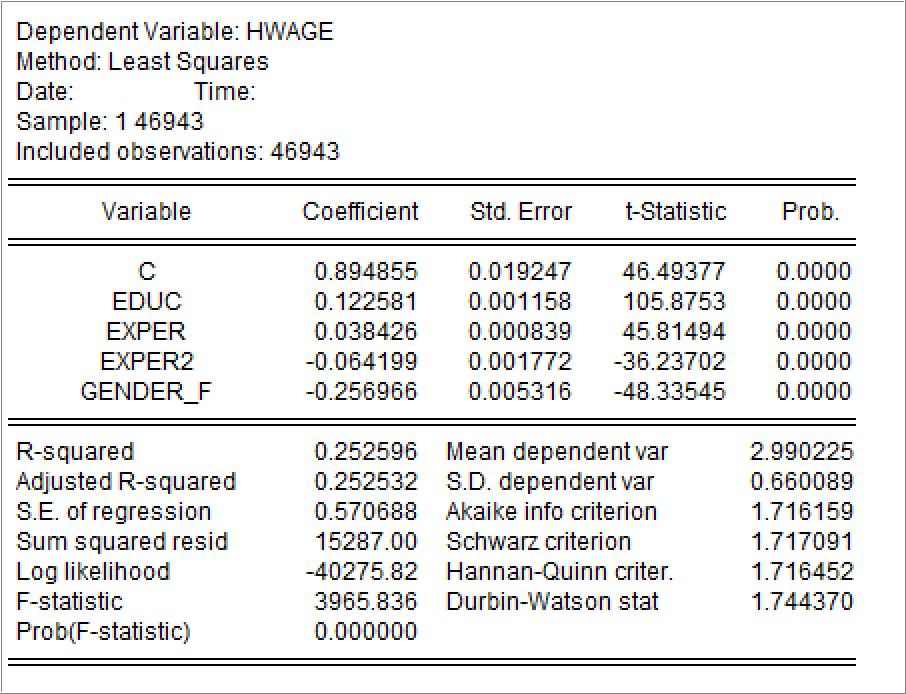
采用EViews软件进行最小二乘法回归，A模型和B模型的结果分别见 图 2 和 图 3 ：

图 2: 模型A的最小二乘回归结果
图 3: 模型B的最小二乘回归结果


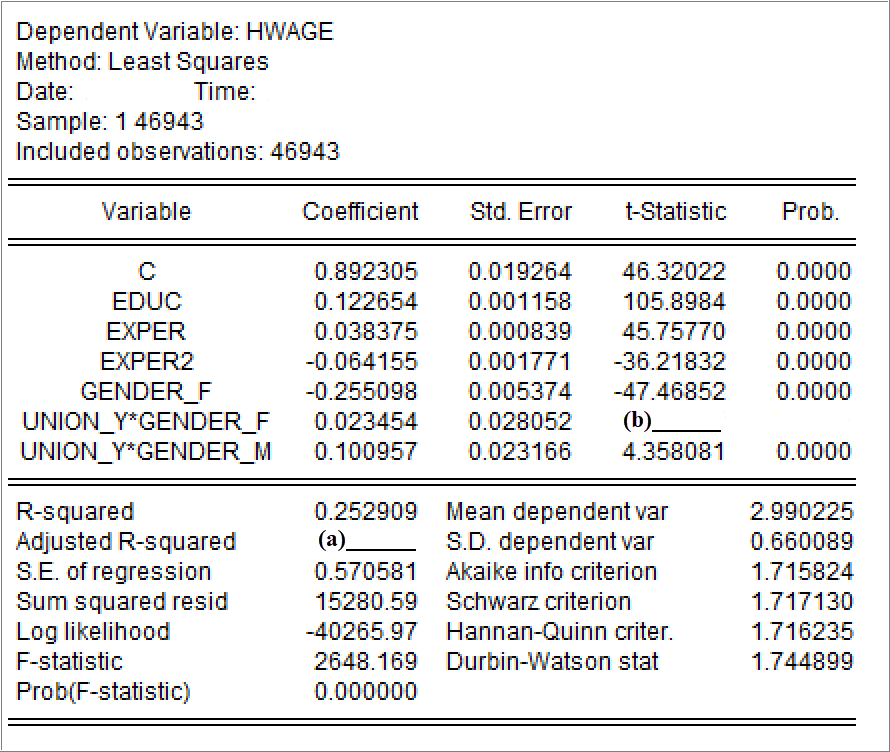
1.（小计10分，共3小题）根据A模型（见 式 1）及其最小二乘法EViews结果（见 图 2），请你依次回答下列问题：

（1）（4分）请你计算出调整可决系数\(\overline{R}^2\)，也即图中空白处(a)____的数值。（要求：写出主要计算过程；结果保留6位小数。）



（2）（3分）请你计算出模型A中交互项\(Union\_y*Gender\_f\)的系数t统计量值\(t^{\ast}_{\hat{\beta}_6}\)，也即图中空白处(b)____的数值。（要求：写出主要计算过程；结果保留4位小数。）



（3）（3分）根据EViews结果（见 图 2），并利用上一题（2）的计算结果，请你对模型A中交互项\(Union\_y*Gender\_f\)的参数\(\beta_6\)和\(Union\_y*Gender\_m\)的参数\(\beta_7\)，分别进行显著性t检验。（提示：给定显著性水平\(\alpha =0.05\)，t查表值\(t_{1-\alpha/2}(n-7) = t_{0.975}(4.6936\times 10^{4}) = 1.96\)；\(t_{1-\alpha/2}(n-8) = t_{0.975}(4.6935\times 10^{4}) = 1.96\)；\(t_{1-\alpha}(n-8) = t_{0.95}(4.6936\times 10^{4}) = 1.64\)。要求：简要写出t检验的主要 依据和结论即可。）




2.（小计10分，共3小题）根据A模型（见 式 1 ）及其最小二乘法EViews结果（见 图 2），请你依次回答下列问题。

（1）（2分）虚拟变量回归模型（见 式 1）中，基础组是哪一个就业群体？（提示：只需要判断性别和工会身份。）



（2）（4分）给定一名受教育年数为15年、从业年数为5年、加入了工会组织的男性就业者，请你计算出该就业者时均薪水的预测值是多少？（要求：写出主要计算步骤和过程；计算结果保留2位小数。）




（3）（4分）在保持其他条件相同（年龄、受教育年数、工作年数）的情况下，一名加入工会的女性就业者与一名加入工会的男性就业者，二者的时均薪资相差多少？（要求：写出主要计算步骤和过程；计算结果保留2位小数。）




3.（小计12分，共4小题）同学C比较感兴趣的一个猜想是：拥有工会成员身份（也即虚拟变量\(Union\_y =1\)），无论对男性还是对女性就业者的时均工资都没有任何影响。因此，同学C综合研究了模型A（见 式 1）和模型B（见 式 2），请结合EViews回归报告（见 图 2 和 图 3），分别回答如下问题。

（1）（2分）对于C同学的猜想（拥有工会成员身份，无论对男性还是对女性就业者的时均工资都没有任何影响），请你写出与该猜想等价的线性约束条件。（要求：请用模型A中的参数进行表达。）




（2）（3分）为了对C同学的猜想进行假设检验，请你提出相应的原假设 \(H_0\) 和备择假设 \(H_1\) 。




（3）（2分）为使用线性约束检验方法，关于模型A（见 式 1）和模型B（见 式 2），哪个是受约束模型，哪个是无约束模型？




（4）（5分）请你用线性约束检验方法，对同学C的猜想进行检验计算并得出检验结论。给定显著性水平\(\alpha = 0.05\)下，F查表值有\(F_{1-\alpha}(q, n-k_u)=F_{0.95}(2,4.6936\times 10^{4}) = 3.00\)；\(F_{1-\alpha}(k_u-1, n-k_u)=F_{0.95}(6,4.6936\times 10^{4}) = 2.10\)。（要求：写出主要计算步骤和过程；计算结果保留2位小数。）







4.（小计8分，共3小题）同学D针对模型A（见 式 1 ）回归结果进行了多重共线性问题诊断，结果如下：

图 4: 对模型A进行的某种多重共线性问题诊断

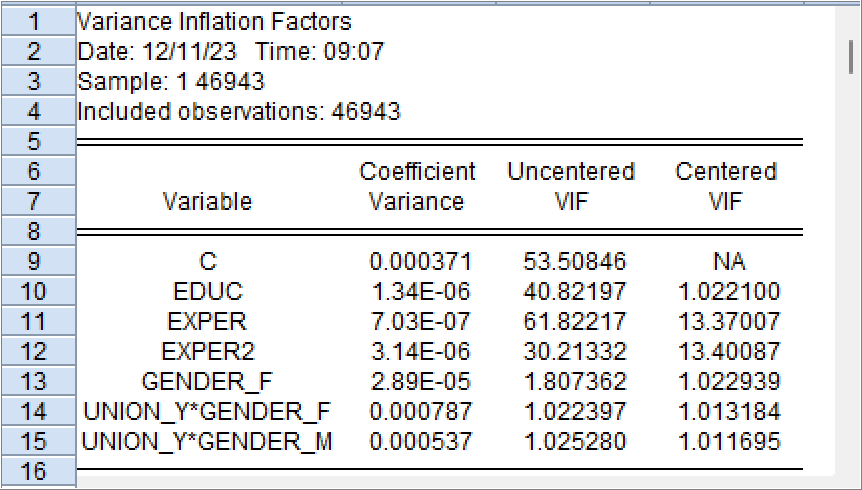
（1）（2分）上图给出的是哪一种多重共线性问题诊断方法？




（2）（3分）请你据此判断模型A是否存在十分严重的多重共线性问题？请给出你的判断依据。




（3）（3分）同学D通过自己思考，始终认为虚拟变量模型A中一定存在严重的多重共线性问题，他的理由是：自变量中\(Exper2\) 就是 \(Exper\) 的平方化计算得到的，二者存在很强联系；而且交互项 \(Union\_y * Gender\_f\) ，也与另一个自变量 \(Gender\_f\) 存在很强联系。你是否认同他的观点和理由？请给出你的依据。




2 参考答案

1.（小计10分，共3小题）

（1）（4分）

答： 已知可决系数\(R^2=0.252909\)，残差平方和\(RSS = 15 280.585765\)，回归系数个数\(k = 7\)， 样本数\(n = 46943\)，则可以计算得到调整可决系数：

\[ \begin{aligned} R^2 &= 1 - \frac{RSS}{TSS} \\ TSS &= \frac{RSS}{1 - R^2} = \frac{15 280.585765}{1 - 0.252909} = 20 453.447715\\ \overline{R}^2 &= 1- \frac{RSS/(n-k)}{TSS/(n-1)} = 1- \frac{15 280.585765/(46943-7)}{20 453.447715/(46943-1)} = 0.252814 \end{aligned} \]

判卷说明：此题还可以利用其他方法，例如利用F统计量 \(\overline{R}^2 = 1- \frac{n-1}{n-k+(k-1) \cdot F^{\ast}}\) ；或者利用 \(\overline{R}^2 = 1- \frac{(1-R^2)\cdot (n-1)}{(n-k)}\)。

（2）（3分）

答： 已知回归系数\(\hat{\beta}_6=0.023454\)，及其标准误差\(S_{\hat{\beta}_6}=0.023454\)，因此有：

\[ t^{\ast}_{\hat{\beta}_6} =\frac{\hat{\beta}_6}{S_{\hat{\beta}_6}} = \frac{0.023454}{0.023454} = 0.8361 \]

（3）（3分）

答： 1）根据题意，已知给定显著性水平\(\alpha =0.05\)，t查表值\(t_{1-\alpha/2}(n-7) = t_{0.975}(4.6936\times 10^{4}) = 1.96\)。2）根据（2）题计算结果，易知 \(t^{\ast}_{\hat{\beta}_6}= 0.8361\)小于t查表值，因此对参数\(\beta_6\)的显著性t检验（\(H_0:\beta_6 =0\)）不显著。3）根据回归报告结果，可以看到 \(t^{\ast}_{\hat{\beta}_7}= 4.3581\) 大于t查表值，因此对参数\(\beta_7\)的显著性t检验（\(H_0:\beta_7 =0\)）是显著的（通过p值也能做出相应判断）。

2.（小计10分，共3小题）

（1）（2分）

答： 根据回归模型设置，可以发现非工会成员的男性就业者群体为基础组（或参照组）。

（2）（4分）

答： 根据给定的条件，可以计算得到：

\[ \begin{aligned} \begin{split} &(\widehat{Hwage}|Educ=15; Exper=5; sqExper=25; Gender\_f=0; Gender\_m=1; Union\_y=1)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(15.0000) +\hat{\beta}_{3}(5.0000) +\hat{\beta}_{4}(25.0000)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(0)\cdot(1) +\hat{\beta}_{7}(1)\cdot(1)\\ =&+[0.8923]\cdot (1)+[0.1227]\cdot (15.0000)+[0.0384]\cdot (5.0000)-[0.0642]\cdot (25.0000)\\&-[0.2551]\cdot (0)+[0.0235]\cdot (0)\cdot(1)+[0.1010]\cdot (1)\cdot(1)\\ =&1.4211 \end{split} \end{aligned} \]

（3）（4分）

答：

  • 对于加入工会的女性就业者，易知：

\[ \begin{aligned} \begin{split} &E(Hwage|Educ; Exper; Exper2; Gender\_f=1; Gender\_m=0; Union\_y=1)\\ =&+\beta_{1}(1) +\beta_{2}Educ +\beta_{3}Exper +\beta_{4}Exper\\&+\beta_{5}\cdot(1) +\beta_{6}(1)\cdot(1) +\beta_{7}(0)\cdot(1)\\ =&\beta_{1} + \beta_{2}Educ + \beta_{3}Exper + \beta_{4} Exper2+ \beta_{5} + \beta_{6} \end{split} \end{aligned} \]

  • 对于加入工会的男性就业者，易知：

\[ \begin{aligned} \begin{split} &E(Hwage|Educ; Exper; Exper2; Gender\_f=0; Gender\_m=1; Union\_y=1)\\ =&+\beta_{1}(1) +\beta_{2}Educ +\beta_{3}Exper +\beta_{4}Exper\\&+\beta_{5}\cdot(0) +\beta_{6}\cdot(0) +\beta_{7}(1)\cdot(1)\\ =&\beta_{1} + \beta_{2}Educ + \beta_{3}Exper + \beta_{4} Exper2 + \beta_{7} \end{split} \end{aligned} \]

  • 在保持其他变量相同过的情况下，上述两式相减得到两人的时均薪水差值的估计值为：\(\beta_5 + \beta_6 -\beta_7 \approx \hat{\beta{}}_5 + \hat{\beta{}}_6 -\hat{\beta}_7 = -0.255098-0.100957=-0.33\)。

3.（小计12分，共4小题）

（1）（2分）

答： 等价的线性约束条件有两个：\(\beta_6=0;\beta_7=0\)。

（2）（3分）

答： 原假设 \(H_0:\beta_6=0;\beta_7=0\) ，备择假设 \(H_1:\beta_6,\beta_7\)不全为零。

（3）（2分）

答： 模型A为无约束模型，模型B为受约束模型。

（4）（5分）

答：可以利用无约束方程和有约束模型的可决系数，构建F统计量并进行检验。

注意：此题也可以利用无约束方程和有约束模型的残差平方和，构建F统计量并进行检验。二者结果和结论都是等价的。

  • 已知无约束模型的可决系数\(R^2_u=0.252909\)，有约束模型的可决系数\(R^2_u=0.252596\)。根据题（1）可知约束条件个数\(q=2\)。

  • 构造并计算线性约束检验的F统计量：

\[ \begin{aligned} F^{\ast}&=\frac{(R^2_u-R^2_r)/q}{(1-R^2_u)/(n-k_f)}\\ &=\frac{( 0.252909 - 0.252596 )/( 2 )}{(1 - 0.252909 )/( 46943 - 7 )}\\ &= 9.85 \end{aligned} \]

  • 进行F检验判断。已知无约束模型的回归元个数\(k_u=7\)，给定显著性水平\(\alpha = 0.05\)下，F查表值为\(F_{1-\alpha}(q, n-k_u)=F_{0.95}(2,4.6936\times 10^{4})=3.00\)。上述样本统计量值\(F^{\ast}=9.85\)大于理论查表值，因此约束条件检验是显著的，表明拥有工会成员身份，对不同性别的就业者时均工资有显著影响。这也表明同学C的猜想是统计上不成立的。

4.（小计8分，共3小题）

（1）（2分）

答： 方差膨胀因子法（或VIF法）

（2）（3分）

答： 认为不存在十分严重的多重共线性问题。根据VIF表中所示，只有从业年数\(Exper\)及其平方项\(Exper2\)的VIF值为13左右，其他变量的VIF值都很小。

（3）（3分）：

答： 不认同他的观点。理由有二：1）题（2）中VIF诊断并没有发现有严重的多重共线性问题。2）多重共线性的来源主要是变量间的线性关系引发的，而C同学理由中都是非线性关系。