| year | month | prcfat | unem |
|---|---|---|---|
| 1981 | JAN | 0.9009899 | 7.9 |
| 1981 | FEB | 0.9130266 | 8.0 |
| 1981 | MAR | 0.9149970 | 7.4 |
| 1981 | APR | 0.9788058 | 7.2 |
| 1981 | MAY | 0.9145713 | 6.1 |
| 1981 | JUN | 1.0848329 | 6.7 |
| 1981 | JUL | 1.2168285 | 7.4 |
| 1989 | JUL | 1.0232056 | 5.8 |
| 1989 | AUG | 0.9798468 | 4.7 |
| 1989 | SEP | 0.9471751 | 5.0 |
| 1989 | OCT | 0.8669214 | 4.6 |
| 1989 | NOV | 0.8254987 | 4.9 |
| 1989 | DEC | 0.8359611 | 4.8 |
1 案例分析题
交通事故案例:一项研究希望交通事故问题及其相关影响因素,共收集了1981年1月到1989年12月期间的月度样本数n=108的数据集(部分数据集见 表 1 ):
其中,相关变量的具体定义见下 表 2):
| 变量 | 定义 | 取值 |
|---|---|---|
| year | 年份 | 整数,1981 ~ 1989年 |
| month | 月度 | 定性变量,月份缩写(如JAN表示1月) |
| prcfat | 交通事故数量 | 定量变量,发生致命交通事故(至少1人死亡)的百分数占比 |
| unem | 失业率 | 定量变量,百分数值(%) |
为了便于分析,研究人员首先把定性变量\(month\)处理成12个虚拟变量,分别为\(JAN_i, FEB_i, MAR_i, APR_i, MAY_i, JUN_i, JUL_i, AUG_i, SEP_i, OCT_i, NOV_i, DEC_i\)。其中:
\[ \begin{align} JAN_i= \begin{cases} 1 \quad \text{是1月份}\\ 0 \quad \text{不是1月份} \end{cases} ; \quad FEB_i= \begin{cases} 1 \quad \text{是2月份}\\ 0 \quad \text{不是2月份} \end{cases} \quad \cdots \quad DEC_i= \begin{cases} 1 \quad \text{是12月份}\\ 0 \quad \text{不是12月份} \end{cases} \end{align} \]
研究人员尝试构建了如下的线性回归模型(见 式 1 ):
\[ \begin{aligned} \begin{split} PRCFAT_t=&+\beta_{1}+\beta_{2}FEB_t+\beta_{3}MAR_t+\beta_{4}APR_t+\beta_{5}MAY_t+\beta_{6}JUN_t+\beta_{7}JUL_t\\&+\beta_{8}AUG_t+\beta_{9}SEP_t+\beta_{10}OCT_t+\beta_{11}NOV_t+\beta_{12}DEC_t+\beta_{13}UNEM_t+u_t \end{split} \end{aligned} \tag{1}\]
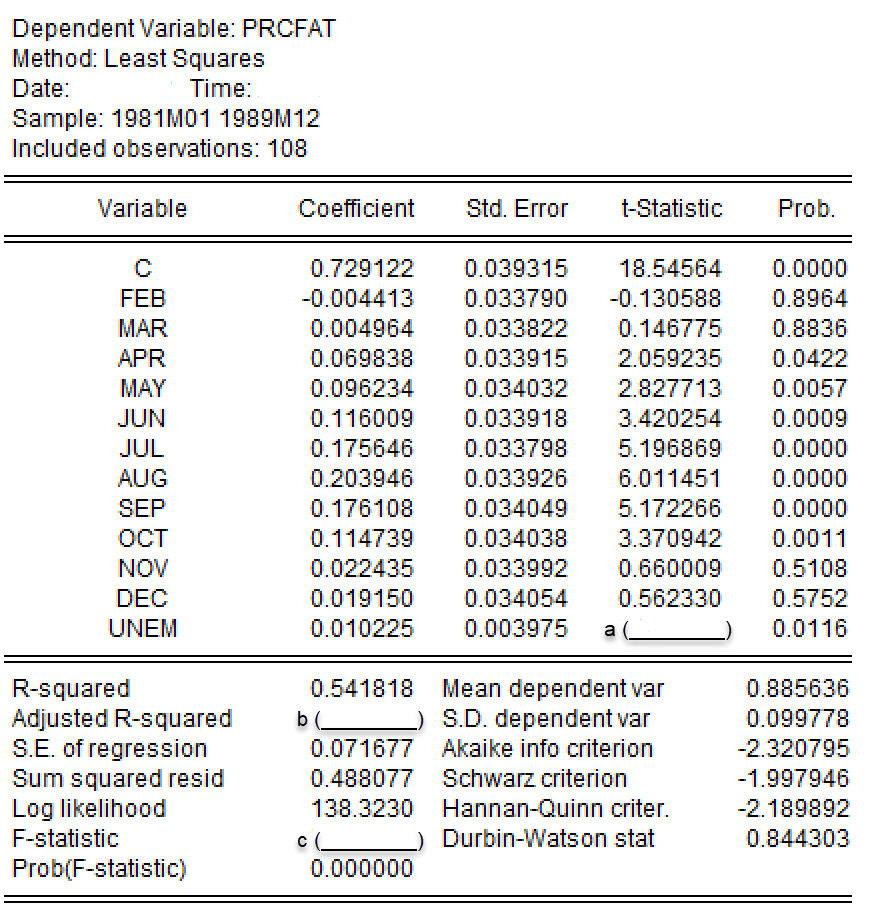
然后采用OLS方法进行估计,并得到如下@ref(fig:eq-season)所示的EViews报告。
下面计算题都是基于以上案例情景和数据集。请认真读题并按要求作答。
1.(5分)根据回归模型 式 1 ,请你指出基础组是什么?请你写出基础组的期望致命交通事故率的理论表达式。(要求:写出主要过程。)
2.(5分)给定失业率\(UNEM_i = 10\),请根据上述EViews的回归结果(见 图 1 )计算十月份(也即\(OCT_i=1\))致命交通事故率的估计值是多少。(要求:写出主要计算过程;结果保留两位小数。)
3.(9分)请分别计算上述EViews的回归结果(见 图 1 )中的空白项a、空白项b和空白项c。(要求:写出主要计算过程;结果保留4位小数。)
4.(6分)研究人员还尝试构建了如下的线性回归模型(见 式 2 ):
\[ \begin{aligned} \begin{split} PRCFAT_t=&+\alpha_{1}+\alpha_{2}JAN_t+\alpha_{3}FEB_t+\alpha_{4}MAR_t+\alpha_{5}APR_t+\alpha_{6}MAY_t+\alpha_{7}JUN_t\\&+\alpha_{8}JUL_t+\alpha_{9}AUG_t+\alpha_{10}SEP_t+\alpha_{11}OCT_t+\alpha_{12}NOV_t+\alpha_{13}UNEM_t+u_t \end{split} \end{aligned} \tag{2}\]
请你结合目前的两次建模(见 式 1 和 式 2 ),以及 图 1 的报告结果,分别计算出参数估计值\(\hat{\alpha}_1\)、\(\hat{\alpha}_{11}\)和\(\hat{\alpha}_{13}\)。(要求:写出主要计算过程;结果保留4位小数。)
5.(5分)研究者怀疑最初的建模(见 式 1 )存在一阶自相关性问题,也即\(u_t=\rho u_{t-1} + \epsilon_t\)(其中\(\epsilon_t \sim N(0, \sigma^2)\))。因此,对OLS分析报告(见 图 1 )的残差做了进一步辅助建模分析。辅助建模分析结果如下(见下 图 2 )
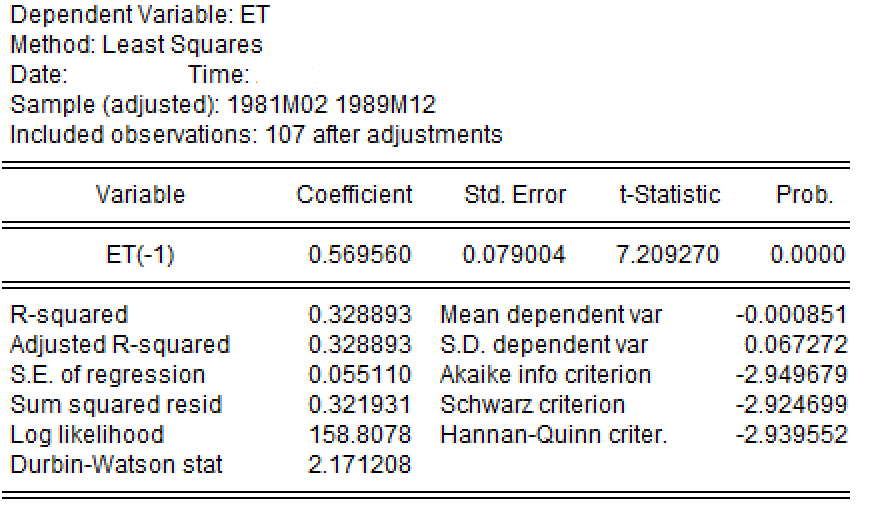
请你根据辅助建模分析报告结果(见 图 2 )进行序列1阶自相关性检验,并得出检验结论。同时,请你计算出自协方差系数的估计值\(\hat{\rho}\)。(要求:写出原假设和备择假设;写出主要检验步骤;得到检验结论。计算结果保留4位小数。)
6.(6分)已知给定95%置信度水平下,\(d_L=1.42\),\(d_U=1.94\)。请你根据OLS分析报告结果(见 图 1 )进行德宾-沃森检验(Durbin-Waston)。同时,请你进一步计算自协方差系数的估计值\(\tilde{\rho}\)。(要求:写出原假设和备择假设;写出主要检验步骤;得到检验结论。计算结果保留4位小数。)
7.(4分)研究者试图进行自相关性问题矫正并得到如下的分析报告。
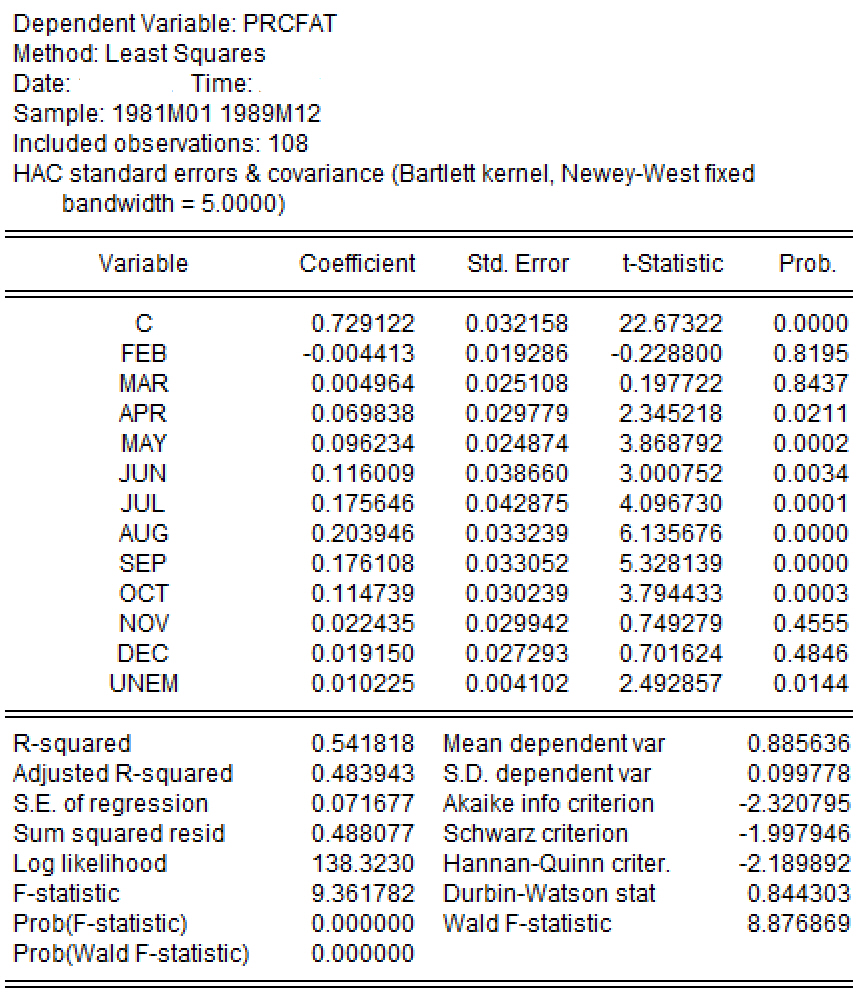
请你指出这种矫正方法是什么?并简要说明矫正前后的主要变化有哪些?
2 参考答案
1.(小计5分)答:
(1)(2分)基础组是一月(JAN);
(2)(3分)基础组的期望致命交通事故率的理论表达式为:
\[\begin{align} &E[PRCFAT_t|(FEB=\cdots=DEC=0,UNEM_t)]\\ &=+\beta_{1}+\beta_{2}FEB_t+\beta_{3}MAR_t+\beta_{4}APR_t+\beta_{5}MAY_t+\beta_{6}JUN_t+\beta_{7}JUL_t\\ &\quad +\beta_{8}AUG_t+\beta_{9}SEP_t+\beta_{10}OCT_t+\beta_{11}NOV_t+\beta_{12}DEC_t+\beta_{13}UNEM_t\\ &=+\beta_{1} + \beta_{13}UNEM_t \end{align}\]
2.(小计5分)答:
给定失业率\(UNEM_i = 10\),根据EViews的回归结果,可以计算出十月份(也即\(OCT_i=1\))致命交通事故率的估计值为:
\[\begin{align} &\widehat{PRCFAT_t}|(FEB=\cdots=DEC=0,OCT_t=1,UNEM_t=10)\\ &=+\hat{\beta}_{1}+\hat{\beta}_{2}FEB_t+\hat{\beta}_{3}MAR_t+\hat{\beta}_{4}APR_t+\hat{\beta}_{5}MAY_t+\hat{\beta}_{6}JUN_t+\hat{\beta}_{7}JUL_t\\ &\quad +\hat{\beta}_{8}AUG_t+\hat{\beta}_{9}SEP_t+\hat{\beta}_{10}OCT_t+\hat{\beta}_{11}NOV_t+\hat{\beta}_{12}DEC_t+\hat{\beta}_{13}UNEM_t\\ &=+\hat{\beta}_{1} + \hat{\beta}_{10} + \hat{\beta}_{13}UNEM_t \\ &=0.7291 + 0.1147 + 0.0102\times 10 \\ &= 0.95 \end{align}\]
3.(小计9分)答:
(1)(3分)EViews的回归结果中的空白项a为t统计量,其结果计算如下:
\[\begin{align} T^{\ast} = \frac{\hat{\beta}_{13}}{S_{\hat{\beta}_{13}}} = \frac{0.0102}{0.0040} = 2.5725 \end{align}\]
(2)(3分)EViews的回归结果中的空白项b为调整判定系数,已知判定系数\(R^2\),则其结果计算如下(方法1:利用判定系数):
\[\begin{align} \overline{R^2} &= 1- \frac{(1-R^2) /(n-k)}{1/(n-1)} \\ &= 1- (1-R^2)\frac{(n-1)}{(n-k)} \\ &= 1 - (1-0.5418)\frac{108-1}{(108-13)} \\ & = 0.4839 \end{align}\]
判卷说明:本题还有其他多种解法,例如(解法2)利用公式\(\bar{R}^{2}=1-\frac{\hat{\sigma}^{2}}{S_{Y}^{2}}\);(解法3)利用公式\(\bar{R}^{2}=1-\frac{RSS/(n-k)}{TSS/(n-1)}\)。计算方法和计算结果正确,则判定相应得分。
(3)(3分)EViews的回归结果中的空白项c为F统计量,已知判定系数\(R^2\),则其结果计算如下(解法1:利用判定系数):
\[\begin{align} F^{\ast} &= \frac{R^2 /(k-1)}{\left(1-R^2\right) /(n-k)} \\ &= \frac{0.5418 /12}{\left(1- 0.5418\right) /(108-13)} \\ & = 9.3618 \end{align}\]
判卷说明:本题还有其他多种解法,例如(解法2)\(F^{\ast}=\frac{ESS/(k-1)}{RSS/(n-k)}=\frac{(TSS-RSS)/(k-1)}{RSS/(n-k)}\)。计算方法和计算结果正确,则判定相应得分。
4.(小计6分)答:
根据题意已知,两个模型之间只是基础组不同,因此利用基础组和比较组系数关系,可以对应地写出所有月份组的对应关系。
(1)(2分)第二次建模中,截距\(\hat{\alpha}_1\)表示的是基础组(12月份,\(DEC\))的水平,也即:
\[\begin{align} \hat{\alpha}_1 = \hat{\beta}_1 + \hat{\beta}_{12} = 0.7291 + 0.0191 = 0.7483 \end{align}\]
(2)(2分)第二次建模中,截距\(\hat{\alpha}_{11}\)表示的是比较组(10月份,\(OCT\))的与基础组(12月份)的差值水平,也即:
\[\begin{align} \hat{\alpha}_{11} = (\hat{\beta}_1 + \hat{\beta}_{10}) - \hat{\alpha}_1 = 0.7291 + 0.1147 - 0.7483 = 0.0956 \end{align}\]
(3)(2分)第二次建模中,截距\(\hat{\alpha}_{13}\)表示的是平行系数(定量变量\(UNEM\)的斜率)。易知,两次建模中平行斜率系数不会发生改变,因此:
\[\begin{align} \hat{\alpha}_{13} = \hat{\beta}_{13} = 0.0102 \end{align}\]
5.(小计5分)答:
根据辅助建模分析报告结果,可以进行如下的序列1阶自相关性检验。
(1)辅助检验模型\(u_t=\rho u_{t-1} + \epsilon_t\)(其中\(\epsilon_t \sim N(0, \sigma^2)\))
(2)原假设和备择假设:\(H_0:\rho =0\)(不存在自相关性);\(H_1:\rho \neq 0\)(存在自相关性)
(3)检验依据及结论:存在一阶正自相关性。根据辅助回归方程报告,t检验结果表明\(t^{\ast}=7.2093\),对应的概率\(p=0.0000\)表明显著拒绝原假设。
(4)根据辅助回归方程报告,自协方差系数估计量为\(\hat{\rho}=0.5696\)。
6.(小计6分)答:
根据EViews分析报告结果,可以进行德宾-沃森检验(Durbin-Waston)1阶自相关性检验。
(1)辅助检验模型\(u_t=\rho u_{t-1} + \epsilon_t\)(其中\(\epsilon_t \sim N(0, \sigma^2)\))
(2)原假设和备择假设:\(H_0:\rho =0\)(不存在自相关性);\(H_1:\rho \neq 0\)(存在自相关性)
(3)检验依据及结论:存在一阶正自相关性。根据回归方程报告,德宾-沃森检验(Durbin-Waston)统计量\(dw=0.84430\),而且已知\(d_L=1.42\),\(d_U=1.94\),因此有\(0< dw< d_L\),表明存在一阶正自相关性。
(4)根据回归方程报告,自协方差系数估计量为\(\tilde{\rho}=1-\frac{dw}{2}=1- \frac{0.84430}{2}=0.5778\)。
7.(小计4分)答:
(1)(2分)这种矫正方法称为稳健标准误法(或者尼威-威斯特标准误法;或异方差-自相关一致性标准误法)。
(2)(2分)稳健标准误法与OLS估计法相比,回归系数估计结果是一致的,只是对回归系数的估计标准误进行了调整(矫正)。