1 案例分析题
一项研究打算分析课程成绩与学生学积分及性别的关系。样本数据来自856名本科生的计量经济学课程考试情况。其中\(score_i\)表示课程成绩(百分制)、\(gpa_i\)表示学积分(积分点数)、\(male_i\)为性别虚拟变量(\(male_i=1\)表示男生,\(male_i=0\)表示女生)。已知全体学生的平均学积分为2.81。
研究人员分别构建了如下4个计量模型并分别得到OLS估计结果(其中:第一行表示回归系数,第二行s表示标准误,第三行t统计量值,第四行fit表示拟合优度,第五行Ftest表示模型整体显著性F检验):
- 【分析1】成绩\(score_i\)对学积分\(gpa_i\)的线性模型及OLS估计:
\[ \begin{aligned} \begin{split} score_i=&+\alpha_{1}+\alpha_{2}gpa_i+u_i \end{split} \end{aligned} \tag{1}\]
\[\begin{equation} \begin{alignedat}{999} &\widehat{score}=&&+32.31&&+14.32gpa_i\\ &(s)&&(2.0049)&&(0.6997)\\ &(t)&&(+16.11)&&(+20.46)\\ &(fit)&&R^2=0.3289&&\bar{R}^2=0.3281 \end{alignedat} \end{equation}\]
- 【分析2】成绩\(score_i\)对性别\(male_i\)和学积分\(gpa_i\)的线性模型及OLS估计:
\[ \begin{aligned} \begin{split} score_i=&+\beta_{1}+\beta_{2}male_i+\beta_{3}gpa_i+u_i \end{split} \end{aligned} \tag{2}\]
\[\begin{equation} \begin{alignedat}{999} &\widehat{score}=&&+29.66&&+3.83male_i&&+14.57gpa_i\\ &(s)&&(2.0409)&&(0.7418)&&(0.6913)\\ &(t)&&(+14.53)&&(+5.16)&&(+21.08)\\ &(fit)&&R^2=0.3492&&\bar{R}^2=0.3477 &&\\ &(Ftest)&&F^*=228.86&&p=0.0000 && \end{alignedat} \end{equation}\]
- 【分析3】成绩对性别、学积分、以及二者交互项\(male_i \ast gpa_i\)的线性模型及OLS估计:
\[ \begin{aligned} \begin{split} score_i=&+\gamma_{1}+\gamma_{2}male_i+\gamma_{3}gpa_i+\gamma_{4}male:gpa_i+u_i \end{split} \end{aligned} \tag{3}\]
\[\begin{equation} \begin{alignedat}{999} &\widehat{score}=&&+30.36&&+2.48male_i&&+14.33gpa_i&&+0.48male:gpa_i\\ &(s)&&(2.8578)&&(3.9646)&&(0.9845)&&(1.3834)\\ &(t)&&(+10.62)&&(+0.62)&&(+14.56)&&(+0.35)\\ &(fit)&&R^2=0.3493&&\bar{R}^2=0.3470 && && \end{alignedat} \end{equation}\]
- 【分析4】成绩对性别、学积分、以及性别和【去均值化后】学积分(也即\((gpa_i-2.81)\))交互项的线性模型及OLS估计:
\[ \begin{aligned} \begin{split} score_i=&+\lambda_{1}+\lambda_{2}male_i+\lambda_{3}gpa_i+\lambda_{4}male:gpa\_2.81_i+u_i \end{split} \end{aligned} \tag{4}\]
\[\begin{equation} \begin{alignedat}{999} &\widehat{score}=&&+30.36&&+3.82male_i&&+14.33gpa_i&&+0.48male:gpa\_2.81_i\\ &(s)&&(2.8578)&&(0.7422)&&(0.9845)&&(1.3834)\\ &(t)&&(+10.62)&&(+5.15)&&(+14.56)&&(+0.35)\\ &(fit)&&R^2=0.3493&&\bar{R}^2=0.3470 && && \end{alignedat} \end{equation}\]
根据上述信息,请依次按要求回答如下问题:
1.(6分)对比【分析1】和【分析2】的OLS估计结果,请你简单解释一下为什么后者的可决系数\(R^2\)大于前者?继续对比【分析3】和【分析4】的OLS估计结果,请你简单解释一下为什么二者的可决系数\(R^2\)会相等?
2.(4分)根据【分析2】中的OLS估计结果,请你计算出参数估计\(\hat{\beta}_3\)的样本t统计量值\(t^{\ast}_{\hat{\beta}_3}\)(也即空白处的值)。(要求:写出主要计算过程,结果保留两位小数。)
3.(8分)根据【分析2】中的OLS估计结果,给定\(TSS=153539.34\)。(1)请你计算OLS估计的回归平方和ESS,及其自由度?(2)请你计算OLS估计的回归误差标准差se(用符号\(\hat{\sigma}\)表达)?(要求:写出主要计算过程,结果保留两位小数。)
4.(6分)观察【分析3】的OLS估计结果,关于性别\(male_i\)估计系数的t检验是否显著?(给定理论查表值为\(t_{(0.975,852)}=1.96\))。如果给定某个女生的学积分为\(gpa_i=2\),请计算出她的预期考试成绩是多少?(要求:写出主要理由;给出计算过程,结果保留两位小数。)
5.(6分)在【分析3】中,有人认为因为自变量\(male_i\)和交互项\(male_i*gpi_i\)之间有线性相关关系(同样也可认为自变量\(gpa_i\)与上述交互项有线性相关关系),因此导致模型出现多重共线性问题。你认为是否需要担心这个问题?请简要说明你的理由。
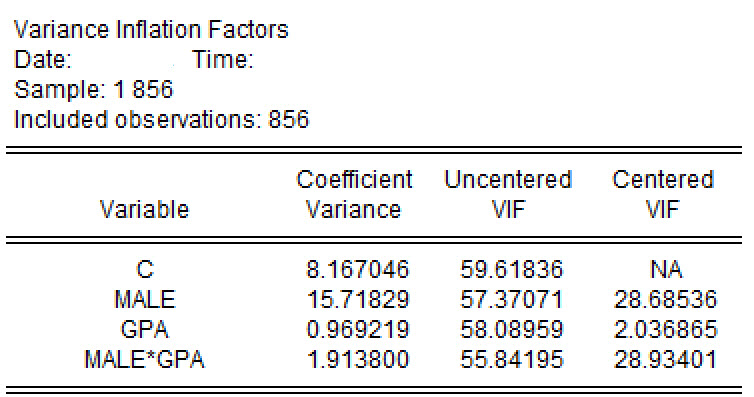
6.(6分)针对【分析3】和【分析4】的OLS估计结果,使用EViews统计软件做出进一步诊断分析,诊断结果分别如下(见 图 1 和 图 2):

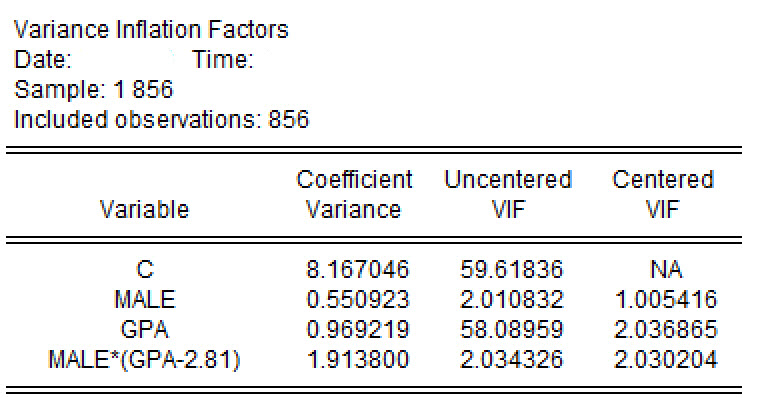
请您根据上述诊断结果回答:(1)上述诊断方法叫什么?(2)上述诊断方法用于诊断什么问题?(3)根据以上诊断结果,你能得到什么结论,请说明理由。
7.(4分)对比【分析3】和【分析4】的OLS估计结果,请你说明二者的估计结果有何异同?根据上述比较,你最终会更倾向于选择采用模型 式 3 还是采用模型 式 4 ?请简要说明你的理由。
2 参考答案
1.(6分) 答:1)(3分)【分析1】和【分析2】的OLS估计结果中,后者的可决系数\(R^2\)大于前者,原因在于后者比前者多引入了一个解释变量\(male_i\)(性别)。而根据计量经济学理论可知,新增加解释变量后,模型的拟合优度至少不会下降。2)(3分)对比【分析3】和【分析4】的模型设定易知,后者只是对其中的一个自变量做了去均值化的线性变换,也即\((gpa_i-2.81)\),因此这本质上并不会改变模型的拟合优度。
2.(4分)答:
\[ \begin{aligned} t^{\ast}_{\hat{\beta}_3} = \frac{\hat{\beta}_3}{\hat{\sigma}_{\hat{\beta}_3}} = \frac{14.5749}{0.6913} = 21.08 \end{aligned} \]
3.(8分)答:我们可以利用判定系数\(R^2\)和统计量\(F^{\ast}\)进行求解。
已知\(R^2=0.3492\)和\(F^{\ast} = 228.8589\),而且已知回归平方和ESS的自由度\(f_1 = 2\),残差平方和RSS的自由度\(f_2 = 853\)。若给定总回归平方和\(TSS=153 539.34\),则根据如下公式:
\[ \begin{aligned} & R^2=\frac{E S S}{T S S}=\frac{E S S}{E S S+R S S}=\frac{E S S / f_2}{E S S / f_2+S e^2} = 0.3492\\ & F^*=\frac{E S S / f_1}{R S S / f_2}=\frac{E S S / f_1}{S e^2} = 228.8589 \end{aligned} \]
可以得到回归平方和\(ESS=53 617.71\);残差平方和\(RSS=99 921.64\),回归误差标准差se,也即\(\hat{\sigma}=10.82\)。
判卷说明:理论过程清楚,公式运用正确,可使用多种计算方法,均可得分。
4.(6分)答:(1)(3分)【分析3】的OLS估计结果表明\(t^{\ast}_{\hat{\gamma}_2}=0.62\),明显小于理论t查表值\(t_{(0.975,852)}=1.96\),因此t检验不显著。(2)(3分)给定学积分为\(gpa_i=2\),则其预期考试成绩为\(E(score|(gpa=2,male=0))=\gamma_1 + \gamma_3gpa_i =30.36+14.33*2=\) 59.02。
5.(6分)答:(1)(2分)首先自变量\(male_i\)和交互项\(male_i*gpi_i\)之间有线性相关关系确实可能会带来多重共线性问题。(2)(4分)主要理由:【分析3】在【分析2】基础上增加交互项之后,\(male_i\)变量t检验不显著,而且其系数的估计精度大大下降(其标准误差从0.7418增大3.9646),因此可以认为多重共线性确实给模型估计带来了干扰。其根源在于给定一个男性,其交互项中的学积分变量\(gpa_i\)基本不大可能为0,从而导致\(male_i\)和交互项\(male_i\times gpi_i\)高度线性相关。
6.(6分)答:(1)上述诊断方法称为方差膨胀因子分析法(VIF);(2)方差膨胀因子分析法(VIF)主要用于诊断原模型是否存在多重共线性问题。(3)根据图1的诊断结果可知,变量\(male_i\)的VIF值为\(28.69>10\);交互项\(male_i \ast gpa_i\)的VIF值为\(28.93>10\)。表明【分析3】中模型存在多重共线性问题。而图2的诊断结果可以看到所有变量的VIF值都小于10,表明【分析4】中模型的多重共线性问题基本得到了缓解,不需要再过度担心。
7.(4分)答:(1)【分析3】和【分析4】的结果可以看出,只有\(male_i\)的系数估计、标准误和t统计量发生了改变,其他变量的这些估计量都不变。(2)结合问题3的相关考虑,我们更应该倾向选择【分析4】设定的计量模型,因为变量的去均值变换是一种有效的缓解多重共线性问题的手段之一。