| obs | salary | phdyrs | servyrs | rank | area | sex |
|---|---|---|---|---|---|---|
| 3 | 79750 | 4 | 3 | Ast | B | M |
| 35 | 80225 | 4 | 2 | Ast | B | F |
| 49 | 140096 | 25 | 25 | Pro | B | F |
| 144 | 89942 | 3 | 3 | Ast | B | M |
| 165 | 88795 | 1 | 0 | Ast | B | M |
| 191 | 180000 | 22 | 9 | Pro | B | M |
| 286 | 81800 | 49 | 49 | Aso | A | M |
| 329 | 99247 | 10 | 10 | Aso | B | M |
| 339 | 128464 | 32 | 25 | Pro | B | M |
| 384 | 105000 | 44 | 44 | Pro | A | M |
1 案例分析题
教师薪水案例数据:一项研究希望分析高校教师薪水\(salary\)的相关影响因素,共收集了样本数n=397的数据集(部分数据集见 表 1 ):
其中,相关变量的具体定义见下面 表 2 :
| 变量 | 定义 | 取值 |
|---|---|---|
| obs | 样本 | 整数,1~397 |
| salary | 薪水 | 定量变量,单位美元 |
| phdyrs | 获得博士学位的年数 | 定量变量,取整数 |
| servyrs | 工作年数 | 定量变量,取整数 |
| rank | 职称 | 定性变量,Pro表示教授、Aso表示副教授、Ast表示助理讲师 |
| area | 研究领域 | 定性变量,A表示理论研究,B表示应用研究 |
| sex | 性别 | 定性变量,M表示男性,F表示女性 |
下面计算题都是基于以上案例情景和数据集。请认真读题并按要求作答。
1.(共12分,共4小题)A研究人员尝试构建了如下的线性回归模型(见 式 1 ):
\[ \begin{align} \begin{split} salary_i &=\beta_{1}+\beta_{2}phdyrs_i+\beta_{3}servyrs_i+u_i && \text{(linear model )} \end{split} \end{align} \tag{1}\]
然后采用OLS方法进行估计,得到如下面 图 1 所示的EViews报告。
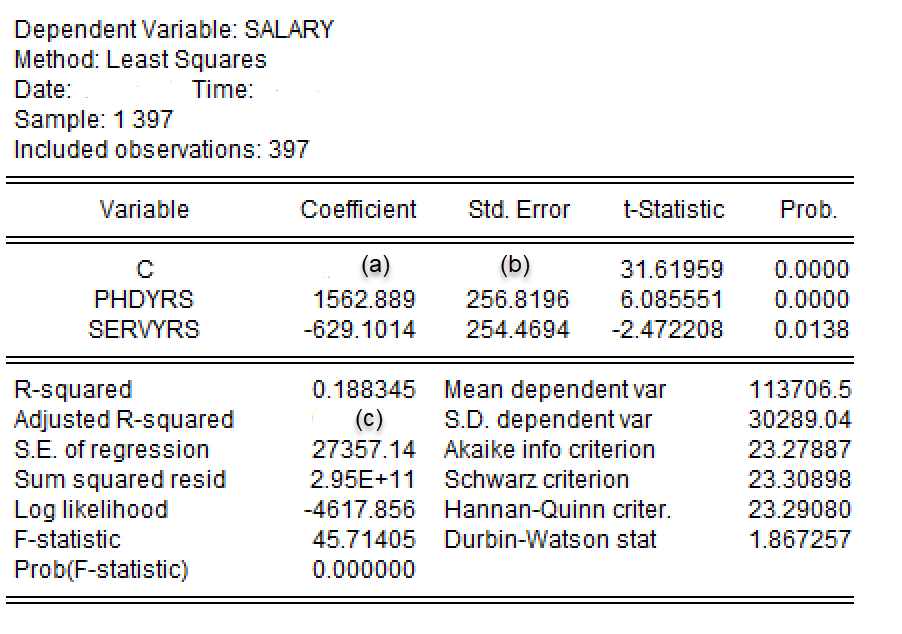
(1)(4分)已知数据集中,平均薪水\(\overline{salary}\)=113706.4584美元、平均博士毕业年数\(\overline{phdyrs}\)=22年、平均工作年数\(\overline{servyrs}\)=18年,请分别计算上述EViews的回归结果中的空白项a和空白项b。(要求:写出主要计算过程;结果保留4位小数。)
(2)(2分)如果某位教师的博士毕业年数为5年(也即\(phdyrs=5\)),而且工作年数为3年(也即\(servyrs=3\)),请根据上述EViews的回归结果计算该教师的薪水的估计值是多少。(要求:写出主要计算过程;结果保留2位小数。)
(3)(3分)根据上述EViews的回归结果,请计算出参数\(\beta_3\)的95%置信区间。(提示:\(t_{0.975}(394)=\) 1.9660;计算结果请保留4位小数。)
(4)(3分)根据上述EViews的回归结果,请计算出空白处c的调整的可决系数\(\overline{R^2}\)。(要求:写出主要计算过程;计算结果保留4位小数。)
2.(共12分,共3小题)A研究人员根据前述EViews回归报告(见 图 1 ),对其回归残差的平方\(e^2_i\)进一步进行了如下的诊断辅助建模:
\[ \begin{align} \begin{split} e^2_i=\delta_{1}+\delta_{2}phdyrs_i+\delta_{3}servyrs_i +\delta_{4}phdyrs^2_i +\delta_{5}servyrs^2_i+v_i \quad \text{(aux model)} \end{split} \end{align} \tag{2}\]
对上述辅助模型使用EViews软件分析得到如下报告(见 图 2 ):
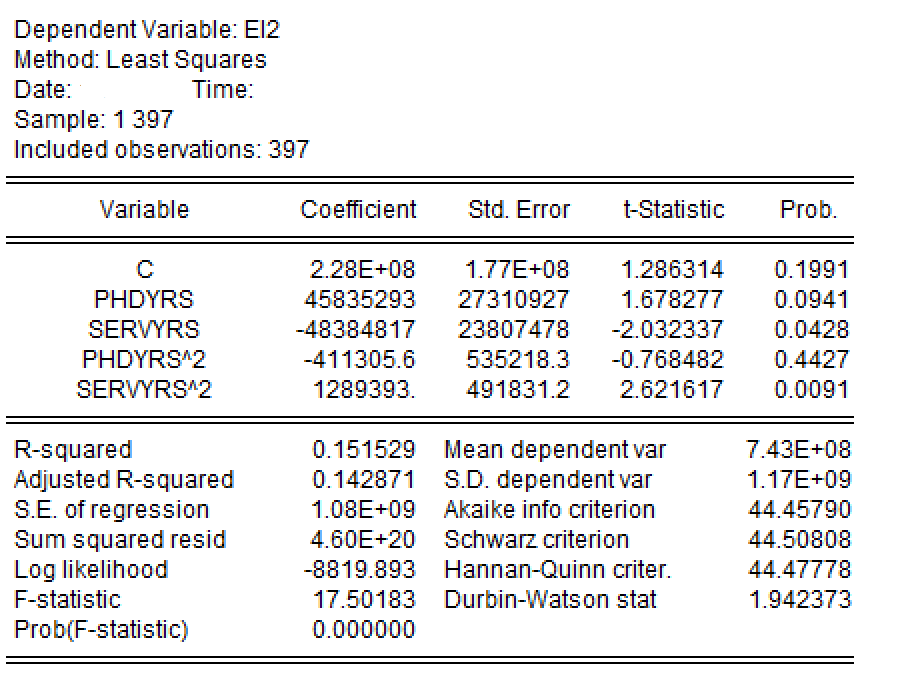
(1)(4分)请你指出上述辅助诊断模型(见 式 2 )可以用于检验(诊断)放宽经典线性回归模型假设的那种问题?这一检验的具体名称是什么?请你写出这一检验的原假设\(H_0\)和备择假设\(H_1\)分别是什么?
(2)(4分)根据上述EViews回归报告(见 图 2 ),请你写出第(1)问中检验方法的统计量理论计算公式,并计算出具体统计量值。给定显著性水平\(\alpha=0.05\),请你得出诊断检验的最终诊断结论。(要求:写出理论过程;计算结果保留4位小数。提示:已知\(\chi^2_{0.95}(5)\)=11.0705;\(\chi^2_{0.95}(4)\)=9.4877;\(\chi^2_{0.95}(2)\)=5.9915)
(3)(4分)A研究人员根据上述的诊断检验分析,如果他认为很有必要对最开始设想的线性模型(见 式 1 )进行加权最小二乘法(WLS)矫正。请你为他写出加权最小二乘法的权重\(\tilde{w}_i\)的正确表达式。(要求:写出理论表达式即可。提示:给定\(\tilde{e}^2_i =\tilde{\delta}_{1}+\tilde{\delta}_{2}phdyrs_i+\tilde{\delta}_{3}servyrs_i +\tilde{\delta}_{4}phdyrs^2_i +\tilde{\delta}_{5}servyrs^2_i\))
3.(共16分,共4小题)为了更好地分析教师薪水\(salary_i\)的决定机制,B研究人员决定将数据中的定性变量(职称\(rank_i\)、研究领域\(area_i\)和性别\(sex_i\),具体见变量定义表 表 2 )也纳入回归分析模型中来,并将这些定性变量依次转换为如下所示的虚拟变量,
\[ \begin{align} rank_i: \begin{cases} rank\_Pro = \begin{cases} 1, & \text{Pro}\\ 0, & \text{not Pro} \end{cases} \\ rank\_Aso = \begin{cases} 1, & \text{Aso}\\ 0, & \text{not Aso} \end{cases} \\ rank\_Ast = \begin{cases} 1, & \text{Ast}\\ 0, & \text{not Ast} \end{cases}\\ \end{cases} \end{align} \]
\[ \begin{align} area_i: \begin{cases} area\_A = \begin{cases} 1, & \text{A}\\ 0, & \text{not A} \end{cases} \\ area\_B = \begin{cases} 1, & \text{B}\\ 0, & \text{not B} \end{cases} \\ \end{cases} \end{align} \]
\[ \begin{align} sex_i: \begin{cases} sex\_M = \begin{cases} 1, & \text{M}\\ 0, & \text{not M} \end{cases} \\ sex\_F = \begin{cases} 1, & \text{F}\\ 0, & \text{not F} \end{cases} \\ \end{cases} \end{align} \]
然后,B研究人员决定将虚拟变量引入线性回归模型,并采用EViews软件分析得到如下所示的回归分析结果(见 图 3 )。请你按要求回答后面的各个小题。
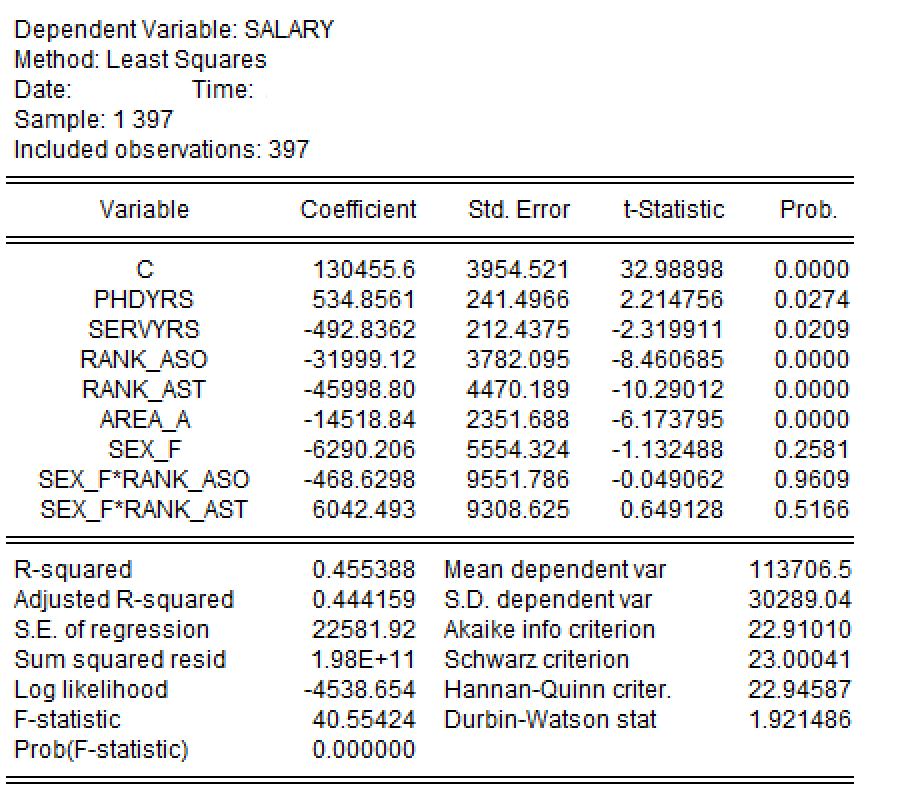
(1)(4分)如果不设定基础组(或参照组),而同时使用上述三个定性变量以及两个定量变量(博士毕业年数\(phdyrs_i\)和工作年数\(servyrs_i\)),来分析它们对教师薪水\(salary_i\)的影响。请你正确写出加法形式的总体线性回归模型。(要求:回归参数使用符号\(\alpha_1,\alpha_2 \cdots\)表达,随机干扰项使用符号\(v_i\)表达。)
(2)(4分)根据B研究人员的回归分析结果(见 图 3 ),请写出在这一回归报告设定下的基础组(或参照组)群体是什么?
(3)(4分)根据B研究人员的回归分析结果(见 图 3 ),请你指出性别变量\(sex_i\)与职称变量\(rank_i\)是否会联合影响到教师薪水\(salary_i\),并简要说明你的判断理由。
(4)(4分)根据B研究人员的回归分析结果(见 图 3 ),在薪资问题上,女性教师是不是受到了性别歧视?请你计算出博士毕业5年、工作年数3年的{应用研究领域的女性副教授}的薪水的估计值是多少?(要求:结果保留2位数。)
2 参考答案
1.(共12分,共4小题):
(1)(小计4分)答:
1)(2分)根据理论公式和已知数值可以计算得到:
\[ \begin{align} \hat{\beta}_1 &= \overline{Y} - \hat{\beta}_2\overline{X}_{2i} - \hat{\beta}_3\overline{X}_{3i} \\ \hat{\beta}_1 &= \overline{salary} - \hat{\beta}_2 \times \overline{phdyrs} - \hat{\beta}_3 \times \overline{phdyrs} \\ \hat{\beta}_1 &= 113706.4584 - 1562.889 \times 22 - (-629.1014) \times 18 = 90646.7256 \end{align} \]
2)(2分)根据理论公式和已知数值可以计算得到:
\[ \begin{align} s_{\hat{\beta}_1} &= \frac{\hat{\beta}_1}{t^{\ast}_{\hat{\beta}_1}} = \frac{90646.7256}{31.61959} = 2866.7900 \end{align} \]
(2)(小计2分)答:根据理论公式和已知数值可以计算得到:
\[ \begin{align} \hat{Y}_i &= \hat{\beta}_1 + \hat{\beta}_2 X_{2i} + \hat{\beta}_3 X_{3i} \\ \widehat{salary}_i &= \hat{\beta}_1 + \hat{\beta}_2 phdyrs_{i} + \hat{\beta}_3 servyrs_{i} \\ & = 90646.7256 + 1562.8890 \times 5 + -629.1014 \times 3\\ &= 96573.87 \end{align} \]
判卷说明:适用矩阵方法计算\(\boldsymbol{\hat{y}}=\boldsymbol{X\hat{\beta}}\),过程和结果正确也可得分。
(3)(小计3分)答:根据理论公式和已知数值可以计算得到:
\[ \begin{align} \beta_3 & \in \left[ \hat{\beta}_3 - t_{1-\alpha/2}(n-3)\cdot s_{\hat{\beta}_3}, \hat{\beta}_3 + t_{1-\alpha/2}(n-3)\cdot s_{\hat{\beta}_3} \right] \\ \beta_3 & \in \left[ -629.1014 - 1.9660\times 254.4694, -629.1014 + 1.9660\times 254.4694 \right] \\ \beta_3 & \in \left[ -1129.3882, -128.8146 \right] \end{align} \]
(4)(3分)答:根据理论公式和已知数值\(n=397,k=2,R^2=0.188345\)可以计算得到:
\[ \begin{align} \overline{R^2} &= 1 - (1-R^2)\frac{n-1}{n-k-1} \\ &= 1- (1-0.188345)\frac{397-1}{397-2-1} = 0.1842 \end{align} \]
判卷说明:本题还可以使用其他如下包括但不限于的方法。a.平方和公式\(\overline{R^2}=1 - \frac{RSS/(n-k-1)}{TSS/(n-1)}\)。b.样本方差公式\(\overline{R^2}=1 - \frac{\hat{\sigma}^2}{S^2_{Y_i}}\)。理论公式无误,计算结果正确即可得分。
2.(共12分,共3小题):
(1)(小计4分)答:
1)(1分)检验主模型是否存在异方差问题。
2)(1分)这一检验方法为怀特异方差检验(White test)。
3)(2分)原假设\(H_0:\delta_{2}=\delta_{3}=\delta_{4}=\delta_{5}=0\),备择假设\(H_1:\delta_{p}\)不全为0, 其中\(p \in c(2,3,\cdots,5)\)。(或者原假设\(H_0:\)同方差;原假设\(H_1:\)怀特辅助模型所示的异方差。)
(2)(小计4分)答:
1)(2分)根据理论公式和已知数值\(n=397\)、\(\chi^2_{0.95}(4)=\) 9.4877、\(R^2_{aux}=\) 0.151529可以计算得到:
\[ \begin{align} {\chi^2}^{\ast} &= n \times R^2_{aux} = 397 \times 0.151529 = 60.1570 \end{align} \]
2)(2分)因为卡方统计量\({\chi^2}^{\ast}=\) 60.1570大于理论查表值\(\chi^2_{0.95}(4)\)=9.4877,因此认为主模型存在怀特辅助方程形式的异方差问题。
判卷说明:a.学生需要使用正确的卡方查表值。b.本题也可以直接通过辅助方程报告中的F检验进行作答。过程说明和结论判断无误,则可相应得分。
(3)(小计4分)答:根据加权最小二乘法(WLS)的原理,结合前述怀特异方差辅助检验的结论,很容易可以得到WLS的一种可行权重,也即:
\[ \begin{align} Var(u_i)& =\sigma^2 \cdot f(X_i) \\ & = \sigma^2 \cdot \left( \delta_{1}+\delta_{2}phdyrs_i+\delta_{3}servyrs_i +\delta_{4}phdyrs^2_i +\delta_{5}servyrs^2_i+v_i\right) \end{align} \]
则有:
\[ \begin{align} \tilde{w}_i& = \frac{1}{\sqrt{\widehat{f(X_i)}}} = \frac{1}{\sqrt{\tilde{e}^2_i}}\\ &= \frac{1}{\sqrt{\tilde{\delta}_{1}+\tilde{\delta}_{2}phdyrs_i+\tilde{\delta}_{3}servyrs_i +\tilde{\delta}_{4}phdyrs^2_i +\tilde{\delta}_{5}servyrs^2_i}} \end{align} \]
判卷说明:只要正确写出后面方程的任何一步都可得满分。
3.(共16分,共4小题):
(1)(小计4分)答:加法形式的总体线性回归模型为:
\[ \begin{align} salary_i &= \alpha_1rank\_{Pro} +\alpha_2 rank\_{Aso} +\alpha_3 rank\_{Ast} \\ &+\alpha_4 area\_{A} +\alpha_5 area\_{B} +\alpha_7 sex\_{M} +\alpha_8 sex\_{F} \\ &+\alpha_8 phdyrs_i + \alpha_9servyrs_i +v_i \end{align} \]
判卷说明:需要正确使用\(\alpha_1,\alpha_2 \cdots\)和随机干扰项符号\(v_i\)。参数的下标和先后顺序可以任意处理。
(2)(小计4分)答:这一回归报告设定下的基础组(或参照组)群体是:在应用研究领域的男性教授。
判卷说明:此处强调具体经济学场景应用。应该根据最开始的数据集和变量定义,恰当写出语句通顺的中文表达。如果仅仅只写是出:基础组群体为\(rank\_Pro,area\_B,sex\_M\),则应相应扣1分。
(3)(小计4分)答:
1)(2分)结论:性别变量\(sex_i\)与职称变量\(rank_i\)是不会联合影响到教师薪水\(salary_i\)。
2)(2分)理由:因为性别变量\(sex_i\)与职称变量\(rank_i\)交叉项的t检验都不显著。
(4)(小计4分)答:
1)(1分)从虚拟变量回归结果看,未能发现女性收到了工资歧视。因为无论是性别的独立性,还是交叉项,其系数的t检验都是不显著的。
2)(3分)根据EViews虚拟变量回归方程的系数:
\[ \begin{align} \boldsymbol{\hat{\beta}}'= &[ 130455.6, 534.8561, -492.8362, -31999.12, -45998.8, \\ &-14518.84, -6290.206, -468.6298, 6042.493 ] \end{align} \]
以及给定的:
\[ \begin{align} X=&[C, phdyrs, servyrs, rank\_Aso, rank\_Ast, area_A, sex_F,\\ &sex_F*rank\_Aso, sex_F*rank\_Ast ] \\ =&\left[1, 5, 3, 1, 0, 0, 1, 1, 0\right] \end{align} \]
则根据理论公式,可以计算得到:
\[ \begin{align} \widehat{salary}_i &= \boldsymbol{X\hat{\beta}} = 92 893.42 \end{align} \]
判卷说明:学生使用上述矩阵计算,或者另外一种代数公式方法计算,结果都是一样的。过程和结果正确即可得分。