1 案例分析题
1.(共12分,共2小题)对于如下的二元线性回归模型:
\[ \begin {align} Y_{i} &={\beta}_{1}+{\beta}_{2} X_{2 i}+{\beta}_{3} X_{3 i}+u_{i} \end {align} \]
现在将对应的样本回归模型(SRM)表达为矩阵形式\(\boldsymbol{y=X \hat{\beta}+e}\),并已知普通最小二乘法(OLS)下,回归系数的估计值为:
\[ \boldsymbol{\hat{\beta}}= \begin{bmatrix} 300.2863 & 0.742 & 8.0436 \end{bmatrix} ^{\prime} \]
回归系数的方差协方差矩阵为:
\[ var-cov(\boldsymbol{\hat{\beta}})= \hat{\sigma}^2\boldsymbol{(X'X)^{-1}} = \begin{bmatrix} 6133.6505&-3.7079&220.2063 \\ -3.7079&0.0023&-0.1371 \\ 220.2063&-0.1371&8.9015 \\ \end{bmatrix} \]
(1)(6分)请你用矩阵符号,写出回归系数向量\(\boldsymbol{\hat{\beta}}\)的理论计算公式。(要求:使用如下的相关矩阵记号\(\boldsymbol{X,y}\),注意加粗)。
(2)(6分)给定 \(\alpha=0.05,n=15\),t分布的理论查表值为 \(t_{1-\alpha/2}(n-k)=t_{0.975}(13)=\) 2.1788。请你根据前述条件,对斜率回归系数分别做出显著性t检验。(要求:基本计算过程,结果保留4位小数,并对检验结论进行简要说明)。
2.(共16分,共4小题)利用某国近8年冰箱销售的季度数据分析冰箱销售的影响因素,A同学设定了如下的虚拟变量模型:
\[ \begin{align} \operatorname{Frig}_{i}=\beta_{0}+\beta_{1} D_{1}+\beta_{2} D_{2}+\beta_{3} D_{3}+\beta_{4} D u r_{i}+u_{i} \quad \text{(dummy mode01) } \end{align} \tag{1}\]
其中:\(Frig\)为冰箱销售数量(单位:千台);\(Dur\)为耐用品支出(单位:亿元); \(D_1=1\)表示第一季度,\(D_1=0\)表示其他;\(D_2=1\)表示第二季;\(D_2=0\)表示其他;\(D_3=1\)表示第三季度,\(D_3=0\)表示其他;\(D_4=1\)表示第四季度,\(D_4=0\)表示其他。
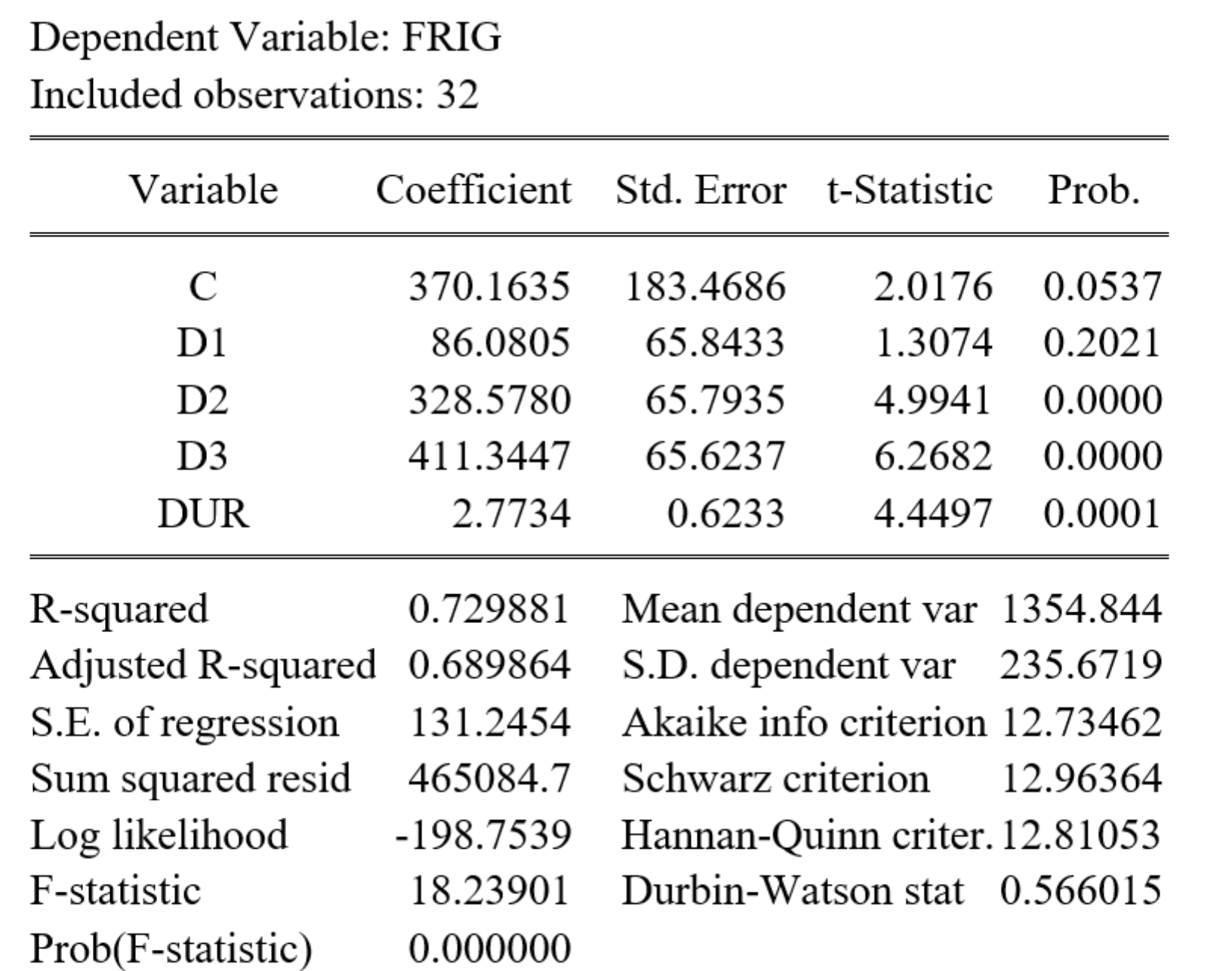
样本数据的OLS回归结果如下:

(1)(6分)上述虚拟变量模型(见 式 1 )中,基础组为哪一季度?根据回归分析报告(见 图 1 ),冰箱的销售量各个季度之间的差异是否显著并简要说明理由?
(2)(2分)若某年第二季度耐用品支出为260亿美元,利用上述回归分析报告(见 图 1 )计算该季度冰箱的销售量。(要求:结果保留4位小数)。
(3)(4分)在置信水平为95%下,请你计算参数\(\beta_4\)的双侧置信区间。计算中可能用到的查表值:\(|t_{0.05} (27)|=1.7032\), \(|t_{0.025} (28)|=2.0484\), \(|t_{0.025}(27)|=2.0518\)。(要求:写出理论公式,列出主要计算过程,结果保留4位小数。)
(4)(4分)如果B同学重新设定如下虚拟变量回归模型:
\[ \begin{align} \operatorname{Frig}_{i}=\alpha_{1}+\alpha_{2} D_{2}+\alpha_{3} D_{3}+\alpha_{4} D_{4}+\alpha_{5} D u r_{i}+v_{i} \quad \text{(dummy mode02) } \end{align} \tag{2}\]
根据虚拟变量的经济学含义,以及 图 1 中的OLS参数估计EViews结果,请你写出上述模型(见 式 2 )的样本回归函数(SRF)。(要求:写出样本回归方程及系数估计值,不用写出系数的t值和标准差,写出简要计算过程,参数估计值保留4位小数)。
3.(12分)假设某商品的总成本(\(Y\))和产出(\(X\))之间存在如下模型关系:
\[ \begin{align} \mathrm{Y}_{i}=\beta_{0}+\beta_{1} X_{i}+u_{i} \end{align} \tag{3}\]
样本数据的OLS回归结果如下:
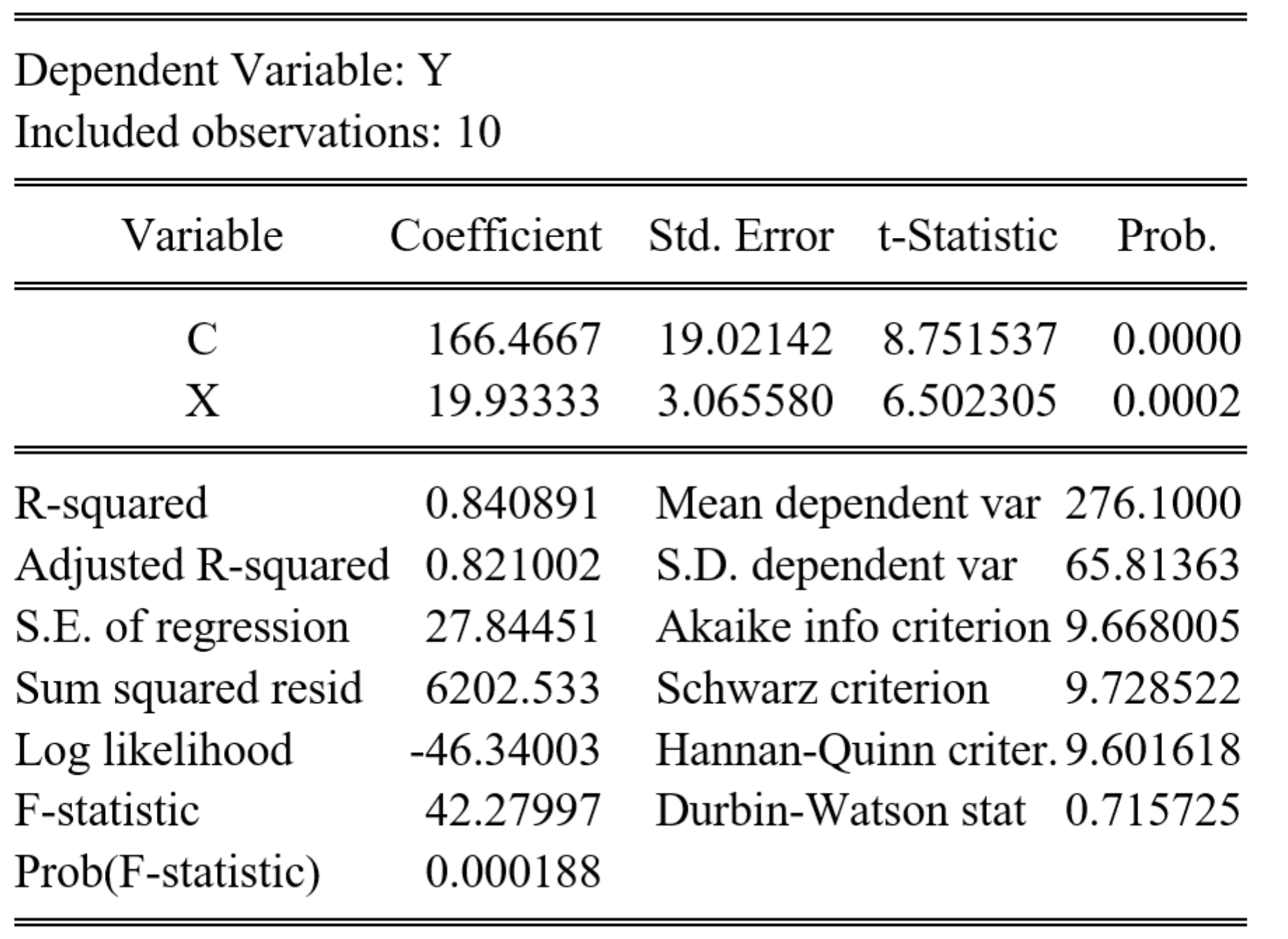
(1)(6分)请根据上述回归结果(见 图 2 ),请你指出Durbin-Watson统计量的\(d\)值是多少?假定主模型(见 式 3 )存在随机干扰项1阶自相关问题,也即\(u_t = \rho u_{t-1} +\varepsilon_t\),请你计算出自相关系数的估计值 \(\hat{\rho}\) 是多少?进一步地,请你进行Durbin-Watson(德宾-沃森)检验,验证主模型(见 式 3 )是否存在随机干扰项序列自相关问题?(提示:给定\(D_L=0.879,D_U=1.32\)。要求:计算值保留4位小数,给出检验依据,进行简要说明)。
(2)(6分)为了进一步分析主模型(见 式 3 )是否存在随机干扰项自相关问题,C同学进一步做了如下形式的某种检验,检验结果如下:
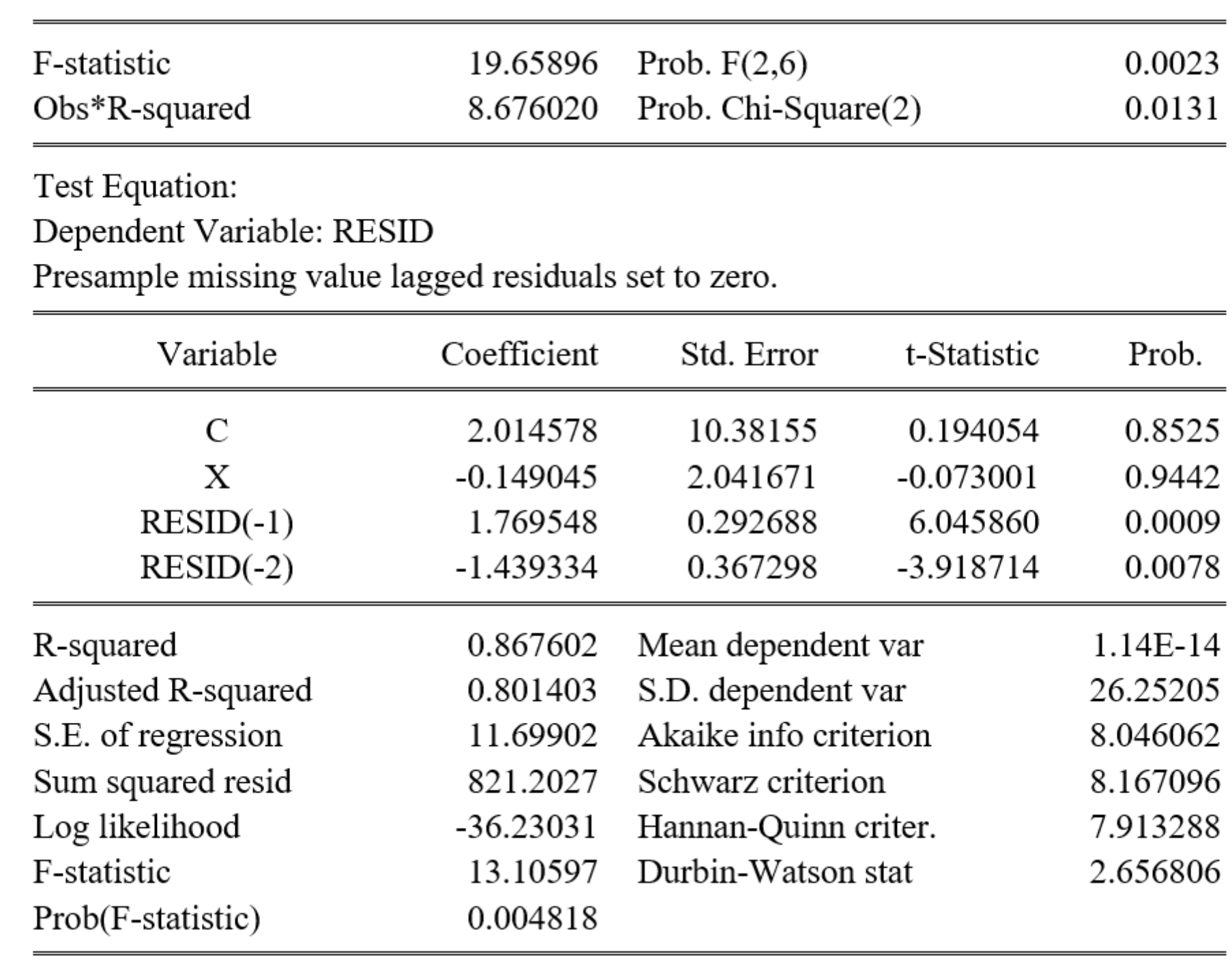
根据上述报告结果(见 图 3 ),请你指出C同学的检验方法名称具体是什么?你能从上述检验种得出什么检验结论?( 提示:已知给定显著性水平\(\alpha=0.05\),理论查表值\(\chi^2 (2)=5.99\)。要求:写出原假设和主要检验过程,并进行简要说明。)
2 参考答案
1.(共12分,共2小题):
(1)(小计6分)答:回归参数估计量为\(\boldsymbol{\hat\beta=(X'X)^{-1}X'Y}\)
(2)(小计6分)本案例中,斜率系数有两个,需要分别对\(\beta_2\)和\(\beta_3\)进行t检验。
原假设和备择假设分别为:\(H_0:\beta_2=0;H_1:\beta_2 \neq 0\);以及 \(H_0:\beta_3=0;H_1:\beta_3 \neq 0\)。下面将使用矩阵计算法直接计算t统计量,并得到t检验结论,具体如下:
已知系数的OLS估计值为:
\[ \boldsymbol{\hat{\beta}}= \begin{bmatrix} 300.2863 & 0.742 & 8.0436 \end{bmatrix} ^{\prime} \]
回归系数的方差协方差矩阵为:
\[ var-cov(\boldsymbol{\hat{\beta}})= \hat{\sigma}^2\boldsymbol{(X'X)^{-1}} = \begin{bmatrix} 6133.6505&-3.7079&220.2063 \\ -3.7079&0.0023&-0.1371 \\ 220.2063&-0.1371&8.9015 \\ \end{bmatrix} \]
因此,OLS系数估计标准方差和标准差分别为:
\[ \begin{equation} S^2(\boldsymbol{\hat{\beta}})= \begin{bmatrix} 6133.6505\\ 0.0023\\ 8.9015 \\ \end{bmatrix} ;\qquad S(\boldsymbol{\hat{\beta}})= \begin{bmatrix} 78.3176257\\ 0.0479583\\ 2.9835382 \\ \end{bmatrix} \end{equation} \]
利用理论公式,可以得到样本t统计量如下:
\[ \begin{align} {t^{\ast}_{\hat{\beta}}} &= \frac{\hat{\beta}}{s_{\hat{\beta}}} = \begin{bmatrix} 3.8342\\ 15.4718\\ 2.6960 \end{bmatrix} \end{align} \]
进一步地,根据理论查表值\(t_{0.975}(12)=2.18\),可以得到样本t统计量与t查表值的对比关系:
\[ \begin{align} {t^{\ast}_{\hat{\beta}}}-t_{0.975}(12) & = \begin{bmatrix} 3.8342\\ 15.4718\\ 2.6960 \end{bmatrix} - 2.18 \\ &= \begin{bmatrix} 1.6542\\ 13.2918\\ 0.5160 \end{bmatrix} > \begin{bmatrix} 0\\ 0\\ 0 \end{bmatrix} \end{align} \]
最后,根据上述结果,可以认为所有斜率回归系数的t检验都是显著的。
2.(共16分,共4小题)
(1)(小计6分)答:1)(2分)上述虚拟变量模型中,基础组为第四季度。2)(4分)根据回归分析报告,可以发现冰箱的销售量在第二季度、第三季度和第四季度上是显著不同的,但是第一季度上并没有表现出与基础组的明显不同。具体依据是各虚拟变量回归系数估计量对应的概率p值。如果概率p值小于0.1,则认为对应的季度与基础组是显著不同的。
(2)(小计2分)答:根据题意可知\(D1=0,D2=1,D3=0;Dur = 260\),进一步根据回归分析报告可知
\[ \begin{align} \hat{Y}_i &= 370.1635 +86.0805\cdot D1 + 328.5780\cdot D2 \\ &+411.3447 \cdot D3 +2.7734 \cdot Dur_i \\ &= 1 419.8255 \end{align} \]
(3)(小计4分)答:根据回归分析报告已知\(\hat{\beta}_4=2.7734\),理论查表值\(|t_{0.025}(27)|=2.0518\),因此可以得到\(\beta_4\)的95%置信区间为:
\[ \begin{align} \hat{\beta}_4 - t \cdot s_{\hat{\beta}_4} \leq \beta_4 \leq \hat{\beta}_4 + t \cdot s_{\hat{\beta}_4} \\ 1.4945 \leq \beta_4 \leq 4.0523 \end{align} \]
(4)(小计4分)答:根据虚拟变量回归模型的含义,以及给出的回归分析报告结果,给定\(Dur_i=0\)可以知道:
第四季度(基础组)销量为:\(E(D1=D2=D3=0,Dur_i=0)=\hat{\beta}_0=370.1635\)
第一季度销量为:\(E(D1=1,D2=D3=0,Dur_i=0)=\hat{\beta}_0 + \hat{\beta}_1=456.244\)
第二季度销量为:\(E(D1=0,D2=1,D3=0,Dur_i=0)=\hat{\beta}_0 + \hat{\beta}_2=698.7415\)
第三季度销量为:\(E(D1=D2=0,D3=1,Dur_i=0)=\hat{\beta}_0 + \hat{\beta}_3=781.5082\)
根据模型(见(2)),我们可以得到如下对应关系:
第四季度销量为:\(E(D2=D3=0,D4=1,Dur_i=0)=\hat{\alpha}_1 + \hat{\alpha}_4=\hat{\beta}_0=370.1635\)
第一季度(基础组)销量为:\(E(D2=D3=D4=0,Dur_i=0)=\hat{\alpha}_1=\hat{\beta}_0 + \hat{\beta}_1=456.244\)
第二季度销量为:\(E(D1=0,D2=1,D3=0,Dur_i=0)=\hat{\alpha}_1 + \hat{\alpha}_2=\hat{\beta}_0 + \hat{\beta}_2=698.7415\)
第三季度销量为:\(E(D1=D2=0,D3=1,Dur_i=0)=\hat{\alpha}_1 + \hat{\alpha}_3=\hat{\beta}_0 + \hat{\beta}_3=781.5082\)
因此,可以得到:
\(\hat{\alpha}_1=\hat{\beta}_0 + \hat{\beta}_1=456.244\)
\(\hat{\alpha}_2=\hat{\beta}_0 + \hat{\beta}_2 - \hat{\alpha}_1=242.4975\)
\(\hat{\alpha}_3=\hat{\beta}_0 + \hat{\beta}_3 - \hat{\alpha}_1=325.2642\)
\(\hat{\alpha}_4=\hat{\beta}_0 - \hat{\alpha}_1=-86.0805\)
\(\hat{\alpha}_5=\hat{\beta}_4 =2.7734\)(斜率不变性)
最后得到模型(见(2))的样本回归方程为:
\[ \begin{align} \widehat{Frig}_{i}&=\hat{\alpha}_{1}+\hat{\alpha}_{2} D_{2}+\hat{\alpha}_{3} D_{3}+\hat{\alpha}_{4} D_{4}+\hat{\alpha}_{5} D u r_{i} \\ &= 456.2440+242.4975D_{2}+325.2642D_{3} -86.0805D_{4}+2.7734Dur_{i} \end{align} \]
3.(共12分,共2小题):
(1)(小计6分)答:1)根据回归分析报告结果可知,Durbin-Watson统计量\(d=0.715725\)。2)一阶自相关系数\(\hat{\rho}=1-d/2=0.6421\)。3)已知\(D_L=0.879,D_U=1.32\),则有\(4-D_L=3.1210\)。因为\(0 \leq d <D_L\),认为主模型存在一阶正自相关问题。
(2)(小计6分)答:1)根据上述检验报告,易知其为拉格朗日乘数检验(LM自相关检验)。2)根据检验结果已知\({{\chi}^2}^{\ast} = 8.67602 > {\chi}^2(2)=5.99\),表明LM检验是在\(\alpha=0.05\)上是显著的,也即认为主模型的随机干扰项存在二阶自相关问题。