| 变量 | 定义 | 取值 |
|---|---|---|
| Lgprice | 对数化价格 | 定量变量,对数化价格 |
| Wd | 工作日 | 定性变量,Mon表示周一;Tue表示周二;Wed表示周三;Turs表示周四;Fri表示周五 |
| Wd1 | 周一 | 虚拟变量, 1表示周一,0表示其他 |
| Wd2 | 周二 | 虚拟变量, 1表示周二,0表示其他 |
| Wd3 | 周三 | 虚拟变量, 1表示周三,0表示其他 |
| Wd4 | 周四 | 虚拟变量, 1表示周四,0表示其他 |
| Wd5 | 周五 | 虚拟变量, 1表示周五,0表示其他 |
| Wave2 | 前两天平均最大浪高 | 定量变量,前两天的平均最大浪高 |
| Wave3 | 后三天平均最大浪高 | 定量变量,后三天的平均最大浪高 |
| Time | 时间 | 定量变量,将全部天数表达为日期序列 |
1 案例分析题
渔业市场案例:一项实证研究某渔业港口城市在工作日中(也即不包括周六和周日)的海鱼产品市场价格问题及其相关影响因素,相关变量的具体定义见 表 1 :
该实证研究共收集了样本数T=97天的数据集,部分数据集见 图 1 :
A同学构建了 式 1 所示的虚拟变量回归模型:
\[ \begin{aligned} \begin{split} Lgprice_t=&+\alpha_{1}+\alpha_{2}Wd1_t+\alpha_{3}Wd2_t+\alpha_{4}Wd3_t+\alpha_{5}Wd4_t\\&+\alpha_{6}Time_t+v_t \end{split} \quad \text{(受约束模型A)}\quad \end{aligned} \tag{1}\]
B同学构建了 式 2 所示的虚拟变量回归模型:
\[ \begin{aligned} \begin{split} Lgprice_t=&+\beta_{1}+\beta_{2}Wd1_t+\beta_{3}Wd2_t+\beta_{4}Wd3_t+\beta_{5}Wd4_t\\&+\beta_{6}Time_t+\beta_{7}Wave2_t+\beta_{8}Wave3_t+u_t \end{split} \quad \text{(无约束模型B)}\quad \end{aligned} \tag{2}\]
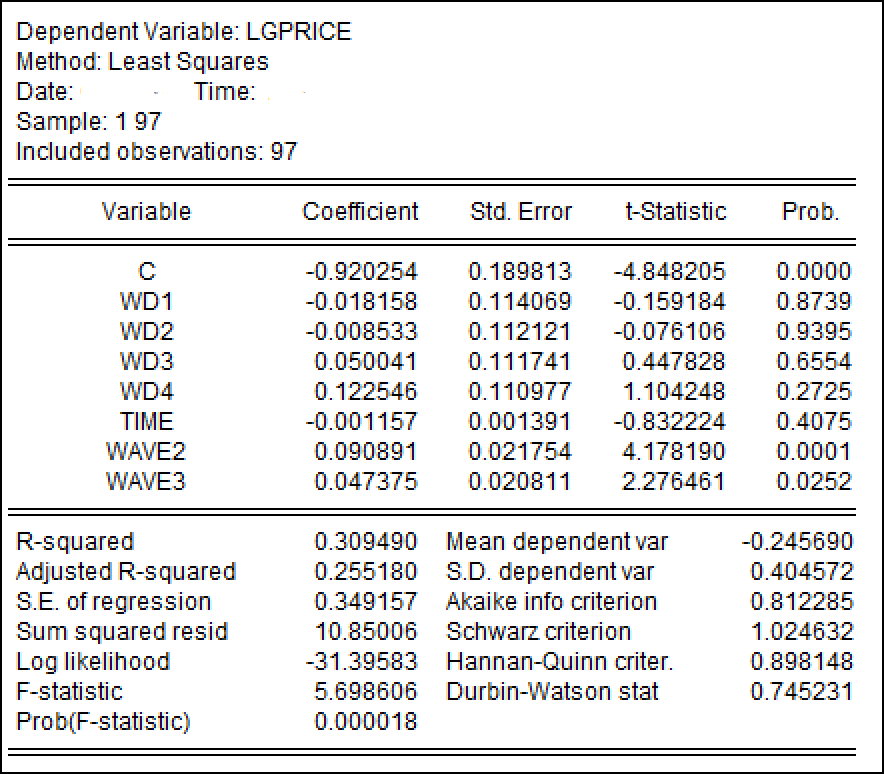
采用EViews软件进行最小二乘法回归,A模型和B模型的结果分别见 图 2 和 图 3 :
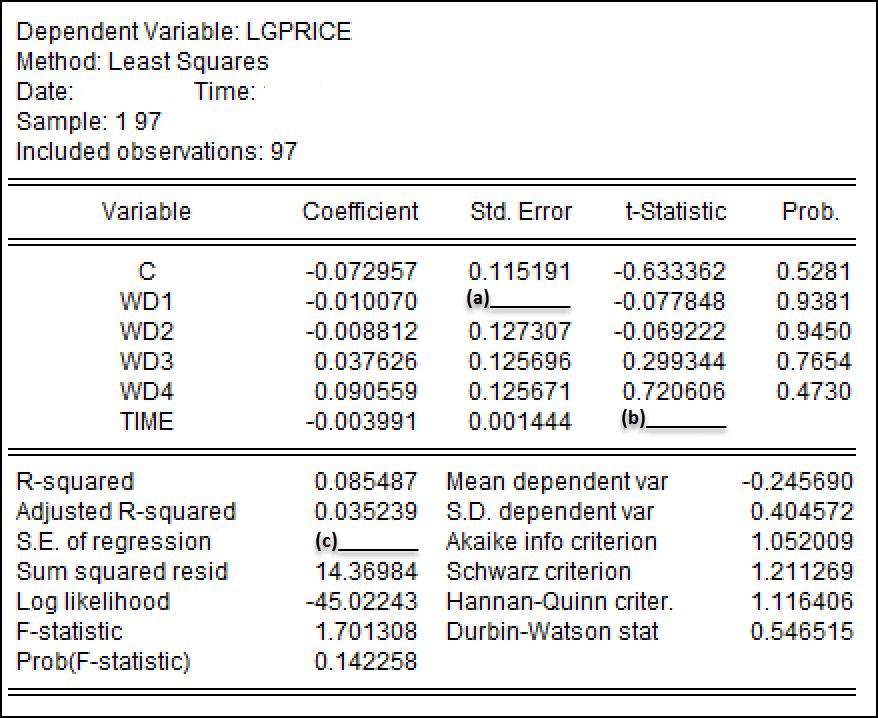
1.(小计10分,共4小题)根据A模型(见 式 1)及其最小二乘法EViews结果(见 图 2),请你依次回答下列问题:
(1)(2分)请你计算出A模型中变量\(Wd1\)的系数估计标准误\(S_{\hat{\alpha}_2}\),也即图中空白处(a)____的数值。(要求:写出主要计算过程;结果保留6位小数。)
(2)(2分)请你计算出模型A中时间变量\(Time\)的系数t统计量值\(t^{\ast}_{\hat{\alpha}_6}\),也即图中空白处(b)____的数值。(要求:写出主要计算过程;结果保留4位小数。)
(3)(3分)根据EViews结果(见 图 2),并利用上一题(2)的计算结果,请你对模型A中时间变量\(Time\)的的参数\(\alpha_6\)进行显著性t检验。(提示:给定显著性水平\(\alpha =0.05\),t查表值\(t_{1-\alpha/2}(n-6) = t_{0.975}(91) = 1.99\);\(t_{1-\alpha/2}(n-7) = t_{0.975}(90) = 1.99\);\(t_{1-\alpha}(n-7) = t_{0.95}(91) = 1.66\)。要求:简要写出t检验的主要依据和结论即可。)
(4)(3分)请你计算出A模型的回归误差标准差\(\hat{\sigma}\),也即图中空白处(c)____的数值。(要求:写出主要计算过程;结果保留6位小数。)
2.(小计10分,共3小题)根据A模型(见 式 1 )及其最小二乘法EViews结果(见 图 2),请你依次回答下列问题。
(1)(2分)虚拟变量回归模型(见 式 1)中,基础组是什么?
(2)(3分)给定某一时期(\(Time\))为100,且当天为周三,请你计算出该天鱼市对数化价格的预测值是多少?(要求:写出主要计算步骤和过程;计算结果保留4位小数。)
(3)(5分)假设将基础组设定为周一,且上述A模型重新设置为\(Lgprice_t=\gamma_{1}+\gamma_{2}Wd2_t+\gamma_{3}Wd3_t+\gamma_{4}Wd4_t+\gamma_{5}Wd5_t+\gamma_{6}Time_t+v_t\)。请你根据受约束模型A的最小二乘回归结果(见 图 2)分别计算得出\(\hat{\gamma}_{1},\hat{\gamma}_{2},\hat{\gamma}_{3},\hat{\gamma}_{4},\hat{\gamma}_{5}\)?(要求:写出主要计算步骤和过程;计算结果保留6位小数。)
3.(小计10分,共3小题)同学C比较感兴趣的一个猜想是:海面越是风大浪急,鱼价就越高,所以两个海浪变量(也即变量\(Wave2,Wave3\))会联合正向影响鱼价。因此,同学C综合研究了受约束模型A(见 式 1)和无约束模型B(见 式 2),请结合EViews回归报告(见 图 2 和 图 3),分别回答如下问题。
(1)(2分)对于C同学的猜想(也即两个海浪变量\(Wave2,Wave3\))会联合正向影响鱼价),请你写出与该猜想等价的线性约束条件。(要求:请用模型B中的参数进行表达。)
(2)(2分)为了对C同学的猜想进行假设检验,请你提出相应的原假设 \(H_0\) 和备择假设 \(H_1\) 。
(3)(6分)请你用线性约束检验方法,对同学C的猜想进行检验计算并得出检验结论。给定显著性水平\(\alpha = 0.05\)下,F查表值有\(F_{1-\alpha}(q, n-k_u)=F_{0.95}(2,89) = 3.10\);\(F_{1-\alpha}(k_u-1, n-k_u)=F_{0.95}(7,89) = 2.11\)。(要求:写出主要计算步骤和过程;计算结果保留2位小数。)
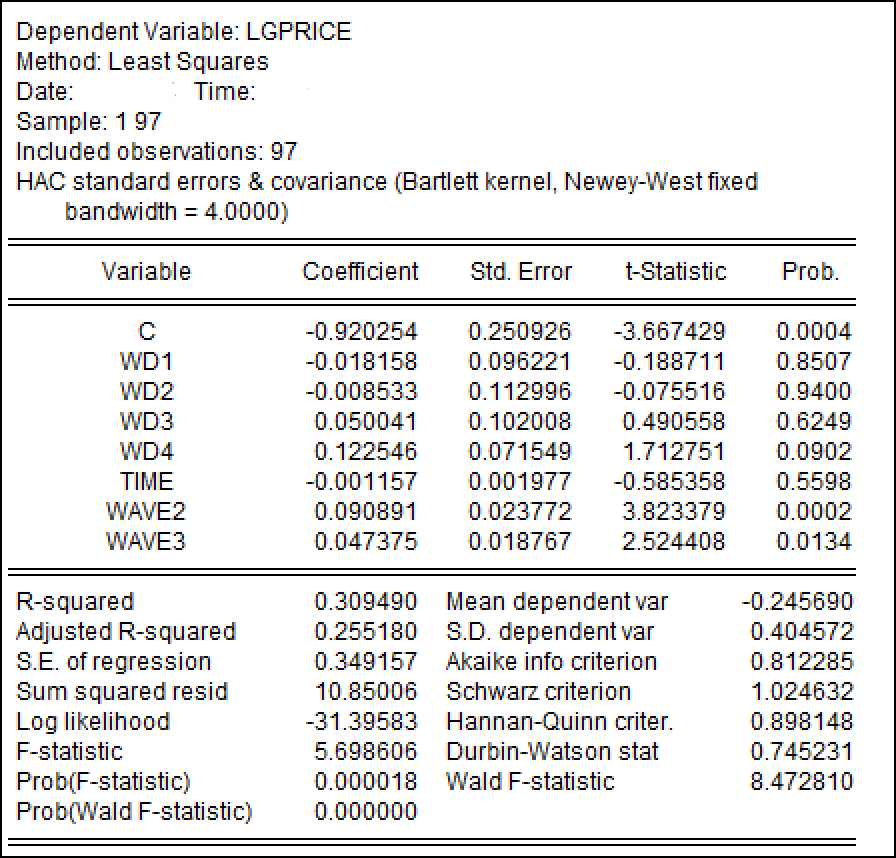
4.(小计10分,共3小题)同学D担心无约束模型B(见 式 2 )可能存在序列自相关性问题,他将进行相关诊断,并得到如下某种方法的模型矫正结果(见 图 4)。
(1)(3分)根据无约束模型B的EViews回归结果(见 图 3),请你采用德斌-沃森检验法(Durbin-Watson)检验是否存在一阶自相关AR(1),也即\(u_t = \rho u_{t-1} + \epsilon_t\)。已知在 \(k = 7, n = 97, \alpha = 1\%\)下的临界值为 \(d_L =1.360, d_U =1.685\)。(要求:写出主要结论,并给出判定理由。)
(2)(3分)如果无约束模型B经诊断发现确实存在一阶自相关AR(1),请你根据德斌-沃森统计量(DW)计算得到自协方差系数估计量\(\hat{\rho}\)。(要求:写出主要计算步骤和过程;计算结果保留4位小数。)
(3)(4分)请根据前述模型矫正结果(见 图 4),请你指出这是哪一种矫正方法?与矫正前相比(对比 图 3)你发现有哪些变化?(要求:请简要给出你的依据。)
2 参考答案
1.(小计10分,共4小题)
(1)(2分)
答: 已知回归系数\(\hat{\alpha}_2=-0.010070\),对应的t统计量\(t_{\hat{\alpha}_2}^{\ast} = -0.077848\),则可以计算得到对应的系数标准误差:
\[ \begin{aligned} S^2_{\hat{\alpha}} &= \frac{\hat{\alpha}_2}{t_{\hat{\alpha}_2}^{\ast}} = \frac{-0.010070}{-0.077848} = 0.129355 \end{aligned} \]
(2)(2分)
答: 已知回归系数\(\hat{\alpha}_6=-0.003991\),及其标准误差\(S_{\hat{\alpha}_6}=0.001444\),因此有:
\[ t^{\ast}_{\hat{\alpha}_6} =\frac{\hat{\alpha}_6}{S_{\hat{\alpha}_6}} = \frac{-0.003991}{0.001444} = -2.7639 \]
(3)(3分)
答: 根据题意,已知给定显著性水平\(\alpha =0.05\),t查表值\(t_{1-\alpha/2}(n-6) = t_{0.975}(91) = 1.99\)。根据(2)题计算结果,易知 \(t^{\ast}_{\hat{\alpha}_6}= -2.7639\)的绝对值大于t查表值,因此对参数\(\alpha_6\)的显著性t检验(\(H_0:\alpha_6 =0\))显著。
(4)(3分)
答:根据题意,已知残差平方和\(RSS=14.36984\),\(k_c=6\),\(n= 97\),因此容易计算得到A模型的回归误差标准差:
\[\hat{\sigma} = \sqrt{\frac{RSS}{n-k_c}} = \sqrt{\frac{14.36984}{91}} = 0.397379\]
2.(小计10分,共3小题)
(1)(2分)
答: 根据回归模型设置,可以发现周五为基础组(或参照组)。
(2)(3分)
答: 根据给定的条件,可以计算得到:
\[ \begin{aligned} \begin{split} &(\widehat{Lgprice}|Wd1=0; Wd2=0; Wd3=1; Wd4=0; Time=100)\\ =&+\hat{\beta}_{1}(1) +\hat{\beta}_{2}(0) +\hat{\beta}_{3}(0) +\hat{\beta}_{4}(1)\\&+\hat{\beta}_{5}(0) +\hat{\beta}_{6}(100.0000)\\ =&-[0.0730]\cdot (1)-[0.0101]\cdot (0)-[0.0088]\cdot (0)+[0.0376]\cdot (1)\\&+[0.0906]\cdot (0)-[0.0040]\cdot (100.0000)\\ =&-0.4344 \end{split} \end{aligned} \]
(3)(5分)
答:根据题意易知,两个方程式具有如下系数等价关系:
(1)周一:\(\hat{\gamma}_1 = \hat{\alpha}_1 +\hat{\alpha}_2=-0.072957 + (-0.010070) = -0.083027\)
(2)周二:\(\hat{\gamma}_1 + \hat{\gamma}_2 = \hat{\alpha}_1 +\hat{\alpha}_3\),因此\(\hat{\gamma}_2 = \hat{\alpha}_1 +\hat{\alpha}_3 - \hat{\gamma}_1 = -0.072957 + -0.008812 - (-0.083027) = 0.001257\)
(3)周三:\(\hat{\gamma}_1 + \hat{\gamma}_3 = \hat{\alpha}_1 +\hat{\alpha}_4\),因此\(\hat{\gamma}_3 = \hat{\alpha}_1 +\hat{\alpha}_4 - \hat{\gamma}_1 = -0.072957 + 0.037626 - (-0.083027) = 0.047696\)
(4)周四:\(\hat{\gamma}_1 + \hat{\gamma}_4 = \hat{\alpha}_1 +\hat{\alpha}_5\),因此\(\hat{\gamma}_4 = \hat{\alpha}_1 +\hat{\alpha}_5 - \hat{\gamma}_1 = -0.072957 + 0.090559 - (-0.083027) = 0.100629\)
(5)周五:\(\hat{\gamma}_1 + \hat{\gamma}_5 = \hat{\alpha}_1\),因此\(\hat{\gamma}_5 = \hat{\alpha}_1 - \hat{\gamma}_1 = -0.072957 - (-0.083027) = 0.010070\)
3.(小计10分,共3小题)
(1)(2分)
答: 等价的线性约束条件有两个:\(\beta_7=0;\beta_8=0\)。
(2)(2分)
答: 原假设 \(H_0:\beta_7=0;\beta_8=0\) ,备择假设 \(H_1:\beta_7,\beta_8\)不全为零。
(4)(6分)
答:可以利用无约束方程和有约束模型的可决系数,构建F统计量并进行检验。
注意:此题也可以利用无约束方程和有约束模型的残差平方和,构建F统计量并进行检验。二者结果和结论都是等价的。
a)已知无约束模型的可决系数\(R^2_u=0.309490\),有约束模型的可决系数\(R^2_u=0.085487\)。根据题(1)可知约束条件个数\(q=2\)。
b)构造并计算线性约束检验的F统计量:
\[ \begin{aligned} F^{\ast}&=\frac{(R^2_u-R^2_r)/q}{(1-R^2_u)/(n-k_f)}\\ &=\frac{( 0.309490 - 0.085487 )/( 2 )}{(1 - 0.309490 )/( 97 - 8 )}\\ &= 14.44 \end{aligned} \]
c)进行F检验判断。已知无约束模型的回归元个数\(k_u=8\),给定显著性水平\(\alpha = 0.05\)下,F查表值为\(F_{1-\alpha}(q, n-k_u)=F_{0.95}(2,89)=3.10\)。上述样本统计量值\(F^{\ast}=14.44\)大于理论查表值,因此约束条件检验是显著的,表明拥有工会成员身份,对不同性别的就业者时均工资有显著影响。这也表明同学C的猜想是统计上不成立的。
4.(小计10分,共3小题)
(1)(3分)
答: 根据根据无约束模型B的EViews回归结果,已知\(DW=0.745231\),又已知在 \(k = 7, n = 97, \alpha = 1\%\)下的临界值为 \(d_L =1.360, d_U =1.685\)。根据德斌-沃森检验法的判断准则,可知\(0< DW < d_L\),则可以判断得出无约束模型B存在一阶正自相关性。
(2)(3分)
答: 根据上述(1)的分析结果,易知\(\hat{\rho} = 1- \frac{DW}{2} = 0.6274\)。
(3)(4分):
答: 该矫正方法具体为尼威-韦斯特序列相关一致性稳健标准误估计法。与矫正前相比,该方法不会影响回归系数的估计结果,主要会矫正系数估计值的标准误差,进而也会改变系数t统计量值。此外,该矫正方法不会改变判定系数、调整判定系数、残差平方和、回归误差方差、F统计量值、DW值等。