拟合数据的多种方法

论文复现读评

OLS
Paper Reading
作者

胡华平

发布于

2025年9月22日

修改于

2025年9月22日

摘要
为了更好地理解拟合数据的多种方法，本文对论文《Locating Hyperplanes to Fitting Set of Points: A General Framework》进行了代码复现和观点读评。
注记论文信息

复现论文：Blanco, V., J. Puerto, and R. Salmerón. Locating Hyperplanes to Fitting Set of Points: A General Framework[J]. Computers & Operations Research, 2018, 95:172-193. html版本浏览;pdf版本下载

  • 论文早前版本发表在arXivhttps://arxiv.org/abs/1505.03451v2：Blanco, V., J. Puerto, and R. Salmerón. A General Framework for Locating Hyperplanes to Fitting Set of Points, arXiv:1505.03451v2 [math.ST].

作者使用R语言实现了论文中的方法，但并没有提供R代码和数据。

观点读评

普通最小二乘法（OLS）是经典计量经济学中最常用的拟合方法，它通过最小化残差平方和\(\Phi=\sum_{i=1}^{n} \varepsilon_{i}^{2}=\sum_{i=1}^{n} (y_i - \hat{y}_i)^{2}\)来拟合数据。

这种数据拟合方法有三个核心要点：

  • 残差\(\varepsilon_i = y_i - \hat{y}_i\)的度量方式表现为“铅垂线距离”，即垂直距离。
  • 残差的距离度量是否进行了加权处理\(\lambda_i\)，OLS没有进行任何加权处理。
  • 最小化算子\(\Phi\)的选择决定了拟合方法的具体形式，OLS选择的是残差平方和（二次方形式）。

实际上我们熟悉的样本回归线（sample regression curve）可以是任意其他一种基于距离测度（distance measure，也即残差）的方法拟合得到的。例如，最小绝对偏差（LAD）方法，最小二乘分位数（LQS）方法，最小截尾平方和（LTS）方法等。当然，也可以考虑其他形式的距离测度，例如，L1距离（绝对值距离）、L2距离（欧氏距离）、L3距离（切比雪夫距离）等。

Blanco等（2018）提出的方法是一个通用框架，它将这些方法统一到一个框架中，并给出了一个统一的数学表达式。这对于我们学习OLS方法和理解其他方法的原理和适用性具有重要意义。此外，论文基于两个案例数据的实证分析，展示了该方法的适用性。

当然，我们还要进一步思考如下问题：

  • 是不是只需要考虑把数据集进行足够好的拟合就可以了？“足够好的拟合”的标准是什么？
  • 为了更好地推断总体参数，上述提到的各种各样的拟合方法，哪种方法会更好？

论文摘要

论文提出了一类用于相对于给定点集定位/拟合超平面的方法族。作者基于有序加权算子（ordered weighted operators）提出了一个以距离型残差为基础的通用聚合框架。文献中最常见的方法（如最小二乘、最小绝对偏差、最小平方分位数、最小截尾平方和等）都可以作为该框架中误差度量与聚合准则的特例统一表示。本文为这些方法给出了统一的数学生成式，并分析了若干重要情形。最一般的设定将导致混合整数非线性规划问题。针对这类问题，作者提出了内外层线性逼近以获得可行的求解流程。此外，作者还提出了一个新的拟合优度指标，它推广了经典的判定系数\(R^2\)，能够用于比较不同拟合超平面。最后，给出了若干示例以及基于R语言的大量计算实验，以展示所提方法的适用性。

通用框架下的超平面定位方法

给定一个在 (d+1) 维空间中的 n 个观测点或需求点（分别使用数据分析或位置分析的术语）的集合，\(\left\{x_{1}, \ldots, x_{n}\right\} \subset\{1\} \times \mathbb{R}^{d}\)（为更清晰地描述模型，我们将假设 \(x_{i}\) 的第一个，即第 0 个分量是用于截距的，即 \(x_{10}=\cdots=x_{n 0}=1\)）。接下来，我们分析定位一个线性形式（超平面）以拟合这些点的问题，该过程最小化不同形式的残差测量及其聚合。对于任何 \(y \in \mathbb{R}^{d+1}\)，我们应将 \(y_{-0}\) 表示为 \(\left(y_{1}, \ldots, y_{d}\right)\)，即 y 的后 d 个坐标（不包括第一个）。首先，我们假设点到超平面的偏差由一个残差映射 \(\varepsilon_{x}: \mathbb{R}^{d+1} \rightarrow \mathbb{R}_{+}\) 建模，即 \(\varepsilon_{x}(\boldsymbol{\beta})=\mathrm{D}\left(x_{-0}, \mathcal{H}(\boldsymbol{\beta})\right)\)，其中 D 是 \(\mathbb{R}^{d}\) 中的一个距离度量。这个残差表示点（观测值）\(x \in \mathbb{R}^{d+1}\) 相对于超平面 \(\mathcal{H}(\boldsymbol{\beta})=\left\{y \in \mathbb{R}^{d}:\left(1, y^{t}\right) \boldsymbol{\beta}=0\right\}\) 的“距离”。有时，为简洁起见，我们会将超平面写为 \(\boldsymbol{\beta}^{t} X=0\)，其中 \(\boldsymbol{\beta}=\left(\beta_{0}, \beta_{1}, \ldots, \beta_{d}\right)^{t} \in \mathbb{R}^{d+1}\)。此外，为简化表示，在不会引起混淆的情况下，我们将点 \(x_{i}\) 的残差称为 \(\varepsilon_{i}\)。

通过使用残差的聚合函数 \(\Phi: \mathbb{R}^{n} \rightarrow \mathbb{R}\)，可以获得整个数据集相对于由 \(\boldsymbol{\beta}\) 导出的超平面的总体偏差度量。在这种设置下，我们试图最小化这样一个聚合函数，而拟合超平面问题（FHP）就在于找到 \(\hat{\boldsymbol{\beta}} \in \mathbb{R}^{d+1}\) 使得： \[ \begin{equation*} \hat{\boldsymbol{\beta}} \in \arg \min _{\boldsymbol{\beta} \in \mathbb{R}^{d+1}} \Phi(\boldsymbol{\varepsilon}(\boldsymbol{\beta})), \tag{1} \end{equation*} \]

其中 \(\boldsymbol{\varepsilon}(\boldsymbol{\beta})=\left(\varepsilon_{1}(\boldsymbol{\beta}), \ldots, \varepsilon_{n}(\boldsymbol{\beta})\right)^{t}\) 是残差向量。

请注意，解决问题 (1) 的难度取决于残差的表达式和聚合标准 \(\Phi\)。如果 \(\Phi\) 和 \(\varepsilon_{X}\) 是线性的，则上述问题变成一个线性规划问题。在本文中，我们考虑了一个通用的聚合标准族，它包括了文献中大多数经典标准作为特例 (Bertsimas and Mazumder, 2014; Giloni and Padberg, 2002; Rousseeuw and Leroy, 2003; Yager and Beliakov, 2010)。

令 \(\lambda_{1}, \ldots, \lambda_{n} \in \mathbb{R}\) 且令 \(\boldsymbol{\varepsilon} \in \mathbb{R}^{n}\) 为给定数据集中所有点的残差向量。我们考虑聚合标准 \(\Phi: \mathbb{R}^{n} \rightarrow \mathbb{R}_{+}\) 定义为： \(\Phi(\boldsymbol{\varepsilon})=\sum_{i=1}^{n} \lambda_{i} \boldsymbol{\varepsilon}_{(i)}^{p}, \quad 1 \leq p<+\infty\), 其中 \(\boldsymbol{\varepsilon}_{(i)} \in\left\{\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right\}\) 满足 \(\boldsymbol{\varepsilon}_{(1)} \leq \cdots \leq \boldsymbol{\varepsilon}_{(n)}\)。可以观察到，这个算子定义了一个多参数族（称为有序中值函数 (Nickel and Puerto, 2005)），根据 \(\lambda\) 权重的选择，可以捕捉文献中提出的许多模型。

大多数经典模型假设残差被定义为点到超平面的垂直距离（相对于最后一个坐标）： \(\boldsymbol{\varepsilon}_{x}(\boldsymbol{\beta})=\left|x_{d}-\sum_{k=0}^{d-1} \frac{\beta_{k}}{\beta_{d}} x_{k}\right|\), （假设 \(\beta_{d} \neq 0\)）。 因此，它们之间的区别来自于聚合标准 \(\Phi\) 的选择。我们下面展示一些经典方法如何适应我们的框架。

  1. 最小二乘和（LSS）方法，归功于高斯（1809），是估计线性模型系数最广泛使用的方法，因其简单性（可以获得最优系数的封闭形式解）及其对总体推断的理论意义。然而，应用它需要一些限制性假设（参见，例如，Giloni and Padberg, 2002）。LSS 标准定义为残差的平方和，即：\(\Phi_{L S S}\left(\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right)=\sum_{i=1}^{n} \boldsymbol{\varepsilon}_{i}^{2}\)，其中残差 \(\boldsymbol{\varepsilon}_{k}\) 由 (3) 给出。读者可能会注意到，LSS 对应于问题 (1) 中 \(\lambda^{t}=(1, \ldots, 1), p=2\) 且 \(\boldsymbol{\varepsilon}\) 为垂直距离的情况。

  2. 最小绝对偏差（LAD）方法（由 Edgeworth, 1887 引入）在于最小化垂直残差绝对值的总和。因此，\(\Phi_{L A D}\left(\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right)=\sum_{i=1}^{n}\left|\boldsymbol{\varepsilon}_{i}\right|\)。注意 LAD 对应于 (1) 中 \(\lambda^{t}=(1, \ldots, 1)\) 和 \(p=1\) 的模型。

  3. 最小二乘分位数（LQS），最近由 Bertsimas and Mazumder (2014) 引入，是 Hampel (1975) 引入的最小二乘中位数（LMS）的推广。它也考虑垂直距离作为残差，但它们被聚合以最小化其分布的 r-分位数（r 的范围是 \(\{1, \ldots, n\}\)）。因此，\(\Phi_{L Q S}\left(\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right)=r-\) quantile \(\left(\boldsymbol{\varepsilon}_{1}^{2}, \ldots, \boldsymbol{\varepsilon}_{n}^{2}\right):=\boldsymbol{\varepsilon}_{(r)}^{2}\)。该方法也符合本文考虑的聚合标准的一般形式。在这种情况下，遵循 (2) 中引入的符号，LQS 超平面可以在 \(p=2\) 和 \(\lambda=(\overbrace{0, \ldots, 0}^{(r-1)}, 1, \overbrace{0, \ldots, 0}^{(n-r)})\) 时获得。（观察到 LMS 超平面在 \(p=2\) 和 \(\lambda=(\overbrace{0, \ldots, 0}^{\left\lfloor\frac{n}{2}\right\rfloor}, 1, \overbrace{0, \ldots, 0}^{\left\lfloor\frac{n}{2}\right\rfloor})\) 时也在同一框架下获得）。

  4. 最小截尾二乘和（LTS）方法由 Rousseeuw (1984) 引入，作为 LSS 方法的一种稳健替代方法，因为它具有高崩溃点。回想一下，直观地说，一个估计量的崩溃点是该估计量在给出不正确（例如，任意大）结果之前可以处理的不正确观测值（例如，任意大的观测值）的比例。用我们的符号表示，它对应于再次选择垂直距离作为残差，\(p=2\)，聚合标准为 \(\Phi_{L T S}\left(\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right)=\sum_{i=1}^{h} \boldsymbol{\varepsilon}_{(i)}^{2}\)，其中 \(\boldsymbol{\varepsilon}_{(i)} \in\left\{\boldsymbol{\varepsilon}_{1}, \ldots, \boldsymbol{\varepsilon}_{n}\right\}\) 且对于 \(i=1, \ldots, n-1\) 有 \(\boldsymbol{\varepsilon}_{(i)} \leq \boldsymbol{\varepsilon}_{(i+1)}\)，以及 \(h \in\{1, \ldots, n\}\)。h 最常见的选择是 \(\left\lfloor\frac{n}{2}\right\rfloor\)，即考虑最好的 50% 的平方残差。

星系数据双变量拟合案例

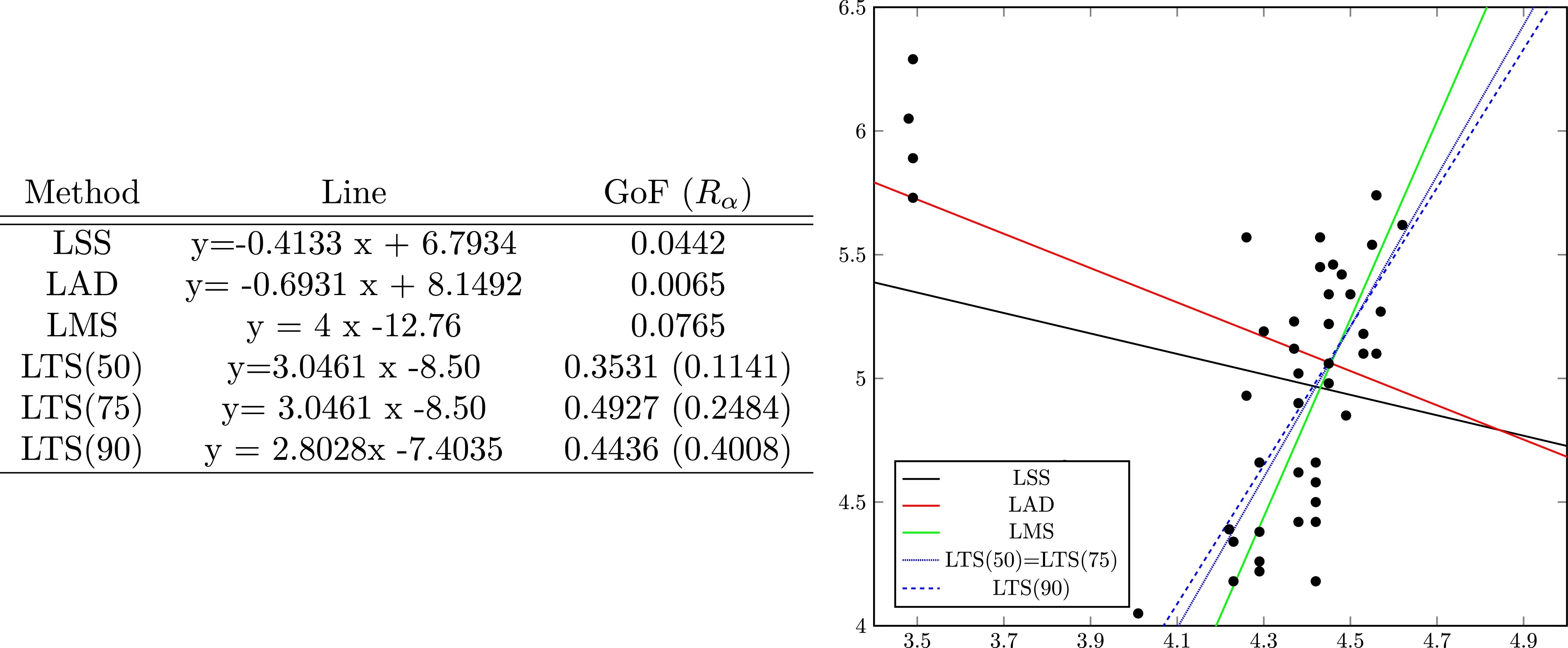
在图 1 中，我们展示了在星系数据集上使用经典方法获得的最佳拟合线。数据集由 \(\mathbb{R}^{2}\) 中的 47 个点组成，这些点对应于天鹅座 (Humphreys, 1978) 中天鹅座 OB1 星团的星星。第一个坐标，\(X_{1}\)，是恒星表面有效温度的对数，第二个坐标，\(X_{2}\)，是恒星光强度的对数。该数据集也在 Rousseeuw and Leroy (2003) 和 Yager and Beliakov (2010) 中进行了分析，以及其他一些研究。我们运行了 LSS、LAD、LMS 和 \(\operatorname{LTS}(\alpha)\)，其中 \(\alpha \in\{50,75,90\}\)。获得的线和拟合优度指标 \(\left(\mathrm{GoF}_{\Phi, \varepsilon}\right)\) 如图 1 所示。读者可能会注意到，LSS 和 LAD 模型无法充分拟合数据，而其他模型（尽管有些相似）显示出对异常值的更好表现。请注意，GoF 也反映了这一点，尽管不清楚 LTS(75)（具有最大 GoF 的模型）是否优于其他模型。

图 1: (原图1). 星系数据集上使用经典方法获得的最佳拟合线。

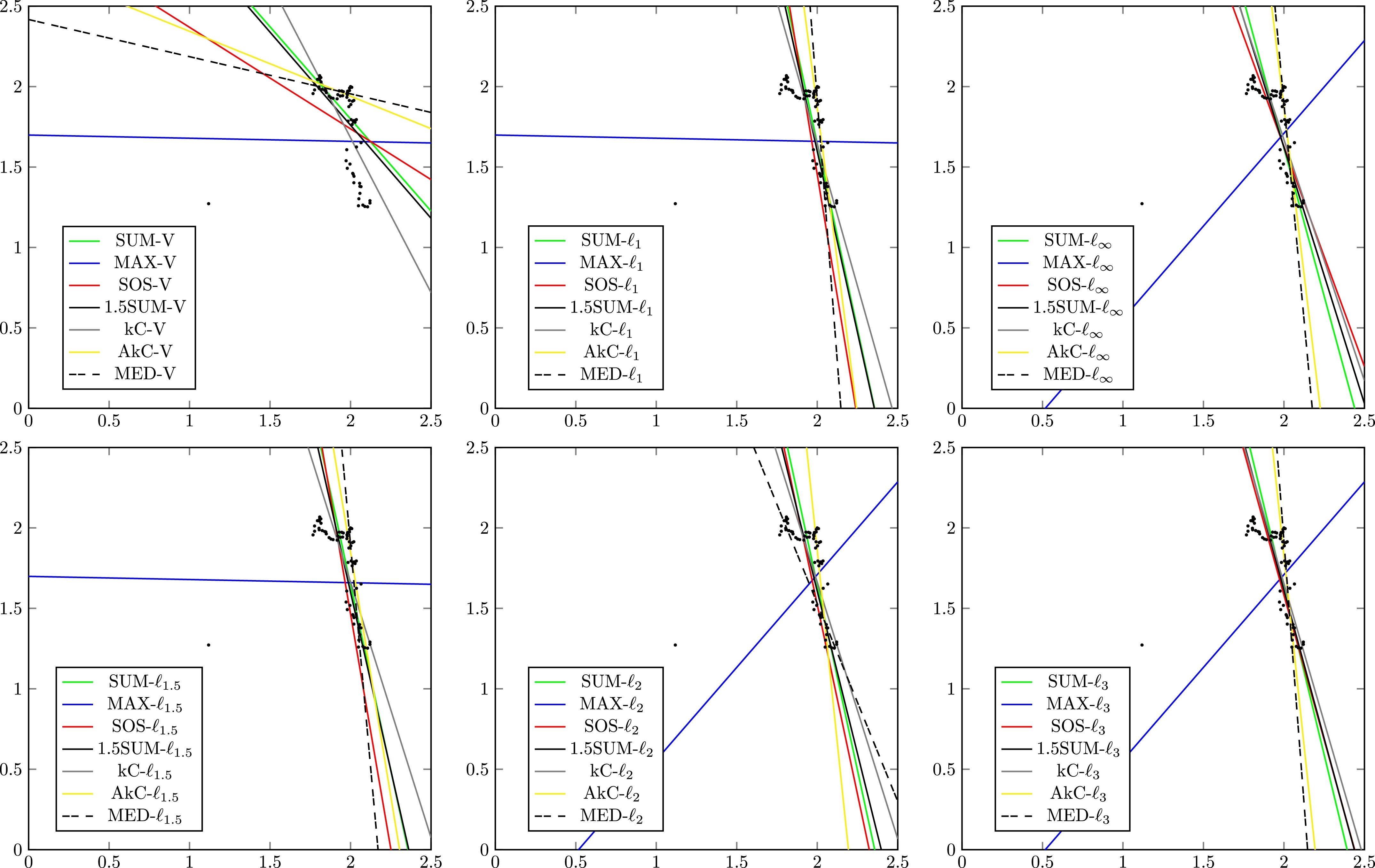
德斌-沃森数据拟合案例

我们还对 Durbin and Watson (1951) 使用的经典真实数据样本进行了一些实验。该数据旨在根据收入和烈酒的相对价格（经生活成本指数平减）来分析 1870 年至 1938 年（\(n=69\)）的年度烈酒消费量。因此，该数据集中观察到的变量是以下度量的对数（系数因此被解释为百分比变化）：\(X_{1}\)（人均实际收入），\(X_{2}\)（烈酒的相对价格）和 \(X_{3}\)（人均烈酒消费量）。

为了说明目的，我们既分析了包含三个变量的全局模型（\(d=3\)），也分析了仅考虑 \(X_{1}\) 和 \(X_{3}\) 并忽略 \(X_{2}\) 的双变量模型（\(d=2\)）。

图 2: (原图6). 德斌-沃森数据的双变量拟合结果。
表 1: （原表4）德斌-沃森数据的双变量拟合结果。
V \(\ell_{1}\) \(\ell_{\infty}\)
SUM (4.0898, -1.1454, -1) (10.8840, -4.6184, -1) (8.9764, -3.6797, -1)
MAX (1.6986, -0.0196, -1) (1.6986, -0.0196, -1) (-0.5963, 1.1530, -1)
SOS (2.9993, -0.6309, -1) (13.5934, -6.0703, -1) (7.0978, -2.7353, -1)
1.5SUM (4.0730, -1.1566, -1) (10.6113, -4.5067, -1) (7.9926, -3.1851, -1)
kC (5.5288, -1.9236, -1) (8.7033, -3.5303, -1) (7.6654, -2.9977, -1)
AkC (2.7467, -0.4031, -1) (17.1272, -7.6311, -1) (18.4349, -8.2833, -1)
MED (2.4167, -0.2310, -1) (28.0156, -13.0469, -1) (23.4462, -10.7748, -1)
\(\ell_{1.5}\) \(\ell_{2}\) \(\ell_{3}\)
SUM (10.8840, -4.6184, -1) (10.8746, -4.6138, -1) (9.8917, -4.1344, -1)
MAX (1.6986, -0.0196, -1) (-0.5963, 1.1530, -1) (-0.5963, 1.1530, -1)
SOS (13.1400, -5.8376, -1) (10.9561, -4.7162, -1) (8.7832, -3.6006, -1)
1.5SUM (10.4466, -4.4233, -1) (9.6868, -4.0399, -1) (8.9821, -3.6851, -1)
kC (8.0130, -3.1750, -1) (8.0455, -3.1914, -1) (8.5389, -3.4427, -1)
AkC (13.9827, -6.0670, -1) (21.0745, -9.6064, -1) (20.6955, -9.4349, -1)
MED (24.0656, -11.0819, -1) (6.4510, -2.4601, -1) (28.0150, -13.0466, -1)