1 多重共线性的理论后果
后果1：估计精度大大下降
后果2：t检验倾向于不显著
后果3：F检验和t检验不一致
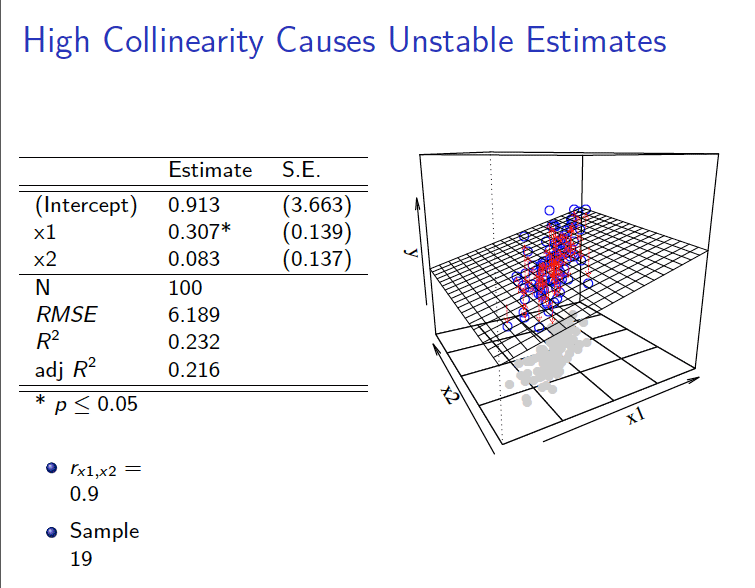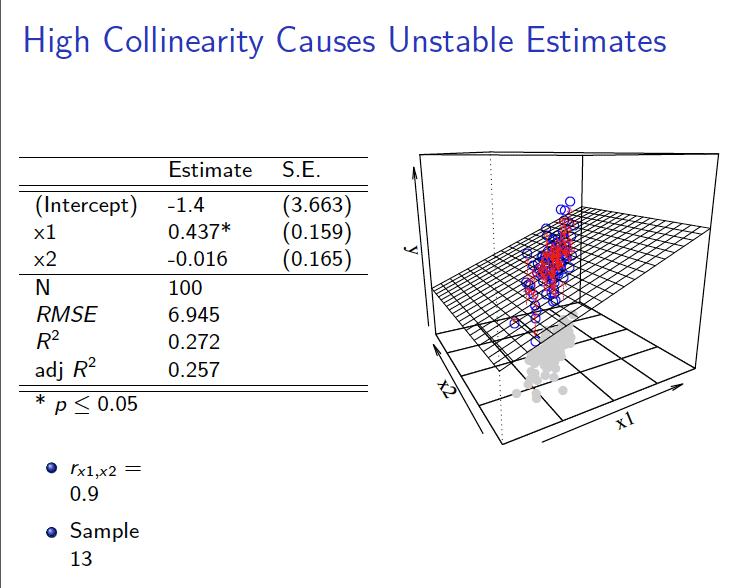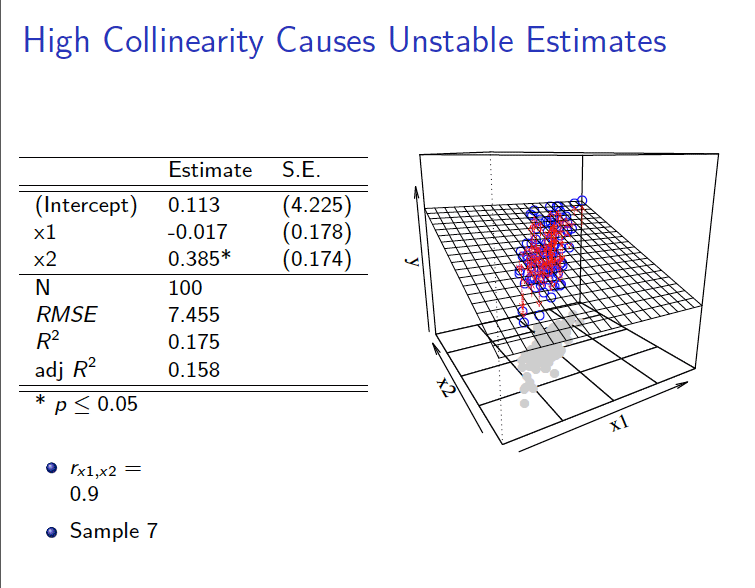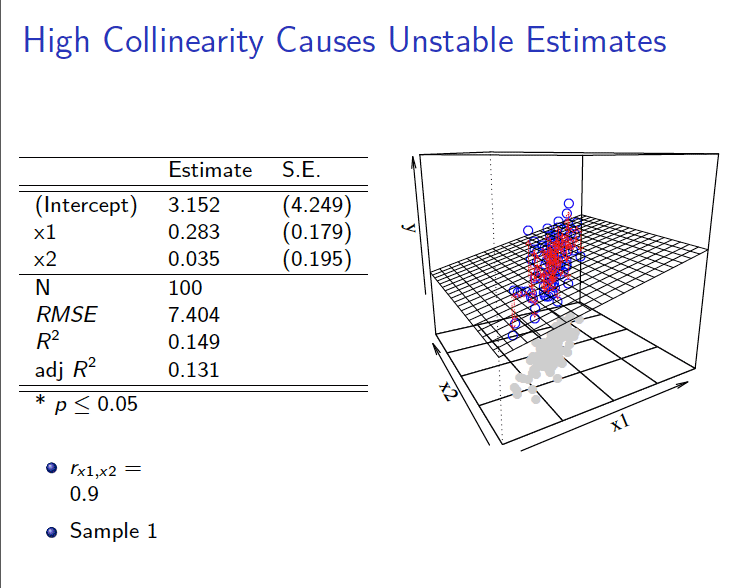
后果4：OLS估计对观测样本敏感
2 数据集
2.1 数据生成机制
模拟的“真实”变量关系为：
\[ \begin{aligned} Y_i&=0.2 X_{1 i}+0.2 X_{2 i}+u_i \\ u_i &\sim N(0, 7^2) \end{aligned} \]
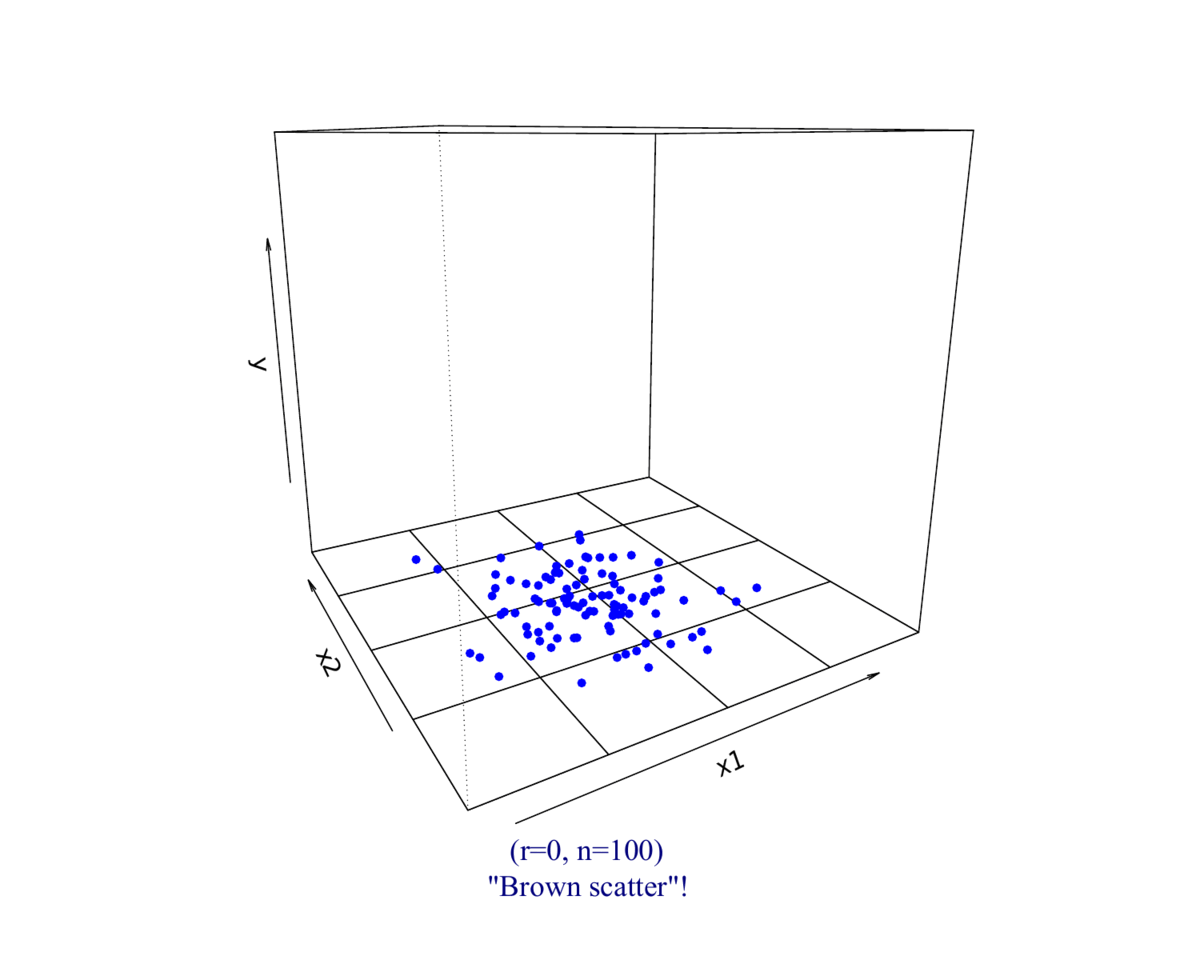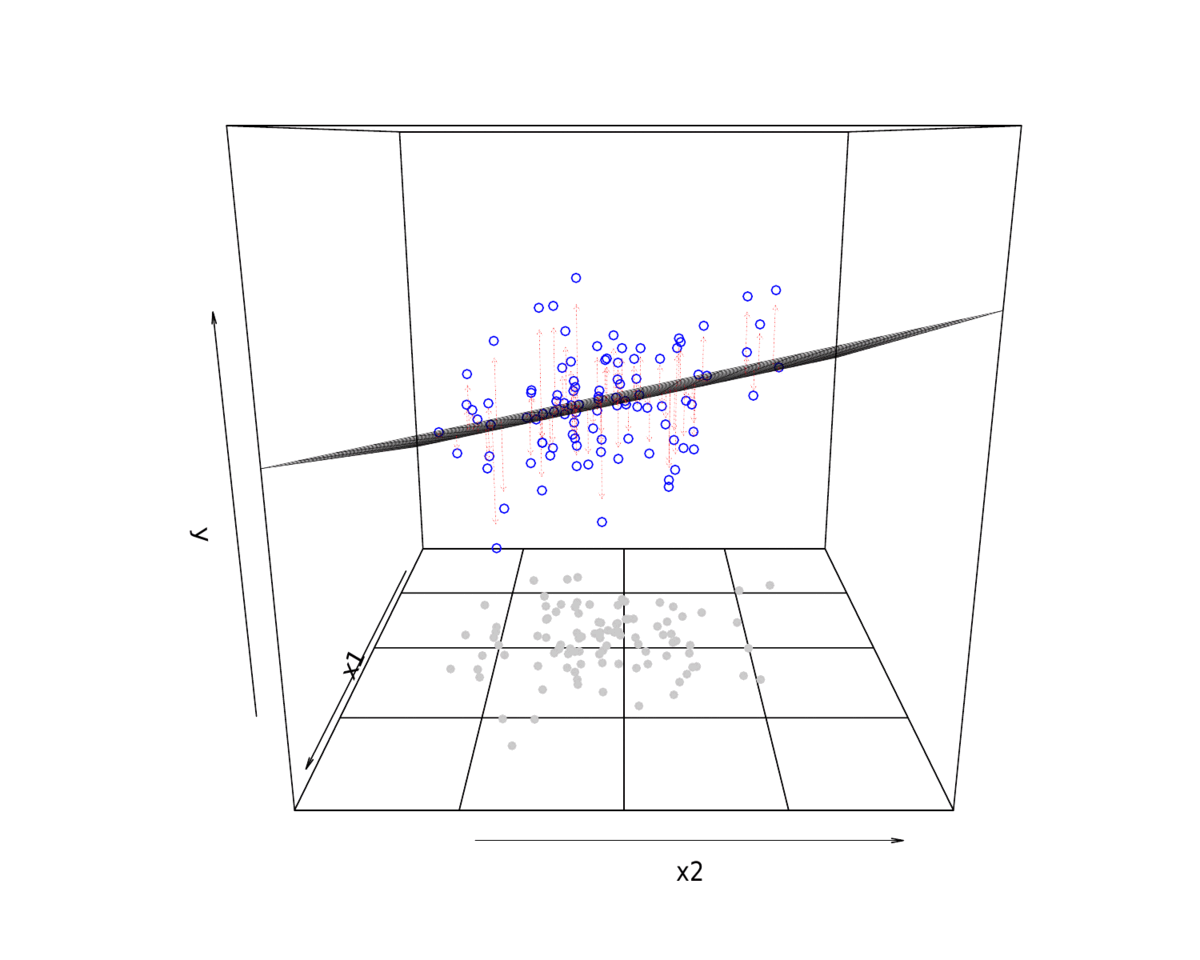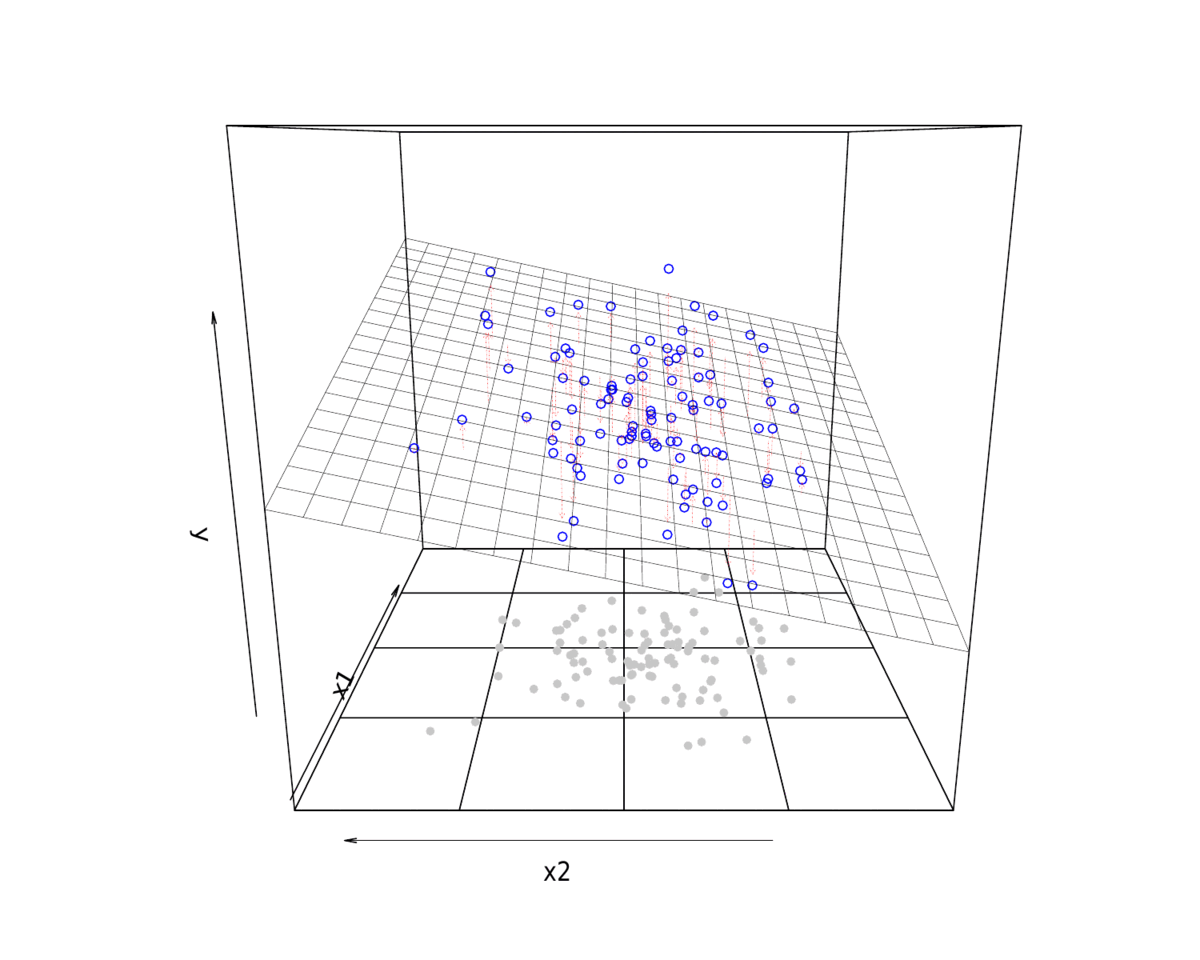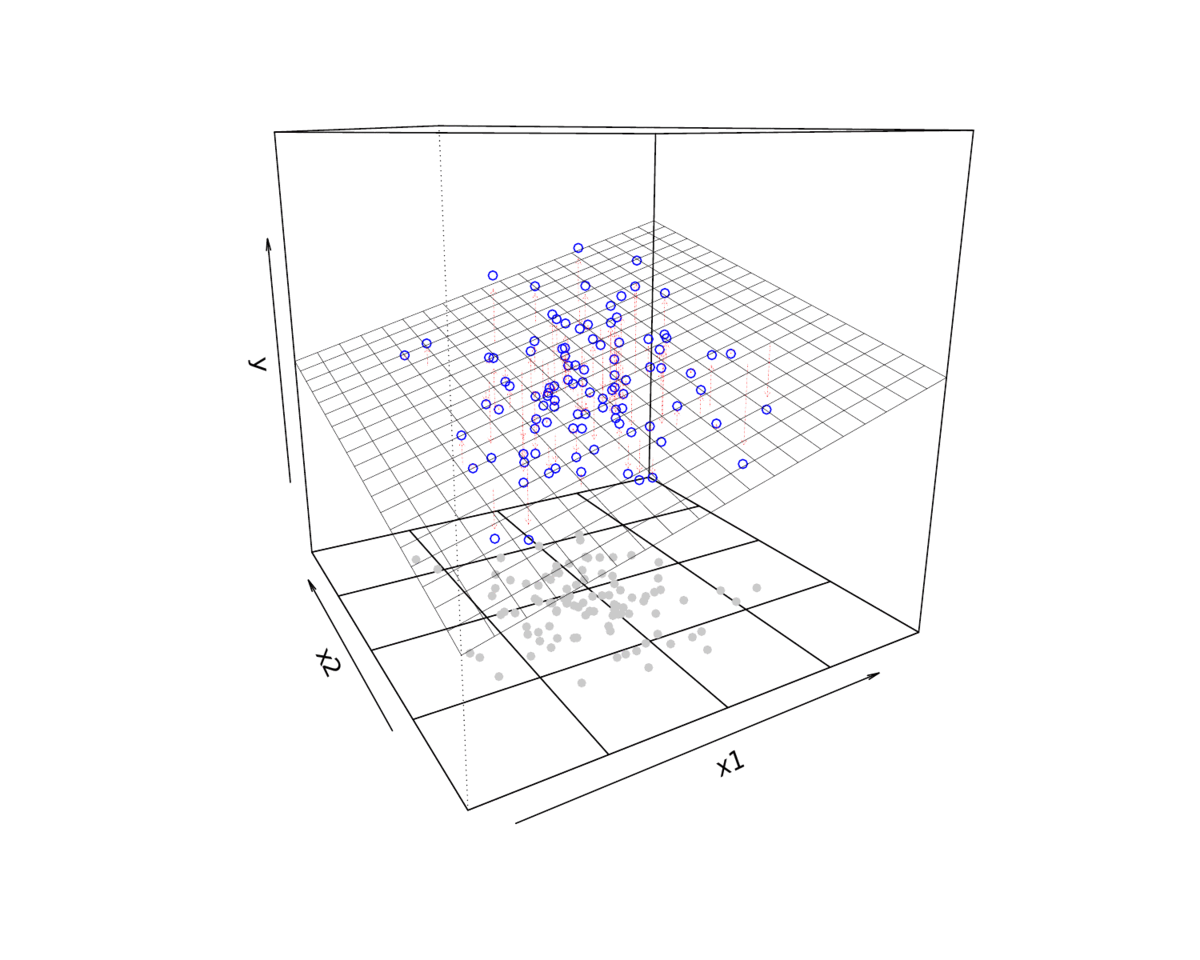
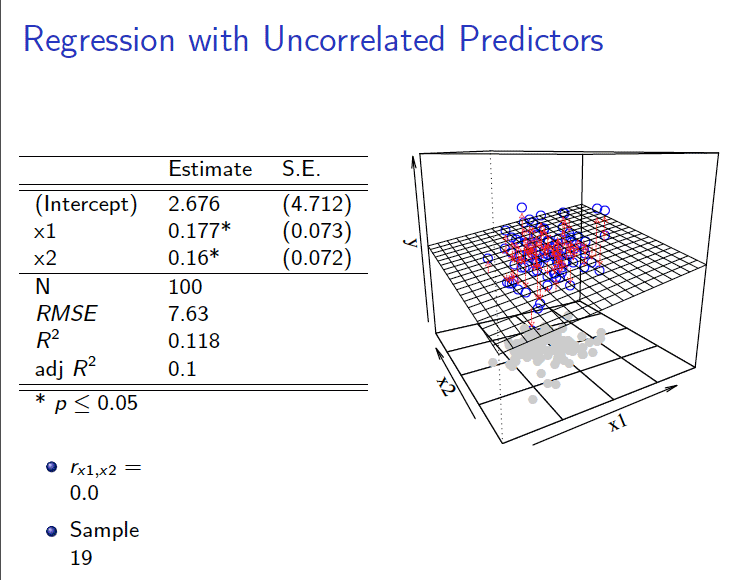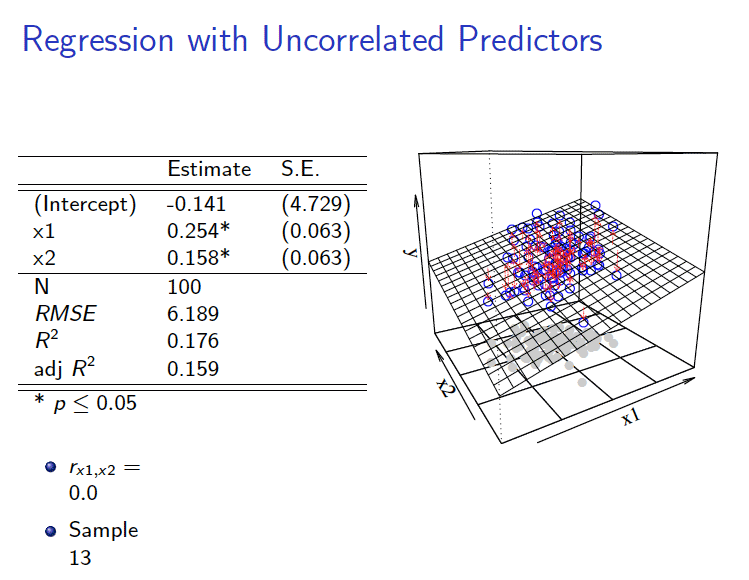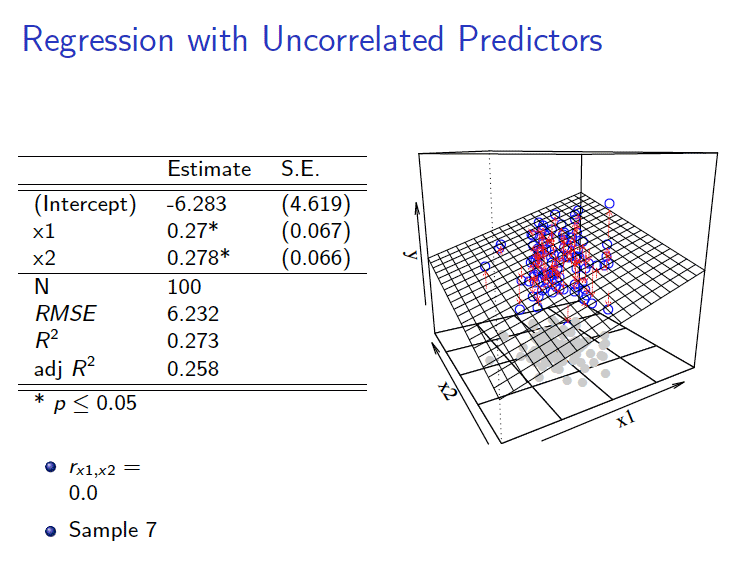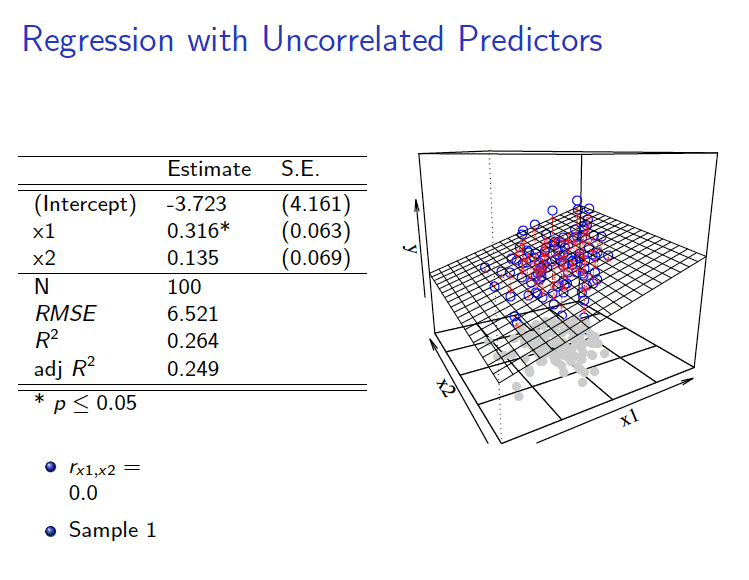
（1）相关系数为\(\rho_{(X_{1},X_2)}=0\)的情形
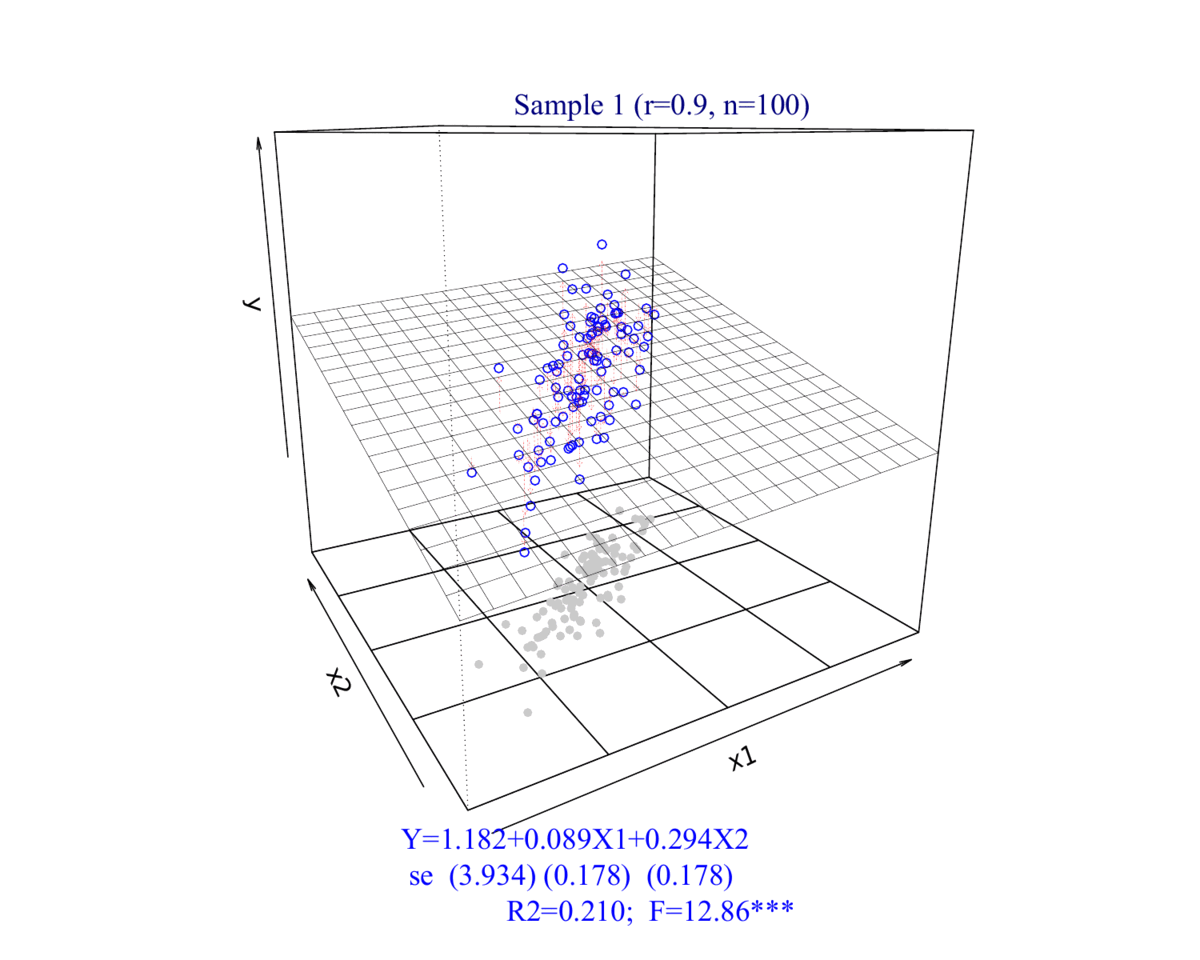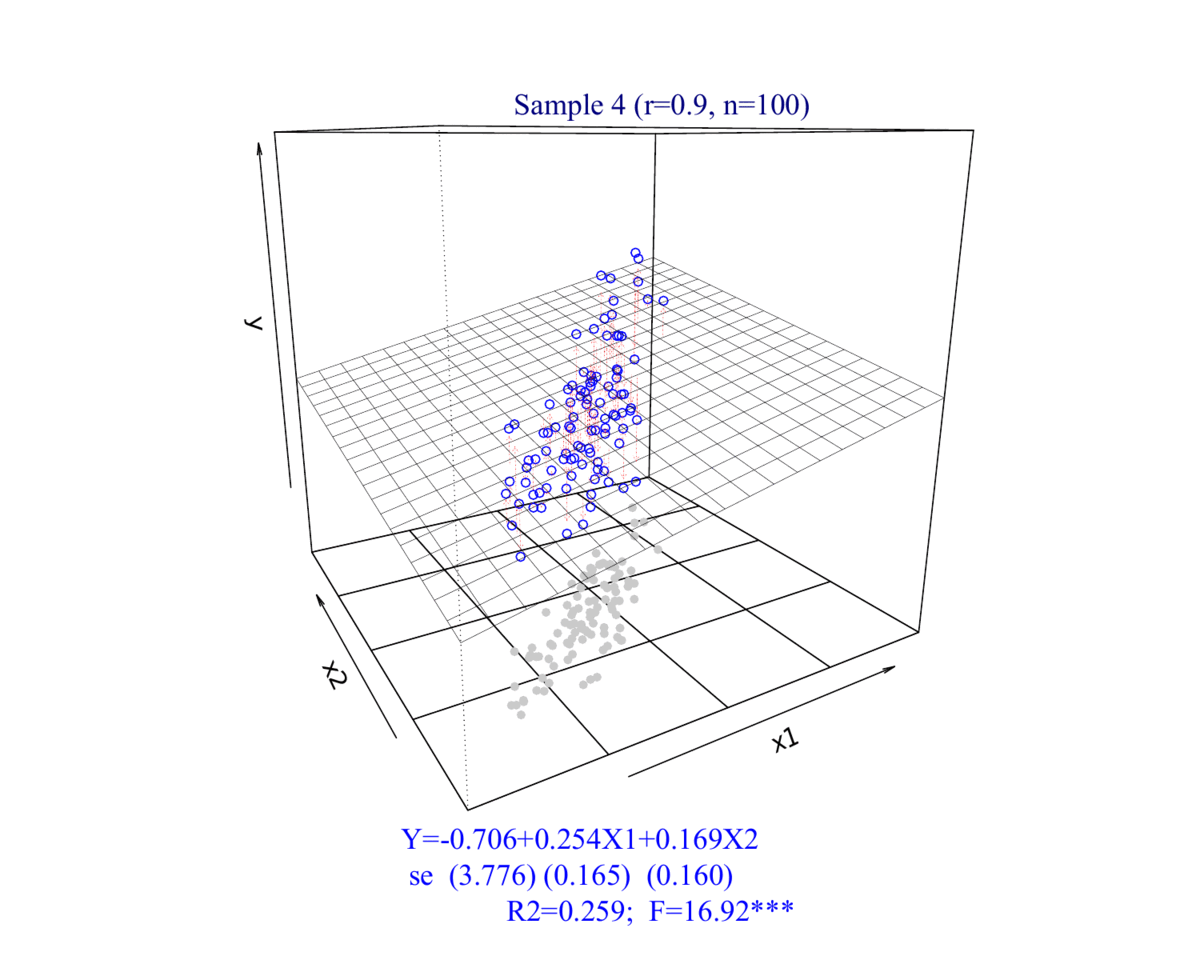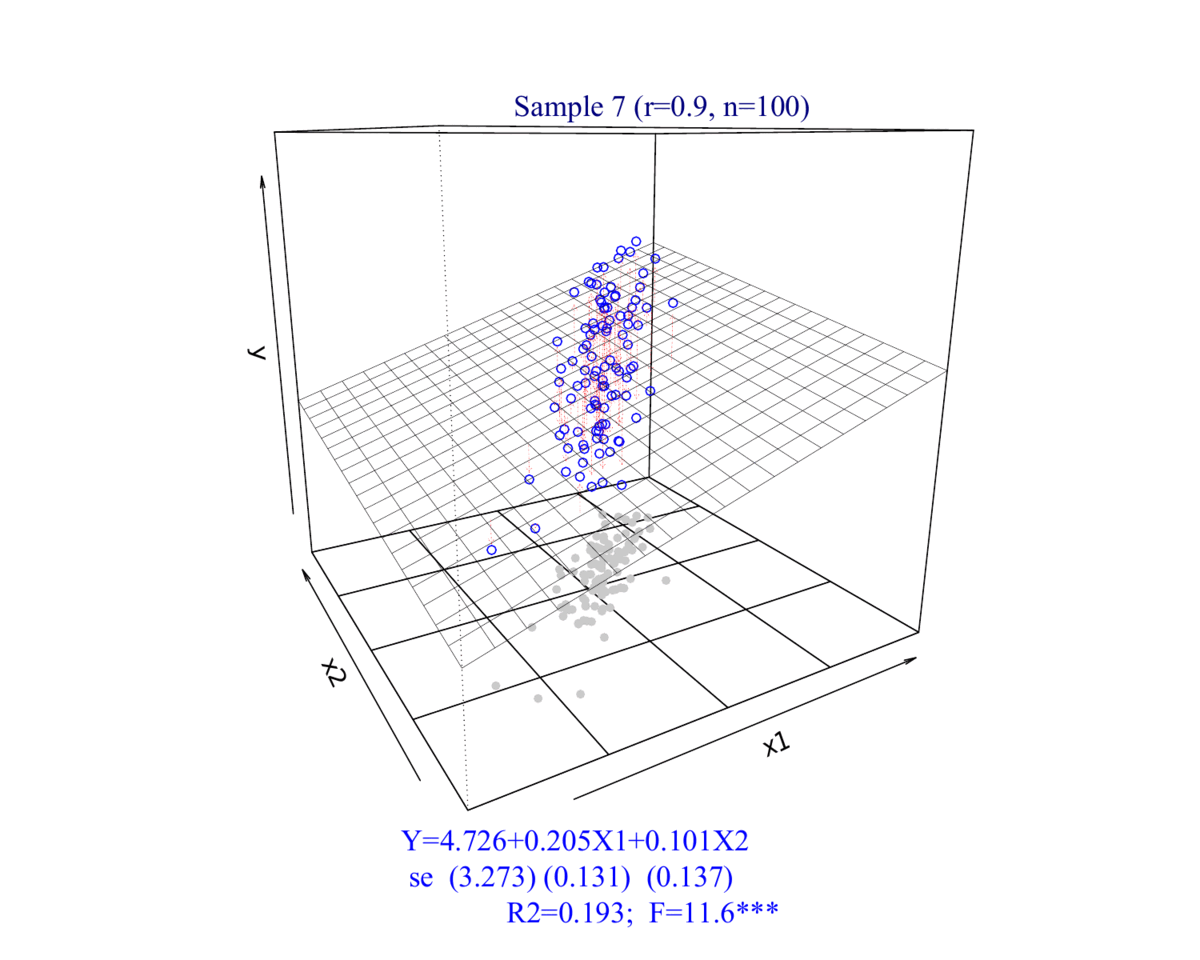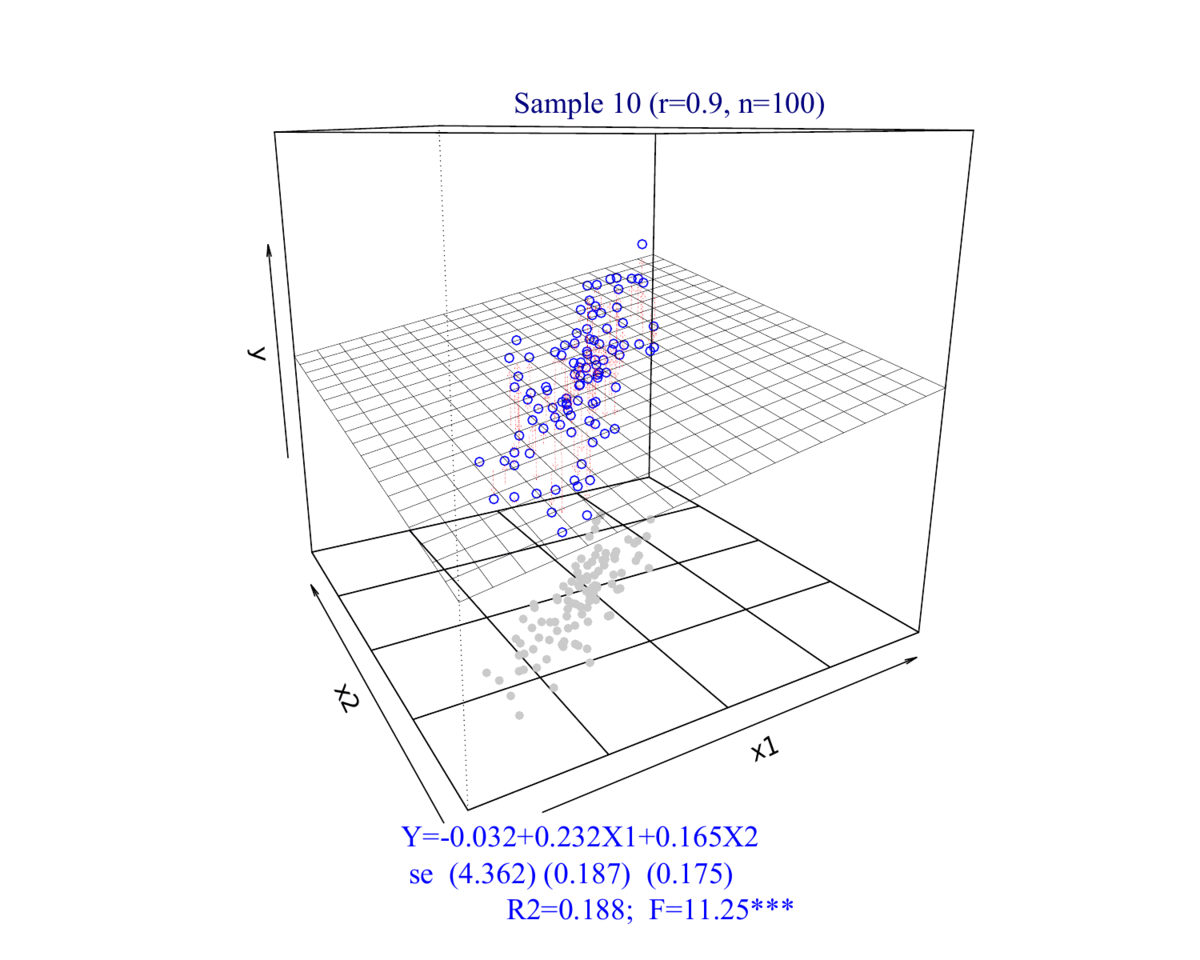
（2）相关系数\(\rho_{(X_{1},X_2)}=0.9\)的情形
对以上两种情形，我们分别生成如下样本数据集\(\{Y_i, X_{1i}, X_{2i}\}\)：
样本容量：\(n =100\)
样本份数：\(sample =10\)
最后我们会利用样本数据，分别对两类情形进行多次的OLS回归，并得到回归结果：
- 相关系数为0时：
\[ \begin{aligned} Y_i = \hat{\alpha}_0+\hat{\alpha}_1 X_{1 i}+\hat{\alpha}_2 X_{2 i} +e_{1i} \end{aligned} \]
- 相关系数为0.9时：
\[ \begin{aligned} Y_i = \hat{\beta}_0+\hat{\beta}_1 X_{1 i}+\hat{\beta}_2 X_{2 i} +e_{2i} \end{aligned} \]
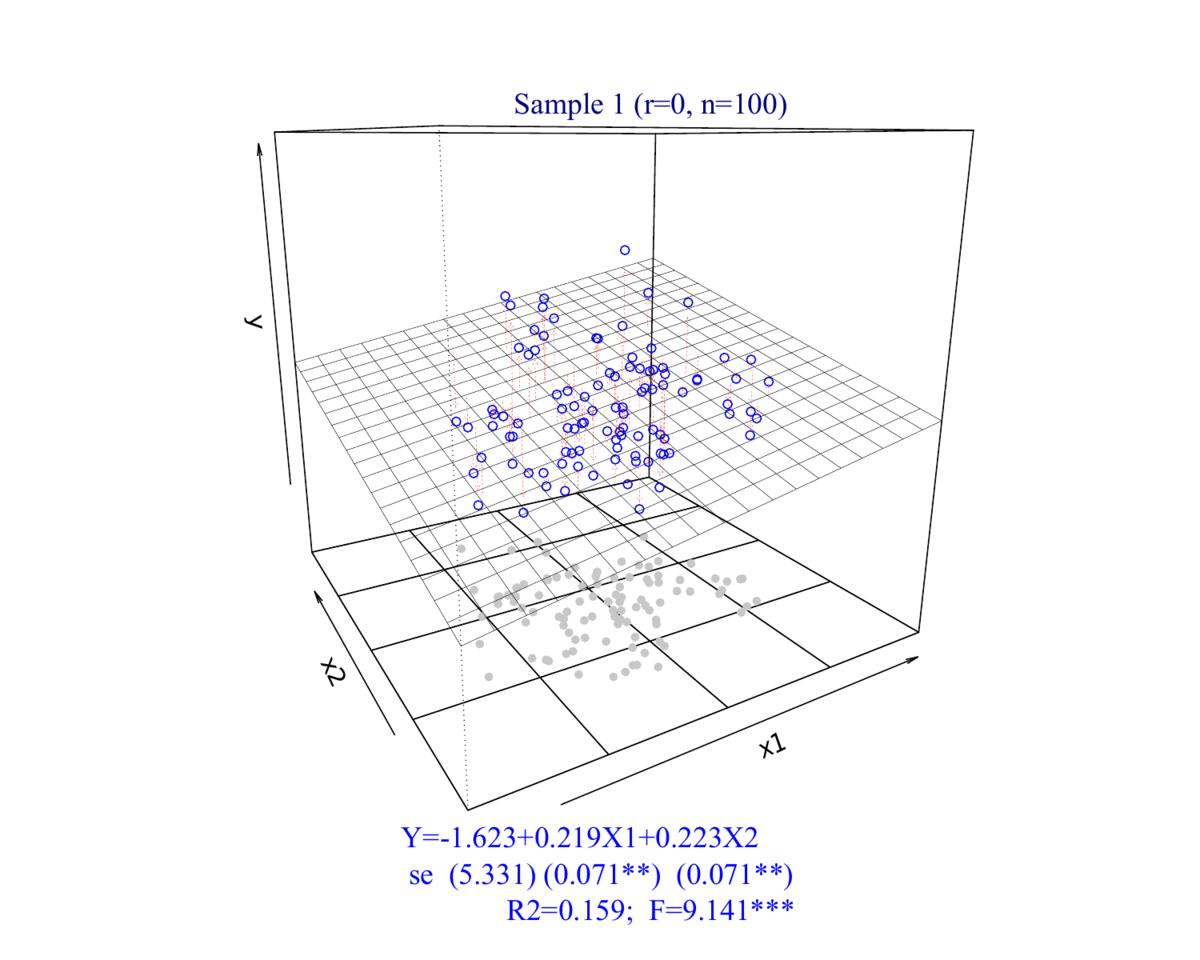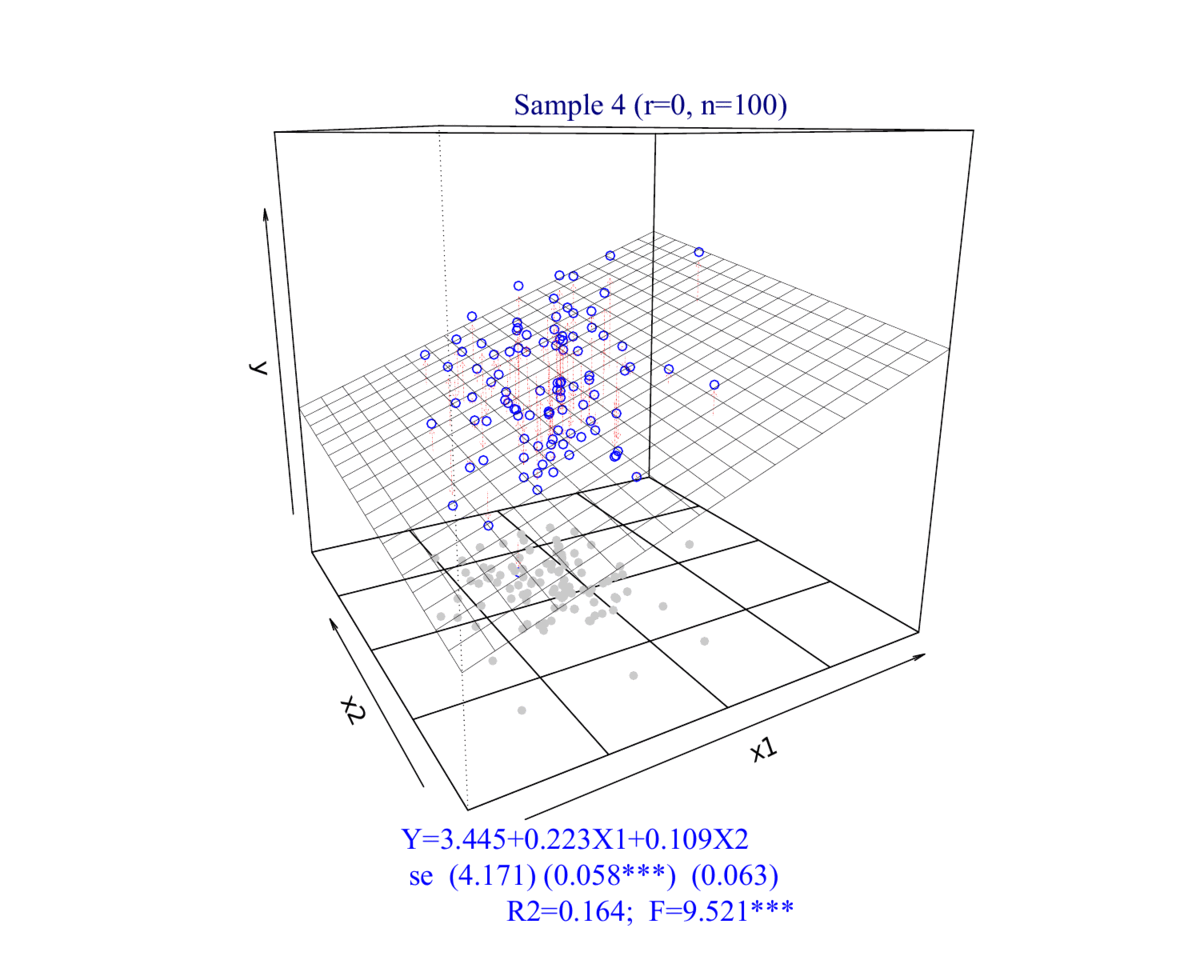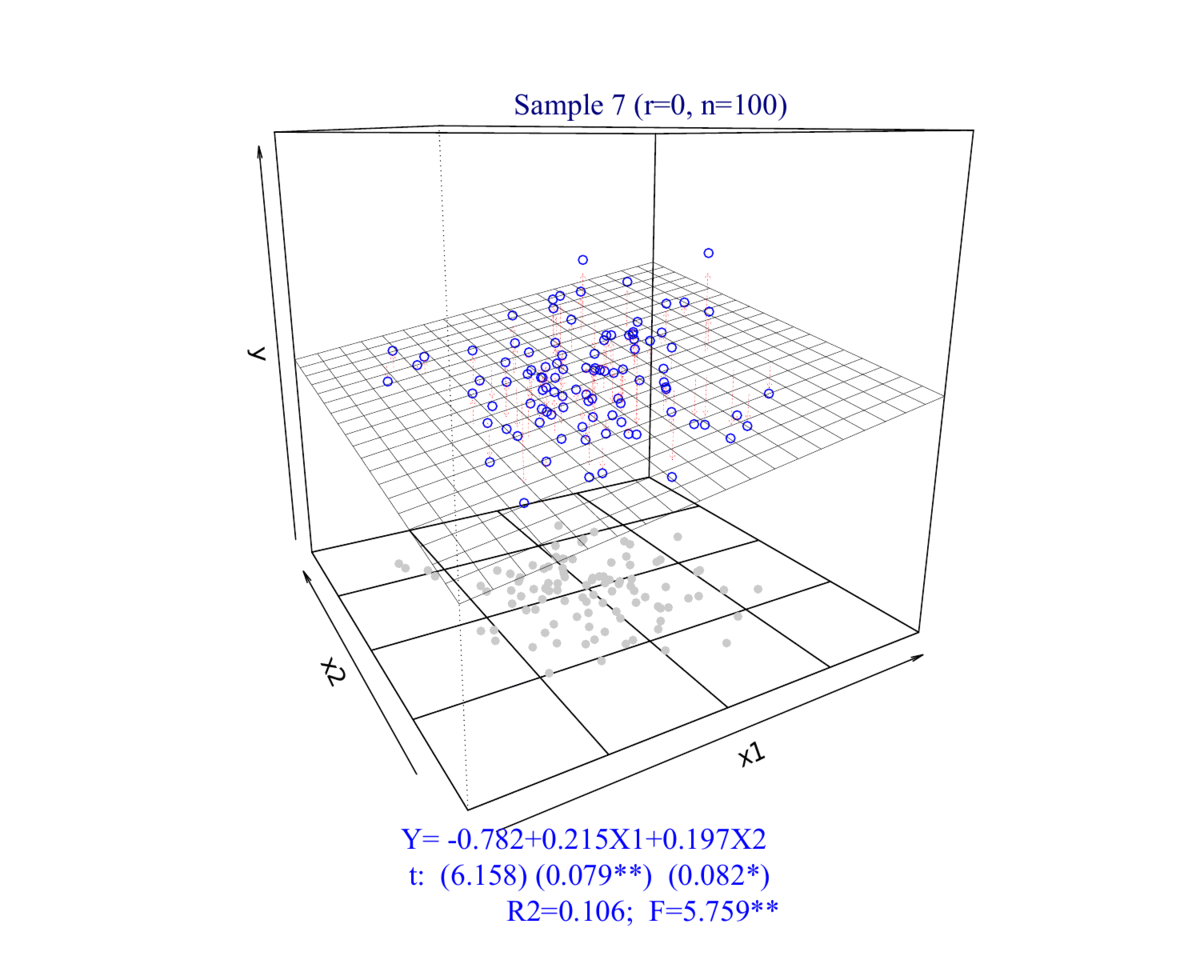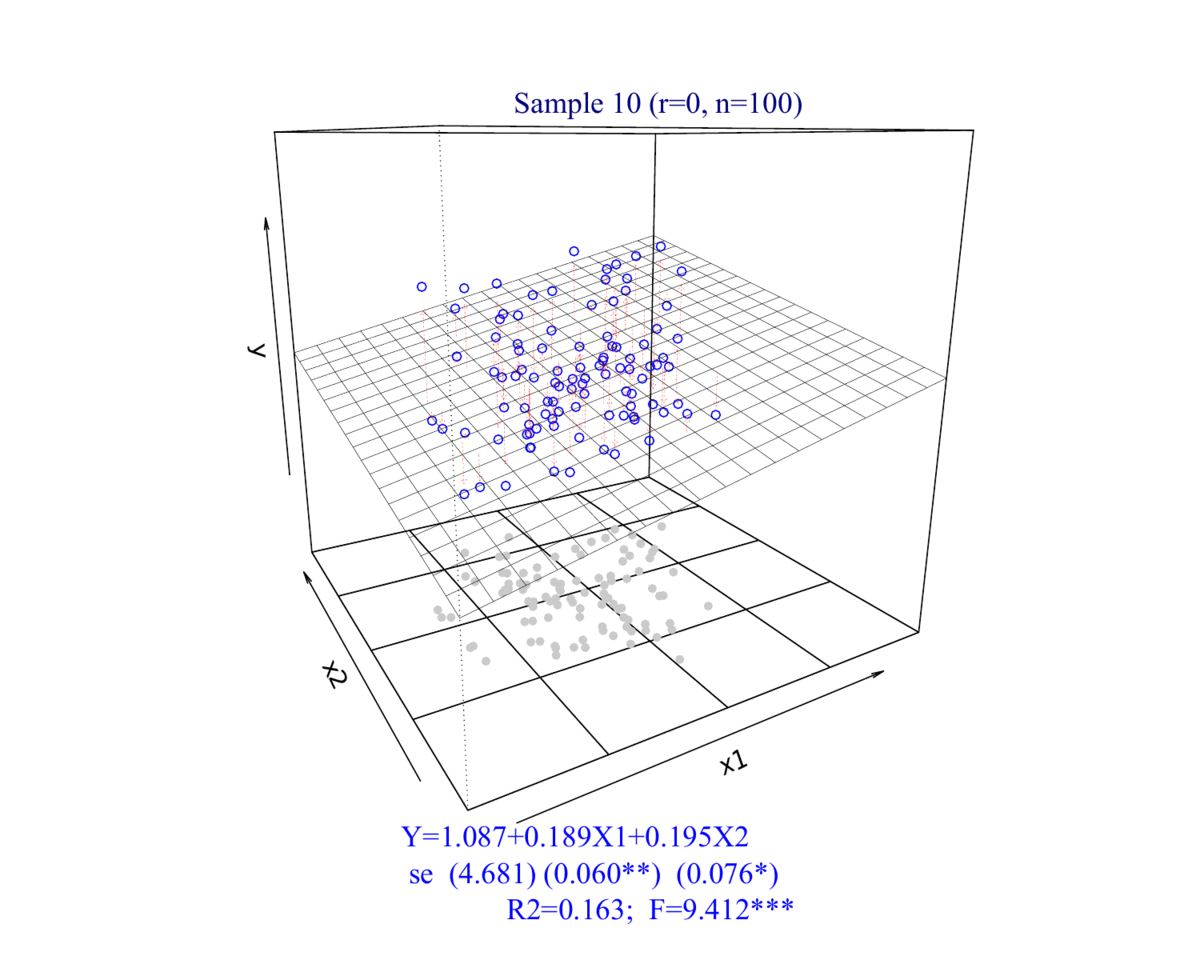
2.2 数据集展示
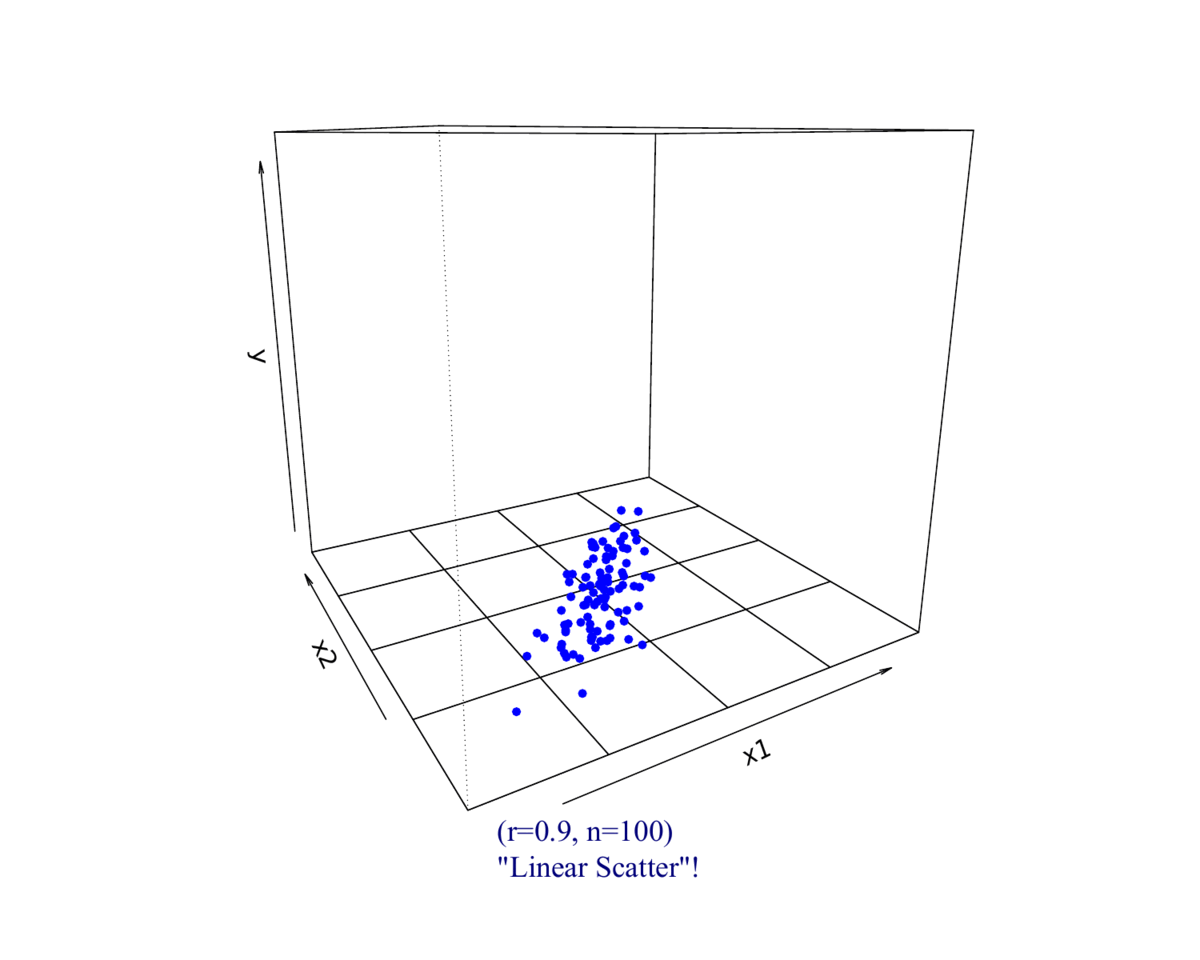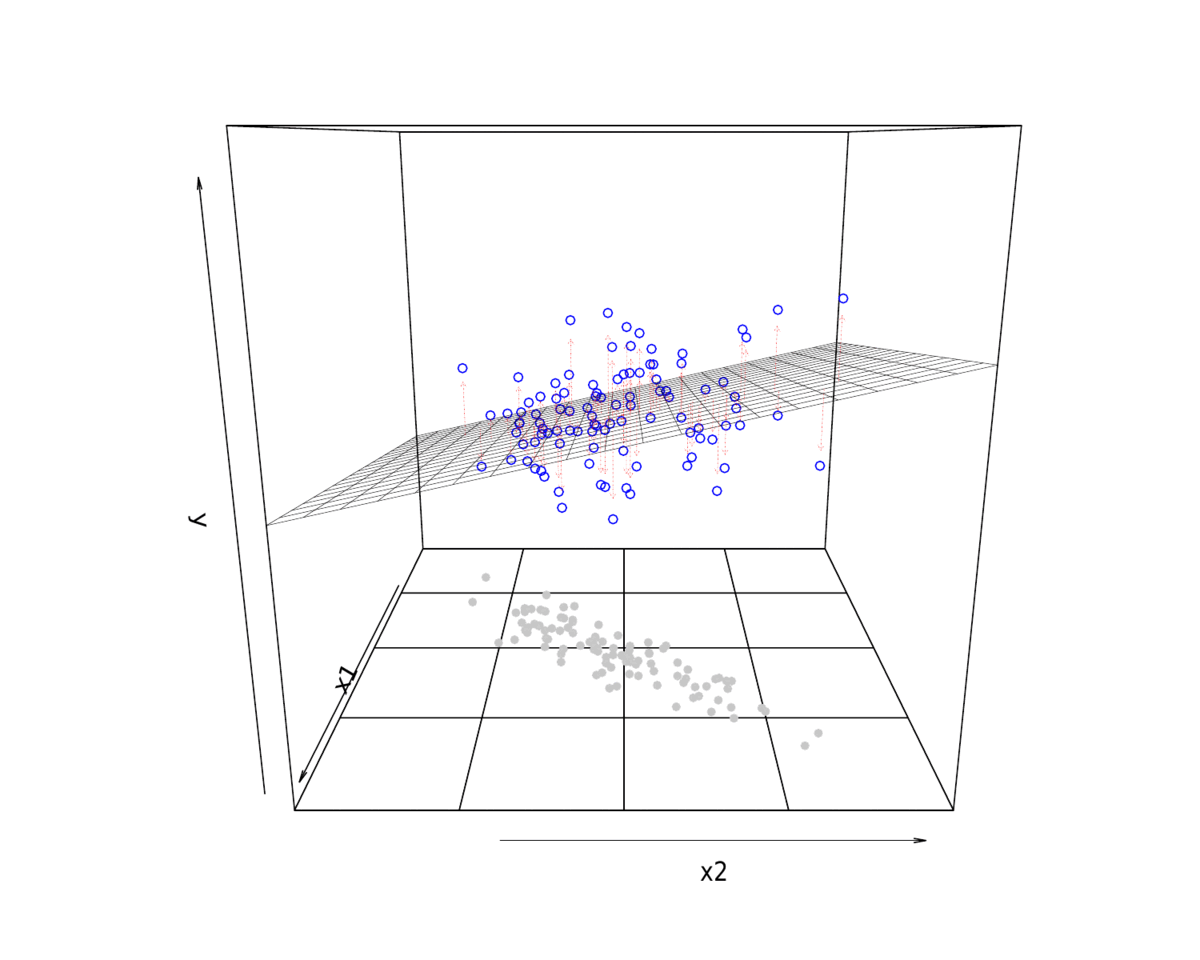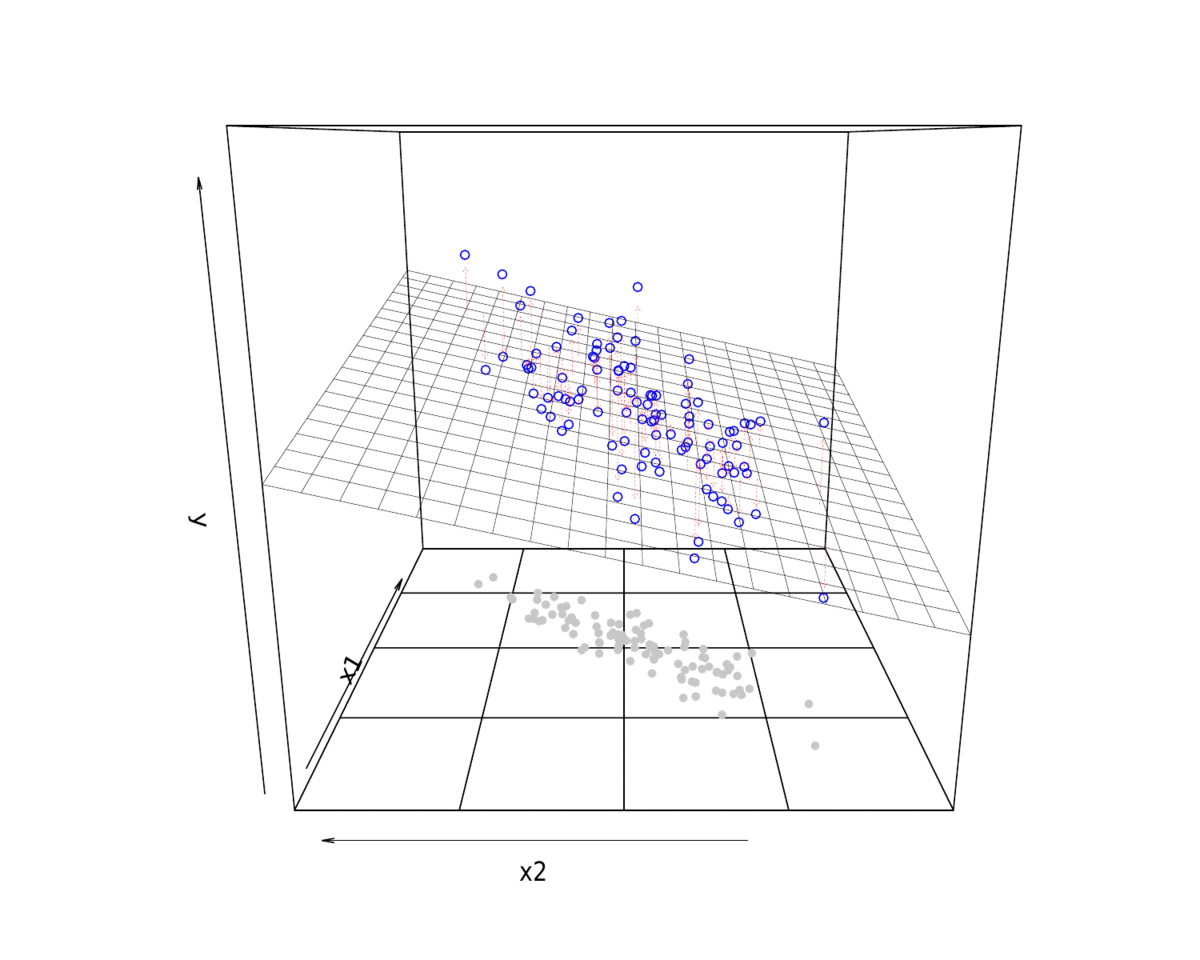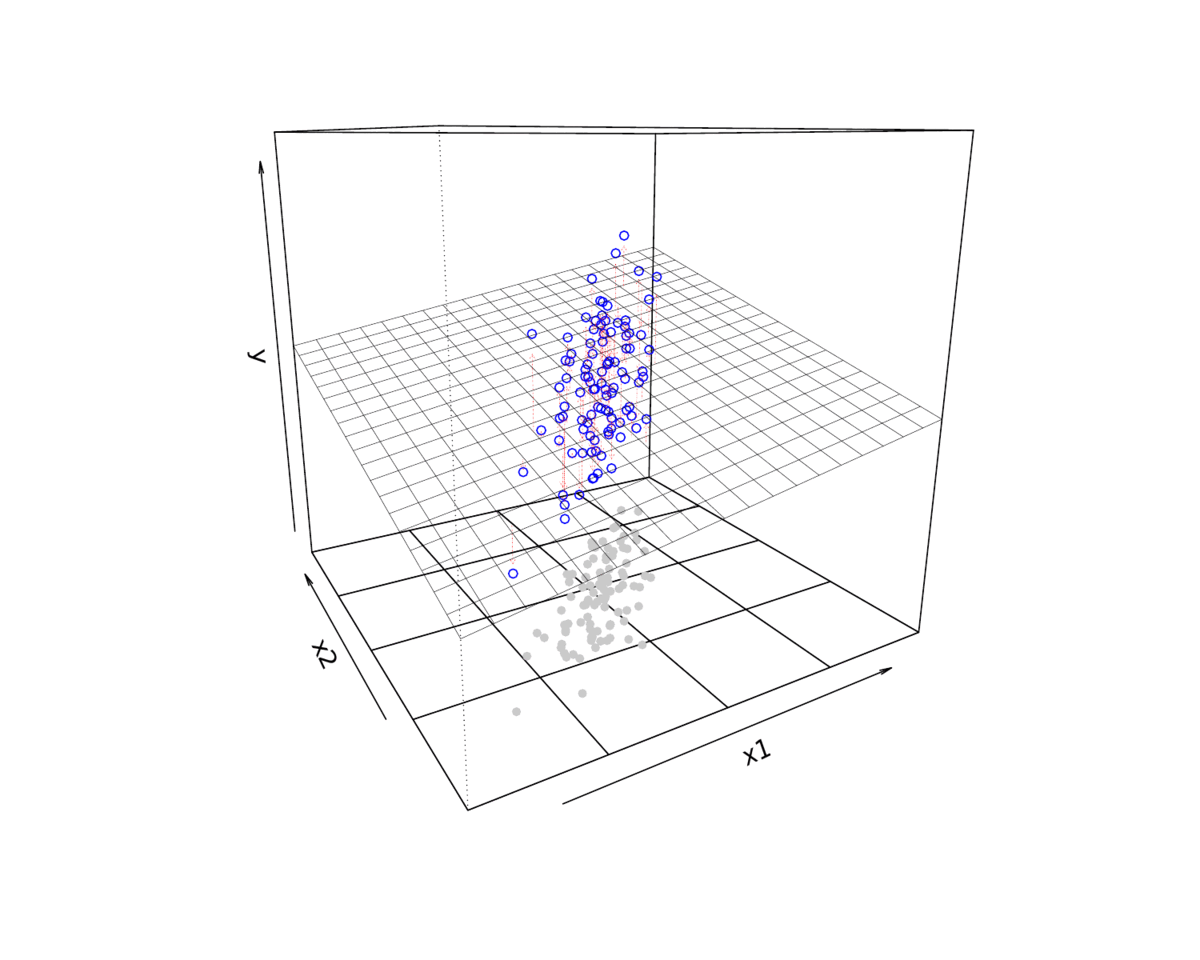
3 拟合展示
4 Paul Johnson教授
提示
我们这里关于多重共线性视觉化的展示源自Paul Johnson教授的课程资料。我曾在2014年就注意到他的这个富有教学意义的展示，并在此基础上做了部分代码改动。
Paul Johnson曾长期在堪萨斯大学担任政治学教授。后来逐步转型为数据科学家，并在私人企业积极探索新的数据分析领域和技术工具。他的个人主页是https://pj.freefaculty.org/。
Paul E. Johnson的多重共线性视觉化的展示在线资源”Stat Writeups”：Regression/Multicollinearity。
交互式课堂版本已经写成 RevealJS 幻灯片：渲染时用 R 生成固定的三档相关系数和 10 份样本，页面里用 plotly 旋转点云、播放抬升，并切换样本与拟合结果。见 多重共线性互动幻灯片。下面仍保留 Johnson 原来的 gif，作为静态记录。
以下为Paul E. Johnson早在2014年完成的最初三维动画演示：
4.1 无多重共线性
4.2 高度多重共线性
