本文将复现Hansen《计量经济学》教材节3.10 “## Model in Matrix Notation”、节3.11 “## Projection Matrix”、节3.12 “## Annihilator Matrix”、节3.19 “## Leverage Values”的内容。重点复现单方程计量模型的一些数学符号体系,内容包括:矩阵模型、投影矩阵、零化矩阵、影响力值。
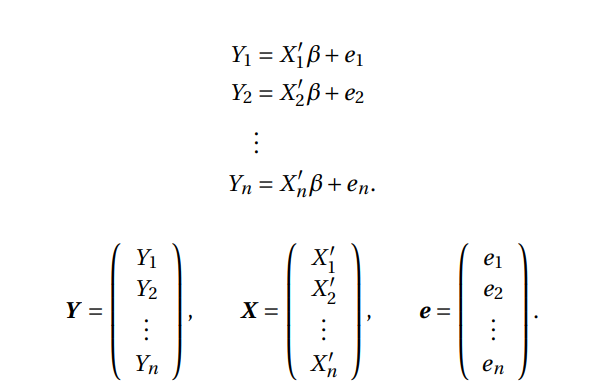
1 矩阵模型1
对于许多目的,包括计算,用矩阵表示法编写模型和统计数据很方便。
在\(n\) 个样本情形下,方程 \(Y_{i}=X_{i}^{\prime} \beta+e_{i}\) 构成了一个 \(n\) 方程组。
\[ Y_{i}=X_{i}^{\prime} \beta+e_{i} \tag{1}\]
- \(X_{i}^{\prime}\) 是 \(X_{i}\) 的转置,即行向量 \(X_{i}^{\prime} = (X_{i1}, X_{i2}, \cdots, X_{ik})\) 包含了第 \(i\) 个样本(观测数量 \(i = 1, 2, \cdots, n\))的 \(k\) 个解释变量(自变量数量 \(k=1, 2, \cdots, k\))。
我们可以将这些 \(n\) 方程堆叠在一起作为
\[ \begin{aligned} &Y_{1}=X_{1}^{\prime} \beta+e_{1} \\ &Y_{2}=X_{2}^{\prime} \beta+e_{2} \\ &\vdots \\ &Y_{n}=X_{n}^{\prime} \beta+e_{n} . \end{aligned} \]
定义
\[ \boldsymbol{Y}= \left( \begin{array}{c} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{n} \end{array} \right), \quad \boldsymbol{X}= \left( \begin{array}{c} X_{1}^{\prime} \\ X_{2}^{\prime} \\ \vdots \\ X_{n}^{\prime} \end{array} \right) = \left( \begin{array}{c} X_{11} & X_{12} & \cdots & X_{1k} \\ X_{21} & X_{22} & \cdots & X_{2k} \\ \vdots & \vdots & \cdots & \vdots \\ X_{n1} & X_{n2} & \cdots & X_{nk} \\ \end{array} \right), \quad \boldsymbol{e}= \left( \begin{array}{c} e_{1} \\ e_{2} \\ \vdots \\ e_{n} \end{array} \right) \]
观察 \(\boldsymbol{Y}\) 和 \(\boldsymbol{e}\) 是 \(n \times 1\) 向量,\(\boldsymbol{X}\) 是 \(n \times k\) 矩阵。 \(n\) 方程组可以紧凑地写成单个方程
\[ \boldsymbol{Y}=\boldsymbol{X} \beta+\boldsymbol{e} \tag{2}\]
样本总和可以用矩阵表示法编写。例如
\[ \begin{aligned} &\sum_{i=1}^{n} X_{i} X_{i}^{\prime}=\boldsymbol{X}^{\prime} \boldsymbol{X} \\ &\sum_{i=1}^{n} X_{i} Y_{i}=\boldsymbol{X}^{\prime} \boldsymbol{Y} . \end{aligned} \]
因此最小二乘估计量可以写成
\[ \widehat{\beta}=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{Y}\right) \]
式 2 的估计版本是
\[ \boldsymbol{Y}=\boldsymbol{X} \widehat{\beta}+\widehat{\boldsymbol{e}} \]
等价的残差向量是
\[ \widehat{\boldsymbol{e}}=\boldsymbol{Y}-\boldsymbol{X} \widehat{\beta} \]
使用残差向量,我们可以将 (3.16) 写为
\[ \boldsymbol{X}^{\prime} \widehat{\boldsymbol{e}}=0 \]
将误差平方和标准写为
\[ \operatorname{SSE}(\beta)=(\boldsymbol{Y}-\boldsymbol{X} \beta)^{\prime}(\boldsymbol{Y}-\boldsymbol{X} \beta) . \]
使用矩阵表示法,我们对大多数估计器都有简单的表达式。这对于计算机编程特别方便,因为大多数语言都允许矩阵表示法和操作。
定理 1 (重要的矩阵表达式) \[ \begin{aligned} \widehat{\beta} &=\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\boldsymbol{X}^{\prime} \boldsymbol{Y}\right) \\ \widehat{\boldsymbol{e}} &=\boldsymbol{Y}-\boldsymbol{X} \widehat{\beta} \\ \boldsymbol{X}^{\prime} \widehat{\boldsymbol{e}} &=0 . \end{aligned} \]
2 投影矩阵2
定义矩阵
\[ \boldsymbol{P}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \]
请注意
\[ \boldsymbol{P} \boldsymbol{X}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \boldsymbol{X}=\boldsymbol{X} . \]
这是投影矩阵的属性。更一般地,对于任何矩阵 \(\boldsymbol{Z}\) 可以写成 \(\boldsymbol{Z}=\boldsymbol{X} \boldsymbol{\Gamma}\) 对于某个矩阵 \(\Gamma\) (我们说 \(\boldsymbol{Z}\) 位于 \(\boldsymbol{X}\) 的范围空间中),然后
\[ \boldsymbol{P Z}=\boldsymbol{P} \boldsymbol{X} \boldsymbol{\Gamma}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \boldsymbol{X} \boldsymbol{\Gamma}=\boldsymbol{X} \boldsymbol{\Gamma}=\boldsymbol{Z} . \]
举一个重要的例子,如果我们将矩阵 \(\boldsymbol{X}\) 划分为两个矩阵 \(\boldsymbol{X}_{1}\) 和 \(\boldsymbol{X}_{2}\),那么 \(\boldsymbol{X}=\) 和 \(\left[\begin{array}{ll}\boldsymbol{X}_{1} & \boldsymbol{X}_{2}\end{array}\right]\) 然后是 \(\boldsymbol{P} \boldsymbol{X}_{1}=\boldsymbol{X}_{1}\)。 (见练习 3.7。)
投影矩阵 \(\boldsymbol{P}\) 具有幂等的代数性质:\(\boldsymbol{P} \boldsymbol{P}=\boldsymbol{P}\)。见下文定理 3.3.2。有关投影矩阵的一般属性,请参见第 A.11 节。
矩阵 \(\boldsymbol{P}\) 在最小二乘回归中创建拟合值:
\[ \boldsymbol{P} \boldsymbol{Y}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \boldsymbol{Y}=\boldsymbol{X} \widehat{\boldsymbol{\beta}}=\widehat{\boldsymbol{Y}} \text {. } \]
由于这个属性,\(\boldsymbol{P}\) 也被称为帽子矩阵。
当 \(X=\mathbf{1}_{n}\) 是一个由 1 组成的 \(n\) 向量时,会出现一个投影矩阵的特殊示例。然后
\[ \boldsymbol{P}=\mathbf{1}_{n}\left(\mathbf{1}_{n}^{\prime} \mathbf{1}_{n}\right)^{-1} \mathbf{1}_{n}^{\prime}=\frac{1}{n} \mathbf{1}_{n} \mathbf{1}_{n}^{\prime} . \]
请注意,在这种情况下
\[ \boldsymbol{P} \boldsymbol{Y}=\mathbf{1}_{n}\left(\mathbf{1}_{n}^{\prime} \mathbf{1}_{n}\right)^{-1} \mathbf{1}_{n}^{\prime} \boldsymbol{Y}=\mathbf{1}_{n} \bar{Y} \]
创建一个 \(n\)-vector,其元素是样本均值 \(\bar{Y}\)。
投影矩阵 \(\boldsymbol{P}\) 经常出现在最小二乘回归的代数运算中。该矩阵具有以下重要性质。
定理 2 (投影矩阵的性质) 任何 \(n \times k \boldsymbol{X}\) 与 \(n \geq\) \(k\) 的投影矩阵 \(\boldsymbol{P}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}\) 具有以下代数性质。
\(\boldsymbol{P}\) 是对称的 \(\left(\boldsymbol{P}^{\prime}=\boldsymbol{P}\right)\)。
\(\boldsymbol{P}\) 是幂等的 \((\boldsymbol{P P}=\boldsymbol{P})\)。
\(\operatorname{tr} \boldsymbol{P}=k\)。
\(\boldsymbol{P}\) 的特征值为 1 和 0 。
\(\boldsymbol{P}\) 的 \(k\) 特征值等于 1 和 \(n-k\) 等于 0 。
\(\operatorname{rank}(\boldsymbol{P})=k\)。
我们通过证明 定理 2 中的主张来结束本节。
第 1 部分成立,因为
\[ \begin{aligned} \boldsymbol{P}^{\prime} &=\left(\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}\right)^{\prime} \\ &=\left(\boldsymbol{X}^{\prime}\right)^{\prime}\left(\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\right)^{\prime}(\boldsymbol{X})^{\prime} \\ &=\boldsymbol{X}\left(\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{\prime}\right)^{-1} \boldsymbol{X}^{\prime} \\ &=\boldsymbol{X}\left((\boldsymbol{X})^{\prime}\left(\boldsymbol{X}^{\prime}\right)^{\prime}\right)^{-1} \boldsymbol{X}^{\prime}=\boldsymbol{P} . \end{aligned} \]
为了建立第 2 部分,\(\boldsymbol{P X}=\boldsymbol{X}\) 的事实意味着
\[ \boldsymbol{P} \boldsymbol{P}=\boldsymbol{P} \boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}=\boldsymbol{P} \]
对于第 3 部分,
\[ \operatorname{tr} \boldsymbol{P}=\operatorname{tr}\left(\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}\right)=\operatorname{tr}\left(\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \boldsymbol{X}\right)=\operatorname{tr}\left(\boldsymbol{I}_{k}\right)=k . \]
跟踪算子的定义和属性见附录 A.5。
附录 A.11 表明第 4 部分适用于任何幂等矩阵。对于第 5 部分,由于 \(\operatorname{tr} \boldsymbol{P}\) 等于第 3 部分的 \(n\) 特征值和 \(\operatorname{tr} \boldsymbol{P}=k\) 之和,因此有 \(k\) 特征值等于 1,其余 \(n-k\) 等于 0。
对于第 6 部分,观察 \(\boldsymbol{P}\) 是半正定的,因为它的特征值都是非负的。根据定理 A.4.5,它的秩等于正特征值的数量,即声称的 \(k\)。
3 零化矩阵3
定义
\[ \boldsymbol{M}=\boldsymbol{I}_{n}-\boldsymbol{P}=\boldsymbol{I}_{n}-\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \]
其中 \(\boldsymbol{I}_{n}\) 是 \(n \times n\) 单位矩阵。
可以看到,
\[ \boldsymbol{M} \boldsymbol{X}=\left(\boldsymbol{I}_{n}-\boldsymbol{P}\right) \boldsymbol{X}=\boldsymbol{X}-\boldsymbol{P} \boldsymbol{X}=\boldsymbol{X}-\boldsymbol{X}=0 . \]
因此 \(\boldsymbol{M}\) 和 \(\boldsymbol{X}\) 是正交的。
我们称 \(\boldsymbol{M}\) 为零化矩阵(Annihilator4 matrix),因为对于 \(\boldsymbol{X}\) 的范围空间中的任何矩阵 \(\boldsymbol{Z}=\boldsymbol{X\Gamma}\),那么
\[ \boldsymbol{M Z}=\boldsymbol{Z}-\boldsymbol{P Z}=\boldsymbol{0} \]
例如,\(\boldsymbol{M} \boldsymbol{X}_{1}=0\) 表示 \(\boldsymbol{X}\) 和 \(\boldsymbol{M P}=0\) 的任何子组件 \(\boldsymbol{X}_{1}\)(参见练习 3.7)。
零化矩阵 \(\boldsymbol{M}\) 与 \(\boldsymbol{P}\) 具有相似的性质,包括 \(\boldsymbol{M}\) 是对称的 \(\left(\boldsymbol{M}^{\prime}=\boldsymbol{M}\right)\) 和幂等的 \((\boldsymbol{M} M=\boldsymbol{M})\)。因此它是一个投影矩阵。
与 定理 2 类似,我们可以计算
\[ \operatorname{tr} \boldsymbol{M}=n-k . \]
(见习题 3.9。)一个暗示是 \(\boldsymbol{M}\) 的秩是 \(n-k\)。
\(\boldsymbol{P}\) 创建拟合值,\(\boldsymbol{M}\) 创建最小二乘残差:
\[ \boldsymbol{M Y}=\boldsymbol{Y}-\boldsymbol{P Y}=\boldsymbol{Y}-\boldsymbol{X \widehat{\beta}}=\widehat{\boldsymbol{e}} \tag{3}\]
如上一节所述,投影矩阵的一个特殊示例出现在 \(\boldsymbol{X}=\mathbf{1}_{n}\) 是一个由 1 组成的 \(n\)-vector 时,因此 \(\boldsymbol{P}=\mathbf{1}_{n}\left(\mathbf{1}_{n}^{\prime} \mathbf{1}_{n}\right)^{-1} \mathbf{1}_{n}^{\prime}\)。相关的零化矩阵是
\[ \boldsymbol{M}=\boldsymbol{I}_{n}-\boldsymbol{P}=\boldsymbol{I}_{n}-\mathbf{1}_{n}\left(\mathbf{1}_{n}^{\prime} \mathbf{1}_{n}\right)^{-1} \mathbf{1}_{n}^{\prime} . \]
\(\boldsymbol{P}\) 创建样本均值向量,\(\boldsymbol{M}\) 创建离均值:
\[ \boldsymbol{M Y}=\boldsymbol{Y}-\mathbf{1}_{n} \bar{Y} \]
为简单起见,我们通常将右侧写为 \(Y-\bar{Y}\)。 \(i^{t h}\) 元素是 \(Y_{i}-\bar{Y}\),\(Y_{i}\) 的离均值
我们还可以使用 式 3 为残差向量写一个替代表达式。将 \(\boldsymbol{Y}=\) \(\boldsymbol{X \beta} +\boldsymbol{e}\) 代入 \(\widehat{\boldsymbol{e}}=\boldsymbol{M} \boldsymbol{Y}\) 并使用 \(\boldsymbol{M} \boldsymbol{X}=\mathbf{0}\) 我们发现
\[ \widehat{\boldsymbol{e}}=\boldsymbol{M} \boldsymbol{Y}=\boldsymbol{M}(\boldsymbol{X \beta} +\boldsymbol{e})=\boldsymbol{M} \boldsymbol{e} \]
它不依赖于回归系数 \(\beta\)。
4 影响力值5
回归矩阵 \(\boldsymbol{X}\) 的影响力值是投影矩阵 \(\boldsymbol{P}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime}\) 的对角线元素。有 \(n\) 影响力值,通常写为 \(h_{i i}\) 对应 \(i=1, \ldots, n\)。自从
\[ \boldsymbol{P}=\left(\begin{array}{c} X_{1}^{\prime} \\ X_{2}^{\prime} \\ \vdots \\ X_{n}^{\prime} \end{array}\right)\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1}\left(\begin{array}{llll} X_{1} & X_{2} & \cdots & X_{n} \end{array}\right) \]
他们是
\[ h_{i i}=X_{i}^{\prime}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} X_{i} \]
影响力值 \(h_{i i}\) 是观察到的回归向量 \(X_{i}\) 的标准化长度。它们经常出现在最小二乘回归的代数和统计分析中,包括留一法回归、有影响的观察、稳健的协方差矩阵估计和交叉验证。
现在列出了影响力值的一些属性。
定理 3 (影响力值的性质)
\(0 \leq h_{i i} \leq 1\)。
\(h_{i i} \geq 1 / n\) 如果 \(X\) 包含截距。
\(\sum_{i=1}^{n} h_{i i}=k\)。
影响力值 \(h_{i i}\) 衡量 \(i^{t h}\) 观察 \(X_{i}\) 相对于样本中其他观察的异常程度。当 \(X_{i}\) 与其他样本值完全不同时,会出现较大的 \(h_{i i}\)。衡量整体异常性的是最大影响力值
\[ \bar{h}=\max _{1 \leq i \leq n} h_{i i} . \tag{4}\]
通常说,当影响力值都大致相等时,回归设计是平衡的。从 定理 3 我们推导出当 \(h_{i i}=\bar{h}=k / n\) 时出现完全平衡。完全平衡的一个例子是,当回归变量都是正交虚拟变量时,每个变量都有相同的 0 和 1 出现。
如果某些影响力值与其他影响力值高度不相等,则回归设计是不平衡的。最极端的情况是 \(\bar{h}=1\)。发生这种情况的一个示例是,当有一个虚拟回归元仅对样本中的一个观察值取值为 1 时。
最大影响力值 式 4 将根据回归变量的选择而变化。例如,考虑方程 (3.13),对具有 \(n=268\) 观察值的单身亚洲男性的工资回归。这个回归有 \(\bar{h}=0.33\)。如果省略平方经验回归量,则影响力值降至 \(\bar{h}=0.10\)。如果添加一个立方经验,它会增加到 \(\bar{h}=0.76\)。如果四次方和五次方相加,则增加到 \(\bar{h}=0.99\)。
一些推理过程(例如稳健的协方差矩阵估计和交叉验证)对高影响力值很敏感。我们稍后会回到这些问题。
我们现在证明 定理 3。
对于第 1 部分,令 \(s_{i}\) 为 \(n \times 1\) 单位向量,其中 \(i^{t h}\) 位置为 1,其他位置为零,因此 \(h_{i i}=s_{i}^{\prime} \boldsymbol{P} s_{i}\)。然后应用二次不等式 (B.18) 和定理 3.3.4,
\[ h_{i i}=s_{i}^{\prime} \boldsymbol{P} s_{i} \leq s_{i}^{\prime} s_{i} \lambda_{\max }(\boldsymbol{P})=1 \]
对于第 2 部分分区 \(X_{i}=\left(1, Z_{i}^{\prime}\right)^{\prime}\)。不失一般性,我们可以用离均值的值 \(Z_{i}^{*}=Z_{i}-\bar{Z}\) 替换 \(Z_{i}\)。然后因为 \(Z_{i}^{*}\) 和截距是正交的
\[ \begin{aligned} h_{i i} &=\left(1, Z_{i}^{* \prime}\right)\left[\begin{array}{cc} n & 0 \\ 0 & Z^{* \prime} Z^{*} \end{array}\right]^{-1}\left(\begin{array}{c} 1 \\ Z_{i}^{*} \end{array}\right) \\ &=\frac{1}{n}+Z_{i}^{* \prime}\left(Z^{* \prime} Z^{*}\right)^{-1} Z_{i}^{*} \geq \frac{1}{n} . \end{aligned} \]
对于第 3 部分,\(\sum_{i=1}^{n} h_{i i}=\operatorname{tr} \boldsymbol{P}=k\),其中第二个等式是定理 3.3.3。
4.1 影响力值的计算
\[ \boldsymbol{P}=\boldsymbol{X}\left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \boldsymbol{X}^{\prime} \]
影响力值\(h_{ii}\)是上述投影矩阵的对角线元素,因此可以表达为:
第一步,先算出平方化矩阵6:
\[ H= \boldsymbol{X} \odot \left( \boldsymbol{X} \otimes \left(\boldsymbol{X}^{\prime} \boldsymbol{X}\right)^{-1} \right) \]
第二步,对上述矩阵进行行加总求和:
\[ h_{ii}= \sum_{i =1}^{n} {H} \]