多方程计量模型数学符号体系

本文梳理和总结了Hansen《计量经济学》教材中多方程计量模型的相关数学符号体系。多方程计量模型（方程系统）是宏观经济学中常用的模型，这类模型的数学符号表达体系与单方程计量模型相比，要更加复杂晦涩。

多方程计量模型

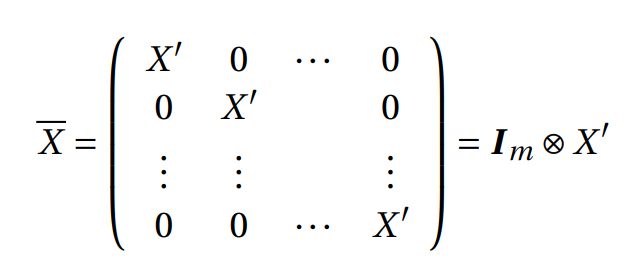
1 回归方程系统¹

1.1 基本符号定义

对于单方程线性回归：\(Y = X' \beta + e\)

相关符号定义为：

• \(Y\)：标量因变量
• \(X\)：\(k \times 1\) 回归元向量
• \(\beta\)：\(k \times 1\) 系数向量
• \(e\)：标量误差项

多方程回归系统中，第\(j\)个（\(j = 1, \ldots, m\)）回归方程可以表示为：

\[ Y_j = X_j' \beta_j + e_j \]

多方程回归系统中符号定义为：

• \(m\)：方程个数
• \(j = 1, \ldots, m\)：方程索引
• \(Y_j\)：第\(j\)个因变量
• \(X_j\)：第\(j\)个方程的\(k_j \times 1\)回归元向量
• \(\beta_j\)：第\(j\)个方程的\(k_j \times 1\)系数向量
• \(e_j\)：第\(j\)个方程的误差项
• \(\bar{k} = \sum_{j=1}^{m} k_j\)：总系数个数

1.2 向量形式

系统方程可以表示为向量形式：

\[ Y = \overline{X} \beta + e \]

因变量向量\(Y = (Y_1, \ldots, Y_m)'\)：\(m \times 1\)因变量向量

回归元矩阵 \(\overline{X}\)：\(m \times \bar{k}\)。具体形式为：

\[ \overline{X} = \begin{pmatrix} X_1' & 0 & \cdots & 0 \\ \vdots & X_2' & & \vdots \\ 0 & 0 & \cdots & X_m' \end{pmatrix} \]

系数向量 \(\beta\)：\(\bar{k} \times 1\)堆叠系数向量。具体形式为：

\[ \beta = \begin{pmatrix} \beta_1 \\ \vdots \\ \beta_m \end{pmatrix} \]

误差向量和协方差矩阵:

• \(e = (e_1, \ldots, e_m)'\)：\(m \times 1\)误差向量
• \(\Sigma = \mathbb{E}[ee']\)：\(m \times m\)误差协方差矩阵
  • 对角元素：\(\text{Var}(e_j)\)
  • 非对角元素：\(\text{Cov}(e_j, e_k)\)

1.3 观测值堆叠形式

系统方程可以表示为：

\[ \boldsymbol{Y} = \overline{\boldsymbol{X}} \beta + \boldsymbol{e} \]

对于\(n\)个观测值，定义：

• \(mn \times 1\)因变量向量。具体形式为：\(\boldsymbol{Y} = \begin{pmatrix} Y_1 \\ \vdots \\ Y_n \end{pmatrix}\)：

• \(mn \times 1\)误差向量 。具体形式为：\(\boldsymbol{e} = \begin{pmatrix} e_1 \\ \vdots \\ e_n \end{pmatrix}\)：

• \(mn \times \bar{k}\)回归元矩阵。具体形式为：\(\overline{\boldsymbol{X}} = \begin{pmatrix} \overline{X}_1 \\ \vdots \\ \overline{X}_n \end{pmatrix}\)：

对于共同回归元情况。当\(X_j = X\)且\(k_j = k\)时（所有方程使用相同的回归元），方程系统可以简化表示为

\[ Y = \boldsymbol{B}' X + e \]

其中：

• 系数矩阵：\(\boldsymbol{B} = (\beta_1, \beta_2, \ldots, \beta_m)\)：\(k \times m\)

此外，观测值堆叠形式还可以表示为：

\[ \boldsymbol{Y} = \boldsymbol{X} \boldsymbol{B} + \boldsymbol{E} \]

其中：

• \(n \times m\)因变量矩阵：\(\boldsymbol{Y} = \begin{pmatrix} Y_1' \\ \vdots \\ Y_n' \end{pmatrix}\)
• \(n \times m\)误差矩阵：\(\boldsymbol{E} = \begin{pmatrix} e_1' \\ \vdots \\ e_n' \end{pmatrix}\)
• \(n \times k\)回归元矩阵：\(\boldsymbol{X} = \begin{pmatrix} X_1' \\ \vdots \\ X_n' \end{pmatrix}\)

1.4 Kronecker积表示

我们可以使用Kronecker积对矩阵\(\overline{X}\)进行简化表示：

\[ \overline{X} = \begin{pmatrix} X' & 0 & \cdots & 0 \\ 0 & X' & & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & X' \end{pmatrix} = \boldsymbol{I}_m \otimes X' \]

其中\(\otimes\)表示Kronecker积。

脚注

1. 见Hansen教材第11章 Multivariate Regression，节11.2 “## Regression Equation System”