Call:
lm(formula = Y ~ X1 + X2, data = data_multiple)
Residuals:
Min 1Q Median 3Q Max
-2.20867 -0.78872 -0.01709 0.94092 1.89296
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.9618 0.2675 7.334 6.79e-11 ***
X1 2.9670 0.1752 16.933 < 2e-16 ***
X2 1.9607 0.1699 11.538 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.981 on 97 degrees of freedom
Multiple R-squared: 0.8296, Adjusted R-squared: 0.8261
F-statistic: 236.2 on 2 and 97 DF, p-value: < 2.2e-16在计量经济学中,当解释变量超过一个时,我们就进入了多元回归的领域。本节我们考虑有两个解释变量的二元回归模型,这是从一元回归到多元回归的重要过渡。
1 模型设定和OLS估计量
考虑二元回归模型: \[ Y_i = X_{1i} \beta_1 + X_{2i} \beta_2 + \varepsilon_i \]
其中:
- \(Y_i\) 是被解释变量
- \(X_{1i}, X_{2i}\) 是解释变量(标量)
- \(\beta_1, \beta_2\) 是回归系数(标量)
- \(\varepsilon_i\) 是误差项
使用矩阵表示,可以写成: \[ Y_i = X_i' \beta + \varepsilon_i \]
其中 \(X_i = (X_{1i}, X_{2i})'\),\(\beta = (\beta_1, \beta_2)'\)。
最小二乘估计的目标是找到参数向量 \(\beta\) 的估计值 \(\hat{\beta}\),使得残差平方和(Sum of Squared Errors, SSE)最小:
\[ \hat{\beta} = \arg\min_{\beta} \sum_{i=1}^{n}(Y_i - X_i' \beta)^2 \]
2 OLS估计量推导
残差平方和函数为: \[ \text{SSE}(\beta) = \sum_{i=1}^{n}(Y_i - X_i' \beta)^2 \]
展开平方项: \[ \text{SSE}(\beta) = \sum_{i=1}^{n}(Y_i^2 - 2Y_i X_i' \beta + \beta' X_i X_i' \beta) \]
整理得到: \[ \text{SSE}(\beta) = \sum_{i=1}^{n} Y_i^2 - 2\beta' \sum_{i=1}^{n} X_i Y_i + \beta' \sum_{i=1}^{n} X_i X_i' \beta \]
这是一个关于向量 \(\beta\) 的二次函数。
2.1 一阶条件
对 \(\text{SSE}(\beta)\) 关于 \(\beta\) 求导: \[ \frac{\partial}{\partial \beta} \text{SSE}(\beta) = -2 \sum_{i=1}^{n} X_i Y_i + 2 \sum_{i=1}^{n} X_i X_i' \beta \]
令导数等于零: \[ -2 \sum_{i=1}^{n} X_i Y_i + 2 \sum_{i=1}^{n} X_i X_i' \hat{\beta} = 0 \]
整理得到: \[ \sum_{i=1}^{n} X_i X_i' \hat{\beta} = \sum_{i=1}^{n} X_i Y_i \]
2.2 矩阵解
这是一个线性方程组 \(\boldsymbol{A} \boldsymbol{b} = \boldsymbol{c}\),其中: - \(\boldsymbol{A} = \sum_{i=1}^{n} X_i X_i'\)(\(k \times k\) 矩阵) - \(\boldsymbol{b} = \hat{\beta}\)(\(k \times 1\) 向量) - \(\boldsymbol{c} = \sum_{i=1}^{n} X_i Y_i\)(\(k \times 1\) 向量)
解为: \[ \hat{\beta} = \left(\sum_{i=1}^{n} X_i X_i'\right)^{-1} \left(\sum_{i=1}^{n} X_i Y_i\right) \]
这就是二元回归的OLS估计量。
2.3 二阶条件
验证二阶条件,计算Hessian矩阵: \[ \frac{\partial^2}{\partial \beta \partial \beta'} \text{SSE}(\beta) = 2 \sum_{i=1}^{n} X_i X_i' \]
这是一个半正定矩阵。如果它是正定的,则二阶条件满足,\(\hat{\beta}\) 是 \(\text{SSE}(\beta)\) 的唯一最小值点。
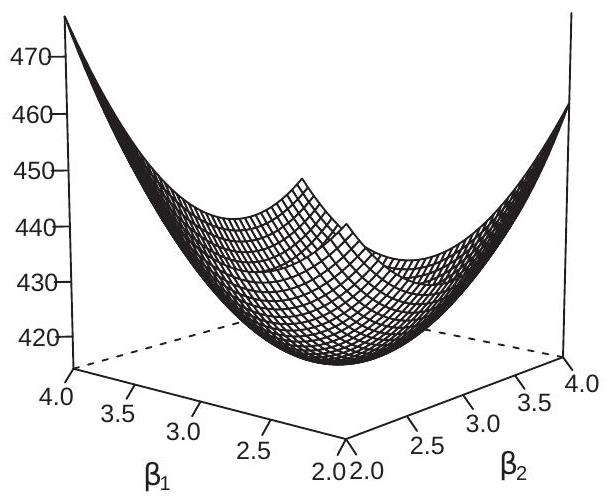
3 残差平方和函数的几何性质
残差平方和函数 \(\text{SSE}(\beta)\) 是关于 \(\beta_1\) 和 \(\beta_2\) 的二次函数,具有以下几何性质:
- 三维表面:\(\text{SSE}(\beta)\) 在 \((\beta_1, \beta_2, \text{SSE})\) 空间中形成一个碗状的三维表面
- 等高线:在 \((\beta_1, \beta_2)\) 平面上的等高线是椭圆形的
- 最小值点:OLS估计量 \(\hat{\beta}\) 对应SSE函数的最小值点
4 R代码复现过程
4.1 1. 数据生成
根据教材内容,我们生成模拟数据: - \(X_1, X_2 \sim U[0,2]\)(均匀分布) - \(Y \sim N(2 + 3X_1 + 2X_2, 1)\)(正态分布,包含截距项)
我们估计如下有截距模型:
\[ Y_i = \beta_0 + \beta_1 X_{1i} + \beta_2 X_{2i} + \varepsilon_i \]
模拟数据集如下:
4.2 2. OLS估计
使用矩阵公式计算OLS估计量。
以下是R估计结果的初始报告摘要:
对上述结果进行整理得到如下估计方程表达式:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y}=&&+1.9618&&+2.9670X1_i&&+1.9607X2_i\\ &(s)&&(0.2675)&&(0.1752)&&(0.1699)\\ &(t)&&(+7.33)&&(+16.93)&&(+11.54)\\ &(over)&&n=100&&\hat{\sigma}=0.9810 &&\\ &(fit)&&R^2=0.8296&&\bar{R}^2=0.8261 &&\\ &(Ftest)&&F^*=236.16&&p=0.0000 && \end{split} \end{alignedat} \]
4.3 3. 计算拟合值和残差
根据OLS估计量计算拟合值和残差。
以下是拟合值和残差的计算结果表:
4.4 4. 绘制图形1:三维回归平面图
根据拟合值和残差计算结果绘制三维图形。图形如下:
4.5 5. 绘制图形2:SSE函数三维表面图
4.6 6. 绘制图形3:SSE等高线图
5 复现结果评注
通过本次复现,我们得到了以下结果:
OLS估计量:通过最小化残差平方和,我们得到了回归系数向量 \(\hat{\beta} = (\hat{\beta}_0, \hat{\beta}_1, \hat{\beta}_2)'\)。
图形分析:
- 图1显示了数据点、回归平面和残差(垂直距离),直观展示了多元最小二乘估计的几何意义
- 图2显示了SSE函数关于 \(\beta_1\) 和 \(\beta_2\) 的三维表面形状,最小值点对应OLS估计量
- 图3显示了SSE函数的等高线图,椭圆形等高线反映了参数之间的相关性
理论验证:通过验证SSE函数的二次形式和Hessian矩阵的正定性,确认了数学推导的正确性。
矩阵运算:展示了如何使用矩阵代数求解多元回归的OLS估计量,为后续更复杂的多元回归模型奠定了基础。
这个复现完整地展示了多元最小二乘估计的理论基础和实际应用。