| 统计 | Y对X | X对Y |
|---|---|---|
| X均值 | 168.2260 | 168.2260 |
| Y均值 | 168.3368 | 168.3368 |
| X标准差 | 15.3921 | 15.3921 |
| Y标准差 | 15.3921 | 15.3921 |
| 相关系数 | 0.5937 | 0.5937 |
| 样本量 | 1000.0000 | 1000.0000 |
| 截距 | 68.4561 | 68.2795 |
| 斜率 | 0.5937 | 0.5937 |
| 错误截距 | NA | -115.2985 |
| 错误斜率 | NA | 1.6843 |
1 计量理论分析过程
1.1 逆回归的基本概念
Galton在双变量分布中发现了一个有趣的特征。除了\(Y\)对\(X\)的回归外,我们也可以进行\(X\)对\(Y\)的回归。(在他的遗传学例子中,这是在给定子女身高的条件下,父母身高的最佳线性预测。)这种回归的形式为:
\[ \begin{aligned} Y &= X\beta + \alpha + e & \text{(式1)}\\ X &= Y\beta^* + \alpha^* + e^* & \text{(式2)} \end{aligned} \]
这时式(2)被称为逆回归(reverse regression)。在这个方程中,系数\(\alpha^{\ast}\)、\(\beta^{\ast}\)和误差项\(e^{\ast}\)由线性投影定义。
1.2 稳定总体中的逆回归
在稳定总体中,我们发现式(2)中的系数\(\alpha^{\ast}\)、\(\beta^{\ast}\)和误差项\(e^{\ast}\)分别为:
\[ \begin{aligned} \beta^* &= \text{corr}(X,Y) = \beta \\ \alpha^* &= (1-\beta)\mu = \alpha \end{aligned} \]
这些系数与\(Y\)对\(X\)投影中的系数完全相同!截距和斜率在正向和逆向投影中具有完全相同的值![这种相等性并不特别重要;它是\(X\)和\(Y\)具有相同方差这一假设的产物。]
1.3 常见的错误理解
虽然这个代数发现相当简单,但它是反直觉的。相反,对于逆回归形式的常见但错误的猜测是取方程\(Y = X\beta + \alpha + e\),两边除以\(\beta\)并重写得到方程:
\[ X = Y\frac{1}{\beta} - \frac{\alpha}{\beta} - \frac{1}{\beta}e \]
这表明\(X\)对\(Y\)的投影应该具有斜率系数\(\frac{1}{\beta}\)而不是\(\beta\),截距为\(-\frac{\alpha}{\beta}\)而不是\(\alpha\)。
哪里出了问题?
方程 \(X = Y\frac{1}{\beta} - \frac{\alpha}{\beta} - \frac{1}{\beta}e\) 是完全有效的,因为它是对有效方程 \(Y = X\beta + \alpha + e\) 的简单操作。问题在于这个方程既不是条件期望函数(CEF)也不是线性投影。投影(或CEF)的逆运算不会产生投影(或CEF)。相反,\(X = Y\beta^* + \alpha^* + e^*\) 是有效的投影,而不是\(X =Y\frac{1}{\beta} - \frac{\alpha}{\beta} - \frac{1}{\beta}e\)。
无论如何,Galton的发现是当变量被标准化时,两个投影(\(Y\)对\(X\),以及\(X\)对\(Y\))中的斜率都等于相关系数,两个方程都表现出回归到均值的现象。这不是因果关系,而是联合分布的自然特征。
2 R代码复现
2.1 复现步骤和基本过程
关于数据生成过程,我们使用Cholesky分解方法生成双变量正态分布数据,分别模拟两种情形:
- 方差相等情形:\(X\)和\(Y\)具有相同的方差(\(\sigma_X^2 = \sigma_Y^2 = 16\))
- 方差不相等情形:\(X\)和\(Y\)具有不同的方差(\(\sigma_X^2 = 16\),\(\sigma_Y^2 = 9\))
对于每种情形,我们分别进行:
- \(Y\)对\(X\)的标准回归:\(Y = \alpha + \beta X + e\)
- \(X\)对\(Y\)的逆回归:\(X = \alpha^* + \beta^* Y + e^*\)
我们比较两种回归的系数是否相等:
(1)方差相等情形:
正回归估计系数:$ = =r_{(X,Y)} $, \(\widehat{\alpha} = \overline{Y} - \widehat{\beta} \overline{X}\);
逆回归估计系数:\(\widehat{\beta^*} =\frac{\sum{y_ix_i}}{\sum{y^2_i}} = r_{X,Y}= \widehat{\beta}\), \(\widehat{\alpha^*} = \overline{X} - \widehat{\beta}^* \overline{Y} \neq \widehat{\alpha}\)
(2)方差不相等情形:
正回归估计系数:$ = r_{(X,Y)} $, \(\widehat{\alpha} = \overline{Y} - \widehat{\beta} \overline{X}\);
逆回归估计系数:\(\widehat{\beta^*} =\frac{\sum{y_ix_i}}{\sum{y^2_i}} \neq r_{X,Y} \neq \widehat{\beta}\),\(\widehat{\alpha^*} = \overline{X} - \widehat{\beta^*} \overline{Y} \neq \widehat{\alpha}\)
最后,我们复现了错误理解的逆回归过程,并进行结果比较。
常见的错误理解是简单地对方程 \(Y = \alpha + \beta X + e\)(正回归)进行代数变换:
\[ X = \frac{1}{\beta}Y - \frac{\alpha}{\beta} - \frac{1}{\beta}e \]
这种方法得到的系数 \(\frac{1}{\beta}\) 和 \(-\frac{\alpha}{\beta}\) 并不是有效的线性投影系数。
2.2 方差相等情形复现结果
为了方便大家复现,我们在这里给出相关的xlsx数据集(点击下载)。
数据集基本情况和回归系数比较表如下:
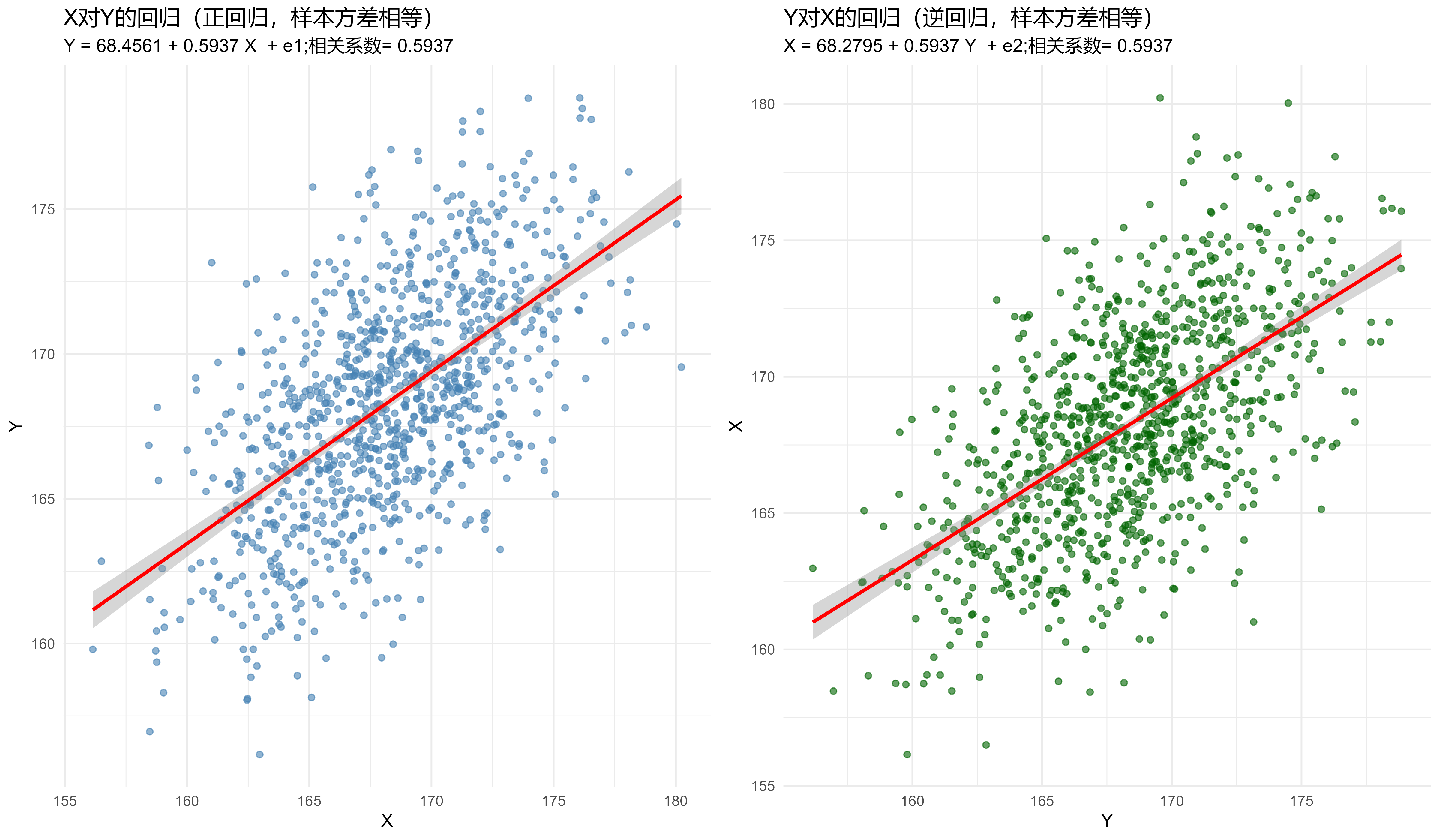
在方差相等的情况下,我们验证了以下重要结论:
- 系数相等性:\(Y\)对\(X\)的回归系数与\(X\)对\(Y\)的逆回归系数完全相等
- 截距相等性:两个回归的截距也相等
- 相关系数性质:相关系数等于两个回归的斜率系数
- 错误理解的逆回归:错误理解的逆回归得到的系数与理论值不一致
2.3 方差不相等情形复现结果
为了方便大家复现,我们在这里给出相关的xlsx数据集(点击下载)。
数据集基本情况和回归系数比较表如下:
| 统计 | X对Y | Y对X |
|---|---|---|
| X均值 | 167.9507 | 167.9507 |
| Y均值 | 168.1132 | 168.1132 |
| X标准差 | 15.9598 | 15.9598 |
| Y标准差 | 8.6626 | 8.6626 |
| 相关系数 | 0.6121 | 0.6121 |
| 样本量 | 1000.0000 | 1000.0000 |
| 截距 | 92.3700 | 28.2678 |
| 斜率 | 0.4510 | 0.8309 |
| 错误截距 | NA | -204.8186 |
| 错误斜率 | NA | 2.2174 |
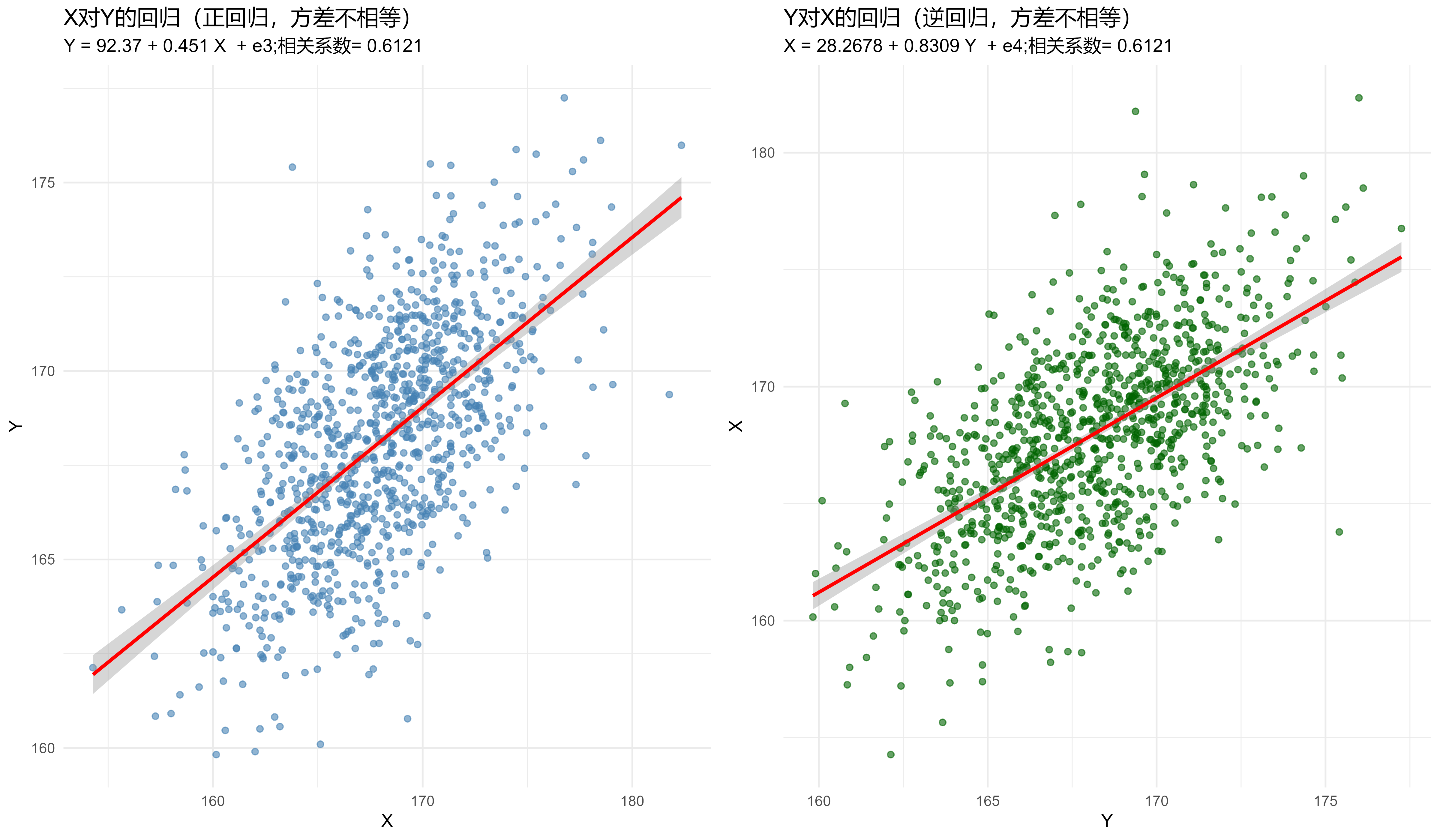
在方差不相等的情况下,我们观察到:
- 系数不相等性:\(Y\)对\(X\)的回归系数与\(X\)对\(Y\)的逆回归系数不相等
- 截距不相等性:两个回归的截距也不相等
- 相关系数性质:相关系数不等于斜率系数
- 错误理解的逆回归:错误理解的逆回归得到的系数与理论值不一致
2.4 理论意义
通过对比两种情形的结果,我们验证了Galton的重要发现:
- 稳定总体的重要性:只有在稳定总体中(\(X\)和\(Y\)具有相同方差),正向和逆向投影才具有相同的斜率系数
- 回归到均值的对称性:在稳定总体中,两个回归方程都表现出回归到均值的特征
- 投影与逆运算的区别:理解投影的逆运算与逆投影之间的区别对于正确理解回归分析至关重要
- 方差相等性的关键作用:方差相等性是逆回归对称性质的必要条件
3 使用Cholesky分解生成相关数据
Cholesky分解是一种将正定对称矩阵分解为下三角矩阵与其转置乘积的方法。在生成相关数据时,我们利用这个性质来构造具有指定协方差结构的多元正态分布数据。
3.1 Cholesky分解的性质和过程
对于正定对称协方差矩阵 \(\Sigma\),存在下三角矩阵 \(L\),使得:
\[ \Sigma = LL^T \]
其中 \(L\) 是下三角矩阵,满足 \(L_{ij} = 0\) 当 \(i < j\) 时。
如果我们有独立的标准正态随机变量 \(Z = (Z_1, Z_2, ..., Z_n)^T\),其中 \(Z_i \sim N(0,1)\) 且相互独立,那么通过线性变换:
\[ X = LZ + \mu \]
其中 \(\mu\) 是均值向量,\(X\) 将具有协方差矩阵 \(\Sigma\) 和均值 \(\mu\)。
对于双变量情况,协方差矩阵为:
\[ \Sigma = \begin{pmatrix} \sigma_X^2 & \rho\sigma_X\sigma_Y \\ \rho\sigma_X\sigma_Y & \sigma_Y^2 \end{pmatrix} \]
其中:
- \(\sigma_X^2\) 是X的方差
- \(\sigma_Y^2\) 是Y的方差
- \(\rho\) 是相关系数
具体过程如下:
- 输入:协方差矩阵 \(\Sigma\)
- 计算:\(L = \text{chol}(\Sigma)\)
- 结果:下三角矩阵 \(L\),满足 \(\Sigma = LL^T\)
数据生成步骤如下:
- 生成独立标准正态变量:\(Z \sim N(0, I)\)
- 应用线性变换:\(XY = ZL^T\)
- 添加均值:\(X = XY_1 + \mu_X\),\(Y = XY_2 + \mu_Y\)
3.2 为什么这种方法有效?
线性变换保持正态性:如果 \(Z\) 是多元正态分布,那么 \(X = LZ + \mu\) 也是多元正态分布。
协方差矩阵的变换:
对于线性变换 \(X = LZ + \mu\),有:
\[ \text{Cov}(X) = L \text{Cov}(Z) L^T = L I L^T = LL^T = \Sigma \]
均值的变换:
\[ \mathbb{E}[X] = L\mathbb{E}[Z] + \mu = L \cdot 0 + \mu = \mu \]
优势如下:
- 精确性:能够精确生成具有指定协方差结构的数据
- 效率:计算复杂度相对较低
- 数值稳定性:Cholesky分解数值稳定性好
- 灵活性:可以轻松扩展到更高维的情况
在逆回归验证中的作用如下:
在逆回归验证中,Cholesky分解确保了:
- X和Y具有指定的方差(\(\sigma_X^2 = \sigma_Y^2 = 16\))
- X和Y具有指定的相关系数(\(\rho = 0.6\))
- 数据服从双变量正态分布
- 为后续验证逆回归性质提供了理想的数据基础
这种方法特别适合验证理论性质,因为它能够精确控制数据的统计特性,使得理论预期与经验结果能够完美匹配。