| 变量_代码 | 变量_中文 | 定义和取值 |
|---|---|---|
| obs | 序号 | 序号 |
| lwage | 对数化工资 | 定量变量:取对数后的工资 |
| edu | 受教育年数 | 定量变量:受教育年数(年) |
| exp | 工作年数 | 定量变量:工作年数(年) |
| exp2 | 工作年数平方 | 定量变量:工作年数平方/100 |
| black | 是否黑人 | 虚拟变量:1=黑人;0=其他 |
| south | 是否南方地区 | 虚拟变量:1=南方地区;0=其他 |
| urban | 是否居住市区 | 虚拟变量:1=居住市区;0=其他 |
| college | 附近是否有大学 | 虚拟变量:1=附近有大学;0=其他 |
| public | 附近是否有公立大学 | 虚拟变量:1=附近有公立大学;0=其他 |
| private | 附近是否有私立大学 | 虚拟变量:1=附近有私立大学;0=其他 |
| age | 年龄 | 定量变量:年龄(年) |
| age2 | 年龄平方 | 定量变量:年龄(年)的平方/100 |
| momedu | 母亲受教育年数 | 定量变量:母亲受教育年数(年) |
| dadedu | 父亲受教育年数 | 定量变量:父亲受教育年数(年) |
工具变量法是处理内生性问题的重要方法,但当工具变量数量超过内生变量数量时,模型会出现过度识别问题。本文基于Hansen教材12章内容,系统阐述了工具变量法的基本原理、2SLS估计方法及其经济含义。通过复现Card(1995)数据,我们构建了不同工具变量组合下的工资结构方程和内生变量的精简方程,并使用R包systemfit进行了2SLS估计。实证结果表明,不同工具变量组合下的2SLS估计结果具有较好的一致性,验证了工具变量法的有效性,为工资决定机制的深入研究提供了可靠的实证基础。
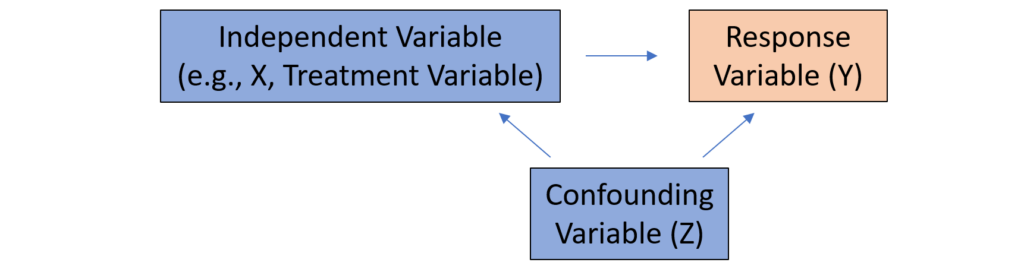
1 案例说明
1.1 初始文献
David Card(1995)在一篇有影响力的论文中提出,如果潜在学生住在大学附近,就可以降低就读成本,从而提高学生上大学的可能性。然而,大学邻近性不会直接影响学生的技能或能力,因此不应对其市场工资产生直接影响。这些考虑因素表明,大学邻近性可以作为工资回归教育的工具。我们使用Card(1995)论文中报告的最简单的模型来说明工具变量的概念。
本文复现使用的R脚本文件和数据集下载链接:
- R脚本文件
hansen21-chpt12-iv.R: - Card数据集
Card1995.dta:
1.2 变量定义
为了研究工资收入(wage,或对数化的工资lwage)是如何决定的,我们考虑如下所示的一些变量(具体定义见 表 1))。
2 准备工作
首先,我们加载所需的包:
require(knitr)
require(here)
require(broom)
require(haven)
require(systemfit)
require(AER)
#renv::install("ivmodel")
require(ivmodel) # for LIML fit
# load package
library(systemfit)我们已经对表12.1和表12.2的估计结果进行了R复现,具体脚本文件见hansen21-chpt12-iv.R。接下来,我们直接运行复现代码脚本,从而得到所有相关分析结果。
source(here("replication", "chpt12-iv", "hansen21-chpt12-iv.R"),
encoding = "UTF-8")
N <- 30003 表12.1:第二阶段方程(工资结构方程)的回归结果比较
3.1 模型1:直接OLS回归(不使用工具变量)
OLS建模表达式为:
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}edu_i+\beta_{3}exp_i+\beta_{4}exp2_i\\&+\beta_{5}black_i+\beta_{6}south_i+\beta_{7}urban_i+u_i \end{split} \quad \text{(OLS directly)}\quad \end{aligned} \tag{1}\]
R代码如下:
# model ols
mod_ls <- formula("lwage ~ edu + exp + exp2 + black + south + urban")
fit_lm <- lm(formula = mod_ls, data = tbl_reg)
smry_lm <- summary(fit_lm)R代码下OLS回归结果初始报告结果如下:
Call:
lm(formula = mod_ls, data = tbl_reg)
Residuals:
Min 1Q Median 3Q Max
-1.59297 -0.22315 0.01893 0.24223 1.33190
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.733664 0.067603 70.022 < 2e-16 ***
edu 0.074009 0.003505 21.113 < 2e-16 ***
exp 0.083596 0.006648 12.575 < 2e-16 ***
exp2 -0.224088 0.031784 -7.050 2.21e-12 ***
black -0.189632 0.017627 -10.758 < 2e-16 ***
south -0.124862 0.015118 -8.259 < 2e-16 ***
urban 0.161423 0.015573 10.365 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.3742 on 3003 degrees of freedom
Multiple R-squared: 0.2905, Adjusted R-squared: 0.2891
F-statistic: 204.9 on 6 and 3003 DF, p-value: < 2.2e-163.2 模型2:一个内生变量且等量工具变量情形下的2SLS分析
edu内生,工具变量为college:
假如我们认为前述OLS模型(见 式 1 )中受教育年数edu为内生自变量,并且认为其他自变量都是外生的。同时,我们选择把附近是否有大学college作为内生自变量edu的一个备选工具变量。
我们进行两阶段最小二乘回归(2SLS),具体两阶段模型见 式 2 和 式 3 ):
\[ \begin{aligned} \begin{split} edu_i=&+\alpha_{1}+\alpha_{2}exp_i+\alpha_{3}exp2_i+\alpha_{4}black_i\\&+\alpha_{5}south_i+\alpha_{6}urban_i+\alpha_{7}college_i+v_i \end{split} \quad \text{(stage 1)}\quad \end{aligned} \tag{2}\]
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}edu_i+\beta_{3}exp_i+\beta_{4}exp2_i\\&+\beta_{5}black_i+\beta_{6}south_i+\beta_{7}urban_i+u_i \end{split} \quad \text{(stage 2)}\quad \end{aligned} \tag{3}\]
我们可以使用如下R代码(AER::ivreg函数)进行两阶段最小二乘估计:
mod_iv_cl <- formula("lwage ~ edu + exp + exp2 + black + south + urban |college + exp + exp2 + black + south + urban")
fit_iv_cl <- AER::ivreg(formula = mod_iv_cl,data = tbl_reg )
smry_iv_cl <- summary(fit_iv_cl)具体2SLS估计的R初始报告结果如下(AER::ivreg函数只显示了第二阶段回归结果):
Call:
AER::ivreg(formula = mod_iv_cl, data = tbl_reg)
Residuals:
Min 1Q Median 3Q Max
-1.82125 -0.24065 0.02368 0.25469 1.43205
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.75278 0.82934 4.525 6.27e-06 ***
edu 0.13229 0.04923 2.687 0.00725 **
exp 0.10750 0.02130 5.047 4.76e-07 ***
exp2 -0.22841 0.03341 -6.836 9.84e-12 ***
black -0.13080 0.05287 -2.474 0.01342 *
south -0.10490 0.02307 -4.546 5.67e-06 ***
urban 0.13132 0.03013 4.359 1.35e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.391 on 3003 degrees of freedom
Multiple R-Squared: 0.2252, Adjusted R-squared: 0.2237
Wald test: 120.8 on 6 and 3003 DF, p-value: < 2.2e-16 3.3 模型3:两个内生变量且等量工具变量情形下的2SLS分析
假如我们认为前述OLS模型(见 式 1 )存在内生性问题,其中受教育年数edu、工作年数及其平方exp和exp2为内生自变量,并且认为其他自变量都是外生的。
同时,我们选择把附近是否有大学college作为内生自变量edu的一个备选工具变量,把年龄及其平方age和age2分别作为exp和exp2的工具变量。
我们可以进行两阶段最小二乘回归(2SLS)分析,具体两阶段模型见 式 4 、式 式 5 、 式 6 ,以及 式 7 ):
\[ \begin{aligned} \begin{split} edu_i=&+\gamma_{1}+\gamma_{2}age_i+\gamma_{3}age2_i+\gamma_{4}black_i\\&+\gamma_{5}south_i+\gamma_{6}urban_i+\gamma_{7}college_i+v1_i \end{split} \quad \text{(stage 1: 1/3)}\quad \end{aligned} \tag{4}\]
\[ \begin{aligned} \begin{split} exp_i=&+\gamma_{1}+\gamma_{2}age_i+\gamma_{3}age2_i+\gamma_{4}black_i\\&+\gamma_{5}south_i+\gamma_{6}urban_i+\gamma_{7}college_i+v2_i \end{split} \quad \text{(stage 1: 2/3)}\quad \end{aligned} \tag{5}\]
\[ \begin{aligned} \begin{split} exp2_i=&+\gamma_{1}+\gamma_{2}age_i+\gamma_{3}age2_i+\gamma_{4}black_i\\&+\gamma_{5}south_i+\gamma_{6}urban_i+\gamma_{7}college_i+v3_i \end{split} \quad \text{(stage 1: 3/3)}\quad \end{aligned} \tag{6}\]
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}edu_i+\beta_{3}exp_i+\beta_{4}exp2_i\\&+\beta_{5}black_i+\beta_{6}south_i+\beta_{7}urban_i+u_i \end{split} \quad \text{(stage 2)}\quad \end{aligned} \tag{7}\]
此时,edu、exp和exp2内生,工具变量为college、age和age2。我们可以使用如下R代码(AER::ivreg函数)进行两阶段最小二乘估计:
mod_iv_ca <- formula("lwage ~ edu + exp + exp2 + black + south + urban |college + age + age2 + black + south + urban")
fit_iv_ca <- AER::ivreg(formula = mod_iv_ca,data = tbl_reg )
smry_iv_ca <- summary(fit_iv_ca) 具体2SLS估计的R初始报告结果如下(AER::ivreg函数只显示了第二阶段回归结果):
Call:
AER::ivreg(formula = mod_iv_ca, data = tbl_reg)
Residuals:
Min 1Q Median 3Q Max
-1.82400 -0.25248 0.02286 0.26349 1.31561
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.06567 0.60850 6.682 2.81e-11 ***
edu 0.13295 0.05138 2.588 0.009712 **
exp 0.05596 0.02599 2.153 0.031412 *
exp2 -0.07957 0.13403 -0.594 0.552796
black -0.10314 0.07737 -1.333 0.182623
south -0.09818 0.02876 -3.413 0.000651 ***
urban 0.10798 0.04974 2.171 0.030010 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4032 on 3003 degrees of freedom
Multiple R-Squared: 0.1764, Adjusted R-squared: 0.1747
Wald test: 148.1 on 6 and 3003 DF, p-value: < 2.2e-16 3.4 模型4:一个内生变量且富余工具变量情形下的2SLS分析
假如我们认为前述OLS模型(见 式 1 )存在内生性问题,其中受教育年数edu为内生自变量,并且认为其他自变量都是外生的。
同时,我们选择把附近是否有公立大学public和附近是否有私立大学private作为内生自变量edu的2个备选工具变量。
我们可以进行两阶段最小二乘回归(2SLS)分析,具体两阶段模型见下面的 式 8 和 式 9 ):
\[ \begin{aligned} \begin{split} edu_i=&+\delta_{1}+\delta_{2}exp_i+\delta_{3}exp2_i+\delta_{4}black_i\\&+\delta_{5}south_i+\delta_{6}urban_i+\delta_{7}public_i+\delta_{8}private_i+v_i \end{split} \quad \text{(stage 1)}\quad \end{aligned} \tag{8}\]
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}edu_i+\beta_{3}exp_i+\beta_{4}exp2_i\\&+\beta_{5}black_i+\beta_{6}south_i+\beta_{7}urban_i+u_i \end{split} \quad \text{(stage 2)}\quad \end{aligned} \tag{9}\]
此时,edu内生,工具变量为public和private。我们可以使用如下R代码(AER::ivreg函数)进行两阶段最小二乘估计:
具体2SLS估计的R初始报告结果如下(AER::ivreg函数只显示了第二阶段回归结果):
Call:
AER::ivreg(formula = mod_tsls_pp, data = tbl_reg)
Residuals:
Min 1Q Median 3Q Max
-1.93985 -0.25152 0.01722 0.27365 1.48154
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.26801 0.68718 4.756 2.07e-06 ***
edu 0.16109 0.04077 3.951 7.96e-05 ***
exp 0.11931 0.01818 6.564 6.16e-11 ***
exp2 -0.23054 0.03503 -6.582 5.46e-11 ***
black -0.10173 0.04531 -2.245 0.0248 *
south -0.09504 0.02165 -4.389 1.18e-05 ***
urban 0.11645 0.02705 4.305 1.73e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4108 on 3003 degrees of freedom
Multiple R-Squared: 0.1447, Adjusted R-squared: 0.143
Wald test: 111 on 6 and 3003 DF, p-value: < 2.2e-16 3.5 模型5:两个内生变量且富余工具变量情形下的2SLS分析
假如我们认为前述OLS模型(见 式 1 )存在内生性问题,其中受教育年数edu、工作年数及其平方exp和exp2为内生自变量,并且认为其他自变量都是外生的。
同时,我们选择把附近是否有公立大学public和附近是否有私立大学private作为内生自变量edu的2个备选工具变量;把年龄及其平方age和age2分别作为exp和exp2的工具变量。
我们可以进行两阶段最小二乘回归(2SLS)分析,具体两阶段模型见下面的 式 10 、 式 11 、 式 12 和 式 13 ):
\[ \begin{aligned} \begin{split} edu_i=&+\gamma_{1}+\gamma_{2}age_i+\gamma_{3}age2_i+\gamma_{4}black_i+\gamma_{5}south_i\\&+\gamma_{6}urban_i+\gamma_{7}public_i+\gamma_{8}private_i+v1_i \end{split} \quad \text{(stage 1: 1/3)}\quad \end{aligned} \tag{10}\]
\[ \begin{aligned} \begin{split} exp_i=&+\delta_{1}+\delta_{2}age_i+\delta_{3}age2_i+\delta_{4}black_i+\delta_{5}south_i\\&+\delta_{6}urban_i+\delta_{7}public_i+\delta_{8}private_i+v2_i \end{split} \quad \text{(stage 1: 2/3)}\quad \end{aligned} \tag{11}\]
\[ \begin{aligned} \begin{split} exp2_i=&+\lambda_{1}+\lambda_{2}age_i+\lambda_{3}age2_i+\lambda_{4}black_i+\lambda_{5}south_i\\&+\lambda_{6}urban_i+\lambda_{7}public_i+\lambda_{8}private_i+v3_i \end{split} \quad \text{(stage 1: 3/3)}\quad \end{aligned} \tag{12}\]
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}edu_i+\beta_{3}exp_i+\beta_{4}exp2_i\\&+\beta_{5}black_i+\beta_{6}south_i+\beta_{7}urban_i+u_i \end{split} \quad \text{(stage 2)}\quad \end{aligned} \tag{13}\]
此时,edu、exp和exp2内生,工具变量为public和private、以及age和age2。我们可以使用如下R代码(AER::ivreg函数)进行两阶段最小二乘估计:
具体2SLS估计的R初始报告结果如下(AER::ivreg函数只显示了第二阶段回归结果):
Call:
AER::ivreg(formula = mod_tsls_ppa, data = tbl_reg)
Residuals:
Min 1Q Median 3Q Max
-1.92063 -0.27218 0.02074 0.28186 1.43044
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.74815 0.48338 7.754 1.21e-14 ***
edu 0.15969 0.04090 3.904 9.65e-05 ***
exp 0.04703 0.02502 1.880 0.060213 .
exp2 -0.03225 0.12811 -0.252 0.801255
black -0.06403 0.06301 -1.016 0.309610
south -0.08573 0.02563 -3.345 0.000834 ***
urban 0.08348 0.04125 2.024 0.043073 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.4327 on 3003 degrees of freedom
Multiple R-Squared: 0.05111, Adjusted R-squared: 0.04921
Wald test: 129.7 on 6 and 3003 DF, p-value: < 2.2e-16 3.6 模型6:使用有限信息极大似然估计(LIML)进行估计
估计结构方程参数的另一种方法是通过最大似然法。 Anderson 和 Rubin (1949) 推导出 \(\vec{Y}=\left(Y_{1}, Y_{2}\right)\) 联合分布的最大似然估计量。该估计量称为有限信息最大似然 (LIML)。
该估计量称为“有限信息”,因为它基于 \(Y\) 的结构方程与 \(X_{2}\) 的简化形式方程相结合。如果最大似然也是基于 \(X_{2}\) 的结构方程导出的,这将导致所谓的全信息最大似然 (FIML)。 LIML 相对于 FIML 的优势在于,前者不需要 \(X_{2}\) 的结构模型,因此允许研究人员专注于感兴趣的结构方程(\(Y\) 的结构方程)。我们不描述 FIML 估计量,因为它在应用计量经济学中并不常用。
3.7 全部工资模型集中展示和综合比较
以上模型的综合汇总结果比较见下表:
说明:
如果使用两阶段最小二乘法,则只列出了第二阶段回归结果
最后一列
LIML_pp采用的是有限信息极大似然估计方法(LIML)。
4 表12.2:第一阶段方程(内生变量的精简方程)估计结果
前述表12.1的工资结构方程的回归中,如果考虑了内生变量并考虑使用了不同的工具变量,则需要估计内生变量的精简方程,也即第一阶段方程(内生变量的精简方程)。
我们可以简单使用OLS方法,针对不同的内生变量和工具变量组合,估计第一阶段方程(内生变量的精简方程),具体估计结果整理后见下表:
5 采用R包systemfit进行2SLS估计
如前所述,AER包的ivreg函数可以进行两阶段最小二乘估计,但是该函数只能估计第二阶段方程(工资结构方程),而不会显示第一阶段方程(内生变量的精简方程)估计结果。
为了完整地展示不同工具变量组合下的第一阶段方程(内生变量的精简方程)估计结果和第二阶段方程(工资结构方程)估计结果,我们可以使用R包systemfit进行估计。
我们下面将展示两种情形下的R包systemfit的2SLS估计结果,即等量工具变量情形和富余工具变量情形。
5.1 模型3:等量工具变量情形
在 小节 3.3 中,给定情形为:edu、exp和exp2内生,工具变量为college、age和age2。作为对比,我们此处使用R包systemfit进行估计。具体结果见 表 4:
方程1.X需要去掉截距项,否则会报错!
hansen2021此时应用的是IV(b)方法。
```{r}
#| label: tbl-just-systemfit-3t3
#| tbl-cap: "等量工具变量下的2SLS结果"
#| eval: true
# load package
library(systemfit)
# set two models
eq_1.1 <- edu ~ -1 + age + age2 +black +south +urban + college
eq_1.2 <- exp ~ -1 + age + age2 +black +south +urban + college
eq_1.3 <- exp2 ~ -1 + age + age2 +black +south +urban + college # important !!
eq_2 <- lwage ~ edu + exp + exp2 +black +south +urban
sys <- list(
eq1.1 = eq_1.1,
eq1.2 = eq_1.2,
eq1.3 = eq_1.3,
eq2 = eq_2)
# specify the instruments
instr <- ~age + age2 +black +south +urban + college
# fit models
fit.sys <- systemfit(
formula = sys,
inst = instr,
method ="2SLS",
data = tbl_reg)
smry <- summary(fit.sys)
out <- broom::tidy(fit.sys) %>%
separate(., col = term,
into = c("eq", "vars"), sep = "_") %>%
select(-all_of(starts_with("conf")))
knitr::kable(out,
#caption ="等量工具变量下的2SLS结果" ,
digits = 4)
```| eq | vars | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| eq1.1 | age | 0.9305 | 0.0164 | 56.6658 | 0.0000 |
| eq1.1 | age2 | -1.6496 | 0.0521 | -31.6411 | 0.0000 |
| eq1.1 | black | -1.4688 | 0.1154 | -12.7254 | 0.0000 |
| eq1.1 | south | -0.4597 | 0.1024 | -4.4879 | 0.0000 |
| eq1.1 | urban | 0.8355 | 0.1092 | 7.6483 | 0.0000 |
| eq1.1 | college | 0.3456 | 0.1069 | 3.2324 | 0.0012 |
| eq1.2 | age | -0.3506 | 0.0164 | -21.3495 | 0.0000 |
| eq1.2 | age2 | 2.3762 | 0.0521 | 45.5726 | 0.0000 |
| eq1.2 | black | 1.4674 | 0.1154 | 12.7116 | 0.0000 |
| eq1.2 | south | 0.4598 | 0.1024 | 4.4888 | 0.0000 |
| eq1.2 | urban | -0.8352 | 0.1093 | -7.6451 | 0.0000 |
| eq1.2 | college | -0.3504 | 0.1069 | -3.2761 | 0.0011 |
| eq1.3 | age | -0.1275 | 0.0035 | -36.7038 | 0.0000 |
| eq1.3 | age2 | 0.5746 | 0.0110 | 52.1129 | 0.0000 |
| eq1.3 | black | 0.2835 | 0.0244 | 11.6143 | 0.0000 |
| eq1.3 | south | 0.1116 | 0.0217 | 5.1534 | 0.0000 |
| eq1.3 | urban | -0.1758 | 0.0231 | -7.6098 | 0.0000 |
| eq1.3 | college | -0.0677 | 0.0226 | -2.9942 | 0.0028 |
| eq2 | (Intercept) | 4.0657 | 0.6085 | 6.6815 | 0.0000 |
| eq2 | edu | 0.1329 | 0.0514 | 2.5876 | 0.0097 |
| eq2 | exp | 0.0560 | 0.0260 | 2.1528 | 0.0314 |
| eq2 | exp2 | -0.0796 | 0.1340 | -0.5936 | 0.5528 |
| eq2 | black | -0.1031 | 0.0774 | -1.3330 | 0.1826 |
| eq2 | south | -0.0982 | 0.0288 | -3.4131 | 0.0007 |
| eq2 | urban | 0.1080 | 0.0497 | 2.1710 | 0.0300 |
5.2 模型5:富余工具变量情形
在 小节 3.5 中,给定情形为:edu、exp和exp2内生,工具变量为public和private、以及age和age2。
作为对比,我们此处使用R包systemfit进行估计。具体结果见表 表 5:
```{r}
#| label: tbl-rich-systemfit
#| tbl-cap: "富余工具变量下的2SLS结果"
#| eval: true
# load package
library(systemfit)
# set two models
eq_1.1 <- edu ~ -1 + age + age2 +black +south +urban + public +private
eq_1.2 <- exp ~ -1 + age + age2 +black +south +urban + public +private
eq_1.3 <- exp2 ~ -1 + age + age2 +black +south +urban + public +private
eq_2 <- lwage ~ edu + exp + exp2 +black +south +urban
sys <- list(
eq1.1 = eq_1.1,
eq1.2 = eq_1.2,
eq1.3 = eq_1.3,
eq2 = eq_2)
# specify the instruments
instr <- ~age + age2 +black +south +urban + public +private
# fit models
fit.sys <- systemfit(
formula = sys,
inst = instr,
method ="2SLS",
data = tbl_reg)
smry <- summary(fit.sys)
out <- tidy(fit.sys) %>%
separate(., col = term,
into = c("eq", "vars"), sep = "_") %>%
select(-all_of(starts_with("conf")))
knitr::kable(out,
#caption ="富余工具变量下的2SLS结果" ,
digits = 4)
```| eq | vars | estimate | std.error | statistic | p.value |
|---|---|---|---|---|---|
| eq1.1 | age | 0.9303 | 0.0164 | 56.7426 | 0.0000 |
| eq1.1 | age2 | -1.6508 | 0.0521 | -31.7135 | 0.0000 |
| eq1.1 | black | -1.4686 | 0.1152 | -12.7435 | 0.0000 |
| eq1.1 | south | -0.4270 | 0.1028 | -4.1551 | 0.0000 |
| eq1.1 | urban | 0.8286 | 0.1091 | 7.5954 | 0.0000 |
| eq1.1 | public | 0.4679 | 0.1132 | 4.1323 | 0.0000 |
| eq1.1 | private | 0.0645 | 0.1376 | 0.4689 | 0.6392 |
| eq1.2 | age | -0.3504 | 0.0164 | -21.3709 | 0.0000 |
| eq1.2 | age2 | 2.3774 | 0.0521 | 45.6667 | 0.0000 |
| eq1.2 | black | 1.4672 | 0.1153 | 12.7297 | 0.0000 |
| eq1.2 | south | 0.4271 | 0.1028 | 4.1560 | 0.0000 |
| eq1.2 | urban | -0.8283 | 0.1091 | -7.5922 | 0.0000 |
| eq1.2 | public | -0.4727 | 0.1133 | -4.1735 | 0.0000 |
| eq1.2 | private | -0.0692 | 0.1376 | -0.5032 | 0.6149 |
| eq1.3 | age | -0.1274 | 0.0035 | -36.7736 | 0.0000 |
| eq1.3 | age2 | 0.5749 | 0.0110 | 52.2594 | 0.0000 |
| eq1.3 | black | 0.2834 | 0.0244 | 11.6387 | 0.0000 |
| eq1.3 | south | 0.1034 | 0.0217 | 4.7617 | 0.0000 |
| eq1.3 | urban | -0.1741 | 0.0231 | -7.5503 | 0.0000 |
| eq1.3 | public | -0.0985 | 0.0239 | -4.1148 | 0.0000 |
| eq1.3 | private | 0.0030 | 0.0291 | 0.1031 | 0.9179 |
| eq2 | (Intercept) | 3.7481 | 0.4834 | 7.7541 | 0.0000 |
| eq2 | edu | 0.1597 | 0.0409 | 3.9044 | 0.0001 |
| eq2 | exp | 0.0470 | 0.0250 | 1.8799 | 0.0602 |
| eq2 | exp2 | -0.0323 | 0.1281 | -0.2517 | 0.8013 |
| eq2 | black | -0.0640 | 0.0630 | -1.0162 | 0.3096 |
| eq2 | south | -0.0857 | 0.0256 | -3.3448 | 0.0008 |
| eq2 | urban | 0.0835 | 0.0412 | 2.0239 | 0.0431 |