\[\begin{aligned} \hat{\beta}_{2} - t_{\alpha / 2} \cdot S_{\hat{\beta}_{2}} \quad \leq & \beta_2 \leq \quad \hat{\beta}_{2} + t_{\alpha / 2} \cdot S_{\hat{\beta}_{2}} \\ 0.5709\quad \leq & \beta_2 \quad \leq0.8772\\ \end{aligned}\]
统计学原理
(Statistics)
第5章 相关和回归分析
05-04 假设检验
Hu Huaping (胡华平)
huhuaping01 at hotmail.com
经济管理学院(CEM)
第五章 相关和回归分析
5.4 假设检验
假设检验
原理和思路
假设检验(Hypothesis Testing):某一给定的观测或发现与某声称的假设是否相符?进行统计假设检验,就是要制定一套步骤和规则,以使决定接受或拒绝一个虚拟假设(原假设)。
虚拟假设(null hypothesis) \(H_0\)
指定或声称的假设,如 \(H_0: \beta_2 = 0\)
它是一个等待被挑战的“靶子”!“稻草人”!
备择假设(alter hypothesis) \(H_1\)
简单备择假设 \(H_1: \beta_2 = 1.5\)
复合备择假设 \(H_1: \beta_2 \neq 1.5\)
假设检验的具体方法:
置信区间检验(confidence interval)
显著性检验(test of significance)
课堂讨论:参数的置信区间检验和显著性检验有什么区别和联系?
置信区间检验法(双侧检验)
双侧或双尾检验(Two-sided or Two-Tail Test)
\[ H_0: \beta_2 =0; \quad H_1: \beta_2 \neq 0 \]
假设检验目的:估计的是否与上述相容?
假设检验决策规则:
构造一个 \(\beta_2\) 的 \(100(1-\alpha)\%\) 置信区间。
如果 \(\beta_2\) 在 \(H_0\) 假设下落入此区间,就不拒绝 \(H_0\) 。
如果它落在此区间之外,就要拒绝 \(H_0\) 。
(示例)教育程度与时均工资回归
对于斜率参数 \(\beta_2\) 的置信区间检验法。
- 步骤1:给出模型,并提出假设:
\[ Y_i = \beta_1 + \beta_2X_i +u_i \]
\[ H_0: \beta_2 =0.5; \quad H_1: \beta_2 \neq 0.5 \]
步骤2:给定 \(\alpha=0.05,\quad (1-\alpha) 100 \%=95 \%\)
步骤3:根据前述计算结果,计算斜率参数 \(\beta_2\) 的95%置信区间为:
- 步骤4:那么我们可以对斜率参数\(\beta_2\)做出如下检验判断:拒绝原假设 \(H_0\),接受\(H_1\)。
认为长期来看很多个区间 [0.5709,0.8772] 有95%的可能性不包含0.5(\(\beta_2 \neq 0.5\))。
(示例)教育程度与时均工资回归
对于截距参数 \(\beta_1\) 的置信区间检验法。
- 步骤1:给出模型,并提出假设:
\[ Y_i = \beta_1 + \beta_2X_i +u_i \]
\[ H_0: \beta_1 =0; \quad H_1: \beta_1 \neq 0 \]
步骤2:给定 \(\alpha=0.05,\quad (1-\alpha) 100 \%=95 \%\)
步骤3:根据前述计算结果,计算截距参数 \(\beta_1\) 的95%置信区间为:
\[\begin{aligned} \hat{\beta}_{1} - t_{\alpha / 2} \cdot S_{\hat{\beta}_{1}} \quad \leq & \beta_1 \leq \quad \hat{\beta}_{1} + t_{\alpha / 2} \cdot S_{\hat{\beta}_{1}} \\ -1.9395\quad \leq & \beta_1 \quad \leq1.9106\\ \end{aligned}\]
- 步骤4:那么我们可以对截距参数 \(\beta_1\) 做出如下检验判断:
认为不能拒绝原假设 \(H_0\) ,暂时接受 \(H_0\) 。认为,长期来看很多个区间[-1.9395,1.9106] 有95%的可能性包含0( \(\beta_1=0\) )。
显著性检验法
显著性检验方法( test-of-significance approach):是一种用样本结果来证实 \(H_0\) 真伪的检验程序。
关键思路:
找到一个适合的检验统计量(test statistic) 。例如t统计量 \(\chi^2\) 统计量、F统计量等。
知道该统计量在 \(H_0\) 下的抽样分布(pdf)。往往与待检验参数有关系。
计算样本统计量的值。也即能用样本数据快速计算出来,例如 \(t^{\ast}_{\hat{\beta_2}}=\frac{\hat{\beta}_2}{S_{\hat{\beta}_2}}\) 。
查表找出给定显著性水平 \(\alpha\) 下的理论统计量的临界值。例如 \(t_{1-\alpha/2}(n-2)=t_{0.975}(11)=\) 2.2010
比较样本统计量值和该临界值的大小。例如,比较 \(t^{\ast}_{\hat{\beta_2}}\) 与 \(t_{0.975}(11)\)
做出拒绝还是接受 \(H_0\) 的判断。
截距参数的t检验
对于截距参数 \(\beta_1\) 的显著性检验(t检验)。
- 步骤1:给出模型,并提出假设:
\[ Y_i = \beta_1 + \beta_2X_i +u_i \]
\[ H_0: \beta_1 =0; \quad H_1: \beta_1 \neq 0 \]
- 步骤2:构造合适的检验统计量
\[ \begin{aligned} T&=\frac{\hat{\beta}_{1}-\beta_{1}}{S_{\hat{\beta}_{1}}} && \leftarrow T \sim t(n-2) \end{aligned} \]
截距参数的t检验
- 步骤3:基于原假设 \(H_0\) 计算出样本统计量。
\[\begin{aligned} \\ T&=\frac{\hat{\beta}_{1}-\beta_{1}}{S_{\hat{\beta}_{1}}} && \leftarrow T \sim t(n-2) \\ t^{\ast}_{\hat{\beta}_1}&=\frac{\hat{\beta}_{1}}{S_{\hat{\beta}_{1}}} && \leftarrow H_0: \beta_1 = 0 \\ t^{\ast}_{\hat{\beta}_1}&= \frac{-0.0145}{0.8746}=-0.0165 \end{aligned}\]
- 步骤4:给定显著性水平 \(\alpha=0.05\) 下,查出统计量的理论分布值。
\(t_{1-\alpha/2}(n-2)=t_{1-0.05/2}(13-2)=t_{0.975}(11)=\) 2.2010
假设检验:截距参数的t检验
步骤5:得到显著性检验的判断结论。
若 \(|t^{\ast}_{\hat{\beta}_1}| > t_{1-\alpha/2}(n-2)\) ,则 \(\beta_1\) 的t检验结果显著。换言之,在显著性水平 \(\alpha=0.05\) 下,应显著地拒绝原假设 \(H_0\) ,接受备择假设 \(H_1\) ,认为截距参数 \(\beta_1 \neq 0\) 。
若 \(|t^{\ast}_{\hat{\beta}_1}| < t_{1-\alpha/2}(n-2)\) ,则 \(\beta_1\) 的t检验结果不显著。换言之,在显著性水平 \(\alpha=0.05\) 下,不能显著地拒绝原假设 \(H_0\) ,只能暂时接受原假设 \(H_0\) ,认为截距参数 \(\beta_1 = 0\) 。
本例中, \(|t^{\ast}_{\hat{\beta}_1}|=\) 0.0165 小于 \(t_{0.975}(11)=\) 2.2010。因此,认为 \(\beta_1\) 的t检验结果不显著。
换言之,在显著性水平 \(\alpha=0.05\) 下,不能显著地拒绝原假设 \(H_0\) ,只能暂时接受原假设 \(H_0\) ,认为截距参数 \(\beta_1 = 0\) 。
斜率参数的t检验
对于斜率参数 \(\beta_2\) 的显著性检验(t检验)。
- 步骤1:给出模型,并提出假设:
\[ Y_i = \beta_1 + \beta_2X_i +u_i \]
\[ H_0: \beta_2 =0; \quad H_1: \beta_2 \neq 0 \]
- 步骤2:构造合适的检验统计量
\[ \begin{aligned} T&=\frac{\hat{\beta}_{2}-\beta_{2}}{{S_{\beta_{2}}}} && \leftarrow T \sim t(n-2) \end{aligned} \]
斜率参数的t检验
- 步骤3:基于原假设 \(H_0\) 计算出样本统计量。
\[\begin{aligned} \\ T&=\frac{\hat{\beta}_{2}-\beta_{2}}{S_{\hat{\beta}_{2}}} && \leftarrow T \sim t(n-2) \\ t^{\ast}_{\hat{\beta}_2}&=\frac{\hat{\beta}_{2}}{S_{\hat{\beta}_{2}}} && \leftarrow H_0: \beta_2 = 0 \\ t^{\ast}_{\hat{\beta}_2}&= \frac{0.7241}{0.0696}=10.4064 \end{aligned}\]
- 步骤4:给定显著性水平 \(\alpha=0.05\) 下,查出统计量的理论分布值。
\(t_{1-\alpha/2}(n-2)=t_{1-0.05/2}(13-2)=t_{0.975}(11)=\) 2.2010
斜率参数的t检验
- 步骤5:得到显著性检验的判断结论。
若 \(|t^{\ast}_{\hat{\beta}_2}| > t_{1-\alpha/2}(n-2)\) ,则 \(\beta_2\) 的t检验结果显著。换言之,在显著性水平 \(\alpha=0.05\) 下,应显著地拒绝原假设 \(H_0\) ,接受备择假设 \(H_1\) ,认为斜率参数 \(\beta_2 \neq 0\) 。
若 \(|t^{\ast}_{\hat{\beta}_2}| < t_{1-\alpha/2}(n-2)\) ,则 \(\beta_2\) 的t检验结果不显著。换言之,在显著性水平 \(\alpha=0.05\) 下,不能显著地拒绝原假设 \(H_0\) ,只能暂时接受原假设 \(H_0\) ,认为斜率参数 \(\beta_2 = 0\) 。
本例中, \(|t^{\ast}_{\hat{\beta}_2}|=\) 10.4064 大于 \(t_{0.975}(11)=\) 2.2010。因此,认为 \(\beta_2\) 的t检验结果显著。
换言之,在显著性水平 \(\alpha=0.05\) 下,应显著地拒绝原假设 \(H_0\) ,接受备择假设 \(H_1\) ,认为斜率参数 \(\beta_2 \neq 0\) 。
显著性水平VS显著性概率
我们可以回顾犯错误类型:
第I类错误:弃真错误 \(\alpha = P(Z > Z_0|H_0=True)\)
第II类错误:取伪错误 \(\beta = P(Z \leq Z_0|H_1=True)\)
[给定样本容量时]如果我们要减少犯第I 类错误, 第II类错误就要增加;反之亦然。
为什么选择显著性水平 \(\alpha\) 通常固定在0.01、0.05、0.1水平上?
约定而已,并非神圣不可改变!
如何改变??
显著性水平VS显著性概率
精确的显著性概率水平p值:
对给定的样本算出一个检验统计量(如t统计量),查到与之对应的概率:p值(p value)或概率值(probability value)
不约定 \(\alpha\) ,而是直接求出犯错误概率p值,由读者自己去评判犯错误的可能性和代价!!因人而异!!
实际操作中的若干问题
关于统计显著性与实际显著性。
不能一味追求统计显著性,有时候还需要考虑“实际显著性”的现实意义。
举例说明:
边际消费倾向(MPC)是指GDP每增加1美元带来消费的增加数;宏观理论表明收入乘数为:1/(1-MPC)。
若MPC的95%置信区间为(0.7129,0.7306),当样本表明MPC的估计值为 \(\widehat{MPC}=0.74\) (此时,即乘数为3.84),你怎样抉择!!!
关于置信区间方法和显著性检验方法的选择。
一般来说,置信区间方法优于显著性检验方法!
例如:假设MPC \(H_0: \beta_2 =0\) 显然荒谬的!
方差分解(ANOVA)
Y变异的分解
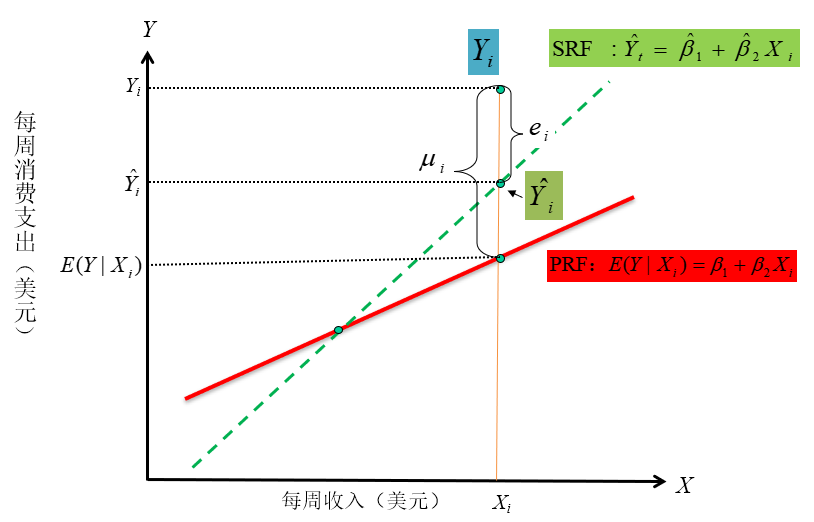
\[ \begin{alignedat}{2} &&(Y_i - \bar{Y}) &&= (\hat{Y}_i - \bar{Y}) &&+ (Y_i - \hat{Y}_i ) \\ &&y_i &&= \hat{y}_i &&+ e_i \end{alignedat} \]
平方和分解
\[ \begin{alignedat}{2} &&(Y_i - \bar{Y}) &&= (\hat{Y}_i - \bar{Y}) &&+ (Y_i - \hat{Y}_i ) \\ &&y_i &&= \hat{y}_i &&+ e_i \\ &&\sum{y_i^2} &&= \sum{\hat{y}_i^2} &&+ \sum{e_i^2} \\ &&TSS &&=ESS &&+RSS \end{alignedat} \]
其中:
- \(TSS\) 表示总离差平方和;
- \(ESS\) 表示回归平方和;
- \(RSS\) 表示残差平方和
(附录):平方和分解证明过程
\[ \begin{aligned} \sum{y_i^2} &= \sum{(\hat{y}_i e_i)^2} \\ &= \sum{(\hat{y}_i^2 +2\hat{y}_ie_i +e_i^2)}\\ &= \sum{\hat{y}_i^2 } +2\sum{\hat{y}_ie_i} + \sum{e_i^2}\\ &= \sum{\hat{y}_i^2 } +2\sum{\left( \hat{(\beta_2}x_i)e_i \right)} + \sum{e_i^2}\\ &= \sum{\hat{y}_i^2 } +2\hat{\beta_2}\sum{\left( x_ie_i \right)} + \sum{e_i^2} && \leftarrow \left[ \sum{x_ie_i} =0 \right]\\ &= \sum{\hat{y}_i^2} + \sum{e_i^2} \end{aligned} \]
双变量分解表
对于一元线性回归(双变量),方差分解的理论值如下:
| 变异来源 | 平方和符号SS | 平方和计算公式 | 自由度df | 均方和符号MSS | 均方和计算公式 |
|---|---|---|---|---|---|
| 回归平方和 | ESS | ((_i-{Y}_i)^2=_i^2) | 1 | (MSS_{ESS}) | (ESS/df_{ESS}=_22x_i2) |
| 残差平方和 | RSS | ((Y_i-_i)2=e_i2) | n-2 | (MSS_{RSS}) | (RSS/df_{RSS}=) |
| 总平方和 | TSS | ((Y_i-{Y}_i)2=y_i2) | n-1 | (MSS_{TSS}) | (TSS/df_{TSS}=) |
模型整体显著性检验
F检验1/4
- 步骤1:给出模型,并提出假设:
一元回归模型下:
\[ Y_i = \beta_1 + \beta_2X_i +u_i \]
\[ H_0: \beta_2 =0; \quad H_1: \beta_2 \neq 0 \]
多元回归模型下:
\[ Y_i = \beta_1 + \beta_2X_{2i} + \beta_3X_{3i}+ \cdots + \beta_kX_{ki}+ u_i \]
\[ H_0: \beta_2 = \beta_3 =\cdots= \beta_k= 0; \quad H_1: \text{not all} \quad \beta_j = 0, \quad j \in 2, 3, \cdots, k \]
F检验2/4
- 步骤2:构造合适的检验统计量
\[ \begin {aligned} \chi^2_1 &= \left( \frac{\hat{\beta}_{2}-\beta_{2} }{\sigma_{\hat{\beta_2}}}\right)^2 = \left( \frac{\hat{\beta}_{2}-\beta_{2} }{\sqrt{\sigma^{2}/\sum x_{i}^{2}}}\right)^2=\frac{\left(\hat{\beta}_{2}-\beta_{2}\right)^{2} \sum x_{i}^{2}}{\sigma^{2}} &&\leftarrow \chi^2_1 \sim \chi^2(1) \end {aligned} \]
\[ \begin {aligned} \chi^2_{2}&=(n-2) \frac{\hat{\sigma}^{2}}{\sigma^{2}}=\frac{\sum e_{i}^{2}}{\sigma^{2}} && \leftarrow \chi^2_2 \sim \chi^2(n-2) \end {aligned} \]
\[ \begin {aligned} F &= \frac{\chi^2_1/1}{\chi^2_2/n-2} = \left( \frac{\left(\hat{\beta}_{2}-\beta_{2}\right)^{2} \sum x_{i}^{2}}{\sigma^{2}} \right ) / \left( \frac{\sum e_{i}^{2}}{(n-2)\sigma^{2}} \right) =\frac{\left(\hat{\beta}_{2}-\beta_{2}\right)^{2} \sum x_{i}^{2}}{\sum e_{i}^{2} /(n-2)}\\ F & \sim F(1,n-2) \end {aligned} \]
F检验3/4
- 步骤3:基于原假设 \(H_0\) 计算出样本统计量。
\[ \begin {aligned} F^{\ast} &= \frac{\left(\hat{\beta}_{2}-\beta_{2}\right)^{2} \sum x_{i}^{2}}{\sum e_{i}^{2} /(n-2)} &&\leftarrow H_0: \beta_2=0 \\ & = \frac{\hat{\beta}_{2}^{2} \sum x_{i}^{2}}{\sum e_{i}^{2} /(n-2)}\\ & = \frac{ESS / df_{ESS}}{RSS / df_{RSS}} =\frac{MSS_{ESS}}{MSS_{RSS}} =\frac{\hat{\beta}_{2}^{2} \sum x_{i}^{2}}{\hat{\sigma}^{2}} \end {aligned} \]
F检验4/4
步骤4:给定显著性水平 \(\alpha=0.05\) 下,查出统计量的理论分布值。 \(F_{1-\alpha}(1,n-2)\)
步骤5:得到显著性检验的判断结论。
若 \(F^{\ast} > F_{1-\alpha}(1,n-2)\) ,则 模型整体显著性的F检验结果显著。换言之,在显著性水平 \(\alpha=0.05\) 下,应显著地拒绝原假设 \(H_0\) ,接受备择假设 \(H_1\) ,认为斜率参数 \(\beta_2 \neq 0\) 。
若 \(F^{\ast} < F_{1-\alpha}(1,n-2)\) ,则 模型整体显著性的F检验结果不显著。换言之,在显著性水平 \(\alpha=0.05\) 下,不能显著地拒绝原假设 \(H_0\) ,只能暂时接受原假设 \(H_0\) ,认为斜率参数 \(\beta_2 = 0\) 。
模型整体显著性检验:比较
F检验与t检验的联系:
在一元回归模型中,t检验与F检验的结论总是一致的。
对于检验斜率参数 \(\beta_2\) 的显著性,两者可相互替代!在一元回归分析中,若假设 \(H_0:\beta_2=0\) ,则 \(F^{\ast} \simeq (t^{\ast})^2\)
F检验与t检验的不同:
检验目的不同。F检验是检验模型的整体显著性;t检验是检验各个回归参数的显著性。
假设的提出不同:
F检验:斜率系数联合假设 \(H_0: \beta_2 =0; \quad H_1: \beta_2 \neq 0\)
t检验:回归系数分别假设 \(H_0: \beta_i =0; \quad H_1: \beta_i \neq 0; \quad i \in 1,2\)
检验原理的不同:F检验需要构造F统计量;t检验需要构造t统计量
(案例)教育程度与时均工资:计算ANOVA表
根据前述理论计算公式,可以算出具体的ANOVA分析表:
| 变异来源 | 平方和SS | 自由度df | 均方和MSS |
|---|---|---|---|
| 回归平方和ESS | 95.425 | 1 | 95.425 |
| 残差平方和RSS | 9.693 | 11 | 0.881 |
| 总平方和TSS | 105.118 | 12 | 7.086 |
(案例)教育程度与时均工资:F检验
步骤1:给出模型 \(Y_i = \beta_1 + \beta_2X_i +u_i\) ,提出假设: \(H_0: \beta_2 =0; \quad H_1: \beta_2 \neq 0\)
步骤2:构造合适检验的分布:
\[ \begin {aligned} F &= \frac{\left(\hat{\beta}_{2}-\beta_{2}\right)^{2} \sum x_{i}^{2}}{\sum e_{i}^{2} /(n-2)} && \leftarrow F \sim F(1,n-2) \end {aligned} \]
- 步骤3:基于原假设 \(H_0: \beta_2=0\) ,可以计算出样本统计量。
\[\begin {aligned} F^{\ast} = \frac{\hat{\beta}_{2}^{2} \sum x_{i}^{2}}{\sum e_{i}^{2} /(n-2)} = \frac{ESS / df_{ESS}}{RSS / df_{RSS}} =\frac{MSS_{ESS}}{MSS_{RSS}} =\frac{95.4253}{0.8812}=108.2924 \end {aligned}\]
(案例)教育程度与时均工资:F检验
步骤4:给定 \(\alpha=0.05\) 下,查出F理论值 \(F_{1-\alpha}(1,n-2)=F_{0.95}(1,11)=\) 4.8443
步骤5:得到显著性检验的判断结论。因为 \(F^{\ast}=\) 108.2924 大于 \(F_{0.95}(1,11)=\) 4.8443,所以模型整体显著性的F检验结果显著。换言之,在显著性水平 \(\alpha=0.05\) 下,应显著地拒绝原假设 \(H_0\) ,接受备择假设 \(H_1\) ,认为斜率参数 \(\beta_2 \neq 0\) 。
本节结束

第5章 相关和回归分析 [05-04] 假设检验