统计学原理
(Statistics)
第5章 相关和回归分析
05-02 回归分析的基本思想
Hu Huaping (胡华平)
huhuaping01 at hotmail.com
经济管理学院(CEM)
第五章 相关和回归分析
5.2 回归分析的基本思想
线性回归分析
从一组样本数据出发,确定变量之间的数学关系式。
对这些关系式的可信程度进行各种统计检验,并从影响某一特定变量的诸多变量中找出哪些变量的影响显著,哪些不显著。
利用所求的关系式,根据一个或几个变量的取值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确程度。
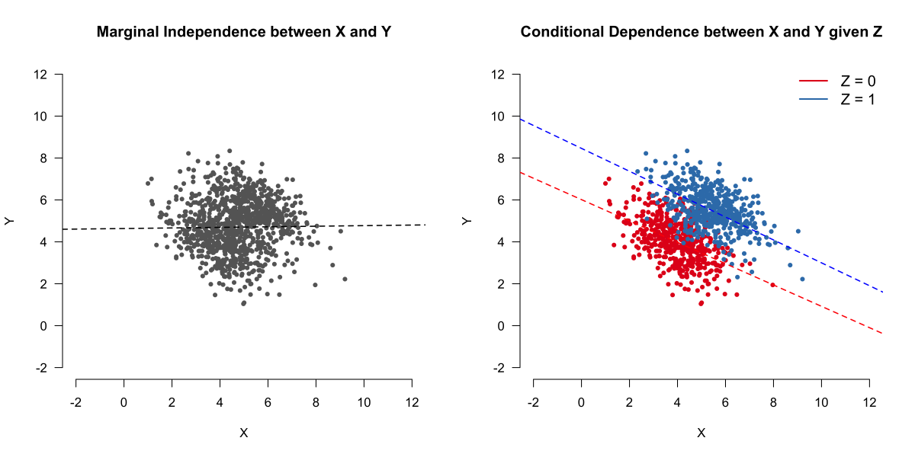
相关关系:边际相关与条件相关1
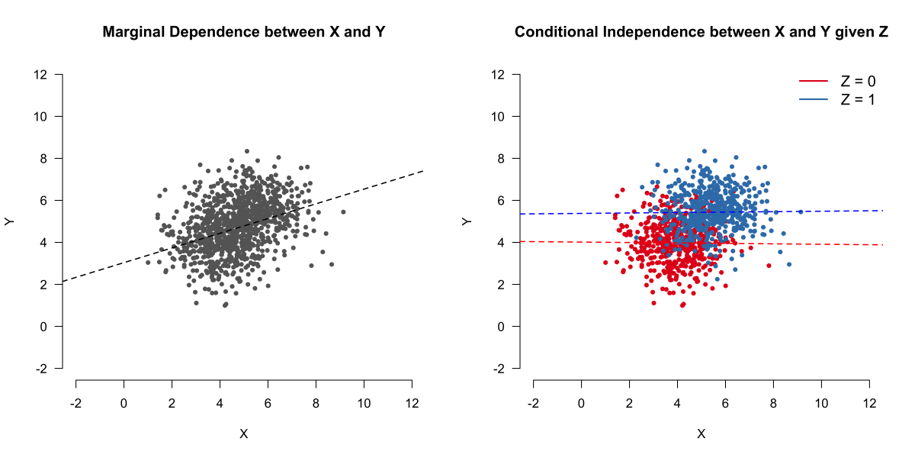
相关关系:边际相关与条件相关2
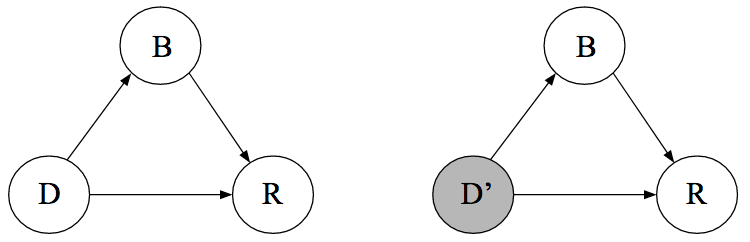
相关关系VS因果关系
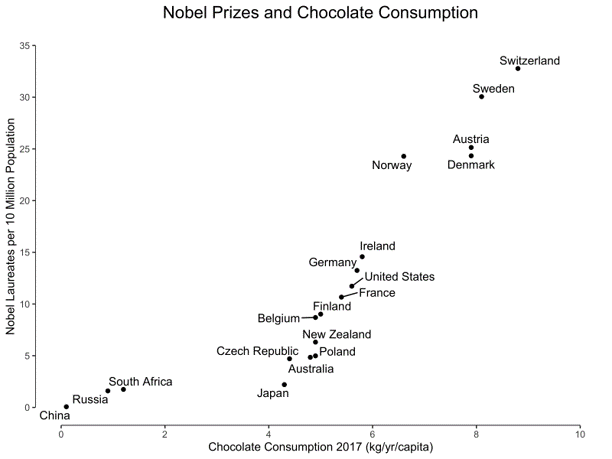
相关关系VS因果关系:性别的作用

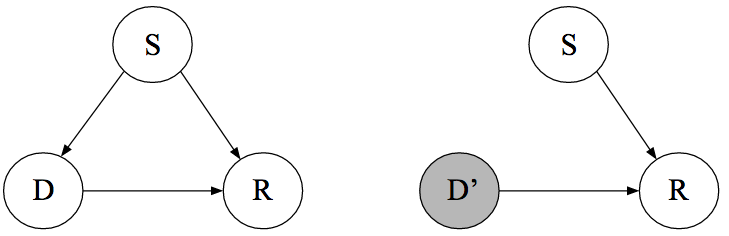
相关关系VS因果关系:血压的作用

(案例)假想总体:60个家庭的收支数据(直观列表)
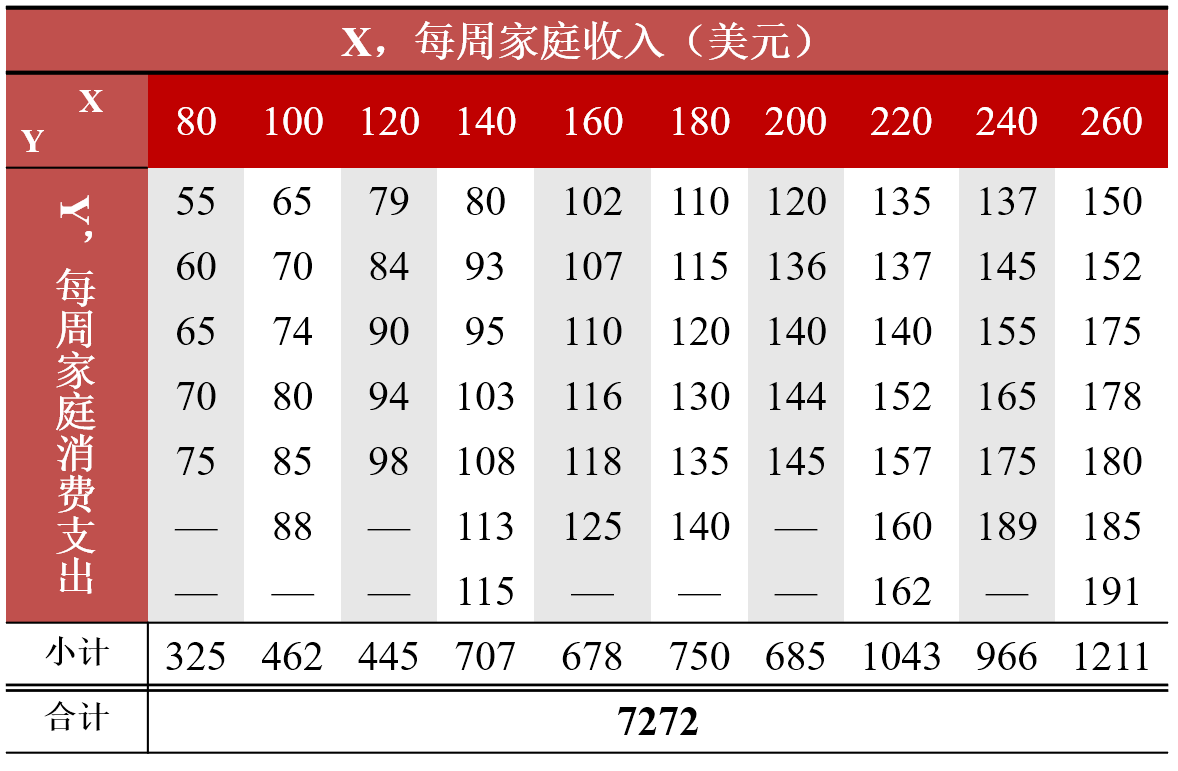
(案例)假想总体:60个家庭的收支数据(扁数据形态)
(案例)假想总体:60个家庭的收支数据(长数据形态)
重要概念:无条件概率和无条件期望
无条件概率:
定义:不受 \(X_i\) 变量取值影响下, \(Y_i\) 出现的可能性。
记号:离散变量 \(P(Y_i)\) ;连续变量 \(g(Y)\)
无条件期望:
定义:不受 \(X_i\) 变量取值影响下,变量 \(Y_i\) 的期望值。
记号: \(g(Y_i)\) 表示连续变量的概率密度函数(cdf)
\[ \begin{aligned} E(Y) &= \sum_1^N{Y_i \cdot P(Y_i)} &&\text{(discrete vars)} \\ E(Y) &= \int{Y_i \cdot g(Y_i)dY} &&\text{(continue vars)} \end{aligned} \]
(示例)无条件概率和无条件期望的示例计算
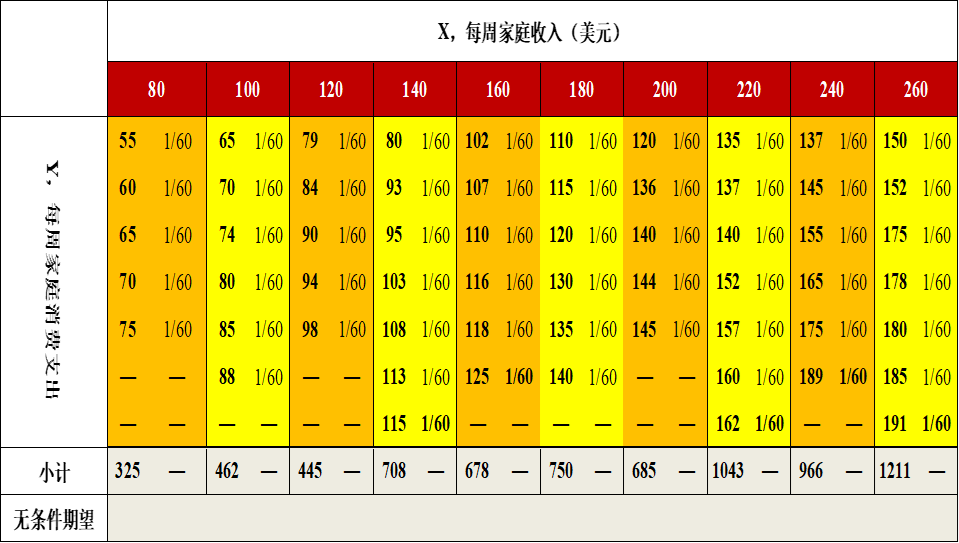
(示例)无条件期望的计算过程
\[ \begin{aligned} E(Y) &= \sum_1^N{Y_i \cdot P(Y_i)} \\ &= \sum_1^{60}\left( 55*\frac{1}{60} + 60*\frac{1}{60} + \cdots + 191*\frac{1}{60} \right) \\ &=\frac{1}{60}\sum_1^{60}Y_i\\ &=\frac{7272}{60}\\ &=121.2 \end{aligned} \]
重要概念:条件概率和条件期望
条件概率:
定义:给定变量 \(X_i\) 的取值条件下, \(Y_i\) 出现的可能性。
记号:离散变量 \(P(Y_i|X_i)\) ;连续变量 \(g(Y|X)\)
条件期望:
在给定变量 \(X_i\) 的取值条件下, \(Y_i\) 的期望值。
记号: \(g(Y|X)\) 表示连续变量的条件概率密度函数(cdf)
\[ \begin{aligned} E(Y|X_i) &= \sum_1^N{(Y_i|X_i) \cdot P(Y_i|X_i)} &&\text{(discrete vars)} \\ E(Y|X_i) &= \int{(Y|X) \cdot g(Y|X)dY} &&\text{(continue vars)} \end{aligned} \]
(示例)条件概率和条件期望的计算
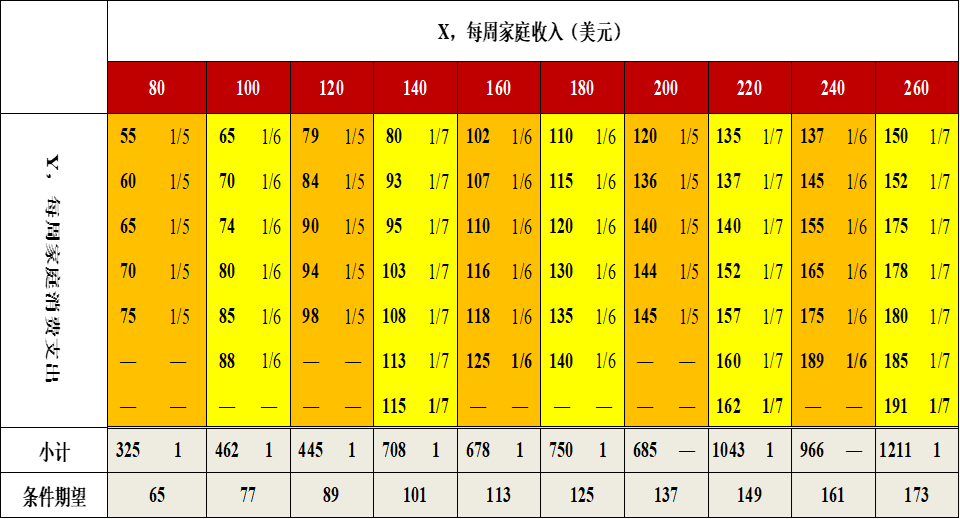
(示例)条件期望的计算过程
\[ \begin{aligned} E(Y|80) &= \sum_1^N{Y_i \cdot P(Y_i|X=80)} \\ &= \sum_1^{5}\left( 55*\frac{1}{5} + 60*\frac{1}{5} + \cdots + 75*\frac{1}{5} \right) \\ &=\frac{1}{5}\sum_1^{5}Y_i\\ &=\frac{325}{5}\\ &=65 \end{aligned} \]
(示例)假想总体的全部数据展示
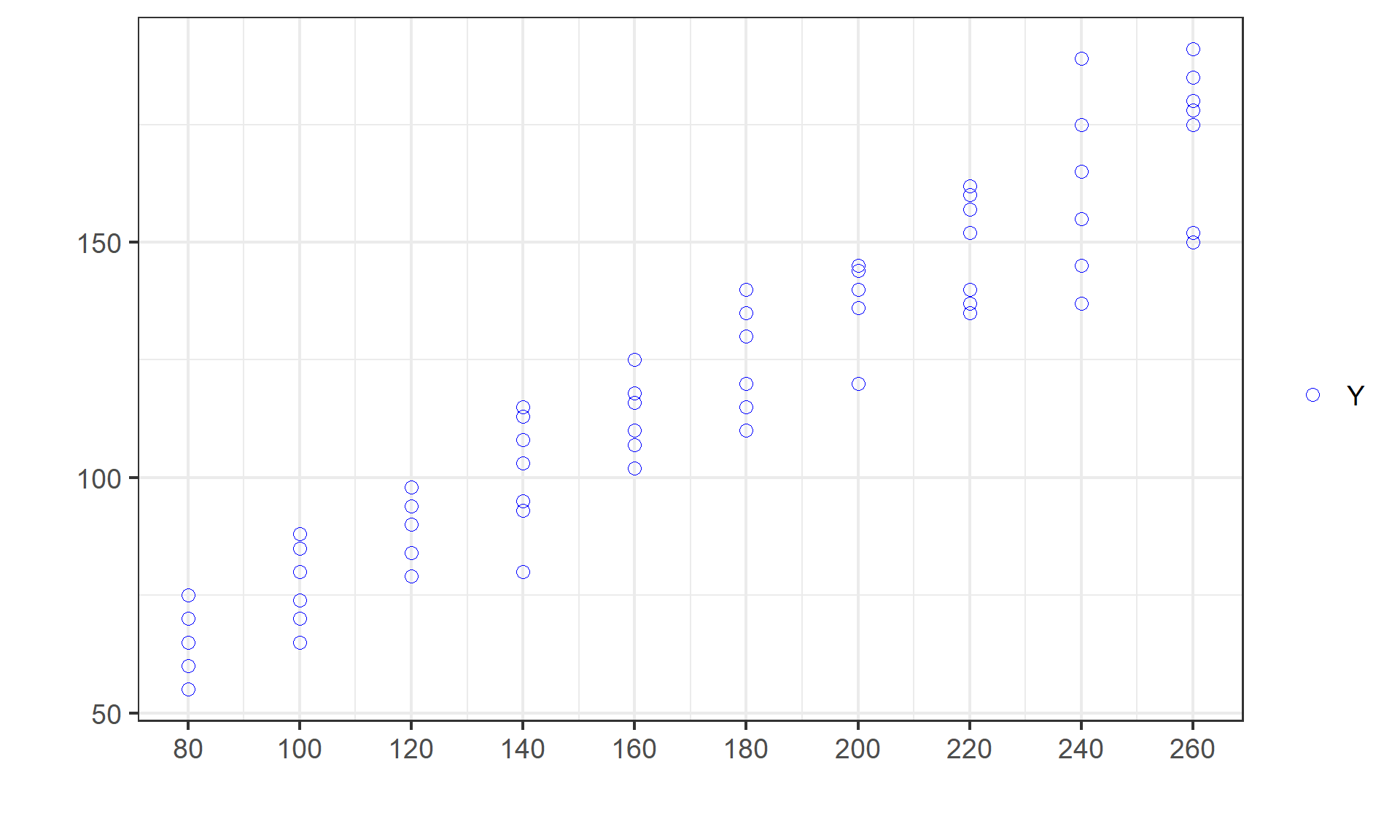
(示例)给定不同X水平下Y条件期望值
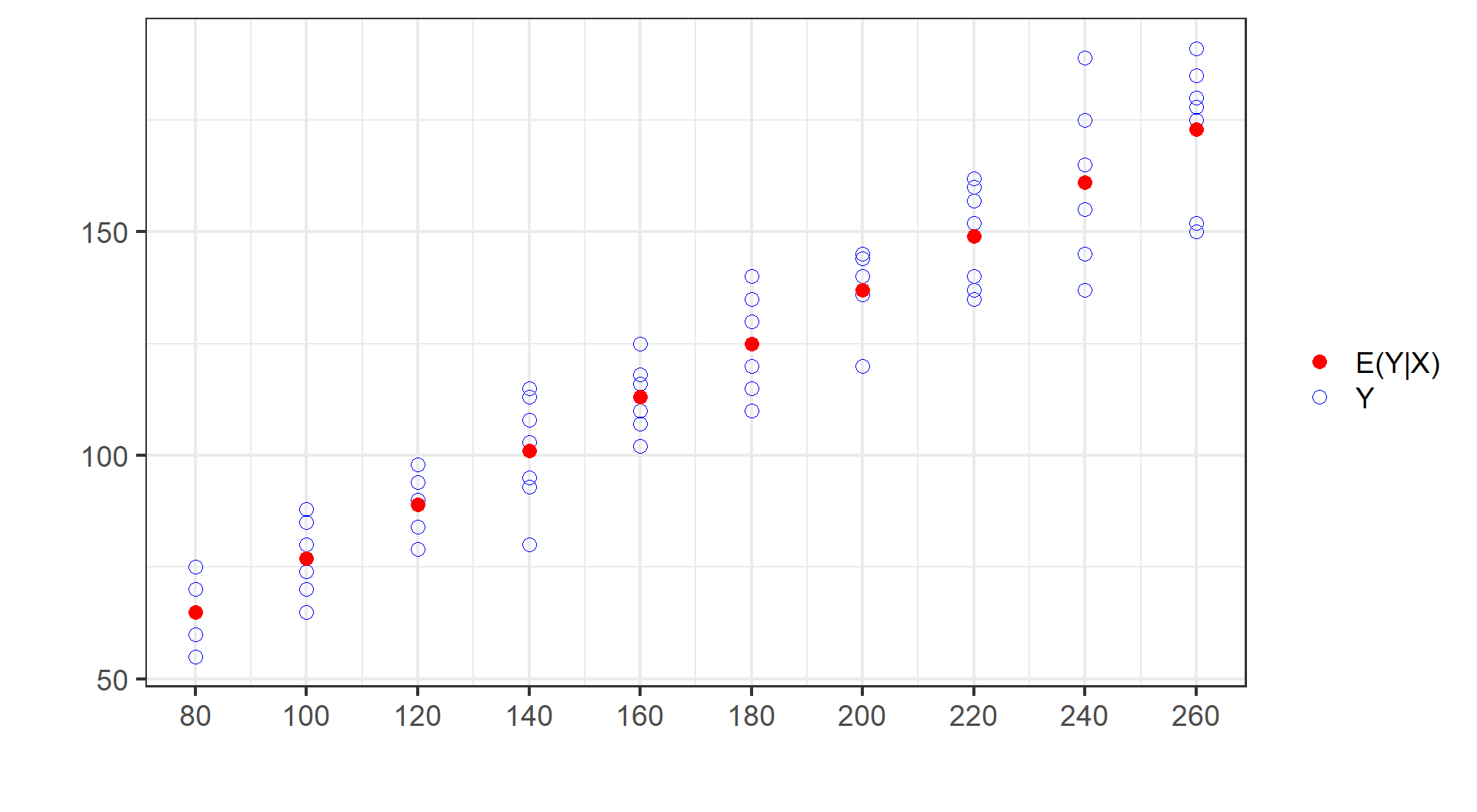
(示例)给定不同X水平下Y条件期望值
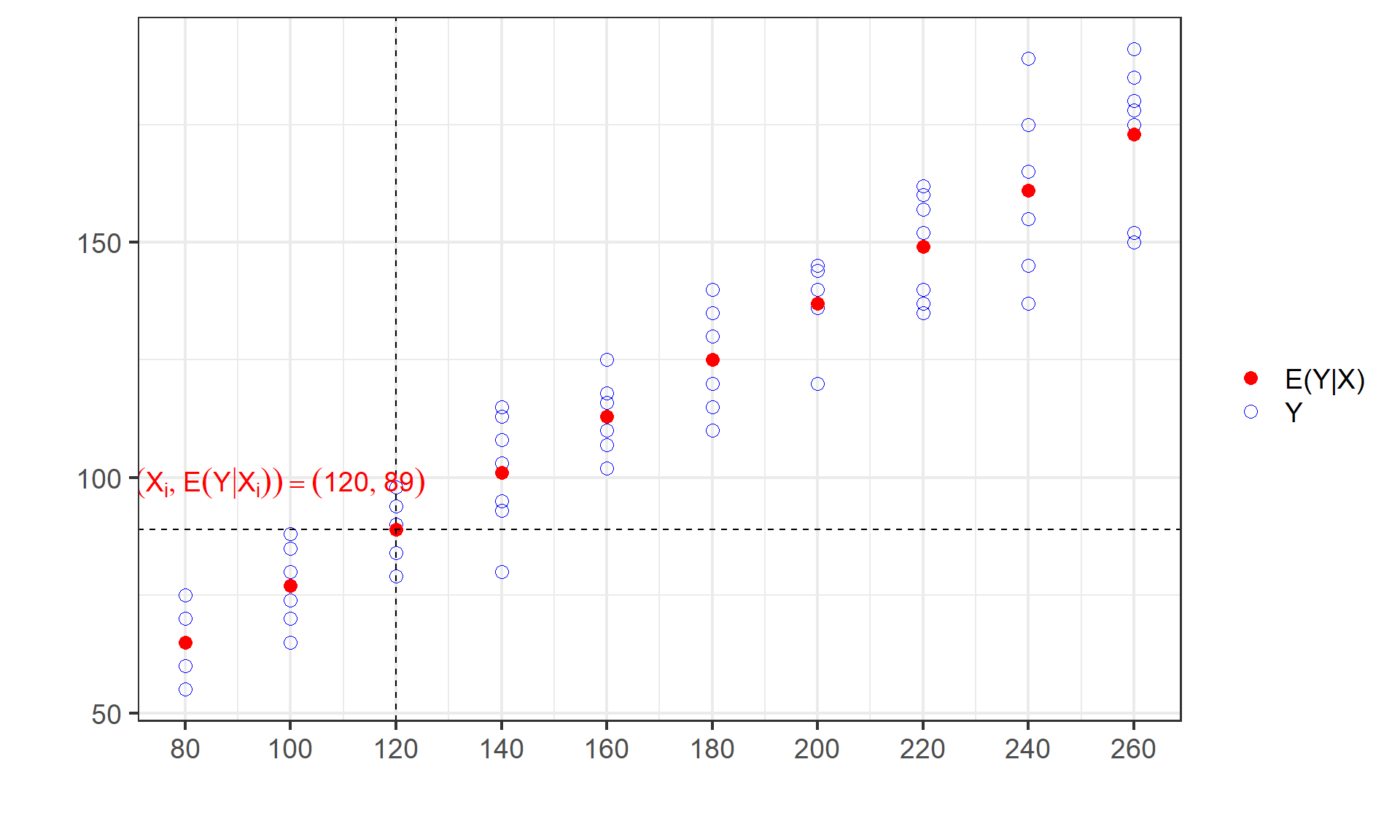
给定 \(X=120\) 水平下 \(Y\) 条件期望值 \(E(Y|X_i=120)\) = 89
(示例)X均值和Y的无条件期望值
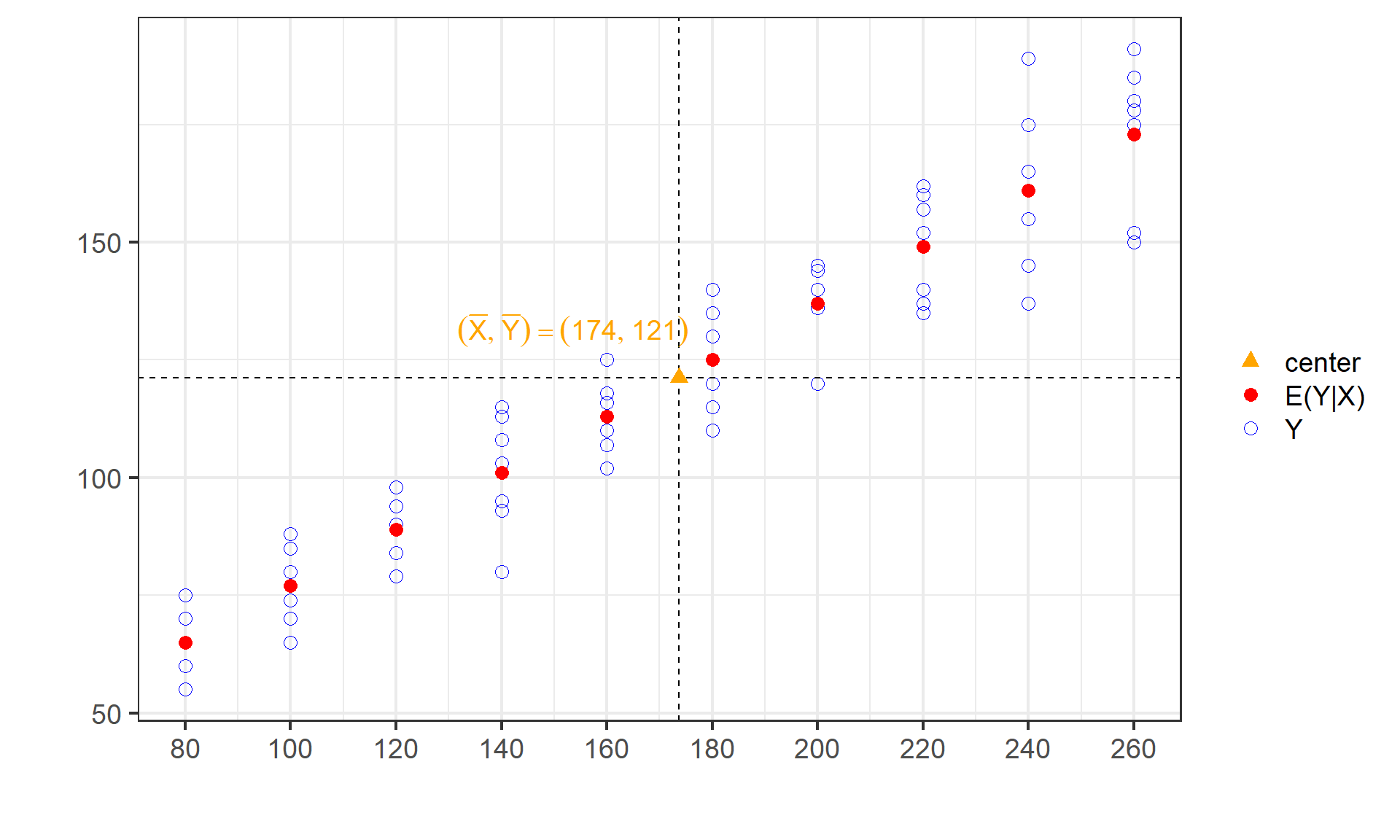
X的均值 \(\bar{X}\) =173.67和Y的无条件期望值 \(E(Y)=\) 121.20
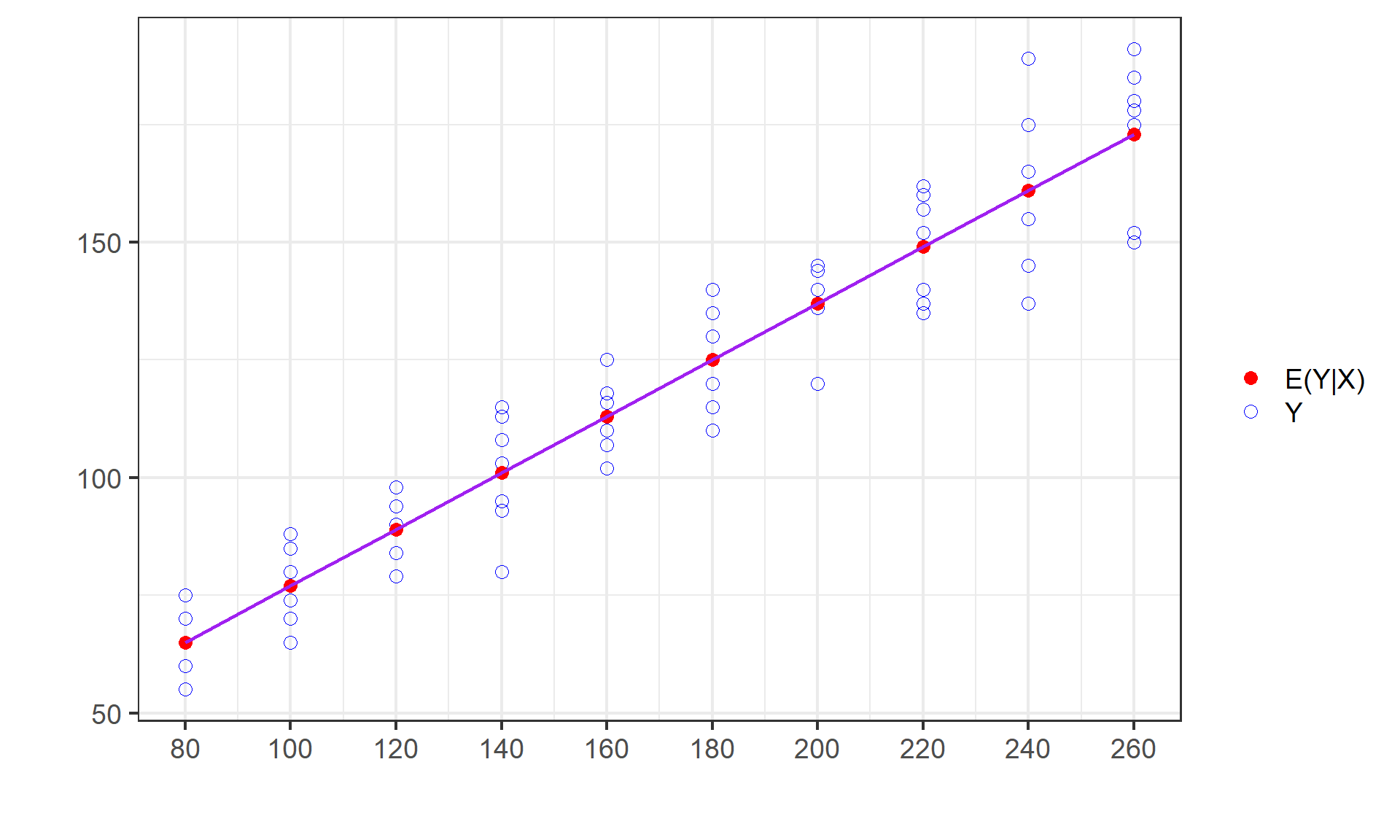
重要概念:总体回归线(PRL)
几何:给定X值时Y的条件期望值的轨迹。
统计:实质上就是Y对X的回归。
总体回归曲线(Population Regression Curve,PRC):条件期望值的轨迹表现为一条曲线(Curve)。
总体回归线(Population Regression Line,PRL):条件期望值的轨迹表现为一条直线(Line)。
重要概念:总体回归线(PRL)
重要概念:总体回归函数(PRF)
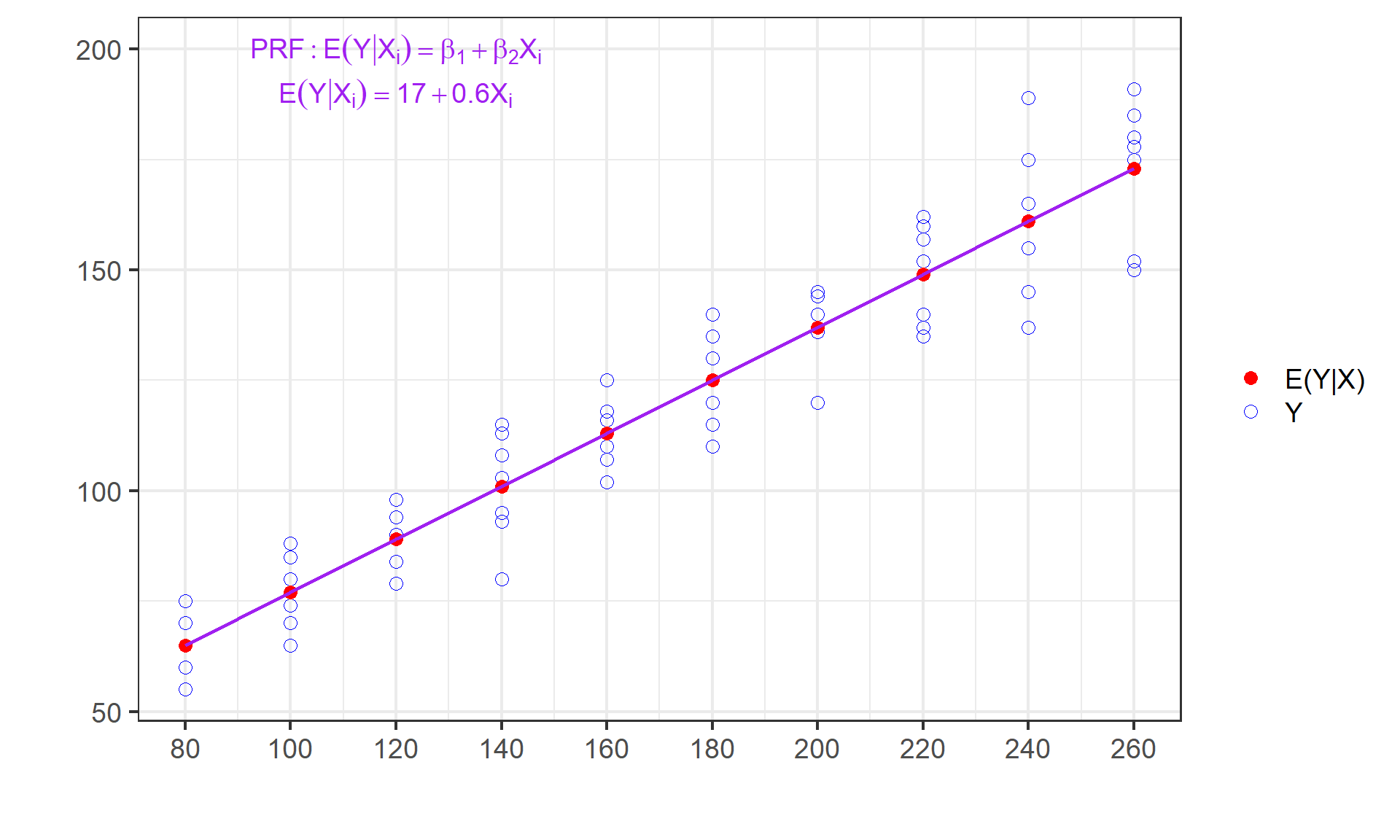
总体回归函数(Population Regression Function,PRF):它是对总体回归曲线(PRC)的数学函数表现形式。
如果不知道总体回归曲线的具体形式,则总体回归函数PRF表达为如下隐函数形式(PRF):
\[ \begin{aligned} E(Y|X_i) & = f(X_i) && \text{(PRF)} \end{aligned} \]
如果总体回归曲线是直线形式,则总体回归函数PRF表达为如下显函数形式(PRF_L):
\[ \begin{aligned} E(Y|X_i) &= \beta_1 +\beta_2X_i && \text{(PRF_L)} \end{aligned} \]
\(\beta_1,\beta_2\) 分别称为截距(intercept)和斜率系数(slope coefficient)。
\(\beta_1,\beta_2\) 称为总体参数或回归系数(regression coefficients)。
\(\beta_1,\beta_2\) 为未知但却是固定的参数。
重要概念:总体回归函数(PRF)
重要概念:总体回归模型(PRM)
总体回归模型(Population Regression model, PRM):把总体回归函数表达成随机设定形式。
如果总体回归函数为隐函数,则总体回归模型记为:
\[ \begin{aligned} Y_i &= E(Y|X_i) + u_i \\ &= f(X_i) +u_i \end{aligned} \]
如果总体回归函数为线性函数,则总体回归模型记为:
\[ \begin{aligned} Y_i &= E(Y|X_i) + u_i \\ &= \beta_1 +\beta_2X_i + u_i \end{aligned} \]
总体回归模型(PRM)属于计量经济学模型,而总体回归函数(PRF)是数量经济学模型(或数学模型)。
总体回归模型(PRM)能充分表达的是现实世界中 \(Y_i\) 变量的行为特征。
重要概念:随机干扰项
总体回归模型(PRM)设定下, \(Y_i\) 将由两个部分组成。
特定家庭的支出( \(Y_i\) ) = 系统性部分( \(E(Y|X_i)\) + 随机部分( \(u_i\) )
特定家庭的支出( \(Y_i\) ) = 系统性部分( \(\beta_1+\beta_2X_i\) ) + 随机部分( \(u_i\) )
随机干扰项:
- 也被称为随机误差项(stochastic error term):总体回归函数中忽略掉的但又影响着Y的全部变量的替代物,它是 \(Y_i\) 与条件期望( \(E(Y|X_i)\) )的离差。
\[ \begin{aligned} u_i &= Y_i - E(Y|X_i) \end{aligned} \]
重要概念:随机干扰项
随机干扰项的来源:
理论的含糊:除了主变量之外,还有其它变量的影响,但不清楚,只能用𝜇_𝑖代替它们。(家庭收入以外?)
数据的不充分:可能知道被忽略的变量,但不能得到这些变量的数量信息。(如家庭财富数据不可得)
核心变量与其它变量:其它变量全部或其中一些合起来影响还是很小的。(如子女、教育、性别、宗教等)
人类行为的内在随机性。(客观存在、固有的)
变量被“移花接木”而产生测量误差(如弗里德曼的持久收入和消费)
节省原则:为了保持一个尽可能简单的回归模型
错误的函数形式:有时根据数据及经验无法确定一个正确的函数形式 (多元回归尤其如此)
重要概念:随机干扰项
为何是“随机的”?
测不准?(误差)
测错了?(误导)
免不了!(内在性)
拥抱随机世界
风筝: \(Y_i\)
风筝线: \(E(Y|X_i)\)
风: \(u_i\)
重要概念:理解PRM和PRF的关系

若给定一个特定家庭 \((X_i=120, Y_i=79)\) ,则条件期望为 \(E(Y|120)=89\)
重要概念:理解PRM和PRF的关系
若给定 \(X_i=120\) ,则5个家庭的真实消费支出分别为:
\[ \begin{aligned} (Y_1|X=120) = 79 &= \beta_1 + \beta_2 \cdot 120 +u_1\\ (Y_2|X=120) = 84 &= \beta_1 + \beta_2 \cdot 120 +u_2\\ (Y_3|X=120) = 90 &= \beta_1 + \beta_2 \cdot 120 +u_3\\ (Y_4|X=120) = 94 &= \beta_1 + \beta_2 \cdot 120 +u_4\\ (Y_5|X=120) = 98 &= \beta_1 + \beta_2 \cdot 120 +u_5 \end{aligned} \]
重要概念:理解PRM和PRF的关系
主要结论:
总体期望刻画总体的“趋势”,总体回归线让“趋势”直观化。
个体随机性是不可避免的,总会“游离”于“趋势”之外。
随机干扰项 \(u_i\) 𝑖携带了随机个体的“游离”信息。
总体回归模型既“提取”了趋势和规律性,又“维系”着个体随机性,从而更好地表达了“真实世界”。
课后思考:
如果是无限总体,总体的规律性在理论上也是可以被严格表达出来么?
如果不告诉你总体,你怎么知道“触碰”到的是“真实的”趋势/规律?
从假想的60个家庭的微型总体中,“随便”抽取10个家庭的数据,你还能看到“直线”趋势么?
重要概念:“线性”的含义
“线性回归模型”中“线性”一词的含义
变量“线性”模型:因变量对于自变量是线性的。
参数“线性”模型:因变量对于参数是线性的。
(测试题)“线性”的含义
下列模型分别属于哪一类?请指出来:
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2 X_i +u_i && \text{(mod1)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2 X_i + \beta_3 X_i^2 +u_i && \text{(mod2)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2 X_i + \beta_3 X_i^2 + \beta_4 X_i^3 +u_i && \text{(mod3)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2 \frac{1}{X_i} +u_i && \text{(mod4)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2 ln(X_i) +u_i && \text{(mod5)} \\ \end{aligned} \]
\[ \begin{aligned} ln(Y_i) &= \beta_1 + \beta_2 X_i +u_i && \text{(mod6)} \end{aligned} \]
(测试题)“线性”的含义
下列模型分别属于哪一类?请指出来:
\[ \begin{aligned} ln(Y_i) &= \beta_1 - \beta_2 \frac{1}{X_i} +u_i && \text{(mod7)} \end{aligned} \]
\[ \begin{aligned} ln(Y_i) &= ln(\beta_1) + \beta_2 ln(X_i) +u_i && \text{(mod8)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \frac{1}{1+e^{(\beta_1 + \beta_2 X_{2i} +u_i) }} && \text{(mod9)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 +(0.75-\beta_1)e^{-\beta_2(X_i-2)} +u_i && \text{(mod10)} \end{aligned} \]
\[ \begin{aligned} Y_i &= \beta_1 + \beta_2^3 X_i +u_i && \text{(mod11)} \end{aligned} \]
重要概念:样本回归线(SRL)
样本(Sample):从总体中随机抽取得到的数据。
样本回归线(Sample Regression Line,SRL):是通过拟合样本数据得到的一条曲线(或直线)。换言之,这条线由拟合值 \(\hat{Y}_i\) 连接而成。
- \(\hat{Y}_i\) 是对条件期望值 \(Y|X_i\) 的拟合。
拟合方法有很多,例如采用OLS方法对样本数据进行拟合。
- 尽可能拟合数据
- 用什么方法拟合?
- 曲线是什么形态?
重要概念:样本回归函数(SRF)
样本回归函数(Sample Regression Function,SRF):是样本回归曲线的数学函数形式,可是是线性的或非线性。如果是直线则可以写成:
\[ \begin{aligned} \hat{Y}_i =\hat{\beta}_1 + \hat{\beta}_2X_i \end{aligned} \]
对比总体回归函数(PRF):
\[ \begin{aligned} E(Y|X_i) =\beta_1 + \beta_2X_i \end{aligned} \]
可以认为:
\(\hat{Y}_i\) 是对 \(E(Y|X_i)\) 的估计量。
\(\hat{\beta}_1\) 是对 \(\beta_1\) 的估计量。
\(\hat{\beta}_2\) 是对 \(\beta_2\) 的估计量。
(示例)第一份随机样本:抽样
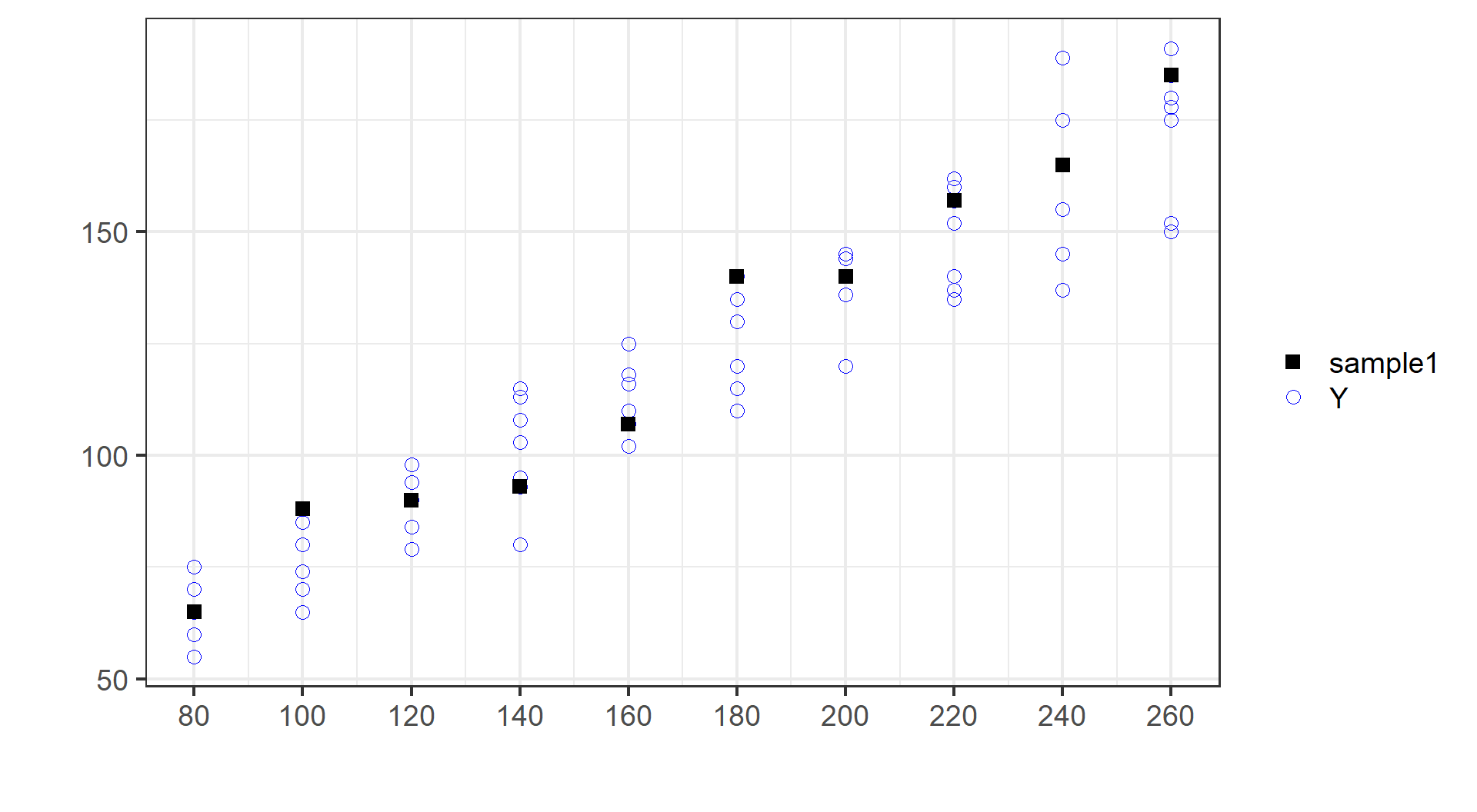
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 65 | 88 | 90 | 93 | 107 | 140 | 140 | 157 | 165 | 185 |
(示例)第一份随机样本:数据
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 65 | 88 | 90 | 93 | 107 | 140 | 140 | 157 | 165 | 185 |
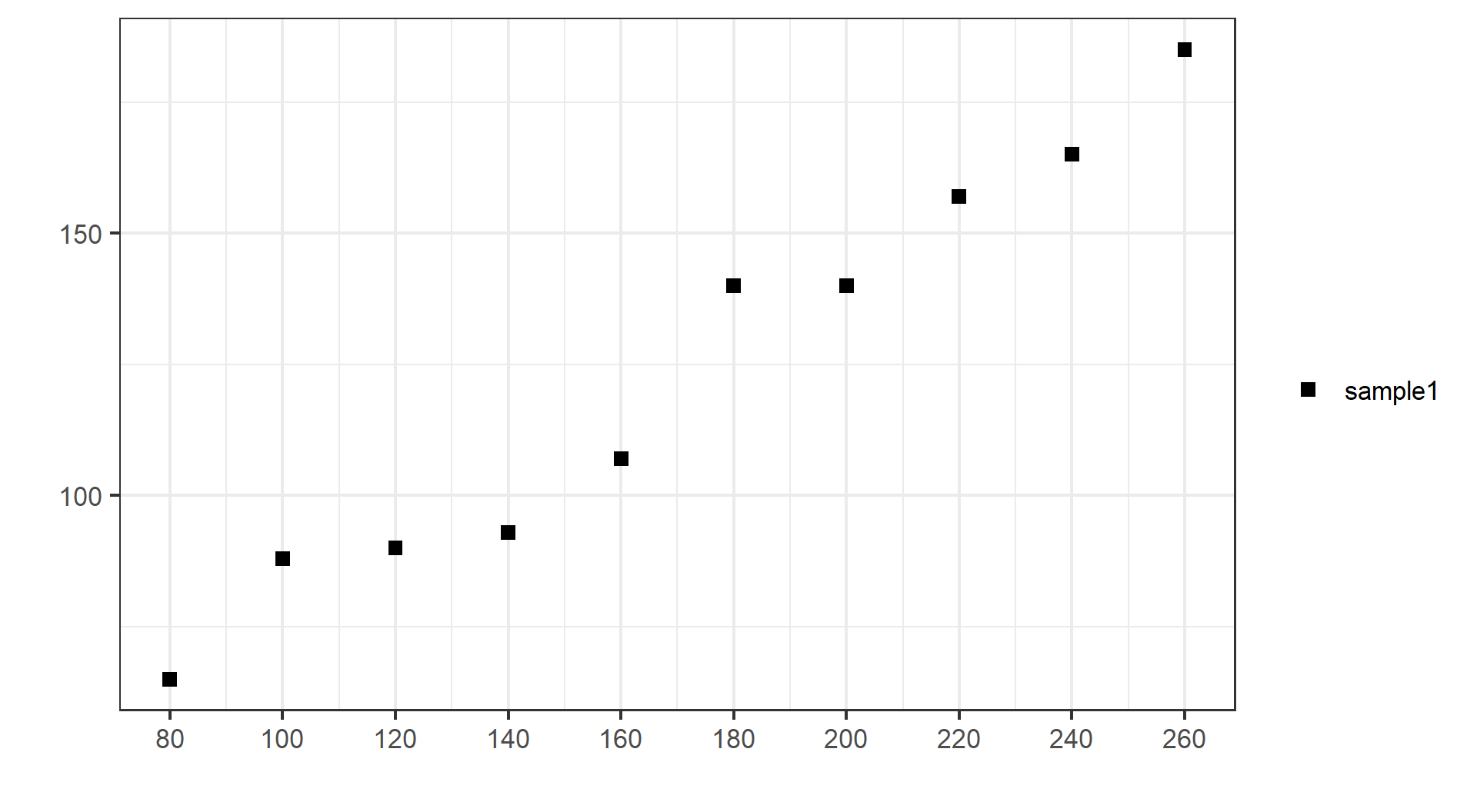
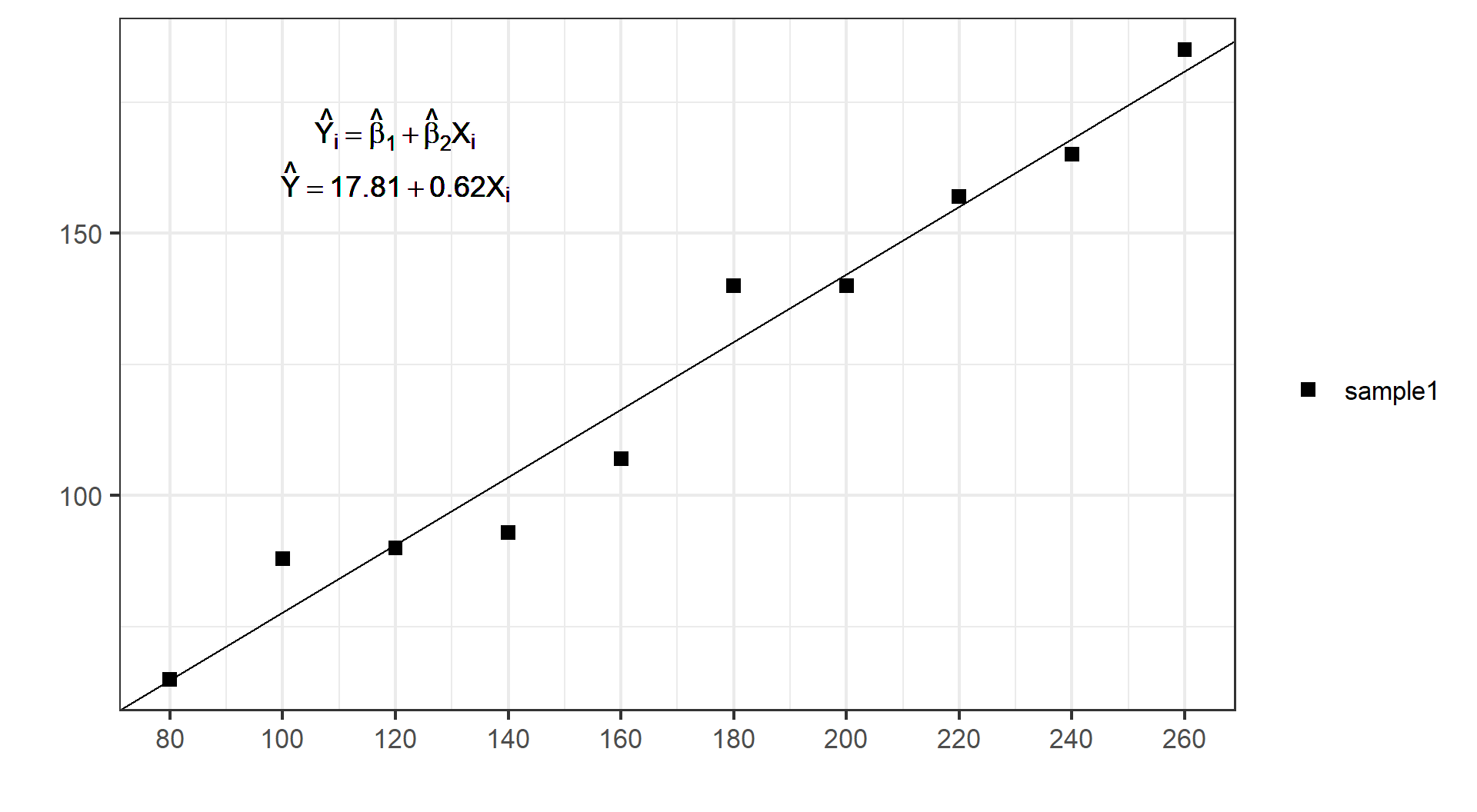
(示例)第一份随机样本:SRL
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 65 | 88 | 90 | 93 | 107 | 140 | 140 | 157 | 165 | 185 |
(示例)第一份随机样本:SRF
根据第一份随机样本拟合得到的样本回归函数SRF:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y}=&&+13.38&&+0.64X_i\\ &(s)&&(7.4383)&&(0.0415)\\ &(t)&&(+1.80)&&(+15.56)\\ &(over)&&n=10&&\hat{\sigma}=7.5301\\ &(fit)&&R^2=0.9680&&\bar{R}^2=0.9640\\ &(Ftest)&&F^*=242.00&&p=0.0000 \end{split} \end{alignedat} \]
样本数据如下:
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 65 | 88 | 90 | 93 | 107 | 140 | 140 | 157 | 165 | 185 |
(示例)第二份随机样本:抽样
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 55 | 70 | 90 | 108 | 125 | 135 | 136 | 135 | 155 | 178 |
(示例)第二份随机样本:数据
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 55 | 70 | 90 | 108 | 125 | 135 | 136 | 135 | 155 | 178 |
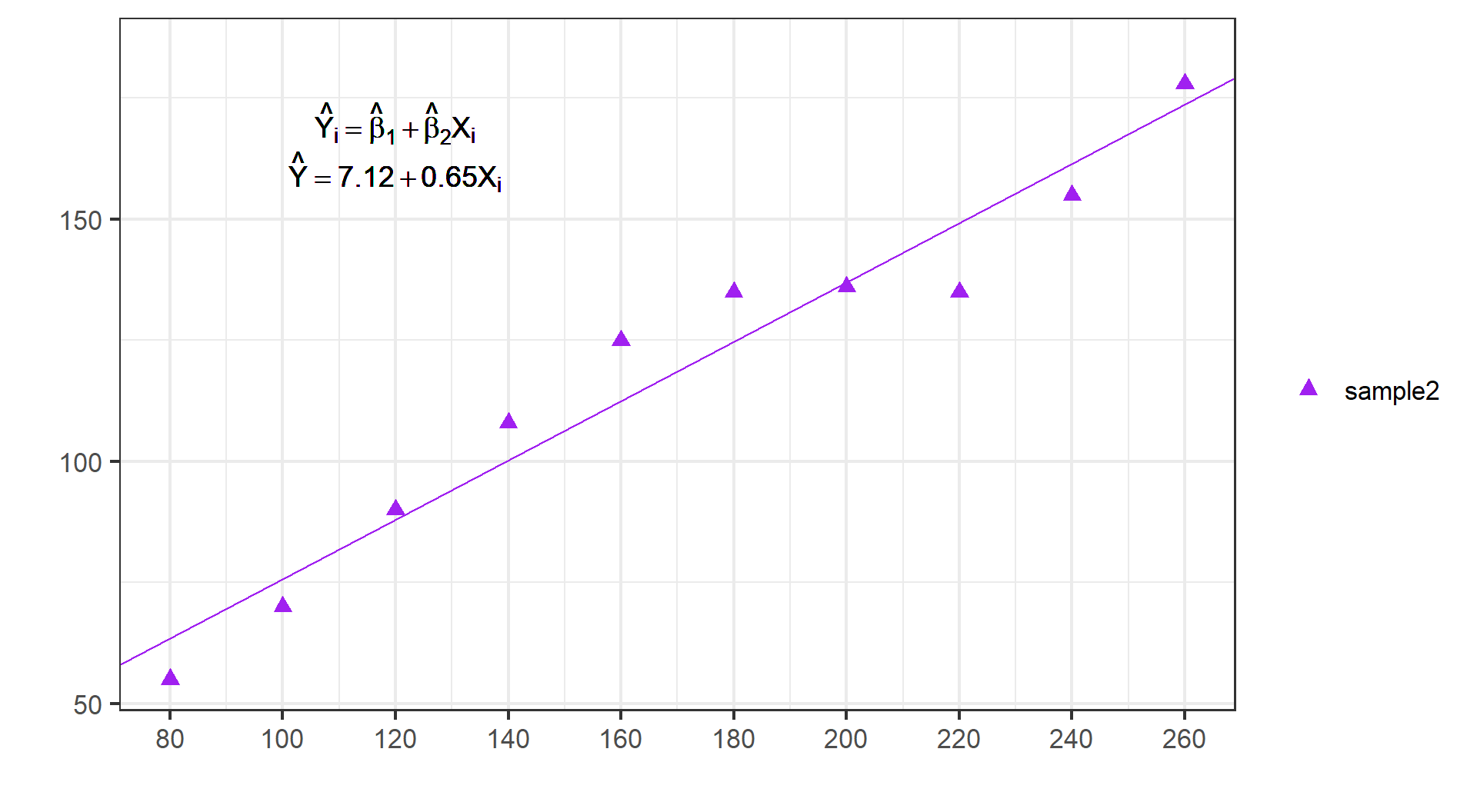
(示例)第二份随机样本:SRL
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 55 | 70 | 90 | 108 | 125 | 135 | 136 | 135 | 155 | 178 |
(示例)第二份随机样本:SRF
根据第二份随机样本拟合得到的样本回归函数SRF:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y}=&&+14.59&&+0.61X_i\\ &(s)&&(9.2070)&&(0.0513)\\ &(t)&&(+1.58)&&(+11.94)\\ &(over)&&n=10&&\hat{\sigma}=9.3207\\ &(fit)&&R^2=0.9468&&\bar{R}^2=0.9402\\ &(Ftest)&&F^*=142.47&&p=0.0000 \end{split} \end{alignedat} \]
样本数据如下:
| var | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | n9 | n10 |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 |
| Y | 55 | 70 | 90 | 108 | 125 | 135 | 136 | 135 | 155 | 178 |
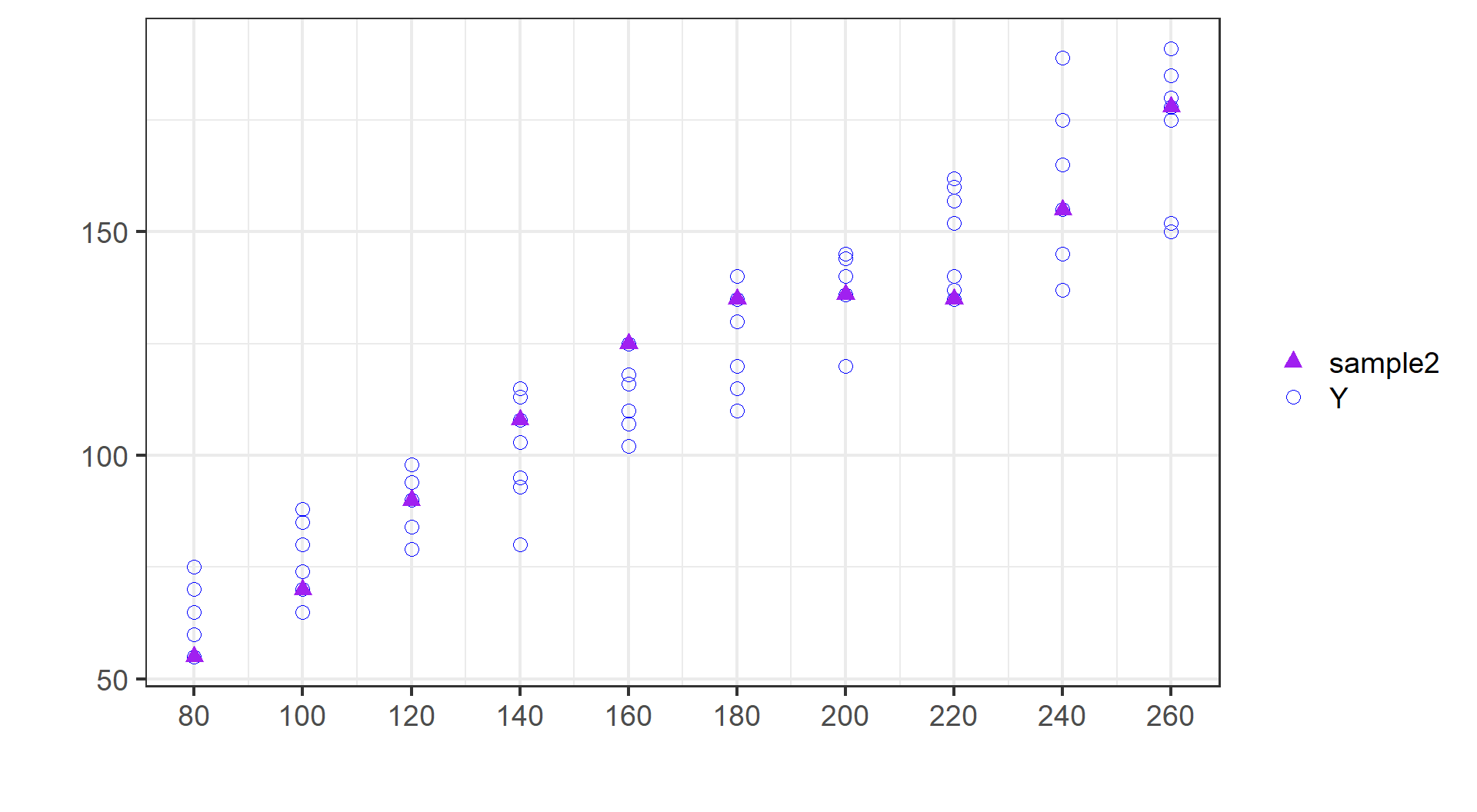
(示例)两份样本同时出现
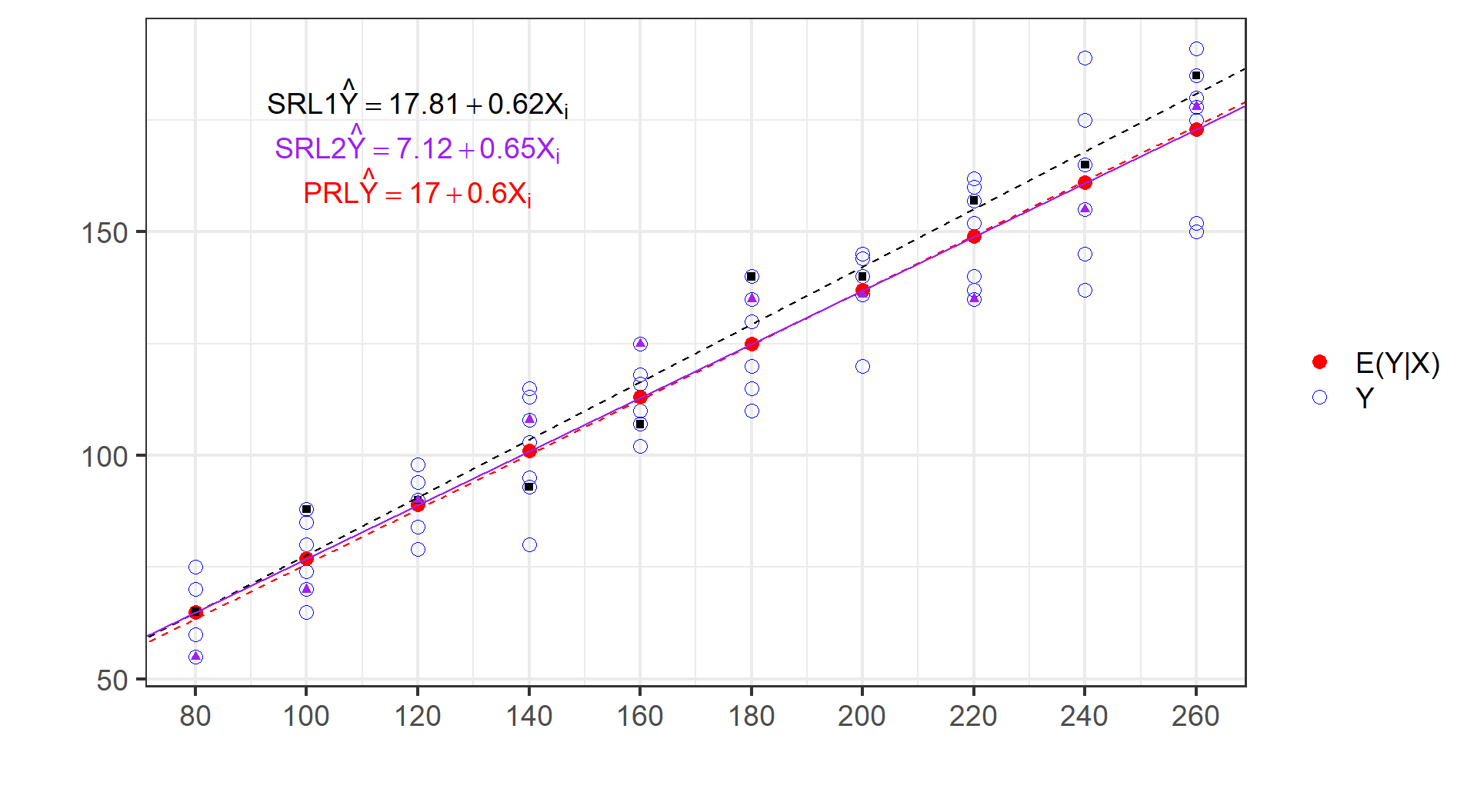
重要概念:样本回归模型(SRM)
样本回归模型(Sample Regression Model,SRM):把样本回归函数表现为“随机”形式。
- 如果样本回归函数为隐函数,则样本回归模型可记为:
\[ \begin{aligned} Y_i &= g(X_i) +e_i \end{aligned} \]
- 如果样本回归函数表现为直线,则样本回归模型可记为:
\[ \begin{align} Y_i &= \hat{\beta}_1 +\hat{\beta}_2X_i +e_i && \text{(SRM_L)} \end{align} \]
其中, \(e_i\) 表示残差(Residual)
重要概念:残差
残差(Residual):
定义:是样本回归函数与Y的样本观测值之间的离差。
记号:
\[ \begin{aligned} e_i &= Y_i - \hat{Y}_i \\ &= Y_i - (\hat{\beta}_1 +\hat{\beta}_2X_i) \end{aligned} \]
重要概念:理解SRF和SRM的关系
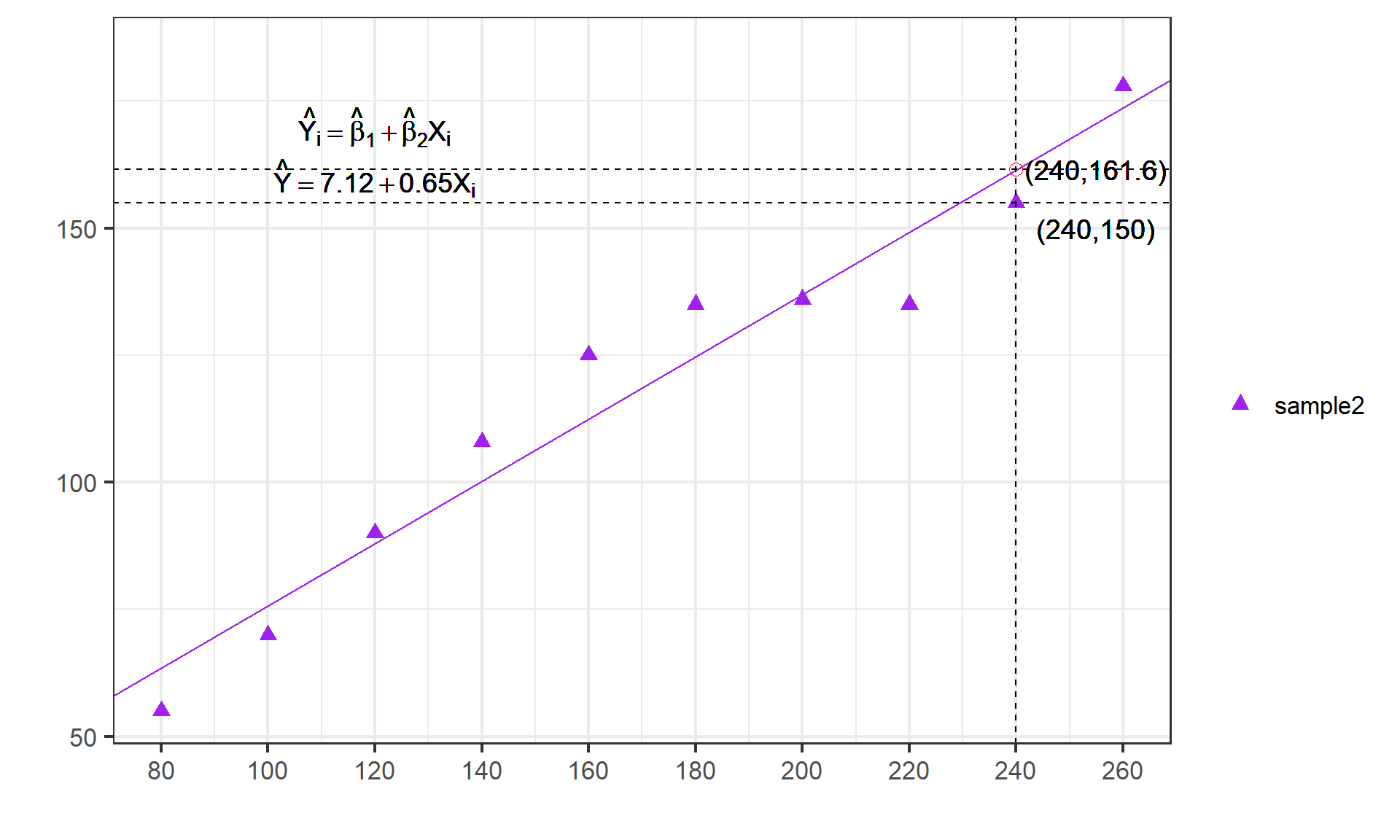
给定 \(x_i=240\) ,样本2的观测值 \(Y_i=240\) ;拟合值 \(\hat{Y}_i=\) 161.6;残差 \(e_i=Y_i- \hat{Y}_i=\) -6.6。
重要概念:样本回归与总体回归的比较
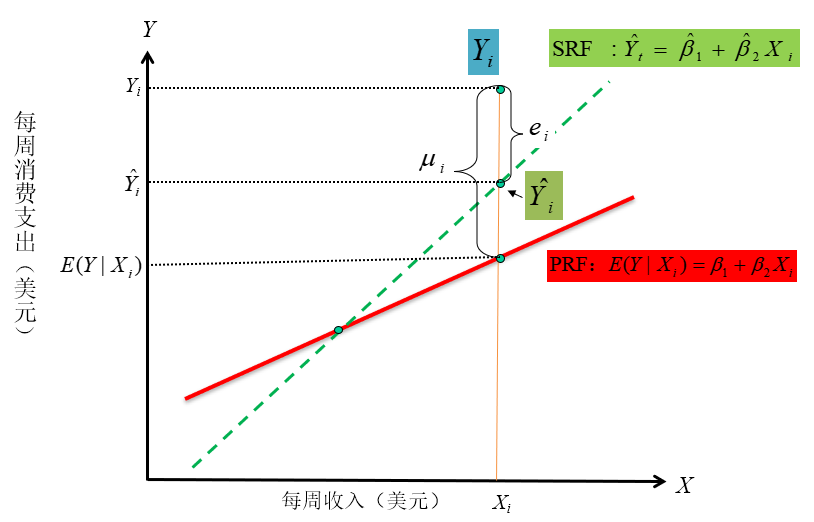
为何不同?继承性和变异性
重要概念:样本回归与总体回归的比较
总体回归函数PRF:
\[ \begin{aligned} E(Y|X_i) &= \beta_1 +\beta_2X_i && \text{(PRF)} \end{aligned} \]
总体回归模型PRM:
\[ \begin{aligned} Y_i &= \beta_1 +\beta_2X_i + u_i && \text{(PRM)} \end{aligned} \]
样本回归函数SRF:
\[ \begin{aligned} \hat{Y}_i =\hat{\beta}_1 + \hat{\beta}_2X_i && \text{(SRF)} \end{aligned} \]
样本回归模型SRM:
\[ \begin{aligned} Y_i &= \hat{\beta}_1 + \hat{\beta}_2X_i +e_i && \text{(SRM)} \end{aligned} \]
思考:
PRF无法直接观测,只能用SRF近似替代
估计值与观测值之间存在偏差
SRF又是怎样决定的呢?
重要概念:样本回归与总体回归的比较
总结:
随机抽样数据继承了总体的特征。
利用随机样本进行数据拟合是对总体规律的“反向追踪”。
样本回归模型中的残差是拟合不完全的产物。
思考与练习
思考:
怎样来判定对随机样本的一次数据拟合是更优的?
存不存在一种“最优”的拟合方法?
课后作业:
请把162名同学的拟合线进行平均化处理(截距和斜率取均值),绘制得到一条“回归线”。
你认为是这根平均化的“回归线”与真相更逼近么?
本节结束

第5章 相关和回归分析 [05-02] 回归分析的基本思想