统计学原理

(Statistics)

第5章 相关和回归分析
05-01 变量间关系的度量


Hu Huaping (胡华平)

huhuaping01 at hotmail.com

经济管理学院(CEM)

第五章 相关和回归分析

5.1 变量间关系的度量

5.2 回归分析的基本思想

5.3 OLS方法与参数估计

5.4 假设检验

5.5 拟合优度与残差分析

5.6 回归预测分析

5.7 回归报告解读

5.1 变量间关系的度量

变量间的关系

相关关系的描述与测度

相关系数的显著性检验

变量间的关系

（示例）变量间的关系：经济学专业解读

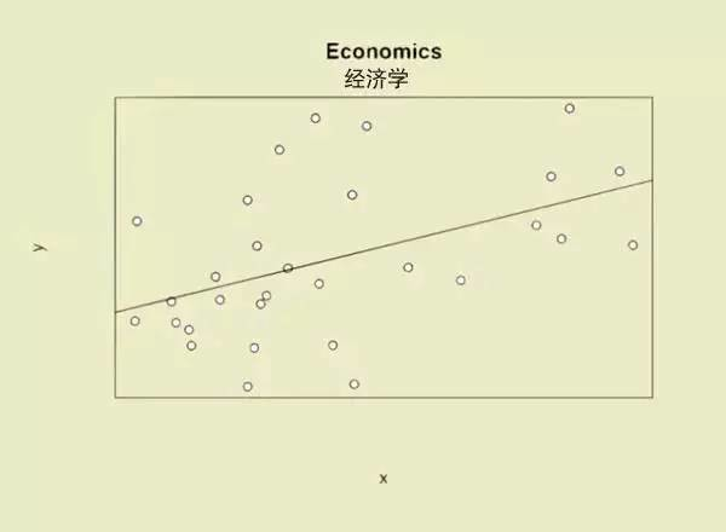
“我们数据不少，做了很严格的回归，但异常值略多略多，符合理论的数值反而难找……”

（示例）变量间的关系：金融学专业解读

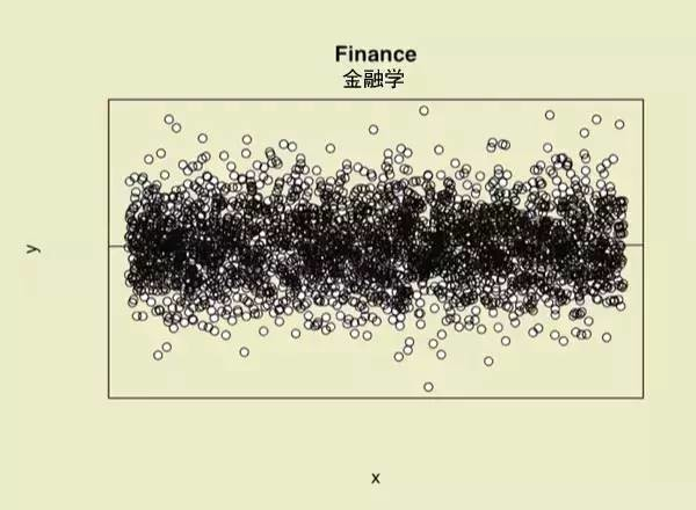
“我们的数据多如牛毛，无孔不入。即使做完回归，也会发现异常值和符合理论的数值多得不忍直视。”

（示例）变量间的关系：土木工程专业解读

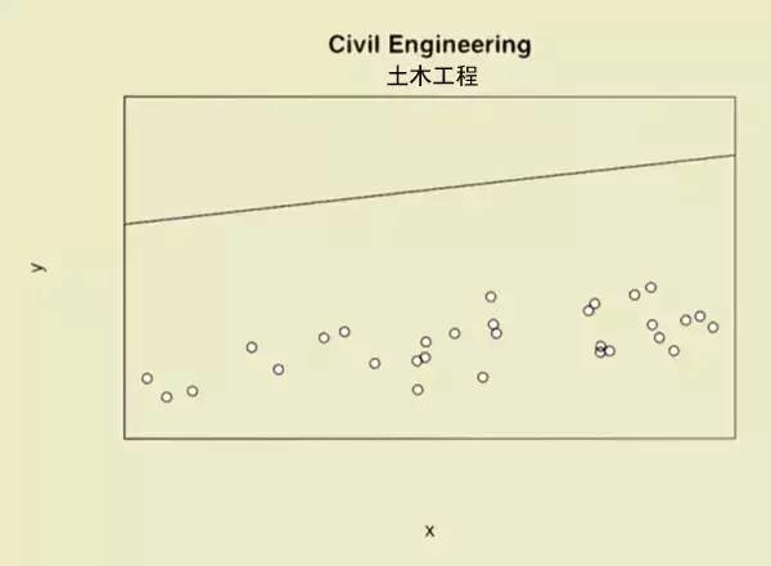
“我们得要设计余量，所以理论设计得远高于实际承受……”

（示例）变量间的关系：物理学专业解读

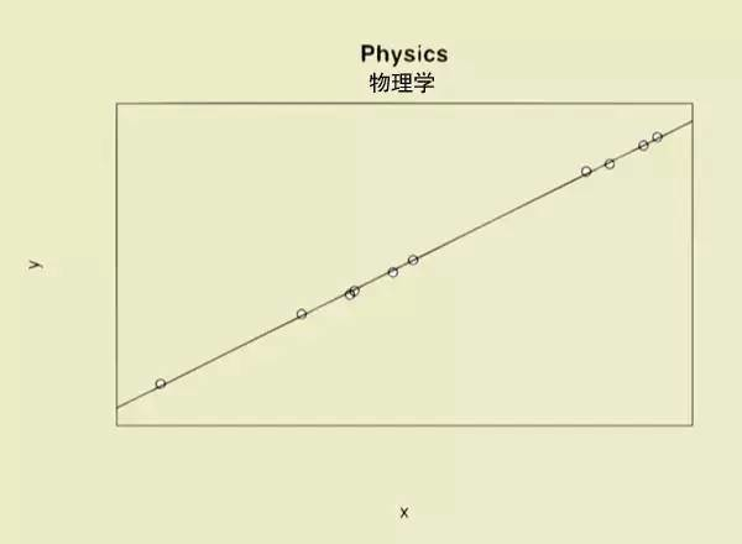
“我们的理论和数据严丝合缝，bingo！”

（示例）变量间的关系：环境科学专业解读

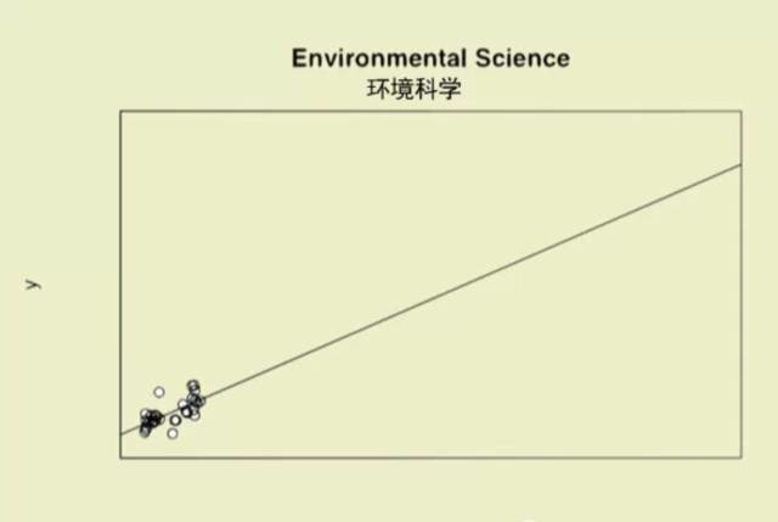
“我们的理论和数据大致吻合，就是……应用范围有点蛋疼。”

（示例）变量间的关系：历史学专业解读

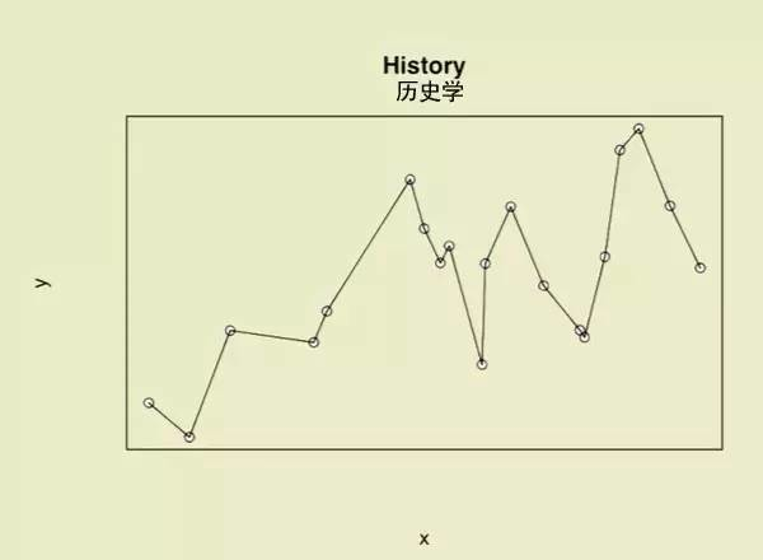
“数据虽然很多，可我们能用理论把他们统统连起来！”

（示例）变量间的关系：政治学专业解读

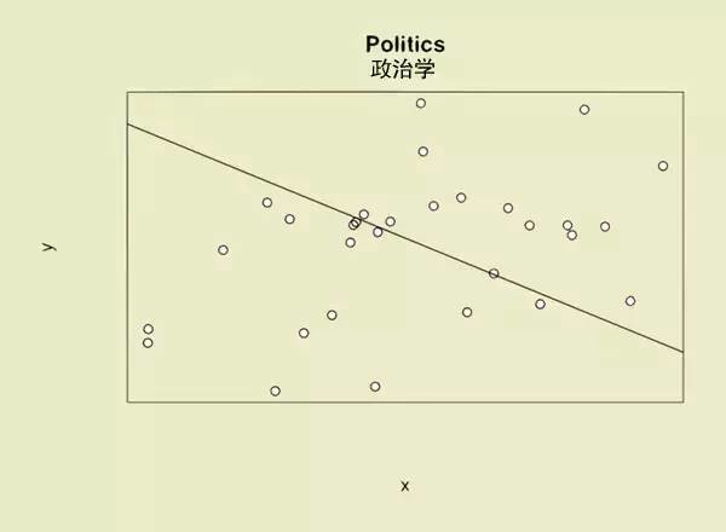
“世界大势一日三变，尽管我们数据不少，可……我们的理论跟数据趋势是反着来的……”

（示例）变量间的关系：社会学专业解读

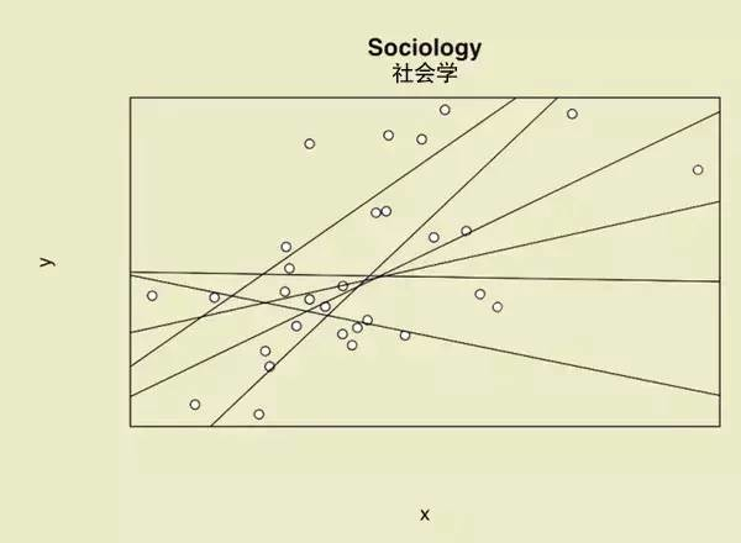
“学海无涯苦作舟。那么多数据，那么多理论，慢慢学，恩……”

（示例）变量间的关系：数学专业解读

“数据很少，但能建立理论～”

（示例）变量间的关系：新闻学专业解读

（示例）“只有一个数据，也能建立理论……”

（示例）变量间的关系：哲学专业解读

“没有数据，依然建立理论……”

（示例）变量间的关系：文学批评专业解读

“如图所示，你懂的……”

变量间的关系：函数关系

两个变量若存在是一一对应的确定关系，则称之为二者具有函数关系。

函数关系

设有两个变量 \(X\) 和 \(Y\) ，变量 \(Y\) 随变量 \(X\) 一起变化，并完全依赖于 \(X\) ，当变量 \(X\) 取某个数值时， \(Y\) 依确定的关系取相应的值，则称 \(Y\) 是 \(X\) 的函数，记为 \(Y = f(X)\) ，其中 \(X\) 称为自变量， \(Y\) 称为因变量。

从几何学角度来看，数据集各观测点会落在一条曲线上。

（示例）函数关系

某种商品的销售额 \(Y\) 与销售量 \(X\) 之间的关系可表示为( \(P\) 为单价)：

\[ Y_i = P_i\cdot X_i \]

圆的面积 \(S\) 与半径 \(R\) 之间的关系可表示为：

\[ S = \pi R^2 \]

企业的原材料消耗额 \(Y\) 与产量 \(X1\) 、单位产量消耗 \(X2\) 、原材料价格 \(X3\) 之间的关系可表示为：

\[ Y = X_1 \cdot X_2 \cdot X_3 \]

变量间的关系：相关关系(correlation)

相关关系的类型

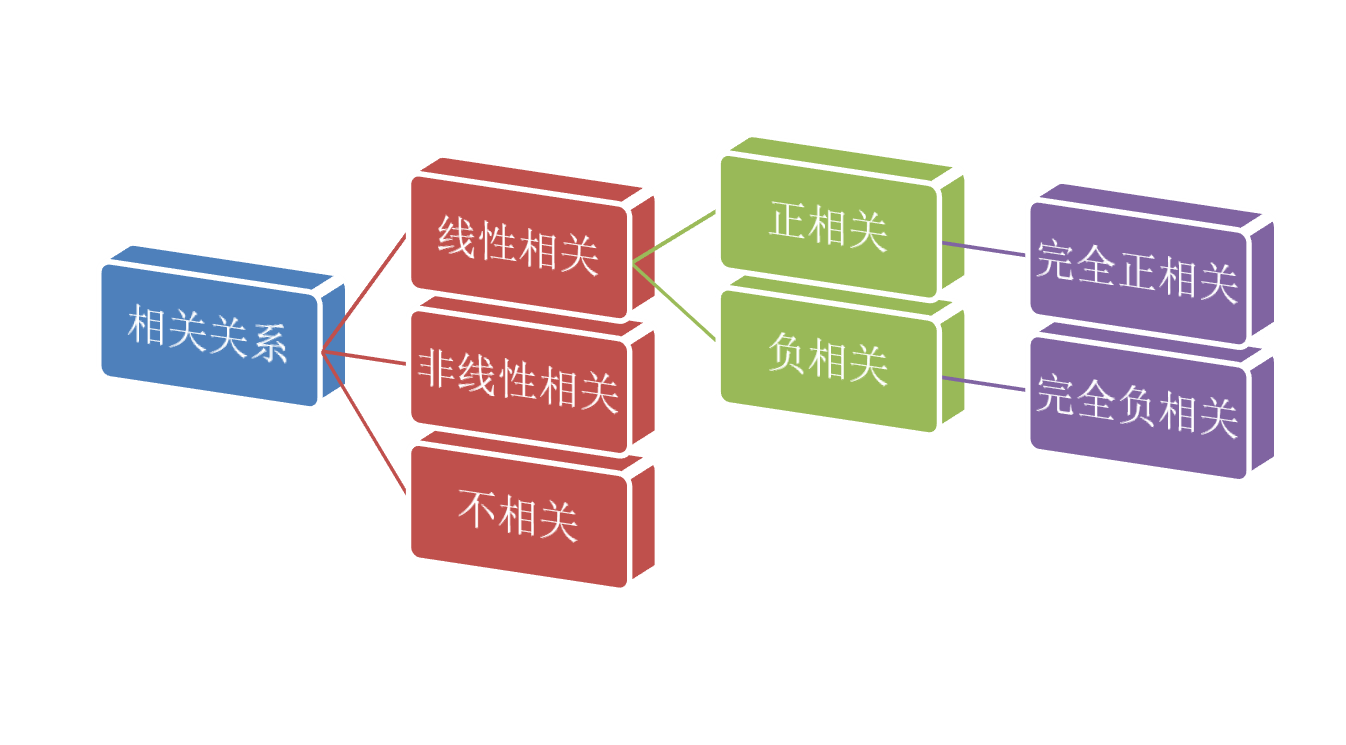
（示例）相关关系

  • 父亲身高 \(Y\) 与子女身高 \(X\) 之间的关系

  • 收入水平 \(Y\) 与受教育程度 \(X\) 之间的关系

  • 粮食单位面积产量 \(Y\) 与施肥量 \(X1\) 、降雨量 \(X2\) 、温度 \(X3\) 之间的关系

  • 商品的消费量 \(Y\) 与居民收入 \(X\) 之间的关系

  • 商品销售额 \(Y\) 与广告费支出 \(X\) 之间的关系

相关关系的描述与测度：问题与假定

相关分析要解决的问题：

  • 变量之间是否存在关系？

  • 如果存在关系，它们之间是什么样的关系？

  • 变量之间的关系强度如何？

  • 样本所反映的变量之间的关系能否代表总体变量之间的关系？

相关分析中的总体假定：

  • 两个变量之间是线性关系

  • 两个变量都是随机变量

相关关系的描述与测度：散点图

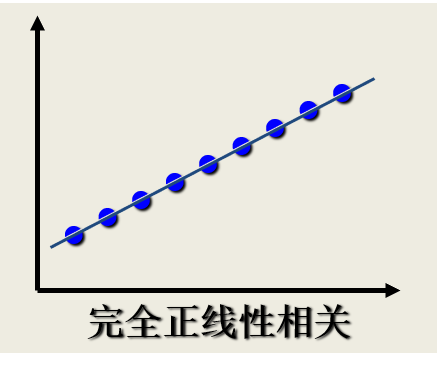
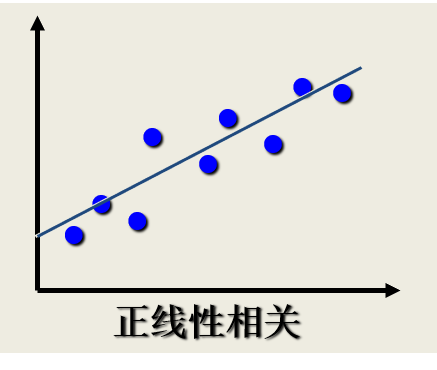
相关关系的描述与测度：散点图

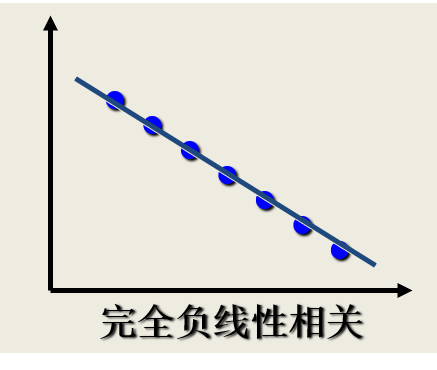
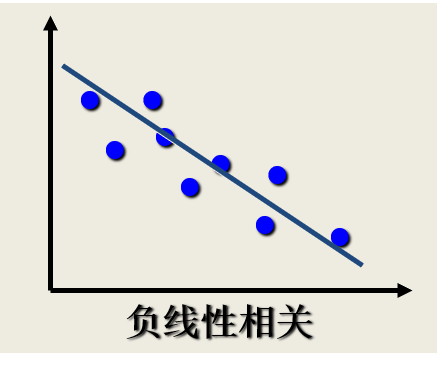
相关关系的描述与测度：散点图

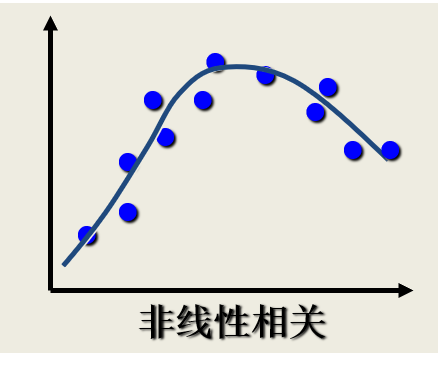
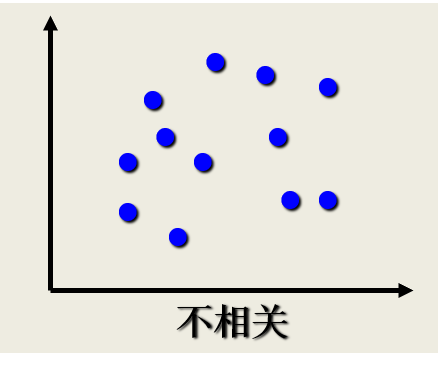
相关关系的描述与测度：散点图

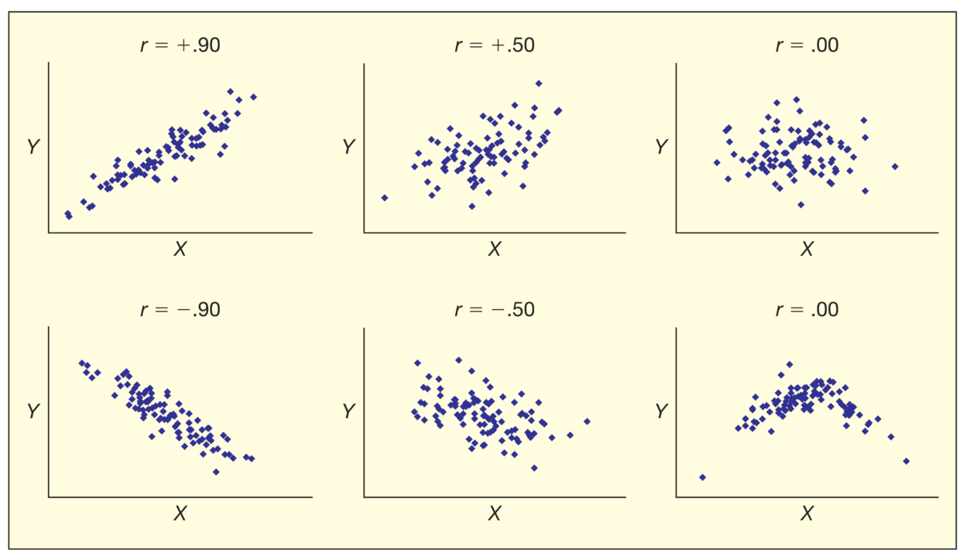
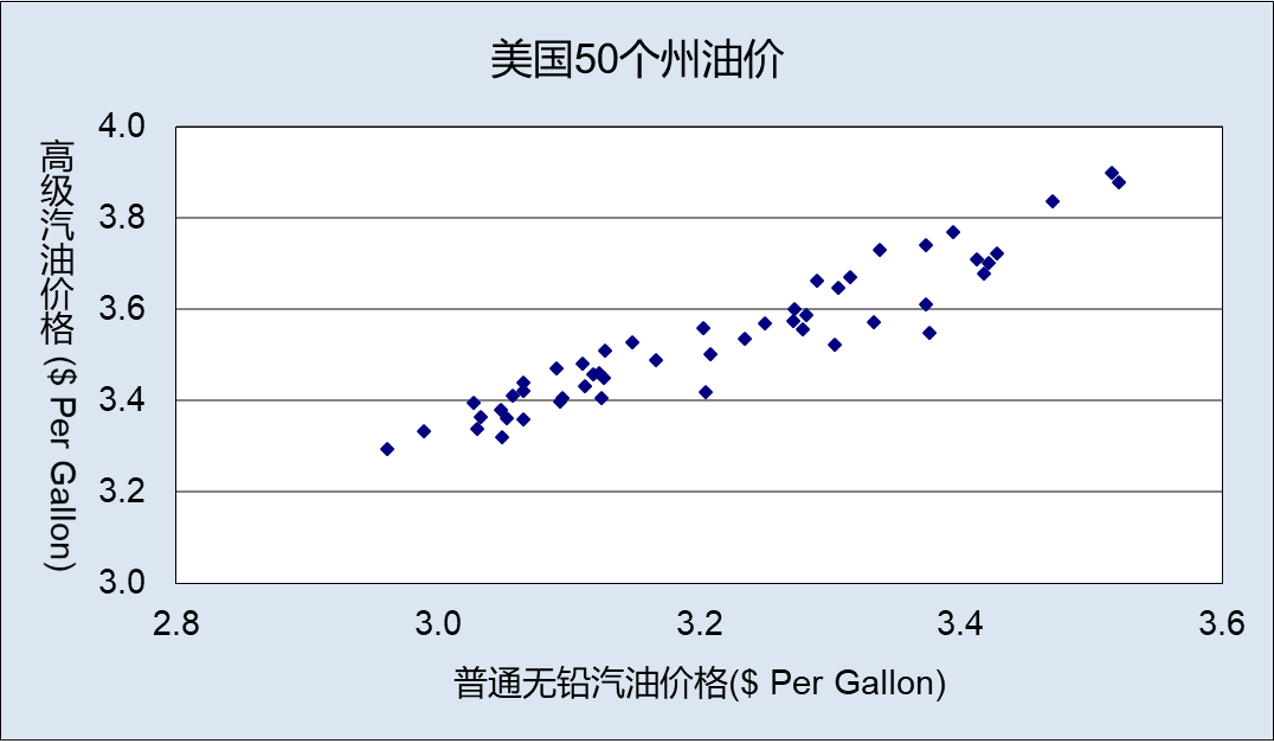
（示例）两类油价的散点图

（示例）传染病与认知水平的散点图

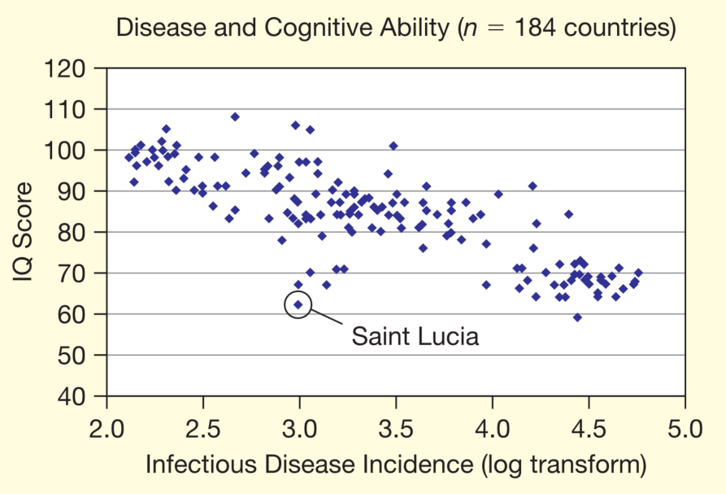
相关关系的描述与测度：相关系数

相关系数(correlation coefficient)：是度量变量之间关系强度的一个统计量。

  • 它是对两个变量之间线性相关强度的一种度量。

  • 一般称为简单相关系数，也称为线性相关系数(linear correlation coefficient) 。

  • 或称为Pearson相关系数(Pearson’s correlation coefficient) 。

相关系数记号表达：

  • 若相关系数是根据总体全部数据计算的，称为总体相关系数，记为 \(\rho\) 。

  • 若是根据样本数据计算的，则称为样本相关系数，简称为相关系数，记为 \(r\) 。

相关关系的描述与测度：计算公式

简单相关系数的大FF计算公式

\[ \begin{align} r & = \frac{n \sum X_i Y_i -\sum X_i \sum Y_i}{\sqrt{n \sum X_i^{2}-\left(\sum X_i\right)^{2}} \cdot \sqrt{n \sum Y_i^{2}-\left(\sum Y_i\right)^{2}}} \tag{eq01} \end{align} \]

简单相关系数的小ff计算公式

\[ \begin{align} r & = \frac{ \sum{\left( (X_i - \overline{X})(Y_i - \overline{Y})\right ) } }{\sqrt{\sum{(X_i - \overline{X})^2 }\sum{(Y_i - \overline{Y})^2}}} = \frac{S S_{XY}}{\sqrt{S S_{XX}} \sqrt{S S_{YY}}} = \frac{\sum{x_iy_i}}{\sqrt{\sum{x_i^2}\sum{y_i^2}}} \tag{eq02} \end{align} \]

\[ \begin{align} S S_{X X} =\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)^{2} ;\quad S S_{Y Y} =\sum_{i=1}^{n}\left(Y_{i}-\overline{Y}\right)^{2} ;\quad S S_{X Y}=\sum_{i=1}^{n}\left(X_{i}-\overline{X}\right)\left(Y_{i}-\overline{Y}\right) \end{align} \]

相关关系的描述与测度：特征

简单相关系数的特征：

性质1： \(r\) 的取值范围是 \([-1,1]\) ， \(|r|\) 越趋于1表示相关关系越强； \(|r|\) 越趋于0表示相关关系越弱。

  • 如果 \(|r|=1\) ，为完全相关。其中 \(r =1\) ，为完全正相关； \(r =-1\) ，为完全负正相关

  • 如果 \(r = 0\) ，不存在线性相关关系

  • 如果 \(-1<r<0\) ，为负相关；如果 \(0<r<1\) ，为正相关。

性质2：r具有对称性。即 \(X\) 与 \(Y\) 之间的相关系数和 \(Y\) 与 \(X\) 之间的相关系数相等，即 \(r_{XY}= r_{YX}\) 。

相关关系的描述与测度：特征

简单相关系数的特征：

性质3： \(r\) 数值大小与 \(X\) 和 \(Y\) 原点及尺度无关，即改变 \(X\) 和 \(Y\) 的数据原点及计量尺度，并不改变 \(r\) 数值大小。

性质4：仅仅是 \(X\) 与 \(Y\) 之间线性关系的一个度量，它不能用于描述非线性关系。这意为着， \(r=0\) 只表示两个变量之间不存在线性相关关系，并不说明变量之间没有任何关系

性质5： \(r\) 虽然是两个变量之间线性关系的一个度量，却不一定意味着 \(X\) 与 \(Y\) 一定有因果关系。

相关关系的描述与测度：解释

相关系数的经验解释

下面给出实证研究时，对相关系数的经验解释：

  • 当 \(|r|<0.8\) 时，可视为两个变量之间高度相关。

  • 当 \(0.5<|r|<0.8\) 时，可视为中度相关。

  • 当 \(0.3<|r|<0.5\) 时，视为低度相关。

  • 当 \(|r|<0.3\) 时，说明两个变量之间的相关程度极弱，可视为不相关。

而且上述解释必须建立在对相关系数的显著性进行检验的基础之上。

相关关系的描述与测度：简单相关系数

简单相关系数（simple correlation coefficient）：

  • \(Y_i\) 和 \(X_{2i}\) 之间的相关系数：

\[ \begin {align} r_{12}=\frac{\sum y_{i} x_{2 i}}{\sqrt{\sum y_{i}^{2}} \sqrt{\sum x_{2 i}^{2}}} \end {align} \]

  • \(Y_i\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{13}=\frac{\sum y_{i} x_{3 i}}{\sqrt{\sum y_{i}^{2}} \sqrt{\sum x_{3 i}^{2}}} \end {align} \]

  • \(X_{2i}\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{23}=\frac{\sum x_{2 i} x_{3 i}}{\sqrt{\sum x_{2 i}^{2}} \sqrt{\sum x_{3 i}^{2}}} \end {align} \]

相关关系的描述与测度：偏相关系数

偏相关系数（partial correlation coefficient）： 一个不依赖于 \(X_{2i}\) 的，对 \(X_{3i}\) 和 \(Y_i\) 的影响的一种相关系数。

  • 保持 \(X_{3i}\) 不变， \(Y_i\) 和 \(X_{2i}\) 之间的相关系数：

\[ \begin {align} r_{12 \cdot 3}=\frac{r_{12}-r_{13} r_{23}}{\sqrt{\left(1-r_{13}^{2}\right)\left(1-r_{23}^{2}\right)}} \end {align} \]

  • 保持 \(X_{2i}\) 不变， \(Y_i\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{13.2}=\frac{r_{13}-r_{12} r_{23}}{\sqrt{\left(1-r_{12}^{2}\right)\left(1-r_{23}^{2}\right)}} \end {align} \]

  • 保持 \(Y_i\) 不变， \(X_{2i}\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{23.1}=\frac{r_{23}-r_{12} r_{13}}{\sqrt{\left(1-r_{12}^{2}\right)\left(1-r_{13}^{2}\right)}} \end {align} \]

相关系数的显著性检验

相关系数的显著性检验，是指检验两个变量之间是否存在线性相关关系。

相关系数的显著性检验方法包括：

  • 等价于对回归斜率系数 \(\beta_1\) 的检验（仅针对一元回归）

  • 采用R. A. Fisher提出的t检验

相关系数的显著性检验

相关系数的显著性检验步骤：

1）提出假设： \(H_0: \rho =0; H_1: \rho \neq 0\)

2）计算样本统计量

\[ T^{\ast} = |r|\sqrt{\frac{n-2}{1-r^2}} \quad \sim t(n-2) \]

3）给定显著性水平 \(\alpha\) ，确定t理论分布值 \(t_{1-\alpha/2}(n-2)\) 。

4）得到假设检验结论：

  • 若 \(T^{\ast}> t_{1-\alpha/2}(n-2)\) ，则拒绝 \(H_0\) ，认为显著存在相关关系；

  • 若 \(T^{\ast} < t_{1-\alpha/2}(n-2)\) ，则无法拒绝 \(H_0\) ，认为相关关系不显著。

附录：假设检验的分布及统计量证明1/3

\[ \begin{align} \sum_y y h(y \mid x)& =\sum_y y \frac{f(x, y)}{f_X(x)}= \beta_1 + \beta_2 x && \text{(1)} \end{align} \]

\[ \begin{align} \sum_y y f(x, y)&=(\beta_1+ \beta_2 x) f_X(x) && \text{(2)}\\ \sum_{x } \sum_y y f(x, y) &=\sum_{x }(\beta_1+ \beta_2 x) f_X(x) && \text{(3)} \\ \sum_{x } \sum_y x y f(x, y) &=\sum_{x }\left(\beta_1 x+ \beta_2 x^2\right) f_X(x) && \text{(4)} \\ E(X Y)&=\beta_1 E(X)+ \beta_2 E\left(X^2\right) && \text{(5)}\\ \end{align} \]

\[ \begin{align} \mu_Y&=\beta_1 + \beta_2 \mu_X && \text{(6 <--2)} \\ \mu_X \mu_Y+\rho \sigma_X \sigma_Y &=\beta_1 \mu_X+\beta_2\left(\mu_X^2+\sigma_X^2\right) && \text{(7 <--5)} \end{align} \]

附录：假设检验的分布及统计量证明2/3

利用上述二元一次方程组，可以解出参数：

\[ \begin{align} \beta_1 &=\mu_Y-\rho \frac{\sigma_Y}{\sigma_X} \mu_X && \text{(8)} \\ \beta_2 &=\rho \frac{\sigma_Y}{\sigma_X} && \text{(9)} \end{align} \]

\[ \begin{align} E(Y \mid X_i)= \beta_1 +\beta_2X_i = \beta_1 + \rho \frac{\sigma_Y}{\sigma_X} X_i && \text{(10)} \end{align} \]

相关系数 \(\rho\) 的显著性检验等价于一元线性回归分析中斜率参数 \(\beta_2\) 的t检验过程，也即： \(H_0: \rho = 0; \quad H_1: \rho \neq 0\) ；等价于 \(H_0: \beta_2 = 0; \quad H_1: \beta_2 \neq 0\)

附录：假设检验的分布及统计量证明3/3

一元线性回归 \(Y_i = \beta_1 +\beta_2X_i + u_i\) ；斜率系数t检验 \(H_0: \beta_2 = 0; H_1: \beta_2 \neq 0\)

$$

\[\begin{align} t=\frac{\hat{\beta_2} -\beta_2}{\hat{\sigma}_{\hat{\beta}_2}} =\frac{\hat{\beta_2}}{\sqrt{\frac{\hat{\sigma}^2}{\sum\left(X_i-\bar{X}\right)^2}}} =\frac{\hat{\beta_2}-0}{\sqrt{\frac{\mathrm{MSE}}{\sum\left(X_i-\bar{X}\right)^2}}} =\frac{r \cdot \left(S_Y / S_X\right)}{\sqrt{\frac{(n-1) S_Y^2 \left(1-r^2\right)}{(n-2) } \cdot \frac{1}{(n-1)S_X^2}}} =\frac{r \sqrt{n-2}}{\sqrt{1-r^2}} \end{align}\]

$$

$$

\[\begin{align} r &= \frac{S_{XY}}{S_X S_Y} \\ \hat{\beta}_2 &=\frac{\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\frac{1}{n-1} \sum_{i=1}^n\left(X_i-\bar{X}\right)^2}=\frac{S_{XY}}{S_X^2}=r \cdot \frac{S_Y}{S_X}\\ \hat{\beta}_1 & = \overline{Y} - \hat{\beta}_2 \overline{X} \\ M S E \equiv \sigma^2 &= \frac{\sum_{i=1}^n\left(Y_i-\hat{Y}_i\right)^2}{n-2}=\frac{\sum_{i=1}^n\left[Y_i-\left(\bar{Y}+\frac{S_{XY}}{S_X^2}\left(X_i-\bar{X}\right)\right)\right]^2}{n-2}=\frac{(n-1) S_Y^2\left(1-r^2\right)}{n-2} \end{align}\]

$$

（案例）银行贷款

（案例）银行贷款：案例数据

案例说明：某银行共有25家分行，分行及所在地区的相关变量数据如下表所示。

（案例）银行贷款：不良贷款VS贷款余额的散点图

不良贷款VS贷款余额散点图

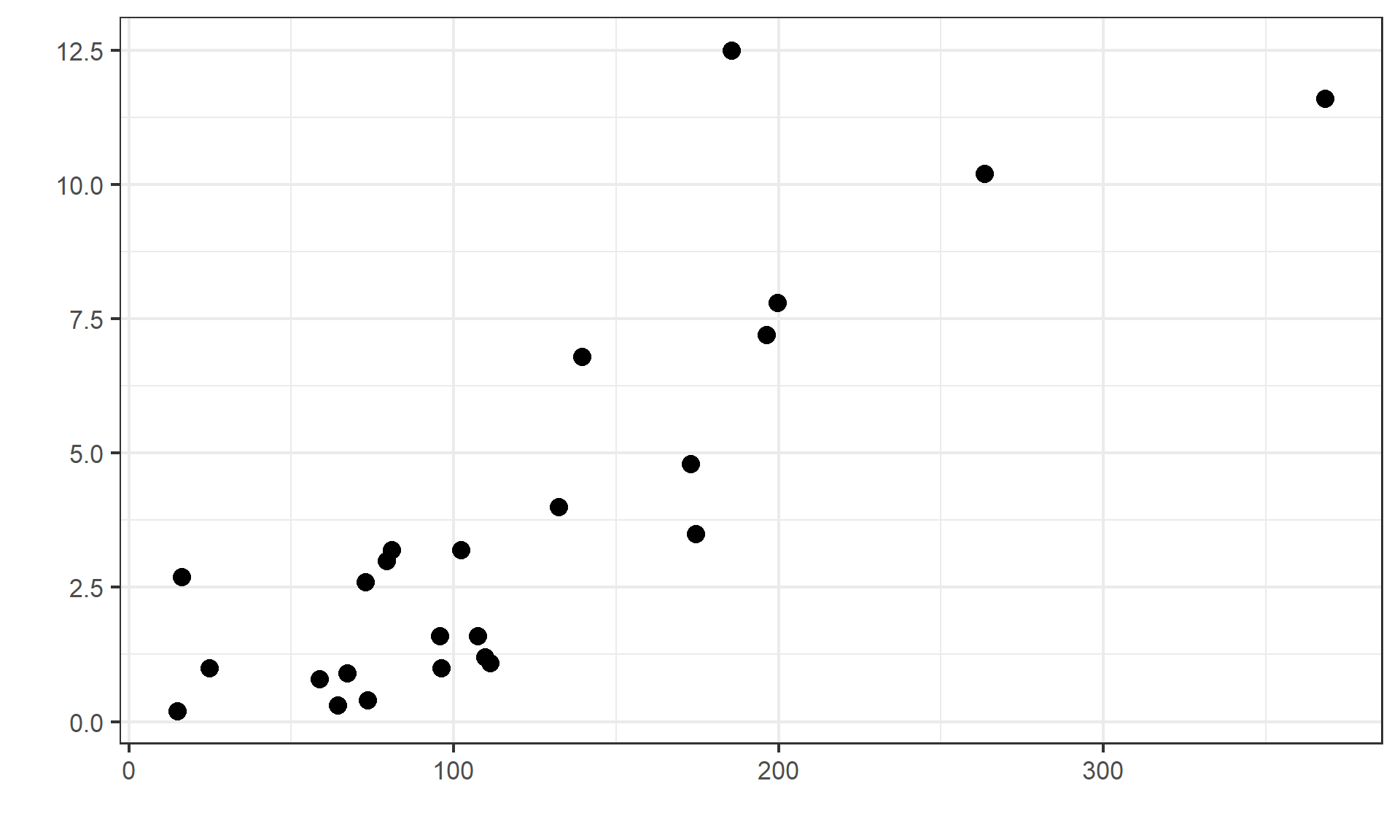
（案例）银行贷款：不良贷款VS贷款余额的相关系数（大FF）

（案例）银行贷款：不良贷款VS贷款余额的相关系数（大FF）

相关系数 \(r\) 的大FF计算公式（eq01）：

\[ \begin{align} r & = \frac{n \sum X_i Y_i -\sum X_i \sum Y_i}{\sqrt{n \sum X_i^{2}-\left(\sum X_i\right)^{2}} \cdot \sqrt{n \sum Y_i^{2}-\left(\sum Y_i\right)^{2}}} \\ & = \frac{25 \times 1.708014\times 10^{4} - 3006.7 \times 93.2}{\sqrt{25 \times 5.1654337\times 10^{5}-\left(3006.7\right)^2} \cdot \sqrt{25 \times 660.1-\left( 93.2\right)^{2}}} \\ & = 0.8436 \end{align} \]

（案例）银行贷款：不良贷款VS贷款余额的相关系数（小ff）

（案例）银行贷款：不良贷款VS贷款余额的相关系数

相关系数 \(r\) 的小FF计算公式（eq02）：

\[ \begin{align} r & = \frac{ \sum{\left( (X_i - \overline{X})(Y_i - \overline{Y})\right ) } }{\sqrt{\sum{(X_i - \overline{X})^2 (Y_i - \overline{Y})^2}}} \\ & = \frac{\sum{x_i y_i}}{\sqrt{\sum{x_i^2}\sum{y_i^2}}} \\ & = \frac{5871.1624}{\sqrt{ 1.5493357\times 10^{5} \times 312.6504}} \\ & = 0.8436 \end{align} \]

（案例）银行贷款：相关系数矩阵表(Pearson)

corl_pearson <- round(cor(df_loan[, -1], method = "pearson"), 4)
corl_pearson[upper.tri(corl_pearson)] <- NA

loan.bad

loan.surplus

loan.receivable

loan.numbers

investment.fixed

loan.bad

1.0000

loan.surplus

0.8436

1.0000

loan.receivable

0.7315

0.6788

1.0000

loan.numbers

0.7003

0.8484

0.5858

1.0000

investment.fixed

0.5185

0.7797

0.4724

0.7466

1.0000

（案例）银行贷款：相关系数矩阵(Spearman)

corl_spearman <- round(cor(df_loan[, -1], method = "spearman"), 4)
corl_spearman[upper.tri(corl_spearman)] <- NA

loan.bad

loan.surplus

loan.receivable

loan.numbers

investment.fixed

loan.bad

1.0000

loan.surplus

0.8339

1.0000

loan.receivable

0.7331

0.8148

1.0000

loan.numbers

0.7172

0.8559

0.7393

1.0000

investment.fixed

0.4407

0.6582

0.5469

0.5975

1.0000

（案例）银行贷款：相关系数矩阵图

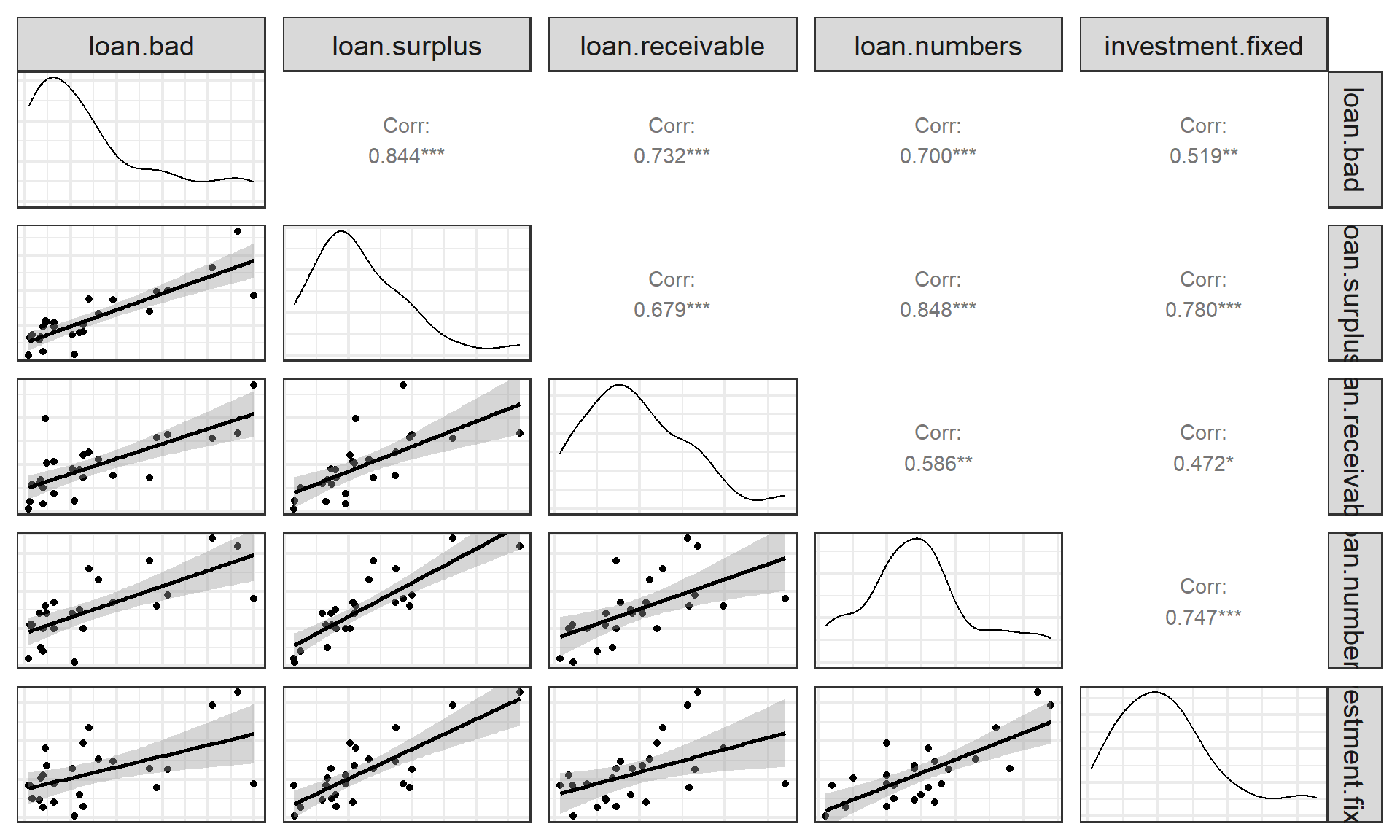
（案例）银行贷款：偏相关系数

假定我们认为不良贷款（loan.bad）与贷款余额（loan.surplus）及贷款项目数（loan.number）存在相互关系。

前面我们已经计算出如下的简单相关系数： \[ r_{12} = r_{_{bad},_{sur}}= 0.8436; \quad r_{13} = r_{_{bad},_{num}}= 0.7003; \quad r_{23} = r_{_{num},_{sur}}= 0.8484 \]

因此我们可以分别计算出偏相关系数

（案例）银行贷款：偏相关系数

  • 保持 \(X_{3i}\) 不变， \(Y_i\) 和 \(X_{2i}\) 之间的相关系数：

\[ \begin {align} r_{12 \cdot 3}=\frac{r_{12}-r_{13} r_{23}}{\sqrt{\left(1-r_{13}^{2}\right)\left(1-r_{23}^{2}\right)}} =\frac{0.8436-0.7003\times 0.8484}{\sqrt{\left(1-0.7003^{2}\right)\left(1-0.8484^{2}\right)}} = 0.6601 \end {align} \]

  • 保持 \(X_{2i}\) 不变， \(Y_i\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{13.2}=\frac{r_{13}-r_{12} r_{23}}{\sqrt{\left(1-r_{12}^{2}\right)\left(1-r_{23}^{2}\right)}} =\frac{0.7003-0.8436 \times 0.8484}{\sqrt{\left(1-0.8436^{2}\right)\left(1-0.8484^{2}\right)}} = -0.0542 \end {align} \]

  • 保持 \(Y_i\) 不变， \(X_{2i}\) 和 \(X_{3i}\) 之间的相关系数：

\[ \begin {align} r_{23.1}=\frac{r_{23}-r_{12} r_{13}}{\sqrt{\left(1-r_{12}^{2}\right)\left(1-r_{13}^{2}\right)}} =\frac{0.8484-0.8436 \times 0.7003}{\sqrt{\left(1-0.8436^{2}\right)\left(1-0.7003^{2}\right)}} = 0.6722 \end {align} \]

（案例）银行贷款：相关系数显著性检验(手算)

对于前述loan.surplus与loan.bad进行相关系数显著性检验（Pearson）：

  • 1）提出假设： \(H_0: \rho =0; H_1: \rho \neq 0\)

  • 2）计算样本统计量：

\[ \begin{align} T^{\ast} = |r|\sqrt{\frac{n-2}{1-r^2}} =0.8436 \times \sqrt{\frac{25-2}{1-0.8436^2}} = 7.5344 \end{align} \]

  • 3）给定显著性水平 \(\alpha=0.05\) ，确定t理论分布值 \(t_{1-\alpha/2}(n-2)=t_{1-0.05/2}(25-2)=t_{0.975}(23)=2.07\) 。

  • 4）得到假设检验结论：因为t样本统计量大于t理论查表值，也即

\[ \left[T^{\ast}= 7.5344\right] > \left[t_{0.975}(23) =2.07\right] \]

因此拒绝原假设 \(H_0\) ，认为变量loan.surplus（贷款余额）与loan.bad（不良贷款）显著存在相关关系。

（案例）银行贷款：相关系数显著性检验(R软件)

我们可以使用R软件函数cor.test()对上述两个变量进行相关系数显著性检验：

cor.test(df_rel1$loan.surplus, df_rel1$loan.bad,
  method = "pearson"
)

    Pearson's product-moment correlation

data:  df_rel1$loan.surplus and df_rel1$loan.bad
t = 7.5335, df = 23, p-value = 1.183e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.6726484 0.9290352
sample estimates:
      cor 
0.8435714

本节结束