统计学原理
(Statistics)
第4章 数据的概括性度量
Hu Huaping (胡华平)
huhuaping01 at hotmail.com
经济管理学院(CEM)
第四章 数据的概括性度量
4.1 总量程度的度量
时期指标
时点指标
内容导航
总量指标:概念和作用
总量指标,又称为绝对指标,是反映社会经济现象一定时间、地点、条件下总的规模、水平的统计指标。
总量指标表现形式是绝对数,也可表现为绝对差数。
例:2009年我国财政收入6.8万亿元,比上年增收近8000亿元。
作用:
- 总量指标能反映一个国家的基本国情和国力,反映某部门、单位等人、财、的基本数据 。
- 总量指标是进行决策和科学管理的依据之一 。
- 总量指标是计算相对指标和平均指标的基础。
总量指标:分类
按其反映的内容不同可分为:
总体单位总量:度量总体的单位数数量。例如,全班学生总人数。
总体标志总量:度量总体中某个标志值总和的量。例如全班所有学生的总成绩。
按其反映的时间状况不同可分为:
- 时期指标:反映现象在某一时期发展过程的总数量。可连续计数,与时间长短有关,是累计结果。
例如:一定时期的产品产量、产值、商品销售量、工资总额等。
- 时点指标:反映现象在某一时刻的状况。间断计数,与时间间隔无关,不能累计。
例如:特定时刻上,人口数、企业数、商品库存数、流动资金额。
总量指标:计算
计算总量指标时需要考虑:
现象的同类性。
明确的统计含义。
计量单位必须一致。
幽默故事
钱是这样贬值的:
\[ \begin{aligned} 10元&=10角\times 10角\\ &=1元\times 1元\\ &=1元 \end{aligned} \]
总量指标:计量单位
总量指标计量单位主要有三种形式:
实物单位
- 自然单位:辆、双、头、根、个……
- 度量衡单位:吨、米、克、立方米……
- 双重单位:公里/小时、吨/台(起重机)、吨/(立方米*座*年)……
- 复合单位:吨公里(货运量)、千瓦小时(度)……
价值单位
- 货币单位有现行价格和不变价格之分。
- 价值单位使不能直接相加的产品产量过渡到能够加总。
劳动单位
- 工时:工人数和劳动时数的乘积。
- 台时:设备台数和开动时数的乘积。
4.2 相对程度的度量
相对指标概述
计划完成相对指标
结构相对指标
比例相对指标
比较相对指标
强度相对指标
动态相对指标
内容导航
相对指标概述:概念和作用
相对指标:是两个有联系的绝对指标之比。
示例:2009年我国对外贸易进口总额增长率为16.3%。
作用:
具体表明社会经济现象之间的比例关系。
使一些不能直接对比的事物找出共同比较的基础。
便于记忆、易于保密。
相对指标概述:类型
计划完成相对指标:用来检查、监督计划执行情况的相对指标。
结构相对指标:利用分组法,将总体区分为不同性质(即差异)的各部分,以部分数值与总体全部数值对比而得出比重或比率,用以反映总体内部构成状况的相对指标。
比例相对指标:同一总体内不同组成部分的指标数值对比的结果,用来反映总体内部的比例关系。
比较相对指标:将两个同类指标做静态对比得出的相对指标,表明同类现象在不同条件下的数量对比关系。
强度相对指标:是两个不同性质的、但有一定联系的总量指标对比的结果,用来表明现象的强度、密度和普遍程度的相对指标。
动态相对指标:后面专门一章学习。
相对指标概述:表现形式
相对指标的表现形式有两大类:
有名数形式
有名数形式:分子分母的单位不能化约。
人口密度:人/平方公里
平均每人分摊的粮食产量:千克/人
无名数形式
无名数形式:分子分母的单位可以化约。
系数或倍数:是将比的基数抽象化为1。例如:固定资产磨损系数、工资等级系数、结构比例系数。
成数:是将比的基数抽象化为10。例如:粮食产量增加一成,即增长1/10。
百分数:是将比的基数抽象化为100。
千分数:是将比的基数抽象化为1000。
相对指标概述:运用原则
相对指标的运用原则:
注意二个对比指标的可比性。
相对指标要和总量指标结合起来运用。
多种相对数结合运用
在比较二个相对数时,是否适宜相除再求一个相对数,应视情况而定。若除出来有实际意义,则除;若不宜相除,只宜相减求差数,用百分点表示之。
(案例)钢产量:案例说明
我国三个时期两个年份的钢产量数据如下:
(案例)钢产量:计算指标
根据以上数据,我们可以计算出:
\[ 产量变化 \Delta =Q_{t_1} - Q_{t_0} \]
\[ 发展速度\% \quad Speed = 100*Q_{t_1} / Q_{t_0} \]
\[ 增长率\% \quad Ratio =100*(Q_{t_1} - Q_{t_0})/Q_{t_0}=100*\Delta/Q_{t_0} \] \[ 增长1\%的绝对值 = \Delta / Ratio = Q_{t_0}/100 \]
(案例)钢产量:计算表1
根据上述指标公式,可以计算得到:
(案例)钢产量:计算表2
前述计算表,也可进一步变形为:
计划完成相对指标:概念和特征
计划完成相对指标:实际完成数与计划任务数对比的比率。根据分子分母是否属于同一时期,可以分为两类,具体计算公式分别为:
- 计划完成程度:分子分母属同一时期。
\[ 计划完成程度 = \frac{实际完成数}{计划完成数}\times 100\% \]
- 计划完成进度:分子分母属不同时期。
\[ 计划完成进度 = \frac{计划初期至某期实际累计完成数}{全期计划数}\times 100\% \]
特征:分子分母不能颠倒位置。
计划完成相对指标:任务下达形式
计划完成相对指标的下达形式主要有三种:
- 以总量指标下达任务,具体计算公式为:
\[ 计划完成相对指标 = \frac{实际水平}{计划水平}\times 100\% \]
- 以平均指标下达任务,具体计算公式为:
\[ 计划完成相对指标 = \frac{实际平均水平}{计划平均水平}\times 100\% \]
- 以相对指标下达任务,具体计算公式为:
\[ \begin{aligned} 计划完成相对指标 = \frac{实际为基数的百分数}{计划为基数的百分数}\times 100\% = \frac{1 \pm 实际增减百分数}{1 \pm 计划增减百分数}\times 100\% \end{aligned} \]
(示例)计算计划完成相对指标:以总量指标为基础
问题:设某公司某年计划工业总产值为200万元,实际完成220万元,则计划完成程度为多少?
答案:
\[ \begin{aligned} \text { 总产值计划完成相对数 }=\frac{220}{200} \times 100 \%=110 \% \end{aligned} \]
(示例)计算计划完成相对指标:以平均指标为基础
问题:某化肥企业某年每吨化肥计划成本为200元,实际成本为180元,则计划完成程度为多少?
答案:
\[ 实际单位成本-计划单位成本=180-200=-20(元) \]
计算结果表明该企业化肥单位成本实际比计划降低了10%,平均每吨化肥节约生产费用20元。
\[ \begin{aligned} \text { 成本计划完成相对数 }=\frac{180}{200} \times 100 \%=90 \% \end{aligned} \]
(示例)计算计划完成相对指标:以相对指标为基础
问题:某企业生产某产品,上年度实际成本为420元/吨,本年度计划单位成本降低6%,实际降低7.6%,则计划完成程度为多少?
答案1:
\[ \begin{aligned} \text { 成本降低率计划完成相对数 }=\frac{1-7.6 \%}{1-6 \%} \times 100 \%=98.29 \% \end{aligned} \]
答案2:本题也可换算成绝对数计算。
\[ \begin{array}{ccc} \text { 计划: } & -6 \% & \sim \text { 394. 8元/吨 } & {[(1-6 \%) \times 420]} \\ \text { 实际: } & -7.6 \% & \sim 388.08 \text { 元 } / \text { 吨 } & {[(1-7.6 \%) \times 420]} \end{array} \]
\[ \begin{aligned} \text { 成本降低率计划完成相对数 }=\frac{388.08}{394.8} \times 100 \%=98.29 \% \end{aligned} \]
计划完成相对指标:中长期计划
中长期计划执行情况检查:
- 水平法:根据计划末期实际达到水平与计划规定末期应达到水平对比,来确定是否完成全期计划。
\[ \begin{aligned} \text { 计划完成程度 }=\frac{\text { 计划末期实际达到水平 }}{\text { 计划末期应达到水平 }} \times 100 \% \end{aligned} \]
- 累计法:整个计划期间实际完成的累计数与全期计划数对比,来确定是否完成全期计划。
\[ \begin{aligned} \text { 计划完成程度 }=\frac{\text { 实际全期累计完成数 }}{\text { 计划全期累计数 }} \times 100 \% \end{aligned} \]
计划完成相对指标:提前完成时间
计算提前完成计划时间
对于水平法:在整个计划期内,只要连续12个月实际完成数达到计划末期水平,就算完成计划,则往后的时间即为提前完成计划的时间。
对于累计法:从计划初开始至某一时期止,实际完成累计数达到计划规定的累计数,就算完成计划,而往后的时间即为提前完成计划的时间。
(示例1)中长期计划提前期:水平法
例题:某地区按五年计划规定,最后一年国民生产总值应达到520亿元,实际国民生产总值如下表所示:
问题:请用水平法计算提前多长时间完成计划任务?
解答:根据水平法,只需要连续一个自然年(12个月)达到年计划产值,就算完成任务 \(^\ast\) 。通过观察和计算可以发现:第4年下半年+第5年第1季度+第5年第2季度= \((220+140+160)=520\) 。因此提前了两个季度完成520亿元的年度计划任务。
(案例)地区生产总值
(示例2)中长期计划提前期:水平法1(例题提问)
例题提问
某产品计划年度任务产量为56万吨,实际第五年产量63万吨,现假定第4年、第5年各月完成情况如下:
问题:请用水平法计算提前多少天完成计划任务?
(示例2)中长期计划提前期:水平法2(解答思路)
解答思路
根据水平法,只需要连续一个自然年(12个月)达到年计划产量,就算完成任务产量56万吨 \(^\ast\) 。容易计算得到,12个月滚动累加的结果如下表。
(示例2)中长期计划提前期:水平法3(分析求解)
分析求解
根据上述滚动12月累加,可以发现正好生产56万吨的时间应是:“第4年8月第31-X天到第5年8月第(31-X)天”的连续12个月。如下图所示。

(示例2)中长期计划提前期:水平法4(计算结果)

假定月内产量是均匀分布的,则有如下等式:
\[ \begin{aligned} \frac{4}{31} X+51+\frac{6}{31}\left(31-X \right) &=56 \\ X &= 15.5 \end{aligned} \]
也即:提前4个月又15天半完成五年计划的年度目标计划任务。
(示例3)中长期计划提前期:累计法
例题:某地区按五年计划规定,固定资产投入额为30亿元,实际投入情况如下表所示:
问题:请用累计法计算提前多长时间完成计划任务?
解答思路
根据累计法,从期初开始累计达到计划投入额30亿元,即为达成目标,剩余日期即为提前期。通过观察和计算可以发现:第1年至第4年实际投入额累加= \((6+7+8+9)=30\) 。因此完成计划时间为第4年,也即意味着提前1年完成五年计划规定任务。
结构相对指标:概念和特征
结构相对指标:反映某个总体内,有机构成的组成部分在系统中的地位,具体通过同一总体中部分数值与总体数值之比来衡量。
指标特征:
子分母不能颠倒
结构相对指标直接相加之和等于1
计算公式:
\[ 结构相对指标 = \frac{总体部分数值}{总体全部数值}\times 100\% \]
结构相对指标:作用
结构相对指标的作用主要体现在:
可以反映总体内部结构的特征
不同时期相对数的比较,可以看出变化过程及趋势
能反映对忍耐力、物力、财力的利用程度及经营效果的好坏
结构相对数在平均数计算中的应用:用于分析加权算术平均数指标的大小极其变动的原因 \(^\ast\) 。
(示例)结构相对指标:企业实收资本
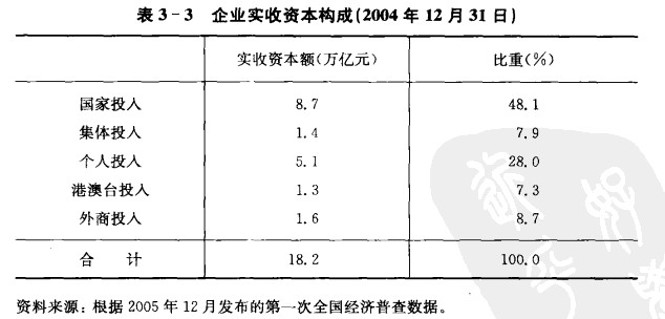
(示例)结构相对指标:国内生产总值构成
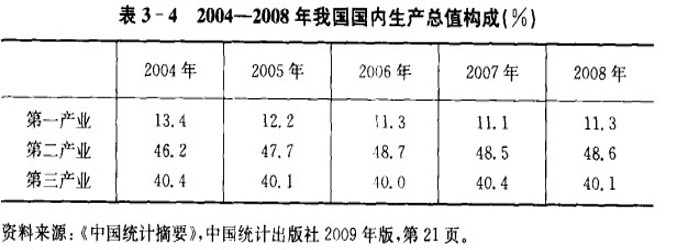
比例相对指标:概念和特征
比例相对指标:反映某个总体内,某一组成部分与其他组成部分的地位对比关系,具体通过同一总体中各组成部分之间数值之比来衡量。
指标特征:分子分母可以颠倒
计算公式:
\[ 比例相对指标 = \frac{总体某一部分数值}{总体中另一部分数值}\times 100\% \]
比例相对指标:类型与形式
比例相对指标有两类表现形式:
- 两两作比:抽象基数为1、10、100或1000。
示例:我国2000年第五次人口普查结果,男女性别比例为106.74:100,这说明以女性为100,男性人口是女性人口数的106.74倍。2009年我国出生人口性别比为119.45,比2008年下降了1.11。
- 多部作比:各部分的百分数连比得比例相对数。
示例:2009年上海GDP抽象化为100,第一产业、第二产业、第三产业的比例为:0.7︰39.9︰59.4
(示例)比例相对指标
示例:某学院两个学科的人数统计表如下:
计算比例相对指标:
此处,我们假定两个学科的地位是平等无差异的的。
学科人数比(经济学=100): \(R_{r1} = \frac{1108}{781}\times 100\%=\) 142.1
学科人数比(管理学=100): \(R_{r2} = \frac{781}{1108}\times 100\%=\) 70.4
比较相对指标:概念和特征
比较相对指标:反映同类现象不同条件下(不同时间/空间之间)的指标对比。
计算公式:
\[ 比较相对指标 = \frac{某一条件下某类指标数值}{另一条件下同类指标数值}\times 100\% \]
指标特征:
比较基数(标准)是一般对象,分子与分母的位置可以互换。
比较基数(标准)具有典型化,分子与分母的位置不能互换。
例如:单位产品的质量、成本、单耗等技术经济指标。
(示例)比较相对指标:两个示例(可互换)
示例1:2015年甲、乙两地国民生产总值分别为50亿元和60亿元。请计算比较相对指标,对比分析两地情况?
计算比较相对指标:
此处,假定以甲乙两地的地位是无差异的,则分子分母可互换。
甲地国民收入是乙地的1.2倍: \(R_{c1} = \frac{60}{50} =1.2\) 。
乙地国民收入是甲地的83.3%: \(R_{c1} = \frac{50}{60}\times 100\% =83.3\%\) 。
(示例)比较相对指标:两个示例(不宜换)
示例2:某年有甲、乙两企业同时生产一种性能相同的产品,甲企业工人劳动生产率为19,307元,乙企业为27,994元。请计算比较相对指标,对比分析两企业情况?
计算比较相对指标:
此处,假定以表现“优秀”的企业为参考系,则分子分母不宜互换。
两企业劳动生产率比较相对数: \(R_{c2} = \frac{19307}{27994} \times 100\% =\) 69.0%。
表明甲企业劳动生产率比乙企业低31%。
强度相对指标:概念和作用
强度相对指标:两个性质不同但又相互联系的总量指标的对比。
计算公式:
\[ 强度相对指标 = \frac{某一总体指标数值}{另一有联系的总体指标数值}\times 100\% \] 指标作用:
说明一个国家、地区、部门的经济实力或为社会服务的能力。
反映和考核社会经济效益。如流通费用率、资金利润率等。
为贬值计划和长远规划提供参考依据。
强度相对指标:表现形式
强度相对数的主要有两种表现形式:
有名数形式:一般用复名数表示,如人/平方公里、部/百人
无名数形式:一般用百分(%)或千分数( \(\unicode{x2030}\) )表示,如流通费用率(%)、人口增长率( \(\unicode{x2030}\) )。
有些强度相对指标有正指标/逆指标两种计算方法。
分子分母可以交换,含义相同,只是表达习惯上的差异。
与术语词义一致的、或广为使用的则称为“正指标”,反之则称为“逆指标”。
(示例)计算强度相对指标
示例:某城市人口100万人,有零售商业机构5000个。请计算强度相对指标,分析商业网点密度情况。
解答:可以分别计算出商业网店密度的正指标和逆指标。
商业网店密度的正指标: \(R_{d1}=\frac{5000个}{1000000人}=5\) (个/千人)
商业网店密度的逆指标: \(R_{d1}=\frac{1000000人}{5000个}=200\) (人/个)
动态相对指标:概念和特征
动态相对指标:同类现象同一空间不同时间指标的对比。
计算公式:其中一个指标为“发展水平”。
\[ 动态相对指标 = \frac{某一现象报告期数值}{同一现象基期数值}\times 100\% \] 指标特征:分子分母不能颠倒。
(示例)计算动态相对指标
案例:某地2014年和2015年国民生产总值分别为56 亿元和60亿元。请计算动态相对指标,分析其经济发展状况。
解答:我们可以计算其国民生产总值的发展水平相对指标。
\[ R_p= \frac{60}{56}\times 100\%=107\% \]
4.3 集中趋势的度量
位置平均数
数值平均数
内容导航
集中趋势:概述
集中趋势(central tendency):一组数据向其中心值靠拢的倾向和程度。
内涵:
测度集中趋势就是寻找数据水平的代表值或中心值。
不同类型的数据用不同的集中趋势测度值。
低层次数据的测度值适用于高层次的测量数据*,但高层次数据的测度值并不适用于低层次的测量数据。
众数:概念和特征
众数(Mode):一组数据中出现次数最多的变量值,一般记为 \(M_o\) 。
众数的特征:
适合于数据量较多时使用。
不受极端值的影响。
一组数据可能没有众数或有几个众数。
主要用于分类数据,也可用于顺序数据和数值型数据。
(示例)众数的表现形式:河流长度(案例说明)
案例说明:对三个地区各6条河流的长度进行测量,得到如下的数据表:
| river | area1 | area2 | area3 |
|---|---|---|---|
| R1 | 10 | 6 | 25 |
| R2 | 5 | 5 | 28 |
| R3 | 9 | 9 | 28 |
| R4 | 12 | 8 | 36 |
| R5 | 6 | 5 | 42 |
| R6 | 8 | 5 | 42 |
(示例)众数的表现形式:河流长度(无众数)
a.频次表:对于地区1(area1)的6条河流,我们可以统计得到不同长度(length)下的河流数(n),得到如下的频次数据表:
| area | length | n |
|---|---|---|
| area1 | 5 | 1 |
| area1 | 6 | 1 |
| area1 | 8 | 1 |
| area1 | 9 | 1 |
| area1 | 10 | 1 |
| area1 | 12 | 1 |
b.示意图:因为每条河流都有不同的长度,出现频次全部等于1。因此,地区1的河流长度无众数。
(示例)众数的表现形式:河流长度(单众数)
a.频次表:对于地区2(area2)的6条河流,我们可以统计得到不同长度(length)下的河流数(n),得到如下的频次数据表:
| area | length | n |
|---|---|---|
| area2 | 5 | 3 |
| area2 | 6 | 1 |
| area2 | 8 | 1 |
| area2 | 9 | 1 |
b.示意图:因为长度为5(百km)出现频次最多(3次)。因此,地区2的河流长度有1个众数,且 \(M_{o1}=5\) 。
(示例)众数的表现形式:河流长度(多众数)
a.频次表:对于地区3(area3)的6条河流,我们可以统计得到不同长度(length)下的河流数(n),得到如下的频次数据表:
| area | length | n |
|---|---|---|
| area3 | 25 | 1 |
| area3 | 28 | 2 |
| area3 | 36 | 1 |
| area3 | 42 | 2 |
b.示意图:因为长度为28(百km)和42(百km)都出现频次最多(2次)。因此,地区3的河流长度有2个众数,且 \(M_{o1}=28;M_{o1}=42\) 。示意简图如下1:
众数计算:概览
A.对于单项式分配数列:观察法,识别频次最多的组。
B.对于组距式分配数列:由最多次数来确定众数所在组;利用比例插值法推算众数的近似值。
- 下限插值公式:
\[ \begin{aligned} M_{0}=X_{L}+\frac{\Delta_{1}}{\Delta_{1}+\Delta_{2}} \cdot d \end{aligned} \]
- 上限插值公式:
\[ \begin{aligned} M_{0}=X_{U} - \frac{\Delta_{2}}{\Delta_{1}+\Delta_{2}} \cdot d \end{aligned} \]
其中:
\(X_{L}\) 表示组下限(Lower limits); \(X_{U}\) 表示组上限(Upper limits);
\(\Delta_{1}\) 表示众数组与前一组的频次之差; \(\Delta_{2}\) 表示众数组与后一组的频次之差;
\(d\) 表示众数组的组距(width)。
众数计算:组距式数列(图形示意)
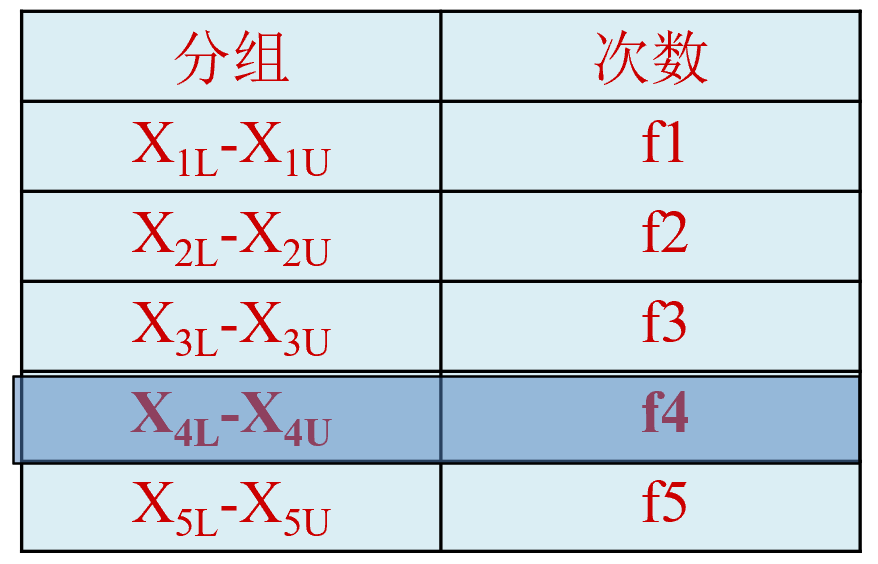
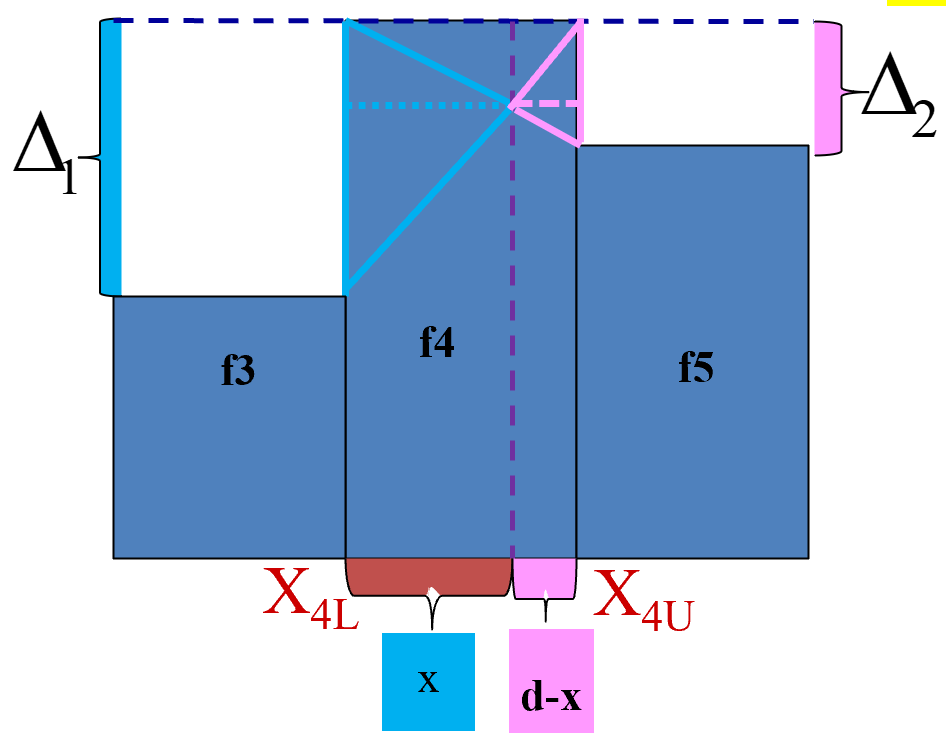
众数计算:组距式数列(上限公式)


给定上限值,则采用上限插值公式:
\[ \begin{aligned} \Rightarrow \frac{x}{d-x}=\frac{\Delta_{1}}{\Delta_{2}} \Rightarrow x=\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \Rightarrow \mathrm{M}_{0}=X_{4 U}-(d-x)=X_{4 U}-\frac{\Delta_{2} \cdot d}{\Delta_{1}+\Delta_{2}} \end{aligned} \]
众数计算:组距式数列(下限公式)


给定下限值,则采用下限插值公式:
\[ \begin{aligned} \Rightarrow \frac{x}{d-x}=\frac{\Delta_{1}}{\Delta_{2}} \Rightarrow x=\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \Rightarrow \mathrm{M}_{0}=\mathrm{X}_{4 L}+\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \end{aligned} \]
众数计算:组距式数列(图形示意)


众数计算:组距式数列(上限公式)


给定上限值,则采用上限插值公式:
\[ \begin{aligned} \Rightarrow \frac{x}{d-x}=\frac{\Delta_{1}}{\Delta_{2}} \Rightarrow x=\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \Rightarrow \mathrm{M}_{0}=X_{4 U}-(d-x)=X_{4 U}-\frac{\Delta_{2} \cdot d}{\Delta_{1}+\Delta_{2}} \end{aligned} \]
众数计算:组距式数列(下限公式)


给定下限值,则采用下限插值公式:
\[ \begin{aligned} \Rightarrow \frac{x}{d-x}=\frac{\Delta_{1}}{\Delta_{2}} \Rightarrow x=\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \Rightarrow \mathrm{M}_{0}=\mathrm{X}_{4 L}+\frac{\Delta_{1} \cdot d}{\Delta_{1}+\Delta_{2}} \end{aligned} \]
(示例):众数计算(单项式数列)1
案例说明:某饮料便利店一天内不同品牌饮料的销售情况如下表所示。请计算众数是什么?
解答:这里的变量为“饮料品牌”,这是个分类变量(nominal),不同类型的饮料就是变量值。所调查的50人中,购买碳酸饮料的人数最多(15人),占总被调查人数的30%,因此众数为“可口可乐”这一品牌,即: \(M_0=\) 碳酸饮料。
(示例):众数计算(单项式数列)2
案例说明:甲城市300家庭对住房状况进行评价,数据统计情况如下表所示。请计算众数是什么?
解答:这里的变量为“住房状况评价”,这是个顺序变量(orderial),不同类型的饮料就是变量值。所调查的300人中,甲城市中对住房表示不满意的户数最多(108户),因此众数为“不满意”这一类别,即: \(M_0=\) 碳酸饮料。
(示例):众数计算(组距式数列)
案例说明:200人的收入水平调查分组数据见右表,请计算收入的众数是多少?
解题思路:先观察众数在第三组(“1500-2000”)。再利用插值公式计算。
\[ \begin{aligned} \text { 下限公式: } M_{o}&=1500+\frac{70-37}{(70-37)+(70-43)} \times 500=1775(\text { 元 }) \end{aligned} \]
\[ \begin{aligned} \text { 上限公式: } M_{o}&=2000-\frac{70-43}{(70-37)+(70-43)} \times 500=1775(\text { 元 }) \end{aligned} \]
众数特征:总结
下面对众数及其计算做一个小结:
众数是一个位置平均数,它只考虑总体分布中最频繁出现的变量值,而不受各单位标志值的影响,从而增强了对变量数列一般水平的代表性。不受极端值和开口组数列的影响。
众数是一个不容易确定的平均指标,当分布数列没有明显的集中趋势而趋均匀分布时,则无众数可言;当变量数列是不等距分组时,众数的位置也不好确定。
在组距式数列的插值近似计算中,众数的确定受相邻两个组频次的影响。
若 \(f_{m-1}=f_{m+1}\) ,则众数取值等于众数组的组中值。
若 \(f_{m-1} < f_{m+1}\) ,则众数取值大于众数组的组中值,从而接近于组上限值。
若 \(f_{m-1} > f_{m+1}\) ,则众数取值小于众数组的组中值,从而接近于组下限值。
中位数:概念和特征
中位数(median) :排序后处于中间位置上的变量值,一般记为 \(M_e\) 。
中位数的特征:
不受极端值的影响
主要用于顺序数据,也可用数值型数据,但不能用于分类数据。
各变量值与中位数的离差绝对值之和最小,即:
\[ \begin{aligned} \sum_{i=1}^{n}\left|X_{i}-M_{\mathrm{e}}\right|=\min \end{aligned} \]
中位数计算:概览
情形1:未分组资料确定中位数;
a.先排序。b.再确定中位数所在位置。c.再确定中位数。
情形2:分组资料确定中位数;
- 情形2-1:单项式分组数列计算中位数数
a.计算累积百分比,确定中位数所在组。b.确定中位数。
- 情形2-2:组距式分组数列计算中位数数
a.计算累积百分比,确定中位数所在组。b.(利用插值公式近似)确定中位数。
中位数计算:未分组资料
第一步:中位数的位置 \(p\) 的确定。
\[ \begin{aligned} p = \left\{ \begin{array}{ll} \frac{n+1}{2} & (n \text {为奇数}) \\ \frac{n}{2}, \frac{n}{2}+1 & (n \text {为偶数}) \end{array}\right. \end{aligned} \]
第二步:数值的确定。
\[ \begin{aligned} M_{e}=\left\{\begin{array}{ll} X_{\left(\frac{n+1}{2}\right)} & (n \text {为奇数}) \\ \frac{1}{2}\left (X_{\left(\frac{n}{2}\right)}+X_{\left(\frac{n}{2}+1\right)}\right) & (n \text {为偶数 }) \end{array}\right. \end{aligned} \]
(示例):未分组数据计算中位数
案例说明:有7名工人生成同种产品,日产量分别为:
W1 W2 W3 W4 W5 W6 W7
10 21 12 15 14 19 17 解题过程:我们注意到数据样本量 \(n=\) 7,为奇数。
- 对原始数据进行排序(由小到大):
W1 W3 W5 W4 W7 W6 W2
10 12 14 15 17 19 21 确定中位数的位置 \(p = \frac{7+1}{2}=\) 4。
因此得到中位数为 \(m_e=\) 15(件)。
(示例):未分组数据计算中位数
案例说明:继续前面案例数据,假设增加另1名工人的日产量数据:
W1 W2 W3 W4 W5 W6 W7 W8
22 10 21 12 15 14 19 17 解题过程:我们注意到数据样本量 \(n=\) 8,为偶数。
- 对原始数据进行排序(由小到大):
W2 W4 W6 W5 W8 W7 W3 W1
10 12 14 15 17 19 21 22 确定中位数的位置 \(p = \frac{8+1}{2}=\) 4.5。
因此得到中位数为 \(m_e=\frac{15+17}{2}\) 16(件)。
中位数计算:单项式分组数列
主要计算步骤:
第一步:先按组顺序,计算累计分布次数(较大制或较小制)。
第二步:再确定中位数所在的位置: \(p= \frac{\sum{f_i}}{2}\) 。
第三步:根据计算的位置,找到该位置所在组,并确定中位数 \(M_e\) 。
示例:单项式数列计算中位数(案例说明)
案例说明:甲城市300家庭对住房状况进行评价,评价(satisfication)采用五分制里克特量表,人数分布的统计情况如下表所示。请计算中位数是什么?
示例:单项式数列计算中位数(分析过程)
解题思路:
首先计算较小累计频数(cumsum *)(见左)。
然后计算中位数的位置 \(p= \frac{300+1}{2}=150.5\)
根据累计频数观察得到中位数为: \(M_e=\) “一般”。
(示例)单项式数列计算中位数:案例说明
案例说明:某工厂共有105个工人,全体工人的日产量( \(X\) ,件/日)经过分组统计后( \(G1 \sim G6\) ),各组工人人数( \(n\) )的数据如下表所示。请计算中位数是什么?
(示例)单项式数列计算中位数:分析过程
解题思路:
首先计算并得到较小累计频数(cumsum*)(见左)。
然后计算中位数的位置 \(p= \frac{(\sum{f_i}+1)}{2}=\frac{105+1}{2}=53\) ,根据累计频数观察得到中位数位置为 \(p =\) 第4组(日产量=8)。
根据中位数所在位置,得到中位数为: \(M_e=8\) (件)。
中位数计算:组距式分组数列
主要计算步骤:
第一步:先按组顺序,计算累计分布次数(较大制或较小制)。
第二步:再确定中位数所在的位置: \(p= \frac{\sum{f_i}}{2}\) 。
第三步:根据计算的位置,找到该位置所在组,初步确定中位数 \(M_{e1}\) 。
第四步:利用合适的插值公式,近似计算得到更为“精确”的中位数数值 \(M_{e2}\) 。
(演示)中位数计算:较小制下限插值公式
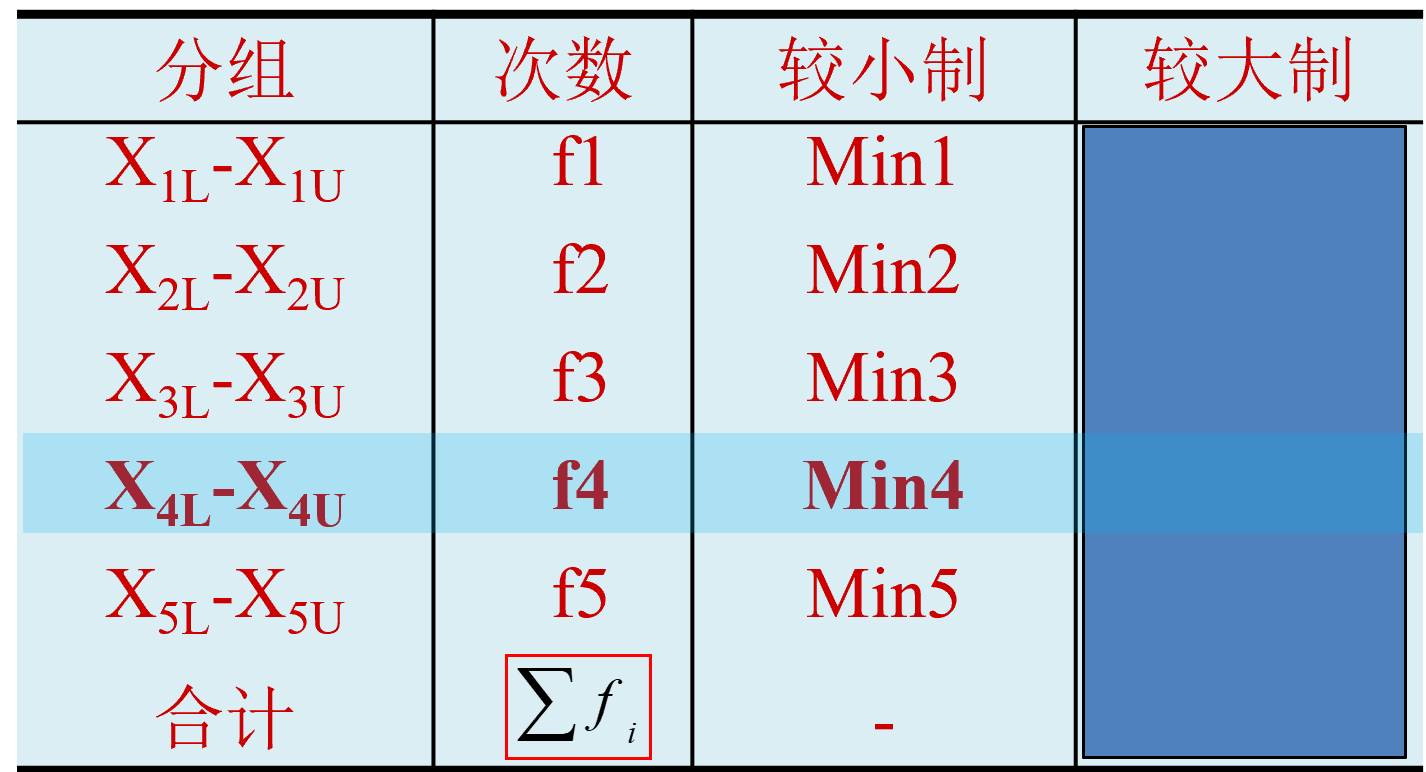
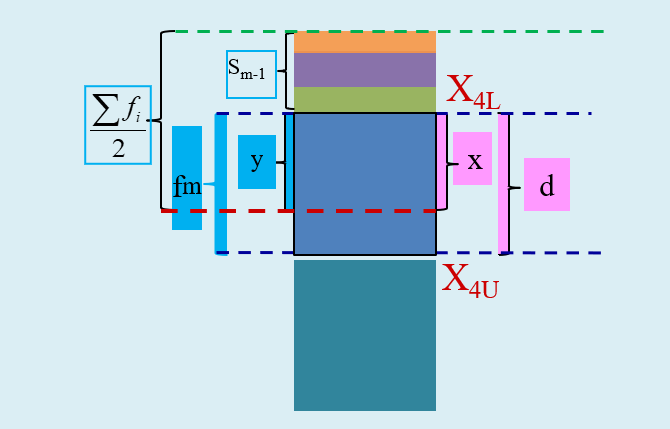
较小制且给定下限值时的相关定义:
\(X_{L}\) 表示组下限(Lower limits); \(X_{U}\) 表示组上限(Upper limits)。
\(d\) 表示众数组的组距(width); \(x\) 表示待求解的组距部分。
\(f_{m}\) 表示中位数组的频次, \(S_{m-1}\) 表示中位数所在组的前一组的较小累计频次; \(y\) 表示与 \(x\) 宽度相对应频次。
(演示)中位数计算:较小制下限插值公式


较小制给定下限值时,则采用较小制下限公式 \((Min, Lower)\) :
\[ \begin{aligned} \frac{x}{d} = \frac{\left(\sum{f_i}/{2}-S_{m-1}\right)}{f_m} \quad \Rightarrow \quad M_{eL}=X_{L}+ x \\ M_{eL}= X_{L}+\frac{\frac{\sum f}{2}-S_{m-1}}{f_{m}} \cdot d \end{aligned} \]
(演示)中位数计算:较小制上限插值公式

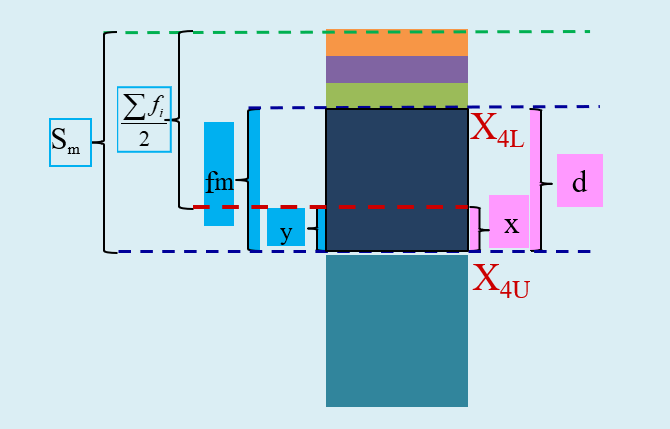
较小制且给定上限值时的相关定义:
\(X_{L}\) 表示组下限(Lower limits); \(X_{U}\) 表示组上限(Upper limits)。
\(d\) 表示众数组的组距(width); \(x\) 表示待求解的组距部分。
\(f_{m}\) 表示中位数组的频次, \(S_{m}\) 表示中位数所在组的较小累计频次; \(y\) 表示与 \(x\) 宽度相对应频次。
(演示)中位数计算:较小制上限插值公式


较小制给定下限值时,则采用较小制上限公式 \((Min, Upper)\) :
\[ \begin{aligned} \frac{x}{d} = \frac{\left(S_{m} - \sum{f_i}/{2}\right)}{f_m} \quad \Rightarrow \quad M_{eU}=X_{U} -x \\ M_{eU}=X_{U} -\frac{S_{m} - \frac{\sum f}{2}}{f_{m}} \cdot d \end{aligned} \]
(演示)中位数计算:较大制下限插值公式
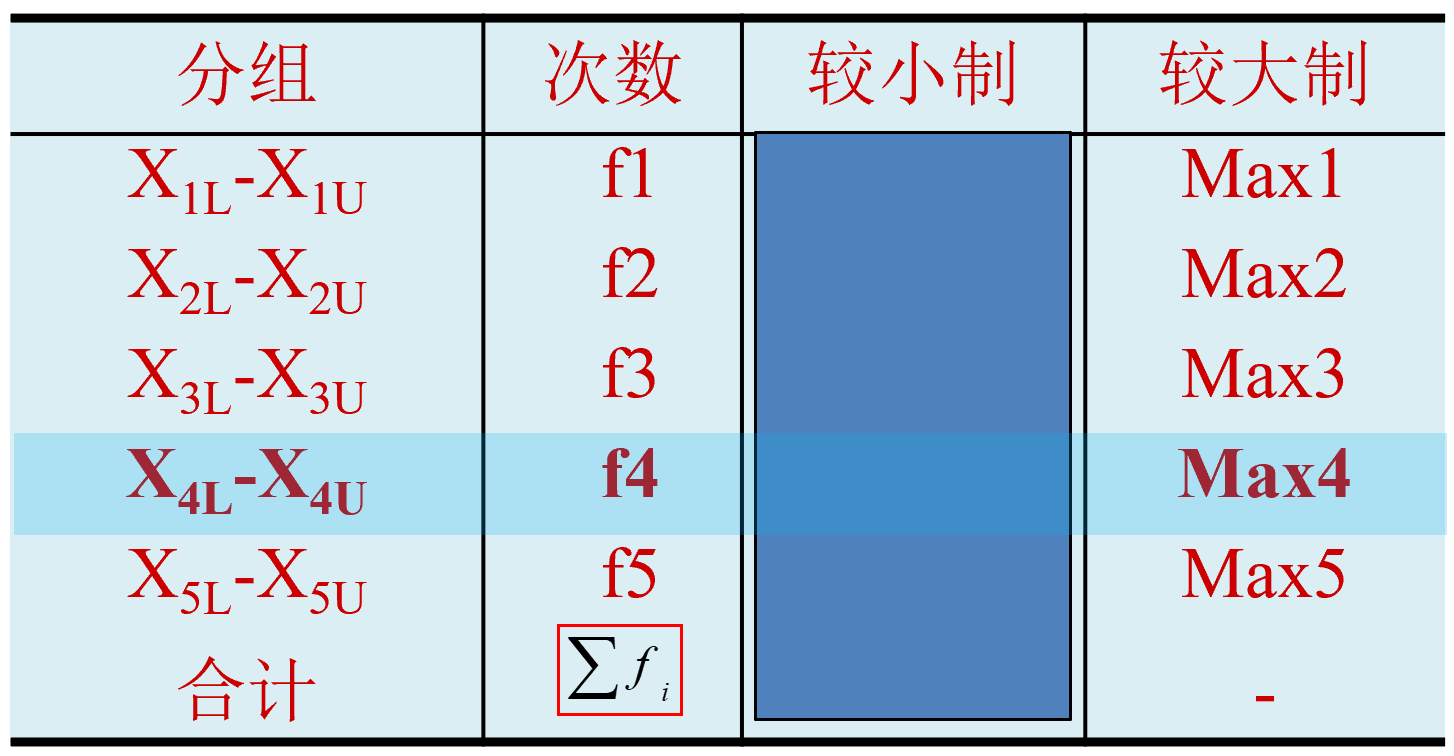
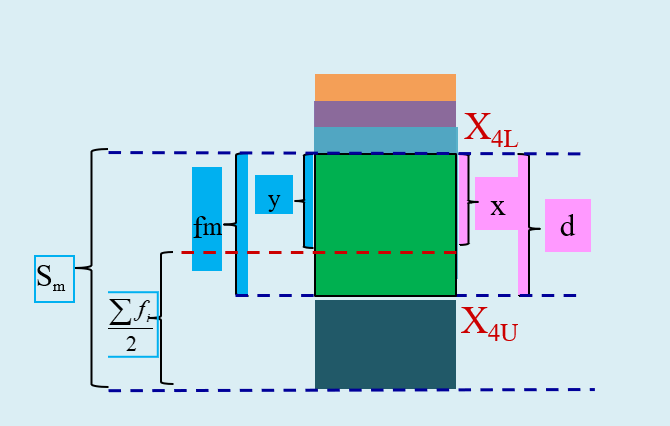
较大制且给定下限值时的相关定义:
\(X_{L}\) 表示组下限(Lower limits); \(X_{U}\) 表示组上限(Upper limits)。
\(d\) 表示众数组的组距(width); \(x\) 表示待求解的组距部分。
\(f_{m}\) 表示中位数组的频次, \(S_{m}\) 表示中位数所在组的较大累计频次; \(y\) 表示与 \(x\) 宽度相对应频次。
(演示)中位数计算:较大制下限插值公式


较大制给定下限值时,则采用较大制下限公式 \((Max, Lower)\) :
\[ \begin{aligned} \frac{x}{d} = \frac{\left(S_{m}- \sum{f_i}/{2}\right)}{f_m} \quad \Rightarrow \quad M_{eL}=X_{L}+ x \\ M_{eL}= X_{L}+\frac{S_{m} -\frac{\sum f}{2}}{f_{m}} \cdot d \end{aligned} \]
(演示)中位数计算:较大制上限插值公式

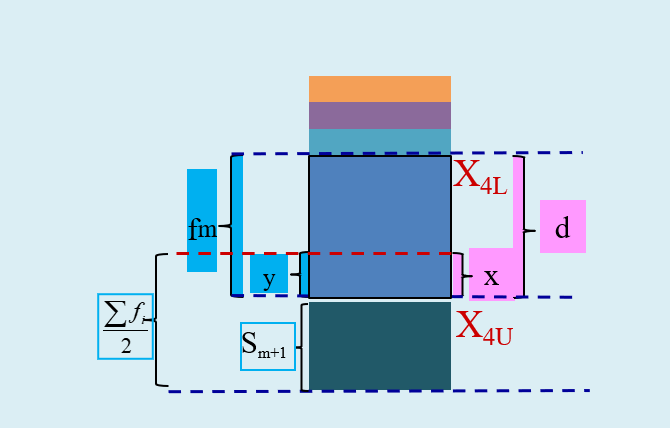
较大制且给定上限值时的相关定义:
\(X_{L}\) 表示组下限(Lower limits); \(X_{U}\) 表示组上限(Upper limits)。
\(d\) 表示众数组的组距(width); \(x\) 表示待求解的组距部分。
\(f_{m}\) 表示中位数组的频次, \(S_{m+1}\) 表示中位数所在组的后一组的较小累计频次; \(y\) 表示与 \(x\) 宽度相对应频次。
(演示)中位数计算:较大制上限插值公式


较大制给定上限值时,则采用较大制上限公式 \((Max, Upper)\) :
\[ \begin{aligned} \frac{x}{d} = \frac{\left( \sum{f_i}/{2} -S_{m+1} \right)}{f_m} \quad \Rightarrow \quad M_{eU}=X_{U} -x \\ M_{eU}=X_{U} -\frac{\frac{\sum f}{2} -S_{m+1} }{f_{m}} \cdot d \end{aligned} \]
(示例)组距式分配数列中位数计算:案例说明
案例说明:某工厂共有164个工人,全体工人的日产量(X)经过分组统计后( \(G1 \sim G7\) ),各组工人人数(n)的分布数据如下表所示。请计算中位数是什么?
| groups | X | n |
|---|---|---|
| G1 | 60Kg以下 | | 0 | |
| G2 | 60-70Kg | 19 |
| G3 | 70-80Kg | 50 |
| G4 | 80-90Kg | 36 |
| G5 | 90-100Kg | 27 |
| G6 | 100-110Kg | 14 |
| G7 | 110Kg以上 | | 8 | |
| Total | - | 164 |
(示例)较小制情形下中位数计算:粗略结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 10 | |
| G2 | 60-70Kg | 19 | 29 |
| G3 | 70-80Kg | 50 | 79 |
| G4 | 80-90Kg | 36 | 115 |
| G5 | 90-100Kg | 27 | 142 |
| G6 | 100-110Kg | 14 | 156 |
| G7 | 110Kg以上 | | 8 | | 164 | |
| Total | - | 164 | NA |
解题思路:
首先计算并得到较小制累计频次表*(cumsum)(见左)。
然后计算中位数的位置 \(p= \frac{(\sum{f_i})}{2}=\frac{164}{2}=82\) ,根据累计频数观察得到中位数位置为 \(p =4\) , 也即第G4组(日产量80-90Kg)。
根据中位数所在位置,初步得到中位数为: \(M_e=\) “80-90Kg”。
(示例)较小制情形下中位数计算:插值公式结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 10 | |
| G2 | 60-70Kg | 19 | 29 |
| G3 | 70-80Kg | 50 | 79 |
| G4 | 80-90Kg | 36 | 115 |
| G5 | 90-100Kg | 27 | 142 |
| G6 | 100-110Kg | 14 | 156 |
| G7 | 110Kg以上 | | 8 | | 164 | |
| Total | - | 164 | NA |
- 较小制下限插值公式计算结果:
\[ \begin{aligned} M_{eL}&=X_{L}+\frac{\frac{\sum f}{2}-S_{m-1}}{f_{m}} \cdot d \\ & =80+\frac{82-79}{36} * 10 \\ & =80.8333 \end{aligned} \]
- 较小制上限插值公式计算结果:
\[ \begin{aligned} M_{eU} &=X_{U}-\frac{S_{m}-\frac{\sum f}{2}}{f_{m}} \cdot d \\ &=90-\frac{115-82}{36} * 10 \\ &=80.8333 \end{aligned} \]
(示例)较大制情形下中位数计算:粗略结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 164 | |
| G2 | 60-70Kg | 19 | 154 |
| G3 | 70-80Kg | 50 | 135 |
| G4 | 80-90Kg | 36 | 85 |
| G5 | 90-100Kg | 27 | 49 |
| G6 | 100-110Kg | 14 | 22 |
| G7 | 110Kg以上 | | 8 | | 8 | |
| Total | - | 164 | NA |
解题思路:
首先计算并得到较大制累计频次表*(cumsum)(见左)。
然后计算中位数的位置 \(p= \frac{(\sum{f_i})}{2}=\frac{164}{2}=82\) ,根据累计频数观察得到中位数位置为 \(p =4\) , 也即第G4组(日产量80-90Kg)。
根据中位数所在位置,初步得到中位数为: \(M_e=\) “80-90Kg”。
(示例)较大制情形下中位数计算:插值公式结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 164 | |
| G2 | 60-70Kg | 19 | 154 |
| G3 | 70-80Kg | 50 | 135 |
| G4 | 80-90Kg | 36 | 85 |
| G5 | 90-100Kg | 27 | 49 |
| G6 | 100-110Kg | 14 | 22 |
| G7 | 110Kg以上 | | 8 | | 8 | |
| Total | - | 164 | NA |
- 较大制下限插值公式计算结果:
\[ \begin{aligned} M_{eU}&=X_{L}+\frac{S_{m} -\frac{\sum f}{2}}{f_{m}} \cdot d \\ & =80+\frac{85-82}{36} * 10 \\ & =80.8333 \end{aligned} \]
- 较大制上限插值公式计算结果:
\[ \begin{aligned} M_{eU} &=X_{U}-\frac{\frac{\sum f}{2} - S_{m+1}}{f_{m}} \cdot d \\ &=90-\frac{82-49}{36} * 10 \\ &=80.8333 \end{aligned} \]
中位数特征:总结1
中位数不受极端值及开口组的影响,具有稳健性。
各单位标志值与中位数离差的绝对值之和是个最小值。
\[ \begin{aligned} \sum\left|X-M_{e}\right|=\min ;\quad or \quad \sum{\left|X-M_{e}\right|f_i}=\min \end{aligned} \]
- 对某些不具有数学特点或不能用数字测定的现象,可用中位数求其一般水平。
中位数特征:总结2
中位数数值 \(M_e\) 受到中位数所在组的较小累计频次 \(S_{(m,Min)}\) 及较大累计频次 \(S_{(m,Max)}\) 数值大小的共同影响。
- 若 \(S_{(m,Min)} = S_{(m,Max)}\) ,则中位数所在组的组中值等于插值近似计算值,也即:
\[ M_e = M_{eL}= M_{eU}= \frac{X_U +X_L}{2} \]
- 若 \(S_{(m,Min)} < S_{(m,Max)}\) ,则插值近似计算值更加接近于中位数所在组的组上限值,也即:
\[ M_e = M_{eL}= M_{eU} \ll X_U \]
- 若 \(S_{(m,Min)} > S_{(m,Max)}\) ,则插值近似计算值更加接近于中位数所在组的组下限值,也即:
\[ M_e = M_{eL}= M_{eU} \gg X_L \]
四分位数:概念和特征
四分位数(Quartile):排序后处于25%和75%位置上的值,包括四分之一位数( \(Q_1\) )和四分之三位数( \(Q_3\) )。
四分位数的特征:
- 不受极端值的影响。
四分位数:计算方法
情形1:未分组资料确定分位数;
a.先排序。b.再确定1/4和3/4分割点位置。c.再确定两个分位数 \(Q_1\) 和 \(Q_3\) 。
情形2:分组资料确定分位数;
- 情形2-1:单项式分组数列计算中位数数
a.确定1/4和3/4分割点位置。b.再确定两个分位数 \(Q_1\) 和 \(Q_3\) 。
- 情形2-2:组距式分组数列计算分位数
a.计算累积频次,确定1/4和3/4分割点位置。b.初步确定两个分位数(所在组) \(Q_1\) 和 \(Q_3\) 。c.最后(利用插值公式近似)相对“精确地”估算两个分位数 \(Q_1\) 和 \(Q_3\) 。
四分位数计算:未分组资料
未分组资料的四分位数计算,主要步骤如下:
第一步:将总体各单位的标志值按大小顺序排列/或分组排序。
第二步:确定1/4和3/4分割点位置 \(p_1\) 和 \(p_3\) 。
\[ \begin{aligned} p_1 = \frac{n+1}{4} ; \quad p_3 = \frac{3(n+1)}{4} \end{aligned} \]
第三步:确定两个分位数 \(Q_1\) 和 \(Q_3\) 。
若 \(\frac{n+1}{4}\) 为整数,则 \(p_1\) 和 \(p_3\) 分割点位置对应的分组标志值则分别为对应的四分位数 \(Q_1\) 和 \(Q_3\) 。
若 \(\frac{n+1}{4}\) 不是整数,则 要用分割点位置对应的两个相邻组近似计算(加权算术平均数)相应的分位数 \(Q_1\) 和 \(Q_3\) 。
(示例):未分组数据计算分位数
案例说明:有11名工人生成同种产品,日产量分别为:
W1 W2 W3 W4 W5 W6 W7 W8 W9 W10 W11
2 7 5 6 8 12 9 10 16 15 20 解题过程:我们注意到数据样本量 \((n+1)/4=\) 3,为整数。
- 对原始数据进行排序(由小到大):
W1 W3 W4 W2 W5 W7 W8 W6 W10 W9 W11
2 5 6 7 8 9 10 12 15 16 20 再确定分位数的位置,其中且 分割点为: \(p_1 =(n+1)/4= (11+1)/4= 3\) 和 \(p_3 =3*(n+1)/4=3*(11+1)/4= 9\) 。
因此得到分位数分别为 \(Q_1=\) 6(件)和 \(Q_3=\) 15(件)。
(示例):未分组数据计算中位数
案例说明:继续前面案例数据,假设增加另1名工人的日产量数据:
W1 W2 W3 W4 W5 W6 W7 W8 W9 W10 W11 W12
22 2 7 5 6 8 12 9 10 16 15 20 解题过程:我们注意到数据样本量 \((n+1)/4=\) 3,不是整数。
- 对原始数据进行排序(由小到大):
W2 W4 W5 W3 W6 W8 W9 W7 W11 W10 W12 W1
2 5 6 7 8 9 10 12 15 16 20 22 再确定分位数的位置,其中且 分割点为: \(p_1 =(n+1)/4= (11+1)/4= 3.25\) 和 \(p_3 =3*(n+1)/4=3*(11+1)/4= 9.75\) 。
得到分位数分别为 \(Q_1=(6+7)/2=6.5\) (件)和 \(Q_3=(15+16)/2=15.5\) (件)。
四分位数计算:单项式数列
单项式数列的四分位数计算,主要步骤如下:
第一步:计算累计频次表。
第二步:确定1/4和3/4分割点位置 \(p_1 =\frac{\sum{f_i}}{4}\) 和 \(p_3 =\frac{3\sum{f_i}}{4}\) 。
第三步:观察比较分割点位置和累计频次,确定得到两个分位数 \(Q_1\) 和 \(Q_3\) 。
(示例):单项式数列计算四分位数
案例说明:继续前面甲城市家庭住房评价案例数据,请你计算出相应的两个四分位数?
| satisfication | n | cumsum |
|---|---|---|
| 非常不满意 | 24 | | 2 | | |
| 不满意 | 1 | 8 | | 32 | |
| 一般 | | 3 | | 225 | |
| 满意 | | 5 | | 270 | |
| 非常满意 | 30 | | 3 | 0 | |
| Total | 300 | NA |
解题过程:
计算累计频次表(见左)。
确定分位数的位置,其中且 分割点为: \(p_1 =\frac{\sum{f_i}}{4}= \frac{300}{4}=75\) 和 \(p_3 =\frac{3\sum{f_i}}{4}= \frac{3*300}{4}=225\) 。
观察累计频次,得到分位数分别为 \(Q_1=\) “不满意”(第二组)和 \(Q_3=\) “一般”(第三组)。
四分位数计算:组距式数列
组距式数列的四分位数计算,主要步骤如下:
第一步:先按组顺序,计算累计分布次数(较大制或较小制)。
第二步:再确定1/4和3/4分割点位置 \(p_1 =\frac{\sum{f_i}}{4}\) 和 \(p_3 =\frac{3\sum{f_i}}{4}\) 。
第三步:根据计算的位置,找到该分割点位置所在组,初步确定四分位数 \(Q_1\) 和 \(Q_3\) 。
第四步:利用合适的插值公式,近似计算得到更为“精确”的中位数数值 \(Q_1\) 和 \(Q_3\) 。
(演示)分位数计算:较小制下限插值公式(定义)
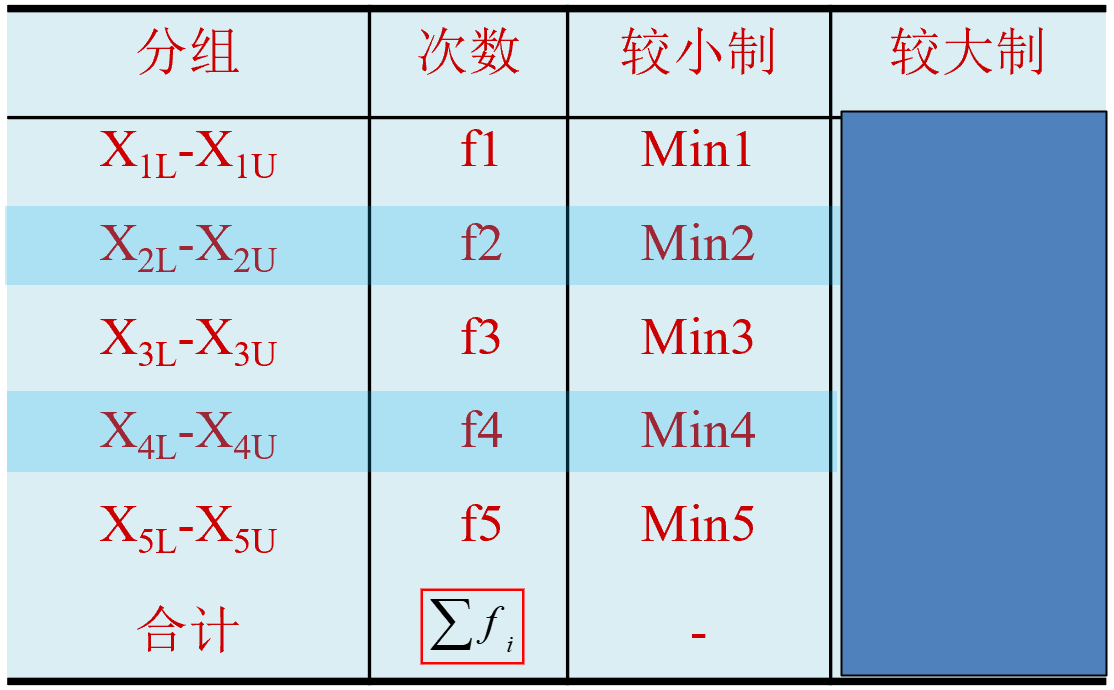
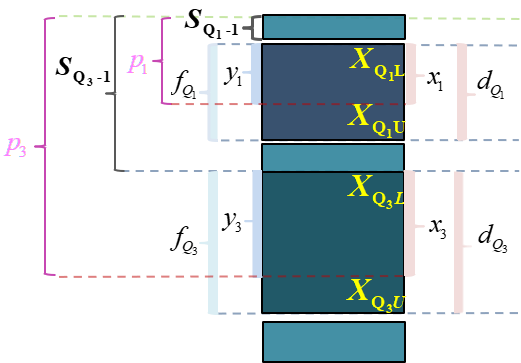
\(Q_{j}\) 表示四分位数,其中 \(j \in 1,3\) 。 \(X_{Q_jL}\) 表示组下限(Lower limits); \(X_{Q_jU}\) 表示组上限(Upper limits)。 \(d_{Q_j}\) 表示分位数组的组距(width); \(x_j\) 表示待求解的组距部分。
\(f_{i}\) 表示各组所对应的频次,其中 \(i \in 1,2,\cdots,5\) 。 \(f_{Q_j}\) 表示分位数组的频次 \(p_j\) 表示1/4或3/4分割位置,其中: \(p_1=\frac{\sum{f_i}}{4}\) , \(p_3=\frac{3\sum{f_i}}{4}\) 。
\(S_{Q_j-1}\) 表示相应分位数所在组的前一组的较小累计频次; \(y_j\) 表示与 \(x_j\) 宽度相对应频次。
(演示)分位数计算:较小制下限插值公式(Q1)


四分之一位数的较小制下限插值公式:
\[ \begin{aligned} \frac{x_1}{d_{Q_1}} = \frac{y_1}{f_{Q_1}} =\frac{p_1-S_{Q_1-1}}{f_{Q_1}} \quad \Rightarrow \quad Q_{1L}=X_{\mathrm{Q}_{1} L}+\frac{\frac{\sum f_i}{4}-S_{Q_{1}-1}}{f_{Q_1}} \cdot d_{Q_1} \end{aligned} \]
(演示)分位数计算:较小制下限插值公式(Q3)


四分之三位数的较小制下限插值公式:
\[ \begin{aligned} \frac{x_3}{d_{Q_3}} = \frac{y_3}{f_{Q_3}} =\frac{p_3-S_{Q_3-1}}{f_{Q_3}} \quad \Rightarrow \quad Q_{3L}=X_{\mathrm{Q}_{3} L}+\frac{\frac{3\sum f_i}{4}-S_{Q_{3}-1}}{f_{Q_3}} \cdot d_{Q_3} \end{aligned} \]
(示例)较小制分位数计算:粗略结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 10 | |
| G2 | 60-70Kg | 19 | 29 |
| G3 | 70-80Kg | 50 | 79 |
| G4 | 80-90Kg | 36 | 115 |
| G5 | 90-100Kg | 27 | 142 |
| G6 | 100-110Kg | 14 | 156 |
| G7 | 110Kg以上 | | 8 | | 164 | |
| Total | - | 164 | NA |
解题思路:
首先计算并得到较小制累计频次表(cumsum)(见左)。
然后计算分位数分割位置 \(p_1= \frac{\sum{f_i}}{4}=\frac{164}{4}=41\) , \(p_3= \frac{3\sum{f_i}}{4}=\frac{3*164}{4}=123\) 。
对照分位数的位置 \(p_j\) 和较小累计频数,初步得到分位数: \(Q_1 =\) “70-80Kg”(G3组); \(Q_3 =\) “90-100Kg”(G5组)。
(示例)较小制分位数计算:下限插值公式
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 10 | |
| G2 | 60-70Kg | 19 | 29 |
| G3 | 70-80Kg | 50 | 79 |
| G4 | 80-90Kg | 36 | 115 |
| G5 | 90-100Kg | 27 | 142 |
| G6 | 100-110Kg | 14 | 156 |
| G7 | 110Kg以上 | | 8 | | 164 | |
| Total | - | 164 | NA |
- 四分之一位数较小制下限公式计算结果:
\[ \begin{aligned} Q_{1L} &=X_{\mathrm{Q}_{1} L}+\frac{\frac{\sum f_i}{4}-S_{Q_{1}-1}}{f_{Q_1}} \cdot d_{Q_1} \\ &= 70+\frac{\frac{164}{4}-29}{50} \times 10=72.4 \end{aligned} \]
- 四分之三位数较小制下限公式计算结果:
\[ \begin{aligned} Q_{3L} &=X_{\mathrm{Q}_{3} L}+\frac{\frac{3\sum f_i}{4}-S_{Q_{3}-1}}{f_{Q_3}} \cdot d_{Q_3} \\ &=90+\frac{3 \times \frac{164}{4}-115}{27} \times 10=92.96 \end{aligned} \]
含义:两个分位数之差,即为四分位差(QD): \(\mathbf{QD} =Q_{3}-Q_{1} =92.96-72.4 =20.56\) 。这表明:有一半工人的日产量分布在72.4 \(\sim\) 92.96之间,他们的最大差异为20.56Kg。
(演示)分位数计算:较小制上限插值公式(情景)
计算情形:只给出较小制累计次数,而且初步已知 \(Q_1\) 和 \(Q_3\) 的粗略位置(如图中所示分别为第2组和第4组)。请精确计算 \(Q_1\) 和 \(Q_3\) 的值。

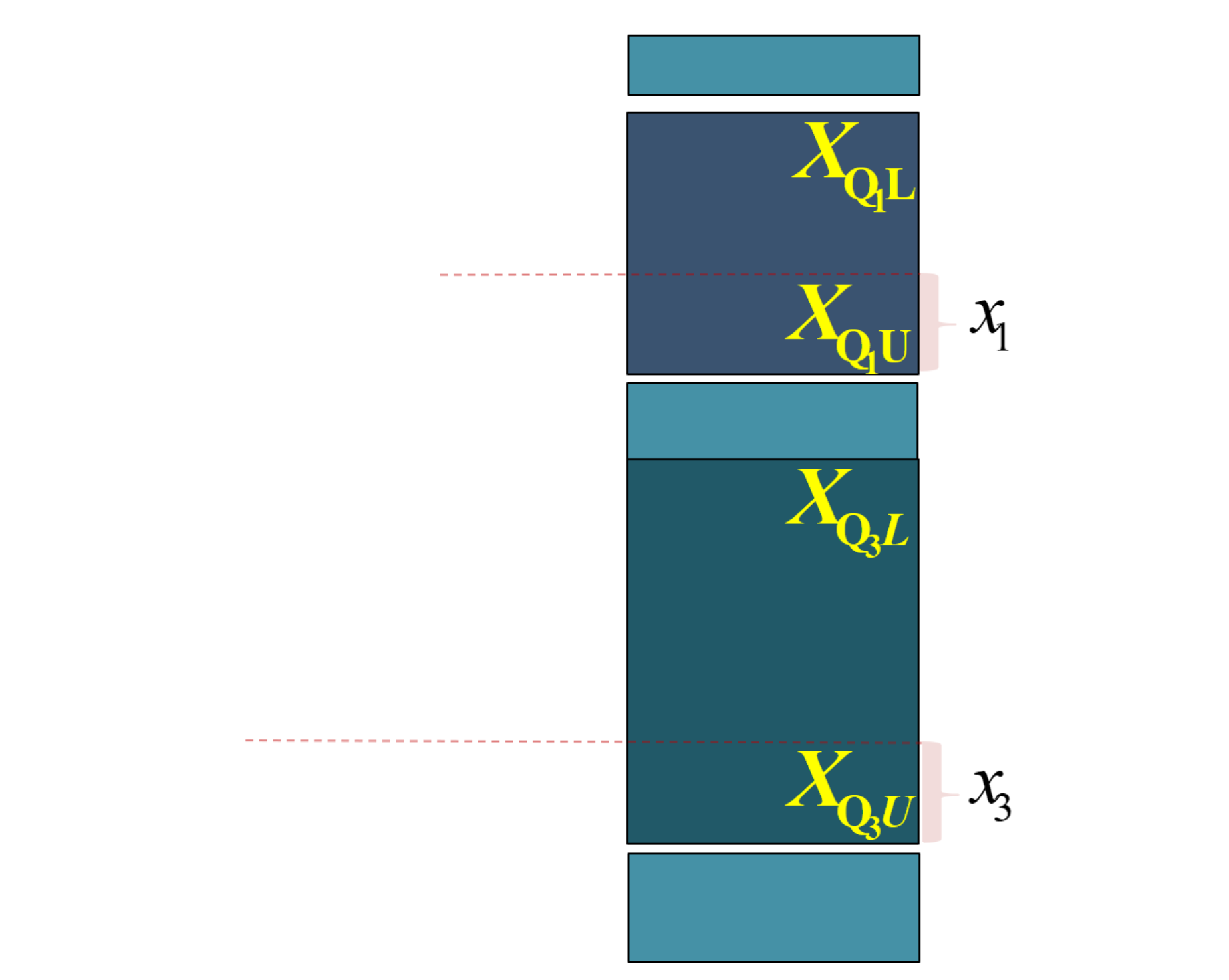
(演示)分位数计算:较小制上限插值公式(推导)
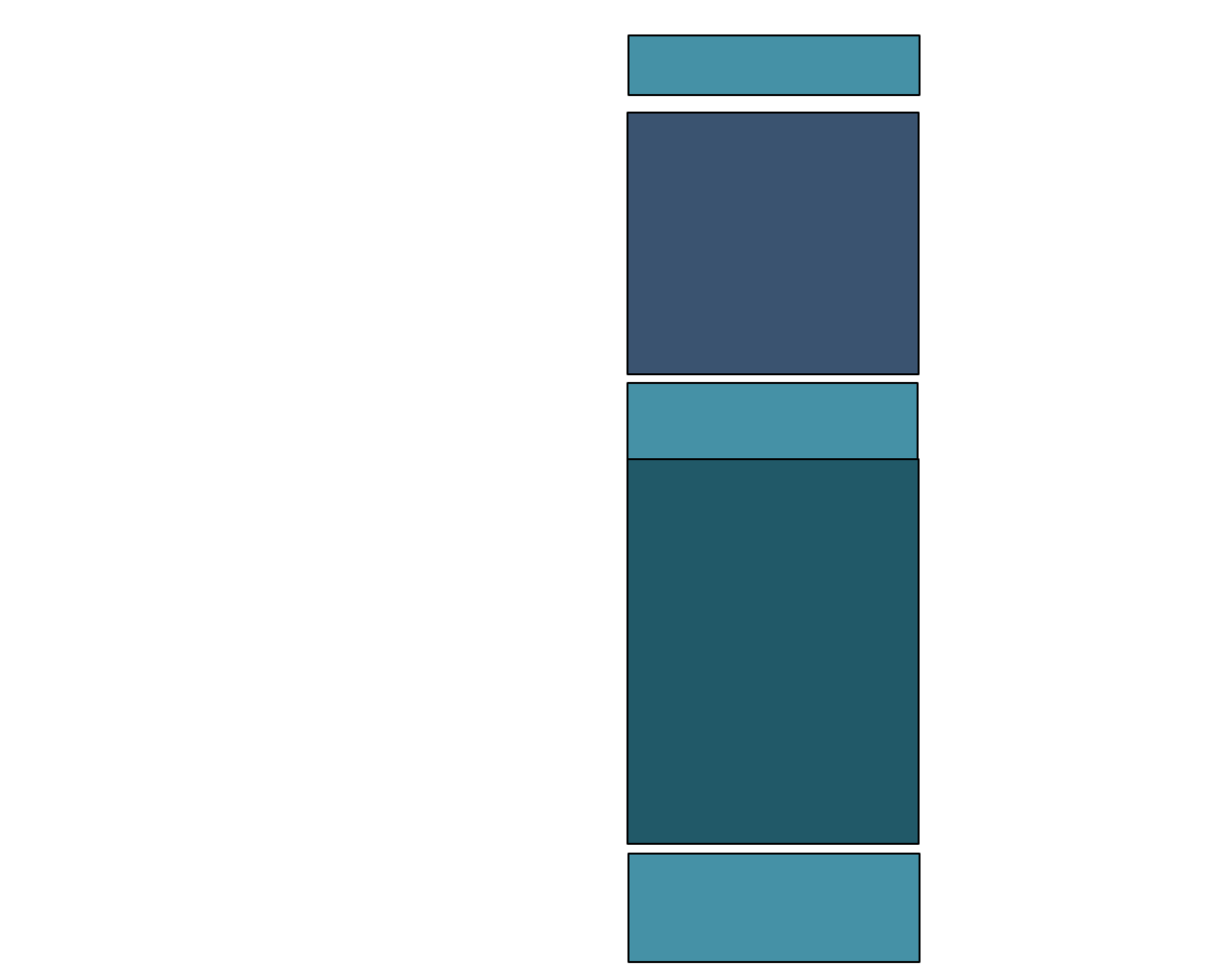
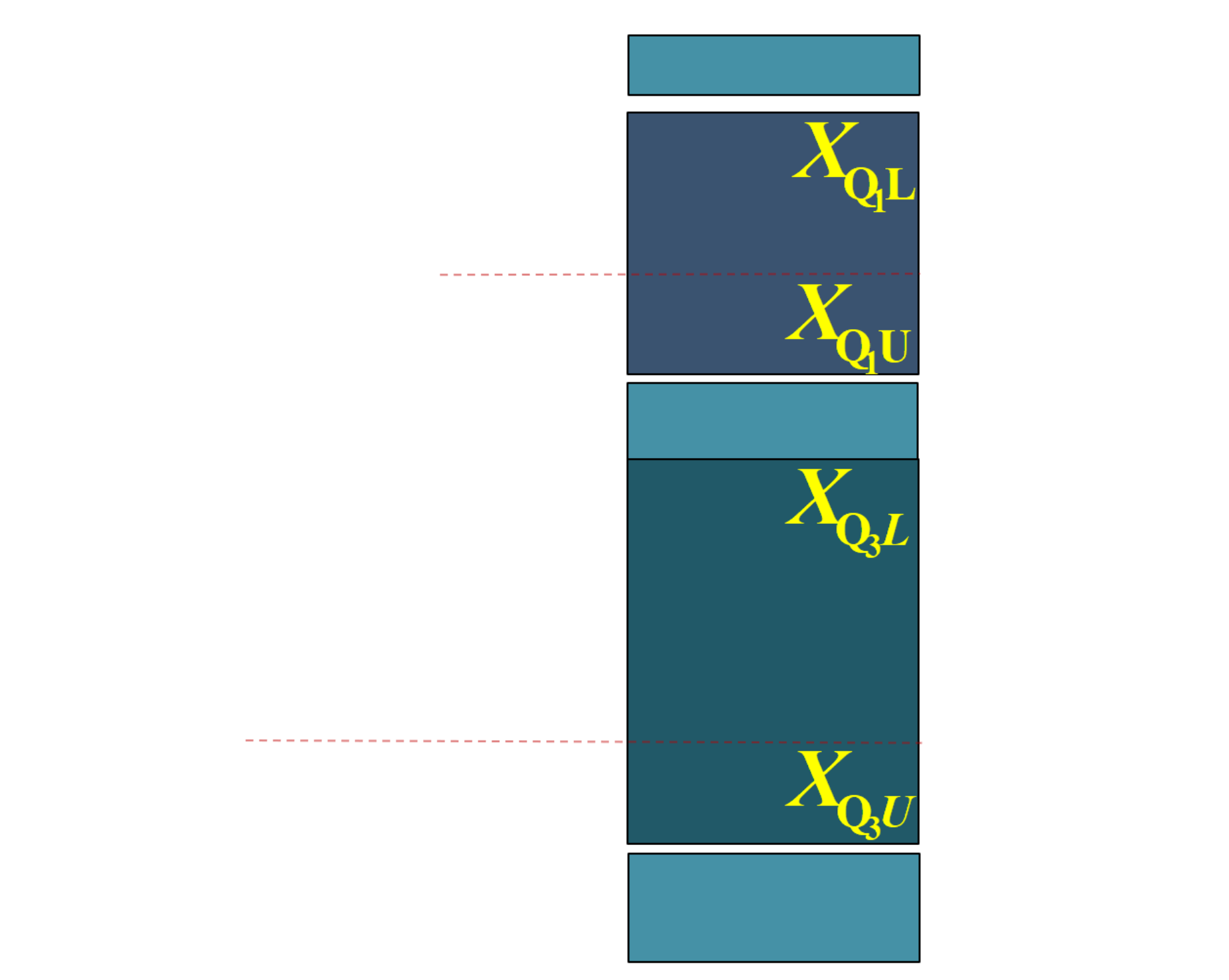

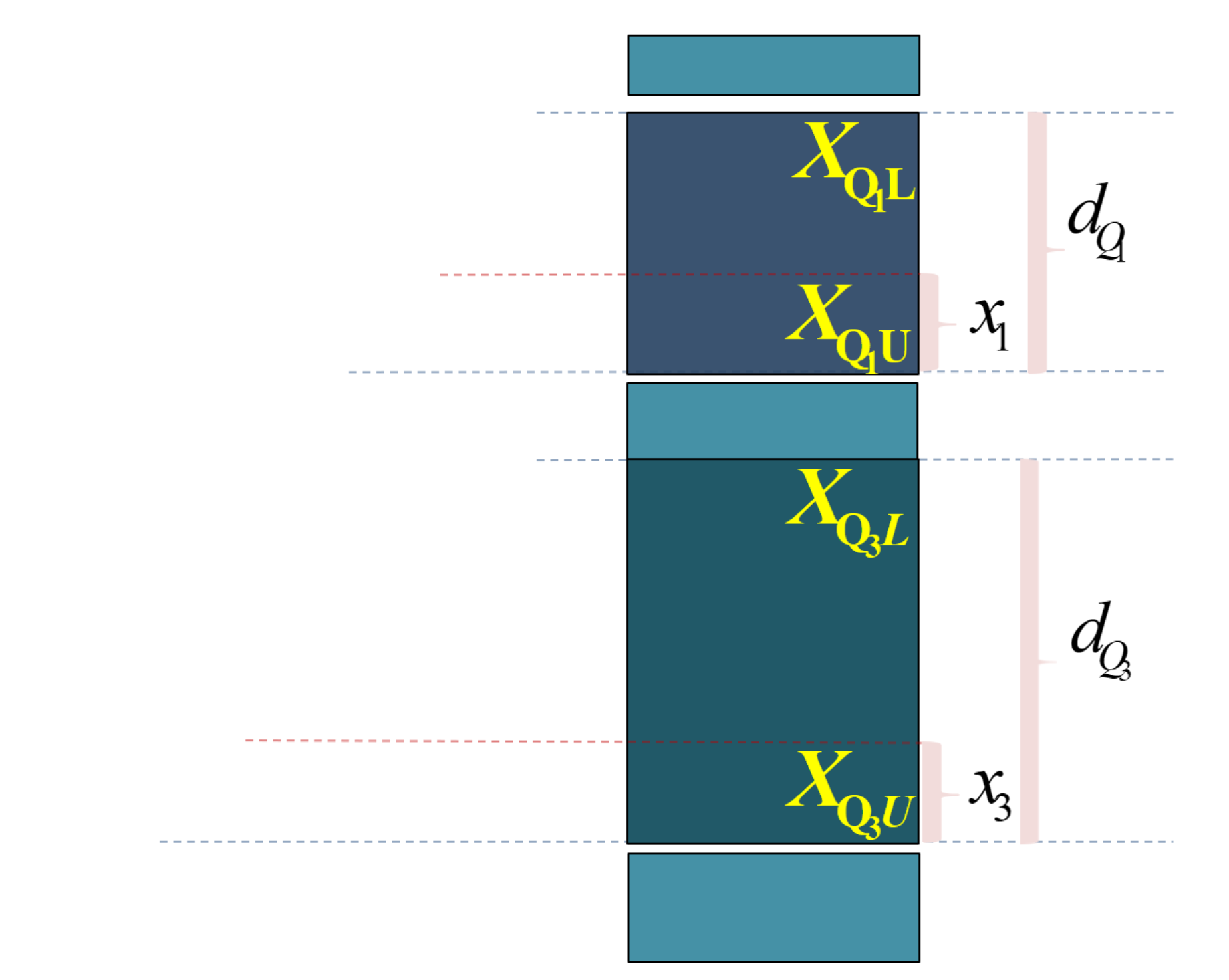
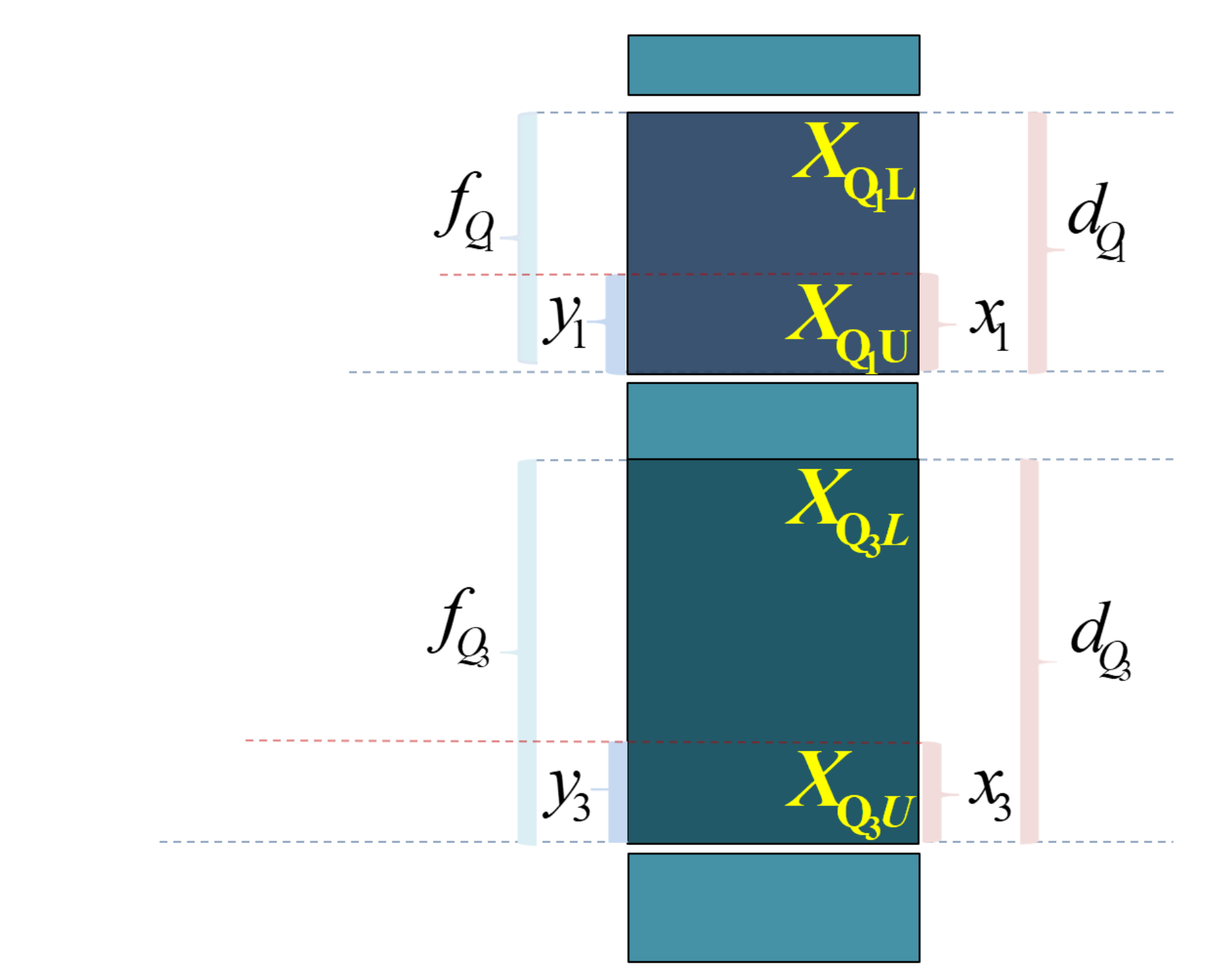
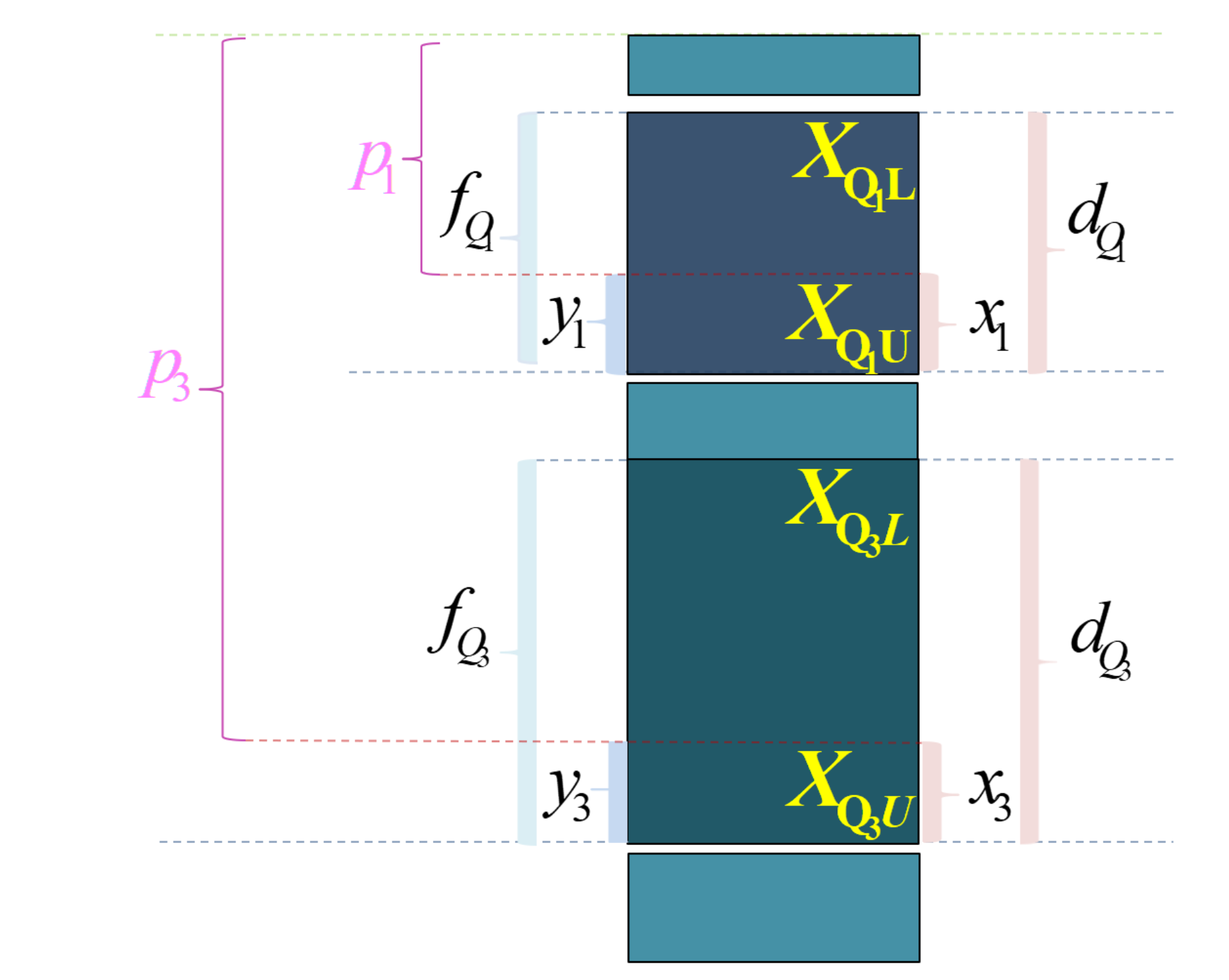
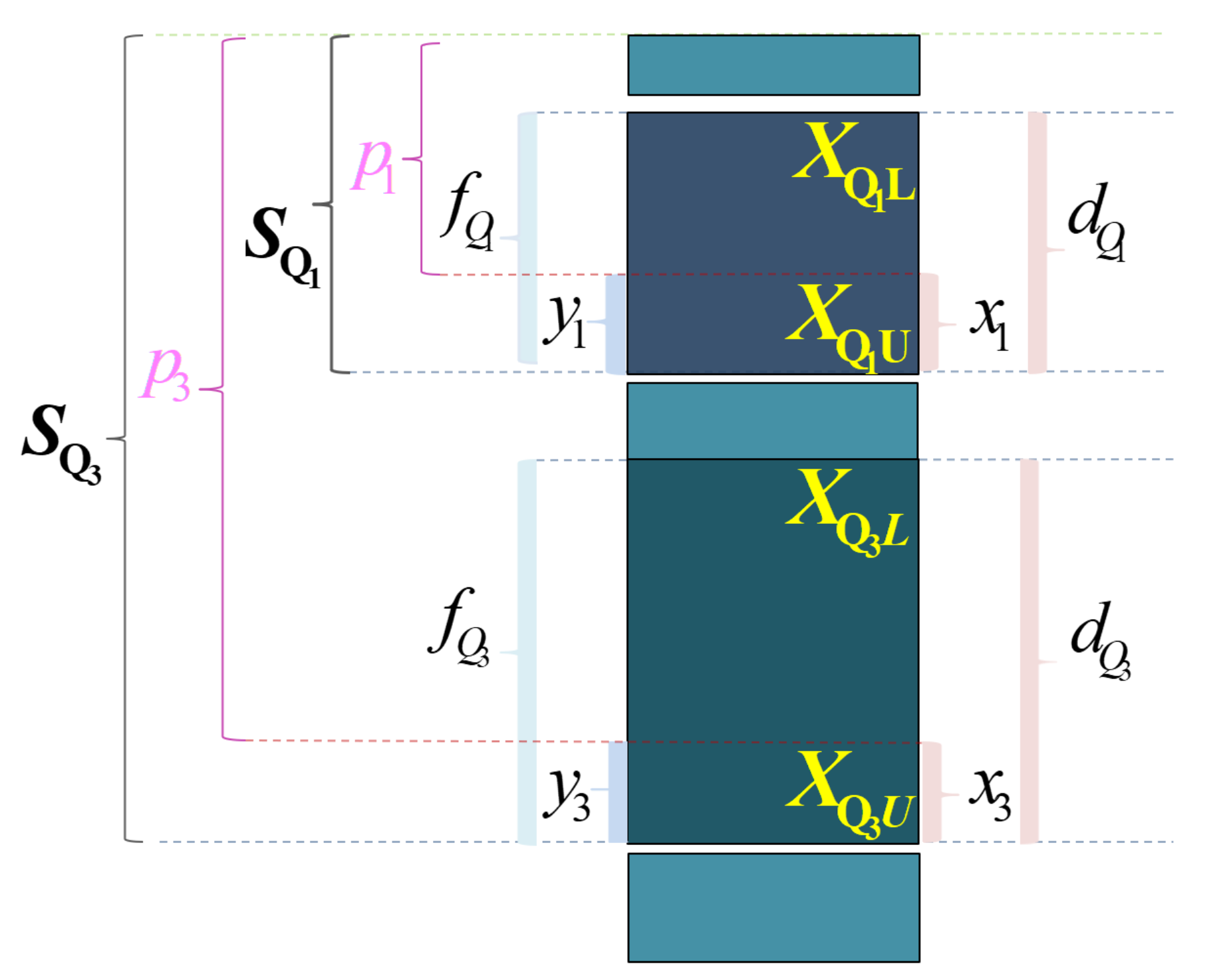
\(Q_{j}\) 表示四分位数,其中 \(j \in 1,3\) 。 \(X_{Q_{jL}}\) 表示组下限(Lower limits); \(X_{Q_{jU}}}\) 表示组上限(Upper limits)。 \(d_{Q_{j}}\) 表示分位数组的组距(width); \(x_j\) 表示待求解的组距部分。
\(f_i\) 表示各组所对应的频次,其中 \(i \in 1,2,\cdots,5\) 。 \(f_{{Q_j}}\) 表示分位数组的频次。 \(p_j\) 表示1/4或3/4分割位置,其中: \(p_1=\frac{\sum{{f_i}}}{4}\) , \(p_3=\frac{{3\sum{f_i}}{4}\) 。
\(S_{{Q_j}}\) 表示相应分位数所在组的较小累计频次; \(y_j\) 表示与 \(x_j\) 宽度相对应频次。
(演示)分位数计算:较小制上限插值公式(Q1)


四分之一位数的较小制上限插值公式:
\[ \begin{aligned} \frac{x_1}{d_{Q_1}} = \frac{y_1}{f_{Q_1}} =\frac{S_{Q_1}-p_1}{f_{Q_1}} \quad \Rightarrow \quad Q_{1U}=X_{\mathrm{Q}_{1} U} - \frac{S_{Q_{1}}-\frac{\sum f_i}{4}}{f_{Q_1}} \cdot d_{Q_1} \end{aligned} \]
(演示)分位数计算:较小制上限插值公式(Q3)


四分之三位数的较小制上限插值公式:
\[ \begin{aligned} \frac{x_3}{d_{Q_3}} = \frac{y_3}{f_{Q_3}} =\frac{S_{Q_3}-p_3}{f_{Q_3}} \quad \Rightarrow \quad Q_{3U}=X_{\mathrm{Q}_{3}U} -\frac{S_{Q_3}- \frac{3\sum f_i}{4}}{f_{Q_3}} \cdot d_{Q_3} \end{aligned} \]
(示例)较小制分位数计算:上限插值公式(案例数据)
案例说明:根据前述工人日产量案例,假如只给出较小累计频次(见下表)。请分别计算精确的两个分位数值。
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 10 | |
| G2 | 60-70Kg | 19 | 29 |
| G3 | 70-80Kg | 50 | 79 |
| G4 | 80-90Kg | 36 | 115 |
| G5 | 90-100Kg | 27 | 142 |
| G6 | 100-110Kg | 14 | 156 |
| G7 | 110Kg以上 | | 8 | | 164 | |
| Total | - | 164 | NA |
(示例)较小制分位数计算:上限插值公式(计算过程)
- 四分之一位数较小制上限公式计算结果:
\[ \begin{aligned} Q_{1L}=X_{\mathrm{Q}_{1} U} - \frac{S_{Q_{1}}-\frac{\sum f_i}{4}}{f_{Q_1}} \cdot d_{Q_1} =80-\frac{79-\frac{164}{4}}{50} \times 10=72.4 \end{aligned} \]
- 四分之三位数较小制上限公式计算结果:
\[ \begin{aligned} Q_{3U}=X_{\mathrm{Q}_{3}U} -\frac{S_{Q_3}- \frac{3\sum f_i}{4}}{f_{Q_3}} \cdot d_{Q_3}=100-\frac{142-\frac{3 \times 164}{4}}{27} \times 10=92.96 \end{aligned} \]
含义:两个分位数之差,即为四分位差(QD): \(\mathbf{QD} =Q_{3}-Q_{1} =92.96-72.4 =20.56\) 。这表明:有一半工人的日产量分布在72.4 \(\sim\) 92.96之间,他们的最大差异为20.56Kg。
(演示)分位数计算:较大制下限插值公式(定义)
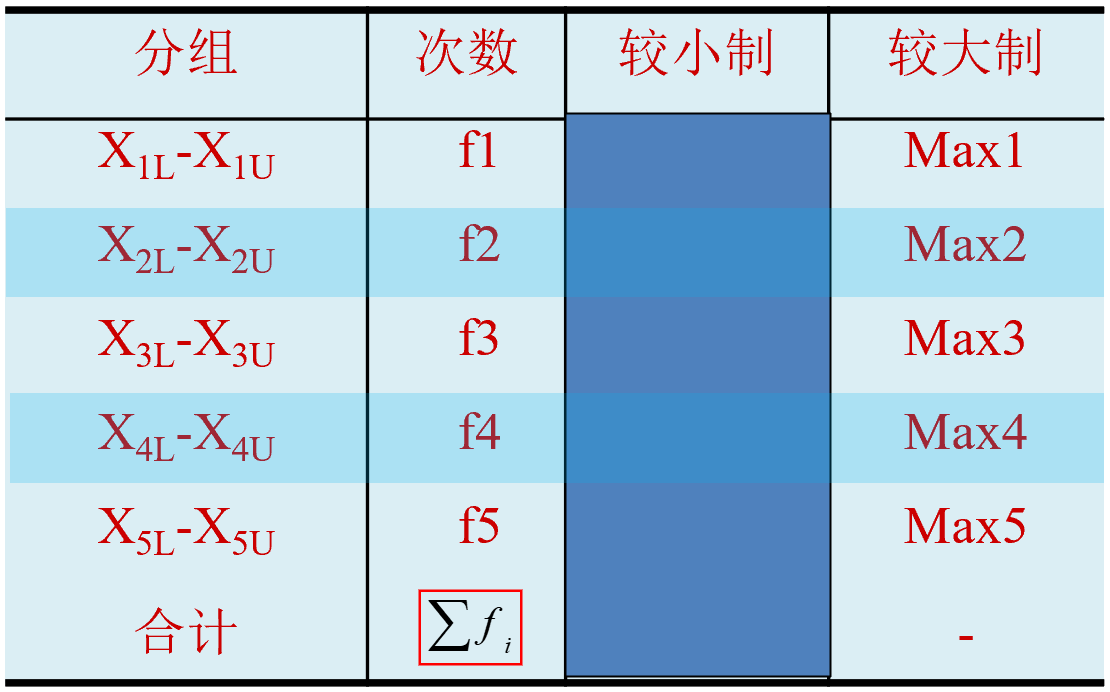
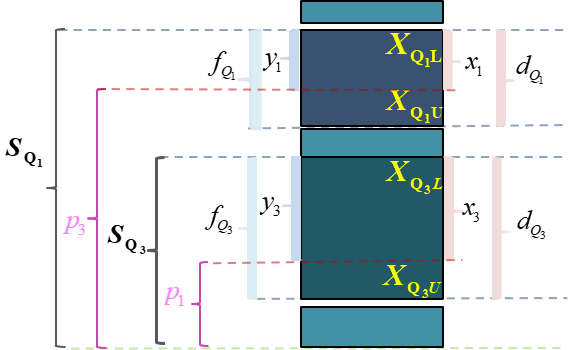
- \(Q_{j}\) 表示四分位数,其中 \(j \in 1,3\) 。 \(X_{Q_jL}\) 表示组下限(Lower limits); \(X_{Q_jU}\) 表示组上限(Upper limits)。 \(d_{Q_j}\) 表示分位数组的组距(width); \(x_j\) 表示待求解的组距部分。
- \(f_{i}\) 表示各组所对应的频次,其中 \(i \in 1,2,\cdots,5\) 。 \(f_{Q_j}\) 表示分位数组的频次 \(p_j\) 表示1/4或3/4分割位置,其中: \(p_1=\frac{\sum{f_i}}{4}\) , \(p_3=\frac{3\sum{f_i}}{4}\) 。
- \(S_{Q_j}\) 表示相应分位数所在组的较大累计频次; \(y_j\) 表示与 \(x_j\) 宽度相对应频次。
(演示)分位数计算:较大制下限插值公式(Q1)


- 四分之一位数的较大制下限插值公式:
\[ \begin{aligned} \frac{x_1}{d_{Q_1}} = \frac{y_1}{f_{Q_1}} =\frac{S_{Q_1} - p_3}{f_{Q_1}} \quad \Rightarrow \quad Q_{1L}=X_{\mathrm{Q}_{1} L}+\frac{S_{Q_1}- \frac{3\sum f_i}{4}}{f_{Q_1}} \cdot d_{Q_1} \end{aligned} \]
(演示)分位数计算:较大制下限插值公式(Q3)


四分之三位数的较大制下限插值公式:
\[ \begin{aligned} \frac{x_3}{d_{Q_3}} = \frac{y_3}{f_{Q_3}} =\frac{S_{Q_3}- p_1}{f_{Q_3}} \quad \Rightarrow \quad Q_{3L}=X_{\mathrm{Q}_{3} L}+\frac{S_{Q_3} -\frac{\sum f_i}{4}}{f_{Q_3}} \cdot d_{Q_3} \end{aligned} \]
(示例)较大制分位数计算:粗略结果
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 164 | |
| G2 | 60-70Kg | 19 | 154 |
| G3 | 70-80Kg | 50 | 135 |
| G4 | 80-90Kg | 36 | 85 |
| G5 | 90-100Kg | 27 | 49 |
| G6 | 100-110Kg | 14 | 22 |
| G7 | 110Kg以上 | | 8 | | 8 | |
| Total | - | 164 | NA |
解题思路:
首先计算并得到较大制累计频次表(cumsum)(见左)。
然后计算分位数分割位置: \(p_1= \frac{3\sum{f_i}}{4}=\frac{3\times 164}{4}=123\) , \(p_3= \frac{\sum{f_i}}{4}=\frac{164}{4}=41\) 。
对照分位数的位置 \(p_j\) 和较大累计频数,初步得到分位数: \(Q_1 =\) “70-80Kg”(G3组); \(Q_3 =\) “90-100Kg”(G5组)。
(示例)较大制分位数计算:下限插值公式
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 164 | |
| G2 | 60-70Kg | 19 | 154 |
| G3 | 70-80Kg | 50 | 135 |
| G4 | 80-90Kg | 36 | 85 |
| G5 | 90-100Kg | 27 | 49 |
| G6 | 100-110Kg | 14 | 22 |
| G7 | 110Kg以上 | | 8 | | 8 | |
| Total | - | 164 | NA |
- 四分之一位数较大制下限公式计算结果:
\[ \begin{aligned} Q_{1L} &=X_{\mathrm{Q}_{1} L}+\frac{S_{Q_1}-\frac{3\sum f_i}{4}}{f_{Q_1}} \cdot d_{Q_1} \\ &= 70+\frac{135-3\times \frac{164}{4}}{50} \times 10=72.4 \end{aligned} \]
- 四分之三位数较大制下限公式计算结果:
\[ \begin{aligned} Q_{3L} &=X_{\mathrm{Q}_{3} L}+\frac{S_{Q_3} - \frac{\sum f_i}{4}}{f_{Q_3}} \cdot d_{Q_3} \\ &=90+\frac{49- \frac{164}{4}}{27} \times 10=92.96 \end{aligned} \]
(演示)分位数计算:较大制上限插值公式(定义)

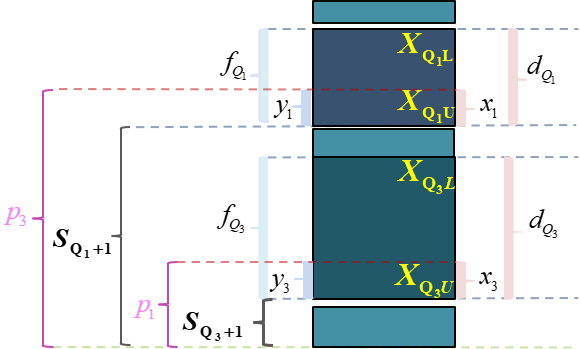
- \(Q_{j}\) 表示四分位数,其中 \(j \in 1,3\) 。 \(X_{Q_jL}\) 表示组下限(Lower limits); \(X_{Q_jU}\) 表示组上限(Upper limits)。 \(d_{Q_j}\) 表示分位数组的组距(width); \(x_j\) 表示待求解的组距部分。
- \(f_{i}\) 表示各组所对应的频次,其中 \(i \in 1,2,\cdots,5\) 。 \(f_{Q_j}\) 表示分位数组的频次。 \(p_j\) 表示1/4或3/4分割位置,其中: \(p_1=\frac{\sum{f_i}}{4}\) , \(p_3=\frac{3\sum{f_i}}{4}\) 。
- \(S_{Q_j+1}\) 表示相应分位数所在组的下一组的较大累计频次; \(y_j\) 表示与 \(x_j\) 宽度相对应频次。
(演示)分位数计算:较大制上限插值公式(Q1)

四分之一位数的较大制上限插值公式:
\[ \begin{aligned} \frac{x_1}{d_{Q_1}} = \frac{y_1}{f_{Q_1}} =\frac{p_3-S_{Q_1}}{f_{Q_1}} \quad \Rightarrow \quad Q_{1U}=X_{\mathrm{Q}_{1} U} - \frac{\frac{3\sum f_i}{4} - S_{Q_{1}+1}}{f_{Q_1}} \cdot d_{Q_1} \end{aligned} \]
(演示)分位数计算:较大制上限插值公式(Q3)

四分之三位数的较大制上限插值公式:
\[ \begin{aligned} \frac{x_3}{d_{Q_3}} = \frac{y_3}{f_{Q_3}} =\frac{p_1- S_{Q_3+1}}{f_{Q_3}} \quad \Rightarrow \quad Q_{3U}=X_{\mathrm{Q}_{3}U} -\frac{\frac{\sum f_i}{4} -S_{Q_3+1}}{f_{Q_3}} \cdot d_{Q_3} \end{aligned} \]
(示例)较大制分位数计算:上限插值公式
| groups | X | n | cumsum |
|---|---|---|---|
| G1 | 60Kg以下 | | 0 | | 164 | |
| G2 | 60-70Kg | 19 | 154 |
| G3 | 70-80Kg | 50 | 135 |
| G4 | 80-90Kg | 36 | 85 |
| G5 | 90-100Kg | 27 | 49 |
| G6 | 100-110Kg | 14 | 22 |
| G7 | 110Kg以上 | | 8 | | 8 | |
| Total | - | 164 | NA |
- 四分之一位数较大制上限公式计算结果:
\[ \begin{aligned} Q_{1U} &=X_{\mathrm{Q}_{1} U} - \frac{\frac{3\sum f_i}{4} - S_{Q_{1}+1}}{f_{Q_1}} \cdot d_{Q_1} \\ &=80-\frac{\frac{3 \times 164}{4}-85}{50} \times 10=72.4 \end{aligned} \]
- 四分之三位数较大制上限公式计算结果:
\[ \begin{aligned} Q_{3U} &=X_{\mathrm{Q}_{3}U} -\frac{\frac{\sum f_i}{4} -S_{Q_3+1}}{f_{Q_3}} \cdot d_{Q_3} \\ &=100-\frac{\frac{164}{4}-22}{27} \times 10=92.96 \end{aligned} \]
含义:两个分位数之差,即为四分位差(QD): \(\mathbf{QD} =Q_{3}-Q_{1} =92.96-72.4 =20.56\) 。这表明:有一半工人的日产量分布在72.4 \(\sim\) 92.96之间,他们的最大差异为20.56Kg。
内容导航
平均数:概念与定义
平均数:是对数据的中心的一种数值化测量指标。
根据总体数据(population)计算的,则称为总体期望(expectation),记为 \(\mu\) ;读作
miu。根据样本数据(sample)计算的,则称为样本平均数,也称为均值(Mean),记为 \(\bar{X}\) ,读作
X bar。
平均数:特征与类型
平均数的特征:
集中趋势的最常用测度值,是一组数据的均衡点(中心点)所在
体现了数据的必然性特征,易受极端值的影响
平均数的类型:
- 算术平均数,记为 \(\bar{X}\) 。具体又分为:
- 简单算数平均数 \(\bar{X}=\frac{\sum{X_i}}{n}\) ; b. 加权算数平均数 \(\bar{X}=\frac{\sum{(f_iX_i)}}{\sum{f_i}}\) 。
调和平均数,记为 \(\bar{X}_H\) 。
几何平均数,记为 \(\bar{X}_G\) 。
算术平均数:概念
设样本量为 \(n\) 的样本数据来自于一个总体(总体数据量为 \(N\) )。
数据来源:
样本数据: \(X_1 ,X_2 , \cdots, X_n\)
总体数据: \(X_1 ,X_2 , \cdots, X_n, \cdots, X_N\)
公式定义:
- 样本平均数计算公式:
\[ \bar{X}=\frac{X_{1}+X_{2}+\cdots+X_{n}}{n}=\frac{\sum_{i=1}^{n} X_{i}}{n} \]
- 总体平均数(期望)计算公式:
\[ \mu=\frac{X_{1}+X_{2}+\cdots+X_{N}}{N}=\frac{\sum_{i=1}^{N} X_{i}}{N} \]
算数平均数:基本公式
样本算术平均数具体包括两类:
简单算数平均数: \(\bar{X}=\frac{X_{1}+X_{2}+\cdots+X_{n}}{n}=\frac{\sum_{i=1}^{n} X_{i}}{n}\)
加权算数平均数:
若给出频次(次数) \(f_i\) 数据:\(\bar{X}=\frac{\sum_1^n{(f_iX_i)}}{\sum_1^n{f_i}}\)
若给出频率(比重) \(w_i = \frac{f_i }{\sum_1^n{f_i}}\) 数据:\(\bar{X}=\sum_1^n{\left(X_i \cdot \left(\frac{f_i }{\sum_1^n{f_i}}\right)\right)}\)
简单算术平均数的计算
适合情形:未分组资料
计算规则:将各总体单位的标志值简单相加,除以总体单位数所求得的结果。
计算公式:
\[ \bar{X}=\frac{X_{1}+X_{2}+\cdots+X_{n}}{n}=\frac{\sum_{i=1}^{n} X_{i}}{n} \]
计算示例:某单位有8名职工,周工资分别为1200元、1400元、1500元、1600元、1650元、1700元、1750元和1800元,则8名职工平均工资为:
\[ \begin{aligned} \bar{X} &=\frac{\sum X}{n}=\frac{X_{1}+X_{2}+X_{3}+\cdots \ldots+X_{n}}{n} \\ &=\frac{1200+1400+1500+1600+1650+1700+1750+1800}{8} \\ &=1575(\text { 元 }) \end{aligned} \]
加权算术平均数:计算概述
适合情形:分组数据且各组次数不完全相同。
计算规则:各组变量值(组中值)乘以各组权数求出标志总量,再将各组权数相加求出总体单位数,二者相除计算出的结果。
一般公式:
\[ \begin{aligned} \bar{X}=\frac{X_{1} f_{1}+X_{2} f_{2}+\ldots \ldots+X_{k} f_{k}}{f_{1}+f_{2}+\ldots \ldots+f_{k}}=\frac{\sum_{i=1}^{k} X_{i} f_{i}}{\sum_{i=1}^{k} f_{i}}=\frac{\sum X f}{\sum f} \end{aligned} \]
加权算术平均数:计算类型
计算类型:
单项式分配数列的计算
组距式分配数列的计算
计算要点: - 变量值( \(X_i\) ):单项式分组为组标志值;组距式分组为组中值。
- 权数( \(f_i\) ):具有权衡轻重的作用。权重既可以是频数(绝对数),也可以是频率(相对数)。
如果是频次(次数) \(f_i\) 数据:
\[ \bar{X}=\frac{\sum_1^n{(f_iX_i)}}{\sum_1^n{f_i}} \]
如果是频率(比重) \(w_i = \frac{f_i }{\sum_1^n{f_i}}\) :
\[ \bar{X}=\sum_1^n{\left(X_i \cdot \left(\frac{f_i }{\sum_1^n{f_i}}\right)\right)} \]
(示例)加权平均数计算:单项式数列
案例说明:某工厂共有105个工人,全体工人的日产量( \(X\) ,件/日)经过分组统计后( \(G1 \sim G6\) ),各组工人人数( \(n\) )的数据如下表所示。请计算全体工人的平均日产量是多少?
| group | X | f |
|---|---|---|
| G1 | 5 | 8 |
| G2 | 6 | 12 |
| G3 | 7 | 19 |
| G4 | 8 | 35 |
| G5 | 9 | 25 |
| G6 | 10 | 6 |
| Total | 45 | 105 |
(示例)加权平均数计算:单项式数列
解答过程:
根据分组标志值(日产量) \(X\) 和频次权重(职工人数) \(f\) ,计算得到各组的日产量 \(Xf\) 。(见右)
利用加权平均数公式计算得到平均日产量。
| group | X | f | Xf |
|---|---|---|---|
| G1 | 5 | 8 | 40 |
| G2 | 6 | 12 | 72 |
| G3 | 7 | 19 | 133 |
| G4 | 8 | 35 | 280 |
| G5 | 9 | 25 | 225 |
| G6 | 10 | 6 | 60 |
| Total | 45 | 105 | 810 |
\[ \begin{aligned} \bar{X}=\frac{X_{1} f_{1}+X_{2} f_{2}+\ldots \ldots+X_{k} f_{k}}{f_{1}+f_{2}+\ldots \ldots+f_{k}}=\frac{810}{105}=7.71(件/人) \end{aligned} \]
(示例)加权平均数计算:组距式数列
案例说明:某工厂共有164个工人,全体工人日产量(X)经过分组统计后( \(G1 \sim G7\) ),各组工人人数(f)分布数据如下所示。请计算全体工人的平均日产量是多少千克?
| groups | X | f |
|---|---|---|
| G1 | 60Kg以下 | | 0 | |
| G2 | 60-70Kg | 19 |
| G3 | 70-80Kg | 50 |
| G4 | 80-90Kg | 36 |
| G5 | 90-100Kg | 27 |
| G6 | 100-110Kg | 14 |
| G7 | 110Kg以上 | | 8 | |
| Total | - | 164 |
(示例)加权平均数计算:组距式数列(频次)
解答过程:
根据组距式分组标志值(日产量) \(X\) ,计算各组的组中值,然后再利用频次权重(职工人数) \(f\) ,计算得到各组的日产量 \(Xf\) 。(见右)
利用加权平均数公式计算得到平均日产量:
\[ \begin{aligned} \bar{X}=\frac{\sum_{i=1}^n (X_i \cdot f_i)}{\sum_{i=1}^n f_i}=\frac{13550}{164}=82.62(\text { 千克 }) \end{aligned} \]
| groups | X | Xi | f | Xf |
|---|---|---|---|---|
| G1 | 60Kg以下 | | 5 | | 0 | | 550 | |
| G2 | 60-70Kg | 65 | 19 | 1235 |
| G3 | 70-80Kg | 75 | 50 | 3750 |
| G4 | 80-90Kg | 85 | 36 | 3060 |
| G5 | 90-100Kg | 95 | 27 | 2565 |
| G6 | 100-110Kg | 105 | 14 | 1470 |
| G7 | 110Kg以上 | | 15 | | 8 | | 920 | |
| Total | - | 595 | 164 | 13550 |
(示例)加权平均数计算:组距式数列(频率)
解答过程:
根据组距式分组标志值(日产量) \(X\) ,计算各组的组中值,然后再利用频次(职工人数) \(f\) 计算出各组的频率权重(职工占比) \(w\) ,计算得到各组的日产量 \(Xw\) 。(见右)
利用加权平均数公式计算得到平均日产量。
\[ \begin{aligned} \bar{X}&=\sum_{i=1}^n{(X_i\cdot w_i)} \\ &=\sum_{i=1}^n{\left( X_i \cdot \frac{f_i}{\sum{f_i}}\right)} \\ &=82.62(\text { 千克 }) \end{aligned} \]
| groups | X | Xi | f | w | Xw |
|---|---|---|---|---|---|
| G1 | 60Kg以下 | | 5 | | 0 | | .06 | | .35 | |
| G2 | 60-70Kg | 65 | 19 | 0.12 | 7.53 |
| G3 | 70-80Kg | 75 | 50 | 0.30 | 22.87 |
| G4 | 80-90Kg | 85 | 36 | 0.22 | 18.66 |
| G5 | 90-100Kg | 95 | 27 | 0.16 | 15.64 |
| G6 | 100-110Kg | 105 | 14 | 0.09 | 8.96 |
| G7 | 110Kg以上 | | 15 | | 8 | | .05 | | .61 | |
| Total | - | 595 | 164 | 1.00 | 82.62 |
算数平均数:总结1
算数平均数 \(\bar{X}\) 的几条性质:
所有的定量数据都有算术平均数。
计算算术平均数时使用了所有数据。
一组样本数据只有一个均值。
简单算术平均数的大小只与变量值的大小有关。
加权算术平均数受各组组中值(变量值)大小,以及各组变量值出现的频数(权数)的影响。
算数平均数:总结2
- 各变量值与均值的离差之和等于零。
简单算数平均数: \(\sum{X_i-\bar{X}} = 0\)
加权算数平均数: \(\sum{\left[(X_i-\bar{X})f_i \right]} = 0\)
- 各变量值与均值的离差平方和等于最小值。
简单算数平均数: \(\sum{(X_i-\bar{X})^2} = min\)
加权算数平均数: \(\sum{\left[ (X_i-\bar{X})^2 f_i \right]} = 0\)
根据原始数据和分组资料计算的结果一般不会完全相等,根据分组数据只能得到近似结果。
只有各组数据在组内呈对称或均匀分布时,根据分组资料的计算结果才会与原始数据的计算结果一致。
(示例)算数平均数:未整理数据 VS 分组整理数据
案例数据:某企业的工会随机调查了50名工人2020年6月加班的小时数,原始数据(左下)和整理数据(右下)结果分别如下:
- 原始未整理数据:
W1 W2 W3 W4 W5 W6 W7 W8 W9 W10 W11 W12 W13 W14 W15 W16 W17 W18 W19 W20
12 14 23 15 16 24 17 9 12 13 21 17 17 16 12 24 17 5 19 13
W21 W22 W23 W24 W25 W26 W27 W28 W29 W30 W31 W32 W33 W34 W35 W36 W37 W38 W39 W40
10 14 10 11 12 7 19 16 9 21 17 14 19 19 19 18 18 15 13 13
W41 W42 W43 W44 W45 W46 W47 W48 W49 W50
12 14 9 26 21 9 13 13 19 15 - 简单算数平均数:
\[ \bar{X} = \frac{\sum{X_i}}{n}=15.22 \]
- 分组整理数据:
| X | Xi | f | Xf |
|---|---|---|---|
| 「 5,10」 | | .5 | | | | 0.0 | |
| (10,15」 | | 12.5 | | 19 | | 237.5 | |
| (15,20」 | | 17.5 | | 16 | | 280.0 | |
| (20,25」 | | 22.5 | | 6 | | 135.0 | |
| (25,30」 | | 27.5 | | 1 | | 27.5 | |
| Total | 87.5 | 50 | 740.0 |
- 加权算数平均数:
\[ \bar{X} = \frac{\sum{(X_i}\cdot f_i)}{\sum{f_i}}=14.8 \]
调和平均数:概念和形式
调和平均数:以变量值的倒数为基础计算的平均数,即标志值的倒数的平均数的倒数,亦称倒数平均数,一般记为 \(\bar{X}_H\) 。
表现形式:
逆向指标的算数平均指标的倒数形式。
算术平均指标的变形形式。
调和平均数:计算公式
调和平均数的理论计算公式为:
\[ \begin{aligned} \bar{X}=\frac{\sum{(X_i f_i)}}{\sum{f_i}}=\frac{\sum{(X_i f_i)}}{\sum \left[\frac{(X_i f_i)}{X_i} \right]} =\frac{\sum{m_i}} {\sum \frac{m_i}{X_i}}=\bar{X}_{H} \end{aligned} \]
其中:
\(m_i=X_i \cdot f_i, f_i=\frac{m_i}{X_i}\) 。
\(m_i\) 是一种特定权数,它不是各组变量值出现的次数,而是各组标志值总量(注意不是“总体标志总量”!!!)。
(示例)调和平均数的应用场景
案例说明:设有一种蔬菜,早、中、晚的价格分别为每千克0.5元、0.2元和0.1元。第一个人早、中、晚各买1千克的菜,第二个人早、中、晚各买1元钱的菜。比较两人所卖菜的平均价格。
\[ \begin{aligned} \text { 平均份格 }=\frac{\text { 购买额 }}{\text { 购买量 }} \end{aligned} \]
- 第一个人平均购买价格:
\[ \begin{aligned} \bar{X}=\frac{0.5+0.2+0.1}{1+1+1}=0.267(\text { 元 }) \end{aligned} \]
- 第二个人平均购买价格:
\[ \begin{aligned} \bar{X_H}=\frac{1+1+1}{1 / 0.5+1 / 0.2+1 / 0.1}=\frac{3}{17}=0.18(\text { 元 }) \end{aligned} \]
调和平均数的计算:主要步骤
简单调和平均数: \(\bar{X}_{H} =\frac{n} {\sum \frac{1}{X_i}}\)
加权调和平均数: \(\bar{X}_{H} =\frac{\sum{m_i}} {\sum \frac{m_i}{X_i}}\)
计算步骤:
先计算各个变量值的倒数 \(\frac{1}{X_i}\) 。
计算变量值的倒数的算数平均数。
简单调和平均数: \(\frac{\sum(\frac{1}{X_i})}{n}\)
加权调和平均数: \(\frac{\sum(\frac{m_i}{X_i})}{\sum{m_i}}\)
- 再计算变量值的倒数的算数平均数 的倒数。
简单调和平均数: \(\bar{X_H} = \frac{n}{\sum(\frac{1}{X_i})}\)
加权调和平均数: \(\bar{X_H} = \frac{\sum{m_i}}{\sum(\frac{m_i}{X_i})}\)
(示例)简单调和平均数的计算:未分组数据(正向指标情形)
示例计算1(正向指标情形):某车间5位工人的劳动生产率(件/小时)资料如下,请分别计算全部工人的平均劳动生产率是多少?
W1 W2 W3 W4 W5
10 12 15 20 30 - 计算分析:因为是正向指标,可以直接使用简单算数平均数计算得到。
\[ \begin{aligned} \bar{X} =\frac{\sum X_i}{n} =\frac{10+12+15+20+30}{5} =\frac{87}{5}=17.4 \text { 件 / 小时 } \end{aligned} \]
(示例)简单调和平均数的计算:未分组数据(逆向指标情形)
示例计算2(逆向指标指标情形):某车间5位工人的劳动生产率(分钟/件)资料如下,请分别计算全部工人的平均劳动生产率是多少?
W1 W2 W3 W4 W5
6 5 4 3 2 - 计算分析:因为是逆向指标,应使用简单调和平均数计算得到。
\[ \begin{aligned} \bar{X}_{H} =\frac{1}{\frac{\sum 1 / X_i}{n}} =\frac{1}{(1/ 6+1 / 5+1 / 4+1 / 3+1 / 2) / 5} =\frac{1}{1.45 / 5}=\frac{1}{0.29}=3.45 \text { 分钟 } / 件 \end{aligned} \]
(示例)加权调和平均数的计算:分组数据A
案例说明:某公司有四个企业,工作完成程度(ratio_do,%)及计划产值(value_plan)如下,请计算全部四个企业的平均工作完成程度?
| firms | ratio_do | value_plan | Xf |
|---|---|---|---|
| 甲 | | 90 | | 100 | | 90 | |
| 乙 | | 100 | | 200 | | 200 | |
| 丙 | | 110 | | 300 | | 330 | |
| 丁 | | 120 | | 400 | | 480 | |
| Total | NA | 1000 | 1100 |
分析过程:此题可以直接使用加权算术平均数公式计算。其中:工作完成程度(ratio_do)为正指标 \(X_i\) ,计划产值(Value_plan)为权重 \(f_i\) 。
\[ \begin{aligned} \bar{X}=\frac{\sum {(X_i f_i)}}{\sum {f_i}}=\frac{1100}{1000} \times 100\%=110 \% \end{aligned} \]
(示例)加权调和平均数的计算:分组数据B
案例说明:某公司有四个企业,工作完成程度(ratio_do,%)及实际产值(value_do)如下,请计算全部四个企业的平均工作完成程度?
| firms | ratio_do | value_do | 1/X | m/X |
|---|---|---|---|---|
| 甲 | | 90 | | 90 | | 1.1111111 | | 100 | |
| 乙 | | 100 | | 200 | | 1.0000000 | | 200 | |
| 丙 | | 110 | | 330 | | 0.9090909 | | 300 | |
| 丁 | | 120 | | 480 | | 0.8333333 | | 400 | |
| Total | NA | 1100 | NA | 1000 |
分析过程:此题需要使用加权调和平均数公式计算。其中:工作完成程度(ratio_do)为正指标 \(X_i\) ,实际产值(Value_do)为特殊权重 \(m_i\) 。
\[ \begin{aligned} \bar{X}==\frac{\sum m_i}{\sum \left(\frac{1}{X_i} m_i \right)}=\frac{1100}{1000} \times 100 \%=110 \% \end{aligned} \]
调和平均数:总结
如果数列中有一标志值等于零,则无法计算调和平均数。
较之算术平均数,调和平均数受极端值的影响要小。
几何平均数:概念与类型
几何平均数(Geometric Mean):对 \(n\) 个变量值连乘之积开 \(n\) 次方根,主要用于计算平均速度和平均比率。
一般公式:
\[ \bar{X_G} = \sqrt[n]{X_1 \cdot X_2 \cdots X_n} = \sqrt[n]{{\prod_{i=1}^n{X_i}}} \]
适合条件:变量值为相乘关系
计算类型:
简单几何平均数
加权几何平均数
简单几何平均数的计算
(方法1)直接开根号:
\[ \bar{X_G} = \sqrt[n]{X_1 \cdot X_2 \cdots X_n} = \sqrt[n]{{\prod_{i=1}^n{X_i}}} \]
(方法2)利用反对数求解:
\[ \begin{aligned} \bar{X_G} &= \left(\prod_{i=1}^n{X_i} \right)^{\frac{1}{n}} \\ log(\bar{X_G}) &= \frac{1}{n} \cdot log\left(\prod_{i=1}^n{X_i}\right) = \frac{1}{n} \cdot \sum_{i =1} ^n{\left(log{X_i} \right)} \\ \bar{X_G} &= arclog\left(\frac{1}{n} \cdot \sum_{i =1} ^n{\left(log{X_i} \right)} \right) = 10^{\left(\frac{1}{n} \cdot \sum_{i =1} ^n{\left(log{X_i} \right)} \right)} \end{aligned} \]
(示例)简单几何平均数的计算
案例说明:某地区工业产品产量在2013-2018年间的产量(output,亿吨)和逐年发展速度*(speed,%)。求该地区五年间的平均发展速度是多少?
| year | output | speed |
|---|---|---|
| 2013 | 9.80 | NA |
| 2014 | 10.54 | 107.5510 |
| 2015 | 10.80 | 102.4668 |
| 2016 | 10.87 | 100.6481 |
| 2017 | 11.16 | 102.6679 |
| 2018 | 11.41 | 102.2401 |
| Total | 64.58 | NA |
(示例)简单几何平均数的计算
解题分析:
方法1:对发展速度(speed)直接连乘开根号。
方法2:对发展速度(speed)取对数(log_speed),再连加对数,最后求反对数。
| year | output | speed | log_speed |
|---|---|---|---|
| 2013 | 9.80 | NA | NA |
| 2014 | 10.54 | 107.5510 | 2.0316 |
| 2015 | 10.80 | 102.4668 | 2.0106 |
| 2016 | 10.87 | 100.6481 | 2.0028 |
| 2017 | 11.16 | 102.6679 | 2.0114 |
| 2018 | 11.41 | 102.2401 | 2.0096 |
| Total | 64.58 | NA | 10.0661 |
\[ \begin{aligned} \bar{X_G} &= \sqrt[n]{{\prod_{i=1}^n{X_i}}}\\ & =\sqrt[n]{1.1643} \\ & = 103.0889 \end{aligned} \]
\[ \begin{aligned} \bar{X_G} &= arclog\left(\frac{1}{n} \cdot \sum_{i =1} ^n{\left(log{X_i} \right)} \right) \\ & = 10^{\left(\frac{1}{n} \cdot \sum_{i =1} ^n{\left(log{X_i} \right)} \right)} = 10^{\left( \frac{1}{5}\cdot 10.0661 \right) } \\ & = 103.0889 \end{aligned} \]
加权几何平均数的计算
(方法1)直接开根号:
\[ \bar{X_G} = \sqrt[(f_1+f_2+\cdots +f_n)]{X_1^{f_1} \cdot X_2^{f_2} \cdots X_n^{f_n}} = \sqrt[\sum_{i=1}^n{f_i}]{{\prod_{i=1}^n{\left( X_i^{f_i}\right)}}} \]
(方法2)利用反对数求解:
\[ \begin{aligned} \bar{X_G} &= \sqrt[\sum{f_i}]{\prod_{i=1}^n{\left( X_i^{f_i}\right)}} \\ log(\bar{X_G} ) &= \frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(log{X_i^{f_i}} \right)} = \frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(f_i \cdot logX_i\right)}\\ \bar{X_G} &= arclog \left(\frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(f_i \cdot logX_i\right)} \right) = 10^{\left(\frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(f_i \cdot logX_i\right)} \right) } \end{aligned} \]
(示例)加权几何平均数的计算
案例说明:某投资银行公布了最近25年间( \(n=25\) )银行年利率的逐年发展速度分组*(speed)和每个分组利率的年数(years)。求该地区25年间的平均发展速度是多少?
| speed | years |
|---|---|
| 1.03 | 1 |
| 1.05 | 4 |
| 1.08 | 8 |
| 1.1 | 10 |
| 1.15 | 2 |
| Total | 25 |
(示例)简单几何平均数的计算
解题分析:
方法1:对发展速度(speed)进行权重 \(f_i\) 的幂指数计算,再连乘,最后再开根号。
方法2:对发展速度(speed)取对数(log_speed),再乘以对应权重 \(f_i\) ,然后加总,最后求反对数。
| speed | years | power | log_speed | f_log_speed |
|---|---|---|---|---|
| 1.03 | 1 | 1.0300 | 0.0128 | 0.0128 |
| 1.05 | 4 | 1.2155 | 0.0212 | 0.0848 |
| 1.08 | 8 | 1.8509 | 0.0334 | 0.2674 |
| 1.1 | 10 | 2.5937 | 0.0414 | 0.4139 |
| 1.15 | 2 | 1.3225 | 0.0607 | 0.1214 |
| Total | 25 | NA | NA | 0.9003 |
\[ \begin{aligned} \overline{X_{\mathrm{g}}}& = \sqrt[\sum_{i=1}^n{f_i}]{{\prod_{i=1}^n{\left( X_i^{f_i}\right)}}}\\ &=\sqrt[25]{1.03^{1 *} 1.05^{4} * 1.08^{8} * 1.10^{10 *}+1.15^{2}}\\ &=\sqrt[25]{7.9489}=1.0865 \end{aligned} \]
\[ \begin{aligned} \overline{X_G} &= arclog \left(\frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(f_i \cdot logX_i\right)} \right) \\ &= 10^{\left(\frac{1}{\sum{f_i}} \cdot \sum_{i =1} ^n{\left(f_i \cdot logX_i\right)} \right) } \\ & = 10^{\left( \frac{1}{25}\cdot 0.9003 \right) } = 1.0865 \end{aligned} \]
几何平均数:总结
几何平均数 \(\bar{X_G}\) 适用于反映特定现象的平均水平,即现象的总标志值是各单位标志值的连乘积。
如果数列中有一个标志值等于零或负值,就无法计算几何平均数 \(\bar{X_G}\) 。
受极端值的影响较算数平均数 \(\bar{X}\) 和调和平均数 \(\bar{X_H}\) 小。
平均数:总结1
位置平均数和数值平均数的图形关系:
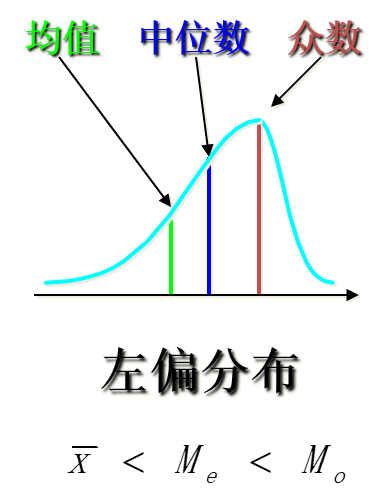
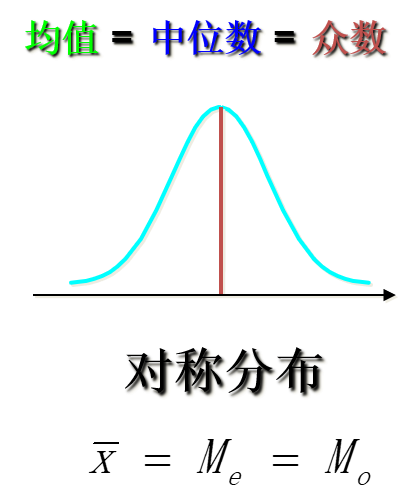
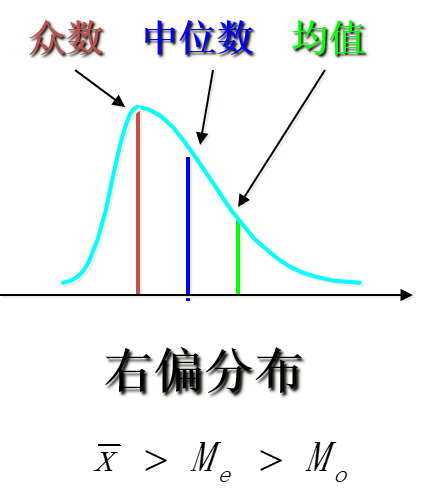
平均数:总结2
- 位置平均数和数值平均数的卡尔·皮尔逊经验公式:
\[ \begin{aligned} \left|\bar{X}-M_{0}\right|=3\left|\bar{X}-M_{e}\right| \end{aligned} \]
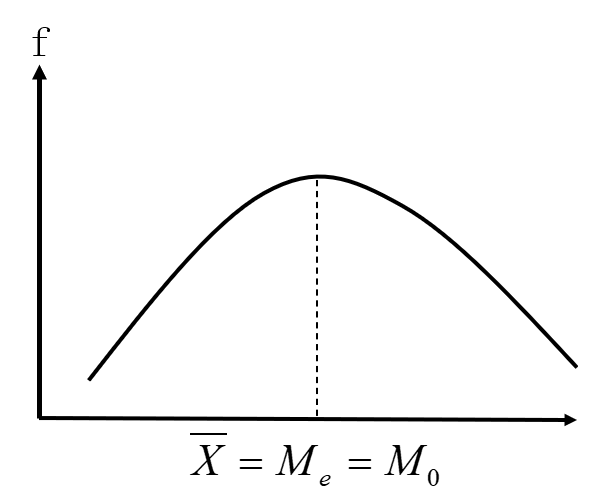
\[ \begin{aligned} M_{0} =3 M_{e}-2 \bar{X}; \end{aligned} \]
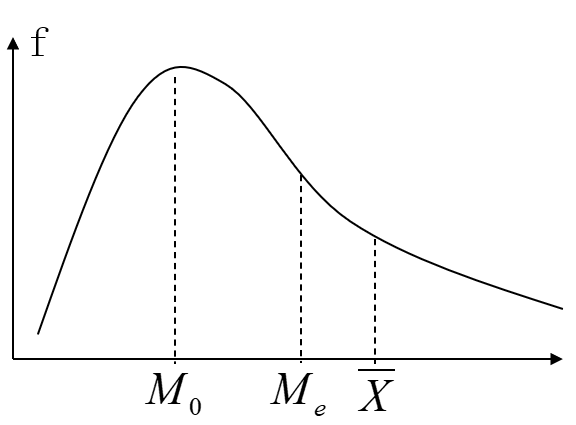
\[ \begin{aligned} \bar{X}=\frac{1}{2}\left(3 M_{e}-M_{o}\right); \end{aligned} \]
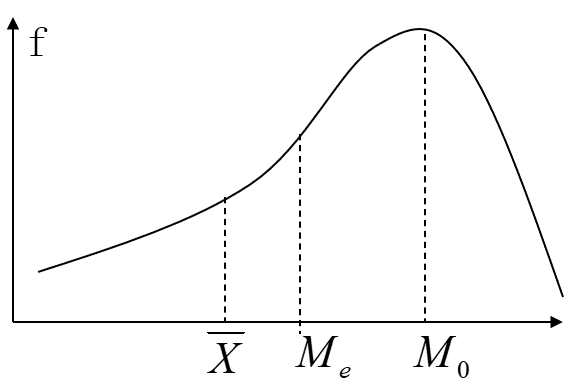
\[ \begin{aligned} M_{e}=\frac{1}{3}\left(M_{o}+2 \bar{X}\right) \end{aligned} \]
4.4 离散程度的度量
内容导航
离散趋势概述:概念内涵
离散趋势的具体内涵有:
是数据分布的一个重要特征
反映各变量值远离其中心值的程度(离散程度)
从另一个侧面说明了集中趋势测度值的代表程度
不同类型的数据有不同的离散程度测度值
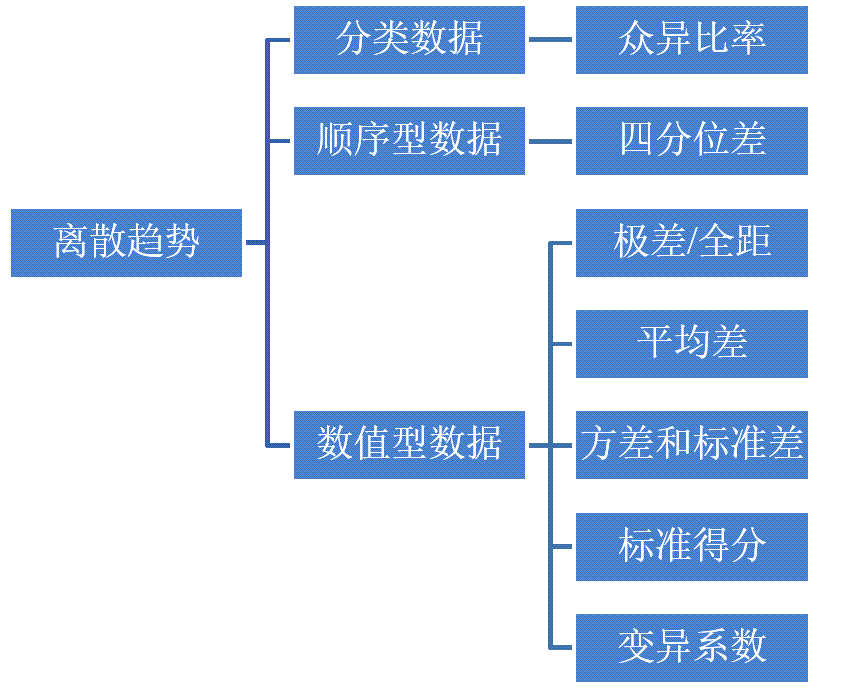
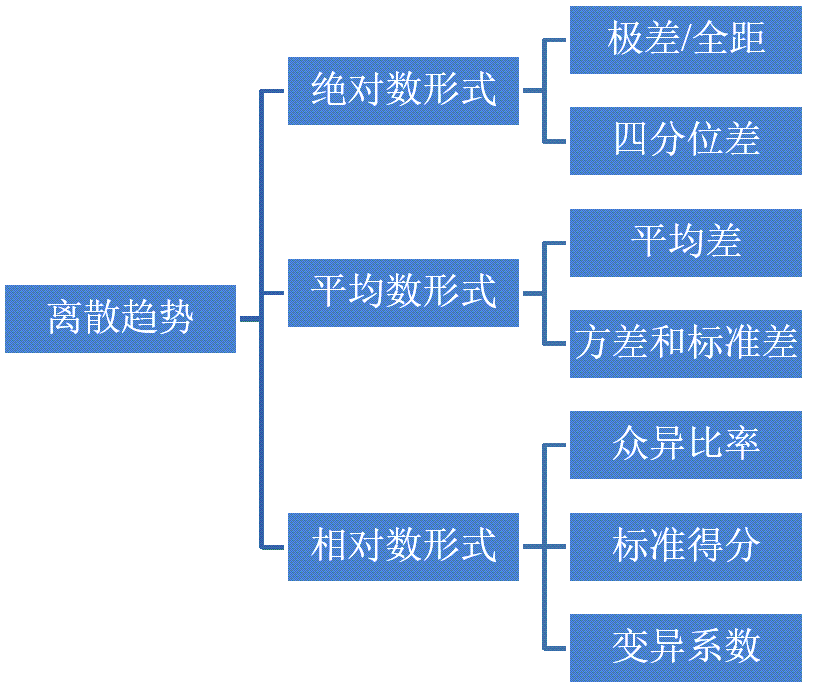
异众比率:概念和特征
异众比率(variation ratio):是对分类数据离散程度的测度,具体表现为非众数组的频数占总频数的比例,一般记为 \(V_r\) 。
异众比率的特征:用于衡量众数的代表性
计算公式:
\[ \begin{aligned} V_{r}=\frac{\sum f_{i}-f_{m}}{\sum f_{i}}=1-\frac{f_{m}}{\sum f_{i}} \end{aligned} \]
(示例)异众比率的计算
案例数据:不同品牌饮料的频数分布如下,请计算该数据集的异众比率是多少
解题分析:
\[ \begin{aligned} V_{r} &=\frac{\sum f_{i}-f_{m}}{\sum f_{i}} =1-\frac{f_{m}}{\sum f_{i}} \\ & =\frac{50-15}{50}=1-\frac{15}{50} \\ &=0.7=70 \% \end{aligned} \]
- 在所调查的50人当中,购买碳酸饮料以外的人数占70%,异众比率比较大。因此,用“碳酸饮料”代表消费者购买饮料品牌的状况,其代表性不是很好。
四分位差:概念和特征
四分位差(quartile deviation):主要用于对顺序尺度/比率尺度数据离散程度的测度,也称为内距或四分间距,它是上四分位数(四分之三位数)与下四分位数(四分之一位数)之差,一般记为 \(Q_d\) :
\[ Q_d = Q_3 – Q_1 \]
四分位差的特征:
反映了中间50%数据的离散程度
不受极端值的影响
用于衡量中位数的代表性
(示例)四分位差的计算:原始未整理数据
案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的四分位差是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213解题步骤:
计算数据集的四分之一位数: \(Q_1 = 170.75\) 。
计算数据集的四分之三位数: \(Q_3 = 197\) 。
最后计算得到四分位差: \(Q_d = Q_3- Q_1 =26.25\)
(示例)四分位差的计算:单项式数列
案例数据:甲城市家庭对住房状况评价的频数分布如下,请计算该数据集的四分位差是多少?
| lable | satisfication | n | cumsum |
|---|---|---|---|
| 1 | 非常不满意 | 24 | | 2 | | |
| 2 | 不满意 | 1 | 8 | | 32 | |
| 3 | 一般 | | 3 | | 225 | |
| 4 | 满意 | | 5 | | 270 | |
| 5 | 非常满意 | 30 | | 3 | 0 | |
| NA | Total | 300 | NA |
解题分析:设非常不满意为1,不满意为2,一般为3,满意为4, 非常满意为5。 已知: \(Q_1 = 不满意 = 2\) ; \(Q_3 = 一般 = 3\) 。则四分位差为:
\[ Q_d = Q_3 - Q_1= 3 – 2 = 1 \]
极差:概念和特征
极差(range):是一组数据的最大值与最小值之差,一般记为 \(R\) ,计算公式为:
\[ R = Max(X_i) - Min(X_i) \]
极差的特征:
离散程度的最简单测度值
易受极端值影响
未考虑数据的分布
(示例)极差的计算:未整理原始数据
案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的极差是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213解题步骤:
- 先排序数据,找到最小值和最大值。
[1] 141 143 144 149 150 152 153 153 154 155 156 158 159 160 160 161 161 162
[19] 163 163 164 165 165 165 166 167 168 168 168 170 171 171 172 172 172 172
[37] 172 173 173 174 174 174 175 175 175 175 176 176 177 177 178 178 178 179
[55] 179 179 180 180 181 182 182 183 184 185 186 186 187 187 187 187 188 188
[73] 188 189 189 189 190 190 191 192 194 194 195 195 196 196 196 196 196 197
[91] 197 198 198 200 201 202 203 203 205 206 207 208 209 210 210 211 211 213
[109] 214 215 218 223 225 226 228 233 233 234 234 237- 最后计算得到四分位差。
\[ R = Max(X_i)- Min(X_i) =237 - 141 = 96 \]
平均差:概念和特征
平均差(mean deviation):是各变量值与其平均数离差绝对值的平均数,一般记为 \(M_d\) 。计算公式根据数据情况分为:
- 未分组数据:
\[ \begin{aligned} M_{\mathrm{d}}=\frac{\sum_{i=1}^{n}\left|X_{i}-\bar{X}\right|}{n} \end{aligned} \]
- 组距分组数据:
\[ \begin{aligned} M_{\mathrm{d}}=\frac{\sum_{i=1}^{k}\left(\left|M_{i}-\bar{X}\right| f_{i}\right)}{\sum{f_i}} \end{aligned} \]
平均差的特征:
能全面反映一组数据的离散程度。
数学性质较差,实际中应用较少。
(示例)平均差的计算:原始未整理数据1
案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的四分位差是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213(示例)平均差的计算:原始未整理数据2
解题步骤:
计算数据集的均值: \(\bar{X} = \frac{\sum{X_i}}{n} = 184.5666667\) 。
计算所有数据的离中心差的绝对值: \(|X_i -\bar{X}|\) ,及其求和项 \(\sum_{i=1}^{n}\left|X_{i}-\bar{X}\right| = 2091.4\) 。
最后利用公式计算得到平均差:
\[ \begin{aligned} M_{\mathrm{d}} &=\frac{\sum_{i=1}^{n}\left|X_{i}-\bar{X}\right|}{n} \\ &=\frac{2091.4}{120} =17.4283333 \end{aligned} \]
[1] 49.43 41.57 2.43 23.57 34.57 43.43 31.57 18.57 30.57 10.57 28.57 18.43
[13] 25.57 13.43 24.57 32.57 23.57 22.57 21.57 11.43 20.57 41.43 19.57 19.57
[25] 2.43 43.57 29.43 35.57 6.57 38.43 33.43 5.57 30.43 4.57 9.57 11.43
[37] 29.57 17.57 16.57 26.43 16.57 14.57 4.57 13.57 48.43 12.57 25.43 12.57
[49] 12.57 9.43 11.57 11.43 10.57 19.57 9.57 48.43 9.57 5.43 22.43 8.57
[61] 1.57 40.43 6.57 49.43 31.57 5.57 40.57 5.57 3.43 12.57 3.57 2.57
[73] 2.57 7.57 0.57 0.43 1.43 1.43 6.57 2.43 52.43 2.43 20.43 3.43
[85] 7.57 4.43 24.43 4.43 5.43 9.57 6.43 11.57 9.43 4.43 10.43 10.43
[97] 21.57 11.43 8.57 11.43 24.57 12.43 12.43 10.57 13.43 15.43 16.43 17.43
[109] 26.57 18.43 3.43 21.43 13.57 23.43 7.43 25.43 16.57 26.43 12.57 28.43(示例)平均差的计算:组距分组数据1
案例数据:A同学将某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的原始数据,并进行如下的组距式分组统计。其中f表示落在各组的天数。请计算该数据集的平均差是多少?
| index | groups | f |
|---|---|---|
| 1 | [140,150) | 4 |
| 2 | [150,160) | 9 |
| 3 | [160,170) | 16 |
| 4 | [170,180) | 27 |
| 5 | [180,190) | 20 |
| 6 | [190,200) | 17 |
| 7 | [200,210) | 10 |
| 8 | [210,220) | 8 |
| 9 | [220,230) | 4 |
| 10 | [230,240] | 5 |
| Total | - | 120 |
(示例)平均差的计算:组距分组数据2
解题步骤:具体计算表见下一页ppt。
计算各组组中值M: \(M_i\) ,以及组中值与权重的乘积Mf: \(M_if_i\) 。然后计算得出均值: \(\bar{X}=\frac{\sum{M_if_i}}{\sum{f_i}}=185\) 。 - 计算得到离中心差demean: \(M_i-\bar{X}\) ,及其绝对值abs_demean \(|M_i-\bar{X}|\) 。
计算离中心差与权重的乘积demean_f: \((M_i-\bar{X})f_i\) ,及其绝对值abs_demean_f: \(|(M_i-\bar{X})|f_i\)
最后,利用公式计算加总项,进一步计算得到平均差。
\[ \begin{aligned} M_{\mathrm{d}} =\frac{\sum_{i=1}^{k}\left(\left|M_{i}-\bar{X}\right| f_{i}\right)}{\sum{f_i}} = \frac{2040}{120} = 17 \end{aligned} \]
- 含义:与销售量平均数相比,日销售量之间平均相差17台。
(示例)平均差的计算:组距分组数据3
| index | groups | M | f | Mf | demean | abs_demean | demean_f | abs_demean_f |
|---|---|---|---|---|---|---|---|---|
| 1 | [140,150) | 145 | 4 | 580 | -40 | 40 | -160 | 160 |
| 2 | [150,160) | 155 | 9 | 1395 | -30 | 30 | -270 | 270 |
| 3 | [160,170) | 165 | 16 | 2640 | -20 | 20 | -320 | 320 |
| 4 | [170,180) | 175 | 27 | 4725 | -10 | 10 | -270 | 270 |
| 5 | [180,190) | 185 | 20 | 3700 | 0 | 0 | 0 | 0 |
| 6 | [190,200) | 195 | 17 | 3315 | 10 | 10 | 170 | 170 |
| 7 | [200,210) | 205 | 10 | 2050 | 20 | 20 | 200 | 200 |
| 8 | [210,220) | 215 | 8 | 1720 | 30 | 30 | 240 | 240 |
| 9 | [220,230) | 225 | 4 | 900 | 40 | 40 | 160 | 160 |
| 10 | [230,240] | 235 | 5 | 1175 | 50 | 50 | 250 | 250 |
| Total | - | 1900 | 120 | 22200 | 50 | 250 | 0 | 2040 |
方差和标准差:概念和特征
方差(variance)和标准差(standard deviation):是数据离散程度的最常用测度指标,反映了各变量值与均值的平均差异。
根据总体数据计算的,称为总体方差(记为 \(\sigma^2\) )以及总体标准差(记为 \(\sigma^2\) )。
根据样本数据计算的,称为样本方差(记为 \(S^2\) )以及样本标准差(记为 \(S\) )。
- 对于未整理原始样本数据:
\[ \begin{aligned} S^{2}&=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1} \\ S&=\sqrt{\frac{\sum_{i=1}^{n}\left(x_{i}-\bar{X}\right)^{2}}{n-1}} \end{aligned} \]
- 对于组距式分组样本数据:
\[ \begin{aligned} S^{2} &=\frac{\sum_{i=1}^{k}\left(\left(M_{i}-\bar{X}\right)^{2} f_{i}\right)}{n-1} \\ S &=\sqrt{\frac{\sum_{i=1}^{k}\left(\left(M_{i}-\bar{X}\right)^{2} f_{i} \right)}{n-1}} \end{aligned} \]
(示例)计算:原始未整理数据1
案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的样本方差和样本标准差分别是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213(示例)计算:原始未整理数据2
解题步骤:
计算数据集的均值: \(\bar{X} = \frac{\sum{X_i}}{n} = 184.5666667\) 。
计算所有数据的离中心差: \(X_i -\bar{X}\) ,及其平方项 \((X_i -\bar{X})^2\) 。
计算离中心差平方项的求和项 \(\sum_{i=1}^{n}\left((X_{i}-\bar{X})^2\right) = 5.5935467\times 10^{4}\) 。
最后利用公式计算得到样本方差和样本标准差:
\[ \begin{aligned} S^{2} &=\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1} \\ &= \frac{5.5935467\times 10^{4}}{119} = 470.0459 \end{aligned} \]
\[ \begin{aligned} S &=\sqrt{\frac{\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}}{n-1}} \\ &= \sqrt{\frac{5.5935467\times 10^{4}}{119} } = 21.6805 \end{aligned} \]
(示例)计算:组距分组数据1
案例数据:A同学将某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的原始数据,并进行如下的组距式分组统计。其中f表示各组的天数。请计算该数据集的样本方差和样本标准分别是多少?
| index | groups | f |
|---|---|---|
| 1 | [140,150) | 4 |
| 2 | [150,160) | 9 |
| 3 | [160,170) | 16 |
| 4 | [170,180) | 27 |
| 5 | [180,190) | 20 |
| 6 | [190,200) | 17 |
| 7 | [200,210) | 10 |
| 8 | [210,220) | 8 |
| 9 | [220,230) | 4 |
| 10 | [230,240] | 5 |
| Total | - | 120 |
(示例)计算:组距分组数据2
解题步骤:具体计算表见下一页ppt。
计算各组组中值M: \(M_i\) ,以及组中值与权重的乘积Mf: \(M_if_i\) 。然后计算得出分组数据的均值: \(\bar{X}=\frac{\sum{M_if_i}}{\sum{f_i}}=185\) 。
计算得到离中心差demean: \(M_i-\bar{X}\) ,以及离中心差的平方项power2: \({(X_{i}-\bar{X})}^2f_i\) ,再计算离中心差平方项与权重的乘积
power2_f: \((X_{i}-\bar{X})^2f_i\) ,然后得到求和项 \(\sum_{i=1}^{n}\left((M_{i}-\bar{X})^2f_i\right)=5.54\times 10^{4}\) 。最后利用公式计算得到样本方差和样本标准差:
\[ \begin{aligned} S^{2} &=\frac{\sum_{i=1}^{n}{\left(\left(M_{i}-\bar{X}\right)^{2}f_i\right)}}{n-1} \\ &= \frac{5.54\times 10^{4}}{119} = 465.5462 \end{aligned} \]
\[ \begin{aligned} S &=\sqrt{\frac{\sum_{i=1}^{n}{\left(\left(M_{i}-\bar{X}\right)^{2}f_i\right)}}{n-1}} \\ &= \sqrt{\frac{5.54\times 10^{4}}{119} } = 21.5765 \end{aligned} \]
(示例)计算:组距分组数据3
| index | groups | M | f | Mf | demean | power2 | power2_f |
|---|---|---|---|---|---|---|---|
| 1 | [140,150) | 145 | 4 | 580 | -40 | 1600 | 6400 |
| 2 | [150,160) | 155 | 9 | 1395 | -30 | 900 | 8100 |
| 3 | [160,170) | 165 | 16 | 2640 | -20 | 400 | 6400 |
| 4 | [170,180) | 175 | 27 | 4725 | -10 | 100 | 2700 |
| 5 | [180,190) | 185 | 20 | 3700 | 0 | 0 | 0 |
| 6 | [190,200) | 195 | 17 | 3315 | 10 | 100 | 1700 |
| 7 | [200,210) | 205 | 10 | 2050 | 20 | 400 | 4000 |
| 8 | [210,220) | 215 | 8 | 1720 | 30 | 900 | 7200 |
| 9 | [220,230) | 225 | 4 | 900 | 40 | 1600 | 6400 |
| 10 | [230,240] | 235 | 5 | 1175 | 50 | 2500 | 12500 |
| Total | - | 1900 | 120 | 22200 | 50 | 8500 | 55400 |
标准分数
标准分数(standard score):也称标准化值,记为 \(Z_i\) ,计算公式为:
\[ Z_i=\frac{(X_i-\bar{X})}{S_{X}} \]
标准分数的特征:
对某一个值在一组数据中相对位置的度量。
可用于判断一组数据是否有离群点(outlier)。
用于对变量的标准化处理。
标准化值 \(Z_i\) 只是将原始数据 \(X_i\) 进行了线性变换,它并没有改变一个数据在该组数据中的位置,也没有改变该组数分布的形状,而只是使该组数据均值为0,标准差为1。因此也被称为标准化变换。
变异系数:概念和作用
变异系数(coefficient of variation):是用相对数表示的变异指标,又称标志变动系数。根据分子的不同,又具体分为:
全距变异系数: \(V_R= \frac{R}{\bar{X}}\)
平均差变异系数: \(V_{AD}= \frac{R}{\bar{X}}\)
标准差变异系数: \(V_{S}= \frac{S}{\bar{X}}\)
变异系数的作用:抽象掉标志值大小及计量单位的影响。
(示例1)计算几类变异系数:案例说明
案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的全距变异系数、平均差变异系数和标准差变异系数分别是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213(示例1)计算几类变异系数:解题分析
根据前面已经得到的相关结算结果:数据集的均值 \(\bar{X} =184.57\) ;全距 \(R=96\) ;平均差 \(AD =17.43\) ;样本标准差 \(S =21.68\) 。
然后,利用公式分别计算得到几类变异系数:
全距变异系数: \(V_R= \frac{R}{\bar{X}}=\frac{96}{184.5666667} =0.5201\)
平均差变异系数: \(V_{AD}= \frac{R}{\bar{X}}=\frac{17.4283333}{184.5666667} =0.0944\)
标准差变异系数: \(V_{S}= \frac{S}{\bar{X}}=\frac{21.6805429}{184.5666667} =0.1175\)
(示例2)计算标准差变异系数:案例说明
案例数据:某工厂有甲、乙两个工人小组,每个小组各有10个工人,两个小组的日产量数据分别如下。请你通过一些计算,比较那个小组的产量更稳定?
- 甲组工人的日产量(件/天)数据:
[1] 68 68 68 62 61 59 69 85 72 83- 乙组工人的日产量(件/天)数据:
[1] 16 15 17 22 12 18 23 20 21 15(示例2)计算标准差变异系数:解题分析
甲组工人产量均值 \(\bar{X_甲}=\frac{\sum{X_i}}{n}=69.5\) ;产量标准差 \(S_甲=\sqrt{\frac{\sum{(X_i -\bar{X}^2)}}{n-1}}=8.6570459\) 。
乙组工人产量均值 \(\bar{X_乙}=\frac{\sum{X_i}}{n}=17.9\) ;产量标准差 \(S_乙=\sqrt{\frac{\sum{(X_i -\bar{X}^2)}}{n-1}}=3.5418137\) 。
显然,从标准差来看甲组离散程度大于乙组 \(S_甲 > S_乙\) ,但是单纯从标准差大小来断定工人产量稳定性,是不恰当的。因为我们还可以看到,甲组的均值也高于乙组 \(\bar{X}_甲 > \bar{X}_乙\) 。
因此,我们需要进一步计算标准差变异系数指标来加以比较。可以发现,甲组要更优。
\[ V_{S甲}= \frac{S_甲}{\bar{X}_甲}=0.1246 < V_{S乙}= \frac{S乙}{\bar{X}_乙}=0.1979 \]
4.5 分布形态的度量
偏态及其测度
峰态及其测度
内容导航
偏态及其测度
偏态(skewness):对数据分布偏斜程度的测度*。
偏态系数SK的特征:
\(SK=0\) 为对称分布
\(SK> 0\) 为右偏分布
\(SK< 0\)为左偏分布
\(|SK|>1\) ,被称为高度偏态分布;
\(0.5<|SK| \leq 1\) ,被认为是中等偏态分布;
\(SK \simeq 0\) ,偏斜程度就越低 。
偏态系数的计算
- 根据原始数据计算:
\[ \begin{aligned} SK = \frac{n}{(n-1)(n-2)}\frac{ \sum_{i=1}^n{(X_i-\bar{X})^3}}{S_X^3} \end{aligned} \]
- 根据分组数据计算:
\[ \begin{aligned} SK = \frac{1}{\sum{f_i}} \cdot \frac{\sum_{i=1}^n{\left((M_i-\bar{X})^3 \cdot f_i\right)}}{S_X^3} \end{aligned} \]
\(n\) 表示总次数; \(f_i\) 表示各组次数; \(M_i\) 表示各组组中值; \(S_X\) 表示样本标准差 \(S_X =\sqrt{\frac{\sum_1^n{(X_i- \bar{X})^2}}{n-1}}\) 。
(示例)偏态系数的计算:未分组原始数据1
Loading required package: moments案例数据:某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的偏度系数SK是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213(示例)偏态系数的计算:未分组原始数据2
解题步骤:
计算数据的均值 \(\bar{X} = \frac{\sum{X_i}}{n}=184.5667\) 。
计算数据的样本标准差 \(S_X =\sqrt{\frac{\sum_{i=1}^n{(X_i- \bar{X})^2}}{n-1}}=21.6805\) 。
利用公式计算得出偏度系数SK。
\[ \begin{aligned} SK = \frac{n}{(n-1)(n-2)}\frac{ \sum_{i=1}^n{(X_i-\bar{X})^3}}{S_X^3} =\frac{120}{(119\times 118)} \frac{5.4\times 10^{5}}{1.0044867\times 10^{4}} = 0.4002 \end{aligned} \]
(示例)偏态系数的计算:分组后组距式数据
案例数据:A同学将某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的原始数据(见前例),并进行如下的组距式分组统计。其中f表示落在各组的天数。请计算所有数据的偏度系数SK是多少?
| index | groups | f |
|---|---|---|
| 1 | [140,150) | 4 |
| 2 | [150,160) | 9 |
| 3 | [160,170) | 16 |
| 4 | [170,180) | 27 |
| 5 | [180,190) | 20 |
| 6 | [190,200) | 17 |
| 7 | [200,210) | 10 |
| 8 | [210,220) | 8 |
| 9 | [220,230) | 4 |
| 10 | [230,240] | 5 |
| Total | - | 120 |
(示例)偏态系数的计算:分组后组距式数据
解题步骤:具体计算表见下一页ppt。
计算各组组中值M: \(M_i\) ,然后计算得出均值: \(\bar{X}=\frac{\sum{M_if_i}}{\sum{f_i}}=185\) 。
计算得到离中心差demean: \(M_i-\bar{X}\) 。
对离中心差分别计算2次方项power2: \((M_i-\bar{X})^2\) 和3次方项power3: \((M_i-\bar{X})^3\) 。以及各自幂指数项与权重f的乘积,power2_f: \((M_i-\bar{X})^2f_i\) 和3次方项power3_f: \((M_i-\bar{X})^3f_i\) 。
分别进行行汇总,得到各项的加总项。
计算出分组后数据的样本标准差 \(S_X =\sqrt{\frac{\sum_1^n{(M_i- \bar{X})^2}}{n-1}}\)
最后,利用公式进一步计算得到偏度系数SK。
\[ \begin{aligned} SK = \frac{1}{\sum{f_i}} \cdot \frac{\sum_{i=1}^n{\left((M_i-\bar{X})^3 \cdot f_i\right)}}{S_X^3} = \frac{1}{120} \cdot \frac{540000}{10044.8673} = 0.4480 \end{aligned} \]
(示例)偏态系数的计算:分组后组距式数据
| index | groups | f | M | Mf | demean | power2 | power2_f | power3 | power3_f |
|---|---|---|---|---|---|---|---|---|---|
| 1 | [140,150) | 4 | 145 | 580 | -40 | 1600 | 6400 | -64000 | -256000 |
| 2 | [150,160) | 9 | 155 | 1395 | -30 | 900 | 8100 | -27000 | -243000 |
| 3 | [160,170) | 16 | 165 | 2640 | -20 | 400 | 6400 | -8000 | -128000 |
| 4 | [170,180) | 27 | 175 | 4725 | -10 | 100 | 2700 | -1000 | -27000 |
| 5 | [180,190) | 20 | 185 | 3700 | 0 | 0 | 0 | 0 | 0 |
| 6 | [190,200) | 17 | 195 | 3315 | 10 | 100 | 1700 | 1000 | 17000 |
| 7 | [200,210) | 10 | 205 | 2050 | 20 | 400 | 4000 | 8000 | 80000 |
| 8 | [210,220) | 8 | 215 | 1720 | 30 | 900 | 7200 | 27000 | 216000 |
| 9 | [220,230) | 4 | 225 | 900 | 40 | 1600 | 6400 | 64000 | 256000 |
| 10 | [230,240] | 5 | 235 | 1175 | 50 | 2500 | 12500 | 125000 | 625000 |
| Total | - | 120 | 1900 | 22200 | 50 | 8500 | 55400 | 125000 | 540000 |
峰态系数的计算
- 根据原始数据计算:
\[ \begin{aligned} KT = \frac{n(n+1)}{(n-1)(n-2)(n-3)} \frac{\sum_{i=1}^n{(X_i-\bar{X})^4}}{S_X^4} - \frac{3(n-1)^2}{(n-2)(n-3)} \end{aligned} \]
- 根据分组数据计算:
\[ \begin{aligned} KT = \frac{\sum_{i=1}^n{\left((M_i-\bar{X})^4 \cdot f_i\right)} }{(\sum{f_i})\cdot S_X^4} \end{aligned} \]
\(n\) 表示总次数; \(f_i\) 表示各组次数; \(M_i\) 表示各组组中值; \(S_X\) 表示样本标准差 \(S_X =\sqrt{\frac{\sum_1^n{(X_i- \bar{X})^2}}{n-1}}\) 。
(示例)峰态系数的计算:未分组原始数据1
案例数据(同前):某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的数据记录如下,请计算该数据集的峰度系数KT是多少?
[1] 234 143 187 161 150 228 153 166 154 174 156 203 159 198 160 152 161 162
[19] 163 196 164 226 165 165 187 141 214 149 178 223 218 179 215 180 175 196
[37] 155 167 168 211 168 170 180 171 233 172 210 172 172 194 173 196 174 165
[55] 175 233 175 190 207 176 183 225 178 234 153 179 144 179 188 172 181 182
[73] 182 177 184 185 186 186 178 187 237 187 205 188 177 189 209 189 190 175
[91] 191 173 194 189 195 195 163 196 176 196 160 197 197 174 198 200 201 202
[109] 158 203 188 206 171 208 192 210 168 211 172 213(示例)峰态系数的计算:未分组原始数据1
解题步骤:
计算数据的均值 \(\bar{X} = \frac{\sum{X_i}}{n}=184.5667\) 。
计算数据的样本标准差 \(S_X =\sqrt{\frac{\sum_{i=1}^n{(X_i- \bar{X})^2}}{n-1}}=21.6805\) 。
利用公式计算得出峰度系数KT。
\[ \begin{aligned} KT &= \frac{n(n+1)}{(n-1)(n-2)(n-3)} \frac{\sum_{i=1}^n{(X_i-\bar{X})^4}}{S_X^4} - \frac{3(n-1)^2}{(n-2)(n-3)}\\ & =\frac{120\times 121}{(119\times 118 \times 117)} \frac{7.01\times 10^{7}}{2.1673328\times 10^{5}} - \frac{3\times 119^2}{118 \times 117} = 2.7353 \end{aligned} \]
(示例)峰态系数的计算:分组后组距式数据
案例数据:A同学将某电脑销售公司在4个月120天( \(n=120\) )的电脑销售台数的原始数据(见前例),并进行如下的组距式分组统计。其中f表示落在各组的天数。请计算所有数据的峰态系数KT是多少?
| index | groups | f |
|---|---|---|
| 1 | [140,150) | 4 |
| 2 | [150,160) | 9 |
| 3 | [160,170) | 16 |
| 4 | [170,180) | 27 |
| 5 | [180,190) | 20 |
| 6 | [190,200) | 17 |
| 7 | [200,210) | 10 |
| 8 | [210,220) | 8 |
| 9 | [220,230) | 4 |
| 10 | [230,240] | 5 |
| Total | - | 120 |
(示例)峰态系数的计算:分组后组距式数据
解题步骤:具体计算表见下一页ppt。
计算各组组中值M: \(M_i\) ,然后计算得出均值: \(\bar{X}=\frac{\sum{M_if_i}}{\sum{f_i}}=185\) 。
计算得到离中心差demean: \(M_i-\bar{X}\) 。对离中心差分别计算2次方项power2: \((M_i-\bar{X})^2\) 和4次方项power4: \((M_i-\bar{X})^4\) 。以及各自幂指数项与权重f的乘积,power2_f: \((M_i-\bar{X})^2f_i\) 和4次方项power4_f: \((M_i-\bar{X})^4f_i\) 。
分别进行行汇总,得到各项的加总项。计算出分组后数据的样本标准差 \(S_X =\sqrt{\frac{\sum_1^n{(M_i- \bar{X})^2}}{n-1}}\)
最后,利用公式进一步计算得到峰度系数KT。
\[ \begin{aligned} KT = \frac{\sum_{i=1}^n{\left((M_i-\bar{X})^4 \cdot f_i\right)} }{(\sum{f_i})\cdot S_X^4} = \frac{1}{120} \cdot \frac{70100000}{216733.2815} = 2.6953 \end{aligned} \]
(示例)峰态系数的计算:分组后组距式数据
| index | groups | f | M | Mf | demean | power2 | power2_f | power4 | power4_f |
|---|---|---|---|---|---|---|---|---|---|
| 1 | [140,150) | 4 | 145 | 580 | -40 | 1600 | 6400 | 2560000 | 10240000 |
| 2 | [150,160) | 9 | 155 | 1395 | -30 | 900 | 8100 | 810000 | 7290000 |
| 3 | [160,170) | 16 | 165 | 2640 | -20 | 400 | 6400 | 160000 | 2560000 |
| 4 | [170,180) | 27 | 175 | 4725 | -10 | 100 | 2700 | 10000 | 270000 |
| 5 | [180,190) | 20 | 185 | 3700 | 0 | 0 | 0 | 0 | 0 |
| 6 | [190,200) | 17 | 195 | 3315 | 10 | 100 | 1700 | 10000 | 170000 |
| 7 | [200,210) | 10 | 205 | 2050 | 20 | 400 | 4000 | 160000 | 1600000 |
| 8 | [210,220) | 8 | 215 | 1720 | 30 | 900 | 7200 | 810000 | 6480000 |
| 9 | [220,230) | 4 | 225 | 900 | 40 | 1600 | 6400 | 2560000 | 10240000 |
| 10 | [230,240] | 5 | 235 | 1175 | 50 | 2500 | 12500 | 6250000 | 31250000 |
| Total | - | 120 | 1900 | 22200 | 50 | 8500 | 55400 | 13330000 | 70100000 |
本章结束

第4章 数据的概括性度量