统计学原理

(Statistics)

第2章 数据收集、整理和清洗
2-7节 抽样分布和抽样误差


Hu Huaping (胡华平)

huhuaping01 at hotmail.com

经济管理学院(CEM)

第二章 数据收集、整理和清洗

2.1 数据目标

2.2 数据收集

2.3 资料整理和数据清洗

2.4 数据的数据库化

2.5 数据质量

2.6 抽样设计

2.7 抽样分布和抽样误差

2.8 问卷设计技术

2.7 抽样分布和抽样误差

离散和连续随机变量

总体和样本特征

抽样误差计算

离散和连续随机变量

离散随机变量：离散事件

六点骰子的样本空间（sample space）为： \(\{1,2,3,4,5,6\}\) ，随机摇一次骰子结果可能是：

set.seed(123)  # 设置随机种子
sample(1:6, 1)  # 随机摇一次骰子
[1] 3

离散随机变量：概率分布

  • 六点骰子的概率分布pdf

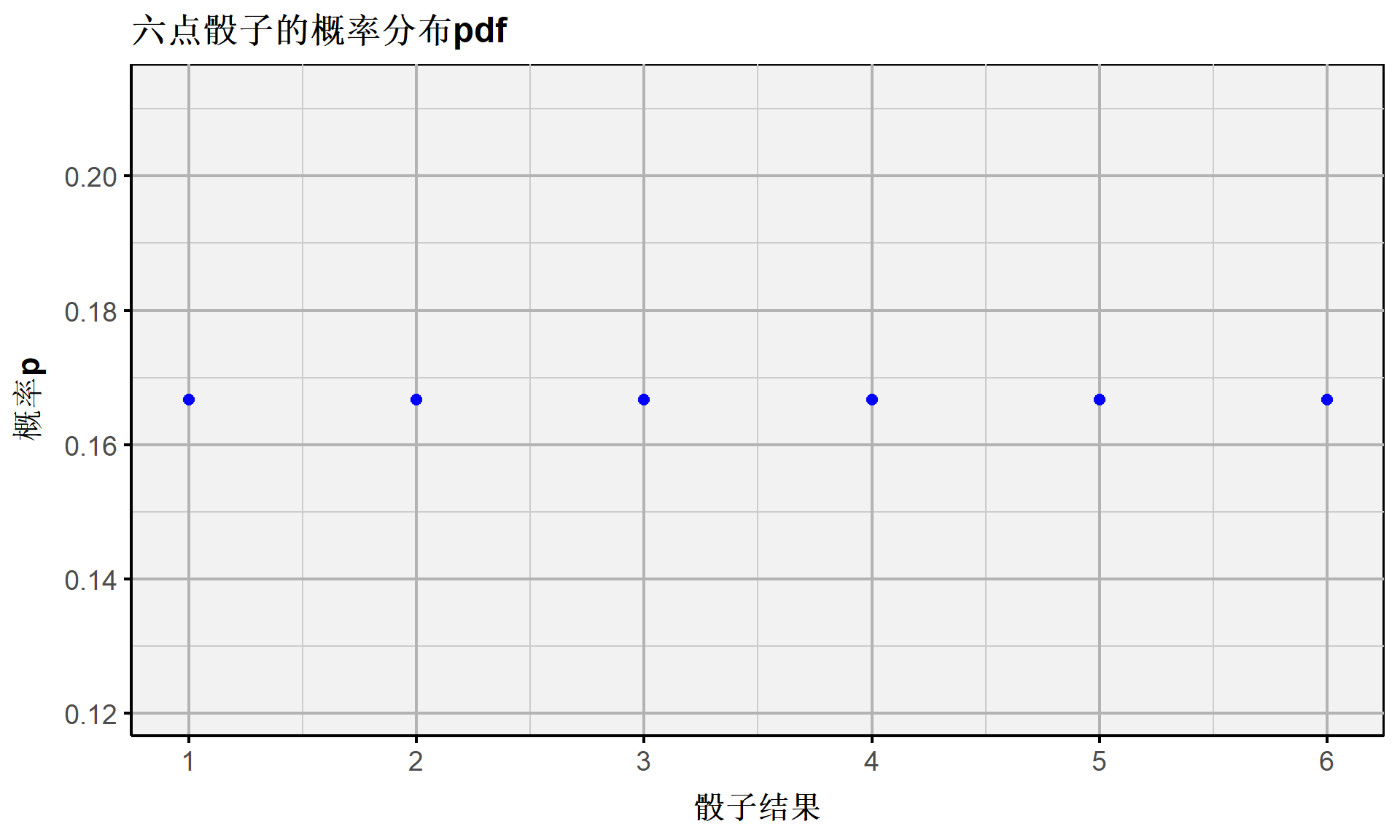
离散随机变量：概率分布

  • 六点骰子的累积概率分布cdf

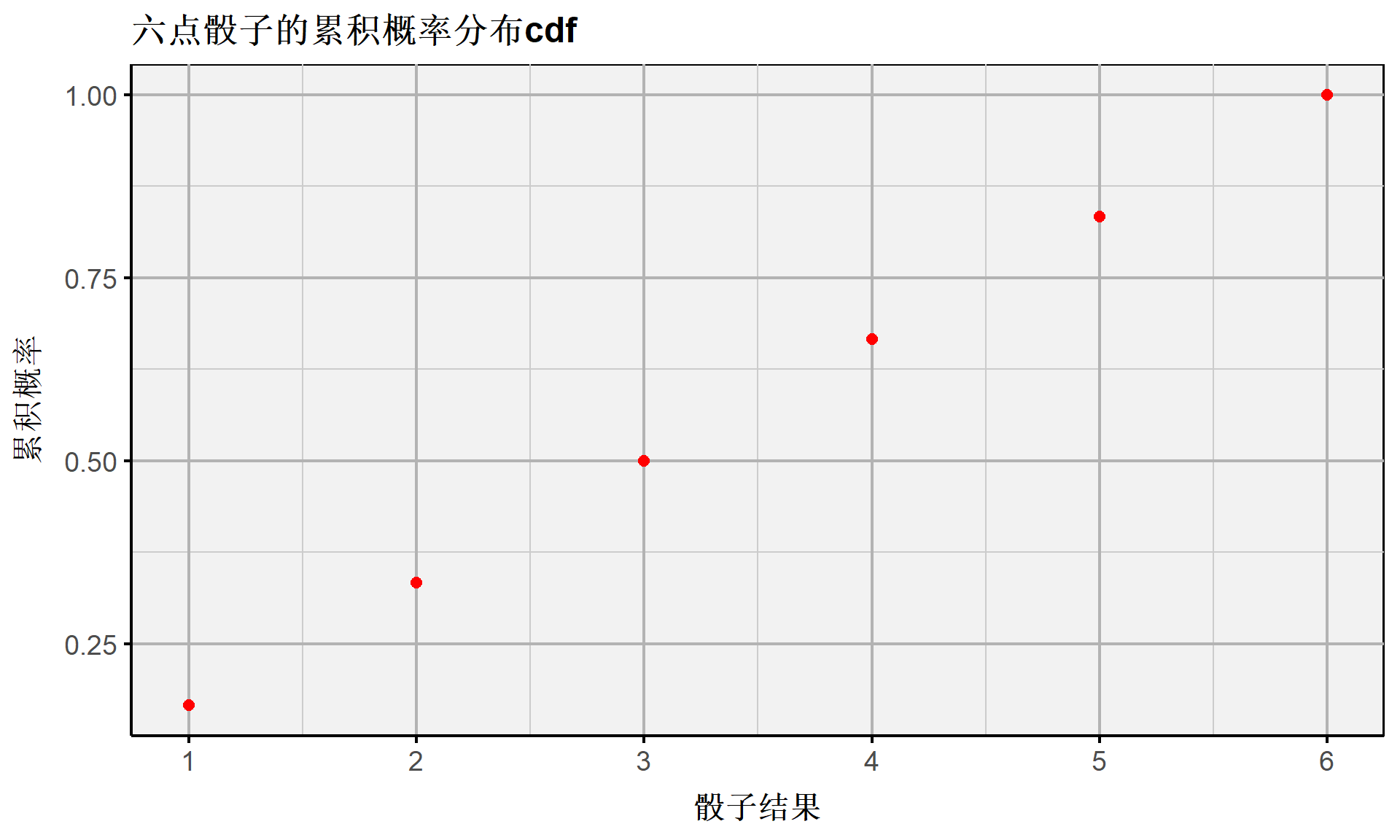
离散随机变量：伯努利事件（概率分布）

抛硬币事件 \(k\) 有两种可能结果： \(H\) （头像）和 \(T\) （花案）。我们随机抛一次硬币的结果可能是：

set.seed(123)  # 设置随机种子
sample(c("H", "T"), 1)  # 随机抛一次硬币
[1] "H"

对于连续 \(n\) 次抛硬币，事件 \(k\) 服从伯努利 \(k \sim B(n,p)\) 分布，其概率为：

\[ f(k)=P(k)=\begin{pmatrix}n\\ k \end{pmatrix} \cdot p^k \cdot (1-p)^{n-k}=\frac{n!}{k!(n-k)!} \cdot p^k \cdot (1-p)^{n-k} \]

离散随机变量：伯努利事件（概率分布）

例如，连续抛10次硬币且其中5次为头像朝上的伯努利概率记为 \(P(k=5\vert n = 10, p = 0.5)\) ，具体计算R函数及其结果为：

p_k5 <- dbinom(
  x = 5,      # 头像朝上次数
  size = 10,  # 抛10次硬币
  prob = 0.5  # H和T的概率均等
  )
[1] "24.609%"
  • 因此，连续抛10次硬币（ \(n=10\) ）且其中5次为头像朝上（ \(k=5\) ）的伯努利事件（ \(p=0.5\) ）出现的概率为24.61%。

离散随机变量：伯努利事件（概率分布）

又例如，连续抛10次硬币且其中头像朝上次数在 \(4 \sim 7\) 次之间的伯努利概率记为 \(P(4 \leq k \leq 7) = P(k \leq 7) - P(k\leq3 )\) ，具体计算R函数及其结果为：

### 先计算头像朝上次数为7次的概率
p_k7 <- pbinom(
  size = 10, # 抛10次硬币
  prob = 0.5, # H和T的概率均等
  q = 7 # 头像朝上次数
  )
### 再计算头像朝上次数为3次的概率
p_k3 <- pbinom(
  size = 10, # 抛10次硬币
  prob = 0.5, # H和T的概率均等
  q = 3 # 头像朝上次数
  )
### 最后计算头像朝上次数为4次到7次的概率
p_k47 <- p_k7 - p_k3
[1] "94.531%"
[1] "17.188%"
[1] "77.344%"
  • 因此，连续抛10次硬币（ \(n=10\) ）且其中头像朝上次数（ \(4 \le k \le 7\) ）的伯努利事件（ \(p=0.5\) ）出现的概率为77.34%。

离散随机变量：伯努利事件（概率分布）

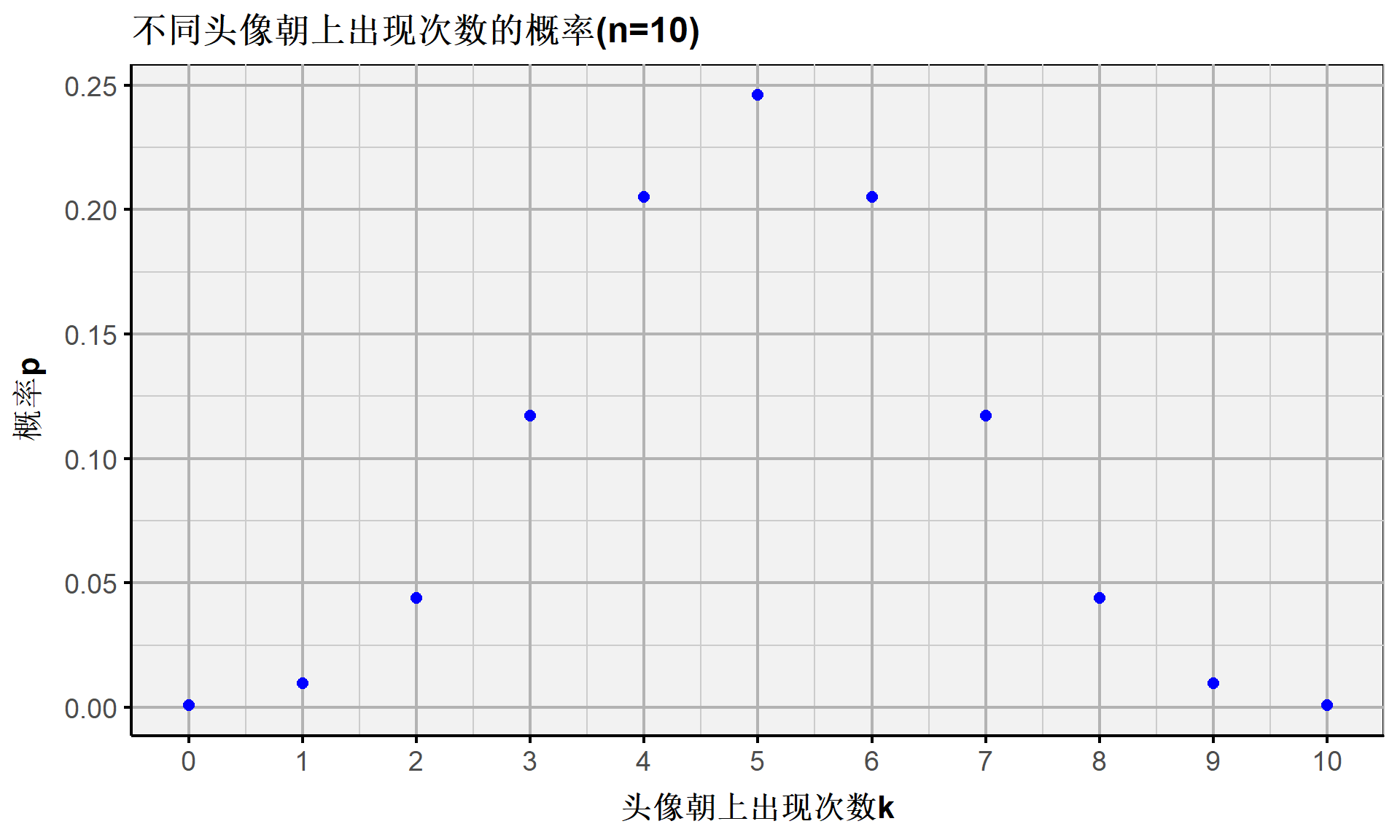
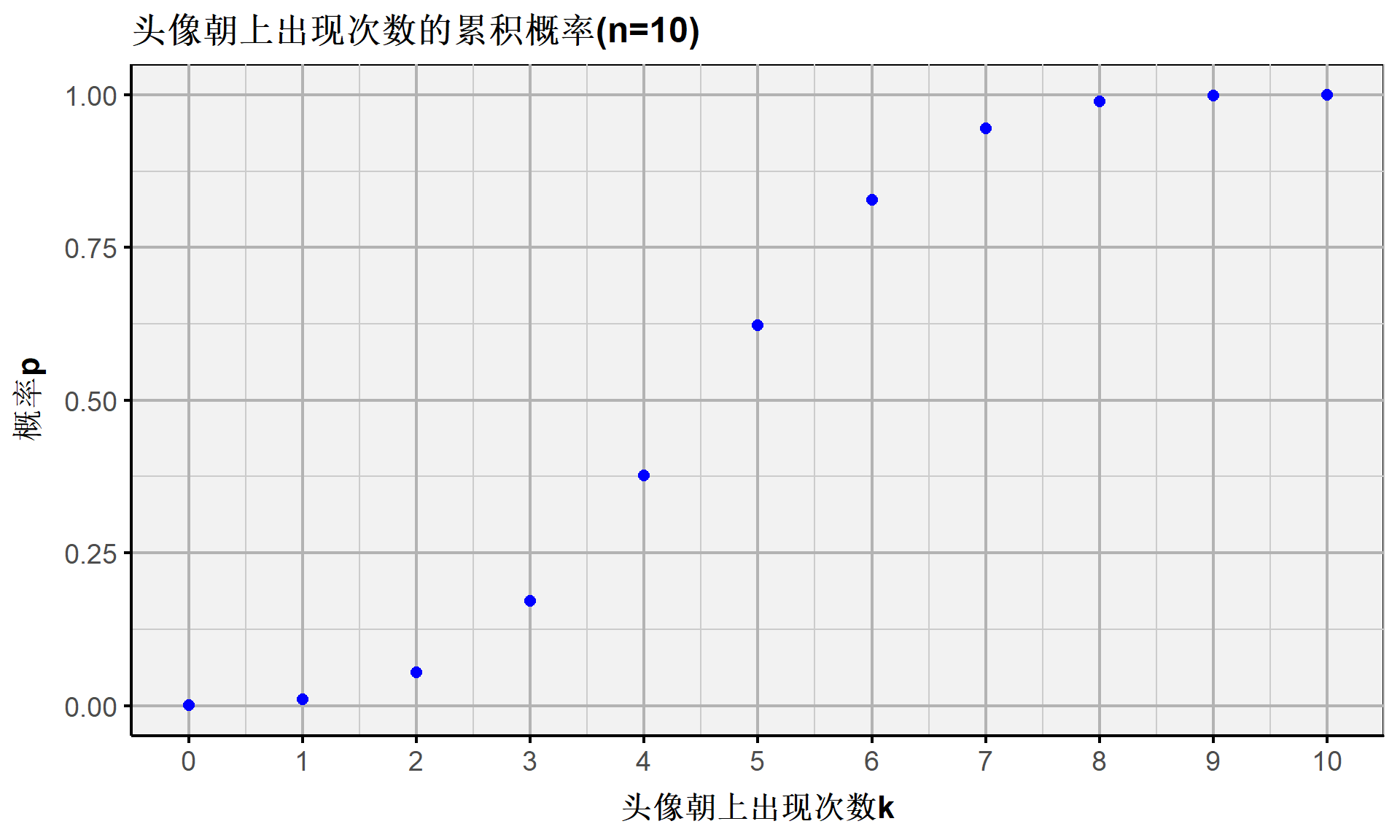
连续随机变量：概率、期望和方差

对于一个连续分布事件 \(X\) ，给定其概率密度函数（PDF）为 \(f_X(x)\) ，那么：

  • 其累积概率密度函数（CDF）： \(P(a \leq X \leq b) = \int_a^b f_X(x) \mathrm{d}x\)

  • 而且有完全概率密度为： \(P(-\infty \leq X \leq \infty) = \int_{-\infty}^{\infty} f_X(x) \mathrm{d}x = 1\) 。

  • 进一步，其期望为： \(E(X) = \mu_X = \int X f_X(x) \mathrm{d}x\) 。

  • 其方差为： \(\text{Var}(X) = \sigma_X^2 = \int (X - \mu_X)^2 f_X(x) \mathrm{d}x\)

连续随机变量：正态分布（PDF、CDF）

一个变量 \(X\) 若服从正态分布，则由两个参数来确定，一个是期望 \(\mu\) ，另一个是方差 \(\sigma^2\) ，并记为： \(Y \sim \mathcal{N}(\mu,\sigma^2)\) 。正态分布的分布密度函数（PDF）的理论表达式为：

\[ \begin{align} f(X) = \frac{1}{\sqrt{2 \pi} \sigma} \exp{[-(X - \mu)^2/(2 \sigma^2)]}. \end{align} \]

其中，标准正态分布属于一种特殊形式的正态分布，其期望为0，方差为1，一般记为： \(X \sim Z(0,1)\) ，其概率密度函数（PDF）一般记为 \(\phi\) ，其累积概率密度函数（CDF）一般记为 \(\Phi\) ，也即有：

\[ \phi(c) = \Phi'(c) \ \ , \ \ \Phi(c) = P(Z \leq c) \ \ , \ \ Z \sim \mathcal{N}(0,1). \] 而且还有：若 \(Y \sim \mathcal{N}(\mu, \sigma^2)\) ，则 \(Y^{\ast} = \frac{Y -\mu}{\sigma} \sim {Z}(0,1)\) 。

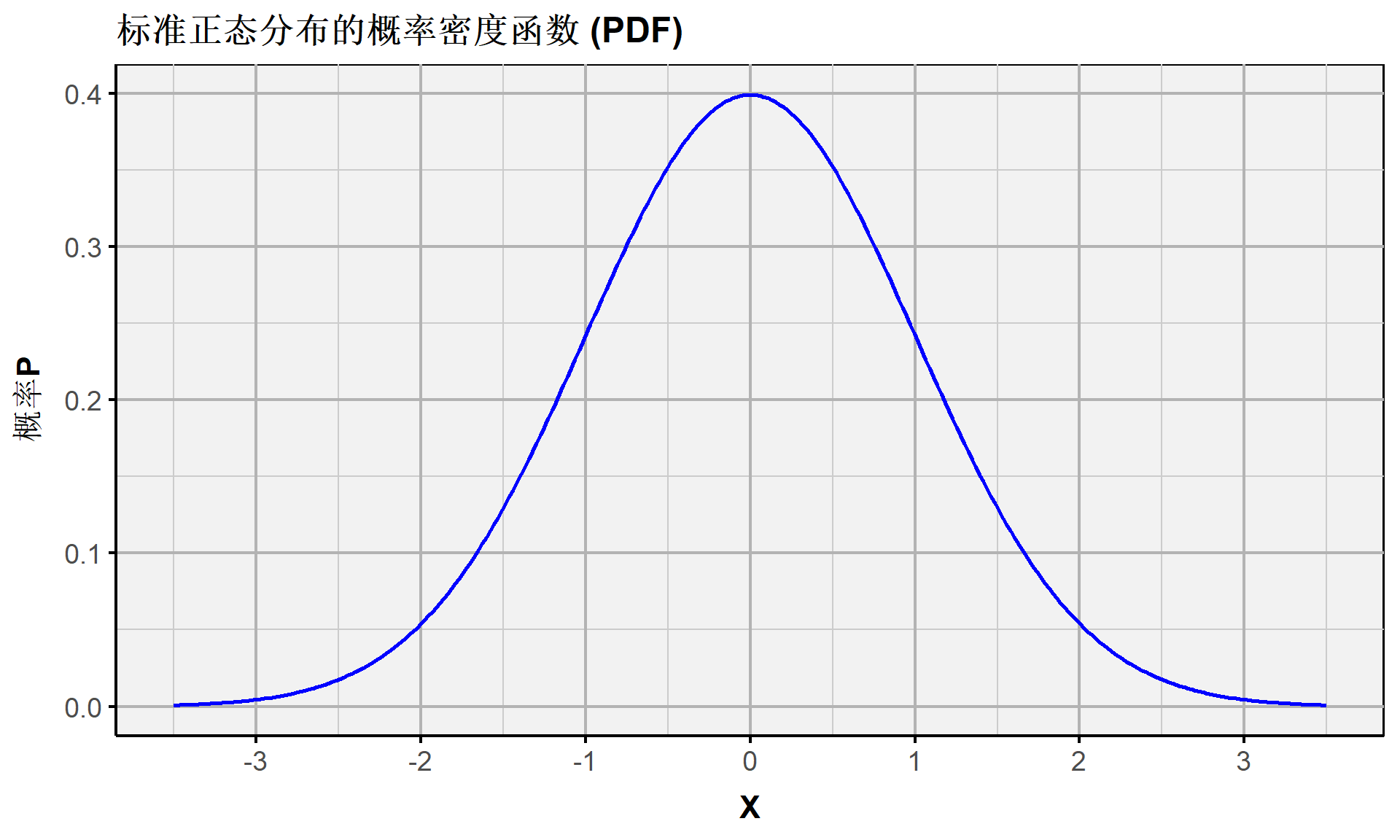
连续随机变量：正态分布（PDF）

正态分布的概率密度函数为：

\[ \phi(X) = \frac{1}{\sqrt{2 \pi} \sigma} \exp{[-(X - \mu)^2/(2 \sigma^2)]} \]

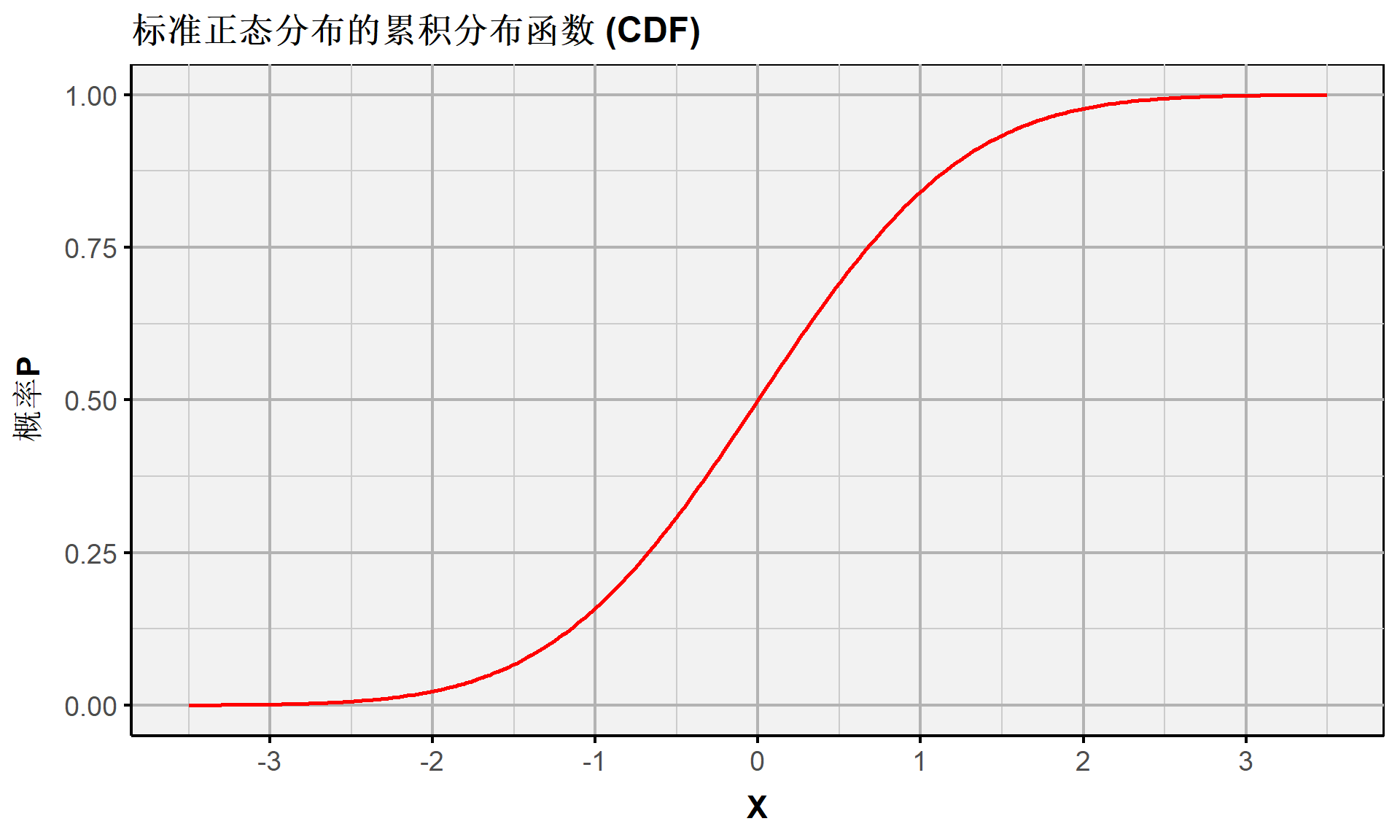
连续随机变量：正态分布（CDF）

正态分布的累积概率密度函数，以及具体的积分过程如下：

\[ \begin{aligned} \Phi(c) &= P(X \leq c) \ \ , \ \ X \sim \mathcal{N}(0,1)\\ &= \int_{-\infty}^{c} \phi(X) \mathrm{d}X \end{aligned} \]

连续随机变量：正态分布（二元联合正态）

连续随机变量：卡方分布（PDF、CDF）

\[ \begin{align} if, \ \ & Z_m \overset{i.i.d.}{\sim} \mathcal{N}(0,1) \\ then, \ \ & Z_1^2 + \dots + Z_M^2 = \sum_{m=1}^M Z_m^2 \sim \chi^2(M) \ \ \end{align} \]

卡方分布的概率密度函数公式为：

\[ f(X) = \frac{1}{2^{\frac{m}{2}} \Gamma\left(\frac{m}{2}\right)} X^{\frac{m}{2}-1} e^{-\frac{X}{2}} \]

连续随机变量：卡方分布（PDF、CDF）

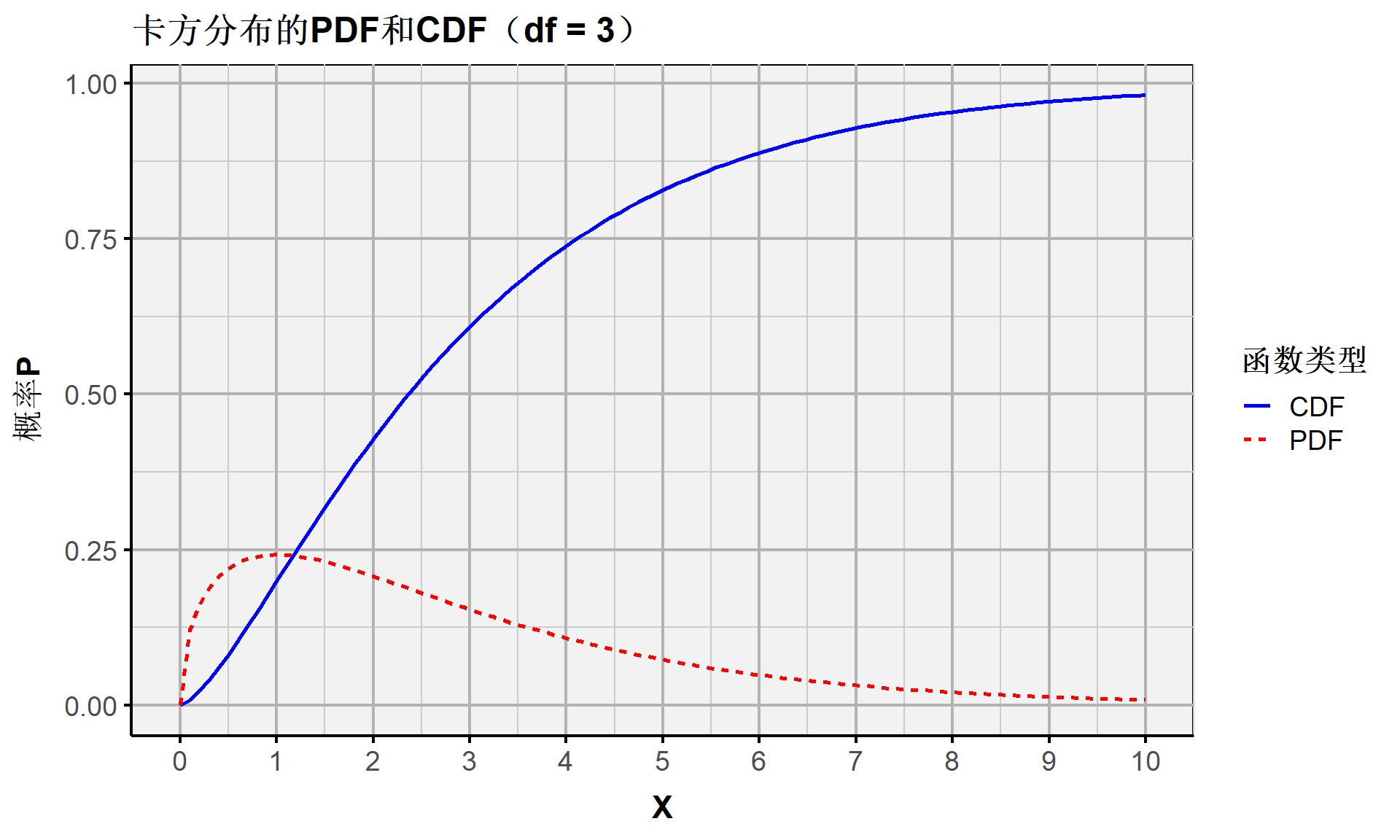
连续随机变量：不同自由度df下卡方分布的概率密度函数

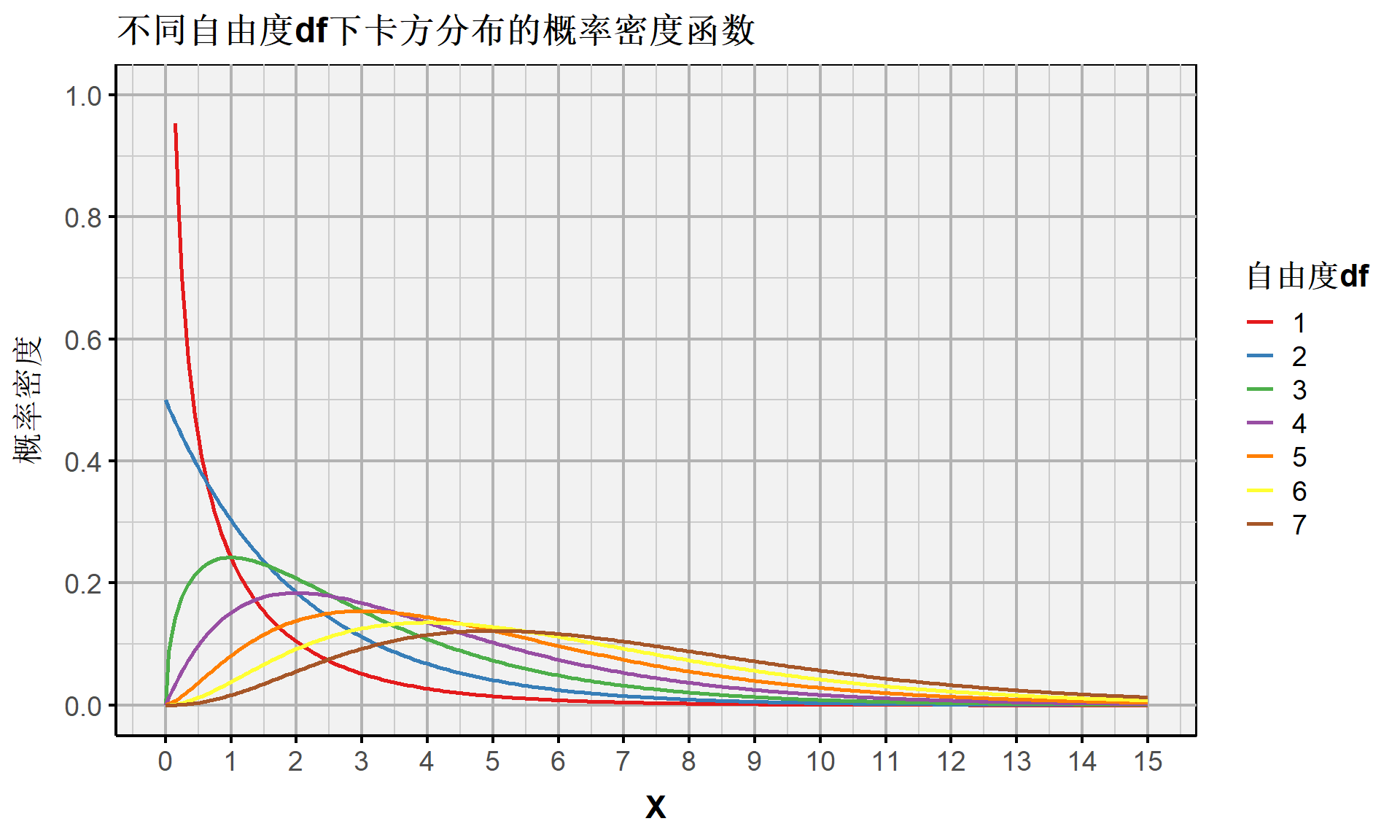
连续随机变量：不同自由度df下卡方分布的累积概率函数

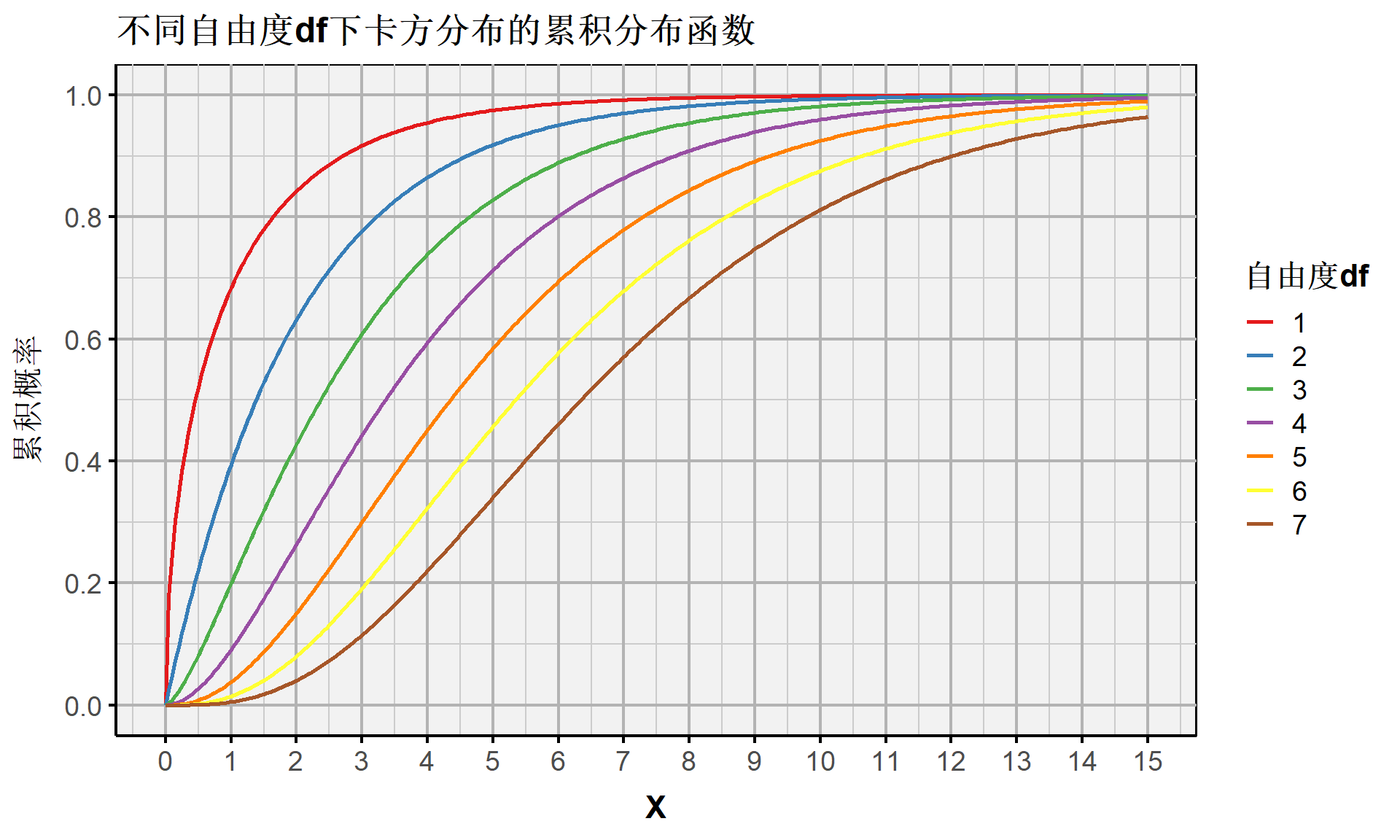
连续随机变量：t分布（PDF、CDF）

假定随机变量 \(Z \sim \mathcal{N}(0,1)\) 服从标准正态分布，随机变量 \(W \sim \chi^2(m)\) 卡方分布，而且二者互相独立，那么可以构造出一个如下的新随机变量 \(T\) ，它将服从t分布：

\[ T= \frac{Z}{\sqrt{W/m}} \sim t(m) \]

t分布的概率密度函数公式为：

\[ f(T) = \frac{\Gamma\left(\frac{m+1}{2}\right)}{\sqrt{m\pi} \Gamma\left(\frac{m}{2}\right)} \left(1 + \frac{T^2}{m}\right)^{-\frac{m+1}{2}} \]

连续随机变量：不同自由度下t分布的概率密度

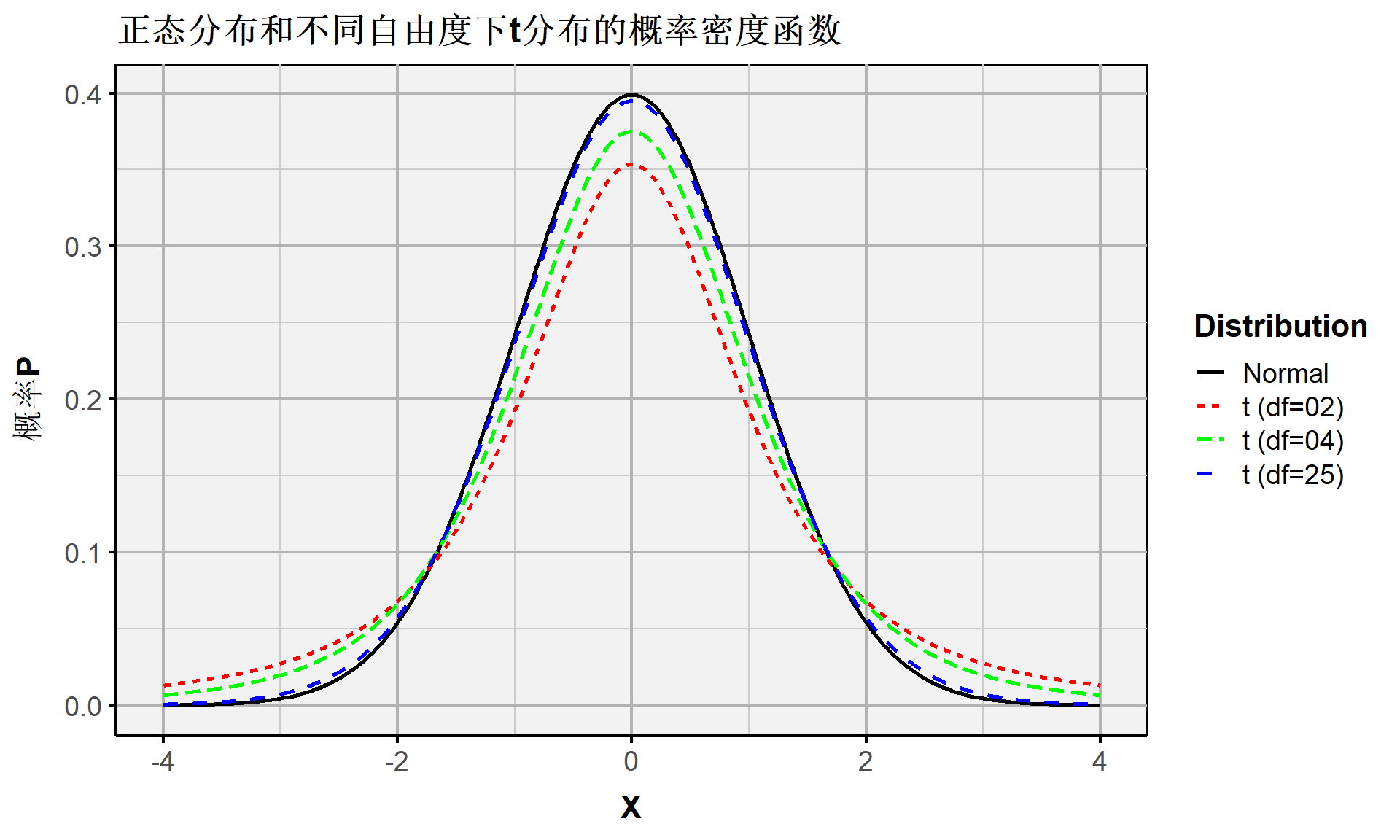
连续随机变量：不同自由度下t分布的累积概率

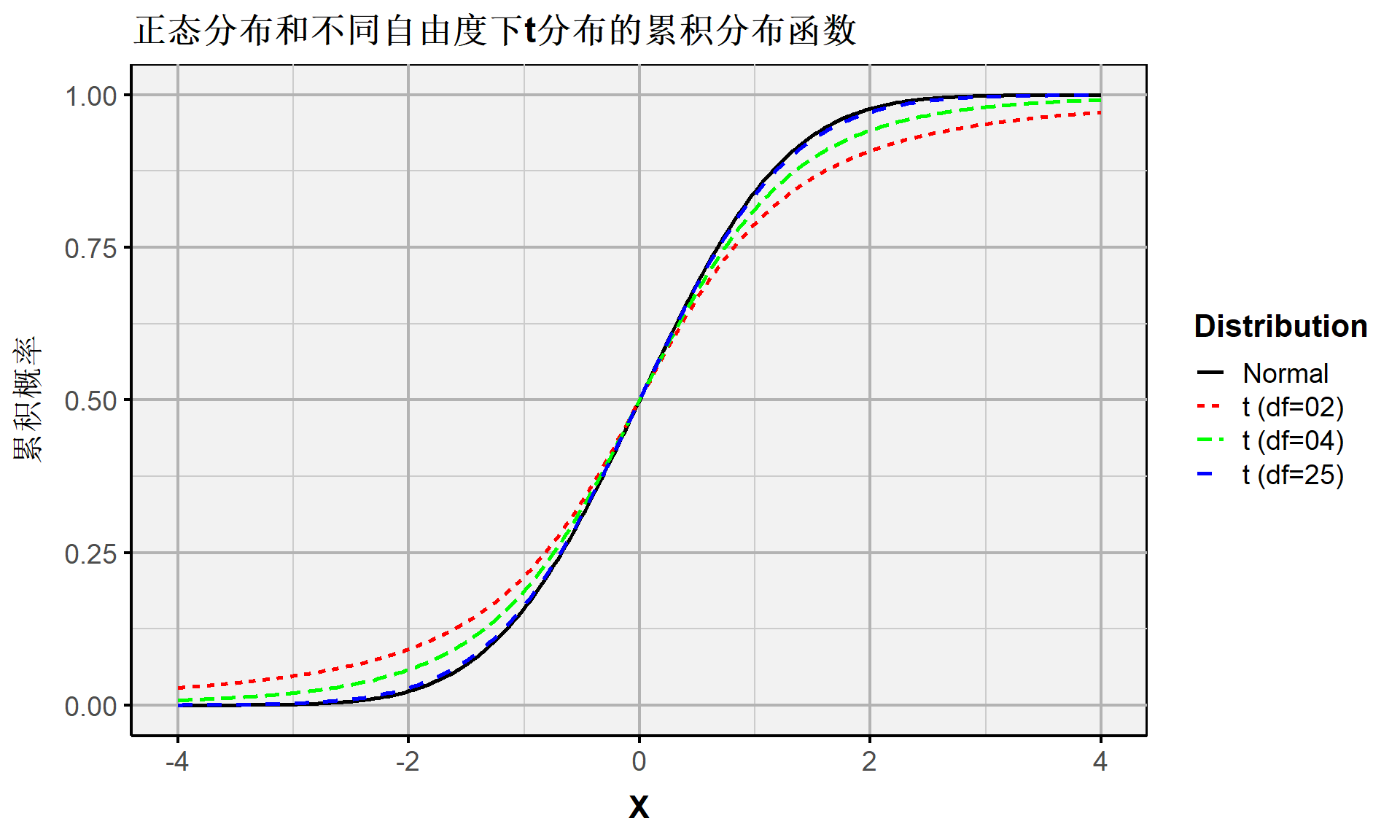
总体和样本特征

总体的特征：总体期望和总体方差

随机变量 \(Y\) 有6种可能取值 \(\{ 1,2,3,4,5,6\}\) ，那么每种可能取值的概率分别为：

总体期望 \(\mu_Y\) 和总体方差 \(\sigma^2_Y\) ：

\[ \begin{align} E(Y) & \equiv \mu_Y= \sum_1^6{(Y_i\cdot p(Y_i))} = \frac{1}{6}\sum_1^6{Y_i} = \frac{1}{6} \times 21 = 3.50 \\ Var(Y)& \equiv \sigma^2_Y= E\left(Y_i - E(Y)\right)^2=E\left(Y_i - \mu \right)^2 = \sum_1^6{\left((Y_i-\mu)p(Y_i)\right)}\\ & = \frac{1}{6}\left[(1-3.5)^2+ (2-3.5)^2+ \cdots + (6-3.5)^2\right] \\ & = 3.89 \end{align} \]

样本的特征：样本均值和样本方差

从上述总体中有放回地随机抽选8次，得到1份样本容量 \(n=8\) 的如下样本数据：

[1] 5 1 5 6 3 5 5 3

样本均值 \(\bar{y}\) 和样本方差 \(s^2_y\) 分别表达并计算为：

\[ \begin{align} \bar{y} &=\frac{1}{n} \sum_{i=1}^{n} y_{i} = \frac{1}{8}\left[5+1+\cdots +3 \right] = 4.125 \\ s^{2}_y &=\frac{\sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}}{n-1} \\ &= \frac{1}{8-1} \times \left[(5- 4.125)^2 + (1-4.125)^2 + \cdots + (3-4.125)^2\right] \\ & = 2.6964 \end{align} \]

样本的特征：样本均值和样本方差

因此，我们可以不断从前述总体 \(Y \in \{1,2,3,4,5,6\}\) 中进行有放回的随机抽样。下表展示了10份随机样本 \(y\) ，每份样本的容量都相同 \(n=8\) 。每份样本的均值 \(\bar{y}\) 见列bar_y，样本方差 \(s^2_y\) 见列s2_y。

总体和样本特征的关系

根据中心极限定理和大数定理，我们可以推导得到总体与样本特征的如下关系：

\[ \begin{align} E(\bar{y}) &= \mu_Y \tag{eq.1} \\ Var(\bar{y}) & = \frac{\sigma^2_Y}{n} \tag{eq.2} \\ E\left(Var(\bar{y}) \right) &= \widehat{Var}(\bar{y}) \equiv \frac{s^2}{n} \tag{eq.3} \end{align} \]

其中， \(s^2 =\frac{\sum_1^n{(y_i - \bar{y})^2}}{n-1}\) 表示随机样本的样本标准差。以上方程蕴含着如下结论：

  • 方程1表明：随机变量 \(\bar{y}\) 的期望是随机变量 \(Y\) 的期望的无偏估计量（unbiased estimator）。

  • 方程2表明：随机变量 \(\bar{y}\) 的方差与随机变量 \(Y\) 的方差存在以上关系。

  • 方程3表明：随机变量 \(\bar{y}\) 的方差的无偏估计量可以通过样本数据计算得到，其结果为 \(\widehat{Var}(\bar{y}) \equiv \frac{s^2}{n}\) 。

抽样分布：骰子游戏

随机样本（random sampling）是从总体中随机抽取个体的集合。

六点骰子的可能结果为 \(\{1,2,3,4,5,6\}\) ，如果随机投掷2次，可以得到2次结果的数值加总：

# 设置随机种子
set.seed(520)
# 随机投掷2次骰子
toll_2 <- sample(1:6, 2, replace = T)
# 计算抽样结果的加总数值
sum_toll_2 <- sum(toll_2)
[1] 3 6
[1] 9

抽样分布：骰子游戏

随机投掷2次的所有可能结果共有 \(6^2=36\) 种可能：

\[ \begin{align*} &(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) \\ &(2,1) (2,2) (2,3) (2,4) (2,5) (2,6) \\ &(3,1) (3,2) (3,3) (3,4) (3,5) (3,6) \\ &(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) \\ &(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) \\ &(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) \end{align*} \]

以上的全部组合，共有11种加总结果 \(S = \left\{2,3,4,5,6,7,8,9,10,11,12 \right\}\) ，每种加总结果的概率分别是：

\[ \begin{align} P(S) = \begin{cases} 1/36, \ & S = 2 \\ 2/36, \ & S = 3 \\ 3/36, \ & S = 4 \\ 4/36, \ & S = 5 \\ 5/36, \ & S = 6 \\ 6/36, \ & S = 7 \\ 5/36, \ & S = 8 \\ 4/36, \ & S = 9 \\ 3/36, \ & S = 10 \\ 2/36, \ & S = 11 \\ 1/36, \ & S = 12 \end{cases} \end{align} \]

抽样分布：骰子游戏

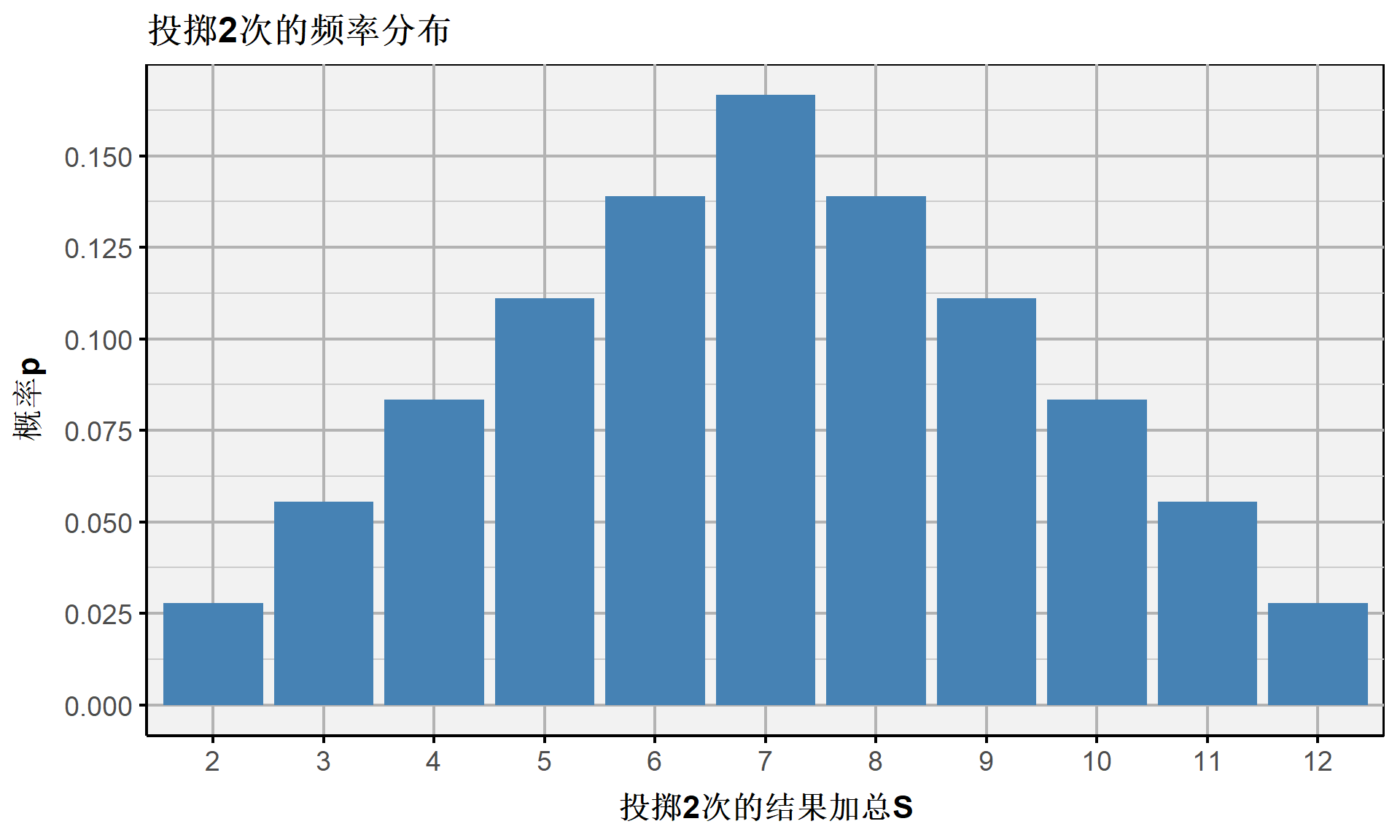
抽样分布：骰子游戏

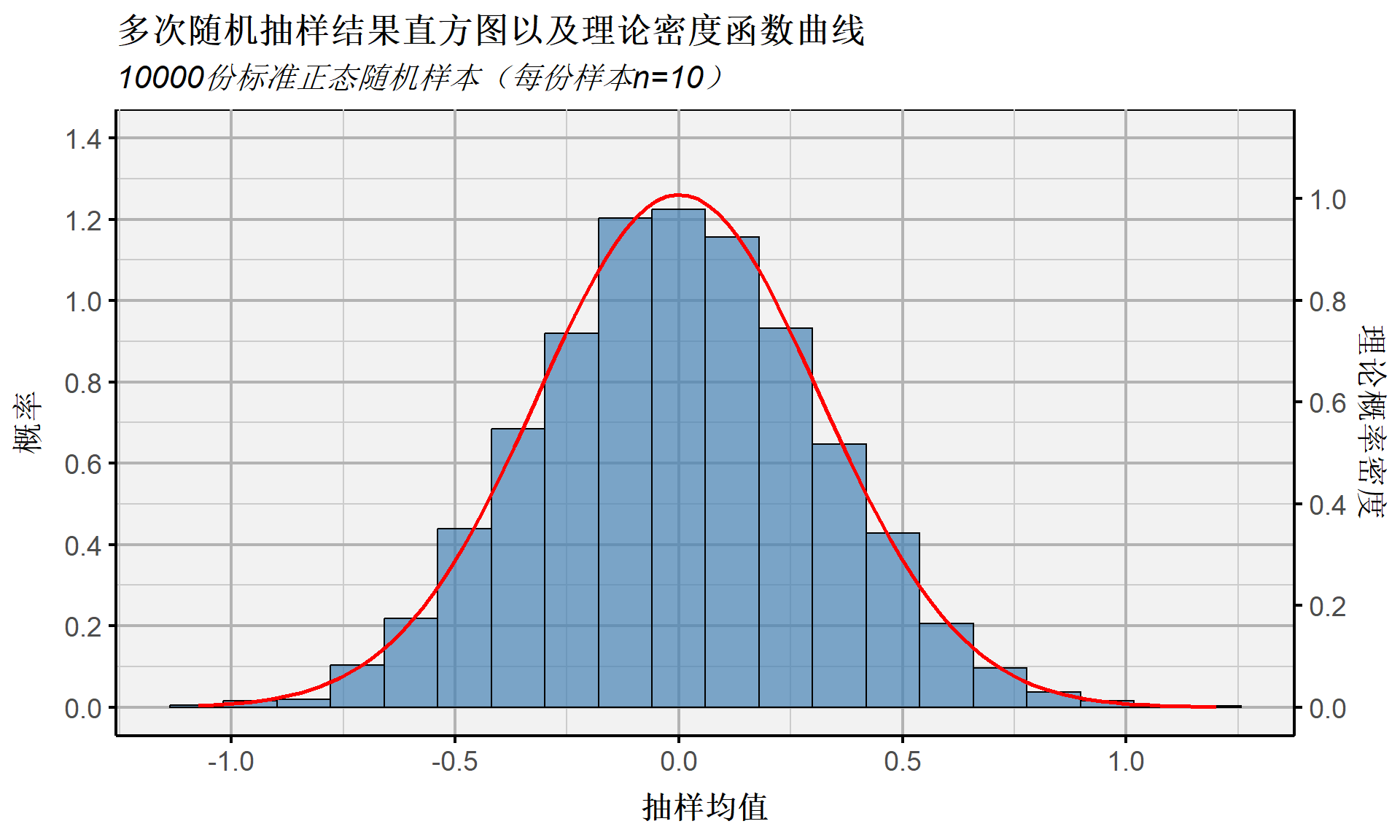
抽样分布：骰子游戏

抽样误差的计算

随机抽样：总体均值和总体方差

\[ \begin{align} E(Y) & \equiv \mu_Y= \sum_{i=1}^N{(Y_i\cdot p(Y_i))} = \frac{1}{N}\sum_{i=1}^N {Y_i} \\ Var(Y)& \equiv \sigma^2_Y= E\left(Y_i - E(Y)\right)^2=E\left(Y_i - \mu \right)^2 \end{align} \]

\[ \begin{align} \bar{y} &= \frac{1}{n}\sum_{i=1}^n {y_i} \\ Var(y_i)& \equiv s^2 = \frac{1}{n-1}\sum_{i=1}^n{\left(y_i - \bar{y} \right)^2} \end{align} \]

对于随机样本下的 \(\overline{y}\) 进一步地，其真实方差和无偏估计方差分别为：

\[ \begin{align} Var(\overline{y})& \equiv \sigma^2_{\overline{y}}= \left(\frac{N-n}{N}\right) \frac{\sigma^2_Y}{n} \\ \widehat{Var}(\overline{y})& \equiv S^2_{\overline{y}}= \left(\frac{N-n}{N}\right) \frac{s^2_y}{n} \\ \end{align} \]

随机抽样：总体总量及其方差

总体 \(Y_i\) 的总量（总和）及其样本估计量分别为：

\[ \begin{aligned} \tau &=\sum_{i=1}^N {Y_i}=N \cdot\mu_Y \\ \hat{\tau} &=N \cdot \bar{y}=\frac{N}{n} \sum_{i=1}^n {y_i} \end{aligned} \]

进一步地，可以获得总体总量估计量的真实方差和样本方差：

\[ \begin{aligned} \operatorname{var}(\hat{\tau}) &=N^2 \cdot \operatorname{var}(\bar{y}) =N^2 \cdot \left(\frac{N-n}{N}\right) \frac{\sigma^2_Y}{n} =N(N-n) \frac{\sigma^2_Y}{n}\\ \widehat{\operatorname{var}}(\hat{\tau}) &=N^2 \cdot \widehat{\operatorname{var}}(\bar{y}) = N^2 \cdot \left(\frac{N-n}{N}\right) \frac{s^2_y}{n} =N(N-n) \frac{s_y^2}{n} \end{aligned} \]

总体均值和总体方差

假定随机样本 \({y_1,\dots,y_n}\) 是独立随机抽取自正态分布总体 \(Y \sim \mathcal{N}(\mu_Y,\sigma_Y^2)\) ，那么前述随机样本数据的均值 \(\overline{y}\) 将服从如下正态分布：

\[ \overline{y} \sim \mathcal{N}(\mu_Y, \sigma_Y^2/n) \tag{2.4} \]

其中：

\[ E(\overline{y}) \equiv \mu_{\bar{y}} = E\left(\frac{1}{n} \sum_{i=1}^n y_i \right) = \frac{1}{n} E\left(\sum_{i=1}^n y_i\right) = \frac{1}{n} \sum_{i=1}^n E\left(y_i\right) = \frac{1}{n} \cdot n \cdot \mu_Y = \mu_Y \]

\[ \begin{align*} \text{Var}(\overline{y}) & \equiv \sigma^2_{\bar{y}} = \text{Var}\left(\frac{1}{n} \sum_{i=1}^n y_i \right) \\ &= \frac{1}{n^2} \sum_{i=1}^n \text{Var}(y_i) + \frac{1}{n^2} \sum_{i=1}^n \sum_{j=1, j\neq i}^n \text{cov}(y_i,y_j) = \frac{\sigma^2_Y}{n} \end{align*} \]

抽样误差：中心极限定理

然而，实际中我们往往并不知道总体方差 \(\sigma^2_Y\) 。此时，上述方差公式是不能够计算的。

有限总体中心极限定理（The finite population Central Limit Theorem）对于随机变量 \(\bar{y}\) 的意义在于：我们可以用样本方差 \(s^2_y\) 来近似替代总体方差 \(\sigma^2_Y\) 。也即：

\[ \begin{align*} \text{Var}(\overline{y}) & \equiv \sigma^2_{\bar{y}} = \frac{\sigma^2_Y}{n} \\ \widehat{Var}(\overline{y}) & \equiv \hat{\sigma}_{\bar{y}} = \frac{s^2_y}{n} \end{align*} \]

抽样误差：中心极限定理

如果样本容量 \(n\) 很小，随机变量 \(\bar{y}\) 的可能分布会是多种多样的。有限总体中心极限定理表明，随着样本容量 \(n\) 的不断增大，随机变量 \(\bar{y}\) 的分布会越来越稳定，并趋向于正态分布（normal distribution），从而有：

\[ \begin{align} \bar{y} & \sim \mathcal{N}(\mu_{\bar{y}}, \sigma^2_{\bar{y}}) \\ \frac{\bar{y} - \mu_{\bar{y}}}{\sigma_{\bar{y}}} = \frac{\bar{y} - \mu_{\bar{y}}}{\sqrt{Var({\bar{y}})}} & \sim \mathcal{Z}(0,1) \end{align} \]

抽样误差：置信区间

如果随机变量 \(\bar{y}\) 的总体方差 \({Var}(\bar{y})\) 未知，则无法使用上述正态分布 \(\mathcal{N}\) 或者标准正态 \(\mathcal{Z}\) 分布，进行有关置信区间的样本推断。幸运的是，我们可以构造出如下服从t分布的随机变量：

\[ \begin{align} \frac{\bar{y} - \mu_{\bar{y}}}{\hat{\sigma}_{\bar{y}}} = \frac{\bar{y} - \mu_{\bar{y}}}{\sqrt{\widehat{Var}(\bar{y})}} = \frac{\bar{y} - \mu_{\bar{y}}}{s_{y}/\sqrt{n}} & \sim t(n-1) \end{align} \]

因此可以进一步得到参数 \(\mu_{\bar{y}}\) 的 \(1-\alpha\) 置信区间：

\[ \begin{align} \bar{y} - t_{1-\alpha / 2} \sqrt{\widehat{Var}(\bar{y})} \leq \mu_{\bar{y}} \leq \bar{y} + t_{1-\alpha / 2} \sqrt{\widehat{Var}(\bar{y})} \end{align} \]

对于有放回的简单随机抽样，参数 \(\mu_{\bar{y}}\) 的 \(1-\alpha\) 置信区间具体为：

\[ \begin{align} \bar{y} - t_{\alpha / 2} \sqrt{\left(\frac{N-n}{N}\right)\left(\frac{s^{2}}{n}\right)} \leq \mu_{\bar{y}} \leq \bar{y} + t_{\alpha / 2} \sqrt{\left(\frac{N-n}{N}\right)\left(\frac{s^{2}}{n}\right)} \end{align} \]

抽样误差：简单随机抽样

对于无放回的简单随机抽样方案，采用无偏估计法（unbiased estimator）下的均值 \(\bar{y}_{\mathrm{st}}\) 和方差 \(\widehat{\operatorname{var}}\left(\bar{y}_{\mathrm{st}}\right)\) 分别为：

\[ \begin{align} \hat{\mu} &=\frac{1}{n} \sum_{i=1}^{n} {y_i} =\bar{y} \\ \widehat{\operatorname{Var}}\left(\hat{\mu}\right) &=\frac{N-n}{N} \cdot \frac{s_y^{2}}{n} \end{align} \]

上述方差公式中， (s^2_y = ) 。而 (=1-) 又被称为有限总体校正比值（finite population correction, fpc）：

  • 如果采用有放回的简单随机抽样，则上述方差公式需要去掉有限总体校正比值。

  • 如果采用无放回的简单随机抽样，但是n相对于N非常小，则上述方差公式中有限总体校正比值会接近于1，因此也可以忽略。

case：田野甲虫数量案例

（示例）田野甲虫数量案例

案例说明：为估计出一片农地中甲虫的总数。研究人员将农地细分为100个大小相等的区块。

研究者决定采用简单随机抽样方案，随机抽选了其中的8个区块（编号见列field），并分别统计出其中的甲虫数量（见列beetles）。最终抽样统计表见右：

简单随机抽样结果
field beetles
41 234
42 256
18 128
13 245
80 211
68 240
25 202
100 267

（示例）简单随机抽样下估计期望和方差：计算结果

根据案例，容易计算得到：全部地块数量 \(N= 100\) ；抽选地块数量 \(n = 8\) 。抽选地块下甲虫数量的样本方差为 \(s^2_y = \frac{\sum_{i=1}^{n}{(y_i - \bar{y})^2}}{n-1}=1932.70\) 。

因此根据简单随机抽样无偏估计法下的计算公式，分别可以计算得到估计的均值 \(\hat{\mu}\) 和方差 \(\widehat{var}(\hat{\mu})\) 分别为：

\[ \begin{align} \hat{\mu} &=\frac{1}{n} \sum_{i=1}^{n} {y_i} =\bar{y} =222.88 \\ \widehat{\operatorname{Var}}\left(\hat{\mu}\right) &=\frac{N-n}{N} \cdot \frac{s_y^{2}}{n} \\ & =\frac{100-8}{100} \cdot \frac{1932.70}{8} = 222.2601 \end{align} \]

（示例）简单随机抽样下估计期望和方差：计算结果

根据上述计算，给定 \(\alpha = 0.05\) 下，平均每个区块甲虫数 \(\mu_{\bar{y}}\) 的置信区间计算结果为：

\[ \begin{align} \hat{\mu} - t_{1-\alpha / 2} \sqrt{\widehat{Var}(\hat{\mu})} \leq & \mu_{\bar{y}} \leq \hat{\mu} + t_{1-\alpha / 2} \sqrt{\widehat{Var}(\hat{\mu})} \\ 222.88 - 2.36 \times \sqrt{222.2601} \leq & \mu_{\bar{y}} \leq 222.88 + 2.36 \times \sqrt{222.2601}\\ 187.62 \leq & \mu_{\bar{y}} \leq 258.13 \end{align} \]

思考提问：全部地块的甲虫数量和置信区间是多少？

必要样本数

不管采用哪种抽样方法，在哪一层抽样，在哪个阶段抽样， 到底要抽多少样本合适啊？

假定 \(\hat{\sigma}\) 是参数 \(\sigma\) 的无偏、正态估计量。则有

\[ \begin{align} \frac{\hat{\theta}-\theta}{\sqrt{\operatorname{Var}(\hat{\theta})}} & \sim \mathcal{Z}(0,1) \\ P\left(\frac{|\hat{\theta}-\theta|}{\sqrt{\operatorname{Var}(\hat{\theta})}}>\mathcal{Z}_{1-\alpha / 2}\right) & =\alpha \\ P\left(|\hat{\theta}-\theta|>\mathcal{Z}_{1-\alpha / 2} \cdot \sqrt{\operatorname{Var}(\hat{\theta})}\right) &=\alpha \end{align} \]

必要样本数（A基于总体均值）

假设我们希望通过考察样本与总体均值的差距，来确定必要抽样样本数。

令 \(d=|\bar{y} - \mu|\) 为抽样极限误差，则简单随机抽样（不放回）方案下必要样本数的计算公式为：

\[ \begin{align} P\left(|\bar{y}-\mu_{\bar{y}}|>\mathcal{Z}_{1-\alpha / 2} \cdot \sqrt{\frac{N-n}{N} \cdot \frac{\sigma^{2}}{n}}\right) & =\alpha \\ \mathcal{Z}_{1-\alpha / 2} \sqrt{\frac{N-n}{N} \cdot \frac{\sigma^{2}}{n}} & \equiv d \\ n &=\frac{1}{\frac{d^{2}}{\mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}+\frac{1}{N}} \end{align} \]

必要样本数（A基于总体均值）

令 \(n_0 = \frac{\mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2}\) ，则上述式子可以进一步写成：

\[ \begin{align} n &=\frac{1}{\frac{d^{2}}{\mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}+\frac{1}{N}} = \frac{1}{1/n_0 + 1/N} \end{align} \]

  • 如果总体规模远大于样本容量，也即 \(N \gg n\) ，则此时有限总体矫正因子fpc一项 \(\frac{N-n}{N} \approx 0\) ，那么必要样本数简化为 \(n = n_0 =\frac{\mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2}\)

示例1：素菜食谱比例案例（必要样本数的计算1/2）

素菜食谱：假设我们想要估计一本食谱中不涉及动物产品的食谱的比例。我们计划对食谱中 \(N = 1251\) 个食谱进行简单随机抽样（SRS-wor，无放回），并希望误差范围为0.03的95% 置信区间。

请计算简单随机抽样方案下的必要样本数？

示例1：素菜食谱比例案例（必要样本数的计算1/2）

解答：根据案例已知 \(N=1251\) ，抽样极限误差为 \(d =0.03\) ，给定 \(\alpha = 0.05\) 下 \(\mathcal{Z}_{1-\alpha/2}=\mathcal{Z}_{0.975}=1.96\) 。

这是一个典型的比率估计问题，在大样本情况下，我们知道总体方差 \(\sigma^2_{\bar{y}} \approx p(1-p)\) ，且在 \(p = 1/2\) 时总体方差取最大值。因此我们可以使用总体方差 \(\sigma^2_{\bar{y}} \approx p(1-p)=0.25\) ，因此必要样本数计算为：

\[ \begin{align} n_0 =\frac{\mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2} = \frac{{1.959964}^{2} \cdot 0.25}{{0.03}^2} = 1 067.0719 \end{align} \]

\[ \begin{align} n = \frac{1}{1/n_0 + 1/N} = \frac{1}{1/1 067.0719 + 1/1251} = 575.8695 \approx 576 \end{align} \]

必要样本数（B基于总体总量）

假设我们希望通过考察样本与总体总量的差距，来确定必要抽样样本数。

令 \(d=|n\bar{y} - N\mu|\) 为抽样极限误差，则简单随机抽样（不放回）方案下必要样本数的计算公式为：

\[ \begin{align} P\left(|n\bar{y} - N\mu|>\mathcal{Z}_{1-\alpha / 2} \cdot \sqrt{N(N-n) \cdot \frac{\sigma^{2}}{n}}\right) & =\alpha \\ \mathcal{Z}_{1-\alpha / 2} \sqrt{N(N-n) \cdot \frac{\sigma^{2}}{n}} & \equiv d \\ n &=\frac{1}{\frac{d^{2}}{N^2\cdot \mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}+\frac{1}{N}} \end{align} \]

必要样本数（B基于总体总量）

令 \(n_0 = \frac{N^2 \cdot \mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2}\) ，则上述式子可以进一步写成：

\[ \begin{align} n &=\frac{1}{\frac{d^{2}}{N^2 \cdot \mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}+\frac{1}{N}} = \frac{1}{1/n_0 + 1/N} \end{align} \]

  • 如果总体规模远大于样本容量，也即 \(N \gg n\) ，则此时有限总体矫正因子fpc一项 \(\frac{N-n}{N} \approx 0\) ，那么必要样本数简化为 \(n = n_0 =\frac{N^2 \cdot \mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2}\)

示例2：昆虫数量案例（必要样本数的计算）1/2

甲虫数量案例：给定 \(\alpha = 0.05\) 下，我们的抽样设计希望是对于整个全部田地中甲虫总数量的抽样极限误差不超过1000只，请计算简单随机抽样方案下的必要样本数？

解答：根据案例已知 \(N=100\) ，抽样极限误差为 \(d =1000\) ，给定 \(\alpha = 0.05\) 下 \(\mathcal{Z}_{1-\alpha/2}=\mathcal{Z}_{0.975}=1.96\) 。

我们已经计算得到了样本方差 \(\widehat{\sigma}^2_{\bar{y}}=s^2_{\bar{y}} =1932.70\)

示例2：昆虫数量案例（必要样本数的计算）2/2

因此必要样本数计算为：

\[ \begin{align} n_0 =\frac{N^2 \cdot \mathcal{Z}_{1-\alpha / 2}^{2} \cdot \sigma^{2}}{d^2} = \frac{{100}^{2} \cdot {1.959964}^{2} \cdot 1932.6964286}{{1000}^2} = 74.2437 \end{align} \]

\[ \begin{align} n = \frac{1}{1/n_0 + 1/N} = \frac{1}{1/74.2437 + 1/100} = 42.6091 \approx 43 \end{align} \]

抽样误差：分层抽样

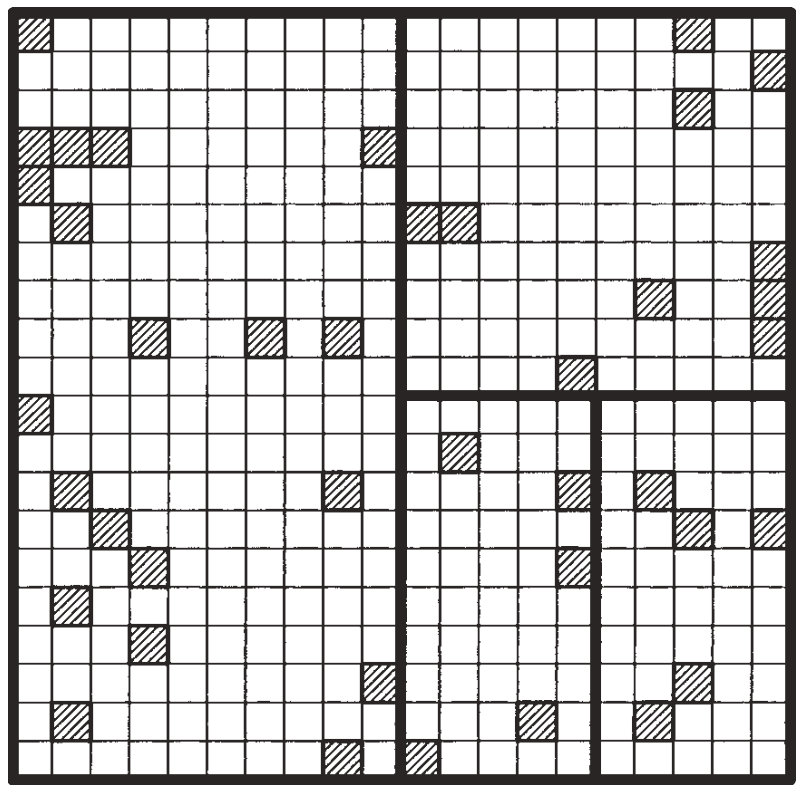
  • 分层数量： \(L=4\) ；各个分层的单位数： \(N_1=200, N_2=100,N_3=N_4=50\) ；全体单位总数 \(N=\sum_{h=1}^L{N_h}=200+100+50+50=400\) 。

  • 各个分层的抽样单位数： \(n_1=20, n_2=10,n_3=n_4=5\) ；全部抽样总数 \(n=\sum_{h=1}^h{n_L}=20+10+5+5=40\) 。

抽样误差：分层抽样

分层抽样的均值 \(\hat{\mu}_{\mathrm{st}}\) 和方差 \(\widehat{\operatorname{Var}}\left(\hat{\mu}_{\mathrm{st}}\right)\) 分别为：

\[ \begin{align} \hat{\mu}_{\mathrm{st}} &=\frac{1}{N} \sum_{h=1}^{L} N_{h} \bar{y}_{h} \\ \widehat{\operatorname{var}}\left(\hat{\mu}_{\mathrm{st}}\right) &=\sum_{h=1}^{L}\left(\frac{N_{h}}{N}\right)^{2}\left(\frac{N_{h}-n_{h}}{N_{h}}\right) \frac{s_{h}^{2}}{n_{h}} \end{align} \]

其中：

  • \(L\) 分层数量； \(N_h\) 表示第 \(h\) 个分层的所有单位数，其中 \(h \in \{ 1, 2, \cdots, L\}\) ； \(N=N_1 +N_2 + \cdots+N_L\) 为所有单位数。 \(n_h\) 表示第 \(h\) 个分层的抽样数； \(n=n_1 +n_2 + \cdots+n_L\) 为所有抽样单位总数。

  • 各个分层的样本方差为： \(s_{h}^{2}=\frac{1}{n_{h}-1} \sum_{i=1}^{n_{h}}\left(y_{h i}-\bar{y}_{h}\right)^{2}\) ； \(\bar{y}_{h}\) 表示各个分层的样本均值。

case：家庭观看电视时长案例

（示例）家庭观看电视时长案例

案例说明：一家广告公司为了有针对性地在某个县投放电视广告，公司决定进行抽样调查，以估计该县家庭每周观看电视的平均小时数。该县有两个镇区A和镇区B，还有农村区域C。A区建在一家工厂周围，大多数家庭都有带学龄儿童的工厂工人。B区主要是退休人员，C区主要是农民。A区有155户，B区有62户，C区有93户。公司决定从A区抽选20户，B区抽选8户，C区抽选12户。具体抽样结果如下：

Stratification sampling n_h N_h
Town A 35, 43, 36, 39, 28, 28, 29, 25, 38, 27, 26, 32, 29, 40, 35, 41, 37, 31, 45, 34 20 155
Town B 27, 15, 4, 41, 49, 25, 10, 30 8 62
Rural Area C 8, 14, 12, 15, 30, 32, 21, 20, 34, 7, 11, 24 12 93

（示例）分层抽样下的抽样误差：计算结果

各分层的计算表如下：

根据该分层抽样，估计的总体均值（该县住户平均收看电视时间）结果为：

\[ \begin{aligned} \hat{\mu}_{s t} &=\frac{1}{N}\left(N_{1} \bar{y}_{1}+N_{2} \bar{y}_{2}+N_{3} \bar{y}_{3}\right) \\ &=\frac{1}{155+62+93}[(155 \times 33.9)+(62 \times 25.12)+(93 \times 19.0)] \\ &=27.7 \end{aligned} \]

（示例）分层抽样下的抽样误差：计算结果

各分层的计算表如下：

根据该分层抽样，上述关于的总体均值估计（住户平均收看电视时间）的方差为：

\[ \begin{align} \widehat{Var} \left(\hat{\mu}_{s t}\right) =\sum_{h=1}^{3}\left(\frac{N_{h}}{N}\right)^{2}\left(\frac{N_{h}-n_{h}}{N_{h}}\right) \frac{s_{h}^{2}}{n_{h}} =\frac{1}{(310)^{2}}\left[\left((155)^{2} \cdot \frac{(155-20)}{155} \cdot \frac{(5.95)^{2}}{20}\right) \\ + \left((62)^{2} \cdot \frac{(62-8)}{62} \cdot \frac{(15.25)^{2}}{8}\right)\right. \left.+\left((93)^{2} \cdot \frac{(93-12)}{93} \cdot \frac{(9.36)^{2}}{12}\right)\right] =1.97 \end{align} \]

（示例）分层抽样下的抽样误差：计算结果

各分层的计算表如下：

根据该分层抽样，上述关于的总体均值估计（住户平均收看电视时间）的95%置信区间为（t查表值为 \(t_{1-0.05/2}(39)=2.02\) ）*：

\[ \begin{aligned} & \hat{\mu}_{s t} \pm t_{1-\alpha/2}(df) \cdot \sqrt{\widehat{Var} \left(\hat{\mu}_{st}\right)} \\ =& 27.7 \pm 2.02 \times \sqrt{1.97} = 27.7 \pm 2.84 \end{aligned} \]

抽样误差：系统抽样和整群抽样的关系

系统抽样示例

整群抽样示例

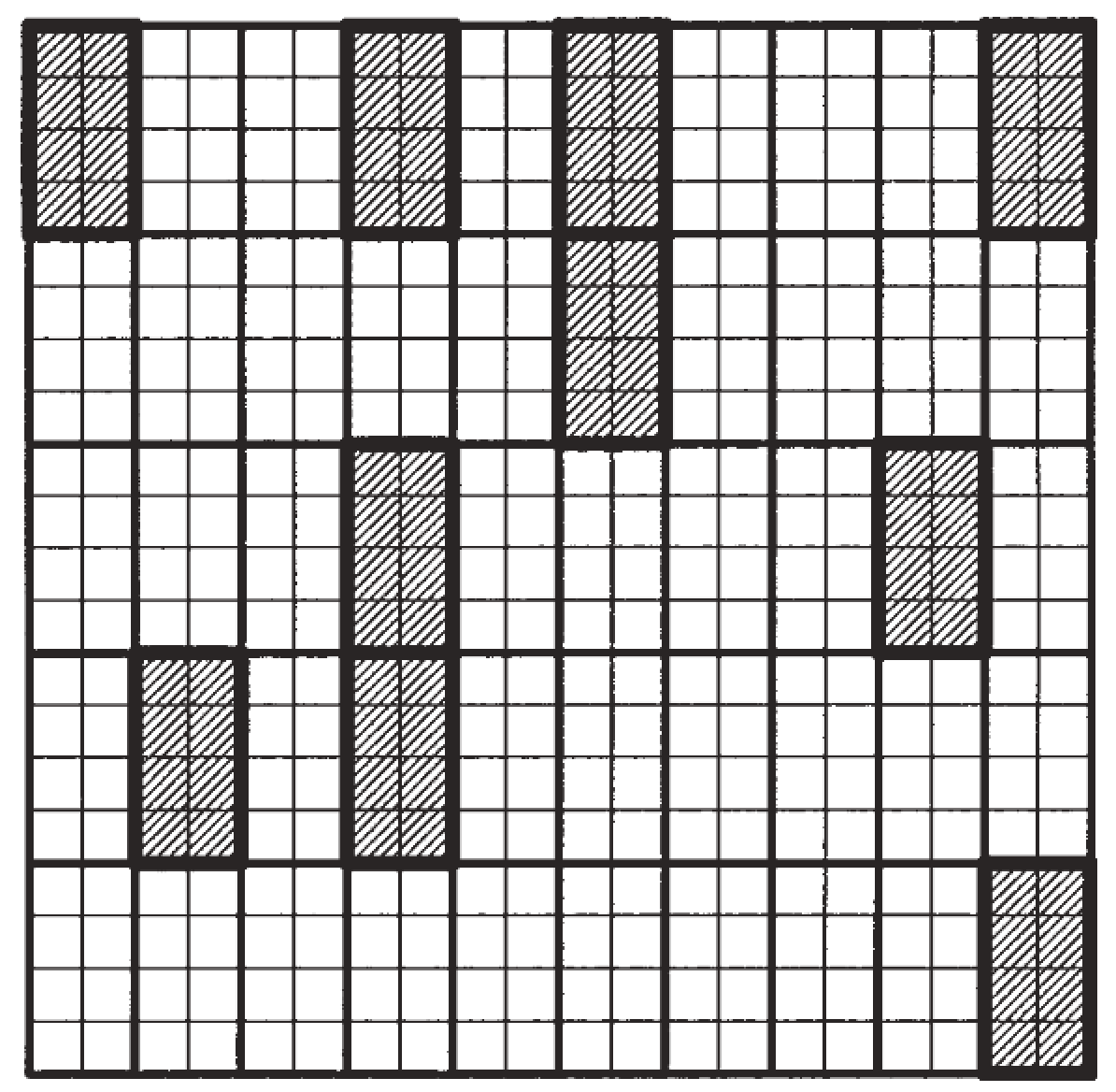
从表面上看，系统抽样（systematic sampling）和整群抽样（cluster sampling）非常不同。实际上，这两种方式具有相同的抽样结构：

  • 利用主要抽样单位（PSU）划分群组，而每个主要抽样单位又是由次要抽样单位（SSU）组成。
  • 如果主要抽样单位（PSU）被随机抽中，则其所有次要单位（SSU）的 \(y\) 值将都会被抽中。

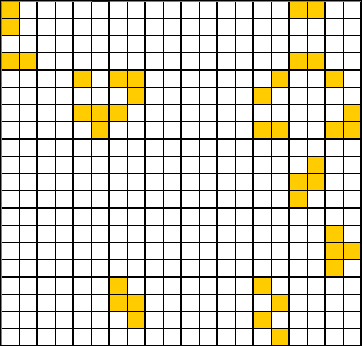
抽样误差：系统抽样和整群抽样的关系

系统抽样示例

  • 该案例共有25个主要抽样单位（PSU）：每个5*5中型方框都有25个小格。

  • 着色色区块是一次典型的随机抽取的系统抽样结果，共抽取样本数 \(n=16\) 。

  • 只有1个主要抽样单位（PSU）被随机抽中：每个5*5中型方框的第1个小格都被抽中，共16个。

整群抽样示例

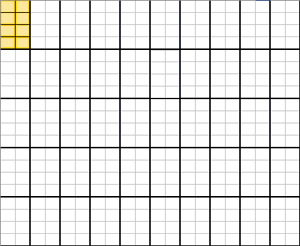
  • 该案例共有50个主要抽样单位（PSU）：共有50个2*4型方框。

  • 着色色区块是一次典型的随机抽取的整群抽样结果，共抽取样本数 \(n=8\) 。

  • 只有1个主要抽样单位（PSU）被随机抽中：第1个2*4型方框的全部小格都被抽中，共8个。

（示例）系统抽样和整群抽样的关系

案例说明：下面展示的是”三采一”的系统采样：我们从前三个主要抽样单元（PSU）中随机选择一个，然后再连续地每隔三个选择一个。

三采一系统抽样示例

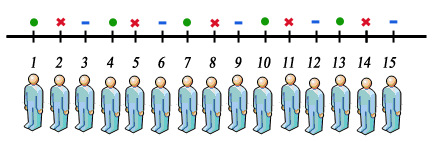
从主要抽样单位PSU {1,2,3}中随机选择一个值。例如，如果选择2，那么我们将选择上图中所有的红叉个体的{2，5，8，8，11 14}。

  • 抽样得到的样本数据{2、5、8、11、14}，只是我们随机选定了1个主要抽样单位（PSU）红叉，因而所有具有该主要抽样单位的全部个体都被抽中（全部红叉）。
  • 实际上，只抽选1个主要抽样单位（PSU）的情况并不少见，例如以上”三采一”的系统样本。我们只采样3个主要抽样单位（分别是绿点、红叉、蓝短线）的1个而已。

抽样误差：系统抽样和整群抽样（记号表达）

我们约定系统抽样和整群抽样的记号表达体系如下：

  • \(N\) 表示总体中的主要抽样单元（PSU）的数量； \(n\) 表示样本中的主要抽样单元（PSU）的数量； \(M_i\) 表示第 \(i\) 个主要抽样单元（PSU）中次要抽样单元（SSU）的数量； \(M=\sum_{i=1}^N M_i\) 表示总体中的所有次要抽样单元（SSU）的数量；

  • \(y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）中第 \(j\) 次要抽样单元（SSU）的个体的变量值。 \(y_i = \sum_{j=1}^{M_i} y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）下所有个体的变量值之和。

  • 主要抽样单元（PSU）的均值记为 \(\mu_1\) ，次要抽样单元（SSU）的均值记为 \(\mu\) ，二者的计算公式分别为：

\[ \begin{align} \mu_1 &= \frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{M_{i}} y_{i j}=\frac{1}{N} \sum_{i=1}^{N} y_{i} \\ \mu &= \frac{1}{M} \sum_{i=1}^{N} \sum_{j=1}^{M_{i}} y_{i j}=\frac{1}{M} \sum_{i=1}^{N} y_{i} \end{align} \]

（示例）系统抽样的记号表达

系统抽样示例

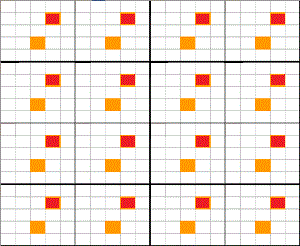
  • 总体的主要抽样单元（PSU）的数量 \(N=25\) ：每个5*5中型方框的全部小格， 共25个。

  • 样本中的主要抽样单元（PSU）的数量 \(n=2\) ：每个5*5中型方框的都抽中了2个着色小格。

  • 每个主要抽样单元（PSU）中次要抽样单元（SSU）的数量 \(M_i=16\) ：所有5*5中型方框，共有16个。

（示例）整群抽样的记号表达

整群抽样示例

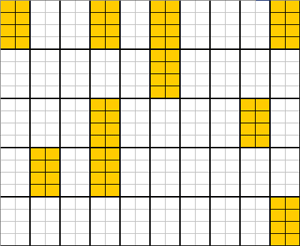
  • 总体的主要抽样单元（PSU）的数量 \(N=50\) ：每个2*4中型方框， 共50个。

  • 样本中的主要抽样单元（PSU）的数量 \(n=10\) ：随机抽中的2*4中型方框，共抽中10个2*4中型着色方框。

  • 每个主要抽样单元（PSU）中次要抽样单元（SSU）的数量 \(M_i=8\) ：每个2*4中型方框中的8个小格。

抽样误差：系统抽样的抽样误差计算

此时估计次要抽样单元（SSU）的均值 \(\hat{\mu}_{sy}\) 和方差 \(\widehat{Var}\left(\hat{\mu}_{sy}\right)\) 分别为：

\[ \begin{align} \hat{\mu}_{sy} &=\bar{y}_{sy}=\frac{1}{n}\sum_{i=1}^{n} \bar{y}_{i} \end{align} \]

\[ \begin{align} \widehat{Var}(\hat{\mu}_{sy}) &=\frac{M-n \cdot \bar{M}}{M\cdot n} \cdot \frac{1}{(n-1)} \cdot \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}\right)^{2} = \frac{M-n \cdot \bar{M}}{M\cdot n} \cdot s^2_{\bar{y}_i} \end{align} \]

其中： - \(\bar{y}_{i}=\frac{y_{i}}{M_{i}}=\frac{\sum_{j=1}^{M_{i}} y_{i j}}{M_{i}}; i \in 1,2, \ldots, n\) 。 \(\bar{M}=M_{1}=M_{2}=\ldots=M_{n}\)

  • 主要抽样单位（PSU）数量为 \(N\) ；样本中的主要抽样单位（PSU）数量为 \(n\) ；第 \(i\) 个主要抽样单位下的次要抽样单位的数量为 \(M_i(i \in 1,2,\cdots, N)\) ；总体的全部次要抽样单位（SSU）数量 \(M = \sum_{i =1}^{50} M_i\)

case：渡船汽车载客量案例

（示例）渡船汽车载客量案例

案例说明：载有汽车横渡海湾的渡轮是按载客量而不是按人收取费用的。轮渡公司希望估算8月份每辆车的平均载人数。该公司知道去年有400辆车乘坐轮渡（见右表）。


  1   2   3   4   5   6   7   8  10 
 12  22  59 102 108  66  24   6   1

公司想对其中80辆车进行采样，为了便于估计系统样本的方差，研究人员决定选择使用系统抽样方法，反复抽取10份样本，每份样本都包含8量汽车的记录数据。

（示例）系统抽样下估计期望和方差：抽样结果

公司决定采用 \(1-in-50(400 / 8)\) 的系统抽样方案，也即：

  • 从1到50的序号中，不重复随机选择10个序号：8、16、40、6、2、26、37、14、47、46；
  • 然后分别以这10个序号作为起始点，每隔50个抽取1个单位，每份样本都会抽取得到8个单位；
  • 最终共获得10份系统抽样样本（每份样本含8个个体）。抽样结果如下（括号内为车内人数）：

（示例）系统抽样下估计期望和方差：计算结果

根据案例，容易计算得到：主要抽样单位（PSU）数量 \(N= 50\) ；样本中的主要抽样单位（PSU）数量 \(n = 10\) ；第 \(i\) 个主要抽样单位下的次要抽样单位的数量 \(M_i = 8(i \in 1,2,\cdots, 50)\) ；总体的全部次要抽样单位（SSU）数量 \(M = \sum_{i =1}^{50} M_i =8 \times 50 =400\)

\[ \begin{align} \hat{\mu}_{sy} &=\frac{1}{n}\sum_{i=1}^{n} \bar{y}_{i}=4.62 \\ \end{align} \]

\[ \begin{align} \widehat{Var}(\hat{\mu}_{sy}) &=\frac{M-n \cdot \bar{M}}{M\cdot n} \cdot \frac{1}{(n-1)} \cdot \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}\right)^{2} = \frac{M-n \cdot \bar{M}}{M\cdot n} \cdot s^2_{\bar{y}_i} \\ &=\frac{400-10 \times 8}{400 \times 10} \cdot 0.4931 = 0.0394 \end{align} \]

  • 其中： \(\bar{y}_{i}=\frac{y_{i}}{M_{i}}=\frac{\sum_{j=1}^{M_{i}} y_{i j}}{M_{i}}; i \in 1,2, \ldots, n\) ；以及 \(\bar{M}=M_{1}=M_{2}=\ldots=M_{n}\)

抽样误差：整群抽样的抽样误差计算方法1

为了次要抽样单元（SSU）均值和方差，我们可以采用无偏估计法（unbiased estimator）：

\[ \begin{align} \hat{\mu} &= \frac{N}{M} \cdot \frac{\sum_{i=1}^{n} y_{i}}{n} \\ \widehat{Var}(\hat{\mu}) &=\frac{N(N-n) }{M^2} \cdot \frac{s_{u}^{2}}{n} \end{align} \]

  • \(s_{u}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}\)
  • \(N\) 表示总体中的主要抽样单元（PSU）的数量； \(n\) 表示样本中的主要抽样单元（PSU）的数量； \(M_i\) 表示第 \(i\) 个主要抽样单元（PSU）中次要抽样单元（SSU）的数量； \(M\) 表示总体中的所有次要抽样单元（SSU）的数量； - \(y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）中第 \(j\) 次要抽样单元（SSU）的个体的变量值。 \(y_i = \sum_{j=1}^{M_i} y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）下所有个体的变量值之和。

抽样误差：整群抽样的抽样误差计算方法2

此外，当群组变量值总和与群组单位数呈正相关关系时，使用比率估计法（ratio estimator）比使用无偏估计更好。此时，估计的次要抽样单元（SSU）均值 \(\hat{\mu}_{r}\) 和方差 \(\widehat{Var}\left(\hat{\mu}_{r}\right)\) 分别为：

\[ \begin{align} \hat{\mu}_{r}& =r =\frac{\sum_{i=1}^n {y_i}}{M} = \frac{\sum_{i=1}^n {y_i}}{\sum_{i=1}^n{M_i}}\\ \widehat{Var}\left(\hat{\mu}_{r}\right) &=\frac{N(N-n)}{n(n-1)} \cdot \frac{1}{M^{2}} \sum_{i=1}^{n}\left(y_{i}-r M_{i}\right)^{2} \end{align} \]

  • \(N\) 表示总体中的主要抽样单元（PSU）的数量； \(n\) 表示样本中的主要抽样单元（PSU）的数量； \(M_i\) 表示第 \(i\) 个主要抽样单元（PSU）中次要抽样单元（SSU）的数量； \(M\) 表示总体中的所有次要抽样单元（SSU）的数量； - \(y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）中第 \(j\) 次要抽样单元（SSU）的个体的变量值。 \(y_i = \sum_{j=1}^{M_i} y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）下所有个体的变量值之和。

case：家庭休假支出案例

（示例）家庭休假支出案例

案例说明：社会学家想要估计某个城市中每个家庭的平均年休假预算。据统计，这个城市有3100户。

社会学家将整个城市划分为400个街区，并将其视为400个集群。然后，他随机抽样了24个集群，采访了该集群中的每个家庭。

整群抽样的结果见右边数据表：

（示例）整群抽样下的抽样误差：相关性分析

初步分析抽样的各群组我们可以发现，主要抽样单元（PSU）的变量总值 \(y_i\) （各群组内全部家庭的旅游支出总和）与主要抽样单元（PSU）的单位规模 \(M_i\) （各群组的家庭数）存在高度正相关关系。

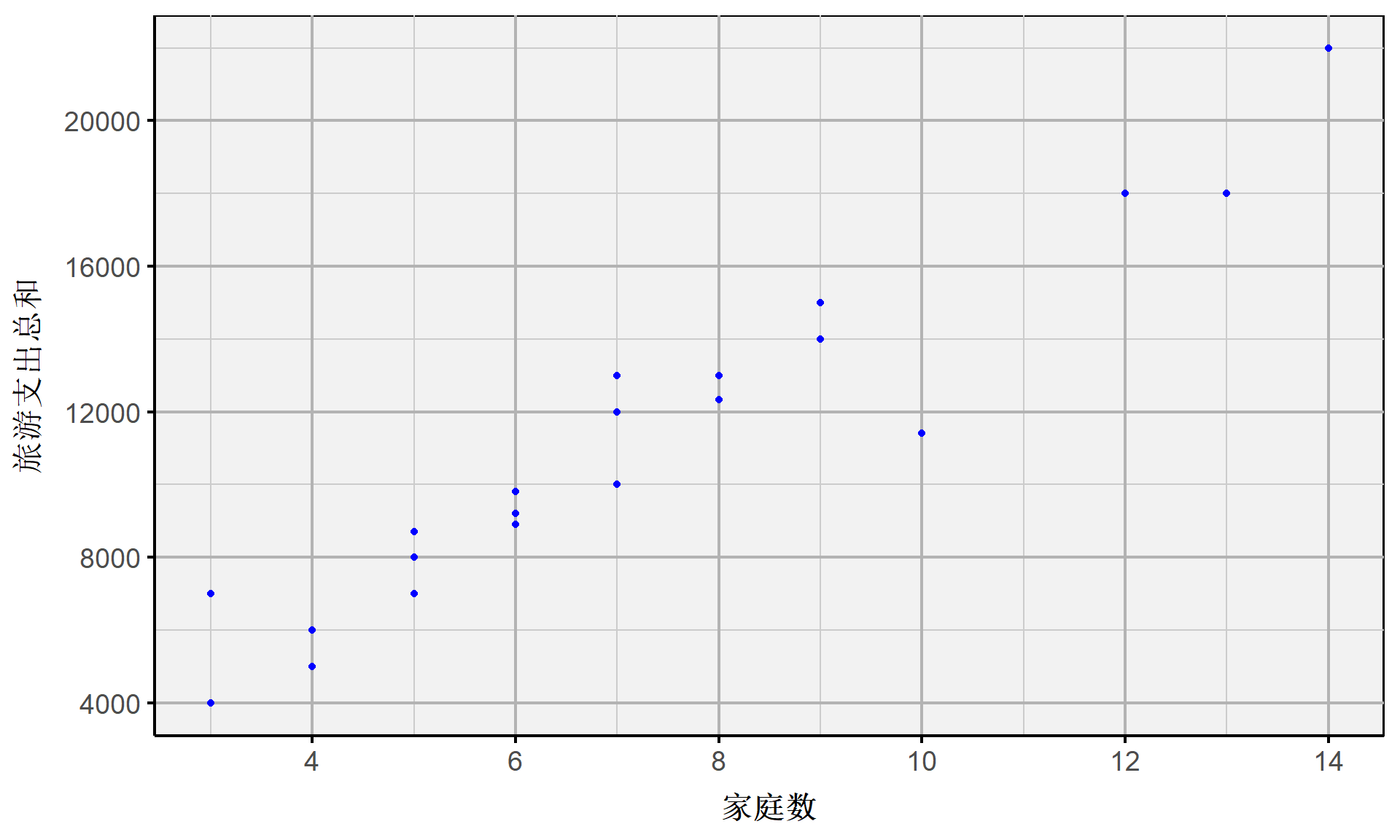
（示例）整群抽样下的抽样误差：回归分析

利用R软件进行回归分析，可以进一步发现二者呈现显著线性关系。

\[ \begin{alignedat}{999} \begin{split} &{total.budget}=&&+647.98&&+1441.94number.households_i &&+e_i\\ &(s)&&(705.8674)&&(92.5852) &&\\ &(t)&&(+0.92)&&(+15.57) &&\\ &(p)&&(0.3686)&&(0.0000) && \end{split} \end{alignedat} \]

（示例）整群抽样下的抽样误差：比率估计法

根据整群抽样数据，我们可以计算得到次要抽样单元（SSU）的均值为：

\[ \begin{align} \hat{\mu}_{r}=r=\frac{\sum_{i=1}^{n} y_{i}}{\sum_{i=1}^{n} M_{i}}=\frac{259240}{169}=1533.96 \\ \widehat{Var}\left(\hat{\mu}_{r}\right)=\frac{N(N-n)}{n \cdot M^{2}} \cdot \frac{1}{n-1} \sum_{i=1}^{n}\left(y_{i}-r M_{i}\right)^{2} \end{align} \]

因为已知： \(M=3100;N=400;n=24\) ，次要抽样单元（SSU）的方差计算结果为：

\[ \begin{align} \widehat{Var}\left(\hat{\mu}_{r}\right)&=\frac{N(N-n)}{n \cdot M^{2}} \cdot \frac{1}{n-1} \sum_{i=1}^{n}\left(y_{i}-r M_{i}\right)^{2} \\ &=\frac{400\times(400-24)}{24 \times 9.61\times 10^{6}} \times \frac{1}{24-1} \times 4.0387519\times 10^{7} \\ &= \frac{1.504\times 10^{5}}{2.3064\times 10^{8}} \times \frac{1}{23 } \times 4.0387519\times 10^{7} = 1145.0713446 \end{align} \]

（示例）整群抽样下的抽样误差：比率估计法

前述比率估计法需要用到的计算表如下所示：

（示例）整群抽样下的抽样误差：无偏估计法

作为对比，下面我们再采用无偏估计法公示进行计算。

容易计算： \(M=3100;N=400;n=24\) ，以及 \(s_{u}^{2}=\frac{1}{n-1} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2}=2.0208762\times 10^{7}\)。因此，次要抽样单元（SSU）的均值和方差计算结果分别为：

\[ \begin{align} \hat{\mu} &=\frac{N}{M}\cdot \frac{\sum_{i=1}^{n} y_{i}}{n} = \frac{400}{3100} \cdot \frac{259240}{24} =1393.81 \end{align} \]

\[ \begin{align} \widehat{Var}(\hat{\mu}) &=\frac{N(N-n)}{M^{2} \cdot n} \cdot \frac{1}{n-1} \sum_{i=1}^{n}\left(y_{i}-\bar{y}\right)^{2} \\ &=\frac{400(400-24)}{(3100)^{2} \cdot 24} \cdot s_{u}^{2} =\frac{400(400-24)}{(3100)^{2} \cdot 24}\times 2.0208762\times 10^{7} = 1.3178104\times 10^{4} \end{align} \]

抽样误差：整群抽样两个误差估计方法的比较

  • 当群组变量值总和与群组单位数大小成正比时，使用比率估计比使用无偏估计更好。因为无偏估计法的方差会非常大，估计结果非常不满意。

我们可以简单使用的随机抽样的公式来计算方差吗？——抱歉不行！

  • 如果采用简单随机抽样，那么就应该相对应使用简单随机抽样公式计算方差，而且必须通过简单随机抽样收集数据。注意：如果不按照抽样方案计算方差，这会是一个很大的错误！

抽样误差：整群抽样的抽样误差计算方法3

有时候，群组被抽中的概率 \(p_i\) 就等于群组单位数占总体单位数的比率，也即 \(p_{i}=M_{i} /M\) 。我们一般称的这种情形为主要抽样单元（PSU）满足比例概率条件（probabilities proportional to size, pps）。那么，在满足pps条件下进行的整群抽样，估计次要抽样单元（SSU）的均值 \(\hat{\mu}_{p}\) 和方差 \(\widehat{Var}\left(\hat{\mu}_{p}\right)\) 分别为：

\[ \begin{align} \hat{\mu}_{p} &=\frac{1}{n} \sum_{i=1}^{n}\left(\frac{y_{i}}{M_{i}}\right) \\ \widehat{Var}\left(\hat{\mu}_{p}\right) &=\frac{1}{n(n-1)} \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}_{p}\right)^{2} \end{align} \]

  • \(\bar{y}_{i}=\frac{y_{i}}{M_{i}}\) 表示第 \(i\) 个群组的抽样均值。 \(n\) 表示样本中的主要抽样单元（PSU）的数量； \(M_i\) 表示第 \(i\) 个主要抽样单元（PSU）中次要抽样单元（SSU）的数量； \(M\) 表示总体中的所有次要抽样单元（SSU）的数量。

  • \(y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）中第 \(j\) 次要抽样单元（SSU）的个体的变量值。 \(y_i = \sum_{j=1}^{M_i} y_{ij}\) 表示第 \(i\) 个主要抽样单元（PSU）下所有个体的变量值之和。

case：请求计算机援助案例

（示例）请求计算机援助案例

案例说明：一家大型公司共有10个部门，每个部门的员工人数各不相同（见下左表）。IT部门主管计划对该公司的3个部门进行随机抽样，以估计该公司平均每个部门的计算机帮助请求数。然后，他采用可重复抽样的比例概率整群抽样法（pps），随机抽取了三个部门的样本数据（见下右表）：

（示例）整群抽样下的抽样误差：计算结果

依据抽样数据，我们知道 \(n =3\) ，容易计算得到 \(\bar{y}_i = \frac{y_i}{M_i}\) ，并进一步计算得到估计的均值 \(\hat{\mu}_{p}\) ，然后再计算出方差 \(\widehat{Var}(\hat{\mu}_{p})\) ：

\[ \begin{align} \hat{\mu}_{p} &=\frac{1}{n} \sum_{i=1}^{n} \frac{y_{i}}{M_{i}} = mean(\bar{y}_i) =\bar{\bar{y}_i}=0.6342 \\ \widehat{Var}\left(\hat{\mu}_{p}\right) &=\frac{1}{n(n-1)} \cdot \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}_{p}\right)^{2} = \frac{1}{n} \cdot s^2(\bar{y}_i) =0.000247 \end{align} \]

抽样误差：多阶段抽样

两阶段抽样示例1：10个PSU，4个SSU/PSU

抽样误差：多阶段抽样

两阶段抽样示例2：20个PSU，2个SSU/PSU

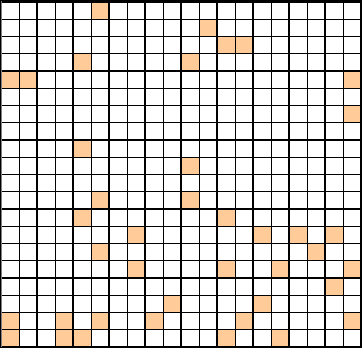
抽样误差：多阶段抽样的符号约定

多阶段抽样下，一些重要的符号约定如下：

  • \(N\) 表示总体中的全部群组数量； \(n\) 表示随机抽样后抽选得到的群组数量； \(M_i\) 表示总体中，第 \(i\) 个群组中的单位数量； \(m_i\) 表示随机抽中的第 \(i\) 个群组中的单位数量； \(M=\sum_{i=1}^N {M_i}\) 表示总体中的所有单位数量；

  • \(y_{ij}\) 表示随机抽中的第 \(i\) 个群组中的第 \(j\) 个单位的变量值； \(\bar{y}_i = \frac{1}{m_i}\sum_{j=1}^{m_i}y_{jij}\) 表示被抽中的第 \(i\) 个群组的样本均值。 \(\hat{y}_{i}=M_{i} \frac{\sum_{j=1}^{m_{i}} y_{i j}}{m_{i}}=M_{i} \bar{y}_{i}\) 表示对总体中第 \(i\) 个群组的变量总值的估计值。

抽样误差：多阶段抽样下的抽样误差计算方法1

多阶段抽样下，次要抽样单元（SSU）均值 \(\hat{\mu}\) 和方差 \(\widehat{Var}\left(\hat{\mu}\right)\) 的无偏估计法（unbiased estimator）计算公式分别为：

\[ \begin{align} \hat{\mu}=\frac{N}{M} \cdot \frac{\sum_{i=1}^{n} \hat{y}_{i}}{n} =\frac{N}{M} \cdot \frac{\sum_{i=1}^{n} M_{i} \bar{y}_{i}}{n} \end{align} \]

\[ \begin{align} \widehat{Var}(\hat{\mu})=\frac{N(N-n)}{M^2} \cdot \frac{s_{u}^{2}}{n}+\frac{N}{nM^2} \sum_{i=1}^{n} M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}} \end{align} \]

两个样本方差，其中 \(s_{u}^{2}\) 表示主要抽样单位（PSU）的样本方差；而 \(s_i^2\) 表示被抽中的第 \(i\) 个群组的样本方差。

\[ \begin{align} s_{u}^{2}&=\frac{1}{n-1} \sum_{i=1}^{n}\left(\hat{y}_{i}-\frac{\sum_{i=1}^{n} \hat{y}_{i}}{n}\right)^{2}\\ s_{i}^{2}&=\frac{1}{m_{i}-1} \sum_{j=1}^{m_{i}}\left(y_{i j}-\bar{y}_{i}\right)^{2} \end{align} \]

]

抽样误差：多阶段抽样下的抽样误差计算方法2

对于两阶段抽样方案：第一阶段和第二阶段都采用简单随机抽样。 - 如果总体的次要抽样单元（SSU）总数 \(M\) 不可知，则不能使用前述的无偏估计法。 - 此外，如果群组的变量加总值（sum value）与群组的个体数量（element size）与呈比率关系，则应该采用下述比率估计法。

对于这样的多阶段抽样方案，次要抽样单元（SSU）均值 \(\hat{\mu}_r\) 和方差 \(\widehat{Var}\left(\hat{\mu}_r\right)\) 的比率估计法（ratio estimator）计算公式分别为：

\[ \begin{align} \hat{\mu}_{r} &= \hat{r}= \frac{\sum_{i=1}^{n} \hat{y}_{i}}{\sum_{i=1}^{n} M_{i}} = \frac{\sum_{i=1}^{n} M_{i} \bar{y}_{i}}{\sum_{i=1}^{n} M_{i}} \end{align} \]

\[ \begin{align} \widehat{Var}\left(\hat{\mu}_{r}\right) &=\frac{N(N-n)}{n M^2} \cdot \frac{1}{n-1} \sum_{i=1}^{n}\left(\hat{y}_{i}-M_{i} \hat{r}\right)^{2}+\frac{N}{n M^2} \sum_{i=1}^{n} M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}} \end{align} \]

case：连锁餐厅满意度案例

（示例）连锁餐厅满意度案例

案例说明：一家餐饮连锁店想估计员工对工作的平均满意度（ 里克特量表1-7分制）。该连锁店共有120家餐厅，连锁店的全体员工总数为6860人。 研究人员决定使用两阶段随机抽样方案，第一阶段采用简单随机抽样来采样10家餐厅（被抽中的序号见列id，餐厅总员工数见列tot_worker）。然后，第二阶段也使用简单随机抽样对这些餐厅中约20％的员工（被抽中的员工数量见列sel_worker）进行抽样和工作满意度采访（见列satisfaction）。最终抽样数据结果如下：

（示例）多阶段抽样的抽样误差：基本计算量

根据案例数据，容易得到：

  • 所有餐厅数量为 \(N =120\) 。

  • 简单随机抽样选中的餐厅数量为 \(n = 10\) 。

  • 第 \(i\) 个餐厅的总员工数为 \(M_i =\) total_worker列。

  • 随机抽中的第 \(i\) 个餐厅中的被抽中的员工数量为 \(m_i=\) sel_worker列。

  • 连锁店全体员工的总人数为 \(M=\sum_{i=1}^N {M_i}=6860\) 。

  • 随机抽中的第 \(i\) 个餐厅中的平均工作满意度评分为 \(\bar{y}_i=\) mean列，工作满意度的样本方差 \(s^2_i=\) variance列。

  • 估计得到的第 \(i\) 个酒店的加总满意度评分为 \(\hat{y}_i=\) y_hat列，10家被抽中酒店估计的平均加总满意度评分为 \(\bar{\hat{y}}=\frac{\sum_{i=1}^{n} \hat{y}_{i}}{n}= 280.29\) 。

（示例）多阶段抽样的抽样误差：无偏估计法的计算量1

我们可以根据无偏估计法的相关理论公式，得到如下的计算表：

（示例）多阶段抽样的抽样误差：无偏估计法的计算量2

从而容易计算得到到如下两个无偏估计法需要用到的样本方差：

\[ \begin{align} s_{u}^{2}&=\frac{1}{n-1} \sum_{i=1}^{n}\left(\hat{y}_{i}-\frac{\sum_{i=1}^{n} \hat{y}_{i}}{n}\right)^{2} =\frac{1}{n-1} \sum_{i=1}^{n}\left(\hat{y}_{i}-\bar{\hat{y}}\right)^{2}=1591.18\\ s_{i}^{2}&=\frac{1}{m_{i}-1} \sum_{j=1}^{m_{i}}\left(y_{i j}-\bar{y}_{i}\right)^{2}=\text{variance} \end{align} \]

上述 \(s_{i}^{2}\) 计算结果见前页ppt的计算表中的variance列。

（示例）多阶段抽样的抽样误差：无偏估计法的结果

因此，采用无偏估计法估计得到的酒店满意度的均值和方差分别为：

\[ \begin{align} \hat{\mu}=\frac{N}{M} \cdot \frac{\sum_{i=1}^{n} \hat{y}_{i}}{n} =\frac{N}{M} \cdot \bar{\hat{y}} = \frac{120}{6860} \times 280.29=4.90 \end{align} \]

\[ \begin{align} \widehat{Var}(\hat{\mu}) &=\frac{N(N-n)}{M^2} \cdot \frac{s_{u}^{2}}{n}+\frac{N}{nM^2} \sum_{i=1}^{n} M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}} \\ & = \frac{120(120-10)}{10\times 6860^2} \times 1591.18+\frac{120}{10\times 6860 ^2} \times 4615.55 \\ &= 0.0458 \end{align} \]

上述求和项内部个值计算结果见前页ppt的计算表，其中： - \(M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}}\) 见计算表中的sum_right列；

（示例）多阶段抽样的抽样误差：比率估计法的计算量1

我们可以根据比率估计法的相关理论公式，得到如下的计算表：

（示例）多阶段抽样的抽样误差：比率估计法的计算量2

容易计算得到到如下比率估计法需要用到的样本方差：

\[ \begin{align} s_{i}^{2}&=\frac{1}{m_{i}-1} \sum_{j=1}^{m_{i}}\left(y_{i j}-\bar{y}_{i}\right)^{2}=\text{variance} \end{align} \]

上述 \(s_{i}^{2}\) 计算结果见前页ppt的计算表中的variance列。

（示例）多阶段抽样的抽样误差：比率估计法的结果

因此，采用比率估计法估计得到的酒店满意度的均值和方差分别为：

\[ \begin{align} \hat{\mu}_{r} = \hat{r} = \frac{\sum_{i=1}^{n} \hat{y}_{i}}{\sum_{i=1}^{n} M_{i}} = \frac{2802.86}{555} =5.05 \end{align} \]

\[ \begin{align} \widehat{Var}\left(\hat{\mu}_{r}\right) &=\frac{N(N-n)}{n M^2} \cdot \frac{1}{n-1} \sum_{i=1}^{n}\left(\hat{y}_{i}-M_{i} \hat{r}\right)^{2}+\frac{N}{n M^2} \sum_{i=1}^{n} M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}} \\ &= \frac{120(120-10)}{10\times 6860^2} \times \frac{1}{10-1} \times 7120.48+\frac{120}{10\times 6860 ^2} \times 4615.55 \\ &= 0.0234 \end{align} \]

上述两个求和项内部个值计算结果见前页ppt的计算表，其中： - \(\left(\hat{y}_{i}-M_{i} \hat{r}\right)^{2}\) 见计算表中的sum1_yi_sqr列； - \(M_{i}\left(M_{i}-m_{i}\right) \frac{s_{i}^{2}}{m_{i}}\) 见计算表中的sum2_si_sqr列。

抽样误差：多阶段抽样下的抽样误差计算方法3

对于两阶段抽样方案：第一阶段采用比例概率抽样法（PPS），第二阶段采用简单随机抽样法： - 那么抽样误差计算应该使用比例概率估计法（pps估计法，具体为Hansen-Hurwitz estimator）。

对于这样的多阶段抽样方案，次要抽样单元（SSU）均值 \(\hat{\mu}_p\) 和方差 \(\widehat{Var}\left(\hat{\mu}_p\right)\) 的比例概率估计法（pps estimator）计算公式分别为：

\[ \begin{align} \hat{\mu}_{p} = \frac{1}{n} \cdot \sum_{i=1}^{n} {\frac{\hat{y}_{i}}{M_i}} =\frac{1}{n} \cdot \sum_{i=1}^{n} {\frac{\bar{y}_{i}*M_i}{M_i}} = \frac{1}{n} \cdot \sum_{i=1}^{n} {\bar{y}_i} \end{align} \]

\[ \begin{align} \widehat{Var}\left(\hat{\mu}_{p}\right) &=\frac{1}{n(n-1)} \cdot \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}_{p} \right)^{2} \end{align} \]

case：学生书本支出案例

（示例）学生书本支出案例

案例说明：一个学院共有36个专业（major）。研究者想估算出上学期学生在教科书上花费（expenses）的平均金额。由于每个专业的规模差异很大，因此采用的两阶段抽样方案，其中第一阶段采用的是pps抽样，第二阶段是简单随机抽样。最终抽样数据结果如下：

（示例）多阶段抽样的抽样误差：PPS估计法的计算表

我们可以根据比例概率估计法的相关理论公式，得到如下的计算表：

（示例）多阶段抽样的抽样误差：PPS估计法的结果

因此，采用比例概率估计法估计得到学生书本支出的均值和方差分别为：

\[ \begin{align} \hat{\mu}_{p} = \frac{1}{n} \cdot \sum_{i=1}^{n} {\frac{\hat{y}_{i}}{M_i}} =\frac{1}{n} \cdot \sum_{i=1}^{n} {\frac{\bar{y}_{i}*M_i}{M_i}} = \frac{1}{n} \cdot \sum_{i=1}^{n} {\bar{y}_i} = \bar{\bar{y_i}} = 412.02 \end{align} \]

\[ \begin{align} \widehat{Var}\left(\hat{\mu}_{p}\right) =\frac{1}{n(n-1)} \cdot \sum_{i=1}^{n}\left(\bar{y}_{i}-\hat{\mu}_{p} \right)^{2} &= \frac{1}{n} \cdot s^2_{\bar{y_i}} \\ & = \frac{1}{4} \times 1214.6406 = 303.6602 \end{align} \]

上述计算结果的中间步骤计算值见前页ppt的计算表。 其中： - \(\bar{y}_i\) 见计算表中的mean列； - \(\hat{y}_i\) 见计算表中的y_hat列。

必要样本数

本学期稍后学习！

（千呼万唤、望穿秋水你们的《概率论与数理统计》啊！！！）

本节结束