统计学原理
(Statistics)
第1章 导论
Hu Huaping (胡华平)
huhuaping01 at hotmail.com
经济管理学院(CEM)
第1章 导论
1.1 为什么学习统计学
统计现象与世界认知
辛普森悖论的警示:女性在求职中被歧视?
故事是这么说的:
辛普森悖论的警示:聚焦六大招聘部门
但故事背后却另有蹊跷:
辛普森悖论的警示:聚焦具体细节
事情的“真相”是:
辛普森悖论的警示:男女对比
对比一下
辛普森悖论的警示:更加细节的数据
更加细节的数据:
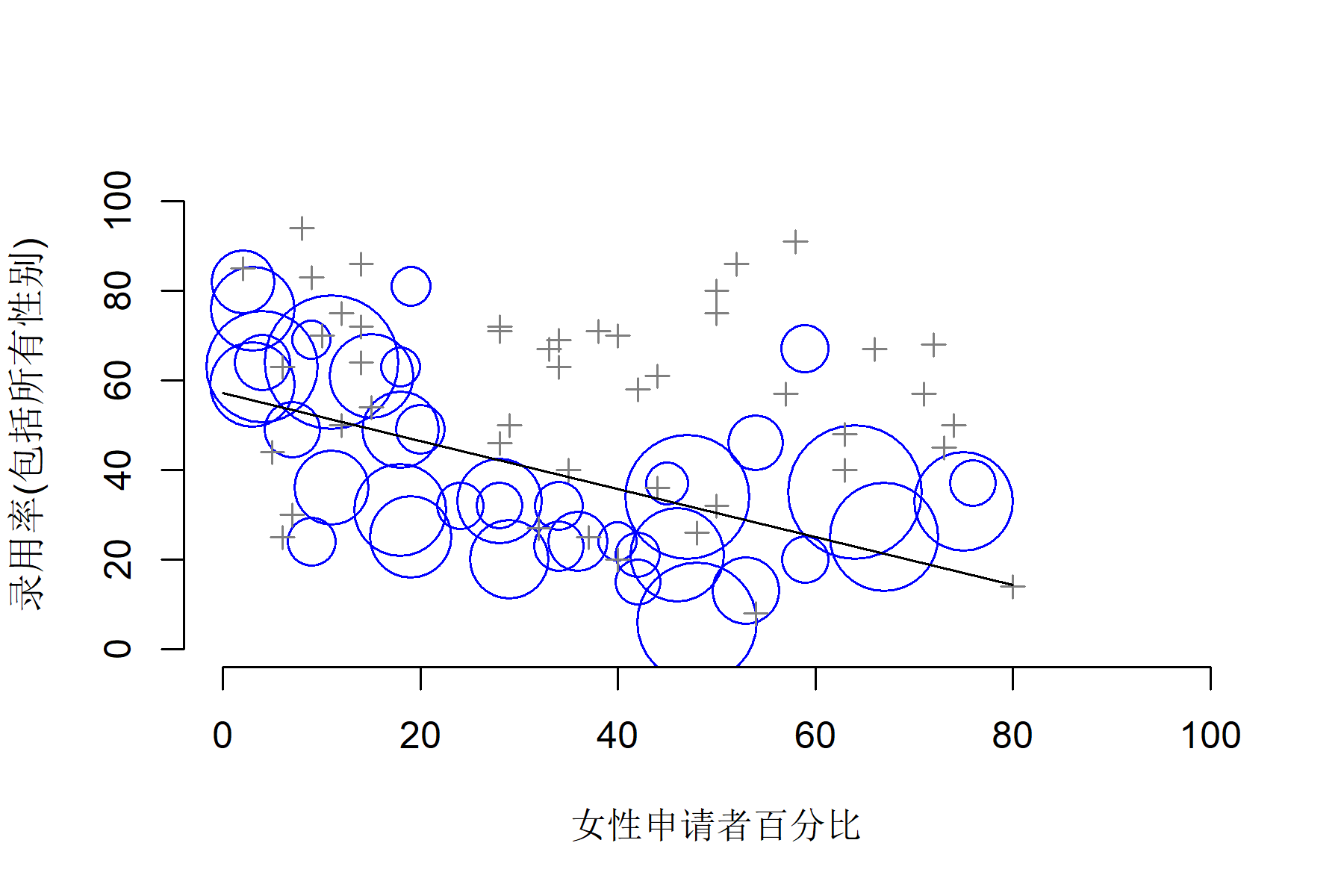
辛普森悖论的警示:令人吃惊的对称性分布
令人吃惊的对称性分布(圆圈表示总申请数大于40人的部门,叉叉表示总申请数小于40人的部门):
信念偏见:论据有效性
信念偏见效应:如果你让人们决定一个特定的论点是否在逻辑上是有效的,我们往往会受到结论可信度的影响,即使我们不应该这样做。
一个有效的论据,其结论是可信的::
没有香烟很便宜(前提1)
有些令人上瘾的东西很便宜(前提2)
因此,有些令人上瘾的东西不是香烟(结论)
一个有效的论据,但其结论是不可信的:
没有令人上瘾的东西很便宜(前提1)
有些香烟很便宜(前提2)
因此,有些香烟不会上瘾(结论)
信念偏见:论据有效性
持枪和控枪的美国现象:素材1
素材1:
- 美国宪法规定,人民持有和携带武器的权利不受侵犯,这是宪法权利。美国历史上地广人稀,一旦发生暴力事件,警察没办法及时赶到现场,所以美国人民应该有枪支自卫。
观点:
A. 宪法很大程度考虑到了公民个人私人持枪的选择权
B. 菜刀在坏人手里会成为凶器,私人持枪以保护自己和身边的人不受侵害也同样重要
C. 其他观点
持枪和控枪的美国现象:素材2
素材2:
1968年美国人口2亿,拥有枪支1.1亿;今天美国人口3.2亿,拥有枪支3.6亿!50年前是两人一支,现在是几乎一人一支。
2016年美国枪支产业雇佣了30多万人,对美国经济的贡献是500亿。美国枪支市场巨大,提供了几十万个工作机会,也养活了很多利益集团,他们不答应禁枪等等。
观点:
A. 军火产业虽然提供了一些就业,但也助长了枪击事件的发生
B. 军火市场根深蒂固,进而让私人禁枪的提案或修宪变得困难
C. 其他观点
持枪和控枪的美国现象:素材3
素材3:
美国有三亿多支枪,每年被枪杀的人3万多。2014年美国有4万人自杀,其中超过一半选择用枪;70岁以上自杀的老人,选择用枪的比例最高,74%。
美国虽然总发生枪击案,但发生的概率仅有千分之0.1。过去23年美国枪杀案的比例整整下降了1倍!
观点:
A. 枪击事件很大程度上是因为影响恶劣而被社会过度关注和解读
B. 引发死亡率的主因很多,私人持枪造成的社会伤害并没有愈演愈烈
C. 其他观点
持枪和控枪的美国现象:素材4
素材4:
美国枪支管理法律不是越来越严,而是越来越松。
正反观点针锋相对:“美国游泳淹死的人是5倍于被枪走火打死的”。“我亲戚三岁的小姑娘被他爸枪走火打死。如果这个小孩是你的,你愿意她成为你玩枪的社会成本吗?”
如果不发生这次拉斯维加斯枪击案,美国又会出台一个放宽枪支管制的议案,要讨论允许私人购买枪支消声器的议案,就是可以公开卖无声枪了。在美国,要自杀的人没枪也会用别的方式死,美国人对死亡的观念:毒药、安乐死与尊严
观点:
A. 控枪政策日趋放松尽管有其可解释之处,但并不是长远明智之举
B. 持枪派,控枪派和中立派或许都无可厚非,各方相互制衡最为重要
C. 其他观点
1.2 变量和数据
变量及其类型
变量及其类型A:按性质划分
变量:描述事物或现象的变化特征。
A.按性质不同可分为:
定性变量:非数值化的变量。
定量变量:数值化的变量。
离散变量:可能的取值比较有限、并能轻松列示的一类定量变量。
连续变量:可能的取值较多、以特定微小数值间隔的一类定量变量。
随堂测验(2min)
请分别说出如下情形分别属于那种变量类型?
- 教育程度(可能取值为:文盲、非文盲)
- 教育程度(可能取值为:小学及以下、初中、高中、大学、研究生及以上)
- 教育程度(可能取值为:1=小学及以下、2=初中、3=高中、4=大学、5=研究生及以上)
- 教育程度(单位为年,可能取值为:6、9、12、15、18、21、24、…)
- 教育程度(单位为年,可能取值为:6、7、8、9、12、14.5、15、18、20、21、…)
变量及其类型B:按变量是否随机
随机变量(random variable):在事件集合上的一个特定函数的随机分布状态。
非随机变量(non-random variable):也称为确定性变量(Deterministic variable)。
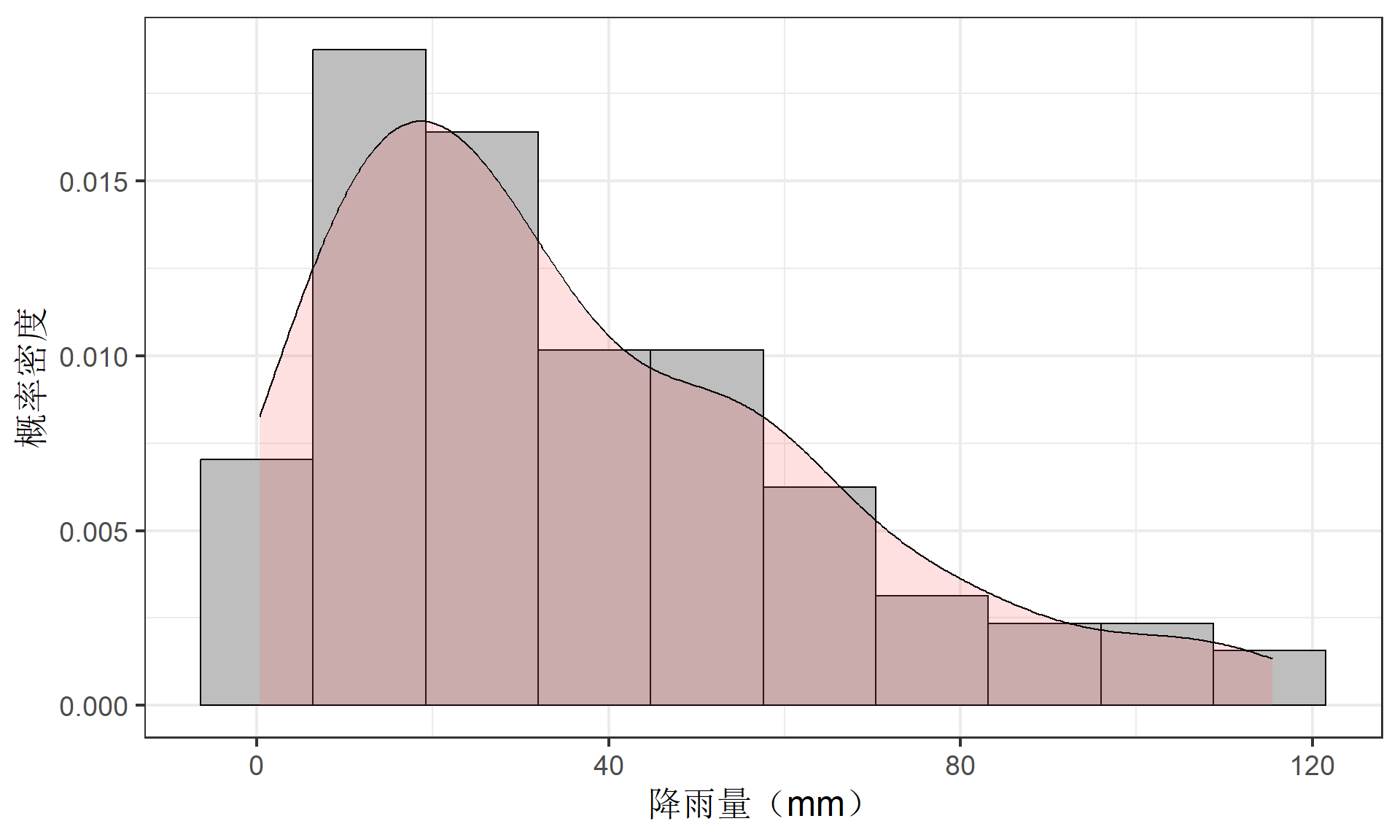
(示例)降雨量记录
100天降雨量记录(mm):下面只列出了前50天
day1 day2 day3 day4 day5 day6 day7
28.023782 11.508874 77.935416 3.525420 6.464387 85.753249 23.045810
day8 day9 day10 day11 day12 day13 day14
63.253062 34.342643 22.283099 61.204090 17.990691 20.038573 5.534136
day15 day16 day17 day18 day19 day20 day21
27.792057 89.345657 24.892524 98.330858 35.067795 23.639570 53.391185
day22 day23 day24 day25 day26 day27 day28
10.898746 51.300222 36.444561 31.251963 84.334666 41.889352 7.668656
day29 day30 day31 day32 day33 day34 day35
56.906847 62.690746 21.323211 14.753574 44.756283 43.906674 41.079054
day36 day37 day38 day39 day40 day41 day42
34.432013 27.695883 3.095586 15.298133 19.023550 34.735349 10.395864
day43 day44 day45 day46 day47 day48 day49
63.269818 108.447798 60.398100 56.155429 20.144242 23.332768 38.998256
day50
4.168453 课堂讨论(2min)
非随机变量(non-random variable)实际存在么?
正方:存在!
- 有随机变量就自然有非随机变量,它取值的产生是经过特意安排的,也即非随机的。
反方:不存在!
- 非随机变量是杜撰的,如果是变量则都应该是随机的。非随机变量其实就是常数(constant),当然不能称为变量,也就不能叫做非随机变量。
变量及其类型C:按变量是否抽象化
C.按变量是否抽象化:
经验变量:经验变量所描述的是我们周围可以观察到的事物。
理论变量:理论变量则是由统计学家用数学方法所构造出来的一些变量,比如z 统计量、t 统计量、 \(\chi^2\) 统计量、F 统计量等。
数据及其类型
数据及其类型A:按数据取值的性质划分
数据:变量的实际具体取值组成的集合。
A.按数据取值的性质分:
定性数据:定性变量的取值。
定量数据:定量变量的取值。
离散数据:离散变量的取值。
连续数据:连续变量的取值。
数据及其类型B:按数据获得是否可控制
观察性数据(observational data):人们在观察性研究中被动性记录下来的数据。
实验性数据(experimental data):人们通过主动控制和改变实验条件获得并记录的数据。
数据与变量的关系
数据和变量共同测度信息
变量是数据存身之所,而数据是变量的现实表达。
变量是一个抽象概念,而数据是实体概念。
数据和变量是相互依存的关系,如同一个硬币的两面。
数据和变量可以进一步共同描述或表达事物或现象的信息(information)。
示例1:SPSS统计软件下的变量和数据
下面给大家展示传统商业(收费)统计分析软件SPSS的变量和数据视窗:
SPSS软件的数据视图
SPSS软件的变量视图
示例2:R统计软件下的变量和数据
下面给大家展示开源(免费)统计分析软件R的变量和数据视窗:
纽约机场数据库:变量视图
Rows: 27,004
Columns: 19
$ year <int> 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2013, 2…
$ month <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ day <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ dep_time <int> 517, 533, 542, 544, 554, 554, 555, 557, 557, 558, 558, …
$ sched_dep_time <int> 515, 529, 540, 545, 600, 558, 600, 600, 600, 600, 600, …
$ dep_delay <dbl> 2, 4, 2, -1, -6, -4, -5, -3, -3, -2, -2, -2, -2, -2, -1…
$ arr_time <int> 830, 850, 923, 1004, 812, 740, 913, 709, 838, 753, 849,…
$ sched_arr_time <int> 819, 830, 850, 1022, 837, 728, 854, 723, 846, 745, 851,…
$ arr_delay <dbl> 11, 20, 33, -18, -25, 12, 19, -14, -8, 8, -2, -3, 7, -1…
$ carrier <chr> "UA", "UA", "AA", "B6", "DL", "UA", "B6", "EV", "B6", "…
$ flight <int> 1545, 1714, 1141, 725, 461, 1696, 507, 5708, 79, 301, 4…
$ tailnum <chr> "N14228", "N24211", "N619AA", "N804JB", "N668DN", "N394…
$ origin <chr> "EWR", "LGA", "JFK", "JFK", "LGA", "EWR", "EWR", "LGA",…
$ dest <chr> "IAH", "IAH", "MIA", "BQN", "ATL", "ORD", "FLL", "IAD",…
$ air_time <dbl> 227, 227, 160, 183, 116, 150, 158, 53, 140, 138, 149, 1…
$ distance <dbl> 1400, 1416, 1089, 1576, 762, 719, 1065, 229, 944, 733, …
$ hour <dbl> 5, 5, 5, 5, 6, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 5, 6, 6, 6…
$ minute <dbl> 15, 29, 40, 45, 0, 58, 0, 0, 0, 0, 0, 0, 0, 0, 0, 59, 0…
$ time_hour <dttm> 2013-01-01 05:00:00, 2013-01-01 05:00:00, 2013-01-01 0…纽约机场数据库:数据视图
只看2013年1月数据集的前500条数据。
数据和信息的关系
数据和信息的联系
数据和信息有何联系与不同?
“The numbers have no way of speaking for themselves. We speak for them. We imbue them with meaning.” —Statistician Nate Silver in the book The Signal and the Noise

大数据的信息特征
大数据(big data)是不是一定好?
- 优点:可能包含更多信息;
- 缺点:信息量太大以至于无法处理。
大数据的四大特征(4V):
- Volume(数据量大)
- Variety(变异性大)
- Veracity(精确记录)
- Velocity(迅疾变化)

更多的数据是否意味更有用的信息?
- 天体运行规律:第谷的海量天文数据VS开普勒筛选分析。

- 总统选举预测:《文学文摘》240万人大调查VS盖洛普5000人调查。

1.3 数据的计量层次
名义数据(nominal data)
名义数据的内涵
取值只用于区分所属类别的定性数据。
对事物进行分类的结果,数据表现为类别,一般用文字来表述。
性别(男、女)
婚姻状况(已婚、未婚、离婚、分居)
(示例)名义数据举例:变量
变量及可能取值VS数据集
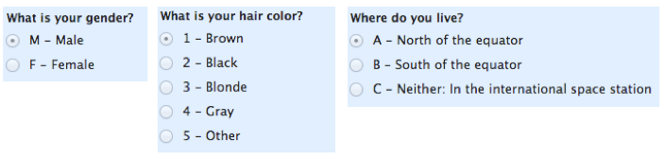
(示例)名义数据举例:数据集
变量及可能取值VS数据集
顺序数据(ordinal data)
顺序数据的内涵
变量的不同取值有顺序差异,即存在自然顺序
变量的不同取值的差值,没有实际意义
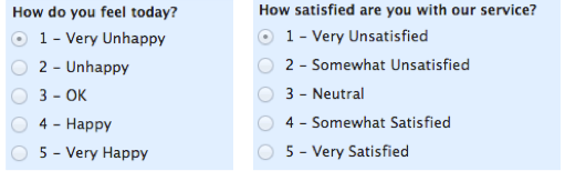
(示例)顺序数据举例
(课堂思考)序数数据如何排序?
课堂思考:序数数据如何排序?如果数据量超级大,怎样快速排序( 数据概览如下):
Rows: 5
Columns: 3
$ weekday <chr> "Mon", "Tue", "Wen", "Thu", "Fri"
$ temp <fct> High, Low, High, Low, Medium
$ feel <fct> VU, VH, UH, OK, H区间数据( interval data)
区间数据的内涵
区间数据( interval data) 的数值存在自然顺序、可以比较大小(加减)、但乘除比率没有意义。
变量的不同取值有顺序差异,即存在自然顺序
变量的不同取值的差值,也具有实际意义
但不同取值的比率是没有实际意义的
- 两个时期之内的距离(如2000 – 1995) 是有意义的,但两个时期的比率(2000/1995) 就没有什么意义。
- 2013年8 月11 日上午11 点天气预报说杨凌的温度是华氏60 度,而长沙达到华氏90 度。长沙比杨凌温度高30华氏度(90-60),是可以的。但说长沙比杨凌暖和1.5倍(90/60),是没有意义。
(示例)起飞延误时长与星期几有关系么?
纽约JKF机场在2013年1月起飞航班数据集:
计划起飞时间(
sched_dep_time)和实际起飞时间(dep_time)能直接相减么?如果延误超过一天,该怎么计算起飞延误时长?
如果取消航班了,该怎么计算起飞延误时长?
(示例)起飞延误时长与星期几有关系么?
(示例)起飞延误时长与星期几有关系么?
比率数据(ratio data)
比率数据的内涵
比率数据(ratio data)的取值存在自然顺序、可以比较大小(加减)、乘除比率有实际意义。
变量存在真实“零点”
变量的不同取值存在自然顺序( \(X_2 \leq X_1\) 或 \(X_2 \geq X_1\) )
变量的不同取值之差是有实际意义的( \(X_2-X_1\) )
变量的不同取值的乘除都是有意义的( \(X_1/X_2\) )
如:GDP(亿元)、个人收入(元)等
小结:数据层次与数据运算可能性
1.4 数据的时间状态
时间序列数据(time series data)
时间序列数据的定义
时间序列数据:对一个变量在不同时间取值的一组观测结果。按取值间隔可分为高频数据和低频数据。
实时牌价:如股票价格
每日(daily):如天气预报
每周(weekly):如货币供给数字
每月(monthly):如失业率和消费者价格指数
每季度(quarterly):如GDP
每年(annually):如政府预算
每5 年(quinquennially):如制造业普查资料
每10 年( decennially):如人口普查资料
时间序列数据的特征
平稳性(stationary):如果一个时间序列的均值和方差不随时间而系统地变化,那它就是平稳的(stationary) 。
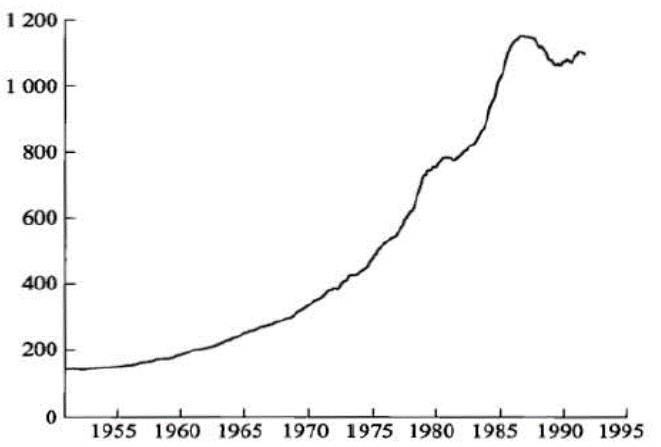
截面数据(cross-section data)
截面数据的定义
横截面数据:对一个或多个变量在同一时间点上收集的数据
异质性(heterogeneity) :当我们的统计分析包含有异质的单位时,我们必须考虑尺度(size)或规模效应(scale effect) 以避免造成混乱。
(示例)鸡蛋价格与鸡蛋产量
其中, \(Y_1\) 代表1990年鸡蛋产量(百万个); \(X_1\) 代表1990年每打鸡蛋的价格(美分/打)。
(示例)鸡蛋价格与鸡蛋产量
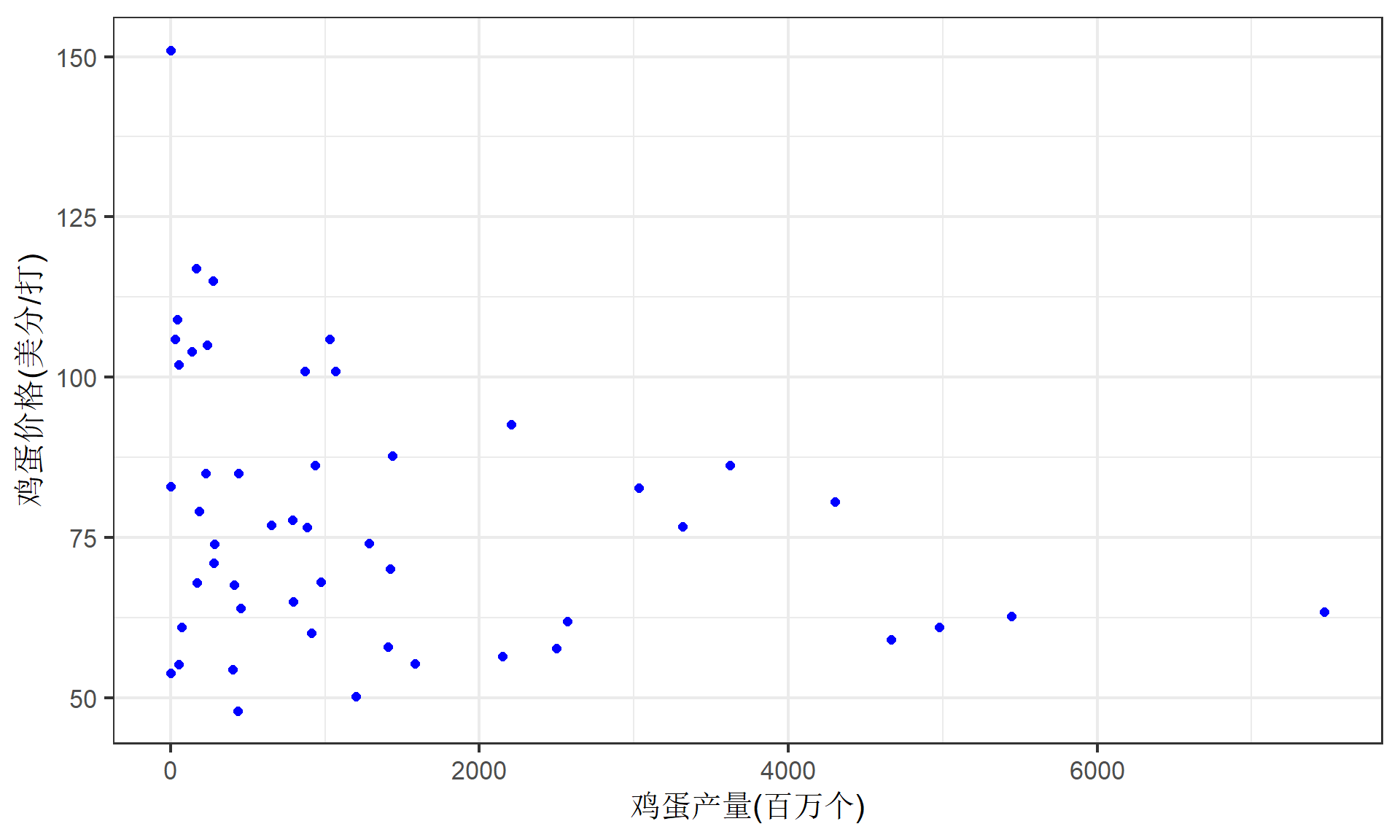
思考提问:图中特征符合经济学理论么?为什么?图中反映了数据可能存在哪些潜在问题?
面板数据(Panel Data)
面板数据的定义及特征
面板数据:是兼有时间序列和横截面数据两种成份,指对相同的横截面单元在时间轴上进行跟踪调查的数据。
平衡面板(balanced panel):所有截面单元都具有相同的观测次数
非平衡面板(unbalanced panel):并非所有截面单元都具有相同的观测次数
数据点(观测数) \(n\) :
- 数据点(观测数)=截面单元数*时期数,也即: \(n=q\ast t\) 。
可能存在的问题:
“平稳性”问题:
“异方差”问题:
(示例)钢铁公司:案例说明
两家钢铁公式的数据案例:
公司:GE=通用公司;US=美国钢铁
I=真实总投资(百万美元)
F=前一年的企业真实价值 (百万美元)
C=前一年的真实资本存量(百万美元)
(示例)钢铁公司:扁数据形式
(示例)钢铁公司:企业投资情况
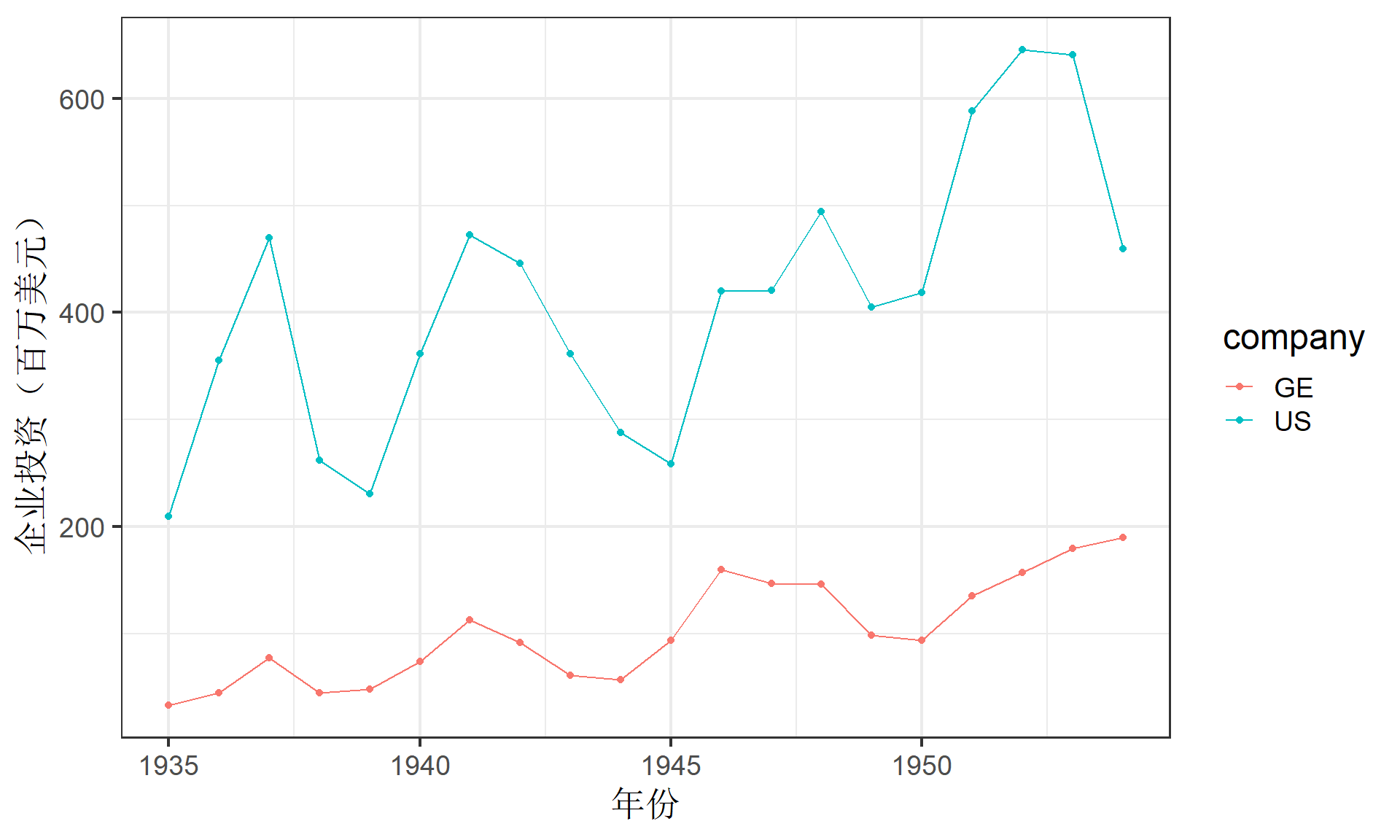
(示例)钢铁公司:长数据形式
(示例)钢铁公司:非平衡情形
1.5 统计学的体系
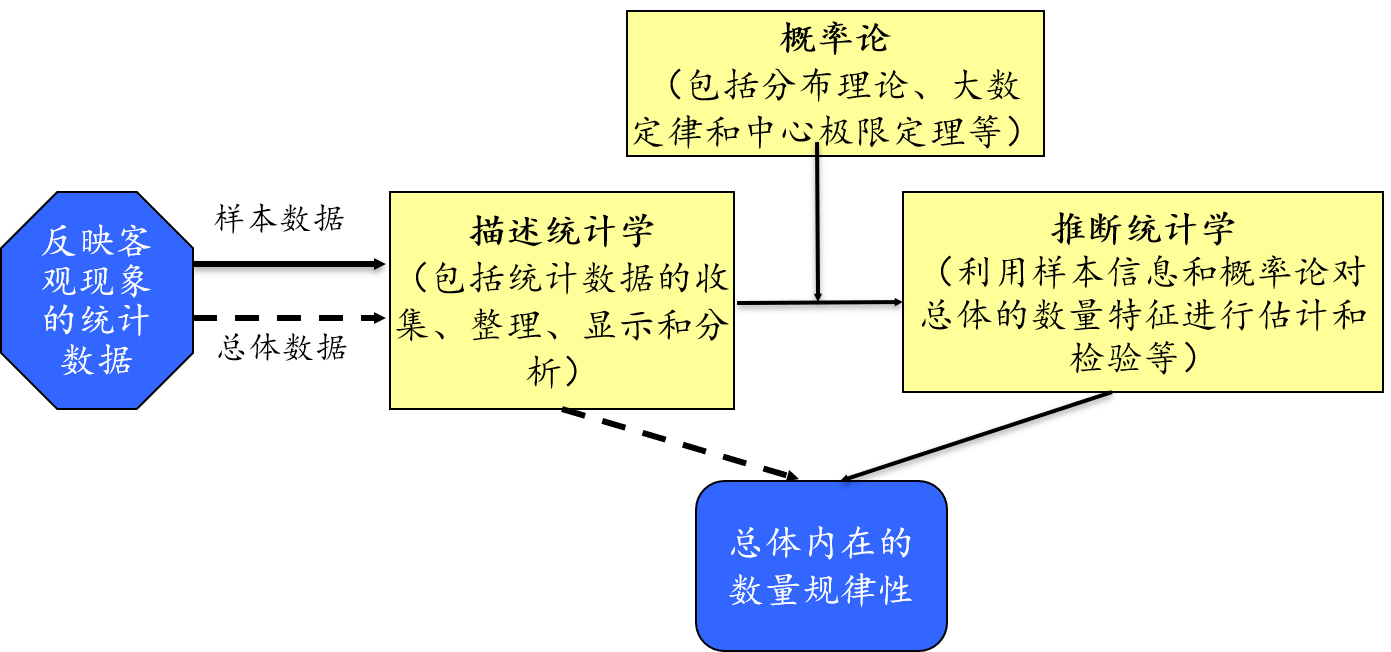
统计学的方法论
概率论在统计学中的价值与作用
方法论:用样本描述或推断总体。
主要途径:概率论在其中发挥着重要作用,也是方法论的分水岭。
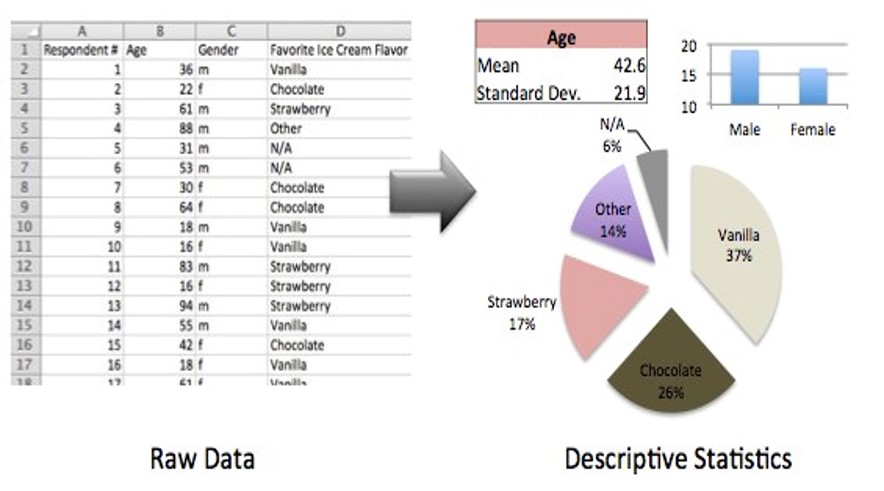
描述性统计(descriptive statistics)
描述性统计的定义和目标
定义:研究数据收集、处理、汇总、图表描述、概括与分析等统计方法
目标:描述数据特征;找出数据的基本规律
内容:
- 搜集数据
- 整理数据
- 展示数据
- 描述性分析
描述性统计展示
推断性统计(inferential statistics)
推断性统计的定义和目标
定义:研究如何利用样本数据来推断总体特征的统计方法
目标:对总体特征作出推断
内容:
- 参数估计
- 假设检验
推断性统计展示
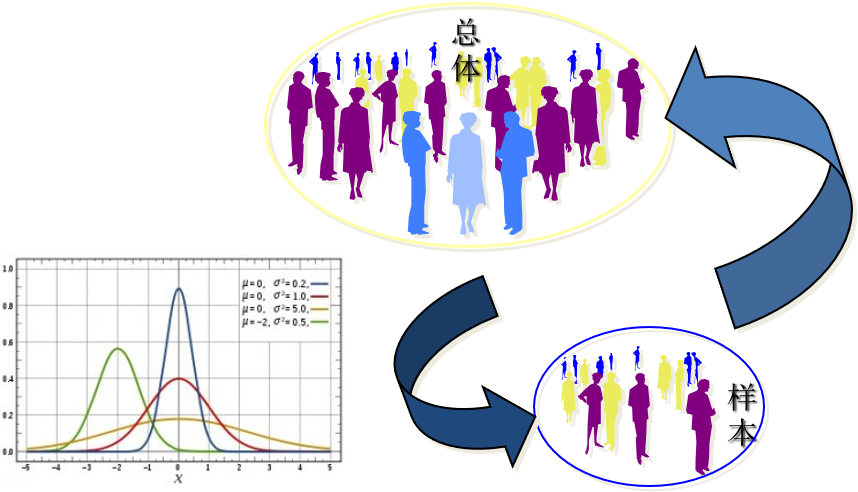
统计学的基本概念
总体和样本
总体(population):
定义:所研究的全部个体(数据) 的集合,其中的每一个个体也称为元素
分类:分为有限总体和无限总体
有限总体的范围能够明确确定,且元素的数目是有限的
无限总体所包括的元素是无限的,不可数的
样本 (sample)
定义:从总体中抽取的一部分元素的集合
样本容量:构成样本的元素的数目称为样本容量或样本量 (sample size)
参数和统计量
参数(parameter):
定义:描述总体特征的概括性数字度量,是研究者想要了解的总体的某种特征值
重要统计量:所关心的参数主要有总体均值( \(\mu\) )、方差( \(\sigma^2\) ) 等
记号:总体参数通常用希腊字母表示 \(\mu,\sigma^2,\Phi,\gamma,\cdots\)
统计量(statistic):
定义:用来描述样本特征的概括性数字度量,它是根据样本数据计算出来的一些量,是样本的函数
重要统计量:所关心的样本统计量有样本均值( \(\bar{X}\) )、样本方差( \(S^2\) ) 等
记号:样本统计量通常用英文字母来表示 \(\bar{X},s^2,w,v,\cdots\)
参数和统计量
(示例)样本如何推断总体?

(示例)样本和总体视角
总体( \([Y_i, X_i],N\) )
总体参数???
变量的总体关系???
样本( \([y_i, x_i],n\) )
样本统计量???
怎么透过样本数据来窥探总体关系的秘密?
(示例)样本和总体视角1

(示例)样本VS总体视角2
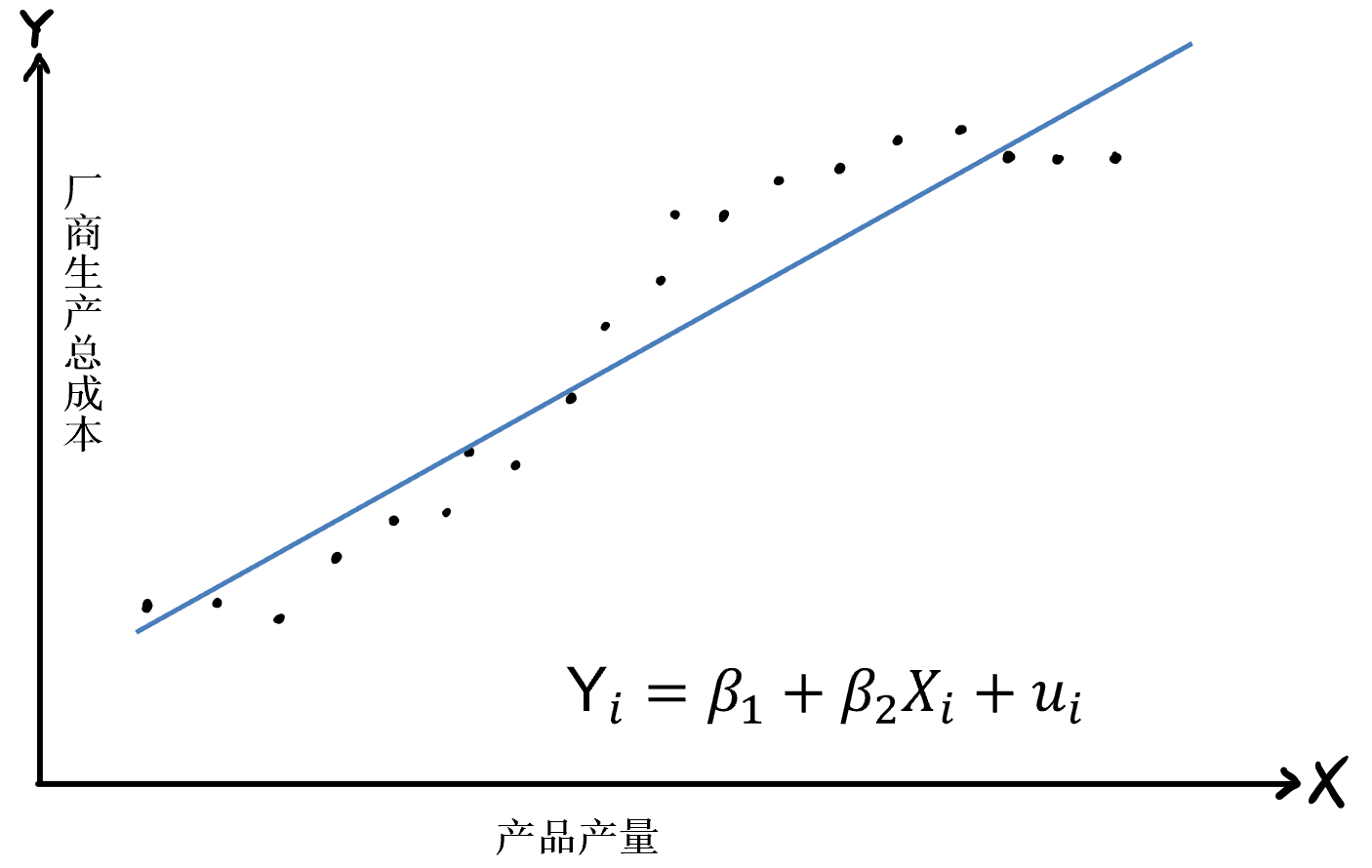
(示例)样本VS总体视角3
(示例)样本VS总体视角4
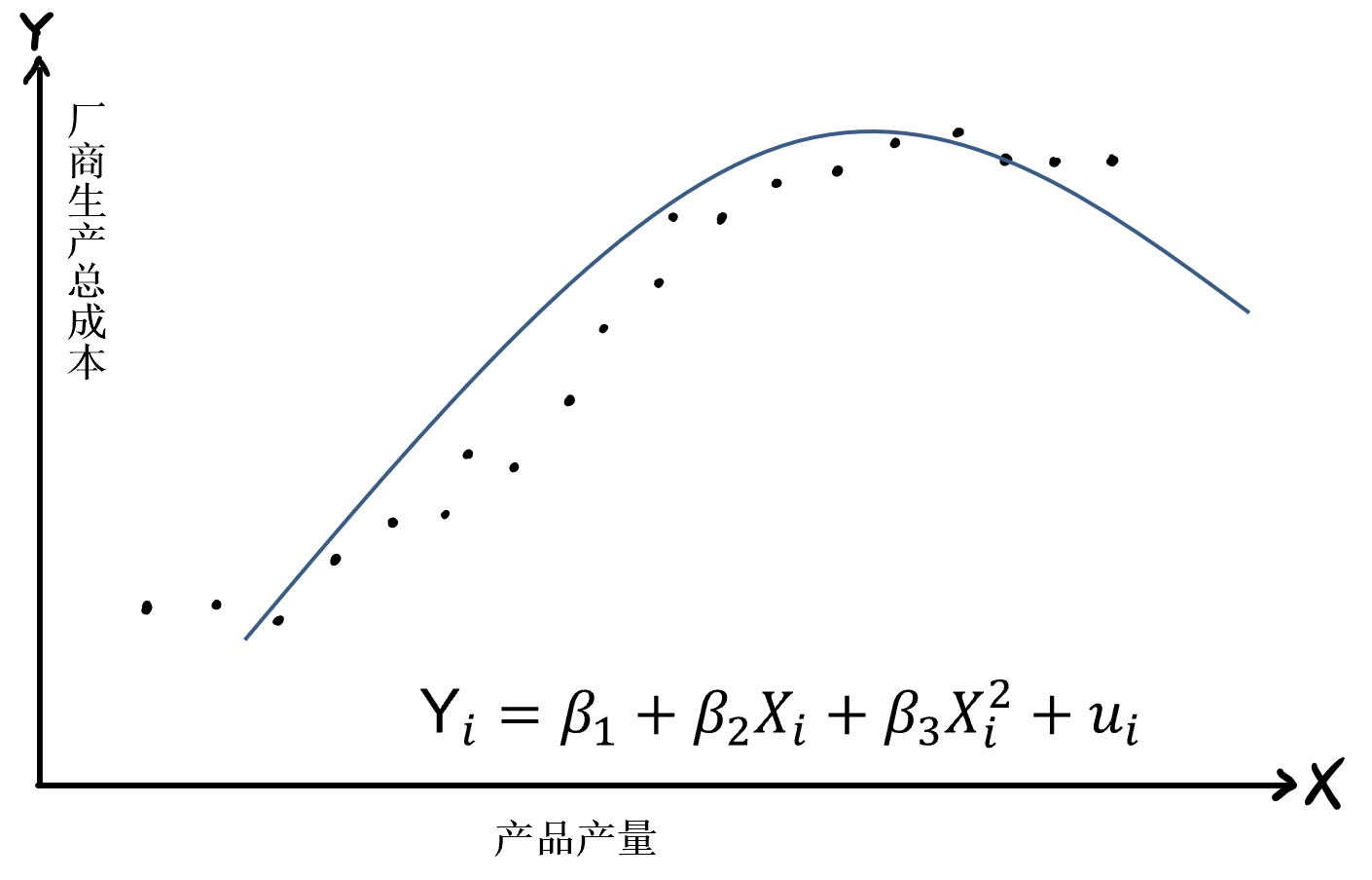
(示例)样本VS总体视角4
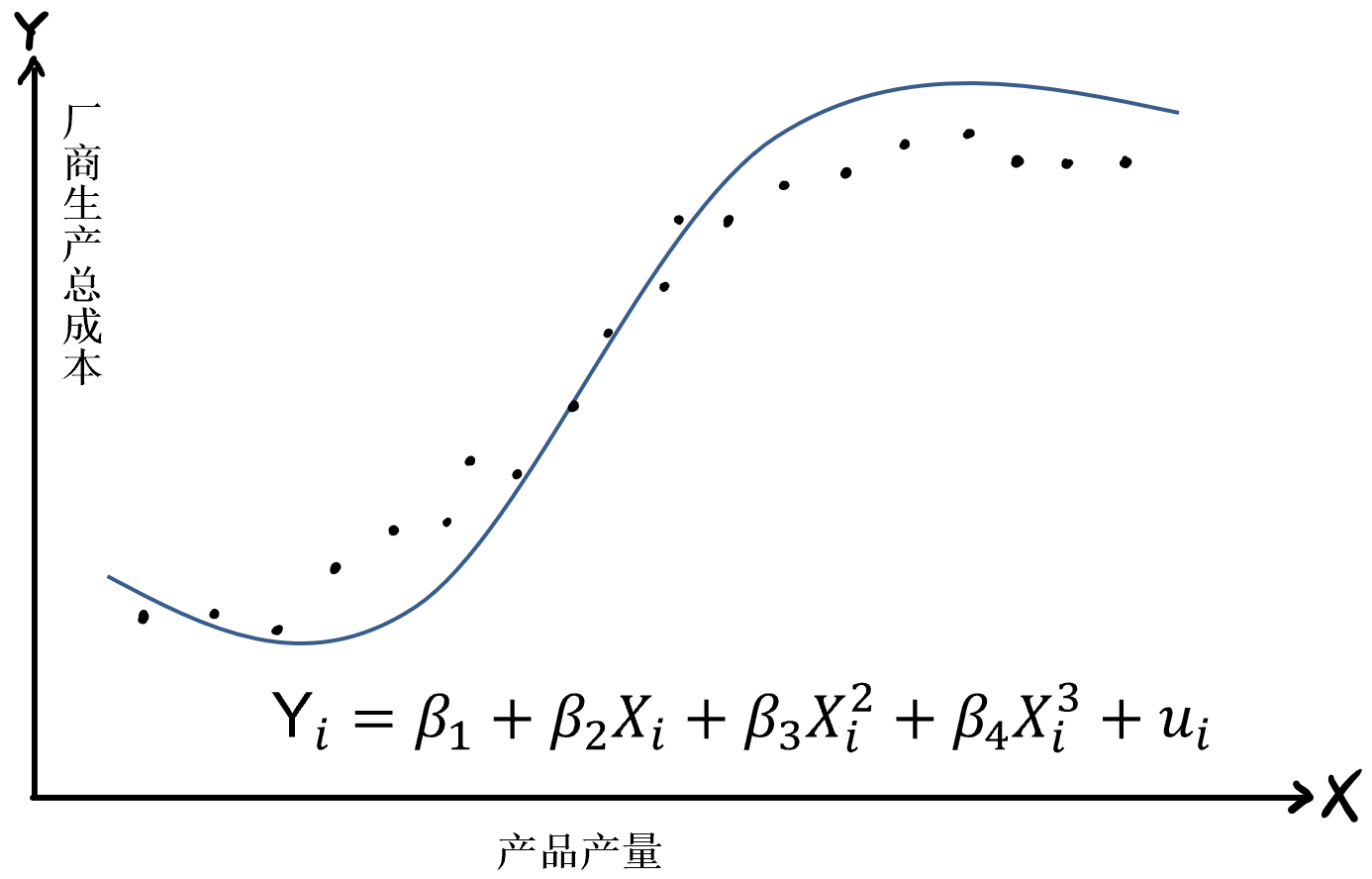
(实验演示)参数和统计量1
总共162名同学参与随机抽样;每个同学都随机抽取 \(n=10\) 个数据点。 因此共有162份样本数据(每份含10个观测数)。
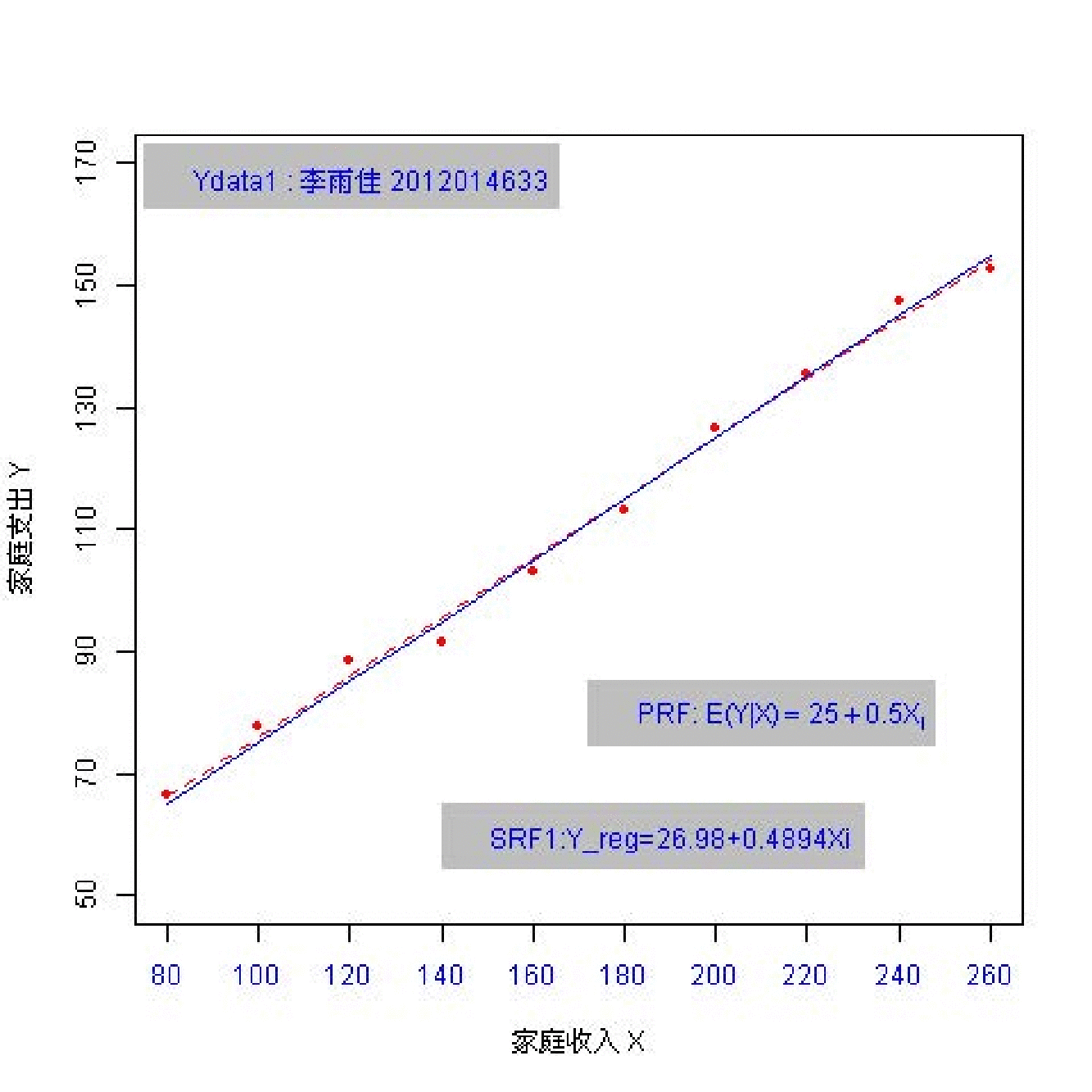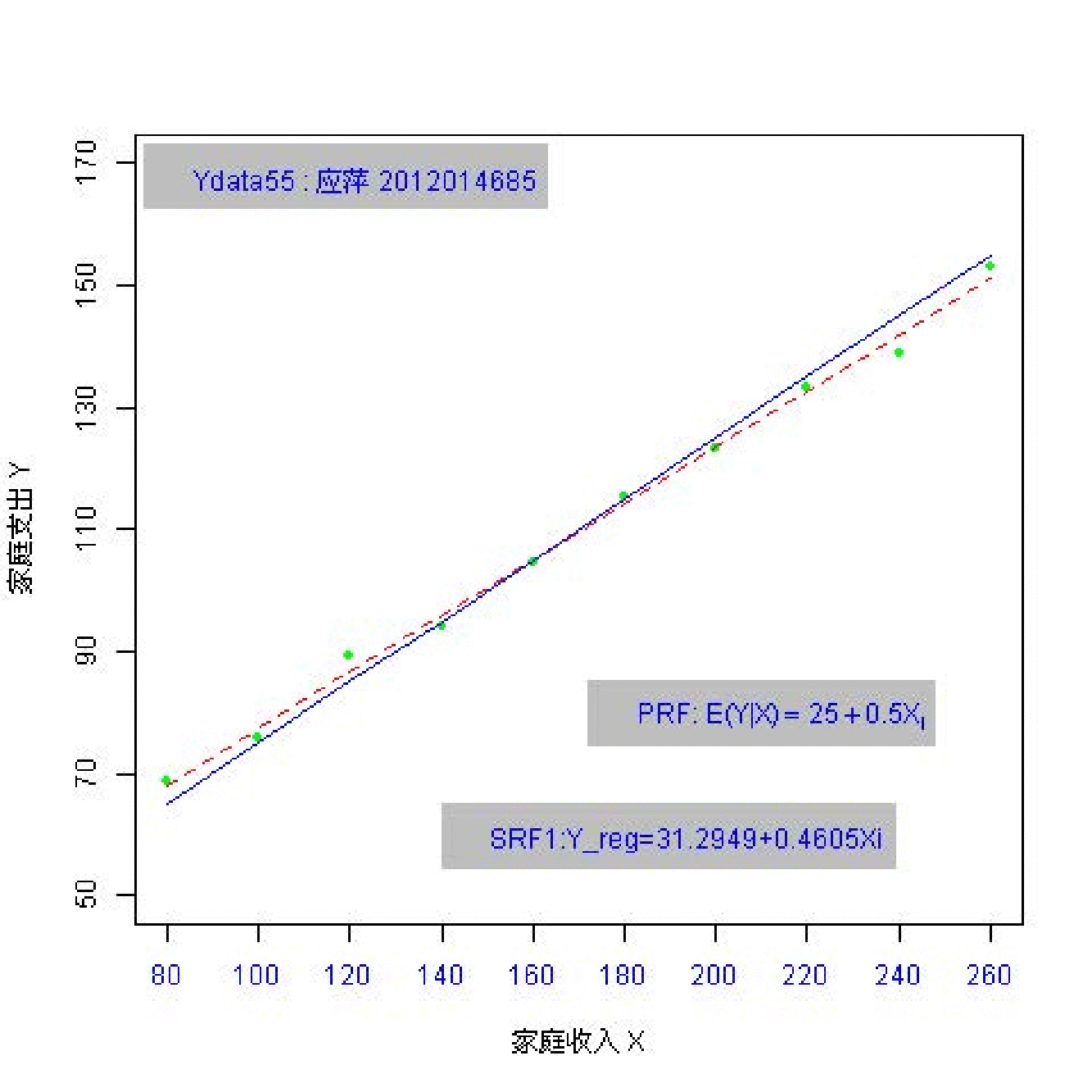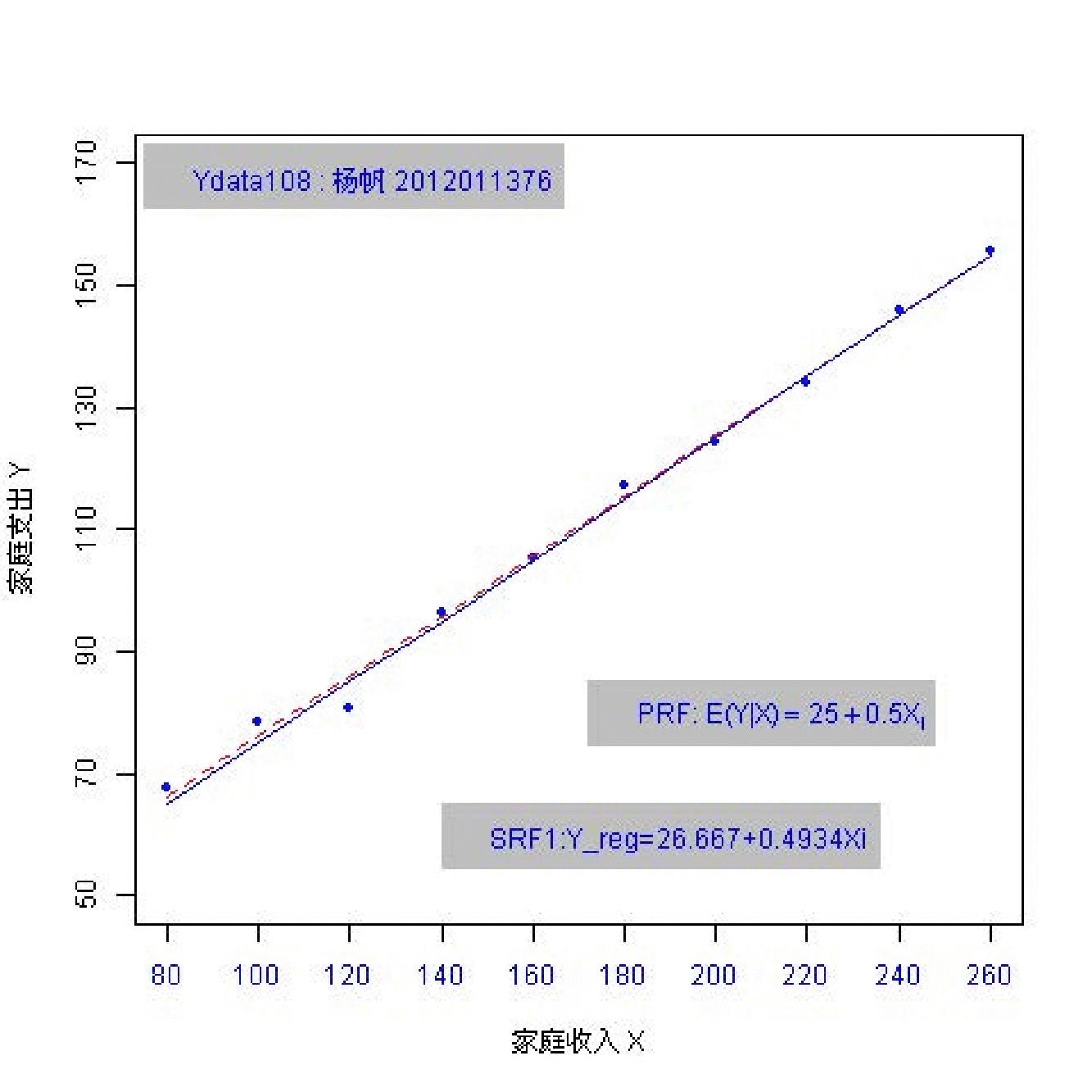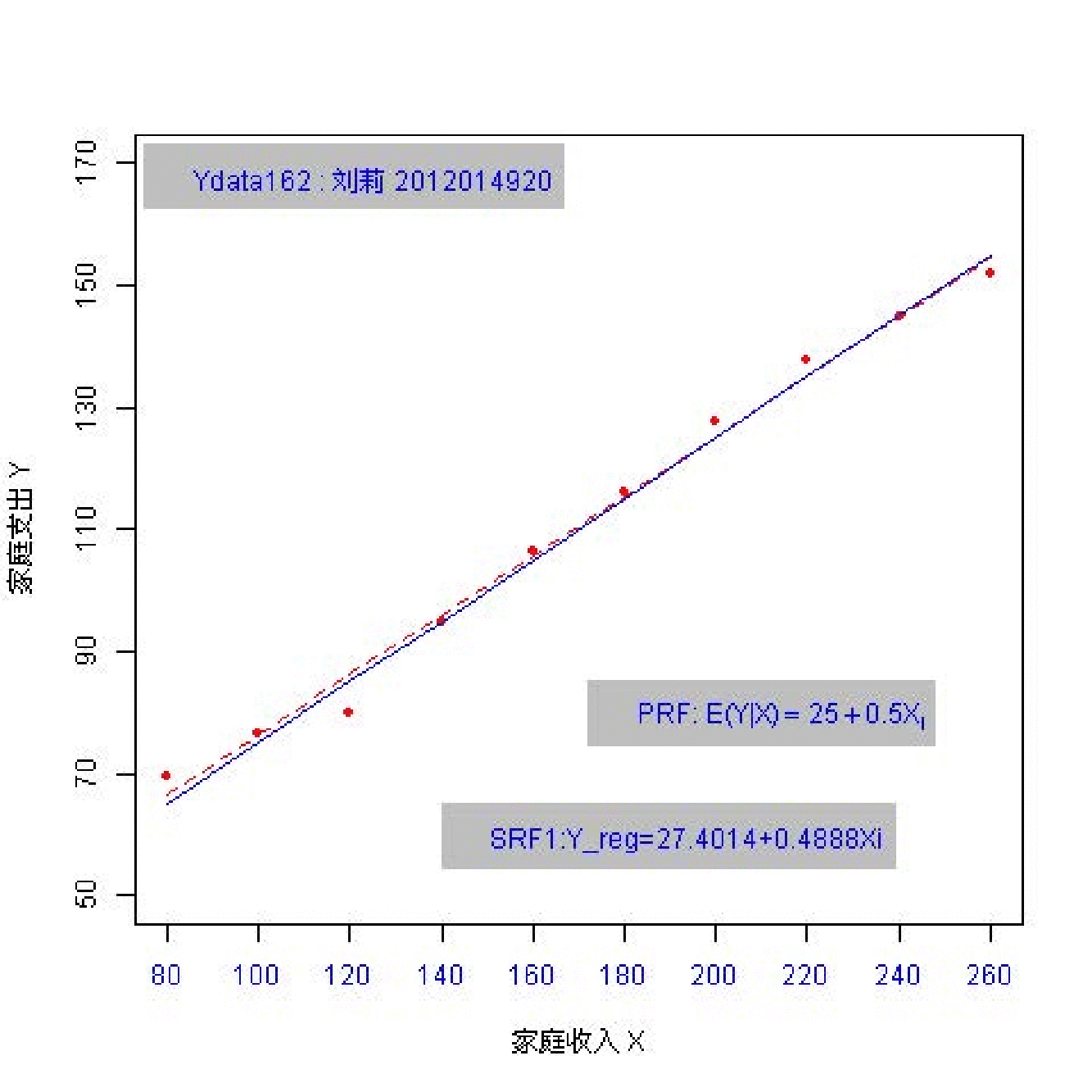
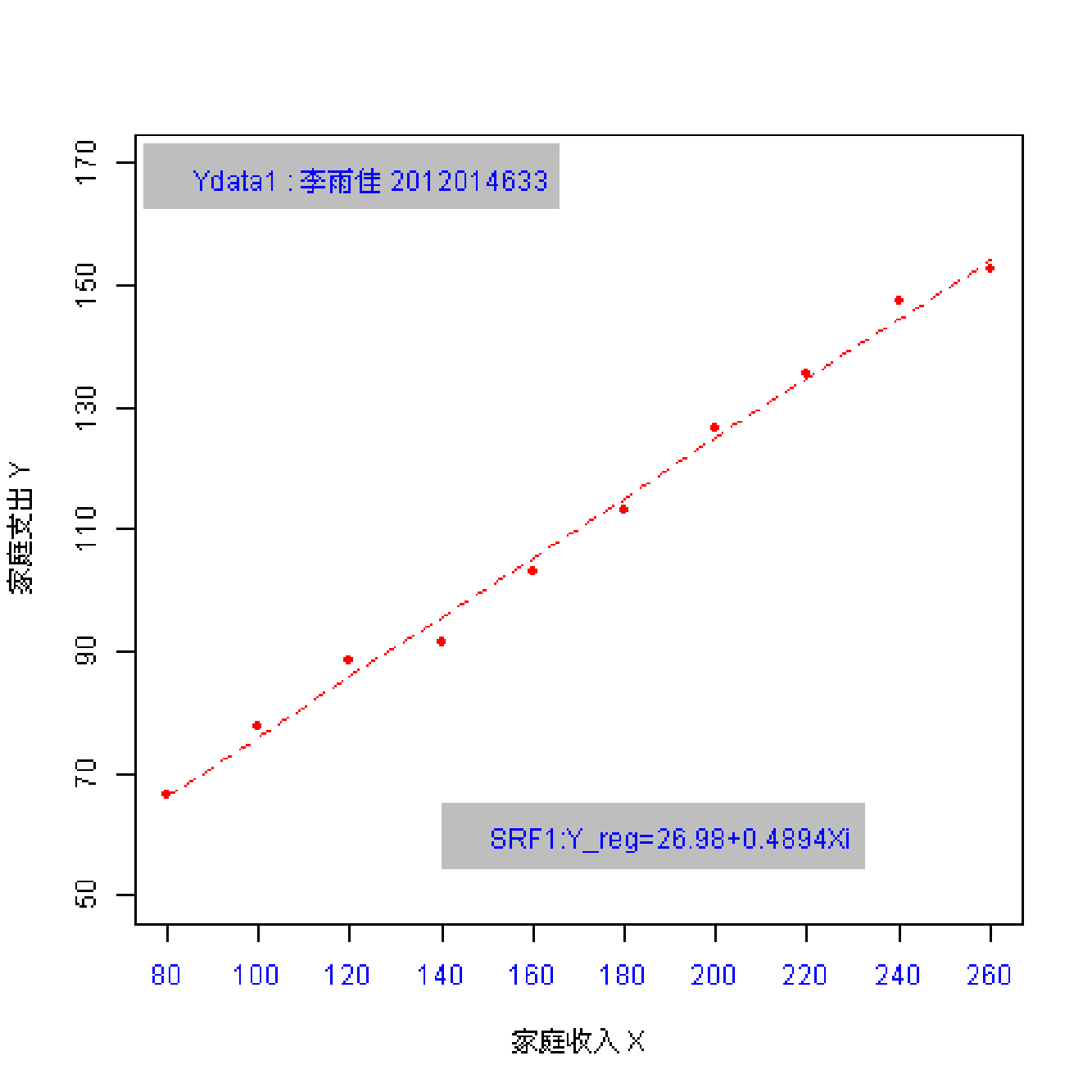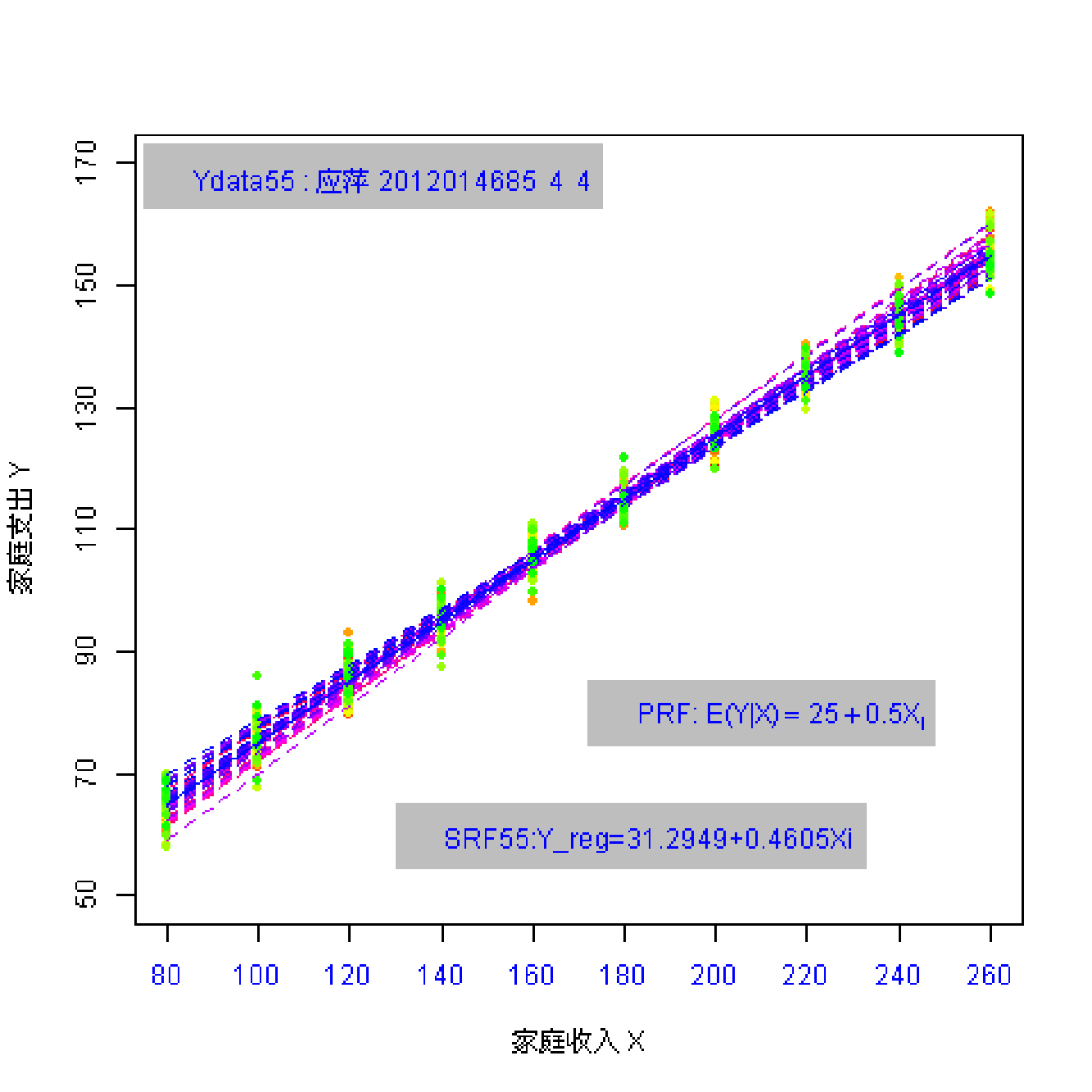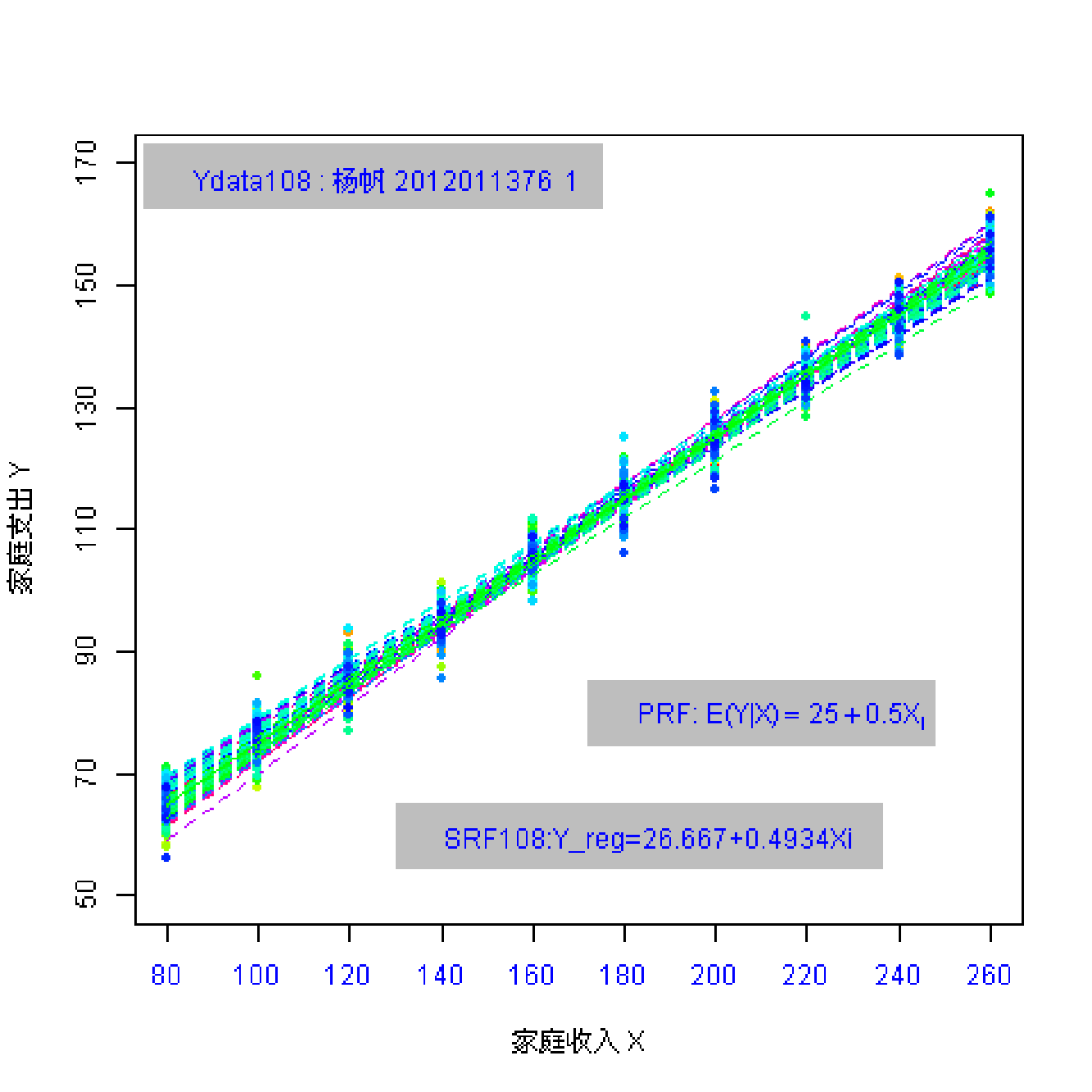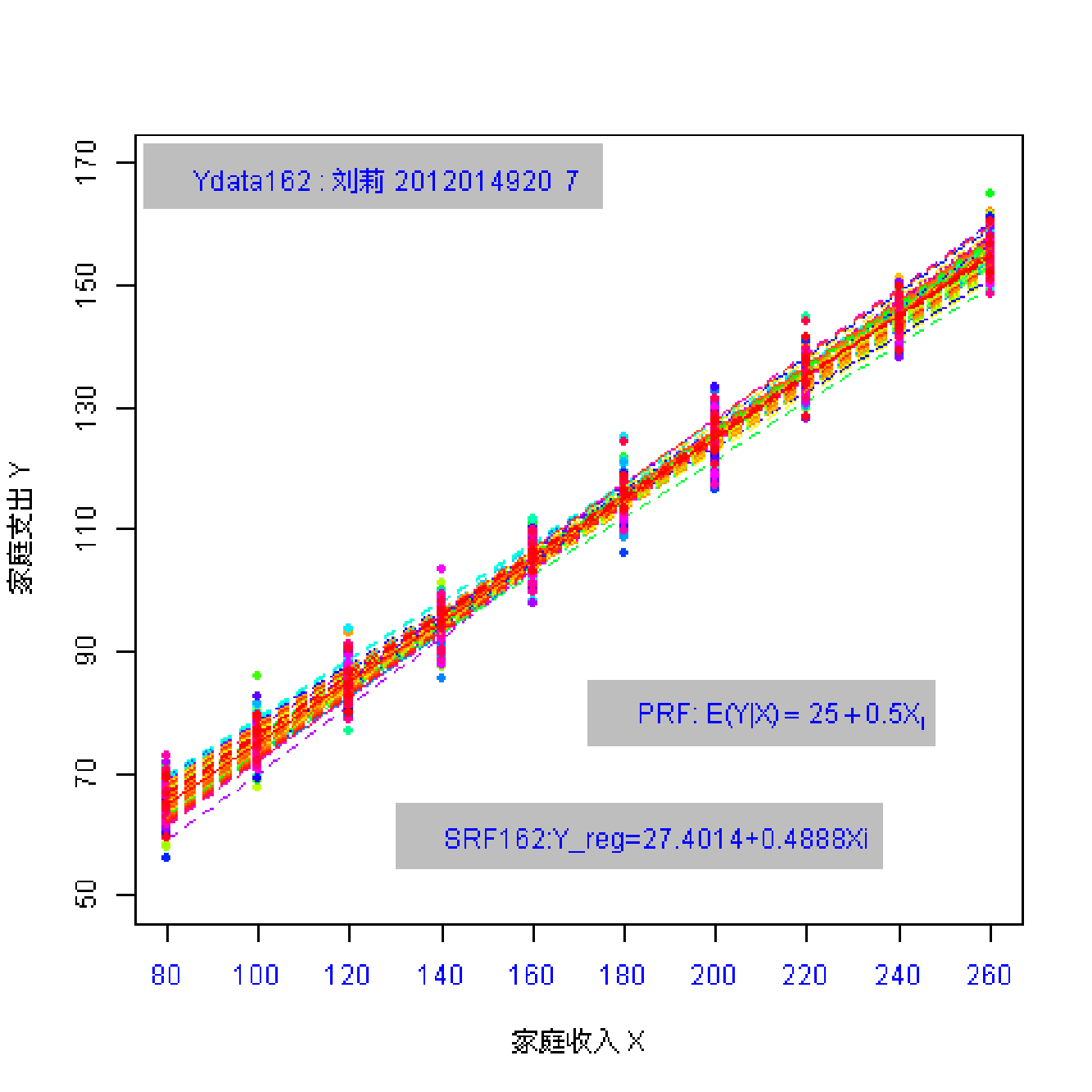
(实验演示)参数和统计量2
总体参数有哪些?
样本统计量又有哪些?
总体:\(Y_i = \beta_0+ \beta_1 X_i + u_i\) ; \(Y_i = 25+ 0.5 X_i + u_i\)
样本: \(Y_i = \hat{\beta}_0+ \hat{\beta}_1 X_i + e_i\)
1.6 统计分析的基本过程
统计分析基本过程:概览
基本过程包括:
实际问题:发现问题
收集数据:取得数据
处理数据:整理与图表展示
分析数据:利用统计方法分析数据
解释数据:结果的说明
得到结论:从数据分析中得出客观结论

统计分析需要具备的能力1
A.基础背景教育:
知识:高等数学、概率论与数理统计、商业经济统计、科学哲学…
技能1:前沿阅读:学术期刊academic journal(西农电子期刊数据库;开源期刊库arXiv.org)、RSS订阅(统计学之都;R-bloggers)、google学术…
技能2:知识管理:Onenote、印象笔记、Mindmanage(思维导图)…
B.广泛数据获取:
- 知识:实验设计、调研经历、数据爬虫
技能:大学生创新创业训练、开源数据库(国内微观调研数据库、国外google dataset search)、问卷星、Chrome开发工具、HTML标记语言、CSS语言、Regex语言、docker操作、Selenium/RSelenium
统计分析需要具备的能力2
C.系统数据管理:
知识:数据库查询语言、连续整合或协作系统(CI)
技能:SQL、DBI、RSQLite;git语言及GitHub自动化托管。
D.数据可视化:
知识:现代图形理论、传统/现代编程语言
技能:Microsoft Excel、SPSS、
E.数据建模分析
知识:数据清洗、数据变换、非结构化数据处理、平行运算、计量建模、深度学习与人工智能…
技能:Hadoop、Machine Learning and AI、交互制图技术(R Graph Gallery)、shinny APP、books(Interpretable Machine Learning)
统计分析需要具备的能力3
F.报告写作交流
知识:学术道德规范、科技论文规则、高效写作工具、论文发表、学术研讨交流
技能:传统写作排版(Word、Latex语言)、现代标记写作语言(Markdown/Rmarkdown)、文献管理工具(Endnote、Zotero)、可复现图文技术、演讲汇报slide(Powerpoint、Xaringan)、个人网站(hugo语言、blogdown)
G.技术技巧之外
知识:对智慧和科学的好奇心、生活或商业上的感知与睿智
技能:沟通技能、团队协作
(示例)纽约案例:背景
航班延误背后的故事:纽约繁忙的天空。数据来源nycflights13
This package contains information about all flights that departed from NYC (e.g. EWR, JFK and LGA) in 2013: 336,776 flights in total. To help understand what causes delays, it also includes a number of other useful datasets. This package provides the following data tables.
flights: all flights that departed from NYC in 2013
weather: hourly meterological data for each airport
planes: construction information about each plane
airports: airport names and locations
airlines: translation between two letter carrier codes and names
实际问题:航班延误有规律可循么?变量情况
从2013-01-01 05:00:00到2013-12-31 23:00:00期间,纽约市三个机场EWR、JFK、LGA,起落航班总数有336776架次。
tibble [336,776 × 19] (S3: tbl_df/tbl/data.frame)
$ year : int [1:336776] 2013 2013 2013 2013 2013 2013 2013 2013 2013 2013 ...
$ month : int [1:336776] 1 1 1 1 1 1 1 1 1 1 ...
$ day : int [1:336776] 1 1 1 1 1 1 1 1 1 1 ...
$ dep_time : int [1:336776] 517 533 542 544 554 554 555 557 557 558 ...
$ sched_dep_time: int [1:336776] 515 529 540 545 600 558 600 600 600 600 ...
$ dep_delay : num [1:336776] 2 4 2 -1 -6 -4 -5 -3 -3 -2 ...
$ arr_time : int [1:336776] 830 850 923 1004 812 740 913 709 838 753 ...
$ sched_arr_time: int [1:336776] 819 830 850 1022 837 728 854 723 846 745 ...
$ arr_delay : num [1:336776] 11 20 33 -18 -25 12 19 -14 -8 8 ...
$ carrier : chr [1:336776] "UA" "UA" "AA" "B6" ...
[list output truncated]分析数据:描述性统计1——1天的航班情况
2013年1月1日这一天的航班总数为842架次。从这样的数据表能看出什么规律?
分析数据:描述性统计2——每天的航班数和平均延误时长
这样的统计分析,能不能看出任何蛛丝马迹呢?
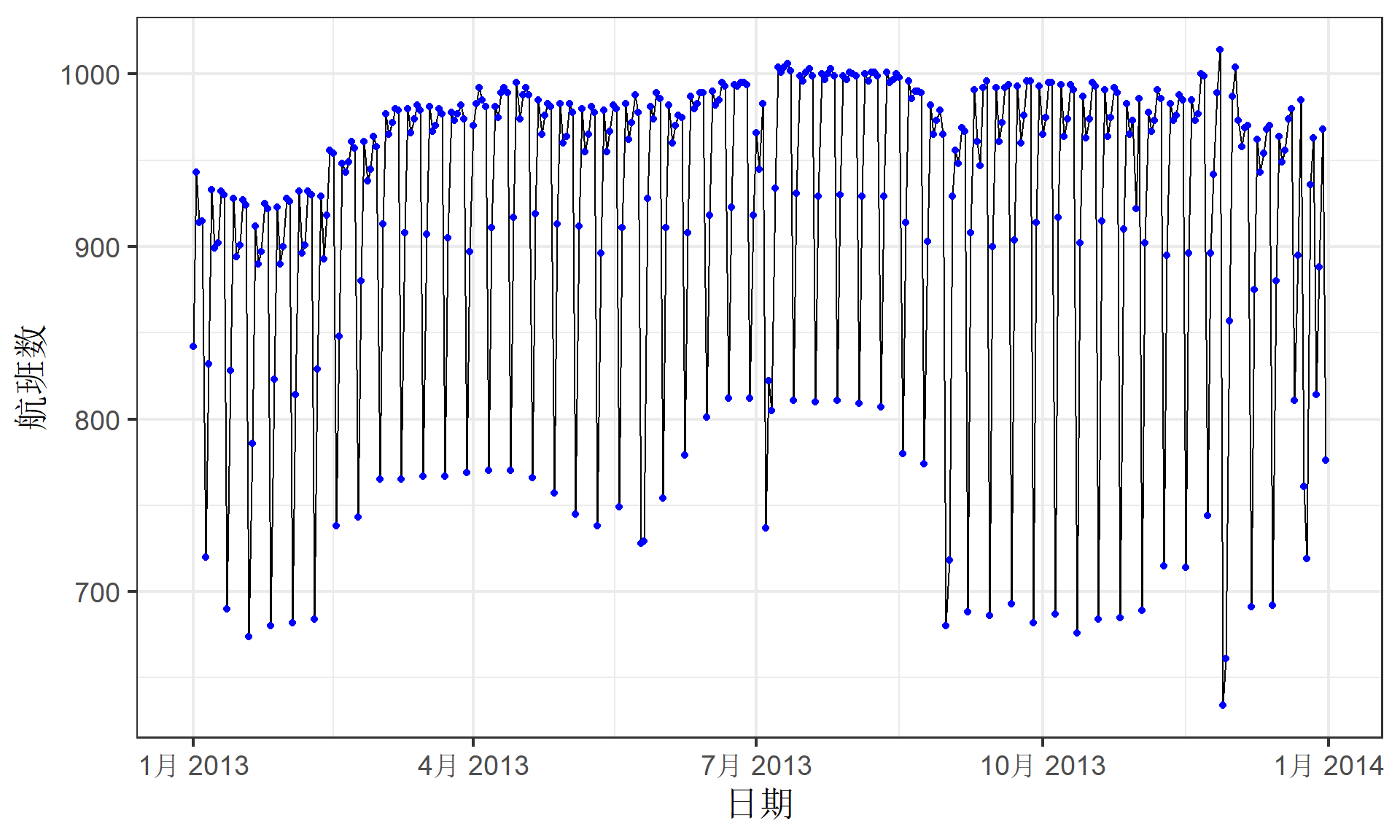
分析数据:描述性统计3(每天航班数)
按时间轴查看每天航班数的全貌图,是不是会更轻松一点?
分析数据:描述性统计4(航班数和平均延误时长)
星期几与航班数和平均延误时长有关系?童鞋们,咱先上一个表:
分析数据:描述性统计5(星期几matter?)
小伙伴们,那咱们再上个图(多批箱线图)瞧一瞧吧
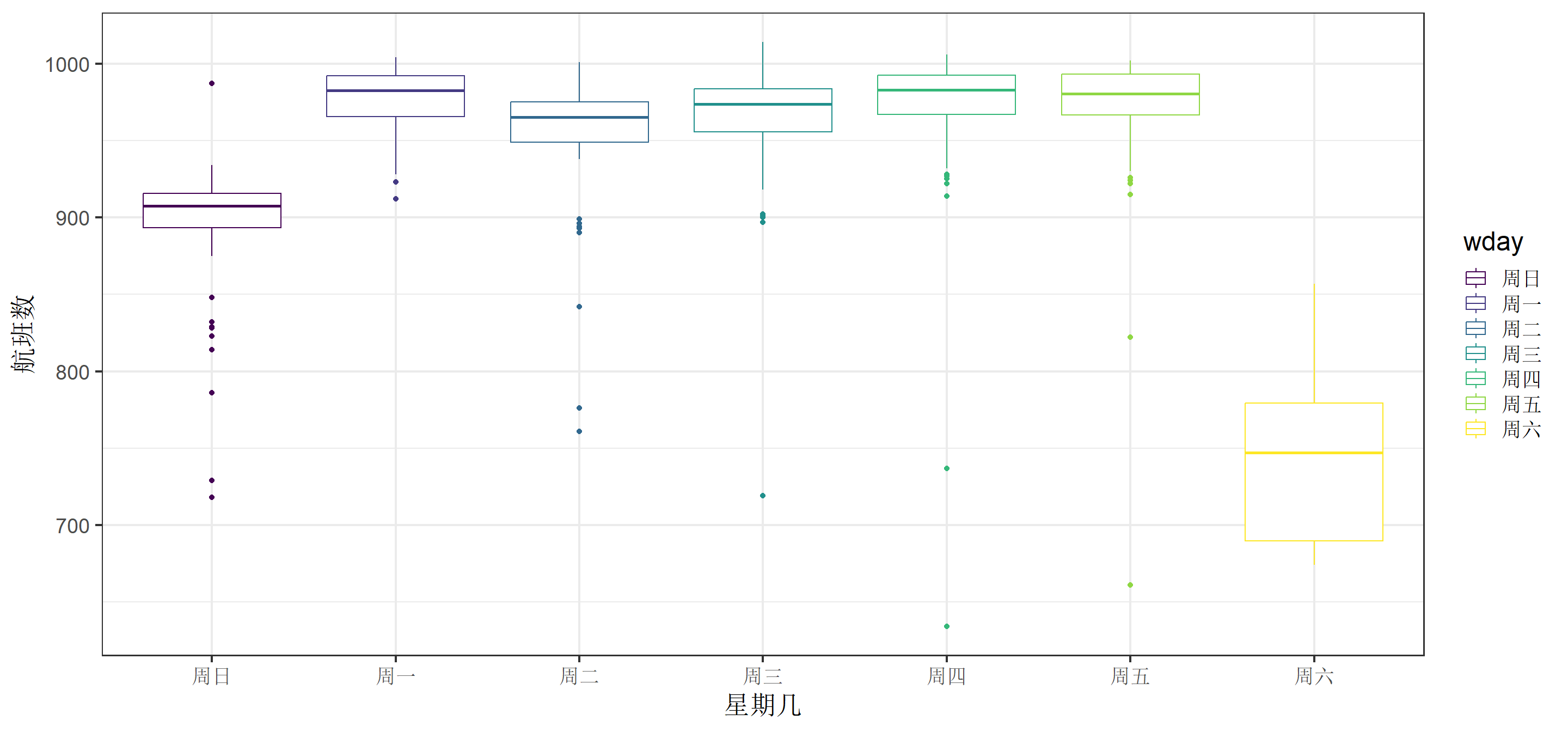
分析数据:描述性统计6(幸运星期六)
星期六会更适合坐飞机么?星期六好像航班很少耶!! 扣扣鼻子问,WHY? 具体是怎样呢??
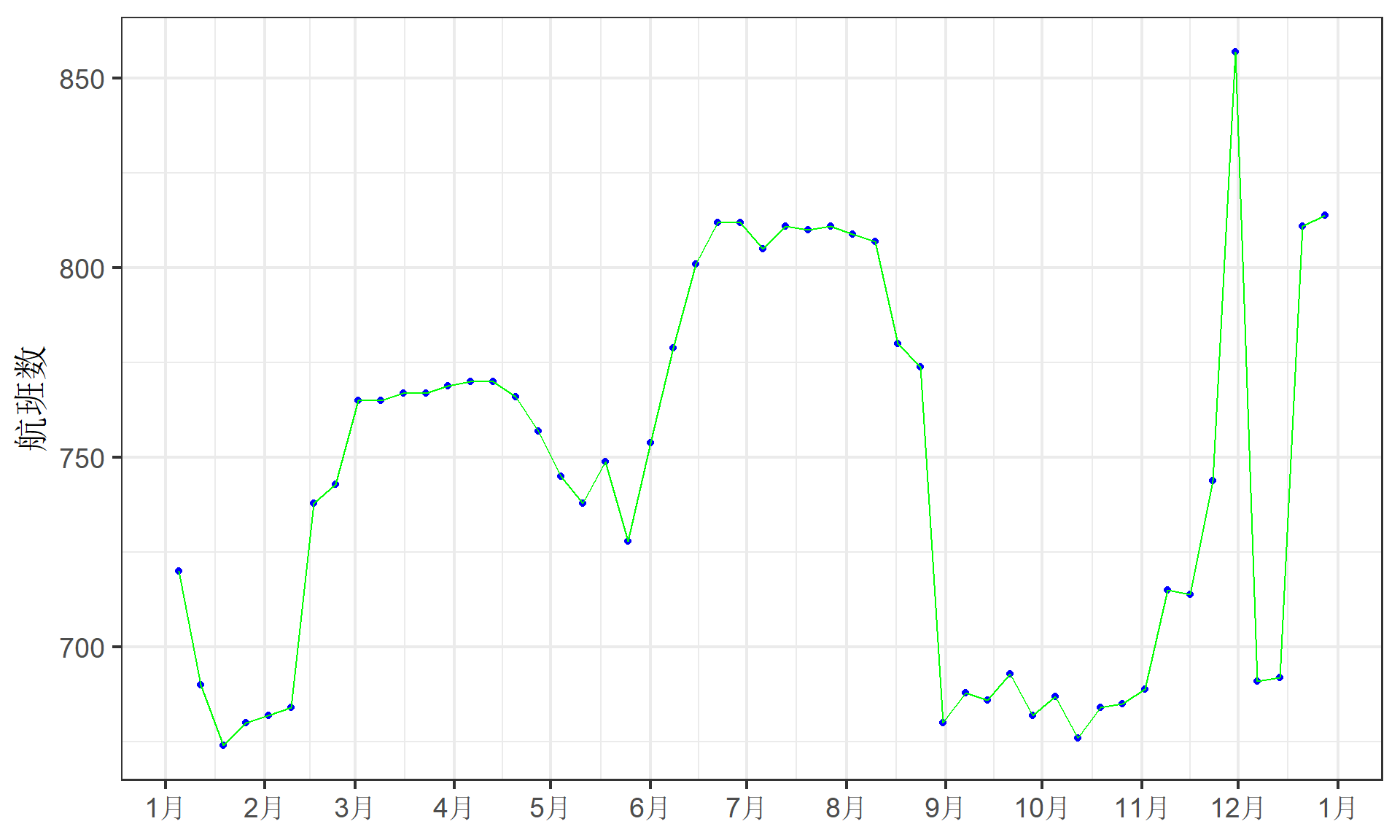
分析数据:描述性统计7(全年的周六)
全年只看星期六的航班数是怎样的赶脚?惊讶的小伙伴们,看看星期六的表现吧!
分析数据:描述性统计8(机场matter?)
选择起飞机场是不是能避免延误?
分析数据:描述性统计9(机场matter?2)
选择起飞机场是不是能避免延误?
分析数据:描述性统计9(机场matter?3)
下面看看美国所有机场信息(airport):变量情况
美国总共有1458个机场。
分析数据:描述性统计10(机场matter?4)
概括地来看看机场数据吧:
Rows: 1,458
Columns: 8
$ faa <chr> "04G", "06A", "06C", "06N", "09J", "0A9", "0G6", "0G7", "0P2", "…
$ name <chr> "Lansdowne Airport", "Moton Field Municipal Airport", "Schaumbur…
$ lat <dbl> 41.13047, 32.46057, 41.98934, 41.43191, 31.07447, 36.37122, 41.4…
$ lon <dbl> -80.61958, -85.68003, -88.10124, -74.39156, -81.42778, -82.17342…
$ alt <dbl> 1044, 264, 801, 523, 11, 1593, 730, 492, 1000, 108, 409, 875, 10…
$ tz <dbl> -5, -6, -6, -5, -5, -5, -5, -5, -5, -8, -5, -6, -5, -5, -5, -5, …
$ dst <chr> "A", "A", "A", "A", "A", "A", "A", "A", "U", "A", "A", "U", "A",…
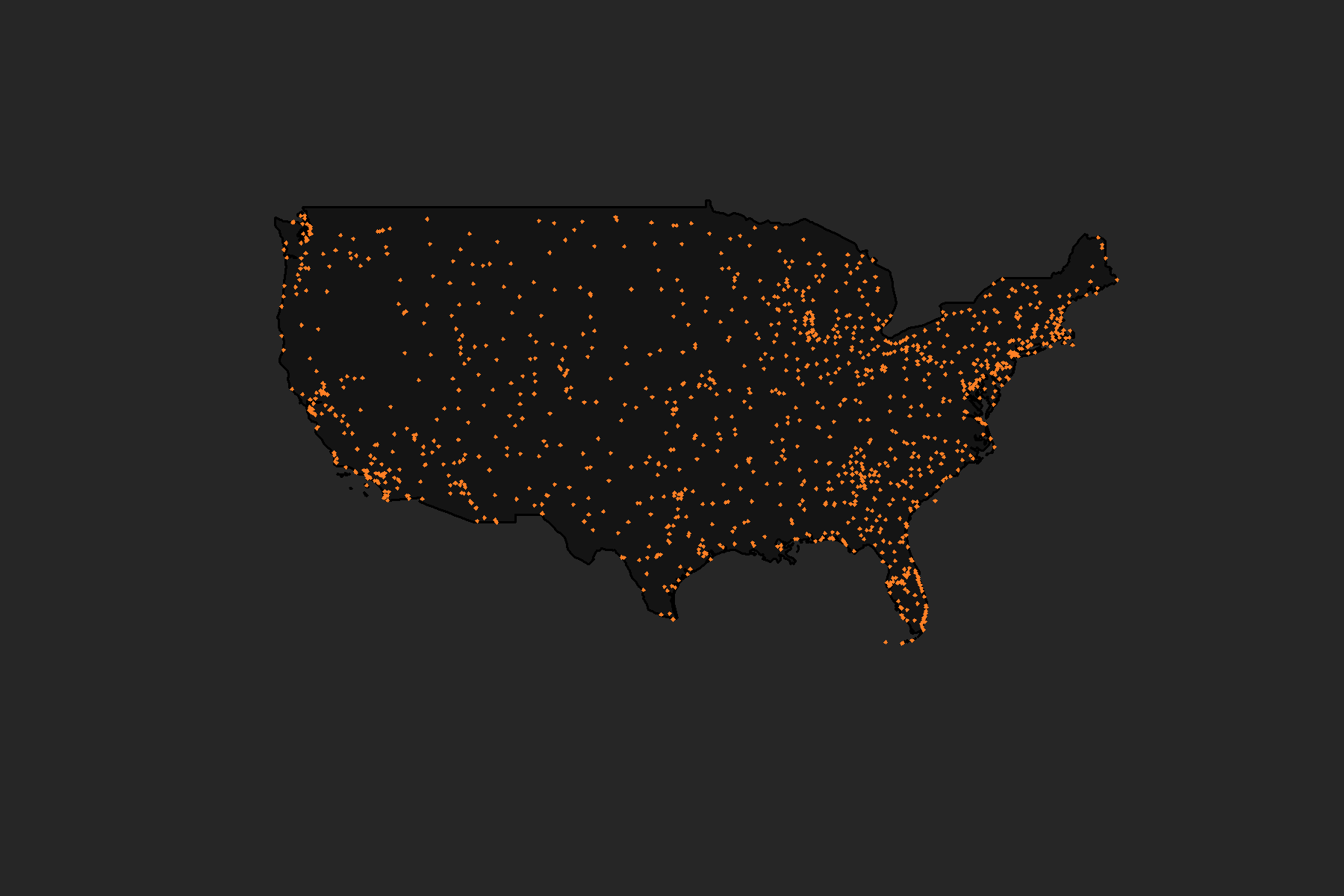
$ tzone <chr> "America/New_York", "America/Chicago", "America/Chicago", "Ameri…分析数据:描述性统计11(机场matter?5)
机场信息(airport):地图可视化点图
分析数据:描述性统计12(机场matter?6)
机场信息(airport):地图可视化线图

分析数据:描述性统计(JFK机场的热力图)
下面重点看看纽约JFK机场全年的起飞延误情况(热力图heat map plot),日期和星期几确实影响起飞延误么?
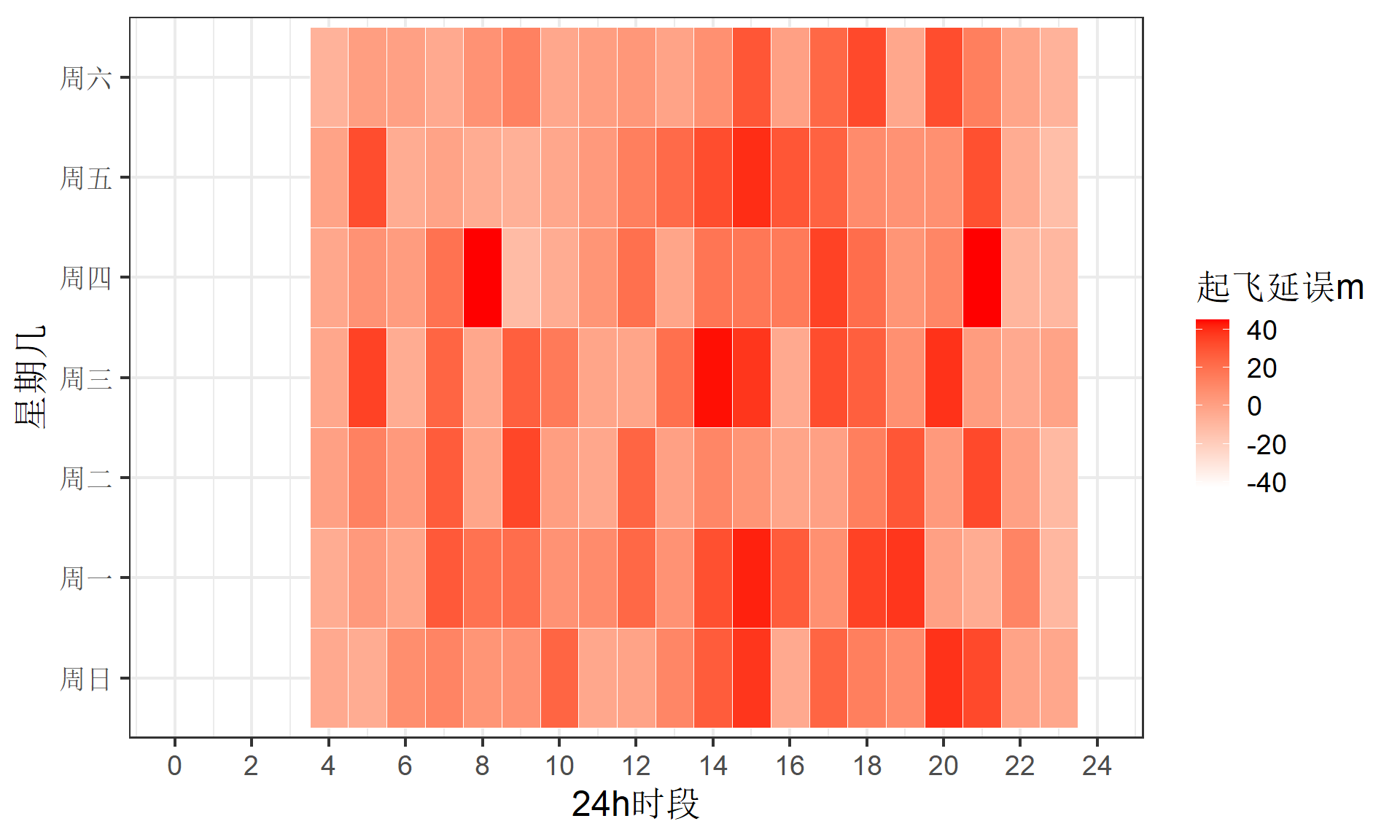
分析数据:推断性统计(JFK机场ANOVA分析1)
分析数据:推断性统计(JFK机场ANOVA分析2)
分析数据:推断性统计(JFK机场回归分析)
\[ \begin{align} dep\_delay &= \beta_0 +\beta_1 Mon +\beta_1 Tue + \beta_1 Wen+ \beta_1 Thu+ \beta_1 Fri + \beta_1 Sta + \beta_1 hh +u_i \end{align} \]
Call:
lm(formula = dep_delay ~ wd + hh, data = flights_jfk_24h)
Residuals:
Min 1Q Median 3Q Max
-63.66 -17.67 -9.43 -0.93 1296.46
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -7.1375 0.3299 -21.633 < 2e-16 ***
wd.L -0.9868 0.3083 -3.201 0.00137 **
wd.Q -1.2321 0.3085 -3.994 6.50e-05 ***
wd.C -1.1929 0.3066 -3.891 1.00e-04 ***
wd^4 -2.4480 0.3060 -7.999 1.27e-15 ***
wd^5 2.2760 0.3049 7.464 8.43e-14 ***
wd^6 -0.5730 0.3059 -1.873 0.06107 .
hh 1.4937 0.0240 62.252 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 38.33 on 109408 degrees of freedom
(1863 observations deleted due to missingness)
Multiple R-squared: 0.03564, Adjusted R-squared: 0.03557
F-statistic: 577.6 on 7 and 109408 DF, p-value: < 2.2e-16得到结论
观点1:
观点2:
观点3:
本章结束

第1章 导论