计量经济学II
(Ecnometrics II)
第20章 联立方程模型的估计方法
胡华平
huhuaping01@hotmail.com
经济管理学院数量经济教研室
2024-09-25
模块4:联立方程模型(SEM)
Chapter 17. 内生性问题与工具变量法
Chapter 18. 为什么要关心联立方程模型?
Chapter 19. 联立方程模型的识别问题
Chapter 20. 联立方程模型的估计方法
20.1 估计方法简介
单方程法和方程组法
为了估计结构方程,可采取两种方法:
单方程法,又称有限息法(limited information methods) 。
我们逐个估计(联立)方程组中的每一个方程,仅考虑对该方程的约束(如对某些变量的排除)而不考虑对其他方程的约束
方程组法(或系统法),又称完全信息法 (full information methods)
我们同时估计模型中的全部方程,适当考虑了因某些变量被排除而对方程组造成的全部约束
工具变量与联立方程
工具变量往往被用于估计联立方程问题,主要又包括三类方法:
三阶段最小二乘法( three-stage least squares, 3SLS):少数情况下可用
广义矩估计方法(Generalized moment method, GMM):普遍用于动态模型问题
完全信息极大似然法( full information maximum likelihood, FIML):更具有理论价值,也优于3SLS,但计算量较大。
单方程法的不足
考虑如下的联立方程模型:
\[ \begin{cases} \begin{alignedat}{9} & Y_{t1} &-\gamma_{21}Y_{t2}&-\gamma_{31}Y_{t3} & &-\beta_{01}&-\beta_{11}X_{t1} & & &= &u_{t1} \\ & & Y_{t2} &-\gamma_{32} Y_{3t} & & -\beta_{02}&-\beta_{12}X_{1t} &- \beta_{22}X_{2t} & &= &u_{t2}\\ &-\gamma_{13}Y_{t1} & &+ Y_{t3} & & -\beta_{03}&-\beta_{13}X_{1t} &-\beta_{23}X_{2t} & &= &u_{t3} \\ &-\gamma_{14}Y_{t1}&-\gamma_{24}Y_{t2} & &+Y_{t4} &-\beta_{04} & & &-\beta_{34}X_{t3} &= &u_{t4} \end{alignedat} \end{cases} \]
- 如果仅仅关注于估计第三个方程,采用单方程法将只考虑此方程,也即仅注意变量\(Y_2,Y_4,X_3\)被排除在此方程之外。
方程组法的不足
如果希望同时估计全部四个方程,采用方程组法将会对方程组中多个方程的全部约束都考虑进来。
为了保持联立方程模型的品质,最理想的应是使用方程组法,比如完全信息极大似然法 (full information maximum likelihood, FIML) 。
然而,实际上方程组法并不常用,主要原因包括:
计算上的负担太大。
像FIML这样的系统方法常常导致参数的高度非线性解,以致难 以确定。
如果方程组中的一个或多个方程有设定误差(比如说,一个错误的函数形式或漏掉有关变量),则误差将传递至其余方程。其结果是,方程组法变得对设定误差非常敏感。
20.2 普通最小二乘法(OLS)
递归模型
模型形式
递归模型(recursive model):也称为三角形模型(triangular model)或因果性(causalmodel)模型。不同方程中的同期干扰项是不相关的,每个方程都展现一种单向的因果依赖关系。
考虑下面的联立方程模型:
\[ \begin{alignat}{6} Y_{t1} = & & & & +\beta_{01}& + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & & +u_{t1} \\ Y_{t2} = & + \gamma_{12}Y_{1t} & & &+\beta_{02} & + \beta_{12}X_{t1} & + \beta_{22}X_{t2} & & + u_{t2}\\ Y_{t3} = & + \gamma_{13}Y_{t1}& + \gamma_{23}Y_{t2}& &+\beta_{03} & + \beta_{13}X_{t1} & + \beta_{23}X_{t2} & & + u_{t3} \\ \end{alignat} \]
OLS方法仍旧适用
\[ \begin{alignat}{6} Y_{t1} = & & & & +\beta_{01}& + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & & +u_{t1} \\ Y_{t2} = & + \gamma_{12}Y_{1t} & & &+\beta_{02} & + \beta_{12}X_{t1} & + \beta_{22}X_{t2} & & + u_{t2}\\ Y_{t3} = & + \gamma_{13}Y_{t1}& + \gamma_{23}Y_{t2}& &+\beta_{03} & + \beta_{13}X_{t1} & + \beta_{23}X_{t2} & & + u_{t3} \\ \end{alignat} \]
我们很容易发现,不同方程中的同期干扰项是不相关的(或者说是零同期相关):
\[ cov(u_{t1},u_{t2})=cov(u_{t1},u_{t3})=cov(u_{t2},u_{t3})=0 \]
对于第一个方程。因为它的右边仅含有外生变量,又因为按假定外生变量与干扰项均不相关,所以此方程满足经典OLS解释变量与干扰项不相关的基本假定。因而 OLS可直接应用于此方程的估计。
对于第二个方程。因为\(cov(u_{t1},u_{t2})=0\),也就意味着\(cov(Y_{t1},u_{t2})=0\)。因而OLS可直接应用于此方程的估计。
对于第三个方程。因为\(cov(u_{t1},u_{t3})=0\),也就意味着\(cov(Y_{t1},u_{t3})=0\)。又因为\(cov(u_{t1},u_{t3})=0\),也就意味着\(cov(Y_{t2},u_{t3})=0\)。因而OLS可直接用于此方程的估计。
递归模型的图形展示
我们也可以用图形进行直观表达:
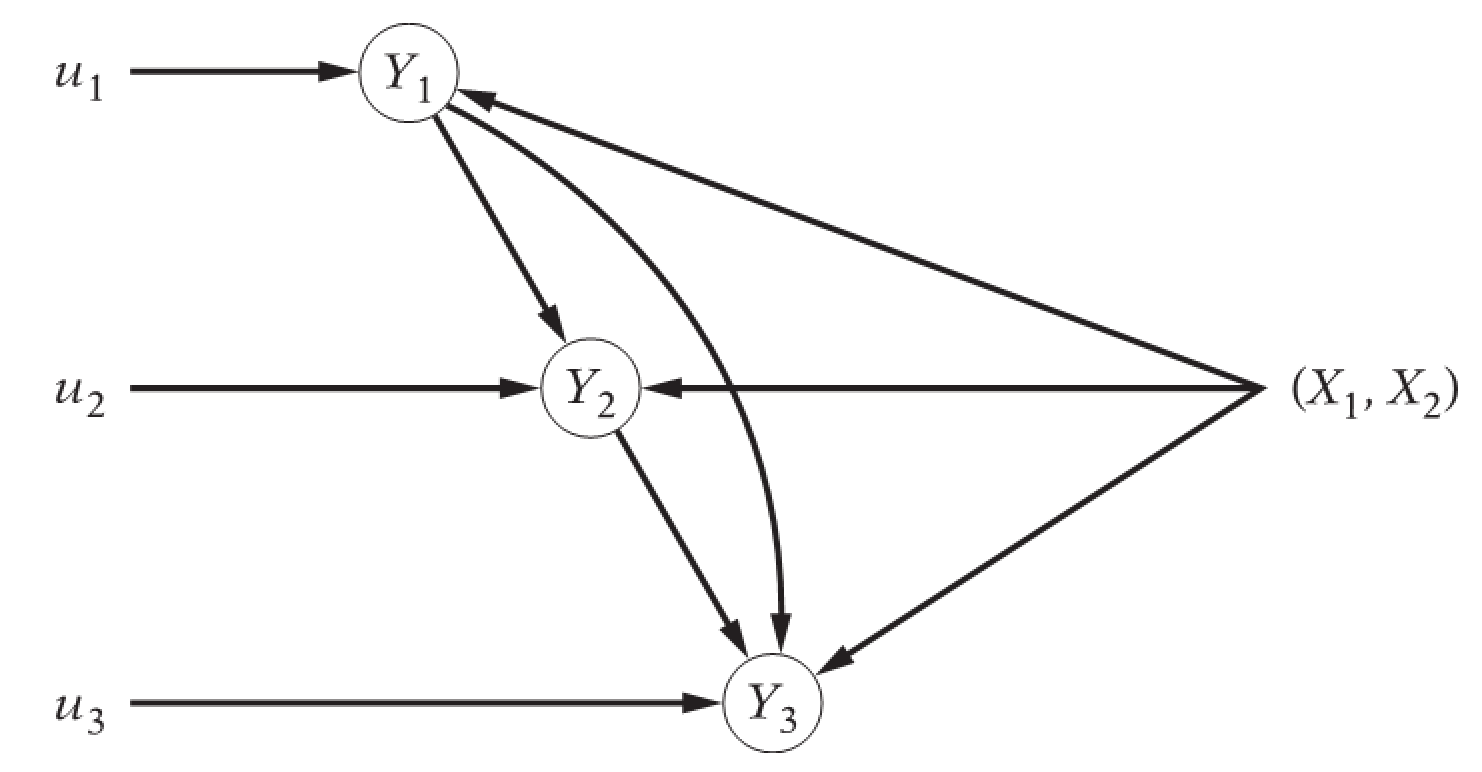
工资价格模型示例
再看一个工资价格模型:
\[ \begin{align} P_t &= \beta_0+\beta_1U_t+\beta_2R_t+\beta_3M_t+u_{t2} &&\text{(价格方程)}\\ W_t &= \alpha_0+\alpha_1UN_t+\alpha_2P_t+u_{t1} &&\text{(工资方程)} \end{align} \]
其中:
价格方程假定当前价格变化率是资本和原料价格变化率、劳动生产率变化率以及前期工资变化率等的函数。
工资方程则表示当前工资变化率取决于当前价格变化率和失业率。
- 货币工资变化率W
- 失业率UN,%
- 价格变化率P
- 资本成本变化率R
- 进口原材料的价格变化率M
20.3 间接最小二乘法(ILS)
间接最小二乘法的估计步骤
对一个恰好识别的结构方程,从约简型系数的OLS估计值获得结构系数估计值的方法叫做间接最小二乘法 (method of indirect least squares, ILS),而如此得到的估计值称间接最小二乘估计值。
间接最小二乘法(ILS方法)包含以下三个步骤:
step 1:先求约简型方程。从结构方程组解出约简型方程,使得在每个方程的因变量都成为唯一的内生变量,并且仅仅是前定变量(外生或滞后内生)和随机误差项的函数。
step 2:对约简型方程逐个应用OLS。因为这些方程中的解释变量是前定的并因而与随机干扰项不相关,所以这种做法是合适的,由此得到的估计值是一致的。
step 3: 从得到的约简型系数的估计值求原始结构系数的估计值 。若方程恰可识别,则结构与约简型系数之间有一一对应关系,就是说可以从后者导出前者的唯一估计值。
案例:美国农作物供需
案例和变量说明
美国农作物供需案例的变量说明如下:
案例数据
美国农作物供需案例的数据如下:
结构化联立方程的设定
因此我们可以构造出如下的联立方程:
\[ \begin{align} Q &= \alpha_0+\alpha_1P_t+\alpha_2X_t+u_{t1} &(\alpha_1<0,\alpha_2>0) &&\text{(需求函数)}\\ Q &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)} \end{align} \]
其中:Q=作物产量指数;P=农产品收购价格指数;X=人均个人消费支出。
约简化联立方程的设定
得到其对应的约简方程形式:
\[ \begin{align} P_t &= \pi_{11}+ \pi_{21}X_t+w_t &&\text{(约简方程1)}\\ Q_t &= \pi_{12}+\pi_{22}X_t+v_t &&\text{(约简方程2)} \\ \end{align} \]
其中,约简系数表达为:
\[ \begin{align} \pi_{11} &= \frac{\beta_0-\alpha_0}{\alpha_1-\beta_1} \\ \pi_{21} &= - \frac{\alpha_2}{\alpha_1-\beta_1}\\ w_t &= \frac{u_{2t}-u_{t1}}{\alpha_1-\beta_1} \\ \end{align} \]
\[ \begin{align} \pi_{12} &= \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1} \\ \pi_{22} &= - \frac{\alpha_2\beta_1}{\alpha_1-\beta_1} \\ v_t &= \frac{\alpha_1u_{t2}-\beta_1u_{1t}}{\alpha_1-\beta_1} \end{align} \]
约简系数的理论估计值
对于上述约简方程形式,我们可以采用OLS方法进行估计,可以得到:
\[ \begin{align} \widehat{\pi}_{21} &= \frac{\sum{p_t x_t}}{\sum{x^2_t}} &&\text{(价格约简方程的斜率)} \\ \widehat{\pi}_{11} &= \overline{P} - \widehat{\pi}_1 \cdot \overline{X} &&\text{(价格约简方程的截距)} \\ \widehat{\pi}_{22} &= \frac{\sum{q_t x_t}}{\sum{x^2_t}} &&\text{(数量约简方程的斜率)} \\ \widehat{\pi}_{12} &= \overline{Q} - \widehat{\pi}_3 \cdot \overline{X} &&\text{(数量约简方程的截距)} \end{align} \]
结构系数的理论估计值
因为我们已经知道(复习阶条件和秩条件),供给方程是恰好可识别的,因此供给方程的结构系数是可以由简约系数唯一地估计得到:
\[ \begin{align} \beta_0 &= \pi_{12}+ \beta_1 \pi_{11} \\ \beta_1 &= \frac{\pi_{22}}{\pi_{21}} \\ \end{align} \]
也即:
\[ \begin{align} \hat{\beta_0} &= \widehat{\pi}_{12}+ \hat{\beta_1} \widehat{\pi}_{11} \\ \hat{\beta_1} &= \frac{\widehat{\pi}_{22}}{\widehat{\pi}_{21}} \\ \end{align} \]
实证估计约简方程
下面我们对约简方程进行OLS回归。
\[ \begin{align} P_t &= \pi_{11}+ \pi_{21}X_t+w_t &&\text{(约简方程1)}\\ Q_t &= \pi_{12}+\pi_{22}X_t+v_t &&\text{(约简方程2)} \\ \end{align} \]
价格约简方程的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{P}=&&+90.96&&+0.00X_i\\ &(s)&&(4.0517)&&(0.0002)\\ &(t)&&(+22.45)&&(+3.01)\\ &(fit)&&R^2=0.2440&&\bar{R}^2=0.2170\\ &(Ftest)&&F^*=9.04&&p=0.0055 \end{split} \end{alignedat} \]
数量约简方程的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+59.76&&+0.00X_i\\ &(s)&&(1.5600)&&(0.0001)\\ &(t)&&(+38.31)&&(+20.93)\\ &(fit)&&R^2=0.9399&&\bar{R}^2=0.9378\\ &(Ftest)&&F^*=437.95&&p=0.0000 \end{split} \end{alignedat} \]
通过约简系数计算结构系数
可以得到约简系数:
\(\widehat{\pi}_{21}=\) 0.00074
\(\widehat{\pi}_{11}=\) 90.96007
\(\widehat{\pi}_{22}=\) 0.00197
\(\widehat{\pi}_{12}=\) 59.76183
由于供给方程是恰好识别的。因此,利用约简系数,进一步可以计算得到供给方程的结构系数:
\(\hat{\beta_1} = \frac{\widehat{\pi}_{22}}{\widehat{\pi}_{12}}\) = 0.00197 / 0.00074 = 2.68052
\(\hat{\beta_0} = \widehat{\pi}_{12}+ \hat{\beta_1} \widehat{\pi}_{11}\) = 59.76183 - 2.68052 \(\cdot\) 90.96007 = -184.05874
因此,基于间接最小二乘法(ILS)估计得到的供给方程是: \(\hat{Q_t}=\) -184.05874 + 2.68052\(P_t\)
对比误设模型的OLS估计结果
作为对比,我们给出一个“有偏误”的估计方法,也即直接对数量Q对价格P采用OLS方法,将得到如下结果:
基于间接最小二乘法(ILS)估计得到的供给方程是: \(\hat{Q_t}=\) -184.05874 + 2.68052\(P_t\)
基于OLS估计方法得到“有偏误”的供给方程是:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+20.89&&+0.67P_i\\ &(s)&&(23.0396)&&(0.2246)\\ &(t)&&(+0.91)&&(+2.99)\\ &(fit)&&R^2=0.2425&&\bar{R}^2=0.2154\\ &(Ftest)&&F^*=8.96&&p=0.0057 \end{split} \end{alignedat} \]
20.4 两阶段最小二乘法(TSLS)
过度识别模型
联立方程示例
考虑下面的联立方程模型:
\[ \begin{alignat}{6} Y_{t1} = & &+ \gamma_{21}Y_{2t} & & +\beta_{01} & + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & +u_{t1} & \text{ (收入方程)} \\ Y_{t2} = & + \gamma_{12}Y_{t1} & & & +\beta_{02} & & & + u_{t2} & \text{ (货币供给方程)} \end{alignat} \]
运用阶条件识别规则和秩条件识别规则(复习提问?),可以知道:
收入方程是不可识别的
如果不改变模型设定,那“神也帮不了你”!
货币供给方程是过度识别的
容易证明,如果采用ILS估计方法,\(\gamma_{21}\)有两个ILS估计值。所以也没办法估计得到!
寻找工具变量
寻找工具变量破解过度识别问题:
从实际考虑,人们也许想用OLS去估计货币供给方程,但却因为\(Y_1\)和\(u_2\) 之间可能存在相关关系而使得估计量有偏。
如果能找到这样的一个代理变量——它和\(Y_1\)高度相关而又与\(u_2\)不相关——则OLS就可直接用于估计货币供给函数。这样的代理变量被称为工具变量(Instrument Variable)
由瑟尔和巴斯曼 (Robert Basmann)各自独立发现的两阶段最小二乘 (two-stage least squares, 2SLS)成为寻找合适工具变量的重要方途径和方法。
2SLS方法:第一阶段
两阶段最小二乘 (two-stage least squares, 2SLS)实际上连续使用两次OLS估计方法的过程:
stage 1: 为摆脱\(Y_1\)和\(u_2\)之间可能的相关性,先求\(Y_1\) 对整个方程组(不仅仅是所考虑的方程中)全部前定变量的回归。也即:
\[ \begin{align} Y_{t1} &= \widehat{\pi}_{01} + \widehat{\pi}_{11} X_{t1} + \widehat{\pi}_{21} X_{t2} + \hat{v}_{t1} \\ &= \hat{Y_{t1} } + \hat{v}_{t1} \\ \hat{Y_{t1} }&= \widehat{\pi}_{01} + \widehat{\pi}_{11} X_{t1} + \widehat{\pi}_{21} X_{t2} \end{align} \]
表明随机的\(Y_1\) 是由两部分构成:
- 随机X的一个线性组合而成的\(\hat{Y}_{t1}\)- 随机成分\(\hat{u}_t\)- 按照OLS理论,\(\hat{Y}_{t1}\)与\(\hat{v}_{t1}\) 是不相关的(Why?提问)。
2SLS方法:第二阶段
stage 2: 现在重新变换过度识别的供给方程如下:
\[ \begin{align} Y_{t2} & = \beta_{02} + \gamma_{12} Y_{t1} + u_{t2} \\ & = \beta_{02} + \gamma_{12} (\hat{Y}_{t1}+\hat{v}_{t1}) + u_{t2} \\ & = \beta_{02} + \gamma_{12} \hat{Y}_{t1}+(\gamma_{12} \hat{v}_{t1} + u_{t2} ) \\ & = \beta_{02} + \gamma_{12} \hat{Y}_{t1}+ u_{t2}^{\ast} \end{align} \]
我们可以证明:
\(Y_{t1}\) 和干扰项\(u_{t2}\) 很可能相关,从而使得OLS估计方法不适用!
但是\(\hat{Y_{1t}}\)和干扰项\(u_{t2}^{\ast}\) 之间,渐进地(随着样本数无限增加时)不相关。从而OLS估计方法又变得适用了!(也即参数估计是一致性的!)
2SLS方法的特点1/2
两阶段最小二乘法(2SLS方法)的特点:
它可以应用于方程组中的某个方程而无需考虑方程组中的其他方程。因此,在求解涉及大量方程的计量经济模型时,2SLS提供了一个经济适用的方法。由于这一原因,此法在实际中被广泛应用。
相对于ILS为过度识别的方程提供参数的多个估计值,而2SLS对每个参数只提供一个估计值。
它只需知道方程组中一共有多少个外生或前定变量,而无需知道方程组中的任何其他变量,故易于应用。
2SLS方法的特点2/2
两阶段最小二乘法(2SLS方法)的特点(续):
此法虽然专为过度识别的方程而设计,但同样适用于恰好识别的方程。但这时ILS和2SLS将给出相同的估计。(为什么?)
如果约简型回归(即阶段1的回归)的F值很高,比如说高于0.8。则经典OLS估计和 2SLS估计将相差无几。
在ILS方法的回归报告中,我们没有给出所估系数的标准误,但我们能对 2SLS估计值给出这些标准误。
2SLS方法下的估计标准误
是否矫正标准误
在ILS方法的回归报告中,我们没有给出所估系数的标准误,但我们能对 2SLS估计值给出这些标准误。
需要注意的是:\(u^{\ast}_{t2}=u_{t2}+\gamma_{12}\hat{v}_{t1}\)
这意味着\(u^{\ast}_{t2} \neq u_{t2}\) ,因此需要进行误差校正
误差矫正的具体办法,可以参考教材附录20A.2
下面的案例展示中,我们将会分别展示没有误差校正的2SLS估计和经过误差矫正的2SLS估计。
重点关注第二阶段模型
误差矫正的计算过程如下:
- stage 2:中供给方程的回归形式为
\[ \begin{align} Y_{t2} & = \beta_{02} + \gamma_{12} Y_{1t} + u_{2t} \\ & = \beta_{02} + \gamma_{12} (\hat{Y_{1t}}+\hat{v}_{t1}) + u_{2t} \\ & = \beta_{02} + \gamma_{12} \hat{Y_{1t}}+(\gamma_{12} \hat{v}_{t1} + u_{t2} ) \\ & = \beta_{02} + \gamma_{12} \hat{Y_{1t}}+ u_{t2}^{\ast} \end{align} \]
- 其中\(u^{\ast}_{t2}=u_{t2}+\gamma_{12}\hat{v}_{t1}\)
标准误校正的计算公式
- stage 2:中对于参数\(\gamma_{12}\)的估计值\(\hat{\gamma}_{12}\),其估计标准误\(s.e_{\hat{\gamma}_{12}}\)的计算公式为:
\[ \begin{align} Y_{t2} & = \beta_{02} + \gamma_{12} \hat{Y_{1t}}+ u_{t2}^{\ast} \end{align} \]
\[ \begin{align} s.e_{\hat{\gamma}_{21}} & = \frac{\hat{\sigma}^2_{u^{\ast}_{t2}}}{\sum{\hat{y}^2_{t1}}}\\ \hat{\sigma}^2_{u^{\ast}_{t2}} & =\frac{ \sum{\left ( u^{\ast}_{t2} \right )^2} }{n-2} = \frac{ \sum{\left (Y_{t2}-\hat{\beta}_{02} -\hat{\gamma}_{12}\hat{Y}_{1t} \right )^2} }{n-2} \end{align} \]
回归误差方差的计算
实际上\(u^{\ast}_{t2} \neq u_{t2}\),也即意味着\(\hat{\sigma}_{u^{\ast}_{t2}} \neq \hat{\sigma}_{u_{t2}}\) 。
下面我们也可以计算得到\(\hat{\sigma}_{u_{t2}}\) 。
\[ \begin{align} \hat{u}_{t2} &= Y_{t2} - \hat{\beta}_{02} - \hat{\gamma}_{12}Y_{t1} \\ \hat{\sigma}^2_{u_{2t}} & =\frac{ \sum{\left ( u_{2t} \right )^2} }{n-2} = \frac{ \sum{\left (Y_{t2}-\hat{\beta}_{02} -\hat{\gamma}_{12}Y_{1t} \right )^2} }{n-2} \end{align} \]
误差矫正因子
误差矫正因子:因此校正stage 2 回归所估计的系数的标准误,需要对每一个系数的标准误乘以如下的误差矫正因子
\[ \begin{align} \eta &= \frac{ \hat{\sigma}^2_{u_{t2}} } {\hat{\sigma}^2_{u^{\ast}_{t2}} } \end{align} \]
\[ \begin{align} s.e^{\ast}_{\hat{\gamma}_{12}} & = s.e_{\hat{\gamma}_{12}} \cdot \eta = s.e_{\hat{\gamma}_{12}} \cdot \frac{ \hat{\sigma}^2_{u_{t2}} } {\hat{\sigma}^2_{u^{\ast}_{t2}} } \\ s.e^{\ast}_{\hat{\beta}_{02}} & = s.e_{\hat{\beta}_{02}} \cdot \eta = s.e_{\hat{\beta}_{20}} \cdot \frac{ \hat{\sigma}^2_{u_{t2}} } {\hat{\sigma}^2_{u^{\ast}_{t2}} } \end{align} \]
20.5 货币市场案例
变量说明
美国货币市场案例的变量说明如下:
数据集
美国货币市场案例的数据如下:
建模情形1:仅货币供给方程过度识别
模型构建及识别情况
因此我们可以构造出如下的联立方程:
\[ \begin{alignat}{6} Y_{t1} = \beta_{01} & &+ \gamma_{21}Y_{t2} & & + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & & +u_{t1} & \text{ (收入方程)} \\ Y_{t2} = \beta_{02} & + \gamma_{12}Y_{1t} & & & & & & + u_{t2} & \quad \text{(货币供给方程)} \end{alignat} \]
其中:
\(Y_1=GDP\)(国内生产总值);\(Y_2=M2\)货币供给;
\(X_1=GDPI\)(私人国内投资);\(X_2=FEDEXP\)(联邦政府的支出)
2SLS:阶段1估计结果
stage 1: 先求\(Y_1\)对整个方程组(不仅仅是所考虑的方程中)全部前定变量的回归,并分别得到\(\hat{Y}_{t1};\hat{v}_{t1}\)。也即:
\[ \begin{align} Y_{1t} &= \widehat{\pi_0} + \widehat{\pi_1} X_{1t} + \widehat{\pi_2} X_{2t} + \hat{v}_{t1} \\ &= \hat{Y_{1t} } + \hat{v}_{t1} \end{align} \]
stage 1的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y1}=&&+2689.85&&+1.87X1_i&&+2.03X2_i\\ &(s)&&(67.9874)&&(0.1717)&&(0.1075)\\ &(t)&&(+39.56)&&(+10.89)&&(+18.93)\\ &(fit)&&R^2=0.9964&&\bar{R}^2=0.9962 &&\\ &(Ftest)&&F^*=4534.36&&p=0.0000 && \end{split} \end{alignedat} \]
2SLS:阶段1估计得到的拟合变量
同时,我们可以得到\(\hat{Y }_{t1} ;\hat{v}_{t1}\)
2SLS:阶段2估计结果
\[ \begin{alignat}{6} Y_{t1} = \beta_{01} & &+ \gamma_{21}Y_{t2} & & + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & & +u_{t2} & \text{ (收入方程)} \\ Y_{t2} = \beta_{02} & + \gamma_{12}Y_{1t} & & & & & & + u_{t2} & \text{ (货币供给方程)} \end{alignat} \]
stage 2: 现在重新变换过度识别的供给方程如下:
\[ \begin{align} Y_{t2} & = \beta_{02} + \gamma_{12} \hat{Y}_{1t}+ u_{t2}^{\ast} \end{align} \]
利用stage 1的结果,采用OLS进一步回归,得到阶段2估计结果:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y2}=&&-2440.20&&+0.79Y1.hat_i\\ &(s)&&(127.3738)&&(0.0178)\\ &(t)&&(-19.16)&&(+44.52)\\ &(fit)&&R^2=0.9831&&\bar{R}^2=0.9826\\ &(Ftest)&&F^*=1982.40&&p=0.0000 \end{split} \end{alignedat} \]
对比有偏误的OLS估计:整理报告
作为对比,我们给出一个“有偏误”的估计方法,也即直接对数量\(Y2\)对\(Y1\) 采用OLS方法,将得到如下结果:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y2}=&&-2430.34&&+0.79Y1_i\\ &(s)&&(127.2148)&&(0.0178)\\ &(t)&&(-19.10)&&(+44.51)\\ &(fit)&&R^2=0.9831&&\bar{R}^2=0.9826\\ &(Ftest)&&F^*=1980.77&&p=0.0000 \end{split} \end{alignedat} \]
对比有偏误的OLS估计:R原始报告
这是原始分析报告:
Call:
lm(formula = models_money$mod.ols, data = us_money_new)
Residuals:
Min 1Q Median 3Q Max
-418.3 -151.7 40.2 143.5 380.8
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.430e+03 1.272e+02 -19.10 <2e-16 ***
Y1 7.905e-01 1.776e-02 44.51 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 229.1 on 34 degrees of freedom
Multiple R-squared: 0.9831, Adjusted R-squared: 0.9826
F-statistic: 1981 on 1 and 34 DF, p-value: < 2.2e-16建模情形2:收入方程和货币供给方程都是过度识别
模型构建及识别情况
因此我们可以构造出如下的联立方程:
\[ \begin{alignat}{6} Y_{t1} = \beta_{01} & &+ \gamma_{12}Y_{t2} & & + \beta_{11}X_{t1} & + \beta_{21}X_{t2} & & & +u_{t1} & \text{ (收入方程)} \\ Y_{t2} = \beta_{02} & + \gamma_{12}Y_{1t} & & & & &+ \beta_{12}Y_{1,t-1} &+ \beta_{22}Y_{2,t-1} & + u_{t2} & \text{ (货币供给方程)} \end{alignat} \]
下面,我们根据阶条件规则2,对上述联立方程模型进行判断:
联立方程模型中前定变量个数\(K=4\) (分别是什么?)
对于第一个方程(收入方程),前定变量个数\(k=2\),则\((K-k)=2\);第一个方程的内生变量个数\(m=2\),则\((m-1)=1\);显然\((K-k)>(m-1)\) 。因此第一个方程是过度识别的
对于第二个方程(货币供给方程),前定变量个数\(k=2\),则\((K-k)=2\);第二个方程的内生变量个数\(m=2\),则\((m-1)=1\);显然\((K-k)>(m-1)\) 。因此第二个方程是过度识别的
结论:收入方程和货币供给方程都是过度识别的
2SLS:阶段1的约简方程表达式
下面我们将使用两阶段最小二乘法(2SLS)对收入方程和货币供给方程进行一致性的估计。
stage 1: 先求\(Y_1\)对整个方程组(不仅仅是所考虑的方程中)全部前定变量的回归,并分别得到\(\hat{Y}_{t1} ;\hat{v}^{\ast}_{t1}\)。同时,求\(Y_2\)对整个方程组(不仅仅是所考虑的方程中)全部前定变量的回归,并分别得到\(\hat{Y}_{t2} ;\hat{v}^{\ast}_{t2}\) 。也即:
\[ \begin{align} Y_{t1} &= \widehat{\pi}_{01} + \widehat{\pi}_{11} X_{t1} + \widehat{\pi}_{21} X_{t2} + \widehat{\pi}_{31} Y_{t-1,1} + \widehat{\pi}_{41} Y_{t-1,2}+ \hat{v}_{t1} \\ &= \hat{Y}_{1t} +\hat{v}_{t1} \\ Y_{t2} &= \widehat{\pi}_{02} + \widehat{\pi}_{12} X_{t1} + \widehat{\pi}_{22} X_{t2} + \widehat{\pi}_{32} Y_{t-1,1} + \widehat{\pi}_{42} Y_{t-1,2}+ \hat{v}_{t2} \\ &= \hat{Y}_{t2} +\hat{v}_{t2} \end{align} \]
2SLS:阶段1的OLS估计结果(收入方程)
- 收入方程在stage 1的OLS回归结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y1}=&&+1098.90&&+0.98X1_i&&+0.77X2_i\\ &(s)&&(185.5566)&&(0.1308)&&(0.1831)\\ &(t)&&(+5.92)&&(+7.50)&&(+4.19)\\ &(cont.)&&+0.59Y1.l1_i&&-0.01Y2.l1_i &&\\ &(s)&&(0.0667)&&(0.0721) &&\\ &(t)&&(+8.87)&&(-0.10) &&\\ &(fit)&&R^2=0.9990&&\bar{R}^2=0.9989 &&\\ &(Ftest)&&F^*=7857.58&&p=0.0000 && \end{split} \end{alignedat} \]
2SLS:阶段1的OLS估计结果(货币供给方程)
- 货币供给方程在stage 1的OLS回归结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y2}=&&-207.14&&+0.20X1_i&&-0.35X2_i\\ &(s)&&(184.9121)&&(0.1303)&&(0.1824)\\ &(t)&&(-1.12)&&(+1.53)&&(-1.95)\\ &(cont.)&&+0.06Y1.l1_i&&+1.06Y2.l1_i &&\\ &(s)&&(0.0665)&&(0.0718) &&\\ &(t)&&(+0.94)&&(+14.78) &&\\ &(fit)&&R^2=0.9985&&\bar{R}^2=0.9983 &&\\ &(Ftest)&&F^*=5050.57&&p=0.0000 && \end{split} \end{alignedat} \]
2SLS:阶段1估计得到的拟合变量
同时,我们可以得到\(\hat{Y}_{t1} ;\hat{v}_{t1}\)以及\(\hat{Y}_{t2} ;\hat{v}_{t2}\)
2SLS:阶段2的估计方程
stage 2: 重新变换过度识别的收入方程和货币供给方程如下:
\[ \begin{align} Y_{t1} &= \beta_{01} + \gamma_{21} \hat{Y}_{t2} + \beta_{11}X_{t1} + \beta_{21}X_{t2} +u^{\ast}_{t1} \\ Y_{t2} &= \beta_{20} + \gamma_{12} \hat{Y}_{1t} + \beta_{12}Y_{t-1,1} + \beta_{22}Y_{t-1,2} + u^{\ast}_{t2} \end{align} \]
2SLS:阶段2的估计结果(收入方程整理报告)
- 收入方程在stage 2的OLS估计结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y1}=&&+2723.68&&+0.22Y2.hat_i&&+1.71X1_i\\ &(s)&&(67.5331)&&(0.1156)&&(0.1848)\\ &(t)&&(+40.33)&&(+1.90)&&(+9.27)\\ &(cont.)&&+1.57X2_i && &&\\ &(s)&&(0.2623) && &&\\ &(t)&&(+5.98) && &&\\ &(fit)&&R^2=0.9966&&\bar{R}^2=0.9963 &&\\ &(Ftest)&&F^*=3073.97&&p=0.0000 && \end{split} \end{alignedat} \]
2SLS:阶段2的估计结果(收入方程原始报告)
- 收入方程在stage 2的OLS估计的原始报告如下:
Call:
lm(formula = models_money2$mod2.stage2.1, data = us_money_new2)
Residuals:
Min 1Q Median 3Q Max
-360.45 -66.79 35.70 81.22 186.18
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2723.6809 67.5331 40.331 < 2e-16 ***
Y2.hat 0.2192 0.1156 1.896 0.0673 .
X1 1.7142 0.1848 9.275 1.87e-10 ***
X2 1.5690 0.2623 5.981 1.29e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 130.1 on 31 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.9966, Adjusted R-squared: 0.9963
F-statistic: 3074 on 3 and 31 DF, p-value: < 2.2e-162SLS:阶段2的估计结果(货币方程整理报告)
- 货币供给方程在stage 2的OLS估计结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y2}=&&-228.13&&+0.11Y1.hat_i&&-0.03Y1.l1_i\\ &(s)&&(153.6925)&&(0.1431)&&(0.1481)\\ &(t)&&(-1.48)&&(+0.77)&&(-0.17)\\ &(cont.)&&+0.93Y2.l1_i && &&\\ &(s)&&(0.0618) && &&\\ &(t)&&(+15.10) && &&\\ &(fit)&&R^2=0.9981&&\bar{R}^2=0.9979 &&\\ &(Ftest)&&F^*=5461.60&&p=0.0000 && \end{split} \end{alignedat} \]
2SLS:阶段2的估计结果(收入方程原始报告)
- 货币供给方程在stage 2的OLS估计的原始报告如下:
Call:
lm(formula = models_money2$mod2.stage2.1, data = us_money_new2)
Residuals:
Min 1Q Median 3Q Max
-360.45 -66.79 35.70 81.22 186.18
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2723.6809 67.5331 40.331 < 2e-16 ***
Y2.hat 0.2192 0.1156 1.896 0.0673 .
X1 1.7142 0.1848 9.275 1.87e-10 ***
X2 1.5690 0.2623 5.981 1.29e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 130.1 on 31 degrees of freedom
(1 observation deleted due to missingness)
Multiple R-squared: 0.9966, Adjusted R-squared: 0.9963
F-statistic: 3074 on 3 and 31 DF, p-value: < 2.2e-16进行误差矫正的2SLS:systemfit下的整理报告
R软件下采用systemfit分析包,得到的“误差矫正”后的两阶段最小二乘法估计结果汇总如下:
进行误差矫正的2SLS:systemfit下的原始报告
R软件下采用systemfit分析包,得到的“误差矫正”后的两阶段最小二乘法估计结果详细报告:
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 70 62 749260 107381032 0.997082 0.998059
N DF SSR MSE RMSE R2 Adj R2
eq1 35 31 549669 17731.24 133.1587 0.996492 0.996153
eq2 35 31 199592 6438.44 80.2399 0.998006 0.997813
The covariance matrix of the residuals
eq1 eq2
eq1 17731.24 -2603.96
eq2 -2603.96 6438.44
The correlations of the residuals
eq1 eq2
eq1 1.00000 -0.24371
eq2 -0.24371 1.00000
2SLS estimates for 'eq1' (equation 1)
Model Formula: Y1 ~ Y2 + X1 + X2
Instruments: ~X1 + X2 + Y1.l1 + Y2.l1
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2723.680944 69.101729 39.41553 < 2.22e-16 ***
Y2 0.219243 0.118317 1.85302 0.07342 .
X1 1.714216 0.189119 9.06422 3.1717e-10 ***
X2 1.569039 0.268427 5.84531 1.9068e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 133.158716 on 31 degrees of freedom
Number of observations: 35 Degrees of Freedom: 31
SSR: 549668.549447 MSE: 17731.243531 Root MSE: 133.158716
Multiple R-Squared: 0.996492 Adjusted R-Squared: 0.996153
2SLS estimates for 'eq2' (equation 2)
Model Formula: Y2 ~ Y1 + Y1.l1 + Y2.l1
Instruments: ~X1 + X2 + Y1.l1 + Y2.l1
Estimate Std. Error t value Pr(>|t|)
(Intercept) -228.1320387 157.9454624 -1.44437 0.15867
Y1 0.1099682 0.1470504 0.74783 0.46020
Y1.l1 -0.0250416 0.1522272 -0.16450 0.87040
Y2.l1 0.9329562 0.0635111 14.68965 1.7764e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 80.239917 on 31 degrees of freedom
Number of observations: 35 Degrees of Freedom: 31
SSR: 199591.774884 MSE: 6438.444351 Root MSE: 80.239917
Multiple R-Squared: 0.998006 Adjusted R-Squared: 0.997813 有偏误的OLS估计结果的对比(收入方程)
- 收入方程的“有偏误”OLS估计结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y1}=&&+2706.39&&+0.17Y2_i&&+1.75X1_i\\ &(s)&&(67.6150)&&(0.1115)&&(0.1864)\\ &(t)&&(+40.03)&&(+1.51)&&(+9.39)\\ &(cont.)&&+1.68X2_i && &&\\ &(s)&&(0.2552) && &&\\ &(t)&&(+6.60) && &&\\ &(fit)&&R^2=0.9966&&\bar{R}^2=0.9963 &&\\ &(Ftest)&&F^*=3139.86&&p=0.0000 && \end{split} \end{alignedat} \]
有偏误的OLS估计结果的对比(货币供给方程)
- 货币供给方程的“有偏误”OLS估计结果
\[ \begin{alignedat}{999} \begin{split} &\widehat{Y2}=&&-206.53&&-0.02Y1_i&&+0.10Y1.l1_i\\ &(s)&&(154.4428)&&(0.1178)&&(0.1252)\\ &(t)&&(-1.34)&&(-0.14)&&(+0.79)\\ &(cont.)&&+0.94Y2.l1_i && &&\\ &(s)&&(0.0622) && &&\\ &(t)&&(+15.14) && &&\\ &(fit)&&R^2=0.9981&&\bar{R}^2=0.9979 &&\\ &(Ftest)&&F^*=5362.58&&p=0.0000 && \end{split} \end{alignedat} \]
20.6 松露供需案例
松露供需案例(背景)



案例和变量说明
数据说明
散点图
下面给出松露数量Q与松露市场价格P的散点图:
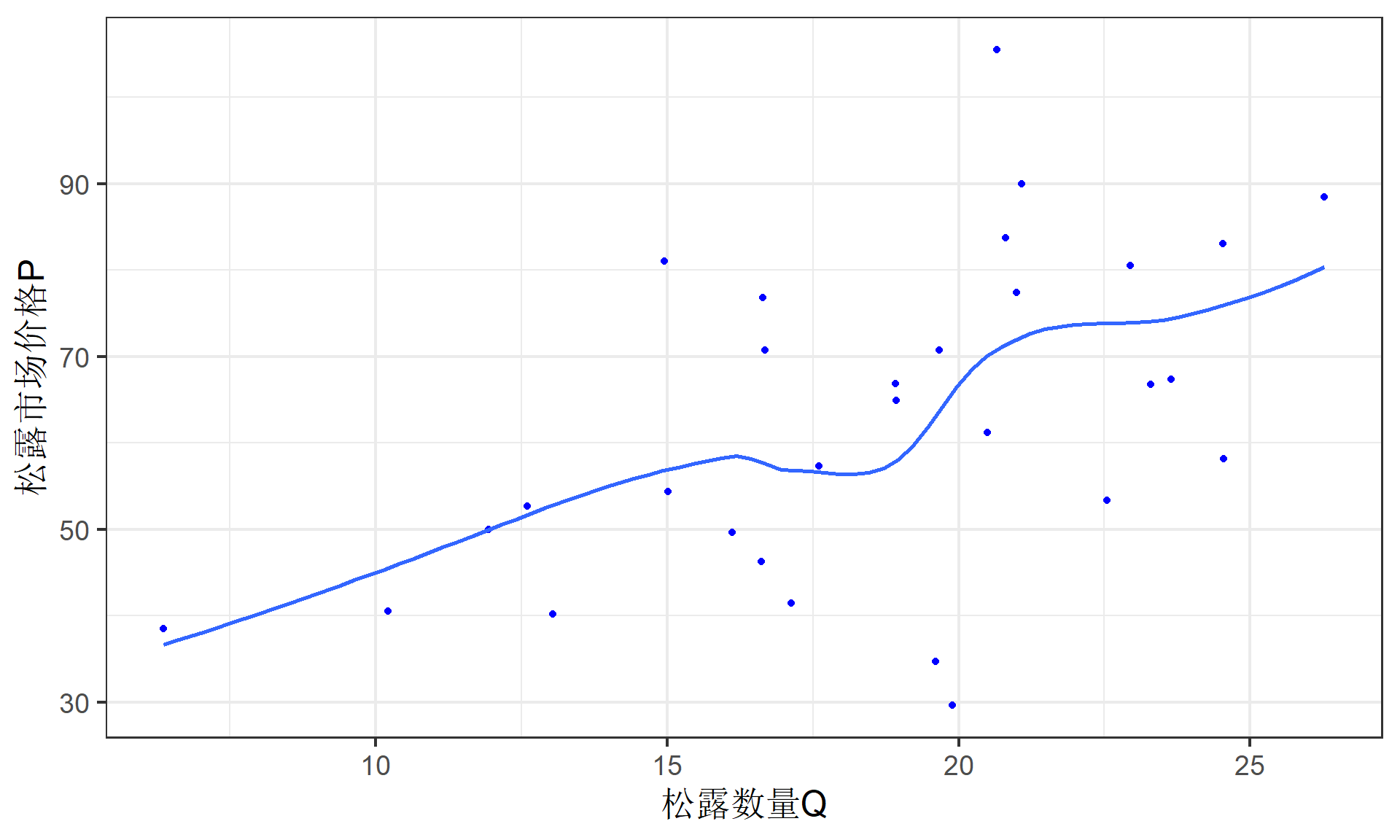
结构方程
给定联立方程:
\[ \begin{align} Q_i &= \alpha_0+\alpha_1P_i+\alpha_2PS_i+\alpha_3DI_i+u_{i1} &&\text{(需求函数)}\\ Q_i &= \beta_0+\beta_1P_i+\beta_2PF_i+u_{i2} &&\text{(供给函数)} \end{align} \]
约简方程
我们可以得到约简方程1:
\[ \begin{cases} \begin{align} P_i &= \pi_{01}+ \pi_{11}PS_i+\pi_{21}DI_i+\pi_{31}PF_i+v_{t1}\\ Q_i &= \pi_{02}+\pi_{12}PS_t+\pi_{22}DI_i+\pi_{32}PF_i+v_{t2} \end{align} \end{cases} \]
结构系数和约简系数
\[ \begin{align} & \pi_{01} = \frac{\beta_0-\alpha_0}{\alpha_1-\beta_1} \\ & \pi_{11} = - \frac{\alpha_2}{\alpha_1-\beta_1} \\ & \pi_{21} = - \frac{\alpha_3}{\alpha_1-\beta_1} \\ & \pi_{31} = \frac{\beta_2}{\alpha_1-\beta_1} \\ & v_{t1} = \frac{u_{2t}-u_{1t}}{\alpha_1-\beta_1} && \end{align} \]
\[ \begin{align} & \pi_{02} = - \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1} \\ & \pi_{12} = - \frac{\alpha_2\beta_1}{\alpha_1-\beta_1} \\ & \pi_{22} = - \frac{\alpha_3\beta_1}{\alpha_1-\beta_1} \\ & \pi_{32} = \frac{\alpha_1\beta_2}{\alpha_1-\beta_1} \\ & v_{t2} = \frac{\alpha_1u_{2t}-\beta_1u_{1t}}{\alpha_1-\beta_1} \end{align} \]
约简模型回归结果
价格约简方程1的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{P}=&&-32.51&&+1.71PS_i&&+7.60DI_i\\ &(s)&&(7.9842)&&(0.3509)&&(1.7243)\\ &(t)&&(-4.07)&&(+4.87)&&(+4.41)\\ &(cont.)&&+1.35PF_i && &&\\ &(s)&&(0.2985) && &&\\ &(t)&&(+4.54) && &&\\ &(fit)&&R^2=0.8887&&\bar{R}^2=0.8758 &&\\ &(Ftest)&&F^*=69.19&&p=0.0000 && \end{split} \end{alignedat} \]
数量约简方程2的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+7.90&&+0.66PS_i&&+2.17DI_i\\ &(s)&&(3.2434)&&(0.1425)&&(0.7005)\\ &(t)&&(+2.43)&&(+4.61)&&(+3.09)\\ &(cont.)&&-0.51PF_i && &&\\ &(s)&&(0.1213) && &&\\ &(t)&&(-4.18) && &&\\ &(fit)&&R^2=0.6974&&\bar{R}^2=0.6625 &&\\ &(Ftest)&&F^*=19.97&&p=0.0000 && \end{split} \end{alignedat} \]
进行误差矫正的2SLS
systemfit下的整理报告
systemfit下的原始报告
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 60 53 692.472 49.8028 0.438964 0.807408
N DF SSR MSE RMSE R2 Adj R2
eq1 30 26 631.9171 24.30450 4.92996 -0.023950 -0.142098
eq2 30 27 60.5546 2.24276 1.49758 0.901878 0.894610
The covariance matrix of the residuals
eq1 eq2
eq1 24.30451 2.16943
eq2 2.16943 2.24276
The correlations of the residuals
eq1 eq2
eq1 1.00000 0.29384
eq2 0.29384 1.00000
2SLS estimates for 'eq1' (equation 1)
Model Formula: Q ~ P + PS + DI
Instruments: ~PS + DI + PF
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.279471 5.543884 -0.77193 0.4471180
P -0.374459 0.164752 -2.27287 0.0315350 *
PS 1.296033 0.355193 3.64881 0.0011601 **
DI 5.013977 2.283556 2.19569 0.0372352 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.92996 on 26 degrees of freedom
Number of observations: 30 Degrees of Freedom: 26
SSR: 631.917143 MSE: 24.304505 Root MSE: 4.92996
Multiple R-Squared: -0.02395 Adjusted R-Squared: -0.142098
2SLS estimates for 'eq2' (equation 2)
Model Formula: Q ~ P + PF
Instruments: ~PS + DI + PF
Estimate Std. Error t value Pr(>|t|)
(Intercept) 20.0328022 1.2231148 16.3785 1.5543e-15 ***
P 0.3379816 0.0249196 13.5629 1.4344e-13 ***
PF -1.0009094 0.0825279 -12.1281 1.9456e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.497585 on 27 degrees of freedom
Number of observations: 30 Degrees of Freedom: 27
SSR: 60.554565 MSE: 2.242762 Root MSE: 1.497585
Multiple R-Squared: 0.901878 Adjusted R-Squared: 0.89461 有偏误的OLS估计:需求方程
作为对比,我们下面给出有偏误的OLS估计——也即不采用2SLS估计联立方程,而是简单而执意地使用OLS方法分别估计需求方程和供给方程!
- 需求方程有偏误的OLS估计结果为:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+1.09&&+0.02P_i&&+0.71PS_i\\ &(s)&&(3.7116)&&(0.0768)&&(0.2143)\\ &(t)&&(+0.29)&&(+0.30)&&(+3.31)\\ &(cont.)&&+0.08DI_i && &&\\ &(s)&&(1.1909) && &&\\ &(t)&&(+0.06) && &&\\ &(fit)&&R^2=0.4957&&\bar{R}^2=0.4375 &&\\ &(Ftest)&&F^*=8.52&&p=0.0004 && \end{split} \end{alignedat} \]
有偏误的OLS估计:供给方程
作为对比,我们下面给出有偏误的OLS估计——也即不采用2SLS估计联立方程,而是简单而执意地使用OLS方法分别估计需求方程和供给方程!
- 供给方程有偏误的OLS估计结果为:
\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+20.03&&+0.34P_i&&-1.00PF_i\\ &(s)&&(1.2220)&&(0.0217)&&(0.0764)\\ &(t)&&(+16.39)&&(+15.54)&&(-13.10)\\ &(fit)&&R^2=0.9019&&\bar{R}^2=0.8946 &&\\ &(Ftest)&&F^*=124.08&&p=0.0000 && \end{split} \end{alignedat} \]
20.7 鳕鱼供需案例
鳕鱼供需案例(背景)



变量说明
数据说明
散点图
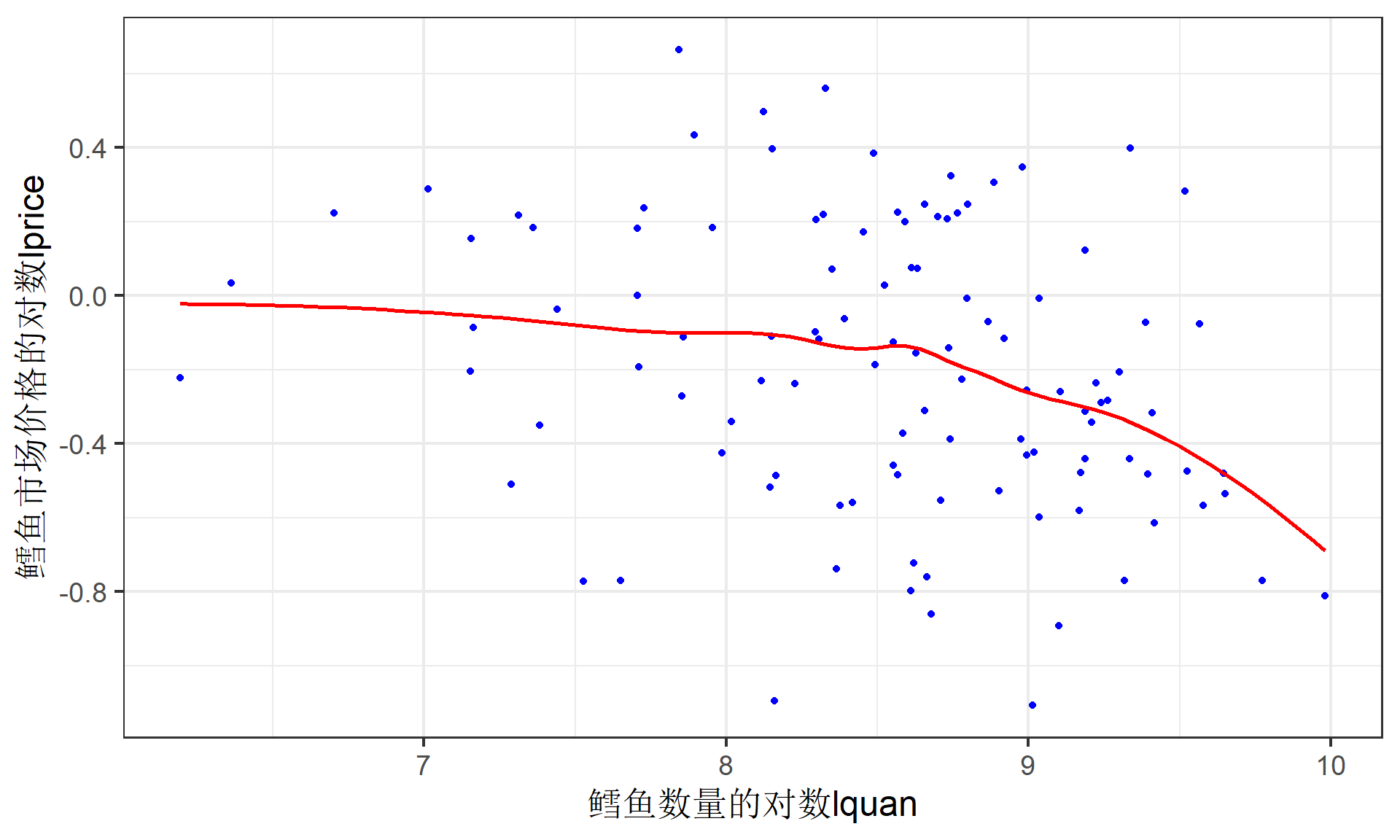
结构方程
给定联立方程:
\[ \begin{align} lquan_t &= \alpha_0+\alpha_1lprice_t+\alpha_2mon_t+\alpha_3tue_t+\alpha_4wen_t+\alpha_5thu_t+u_{1t} &&\text{(需求函数)}\\ lquan_t &= \beta_0+\beta_1lprice_t+\beta_3stormy_t+u_{2t} &&\text{(供给函数)} \end{align} \]
约简方程
可得到约简方程:
\[ \begin{align} lquan_t &= \pi_0 + \pi_1mon_t+\pi_2tue_t+\pi_3wen_t+\pi_4thu_t\\ &+\pi_5stormy_t+v_t &&\text{(约简方程1)}\\ lprice_t &= \pi_0 + \pi_1mon_t+\pi_2tue_t+\pi_3wen_t+\pi_4thu_t\\ &+\pi_5stormy_t+v_t &&\text{(约简方程2)}\\ \end{align} \]
约简方程估计结果(数量方程)
数量约简方程的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lquan}=&&+8.81&&+0.10mon_i&&-0.48tue_i&&-0.55wed_i&&+0.05thu_i&&-0.39stormy_i\\ &(s)&&(0.1470)&&(0.2065)&&(0.2011)&&(0.2058)&&(0.2010)&&(0.1437)\\ &(t)&&(+59.92)&&(+0.49)&&(-2.41)&&(-2.69)&&(+0.27)&&(-2.70)\\ &(fit)&&R^2=0.1934&&\bar{R}^2=0.1550 && && && &&\\ &(Ftest)&&F^*=5.03&&p=0.0004 && && && && \end{split} \end{alignedat} \]
约简方程估计结果(价格方程)
价格约简方程的回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lprice}=&&-0.27&&-0.11mon_i&&-0.04tue_i&&-0.01wed_i&&+0.05thu_i&&+0.35stormy_i\\ &(s)&&(0.0764)&&(0.1073)&&(0.1045)&&(0.1069)&&(0.1045)&&(0.0747)\\ &(t)&&(-3.56)&&(-1.05)&&(-0.39)&&(-0.11)&&(+0.48)&&(+4.64)\\ &(fit)&&R^2=0.1789&&\bar{R}^2=0.1398 && && && &&\\ &(Ftest)&&F^*=4.58&&p=0.0008 && && && && \end{split} \end{alignedat} \]
进行误差矫正的2SLS
systemfit下的整理报告
systemfit下的原始报告
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 222 213 109.612 0.107301 0.094242 -0.597812
N DF SSR MSE RMSE R2 Adj R2
eq1 111 105 52.0903 0.496098 0.704342 0.139124 0.098130
eq2 111 108 57.5218 0.532610 0.729801 0.049360 0.031755
The covariance matrix of the residuals
eq1 eq2
eq1 0.496098 0.396138
eq2 0.396138 0.532610
The correlations of the residuals
eq1 eq2
eq1 1.000000 0.770653
eq2 0.770653 1.000000
2SLS estimates for 'eq1' (equation 1)
Model Formula: lquan ~ lprice + mon + tue + wed + thu
Instruments: ~mon + tue + wed + thu + stormy
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.5059113 0.1661669 51.18896 < 2.22e-16 ***
lprice -1.1194169 0.4286450 -2.61152 0.0103334 *
mon -0.0254022 0.2147742 -0.11827 0.9060766
tue -0.5307694 0.2080001 -2.55177 0.0121574 *
wed -0.5663511 0.2127549 -2.66199 0.0089895 **
thu 0.1092673 0.2087866 0.52334 0.6018373
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.704342 on 105 degrees of freedom
Number of observations: 111 Degrees of Freedom: 105
SSR: 52.090321 MSE: 0.496098 Root MSE: 0.704342
Multiple R-Squared: 0.139124 Adjusted R-Squared: 0.09813
2SLS estimates for 'eq2' (equation 2)
Model Formula: lquan ~ lprice + stormy
Instruments: ~mon + tue + wed + thu + stormy
Estimate Std. Error t value Pr(>|t|)
(Intercept) 8.62835440 0.38897023 22.18256 < 2e-16 ***
lprice 0.00105931 1.30954697 0.00081 0.99936
stormy -0.36324606 0.46491248 -0.78132 0.43632
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.729801 on 108 degrees of freedom
Number of observations: 111 Degrees of Freedom: 108
SSR: 57.521843 MSE: 0.53261 Root MSE: 0.729801
Multiple R-Squared: 0.04936 Adjusted R-Squared: 0.031755 有偏误的OLS估计结果(需求方程)
- 需求方程有偏误的OLS估计结果为:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lquan}=&&+8.61&&-0.56lprice_i&&+0.01mon_i&&-0.52tue_i&&-0.56wed_i&&+0.08thu_i\\ &(s)&&(0.1430)&&(0.1682)&&(0.2026)&&(0.1977)&&(0.2023)&&(0.1978)\\ &(t)&&(+60.17)&&(-3.34)&&(+0.07)&&(-2.61)&&(-2.75)&&(+0.41)\\ &(fit)&&R^2=0.2205&&\bar{R}^2=0.1834 && && && &&\\ &(Ftest)&&F^*=5.94&&p=0.0001 && && && && \end{split} \end{alignedat} \]
有偏误的OLS估计结果(供给方程)
- 供给方程有偏误的OLS估计结果为:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lquan}=&&+8.50&&-0.44lprice_i&&-0.22stormy_i\\ &(s)&&(0.0981)&&(0.1942)&&(0.1630)\\ &(t)&&(+86.69)&&(-2.26)&&(-1.33)\\ &(fit)&&R^2=0.0923&&\bar{R}^2=0.0755 &&\\ &(Ftest)&&F^*=5.49&&p=0.0053 && \end{split} \end{alignedat} \]
本章结束

第20章 联立方程模型的估计方法