计量经济学II

(Ecnometrics II)

第19章联立方程模型的识别问题？

胡华平

huhuaping01@hotmail.com

经济管理学院数量经济教研室

2024-09-25

模块4：联立方程模型（SEM）

Chapter 17. 内生性问题与工具变量法
Chapter 18. 为什么要关心联立方程模型？
Chapter 19. 联立方程模型的识别问题
Chapter 20. 联立方程模型的估计方法

19.1 识别类型

识别问题的定义

识别问题 (identification problem)，是指能否从所估计的约简型系数求出一个结构方程参数的估计值。

识别的情形：

如果能够求出估计值，就说该方程是可以识别的，具体又分为：
恰好识别的（充分或刚好识别的，Just/Exact Identiﬁcation）：是指能够得到结构参数的唯一数值。
过度识别的(Overidentiﬁcation)：是指可获得结构参数不止一个的值。
如果不能求出估计值，就说所考虑的方程是不可识别的或识别不足的 (Underidentiﬁcation)。

识别问题的演示

联立方程

考虑如下的供需联立方程：

\[ \begin{align} Q &= \alpha_0+\alpha_1P_t+u_{t1} &(\alpha_1<0) &&\text{(需求函数)}\\ Q &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)}\\ \end{align} \]

散点图

供需均衡点

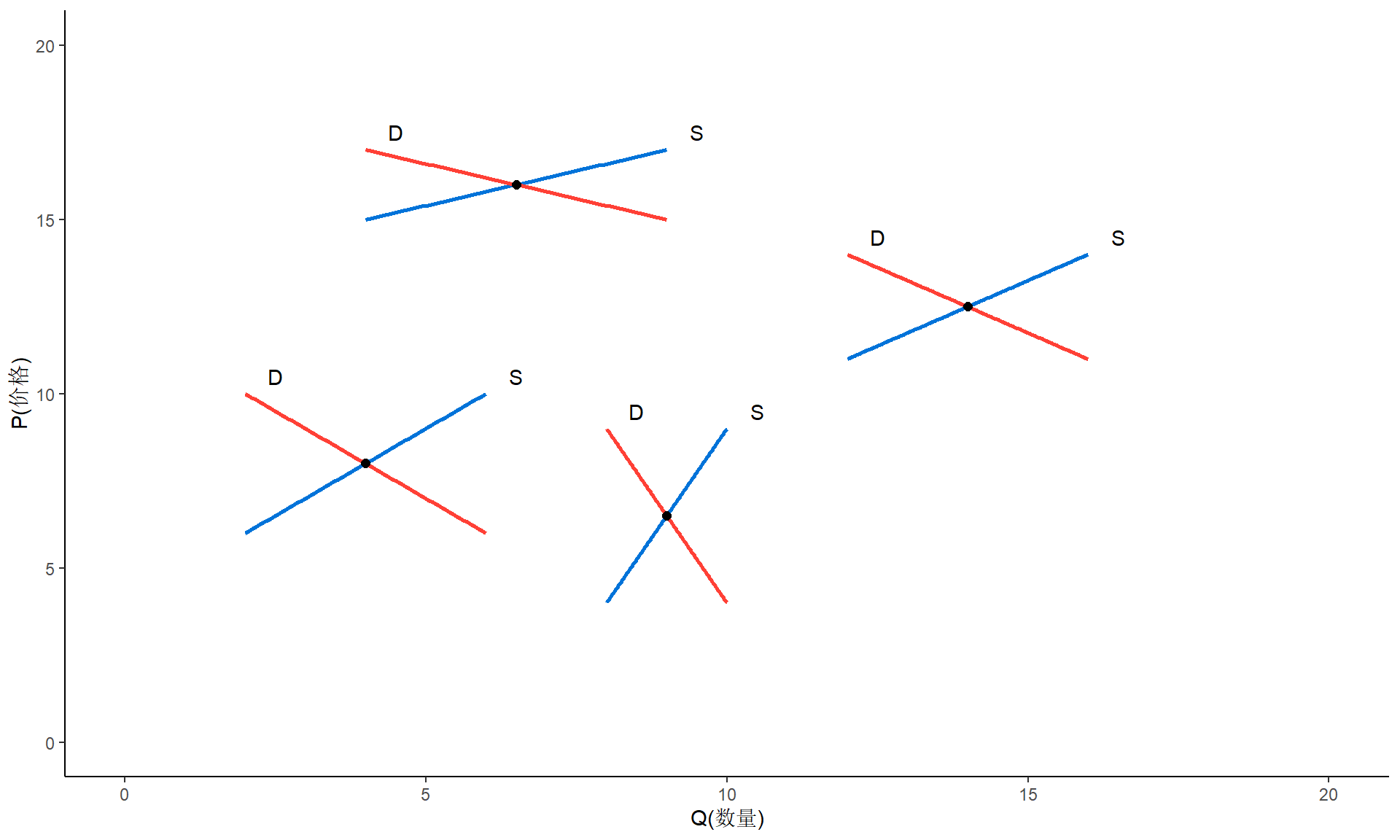
不可识别

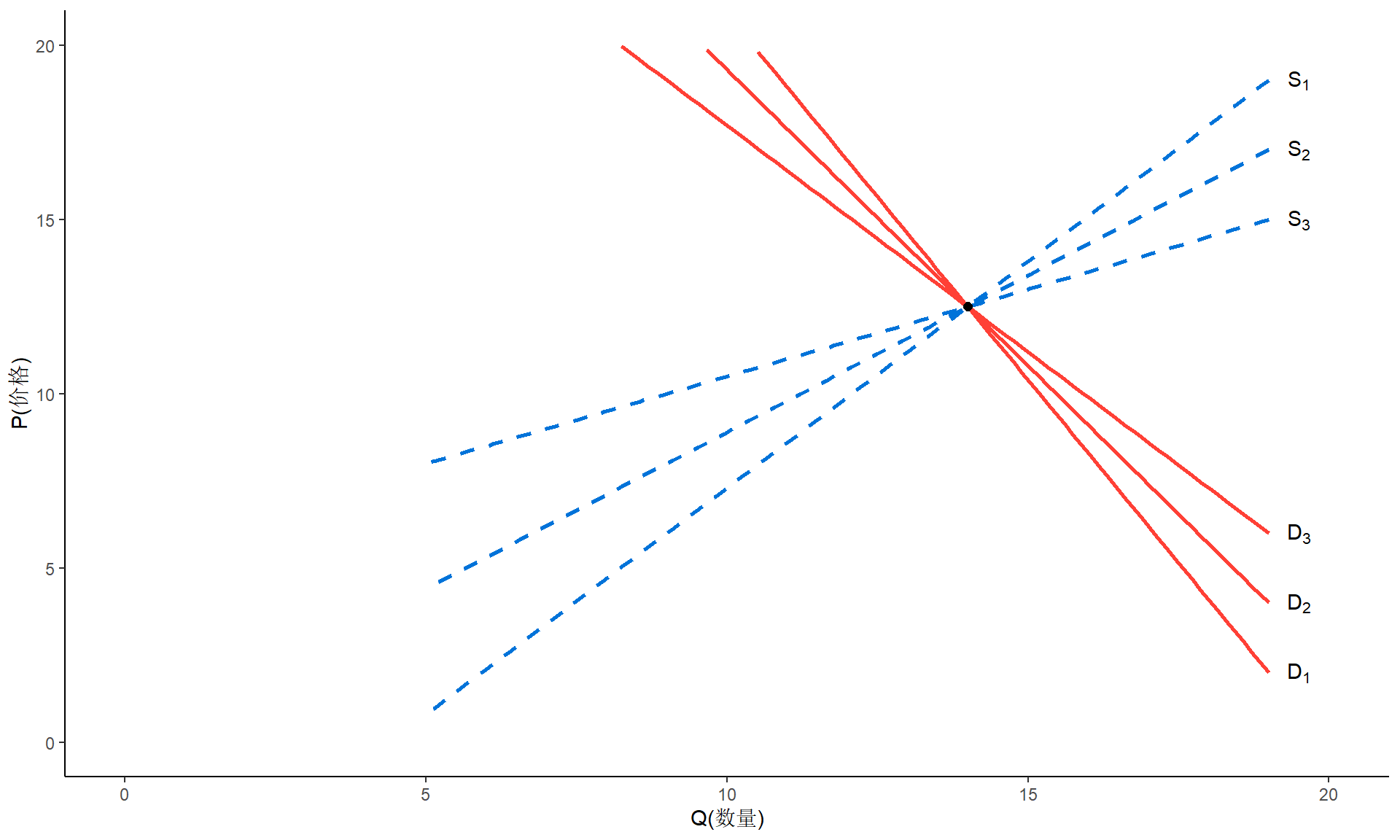
我们无法肯定这个点是由图中整个(供求)曲线族中的哪对供求曲线产生的。这时，我们就说供需曲线是不可识别的。

能识别出供给曲线

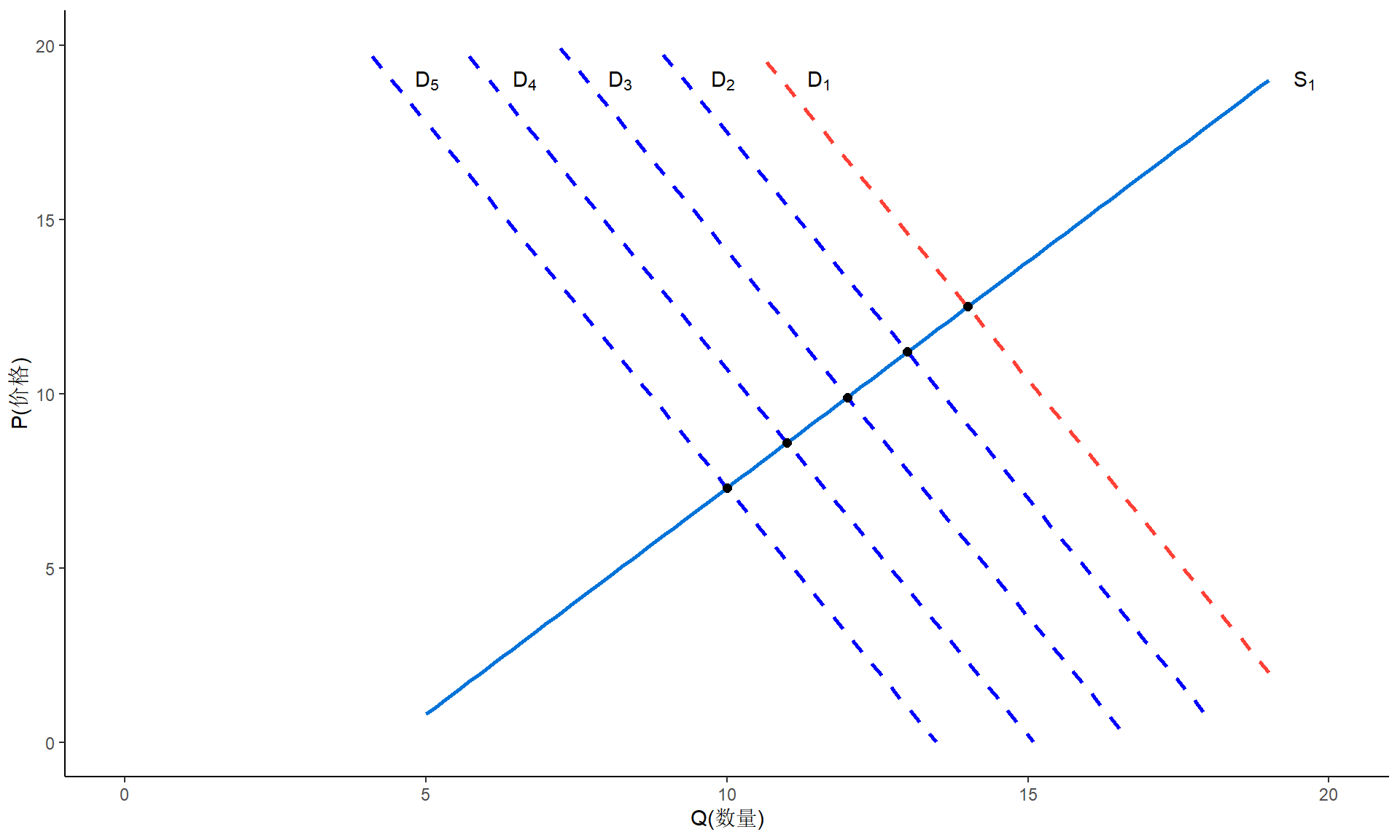
如果由于收入、嗜好等等的变化，需求曲线随时间而移动，而供给曲线则保持相对稳定，则散点将展现出一条供给曲线。这时，我们就说供给曲线是可识别的。

能识别出需求曲线

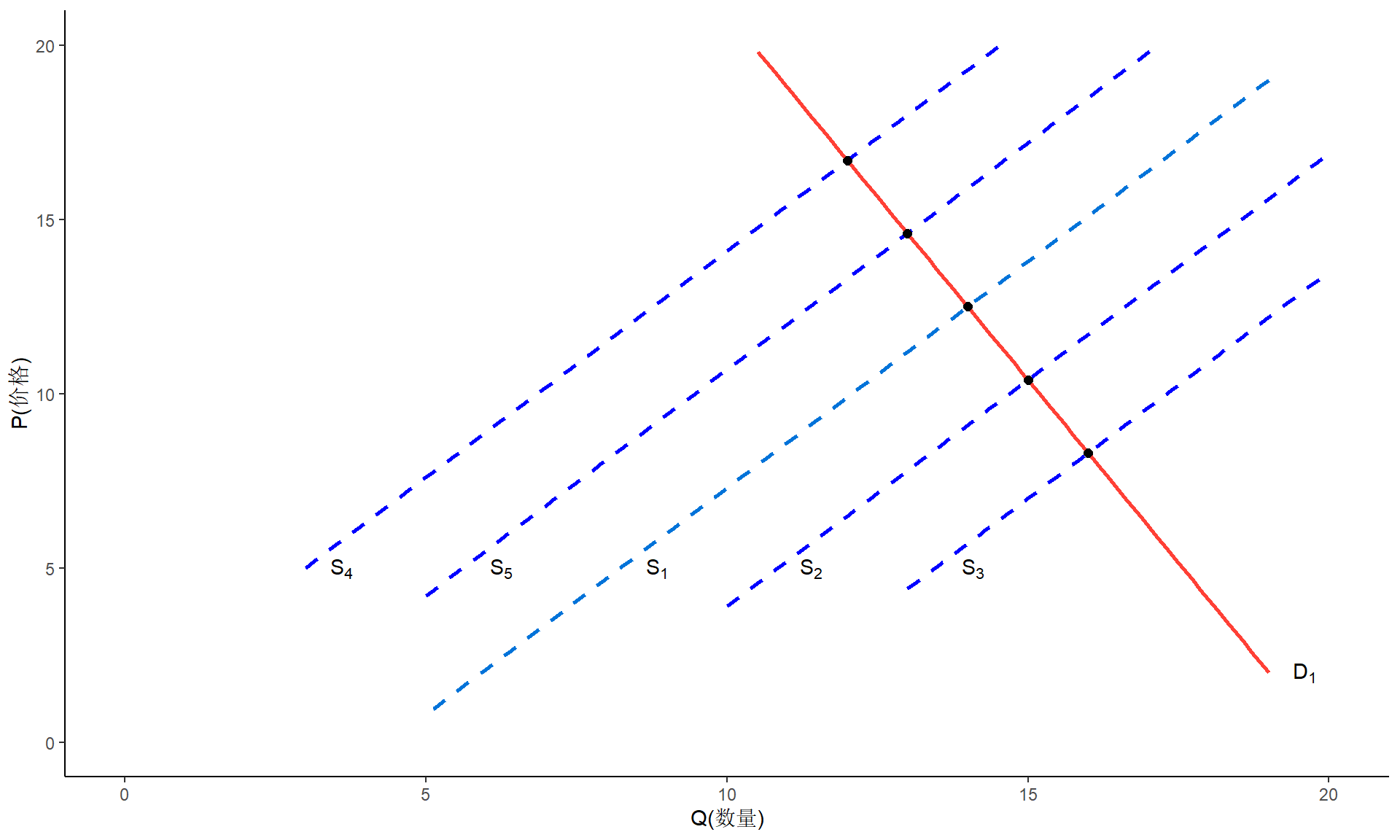
如果由于气候条件的变化或其他外部因素的变化，供给曲线随时间而移动，但需求曲线保持相对稳定，则散点将展现出一条需求曲线。这时，我们就说需求曲线是可识别的。

识别不足

结构方程和约简方程

给定联立方程：

\[ \begin{cases} \begin{align} Q_t &= \alpha_0+\alpha_1P_t+u_{t1} &(\alpha_1<0) &&\text{(需求函数)}\\ Q_t &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)}\\ \end{align} \end{cases} \]

则容易得到约简方程形式：

\[ \begin{cases} \begin{align} P_t &= \pi_{11}+v_{t1} \\ Q_t &= \pi_{12}+v_{t2} \end{align} \end{cases} \]

其中，约简参数和结构参数的关系为： \[ \begin{cases} \begin{align} \pi_{11} & = -\frac{\alpha_0 - \beta_0}{\alpha_1-\beta_1} ;&& \pi_{21} = \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1} \\ v_{t1} &= - \frac{u_{t1} - u_{t2}}{\alpha_1-\beta_1} ;&& v_{t2} = \frac{\alpha_1 u_{t2}- \alpha_0 u_{t1}}{\alpha_1-\beta_1} \end{align} \end{cases} \]

显然，前述的结构方程是不可识别的！

结构参数个数？
约简参数个数？

虚构的一个“混杂”方程

针对结构方程，我们可以变换得到：

\[ \begin{cases} \begin{align} \lambda Q &= \lambda\alpha_0+\lambda\alpha_1P_t+\lambda u_{t1} &(\alpha_1<0) &&\text{(需求函数变换)}\\ (1-\lambda)Q &= (1-\lambda)\beta_0+(1-\lambda)\beta_1P_t+(1-\lambda)u_{t2} &(\beta_1>0) &&\text{(供给函数变换)} \end{align} \end{cases} \]

进一步，我们可以构造一个如下的“混杂”方程：

\[ \begin{align} Q_t &= \lambda\alpha_0+(1-\lambda)\beta_0 +(\lambda\alpha_1+(1-\lambda)\beta_1 )P_t+ \lambda u_{1t}+(1-\lambda)u_{t2} & && \text{(混杂方程)} \\ \end{align} \]

并记为：$Q_t = \gamma_0 +\gamma_1P_t+w_t$

其中：

\[ \begin{cases} \begin{align} \gamma_0 & = \lambda\alpha_0+(1-\lambda)\beta_0 \\ \gamma_1 &= \lambda\alpha_1+(1-\lambda)\beta_1 \\ w_t &= \lambda u_{1t}+(1-\lambda)u_{t2} \end{align} \end{cases} \]

该虚构的混杂方程与结构方程中的任何一个都是无差异的！
因此表明原来的结构方程是不可识别的！

恰好识别

结构方程和约简方程

给定结构方程方程：

\[ \begin{cases} \begin{align} Q_t &= \alpha_0+\alpha_1P_t+\alpha_2I_t+u_{t1} &(\alpha_1<0,\alpha_2>0) &&\text{(需求函数)}\\ Q_t &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)} \end{align} \end{cases} \]

得到约简方程形式：

\[ \begin{cases} \begin{align} P_t &= \pi_{11}+ \pi_{21}I_t+v_{t1} \\ Q_t &= \pi_{12}+ \pi_{22}I_t+v_{t2}\\ \end{align} \end{cases} \]

其中：

\[ \begin{alignedat}{3} & \pi_{11} = \frac{\beta_0-\alpha_0}{\alpha_1-\beta_1}; \quad & \pi_{21} = - \frac{\alpha_2}{\alpha_1-\beta_1} ; \quad & v_{t1} = \frac{u_{t2}-u_{t1}}{\alpha_1-\beta_1} \\ & \pi_{12} = \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1};\quad & \pi_{22} = - \frac{\alpha_2\beta_1}{\alpha_1-\beta_1} ;\quad & v_{t2} = \frac{\alpha_1u_{t2}-\beta_1u_{t1}}{\alpha_1-\beta_1} \end{alignedat} \]

只有一个方程能恰好识别

前述结构方程能否识别么？

约简参数个数？
结构参数个数？

答案：

只有4个约简参数：$\pi_{11},\pi_{21},\pi_{12},\pi_{22}$- 但是有5个结构参数：$\alpha_0,\alpha_1,\alpha_2,\beta_0,\beta_1$
因此不可能完全求解全部5个结构参数

然而，供给方程的结构参数是恰好识别的，因为：

\[ \begin{align} \beta_0 = \pi_{12}-\beta_1\pi_{11} ; \quad \beta_1 = \frac{\pi_{22}}{\pi_{21}} \end{align} \]

过度识别

结构方程

给定结构方程：

\[ \begin{cases} \begin{align} Q_t &= \alpha_0+\alpha_1P_t+\alpha_2I_t+\alpha_3R_t+u_{t1} &(\alpha_1<0,\alpha_2>0) &&\text{(需求函数)}\\ Q_t &= \beta_0+\beta_1P_t+\beta_2P_{t-1}+u_{t2} &(\beta_1,\beta_2>0) &&\text{(供给函数)} \end{align} \end{cases} \]

提问：请变换得到约简方程？

约简方程

得到约简方程形式：

\[ \begin{cases} \begin{align} P_t &= \pi_{11}+ \pi_{21}I_t+\pi_{31}R_t+\pi_{41}P_{t-1}+v_{t1} \\ Q_t &= \pi_{12}+\pi_{22}I_t+\pi_{32}R_t+\pi_{42}P_{t-1}+v_{t2} \end{align} \end{cases} \]

\[ \begin{cases} \begin{align} & \pi_{11} = \frac{\beta_0-\alpha_0}{\alpha_1-\beta_1} \\ & \pi_{21} = - \frac{\alpha_2}{\alpha_1-\beta_1} \\ & \pi_{31} = - \frac{\alpha_3}{\alpha_1-\beta_1} \\ & \pi_{41} = \frac{\beta_2}{\alpha_1-\beta_1} \\ & v_{t1} = \frac{u_{t2}-u_{t1}}{\alpha_1-\beta_1} \end{align} \end{cases} \]

\[ \begin{cases} \begin{align} & \pi_{12} = - \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1} \\ & \pi_{22} = - \frac{\alpha_2\beta_1}{\alpha_1-\beta_1} \\ & \pi_{32} = - \frac{\alpha_3\beta_1}{\alpha_1-\beta_1} \\ & \pi_{42} = \frac{\alpha_1\beta_2}{\alpha_1-\beta_1} \\ &v_{t2} = \frac{\alpha_1u_{t2}-\beta_1u_{t1}}{\alpha_1-\beta_1} \end{align} \end{cases} \]

存在多个满足条件的解

前述结构方程能否识别么？

约简参数个数？
结构参数个数？

答案：

有8个约简参数：$\pi_{11},\pi_{12},\pi_{13},\pi_{14},\pi_{21},\pi_{22},\pi_{23},\pi_{24}$- 只有7个结构参数：$\alpha_0,\alpha_1,\alpha_2,\alpha_3,\beta_0,\beta_1,\beta_2$
因此方程数多于未知系数个数，不能求解得出全部7个结构系数的唯一估计值。

结论：结构方程存在多个满足条件的解，是过度识别的。

19.2 识别规则

符号约定

首先给出结构方程中变量个数的记号约定：

-$M=$ 结构方程中全部内生变量的个数 -$m=$ 某个方程中内生变量的个数 -$K=$ 结构方程中全部前定变量的个数（包括截距项） -$k=$ 某定方程中前定变量的个数

可识别的阶条件

阶条件规则1

阶条件规则1：

在一个含有M个方程的结构模型中，一个方程能被识别，它必须排除——在联立模型中出现而它自己不出现的——至少M-1个变量（包括内生或前定）。也即$M+K-(k+m) \geq (M-1)$。

如果它恰好有M-1个（内生或前定）变量没有出现，则该方程是恰好识别的。也即，$M+K-(k+m) = (M-1)$- 如果它超过M-1个（内生或前定）变量没有出现，则该方程是过度识别的；也即，$M+K-(k+m) > (M-1)$

阶条件规则2

阶条件规则2：

在一个含有M个方程的结构模型中，一个方程能被识别，该方程所排除的——在联立模型中出现而它自己不出现——前定变量个数必须多于它所含的内生变量的个数减1，也即$K-k \geq m-1$。

如果$K-k = m-1$ ，则该方程是恰好识别的；
如果$K-k \geq m-1$ ，则该方程是过度识别的。

应用示例：阶条件识别

阶条件1：都不可识别

有如下的结构方程：

阶条件规则1的结论：

结构方程的全部变量有(M+K)=2+0=2个，且(M-1)=2-1=1
对于第1个方程，因为其全部变量数有(m+k)=2+0=2个，所以(M+K)-(m+k)=2-2=0，显然(M+K)-(m+k)<(M-1)。因此第一个方程（需求方程）是不可识别的
对于第二个方程，因为(m+k)=2+0=2，所以(M+K)-(m+k)=2-2=0，显然(M+K)-(m+k)<(M-1)。因此第二个方程（供给方程）也是不可识别的

阶条件2：都不可识别

有如下的结构方程：

阶条件规则2的结论：

结构方程中前定变量个数K=0
对于第1个方程，前定变量个数k=0，则(K-k)=0；第1个方程的内生变量个数m=1，则(m-1)=1；显然(K-k)<(m-1)。因此第1个方程（需求方程）是不可识别的
对于第2个方程，前定变量个数k=0，则(K-k)=0；第2个方程的内生变量个数m=1，则(m-1)=1；显然(K-k)<(m-1)。因此第2个方程（供给方程）是不可识别的

阶条件1：不可识别+恰好识别

给定结构方程方程：

阶条件规则1的结论：

结构方程中(M+K)=2+1=3，且(M-1)=2-1=1
对于第1个方程，因为(m+k)=2+1=3，所以(M+K)-(m+k)=3-3=0，显然(M+K)-(m+k)<(M-1)。第1个方程（需求方程）是不可识别的
对于第2个方程，因为(m+k)=2+0=2，所以(M+K)-(m+k)=3-2=1，显然(M+K)-(m+k)=(M-1)。第2个方程（供给方程）是恰好识别的

阶条件2：不可识别+恰好识别

给定结构方程方程：

阶条件规则2的结论：

结构方程中前定变量个数K=1
对于第1个方程，前定变量个数k=1，则(K-k)=0；第一个方程的内生变量个数m=2，则(m-1)=1；显然(K-k)<(m-1)。因此第一个方程（需求方程）是不可识别的
对于第2个方程，前定变量个数k=0，则(K-k)=1；第二个方程的内生变量个数m=2，则(m-1)=1；显然(K-k)=(m-1)。因此第二个方程（供给方程）是恰好识别的

阶条件1：恰好识别+过度识别

给定结构方程：

阶条件规则1的结论：

结构方程中(M+K)=2+3=5，且(M-1)=2-1=1
对于第1个方程，因为(m+k)=2+2=4，所以(M+K)-(m+k)=5-4=1，显然(M+K)-(m+k)=(M-1)。第1个方程（需求方程）是恰好识别的
对于第二个方程，因为(m+k)=2+1=3，所以(M+K)-(m+k)=5-3=2，显然(M+K)-(m+k)>(M-1)。第2个方程（供给方程）是过度识别的

阶条件2：恰好识别+过度识别

给定结构方程：

阶条件规则2的结论：

结构方程中前定变量个数K=3
对于第1个方程，前定变量个数k=2，则(K-k)=1；第1个方程的内生变量个数m=2，则(m-1)=1；显然(K-k)=(m-1)。因此第1个方程（需求方程）是恰好识别的
对于第2个方程，前定变量个数k=1，则(K-k)=2；第2个方程的内生变量个数m=2，则(m-1)=1；显然(K-k)>(m-1)。因此第2个方程（供给方程）是过度识别的

可识别的阶条件：总结

阶条件规则是识别的必要而非充分条件，即使它得到满足，方程也会出现不能识别的情形。例如：

\[ \begin{align} Q &= \alpha_0+\alpha_1P_t+\alpha_2I_t+u_{t1} &(\alpha_1<0,\alpha_2>0) &&\text{(需求函数)}\\ Q &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)} \end{align} \]

根据阶条件规则，我们判断第二个方程（供给方程）是恰好可识别的。但实际上，我们还需要确保第一个方程中的收入$I_t$前面的系数$\alpha_2 \neq 0$ 。也就是说，收入变量不仅仅有可能进入而且确实进入了需求函数。

阶条件规则1和阶条件规则2是等价的。
利用阶条件规则判断识别问题，适合于比较简单的联立方程情形。

可识别的秩条件

秩条件规则

秩条件规则：

在一个包含M个内生变量的M个方程的联立模型中，一个方程可识别的充分必要条件是，我们能从模型所含而该方程所不含的（内生或前定）变量系数矩阵中构造出至少1个$(M-1)\ast(M-1)$ 阶的非零行列式来。

主要操作步骤：

把结构模型移项，写出代数式2
按方程写出对应的系数列表
找到该方程不含的所有列
从这些列中随意找出1个$(M-1)\ast(M-1)$的矩阵
判断并得出结论：如果能找到任何1个行列式为0的矩阵，则该方程就是不可识别的

应用示例：秩条件识别

步骤1：写出代数式2，写出系数列表

\[ \begin{cases} \begin{alignedat}{9} & Y_{t1} &-\gamma_{21}Y_{t2}&-\gamma_{31}Y_{t3} & &-\beta_{01}&-\beta_{11}X_{t1} & & &= &u_{t1} \\ & & Y_{t2} &-\gamma_{32} Y_{3t} & & -\beta_{02}&-\beta_{12}X_{1t} &- \beta_{22}X_{2t} & &= &u_{t2}\\ &-\gamma_{13}Y_{t1} & &+ Y_{t3} & & -\beta_{03}&-\beta_{13}X_{1t} &-\beta_{23}X_{2t} & &= &u_{t3} \\ &-\gamma_{14}Y_{t1}&-\gamma_{24}Y_{t2} & &+Y_{t4} &-\beta_{04} & & &-\beta_{34}X_{t3} &= &u_{t4} \end{alignedat} \end{cases} \]

可以将上述结构方程的参数写成如下的形式：

\[ \begin{matrix} -- & -- & -- & -- & -- & --& -- & -- & -- \\ eq & Y_1 & Y_2 & Y_3 & Y_4 & 1& X_1 & X_2 & X_3 \\ -- & -- & -- & -- & -- & -- & -- & -- & -- \\ 1 & 1 & -\gamma_{21} & -\gamma_{31} & 0 & -\beta_{01}& -\beta_{11} & 0 & 0 \\ 2 & 0 & 1 & -\gamma_{32} & 0 & -\beta_{02}& -\beta_{12} & -\beta_{22} & 0 \\ 3 & -\gamma_{13} & 0 & 1 & 0 & -\beta_{03}& -\beta_{13} & -\beta_{23} & 0 \\ 4 & -\gamma_{14} & -\gamma_{24} & 0 & 1 & -\beta_{04}& 0 & 0 & -\beta_{34} \\ \end{matrix} \]

步骤2：分析第1个方程的变量数，找到缺失列

第1个方程不包含的内生变量有：$Y_{t4}$；不包含的前定变量有：$X_{t2},X_{t3}$

\[ \begin{matrix} -- & -- & -- & -- & -- & --& -- & -- & -- \\ eq & Y_1 & Y_2 & Y_3 & [Y_4] & 1& X_1 & [X_2] & [X_3] \\ -- & -- & -- & -- & -- & -- & -- & -- & -- \\ 1 & 1 & -\gamma_{21} & -\gamma_{31} & 0 & -\beta_{01}& -\beta_{11} & 0 & 0 \\ 2 & 0 & 1 & -\gamma_{32} & 0 & -\beta_{02}& -\beta_{12} & -\beta_{22} & 0 \\ 3 & -\gamma_{13} & 0 & 1 & 0 & -\beta_{03}& -\beta_{13} & -\beta_{23} & 0 \\ 4 & -\gamma_{14} & -\gamma_{24} & 0 & 1 & -\beta_{04}& 0 & 0 & -\beta_{34} \\ \end{matrix} \]

步骤3：找1个目标矩阵，计算其行列式

\[ \begin{alignat}{3} A= \begin{bmatrix} 0 & -\beta_{22} & 0 \\ 0 & -\beta_{32} & 0 \\ 1 & 0 & -\beta_{43} \\ \end{bmatrix} \end{alignat} \]

\[ \begin{alignat}{3} det(A)= \begin{vmatrix} 0 & -\beta_{22} & 0 \\ 0 & -\beta_{32} & 0 \\ 1 & 0 & -\beta_{43} \\ \end{vmatrix} =0 \end{alignat} \]

这意味着，矩阵的秩$rank(A)=\mathbf{\rho}(A)<3$。因此，第一个方程不满足秩条件，不能识别。

秩条件识别小结

总结起来，秩条件识别规则的步骤如下：

把结构方程写成代数式2
把系数写成表格形式
划掉被考虑的方程所在行
再划掉被考虑的方程中非零系数对应的列
余下的系数将构成一个系数矩阵

利用系数矩阵，构造任意的$(M-1)*(M-1)$ 阶方阵，并计算方阵的行列式
如果能找到至少一个行列式不等于零的$(M-1)*(M-1)$ 阶方阵，也即该方阵的秩为M-1，则表明被考虑方程是可识别的（恰好或多度识别）
如果所有可能的$(M-1)*(M-1)$阶方阵，它们的行列式全等于零，也即所有可能$(M-1)*(M-1)$ 阶方阵的秩都小于M-1，则表明被考虑方程是不可识别的

识别练习：其他3个方程是否可识别？

答案：

第1个方程：不可识别
第2个方程：？
第3个方程：？
第4个方程：？

秩条件与阶条件的比较

下面我们再运用识别的阶条件对所有方程进行判断，可以得到下面结果：

识别规则的总结

下面对识别规则进行一个全面总结：

阶条件是识别的必要但非充分条件，即使它得到满足，方程也会出现不能识别的情形。
秩条件是识别的充分必要条件
秩条件告诉我们所考虑的方程是否可识别，而阶条件告诉我们它是恰好识别还是过度识别
严格地，我们需要先分析秩条件，确定方程是否可识别；然后再利用阶条件，判断是恰好识别还是过度识别！

19.3 内生性检验

内生性检验（联立性检验）

概念与定义

联立性检验在本质上是检验一个（内生）回归元是否与误差项（$u_t$ ）相关。

如果相关，就存在联立性问题，从而需要找到不同于OLS的估计方法；
如果不相关，则认为不存在联立性问题，可以继续使用OLS方法

豪斯曼设定误差检验 (Hausman specification error test)的一种形式可用于检验联立性问题。

豪斯曼联立性检验又被称为豪斯曼内生性检验 (Hausman test of endogeneity)

检验的原理

给定联立方程：

\[ \begin{align} Q &= \alpha_0+\alpha_1P_t+\alpha_2I_t+\alpha_3R_t+u_{t1} &(\alpha_1<0,\alpha_2>0) &&\text{(需求函数)}\\ Q &= \beta_0+\beta_1P_t+u_{t2} &(\beta_1>0) &&\text{(供给函数)} \end{align} \]

其中： P=价格；I=收入；R=财富

很容易得到约简方程：

\[ \begin{align} P_t &= \pi_{11}+ \pi_{21}I_t + \pi_{31} R_t + v_{t1} &&\text{(约简方程1)}\\ Q_t &= \pi_{12}+ \pi_{22}I_t + \pi_{33} R_t + v_{t2} &&\text{(约简方程2)} \end{align} \]

检验的原理

我们可以直接用OLS方法估计约简方程1（价格方程），得到：

\[ \begin{align} P_t &= \hat{\pi}_{11}+ \hat{\pi}_{21}I_t + \hat{\pi}_{31} R_t + \hat{v}_{t1} &&\text{(价格方程的OLS估计)} \\ &= \hat{P_t} +\hat{v}_{t1} \end{align} \]

进而可以将价格方程的OLS估计结果带入如下检验方程，并做如下的OLS估计：

\[ \begin{align} Q_t &= \beta_0+\beta_1\hat{P_t} + \beta_1 \hat{v}_{t1} +u_{t2} & && \text{(豪斯曼检验方程)}\\ Q_t &= \beta_0+\beta_1 {P_t} + \beta_1\hat{v}_{t1} +u_{t2} & &&\text{(平狄克检验方程)} \\ \end{align} \]

检验的原理

豪斯曼联立性检验下：

原假设$H_0$：无联立性问题，要求$\hat{v}_{t1}$和$u_{t2}$ 不相关；
备择假设$H_1$：有联立性问题，要求$\hat{v}_{t1}$和$u_{t2}$ 相关；

因此，只需要检验方程参数$\beta_1$ 进行检验：

如果$\beta_1$统计上不显著，则不能拒绝原假设$H_0$ ，认为无联立性问题
如果$\beta_1$统计显著，则拒绝原假设$H_0$，接受备择假设$H_1$ ，认为存在联立性问题

内生性检验

因此，豪斯曼检验的步骤包括：

step 1：利用OLS方法，做$P_t = \hat{\pi}_{11}+ \hat{\pi}_{21}I_t + \hat{\pi}_{31} R_t + \hat{v}_{t1}$的回归，得到$\hat{v_t}$
step 2：利用OLS方法，做$Q_t = \beta_0+\beta_1 \hat{P_t} + \beta_1\hat{v}_{t1} +u_{t2}$的回归，并对$\hat{v}_{1t}$的系数进行t检验，并作出联立性问题的判断。需要注意的是，为了更有效地估计，平狄克 (Pindyck) 和鲁宾费尔德 (Rubinfeld) 建议对$Q_t = \beta_0+\beta_1 P_t + \beta_1\hat{v}_{t1} +u_{t2}$ 的回归。

案例：松露市场

结构和约简方程

我们仍旧以松露案例模型为例，给定如下联立方程：

\[ \begin{align} Q_i &= \alpha_0+\alpha_1P_i+\alpha_2PS_i+\alpha_3DI_i+u_{i1} &&\text{(需求函数)}\\ Q_i &= \beta_0+\beta_1P_i+\beta_2PF_i+u_{i2} &&\text{(供给函数)} \end{align} \]

很快可以得到约简方程：

\[ \begin{align} P_i &= \pi_{11}+ \pi_{21}PS_i+\pi_{31}DI_i+\pi_{41}PF_i+v_{i1} \\ Q_i &= \pi_{12}+\pi_{22}PS_t+\pi_{32}DI_t+\pi_{42}PF_i+v_{i2} \end{align} \]

结构和约简系数

其中约简系数和结构系数的关系为：

\[ \begin{cases} \begin{align} & \pi_{11} = \frac{\beta_0-\alpha_0}{\alpha_1-\beta_1}\\ & \pi_{21} = - \frac{\alpha_2}{\alpha_1-\beta_1}\\ & \pi_{31} = - \frac{\alpha_3}{\alpha_1-\beta_1}\\ & \pi_{41} = \frac{\beta_2}{\alpha_1-\beta_1}\\ & v_{i1} = \frac{u_{i2}-u_{i1}}{\alpha_1-\beta_1} \end{align} \end{cases} \]

\[ \begin{cases} \begin{align} & \pi_{12} = - \frac{\alpha_1\beta_0-\alpha_0\beta_1}{\alpha_1-\beta_1} \\ & \pi_{22} = - \frac{\alpha_2\beta_1}{\alpha_1-\beta_1} \\ & \pi_{32} = - \frac{\alpha_3\beta_1}{\alpha_1-\beta_1} \\ & \pi_{42} = \frac{\alpha_1\beta_2}{\alpha_1-\beta_1} \\ & v_{i2} = \frac{\alpha_1u_{i2}-\beta_1u_{i1}}{\alpha_1-\beta_1} \end{align} \end{cases} \]

OLS估计价格方程：约简方程

按照豪斯曼联立性检验的第一个步骤，利用OLS方法回归如下价格约简方程，并得到$\hat{P_i},\hat{v}_{i1}$

\[ \begin{align} P_i & = \hat{\pi}_{11}+ \hat{\pi}_{21} PS_i + \hat{\pi}_{31} DI_i + \hat{\pi}_{41} PF_i + \hat{v}_{i1} \\ & = \hat{P_i} + \hat{v}_{i1} \end{align} \]

OLS估计价格方程：`R`程序报告

约简方程1（价格方程）的原始回归结果报告如下：


Call:
lm(formula = Hausman_models$mod.P, data = truffles)

Residuals:
     Min       1Q   Median       3Q      Max 
-20.4825  -3.5927   0.2801   4.5326  12.9210 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -32.5124     7.9842  -4.072 0.000387 ***
PS            1.7081     0.3509   4.868 4.76e-05 ***
DI            7.6025     1.7243   4.409 0.000160 ***
PF            1.3539     0.2985   4.536 0.000115 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.597 on 26 degrees of freedom
Multiple R-squared:  0.8887,    Adjusted R-squared:  0.8758 
F-statistic: 69.19 on 3 and 26 DF,  p-value: 1.597e-12

OLS估计价格方程：精简报告

约简方程1（价格方程）的精简回归报告如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{P}=&&-32.51&&+1.71PS_i&&+7.60DI_i&&+1.35PF_i\\ &(s)&&(7.9842)&&(0.3509)&&(1.7243)&&(0.2985)\\ &(t)&&(-4.07)&&(+4.87)&&(+4.41)&&(+4.54)\\ &(fit)&&R^2=0.8887&&\bar{R}^2=0.8758 && &&\\ &(Ftest)&&F^*=69.19&&p=0.0000 && && \end{split} \end{alignedat} \]

请解释回归结果？？

OLS估计价格方程：估计得到的变量

进而可以分别估计得到$\hat{P_i},\hat{v}_{i1}$

联立性检验：模型设定

下面，我们继续进行豪斯曼联立性检验的第二个步骤（采用平狄克和鲁宾费尔德的建议），采用OLS方法估计如下豪斯曼检验方程和平狄克检验方程：

\[ \begin{align} Q_i &= \beta_0+\beta_1 \hat{P_i} +\beta_1 \hat{v}_{i1} +u_{i2} &&\text{(豪斯曼检验方程)} \\ Q_i &= \beta_0+\beta_1P_i +\beta_1 \hat{v}_{i1} +u_{i2} &&\text{(平狄克检验方程)} \end{align} \]

因此，我们马上可以得到第二个步骤的检验结果。

豪斯曼检验：原始报告

如果采用豪斯曼检验方程，则有原始报告结果如下：


Call:
lm(formula = Hausman_models$mod.Q.Hausman, data = truffles_Hausman)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.4756 -2.8917  0.2775  3.3937  5.3796 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.94585    2.60369   4.588 9.21e-05 ***
hat.Pi       0.10383    0.04001   2.595  0.01510 *  
hat.vi       0.33801    0.11304   2.990  0.00589 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.803 on 27 degrees of freedom
Multiple R-squared:  0.3673,    Adjusted R-squared:  0.3205 
F-statistic: 7.838 on 2 and 27 DF,  p-value: 0.00207

豪斯曼检验：精简报告

如果采用豪斯曼检验方程，上述精简报告结果如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+11.95&&+0.10hat.Pi_i&&+0.34hat.vi_i\\ &(s)&&(2.6037)&&(0.0400)&&(0.1130)\\ &(t)&&(+4.59)&&(+2.60)&&(+2.99)\\ &(fit)&&R^2=0.3673&&\bar{R}^2=0.3205 &&\\ &(Ftest)&&F^*=7.84&&p=0.0021 && \end{split} \end{alignedat} \]

豪斯曼联立性检验的结论：

-$\hat{v}_{1i}$前的系数等于0.34，$t^{}=2.9901>t{(/2,n-3)}=$2.4726599。(给定$$ )

因此，$\hat{v}_{i1}$前系数的t检验是极显著的(给定$\alpha=0.01$水平下)，从而拒绝原假设$H_0$（无联立性问题），接受备择假设$H_1$ ，认为存在联立性问题。

平狄克检验：原始报告

如果采用平狄克检验方程，则R原始报告结果如下：


Call:
lm(formula = Hausman_models$mod.Q.Pindyck, data = truffles_Hausman)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.4756 -2.8917  0.2775  3.3937  5.3796 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.94585    2.60369   4.588 9.21e-05 ***
P            0.10383    0.04001   2.595   0.0151 *  
hat.vi       0.23418    0.11991   1.953   0.0613 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.803 on 27 degrees of freedom
Multiple R-squared:  0.3673,    Adjusted R-squared:  0.3205 
F-statistic: 7.838 on 2 and 27 DF,  p-value: 0.00207

平狄克检验：精简报告

如果采用平狄克检验方程，可以得到如下精简报告结果：

\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+11.95&&+0.10P_i&&+0.23hat.vi_i\\ &(s)&&(2.6037)&&(0.0400)&&(0.1199)\\ &(t)&&(+4.59)&&(+2.60)&&(+1.95)\\ &(fit)&&R^2=0.3673&&\bar{R}^2=0.3205 &&\\ &(Ftest)&&F^*=7.84&&p=0.0021 && \end{split} \end{alignedat} \]

联立性问题检验结论：

-$\hat{v}_{i1}$前的系数等于0.23，$t^{}=1.9529>t{(/2,n-3)}=$1.7032884。(给定$$)

因此，$\hat{v}_{1i}$前系数的t检验是显著的(给定$\alpha=0.1$水平下)，从而拒绝原假设$H_0$（无联立性问题），接受备择假设$H_1$，认为存在联立性问题

19.4 外生性检验

外生性检验

略

要点与结论1/2

识别问题的考虑应先于估计问题。
识别问题是问我们能否从约简系数估计值求出结构系的唯一数值估计值。
如果能做到，就说联立方程组中的某个方程是可识别的；如果做不到，该方程就是不可识别或识別不足的。
一个可识别的方程可以是恰好识别的或过度识别的。在前一种情形中，可以得到的唯一值；而在后一种情形中，可以得到不止一个估计值。
识別问题之所以出现，是因为同样的数据集适合于不同的的模型。

要点与结论2/2

要判断一个结构方程的可识别性，我们可以应用约简型方程的技术，把一个内生变量表达为前定变量的函数。
这种耗时的程序由于阶条件或秩条件的利用而得以避免。阶条件虽然易用应用，但它仅是可识别性的必要而非充分条件；秩条件则是可识别性的充分必要条件。
当出现联立性问题时，OLS一般而言是不适用的。但如果我们仍想用它，则必须明确地进行联立性检验，为此，可利用豪斯曼内生性检验方法。
虽然在实践中一个变量是内生或外生的，是凭判断而决定的，但我们可以用豪斯曼设定检验判定一个或一组变量是内生的还是外生的。
因果关系和外生性虽属于同一类问题，但它们的概念却是不同的。其中一个概念并不蕴含另一个概念。在实践中，仍然是把这两个概念区分开来为好。

计量经济学II

(Ecnometrics II)

第19章 联立方程模型的识别问题？

胡华平

huhuaping01@hotmail.com

经济管理学院数量经济教研室

2024-09-25

模块4：联立方程模型（SEM）

19.1 识别类型

识别问题的定义

识别问题的演示

联立方程

散点图

供需均衡点

不可识别

能识别出供给曲线

能识别出需求曲线

识别不足

结构方程和约简方程

虚构的一个“混杂”方程

恰好识别

结构方程和约简方程

只有一个方程能恰好识别

过度识别

结构方程

约简方程

存在多个满足条件的解

19.2 识别规则

符号约定

可识别的阶条件

阶条件规则1

阶条件规则2

应用示例：阶条件识别

阶条件1：都不可识别

阶条件2：都不可识别

阶条件1：不可识别+恰好识别

阶条件2：不可识别+恰好识别

阶条件1：恰好识别+过度识别

阶条件2：恰好识别+过度识别

可识别的阶条件：总结

可识别的秩条件

秩条件规则

应用示例：秩条件识别

步骤1：写出代数式2，写出系数列表

步骤2：分析第1个方程的变量数，找到缺失列

步骤3：找1个目标矩阵，计算其行列式

秩条件识别小结

识别练习：其他3个方程是否可识别？

秩条件与阶条件的比较

识别规则的总结

19.3 内生性检验

内生性检验（联立性检验）

概念与定义

检验的原理

检验的原理

检验的原理

内生性检验

案例：松露市场

结构和约简方程

结构和约简系数

OLS估计价格方程：约简方程

OLS估计价格方程：R程序报告

OLS估计价格方程：精简报告

OLS估计价格方程：估计得到的变量

联立性检验：模型设定

豪斯曼检验：原始报告

豪斯曼检验：精简报告

平狄克检验：原始报告

平狄克检验：精简报告

19.4 外生性检验

外生性检验

要点与结论1/2

要点与结论2/2

本章结束

第19章联立方程模型的识别问题？

OLS估计价格方程：`R`程序报告