计量经济学II

(Ecnometrics II)

第18章为什么要关心联立方程模型？

胡华平

huhuaping01@hotmail.com

经济管理学院数量经济教研室

2024-09-25

18.1 联立方程模型的本质

联立方程模型的概念

联立方程模型（simultaneous equations model,SEM）：由多个方程组成的、方程之间存在相互关联的、联合影响的内生变量的方程系统。其基本形式如下：

\[ \begin{cases} \begin{align} Y_{1 i}=\beta_{10}+\gamma_{12} Y_{2 i}+\beta_{11} X_{1 i}+u_{i1} \\ Y_{2 i}=\beta_{20}+\gamma_{21} Y_{1 i}+\beta_{21} X_{1 i}+u_{i2} \end{align} \end{cases} \]

常见的经济模型

需求-供给模型

需求-供给模型：

\[ \begin{align} \text { Demand function: } & {Q_{t}^{d}=\alpha_{0}+\alpha_{1} P_{t}+u_{ t1}, \quad \alpha_{1}<0} \\ {\text { supply function: }} & {Q_{t}^{s}=\beta_{0}+\beta_{1} P_{t}+u_{ t2}, \quad \beta_{1}>0} \\ {\text {Equilibrium condition:}} & {Q_{t}^{d}=Q_{t}^{s}} \end{align} \]

凯恩斯收入决定模型

凯恩斯收入决定模型（Keynesian model of income determination）：

\[ \begin{cases} \begin{align} C_t &= \beta_0+\beta_1Y_t+\varepsilon_t &&\text{(消费函数)}\\ Y_t &= C_t+I_t &&\text{(收入恒等式)} \end{align} \end{cases} \]

IS模型

投资储蓄的IS宏观经济模型：

\[ \begin{align} \text { Consumption function: } & C_{t}=\beta_{0}+\beta_{1} Y_{d t} & <\beta_{1}<1 \\ \text { Tax function: } & T_{t}=\alpha_{0}+\alpha_{1} Y_{t} & \quad 0<\alpha_{1}<1 \\ \text { Investment function: } & I_{t}=\gamma_{0}+\gamma_{1} r_{t} \\ \text { Definition: } & \gamma_{d t}=Y_{t}-T_{t} \\ \text { Government expenditure: } & G_{t}=\bar{G} \\ \text { National income identity: } & Y_{t}=C_{t}+I_{t}+G_{t} \end{align} \]

其中：\(Y\)表示国民收入；\(Y_d\)表示可支配收入；\(r\)表示利率；\(\bar{G}\)表示给定政府支出水平。

LM模型

货币市场均衡的LM宏观经济模型：

\[ \begin{align} {\text { Money demand function: }} & {M_{t}^{d}=a+b Y_{t}-c r_{t}} \\ {\text { Money supply function: }} & {M_{t}^{s}=\bar{M}} \\ {\text { Equilibrium condition: }} & {M_{t}^{d}=M_{t}^{s}} \end{align} \]

其中：\(Y\)表示收入；\(r\)表示利率;\(\bar{M}\)表示给定货币供给量。

克莱因模型

克莱因模型（Llein’s model）：

\[ \begin{align} \text { Consumption function: } & C_{t}=\beta_{0}+\beta_{1} P_{t}+\beta_{2}\left(W+W^{\prime}\right)_{t}+\beta_{3} P_{t-1}+u_{ t1} \\ \text { Investment function: } & I_{t} =\beta_{4}+\beta_{5} P_{t}+\beta_{6} P_{t-1}+\beta_{7} K_{t-1}+u_{ t2} \\ \text { Demand for labor: } & w_{t}= \beta_{8}+\beta_{9}\left(Y+T-W^{\prime}\right)_{t} +\beta_{10}\left(Y+T-W^{\prime}\right)_{t-1}+\beta_{11} t+u_{ t3} \\ \text { Identity: } & Y_{t} = C_{t}+I_{t}+C_{t} \\ \text { Identity: } & Y_{t}=W_{t}^{\prime}+W_{t}+P_{t} \\ \text { Identity: } & K_{t}=K_{t-1}+I_{t} \end{align} \]

其中：\(C\)表示消费支出；\(Y\)表示税后收入；\(P\)表示利润；\(W\)表示个人工资；\(W^{\prime}\)表示政府工资；\(K\)表示资本存货；\(T\)表示税收。

生活中的模型

凶杀犯罪率模型

\[ \begin{align} \operatorname{murdpc} &=\alpha_{1} \operatorname{polpc}+\beta_{10}+\beta_{11} \text {incpc}+u_{1} \\ \text { polpc } &=\alpha_{2} \operatorname{murdpc}+\beta_{20}+\text { other factors. } \end{align} \]

其中：\(murdpc\)表示人均凶杀犯罪数；\(polpc\)表示人均警员数；\(incpc\)表示人均收入。

住房支出-储蓄模型

\[ \begin{align} \text {housing } & =\alpha_{1} \text {saving}+\beta_{10}+\beta_{11} \text {inc}+\beta_{12} e d u c+\beta_{13} \text {age}+u_{1} \\ \text {saving} &=\alpha_{2} \text {housing }+\beta_{20}+\beta_{21} \text {inc}+\beta_{22} e d u c+\beta_{23} \text {age}+u_{2} \end{align} \]

其中：\(housing\)表示住房支出；\(saving\)表示家庭储蓄；\(inc\)表示家庭收入；\(educ\)表示教育水平;\(age\)表示年龄。

联立方程模型的特点

联立方程模型的本质是内生变量问题：

每一个方程都有其经济学因果关系（保持其他条件不变的）
样本数据只是各种变量的最终结果，但其中蕴含复杂相互因果互动关系
特定方程的参数估计，往往跟其他方程有联系
直接使用OLS方法估计参数将会不可靠

案例：松露市场

案例说明

松露是美味的食材。它们是生长在地下的食用菌。我们考虑如下的松露供求模型:

\[ \begin{cases} \begin{align} \text { Demand: } & Q_{di}=\alpha_{1}+\alpha_{2} P_{i}+\alpha_{3} P S_{i}+\alpha_{4} D I_{i}+e_{d i} \\ \text { Supply: } & Q_{si}=\beta_{1}+\beta_{2} P_{i}+\beta_{3} P F_{i}+e_{s i}\\ \text { Equity: } & Q_{di}= Q_{si} \end{align} \end{cases} \]

其中： -\(Q_i=\)某一特定市场上松露的交易量;-\(P_i=\)松露的市场价格;-\(PS_i=\)松露替代物的市场价格;-\(DI_i=\)当地居民每月人均可支配收入;-\(PF_i=\)生产要素的价格，在本例中是搜索松露过程中租用小猪的每小时租金。

变量说明

数据表

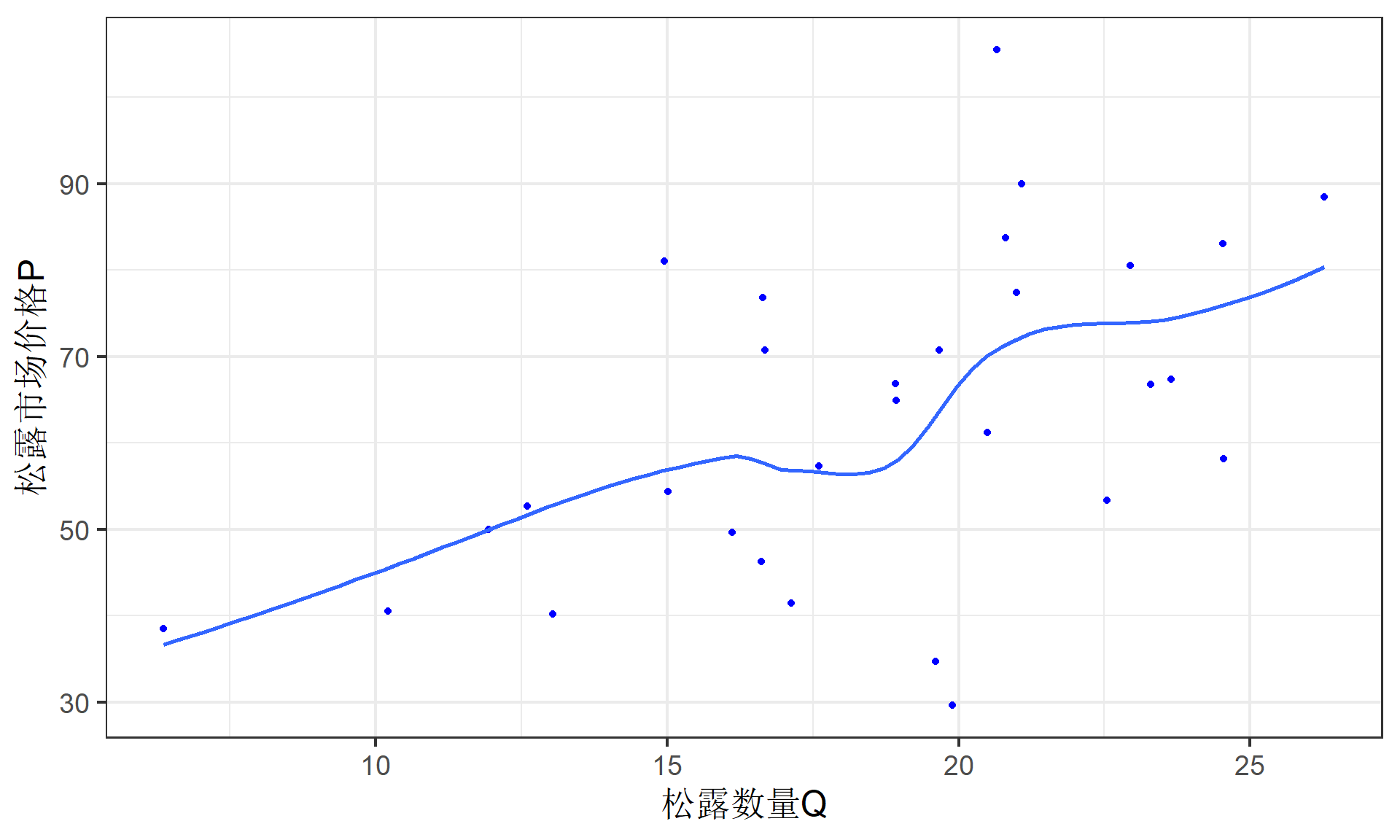
散点图(价格P VS 数量Q)

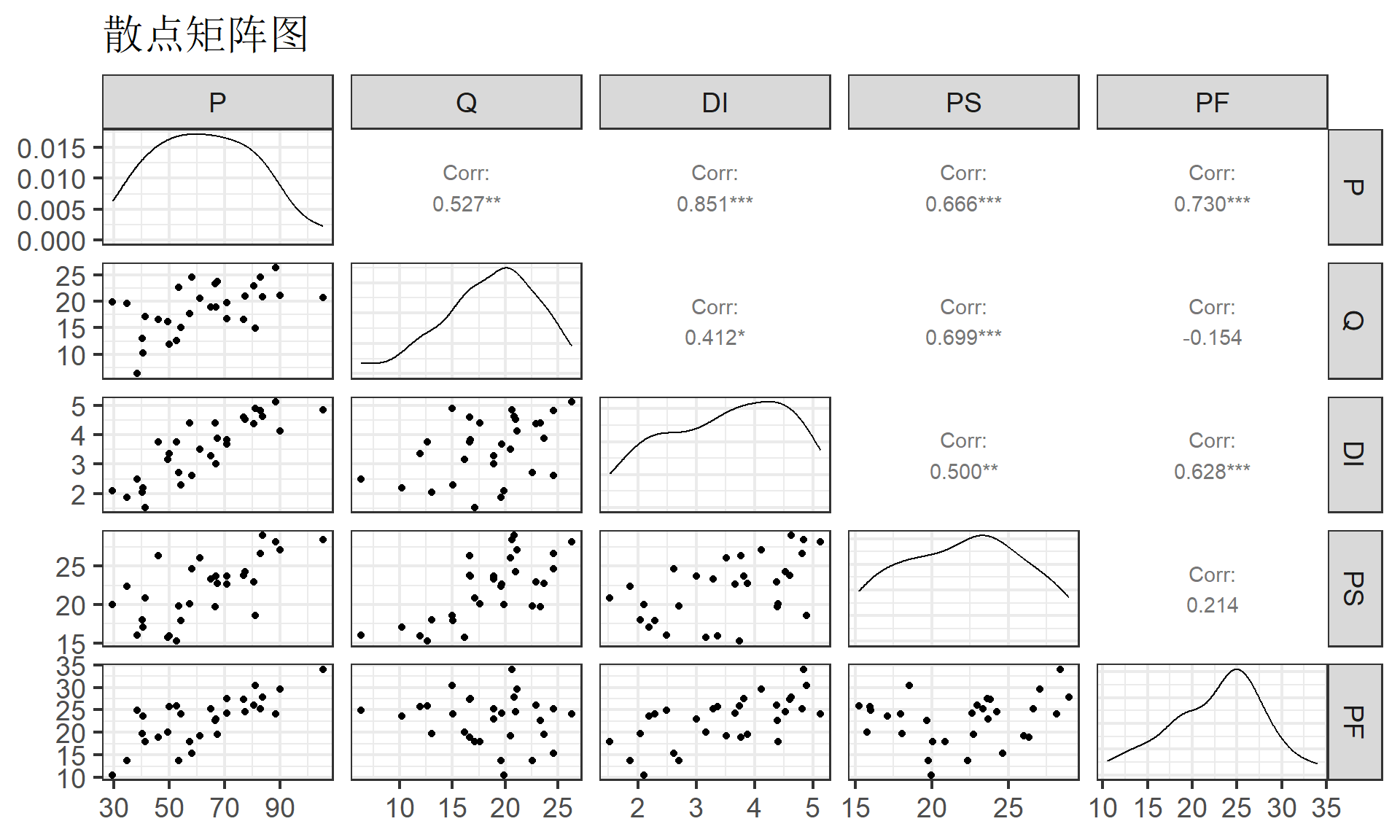
矩阵散点图

简单线性回归：模型设定

从最简单线性回归模型开始。通常我们会使用价格(P)和产量(Q)数据直接做简单线性回归建模：

\[ \begin{align} P & = \hat{\beta}_1+\hat{\beta}_2Q +e_1 && \text{(simple P model)}\\ Q & = \hat{\beta}_1+\hat{\beta}_2P +e_2 && \text{(simple Q model)} \end{align} \]

简单线性回归：估计结果

我们都知道，两个变量的线性回归是不对称的，因此有：

简单的价格(P)模型回归结果如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{P}=&&+23.23&&+2.14Q_i\\ &(s)&&(12.3885)&&(0.6518)\\ &(t)&&(+1.87)&&(+3.28)\\ &(fit)&&R^2=0.2780&&\bar{R}^2=0.2522\\ &(Ftest)&&F^*=10.78&&p=0.0028 \end{split} \end{alignedat} \]

简单的数量(Q)模型回归结果如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+10.31&&+0.13P_i\\ &(s)&&(2.5863)&&(0.0396)\\ &(t)&&(+3.99)&&(+3.28)\\ &(fit)&&R^2=0.2780&&\bar{R}^2=0.2522\\ &(Ftest)&&F^*=10.78&&p=0.0028 \end{split} \end{alignedat} \]

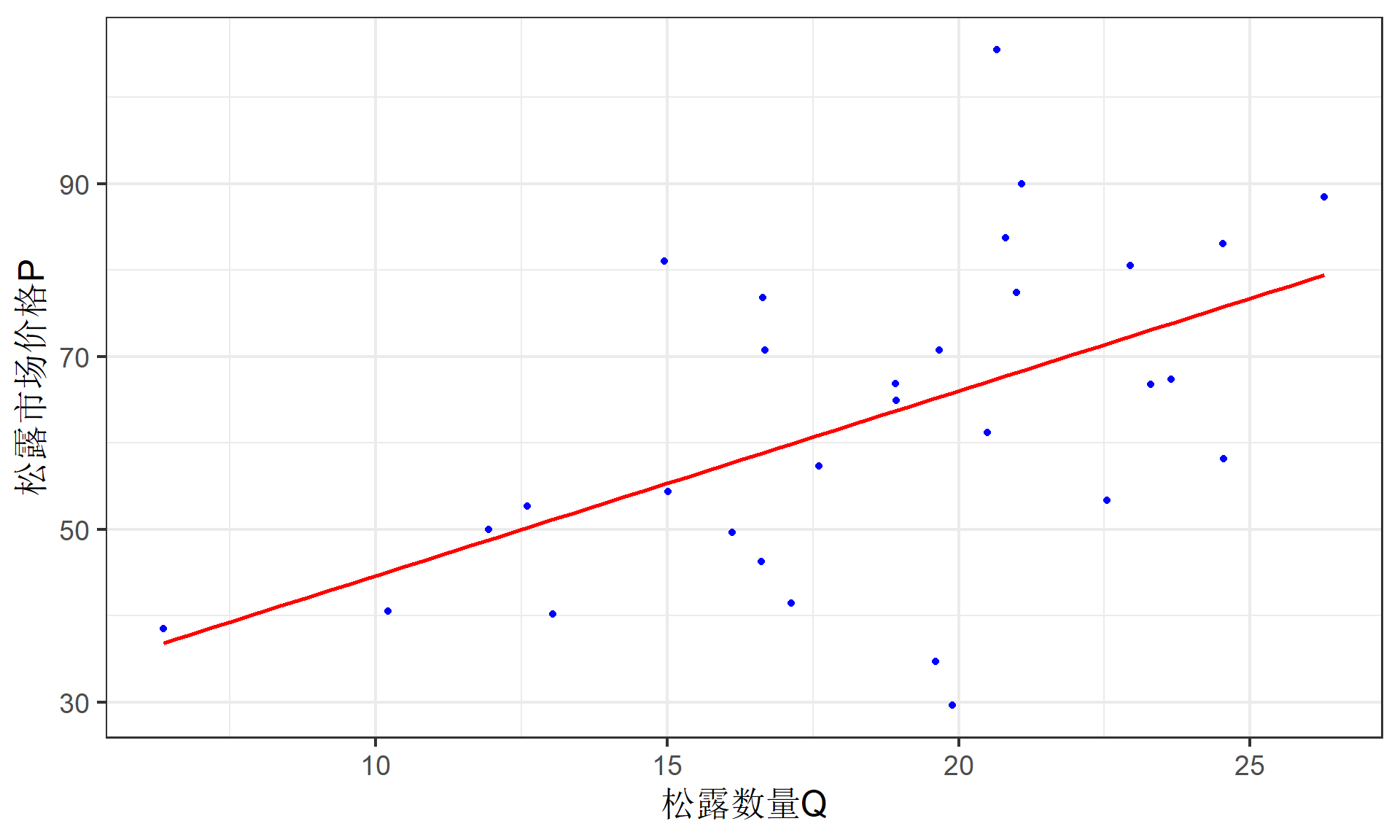
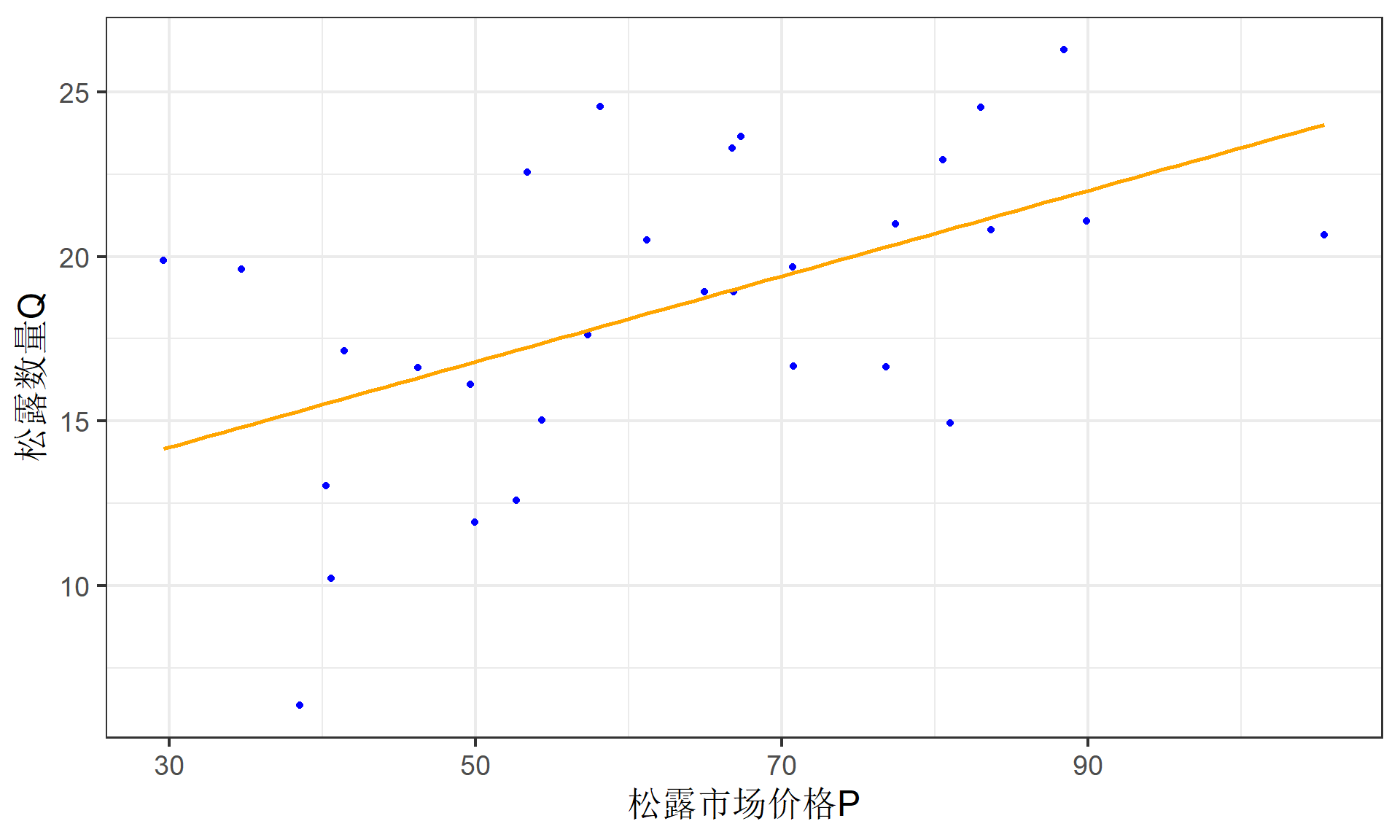
样本回归线

多元线性回归：模型设定

当然，我们也可以继续使用更多的变量作为自变量X，构建如下的回归模型：

\[ \begin{align} P & = \hat{\beta}_1+\hat{\beta}_2Q +\hat{\beta}_3DI+\hat{\beta}_2PS +e_1 && \text{(added P model)}\\ Q & = \hat{\beta}_1+\hat{\beta}_2P +\hat{\beta}_2PF+e_2 && \text{(added Q model)} \end{align} \]

我们努力地想让这些方程更加“合理”、“可信”。

多元线性回归：估计结果

增加变量的价格(P)模型回归结果如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{P}=&&-13.62&&+0.15Q_i&&+12.36DI_i\\ &(s)&&(9.0872)&&(0.4988)&&(1.8254)\\ &(t)&&(-1.50)&&(+0.30)&&(+6.77)\\ &(cont.)&&+1.36PS_i && &&\\ &(s)&&(0.5940) && &&\\ &(t)&&(+2.29) && &&\\ &(fit)&&R^2=0.8013&&\bar{R}^2=0.7784 &&\\ &(Ftest)&&F^*=34.95&&p=0.0000 && \end{split} \end{alignedat} \]

增加变量的数量(Q)模型回归结果如下：

\[ \begin{alignedat}{999} \begin{split} &\widehat{Q}=&&+20.03&&+0.34P_i&&-1.00PF_i\\ &(s)&&(1.2220)&&(0.0217)&&(0.0764)\\ &(t)&&(+16.39)&&(+15.54)&&(-13.10)\\ &(fit)&&R^2=0.9019&&\bar{R}^2=0.8946 &&\\ &(Ftest)&&F^*=124.08&&p=0.0000 && \end{split} \end{alignedat} \]

18.2 联立方程模型的表达和定义

结构化SEM

代数表达（式A）

结构化的SEM(Structural SEM system)：是直接描述经济结构或行为的方程组。

结构化的SEM代数表达式（形式A）可以表达为:

\[ \begin{cases} \begin{alignat}{5} Y_{t1}&= & &+\gamma_{21}Y_{t2}+&\cdots &+\gamma_{m1}Y_{tm} & +\beta_{11}X_{1t}+\beta_{21}X_{t2} &+\cdots+\beta_{k1}X_{tk} &+\varepsilon_{t1} \\ Y_{t2}&=&\gamma_{12}Y_{t1} &+ & \cdots &+\gamma_{m2}Y_{tm}&+\beta_{12}X_{t1}+\beta_{22}X_{t2} &+\cdots+\beta_{k2}X_{tk} &+\varepsilon_{t2}\\ & \vdots &\vdots &&\vdots &&\vdots \\ Y_{tm}&=&\gamma_{1m}Y_{t1}&+\gamma_{2m}Y_{t2}+& \cdots & &+\beta_{1m}X_{t1} +\beta_{2m}X_{t2} &+\cdots+\beta_{km}X_{tk} &+\varepsilon_{tm} \end{alignat} \end{cases} \]

内生变量或联合应变量(m个)：\(Y_{1},Y_{2},\cdots,Y_{m}\)- 前定变量(K个):\(X_{1},X_{2},\cdots,X_{k}\)- 结构随机干扰项(m个):\(\varepsilon_{1},\varepsilon_{2},\cdots,\varepsilon_{m}\)

内生变量系数\(\gamma\)- 前定变量系数\(\beta\)- 观测个数\(t=1,2,\cdots,T\)

结构系数

结构系数(Structural coefficients)：是结构化SEM中的参数，它们反映了经济结果或行为的关系。包括：

内生结构系数:\(\gamma_{11}, \gamma_{21},\cdots, \gamma_{m1}; \cdots; \gamma_{1m}, \gamma_{2m},\cdots, \gamma_{mm}\)

外生结构系数:\(\beta_{11}, \beta_{21},\cdots, \beta_{m1}; \cdots; \beta_{1m}, \beta_{2m},\cdots, \beta_{mm};\)

结构变量

内生变量(Endogenous variables)：由SEM决定的那些变量。
前定变量(Predetermined variables)：那些不由SEM本身在当期（current time period）决定的变量。

内生变量，例如:\(Y_{t1};Y_{t2}; \cdots; Y_{tm}\)

前定变量，例如:\(X_{..}\)

结构随机干扰项(Structural disturbance)：也即结构化SEM系统中的随机干扰项。例如：\(\varepsilon_{t1};\varepsilon_{t2}; \cdots; \varepsilon_{tm}\)

前定变量1/2

前定变量(Predetermined variables)：那些不由SEM本身在当期（current time period）决定的变量。具体又包括：

外生变量(exogenous variables)
滞后内生变量(lagged endogenous variables)

前定变量2/2

外生变量: 那些不被SEM本身决定的变量，它们既不会在当期（current period)被SEM决定，也不是在滞后期(lagged period)被SEM说决定。
滞后内生变量(Lagged en]dogenous variables)：是当期内生变量的滞后变量。

当期外生变量: -\(X_{t1}, X_{t2},\cdots, X_{tk}\).

滞后外生变量: - 变量\(X_{t1}\)的滞后期变量:\(X_{t-1,1}; X_{t-2,1};\cdots; X_{t-(T-1),1}\)- 变量\(X_{tk}\)的滞后期变量:\(X_{t-1,k}; X_{t-2,k};\cdots; X_{t-(T-1),k}\)-\(\cdots\)

滞后内生变量: - 变量\(Y_{t1}\)的滞后变量:\(Y_{t-1,1}; Y_{t-2,1}; \cdots, Y_{t-(T-1),1}\)- 变量\(Y_{tm}\)的滞后变量：\(Y_{t-1,m}; Y_{t-2,m}; \cdots;Y_{t-(T-1),m}\)-\(\cdots\)

前定系数

前定系数(Predetermined coefficients): 是指前定变量前的系数.

例如: - 所有的\(\beta_{..}\)

另一种代数表达（式B）

通过简单的变形，结构化SEM的代数表达式A，可以转换为如下的代数表达式B :

\[ A: \begin{cases} \begin{alignat}{5} Y_{t1}&= & &+\gamma_{21}Y_{t2}+&\cdots &+\gamma_{m1}Y_{tm} & +\beta_{11}X_{1t}+\beta_{21}X_{t2} &+\cdots+\beta_{k1}X_{tk} &+\varepsilon_{t1} \\ Y_{t2}&=&\gamma_{12}Y_{t1} &+ & \cdots &+\gamma_{m2}Y_{tm}&+\beta_{12}X_{t1}+\beta_{22}X_{t2} &+\cdots+\beta_{k2}X_{tk} &+\varepsilon_{t2}\\ & \vdots &\vdots &&\vdots &&\vdots \\ Y_{tm}&=&\gamma_{1m}Y_{t1}&+\gamma_{2m}Y_{t2}+& \cdots & &+\beta_{1m}X_{t1} +\beta_{2m}X_{t2} &+\cdots+\beta_{km}X_{tk} &+\varepsilon_{tm} \end{alignat} \end{cases} \]

.small[

\[ \Rightarrow B: \begin{cases} \begin{alignat}{5} \gamma_{11}Y_{t1} &+ \gamma_{21}Y_{t2}&+\cdots &+\gamma_{m-1,1}Y_{t,m-1} &+\gamma_{m1}Y_{tm} & +\beta_{11}X_{t1}+\beta_{21}X_{t2} &+\cdots+\beta_{k1}X_{tk} &=\varepsilon_{t1} \\ \gamma_{12}Y_{t1} &+\gamma_{22}Y_{t2} &+ \cdots&+\gamma_{m-1,2}Y_{t,m-1} &+\gamma_{m2}Y_{tm}&+\beta_{12}X_{t1}+\beta_{22}X_{t2} &+\cdots+\beta_{k2}X_{tk} &= \varepsilon_{t2}\\ & \vdots &\vdots &&\vdots &&\vdots \\ \gamma_{1m}Y_{t1}&+\gamma_{2m}Y_{t2}&+ \cdots &+\gamma_{m-1,m}Y_{t,m-1} & +\gamma_{mm}Y_{tm} &+\beta_{1m}X_{t1} +\beta_{2m}X_{t2} &+\cdots+\beta_{km}X_{tk} &=\varepsilon_{tm} \end{alignat} \end{cases} \]

]

矩阵表达式1/2

采用矩阵语言(Matrix language)，前述结构化SEM还可以进一步表达为 矩阵形式(matrix expression):

\[ \begin{equation} \begin{bmatrix} Y_1 & Y_2 & \cdots & Y_m \\ \end{bmatrix} _t \begin{bmatrix} \gamma_{11} & \gamma_{12} & \cdots & \gamma_{1m} \\ \gamma_{21} & \gamma_{22} & \cdots & \gamma_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ \gamma_{m1} & \gamma_{m2} & \cdots & \gamma_{mm} \\ \end{bmatrix} + \\ \begin{bmatrix} X_1 & X_2 & \cdots & X_m \\ \end{bmatrix} _t \begin{bmatrix} \beta_{11} & \beta_{12} & \cdots & \beta_{1m} \\ \beta_{21} & \beta_{22} & \cdots & \beta_{2m} \\ \cdots & \cdots & \cdots & \cdots\\ \beta_{k1} & \beta_{k2} & \cdots & \beta_{km} \\ \end{bmatrix} \\ = \begin{bmatrix} \varepsilon_1 & \varepsilon_2 & \cdots & \varepsilon_m \\ \end{bmatrix} _t \end{equation} \]

矩阵表达式2/2

简单起见，我们可以将结构化SEM的矩阵形式一般化记为：

\[ \begin{aligned} & \boldsymbol{y^{\prime}_t} \boldsymbol{\Gamma} &+ & \boldsymbol{x^{\prime}_t} \boldsymbol{B} &= & \boldsymbol{{\varepsilon^{\prime}_t}} \\ &(1 \ast m)(m \ast m) & & (1 \ast k)(k \ast m) & & (1 \ast m) \end{aligned} \]

其中： - 粗体大写英文字母和希腊字母表示矩阵(matrix)

粗体小写英文字母和希腊字母表示列向量(column vector)

内生系数矩阵

对于 内生系数矩阵\(\boldsymbol{\Gamma}\)：

\[ \begin{equation} \boldsymbol{\Gamma} = \begin{bmatrix} \gamma_{11} & \gamma_{12} & \cdots & \gamma_{1m} \\ \gamma_{21} & \gamma_{22} & \cdots & \gamma_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ \gamma_{m1} & \gamma_{m2} & \cdots & \gamma_{mm} \\ \end{bmatrix} \\ \text{if }\Rightarrow \begin{bmatrix} \gamma_{11} & \gamma_{12} & \cdots & \gamma_{1m} \\ 0 & \gamma_{22} & \cdots & \gamma_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & \gamma_{mm} \\ \end{bmatrix} \end{equation} \]

\[ \begin{cases} \begin{aligned} y_{1t} &=& f_{1}\left(\mathbf{x}_{t}\right)+\varepsilon_{t1} \\ y_{2t} &=& f_{2}\left(y_{t1}, \mathbf{x}_{t}\right)+\varepsilon_{t2} \\ & \vdots & \vdots \\ y_{mt} &=& f_{m}\left(y_{t1}, y_{t2}, \ldots, \mathbf{x}_{t}\right)+\varepsilon_{mt} \end{aligned} \end{cases} \]

为了确保每一个方程起码有1个 因变量，则矩阵\(\boldsymbol{\Gamma}\) 的每1列起码要有1个元素含有常数1
如果矩阵\(\boldsymbol{\Gamma}\) 是一个上三角矩阵(upper triangular matrix)，那么SEM将会是一个递归模型(recursive model)系统。
同时，为了保证SEM的参数估计解存在，矩阵\(\boldsymbol{\Gamma}\) 必须是非奇异矩阵(nonsingular matrix).

外生系数矩阵

外生系数矩阵\(\boldsymbol{B}\)：

\[ \begin{equation} \boldsymbol{B} = \begin{bmatrix} \beta_{11} & \beta_{12} & \cdots & \beta_{1m} \\ \beta_{21} & \beta_{22} & \cdots & \beta_{2m} \\ \cdots & \cdots & \cdots & \cdots\\ \beta_{k1} & \beta_{k2} & \cdots & \beta_{km} \\ \end{bmatrix} \end{equation} \]

需要注意的是：SEM系统是有截距的，因此我们要记住外生系数矩阵的第1列都是截距系数。

约简化SEM

代数表达式

约简方程(Reduced equations): 将1个内生变量(endogenous variable)，表达成只包含前定变量(predetermined variables)和随机干扰项的方程。

\[ \begin{cases} \begin{alignat}{5} Y_{t1}&= & +\pi_{11}X_{t1}+\pi_{21}X_{t2} &+\cdots+\pi_{k1}X_{tk} & + v_{t1} \\ Y_{t2}&=&+\pi_{12}X_{t1}+\pi_{22}X_{t2} &+\cdots+\pi_{k2}X_{tk} & + v_{t2}\\ & \vdots &\vdots &&\vdots & \\ Y_{tm}&=&+\pi_{1m}X_{t1} +\pi_{2m}X_{t2} &+\cdots+\pi_{km}X_{tk} & + v_{tm} \end{alignat} \end{cases} \]

上面，我们把结构化方程里的每1个内生变量，都表达为了约简方程，这样的方程系统被称为约简化SEM系统。

约简系数和随机干扰项

约简系数(Reduced coefficients): 也即约简化SEM系统里的所有参数.
约简随机干扰项(Reduced disturbance): 也即约简化SEM系统里随机干扰项

约简系数:

\(\pi_{11},\pi_{21},\cdots, \pi_{k1}\)
\(\pi_{1m},\pi_{2m},\cdots, \pi_{km}\).

约简随机干扰项:

\(v_{1},v_2,\cdots, v_m\)。

矩阵表达式1/2

对于上述代数形式的约简SEM，我们也可以表达为如下矩阵形式的约简SEM:

\[ \begin{equation} \begin{bmatrix} Y_1 & Y_2 & \cdots & Y_m \\ \end{bmatrix} _t = \\ \begin{bmatrix} X_1 & X_2 & \cdots & X_m \\ \end{bmatrix} _t \begin{bmatrix} \pi_{11} & \pi_{12} & \cdots & \pi_{1m} \\ \pi_{21} & \pi_{22} & \cdots & \pi_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ \pi_{m1} & \pi_{m2} & \cdots & \pi_{mm} \\ \end{bmatrix} + \begin{bmatrix} v_1 & v_2 & \cdots & v_m \\ \end{bmatrix} _t \end{equation} \]

矩阵表达式2/2

简单起见，我们可以把矩阵形式的约简SEM，进一步记为：

\[ \begin{aligned} & \boldsymbol{y^{\prime}_t} & = &\boldsymbol{x^{\prime}_t} \boldsymbol{\Pi} & + & \boldsymbol{{v^{\prime}_t}} \\ &(1 \ast m) & & (1 \ast k)(k \ast m) & & (1 \ast m) \end{aligned} \]

约简系数矩阵记为:

\[ \begin{equation} \boldsymbol{\Pi} = \begin{bmatrix} \pi_{11} & \pi_{12} & \cdots & \pi_{1m} \\ \pi_{21} & \pi_{22} & \cdots & \pi_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ \pi_{m1} & \pi_{m2} & \cdots & \pi_{mm} \\ \end{bmatrix} \end{equation} \]

约简随机干扰项记为:

\[ \begin{equation} \boldsymbol{{v^{\prime}_t}}= \begin{bmatrix} v_1 & v_2 & \cdots & v_m \\ \end{bmatrix}_t \end{equation} \]

结构化SEM与约简化SEM的关系

方程系统

显然，我们可以从结构化SEM推导得到约简化SEM:

\[ \Rightarrow\begin{cases} \begin{alignat}{5} Y_{t1}&= & +\pi_{11}X_{t1}+\pi_{21}X_{t2} &+\cdots+\pi_{k1}X_{tk} & + v_{t1} \\ Y_{t2}&=&+\pi_{12}X_{t1}+\pi_{22}X_{t2} &+\cdots+\pi_{k2}X_{tk} & + v_{t2}\\ & \vdots &\vdots &&\vdots & \\ Y_{tm}&=&+\pi_{1m}X_{t1} +\pi_{2m}X_{t2} &+\cdots+\pi_{km}X_{tk} & + v_{tm} \end{alignat} \end{cases} \]

系数关系

对于结构化SEM的矩阵形式：

\[ \begin{aligned} \boldsymbol{y^{\prime}_t} \boldsymbol{\Gamma} + \boldsymbol{x^{\prime}_t} \boldsymbol{B} = \boldsymbol{{\varepsilon^{\prime}_t}} \end{aligned} \]

以及约简化SEM的矩阵形式：

\[ \begin{aligned} \boldsymbol{y^{\prime}_t} = \boldsymbol{x^{\prime}_t} \boldsymbol{\Pi} + \boldsymbol{{v^{\prime}_t}} \end{aligned} \]

不难发现二者系数矩阵存在如下关系:

\[ \begin{align} \boldsymbol{\Pi} &= - \boldsymbol{B} \boldsymbol{\Gamma^{-1}}\\ \boldsymbol{{v^{\prime}_t}} &= \boldsymbol{{\varepsilon^{\prime}_t}} \boldsymbol{\Gamma}^{-1} \end{align} \]

其中:

矩关系(Moments)

下面，我们来关注一下二者随机干扰项的一阶矩和二阶矩，以及它们之间的关系：

首先, 我们假定结构随机干扰项满足如下条件：

\[ \begin{align} \mathbf{E[\varepsilon_t | x_t]} &= \mathbf{0} \\ \mathbf{E[\varepsilon_t \varepsilon^{\prime}_t |x_t]} &= \mathbf{\Sigma} \\ E\left[\boldsymbol{\varepsilon}_{t} \boldsymbol{\varepsilon}_{s}^{\prime} | \mathbf{x}_{t}, \mathbf{x}_{s}\right] &=\mathbf{0}, \quad \forall t, s \end{align} \]

随后，我们将能够证明约简随机干扰项将满足:

\[ \begin{align} E\left[\mathbf{v}_{t} | \mathbf{x}_{t}\right] &=\left(\mathbf{\Gamma}^{-1}\right)^{\prime} \mathbf{0}=\mathbf{0} \\ E\left[\mathbf{v}_{t} \mathbf{v}_{t}^{\prime} | \mathbf{x}_{t}\right] &=\left(\mathbf{\Gamma}^{-1}\right)^{\prime} \mathbf{\Sigma} \mathbf{\Gamma}^{-1}=\mathbf{\Omega} \\ \text{where: }\mathbf{\Sigma} &=\mathbf{\Gamma}^{\prime} \mathbf{\Omega} \mathbf{\Gamma} \end{align} \]

给定样本数据1/2

在给定的样本数据下，我们可以按行来得到数据矩阵（假设总共有\(T\)个样本观测数）:

\[ \begin{align} \left[\begin{array}{lll}{\mathbf{Y}} & {\mathbf{X}} & {\mathbf{E}}\end{array}\right]=\left[\begin{array}{ccc}{\mathbf{y}_{1}^{\prime}} & {\mathbf{x}_{1}^{\prime}} & {\boldsymbol{\varepsilon}_{1}^{\prime}} \\ {\mathbf{y}_{2}^{\prime}} & {\mathbf{x}_{2}^{\prime}} & {\boldsymbol{\varepsilon}_{2}^{\prime}} \\ {\vdots} & {} \\ {\mathbf{y}_{T}^{\prime}} & {\mathbf{x}_{T}^{\prime}} & {\boldsymbol{\varepsilon}_{T}^{\prime}}\end{array}\right] \end{align} \]

那么，结构化SEM可以表达为：

\[ \begin{align} \mathbf{Y} \mathbf{\Gamma}+\mathbf{X} \mathbf{B}=\mathbf{E} \end{align} \]

结构随机干扰项的1阶矩和2阶矩可以表达为:

\[ \begin{align} E[\mathbf{E} | \mathbf{X}] &=\mathbf{0} \\ E\left[(1 / T) \mathbf{E}^{\prime} \mathbf{E} | \mathbf{X}\right] &=\mathbf{\Sigma} \end{align} \]

给定样本数据2/2

假定:

\[ \begin{align} (1 / T) \mathbf{X}^{\prime} \mathbf{X} & \rightarrow \mathbf{Q} \text{ ( a finite positive definite matrix)} \\ (1 / T) \mathbf{X}^{\prime} \mathbf{E} & \rightarrow \mathbf{0} \end{align} \]

那么约简化SEM可以表达为:

\[ \begin{align} \mathbf{Y} & =\mathbf{X} \boldsymbol{\Pi}+\mathbf{V} && \leftarrow \mathbf{V}=\mathbf{E} \mathbf{\Gamma}^{-1} \end{align} \]

此外，我们还可以得到如下一些有用的样本统计量：

\[ \begin{align} \frac{1}{T} \begin{bmatrix} {\mathbf{Y}^{\prime}} \\ {\mathbf{X}^{\prime}} \\ {\mathbf{V}^{\prime}} \end{bmatrix} \begin{bmatrix} {\mathbf{Y}} & {\mathbf{X}} & {\mathbf{V}} \end{bmatrix} \quad \rightarrow \quad \begin{bmatrix} {\mathbf{I}^{\prime} \mathbf{Q} \mathbf{I}+\mathbf{\Omega}} & {\mathbf{I} \mathbf{I}^{\prime} \mathbf{Q}} & {\mathbf{\Omega}} \\ {\mathbf{Q} \mathbf{I}} & {\mathbf{Q}} & {\mathbf{0}^{\prime}} \\ {\mathbf{\Omega}} & {\mathbf{0}} & {\mathbf{\Omega}} \end{bmatrix} \end{align} \]

案例：凯恩斯收入决定模型

结构模型：2方程模型

以凯恩斯收入决定的联立方程为例（结构模型）：

\[ \begin{cases} \begin{align} C_t &= \beta_0+\beta_1Y_t+\varepsilon_t &&\text{(消费函数)}\\ Y_t &= C_t+I_t &&\text{(收入恒等式)} \end{align} \end{cases} \]

上述结构模型中：

内生变量有2个：\(c_t;Y_t\)

前定变量有1个，其中：

外生变量有1个：\(I_t\)
滞后内生变量有0个

思考提问：怎样把这个结构模型转变为约简模型？（考点）

约简方程

上述结构模型，可以变换为为如下约简方程：

\[ \begin{cases} \begin{align} Y_t &=\frac{\beta_0}{1-\beta_1}+\frac{1}{1-\beta_1}I_t+\frac{\varepsilon_t}{1-\beta_1} &&\text{(变换方程1)} \\ C_t &=\frac{\beta_0}{1-\beta_1}+\frac{\beta_1}{1-\beta_1}I_t+\frac{\varepsilon_t}{1-\beta_1} &&\text{(变换方程2)} \end{align} \end{cases} \]

进一步可记为如下约简方程形式：

\[ \begin{cases} \begin{align} Y_t &= \pi_{11}+\pi_{21}I_t+v_{t1} &&\text{(约简方程1)}\\ C_t &= \pi_{12}+\pi_{22}I_t+v_{t2} &&\text{(约简方程2)} \end{align} \end{cases} \]

易知：结构系数共有2个\(\beta_0;\beta_1\)；而约简系数共有4个\(\pi_{11},\pi_{21};\pi_{12},\pi_{22}\)（实际上只有3个！）

约简系数和结构系数

其中约简系数和结构系数的关系为：

\[ \begin{cases} \begin{align} \pi_{11} & = \frac{\beta_0}{1-\beta_1}; & \pi_{12} & = \frac{1}{1-\beta_1} & \\ \pi_{21} & = \frac{\beta_0}{1-\beta_1}; & \pi_{22} & = \frac{\beta_1}{1-\beta_1} \\ v_{t1} & = \frac{\varepsilon_t}{1-\beta_1}; & v_{t2} & = \frac{\varepsilon_t}{1-\beta_1} \end{align} \end{cases} \]

案例：小型宏观经济模型

结构方程：3方程联立模型

考虑如下的小型宏观经济模型（结构方程）：

\[ \begin{cases} \begin{aligned} \text { consumption: } c_{t} &=\alpha_{0}+\alpha_{1} y_{t}+\alpha_{2} c_{t-1}+\varepsilon_{t, c} \\ \text { investment: } i_{t} &=\beta_{0}+\beta_{1} r_{t}+\beta_{2}\left(y_{t}-y_{t-1}\right)+\varepsilon_{t, j} \\ \text { demand: } y_{t} &=c_{t}+i_{t}+g_{t} \end{aligned} \end{cases} \]

内生变量有3个：\(c_t;i_t;Y_t\)

前定变量有4个，其中：

外生变量有2个：\(r_t;g_t\)
滞后内生变量有2个：\(y_{t-1};c_{t-1}\)

结构系数共有6个：\(\alpha_0,\alpha_1,\alpha_2;\beta_0,\beta_1,\beta_2;\)

约简方程

上述结构方程可以变换为如下约简方程：（HOW TO??）

\[ \begin{cases} \begin{align} c_{t} = & [{\alpha_{0}}{\left(1-\beta_{2}\right)}+\beta_{0} \alpha_{1}+\alpha_{1} \beta_{1} r_{t}+\alpha_{1} g_{t}+\alpha_{2}\left(1-\beta_{2}\right) c_{t-1}-\alpha_{1} \beta_{2} y_{t-1} \\ +&\left(1-\beta_{2}\right) \varepsilon_{t, c}+\alpha_{1} \varepsilon_{t, j}] /{\Lambda} \\ i_{t} = & [\alpha_{0} \beta_{2}+\beta_{0}\left(1-\alpha_{1}\right)+\beta_{1}\left(1-\alpha_{1}\right) r_{t}+\beta_{2} g_{t}+\alpha_{2} \beta_{2} c_{t-1}-\beta_{2}\left(1-\alpha_{1}\right) y_{t-1} \\ +&\beta_{2} \varepsilon_{t, c}+\left(1-\alpha_{1}\right) \varepsilon_{t, j}]/{\Lambda} \\ y_{t} = & [\alpha_{0}+\beta_{0}+\beta_{1} r_{t}+g_{t}+\alpha_{2} c_{t-1}-\beta_{2} y_{t-1} +\varepsilon_{t, c}+\varepsilon_{t, j}] /{\Lambda} \end{align} \end{cases} \]

其中：\(\Lambda = 1- \alpha_1 -\beta_2\)。或者将上述约简方程记为：

\[ \begin{cases} \begin{aligned} c_{t} & = \pi_{11} +\pi_{21}r_t +\pi_{31}g_t +\pi_{41}c_{t-1} +\pi_{51}y_{t-1} +v_{t1} \\ i_{t} & = \pi_{12} +\pi_{22}r_t +\pi_{32}g_t +\pi_{42}c_{t-1} +\pi_{52}y_{t-1} +v_{t2} \\ i_{t} & = \pi_{13} +\pi_{23}r_t +\pi_{33}g_t +\pi_{43}c_{t-1} +\pi_{53}y_{t-1} +v_{t3} \end{aligned} \end{cases} \]

易知约简系数共有15个！！

思考

思考：

结构方程和约简方程有什么用？

（结构方程中的）消费函数，利率\(i_t\)不会对消费\(c_t\)产生影响？
从约简方程中则可以很快得到答案\(\frac{\Delta c_t}{\Delta r_t} = \frac{\alpha_1 \beta_1}{\Lambda}\)

（结构方程中的）消费函数，收入\(y_t\)对消费\(c_t\)产生影响，具体是来自什么原因？
进行中介变换也容易得到答案\(\frac{\Delta c_t}{ \Delta y_t} = \frac{\Delta c_t / \Delta r_t}{\Delta y_t / \Delta r_t} = \frac{\alpha_1 \beta_1 / \Lambda}{ \beta_1 / \Lambda} = \alpha_1\)

约简方程的矩阵形式

因为约简方程的矩阵形式可以表达为：

\[ \begin{aligned} \boldsymbol{y^{\prime}_t} = &-\boldsymbol{x^{\prime}_t} \boldsymbol{\Pi} + \boldsymbol{{v^{\prime}_t}} = -\boldsymbol{x^{\prime}_t} \boldsymbol{B} \boldsymbol{\Gamma^{-1}} + \boldsymbol{{\varepsilon^{\prime}_t}} \boldsymbol{\Gamma}^{-1} \end{aligned} \]

容易得到如下相关矩阵：

\[ \begin{align} \mathbf{y}^{\prime} & = \begin{bmatrix} c & i & y \end{bmatrix}\\ \mathbf{x}^{\prime} & = \begin{bmatrix} 1 & r & g & c_{-1} & y_{-1} \end{bmatrix} \end{align} \]

\[ \begin{align} \mathbf{B}= \begin{bmatrix} {-\alpha_{0}} & {-\beta_{0}} & {0} \\ {0} & {-\beta_{1}} & {0} \\ {0} & {0} & {-1} \\ {-\alpha_{2}} & {0} & {0} \\ {0} & {\beta_{2}} & {0} \end{bmatrix} \end{align} \]

\[ \begin{align} \Gamma &= \begin{bmatrix} {1} & {0} & {-1} \\ {0} & {1} & {-1} \\ {-\alpha_{1}} & {-\beta_{2}} & {1} \end{bmatrix} \\ \mathbf{\Gamma}^{-1} &=\frac{1}{\Lambda} \begin{bmatrix} {1-\beta_{2}} & {\beta_{2}} & {1} \\ {\alpha_{1}} & {1-\alpha_{1}} & {1} \\ {\alpha_{1}} & {\beta_{2}} & {1} \end{bmatrix} \end{align} \]

约简系数与结构系数

根据约简方程的矩阵表达式：

根据前述计算结果，则可以得到约简系数与结构系数的关系为：

\[ \begin{align} \boldsymbol{\Pi}^{\prime}=\frac{1}{\Lambda} \begin{bmatrix} {\alpha_{0}\left(1-\beta_{2}\right)+\beta_{0} \alpha_{1}} & {\alpha_{1} \beta_{1}} & {\alpha_{1}} & {\alpha_{2}\left(1-\beta_{2}\right)} & {-\beta_{2} \alpha_{1}} \\ {\alpha_{0} \beta_{2}+\beta_{0}\left(1-\alpha_{1}\right)} & {\beta_{1}\left(1-\alpha_{1}\right)} & {\beta_{2}} & {\alpha_{2} \beta_{2}} & {-\beta_{2}\left(1-\alpha_{1}\right)} \\ {\alpha_{0}+\beta_{0}} & {\beta_{1}} & {1} & {\alpha_{2}} & {-\beta_{2}} \end{bmatrix} \end{align} \]

其中：\(\Lambda = 1- \alpha_1 -\beta_2\)。

难点：矩阵的逆的计算。

掌握了就是快刀一把，手起刀落，麻利干脆！

附录

逆矩阵求解方法和步骤

A.用初等行运算（高斯－若尔当）来求逆矩阵：

构造增广矩阵
对增广矩阵进行多次变换，直至达到目标。

B.用余子式、代数余子式和伴随来求逆矩阵

计算余子式矩阵和代数余子式矩阵
计算伴随矩阵：就是代数余子式矩阵的转置
计算原矩阵行列式：原矩阵顶行的每个元素乘以其对应”代数余子式矩阵”顶行元素。
计算得出逆矩阵：1/行列式 X 伴随矩阵

18.3 OLS估计方法还合适么？

内生变量问题

违背CLRM假设

以凯恩斯收入决定模型为例，我们将可以证明\(Y_t\)和\(u_t\)将会出现相关，从而违背CLRM假设。

\[ \begin{cases} \begin{align} C_t &= \beta_0+\beta_1Y_t+u_t &(0<\beta_1<1) &&\text{(消费函数)}\\ Y_t &= C_t+I_t & &&\text{(收入恒等式)} \end{align} \end{cases} \]

将上述结构方程进行变换，得到：

\[ \begin{align} Y_t &= \beta_0+\beta_1Y_t+ I_t +u_t \\ Y_t &= \frac{\beta_0}{1-\beta_1}+\frac{1}{1-\beta_1}I_t+\frac{1}{1-\beta_1}u_t && \text{(式1：约简方程)}\\ E(Y_t)&=\frac{\beta_0}{1-\beta_1}+\frac{1}{1-\beta_1}I_t && \text{(式2：两边取期望)} \end{align} \]

无法得到BLUE

进一步地：

\[ \begin{align} Y_t - E(Y_t)& = \frac{u_t}{1-\beta_1} && \text{(式1 - 式2)}\\ u_t-E(u_t) &= u_t && \text{(式3：期望等于0)} \\ cov(Y_t,u_t) &= E([Y_t-E(Y_t)][u_t-E(u_t)]) && \text{(式4：协方差定义式)}\\ &=\frac{E(u^2_t)}{1-\beta_1} && \text{(式5：方差定义式)}\\ &=\frac{\sigma^2}{1-\beta_1}\neq 0 && \text{(式6：方差不为0)} \end{align} \]

因此，凯恩斯模型的需求方程，将会不满足CLRM假设中\(Y_t\)与\(u_t\)不相关的假设。从而使用OLS方法对需求方程不能得到最优线性无偏估计量（BLUE）。

系数的OLS估计量是有偏的

下面将进一步证明，使用OLS方法估计\(\beta_1\)是有偏的，也即\(E(\hat{\beta}_1) \neq \beta_1\)。证明过程如下：

\[ \begin{cases} \begin{align} C_t &= \beta_0+\beta_1Y_t+u_t &(0<\beta_1<1) &&\text{(消费函数)}\\ Y_t &= C_t+I_t & &&\text{(收入恒等式)} \end{align} \end{cases} \]

\[ \begin{align} \hat{\beta}_1 = \frac{\sum{c_ty_t}}{\sum{y^2_t}} = \frac{\sum{C_ty_t}}{\sum{y^2_t}} = \frac{\sum{\left [ (\beta_0+\beta_1Y_t+u_t)y_t \right ]}}{\sum{y^2_t}} = \beta_1 + \frac{\sum{u_ty_t}}{\sum{y^2_t}} && \text{(式1)} \end{align} \]

对式1两边取期望，因此有：

\[ \begin{align} E(\hat{\beta}_1) &= \beta_1 + E \left ( \frac{\sum{u_ty_t}}{\sum{y^2_t}} \right ) \end{align} \]

问题是：\(E \left ( \frac{\sum{u_ty_t}}{\sum{y^2_t}} \right )\) 是否等于0？我们可以证明它将不等于0（证明过程见后）。

附录

证明附录1/2

\[ \begin{align} \frac{\sum{c_ty_t}}{\sum{y^2_t}} &= \frac{\sum{(C_t-\bar{C})(Y_t - \bar{Y})}}{\sum{y^2_t}} = \frac{\sum{(C_t-\bar{C})y_t}}{\sum{y^2_t}} \\ & =\frac{\sum{C_ty_t}-\sum{\bar{C}y_t}}{\sum{y^2_t}} =\frac{\sum{C_ty_t}-\sum{\bar{C}(Y_t- \bar{Y})}}{\sum{y^2_t}} \\ & = \frac{\sum{C_ty_t}-\bar{C}\sum{Y_t}- \sum{\bar{C}\bar{Y}}}{\sum{y^2_t}} = \frac{\sum{C_ty_t}-\bar{C}\sum{Y_t}- n{\bar{C}\bar{Y}}}{\sum{y^2_t}} = \frac{\sum{C_ty_t}}{\sum{y^2_t}} \end{align} \]

\[ \begin{align} \hat{\beta_1} & = \frac{\sum\left(\beta_{0}+\beta_{1} Y_{t}+u_{t}\right) y_{t}}{\sum y_{t}^{2}} = \frac{\sum{\beta_{0}y_t} +\sum{\beta_1Y_ty_t}+\sum{u_{t}y_t} }{\sum y_{t}^{2}} \\ & = \frac{\beta_1\sum{(y_t+\bar{Y})y_t}+\sum{u_{t}y_t} }{\sum y_{t}^{2}} =\beta_{1}+\frac{\sum y_{t} u_{t}}{\sum y_{t}^{2}} \end{align} \]

\[ \begin{align} \Leftarrow &\sum{y_t} =0 ; && \frac{\sum{Y_ty_t}}{y^2_t} = 1 \end{align} \]

证明附录2/2

依概率取极限：

\[ \begin{align} \operatorname{plim}\left(\hat{\beta}_{1}\right) &=\operatorname{plim}\left(\beta_{1}\right)+\operatorname{plim}\left(\frac{\sum y_{t} u_{t}}{\sum y_{t}^{2}}\right) \\ &=\operatorname{plim}\left(\beta_{1}\right)+\operatorname{plim}\left(\frac{\sum y_{t} u_{t} / n}{\sum y_{t}^{2} / n}\right) =\beta_{1}+\frac{\operatorname{plim}\left(\sum y_{t} u_{t} / n\right)}{\operatorname{plim}\left(\sum y_{t}^{2} / n\right)} \end{align} \]

而我们已经证明过：

\[ \begin{align} cov(Y_t,u_t) &= E([Y_t-E(Y_t)][u_t-E(u_t)]) =\frac{E(u^2_t)}{1-\beta_1} =\frac{\sigma^2}{1-\beta_1}\neq 0 \end{align} \]

因此，\(E \left ( \frac{\sum{u_ty_t}}{\sum{y^2_t}} \right ) \neq 0\)得证。

数值模拟

人为控制的总体

\[ \begin{align} C_t &= \beta_0+\beta_1Y_t+u_t &(0<\beta_1<1) &&\text{(消费函数)}\\ Y_t &= C_t+I_t & &&\text{(收入恒等式)} \end{align} \]

\[ \begin{align} C_t &= 2+ 0.8Y_t+u_t &(0<\beta_1<1) &&\text{(消费函数)}\\ Y_t &= C_t+I_t & &&\text{(收入恒等式)} \end{align} \]

人为控制的总体被设置为：

\(\beta_0=2, \beta_1=0.8, I_t \leftarrow \text{给定值}\)
\(E(u_t)=0, var(u_t)=\sigma^2=0.04\)
\(E(u_tu_{t+j})=0,j \neq 0\)
\(cov(u_t,I_t)=0\)

模拟数据集

给定条件下的模拟数据为：

手工计算

根据前述公式，可以计算得到回归系数：

容易计算出：\(\sum{u_ty_t}\) =3.8000

以及:\(\sum{y^2_t}\) =184.0000

以及：\(\frac{\sum{u_ty_t}}{\sum{y^2_t}}\) =0.0207

因此：\(\hat{\beta}_1 = \beta_1 + \frac{\sum{u_ty_t}}{\sum{y^2_t}}\) =0.8+0.0207= 0.8207

这也意味着：\(\hat{\beta_1}\)比真值\(\beta_1=0.8\) 有0.0207的偏差。

散点图

回归报告：R报告

下面我们利用模拟的数据，进行回归分析，得到原始报告：


Call:
lm(formula = mod_monte$mod.C, data = monte)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.27001 -0.15855 -0.00126  0.09268  0.46310 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.49402    0.35413   4.219 0.000516 ***
Y            0.82065    0.01434  57.209  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.1946 on 18 degrees of freedom
Multiple R-squared:  0.9945,    Adjusted R-squared:  0.9942 
F-statistic:  3273 on 1 and 18 DF,  p-value: < 2.2e-16

回归报告：四行式整理

下面我们对原始报告进行整理，得到精简报告：

\[ \begin{alignedat}{999} \begin{split} &\widehat{C}=&&+1.49&&+0.82Y_i\\ &(s)&&(0.3541)&&(0.0143)\\ &(t)&&(+4.22)&&(+57.21)\\ &(fit)&&R^2=0.9945&&\bar{R}^2=0.9942\\ &(Ftest)&&F^*=3272.87&&p=0.0000 \end{split} \end{alignedat} \]

这样直接OLS回归的结果也表明是有偏的。

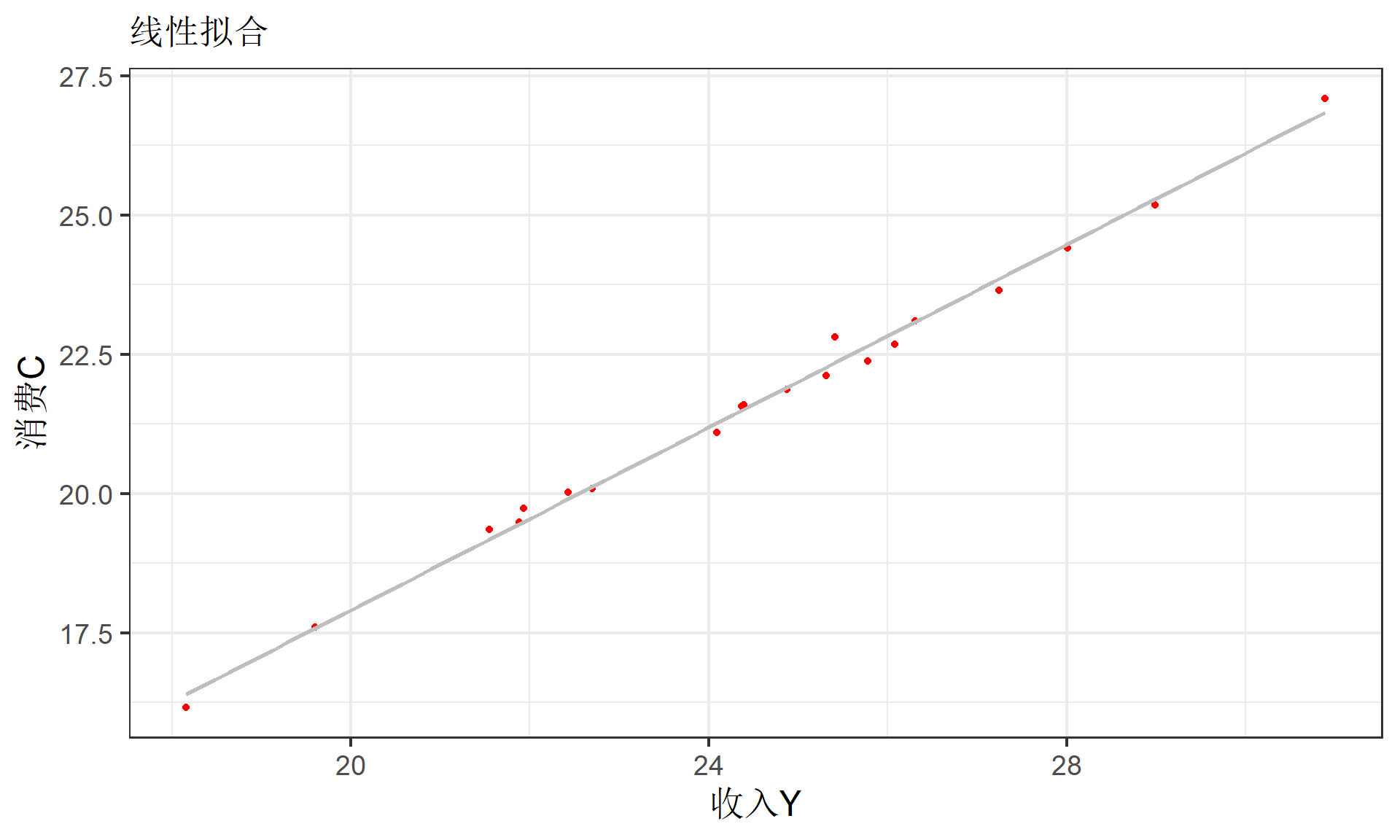
样本回归线

这是样本回归线：

本章小结

结论和要点

与单方程模型对比，联立方程模型涉及多于一个因变量或内生变量，从而有多少个内生变量就需要有多少个方程。
联立方程模裂的一个特有性质是，一个方程中的内生变量(即回归子)作为解释变量而出现在方程组的另一个方程之中。
这使得内生解释变量变成了随机的，而且常常和它作为解释变量所在方程中的误差项有相关关系。
在这种情况下，经典OLS未必适用，因为这样得到的估计量是不一致的。就是说，不管样本容量有多大，这些估计量都不会收敛于其真实总体值
凯恩斯模型的蒙特卡洛模拟，说明了当一个回归方程中的回归元与干扰项相关时(这正是联立方程模型的典型情况) ，用OLS方法估计其参数会内在地导致偏误。

计量经济学II

(Ecnometrics II)

第18章 为什么要关心联立方程模型？

胡华平

huhuaping01@hotmail.com

经济管理学院数量经济教研室

2024-09-25

18.1 联立方程模型的本质

联立方程模型的概念

常见的经济模型

需求-供给模型

凯恩斯收入决定模型

IS模型

LM模型

克莱因模型

生活中的模型

凶杀犯罪率模型

住房支出-储蓄模型

联立方程模型的特点

案例：松露市场

案例说明

变量说明

数据表

散点图(价格P VS 数量Q)

矩阵散点图

简单线性回归：模型设定

简单线性回归：估计结果

样本回归线

多元线性回归：模型设定

多元线性回归：估计结果

18.2 联立方程模型的表达和定义

结构化SEM

代数表达（式A）

结构系数

结构变量

前定变量1/2

前定变量2/2

前定系数

另一种代数表达（式B）

矩阵表达式1/2

矩阵表达式2/2

内生系数矩阵

外生系数矩阵

约简化SEM

代数表达式

约简系数和随机干扰项

矩阵表达式1/2

矩阵表达式2/2

结构化SEM与约简化SEM的关系

方程系统

系数关系

矩关系(Moments)

给定样本数据1/2

给定样本数据2/2

案例：凯恩斯收入决定模型

结构模型：2方程模型

约简方程

约简系数和结构系数

案例：小型宏观经济模型

结构方程：3方程联立模型

约简方程

思考

约简方程的矩阵形式

约简系数与结构系数

附录

逆矩阵求解方法和步骤

18.3 OLS估计方法还合适么？

内生变量问题

违背CLRM假设

无法得到BLUE

系数的OLS估计量是有偏的

附录

证明附录1/2

证明附录2/2

数值模拟

人为控制的总体

模拟数据集

手工计算

散点图

回归报告：R报告

第18章为什么要关心联立方程模型？