计量经济学II
(Ecnometrics II)
第17章 内生性问题与工具变量法
胡华平
huhuaping01@hotmail.com
经济管理学院数量经济教研室
2024-09-25
17.1 内生自变量问题
CLRM假设A2
对于总体回归模型:
\[ \begin{align} Y_i &= \beta_1 +\beta_2X_i + u_i && \text{(PRM)} \end{align} \]
- 在CLRM假设下:CLRM假设A2——X是固定的(给定的)或独立于误差项。也即自变量X不是随机变量。也即:
\[ \begin{align} Cov(X_i, u_i)= 0\\ E(X_i u_i)= 0 \end{align} \]
此时,我们可以使用OLS方法,并得到BLUE。
放宽/违背CLRM假设A2
对于总体回归模型:
\[ \begin{align} Y_i &= \beta_1 +\beta_2X_i + u_i && \text{(PRM)} \end{align} \]
- 如果违背上述假设,也即自变量X与随机干扰项相关。
\[ \begin{align} Cov(X_i, u_i) \neq 0\\ E(X_i u_i) \neq 0 \end{align} \]
此时使用OLS估计将不再能得到BLUE,而应该采用工具变量法(IV)进行估计。
事实上,无论\(X_i\)与\(u_i\)是否相关,我们都可以采用IV法得到BLUE。
好模型的标准
随机控制实验
\[ \begin{equation} \boldsymbol{y= X \beta+u} \end{equation} \]
随机控制实验(randomized controlled experiment):理想情形下,自变量X的取值是随机分配变化的(原因),然后我们再来观测因变量Y的变化(结果)。
如果\(Y_i\)和\(X_i\)确实存在系统性的关系(线性关系),那么改变\(X_i\)则导致\(Y_i\)的相应变化。
除此之外的任何其他随机因素,都将放到随机干扰项 \(u_i\)中,它对因变量\(Y_i\)的变动影响,应该是独立于\(X_i\)的影响作用的。
外生自变量
外生自变量(exogenous regressors):如果自变量 \(X_i\)真的是如上所说的完美的随机取值(randomly assigned),则称之为外生自变量。更准确地,可以定义为:
严格外生性假设(strictly exogeneity): \(E\left(u_{i} \mid X_{1}, \ldots, X_{N}\right)=E\left(u_{i} \mid \mathbf{x}\right)=0\)。
因为在随机控制实验,给定样本 \(i\)和样本 \(j\),自变量的取值分别为 \(X_i\)和 \(X_j\),它们应该是相互独立的。因此可以把上述假设进一步简化为:
同期外生性假设(contemporaneously exogeneity): \(E(u_i|X_{i})=0, \text{for } i =1, \ldots,N\)。
大样本情况下OLS方法
在大样本情形下,上述严格外生性假设可以进一步转换为同期不相关假设:
\(E(u_i)=0\),而且
\(\operatorname{cov}(X_i, u_i)=0\)
因为我们可以证明(证明略),在大样本情况OLS方法下:
\(E(u_i|X_{i})=0 \quad \Rightarrow \quad E(u_i)=0\)
\(E(u_i|X_{i})=0 \quad \Rightarrow \quad \operatorname{cov}(X_i, u_i)=0\)
内生自变量问题的定义
\[ \begin{equation} \boldsymbol{y= X \beta+u} \end{equation} \]
在经典线性回归模型假设(CLRM)中,我们假设所有回归元 \(X_{i}\)是给定的,且随机干扰项的条件期望为0( \(E(u_i|X_{i})=0\))。
回归元是严格外生性具有重要意义,因为理论上将表明模型的预测误差将是最小的(等于0)
实际上,我们的这一假设要求非常高,在随机控制实验中要求 \(X_{ki}\)是同期外生性的 \(E(u_i|X_{i})=0, \text{for } i =1, \ldots,N\)。
然而,现实中,回归元 \(X_{i}\)可能是随机的;而且回归元与随机干扰项可以能是相关的。此时,我们称模型存在内生自变量(endogenous regressors)问题。正式地:
如果自变量与随机干扰项无关,则称之为外生变量(.red[ex]ogenous)
如果自变量与随机干扰项相关,则称之为内生变量(.red[en]dogenous)。
引发内生自变量问题的4种情形
在应用计量经济学中,内生性通常以以下四种方式之一出现:
遗漏变量(Omitted variables)
测量误差(Measurement errors)
自相关问题(Autocorrelation)
方程联立性问题(Simultaneity)
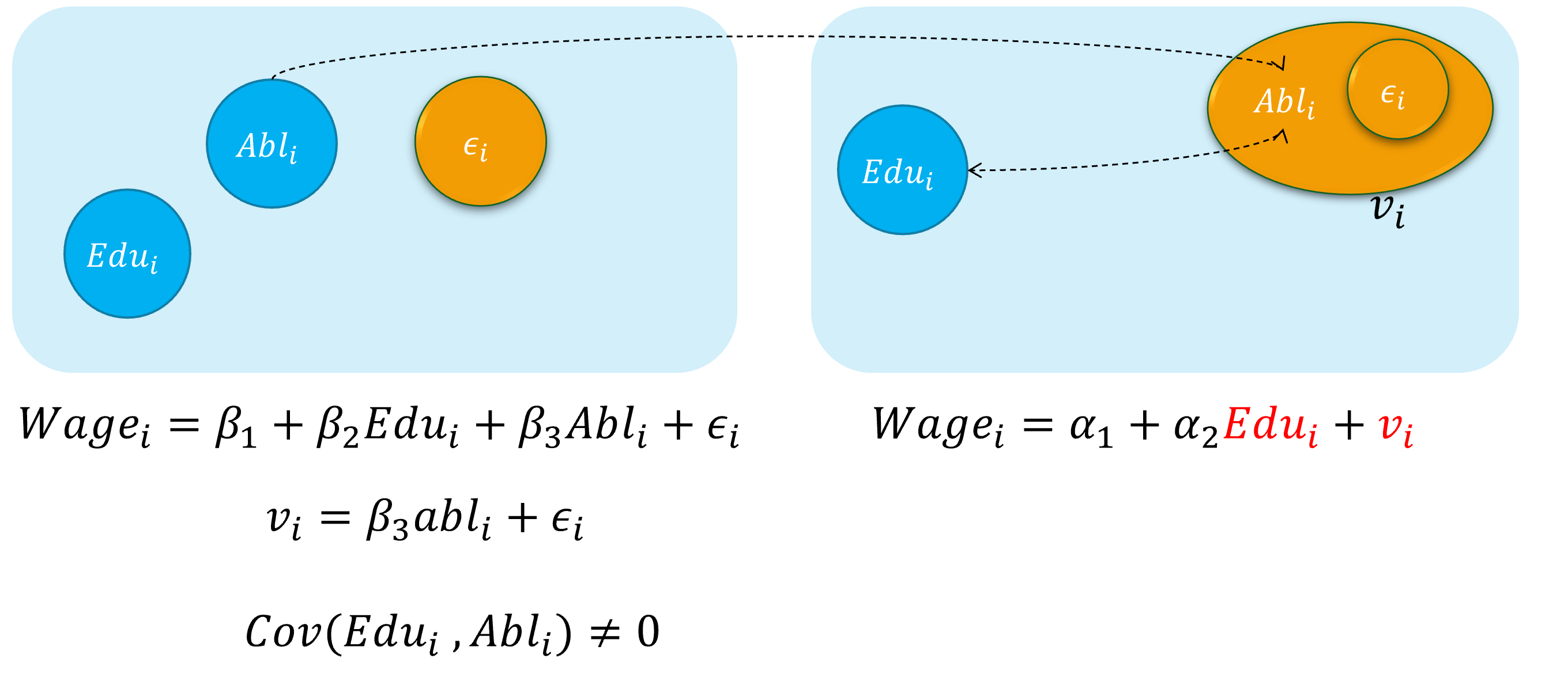
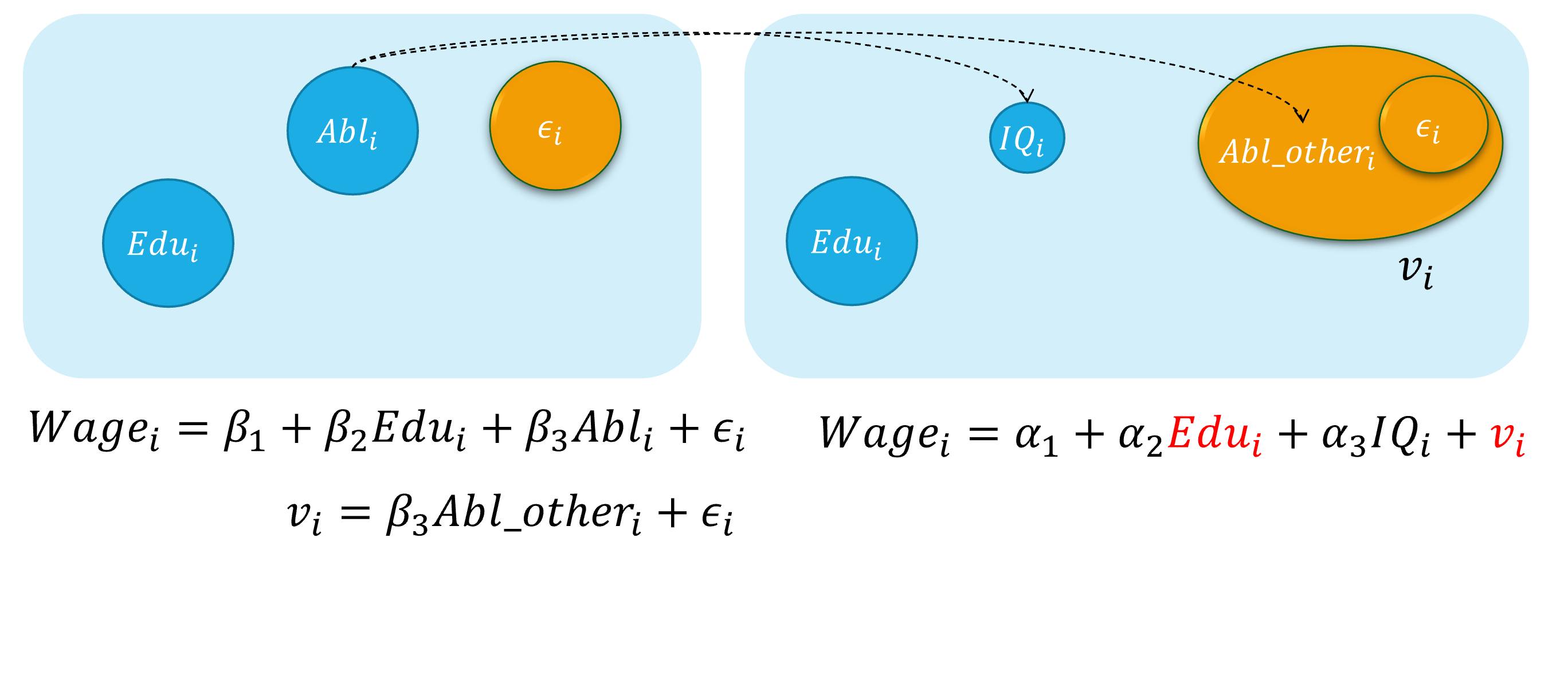
内生自变量情形1:遗漏变量
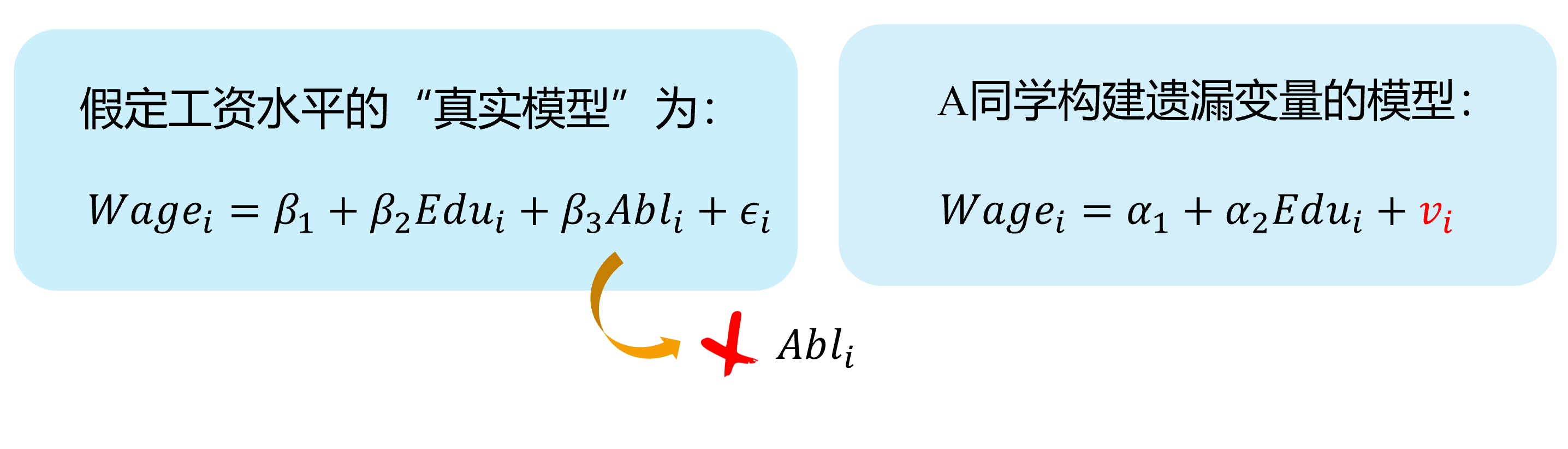
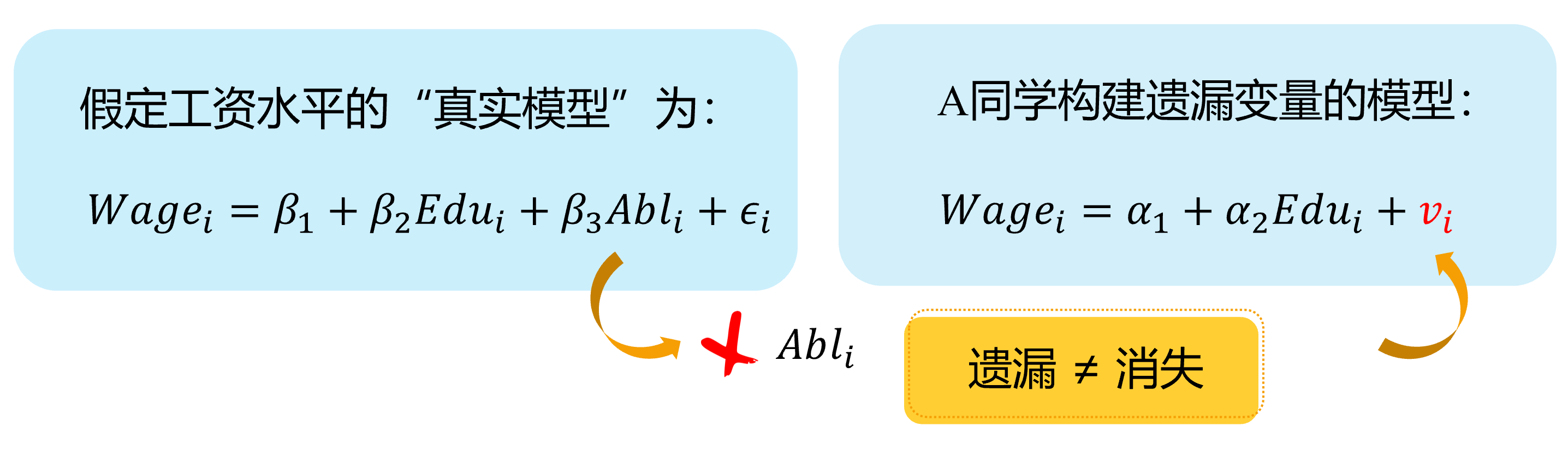
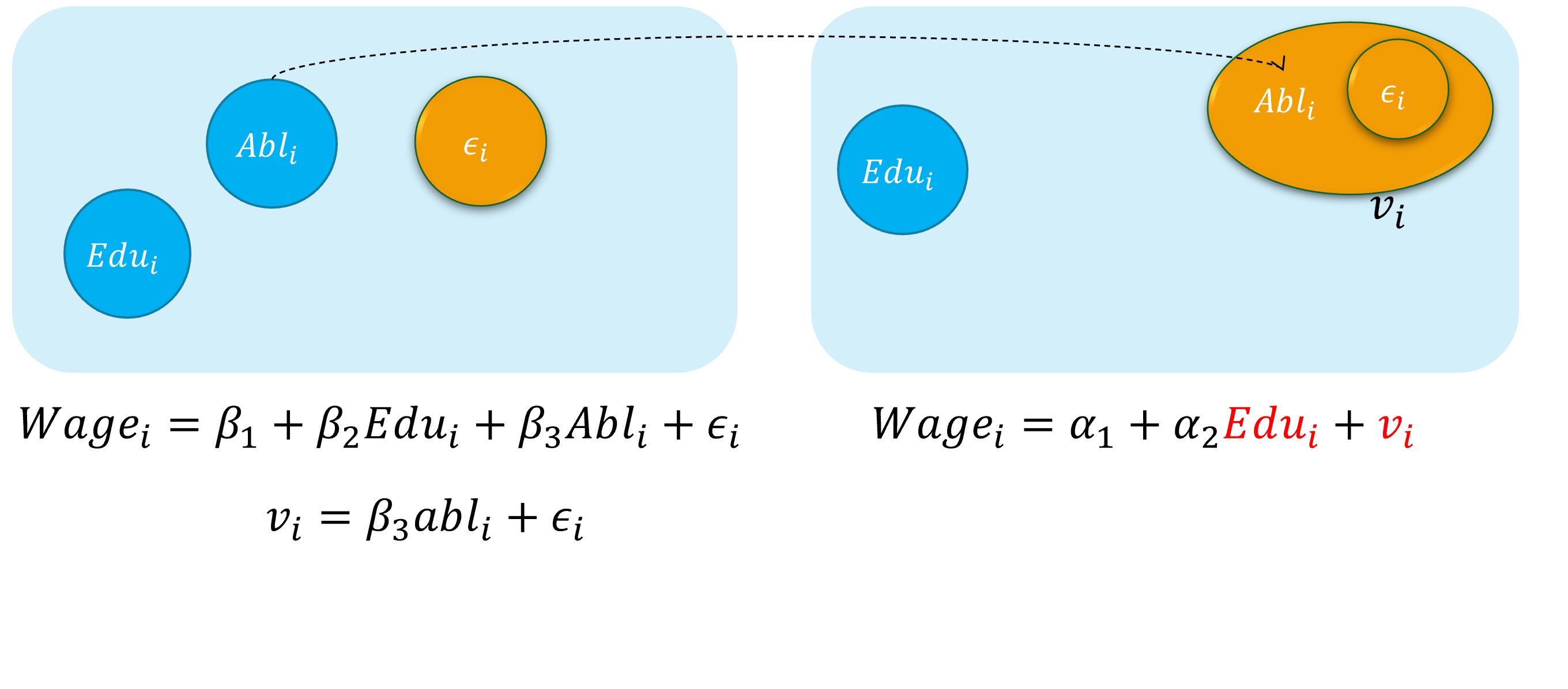
假定假定工资水平的“真实模型”为:
\[ \begin{align} Wage_{i}=\beta_{1}+\beta_{2} Edu_{i}+\beta_{3} Abl_{i}+\epsilon_{i} \quad \text{(the assumed true model)} \end{align} \]
然而,因为个体的能力变量 \(Abl\) 往往无法直接观测得到,因此我们往往不能放入到模型中,并构建了一个有偏误的模型。
\[ \begin{align} Wage_{i}=\alpha_{1}+\alpha_{2} Edu_{i}+v_{i} \quad \text{(the error specified model)} \end{align} \]
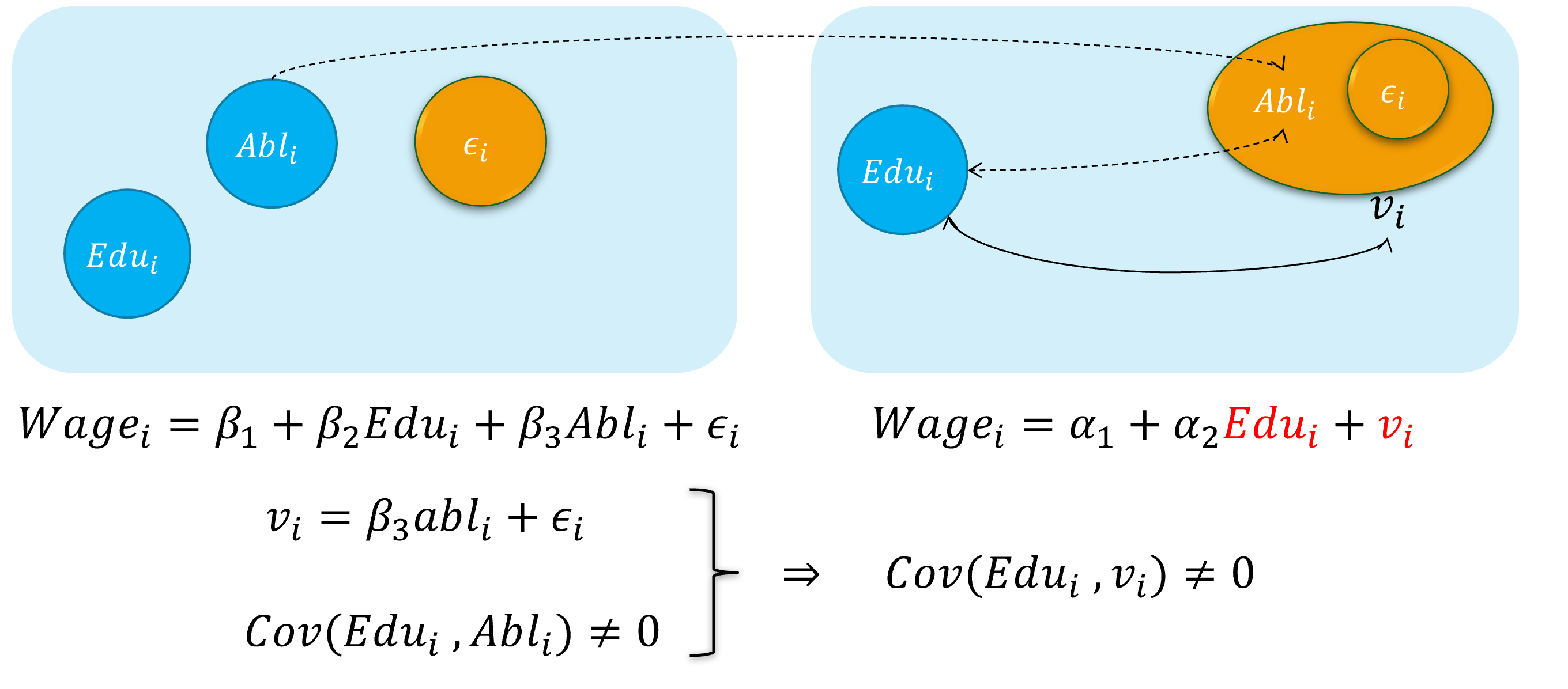
其中能力变量 \(Abl\) 被包含到新的随机干扰项 \(v_i\)中,也即: \(v_{i}=\beta_{3} abl_{i}+u_{i}\)
显然,我们认为偏误模型中,忽略了能力变量 \(Abl\),而受教育年数变量 \(Edu\)实际上又与之有相关关系。进而偏误模型中, \(cov(Edu_i, v_i) \neq 0\),从而受教育年数变量 \(Edu\)具有内生自变量问题。
遗漏变量:演示1
下面我们对遗漏变量情形做一个整体的直观演示:

遗漏变量:演示2
具体地,遗漏变量引发内生自变量问题的直观演示如下:


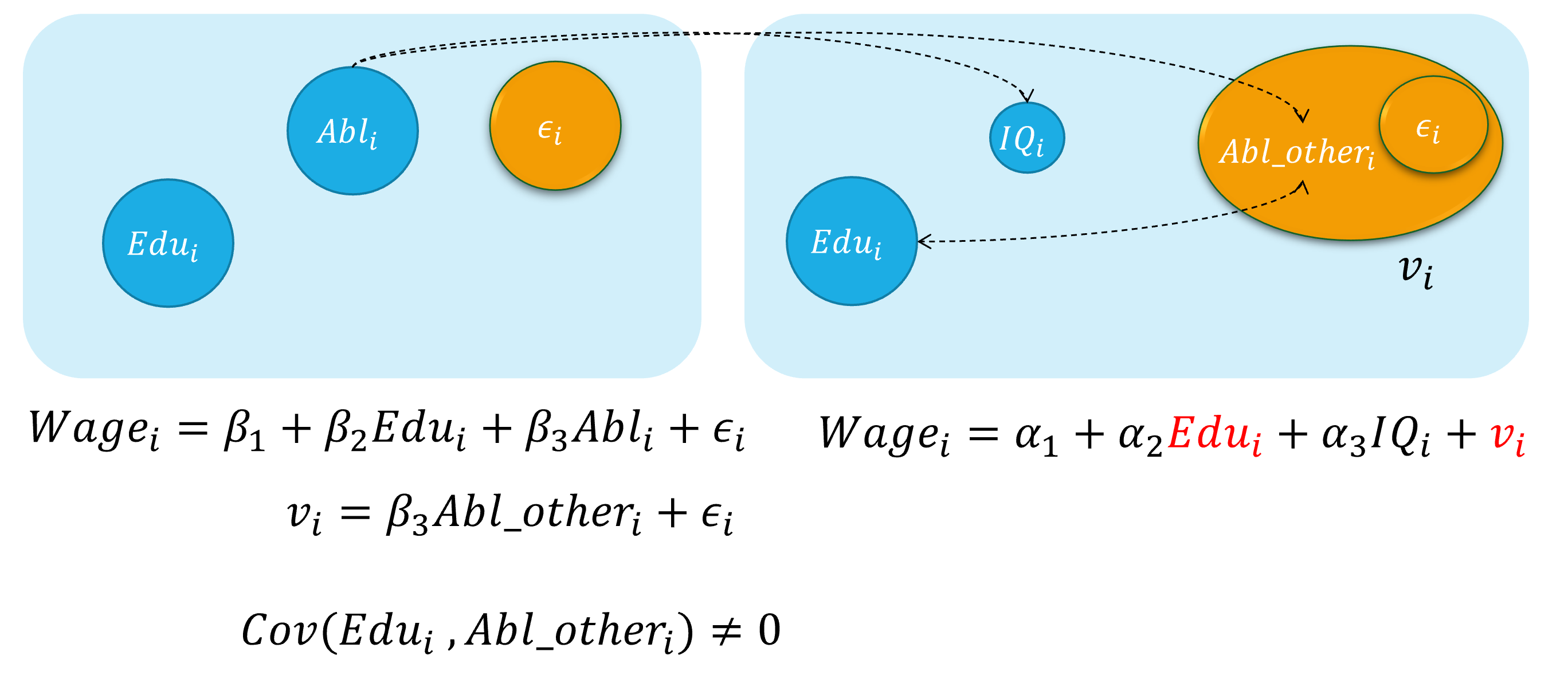
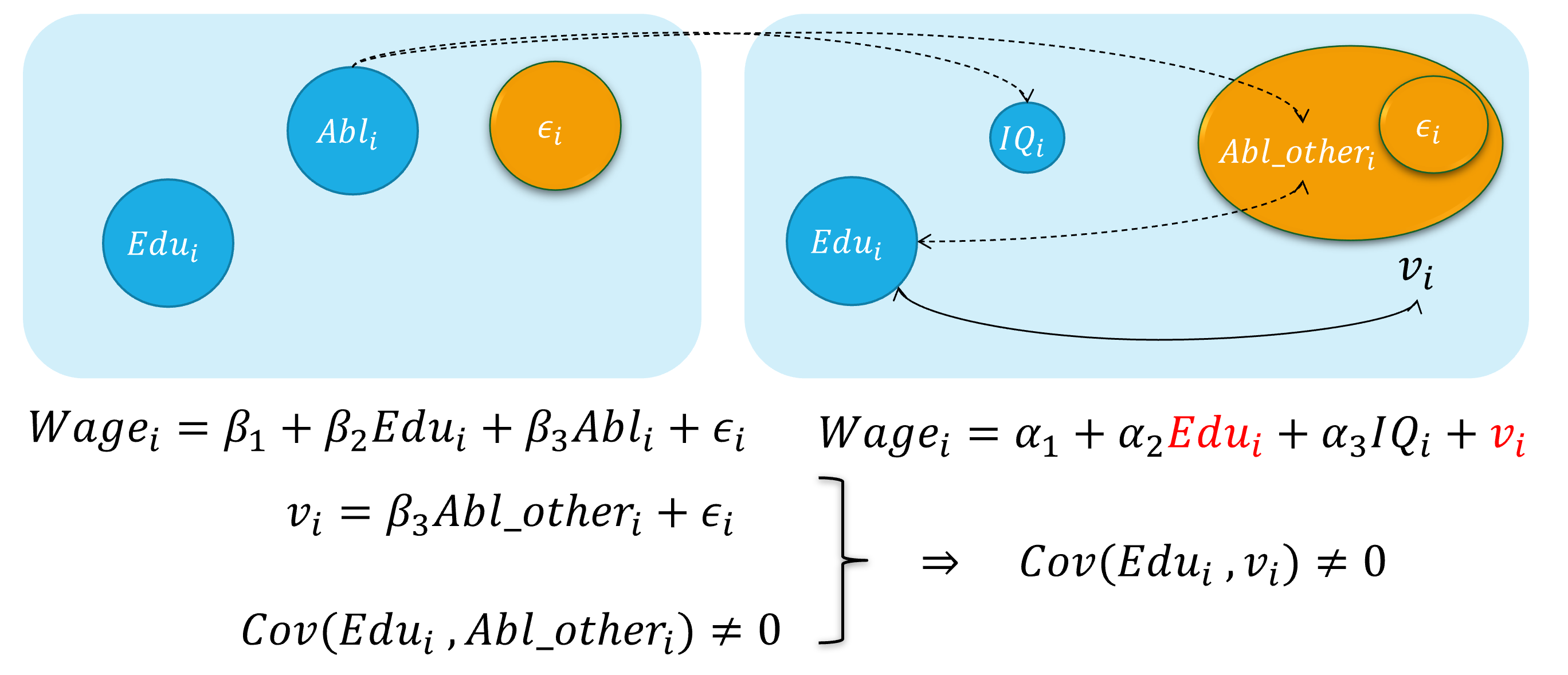
内生自变量情形2:测量误差
概念
很多时候的模型中实际使用的某个自变量本身并不是准确观测的,而只是“近似物”,因此模型自变量中存在测量误差(measurement error)。
示例
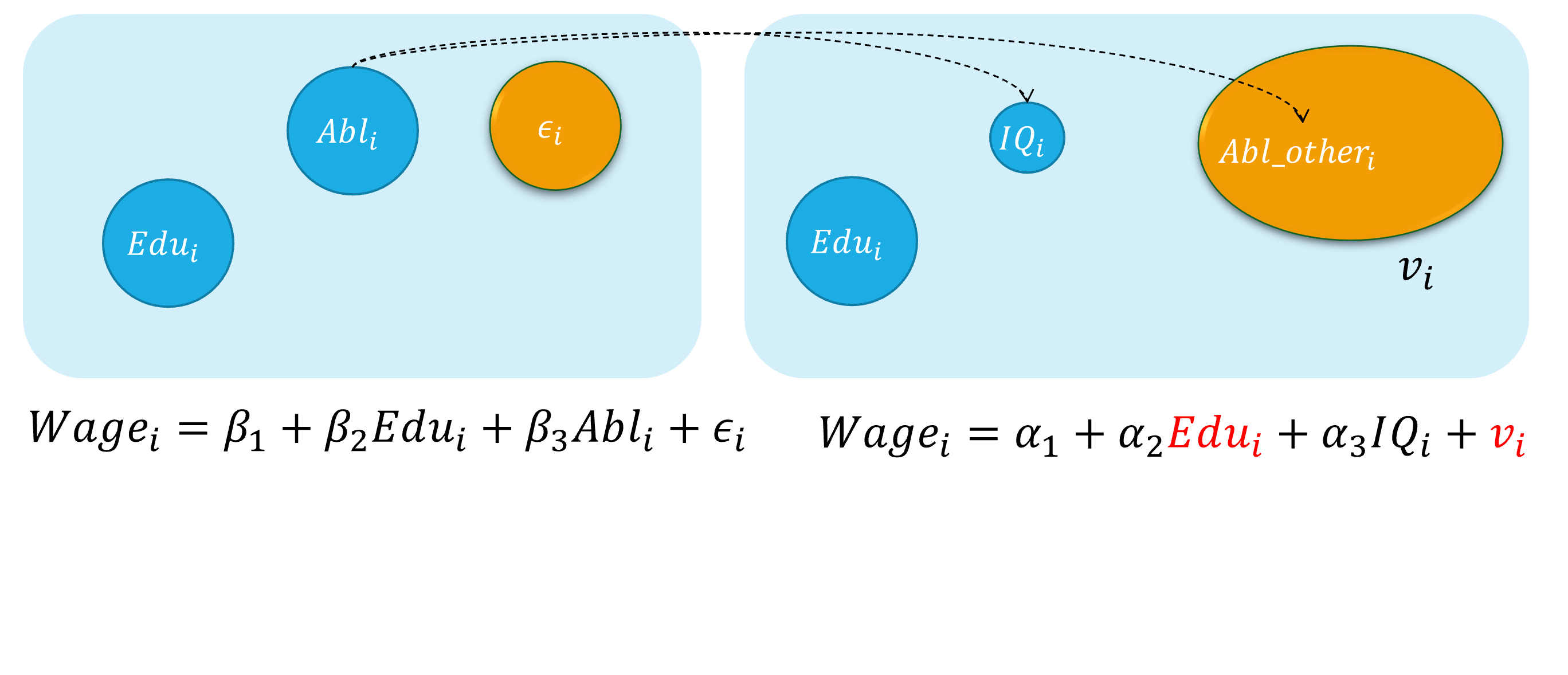
再次,假定工资决定的真实模型(real model)是:
\[ \begin {align} Wage_i=\beta_{1}+\beta_{2} Edu_i+\beta_{3} Abl_i+\epsilon_i \quad \text{(the assumed true model)} \end {align} \]
然而, 因为个体的能力变量 \(Abl\) 往往无法直接观测得到,我们便会考虑使用 智商水平 变量 ( \(IQ_i\)),并构建如下有偏误的代理变量模型(proxy variable model):
\[ \begin {align} Wage_i=\alpha_{1}+\alpha_{2} Edu_i+\alpha_{3} IQ_i+v_i \quad \text{(the error specified model)} \end {align} \]
此时,智商水平 \(IQ_i\)被认为是能力变量 \(Abl_i\)的一个代理变量(proxy variable)。
而实际上,能力水平变量 \(Abl_i\)的内涵要远远大于智商水平变量 \(IQ_i\)。因此,受教育年数变量 \(Edu\)会与随机干扰项中未纳入模型的 \(Abl_i\)变量的测量误差部分存在相关关系。进而偏误模型中, \(cov(Edu_i, v_i) \neq 0\),从而受教育年数变量 \(Edu\)具有内生自变量问题。
测量误差:演示1
下面我们对测量误差情形做一个整体的直观演示:




测量误差:演示2
具体地,测量误差引发内生自变量问题的直观演示如下:

内生自变量情形3:序列自相关问题
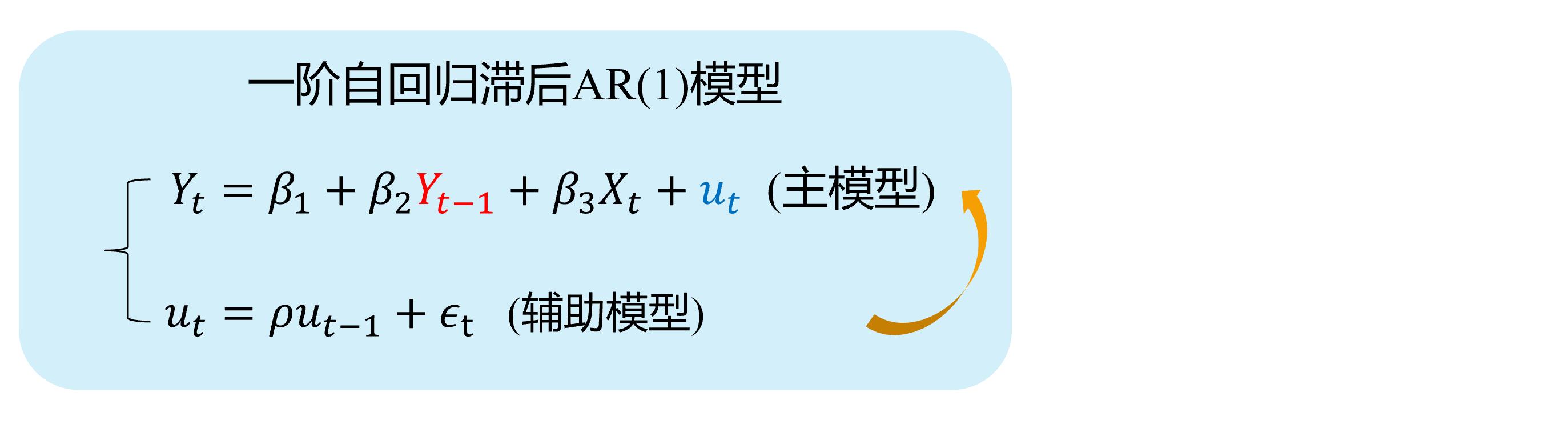
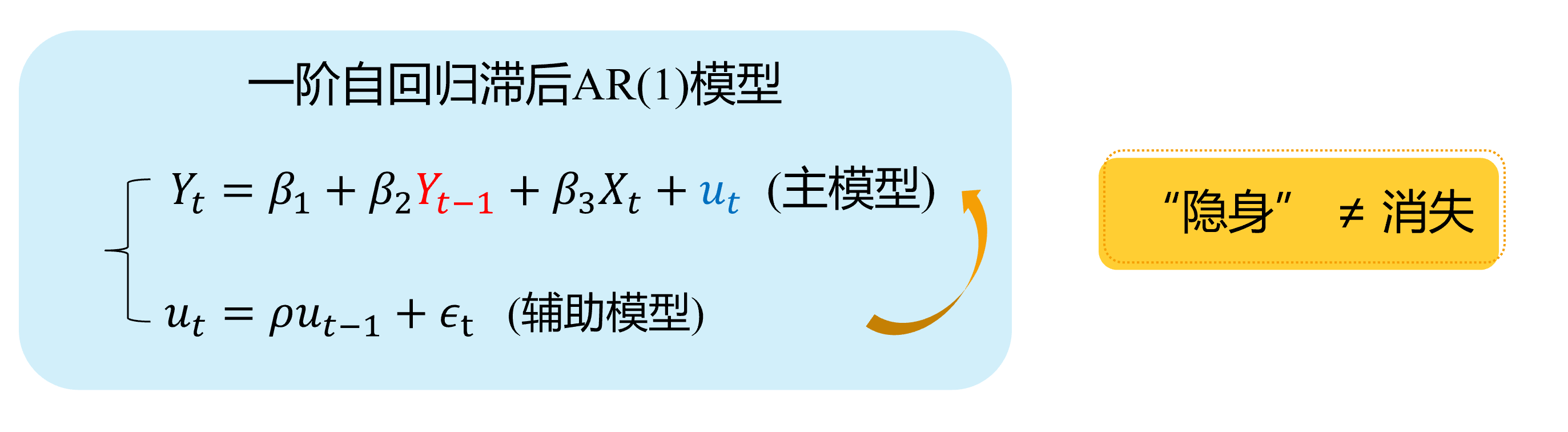
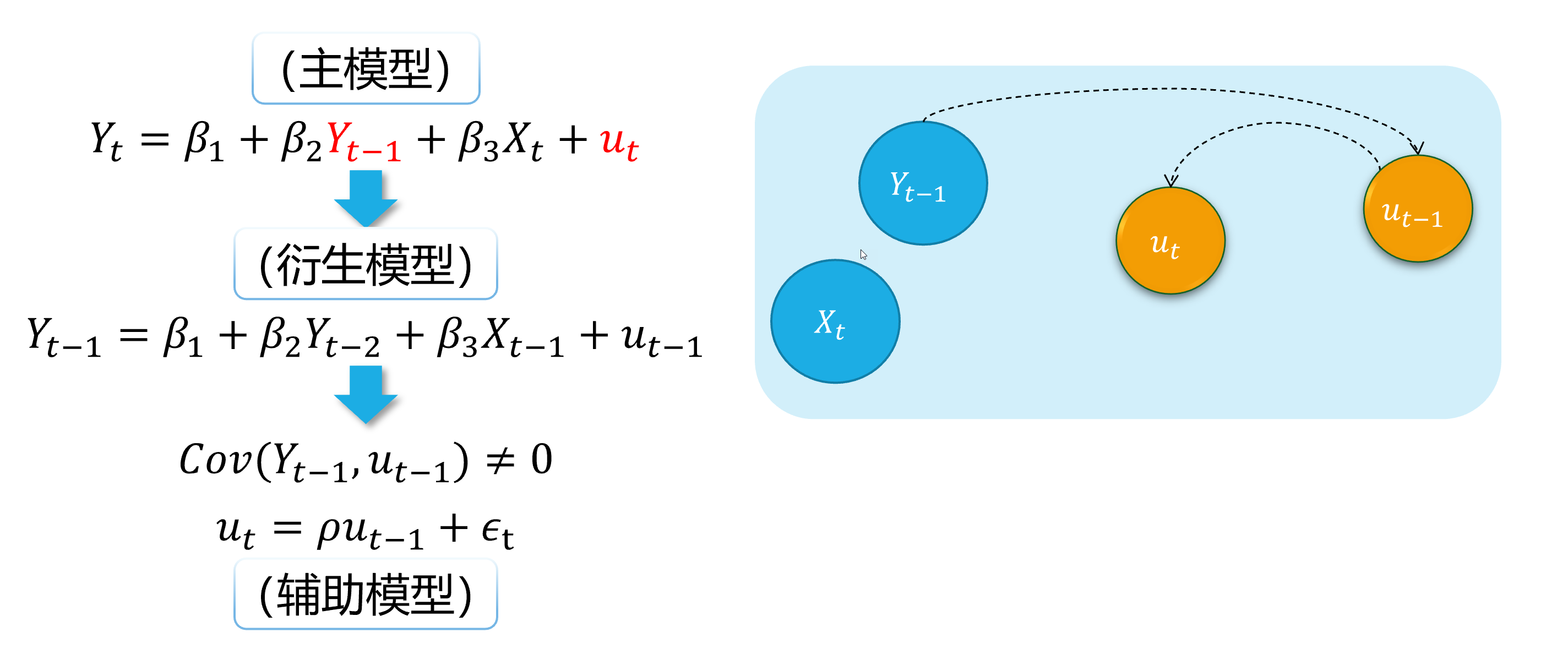
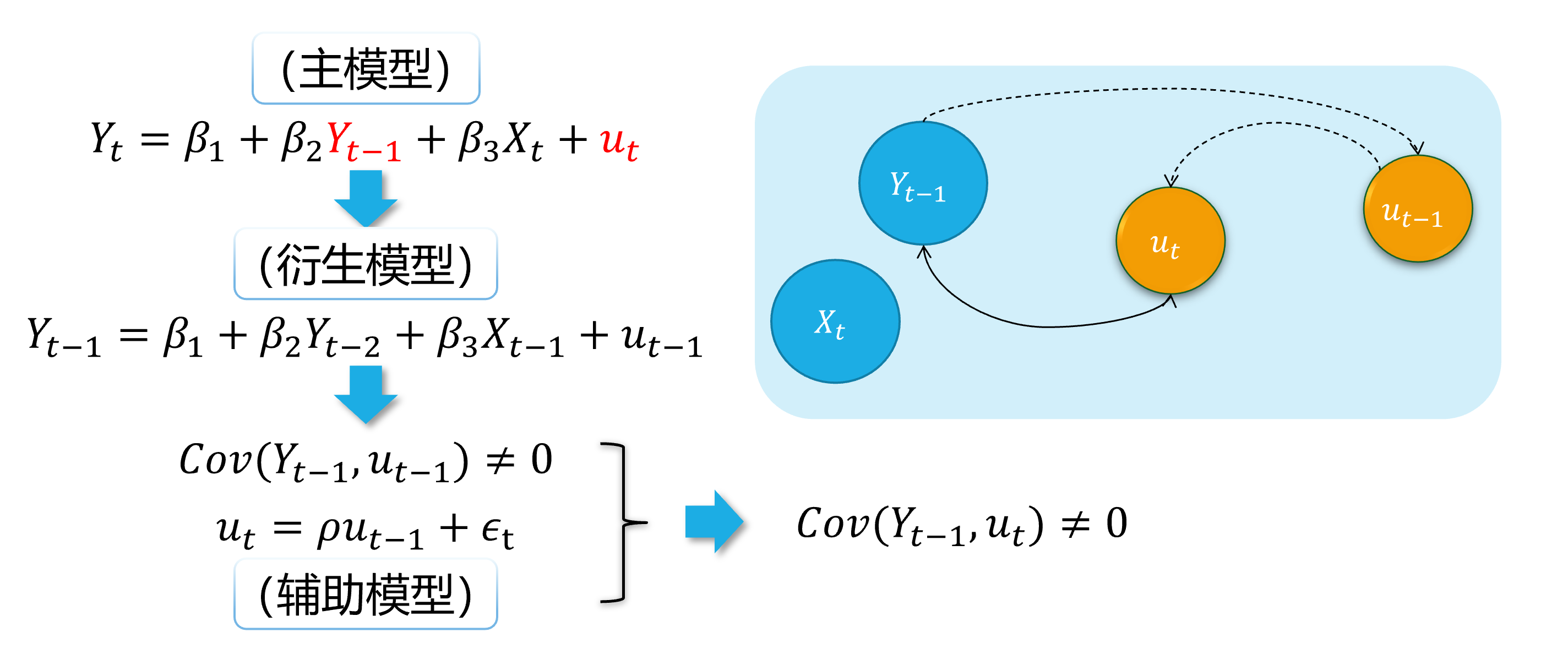
自回归滞后变量模型:因变量的滞后变量( \(Y_{t-1}, \ldots, Y_{t-p},\ldots\))作为回归元,出现在模型中。
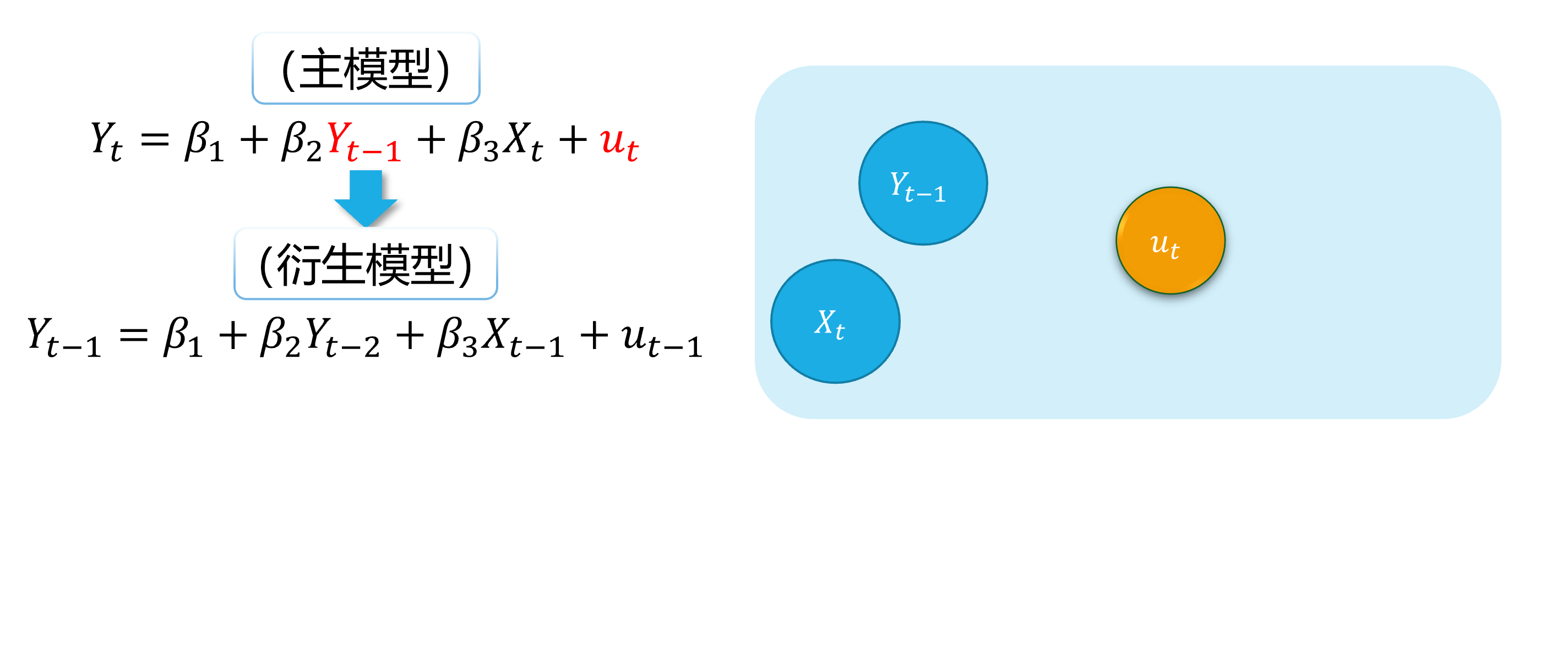
\[ \begin {align} Y_t=\beta_{1}+\beta_{2} Y_{t-1}+\beta_{3}X_t+u_t \end {align} \]
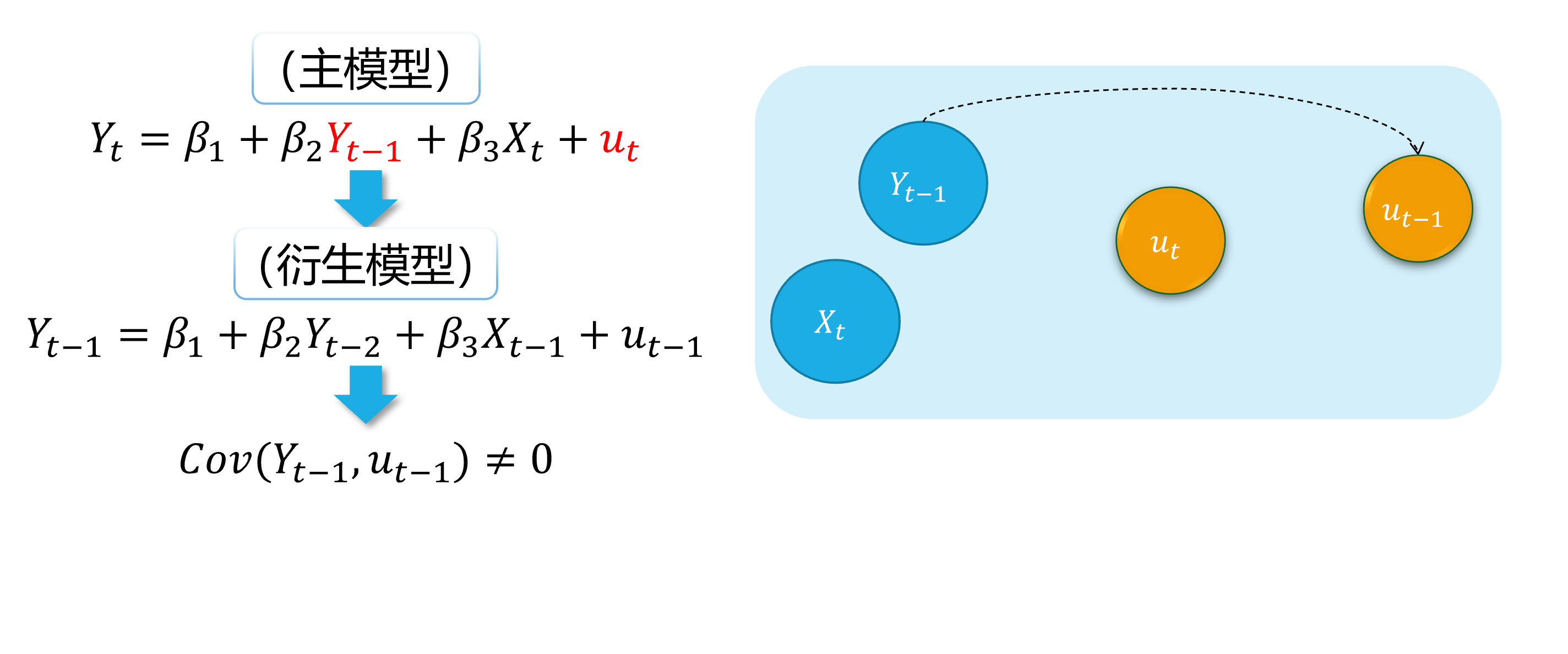
如果随机干扰项表现为一阶自相关AR(1),也即:
\[ \begin {align} u_t=\rho u_{t-1}+ \epsilon_t \end {align} \]
那么,显然 \(cov(Y_{t-1}, u_{t-1}) \neq 0\),进而 \(cov(Y_{t-1}, u_{t}) \neq 0\)。因此,受教育年数变量 \(Y_{t-1}\)具有内生自变量问题。
序列自相关:演示1
下面我们对序列自相关情形做一个整体的直观演示:


序列自相关:演示2
具体地,序列自相关引发内生自变量问题的直观演示如下:
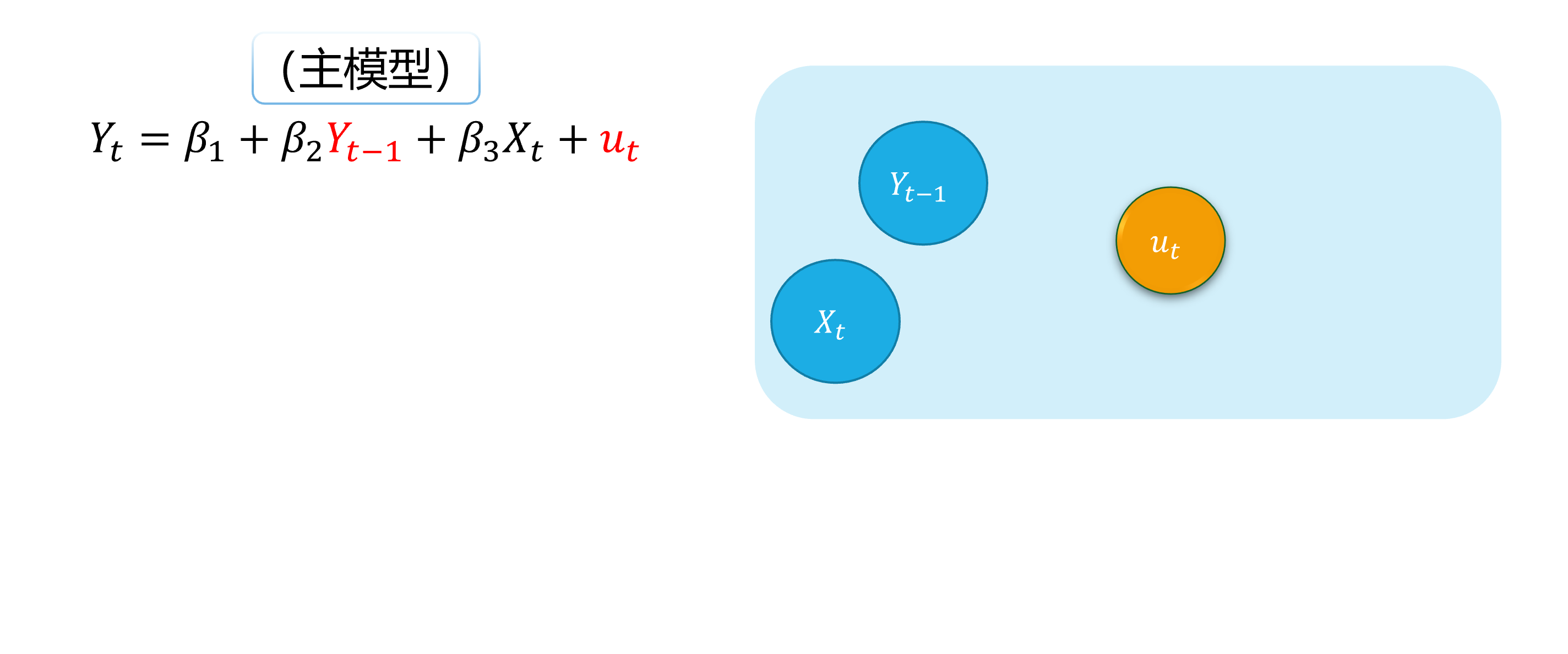
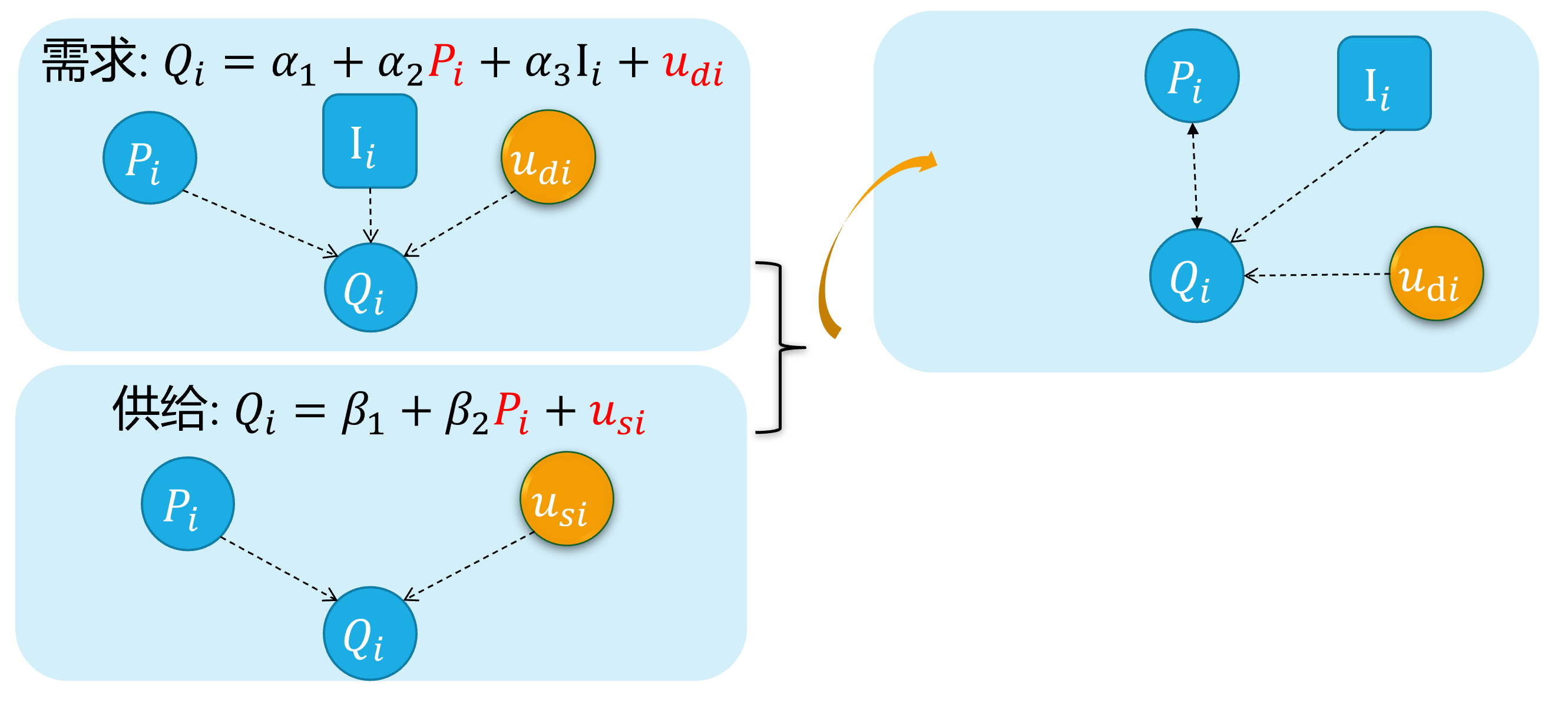
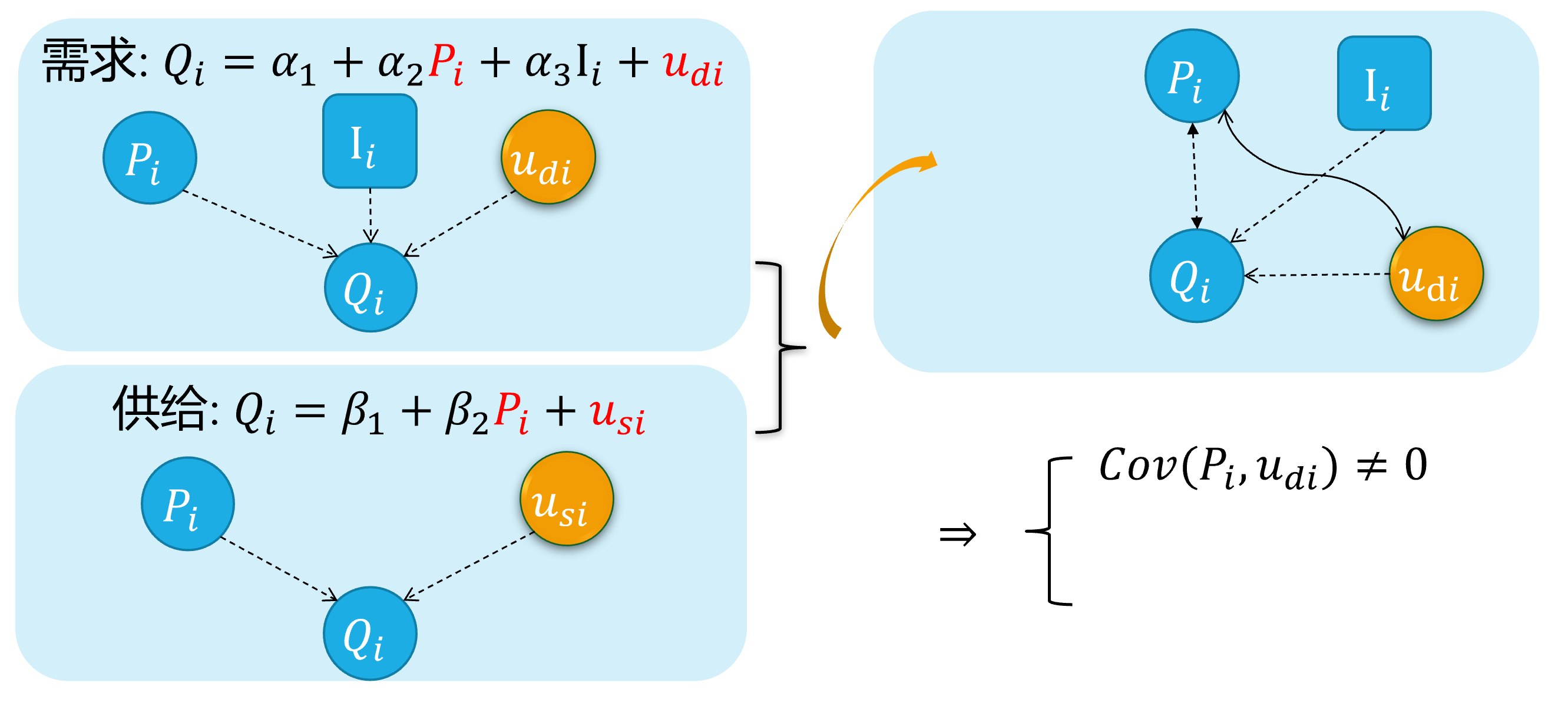
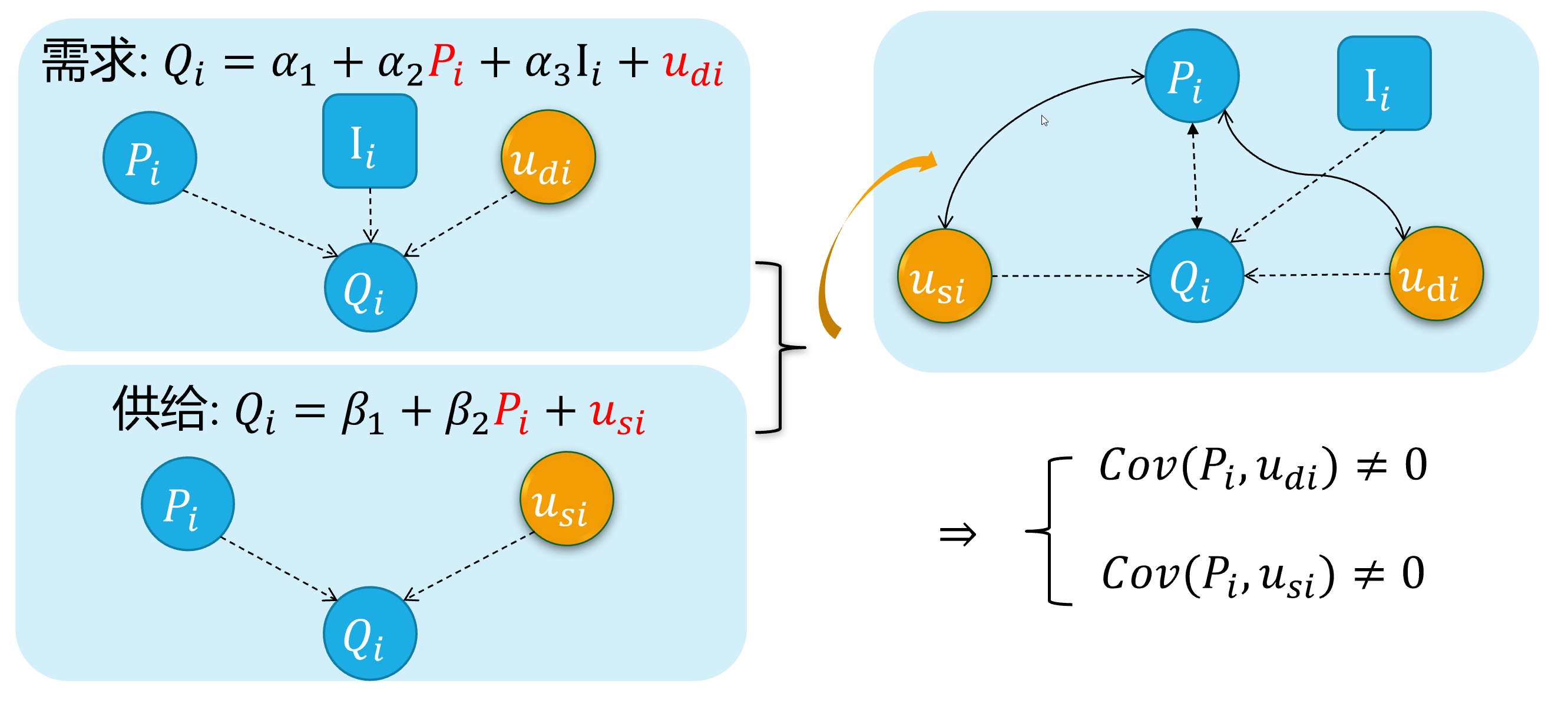
内生自变量情形4:方程联立性
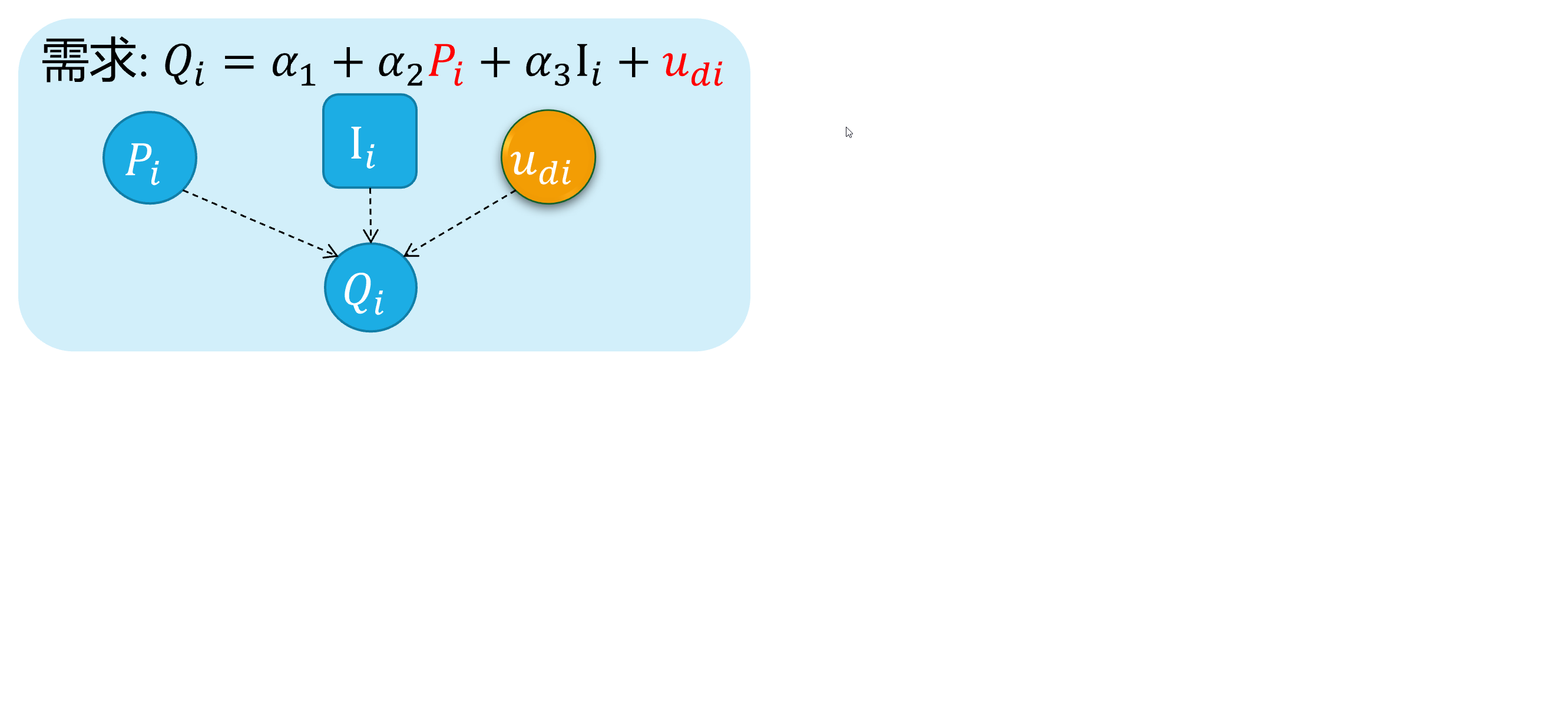
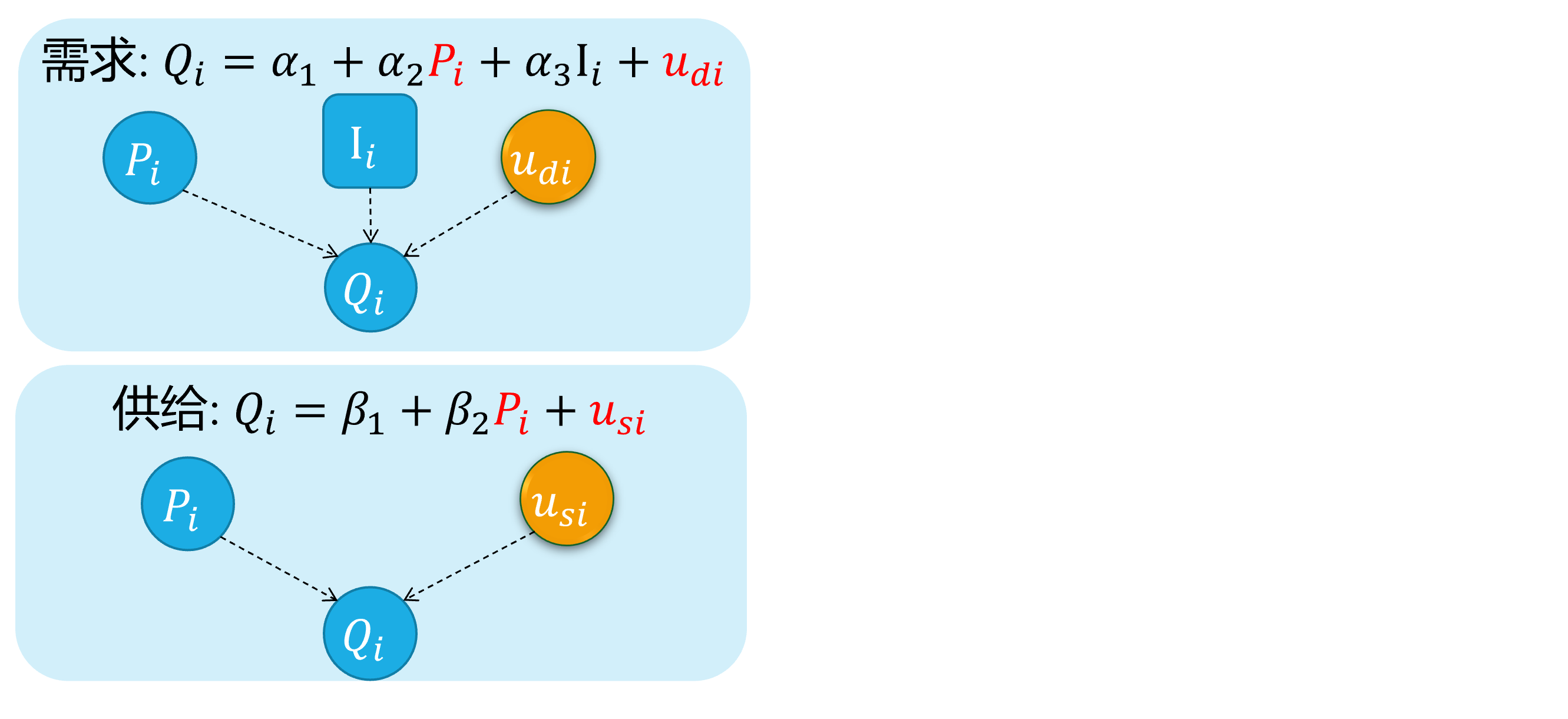
对于供需联立方程的结构化形式:
\[ \begin{cases} \begin{align} \text { Demand: } & Q_{i}=\alpha_{1}+\alpha_{2} P_{i}+u_{d i} \\ \text { Supply: } & Q_{i}=\beta_{1}+\beta_{2} P_{i} + u_{s i} \end{align} \end{cases} \]
众所周知,因为价格 \(P_i\)变动会影响供给量和需求量 \(Q_i\)的变动;反之亦然。两者之间存在相互反馈影响机制。
因此,可以证明 \(cov(P_i, u_{di}) \neq 0\),而且 \(cov(P_i, u_{si}) \neq 0\),从而产生内生性问题。
方程联立性:演示1
下面我们对方程联立性情形做一个整体的直观演示:




方程联立性:演示2
具体地,方程联立性引发内生自变量问题的直观演示如下:
学习成绩与逃课次数案例
案例背景
假设“真实模型”是:
\[ \begin {align} score_i=\alpha_{1}+\alpha_{2}skipped_i+ \alpha_3 abil_i + \alpha_4 mot_i + \alpha_5 income_i +\epsilon_i \end {align} \]
一个遗漏了重要变量的“偏误模型”是:
\[ \begin {align} score_i=\beta_{1}+\beta_{2}skipped_i+v_i \end {align} \]
学习成绩受到逃课次数的影响,但是我们也很担心以上模型中 \(skipped_i\)与 \(v_i\)中的某些因素相关,例如越有能力 \(abil_i\)、越积极 \(mot_i\)的学生,逃课也越少。
因为自变量 \(skipped_i\)可能与随机干扰项 \(v_i\)相关。此时,对于以上简单的回归,可能得不出可靠的估计。
可选工具变量
\[ \begin {align} score_i=\beta_{1}+\beta_{2}skipped_i+v_i \end {align} \]
逃课次数 \(skipped_i\)的工具变量 \(Z_i\)有哪些可供备选的呢?
宿舍跟上课地点的距离 \(distance\)。我们一般认为,它与逃课次数相关 \(skipped_i\),但是它与 \(v_i\)中的某些因素也会相关么?
如果收入水平 \(income\)确实影响了学习成绩,但是模型却没有引入收入水平 \(income\)变量,也就意味着 \(v_i\)中包含了遗漏的重要变量——收入水平 \(income\)。此时,距离 \(distance\)就会与收入水平 \(income\)相关,进而与 \(v_i\)相关。——因为收入少的学生,更倾向于在外租房(合租);收入多的学生,更倾向于住校。
17.2 内生变量法下的估计问题
造成不一致性估计
遗漏变量情形
一般而言,由于A2不成立,相关重要变量的遗漏,会导致OLS方法的估计不一致。
假设真实的工资模型是教育和能力的函数:
\[ \begin{align} Wage_{i}=\beta_{1}+\beta_{2} Edu_{i}+\beta_{3} Abl_{i}+\epsilon_{i} \quad \text{(a)} \end{align} \]
- 然而个人能力往往是不能被观察到的。
因此能力被包含在误设模型的随机干扰项中:
\[ \begin{align} Wage_{i}=\beta_{1}+\beta_{2} Edu_{i}+e_{i} \quad \text{(b)} \end{align} \]
- 其中\(e_{i}=\beta_{3} Abl_{i}+\epsilon_{i}\)
问题是能力不仅影响工资,而且能力越强的人受教育的时间越长,这就导致了随机误差项和教育变量之间的正相关 \(\operatorname{Cov}\left(Edu_{i}, e_{i}\right)>0\)。
牢记:遗漏并不等于消失!“omission” does not means “disappear” !
测量误差情形1/3
如果真实模型为:
\[ \begin{align} Y_{i}=\beta_{0}+\beta_{1} X_{i}+\epsilon_{i} \quad \text{(1)} \end{align} \]
我们希望观测自变量 \(X\)对因变量 \(Y\)的真实影响,但是很可能我们无法完全地观测得到自变量 \(X\),从而退一步采用一个可以观测到的代理变量(如 \(X^{\ast}\))。
\[ \begin{align} X^{\ast}_{i}=X_{i} - v_{i} \quad \text{(2)} \end{align} \]
其中: - 随机变量 \(v_i\)的期望为0,方差为 \(\sigma_{v}^{2}\) - \(X_i, \epsilon_i\) 与 \(v_i\)是互为独立的(pairwise independent)。
从而,我们构造了一个包含测量误差的误设模型:
\[ \begin{align} Y_{i}=\alpha_{0}+\alpha_{1} X^{\ast}_{i}+v_{i} \quad \text{(3)} \end{align} \]
测量误差情形2/3
更一般地:
\[ \begin{align} Y_{i} &=\beta_{0}+\beta_{1} X_{i}+\epsilon_{i} && \text{ eq(1) assumed true model } \end{align} \]
\[ \begin{align} X^{\ast}_i &= X_i - v_i && \text{ eq(2) proxy variable }\\ X_i &= X^{\ast}_i + v_i && \text{ eq(3)}\\ Y_{i} &=\beta_{0}+\beta_{1} X^{\ast}_{i}+u_{i} && \text{ eq(4) error specified model} \end{align} \]
把方程 (3) 带入方程 (1),可以得到方程(5):
\[ \begin{align} Y_{i} =\beta_{0}+\beta_{1} X_{i}^{*}+\epsilon_{i} =\beta_{0}+\beta_{1}\left(X^{\ast}_{i} + v_{i}\right)+\epsilon_{i} =\beta_{0}+\beta_{1} X^{\ast}_{i}+\left(\epsilon_{i} + \beta_{1} v_{i}\right) \quad \text{eq(5)} \end{align} \]
这将表明误设模型中的随机误差项 \(u_{i}=\left(\epsilon_{i}+\beta_{1} v_{i}\right)\),从而导致 \(\operatorname{Cov}\left(X^{\ast}_{i}, u_{i}\right) \neq 0\),根据高斯马尔可夫定量,OLS方法将不能得到一致性估计量(具体见下一页)。
测量误差情形3/3
容易证明: \(E\left(u_{i}\right)=E\left(\epsilon_{i} +\beta_{1} v_{i}\right)=E\left(\epsilon_{i}\right)+\beta_{1} E\left(v_{i}\right)=0\)
然而:
\[ \begin{aligned} \operatorname{Cov}\left(X^{\ast}_{i}, u_{i}\right) &=E\left[\left(X^{\ast}_{i}-E\left(X^{\ast}_{i}\right)\right)\left(u_{i}-E\left(u_{i}\right)\right)\right] \\ &=E\left(X^{\ast}_{i} u_{i}\right) \\ &=E\left[\left(X_{i}-v_{i}\right)\left(\epsilon_{i} +\beta_{1} v_{i}\right)\right] \\ &=E\left[X_{i} \epsilon_{i}+\beta_{1} X_{i} v_{i}- v_{i}\epsilon_{i}- \beta_{1} v_{i}^{2}\right] \leftarrow \quad \text{(pairwise independent)} \\ &=-E\left(\beta_{1} v_{i}^{2}\right) =-\beta_{1} \operatorname{Var}\left(v_{i}\right) =-\beta_{1} \sigma_{v_i}^{2} \neq 0 \end{aligned} \]
因此,方程4中的自变量\(X^{\ast}\)是内生自变量(endogenous),从而OLS的系数估计量\(\beta_{1}\)是不一致的。
OLS不一致估计量
一般而言,如果CLRM假设中的A2被违背,OLS估计量将会是有偏的(biased estimator)。
下面我们分别进行矩阵和代数形式的证明。
违背CLRM假设A2(矩阵证明)
我们已知,真实参数\(\hat{\beta}\)的OLS估计量理论公式为:
\[ \begin{align} \widehat{\beta} &=\beta+\left(X^{\prime} X\right)^{-1} X^{\prime} \epsilon && \text{(6)} \end{align} \]
我们可以两边同时取期望:
\[ \begin{equation} \begin{aligned} E(\widehat{\beta}) &=\beta+E\left(\left(X^{\prime} X\right)^{-1} X^{\prime} \epsilon\right) \\ &=\beta+E\left(E\left(\left(X^{\prime} X\right)^{-1} X^{\prime} \epsilon | X\right)\right) \\ &=\beta+E\left(\left(X^{\prime} X\right)^{-1} X^{\prime} E(\epsilon | X)\right) \neq \beta \end{aligned} \end{equation} \]
如果CLRM假设中A2:\(E(\epsilon | X) = 0\)被违背,也即意味着\(E(\epsilon | X) \neq 0\),从而OLS估计量是有偏的。
违背CLRM假设A2(代数证明1/3)
根据总体回归模型PRM可以分步得到:
\[ \begin{align} Y_i&=\beta_1+\beta_2 X_i+u_i && \text{(式1)}\\ E\left(Y_i\right)&=\beta_1+\beta_2 E\left(X_i\right) &&\text{(式2)}\\ Y_i-E\left(Y_i\right)&=\beta_2\left[X_i-E\left(X_i\right)\right]+u_i &&\text{(式3)}\\ \end{align} \]
\[ \begin{align} \left[X_i-E\left(X_i\right)\right]\left[Y_i-E\left(Y_i\right)\right] &=\beta_2\left[X_i-E\left(X_i\right)\right]^2+\left[X_i-E\left(X_i\right)\right] u_i &&\text{(式4)}\\ E\left[X_i-E\left(X_i\right)\right]\left[Y_i-E\left(Y_i\right)\right] &=\beta_2 E\left[X_i-E\left(X_i\right)\right]^2+E\left\{\left[X_i-E\left(X_i\right)\right] u_i\right\} &&\text{(式5)}\\ \operatorname{cov}\left(X_i, Y_i\right) & =\beta_2 \operatorname{var}\left(X_i\right)+\operatorname{cov}\left(X_i, u_i\right) &&\text{(式6)} \end{align} \]
最后得到:
\[ \begin{align} \beta_2=\frac{\operatorname{cov}\left(X_i, Y_i\right)}{\operatorname{var}\left(X_i\right)}-\frac{\operatorname{cov}\left(X_i, u_i\right)}{\operatorname{var}\left(X_i\right)} &&\text{(式7)}\\ \end{align} \]
违背CLRM假设A2(代数证明2/3)
给定样本数据,我们已经知道OLS下的斜率估计为:
\[ \begin{align} b_2=\frac{\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sum\left(X_i-\bar{X}\right)^2}=\frac{\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right) /(N-1)}{\sum\left(X_i-\bar{X}\right)^2 /(N-1)}=\frac{\widehat{\operatorname{cov}}(X, Y)}{\widehat{\operatorname{var}}(X)} \end{align} \]
- 这意味着,如果 \(\operatorname{cov}\left(X_i, u_i\right)=0\),那么则有:
\[ \begin{align} b_2=\frac{\widehat{\operatorname{cov}}(X, Y)}{\widehat{\operatorname{var}}(X)} \rightarrow \frac{\operatorname{cov}(X, Y)}{\operatorname{var}(X)}=\beta_2 \end{align} \]
违背CLRM假设A2(代数证明3/3)
给定样本数据,我们已经知道OLS下的斜率估计为:
\[ \begin{align} b_2=\frac{\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\sum\left(X_i-\bar{X}\right)^2}=\frac{\sum\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right) /(N-1)}{\sum\left(X_i-\bar{X}\right)^2 /(N-1)}=\frac{\widehat{\operatorname{cov}}(X, Y)}{\widehat{\operatorname{var}}(X)} \end{align} \]
- 反之,如果 \(\operatorname{cov}\left(X_i, u_i\right)\neq 0\),那么则有:
\[ \begin{align} b_2 \rightarrow \frac{\operatorname{cov}(X, Y)}{\operatorname{var}(X)}=\beta_2+\frac{\operatorname{cov}(X, u)}{\operatorname{var}(X)} \neq \beta_2 \end{align} \]
OLS一致性估计量
那么,在什么条件下我们才能得到一致估计量呢?
\[ \begin{equation} \begin{aligned} p \lim \widehat{\beta} &=\beta+p \lim \left(\left(X^{\prime} X\right)^{-1} X^{\prime} \epsilon\right) =\beta+p \lim \left(\left(\frac{1}{n} X^{\prime} X\right)^{-1} \frac{1}{n} X^{\prime} \epsilon\right) \\ &=\beta+p \lim \left(\frac{1}{n} X^{\prime} X\right)^{-1} \times p \lim \left(\frac{1}{n} X^{\prime} \epsilon\right) \end{aligned} \end{equation} \]
弱大数定理
通过弱大数定律(Weak Law of Large Numbers, WLLN):
\[ \begin{equation} \frac{1}{n} X^{\prime} \epsilon=\frac{1}{n} \sum_{i=1}^{n} X_{i} \epsilon_{i} \xrightarrow{p} E\left(X_{i} \epsilon_{i}\right) \end{equation} \]
因此如果 \(E\left(X_{i} \epsilon_{i}\right)=0\),则\(\widehat{\beta}\)是一致估计量。
需要注意的是:
\(E\left(X_{i} \epsilon_{i}\right)=0\)比CLRM假设中的A2 \(E(\epsilon | X) = 0\)更容易满足。
因此,一些有偏的估计量,在大样本情况下也可以是渐进一致的。
工资案例
误设模型
考虑如下的“误设模型”:
\[ \begin{align} lwage_i = \beta_1 +\beta_2educ_i + \beta_3exper_i +\beta_4expersq_i + v_i \end{align} \]
如前所述,该“误设模型”的问题在于,随机误差项中包含不可观测的重要变量,例如个人能力水平( \(Abl_i\)), 它同时对工资水平因变量和受教育程度自变量产生影响。
换言之,自变量工资水平与随机干扰项相关,也即 \(cov(educ_i, v_i) \neq 0\),因此它是内生自变量(endogenous regressor)。
在实践中,我们将使用受教育年数作为educ的代理变量,这本身也会带来前面提到的误差测量问题。
变量说明
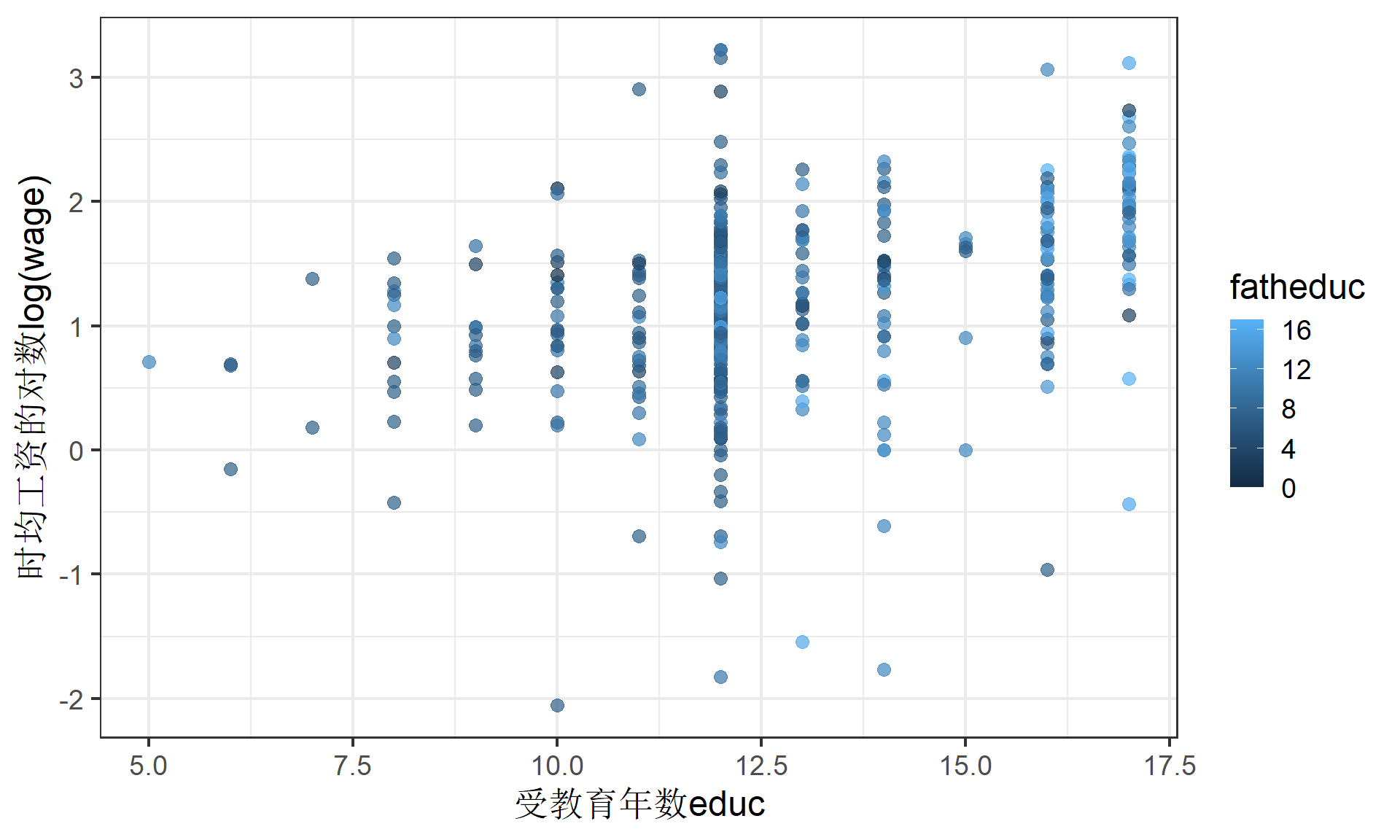
研究者关注1388名已婚女性时均工资 \(wage\)与受教育年数\(educ\)之间的关系,考虑如下变量:
原始数据
散点图1
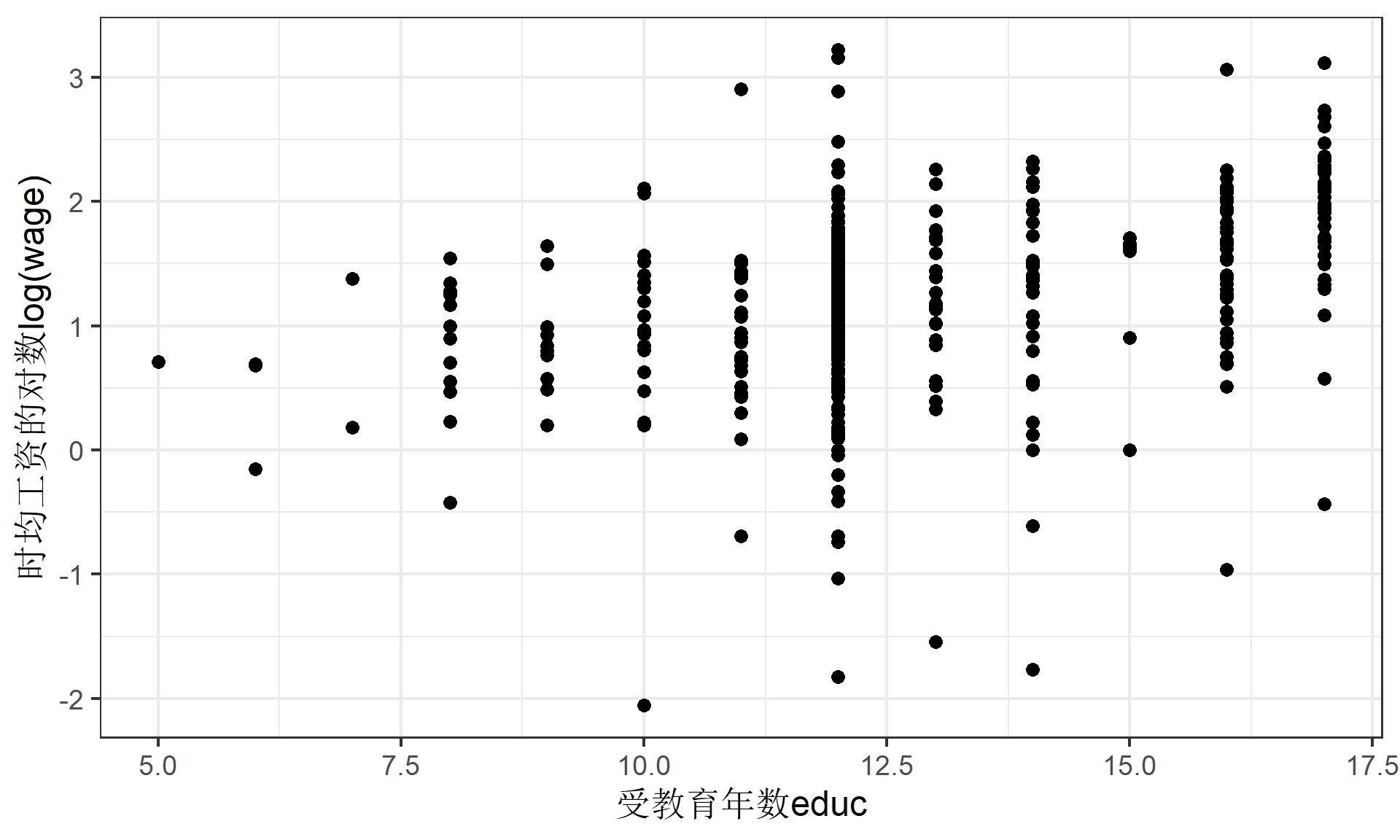
散点图2
OLS回归
如果直接构建如下的“偏误模型”,并坚持采用OLS估计:
\[ \begin{aligned} \begin{split} lwage_i=&+\beta_{1}+\beta_{2}educ_i+\beta_{3}exper_i+\beta_{4}expersq_i+u_i \end{split} \end{aligned} \]
\[ \begin{alignedat}{999} \begin{split} &\widehat{lwage}=&&-0.52&&+0.11educ_i&&+0.04exper_i&&-0.00expersq_i\\ &(s)&&(0.1986)&&(0.0141)&&(0.0132)&&(0.0004)\\ &(t)&&(-2.63)&&(+7.60)&&(+3.15)&&(-2.06)\\ &(over)&&n=428&&\hat{\sigma}=0.6664 && &&\\ &(fit)&&R^2=0.1568&&\bar{R}^2=0.1509 && &&\\ &(Ftest)&&F^*=26.29&&p=0.0000 && && \end{split} \end{alignedat} \]
17.3 工具变量选择与估计方法
工具变量
缘由
至此,我们已经了解到如果模型出现一个或多个内生自变量,则参数\(\beta\)的OLS估计是有偏的。
OLS方法的估计“问题”,来自于我们要求的CLRM假设中的\(E(X_i\epsilon_i)=0\),这意味着我们相信样本数据满足:
\[ \boldsymbol{X^{\prime} {e}=0} \]
但是,实际上自变量与随机误差项存在相关关系,也即\(E(X_i\epsilon_i) \neq 0\).
条件
如果我们能够找到这样的一些解释变量(explanatory variables)\(\boldsymbol{Z}\),它们满足如下条件:
相关性(Relevance):\(\boldsymbol{Z}\)与\(\boldsymbol{X}\)相关
外生性(Exogeneity):\(\boldsymbol{Z}\) 与随机干扰项\(\boldsymbol{\epsilon}\)不相关
我们称满足以上条件的变量\(\boldsymbol{Z}\)为工具变量(Instrumental Variables , IV )。
估计量
正确使用工具变量后,参数估计量\(\hat{\beta}_{IV}\)可以表达为如下的正则表达式(normal equation)——更准确地是矩条件(moment condition)形式:
\[ \begin{align} \boldsymbol{Z^{\prime} \hat{\epsilon}=Z^{\prime}\left(y-X \hat{\beta}_{IV}\right)=0} \end{align} \]
假定\(Z^{\prime} X\) 是非奇异方阵(non singular square matrix),则有:
\[ \begin{align} \boldsymbol{\hat{\beta}_{IV}=\left(Z^{\prime} X\right)^{-1} Z^{\prime} y} \end{align} \]
上述关于\(\boldsymbol{Z^{\prime} X}\)是非奇异方阵的条件,直觉上是可以得到满足的,只要我们的工具变量[1]数量不少于模型中的自变量数。
尽管如此,工具变量法下的参数估计量\(\boldsymbol{\hat{\beta}_{IV}}\)在有限样本下仍然是有偏的,但是可以证明它是渐进一致的。
一致性
下面我们来证明\(\boldsymbol{\hat{\beta}_{IV}}\)是渐进一致的。
\[ \begin{align} \boldsymbol{\hat{\beta}_{IV} =\left(Z^{\prime} X\right)^{-1} Z^{\prime} y =\left(Z^{\prime} X\right)^{-1} Z^{\prime} (X\beta +\epsilon) =\beta+\left(Z^{\prime} X\right)^{-1} Z^{\prime} \epsilon} \end{align} \]
\[ \begin{align} p \lim \boldsymbol{{\hat{\beta}_{IV}}} &=\boldsymbol{\beta+p \lim \left(\left(Z^{\prime} X\right)^{-1} Z^{\prime} \epsilon\right)} \\ &=\boldsymbol{\beta+\left(p \lim \left(\frac{1}{n} Z^{\prime} X\right)\right)^{-1} \operatorname{plim}\left(\frac{1}{n} Z^{\prime} \epsilon\right) =\beta} \end{align} \]
- 保证相关性条件(Relevance)
\[ \begin{align} p \lim \left(\frac{1}{n} \boldsymbol{Z^{\prime} X}\right) &=p \lim \left(\frac{1}{n} \sum z_{i} X_{i}^{\prime}\right) \\ &=E\left(Z_{i} X_{i}^{\prime}\right) \neq 0 \end{align} \]
- 保证内生性条件(Exogeneity)
\[ \begin{align} p \lim \left(\frac{1}{n} \boldsymbol{Z^{\prime} \epsilon}\right) &=p \lim \left(\frac{1}{n} \sum Z_{i} \epsilon_{i}\right) \\ &=E\left(Z_{i} \epsilon_{i}\right)=0 \end{align} \]
推断
下面我们来看一下随机干扰项方差\(\sigma^{2}\) 的工具变量法估计情况。
\[ \begin{align} \hat{\sigma}_{I V}^{2} =\frac{\sum e_{i}^{2}}{n-k} =\frac{\boldsymbol{\left(y-X \hat{\beta}_{IV}\right)^{\prime}\left(y-X \hat{\beta}_{I V}\right)}}{n-k} \end{align} \]
可以证明它是真实参数的无偏估计了(证明略)。
基于此,我们才可以进行后续各种假设检验。
工具变量的选择
现实困难
然而,找到有效的工具量并非易事,它本身就是工具变量估计方法的一大现实困难。因为:
优良的工具变量需要同时满足相关性和外生性两个严苛的条件。
一个段子: If you can find a valid instrumental variable, you can get PhD from MIT.
渐进方差
我们可以证明IV估计量\(\hat{\beta}_{I V}\) 的渐进方差(asymptotic variance)等于(证明略):
\[ \begin{align} \operatorname{Var}\left(\boldsymbol{\hat{\beta}_{I V}}\right)=\sigma^{2}\boldsymbol{\left(Z^{\prime} X\right)^{-1}\left(Z^{\prime} Z\right)\left(X^{\prime} Z\right)^{-1}} \end{align} \]
其中:
- \(\boldsymbol{X^{\prime} Z}\)是工具变量和自变量的协方差矩阵(covariances matrix )。
- 如果二者的相关程度较低,则协方差矩阵\(\boldsymbol{X^{\prime} Z}\)的元素取值会接近于0,因此逆矩阵\(\boldsymbol{\left(X^{\prime} Z\right)^{-1}}\)元素取值会非常大。 最后,参数估计量的方差\(\operatorname{Var}\left(\boldsymbol{\hat{\beta}_{IV}}\right)\) 也会非常大,也即估计精度会非常低。
基本策略
对于误设模型(存在内生自变量问题):
\[ \begin{equation} \boldsymbol{y= X \beta+v} \end{equation} \]
一个基本策略是构造全体工具变量\(\boldsymbol{Z}=(X_{ex}, X^{\ast})\),其中:
工具变量\(X_{ex}\)是那些明确出现在模型中的、且被认定为外生的自变量.
其他工具变量\(\boldsymbol{X^{\ast}}\)是那些没有明确出现在模型中、但是与模型密切相关的、通过某种努力找到的外生变量。
估计效率
显然,如果模型中的自变量\(X\)被认定为都是外生的,那么\(X=Z\),因而高斯马尔可夫定律(Gauss-Markov theorem)是成立的。并且我们需要注意的是:
IV估计量\(\mathbf{\hat{\beta}}_{IV}\) 并不会显示任何绝对估计效率的特征。
我们只能够说它具有相对估计效率。换言之,我们只能通过不断选择更优的工具变量积合,从而使得在众多IV估计量中,能够找到相对更好的估计量。
多个工具变量与模型识别
下面考虑另一种情形,此时我们找到的工具变量数目要远多于内生自变量数目(后面我们会知道,这属于过度识别情形,over-identification)。
根据相对估计效率原则,我们将会从工具变量集中找到那些与自变量\(X\)高度相关的,从而使得IV估计量的方差最小化!
多个工具变量的运用
最好的办法就是:
- 我们首先使用OLS方法,把\(\boldsymbol{X}\)的每一列,都对全部工具变量\(\boldsymbol{Z}\)进行回归,从而得到拟合变量\(\boldsymbol{\hat{X}}\):
\[ \begin{align} \boldsymbol{\hat{X}=Z\left(Z^{\prime} Z\right)^{-1} Z^{\prime} X=ZF} \end{align} \]
- 然后,我们使用拟合得到的\(\boldsymbol{\hat{X}}\)作为新的自变量, 再与因变量\(\mathbf{y}\)进行OLS回归,从而得到高斯马尔可夫一致性估计量(证明过程见下一页):
\[ \begin{align} \boldsymbol{\hat{\beta}_{I V} =\left(\hat{X}^{\prime} X\right)^{-1} \hat{X}^{\prime} y=\left(X^{\prime} Z\left(Z^{\prime} Z\right)^{-1} Z^{\prime} X\right)^{-1} X^{\prime} Z\left(Z^{\prime} Z\right)^{-1} Z^{\prime} y } \end{align} \]
实际上,这就是我们经常听说的两阶段最小二乘法(2SLS)。
工具变量法解决方案
遗漏变量情形:真实模型和误设模型
假定如下的故事背景:
\[ Wage_{i}=\beta_{0}+\beta_{1} Edu_{i}+\beta_{2} Abl_{i}+\epsilon_{i} \quad \text{(ture model}) \]
\[ Wage_{i}=\beta_{0}+\beta_{1} Edu_{i}+v_{i} \quad \text{(error specification model}) \]
其中,\(v_{i}=\beta_{2} Abl_{i}+\epsilon_{i}\)。此时,\(Edu\) 是一个内生自变量。
遗漏变量情形:工具变量条件
假设我们能够找到满足如下条件的工具变量\(Z\):
首先:
\(Z\) 不会直接影响因变量\(Wages\)
\(Z\) 与\(v\) 不相关,也即:\(\operatorname{Cov}(v, z)=0\)
其次:
- \(Z\) 至少要与内生变量\(Edu\) 相关 (relevance)。$(Z, Edu) $
这一条件是否满足,可以利用如下简单OLS回归的\(\alpha_{2}\)显著性检验进行判断:\(Edu_{i}=\alpha_{1}+\alpha_{2}Z_{i}+u_{i}\)
至此,\(Z\) 才是内生自变量\(Edu_i\)的一个有效工具变量(valid instrument),然后我们才能进一步做出一致性参数估计。
遗漏变量情形:可选的工具变量
一些经济学家建议使用家庭背景变量作为内生自变量\(Edu\)的工具变量:
例如, 母亲受教育程度\(motherEdu\)与子代的受教育程度\(Edu\)相关。然而它跟子代的能力\(Abl\)可能存在一定相关关系。
又例如,家庭中兄弟姐妹数量\(Siblings\)与受教育程度\(Edu\)一般呈现负相关关系,而且它与能力\(Abl\)应该不相关
测量误差情形:真实模型和误设模型
下面我们看一下,IV方法如何处理测量误差导致的内生自变量问题。
\[ \begin {align} \log (Wage_i)=\beta_{0}+\beta_{1} Edu_i+\beta_{2} Abl_i+u_i \quad \text{(true model)} \end {align} \]
\[ \begin {align} \log (Wage_i)=\beta_{0}+\beta_{1} Edu_i+\beta_{2} IQ_i+u_i^{\ast} \quad \text{(error specification model)} \end {align} \]
此时, 智商水平\(IQ_i\) 可以考虑作为内生自变量受教育程度\(Edu\)的工具变量。但是要注意的是,工具变量\(IQ_i\) 还是可能与随机干扰项\(u_i^{\ast}\)相关。
工具变量法下的系数估计过程
把上述“偏误模型”记为:
\[ \begin {align} score_i & =\beta_{1}+\beta_{2}skipped_i+u_i \\ Y_i & = \beta_{1}+\beta_{2}X_i+u_i \end {align} \]
假设我们找到了理想的工具变量\(Z_i\),并构建如下的工具变量模型:
\[ \begin {align} Y_i & = \alpha_{1}+\alpha_{2}Z_i+v_i \end {align} \]
\[ \begin {align} cov(Z_i, Y_i) & = \alpha_{2}cov(Z_i,X_i)+ cov(Z_i,u_i) && \leftarrow [cov(Z_i,u_i)=0] \\ \alpha_2|_{IV}^{plim} & = \frac{cov(Z_i, Y_i)}{cov(Z_i, X_i)} = \frac{\sum{z_iy_i}}{\sum{z_ix_i}} = \frac{\sum{x_iy_i}}{\sum{x_i^2}} && \leftarrow [if \quad X_i=Z_i] \\ &=\beta_2 \end {align} \]
工具变量法下系数的真实方差
对于“偏误模型”和工具变量模型:
\[ \begin{align} Y_i &= \beta_1 +\beta_2X_i + u_i && \text{(PRM)} \\ Y_i &= \alpha_1 +\alpha_2Z_i + v_i && \text{(IV)} \end{align} \]
如果如下三个条件成立:
\[ \begin{align} Cov(Z_i, u_i) & = 0 \\ Cov(Z_i, X_i) & \neq 0 \\ E(v_i^2|Z_i) & \equiv \sigma^2 \equiv var(u_i) \end{align} \]
可证明斜率系数\(\alpha_2\)渐近方差为:
\[ \begin{align} var(\alpha_2) \simeq \frac{\sigma^2}{n \sigma^2_{X_i} \rho^2_{(X_i,Z_i)}} \end{align} \]
其中:
\(\sigma^2\)是\(v_i\)的总体方差,也即\(var(v_i) \equiv \sigma^2\)。
\(\sigma^2_{X_i}\)是\(X_i\)的总体方差,也即\(var(X_i) \equiv \sigma^2_{X_i}\)。
\(\rho^2_{(X_i,Z_i)}\)是\(X_i\)和\(Z_i\)的总体相关系数的平方,也即\(\rho^2_{(X_i,Z_i)} \equiv \frac{[cov(X_i,Z_i)]^2}{var(X_i)var(Z_i)}\);
工具变量法下系数的样本方差
对于给定的样本数据,我们可以计算出
\[ \begin{align} var(\alpha_2) \simeq \frac{\sigma^2}{n \sigma^2_{X_i} \rho^2_{(X_i,Z_i)}} \simeq \frac{\hat{\sigma}^2}{n S^2_{X_i} R^2_{(X_i,Z_i)}} \end{align} \]
其中:
\(\sigma^2_{X_i} \simeq S^2_{X_i}=\frac{\sum{(X_i-\bar{X})^2}}{n-1}\)。
\(\rho^2_{(X_i,Z_i)}\simeq R^2\),其中\(R^2\)为通过做\(X_i\)对\(Z_i\)的回归来获得的判定系数。\(X_i = \hat{\pi}_1 +\hat{\pi}_2 Z_i + \epsilon_i\)
\(\hat{\sigma}^2 = \frac{\sum{e_i^2}}{n-2}\),是来自对工具变量回归的残差计算。\(Y_i = \hat{\alpha}_1 +\hat{\alpha}_2 Z_i + e_i\)
案例:IV回归分析法实践
IV模型设定
下面给出一个已婚女性的教育回报案例,对上述结论进行论证和分析。
工具变量回归模型:
\[ \begin{align} log(wage) = \lambda_1 + \lambda_2educ|fatheduc + \epsilon_i \end{align} \]
IV回归下的手动两步估计结果
采用工具变量法的第一阶段回归:
\[ \begin{aligned} \begin{split} educ_i=&+\delta_{1}+\delta_{2}fatheduc_i+u_i \end{split} \end{aligned} \]
\[ \begin{alignedat}{999} \begin{split} &\widehat{educ}=&&+10.24&&+0.27fatheduc_i\\ &(s)&&(0.2759)&&(0.0286)\\ &(t)&&(+37.10)&&(+9.43)\\ &(fit)&&R^2=0.1726&&\bar{R}^2=0.1706\\ &(Ftest)&&F^*=88.84&&p=0.0000 \end{split} \end{alignedat} \]
采用工具变量法的第二阶段回归:
\[ \begin{aligned} \begin{split} lwage_i=&+\gamma_{1}+\gamma_{2}educ.hat_i+v_i \end{split} \end{aligned} \]
\[ \begin{alignedat}{999} \begin{split} &\widehat{lwage}=&&+0.44&&+0.06educ.hat_i\\ &(s)&&(0.4671)&&(0.0368)\\ &(t)&&(+0.94)&&(+1.61)\\ &(fit)&&R^2=0.0060&&\bar{R}^2=0.0037\\ &(Ftest)&&F^*=2.59&&p=0.1086 \end{split} \end{alignedat} \]
IV回归下R包ivreg的自动计算结果
采用R包AER的工具变量回归函数ivreg(),可以得到如下回归结果:
Call:
ivreg(formula = lwage ~ educ | fatheduc, data = mroz)
Residuals:
Min 1Q Median 3Q Max
-3.0870 -0.3393 0.0525 0.4042 2.0677
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.44110 0.44610 0.989 0.3233
educ 0.05917 0.03514 1.684 0.0929 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6894 on 426 degrees of freedom
Multiple R-Squared: 0.09344, Adjusted R-squared: 0.09131
Wald test: 2.835 on 1 and 426 DF, p-value: 0.09294 提问:
手工分步计算与软件自动计算有哪些不同?
判定系数和系数标准误差为什么会不同?
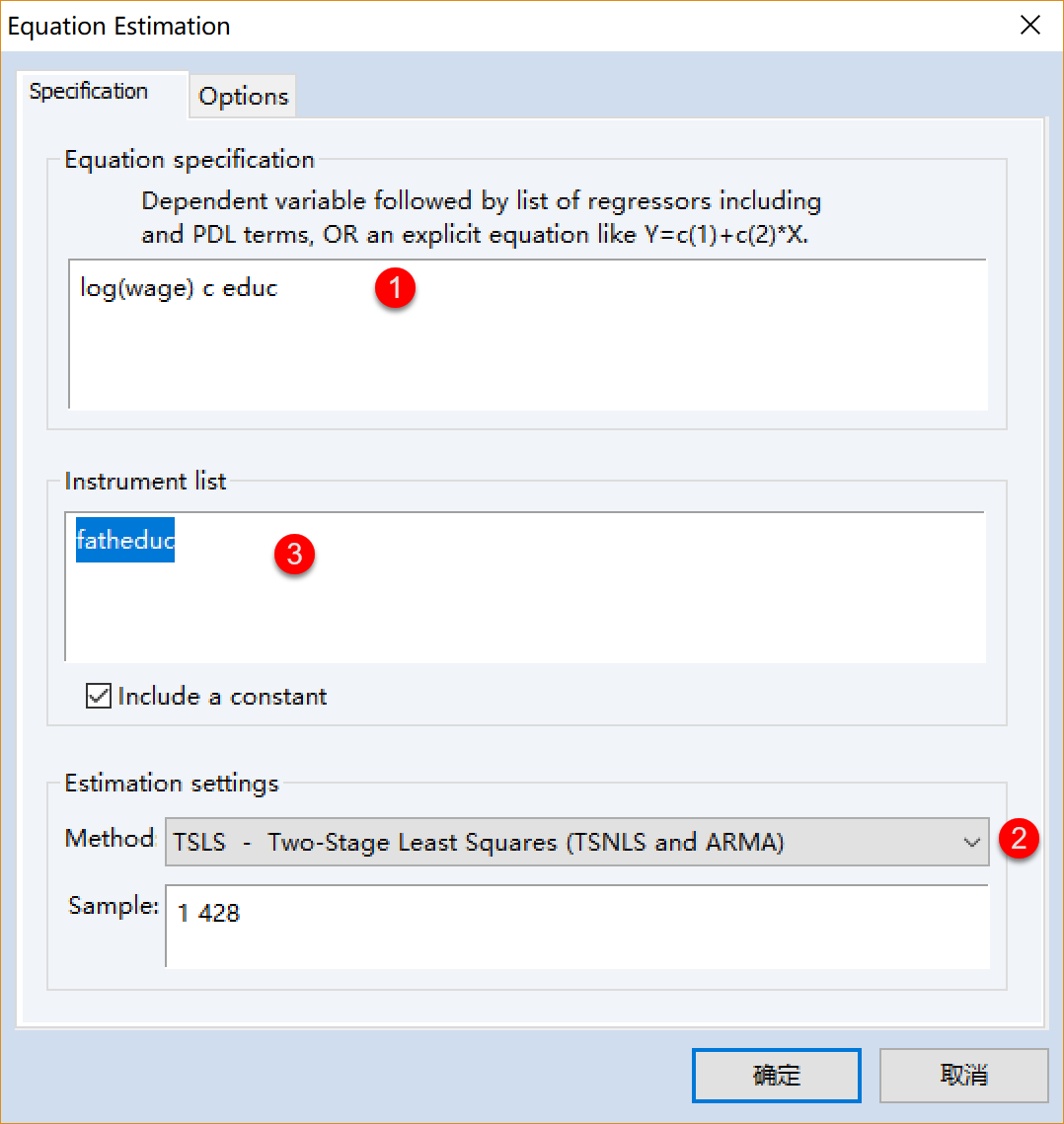
IV回归下EViews软件操作步骤
EViews软件下工具变量法的实现:
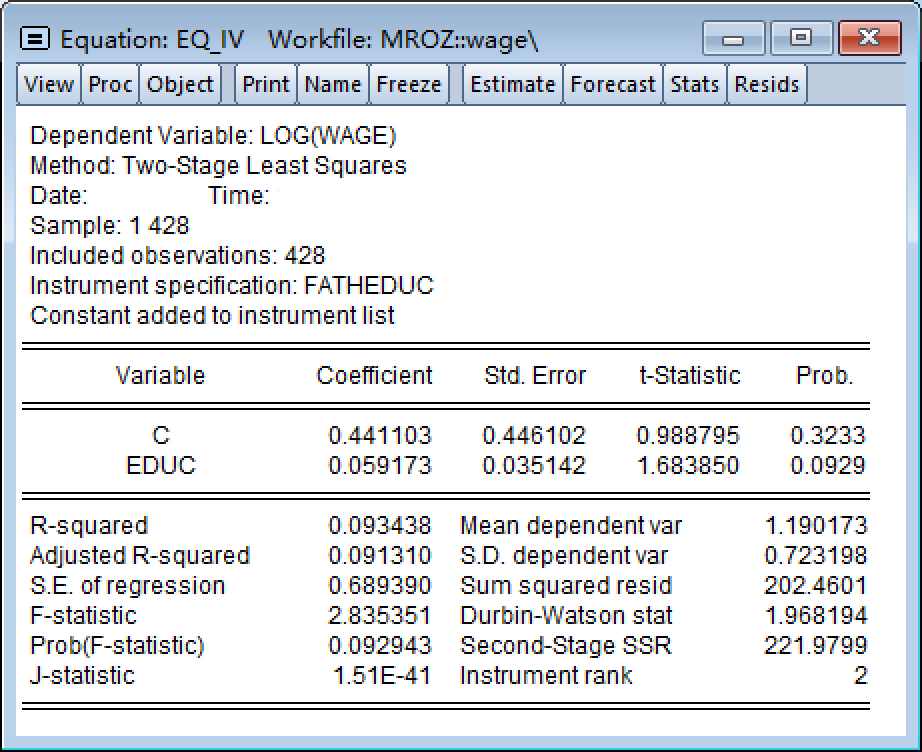
IV回归下EViews软件估计结果
EViews软件下工具变量法的结果:
17.4 两阶段最小二乘法(2SLS)
2SLS的基本过程
如果我们的工具变量数目多于内生自变量数目,则一致性估计量\(\boldsymbol{\hat{\beta}_{IV}}\) 可以通过两步法实现:
第1阶段:对自变量矩阵\(\mathbf{X}\) 的每1列都对全部工具变量\(\mathbf{Z}\)进行OLS回归。从而得到矩阵\(\mathbf{X}\)的拟合值矩阵\(\mathbf{\hat{X}}\)。
第2阶段: 将因变量\(\mathbf{y}\) 对拟合值矩阵\(\hat{X}\)进行OLS回归。
以上两个步骤,一起被称为 两阶段最小二乘法(two-stage least squares, 2SLS/TSLS)。
案例:手动2SLS法(无方差矫正)
阶段1:模型设定
首先,我们考虑使用母亲受教育情况\(motherduc\) 作为内生自变量\(educ\)的工具变量:
2SLS的第1阶段:内生自变量对全部工具变量进行OLS回归.
这一阶段中,我们将能够得到内生自变量的拟合变量 \(\widehat{educ}\):
\[ \begin{align} \widehat{educ} = \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\gamma}_3expersq +\hat{\gamma}_4mothereduc \end{align} \]
阶段1:回归结果
以下是 2SLS的第1阶段估计过程和结果(R代码):
\[ \begin{alignedat}{999} \begin{split} &\widehat{educ}=&&+9.78&&+0.05exper_i&&-0.00expersq_i&&+0.27motheduc_i\\ &(s)&&(0.4239)&&(0.0417)&&(0.0012)&&(0.0311)\\ &(t)&&(+23.06)&&(+1.17)&&(-1.03)&&(+8.60)\\ &(fit)&&R^2=0.1527&&\bar{R}^2=0.1467 && &&\\ &(Ftest)&&F^*=25.47&&p=0.0000 && && \end{split} \end{alignedat} \]
我们可以看到:\(mothereduc\)系数的样本t值大于2(2t法则),因此t检验显著(\(\alpha =0.05\)水平下),意味着工具变量和内生自变量之间存在明显的线性关系,而且是我们已经控制了其他变量的情况下。
阶段1:拟合结果
在2SLS的第1阶段过程中,我们很快可以获得内生自变量的OLS拟合值\(\widehat{educ}\),并把它列添加到数据集中:
阶段2:模型设定
2SLS的第2阶段: 使用母亲受教育情况\(motherduc\) 作为内生自变量\(educ\)的工具变量。
在第2阶段中,我们将因变量\(log(wage)\)对前面得到的拟合值\(\widehat{educ}\)以及原来模型中的外生自变量继续进行OLS回归。
\[ \begin{align} lwage = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} \end{align} \]
阶段2:回归结果
通过利用新的数据集mroz_add,2SLS的第2阶段回归结果如下:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lwage}=&&+0.20&&+0.05educHat_i&&+0.04exper_i&&-0.00expersq_i\\ &(s)&&(0.4933)&&(0.0391)&&(0.0142)&&(0.0004)\\ &(t)&&(+0.40)&&(+1.26)&&(+3.17)&&(-2.17)\\ &(fit)&&R^2=0.0456&&\bar{R}^2=0.0388 && &&\\ &(Ftest)&&F^*=6.75&&p=0.0002 && && \end{split} \end{alignedat} \]
但是请记住,用这种“step by step”的过程计算的标准误差是不正确的(为什么?)。
而正确的方法应该使用专用软件来求解工具变量模型。在R中,这样的函数是AER::ivreg()。
广义工具变量回归模型
定义
我们将内生自变量模型表达为:
\[ \begin{align} Y_{i}=\beta_{0}+\sum_{j=1}^{k} \beta_{j} X_{j i}+\sum_{s=1}^{r} \beta_{k+s} W_{ri}+\epsilon_{i} \end{align} \]
其中,\(\left(X_{1 i}, \ldots, X_{k i}\right)\) 是内生自变量 (endogenous regressors);\(\left(W_{1 i}, \ldots, W_{r i}\right)\) 是外生自变量 (exogenous regressors)。而且假定我们还找到了\(m\)个工具变量(instrumental variables)\(\left(Z_{1 i}, \ldots, Z_{m i}\right)\),它们都满足工具相关性(instrument relevance)和工具外生性(instrument exogeneity)两大条件。
如果\(m=k\),则参数估计将是恰好识别的(exactly identified).
如果\(m>k\),则参数估计将是过度识别的(over-identified).
When\(m<k\),则参数估计将是无法识别的(underidentified).
最后,只有\(m \geq k\)时,参数估计才是可识别的(identified)
2SLS估计过程
两阶段最小二乘法(2SLS):
第1阶段: 将自变量矩阵中的第1列\(X_{1i}\) 都对常数1、所有工具变量\(\left(Z_{1i}, \ldots, Z_{m i}\right)\) 以及所有外生自变量\(\left(W_{1i}, \ldots, W_{ri}\right)\) 进行OLS估计,并得到内生自变量的拟合值\(\hat{X}_{1 i}\)。对所有内生自变量都重复此步骤,最后得到\(\left(\hat{X}_{1 i}, \ldots, \hat{X}_{k i}\right)\)。
第2阶段: 将因变量\(Y_{i}\) 对常数、所有拟合变量\(\left(\hat{X}_{1 i}, \ldots, \hat{X}_{k i}\right)\)、以及所有外生自变量 \(\left(W_{1 i}, \ldots, W_{r i}\right)\) 继续进行OLS估计,并得到参数估计值\(\left(\hat{\beta}_{0}^{IV}, \hat{\beta}_{1}^{IV}, \ldots, \hat{\beta}_{k+r}^{IV}\right)\)
下面的几个例子中,我们将使用一次性的、整体性的2SLS估计方案,直接得到2SLS估计结果。也即:
- 对估计样本标准差进行某种合理矫正
- 一次性完成两个OLS估计步骤,直接得到最后估计结果。
- 我们这里将使用
R函数ARE::ivreg()来执行具体分析。
案例:2SLS仅使用母亲教育作为工具变量
2SLS的模型设定
工资案例中,我们首先仅使用\(mothereduc\)作为内生自变量\(educ\)的工具变量。
\[ \begin{cases} \begin{align} \widehat{educ} &= \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\gamma}_3expersq +\hat{\gamma}_4motheduc && \text{(stage 1)}\\ lwage & = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} && \text{(stage 2)} \end{align} \end{cases} \]
2SLS的估计结果
- 这里我们可以看到变量
educ的系数的t检验结果是显著的(给定\(\alpha =0.05\))。
附录:systemfit::systemfit()的R代码(m)
R软件中有两个包可以实现2SLS分析。其中之一为systemfit包,具体函数为systemfit::systemfit()。以下为R代码:
# load pkg
require(systemfit)
# set two models
eq_1 <- educ ~ exper + expersq + motheduc
eq_2 <- lwage ~ educ + exper + expersq
sys <- list(eq1 = eq_1, eq2 = eq_2)
# specify the instruments
instr <- ~ exper + expersq + motheduc
# fit models
fit.sys <- systemfit(
sys, inst=instr,
method="2SLS", data = mroz)
# summary of model fit
smry.system_m <- summary(fit.sys)附录:systemfit::systemfit()的R报告(m)
以下为systemfit::systemfit()2SLS的分析报告:
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 856 848 2085.49 1.96552 0.150003 0.112323
N DF SSR MSE RMSE R2 Adj R2
eq1 428 424 1889.658 4.456742 2.111100 0.152694 0.146699
eq2 428 424 195.829 0.461861 0.679604 0.123130 0.116926
The covariance matrix of the residuals
eq1 eq2
eq1 4.456742 0.304759
eq2 0.304759 0.461861
The correlations of the residuals
eq1 eq2
eq1 1.000000 0.212418
eq2 0.212418 1.000000
2SLS estimates for 'eq1' (equation 1)
Model Formula: educ ~ exper + expersq + motheduc
Instruments: ~exper + expersq + motheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.77510269 0.42388862 23.06055 < 2e-16 ***
exper 0.04886150 0.04166926 1.17260 0.24161
expersq -0.00128106 0.00124491 -1.02905 0.30404
motheduc 0.26769081 0.03112980 8.59918 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.1111 on 424 degrees of freedom
Number of observations: 428 Degrees of Freedom: 424
SSR: 1889.658428 MSE: 4.456742 Root MSE: 2.1111
Multiple R-Squared: 0.152694 Adjusted R-Squared: 0.146699
2SLS estimates for 'eq2' (equation 2)
Model Formula: lwage ~ educ + exper + expersq
Instruments: ~exper + expersq + motheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.198186056 0.472877230 0.41911 0.6753503
educ 0.049262953 0.037436026 1.31592 0.1889107
exper 0.044855848 0.013576817 3.30386 0.0010346 **
expersq -0.000922076 0.000406381 -2.26899 0.0237705 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.679604 on 424 degrees of freedom
Number of observations: 428 Degrees of Freedom: 424
SSR: 195.829058 MSE: 0.461861 Root MSE: 0.679604
Multiple R-Squared: 0.12313 Adjusted R-Squared: 0.116926 附录:ARE::ivreg()的R代码(m)
R软件中有另一个包函数ARE::ivreg()也可以实现2SLS分析。以下为相应的R代码及其分析报告:
附录:ARE::ivreg()的R报告(m)
运行上述ARE::ivreg()方法的R代码块,得到相应的R分析报告:
Call:
ivreg(formula = mod_iv_m, data = mroz)
Residuals:
Min 1Q Median 3Q Max
-3.10804 -0.32633 0.06024 0.36772 2.34351
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.1981861 0.4728772 0.419 0.67535
educ 0.0492630 0.0374360 1.316 0.18891
exper 0.0448558 0.0135768 3.304 0.00103 **
expersq -0.0009221 0.0004064 -2.269 0.02377 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6796 on 424 degrees of freedom
Multiple R-Squared: 0.1231, Adjusted R-squared: 0.1169
Wald test: 7.348 on 3 and 424 DF, p-value: 8.228e-05 我们可以看到\(educ\)前的t检验结果是不显著的。
案例:2SLS仅使用父亲教育为IV
2SLS的模型设定
这里,我们再考虑仅使用\(fatheduc\) 作为内生自变量\(educ\)的工具变量:
\[ \begin{cases} \begin{align} \widehat{educ} &= \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\gamma}_3expersq +\hat{\gamma}_4fatheduc && \text{(stage 1)}\\ lwage & = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} && \text{(stage 2)} \end{align} \end{cases} \]
同样,我们使用R软件进行2SLS估计。
2SLS的估计结果
这里我们可以看到变量
educ的系数的t检验结果是显著的(给定\(\alpha =0.05\))。
附录:systemfit::systemfit()的R代码(f)
R软件中有两个包可以实现2SLS分析。其中之一为systemfit包,具体函数为systemfit::systemfit()。以下为R代码:
# load pkg
require(systemfit)
# set two models
eq_1 <- educ ~ exper + expersq + fatheduc
eq_2 <- lwage ~ educ + exper + expersq
sys <- list(eq1 = eq_1, eq2 = eq_2)
# specify the instruments
instr <- ~ exper + expersq + fatheduc
# fit models
fit.sys <- systemfit(
sys, inst=instr,
method="2SLS", data = mroz)
# summary of model fit
smry.system_f <- summary(fit.sys)附录:systemfit::systemfit()的R报告(f)
以下为systemfit::systemfit()2SLS的分析报告:
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 856 848 2030.11 1.91943 0.172575 0.134508
N DF SSR MSE RMSE R2 Adj R2
eq1 428 424 1838.719 4.336602 2.082451 0.175535 0.169701
eq2 428 424 191.387 0.451384 0.671851 0.143022 0.136959
The covariance matrix of the residuals
eq1 eq2
eq1 4.336602 0.195036
eq2 0.195036 0.451384
The correlations of the residuals
eq1 eq2
eq1 1.000000 0.139402
eq2 0.139402 1.000000
2SLS estimates for 'eq1' (equation 1)
Model Formula: educ ~ exper + expersq + fatheduc
Instruments: ~exper + expersq + fatheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.88703429 0.39560779 24.99201 < 2e-16 ***
exper 0.04682433 0.04110742 1.13907 0.25532
expersq -0.00115038 0.00122857 -0.93636 0.34962
fatheduc 0.27050610 0.02887859 9.36701 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.082451 on 424 degrees of freedom
Number of observations: 428 Degrees of Freedom: 424
SSR: 1838.719104 MSE: 4.336602 Root MSE: 2.082451
Multiple R-Squared: 0.175535 Adjusted R-Squared: 0.169701
2SLS estimates for 'eq2' (equation 2)
Model Formula: lwage ~ educ + exper + expersq
Instruments: ~exper + expersq + fatheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.061116933 0.436446128 -0.14003 0.8887003
educ 0.070226291 0.034442694 2.03893 0.0420766 *
exper 0.043671588 0.013400121 3.25904 0.0012079 **
expersq -0.000882155 0.000400917 -2.20034 0.0283212 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.671851 on 424 degrees of freedom
Number of observations: 428 Degrees of Freedom: 424
SSR: 191.386653 MSE: 0.451384 Root MSE: 0.671851
Multiple R-Squared: 0.143022 Adjusted R-Squared: 0.136959 附录:ARE::ivreg()的R代码(f)
R软件中有另一个包函数ARE::ivreg()也可以实现2SLS分析。以下为相应的R代码及其分析报告:
附录:ARE::ivreg()的R报告(f)
运行上述ARE::ivreg()方法的R代码块,得到相应的R分析报告:
Call:
ivreg(formula = mod_iv_f, data = mroz)
Residuals:
Min 1Q Median 3Q Max
-3.09170 -0.32776 0.05006 0.37365 2.35346
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.0611169 0.4364461 -0.140 0.88870
educ 0.0702263 0.0344427 2.039 0.04208 *
exper 0.0436716 0.0134001 3.259 0.00121 **
expersq -0.0008822 0.0004009 -2.200 0.02832 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6719 on 424 degrees of freedom
Multiple R-Squared: 0.143, Adjusted R-squared: 0.137
Wald test: 8.314 on 3 and 424 DF, p-value: 2.201e-05 教育回报案例:2SLS同时使用父亲和母亲教育为IV
2SLS的模型设定
当然,我们实际上也可以同时使用\(motheduc\)和\(fatheduc\)作为内生自变量\(educ\)的工具变量。
\[ \begin{cases} \begin{align} \widehat{educ} &= \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\beta}_3expersq +\hat{\beta}_4motheduc + \hat{\beta}_5fatheduc && \text{(stage 1)}\\ lwage & = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} && \text{(stage 2)} \end{align} \end{cases} \]
2SLS的估计结果
- 这里我们可以看到 变量
educ的系数的t检验结果是显著的(p值小于0.1)。
附录:systemfit::systemfit()的R代码(mf)
R软件中有两个包可以实现2SLS分析。其中之一为systemfit包,具体函数为systemfit::systemfit()。以下为R代码:
# load pkg
require(systemfit)
# set two models
eq_1 <- educ ~ exper + expersq + motheduc + fatheduc
eq_2 <- lwage ~ educ + exper + expersq
sys <- list(eq1 = eq_1, eq2 = eq_2)
# specify the instruments
instr <- ~ exper + expersq + motheduc + fatheduc
# fit models
fit.sys <- systemfit(
sys, inst=instr,
method="2SLS", data = mroz)
# summary of model fit
smry.system_mf <- summary(fit.sys)附录:systemfit::systemfit()的R报告(mf)
以下为systemfit::systemfit()2SLS的分析报告:
systemfit results
method: 2SLS
N DF SSR detRCov OLS-R2 McElroy-R2
system 856 847 1951.6 1.83425 0.204575 0.149485
N DF SSR MSE RMSE R2 Adj R2
eq1 428 423 1758.58 4.157388 2.038967 0.211471 0.204014
eq2 428 424 193.02 0.455236 0.674712 0.135708 0.129593
The covariance matrix of the residuals
eq1 eq2
eq1 4.157388 0.241536
eq2 0.241536 0.455236
The correlations of the residuals
eq1 eq2
eq1 1.000000 0.175571
eq2 0.175571 1.000000
2SLS estimates for 'eq1' (equation 1)
Model Formula: educ ~ exper + expersq + motheduc + fatheduc
Instruments: ~exper + expersq + motheduc + fatheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) 9.10264011 0.42656137 21.33958 < 2.22e-16 ***
exper 0.04522542 0.04025071 1.12359 0.26182
expersq -0.00100909 0.00120334 -0.83857 0.40218
motheduc 0.15759703 0.03589412 4.39061 1.4298e-05 ***
fatheduc 0.18954841 0.03375647 5.61517 3.5615e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.038967 on 423 degrees of freedom
Number of observations: 428 Degrees of Freedom: 423
SSR: 1758.575263 MSE: 4.157388 Root MSE: 2.038967
Multiple R-Squared: 0.211471 Adjusted R-Squared: 0.204014
2SLS estimates for 'eq2' (equation 2)
Model Formula: lwage ~ educ + exper + expersq
Instruments: ~exper + expersq + motheduc + fatheduc
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.048100307 0.400328078 0.12015 0.9044195
educ 0.061396629 0.031436696 1.95302 0.0514742 .
exper 0.044170393 0.013432476 3.28833 0.0010918 **
expersq -0.000898970 0.000401686 -2.23799 0.0257400 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.674712 on 424 degrees of freedom
Number of observations: 428 Degrees of Freedom: 424
SSR: 193.020015 MSE: 0.455236 Root MSE: 0.674712
Multiple R-Squared: 0.135708 Adjusted R-Squared: 0.129593 附录:ARE::ivreg()的R代码(mf)
R软件中有另一个包函数ARE::ivreg()也可以实现2SLS分析。以下为相应的R代码及其分析报告:
附录:ARE::ivreg()的R报告(mf)
运行上述ARE::ivreg()方法的R代码块,得到相应的R分析报告:
Call:
ivreg(formula = mod_iv_mf, data = mroz)
Residuals:
Min 1Q Median 3Q Max
-3.0986 -0.3196 0.0551 0.3689 2.3493
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0481003 0.4003281 0.120 0.90442
educ 0.0613966 0.0314367 1.953 0.05147 .
exper 0.0441704 0.0134325 3.288 0.00109 **
expersq -0.0008990 0.0004017 -2.238 0.02574 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6747 on 424 degrees of freedom
Multiple R-Squared: 0.1357, Adjusted R-squared: 0.1296
Wald test: 8.141 on 3 and 424 DF, p-value: 2.787e-05 多模型比较
构建的多个模型
我们简单把前面的几类分析汇总一下。目前为止,我们实际上实施了总共 5 种参数估计,它们的估计方法或估计流程各有不同:
直接对误设模型(存在内生自变量问题)进行OLS估计。
一步一步的、“手动的”2SLS估计流程(仅使用\(motheduc\)作为工具变量),而且没有进行方差协方差矫正。
一次性的、“专门的”2SLS估计流程,并进行了方差协方差矫正。这里使用的是
R软件里的专用函数ARE::ivreg()进行整体“打包式”估计。具体我们估计了3个模型:
- 仅使用\(motheduc\)作为工具变量- 仅使用\(fatheduc\)作为工具变量- 同时使用\(motheduc\) 和\(fatheduc\) 作为工具变量
估计结果对比(图片形式)
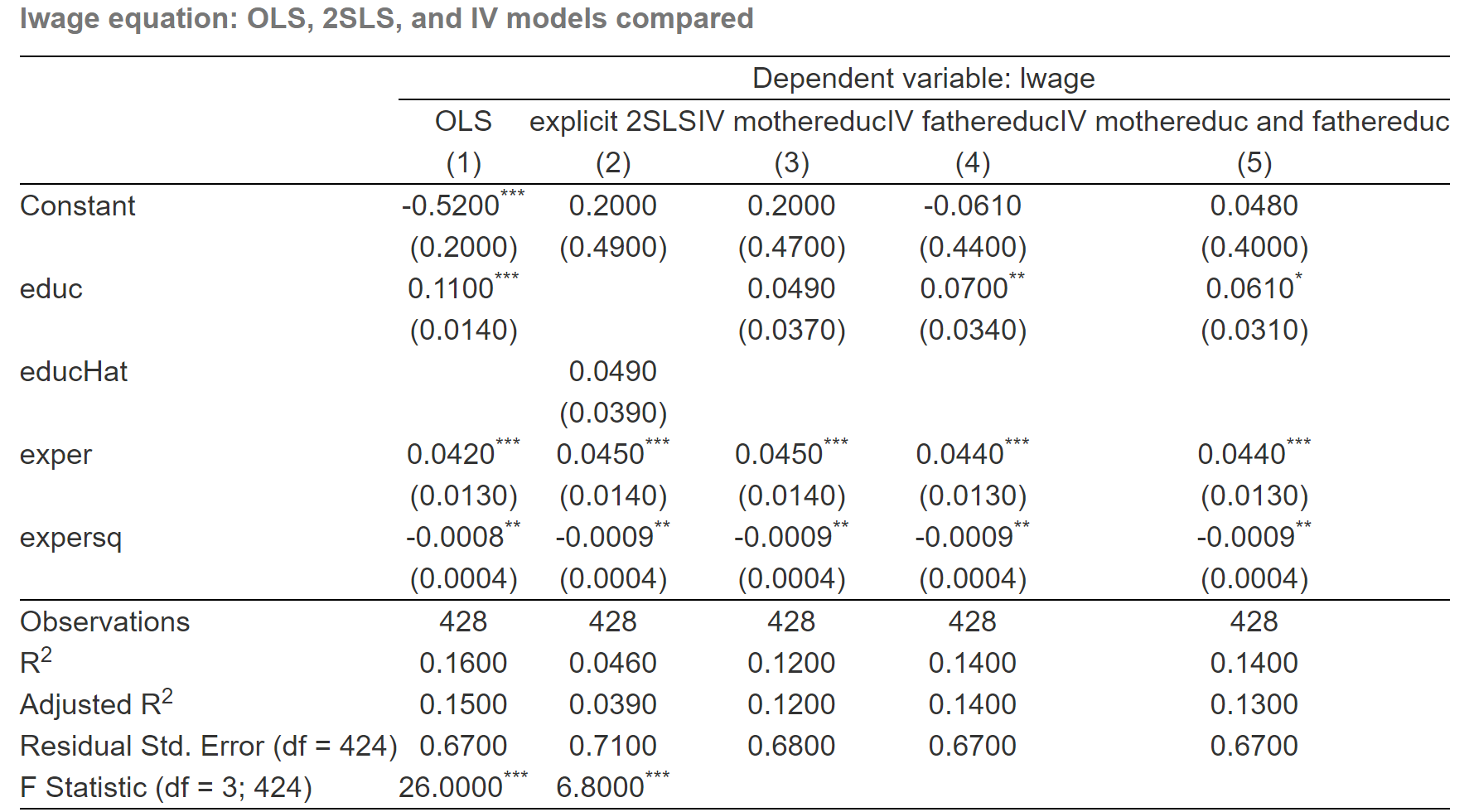
估计结果对比(表格形式7)
| Dependent variable: lwage | |||||
| OLS | explicit 2SLS | IV mothereduc | IV fathereduc | IV mothereduc and fathereduc | |
| (1) | (2) | (3) | (4) | (5) | |
| Constant | -0.5220*** | 0.1982 | 0.1982 | -0.0611 | 0.0481 |
| (0.1986) | (0.4933) | (0.4729) | (0.4364) | (0.4003) | |
| educ | 0.1075*** | 0.0493 | 0.0702** | 0.0614* | |
| (0.0141) | (0.0374) | (0.0344) | (0.0314) | ||
| educHat | 0.0493 | ||||
| (0.0391) | |||||
| exper | 0.0416*** | 0.0449*** | 0.0449*** | 0.0437*** | 0.0442*** |
| (0.0132) | (0.0142) | (0.0136) | (0.0134) | (0.0134) | |
| expersq | -0.0008** | -0.0009** | -0.0009** | -0.0009** | -0.0009** |
| (0.0004) | (0.0004) | (0.0004) | (0.0004) | (0.0004) | |
| Observations | 428 | 428 | 428 | 428 | 428 |
| R2 | 0.1568 | 0.0456 | 0.1231 | 0.1430 | 0.1357 |
| Adjusted R2 | 0.1509 | 0.0388 | 0.1169 | 0.1370 | 0.1296 |
| Residual Std. Error (df = 424) | 0.6664 | 0.7090 | 0.6796 | 0.6719 | 0.6747 |
| F Statistic (df = 3; 424) | 26.2862*** | 6.7510*** | |||
估计结果说明
表格中的主要信息说明如下:
列(1)\(\ldots\)(5)分别表示前述5个模型的估计结果,其中(1)和(2)没有进行方差矫正,而(3)、(4)、(5)则进行了方差矫正。
需要注意的是,(3)、(4)、(5)中的\(educ\)与(2)中的\(educHat\)是等价的。
括号里显示的是参数估计了的样本标准误差(standard error of the estimator)。
估计结果分析
5个模型估计结果比较的主要要点有:
首先,由表可知,教育在决定工资方面的重要性在模型(3)、(4)和(5)中相对要更小,系数分别为0.049,0.07,0.061。标准误差也随着估计模型(3)、(4)、(5)而减小。
其次,它还表明,明确的2SLS模型(2)和仅使用\(motheduc\)为工具变量的模型(3)产生相同的系数估计值,但标准误差不同。模型(2)中的2SLS的标准误差为0.039,比模型(3)估计值的标准误差0.037略大。
第三,当仅使用motheduc作为唯一工具变量时,模型(2)和模型(3)的教育系数的t检验不显著。
第四,我们这里可以充分感受和理解一下2SLS的“相对估计效率”!
17.5 检验工具变量的有效性(Instrument validity)
工具变量有效性
模型设定
考虑如下一般化的模型:
\[ \begin{align} Y_{i}=\beta_{0}+\sum_{j=1}^{k} \beta_{j} X_{j i}+\sum_{s=1}^{r} \beta_{k+s} W_{ri}+u_{i} \end{align} \]
\(Y_{i}\) 是因变量
\(\beta_{0}, \ldots, \beta_{k+1}\) 是\(1+k+r\)个 待估计回归系数- \(X_{1 i}, \ldots, X_{k i}\) 是\(k\)个 内生自变量- \(W_{1 i}, \ldots, W_{r i}\) 是\(r\)个 模型中外生自变量,它们都与\(u_{i}\)不相关
\(u_{i}\) 是随机干扰项
\(Z_{1 i}, \ldots, Z_{m i}\) 是 \(m\)个工具变量。
条件要求
工具变量有效性(Instrument valid)意味着工具变量必须同时满足工具相关性(Instrument Relevance)和工具外生性(Instrument Exogeneity)两个条件:
\[ E\left(Z_{i} X_{i}^{\prime}\right) \neq 0 \]
\[ E\left(Z_{i} u_{i}\right)=0 \]
检验工具相关性(弱工具变量)
放松条件
实际研究中,工具相关性也意味着,如果存在\(k\) 个内生自变量和\(m\) 个工具变量\(Z\),只要\(m \geq k\),则一定可以得到如下的外生变量向量:
\[ \left(\hat{X}_{1 i}^{*}, \ldots, \hat{X}_{k i}^{*}, W_{1 i}, \ldots, W_{r i}, 1\right) \]
而且,它也不应该 是完全共线性(perfectly multicollinear)。
其中: - \(\hat{X}_{1i}^{\ast}, \ldots, \hat{X}_{ki}^{\ast}\) 是2SLS中第1阶段得到的\(k\)个内生自变量的OLS估计拟合值. - 1 代表常数回归元,对于有截距回归模型,所有样本的常数回归元取值都等于1。
显然,完全多重共线是比较少见的,我们完全可以不用大费周章来仔细检验这种情形。
事实上,我们真正需要注意的是被称为“弱工具性”(weak instruments)的问题。
弱工具变量问题
弱工具变量:如果我们找到的工具变量只能解释内生自变量变异的很少部分,那么我们就称这样的工具变量为弱工具变量(weak instruments)。
正式地,当\(\operatorname{corr}\left(Z_{i}, X_{i}\right)\) 接近于0时,\(z_{i}\)被称作为弱工具变量。
考虑简单回归的情形\(Y_{i}=\beta_{0}+\beta_{1} X_{i}+\epsilon_{i}\)
参数\(\beta_{1}\)的IV估计值为\(\widehat{\beta}_{1}^{IV}=\frac{\sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)\left(Y_{i}-\bar{Y}\right)}{\sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)\left(X_{i}-\bar{X}\right)}\)
Note that\(\frac{1}{n} \sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)\left(Y_{i}-\bar{Y}\right) \xrightarrow{p} \operatorname{Cov}\left(Z_{i}, Y_{i}\right)\)
and\(\frac{1}{n} \sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)\left(X_{i}-\bar{X}\right) \xrightarrow{p} \operatorname{Cov}\left(Z_{i}, X_{i}\right)\).
- 因此,如果\(\operatorname{Cov}\left(Z_{i},X_{i}\right) \approx 0\), 那么IV估计值 \(\widehat{\beta}_{1}^{IV}\) 也将是无意义的。
案例:婴儿出生体重
模型以及可能的工具变量
下面的案例中,我们考察吸烟(smoking)对出生婴儿体重(birth weight)的影响,构建的模型如下:
\[ \begin{align} \log (\text {bwght})=\beta_{0}+\beta_{1} \text {packs}+\epsilon_{i} \end{align} \]
其中\(packs\) 时妈妈每天抽烟的盒数,我们有理由认为这个变量是内生自变量 (为什么?) 。另外,假定我们使用香烟平均价格\(cigprice\)作为内生自变量\(packs\)的一个工具变量,并假设它与随机干扰项\(\epsilon\)不相关。
TSLS回归结果
然而,妈妈抽烟盒数\(packs\)对香烟平均价格\(cigprice\)第1阶段OLS回归分析,我们发现基本上二者并没有相关关系。
\[ \begin{alignedat}{999} \begin{split} &\widehat{packs}=&&+0.0674&&+0.0003cigprice_i\\ &(s)&&(0.1025)&&(0.0008)\\ &(t)&&(+0.66)&&(+0.36)\\ &(Ftest)&&F^*=0.13&&p=0.7179 \end{split} \end{alignedat} \]
在这种情况下,如果我们执意使用\(cigprice\)作为工具变量,并进行第2阶段的OLS回归,我们会得到:
\[ \begin{alignedat}{999} \begin{split} &\widehat{lbwght}=&&+4.4481&&+2.9887packs\_hat_i\\ &(s)&&(0.1843)&&(1.7654)\\ &(t)&&(+24.13)&&(+1.69)\\ &(Ftest)&&F^*=2.87&&p=0.0907 \end{split} \end{alignedat} \]
显然,即便第2阶段的结果t检验是显著的,但它已经完全没有的检验的意义和价值。因为\(cigprice\)表现为弱工具变量,在第1阶段的回归就已经暴露出问题了。
弱工具变量策略
如果手里拿到的是弱工具变量,那么我们有两个实施策略:
- 忍爱放弃 弱工具变量 ,再次开始寻找强工具变量:
虽然前者只是一个选项,如果待估计参数仍然可识别时,即便弱工具变量被舍弃,参数估计还是可能的。但是后者可能就是极其困难的,甚至可能需要我们重新设计整个研究。
- 坚持使用弱工具变量,但要使用改进的2SLS方法。
这样的改进方法包括,诸如有限信息极大似然估计法(limited information maximum likelihood estimation, LIML)。
弱工具变量的受约束F检验(仅含1个内生自变量时)
下面先简单考虑只有一个内生自变量的情况。如果在2SLS估计的第1阶段回归中所有工具变量的系数联合F检验不显著(接受\(H_0: \alpha_1=\alpha2=\cdots=0\))则该工具变量显然不具备工具相关性的要求。
我们可以使用以下经验法则:
- 进行2SLS估计的第1阶段回归
\[ \begin{align} X_{i}=\hat{\alpha}_{0}+\hat{\alpha}_{1} Z_{1 i}+\ldots+\hat{\alpha}_{m} Z_{m i}+\hat{u}_{i} \quad \text{(3)} \end{align} \]
通过计算F统计量,对如下联合假设进行检验:\(H_0: \hat{\alpha}_1=\ldots=\hat{\alpha}_m=0\)。
如果计算得到的样本统计量\(F^{\ast}\)比理论查表值小,则不能拒绝\(H_0\) ,表明这些工具变量都是弱工具变量.。
这一经验法则在
R中很容易实现。使用lm()函数运行第1阶段回归,然后通过car::linearHypothesis()函数计算得到统计量\(F^{\ast}\)。
弱工具变量检验的Cragg-Donald检验(包含多个内生自变量时)
然而,如果模型中存在多个内生自变量,前述的F检验就变得不可靠了。——即便我们确实也可以对每1个内生自变量分别进行\(F\)检验。
此时,一个可行的检验方法是Cragg-Donald test,这一检验将依赖于计算如下的统计量:
\[ \begin{align} F=\frac{N-G-B}{L} \frac{r_{B}^{2}}{1-r_{B}^{2}} \end{align} \]
- 其中:\(G\) 是外生自变量的个数;\(B\) 是内生自变量的个数;\(L\) 是工具变量的个数;\(r_B\) 是最小的canonical相关系数(lowest canonical correlation)。
案例: 弱工具变量的受约束F检验
案例说明及3种模型设定
对于前面工资案例中的3个工具变量,我们可以依次检验它们的工具相关性:
\[ \begin{align} educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_1motheduc +v && \text{(relevance test 1)}\\ educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_2fatheduc +v && \text{(relevance test 2)} \\ educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_1motheduc + \theta_2fatheduc +v && \text{(relevance test 3)} \end{align} \]
受约束F检验:模型1(mothedu)检验结果
\[ \begin{align} educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_1motheduc +v \end{align} \]
Linear hypothesis test
Hypothesis:
motheduc = 0
Model 1: restricted model
Model 2: educ ~ exper + expersq + motheduc
Res.Df RSS Df Sum of Sq F Pr(>F)
1 425 2219.2
2 424 1889.7 1 329.56 73.946 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1知识回顾: 受约束F检验VS经典F检验
需要注意的是:受约束F检验(Restriced F test)是不同于 经典F检验(classical F test)的。我们可以简单比较一下。
这是经典F检验(classical F test)结果:
\[ \begin{alignedat}{999} \begin{split} &\widehat{educ}=&&+9.78&&+0.05exper_i&&-0.00expersq_i&&+0.27motheduc_i\\ &(s)&&(0.4239)&&(0.0417)&&(0.0012)&&(0.0311)\\ &(t)&&(+23.06)&&(+1.17)&&(-1.03)&&(+8.60) \end{split} \end{alignedat} \]
受约束F检验:模型2(fathedu)检验结果
\[ \begin{align} educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_1fatheduc +v && \text{(relevance test 2)} \end{align} \]
Linear hypothesis test
Hypothesis:
fatheduc = 0
Model 1: restricted model
Model 2: educ ~ exper + expersq + fatheduc
Res.Df RSS Df Sum of Sq F Pr(>F)
1 425 2219.2
2 424 1838.7 1 380.5 87.741 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1受约束F检验:模型3(mothedu和fathedu)检验结果
\[ \begin{align}educ &= \gamma_1 +\gamma_2exper +\gamma_2expersq + \theta_1motheduc + \theta_2fatheduc +v&& \text{(relevance test 3)}\end{align} \]
Linear hypothesis test
Hypothesis:
motheduc = 0
fatheduc = 0
Model 1: restricted model
Model 2: educ ~ exper + expersq + motheduc + fatheduc
Res.Df RSS Df Sum of Sq F Pr(>F)
1 425 2219.2
2 423 1758.6 2 460.64 55.4 < 2.2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1案例:弱工具变量的Cragg-Donald检验
案例说明及模型设定
下面,我们将构造含有2个内生自变量的模型,并尝试使用Cragg-Donald test方法来检验我们的工具变量是否是弱工具变量。假定如下误设工作时长回归模型(包含2个内生自变量):
\[ \begin{equation}hushrs=\beta_{1}+\beta_{2} mtr+\beta_{3} educ+\beta_{4} kidsl6+\beta_{5} nwifeinc+e\\ \end{equation} \]
- 2个 内生自变量: \(educ\) and \(mtr\)
- 2个 外生自变量: \(nwifeinc\) and \(kidslt6\)
- 2个 工具变量: \(motheduc\) and \(fatheduc\).
Cragg-Donald检验结果
我们仍旧使用前面的数据集mroz,且只用女性参加工作的样本数据集mroz1(\(inlf=1\))。
mroz1 <- wooldridge::mroz %>% filter(wage > 0, inlf == 1)
G <-2; L <-2; N <-nrow(mroz1)
x1 <- resid(lm(mtr ~ kidslt6 + nwifeinc, data = mroz1))
x2 <- resid(lm(educ ~ kidslt6 + nwifeinc, data = mroz1))
z1 <-resid(lm(motheduc ~ kidslt6 + nwifeinc, data = mroz1))
z2 <-resid(lm(fatheduc ~ kidslt6 + nwifeinc, data = mroz1))
X <- cbind(x1,x2)
Y <- cbind(z1,z2)
rB <- min(cancor(X, Y)$cor)
CraggDonaldF <- ((N-G-L)/L)/((1-rB^2)/rB^2)| G | L | B | N | rb | CraggDonaldF |
|---|---|---|---|---|---|
| 2 | 2 | 2 | 428 | 0.0218 | 0.1008 |
运行上述R代码,结果显示 Cragg-Donald统计量 \(F^{\ast}=\) 0.1008 ,它远小于理论查表值4.58[1]。
因此,我们无法拒绝 \(H_0\),认为工具变量\(motheduc\)和\(fatheduc\)两个都是弱工具变量。
检验工具外生性
主要的困难
工具变量外生性(Instrument Exogeneity) 意味着所有\(m\)个工具变量必须与随机干扰项不相关:
\[ Cov{(Z_{1 i}, \epsilon_{i})}=0; \quad \ldots; \quad Cov{(Z_{mi}, \epsilon_{i})}=0. \]
在只有少数工具变量情形下,我们会发现工具变量外生性的要求几乎无法被检验。(为什么?)
然而,如果我们有比我们需要的更多工具变量,那么我们可以有效地测试是否其中一些工具变量与随机干扰项无关。
因此,下面我们将主要讨论过度识别(over-identification)的内生自变量问题模型。
过度识别情形
我们已经知道,过度识别(over-identification)情况下\((m>k)\),我们可以通过尝试组合不同的工具变量来进行IV法参数估计。显然,理论上我们认为:
如果工具变量都是外生的,组合不同工具变量,那么得到的估计值应该是近似的。
如果估计值非常不同,则一些或所有工具变量可能不是外生的。
我们下面介绍的过度识别的受约束检验(overidentifying restrictions test) ——J test,正是基于这一检验思想:
- J test原假设为工具变量是外生性的:
\[ H_{0}: E\left(Z_{h i} \epsilon_{i}\right)=0, \text { for all } h=1,2, \dots, m \]
J test检验流程1/2
过度识别约束检验 (overidentifying restrictions test),又被称为\(J\)-test检验,或者Sargan test检验。这种检验的原假设为工具变量都是外生性的。
过度识别约束检验 的主要流程是:
- Step 1: 计算IV回归残差(IV regression residuals) :
\[ \widehat{\epsilon}_{i}^{IV}=Y_{i}-\left(\hat{\beta}_{0}^{ IV}+\sum_{j=1}^{k} \hat{\beta}_{j}^{IV} X_{j i}+\sum_{s=1}^{r} \hat{\beta}_{k+s}^{IV} W_{s i}\right) \]
- Step 2: 运行辅助回归,也即将IV回归残差对工具变量和外生自变量进行OLS回归估计。然后对该辅助回归进行如下的联合假设检验\(H_{0}: \alpha_{1}=0, \ldots, \alpha_{m}=0\)
\[ \widehat{\epsilon}_{i}^{IV}=\alpha_{0}+\sum_{h=1}^{m} \alpha_{h} Z_{h i}+\sum_{s=1}^{r} \alpha_{m+s} W_{s i}+v_{i} \quad \text{(2)} \]
J test检验流程2/2
- Step3: 根据上述受约束联合F检验计算得到 如下J统计量:\(J=m F^{\ast}\)
其中\(F^{\ast}\) 是前述\(m\)个受约束回归检验中的F统计量值。其约束条件为\(H_0: \alpha_{1}=\ldots=\alpha_{m}=0\) in eq(2)
在 原假设\(H_0\)下,上面计算得到的J统计量统计量在大样本情况下服从卡方分布\(\chi^{2}(m-k)\)。
\[ \boldsymbol{J} \sim \chi^{2}({m-k}) \]
如果\(J\) 小于卡方分布理论查表值,则J检验不显著,不能拒绝\(H_0\),意味着所有工具变量都是外生性的。
如果\(J\) 大于卡方分布理论查表值,则J检验显著,拒绝\(H_0\),接受\(H_1\),意味着所有至少有1个工具变量不是外生性的。
案例:工具外生性检验
主模型和辅助模型设定
继续讨论工资案例,这里我们考虑同时使用 \(motheduc\)和 \(fatheduc\)作为内生自变量 \(educ\)的工具变量。
初步可以判断,下述的IV模型是过度识别的,因此我们采用J-test来检验两个工具变量是不是全都是外生性的。
2SLS模型中,我们设定为:
\[ \begin{cases} \begin{align} \widehat{educ} &= \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\beta}_3expersq +\hat{\beta}_4motheduc + \hat{\beta}_5fatheduc && \text{(stage 1)}\\ lwage & = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} && \text{(stage 2)} \end{align} \end{cases} \]
那么辅助回归,我们相应地设定为:
\[ \begin{align} \hat{\epsilon}^{IV} &= \hat{\alpha}_1 +\hat{\alpha}_2exper + \hat{\alpha}_3expersq +\hat{\alpha}_4motheduc + \hat{\alpha}_5fatheduc + v && \text{(auxiliary model)} \end{align} \]
拟合模型并得到IV估计法下的残差(代码)
拟合模型并得到IV估计法下的残差(数据集)
利用残差执行辅助回归分析
下一步,我们运行前面设定的辅助回归,并得到如下结果(事实上这里不能得到外生性的任何结论):
Call:
lm(formula = mod_jtest, data = mroz_resid)
Residuals:
Min 1Q Median 3Q Max
-3.1012 -0.3124 0.0478 0.3602 2.3441
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.096e-02 1.413e-01 0.078 0.938
exper -1.833e-05 1.333e-02 -0.001 0.999
expersq 7.341e-07 3.985e-04 0.002 0.999
motheduc -6.607e-03 1.189e-02 -0.556 0.579
fatheduc 5.782e-03 1.118e-02 0.517 0.605
Residual standard error: 0.6752 on 423 degrees of freedom
Multiple R-squared: 0.0008833, Adjusted R-squared: -0.008565
F-statistic: 0.0935 on 4 and 423 DF, p-value: 0.9845对辅助回归模型进行受约束F检验
实际上,关键的步骤是我们对辅助回归进行如下的受约束联合F检验,并得到F统计量值\(F^{\ast} =0.19\)
Linear hypothesis test
Hypothesis:
motheduc = 0
fatheduc = 0
Model 1: restricted model
Model 2: resid_iv_mf ~ exper + expersq + motheduc + fatheduc
Res.Df RSS Df Sum of Sq F Pr(>F)
1 425 193.02
2 423 192.85 2 0.1705 0.187 0.8295对辅助回归模型进行卡方检验(获得J统计量)
此外我们还可以根据受约束联合F检验可计算出卡方统计量,并得到检验结论。
Linear hypothesis test
Hypothesis:
motheduc = 0
fatheduc = 0
Model 1: restricted model
Model 2: resid_iv_mf ~ exper + expersq + motheduc + fatheduc
Res.Df RSS Df Sum of Sq Chisq Pr(>Chisq)
1 425 193.02
2 423 192.85 2 0.1705 0.374 0.8294对辅助回归模型进行卡方检验(获得J统计量的p值)
因为R软件中linearHypothesis()默认卡方自由度是\(m\)。现在,我们需要设定正确的卡方检验自由度为\(f=m-k=2-1=1\):
R软件中,我们可以直接使用pchisq()函数,计算卡方统计量\({\chi^2}^{\ast} =0.3740\)对应的概率p值,并做出假设检验的判断。(当然,我们也可以通过卡方分布的理论查表值做出假设检验判断)
因为计算得到的卡方概率值\(p=\) 0.5408,比0.1还要大。因此,我们不能拒绝原假设,从而认为所有工具变量\(motheduc\)和\(fatheduc\)都是外生性的!
17.6 检验自变量的内生性
检验自变量的内生性
自变量内生性的含义
由于OLS通常比IV方法更有效(回想一下,如果高斯-马尔科夫假设成立,则OLS估计为BLUE)。
这也就以为着,如果我们并不想得到一致性估计量时,我们实际上并不需要使用IV方法。
当然,如果我们确实想要得到一致性估计量,面对内生自变量问题模型,我们还需要检验内生自变量是不是真的是内生性的,也即:
\[ H_{0}: \operatorname{Cov}(X, \epsilon)=0 \text { vs. } H_{1}: \operatorname{Cov}(X, \epsilon) \neq 0 \]
Hausman检验的基本思路
Hausman test将会告诉我们:如果不能拒绝原假设\(H_{0}\),我们直接使用OSL方法估计就很有效;如果显著拒绝原假设\(H_{0}\),那么使用IV法才能得到参数的一致性估计量。
下面给出的是Hausman test检验的基本思想和逻辑:
如果自变量\(X\) 确实是 外生性的,那么我们采用OLS方法和采用IV方法,两者的参数估计结果应该是一样的。
如果自变量\(X\) 确实存在 内生性,那么我们采用OLS方法和采用IV方法,两者的参数估计结果应该是不一样的。
Hausman检验的关键
Hausman test检验的关键,就是比较OLS方法和IV方法下参数估计值之间的差异性。
如果两种估计方法的差异是微小,我们可以推测OLS和IV是一致的,也即模型中自变量都是外生的。我们可以直接使用OLS方法。
如果两种估计方法的差异很大,意味着OLS和IV估计量是不一致的。在这种情况下,模型可能存在内生自变量问题,那么我们应该使用IV法。
Hausman检验的模型形式
下面给出的是Hausman test的具体检验形式:
\[ \begin{align} \hat{H}=n\boldsymbol{\left[\hat{\beta}_{IV}-\hat{\beta}_{\text {OLS}}\right] ^{\prime}\left[\operatorname{Var}\left(\hat{\beta}_{IV}-\hat{\beta}_{\text {OLS}}\right)\right]^{-1}\left[\hat{\beta}_{IV}-\hat{\beta}_{\text {OLS}}\right]} \xrightarrow{d} \chi^{2}(k) \end{align} \]
如果样本统计量\(\hat{H}\) 比卡方理论查表值 小,则Hausman test不显著,不能显著拒绝\(H_0\),从而认为所有自变量应该不是内生性的。
如果样本统计量\(\hat{H}\) 比卡方理论查表值 大,则Hausman test是显著的,显著拒绝\(H_0\),接受\(H_1\),从而认为至少有部分自变量是内生性的。
案例:Hausman检验
工具变量模型设定
再次使用工资案例进行说明。我们继续同时使用\(motheduc\) 和\(fatheduc\) 作为内生自变量\(educ\)的工具变量。并做出如下的2SLS模型设定:
\[ \begin{cases} \begin{align} \widehat{educ} &= \hat{\gamma}_1 +\hat{\gamma}_2exper + \hat{\beta}_3expersq +\hat{\beta}_4motheduc + \hat{\beta}_5fatheduc && \text{(stage 1)}\\ lwage & = \hat{\beta}_1 +\hat{\beta}_2\widehat{educ} + \hat{\beta}_3exper +\hat{\beta}_4expersq + \hat{\epsilon} && \text{(stage 2)} \end{align} \end{cases} \]
在
R软件中,我们可以使用IV模型诊断工具来进行Hausman test。其中只需要设定函数summary(lm_iv_mf, diagnostics = TRUE)中的参数diagnostics = TRUE,我们就能得到Hausman test结论。
Hausman检验结果
Call:
ivreg(formula = mod_iv_mf, data = mroz)
Residuals:
Min 1Q Median 3Q Max
-3.0986 -0.3196 0.0551 0.3689 2.3493
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.0481003 0.4003281 0.120 0.90442
educ 0.0613966 0.0314367 1.953 0.05147 .
exper 0.0441704 0.0134325 3.288 0.00109 **
expersq -0.0008990 0.0004017 -2.238 0.02574 *
Diagnostic tests:
df1 df2 statistic p-value
Weak instruments 2 423 55.400 <2e-16 ***
Wu-Hausman 1 423 2.793 0.0954 .
Sargan 1 NA 0.378 0.5386
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6747 on 424 degrees of freedom
Multiple R-Squared: 0.1357, Adjusted R-squared: 0.1296
Wald test: 8.141 on 3 and 424 DF, p-value: 2.787e-05 Hausman检验结果
我们来解读一下这份模型诊断报告:
- (Wu-)Hausman test用于内生性检验, 拒绝原假设,认为自变量\(Educ\)是内生性的。
- Weak instruments test用于弱工具变量检验,拒绝原假设,认为至少有1个工具变量不是弱工具变量。
- Sargan overidentifying restrictions用于检验外生性。结果发现不能拒绝原假设,意味着工具变量随机干扰项是不相关的(外生性的)。
本章小结
知识小结
一个工具变量必须有两个属性:
- 必须与随机干扰项不相关(工具外生性);
- 必须与内生解释变量部分相关(工具相关性)。
找到具有上述两个属性的变量通常很有挑战性。
虽然我们永远不能测试所有的工具变量是否是外生的,但我们至少可以测试它们中的一些否是外生的。
当工具变量有效时,我们可以进一步检验解释变量是否为内生性的。
两阶段最小二乘(2SLS)方法在社会科学中经常使用。但是当工具变量很差时,2SLS可能比OLS方法更糟糕。
案例学习
案例1: Card (1995) 1/2
In Card (1995) education is assumed to be endogenous due to omitted ability or measurement error. The standard wage function
\[ \ln \left(w a g e_{i}\right)=\beta_{0}+\beta_{1} E d u c_{i}+\sum_{m=1}^{M} \gamma_{m} W_{m i}+\varepsilon_{i} \]
is estimated by Two Stage Least Squares using a binary instrument, which takes value 1 if there is an accredited 4-year public college in the neighborhood (in the “local labour market”), 0 otherwise.
案例1: Card (1995) 2/2
The dataset is available online at http://davidcard.berkeley.edu/data_sets.html and consists of 3010 observations from the National Longitudinal Survey of Young Men.
- Education is measured by the years of completed schooling and varies we between 2 and 18 years.
案例2: Angrist and Krueger (1991) 1/2
The data is available online at http://economics.mit.edu/faculty/angrist/data1/data/angkru1991 and consists of observations from 1980 Census documented in Census of Population and Housing, 1980: Public Use Microdata Samples.
练习案例2: Angrist and Krueger (1991) 2/2
- They observe that individuals born earlier in the year (first two quarters) have less schooling than those born later in the year.
It is a consequence of the compulsory schooling laws, as individuals born in the first quarters of the year reach the minimum school leaving age at the lower grade and might legally leave school with less education.
The main criticism of Angrist and Krueger (1991) analysis, pointed out by Bound, Jaeger and Baker (1995) is that the quarter of birth is a weak instrument.
A second criticism of Angrist and Krueger (1991) results, discussed by Bound and Jaeger (1996) is that quarter of birth might be correlated with unobserved ability and hence does not satisfy the instrumental exogeneity condition.
本章结束

第17章 内生性问题与工具变量法