计量经济学实验
(Econometrics Lab)
基于EViews软件的实验设计与应用
Hu Huaping (胡华平)
huhuaping01 at hotmail.com
经济管理学院(CEM)
2025年11月24日
Lab 02: 一元线性回归
实验目的与原理
实验目的及要求
目的:熟悉一元回归建模和分析的基本原理。
要求:
- 熟练利用EViews软件进行一元回归分析
- 进行计量经济检验
- 能快速看懂EViews分析报告,并理解报告内容的内部关系
实验原理要点
- 经济建模要点
- 参数估计(最小二乘法)
- 参数推断
- 拟合优度(判定系数)
- 模型检验(经济学检验、统计学检验:t检验和F检验)
- 样本外预测
回归的本质
回归是对个体值\(Y_i\)有”回归”到条件期望值\(E(Y|X_i)\)这一现象的形象表达。
- 线性回归:条件期望值\(E(Y|X_i)\)的轨迹表现为直线
- 在给定不同的\(X_i\),个体值\(Y_i\)有”回归”到一条直线的趋势
- 回归分析是对总体真实规律的探索,通过样本来猜测和推断
注记
回归:通过解释变量\(X_i\)(在重复抽样中)的已知或设定值,去估计和(或)预测应变量\(Y_i\)的总体均值。
核心概念:总体与样本
总体回归模型(PRM):
- \(\beta_1+\beta_2X_i\):确定性部分(总体回归函数PRF)
- \(u_i\):随机干扰项(随机性部分)
样本回归模型(SRM):
\[ \begin{aligned} Y_i=\hat{\beta}_1+\hat{\beta}_2X_i+e_i \end{aligned} \]
- \(\hat{\beta}_1+\hat{\beta}_2X_i\):样本回归函数(SRF)
- \(e_i\):残差
参数估计方法
用样本数据估计总体参数,有三种指导理念不同的方法:
- 最小二乘法(LS):使拟合的样本回归线与样本观测点之间的欧几里得空间距离最小化
- 极大似然法(ML):使实验样本在下次抽样时能最大可能再次出现
- 矩估计法(MM):通过样本矩等于总体矩求解参数
提示
本章重点介绍最小二乘法(LS)在线性回归模型中的使用。
参数估计与检验
最小二乘法(LS)估计
对于线性模型:
\[ \begin{aligned} Y_i &=\beta_1+\beta_2X_i+u_i && \text{(PRM)} \\ Y_i &=\hat{\beta}_1+\hat{\beta}_2X_i+e_i && \text{(SRM)} \end{aligned} \]
求解最小化过程:
\[ \begin{aligned} Min(Q) &=\sum{(Y_i-\hat{Y}_i)^2}\\ &=\sum{\left ( Y_i-(\hat{\beta}_1+\hat{\beta}_2X_i) \right )^2} \end{aligned} \]
回归系数估计公式
FF公式(Favorite Five):
\[ \begin{aligned} \hat{\beta}_2 &=\frac{n\sum{X_iY_i}-\sum{X_i}\sum{Y_i}}{n\sum{X_i^2}-\left ( \sum{X_i} \right)^2}\\ \hat{\beta_1} &=\frac{n\sum{X_i^2Y_i}-\sum{X_i}\sum{X_iY_i}}{n\sum{X_i^2}-\left ( \sum{X_i} \right)^2} \end{aligned} \]
ff公式(离差形式):
\[ \begin{aligned} \hat{\beta}_2 &=\frac{\sum{x_iy_i}}{\sum{x_i^2}}\\ \hat{\beta_1} &=\bar{Y}_i-\hat{\beta}_2\bar{X}_i \end{aligned} \]
其中:\(x_i=X_i-\bar{X}\),\(y_i=Y_i-\bar{Y}\)
误差方差估计
\[ \begin{aligned} \hat{\sigma}^2 &=\frac{\sum{e_i^2}}{n-2}=\frac{\sum{(Y_i-\hat{Y}_i)^2}}{n-2} \end{aligned} \]
高斯-马尔可夫定理
重要
在正态经典线性回归模型假设(N-CLRM)下,采用普通最小二乘法(OLS),得到的估计量\(\hat{\beta}\),是真实参数\(\beta\)最优的、线性的、无偏估计量(BLUE)。
\[ \begin{aligned} \xrightarrow{\text{N-CLRM}} {\text{OLS}}(\hat{\beta})\xrightarrow[\text{}]{\text{BLUE}}\beta \end{aligned} \]
拟合优度:判定系数
通过平方和分解:
\[ \begin{aligned} TSS&=ESS+RSS\\ \sum{y_i^2} &= \sum{\hat{y_i}^2} +\sum{e_i^2} \end{aligned} \]
判定系数:
\[ \begin{aligned} r^2 &=\frac{ESS}{TSS}=\frac{\sum{(\hat{Y_i}-\bar{Y})^2}}{\sum{(Y_i-\bar{Y})^2}}\\ &=1-\frac{RSS}{TSS} \end{aligned} \]
注记
一元回归中,判定系数\(r^2\)等于简单相关系数\(r_{X_i,Y_i}\)的平方。
回归系数的t检验
在N-CLRM下,可以构造t统计量:
\[ \begin{aligned} t_{\hat{\beta_2}}^{\ast}&=\frac{\hat{\beta_2}}{S_{\hat{\beta_2}}} \sim t(n-2)\\ t_{\hat{\beta_1}}^{\ast}&=\frac{\hat{\beta_1}}{S_{\hat{\beta_1}}} \sim t(n-2) \end{aligned} \]
其中:
\[ \begin{aligned} S_{\hat{\beta}_2} &=\sqrt{\frac{1}{\sum{x_i^2}}}\cdot\hat{\sigma}\\ S_{\hat{\beta}_1} &=\sqrt{\frac{\sum{X_i^2}}{n\sum{x_i^2}}}\cdot\hat{\sigma} \end{aligned} \]
模型整体显著性:F检验
F统计量:
\[ \begin{aligned} F^{\ast}&=\frac{ESS/df_{ESS}}{RSS/df_{RSS}}=\frac{MSS_{ESS}}{MSS_{RSS}} \\ &\sim F(df_{ESS},df_{RSS}) \end{aligned} \]
对于一元回归:\(df_{ESS}=1\),\(df_{RSS}=n-2\)
样本外预测
均值预测:
给定\(X_0\),预测\(E(Y|X=X_0)\):
\[ \begin{aligned} \hat{Y}_0&=\hat{\beta}_1+\hat{\beta}_2X_0\\ S_{\hat{Y}_0}&=\sqrt{\hat{\sigma}^2 \left( \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right)} \end{aligned} \]
个值预测:
给定\(X_0\),预测\((Y_0|X=X_0)\):
\[ \begin{aligned} S_{(Y_0-\hat{Y}_0)}&=\sqrt{\hat{\sigma}^2 \left(1+ \frac{1}{n}+ \frac{(X_0-\bar{X})^2}{\sum{x_i^2}} \right)} \end{aligned} \]
看懂EViews报告
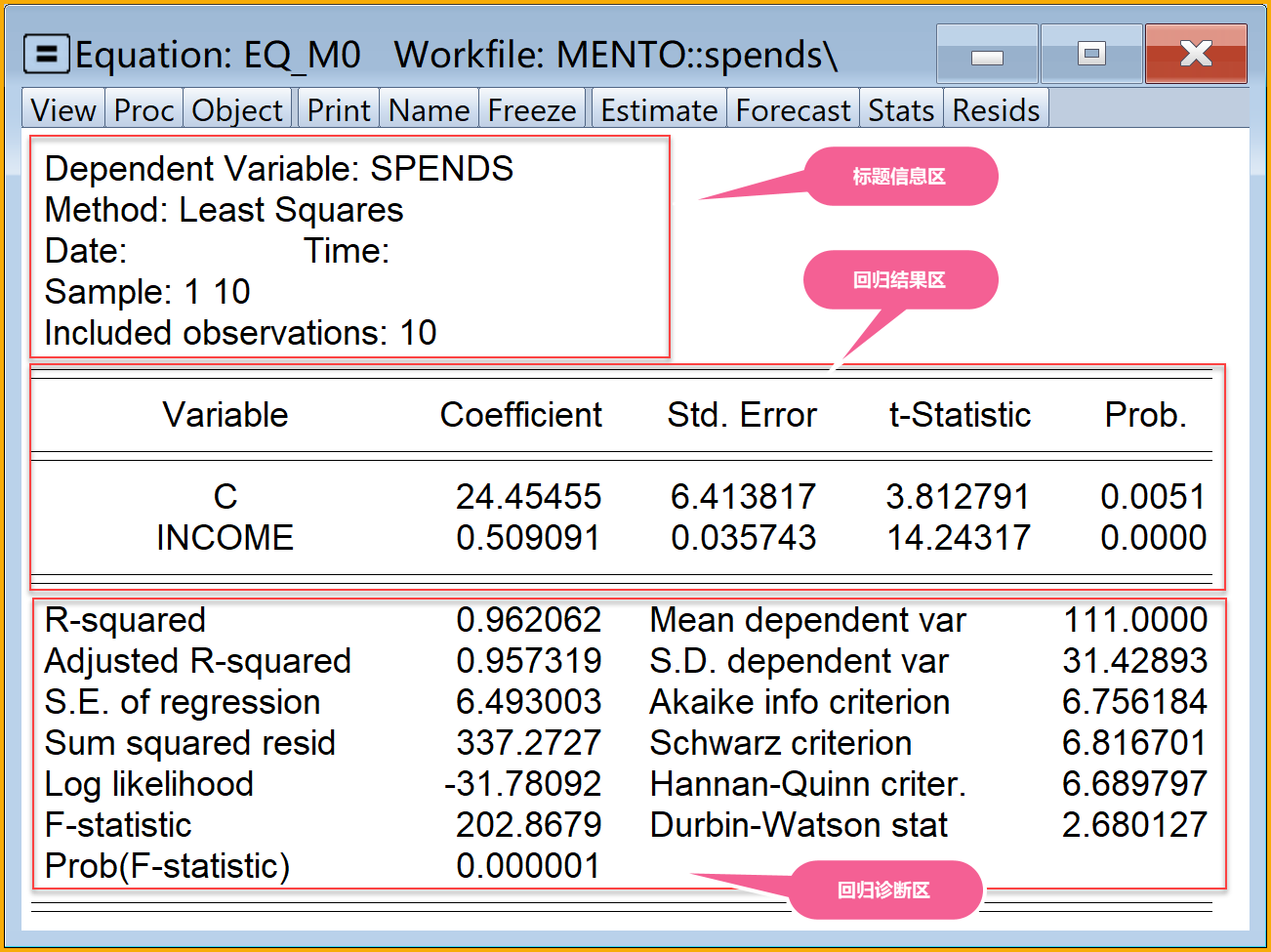
EViews回归报告结构
标题信息区
| row | content | mark |
|---|---|---|
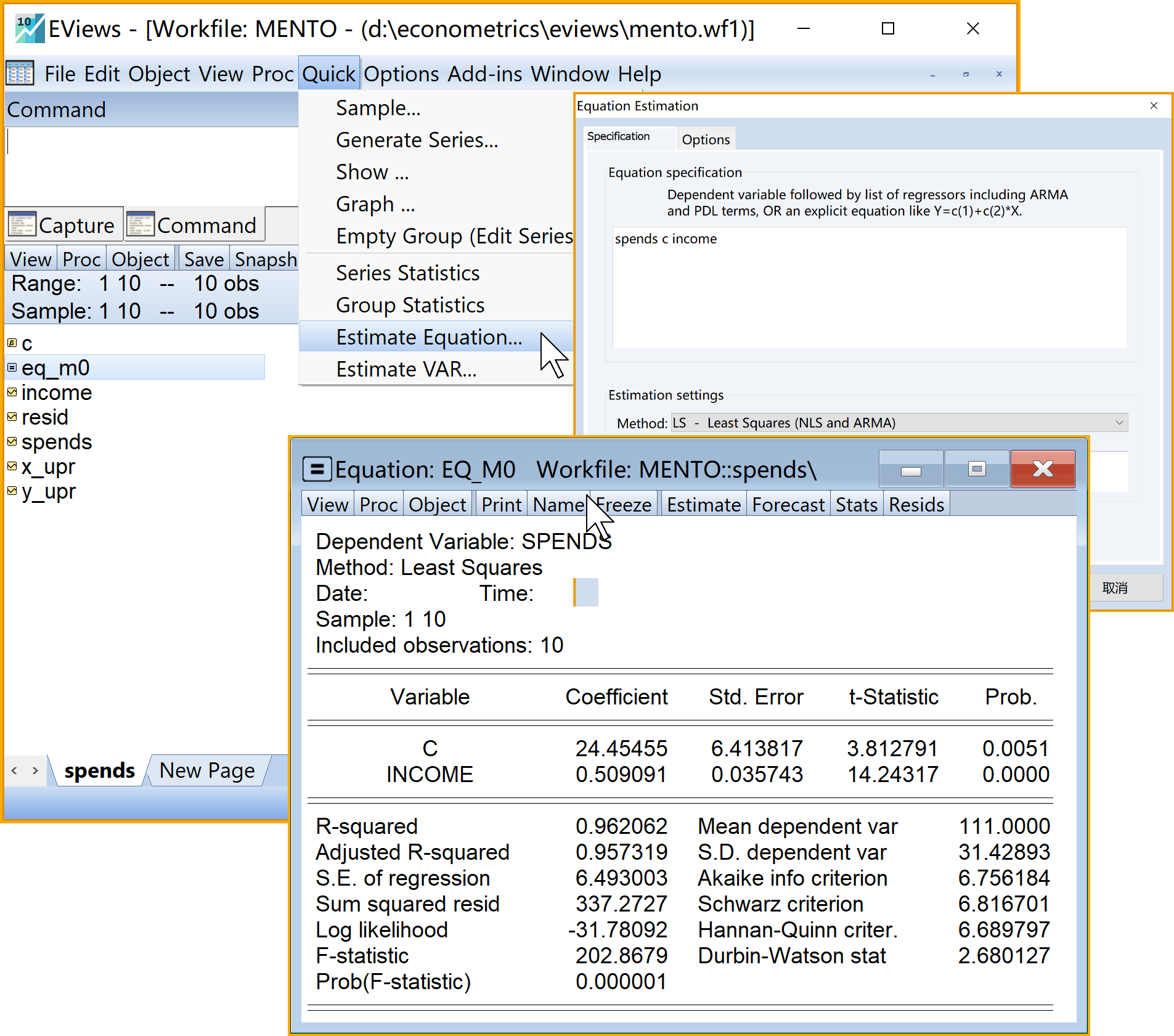
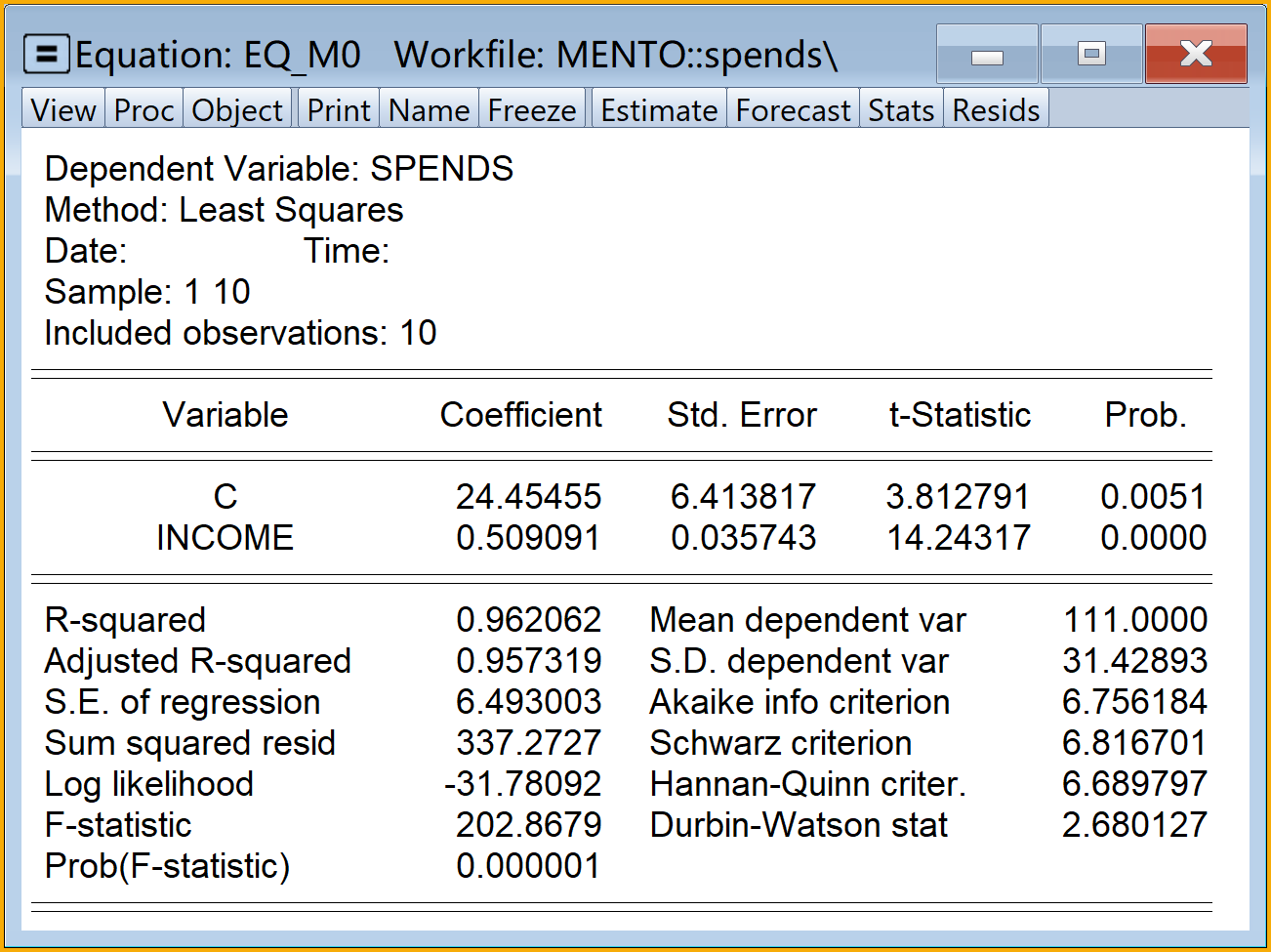
| 第1行 | Dependent Variable: SPENDS | 因变量 |
| 第2行 | Method: Least Squares | 方法 |
| 第3行 | Date: Time: | 日期、时间 |
| 第4行 | Sample: 1 10 | 样本框 |
| 第5行 | Included observations: 10 | 样本数 |
回归结果区
| row | column | content | mark | math |
|---|---|---|---|---|
| 第1行 | 第1列 | Variable | 方程变量 | |
| 第2行 | 第1列 | C | 回归方程的截距 | |
| 第3行 | 第1列 | INCOME | 回归方程的变量X | |
| 第1行 | 第2列 | Coefficient | 系数(回归参数的点估计值) | |
| 第2行 | 第2列 | … | 截距系数 | \(\hat{\beta}_1\) |
| 第3行 | 第2列 | … | 斜率系数 | \(\hat{\beta}_2\) |
| 第1行 | 第3列 | Std. Error | 系数的样本标准差 | |
| 第2行 | 第3列 | … | 截距系数的样本标准差 | \(S_{\hat{\beta}_1}\) |
| 第3行 | 第3列 | … | 斜率系数的样本标准差 | \(S_{\hat{\beta}_2}\) |
| 第1行 | 第4列 | t-Statistic | 系数的样本t值 | |
| 第2行 | 第4列 | … | 截距系数的样本t值 | \(t^{\ast}_{\hat{\beta}_1}\) |
| 第3行 | 第4列 | … | 斜率系数的样本t值 | \(t^{\ast}_{\hat{\beta}_2}\) |
| 第1行 | 第5列 | Prob. | 系数的样本t值对应的概率值p | |
| 第2行 | 第5列 | … | 截距系数的样本t值对应的概率值p | \(p(\alpha/2, t^{\ast}_{\hat{\beta}_1}, f)\) |
| 第3行 | 第5列 | … | 斜率系数的样本t值对应的概率值p | \(p(\alpha/2, t^{\ast}_{\hat{\beta}_2}, f)\) |
回归诊断区
| row | column | content | mark | math |
|---|---|---|---|---|
| 第1行 | 第1列 | R-squared | 判定系数 | \(R^2\) |
| 第2行 | 第1列 | Adjusted R-squared | 调整判定系数 | \(\bar{R}^2\) |
| 第3行 | 第1列 | S.E. of regression | 回归标准误 | \(\hat{\sigma}\) |
| 第4行 | 第1列 | Sum squared resid | 残差平方和 | \(RSS=\sum{e_i^2}\) |
| 第5行 | 第1列 | Log likelihood | 对数似然值 | |
| 第6行 | 第1列 | F-statistic | 回归方程的F统计量值 | \(F^{\ast}\) |
| 第7行 | 第1列 | Prob(F-statistic) | F统计量值对应的概率值p | \(p(\alpha, F^{\ast}, f_1,f_2)\) |
| 第1行 | 第3列 | Mean dependent var | 因变量的均值 | \(\bar{Y}\) |
| 第2行 | 第3列 | S.D. dependent var | 应变量的标准差 | \(S_{Y_i}=\sqrt{\frac{\sum{(Y_i-\bar{Y})^2}}{(n-1)}}\) |
| 第3行 | 第3列 | Akaike info criterion | AIC指数 | |
| 第4行 | 第3列 | Schwarz criterion | SC指数 | |
| 第5行 | 第3列 | Hannan-Quinn criter. | HQ指数 | |
| 第6行 | 第3列 | Durbin-Watson stat | DW统计量 | 德宾沃森统计量 |
实验准备
实验软件
- EViews ≥ 9.0(推荐 10)
- Mathtype ≥ 6.0
- Office Word/Excel ≥ 2010
- 浏览器:Chrome ≥ 66 或 360 极速 ≥ 9.5
实验数据
蒙特卡洛模拟数据:下面给出了10个家庭在spends家庭收入,income家庭支出等方面的数据。
| obs | spends | income |
|---|---|---|
| 1 | 70 | 80 |
| 2 | 65 | 100 |
| 3 | 90 | 120 |
| 4 | 95 | 140 |
| 5 | 110 | 160 |
| 6 | 115 | 180 |
| 7 | 120 | 200 |
| 8 | 140 | 220 |
| 9 | 155 | 240 |
| 10 | 150 | 260 |
| variable | label |
|---|---|
| obs | 样本编号 |
| spends | 家庭收入 |
| income | 家庭支出 |
实验模型
如果消费和收入之间可以构造如下一元线性回归模型:
\[ \begin{aligned} Y_i & =\hat{\beta}_1+\hat{\beta}_2X_i+e_i && \text{(SRM)} \\ \hat{Y}_i & =\hat{\beta}_1+\hat{\beta}_2X_i && \text{(SRF)} \end{aligned} \]
对象命名规则1/2
| remark | mean | word | example |
|---|---|---|---|
| upr | 字母大写 | uper | 样本序列\(Y_i\),可记为y_upr |
| lwr | 字母小写 | lower | 离差序列\(y_i\),可记为y_lwr |
| avr | 均值 | average | 样本均值\(\bar{X}\),可记为x_avr |
| sqr | 平方 | square | 样本序列\(Y^2_i\),可记为y_upr_sqr |
| hat | 估计值 | hat | \(\hat{\beta}_2\)和\(\hat{Y}_i\),可分别记为b2_hat和y_upr_hat |
| str | 星号 | star | 斜率系数的样本t值\(t^{\ast}_{\hat{\beta}_2}\),可记为t_str_b2_hat |
| scl | 标量 | scalar | 样本均值\(\bar{X}\)作为标量,可记为x_avr_scl |
| ser | 序列 | series | 样本均值\(X_i\)可作为有 n个数值的序列,可记为x_avr_ser |
对象命名规则2/2
| remark | mean | word | example |
|---|---|---|---|
| sgm | 方差参数 | sigma | 回归误差方差\(\hat{\sigma}^2\),可记为sgm_hat_sqr |
| b | 回归参数 | beta | 斜率参数\(\beta_2\),可记为b2 |
| mns | 减号 | minus | 样本标准差\(S_{(\hat{Y}_0-Y_0)}\),可记为s_y0h_mns_y0 |
| fst | 预测 | forecast | 均值预测值\(E(Y{\mid}X=X_0)\),可记为fst_exp |
| exp | 期望值 | expect | 均值预测值\(E(Y{\mid}X=X_0)\),可记为fst_ex |
| ind | 个值 | individual | 个值预测值\((Y_0{\mid}X=X_0)_L\),可记为fst_ind |
| lft | 左界 | left | 均值区间预测的左界值\(E(Y{\mid}X=X_0)_L\),可记为y_exp_lft |
| rht | 右界 | right | 均值区间预测的右界值\(E(Y{\mid}X=X_0)_R\),可记为y_exp_rht |
实验操作步骤
主要实验步骤概览
- 1.新建工作文件并导入数据
- 2.进行EViews回归分析
- 3.构建重要变量对象
- 4.计算FF原序列和ff离差序列
- 5.计算回归系数估计值
- 6.计算回归拟合值、残差等
- 7.计算误差方差及标准差
- 8.计算回归系数的样本方差和标准差
- 9.进行平方和分解(ANOVA)
- 10.计算相关系数和判定系数
- 12.回归系数的t检验
- 13.模型整体显著性F检验
- 14.样本外预测(均值预测和个值预测)
步骤1:新建工作文件并导入数据1/3
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
'创建工作文件(工作文件名=mento,子页命名=spend),无结构无日期,样本数为10
wfcreate(wf=mento,page=spend) u 10
'导入外部数据
import d:\github\books\data\lab2-mento-demon.xlsx步骤1:新建工作文件并导入数据2/3
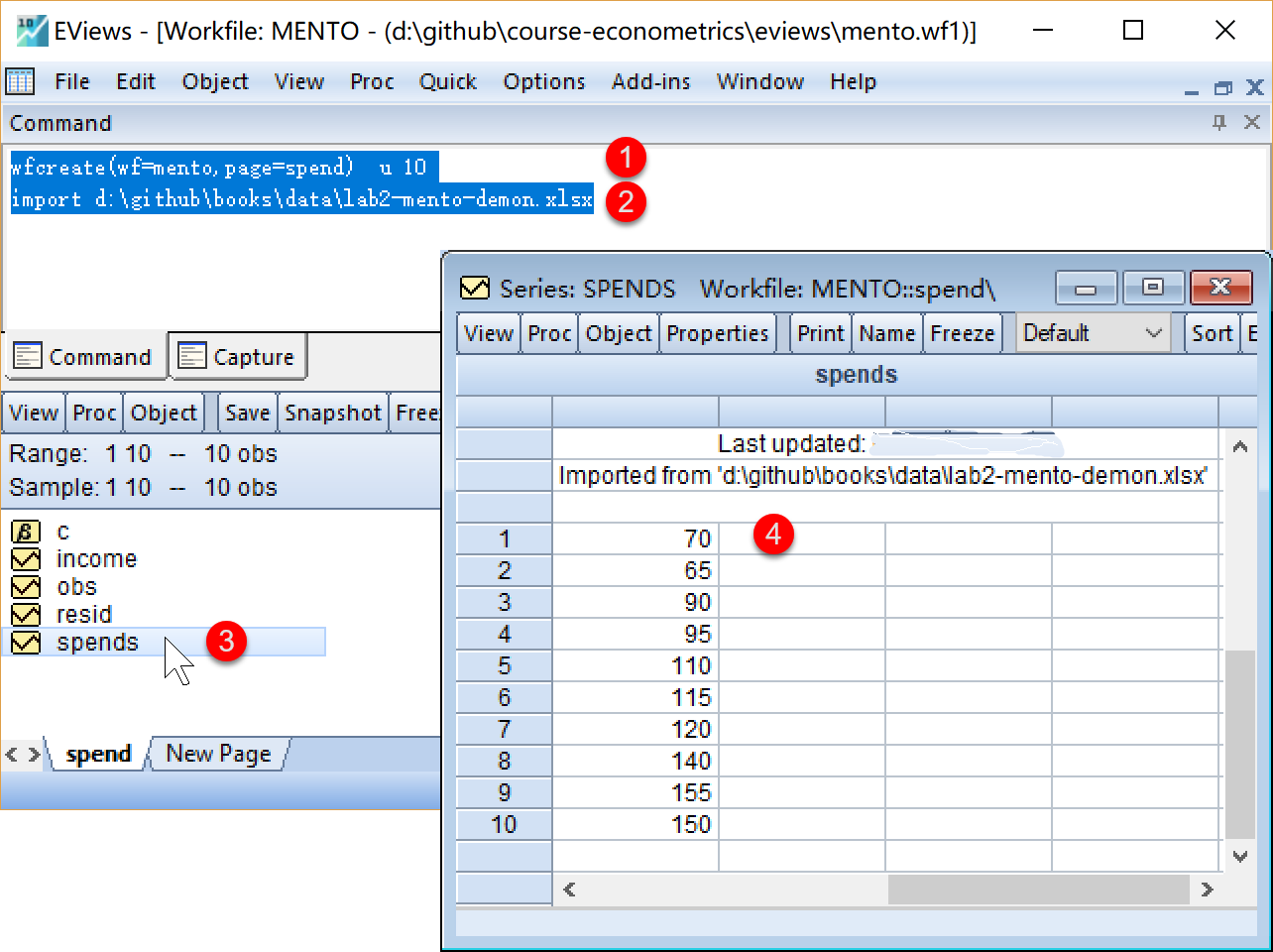
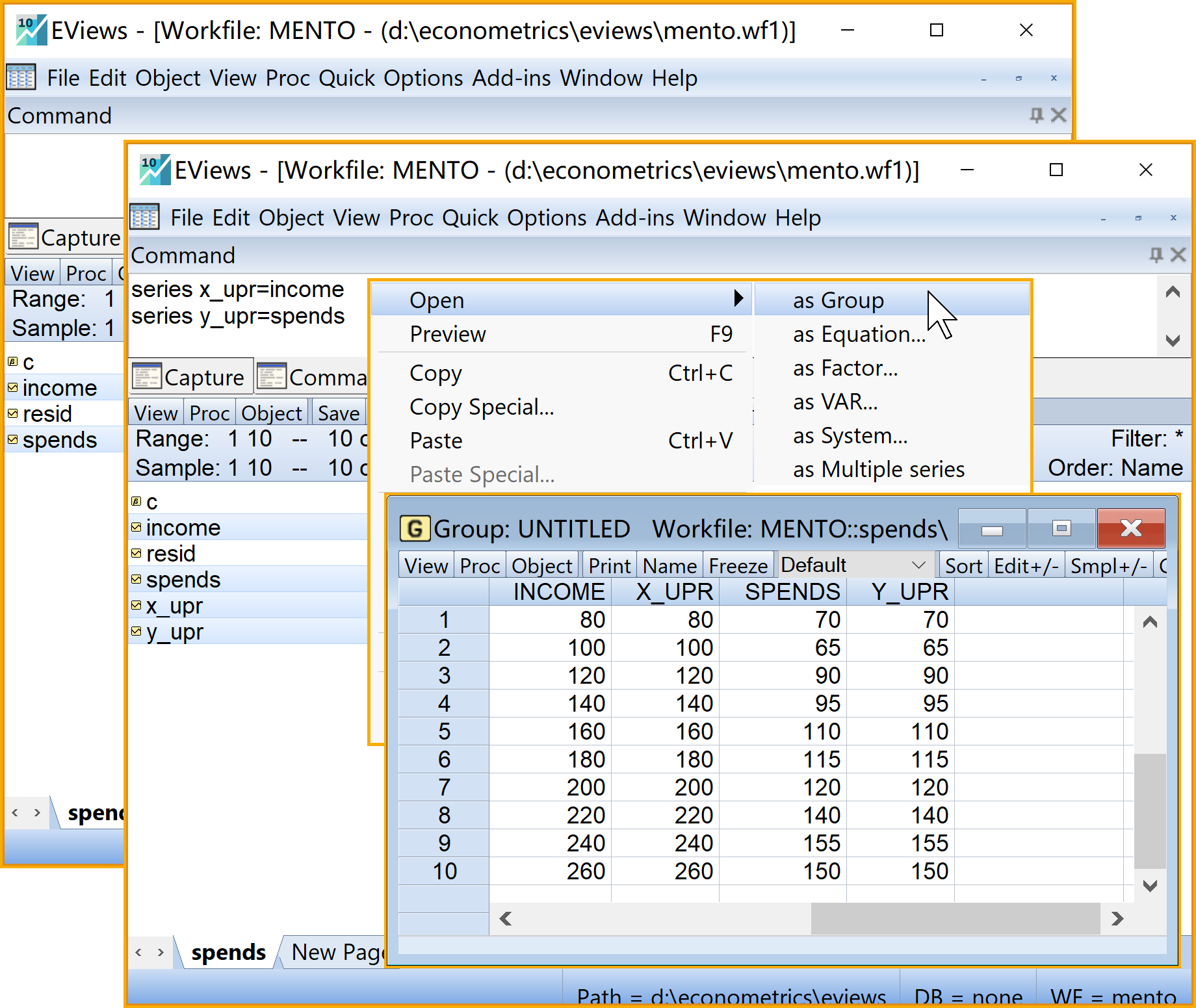
步骤1:新建工作文件并导入数据3/3
步骤2:进行EViews回归分析1/4
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 生成线性回归方程对象eq_m0
equation eq_m0.ls spends c income步骤2:进行EViews回归分析2/4
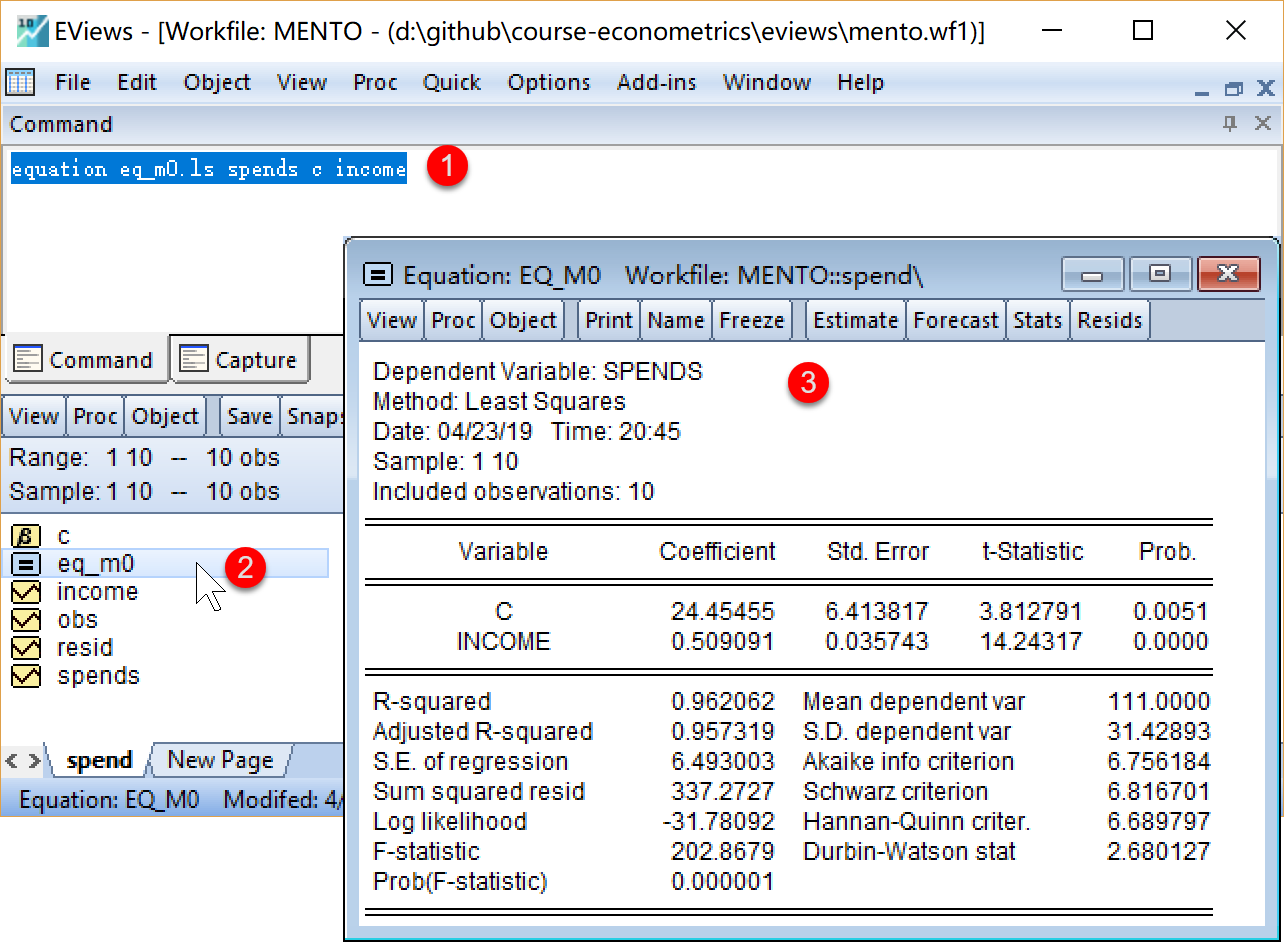
步骤2:进行EViews回归分析3/4
步骤2:进行EViews回归分析4/4
步骤3:构建重要变量对象1/3
EViews命令
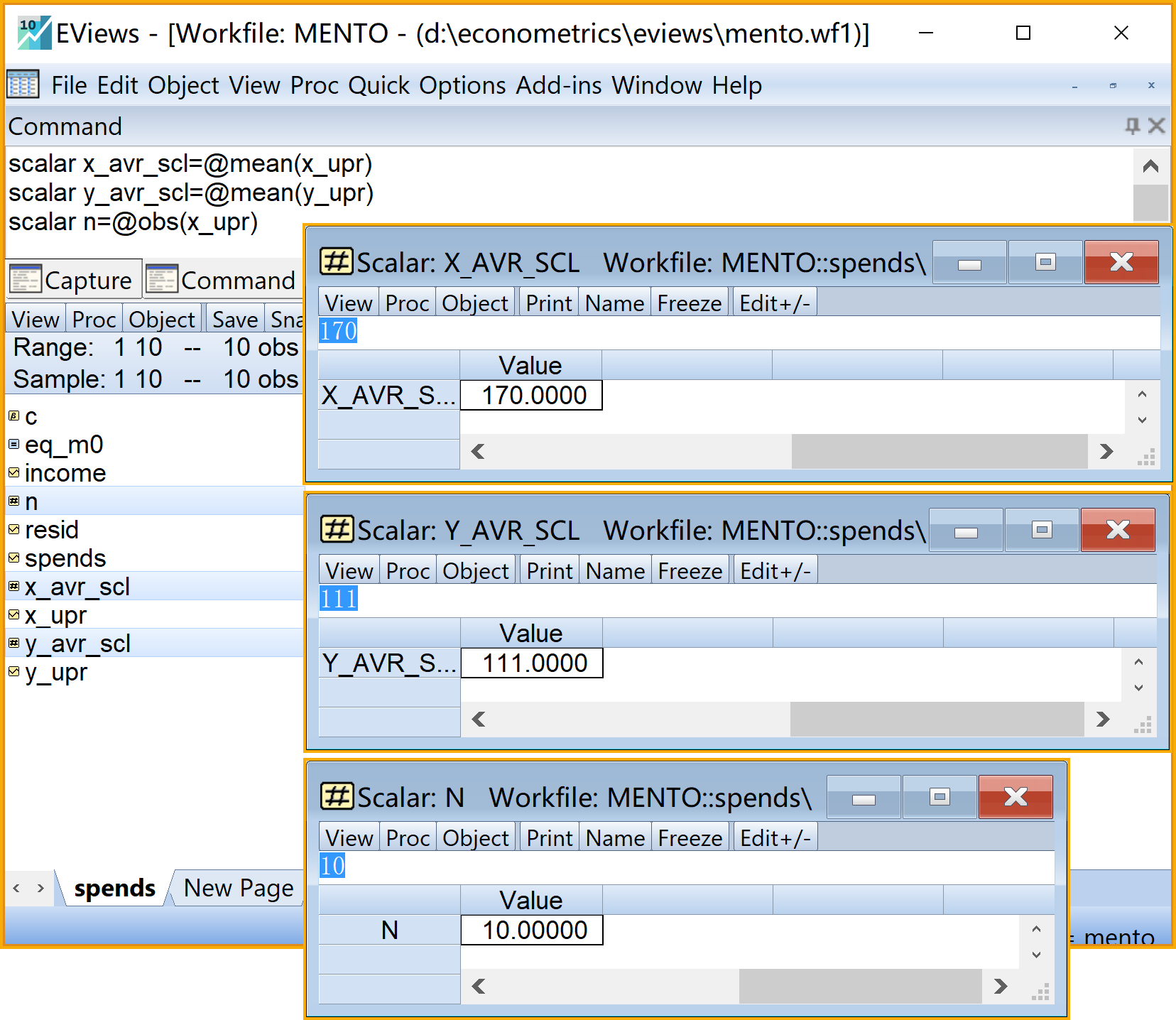
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 转换变量名
series x_upr=x '序列X
series y_upr=y '序列Y
'计算三个重要标量
scalar x_avr_scl=@mean(x_upr) 'X的均值(标量)
scalar y_avr_scl=@mean(y_upr) 'Y的均值(标量)
scalar n=@obs(x_upr) '样本数n(标量)
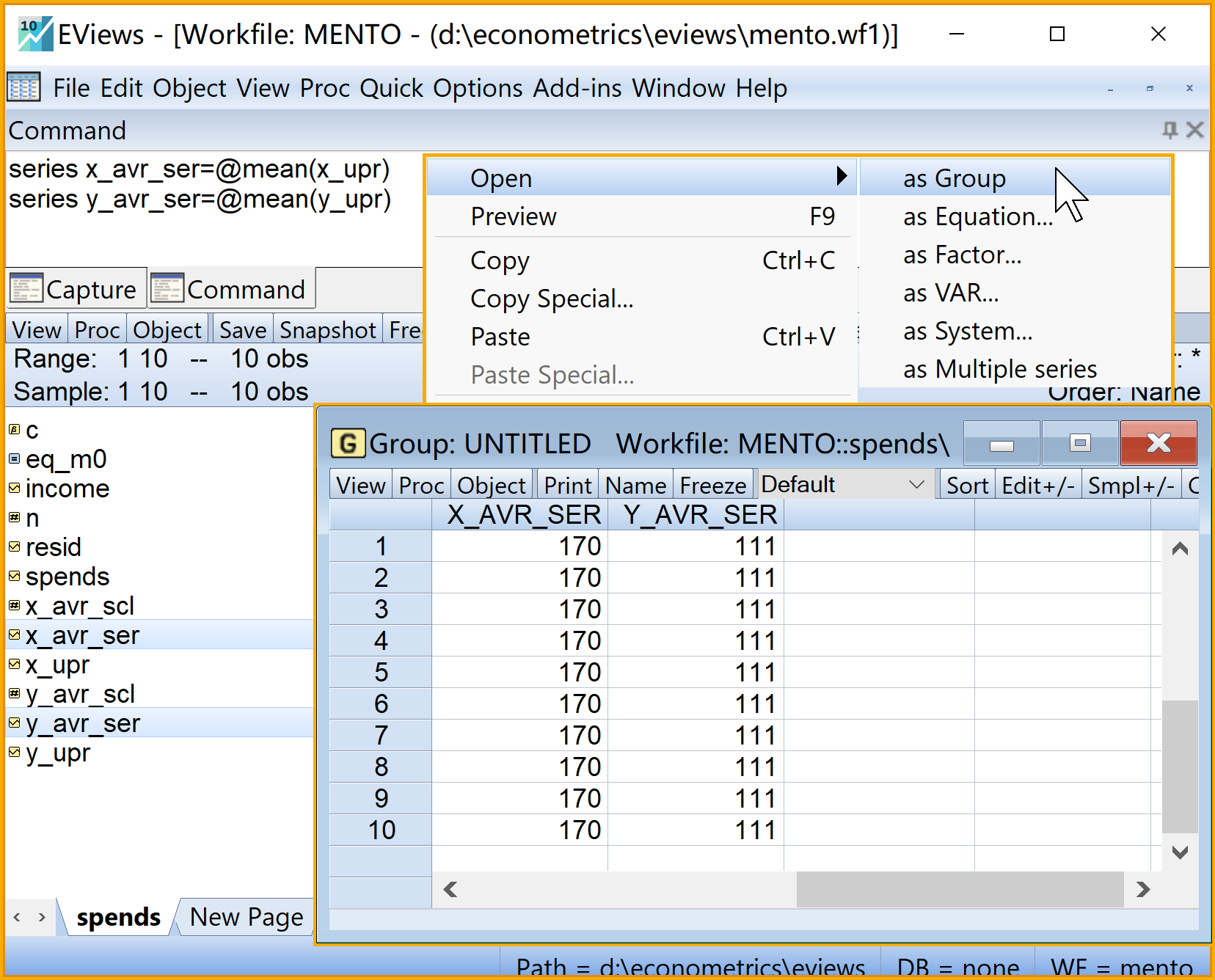
'计算均值序列
series x_avr_ser=@mean(x_upr) 'X的均值(序列)
series y_avr_ser=@mean(y_upr) 'Y的均值(序列)步骤3:构建重要变量对象2/3
步骤3:构建重要变量对象3/3
步骤4:计算FF原序列1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
'计算FF,并以group形式打开
series x_upr_sqr=x_upr^2 '序列X^2
series y_upr_sqr=y_upr^2 '序列Y^2
series xy_upr= x_upr*y_upr '序列XY
group ff_upr x_upr y_upr x_upr_sqr y_upr_sqr xy_upr步骤4:计算FF原序列2/2
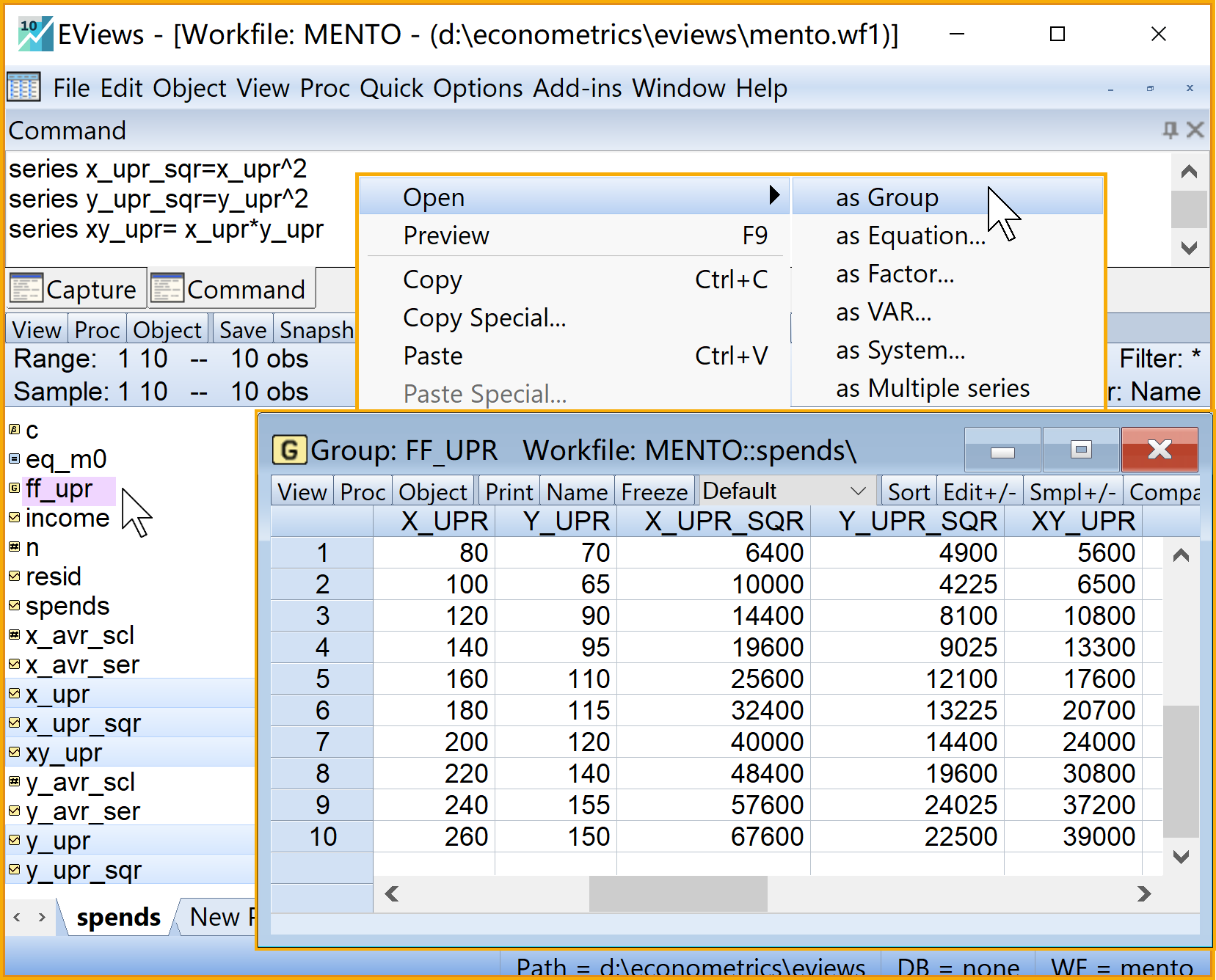
步骤4:计算ff离差序列1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
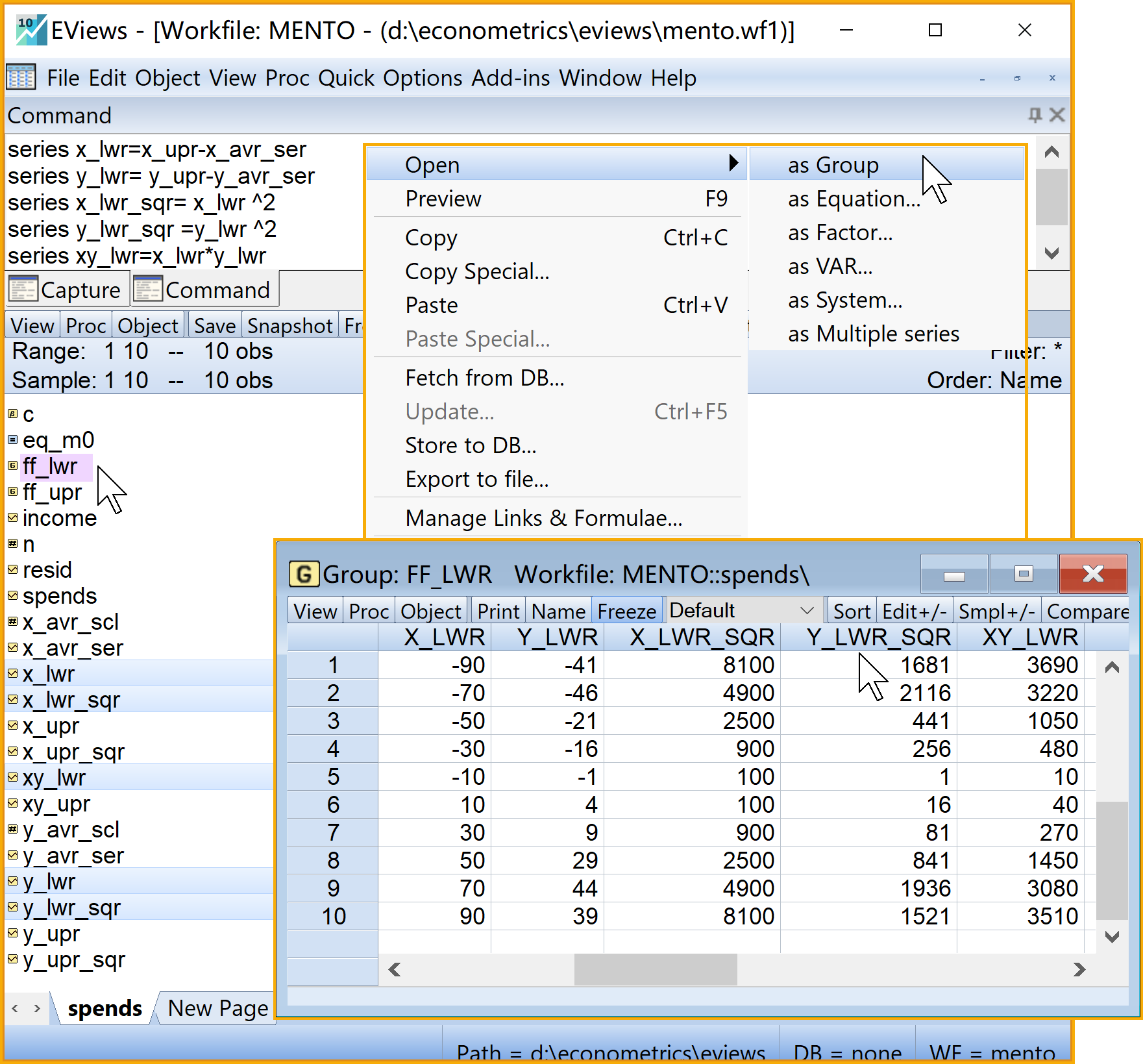
'计算ff离差series,并构建group
series x_lwr=x_upr-x_avr_ser '离差序列x
series y_lwr= y_upr-y_avr_ser '离差序列y
series x_lwr_sqr= x_lwr ^2 '离差序列x^2
series y_lwr_sqr =y_lwr ^2 '离差序列y^2
series xy_lwr=x_lwr*y_lwr '离差序列xy
group ff_lwr x_lwr y_lwr x_lwr_sqr y_lwr_sqr xy_lwr步骤4:计算ff离差序列2/2
步骤5:计算回归系数估计值1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
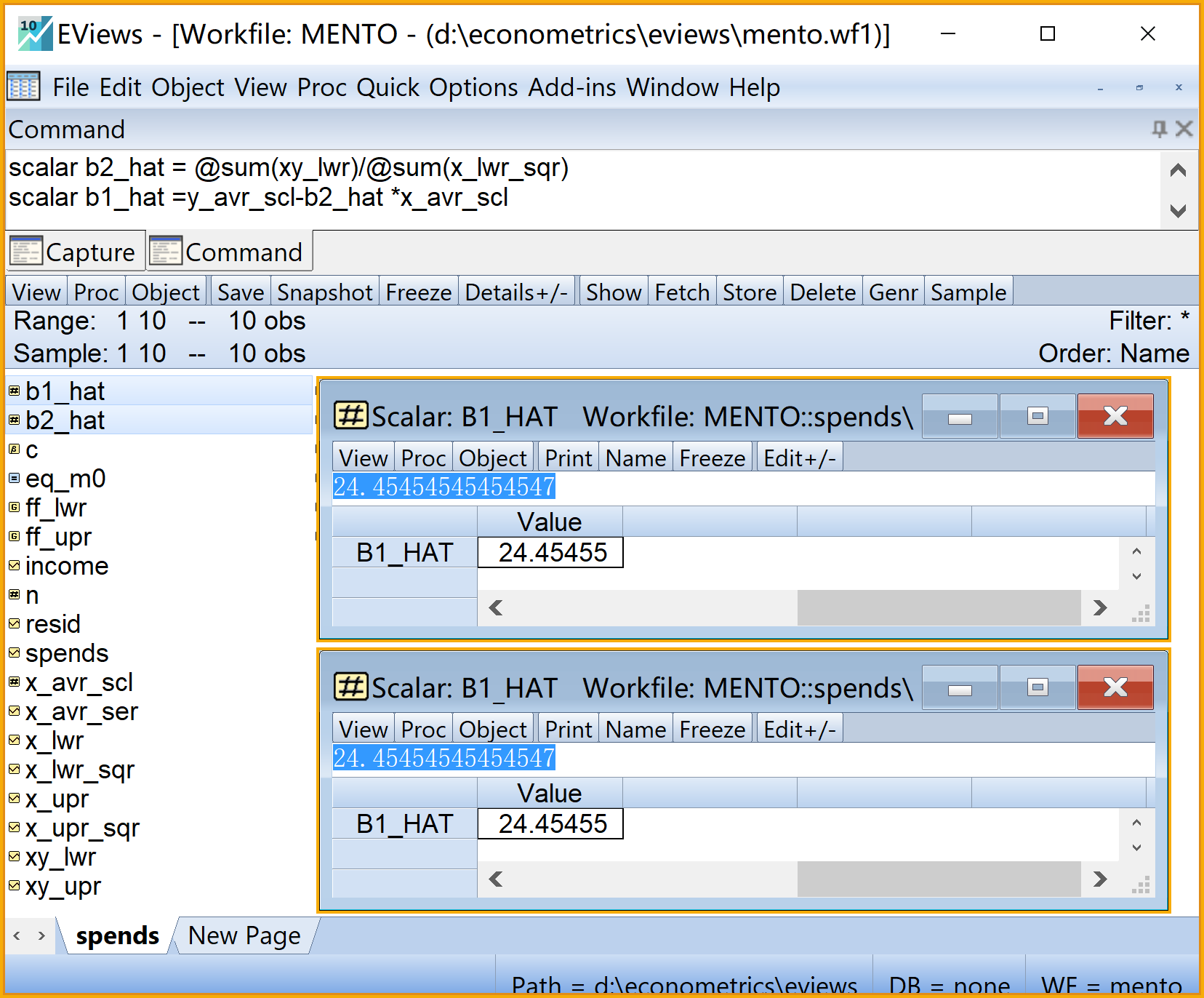
' 计算回归系数scalar:b2和b1
scalar b2_hat = @sum(xy_lwr)/@sum(x_lwr_sqr) '斜率系数
scalar b1_hat =y_avr_scl-b2_hat *x_avr_scl '截距系数步骤5:计算回归系数估计值2/2
步骤6:计算回归拟合值和残差1/3
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 计算回归预测值及其离差series
series y_upr_hat= b1_hat+ b2_hat*x_upr '回归预测值
series y_lwr_hat= y_upr_hat-y_avr_ser '回归预测的离差值
' 计算残差及残差平方series
series ei=y_upr-y_upr_hat '残差序列
series ei_sqr= ei^2 '残差平方序列步骤6:计算回归拟合值和残差2/3
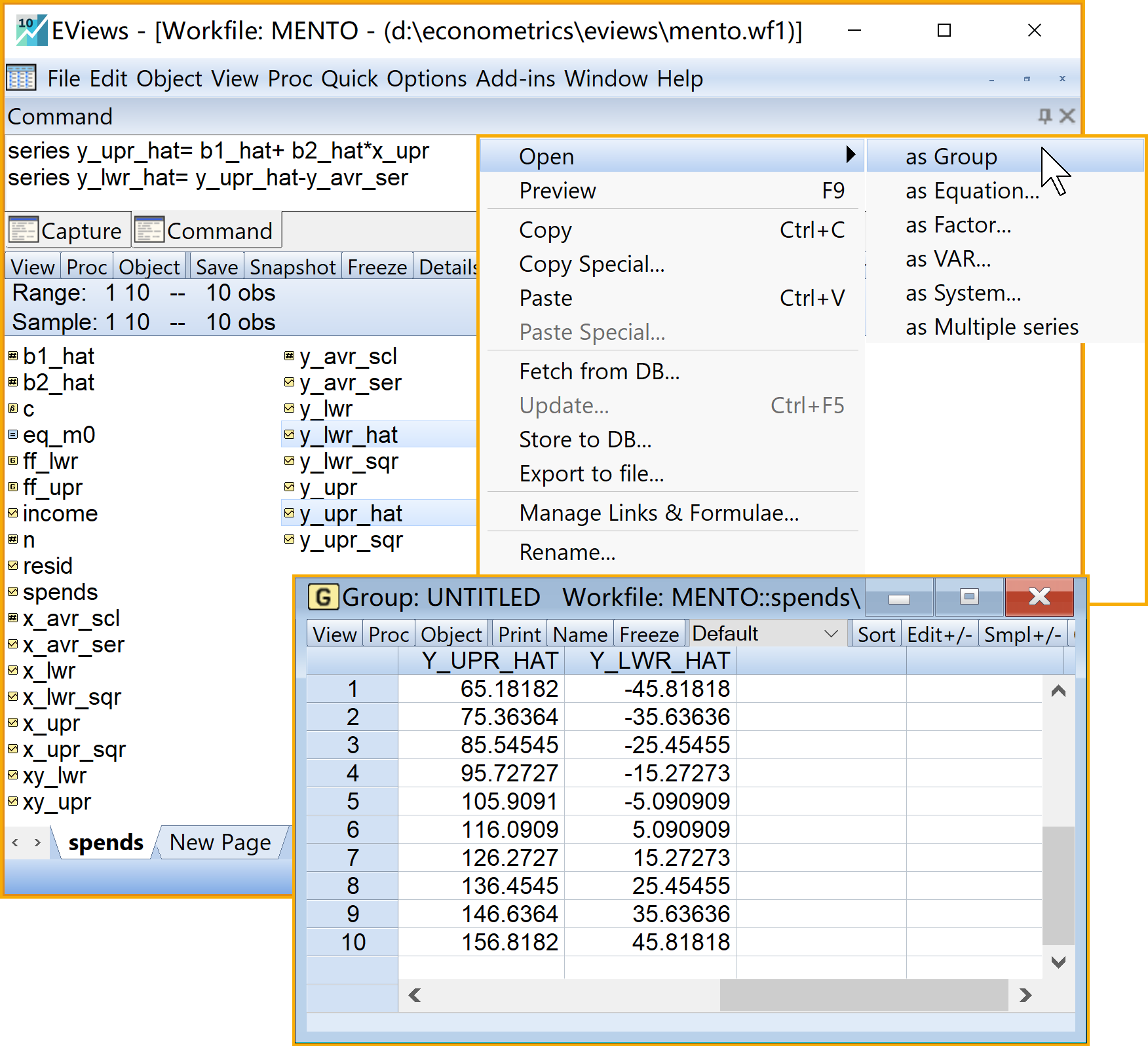
步骤6:计算回归拟合值和残差3/3
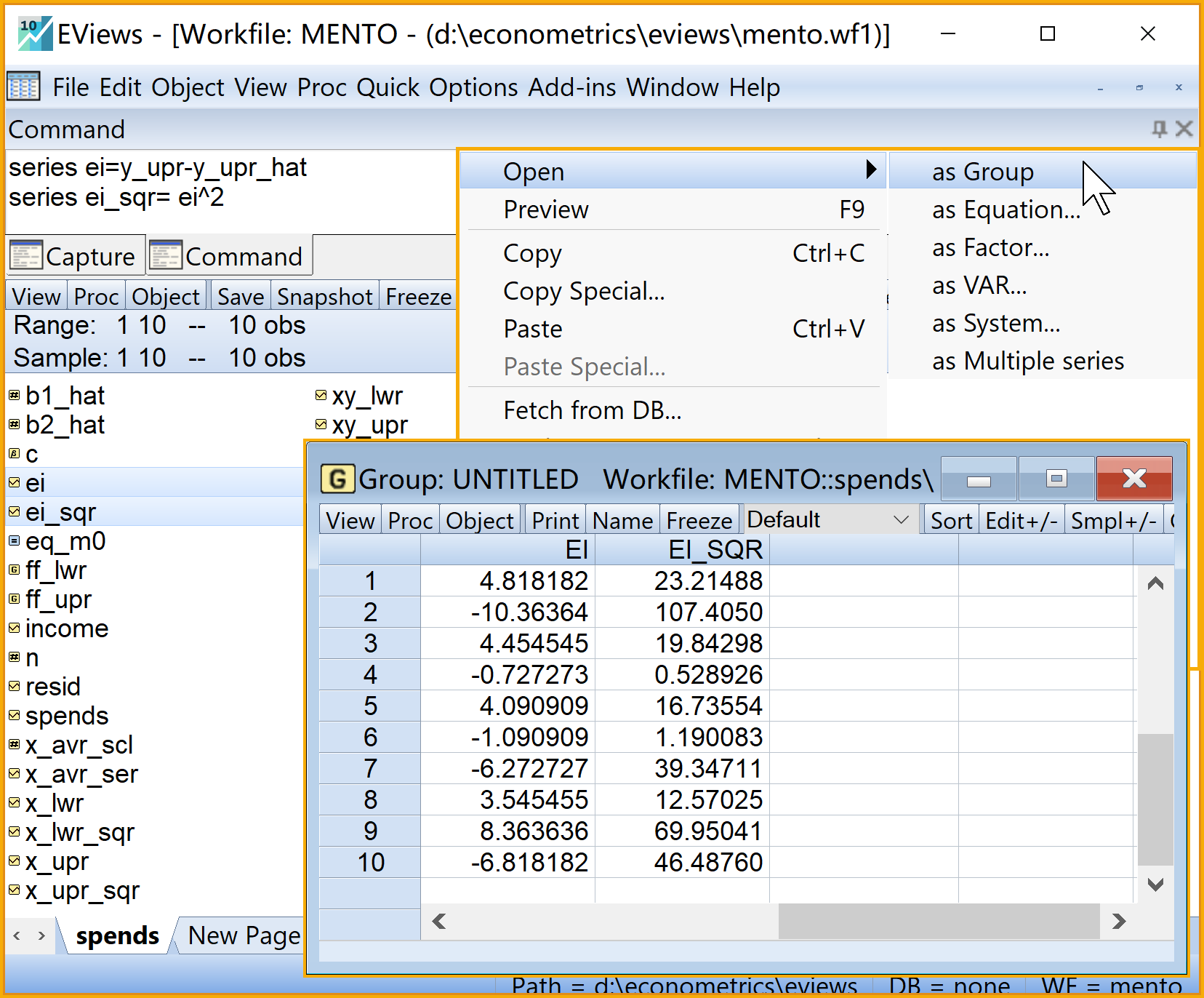
步骤7:计算误差方差及标准差1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 计算回归误差方差及其标准差scalar
scalar sgm_hat_sqr=@sum(ei_sqr)/(n-2) '方程的回归误差方差
scalar sgm_hat= sgm_hat_sqr^0.5 '方程的回归误差标准差步骤7:计算误差方差及标准差2/2
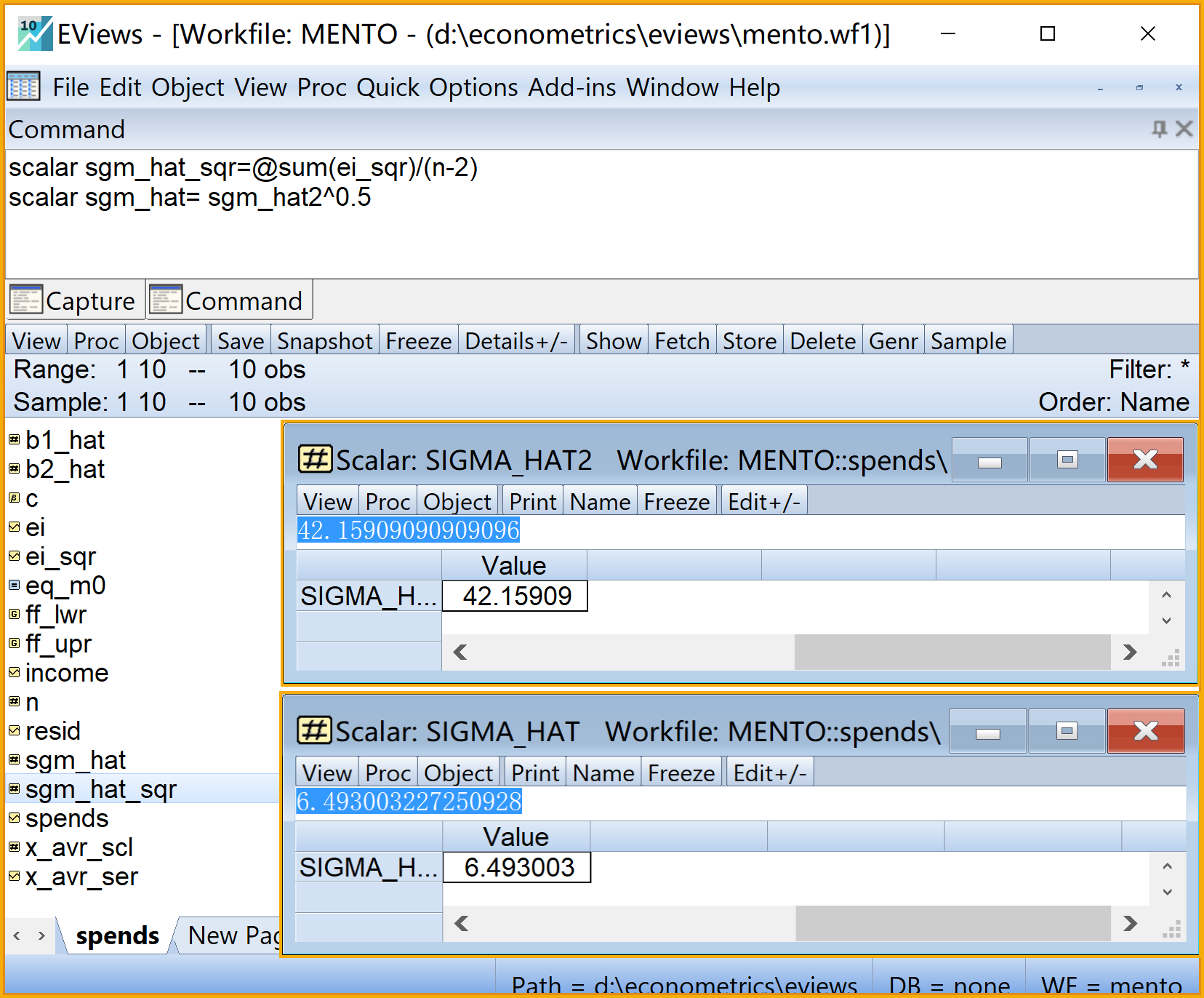
步骤8:计算回归系数的样本方差和标准差1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 计算回归系数的样本方差和标准差scalar
scalar ss_b2_hat=sgm_hat_sqr/@sum(x_lwr_sqr) '斜率系数的样本方差
scalar ss_b1_hat=ss_b2_hat*(@sum(x_upr_sqr)/n) '截距系数的样本方差
scalar s_b2_hat=ss_b2_hat^0.5 '斜率系数的样本标准差
scalar s_b1_hat=ss_b1_hat^0.5 '截距系数的样本标准差步骤8:计算回归系数的样本方差和标准差2/2
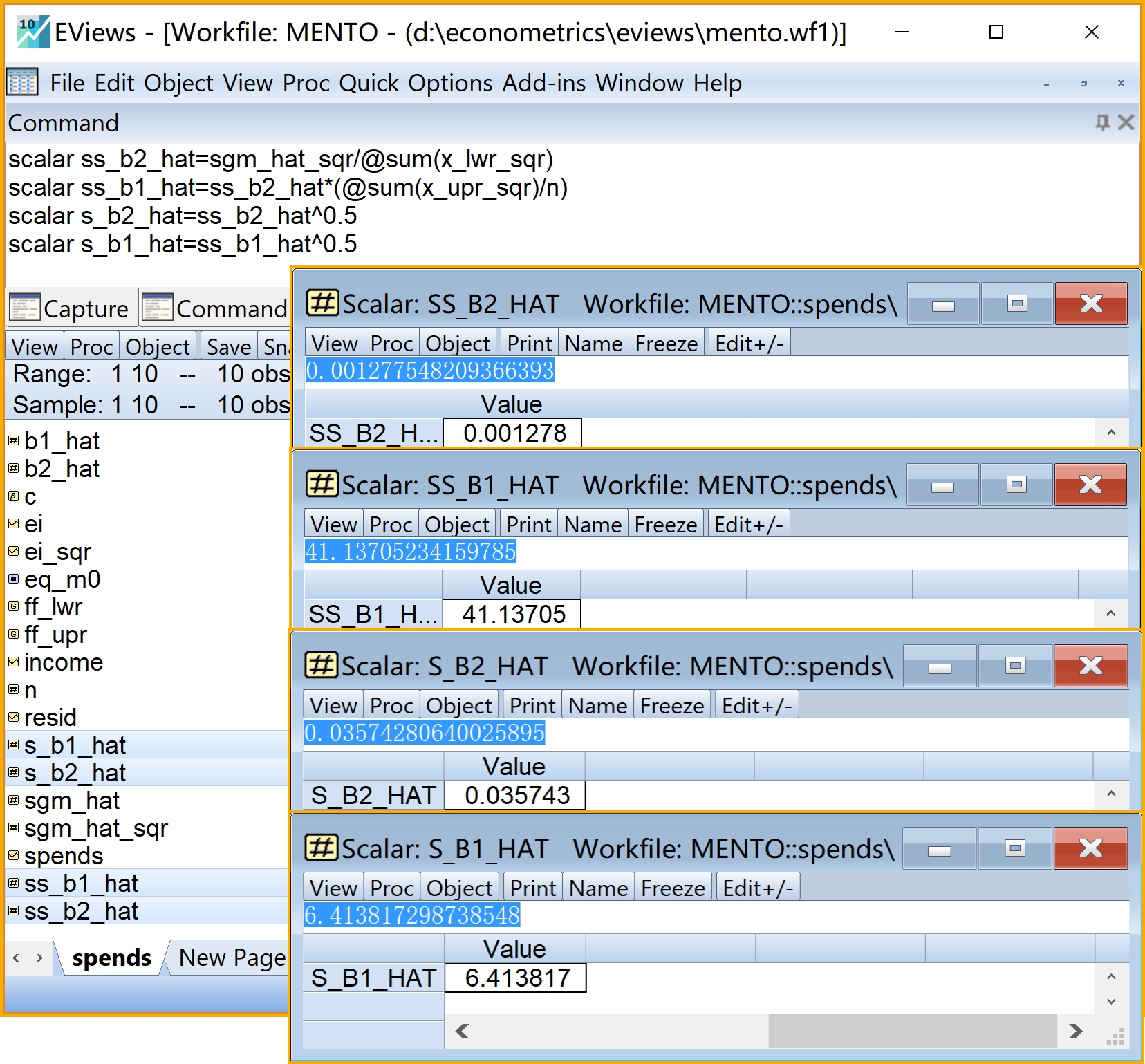
步骤9:平方和分解(ANOVA)1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 进行平方和分解并得到相应自由度(标量scalar)
scalar tss=@sum(y_lwr_sqr) '总平方和TSS
scalar rss=@sum(ei_sqr) '残差平方和RSS
scalar ess=tss-rss '回归平方和ESS
scalar df_tss=n-1 ' TSS的自由度
scalar df_rss=n-2 ' RSS的自由度
scalar df_ess=1 ' ESS的自由度步骤9:平方和分解(ANOVA)2/2
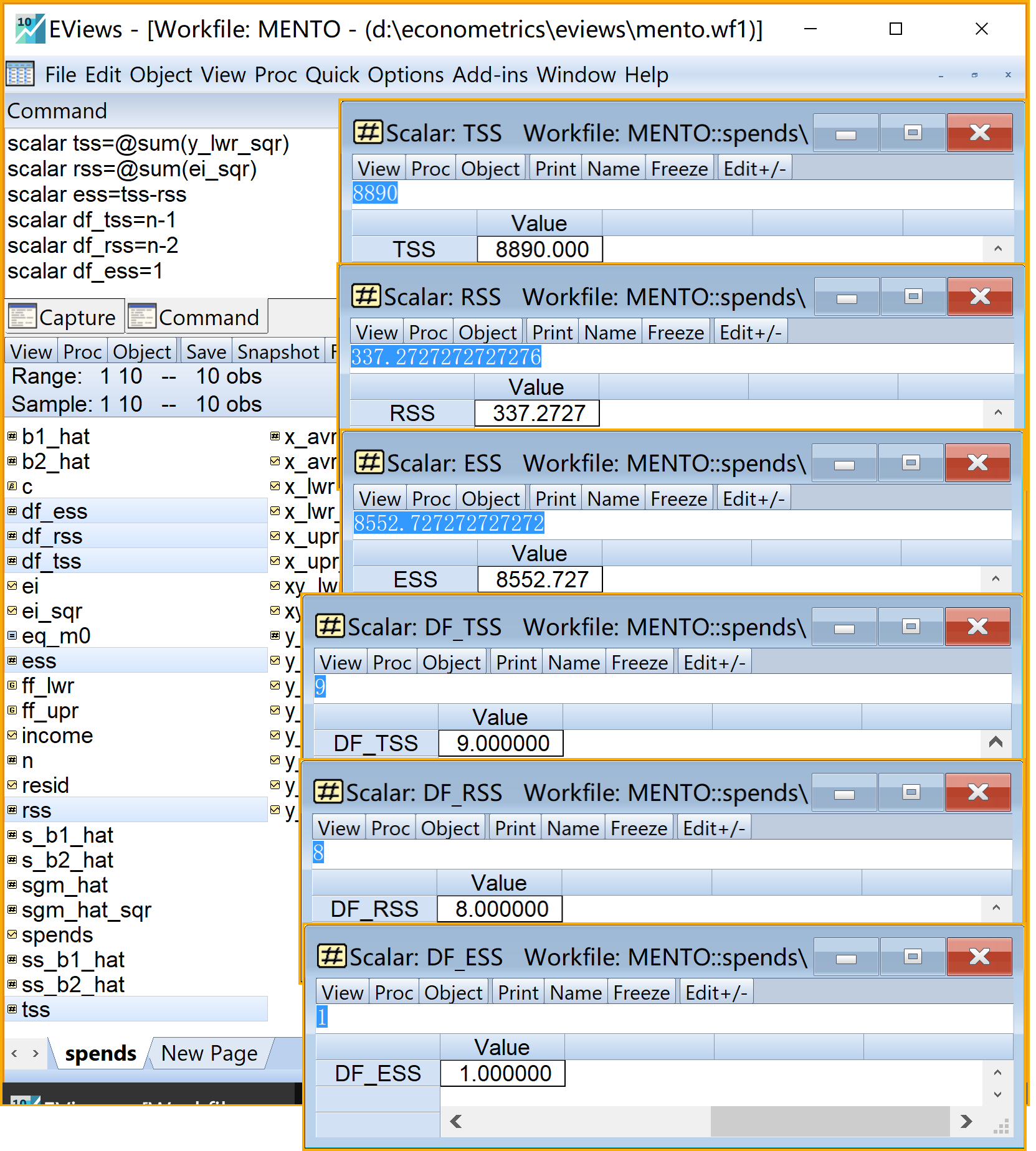
步骤10:计算相关系数和判定系数1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 计算相关系数r和判定系数(标量scalar)
scalar r=@cor(x_upr,y_upr) 'X和Y变量的相关系数
scalar r_sqr=ess/tss '回归方程的判定系数步骤10:计算相关系数和判定系数2/2
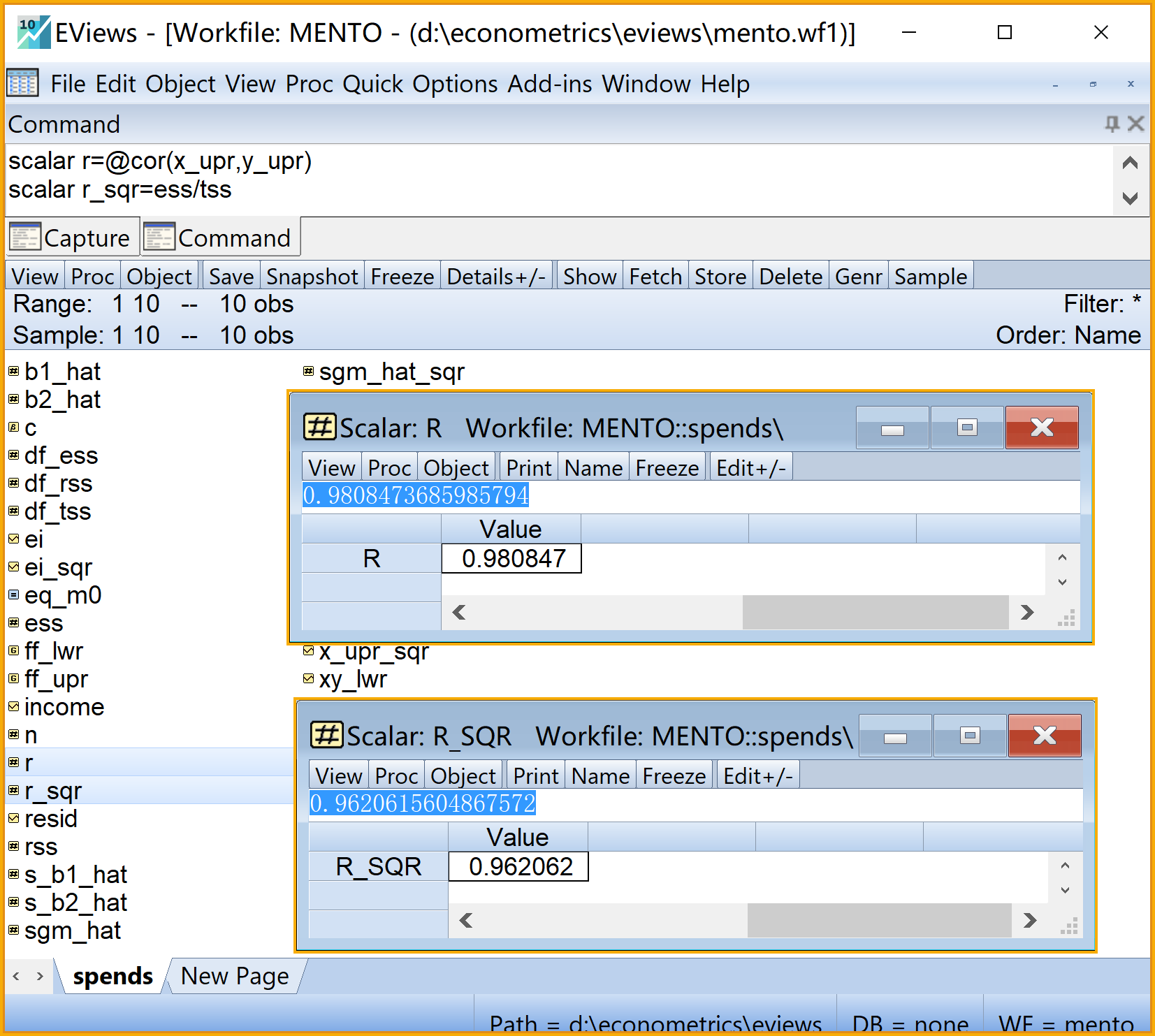
步骤11:回归系数的t检验1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 回归系数的t检验
scalar t_str_b2_hat =b2_hat/s_b2_hat '斜率的t统计量
scalar t_str_b1_hat =b1_hat/s_b1_hat '截距的t统计量
scalar t_value =@qtdist(0.975,8) 'a=0.05下的t查表值(右侧正值)
scalar t_value2 =@qtdist(0.025,8) 'a=0.05下的t查表值(左侧负值)步骤11:回归系数的t检验2/2
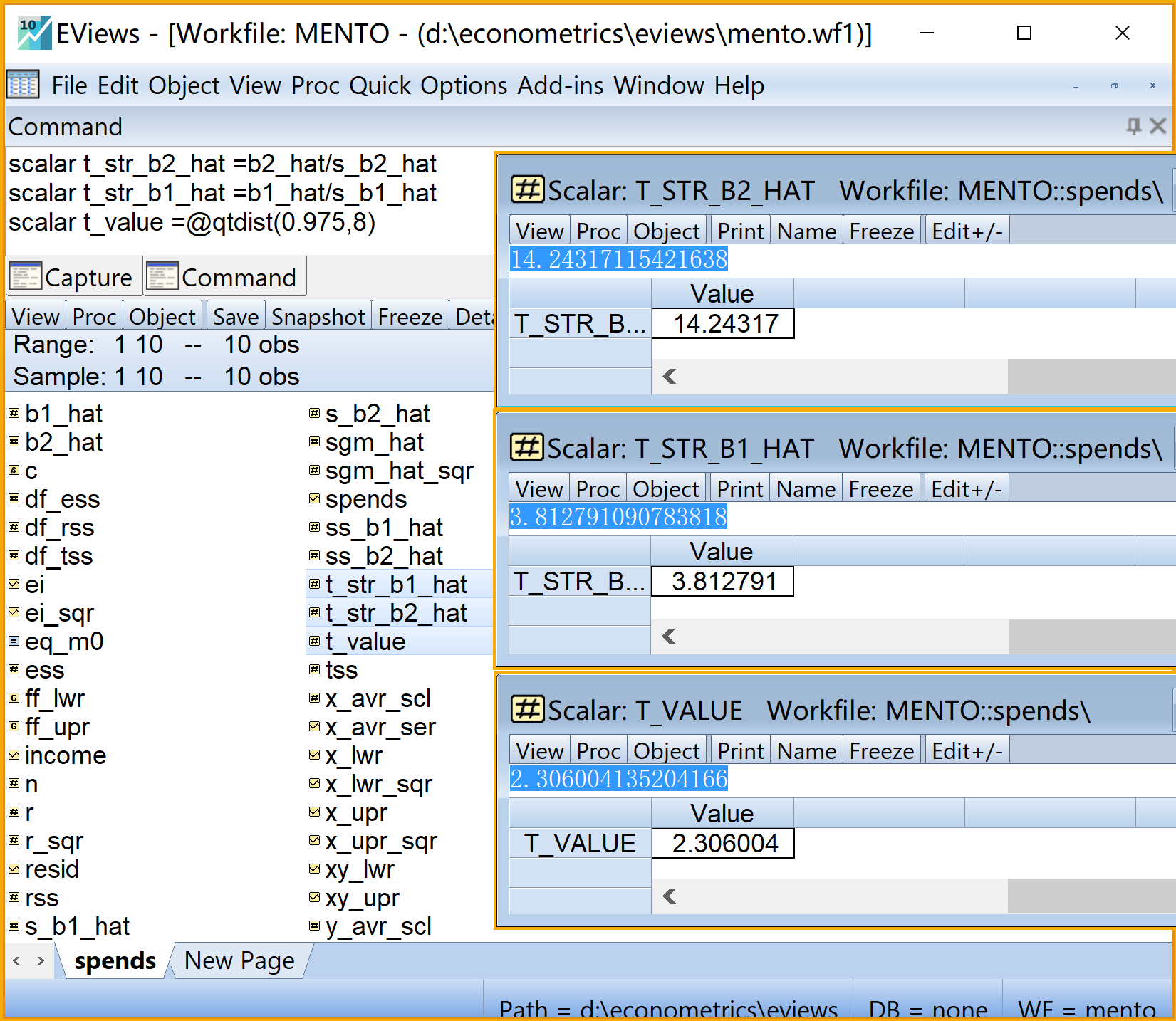
步骤12:模型整体显著性F检验1/2
EViews命令
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 回归方程的F检验
scalar f_str =(ess/df_ess)/(rss/df_rss) '回归方程的F统计量值
scalar f_value=@qfdist(0.95,df_ess,df_rss) 'a=0.05下的F查表值(右侧大值)
scalar f_value2=@qfdist(0.05,df_ess,df_rss) 'a=0.05下的F查表值(左侧小值)步骤12:模型整体显著性F检验2/2
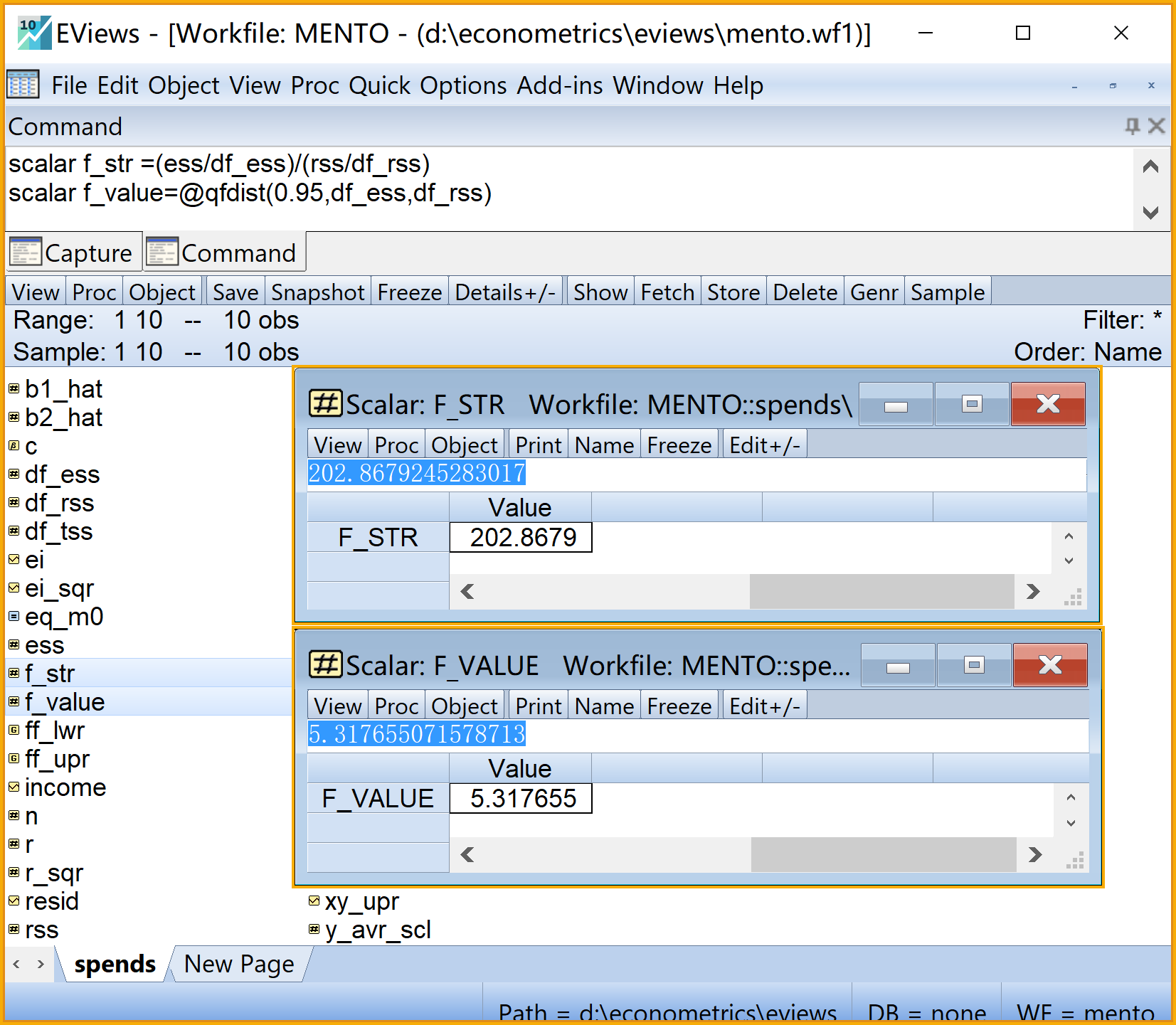
步骤13:样本外预测1/3
EViews命令
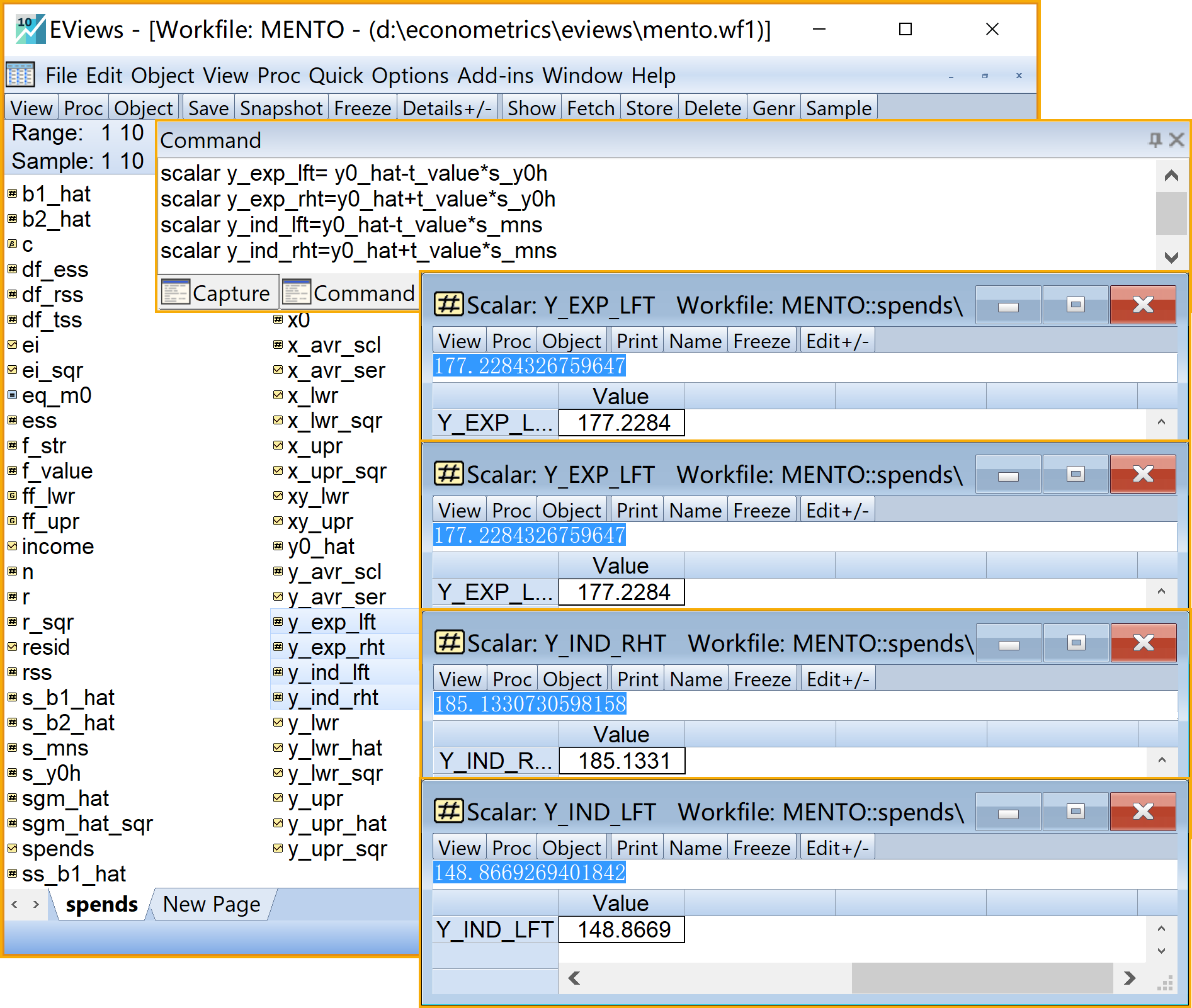
我们可以在命令视窗中依次输入并运行如下EViews命令:
' 计算样本外预测(标量scalar)
scalar x0 =280 '样本外X值
scalar y0_hat =b1_hat+b2_hat*x0 '样本外估计Y值
scalar s_y0h=(sgm_hat_sqr*(1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr)))^0.5 '均值预测的样本标准差
scalar s_mns = (sgm_hat_sqr*(1+1/n+(x0-x_avr_scl)^2/@sum(x_lwr_sqr) ))^0.5 '个值预测的样本标准差
scalar y_exp_lft= y0_hat-t_value*s_y0h '均值预测的置信区间的左界值
scalar y_exp_rht= y0_hat+t_value*s_y0h '均值预测的置信区间的右界值
scalar y_ind_lft= y0_hat-t_value*s_mns '个值预测的置信区间的左界值
scalar y_ind_rht= y0_hat+t_value*s_mns '个值预测的置信区间的右界值步骤13:样本外预测2/3
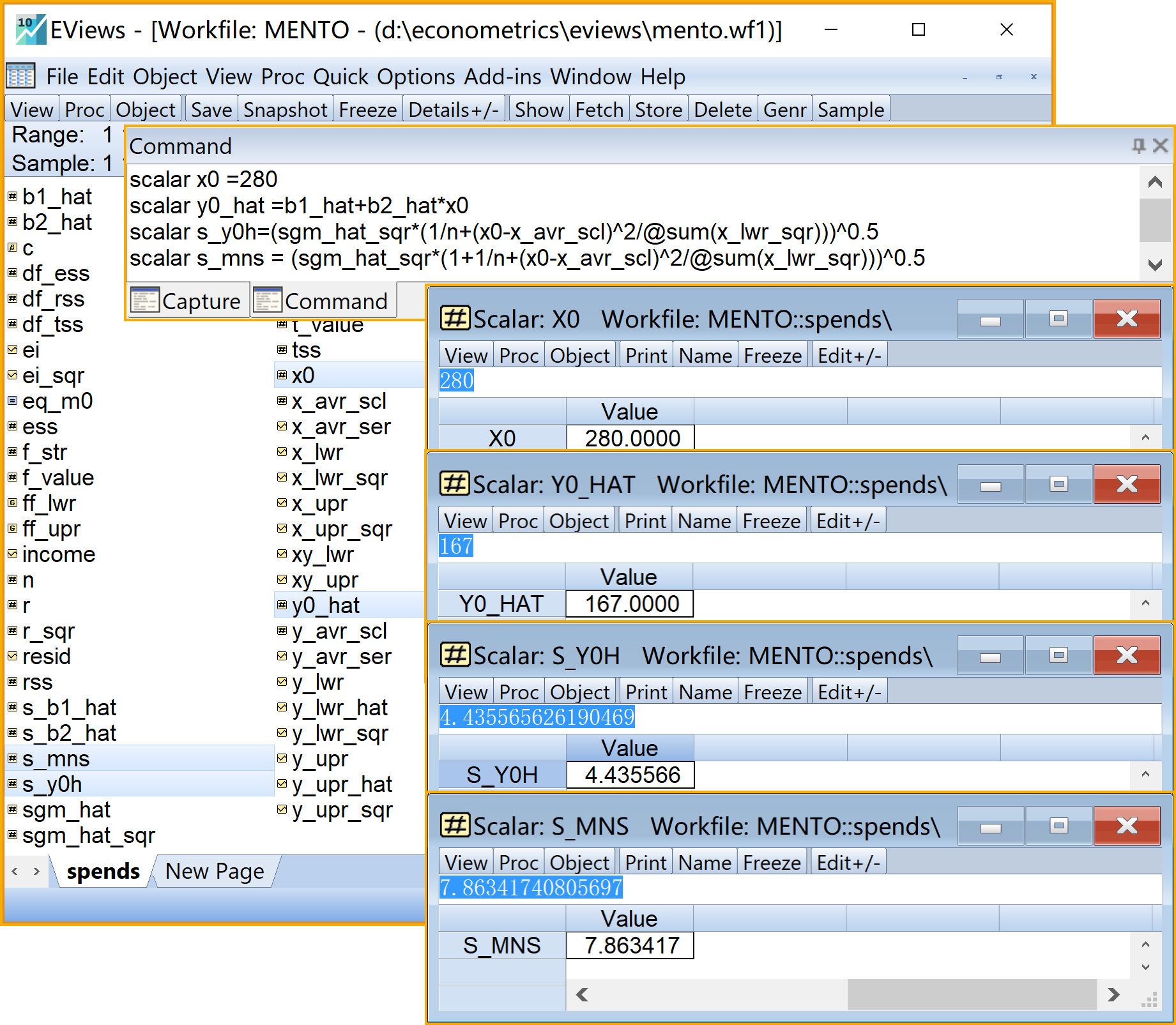
步骤13:样本外预测3/3
本章结束

Lab 02: 简单回归 | Hu Huaping (胡华平)